Recent Progress in Liquid Microlenses and Their Arrays for Adaptive and Applied Optical Systems
Abstract
1. Introduction
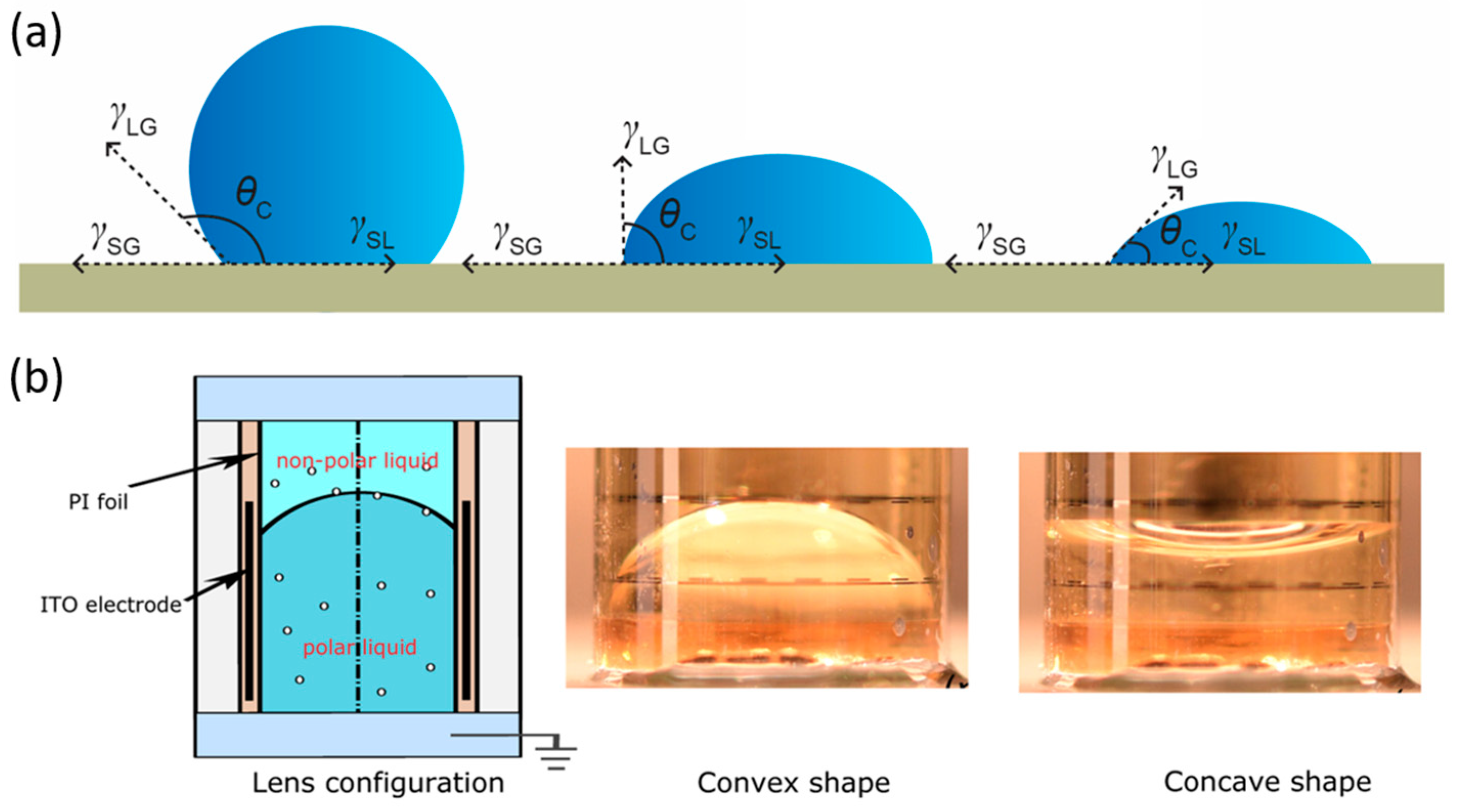
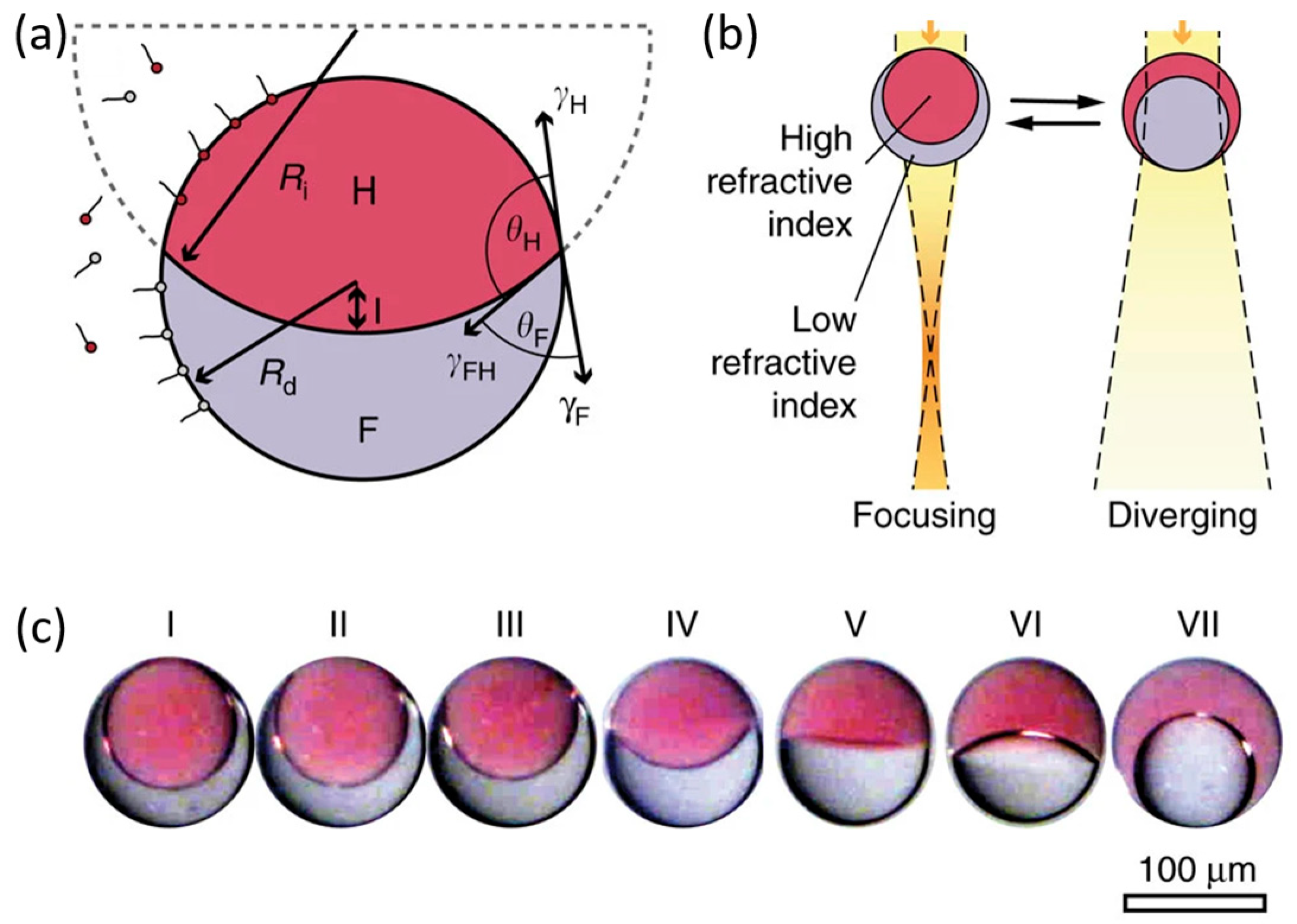
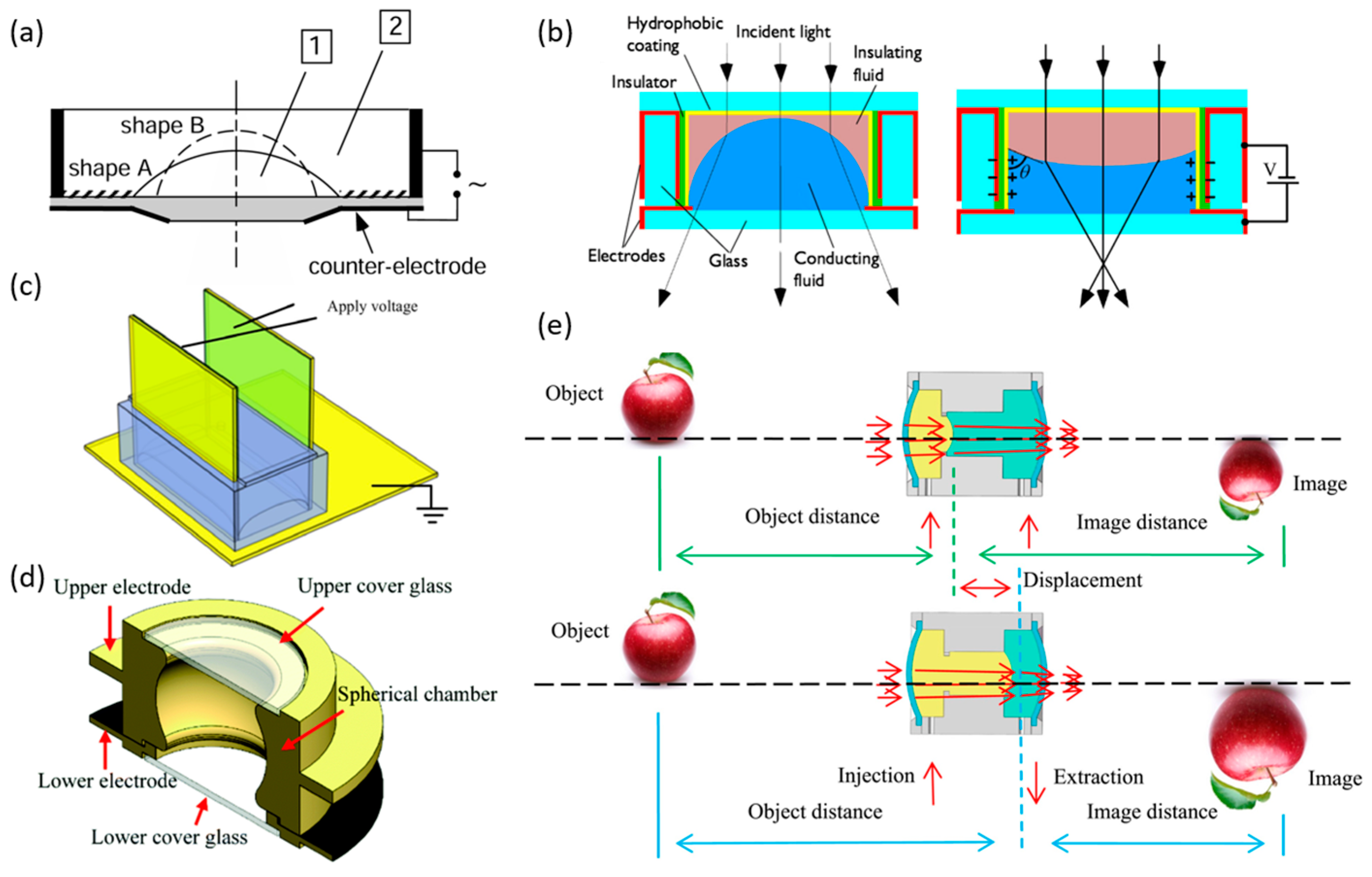
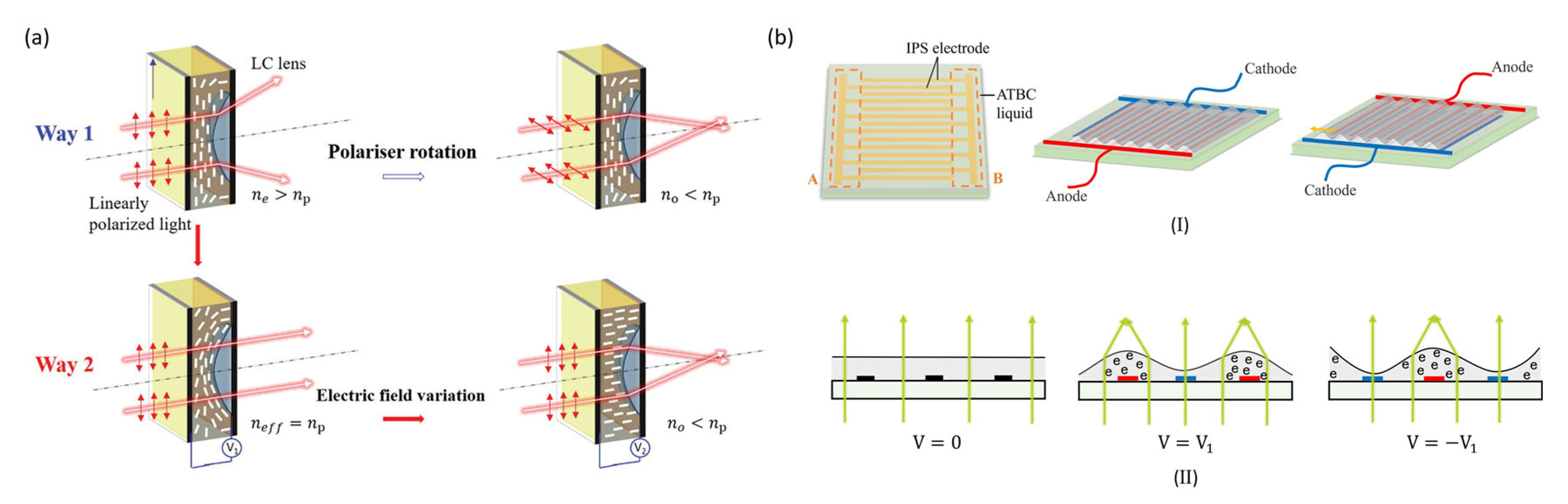
2. Actuation Mechanism
3. Materials and Fabrication Methodologies
3.1. Materials
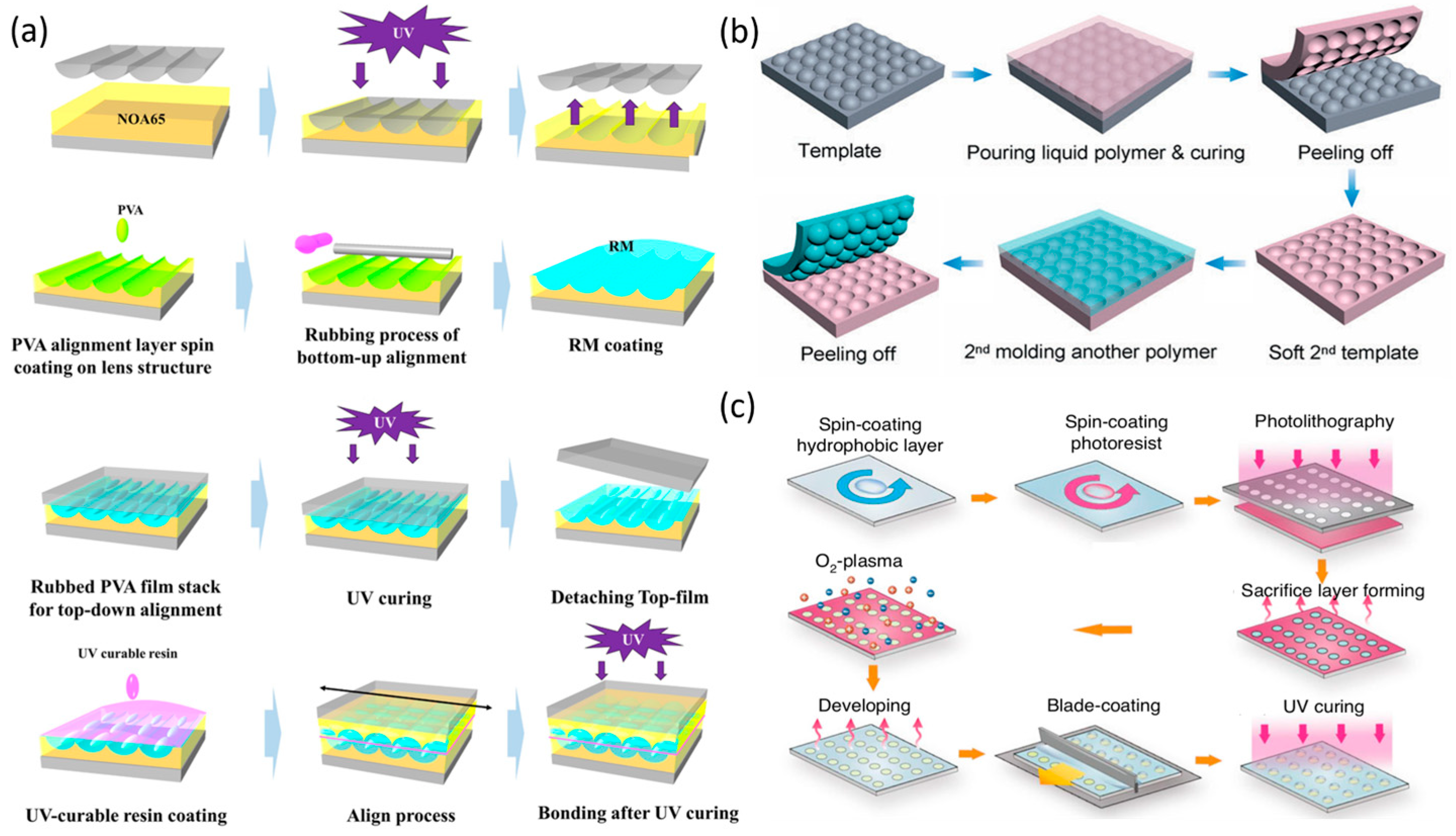
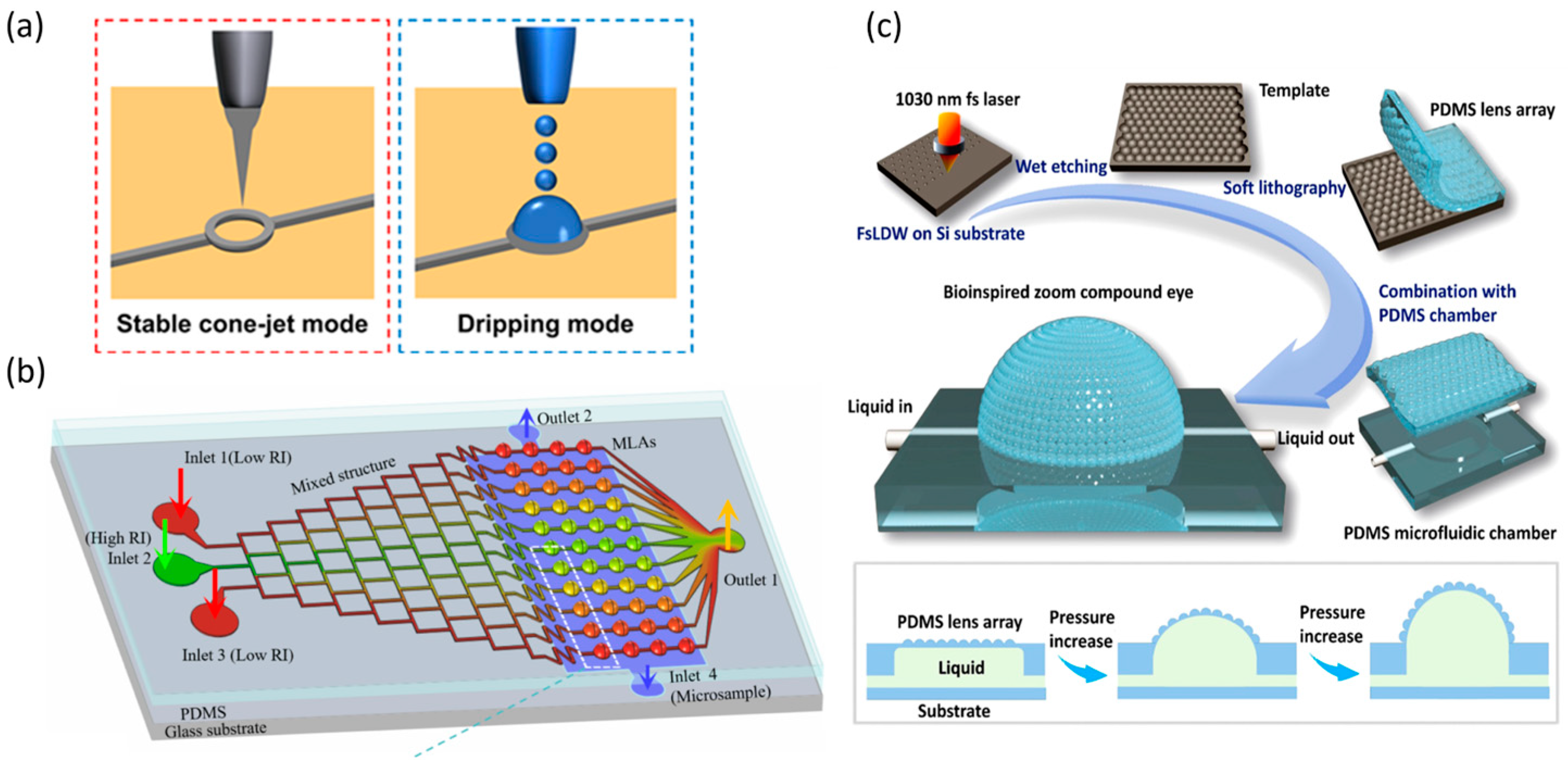
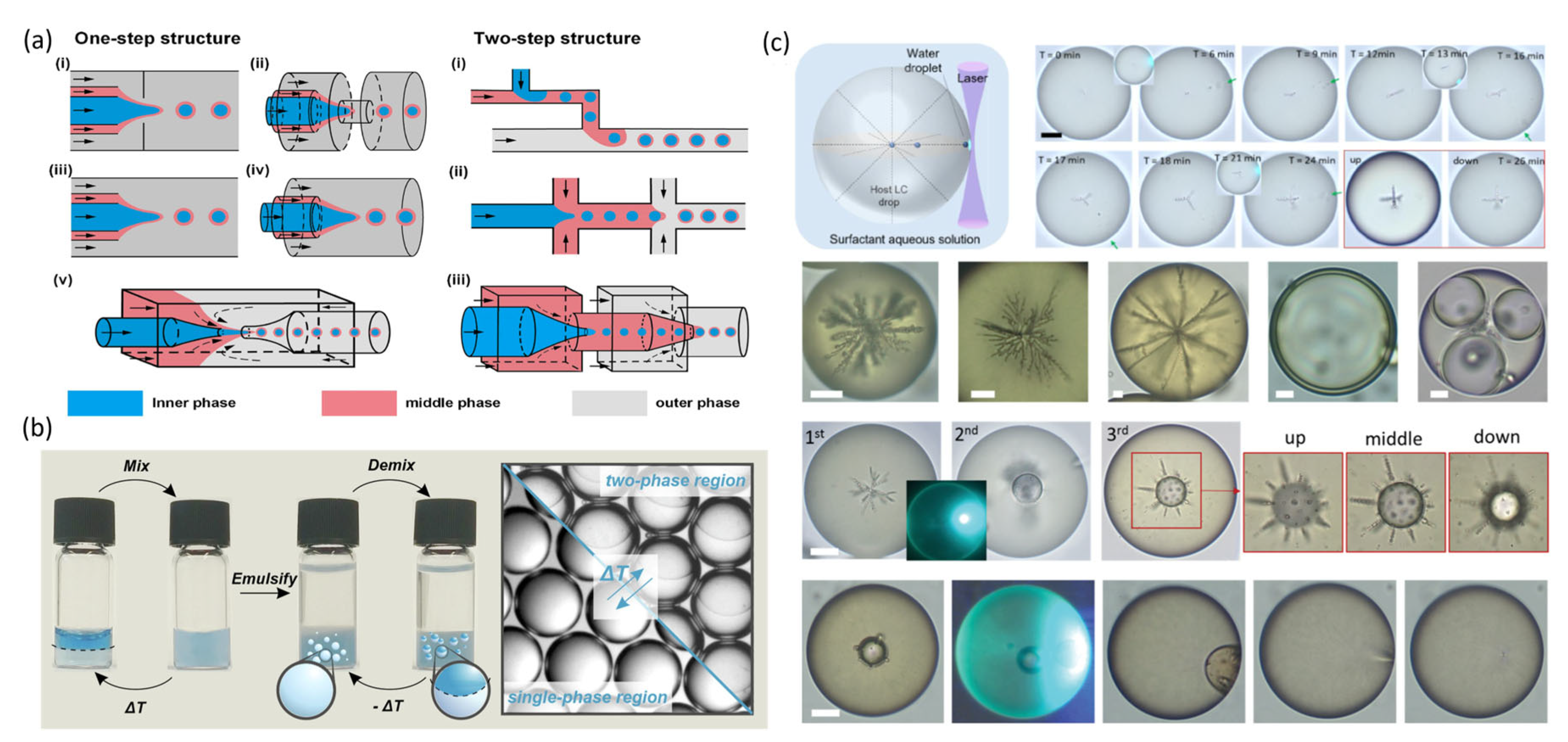
3.2. Fabrication Method
4. Core Functions
4.1. Focal Length Tuning
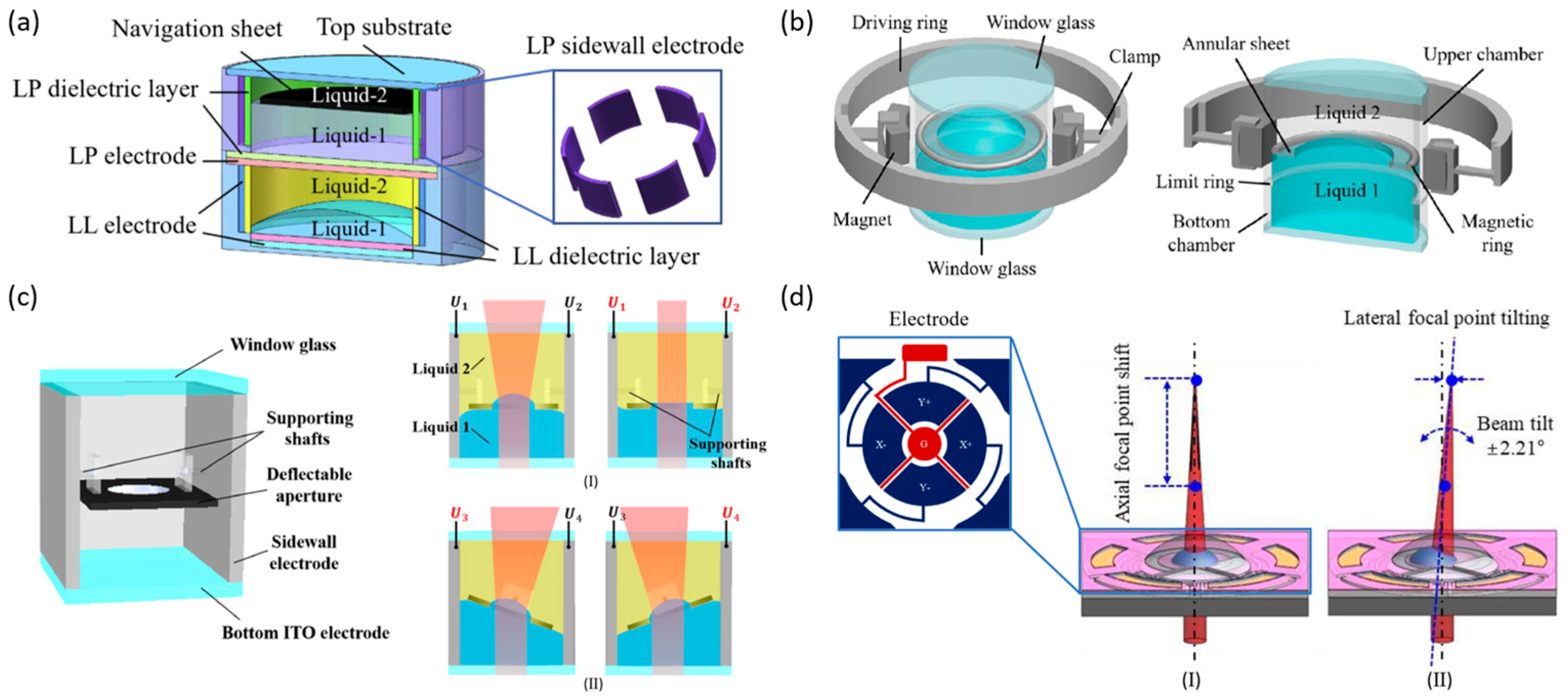
4.2. Field of View Expansion
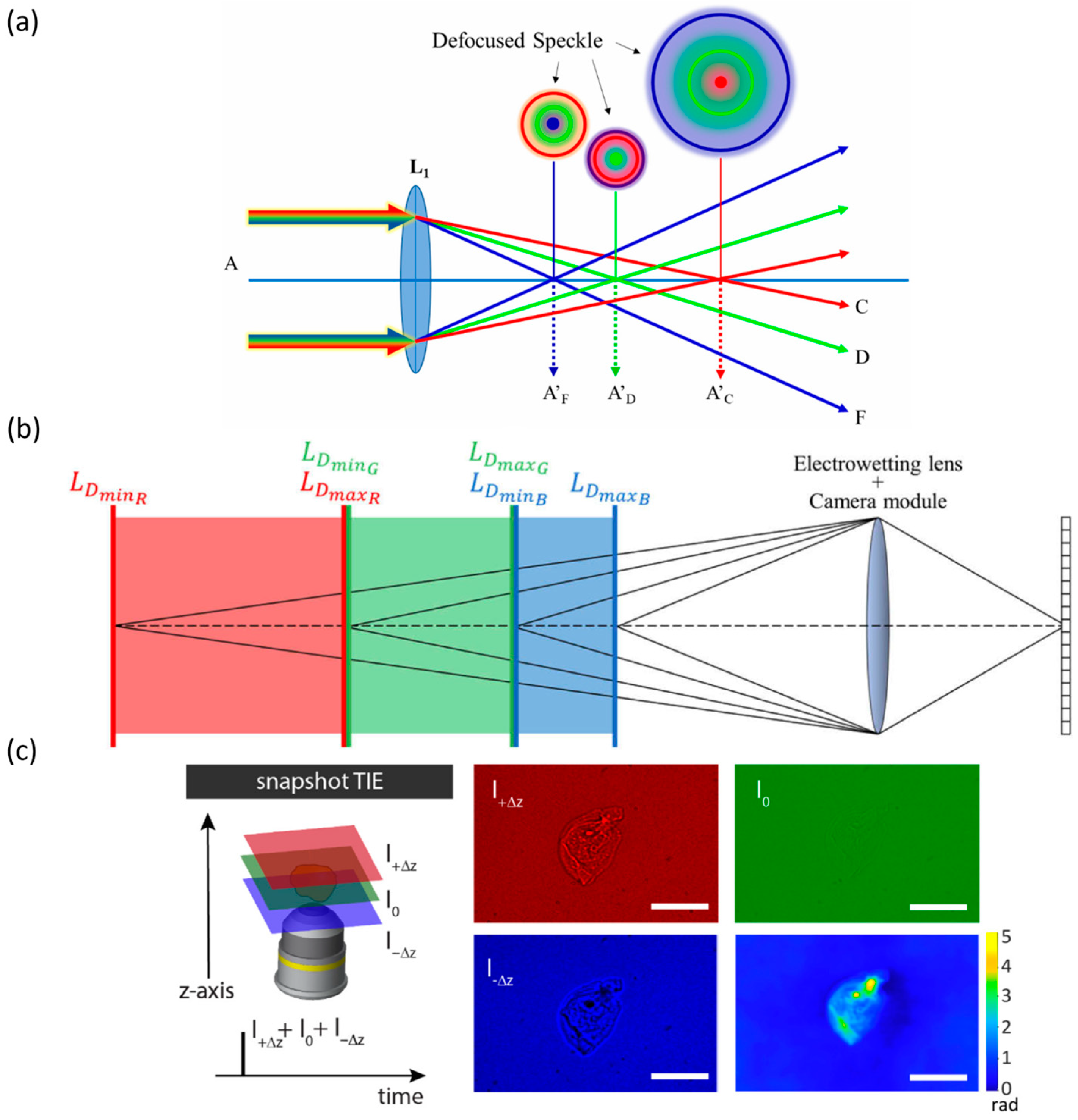
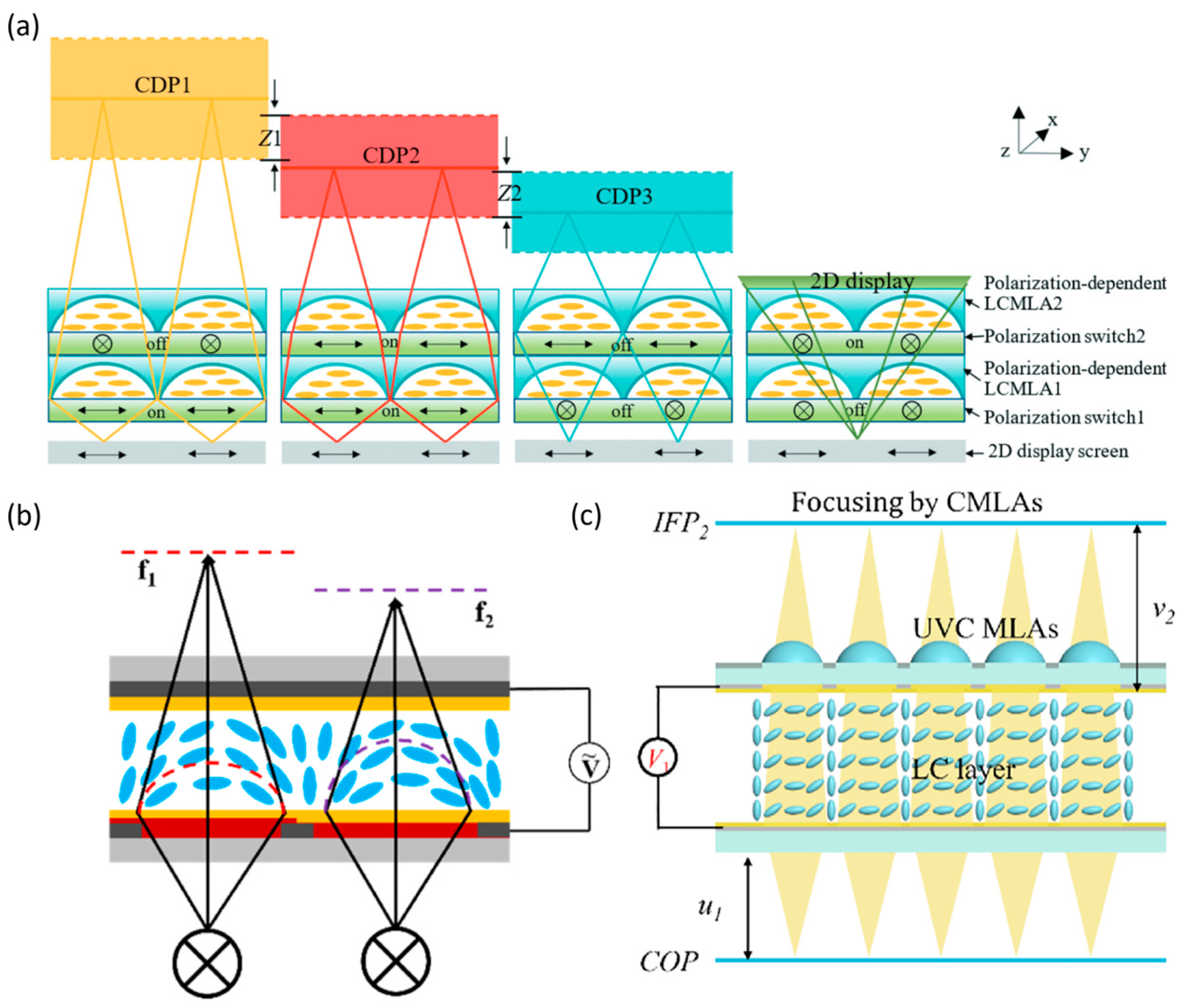
4.3. Depth of Field Extension
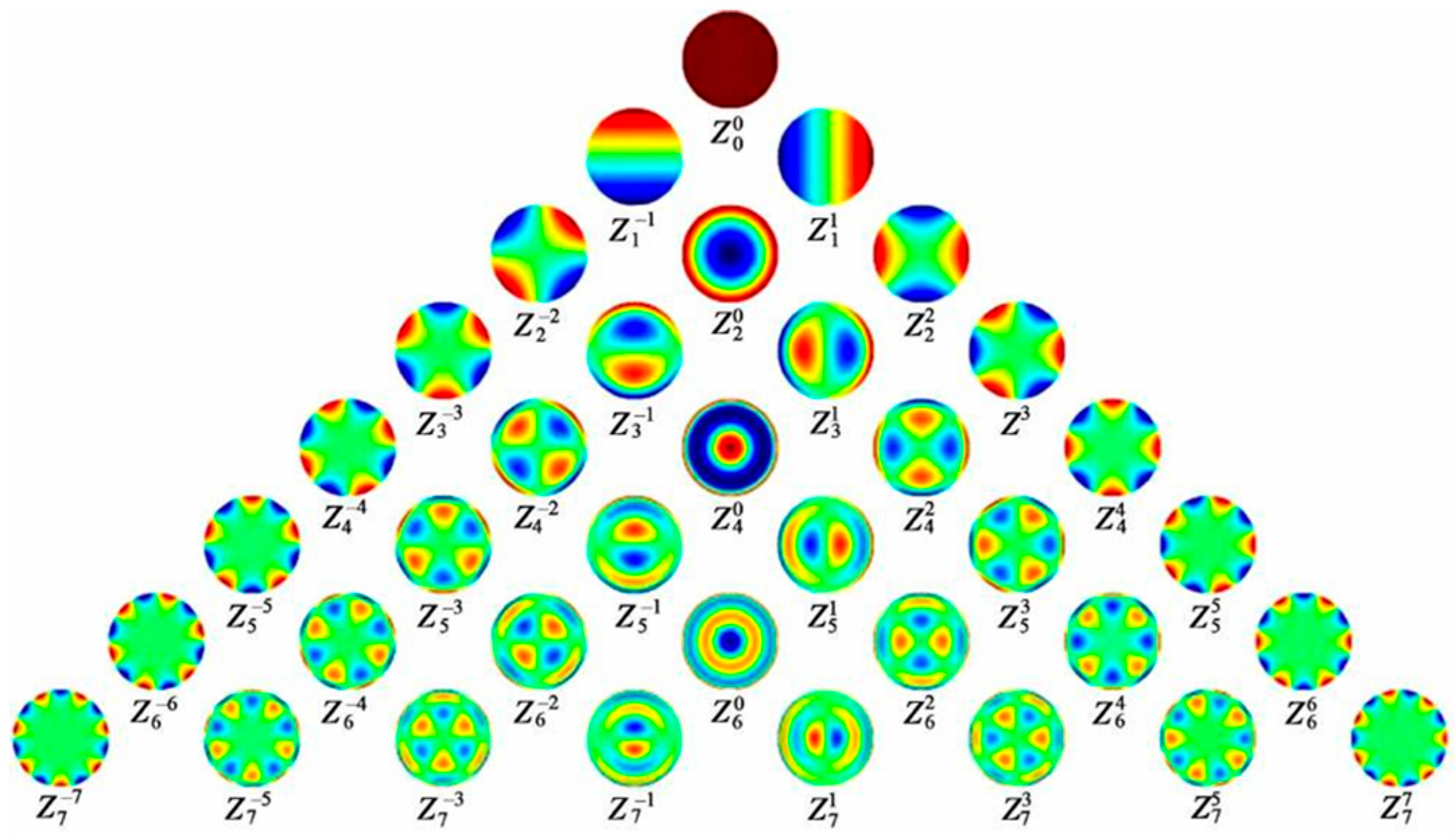
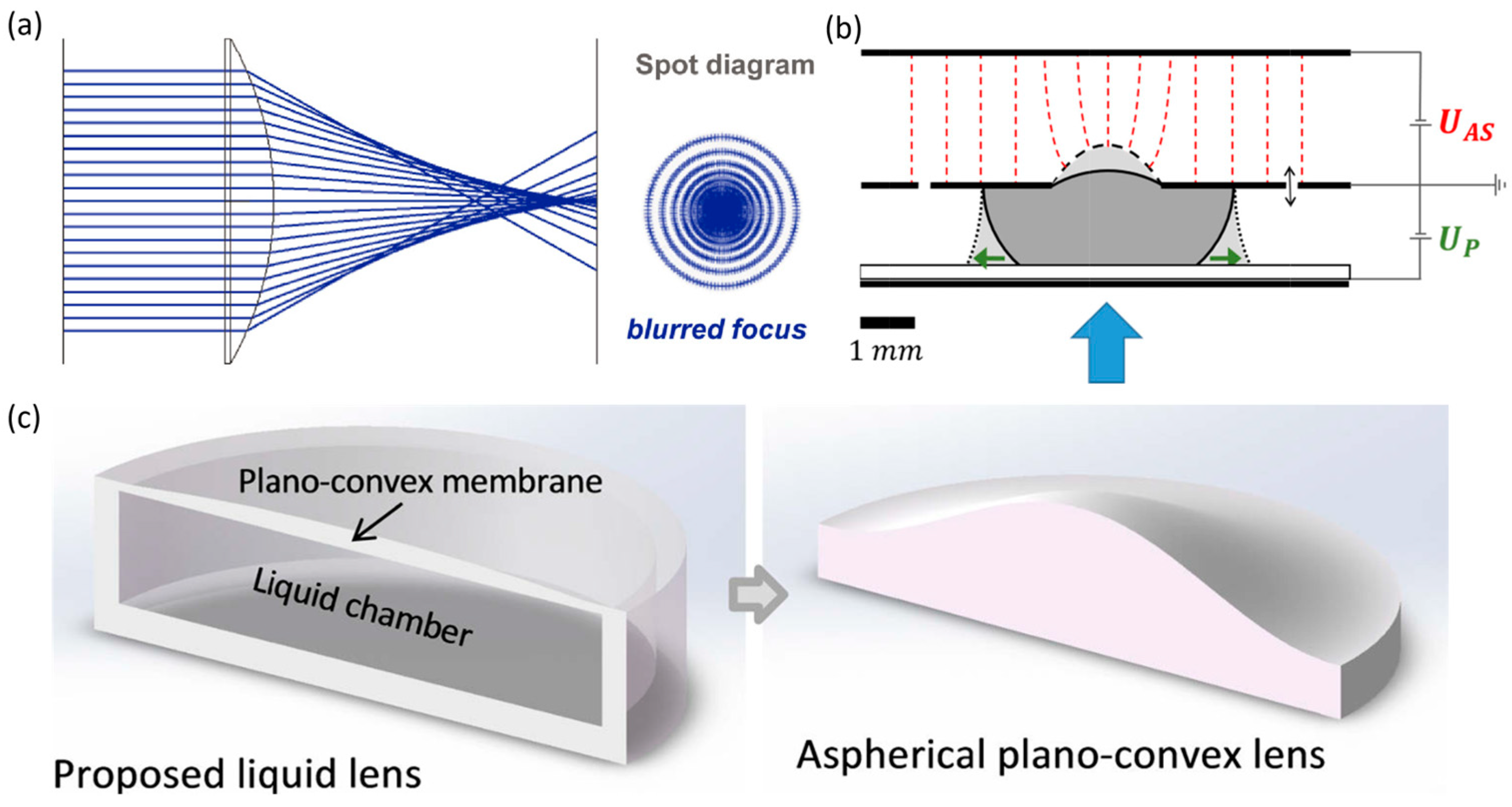
4.4. Aberration Correction
4.4.1. Chromatic Aberration
4.4.2. Spherical Aberration
4.4.3. Complex Aberrations
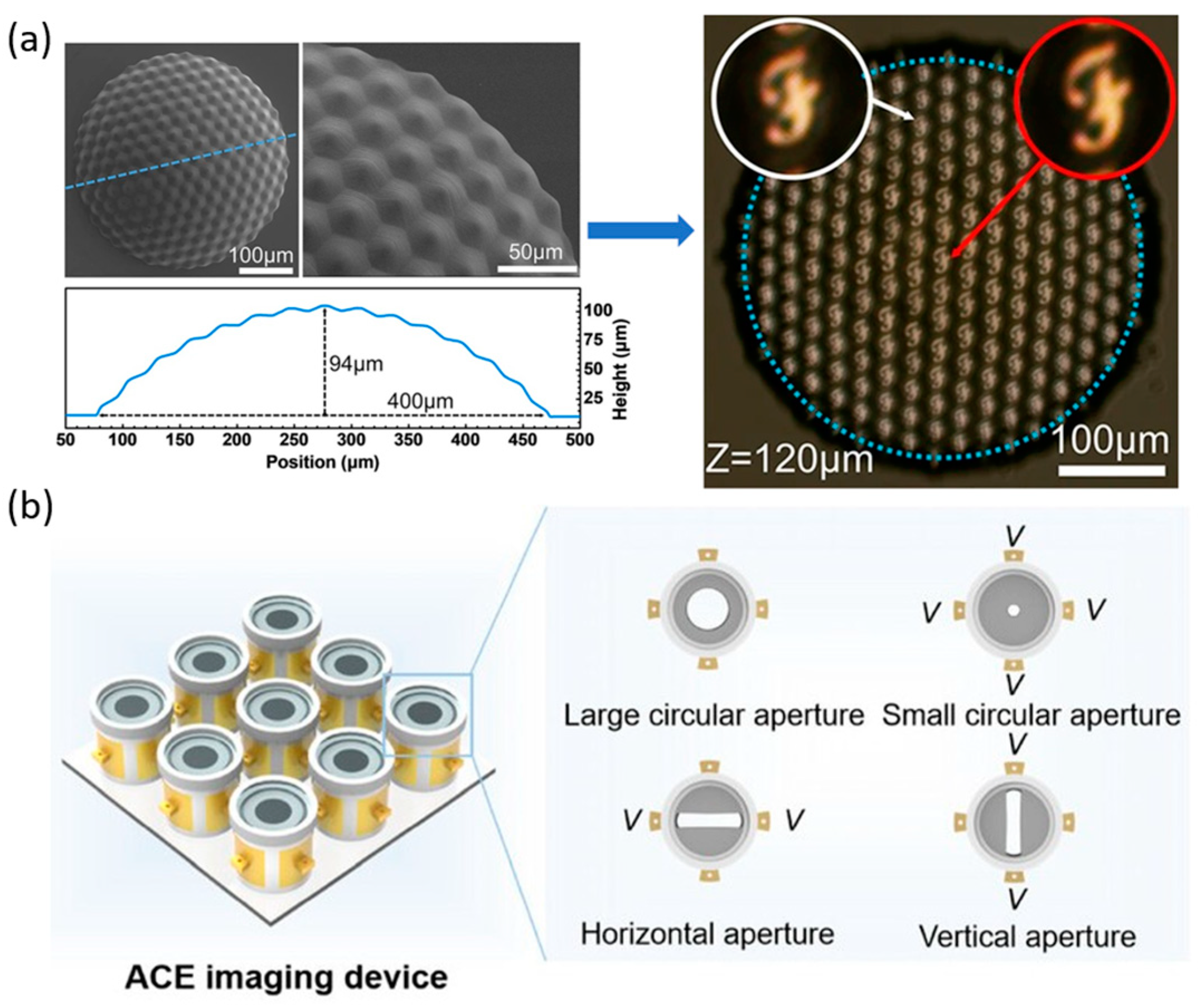
4.4.4. Aberration Correction of Liquid Lens Arrays

5. Perspective and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Zheng, Y.; Yuan, R.-Y.; Jiang, Z.; Xu, J.-B.; Zhao, Y.-R.; Wang, X.; Li, X.-W.; Xing, Y.; Wang, Q.-H. Tunable Liquid Lenses: Emerging Technologies and Future Perspectives. Laser Photonics Rev. 2023, 17, 2300274. [Google Scholar] [CrossRef]
- Liu, H.-B.; Hu, Y.; Li, Y.-Z.; Zhao, J.-H. Review of Current Status and Development of Liquid Lens. Laser Optoelectron. Prog. 2024, 61, 0900005. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, H.-X.; Jia, D.-G.; Liu, T.-G. Recent Development of Tunable Optical Devices Based on Liquid. Molecules 2022, 27, 8025. [Google Scholar] [CrossRef]
- Sun, Z.-J.; Han, D.-D.; Zhang, Y.-L. China’s Top 10 Optical Breakthroughs: Research Progress of Tunable Microlens Arrays (Invited). Laser Optoelectron. Prog. 2024, 61, 1000002. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.-J.; Chu, C.-Y.; Lu, W.-T.; Zhang, P.-P.; Yang, G.-L.; Zhong, H.-Z.; Zhao, Y.-J. Development of Microlens Arrays: From Fabrication to Photonic Applications. Acta Opt. Sin. 2021, 41, 2100001. [Google Scholar] [CrossRef]
- Guo, J.-K.; Sandaruwan, W.-D.-N.; Li, J.-W.; Ling, J.-Z.; Yuan, Y.; Liu, X.; Li, Q.; Wang, X.-R. Recent Progress in Droplet Structure Machining for Advanced Optics. Micromachines 2024, 15, 337. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.-W.; Peng, Y.-Y.; Weng, X.-Y.; Jin, Y.-Q.; Zhou, X.-T.; Yan, Q.; Guo, T.-L.; Wu, C.-X.; Zhang, Y.-A. Flexible Liquid Crystal Micro-Lens Arrays for Curved Integral Imaging 2D/3D Convertible Display. Liq. Cryst. 2023, 50, 1666–1678. [Google Scholar] [CrossRef]
- Aljohani, O.; Dierking, I. Modern Developments in Lasing with Liquid Crystals. Front. Mater. 2024, 11, 1453744. [Google Scholar] [CrossRef]
- Guo, J.-K.; Gao, Y.-X.; Ling, J.-Z.; Yuan, Y.; Wang, X.-R.; Song, J.-K. Laser Processing of Microdroplet Structure of Liquid Crystal in 3D. Opt. Express 2022, 30, 26018–26026. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Jin, N. The Applications of Ionic Liquid as Functional Material: A Review. Curr. Org. Chem. 2016, 20, 2109–2116. [Google Scholar] [CrossRef]
- Xu, M.; Liu, Y.; Yuan, Y.; Lu, H.; Qiu, L. Variable-Focus Liquid Lens Based on Electrically Responsive Fluid. Opt. Lett. 2022, 47, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Warner, M.; Terentjev, E.-M. Liquid Crystal Elastomers; Oxford Academic: Oxford, UK, 2003. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, L.; Bae, J. Advances in 4D Printing of Liquid Crystalline Elastomers: Materials, Techniques, and Applications. Mater. Horiz. 2022, 9, 1825–1849. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, J.; Yang, S. Multi-Functional Liquid Crystal Elastomer Composites. Appl. Phys. Rev. 2022, 9, 011301. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, M.; Gan, Z.; Lv, J.; Lin, Z.; Hong, H. Tuneable Lenses Driven by Dielectric Elastomers: Principles, Structures, Applications, and Challenges. Appl. Sci. 2025, 15, 6926. [Google Scholar] [CrossRef]
- Chen, S.; Potsaid, B.; Li, Y.; Lin, J.; Hwang, Y.; Moult, E.M.; Zhang, J.; Huang, D.; Fujimoto, J.G. High Speed, Long Range, Deep Penetration Swept Source OCT for Structural and Angiographic Imaging of the Anterior Eye. Sci. Rep. 2022, 12, 992. [Google Scholar] [CrossRef]
- Li, H.; He, Y.-C.; Yu, Y.; Wu, Y.-T.; Zhang, S.-P.; Zhang, Y.-D. A Light Field Display Realization with a Nematic Liquid Crystal Microlens Array and a Polymer Dispersed Liquid Crystal Film. Photonics 2022, 9, 244. [Google Scholar] [CrossRef]
- Hsiao, Y.-C.; Zeng, Y.; Liu, H.-C.; Shung, K.-K.; Zhou, Q.-F.; Wu, J.-X. A Wireless Capsule Ultrasound Endoscopy Using Electrowetting Liquid Lens Scanning Device. In Proceedings of the 2023 IEEE International Ultrasonics Symposium (IUS), Montreal, QC, Canada, 3–8 September 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Pu, Y.-R.; Xiong, W.-P.; Yu, X.-L.; Zou, R.-M.; Huang, J.-C.; Liu, X.-J.; Sun, Y. Liquid Lens-Based Endoscopic OCT Probe with Adjustable Focus for 3D Imaging in Cross-Sectionally Irregular Lumens. Opt. Express 2025, 33, 29880–29894. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Y.; He, Z.-Z.; Chen, B.-W.; Liu, J. A Personal Desktop Liquid-Metal Printer as a Pervasive Electronics Manufacturing Tool for Society in the Near Future. Engineering 2015, 1, 506–512. [Google Scholar] [CrossRef]
- Zhao, P.-P.; Li, Y.; Zappe, H. Accelerated Electrowetting-Based Tunable Fluidic Lenses. Opt. Express 2021, 29, 15733–15746. [Google Scholar] [CrossRef]
- Chen, L.-J.; Liang, S.-J.; Chen, Z.-S.; Liang, X.-F.; Chen, Q.-M. Electrically Tunable Lenses for Imaging and Light Manipulation. Micromachines 2023, 14, 319. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Wang, Y.-J.; Reshetnyak, V. Liquid Crystal Lenses with Tunable Focal Length. Liq. Cryst. Rev. 2017, 5, 111–143. [Google Scholar] [CrossRef]
- Sato, S. Liquid-Crystal Lens-Cells with Variable Focal Length. Jpn. J. Appl. Phys. 1979, 18, 1679–1684. [Google Scholar] [CrossRef]
- Guo, J.-K.; Ling, J.-Z.; Yuan, Y.; Chang, F.; Wang, X.-R.; Song, J.-K. Laser Processing of Liquid Crystal Droplets with Diverse Internal Structures. Crystals 2023, 13, 683. [Google Scholar] [CrossRef]
- Zarzar, L.-D.; Sresht, V.; Sletten, E.-M.; Kalow, J.-A.; Blankschtein, D.; Swager, T.-M. Dynamically Reconfigurable Complex Emulsions via Tunable Interfacial Tensions. Nature 2015, 518, 520–524. [Google Scholar] [CrossRef]
- Nagelberg, S.; Zarzar, L.-D.; Nicolas, N.; Subramanian, K.; Kalow, J.-A.; Sresht, V.; Blankschtein, D.; Barbastathis, G.; Kreysing, M.; Swager, T.-M.; et al. Reconfigurable and Responsive Droplet-Based Compound Micro-Lenses. Nat. Commun. 2017, 8, 14673. [Google Scholar] [CrossRef]
- Concellón, A.; Zentner, C.-A.; Swager, T.-M. Dynamic Complex Liquid Crystal Emulsions. J. Am. Chem. Soc. 2019, 141, 18246–18255. [Google Scholar] [CrossRef]
- Wang, H.-J.; Shi, W.-X.; Wang, J.-J.; Zhou, X.-K.; Li, P. Converting Evanescent Waves into Propagating Waves by Hyper-Hemi-Microsphere. Opt. Express 2024, 32, 25451–25462. [Google Scholar] [CrossRef]
- Guo, J.-K.; Wang, H.-J.; Chang, F.-J.; Ling, J.-Z.; Yuan, Y.; Zhang, X.-T.; Wang, X.-R. Production and Reconfiguration of Double Emulsions by Temperature Control. Langmuir 2023, 39, 13296–13302. [Google Scholar] [CrossRef]
- Xu, X.-Q.; Wang, R.-K. Synergistic effect of hyperosmotic agents of dimethyl sulfoxide and glycerol on optical clearing of gastric tissue studied with near infrared spectroscopy. Phys. Med. Biol. 2004, 49, 457–468. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Shen, Z.; Wang, J.; Li, X.; Zeng, Y.; Wang, B.; He, Y.; Du, Y. Glycerol-Mediated Nanostructure Modification Leading to Improved Transparency of Porous Polymeric Scaffolds for High Performance 3D Cell Imaging. Biomacromolecules 2014, 15, 2521–2531. [Google Scholar] [CrossRef] [PubMed]
- Bogi, A.; Faetti, S. Elastic, Dielectric and Optical Constants of 4′-Pentyl-4-Cyanobiphenyl. Liq. Cryst. 2001, 28, 729–739. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ozdemir, O.; Karakashev, S.-I.; Nguyen, A.-V.; Miller, J.-D. Adsorption and Surface Tension Analysis of Concentrated Alkali Halide Brine Solutions. Miner. Eng. 2009, 22, 263–271. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, S.; Panagiotopoulos, A.-Z.; Klein, M.-L.; Wu, X. Why Dissolving Salt in Water Decreases Its Dielectric Permittivity. Phys. Rev. Lett. 2023, 131, 076801. [Google Scholar] [CrossRef]
- Shimizu, K.; Murakami, K.; Ogawa, N.; Akai, H.; Shintake, J. Polyvinyl Chloride-Added Dibutyl Adipate for High-Performance Electrohydrodynamic Pumps. Front. Robot. AI 2023, 10, 1109563. [Google Scholar] [CrossRef] [PubMed]
- Fredlake, C.-P.; Crosthwaite, J.-M.; Hert, D.-G.; Aki, S.-N.-V.-K.; Brennecke, J.-F. Thermophysical Properties of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2004, 49, 954–964. [Google Scholar] [CrossRef]
- Nikitina, V.-A.; Nazet, A.; Sonnleitner, T.; Buchner, R. Properties of Sodium Tetrafluoroborate Solutions in 1-Butyl-3-Methylimidazolium Tetrafluoroborate Ionic Liquid. J. Chem. Eng. Data 2012, 57, 3019–3025. [Google Scholar] [CrossRef]
- Arosa, Y.; Algnamat, B.-S.; Rodríguez, C.-D.; Lago, E.-L.; Varela, L.-M.; De La Fuente, R. Modeling the Temperature-Dependent Material Dispersion of Imidazolium-Based Ionic Liquids in the VIS-NIR. J. Phys. Chem. C 2018, 122, 29470–29478. [Google Scholar] [CrossRef]
- Klomfar, J.; Součková, M.; Pátek, J. Surface tension measurements with validated accuracy for four 1-alkyl-3-methylimidazolium based ionic liquids. J. Chem. Thermodyn. 2010, 42, 323–329. [Google Scholar] [CrossRef]
- Huang, M.-M.; Jiang, Y.; Sasisanker, P.; Driver, G.-W.; Weingärtner, H. Static Relative Dielectric Permittivities of Ionic Liquids at 25 °C. J. Chem. Eng. Data 2011, 56, 1494–1499. [Google Scholar] [CrossRef]
- XIAMETERTM PMX-200 Silicone Fluid, 50–1000 cSt. Available online: https://www.dow.com/zh-cn/pdp.xiameter-pmx-200-silicone-fluid-50-cst.01013181z.html#overview (accessed on 27 August 2025).
- Hsu, C.-J.; Singh, B.-P.; Antony, M.; Selvaraj, P.; Manohar, R.; Huang, C.-Y. Liquid Crystal Lens with Doping of Rutile Titanium Dioxide Nanoparticles. Opt. Express 2020, 28, 22856–22866. [Google Scholar] [CrossRef]
- Li, Y.; Guo, M.-F.; Li, Y.-B. Recent advances in plasticized PVC gel for soft actuators and devices: A review. J. Mater. Chem. C 2019, 7, 12991–13009. [Google Scholar] [CrossRef]
- Ghevondyan, M.; Davtyan, M.; Aghayan, M. Dielectric Elastomer Actuators: Medical Applications Review. Discov. Mater. 2025, 5, 43. [Google Scholar] [CrossRef]
- Lu, X.; Xu, M.; Li, Z.-P.; Li, H.-M.; Zhang, W.-H. Preparation of polyurethanes with broad temperature range and highdamping factor. Chin. J. Eng. 2020, 42, 365–371. [Google Scholar] [CrossRef]
- White, T.-J.; Broer, D.-J. Programmable and Adaptive Mechanics with Liquid Crystal Polymer Networks and Elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Herbert, K.-M.; Fowler, H.-E.; McCracken, J.-M.; Schlafmann, K.R.; Koch, J.A.; White, T.J. Synthesis and Alignment of Liquid Crystalline Elastomers. Nat. Rev. Mater. 2022, 7, 23–38. [Google Scholar] [CrossRef]
- Shi, L.; Yang, R.; Lu, S.; Jia, K.; Xiao, C.; Lu, T.; Wang, T.; Wei, W.; Tan, H.; Ding, S. Dielectric Gels with Ultra-High Dielectric Constant, Low Elastic Modulus, and Excellent Transparency. NPG Asia Mater. 2018, 10, 821–826. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, D.; Wang, F.; Han, S.; Yu, D.; Li, F. Variable-Focus Flexible Cylindrical Lens Based on near-Infrared Light-Driven Liquid Crystal Elastomers. Opt. Express 2025, 33, 7813–7829. [Google Scholar] [CrossRef]
- Hirankittiwong, P.; Laeim, H.; Molahalli, V.; Alodhayb, A.; Chattham, N.; Hegde, G. Tunable Focusing Liquid Crystal Lenses: The Challenges and the Opportunities. ChemPhysChem 2025, 26, e202401113. [Google Scholar] [CrossRef]
- Nesterenko, P.-N. 3D Printing in Analytical Chemistry: Current State and Future. Pure Appl. Chem. 2020, 92, 1341–1355. [Google Scholar] [CrossRef]
- Ula, S.-W.; Traugutt, N.-A.; Volpe, R.-H.; Patel, R.-R.; Yu, K.; Yakacki, C.-M. Liquid Crystal Elastomers: An Introduction and Review of Emerging Technologies. Liq. Cryst. Rev. 2018, 6, 78–107. [Google Scholar] [CrossRef]
- Kim, C.; Shin, D.; Koo, G.; Won, Y.-H. Fabrication of an Electrowetting Liquid Microlens Array for a Focus Tunable Integral Imaging System. Opt. Lett. 2020, 45, 511–514. [Google Scholar] [CrossRef]
- Gu, T.-K.; Wang, L.-L.; Guo, Y.; Jiang, W.-T.; Shi, Y.-S.; Yang, S.; Chen, J.-J.; Liu, H.-Z. Realization of reconfigurable super-resolution imaging by liquid microlens arrays integrated on light disk. Acta Phys. Sin. 2023, 72, 099501. [Google Scholar] [CrossRef]
- Qiao, C.; Li, H.; Li, Z.-K.; Wu, Y.-T. Liquid Crystal Microlens Arrays Based on Aluminum-Doped Zinc Oxide Oriented Microstructure Facilitate Light Field Image Resolution Enhancement. IEEE Sens. J. 2025, 25, 5995–6006. [Google Scholar] [CrossRef]
- Bian, Z.-Y.; Fang, F.; Wang, W.-Q.; Lu, H.-B.; Xu, M. Low scattering and fast response polymer brush-stabilized liquid crystal microlens array with tunable focal length. Displays 2025, 89, 103085. [Google Scholar] [CrossRef]
- Lee, J.; Park, Y.; Chung, S.-K. Multifunctional Liquid Lens for Variable Focus and Aperture. Sens. Actuators A Phys. 2019, 287, 177–184. [Google Scholar] [CrossRef]
- Wang, W.-W.; Li, S.-Y.; Liu, P.-H.; Zhang, Y.-G.; Yan, Q.; Guo, T.-L.; Zhou, X.-T.; Wu, C.-X. Improved depth of field of the composite micro-lens arrays by electrically tunable focal lengths in the light field imaging system. Opt. Laser Technol. 2022, 148, 107748. [Google Scholar] [CrossRef]
- Li, S.-X.; Yang, C.-L.; Peng, Z.-H.; Liu, Y.-G.; Diao, Z.-H.; Lu, X.-H.; Yu, Y.; Wang, Q.-D.; Mu, Q.-Q. Continuously Focus Tunable 2D/3D Switchable Cylindrical Liquid Crystal Microlens Arrays for Autostereoscopic Displays. Opt. Express 2025, 33, 1594–1608. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.-H.; Park, M.-K.; Erdenebat, M.-U.; Seo, J.-H.; Lee, J.-W.; Joo, K.-I.; Kim, Y.-S.; Lee, G.; Lee, H.; Choi, H.-J.; et al. Resolution Enhancement of Light Field Displays Using a Polarization-Dependent Virtual-Moving Liquid Crystalline Polymer-Lenticular Lens Array with Rapid Switching Operation. Opt. Laser Technol. 2025, 187, 112794. [Google Scholar] [CrossRef]
- Wan, Y.-B.; Qiu, Z.-G.; Kang, L.-F.; Deng, Z.-J.; Li, J.-Z. Flexible MEMS Techniques for Multi-Physical Sensors. In Microelectromechanical Systems; IntechOpen: London, UK, 2024. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Hu, G.-W.; Ye, H.-P.; Wei, M.-Y.; Guo, Z.-H.; Chen, K.-X.; Liu, C.; Tang, B.; Zhou, G.-F. Mold-Free Self-Assembled Scalable Microlens Arrays with Ultrasmooth Surface and Record-High Resolution. Light Sci. Appl. 2023, 12, 1318–1326. [Google Scholar] [CrossRef]
- Liang, L.; Hu, X.-J.; Shi, Y.; Zhao, S.-K.; Hu, Q.-H.; Liang, M.-H.; Ai, Y. Tunable and Dynamic Optofluidic Microlens Arrays Based on Droplets. Anal. Chem. 2022, 94, 14938–14946. [Google Scholar] [CrossRef]
- Hu, X.; Zhu, J.; Hu, Q.; Zheng, J.; Yang, D.; Zhou, F.; Cheng, Y.; Yang, Y. Digital Optofluidic Compound Eyes with Natural Structures and Zooming Capability for Large-Area Fluorescence Sensing. Biosens. Bioelectron. 2022, 195, 113670. [Google Scholar] [CrossRef]
- Chen, Q.; Bian, Z.-Y.; Wang, H.-R.; Chang, X.-Y.; Fang, Y.; Lu, H.-B.; Xu, M. Fabrication of Liquid-Filled Zoom Compound Eyes with a Tunable Focal Length. Appl. Opt. 2024, 63, 5973–5979. [Google Scholar] [CrossRef]
- Wang, S.-J.-Y.; Liu, Y.-B. Recent Development of Lens Array Fabrication: A Review. J. Comb. Math. Comb. Comput. 2023, 118, 191–205. [Google Scholar] [CrossRef]
- Jing, X.; Li, S.; Zhu, R.; Ning, X.; Lin, J. Miniature Bioinspired Artificial Compound Eyes: Microfabrication Technologies, Photodetection and Applications. Front. Bioeng. Biotechnol. 2024, 12, 1342120. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, Y.-H.; Wang, X.-Q.; Ning, F.-G.; Wen, S.-P.; Zhou, Y.-F.; Chen, S.-J.; Betts, A.; Jerrams, S.; Zhou, F.-L. Electrohydrodynamic Printing of a Dielectric Elastomer Actuator and Its Application in Tunable Lenses. Compos. Part A Appl. Sci. Manuf. 2021, 147, 106461. [Google Scholar] [CrossRef]
- Zhong, Y.; Yu, H.-B.; Zhou, P.-L.; Wen, Y.-D.; Zhao, W.-X.; Zou, W.-H.; Luo, H.; Wang, Y.-C.; Liu, L.-Q. In Situ Electrohydrodynamic Jet Printing-Based Fabrication of Tunable Microlens Arrays. ACS Appl. Mater. Interfaces 2021, 13, 39550–39560. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Du, J.; Zhang, W.; Zhang, H.-Y.; Wang, Y.-F.; Liang, M.-H.; Liao, F.; Shi, J.-P.; Yang, J.-K.-W.; Zuo, Z.-W.; et al. Dynamically Tunable Optofluidic Multifocal Microlens Arrays by 3D Printing. ACS Sens. 2025, 10, 4172–4183. [Google Scholar] [CrossRef]
- Cao, J.-J.; Hou, Z.-S.; Tian, Z.-N.; Hua, J.-G.; Zhang, Y.-L.; Chen, Q.-D. Bioinspired Zoom Compound Eyes Enable Variable-Focus Imaging. ACS Appl. Mater. Interfaces 2020, 12, 10107–10117. [Google Scholar] [CrossRef]
- Huang, L.-Y.; Wu, K.; Cai, S.-H.; Yu, H.-S.; Liu, D.-F.; Yuan, W.-B.; Chen, X.; Ji, H.-B. Understanding the Microfluidic Generation of Double Emulsion Droplets with Alginate Shell. Colloids Surf. B Biointerfaces 2023, 222, 113114. [Google Scholar] [CrossRef]
- Jiang, L.; Guo, K.-F.; Chen, Y.; Xiang, N. Droplet Microfluidics for Current Cancer Research: From Single-Cell Analysis to 3D Cell Culture. ACS Biomater. Sci. Eng. 2024, 10, 1335–1354. [Google Scholar] [CrossRef]
- Moragues, T.; Arguijo, D.; Beneyton, T.; Modavi, C.; Simutis, K.; Abate, A.R.; Baret, J.-C.; deMello, A.J.; Densmore, D.; Griffiths, A.D. Droplet-Based Microfluidics. Nat. Rev. Methods Primers 2023, 3, 32. [Google Scholar] [CrossRef]
- Park, S.-H.; Lee, S.-S.; Kim, S. Photonic Multishells Composed of Cholesteric Liquid Crystals Designed by Controlled Phase Separation in Emulsion Drops. Adv. Mater. 2020, 32, 2002166. [Google Scholar] [CrossRef]
- Li, Y.-L.; Zhou, T.; Li, Y.-Y.; Zhang, Q.; You, Z.-H. Manipulating liquid-liquid phase separation using patterned flow. arXiv 2024. [Google Scholar] [CrossRef]
- Pavlovic, M.; Antonietti, M.; Schmidt, B.-V.-K.-J.; Zeininger, L. Responsive Janus and Cerberus Emulsions via Temperature-Induced Phase Separation in Aqueous Polymer Mixtures. J. Colloid Interface Sci. 2020, 575, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.-K.; Zhao, Z.-J.; Ling, J.-Z.; Yuan, Y.; Wang, X.-R. Laser micro/nanomachining technology for soft matter. Acta Phys. Sin. 2022, 71, 174203. [Google Scholar] [CrossRef]
- Berge, B.; Peseux, J. Variable Focal Lens Controlled by an External Voltage: An Application of Electrowetting. Eur. Phys. J. E 2000, 3, 159–163. [Google Scholar] [CrossRef]
- Kuiper, S.; Hendriks, B.H.W. Variable-Focus Liquid Lens for Miniature Cameras. Appl. Phys. Lett. 2004, 85, 1128–1130. [Google Scholar] [CrossRef]
- Wang, D.-D.; Hu, D.-G.; Zhou, Y.-W.; Sun, L.-C. Design and Fabrication of a Focus-Tunable Liquid Cylindrical Lens Based on Electrowetting. Opt. Express 2022, 30, 47430–47439. [Google Scholar] [CrossRef]
- Xu, J.-B.; Zhao, Y.-R.; Liu, C.; Wang, Q.-H. Non-Aqueous Organic Solution Based on a Large-Aperture Spherical Electrowetting Liquid Lens with a Wide Tunable Focal Length Range. J. Mater. Chem. C 2022, 10, 6778–6793. [Google Scholar] [CrossRef]
- Zhang, N.-H.; Yuan, R.-Y.; Zhao, Z.-Z.; Li, L. Multi-Curved Variable-Focus Liquid Lens. Opt. Commun. 2022, 508, 127781. [Google Scholar] [CrossRef]
- Xu, J.-B.; Zhao, Y.-R.; Liu, C.; Wang, Q.-H. Triple-Layer Spherical Electrowetting Liquid Lens with Large-Aperture and High Zoom Ratio. Opt. Lasers Eng. 2023, 160, 107311. [Google Scholar] [CrossRef]
- Chen, T.; Sun, J.-Y.; Ding, T.-X.; Zheng, P.-T.; Chen, Q.-R.; Chen, Y.; Liang, Z.-C. Flexible Wire Electrode Driving Focus-Tunable Electrowetting Optofluidic Lens. IEEE Photonics Technol. Lett 2022, 34, 537–540. [Google Scholar] [CrossRef]
- Chen, T.; Hu, Q.-Y.; Shang, X.-T.; Ding, K.; Chen, J.; Guan, J.-F.; Deng, L.-L.; Yang, H.-X. Double-Coil Driving Electrowetting Liquid Lens with Dual-Cavity Structure. Opt. Lett. 2025, 50, 2703–2706. [Google Scholar] [CrossRef] [PubMed]
- Li, L.-Y.; Yuan, R.-Y.; Wang, J.-H.; Li, L.; Wang, Q.-H. Optofluidic Lens Based on Electrowetting Liquid Piston. Sci. Rep. 2019, 9, 13062. [Google Scholar] [CrossRef]
- Kopp, D.; Brender, T.; Zappe, H. All-Liquid Dual-Lens Optofluidic Zoom System. Appl. Opt. 2017, 56, 3758–3763. [Google Scholar] [CrossRef]
- Park, I.-S.; Park, Y.; Oh, S.-H.; Yang, J.-W.; Chung, S.-K. Multifunctional Liquid Lens for Variable Focus and Zoom. Sens. Actuators A Phys. 2018, 273, 317–323. [Google Scholar] [CrossRef]
- Xue, Y.-Y.; Zhou, Z.-W.; Xu, M.; Lu, H.-B. Tunable Liquid Crystal Microlens Array with Negative and Positive Optical Powers Based on a Self-Assembled Polymer Convex Array. Liq. Cryst. 2021, 48, 1806–1814. [Google Scholar] [CrossRef]
- Xu, M.; Li, J.; Wang, H.-R.; Chen, Q.-L.; Lu, H.-B. Adaptive Lenticular Microlens Array Based on a Transparent Electrically Responsive Fluid. J. Mol. Liq. 2023, 392, 123467. [Google Scholar] [CrossRef]
- Xu, M.; Chen, C.-F.; Chang, X.-Y.; Chen, Q.-L.; Lu, H.-B. Dielectric Liquid Microlens Array with Tunable Focal Length Based on Microdroplet Array Created via Dip-Coating Method. Langmuir 2024, 40, 5809–5817. [Google Scholar] [CrossRef]
- Takei, A.; Matsumoto, K.; Shimoyama, I. A Thin Electrowetting Controlled Optical System with Pan/Tilt and Variable Focus Functions. Sens. Actuators A Phys. 2013, 194, 112–118. [Google Scholar] [CrossRef]
- Liu, C.; Wang, D.; Wang, Q.-H.; Xing, Y. Multifunctional Optofluidic Lens with Beam Steering. Opt. Express 2020, 28, 7734–7745. [Google Scholar] [CrossRef]
- Tian, J.-Q.; Zhao, Z.-Z.; Li, L. Adaptive Liquid Lens with a Tunable Field of View. Opt. Express 2022, 30, 40991–41001. [Google Scholar] [CrossRef]
- Yin, W.-Q.; Wang, Z.-Y.; Li, L. FOV Adjustable Liquid Lens Driven by Electrowetting Effect. Opt. Express 2024, 32, 27268–27277. [Google Scholar] [CrossRef]
- Seo, S.; Lee, K.; Yoo, S.-K.; Eom, J.; Park, Y. Photoacoustic Endoscopic Probe Based on Lens Scanning Using a Laterally Tunable Electrowetting Liquid Lens. Opt. Express 2025, 33, 21016–21029. [Google Scholar] [CrossRef]
- Zohrabi, M.; Cormack, R.-H.; Gopinath, J.-T. Wide-Angle Nonmechanical Beam Steering Using Liquid Lenses. Opt. Express 2016, 24, 23798–23809. [Google Scholar] [CrossRef]
- Choi, H.; Park, N.-C.; Kim, W.-C. Optical System Design for Light Detection and Ranging with Ultra-Wide Field-of-View Using Liquid Lenses. Microsyst. Technol. 2020, 26, 121–131. [Google Scholar] [CrossRef]
- Shin, K.-S.; Hong, J.; Han, W.; Park, J.-H. Field of View and Angular-Resolution Enhancement in Microlens Array Type Virtual Reality near-Eye Display Using Polarization Grating. Opt. Express 2025, 33, 263–278. [Google Scholar] [CrossRef]
- Sun, Z.-J.; Liu, Y.-Q.; Wan, J.-Y.; Liu, X.-Q.; Han, D.-D.; Chen, Q.-D.; Zhang, Y.-L. Reconfigurable Microlens Array Enables Tunable Imaging Based on Shape Memory Polymers. ACS Appl. Mater. Interfaces 2024, 16, 9581–9592. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.-Y.; Zhang, Y.-L.; Pan, C.; Dou, J.-Y.; Li, Z.-Z.; Tian, Z.-N.; Mao, J.-W.; Chen, Q.-D.; Sun, H.-B. Miniature Optoelectronic Compound Eye Camera. Nat. Commun. 2022, 13, 5634. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Lu, X.-K.; Li, J.-N.; Zhao, Y.-R.; Lin, Y.-C.; Zhang, H.-R.; Li, R.-Q.; Wang, Q.-H.; Liu, C. Adaptive Compound Eye Imaging Device Based on Electrowetting Liquid Aperture with Adjustable Shape. Adv. Intell. Syst. 2025, 2500412. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, H.-R.; Li, X.-W.; Zhao, Y.-R.; Li, Z.-S.; Hou, Y.-H.; Liu, C.; Wang, Q.-H. Fast-Zoom and High-Resolution Sparse Compound-Eye Camera Based on Dual-End Collaborative Optimization. Opto-Electron. Adv. 2025, 8, 240285. [Google Scholar] [CrossRef]
- Jütte, L.; Yang, Z.-Y.; Sharma, G.; Roth, B. Focus Stacking in Non-Contact Dermoscopy. Biomed. Phys. Eng. Express 2022, 8, 065022. [Google Scholar] [CrossRef]
- Barak, N.; Kumari, V.; Sheoran, G. Measurement of Specular Surfaces Using Electrically Tunable Lens in Digital Holography. J. Opt. 2022, 24, 125603. [Google Scholar] [CrossRef]
- Español, E.; Tolosa, A.; Saavedra, G.; Martinez-Corral, M.; Incardona, N. Compact extended-DOF microscope through electrowetting lens. Opt. Express 2025, 33, 9199–9212. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-Y.; Xu, Y.-X.; Zhang, X.-Y. Rapid Depth Estimation Based on a Key Electrowetting Liquid-Lens with Electrically Adjusted Imaging Focus. Rev. Sci. Instrum. 2025, 96, 053704. [Google Scholar] [CrossRef]
- Jiang, P.; Chen, T.-T.; Chen, W.; Wang, S.-Y. Real-Time Extend Depth of Field Imaging Based on Liquid Lens and Deblur-Unet in Automated Optical Inspection. Opt. Lasers Eng. 2025, 192, 109022. [Google Scholar] [CrossRef]
- Xu, J.-B.; Zhao, Y.-R.; Yuan, R.-Y.; Li, X.-W.; Liu, C.; Wang, Q.-H. Electrowetting Liquid Lens Integrating Adaptive Liquid Iris. Opt. Laser Technol. 2024, 169, 110023. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, Z.; Wang, X.; Zheng, Y.; Zheng, Y.-W.; Wang, Q.-H. Continuous Optical Zoom Microscope with Extended Depth of Field and 3D Reconstruction. PhotoniX 2022, 3, 20. [Google Scholar] [CrossRef]
- Zhang, R.-N.; Zhou, N.; Tang, H.-C.; Xia, M.-H.; Cai, Z.-W.; Sun, J.-S.; Chen, Q.; Zuo, C. High-Speed Multi-Modal Extended Depth-of-Field Microscopy with an Electrically Tunable Lens. Laser Photonics Rev. 2024, 18, 2300770. [Google Scholar] [CrossRef]
- Cai, W.-B.; Zhang, X.-M.; Li, H.; Liao, Z. Large Depth of Field Structured Light Micro-Vision System for 3D Measurement Based on Dual Electrically Tunable Lenses. Opt. Express 2025, 33, 34138–34152. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.-L.; Piao, X.-Z.; Zhuang, J.-Y.; Wu, C.-H.; Zhang, D.-R.; Cheng, X.; Stoeber, B. 3D imaging of moving cells within droplets with a staggered bifocal microlens array. Opt. Express 2025, 33, 26152–26163. [Google Scholar] [CrossRef]
- Peng, Y.-Y.; Wang, W.-W.; Zhang, J.-Z.; Zou, Z.-Y.; Chen, C.-L.; Zhou, X.-T.; Guo, T.-L.; Yan, Q.; Zhang, Y.-G.; Wu, C.-X. Integral imaging 3D display using triple-focal microlens arrays for near-eye display with enhanced depth of field. Displays 2025, 87, 102986. [Google Scholar] [CrossRef]
- Li, Q.; Zhong, F.-Y.; Deng, H.; He, W. Depth-enhanced 2D/3D switchable integral imaging display by using n-layer focusing control units. Liq. Cryst. 2022, 49, 1367–1375. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Zou, Z.-Z.; Peng, Y.-Y.; Zhou, X.-T.; Guo, T.-L.; Wu, C.-X.; Kang, J.-X.; Zang, Y.-A. Stacked High-Resistance Layer Induced Dual-Focal Liquid Crystal Microlens Array for Enhanced Depth-of-Field Integral Imaging 3D Display. Opt. Commun. 2025, 577, 131416. [Google Scholar] [CrossRef]
- Robert, J.-N. Zernike Polynomials and Atmospheric Turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Otsu-Hyodo, T.; Ohtake, Y.; Ando, T. In-situ aberration correction for Laguerre-Gaussian optical tweezers via optimization of orbit shape. Opt. Express 2024, 32, 30943–30954. [Google Scholar] [CrossRef]
- Spors, F.; Egan, D.J.; Shen, J.; McNaughton, L.E.; Mann, S.; Patel, N.M. Corneal Wavefront Aberrations in Patients Wearing Multifocal Soft Contact Lenses for Myopia Control. Open J. Ophthalmol. 2012, 2, 45–53. [Google Scholar] [CrossRef]
- Novák, J.; Mikš, A. Third-Order Aberration Analysis of a Thin Air-Spaced Aplanatic Doublet with Variable Focal Length Composed of Tunable Focus Lenses. Appl. Opt. 2025, 64, 6308–6314. [Google Scholar] [CrossRef]
- Zhao, P.-P.; Sauter, D.; Zappe, H. Tunable Fluidic Lens with a Dynamic High-Order Aberration Control. Appl. Opt. 2021, 60, 5302–5311. [Google Scholar] [CrossRef]
- Lloret, T.; Navarro-Fuster, V.; Ramírez, M.G.; Morales-Vidal, M.; Beléndez, A.; Pascual, I. Aberration-Based Quality Metrics in Holographic Lenses. Polymers 2020, 12, 993. [Google Scholar] [CrossRef] [PubMed]
- Reichelt, S.; Zappe, H. Design of Spherically Corrected, Achromatic Variable-Focus Liquid Lenses. Opt. Express 2007, 15, 14146–14154. [Google Scholar] [CrossRef]
- Sigler, R.D. Apochromatic Color Correction Using Liquid Lenses. Appl. Opt. 1990, 29, 2451–2459. [Google Scholar] [CrossRef]
- Lenk, L.; Sinzinger, S. Diffractive Alvarez-Lohmann Lenses for Correcting Aberrations of Tunable Membrane Lenses. Opt. Eng. 2023, 62, 035103. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Zhao, Y. Aberration Analyses for Liquid Zooming Lenses without Moving Parts. Opt. Commun. 2007, 275, 22–26. [Google Scholar] [CrossRef]
- Waibel, P.; Mader, D.; Liebetraut, P.; Zappe, H.; Seifert, A. Chromatic Aberration Control for Tunable All-Silicone Membrane Microlenses. Opt. Express 2011, 19, 18584–18592. [Google Scholar] [CrossRef]
- Li, L.; Wang, Q.-H. Zoom Lens Design Using Liquid Lenses for Achromatic and Spherical Aberration Corrected Target. Opt. Eng. 2012, 51, 043001. [Google Scholar] [CrossRef]
- Wang, L.-H.; Oku, H.; Ishikawa, M. An Adaptive Achromatic Doublet Design by Double Variable Focus Lenses. In Proceedings of the Novel Optical Systems Design and Optimization XVII, San Diego, CA, USA, 17–21 August 2014; Volume 9193. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.-H.; Yu, Y.-J.; Wu, L.-A.; Song, M.-Y.; Zhao, Z.-H. Chromatic-Aberration-Corrected Hyperspectral Single-Pixel Imaging. Photonics 2022, 10, 7. [Google Scholar] [CrossRef]
- Jung, G.-S.; Won, Y.-H. Compact and Fast Depth Sensor Based on a Liquid Lens Using Chromatic Aberration to Improve Accuracy. Opt. Express 2021, 29, 15786–15801. [Google Scholar] [CrossRef] [PubMed]
- Alexandropoulos, C.; Rodríguez-Suñé, L.; Duocastella, M. Snapshot Quantitative Phase Imaging with Acousto-Optic Chromatic Aberration Control. Sensors 2025, 25, 4503. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Liu, C.; Li, N.-N.; Wang, Q.-H. Holographic Zoom System With Large Focal Depth Based on Adjustable Lens. IEEE Access 2020, 8, 85784–85792. [Google Scholar] [CrossRef]
- Wang, D.; Liu, C.; Shen, C.; Xing, Y.; Wang, Q.-H. Holographic Capture and Projection System of Real Object Based on Tunable Zoom Lens. PhotoniX 2020, 1, 6. [Google Scholar] [CrossRef]
- Eppig, J.; Schrecker, A.; Messner, A.; Langenbucher, A. Aberration Correction with Aspheric Intraocular Lenses. In Intraocular Lens; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Mishra, K.; Narayanan, A.; Mugele, F. Design and Wavefront Characterization of an Electrically Tunable Aspherical Optofluidic Lens. Opt. Express 2019, 27, 17601–17609. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, X.-F.; Xu, Z.-J.; Wu, P.; Yu, H.-B. Universal Membrane-Based Tunable Liquid Lens Design for Dynamically Correcting Spherical Aberration over User-Defined Focal Length Range. Opt. Express 2019, 27, 37667–37679. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Li, H.-T.; Yu, H.-B. Uniform Design and Deep Learning Based Liquid Lens Optimization Strategy toward Improving Dynamic Optical Performance and Lowering Driving Force. Opt. Express 2023, 31, 20174–20186. [Google Scholar] [CrossRef]
- Wang, J.-H.; Zhou, X.; Luo, L.; Yuan, R.-Y.; Wang, Q.-H. Tunable Liquid Lens Integrated with Aspheric Surface. Opt. Commun. 2019, 445, 56–63. [Google Scholar] [CrossRef]
- Chen, Q.-M.; Tang, X.-L.; Zhou, Y.-J.; Tsoi, C.-C.; Li, Z.-H.; Zhang, X.-M. Aberration-Free Aspherical in-Plane Tunable Liquid Lenses by Regulating Local Curvatures. Lab Chip 2020, 20, 995–1001. [Google Scholar] [CrossRef] [PubMed]
- Furieri, T.; Ancora, D.; Calisesi, G.; Morara, S.; Bassi, A.; Bonora, S. Aberration Measurement and Correction on a Large Field of View in Fluorescence Microscopy. Biomed. Biomed. Opt. Express 2022, 13, 262–273. [Google Scholar] [CrossRef] [PubMed]
- Furieri, T.; Bassi, A.; Bonora, S. Large Field of View Aberrations Correction with Deformable Lenses and Multi Conjugate Adaptive Optics. J. Biophotonics 2023, 16, e202300104. [Google Scholar] [CrossRef] [PubMed]
- Zohrabi, M.; Cormack, R.-H.; Mccullough, C.; Supekar, O.-D.; Gibson, E.-A.; Bright, V.-M.; Gopinath, J.-T. Numerical Analysis of Wavefront Aberration Correction Using Multielectrode Electrowetting-Based Devices. Opt. Express 2017, 25, 31451–31461. [Google Scholar] [CrossRef]
- Cai, S.-X.; Sun, Y.-L.; Chu, H.-H.; Yang, W.-G.; Yu, H.-B.; Liu, L.-Q. Microlenses Arrays: Fabrication, Materials, and Applications. Microsc. Res. Tech. 2021, 84, 2784–2806. [Google Scholar] [CrossRef]
- Zhou, H.-Y.; Zhu, Y.-M.; Liang, H.-X.; Zhang, J.; Kou, S.-F.; Liang, Z.-C.; Zhao, R. Wavefront Correction Using Liquid Lens Array Based on Electrowetting-on-Dielectric. Laser Optoelectron. Prog. 2025, 62, 0923001. [Google Scholar] [CrossRef]
- Li, H.-Y.; Zhang, H.-X.; Liu, X.; Jia, D.-G.; Liu, T.-G. Curved Fiber Compound Eye Camera Inspired by the Strepsiptera Vision. Opt. Express 2023, 31, 36903–36914. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Won, Y.H. Method to Reduce the Aberration of a Polygonal Aperture Focus-Tunable Lens Array for High Fill Factor. Opt. Lett. 2019, 44, 2554–2557. [Google Scholar] [CrossRef]
- Shahini, A.; Jin, H.; Zhou, Z.-X.; Zhao, Y.; Chen, P.-Y.; Hua, J.; Cheng, M.-M.-C. Toward Individually Tunable Compound Eyes with Transparent Graphene Electrode. Bioinspir. Biomim. 2017, 12, 046002. [Google Scholar] [CrossRef]
- Cheng, Y.; Cao, J.; Meng, L.-T.; Wang, Z.-H.; Zhang, K.Y.; Ning, Y.; Hao, Q. Reducing Defocus Aberration of a Compound and Human Hybrid Eye Using Liquid Lens. Appl. Opt. 2018, 57, 1679–1688. [Google Scholar] [CrossRef]
- Zhao, R.; Peng, C.; Zhang, K.; Kong, M.-M.; Chen, T.; Guan, J.-F.; Liang, Z.-C. Design and simulation of bionic compound eye with electrowetting liquid lens. Opto-Electron. Eng. 2021, 48, 200120. [Google Scholar] [CrossRef]
- Tang, C.; Hou, C.-P.; Song, Z.-J. Depth Recovery and Refinement from a Single Image Using Defocus Cues. J. Mod. Opt. 2015, 62, 204–211. [Google Scholar] [CrossRef]
- Zohrabi, M.; Lim, W.-Y.; Gilinsky, S.; Bright, V.-M.; Gopinath, G.-T. Adaptive aberration correction using an electrowetting array. Appl. Phys. Lett. 2023, 122, 081102. [Google Scholar] [CrossRef]

| Material Name | Water-Based Conductive Liquid | Electronegative Fluid | Ionic Liquid | Propylene Carbonate (PC) | Glycerol | |
|---|---|---|---|---|---|---|
| NaCI *, KCI | Tetradecanedioic Acid | EMIMBF4, BMIMBF4 *, EMIMN(CN)2 | ||||
| Surface Tension | γ (mN/m) | 72.72 to 81.75 | 31.0 | 44.41 | - | 62.5 |
| Viscosity | (mPa·s) | 1.004 to 1.990 | 5.11 | 112.3 | - | 934 |
| Boiling Point Temperature | Tb (°C) | 100.05 to 101.80 | 165 | 290 | 241.6 | 98 |
| Freezing/Normal Melting Point Temperature | Tf/m (°C) | −2.60 to −0.18 | −32.4 | −85 | −48.8 | 18.2 |
| Conductivity | κ (mS/cm) | 8.2 to 222 | 2.4 × 10−11 | 3.53 | - | - |
| Dielectric Constant | ε | <78.0 | 5.85 | 13.9 0.8 | 66.14 | 46.53 |
| Refractive Index | n | 1.3332 to 1.3795 | 1.4369 | 1.4156 0.0012 | 1.4189 | 1.4746 |
| Qualitative Solubility | sl EtOH | i H2O; msc EtOH, eth | - | vs·H2O, EtOH, eth, ace, bz | msc H2O, EtOH; sl eth; i bz, ctc, chl | |
| Actuation Type | Electrowetting | Electrowetting | Electrowetting Dielectrophoresis | Electrowetting Dielectrophoresis Liquid-filled type | ||
| Reference | [34,35,36] | [34,37] | [34,38,39,40,41,42] | [34] | [34] | |
| Material Name | Alkane | Fluorocarbon | Silicone Oil | Liquid Crystals | ||
|---|---|---|---|---|---|---|
| Dodecane *, Ethane, Hexane | Perfluorocarbon, Perfluorohexane * | E7 *, 5CB | E7 + 0.5 wt% TiO2 | |||
| Surface Tension | γ (mN/m) | 24.93 | - | 20.8 | - | - |
| Viscosity | (mPa·s) | 1.383 | - | 50cst | - | - |
| Boiling Point Temperature | Tb (°C) | 216.3 | 57.2 | >300 (flash point) | TNI: 61.5 | TNI: 63.5 |
| Freezing/Normal melting Point Temperature | Tf/m (°C) | −9.55 | −86.1 | −41 | ||
| Conductivity | κ (mS/cm) | - | - | - | - | - |
| Dielectric Constant | ε | 2.0120 | - | - | : 14.1 | - |
| Refractive index | n | 1.4210 | 1.2515 | 1.4022 | : 0.216 | : 0.25 |
| Qualitative Solubility | i H2O; vs EtOH, eth, ace, ctc, chl | i H2O; s eth, bz, chl | i H2O; | i H2O; | - | |
| Actuation Type | Janus/double-emulsion droplets | Electrowetting Dielectrophoresis Liquid-filled type | electric driving | |||
| Reference | [34] | [43] | [44] | |||
| Elastomer | Dielectric Elastomer | Liquid Crystal Elastomer | Hydrogel | |||
|---|---|---|---|---|---|---|
| VHB | PDMS | PU | Polyvinyl Chloride Gel (PVC) | Hydrogel Dielectric Gel | ||
| Temperature range (°C) | −10 to 90 | −100 to 250 | −40 to 10 | −20 to 125 | - | - |
| Dielectric constant (@ 1 Hz) | 4.8 | 3 | 7 | - | Pure PVC: 5–10 | 30 to 50 |
| Young’s Modulus | 1.0 to 3.0 MPa | 0.1 to 1.0 MPa | 10 to 17 MPa | kPa-Mpa range | PVC:DBA-1:9 to 1:1 10 kpa to 480 kpa | 20–60 kPa |
| Strain (%) | Max. 120 | Max. 380 | 100 | Max. 400 | Max. 76 | 500 |
| Fatigue Life | >107 @ 5% | >107 Max 5% | - | - | >108 | - |
| Reference | [46] | [46] | [46,47] | [48,49] | [45] | [50] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Cao, Z.; Ling, J.; Yuan, Y.; Liu, X.; Wang, X.; Guo, J.-K. Recent Progress in Liquid Microlenses and Their Arrays for Adaptive and Applied Optical Systems. Micromachines 2025, 16, 1158. https://doi.org/10.3390/mi16101158
Lu S, Cao Z, Ling J, Yuan Y, Liu X, Wang X, Guo J-K. Recent Progress in Liquid Microlenses and Their Arrays for Adaptive and Applied Optical Systems. Micromachines. 2025; 16(10):1158. https://doi.org/10.3390/mi16101158
Chicago/Turabian StyleLu, Siyu, Zheyuan Cao, Jinzhong Ling, Ying Yuan, Xin Liu, Xiaorui Wang, and Jin-Kun Guo. 2025. "Recent Progress in Liquid Microlenses and Their Arrays for Adaptive and Applied Optical Systems" Micromachines 16, no. 10: 1158. https://doi.org/10.3390/mi16101158
APA StyleLu, S., Cao, Z., Ling, J., Yuan, Y., Liu, X., Wang, X., & Guo, J.-K. (2025). Recent Progress in Liquid Microlenses and Their Arrays for Adaptive and Applied Optical Systems. Micromachines, 16(10), 1158. https://doi.org/10.3390/mi16101158






