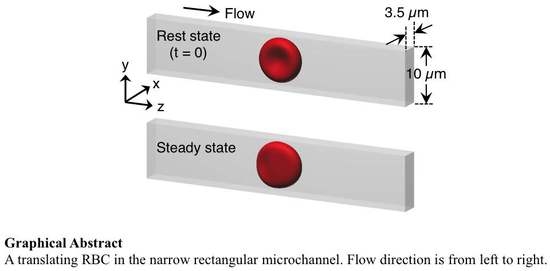
Deformation of a Red Blood Cell in a Narrow Rectangular Microchannel
Abstract
1. Introduction
2. Materials and Methods
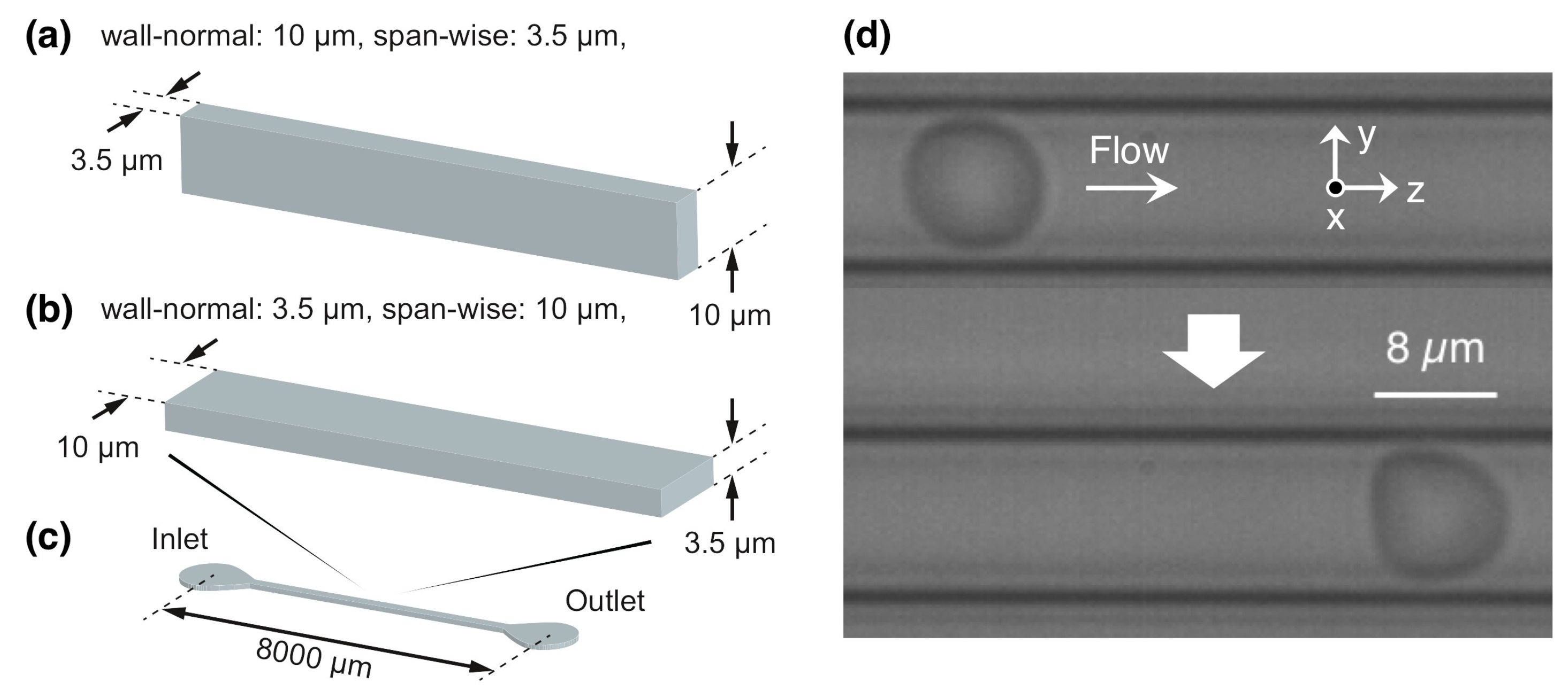
2.1. Flow and RBC Model
2.2. Numerical Simulation
3. Results
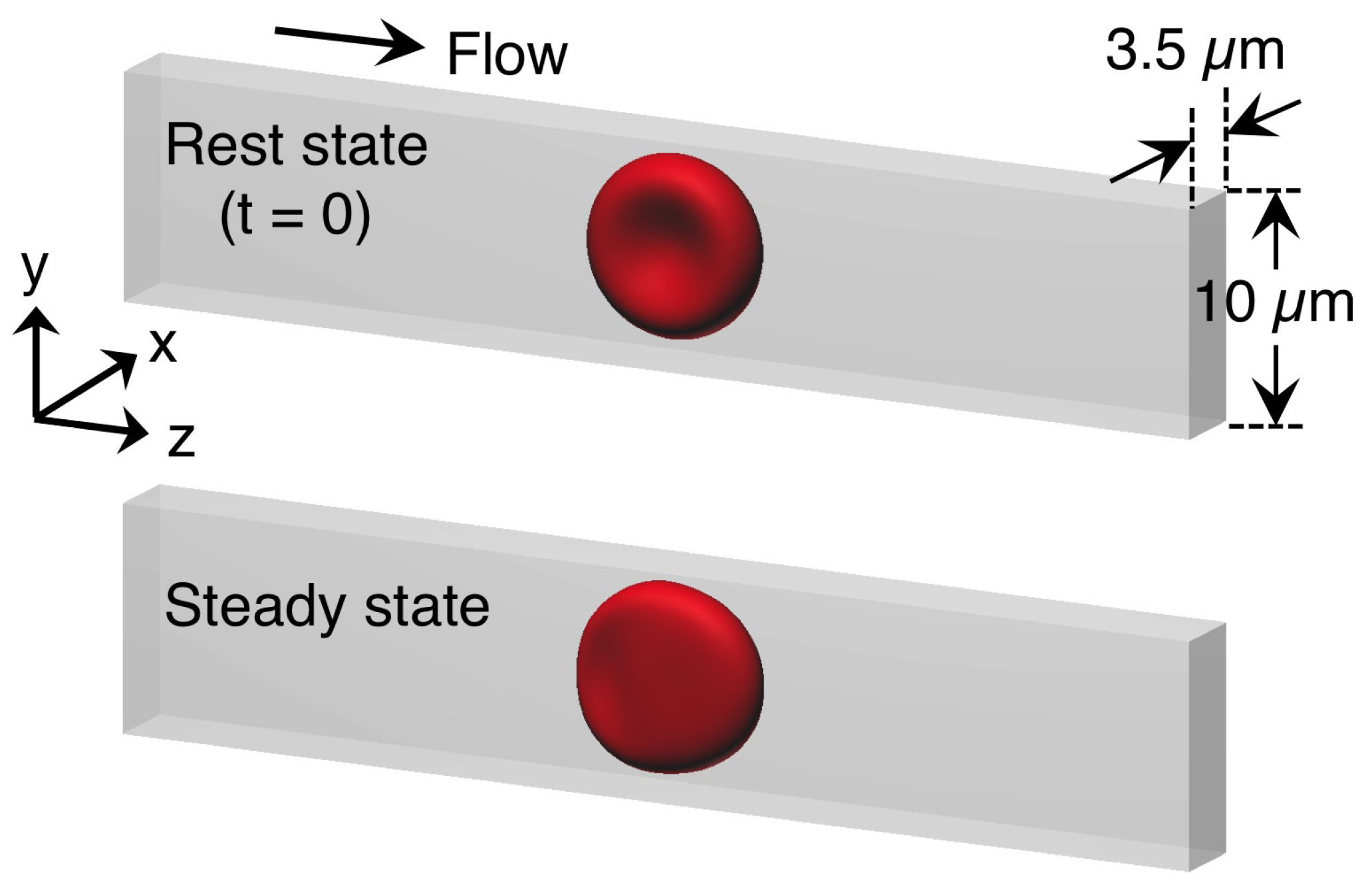
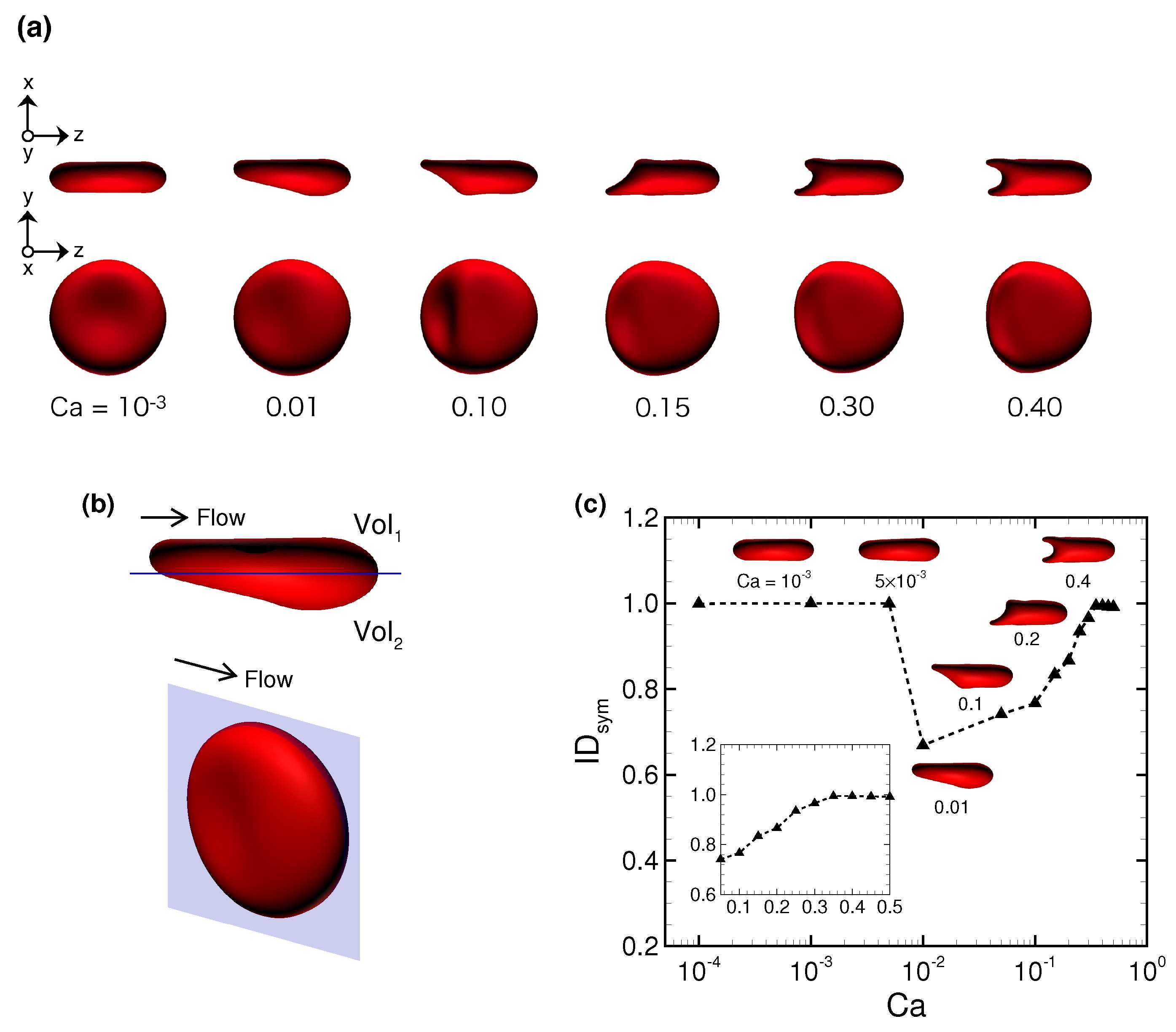
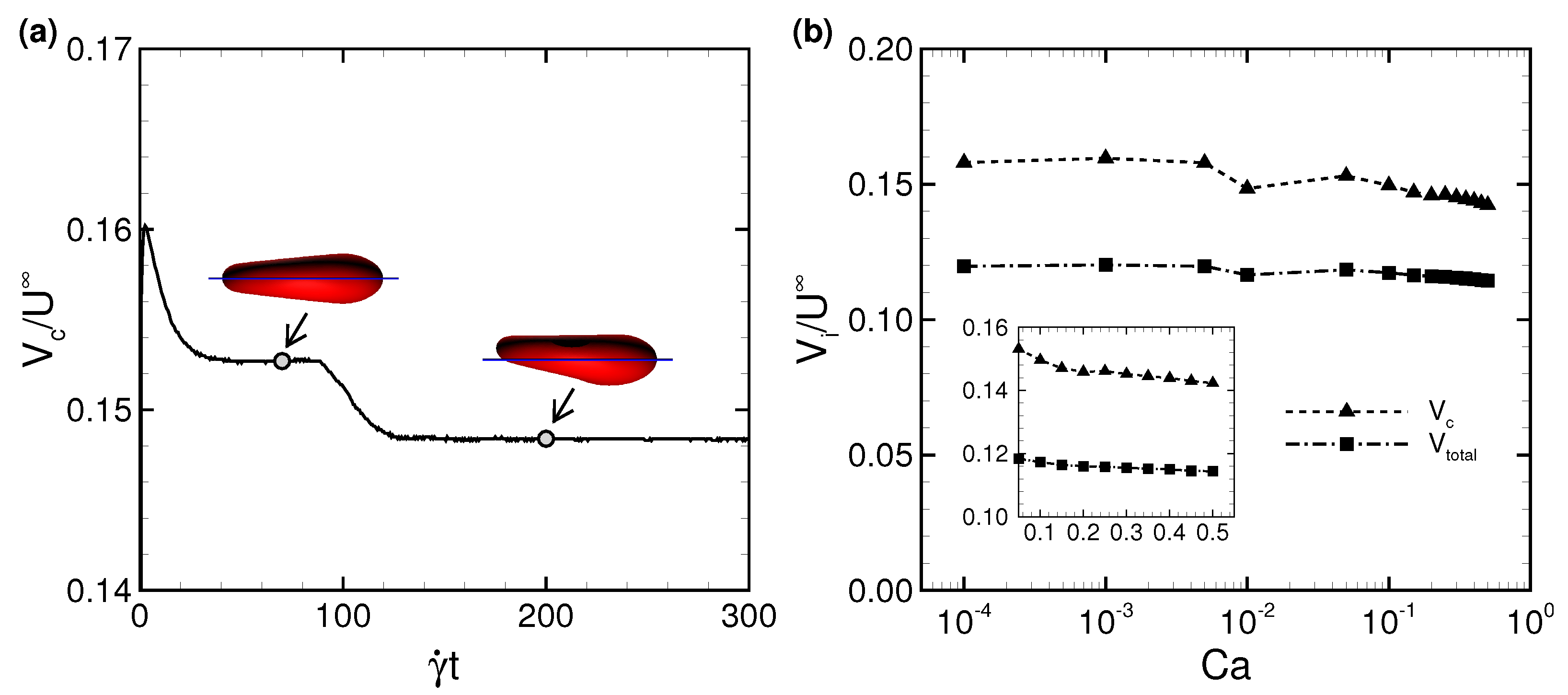
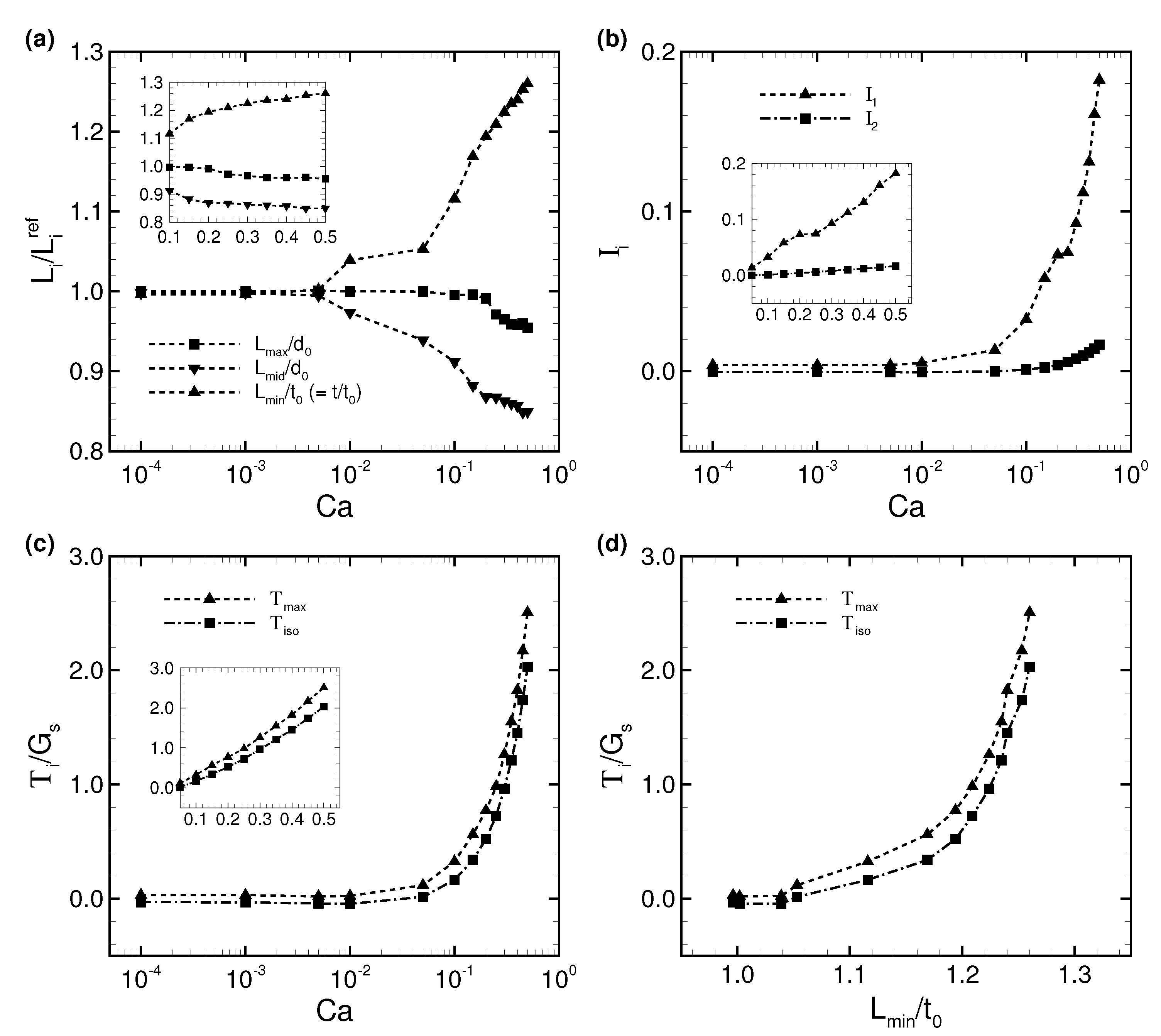
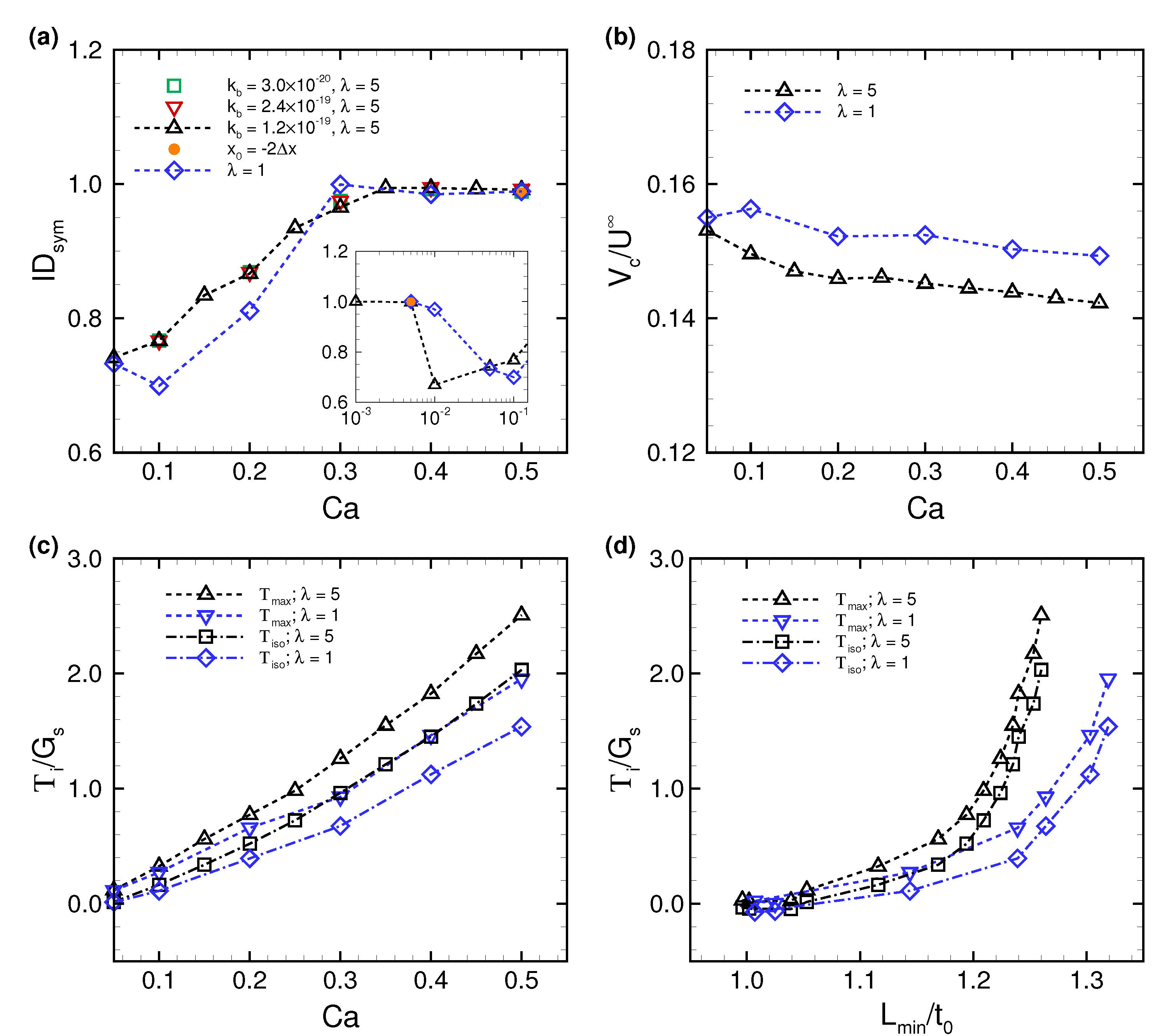
3.1. Deformation of a Translating RBC in a Narrow Rectangular Microchannel
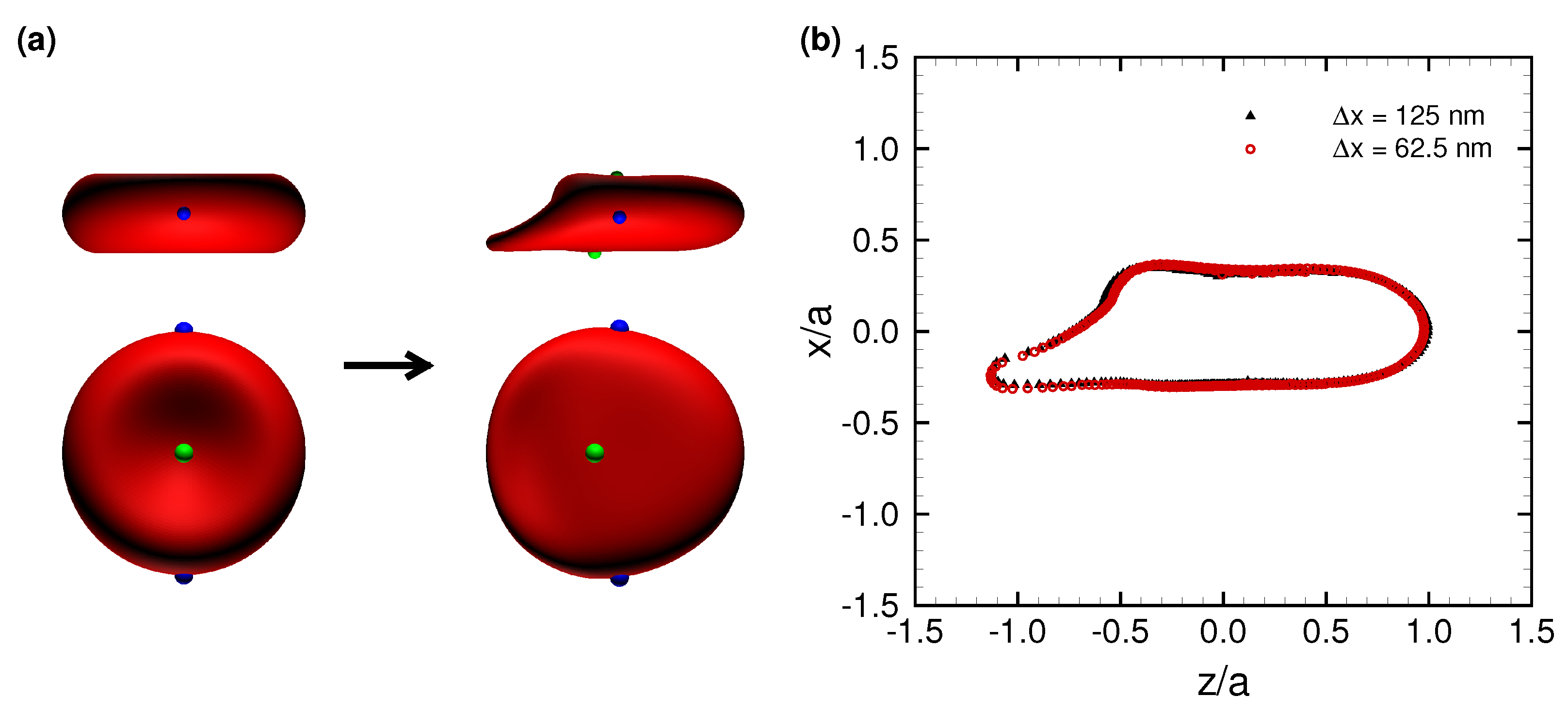
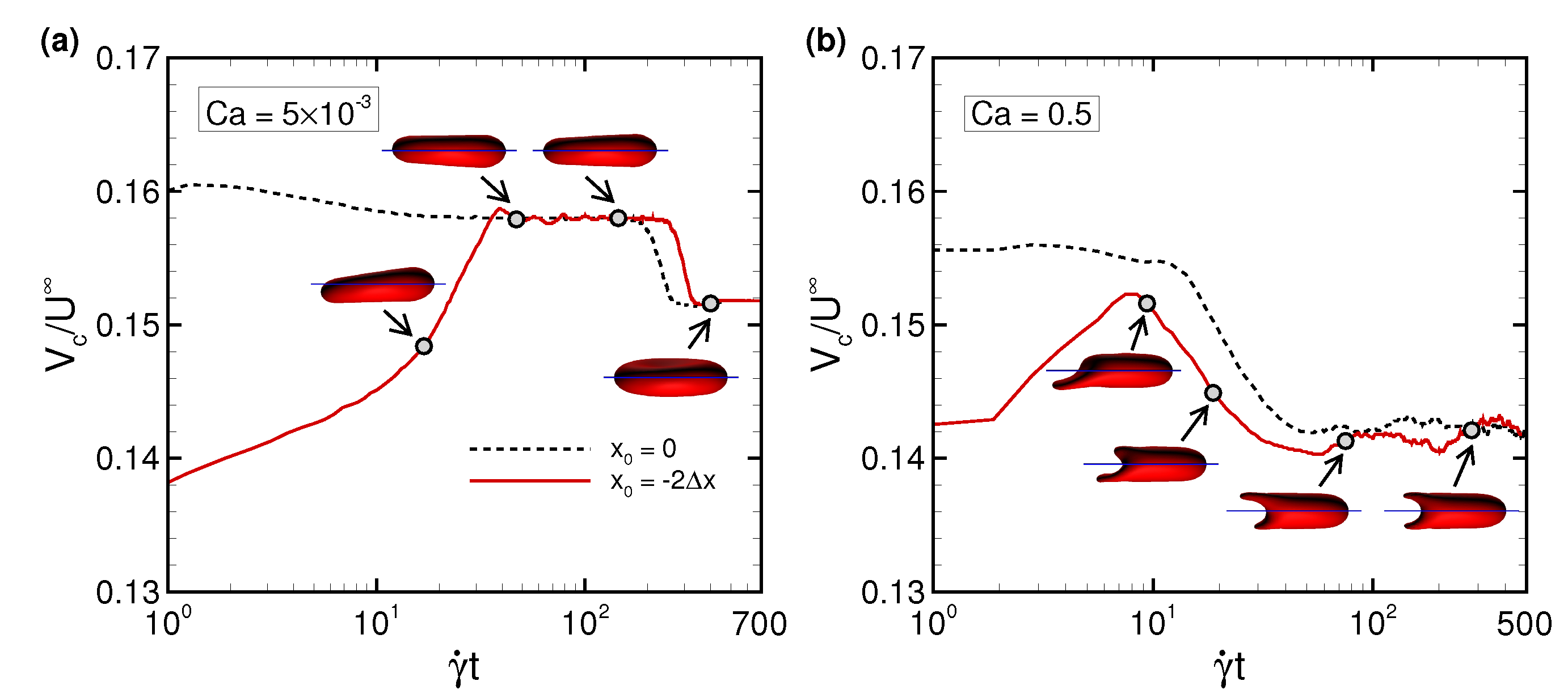
3.2. Effects of Perturbations on Stable Membrane Configuration
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RBC | Red blood cell |
| LBM | Lattice–Boltzmann method |
| FEM | Finite element method |
| IBM | Immersed boundary method |
| GPU | Graphics processing unit |
Appendix A. Sample Preparation and Observation

References
- Chen, S. Red cell deformability and its relevance to blood flow. Annu. Rev. Physiol. 1987, 49, 177–192. [Google Scholar] [CrossRef]
- Caimi, G.; Presti, R.L. Techniques to evaluate erythrocyte deformability in diabetes mellitus. Acta Diabetol. 2004, 41, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Johannes, M.B.P.; Leray, C.; Ruef, P.; Cazenave, J.P.; Linderkamp, O. Endotoxin binding to erythrocyte membrane and erythrocyte deformability in human sepsis and in vitro. Crit. Care Med. 2003, 31, 924–928. [Google Scholar]
- Glenister, F.K.; Coppel, R.L.; Cowman, A.F.; Mohandas, N.; Cooke, B.M. Contribution of parasite proteins to altered mechanical properties of malaria-infected red blood cells. Blood 2002, 99, 1060–1063. [Google Scholar] [CrossRef]
- Park, Y.; Diez-Silva, M.; Popescu, G.; Lykotrafitis, G.; Choi, W.; Feld, M.S.; Suresh, S. Refractive index maps and membrane dynamics of human red blood cells parasitized by Plasmodium falciparum. Proc. Natl. Acad. Sci. USA 2008, 112, 6068–6073. [Google Scholar] [CrossRef] [PubMed]
- Suresh, S.; Spatz, J.; Mills, J.P.; Micoulet, A.; Dao, M.; Lim, C.T.; Beil, M.; Seufferlein, T. Connections between single-cell biomechanics and human disease states: Gastrointestinal cancer and malaria. Acta Biomater. 2005, 1, 15–30. [Google Scholar] [CrossRef]
- Fregin, B.; Czerwinski, F.; Biedenweg, D.; Girardo, S.; Gross, S.; Aurich, K.; Otto, O. High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry. Nat. Commun. 2019, 10, 415. [Google Scholar] [CrossRef] [PubMed]
- Gossett, D.R.; Tse, H.T.K.; Lee, S.A.; Ying, Y.; Lindgren, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Carloa, D.D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar] [CrossRef]
- Ito, H.; Murakami, R.; Sakuma, S.; Tsai, C.-H.D.; Gutsmann, T.; Brandenburg, K.; Poöschl, J.M.B.; Arai, F.; Kaneko, M.; Tanaka, M. Mechanical diagnosis of human eryhrocytes by ultra-high speed manipulation unraveled critical time window for global cytoskeletal remodeling. Sci. Rep. 2017, 7, 43134. [Google Scholar] [CrossRef]
- Otto, O.; Rosendahl, P.; Mietke, A.; Golfier, S.; Herold, C.; Klaue, D.; Girardo, S.; Pagliara, S.; Ekpenyong, A.; Jacobi, A.; et al. Real-time deformability cytometry: On-the-fly cell mechanical phenotyping. Nat. Methods 2015, 12, 199–202. [Google Scholar] [CrossRef]
- Tsai, C.-H.D.; Tanaka, J.; Kaneko, M.; Horade, M.; Ito, H.; Taniguchi, T.; Ohtani, T.; Sakata, Y. An on-chip RBC deformability checker significantly improves velocity-deformation correlation. Micromachines 2016, 7, 176. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y.; Ishida, S.; Omori, T.; Kamm, R.D.; Ishikawa, T. Cell adhesion during bullet motion in capillaries. Am. J. Physiol. Heart Circ. Physiol. 2016, 311, H395–H403. [Google Scholar] [CrossRef] [PubMed]
- Mokbel, M.; Mokbel, D.; Mietke, A.; Träber, N.; Girardo, S.; Otto, O.; Guck, J.; Aland, S. Numerical simulation of real-time deformability cytometry to extract cell mechanical properties. ACS Biomater. Sci. Eng. 2017, 3, 2962–2973. [Google Scholar] [CrossRef]
- Mauer, J.; Mendez, S.; Lanotte, L.; Nicoud, F.; Abkarian, M.; Gompper, G.; Fedosov, D.A. Flow-induced transitions of red blood cell shapes under shear. Phys. Rev. Lett. 2018, 121, 118103. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.-Y.; Yazdani, A.; Li, X.; Douglas, K.A.A.; Mantzoros, C.S.; Karniadakis, G.E. Quantifying platelet margination in diabetic blood flow. Biophys. J. 2018, 115, 1–12. [Google Scholar] [CrossRef]
- Li, X.; Du, E.; Lei, H.; Tang, Y.-H.; Dao, M.; Suresh, S.; Karniadakis, G.E. Patient-specific blood rheology in sickle-cell anaemia. Interf. Focus 2016, 6, 20150065. [Google Scholar] [CrossRef] [PubMed]
- Ito, H.; Takeishi, N.; Kirimoto, A.; Chimura, M.; Ohtani, T.; Sakata, Y.; Horade, M.; Takayama, T.; Wada, S.; Kaneko, M. How to measure cellular shear modulus inside a chip: Detailed correspondence to the fluid-structure coupling analysis. In Proceedings of the MEMS2019, Seoul, Korea, 27–31 January 2019; pp. 336–433. [Google Scholar]
- Kirimoto, A.; Ito, H.; Tsai, C.D.; Kaneko, M. Measurement of both viscous and elasticc constants of a red blood cell in a microchannel. In Proceedings of the MEMS2018, Belfast, UK, 21–25 January 2018. [Google Scholar] [CrossRef]
- Abkarian, M.; Faivre, M.; Horton, R.; Smistrup, K.; Best-Popescu, C.A.; Stone, H.A. Cellular-scale hydrodynamics. Biomed. Mater. 2008, 3, 034011. [Google Scholar] [CrossRef] [PubMed]
- Guckenberger, A.; Kihm, A.; John, T.; Wagner, C.; Gekle, S. Numerical-experimental observation of shape bistability of red blood cells flowing in a microchannel. Soft Matter 2018, 14, 2032–2043. [Google Scholar] [CrossRef]
- Prado, G.; Farutin, A.; Misbah, C.; Bureau, L. Viscoelastic transient of confined red blood cells. Biophys. J. 2015, 108, 2126–2136. [Google Scholar] [CrossRef]
- Suzuki, Y.; Tateishi, N.; Soutani, M.; Maeda, N. Deformation of erythrocytes in microvessels and glass capillaries: Effects of erythrocyte deformability. Microcirculation 1996, 3, 49–57. [Google Scholar] [CrossRef]
- Tomaiuolo, G.; Simeone, M.; Martinelli, V.; Rotolib, B.; Guido, S. Red blood cell deformation in microconfined flow. Soft Matter 2009, 5, 3736–3740. [Google Scholar] [CrossRef]
- Tomaiuolo, G.; Lanotte, L.; D’Apolito, R.; Cassinese, A.; Guido, S. Microconfined flow behavior of red blood cells. Med. Eng. Phys. 2016, 38, 11–16. [Google Scholar] [CrossRef] [PubMed]
- Brust, M.; Aouane, O.; Thiébaud, M.; Flormann, D.; Verdier, C.; Kaestner, L.; Laschke, M.W.; Selmi, H.; Benyoussef, A.; Podgorski, T.; et al. The plasma protein fibrinogen stabilizes clusters of red blood cells in microcapillary flows. Sci. Rep. 2014, 4, 4348. [Google Scholar] [CrossRef] [PubMed]
- Kaoui, B.; Biros, G.; Misbah, C. Why do red blood cells have asymmetric shapes even in a symmetric flow? Phys. Rev. Lett. 2009, 103, 188101. [Google Scholar] [CrossRef] [PubMed]
- Lázaro, G.R.; Hernández-Machadoa, A.; Pagonabarraga, I. Rheology of red blood cells under flow in highly confined microchannels. II. Effect of focusing and confinement. Soft Matter 2014, 10, 7207–7217. [Google Scholar] [CrossRef] [PubMed]
- Tahiri, N.; Biben, T.; Ez-Zahraouy, H.; Benyoussef, A.; Misbah, C. On the problem of slipper shapes of red blood cells in the microvasculature. Microvasc. Res. 2013, 85, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Secomb, T.W.; Skalak, R. A two-dimensional model for capillary flow of an asymmetric cell. Microvasc. Res. 1982, 24, 194–203. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Peltomäki, M.; Gompper, G. Deformation and dynamics of red blood cells in flow through cylindrical microchannels. Soft Matter 2014, 10, 4258–4267. [Google Scholar] [CrossRef]
- Zhu, L.; Gallaire, F. A pancake droplet translating in a Hele-Shaw cell: Lubrication film and flow field. J. Fluid Mech. 2016, 798, 955–969. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.P.; Chien, S. Strain energy function of red blood cell membranes. Biophys. J. 1973, 13, 245–264. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y.; Nakaaki, K.; Yamaguchi, T.; Ishikawa, T. Leukocyte margination at arteriole shear rate. Physiol. Rep. 2014, 2, e12037. [Google Scholar] [CrossRef] [PubMed]
- Takeishi, N.; Imai, Y.; Yamaguchi, T.; Ishikawa, T. Flow of a circulating tumor cell and red blood cells in microvessels. Phys. Rev. E 2015, 92, 063011. [Google Scholar] [CrossRef]
- Takeishi, N.; Imai, Y. Capture of microparticles by bolus of red blood cells in capillaries. Sci. Rep. 2017, 7, 5381. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Dao, M.; Lim, C.T.; Suresh, S. Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Phys. Fluid 2005, 88, 3707–6719. [Google Scholar] [CrossRef] [PubMed]
- Puig-de-Morales-Marinkovic, M.; Turner, K.T.; Butler, J.P.; Fredberg, J.J.; Suresh, S. Viscoelasticity of the human red blood cell. Am. J. Physiol. Cell Physiol. 2007, 293, C597–C605. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flow. Annu. Rev. Fluid. Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Walter, J.; Salsac, A.V.; Barthès-Biesel, D.; Le Tallec, P. Coupling of finite element and boundary integral methods for a capsule in a stokes flow. Int. J. Numer. Meth. Eng. 2010, 83, 829–850. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Miki, T.; Wang, X.; Aoki, T.; Imai, Y.; Ishikawa, T.; Takase, K.; Yamaguchi, T. Patient-specific modeling of pulmonary air flow using GPU cluster for the application in medical particle. Comput. Meth. Biomech. Biomed. Eng. 2012, 15, 771–778. [Google Scholar] [CrossRef] [PubMed]
- Skalak, R.; Branemark, P.I. Deformation of red blood cells in capillaries. Science 1969, 164, 717–719. [Google Scholar] [CrossRef] [PubMed]
- Kuriakose, S.; Dimitrakopoulos, P. Motion of an elastic capsule in a square microfluidic channel. Phys. Rev. E 2011, 84, 011906. [Google Scholar] [CrossRef]
- Rorai, C.; Touchard, A.; Zhu, L.; Brandt, L. Motion of an elastic capsule in a constricted microchannel. Eur. Phys. J. E 2015, 38, 49. [Google Scholar] [CrossRef]
- Omori, T.; Ishikawa, T.; Barthés-Biesel, D.; Salsac, A.-V.; Imai, Y.; Yamaguchi, T. Tension of red blood cell membrane in simple shear flow. Phys. Rev. E 2012, 86, 056321. [Google Scholar] [CrossRef]
- Lanotte, L.; Mauer, J.; Mendez, S.; Fedosov, D.A.; Fromental, J.-M.; Claveria, V.; Nicoul, F.; Gompper, G.; Abkarian, M. Red cells’ dynamic morphologies govern blood shear thinning under microcirculatory flow conditions. Proc. Natl. Acad. Sci. USA 2016, 113, 13289–13294. [Google Scholar] [CrossRef]
- Peng, Z.; Mashayekh, A.; Zhu, Q. Erythrocyte responses in low-shear-rate flows: Effects of non-biconcave stress-free state in the cytoskeleton. J. Fluid. Mech. 2014, 742, 96–118. [Google Scholar] [CrossRef]
- Sinha, K.; Graham, M.D. Dynamics of a single red blood cell in simple shear flow. Phys. Rev. E 2015, 92, 042710. [Google Scholar] [CrossRef]
- Tsubota, K.; Wada, S.; Liu, H. Elastic behavior of a red blood cell with the membrane’s nonuniform natural state: Equilibrium shape, motion transition under shear flow, and elongation during tank-treading motion. Biomech. Model. Mechanobiol. 2014, 13, 735–746. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takeishi, N.; Ito, H.; Kaneko, M.; Wada, S. Deformation of a Red Blood Cell in a Narrow Rectangular Microchannel. Micromachines 2019, 10, 199. https://doi.org/10.3390/mi10030199
Takeishi N, Ito H, Kaneko M, Wada S. Deformation of a Red Blood Cell in a Narrow Rectangular Microchannel. Micromachines. 2019; 10(3):199. https://doi.org/10.3390/mi10030199
Chicago/Turabian StyleTakeishi, Naoki, Hiroaki Ito, Makoto Kaneko, and Shigeo Wada. 2019. "Deformation of a Red Blood Cell in a Narrow Rectangular Microchannel" Micromachines 10, no. 3: 199. https://doi.org/10.3390/mi10030199
APA StyleTakeishi, N., Ito, H., Kaneko, M., & Wada, S. (2019). Deformation of a Red Blood Cell in a Narrow Rectangular Microchannel. Micromachines, 10(3), 199. https://doi.org/10.3390/mi10030199