Abstract
The temporal variations and spatial variations in the ionosphere during geomagnetic storms are exceptionally complex and drastic, significantly complicating ionospheric model construction. In this study, we present a multi-site, high-precision ionospheric vertical total electron content () estimation method by constraining the when the locations of ionospheric pierce points (IPPs), determined by multiple sites, are nearby. The root mean square error (RMSE) relative to the global ionospheric map (GIM) is 3.22 TEC units (TECU), with a correlation coefficient of 0.98. This method enables the high-precision estimation of at IPPs. Utilizing the Gauss–Markov Kalman filter data assimilation algorithm, we consider the relationship between various Dst indices and the ionospheric temporal scales, achieving a regional ionospheric total electron content Map during geomagnetic storms. This approach effectively monitors the impact of geomagnetic storms on the ionospheric total electron content and provides a more accurate representation of ionospheric changes during geomagnetic storms compared to the GIM Map and the International Reference Ionosphere (IRI)-2020 model.
1. Introduction
The space environment plays a crucial role in the Sun–Earth relationship and significantly impacts various electronic and space systems. The ionosphere is closely connected to human life. The ionosphere is influenced by human activities and natural disasters [1,2]. Modern daily life increasingly depends on advanced systems such as satellite communication and navigation. Since the radio signals used by these systems must pass through the ionosphere, they are inevitably affected [3,4]. During geomagnetic storms and other severe ionospheric disturbances, these effects become more pronounced, resulting in higher communication bit error rates, demodulation loss, interruptions, and reduced navigation and positioning accuracy. The real-time monitoring of ionospheric changes during geomagnetic storms is essential for ensuring the reliability of satellite communication and navigation systems.
The ionosphere can cause radio waves of different frequencies to experience varying time delays. By leveraging the dispersive properties of the ionosphere and the dual-frequency coherence of Global Navigation Satellite System (GNSS) signals, the slant total electron content () can be calculated. The existing models for estimating based on GNSS signals include the polynomial model, trigonometric series model, spherical harmonic series model, spline function model, and generalized trigonometric series model, among others [5,6,7,8]. However, with the increasing number of GNSS monitoring stations, if the constraints of total ionospheric electron content are not accounted for when the IPP locations of a multi-site solution are nearby, the estimation accuracy of measurement in localized regions of the ionosphere may be compromised, thereby reducing the quality of GNSS observations.
The ionosphere exhibits highly complex physical and chemical processes [9,10]. This complexity becomes particularly pronounced during geomagnetic storms, which greatly increase the challenges associated with estimating the ionospheric Map [11,12,13]. Many scholars have studied these processes and developed ionospheric physical models, such as TIME-GCM [14], CTIM [15], and GITM [16]. However, the accuracy of the inversions derived from these physical models is highly sensitive to the precision of the initial conditions and external driving parameters, owing to their limited constraints from observational data.
The proliferation of ionospheric observational data has driven the development of empirical models like NeQuick, Klobuchar, and IRI, which leverage large-scale datasets to characterize ionospheric behavior [17,18,19]. Although these empirical models can provide medium- and long-term forecasts, their estimation and forecasting accuracies are limited due to their reliance on statistical methods.
Data assimilation effectively integrates observational field data with background field data, acting as a crucial bridge between observed data and ionospheric models to produce more accurate and objective results [20,21,22,23]. Compared to traditional remote sensing inversion methods, data assimilation better utilizes the authenticity of observational data and the spatial and temporal completeness of background field data. As a result, the quality of both the observational and background field data is critical for the success of data assimilation [24,25,26,27].
In this study, we employed a multi-site, high-precision estimation method to obtain accurate GNSS at IPPs. The IRI-2020 model provided the background field data, while the Gauss–Markov Kalman filter technique was applied to estimate the regional ionospheric Map during geomagnetic storms by considering the relationship between various geomagnetic indices and the ionospheric temporal scales.
2. Materials and Methods
2.1. US CORS Station Data
Using data from the National Geodetic Survey (NGS) (https://geodesy.noaa.gov/corsdata/rinex/, accessed on 16 December 2024), which maintains the Continuously Operating Reference System (CORS) comprising over 1000 GNSS monitoring stations, the distribution of GNSS stations within the regional range (25°N–50°N, 70°W–130°W) is shown in Figure 1. Considering factors such as the sparse station distribution and computation time, 300 GNSS monitoring stations were selected for analysis. The method described in Section 2.3 was applied to the data from these stations to extract the results at the IPPs during geomagnetic storms, which will serve as observational field data for the subsequent ionospheric data assimilation process.
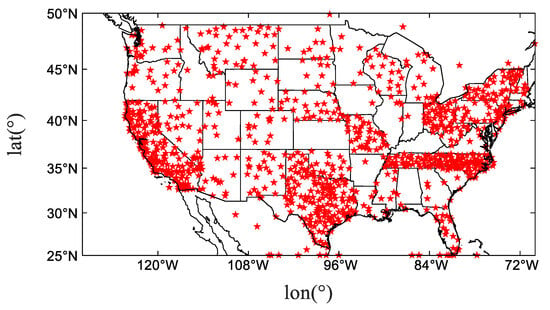
Figure 1.
The distribution of GNSS monitoring stations, from the National Atmospheric Survey Agency of the United States.
2.2. Dst and F01.7 Data
A geomagnetic storm is a short-term geomagnetic disturbance [22] caused by the interaction between high-speed solar wind plasma and the magnetosphere. The magnetosphere plays a critical role in controlling the movement of charged particles in the ionosphere. Consequently, the ionosphere experiences significant disturbances on a global scale during geomagnetic storms. These disturbances are evident in variations in and other related parameters during the geomagnetic storm period compared to quiet conditions. Based on these variations, geomagnetic storms are classified into positive-phase storms and negative-phase storms. The strength and intensity of geomagnetic storms are described by the Dst index. The Dst index is calculated based on data from global geomagnetic observatories at middle and low latitudes, reflecting the degree of weakening of the horizontal magnetic field component on the Earth’s surface. The Dst index is directly affected by intensity variation in the equatorial ring current (composed of energy ions and electrons). The ring current intensifies due to particle injections from the magnetotail during a geomagnetic storm. Its westward-flowing current generates a magnetic field opposing Earth’s intrinsic field, causing the Dst index to decrease. Therefore, the Dst index is a critical indicator for quantifying the dynamics of loop currents and the intensity of geomagnetic storms [28,29]. Table 1 provides the classification criteria for different types of geomagnetic storms.

Table 1.
Geomagnetic storm classification [30].
Geomagnetic disturbances are strongly correlated with solar activity levels, with a higher frequency of storms occurring during periods of elevated solar activity. Solar activity is often quantified using the solar radio flux F10.7 index, measured in solar flux units (sfu). Typically, solar activity is considered high when F10.7 exceeds 120 sfu. Using data provided by the National Aeronautics and Space Administration (NASA, https://omniweb.gsfc.nasa.gov/, accessed on 6 December 2024), the variations in Dst and F10.7 since 2023 are illustrated in Figure 2. The accuracy of the GNSS VTEC and data assimilation results was validated using data from GNSS monitoring stations (NGS, https://geodesy.noaa.gov/corsdata/rinex/, accessed on 16 December 2024) during three geomagnetic storms: 23–25 March 2023; 23–25 April 2023; and 24–26 March 2024, as indicated by the Dst values shown in Figure 3.
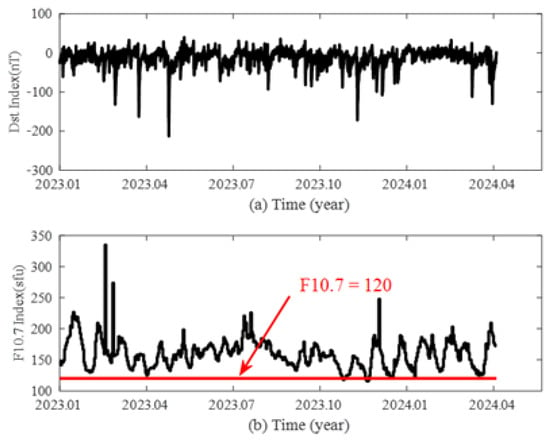
Figure 2.
The variations in Dst and F10.7 from January 2023 to April 2024. (a) The variation in Dst from January 2023 to April 2024; (b) the variation in F10.7 from January 2023 to April 2024.
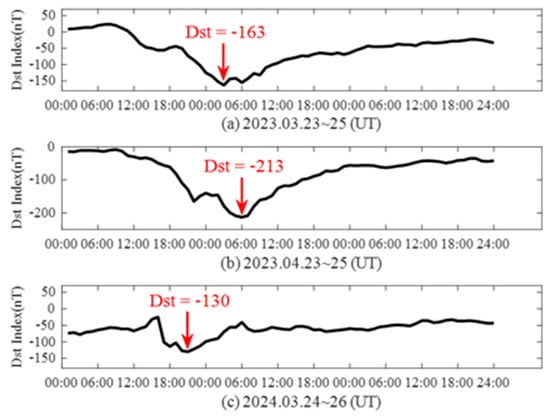
Figure 3.
The changes in Dst during three geomagnetic storms. (a) The variation in Dst during 23–25 March 2023; (b) the variation in Dst during 23–25 April 2023; (c) the variation in Dst during 24–26 March 2024.
As shown in Figure 2, the F10.7 index has consistently exceeded 120 sfu since early 2023, indicating a high level of solar activity. The Dst index, a critical metric for quantifying ring current dynamics and geomagnetic storm intensity, reveals that multiple geomagnetic storms have occurred since 2023. According to the classification of geomagnetic storm, the three geomagnetic disturbances shown in Figure 3 are strong (23–25 March 2023), severe (23–25 April 2023), and strong (24–26 March 2024).
2.3. Multi-Site High-Precision Ionospheric Estimation
By leveraging frequency-dependent delays, the dual-frequency GNSS signal coherence technique was employed to perform inversion along the signal propagation path.
Calculation: Based on dual-frequency GNSS signal pseudo-range and carrier-phase measurements, the formula for calculating is as follows [31].
Here, and are calculated using the carrier-phase measurements and code pseudo-range, respectively. and represent the frequencies of the GNSS signals, while and are their corresponding wavelengths. and refer to the code pseudo-range measurements and and refer to the carrier-phase measurements. The carrier-phase measurements include whole-cycle ambiguity but offer higher accuracy compared to the code pseudo-range. Consequently, provides an absolute value with lower precision, whereas yields a relative value with higher accuracy. To calculate the high-accuracy STEC value, the carrier-phase smoothing pseudo-range method was applied, which detects cycle slips and accounts for hardware delay ().
Here, and are the receiver hardware delays and the satellite hardware delays. is the real .
The ionosphere was modeled as a monolayer thin-shell configuration, and the projection function was expressed as ( [32]:
Here, is the zenith angle, is the GNSS satellite elevation angle, is the ionospheric equivalent height, and is the Earth’s radius. Figure 4 illustrates the monolayer thin-shell configuration of the ionosphere.
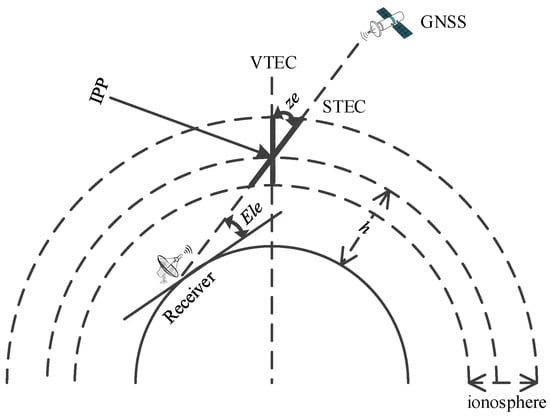
Figure 4.
The monolayer thin-shell configuration of the ionosphere.
Using the tilt factor , the was transformed into the at the IPPs. The GNSS receiver and GNSS satellite hardware delays were utilized to calculate the true at the IPPs.
The region was divided into monitoring grids of 2.5° × 2.5° in longitude and latitude, adaptively configured based on the location and distribution of the IPPs. It was assumed that all IPPs within the same grid shared the same value. Differential equations were established at 15 min intervals. For the -th GNSS receiver linked to the -th GNSS satellite, and the -th GNSS receiver linked to the -th GNSS satellite, the differential equation for a specific grid is expressed as the following equation:
where represents the number of stations and denotes the number of satellites. Data from one full day of observations were accumulated to construct a system of overdetermined linear equations:
Here, is the matrix, with being the total number of valid observations in a day. The vector is the column vector containing the parameters to be solved, including (for receivers) and (for GNSS satellites). The vector is an column vector.
The least squares method was applied to solve for the unknown vector , yielding the hardware delays for each receiver and for each satellite. The detailed implementation process is illustrated in Figure 5.
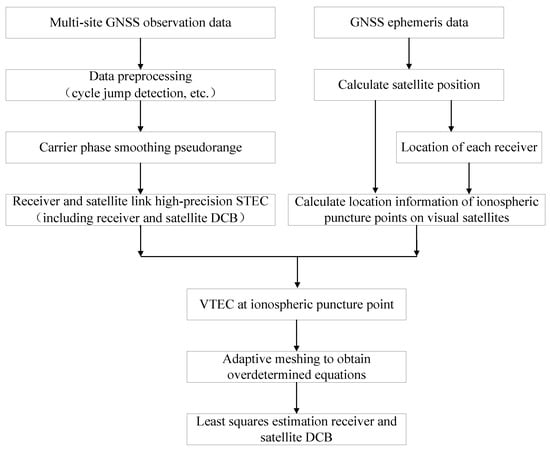
Figure 5.
High-precision estimation based on multiple sites.
2.4. Gauss–Markov Kalman Filtering
The Kalman filtering algorithm is a widely used method for data assimilation. Compared to the variational approach, the Kalman filtering algorithm does not require the development of a complex adjoint model, making the forward error covariance easier to interpret and its implementation more straightforward. Additionally, it provides optimal estimations in both time and space. Due to these advantages, the Kalman filtering algorithm is increasingly applied in data assimilation.
According to the Kalman filter theory, the assimilation process of observed data can be expressed as follows:
where denotes the analyzed field value after assimilation, denotes the background field value given by the IRI model, denotes the background field error covariance matrix, denotes the state value of the observed field, denotes the observation operator, denotes the transpose of , denotes the inverse of , and denotes the observation field error covariance matrix. is the gain matrix, which serves as an adjustment of the observed data to the background field. denotes the analyzed field covariance matrix after assimilation.
Data assimilation produces an optimized combination of observational data and background values, scaled by their respective uncertainties. Therefore, the accuracy in describing the errors and covariances of the background and observed fields directly impacts the assimilation outcome.
In previous research, it has been assumed that observations are uncorrelated, observation errors are unbiased, and these errors are independent of each other and proportional to the square of the observations [22]. Consequently, the observation field covariance matrix has been modeled as a diagonal matrix, with the diagonal elements being the product of a scaling factor and the square of the observations. This relationship is expressed by the following equation:
where denotes the observation point; denotes the value of error covariance between observations; denotes the standard deviation of the IPP at each observation point; denotes the IPP at each observation point; denotes the correlation coefficient; and denotes the scale factor as a hyperparameter [33].
The background field error covariance matrix was derived using the IRI-2020 model by calculating the deviation of the background field error at the current time from the monthly mean background field error. The Map result of the monthly average value of the background field at the time of was calculated using the following formula:
In this formula, denotes the Map result of the background field on the -th day of the current month at the time of . denotes the number of days in the current month.
The background field error of the -th day of the current month at the time of was calculated using the following formula:
The background field error of the monthly mean value at the time of was calculated using the following formula:
To ensure the matching of matrix dimensions in the process of data assimilation needs to be expanded according to the rows.
The deviation of the background field error from the monthly mean background field error at the time of was calculated using the following formula:
The background field error covariance matrix was calculated using the following formula:
In this study, the background field was derived using the IRI-2020 model. However, as an empirical model, the IRI-2020 model lacks forward-forecasting capabilities. To overcome this limitation, the widely used Gauss–Markov Kalman filter algorithm was employed for short-term forecasts. This algorithm assumes that the value at the subsequent time point is related to the current observation, enabling the correction of background field predictions based on the latest data. During the correction process, the influence of the current observation on the background field correction decays exponentially over time, resulting in more-accurate short-term predictions. These predictions can be calculated using the following formula:
In this formula, denotes the background field value corrected by the observed values, denotes the background field corrected by the covariance matrix of the analyzed field, denotes the time step, and denotes the ionospheric temporal scale. As time progresses, the influence of the observed data on the background field diminishes, eventually converging to the background field.
For the ionospheric temporal scale , it is generally accepted that the value of is 1 h during geomagnetic storm and 3 h during quiet conditions [33,34,35]. To better characterize the variation in the ionospheric temporal scale during geomagnetic storms, the correlation of ionospheric electron density at different time intervals can be analyzed.
The values calculated at each station were used as the ionospheric temporal scale data to minimize the impact of spatial factors on the correlation of ionospheric electron density. Considering the diurnal variation characteristics of the ionosphere, the IRI-2020 model was utilized to calculate the of the corresponding station as the background value. The effect of diurnal changes and the influence of day change on the temporal scale analysis results of the ionosphere were reduced by subtracting the background .
where is the time series in which the day change of the is removed and is the time series in which the day change of the is removed after the delay time . In the analysis process, each time series had a length of 6 h, equivalent to 720 sampling points, as the GNSS monitoring station data sampling rate was 30 s.
2.5. Assessment Methodology
To assess the accuracy of assimilation results, the root to mean square error (RMSE) and correlation coefficient (R) could be used as criteria for accuracy assessment. They are defined as follows:
where is the total number of samples, is the value at point obtained by data assimilation, and is the of the observed value or background value.
When calculating the ionospheric temporal scale , is replaced by and by .
3. Results
3.1. Multi-Site High-Precision Estimation Results
Geomagnetic storms typically cause changes in ionospheric electron density within a few hours of their onset. To assess the accuracy of estimation using multiple stations, the copr (34.41°N, 119.88°W), flwe (28.44°N, 81.09°W), leba (39.43°N, 84.28°W), and gobs (45.84°N, 120.82°W) stations were selected due to their diverse latitudes and longitudes (Figure 6). These stations were chosen based on the temporal variations in Dst during three geomagnetic disturbances depicted in Figure 3. The GNSS results during the geomagnetic storms were calculated and compared with the GIM results. This comparison validated the accuracy of our multi-site estimation, as illustrated in Figure 7 and Figure 8.
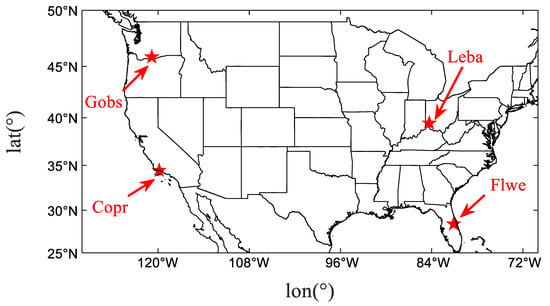
Figure 6.
Distribution map of accuracy verification stations.
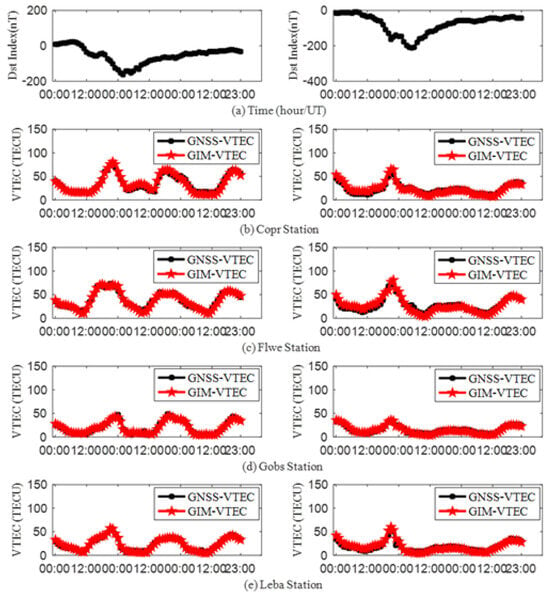
Figure 7.
The variation in from 23 to 25 March 2023 and 23–25 April 2023. (a) The variation in Dst; (b) the variation in at the copr station; (c) the variation in at the flwe station; (d) the variation in at the gobs station. (e) the variation in at the leba station.
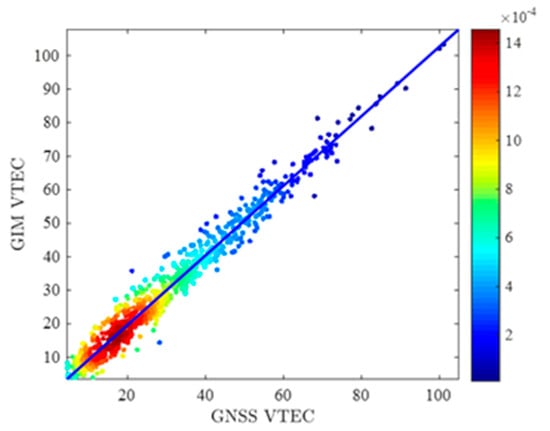
Figure 8.
Correlation between GNSS and GIM during three geomagnetic storms.
Figure 8 shows the comparison of the correlation between GNSS VTEC and GIM VTEC. From the degree of dispersion of the distribution points, it can be seen that GNSS VTEC and GIM VTEC have good consistency. The color scale represents the ratio of the corresponding number of samples to the total number of samples, where the larger the value is, the more samples fall within this range. From the distribution point color scale, it can be seen that the is mainly distributed in the range of 10TECU~40TECU.
Using the multi-site high-precision estimation method, the RMSE statistics for GNSS and GIM during three geomagnetic storms are presented in Table 2. The average of the RMSEs for the four GNSS sites, copr, flwe, leba, and gobs, are 3.64 TECU, 4.12 TECU, 2.21 TECU, and 2.92 TECU, respectively, with an overall average of 3.22 TECU. The ionosphere is mainly formed by solar radiation ionization. When the sun shines directly on low-latitude areas, solar radiation ionization is stronger, resulting in a larger TEC. Due to the influence of the geomagnetic storms, the equatorial ionization anomaly (EIA) may occur in low-latitude regions, resulting in drastic changes in ionospheric TEC in these areas. All of these factors will increase the accuracy of ionospheric TEC forecasting in low-latitude regions, including the lower latitude of the copr and flwe stations compared to the leba and gobs stations and the fact that the TEC calculation accuracy of the leba and gobs stations is better than that of the copr and flwe stations. As shown in Figure 8, the GNSS values during the three geomagnetic storms align well with the GIM , with a calculated correlation coefficient of 0.98.

Table 2.
RMSE statistical results of GNSS and GIM .
Observations from 300 GNSS monitoring stations in the U.S. CORS network during the geomagnetic storms were used to apply the multi-site high-precision estimation method. This approach provided IPP values for the U.S. regional ranges (25°N–50°N, 70°W–130°W) during the geomagnetic storms. Figure 9 illustrates the spatial distribution of IPP for the GNSS stations at 19:00 UT on 23 March 2023. Since GNSS monitoring stations are ground-based, the distribution of IPP is concentrated within U.S. territory and its surrounding areas, extending monitoring capabilities into adjacent sea regions. Due to the geographical locations of these GNSS monitoring stations, the IPP distribution is densest in the eastern U.S., followed by the western U.S., and most sparse in the central U.S.
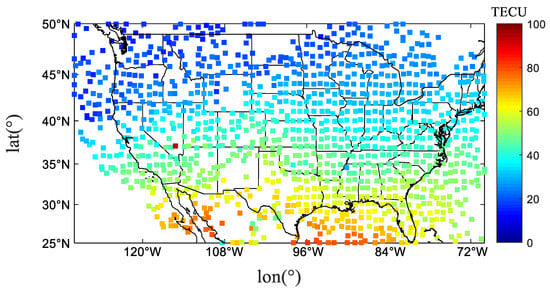
Figure 9.
Distribution of IPP on 23 March 2023 at 19:00 (UT).
Figure 9 shows that the resulting spatial distribution of the observations of IPP VTEC from 300 GNSS monitoring stations in the area with coordinates 25°N–50°N, 70°W–130°W at 19:00 UT on 23 March 2023 has a definite longitudinal and latitudinal structure. There is a significant equatorial ionization anomaly south of latitude 35°N [36,37]. Solar EUV radiation, Equatorial Electrojet, geomagnetic field geometry and thermospheric winds are the major influencing factors of the equatorial ionization anomaly, and the range of the ionospheric equatorial anomaly area will change during magnetic storms.
3.2. Gauss–Markov Kalman Filter Data Assimilation Results
Using the methods described in Section 2.2, GNSS was calculated during the three geomagnetic storms, as well as one day before and after each storm; the influence of daily variations on the results of the ionospheric temporal scale analysis was minimized by deducting the day-to-day variations in IRI . Utilizing the correspondence between the Dst index and the classification of geomagnetic storm levels, as provided in Table 1, the ionospheric temporal scale is defined as the time when the correlation drops to 0.8.
Figure 10 illustrates the changes in the ionospheric temporal scale for different storm classification. The ionospheric TEC changes dramatically during geomagnetic storms, resulting in a decrease in ionospheric TEC correlation. When −200 nT < Dst < −300 nT, the ionospheric temporal scale is defined as 0.84 h, reflecting a weaker temporal correlation. As the Dst index increases, the level of geomagnetic storm decreases, and the ionospheric temporal scale gradually increases. When −30 nT < Dst, the ionospheric temporal scale is defined as 3.02 h, reflecting enhanced temporal correlation. When using Gauss–Markov Kalman filtering for ionospheric assimilation during geomagnetic storms, it is necessary to select the corresponding ionospheric temporal scale based on the level of the geomagnetic storm.
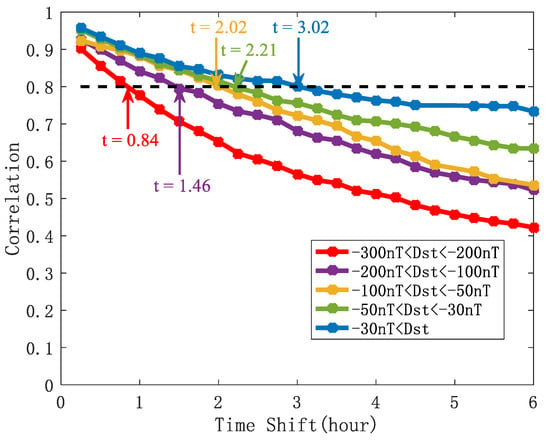
Figure 10.
Variation in ionospheric temporal scale with correlation.
The Gauss–Markov Kalman filter data assimilation algorithm was applied using the IPP measured by the GNSS monitoring stations as the observation and the obtained by the IRI-2020 model serving as the background field, combined with the ionospheric temporal scale results corresponding to different geomagnetic indices. Figure 11, Figure 12 and Figure 13 show the IPP , IRI , and the assimilated at 19:00 UT for the distribution in the United States and the surrounding region during the geomagnetic storms.
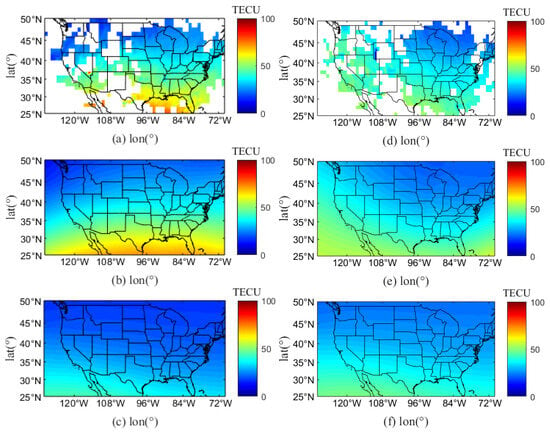
Figure 11.
The comparison results of on 23 and 24 March 2023 at 19:00 (UT); (a,d) the distribution of IPP in the United States and the surrounding region; (b,e) the distribution of assimilated in the United States and the surrounding region; (c,f) the distribution of IRI in the United States and the surrounding region.
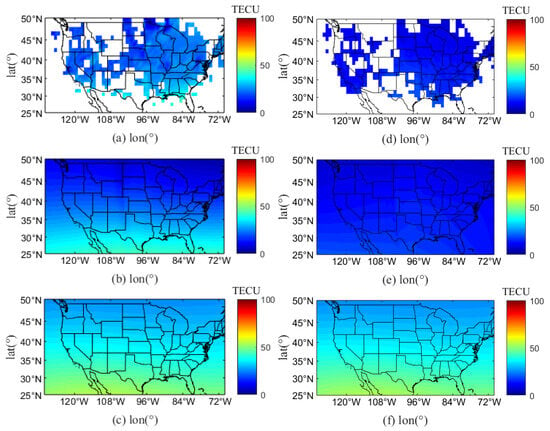
Figure 12.
The comparison results of on 23 and 24 April 2023 at 19:00 (UT); (a,d) the distribution of IPP in the United States and the surrounding region; (b,e) the distribution of assimilated in the United States and the surrounding region; (c,f) the distribution of IRI in the United States and the surrounding region.
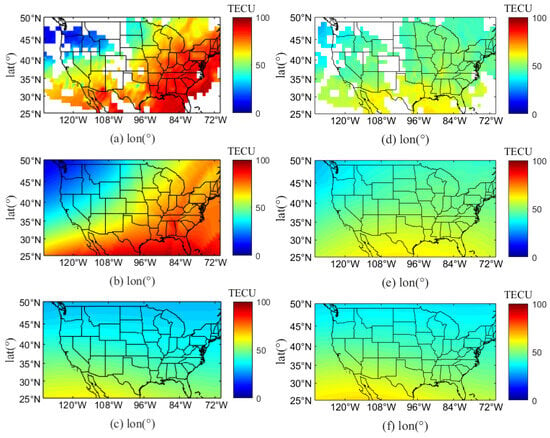
Figure 13.
The comparison results of on 24 and 25 March 2024 at 19:00 (UT). (a,d) The distribution of IPP in the United States and the surrounding region; (b,e) the distribution of assimilated in the United States and the surrounding region; (c,f) the distribution of IRI in the United States and the surrounding region.
As shown in Figure 11, Figure 12 and Figure 13, the Gauss–Markov Kalman filter assimilation algorithm, based on IPP , effectively reconstructs the electron density in the observation area and the surrounding ionosphere compared to the IRI-2020 model. From Figure 3 and Figure 12, the Dst minimum of −213 nT on 24 April 2023 is classified as a very large geomagnetic storm according to the classification of geomagnetic storms in Table 1. The significantly decreased at 19:00 UT (15:00 CET) on 23 and 24 April 2023 under the influence of this geomagnetic storm, which was negative. As shown in Figure 13, the maxima at 19:00 UT on 24 March 2024, were approximately 100 TECU, while the maxima at 19:00 UT on 25 March 2024, were approximately 60 TECU.
4. Discussion
The research on ionospheric data assimilation has evolved significantly over the past decade, with several key studies contributing to the advancement of the field. Aa et al. [38] developed a regional ionospheric TEC mapping technique over China using a 3D variational method to assimilate ground-based GNSS and radio occultation data, demonstrating improved accuracy in ionospheric modeling. Mengist et al. [22] furthered this work by assimilating multiple data types into a regional ionosphere model using a 3D-var algorithm (IDA4D), enhancing the model’s ability to capture ionospheric dynamics during both quiet and storm conditions. Ou et al. [39] introduced a near-real-time global ionospheric data assimilation and forecast system utilizing an ensemble Kalman filter (EnKF) to assimilate global GNSS TEC data, providing timely and accurate ionospheric forecasts. Qiao et al. [33] explored the use of a Gauss–Markov Kalman filter (GMKF) for assimilating ionospheric TEC data, showing significant improvements in modeling accuracy. Most recently, Forootan et al. [40] developed an empirical data assimilation method to merge TEC data with empirical and physical models, enhancing the accuracy of thermospheric neutral density and ionospheric electron content forecasts.
The aforementioned studies have determined ionospheric temporal scale based on empirical values; for example, the ionospheric temporal scale is 1 h during geomagnetic storms and 3 h during quiet conditions. In this study, by analyzing GNSS VTEC during geomagnetic storms, we quantitatively established the correspondence between the ionospheric temporal scale and the Dst index. To generate regional high-precision Map results during geomagnetic storms, three geomagnetic disturbances from 2023 to 2024 were selected. Based on the geomagnetic storm classifications in Table 1, geomagnetic storm classification was strong during 23~24 March 2023 (Dstmin = −163 nT), geomagnetic storm classification was severe during 23~24 April 2023 (Dstmin = −213 nT), and geomagnetic storm classification was strong during 24~25 March 2024 (Dst min = −130 nT), lasting for more than two days. GNSS measurements from the copr, flwe, leba, and gobs stations were selected and compared with GIM to validate the accuracy of the multi-site high-precision estimation. The statistically significant RMSE between GNSS and GIM was 3.22 TECU, as shown in Table 2. Additionally, the average RMSEs for the copr and flwe stations were higher than those of the leba and gobs stations, primarily due to the leba and gobs stations being located in mid-latitude regions, while the copr and flwe stations are near low-latitude areas. The ionospheric TEC variations in low-latitude regions are usually more severe compared to mid-latitude regions, which affects the estimation accuracy.
By analyzing the change in ionospheric temporal scale during geomagnetic storms, it can be seen from Figure 10 that the ionospheric temporal scale decreases with the increase in Dst. The ionospheric temporal scale was 0.83 h at −300 nT < Dst< −200 nT, and 3.02 h at Dst > −30 nT, which is consistent with the generally accepted ionospheric temporal scale of 1 h during geomagnetic storms and 3 h during quiet conditions, but the relationship between ionospheric time correlation and Dst is clear. Using IPP as the observed value, a comparison of (a) to (c) in Figure 11, Figure 12 and Figure 13 shows that the assimilation results of the during the geomagnetic storms had a significantly improved accuracy compared to the IRI-2020 model results. From Figure 12, it is evident that the decreased significantly from 23 to 24 April 2023 under the influence of the geomagnetic storm. Combined with Figure 7, it becomes clear that the decrease in on 24 April 2023 was particularly prominent, characterizing this geomagnetic disturbance as a typical negative-phase storm. Figure 13 illustrates that GNSS fluctuated more drastically at the same time on two consecutive days during the same geomagnetic storm, with the on 24 March 2024, being 66.67% higher than on 25 March 2024.
To further analyze the performance of this method compared to other assimilation methods during geomagnetic storms, Figure 14 compares the Map generated by this method with the Map of GIM, and Figure 15 provides the quantitative analysis results.
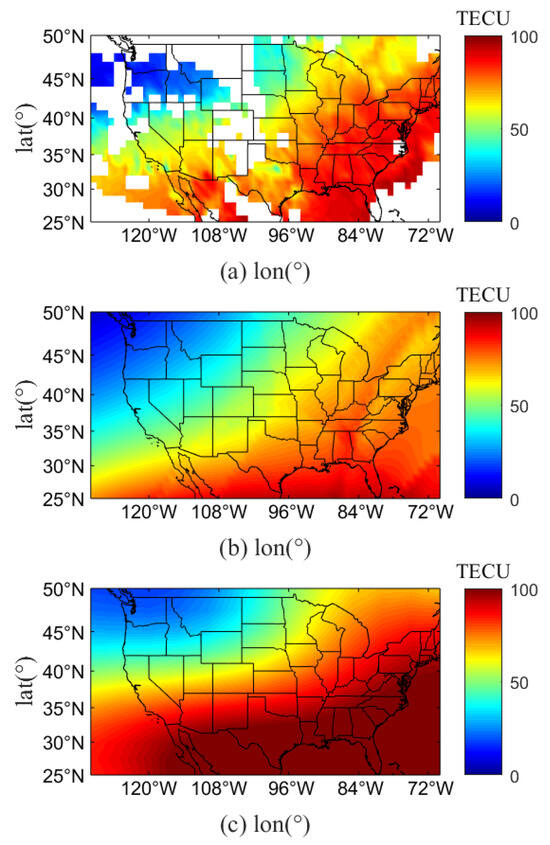
Figure 14.
The comparison results of on 24 March 2024 at 19:00 (UT). (a) The distribution of IPP in the United States and the surrounding region; (b) the distribution of assimilated in the United States and the surrounding region; (c) the distribution of GIM in the United States and the surrounding region.
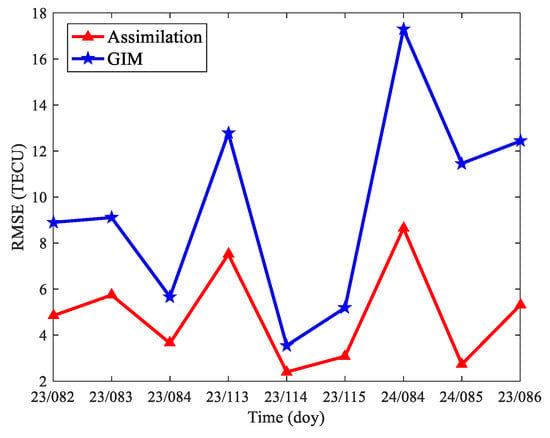
Figure 15.
RMSE between assimilation results and GNSS .
From Figure 13 and Figure 14, it can be seen that both this method and the GIM method can accurately reflect the variations in TEC during magnetic storms. However, this method is closer to GNSS (observations) compared to the GIM results, which exhibit a significant overestimation relative to the observations. Figure 15 shows a quantitative comparison between the results generated by the two methods and GNSS . The average RMSE between our method and GNSS is calculated as 4.88 TECU at 19:00 (UT), whereas the average RMSE between the GIM method and GNSS reaches 9.60 TECU at the same time. These results demonstrate that our method effectively enables the reconstruction of ionospheric TEC within localized regions.
5. Conclusions
In this paper, we constrain when IPP locations are nearby to each other in the multi-site solution. Data from multiple GNSS monitoring stations during geomagnetic storms were selected, and the site–satellite link was solved using the carrier-phase smoothing pseudo-ranging method to obtain high-precision relative . Based on the distribution of the links, we adaptively divided the grid and estimated the hardware delays of both the receivers at the sites and the satellites with high accuracy. The positive response of the ionosphere as a result of the equatorial ionization anomaly and the corresponding low- and mid-latitude effects is seen. The GNSS exhibited strong agreement with the GIM . The multi-site high-precision ionospheric estimation method achieved an RMSE of 3.22 TECU and a correlation coefficient of 0.98 with GIM during the three-day period of geomagnetic storms, verifying the accuracy of this method. From the GNSS VTEC calculation results, the GNSS is mainly distributed in the range of 10 TECU~40 TECU, but the GNSS can also exceed 100 TECU due to the influence of geomagnetic storms.
By summarizing the previous research on ionospheric assimilation, the ionospheric temporal scale is generally, based on experience, 1 h during geomagnetic storms and 3 h during quiet conditions. This article uses high-precision GNSS data to establish a quantitative relationship between the important parameter, the Dst index, which measures the level of geomagnetic storms, and the ionospheric temporal scale. The IPP values determined by the GNSS monitoring stations were used as the observation field data, while the values obtained from the IRI-2020 model served as the background field data. By employing the Gauss–Markov Kalman filter data assimilation algorithm, a regional Map was generated during geomagnetic storms by giving the ionospheric temporal scale corresponding to different storm classifications. The Maps effectively monitored the impact of geomagnetic storms on the and captured changes in the during geomagnetic storms with greater accuracy compared to the IRI-2020 model. To further demonstrate the accuracy of the ionospheric TEC Map constructed by this method, a quantitative comparison was made with the GIM TEC Map at 19:00 (UT). Within the range of 25°N–50°N and 70°W–130°W in the region, the average of RMSE between the TEC Map generated by this method and GNSS VTEC is 4.88 TECU, and the average of RMSE between the GIM TEC Map and GNSS VTEC is 9.60 TEUC. The TEC Map generated by this method is closer to GNSS VTEC compared to the GIM TEC Map. This article selects three typical geomagnetic disturbances in a high-solar-activity years and analyzes the quantitative relationship between the ionospheric temporal scale and Dst index. Further research can be conducted on the GNSS VTEC data of geomagnetic disturbances in different solar cycle years to continuously improve this quantitative relationship.
Author Contributions
Conceptualization, Q.-L.Z., H.-N.W., X.D., B.X., C.Z. and Y.-F.Z.; Methodology, H.-N.W. and M.O.; Experiment, H.-N.W., X.D. and M.O.; Software H.-N.W.; Validation, H.-N.W., M.O. and Y.-F.Z.; Formal Analysis, H.-N.W., B.X. and Y.-F.Z.; Investigation, H.-N.W.; Resources, H.-N.W. and Q.-L.Z.; Data Curation, H.-N.W. and M.O.; Writing—Original Draft Preparation, H.-N.W.; Writing—Review and Editing, H.-N.W., Y.-F.Z., C.Z. and B.X.; Supervision, Y.-F.Z. and C.Z.; Project Administration, X.D.; Funding Acquisition, Y.-F.Z. and Q.-L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fund project: National Key R&D Program of China (Grant No. 2022YFF0503900).
Data Availability Statement
The GIM products were obtained online (https://cddis.nasa.gov/archive/gnss/products/ionex/, accessed on 16 December 2024). The OMNI data was obtained online (https://omniweb.gsfc.nasa.gov, accessed on 6 December 2024). The GNSS data was obtained online (https://geodesy.noaa.gov/corsdata/rinex/, accessed on 16 December 2024).
Acknowledgments
The authors would like to thank the IGS for providing the GIM products. The authors would like to thank the GSFC/SPDF OMNI Web interface for the OMNI data. The authors would also like to thank the National Geodetic Survey (NGS) for providing the GNSS data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jin, S.; Jin, R.; Li, D. GPS detection of ionospheric rayleigh wave and its source following the 2012 Haida Gwaii earthquake. J. Geophys. Res. Space Phys. 2017, 122, 1360–1372. [Google Scholar] [CrossRef]
- Jin, S. Two-mode ionospheric disturbances following the 2005 Northern California offshore earthquake from GPS measurements. J. Geophys. Res. Space Phys. 2018, 123, 8587–8598. [Google Scholar] [CrossRef]
- Goodman, J.M. Operational communication systems and relationships to the ionosphere and space weather. Adv. Space Res. 2005, 36, 2241–2252. [Google Scholar] [CrossRef]
- Ritchie, S.E.; Honary, F. Storm sudden commencement and its effect on high-latitude HF communication links. Space Weather 2009, 7, S06005. [Google Scholar] [CrossRef]
- Ma, G.; Gao, W.; Li, J.; Chen, Y.; Shen, H. Estimation of GPS instrumental biases from small scale network. Adv. Space Res. 2014, 54, 871–882. [Google Scholar] [CrossRef]
- Cai, H.; Wang, Q. Resolving the Regional Ionospheric Grid Model by Applying Kalman Filter. In Proceedings of the China Satellite Navigation Conference (CSNC) 2016, Changsha, China, 18–20 May 2016; Volume III, pp. 425–434. [Google Scholar]
- Cooper, C.; Mitchell, C.N.; Wright, C.J.; Jackson, D.R.; Witvliet, B.A. Measurement of ionospheric total electron content using single-frequency geostationary satellite observations. Radio Sci. 2019, 54, 10–19. [Google Scholar] [CrossRef]
- Wang, H.-N.; Zhu, Q.-L.; Dong, X.; Sheng, D.-S.; Zhi, Y.-F.; Zhou, C.; Xu, B. A Novel Technique for High-Precision Ionospheric VTEC Estimation and Prediction at the Equatorial Ionization Anomaly Region: A Case Study over Haikou Station. Remote Sens. 2023, 15, 3394. [Google Scholar] [CrossRef]
- Chetia, B.; Barman, M.K.; Devi, M.; Barbara, A.K. Study of Physical and Dynamical Processes in the Ionosphere at Equatorial Anomaly Crest Region during Magnetic Storm for High and Low Solar Activity Period. In Geostatistical and Geospatial Approaches for the Characterization of Natural Resources in the Environment, Proceedings of the International Association for Mathematical Geosciences Annual Conferences, New Delhi, India, 17–20 October 2014; Springer Nature: London, UK, 2016; pp. 861–866. [Google Scholar]
- Deng, Y.; Ridley, A.J. The Global Ionosphere-Thermosphere Model and the Nonhydrostatic Processes. In Geophysical Monograph Series; Wiley: Hoboken, NJ, USA, 2014; pp. 85–100. [Google Scholar]
- Kouris, S.S.; Xenos, T.D.; Polimeris, K.V.; Stergiou, D. TEC and foF2 variations: Preliminary results. Ann. Geophys. 2004, 47, 1325–1332. [Google Scholar] [CrossRef]
- Sai Gowtam, V.; Tulasi Ram, S. Ionospheric annual anomaly New insights to the physical mechanisms. J. Geophys. Res. Space Phys. 2017, 122, 8816–8830. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.B.; Le, H.J. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 257–275. [Google Scholar] [CrossRef]
- Gan, Q.; Wang, W.; Yue, J.; Liu, H.; Chang, L.C.; Zhang, S.; Burns, A.; Du, J. Numerical simulation of the 6 day wave effects on the ionosphere: Dynamo modulation. J. Geophys. Res. Space Phys. 2016, 121, 10103–10116. [Google Scholar] [CrossRef]
- Ferdousi, B.; Raeder, J. Signal propagation time from the magnetotail to the ionosphere: OpenGGCM simulation. J. Geophys. Res. Space Phys. 2016, 121, 6549–6561. [Google Scholar] [CrossRef]
- Ridley, A.J.; Deng, Y.; Tóth, G. The global ionosphere–thermosphere model. J. Atmos. Sol.-Terr. Phys. 2006, 68, 839–864. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: Fromionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z.; Yuan, Y.; Li, M.; Huo, X.; Yuan, C. Ionospheric correction using GPS Klobuchar coefficients with an empirical nigh-time delay model. Adv. Space Res. 2018, 63, 886–896. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, J.; Wang, Z.; An, J.; Ou, J.; Liu, S.; Wang, N. Assessment of spatial and temporal TEC variations derived from ionospheric models over the polar regions. J. Geod. 2019, 93, 455–471. [Google Scholar] [CrossRef]
- Chartier, A.T.; Matsuo, T.; Anderson, J.L.; Collins, N.; Hoar, T.J.; Lu, G.; Mitchell, C.N.; Coster, A.J.; Paxton, L.J.; Bust, G.S. Ionospheric data assimilation and forecasting during storms. J. Geophys. Res. Space Phys. 2016, 121, 764–778. [Google Scholar] [CrossRef]
- Gardner, L.C.; Schunk, R.W.; Scherliess, L.; Eccles, V.; Basu, S.; Valladeres, C. Modeling the midlatitude ionosphere storm-enhanced density distribution with a data assimilation model. Space Weather 2018, 16, 1539–1548. [Google Scholar] [CrossRef]
- Mengist, C.K.; Ssessanga, N.; Jeong, S.-H.; Kim, J.-.H.; Kim, Y.H.; Kwak, Y.-.S. Assimilation of multiple data types to a regional ionosphere model with a 3D-Var algorithm (IDA4D). Space Weather 2019, 17, 1018–1039. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, S.; Yang, D.; Wu, X. Assimilating GNSS TEC with an LETKF over Yunnan, China. Remote Sens. 2023, 15, 3547. [Google Scholar] [CrossRef]
- Wu, M.J.; Guo, P.; Xu, T.L.; Fu, N.F.; Xu, X.S.; Jin, H.L.; Hu, X.G. Data assimilation of plasmasphere and upper ionosphere using COSMIC/GPS slant TEC measurements. Radio Sci. 2015, 50, 1131–1140. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, X. A multigrid nonlinear least squares four-dimensional Variational data assimilation scheme the with Advanced Research Weather Research and Forecasting Model. J. Geophys. Res. Atmos. 2018, 123, 5116–5129. [Google Scholar] [CrossRef]
- He, J.; Yue, X.; Hu, L.; Wang, J.; Li, M.; Ning, B.; Wan, W.; Xu, J. Observing system impact on ionospheric specification over China using EnKF assimilation. Space Weather 2020, 18, e2020SW002527. [Google Scholar] [CrossRef]
- Lin, X.; Wang, H.; Zhang, Q.; Yao, C.; Chen, C.; Cheng, L.; Li, Z. A Spatiotemporal Network Model for Global Ionospheric TEC Forecasting. Remote Sens. 2022, 14, 1717. [Google Scholar] [CrossRef]
- Kumar, S.; Veenadhari, B.; Ram, S.T.; Su, S.Y.; Kikuchi, T. Possible relationship between the equatorial electrojet (EEJ) and daytime vertical E×B drift velocities in F region from ROCSAT observations. Adv. Space Res. 2016, 58, 1168–1176. [Google Scholar] [CrossRef]
- Mungufeni, P.; Habarulema, J.B.; Migoya-Orué, Y.; Jurua, E. Statistical analysis of the correlation between the equatorial electrojet and the occurrence of the equatorial ionisation anomaly over the East African sector. Ann. Geophys. 2018, 36, 841–853. [Google Scholar] [CrossRef]
- Loewe, C.A.; Prölls, G.W. Classification and mean behavior of magnetic storms. J. Geophys. Res. 1997, 102, 14209–14213. [Google Scholar] [CrossRef]
- Ping, J.; Kono, Y.; Matsumoto, K.; Otsuka, Y.; Saito, A.; Shum, C.; Heki, K.; Kawano, N. Regional ionosphere map over Japanese islands. Earth Planets Space 2002, 54, 13–16. [Google Scholar] [CrossRef]
- Otsuka, Y.; Ogawa, T.; Saito, A.; Tsugawa, T.; Fukao, S.; Miyazaki, S. A new technique for mapping of total electron content using GPS network in Japan. Earth Planets Space 2002, 54, 63–70. [Google Scholar] [CrossRef]
- Qiao, J.; Liu, Y.; Fan, Z.; Tang, Q.; Li, X.; Zhang, F.; Song, Y.; He, F.; Zhou, C.; Qing, H.; et al. Ionospheric TEC data assimilation based on Gauss–Markov Kalman filter. Adv. Space Res. 2021, 68, 4189–4204. [Google Scholar] [CrossRef]
- Ou, M.; Fan, D.; Wang, C.; He, L. A simulation study of the Argo program-enhanced global ionospheric modeling. Adv. Space Res. 2024, 73, 1865–1874. [Google Scholar] [CrossRef]
- Aa, E.; Liu, S.; Huang, W.; Shi, L.; Gong, J.; Chen, Y.; Shen, H.; Li, J. Regional 3-D ionospheric electron density specification on the basis of data assimilation of ground-based GNSS and radio occultation data. Space Weather 2016, 14, 433–448. [Google Scholar] [CrossRef]
- Pancheva, D.; Mukhtarov, P.; Bojilova, R. Response to geomagnetic storm on 23–24 March 2023 long-lasting longitudinal variations of the global ionospheric TEC. Adv. Space Res. 2024, 73, 6006–6028. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H.; Oikonomou, C. Ionospheric response of the March 2023 geomagnetic storm over European latitudes. Adv. Space Res. 2024, 73, 6029–6040. [Google Scholar] [CrossRef]
- Aa, E.; Huang, W.; Yu, S.; Liu, S.; Shi, L.; Gong, J.; Chen, Y.; Shen, H. A regional ionospheric TEC mapping technique over China and adjacent areas on the basis of data assimilation. J. Geophys. Res.-Space Phys. 2015, 120, 5049–5061. [Google Scholar] [CrossRef]
- Ou, M.; Chen, L.; Xu, N.; Zhen, W.; Chen, L. A near real-time global ionospheric data assimilation and forecast system. In Proceedings of the 2021 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Zhuhai, China, 1–4 December 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Forootan, E.; Kosary, M.; Farzaneh, S.; Schumacher, M. Empirical Data Assimilation for Merging Total Electron Content Data with Empirical and Physical Models. Surv. Geophys. 2023, 44, 2011–2041. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).