Impact of Parameters and Tree Stand Features on Accuracy of Watershed-Based Individual Tree Crown Detection Method Using ALS Data in Coniferous Forests from North-Eastern Poland
Abstract
1. Introduction
2. Materials and Methods
2.1. ALS Materials and Field Data Inventory
2.1.1. Study Area and Sample Plots Data Inventory
2.1.2. Airborne Laser Scanning Point Clouds
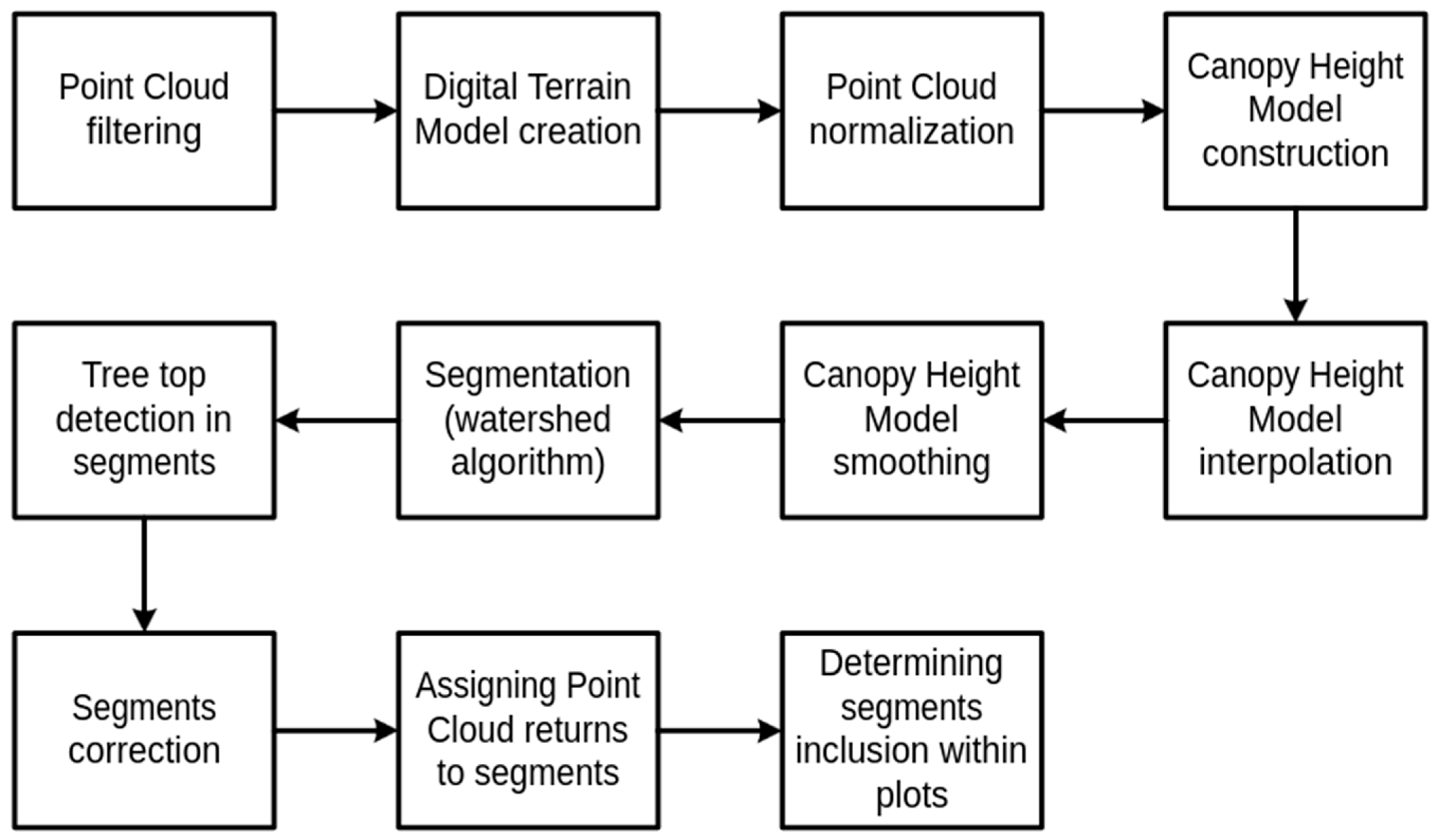
2.2. Individual Tree Crown Detection Algorithm and Parameter Fitting Benchmark
- Point Cloud Filtering. The raw point cloud is filtered to remove points of noise class and irrelevant points with a Z coordinate that is too large.
- Digital Terrain Model (DTM) Creation. A DTM raster is generated to represent the bare ground surface by isolating returns of ground class from the point cloud. There are various algorithms to create a DTM, but we used the TIN algorithm, which is a spatial interpolation based on a Delaunay triangulation. This model serves as a reference for tree height calculations and assists in the normalization of the canopy.
- Point Cloud Normalization. The point cloud is normalized by subtracting the DTM height from each point, resulting in a height-above-ground metric. This normalization step transforms the data so that each point’s height represents its distance from the ground, not from sea level, which is essential for accurately measuring tree heights.
- Canopy Height Model (CHM) Construction. The CHM raster is created by using the normalized point cloud to identify the highest points within the canopy at each pixel location. Points lower than 5 m above the ground are omitted due to the irrelevance of small trees and bushes. The size of the pixel is one of the parameters of the described method.
- CHM Raster Interpolation. The CHM is interpolated into a continuous raster format to fill gaps (empty pixels) resulting from insufficient scanning density. We used our proprietary method presented in [10]. It fills missing pixels inside crowns without extending their size. We repeat the procedure of filling the empty pixels that have more than four non-empty pixels as long as no more pixels can be further filled.
- CHM Raster Smoothing. Gaussian smoothing is applied to the CHM raster to reduce noise and small irregularities that could interfere with watershed segmentation. This step simplifies the canopy structure, making it easier to delineate individual tree crowns. We parameterize the smoothing with the smoothing window (mask) size and the standard deviation of the Gaussian distribution used as smoothing mask.
- Segmentation Using the Watershed Algorithm. The watershed algorithm [9] is applied to the smoothed CHM raster to segment individual tree crowns. This algorithm treats the CHM as a topographic surface, dividing the canopy into distinct regions that correspond to individual crowns based on height variations.
- Tree Top Detection in Segments. Within each tree crown segment, treetops are detected by identifying the highest point. Treetop detection is critical for measuring tree height.
- Correction by Merging Trees of a Crown Segment that is Too Small. Detected segments that are too small or represent isolated points are removed or merged with nearby larger tree crown segments. A particular threshold function of height is used to ensure the minimal tree crown size.
- Assigning Point Cloud Returns to Tree Crown Segments. All the relevant points in the point cloud are assigned to their respective tree segments based on spatial alignment with the segmented crowns.
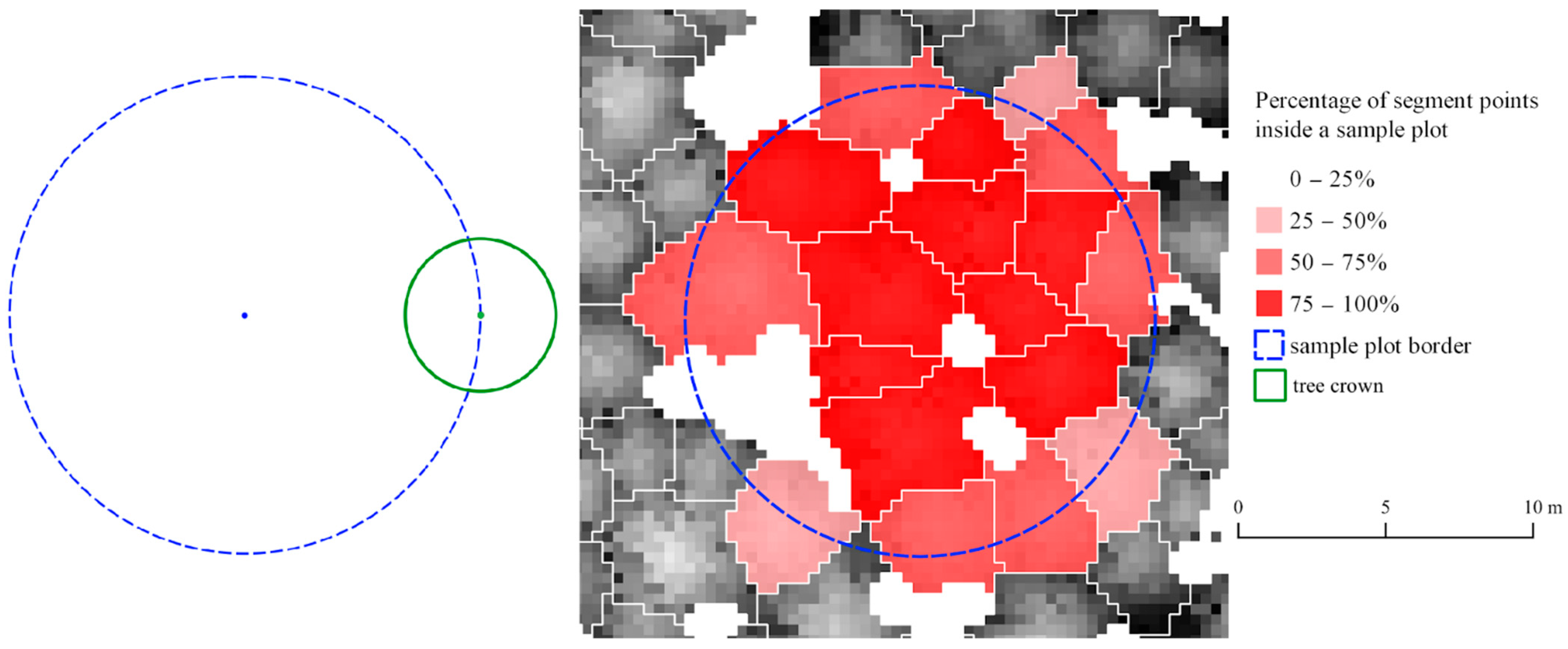
- Determining Segments Inclusion within the analyzed area. For each segment, it is assessed whether the segment belongs to a defined area under consideration based on the assigned points from the point cloud to the tree crown segment. The tree crown is considered to lay in the plot’s area when the percentage of points falling into the SP exceeds the assumed threshold, which can be parameterized.
2.3. Bayesian Networks
2.4. Strength of Influence Metrics
2.4.1. Euclidean Distance
2.4.2. Hellinger Distance
2.4.3. Normalized J-Divergence
2.5. Dataset of the ITCD Results
2.6. Utilizing a BN Model for Parameters Recommendation
3. Results
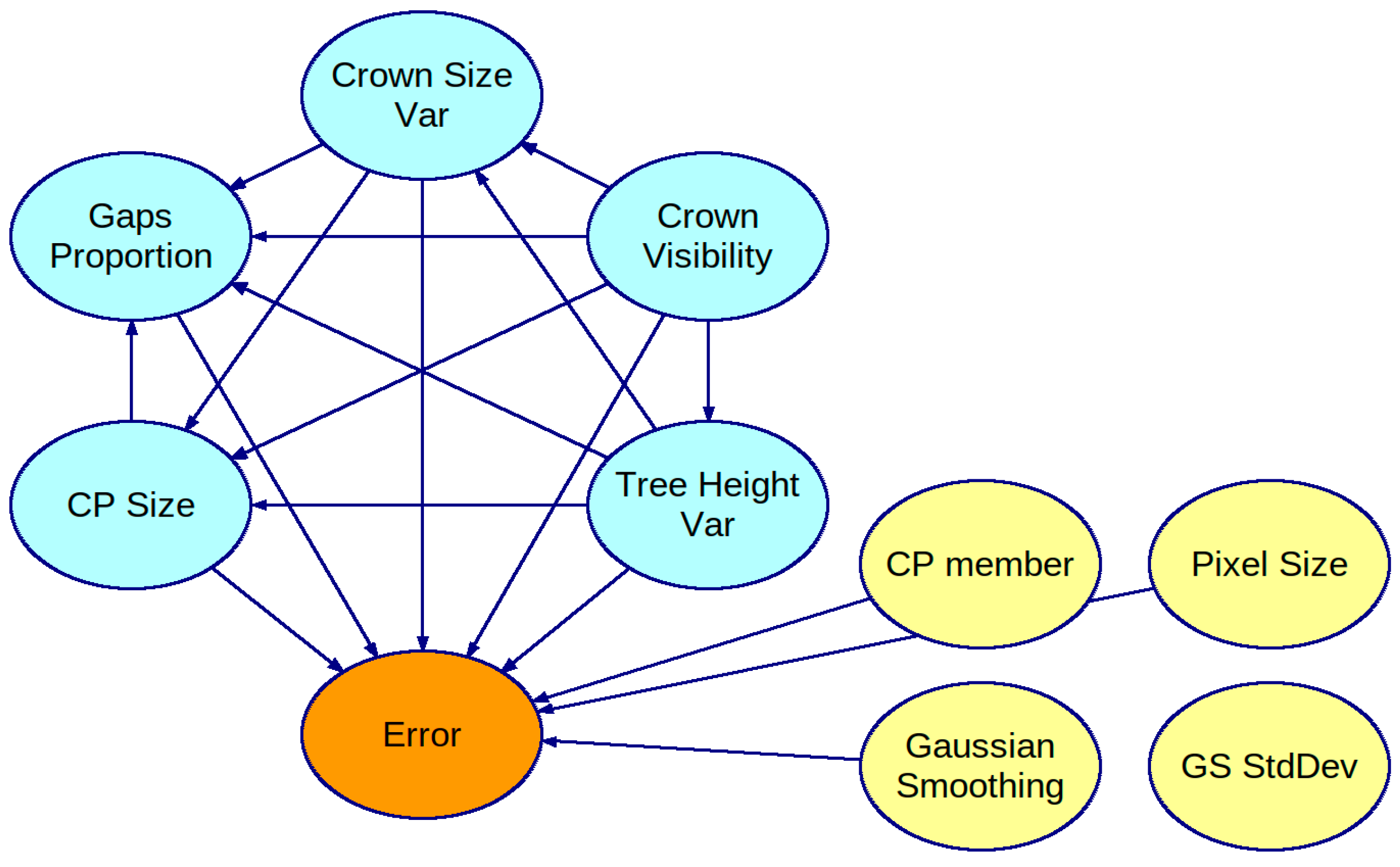
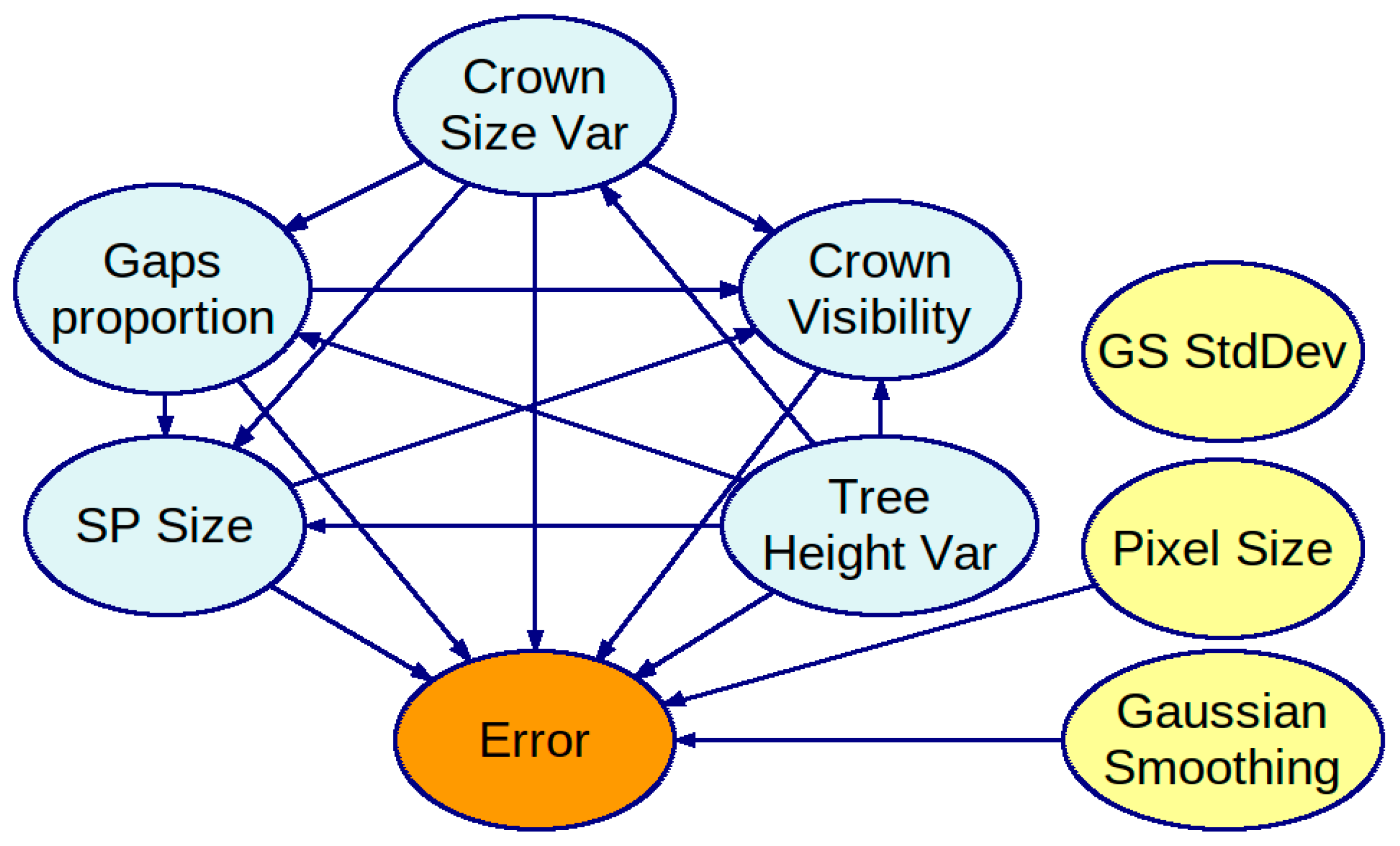
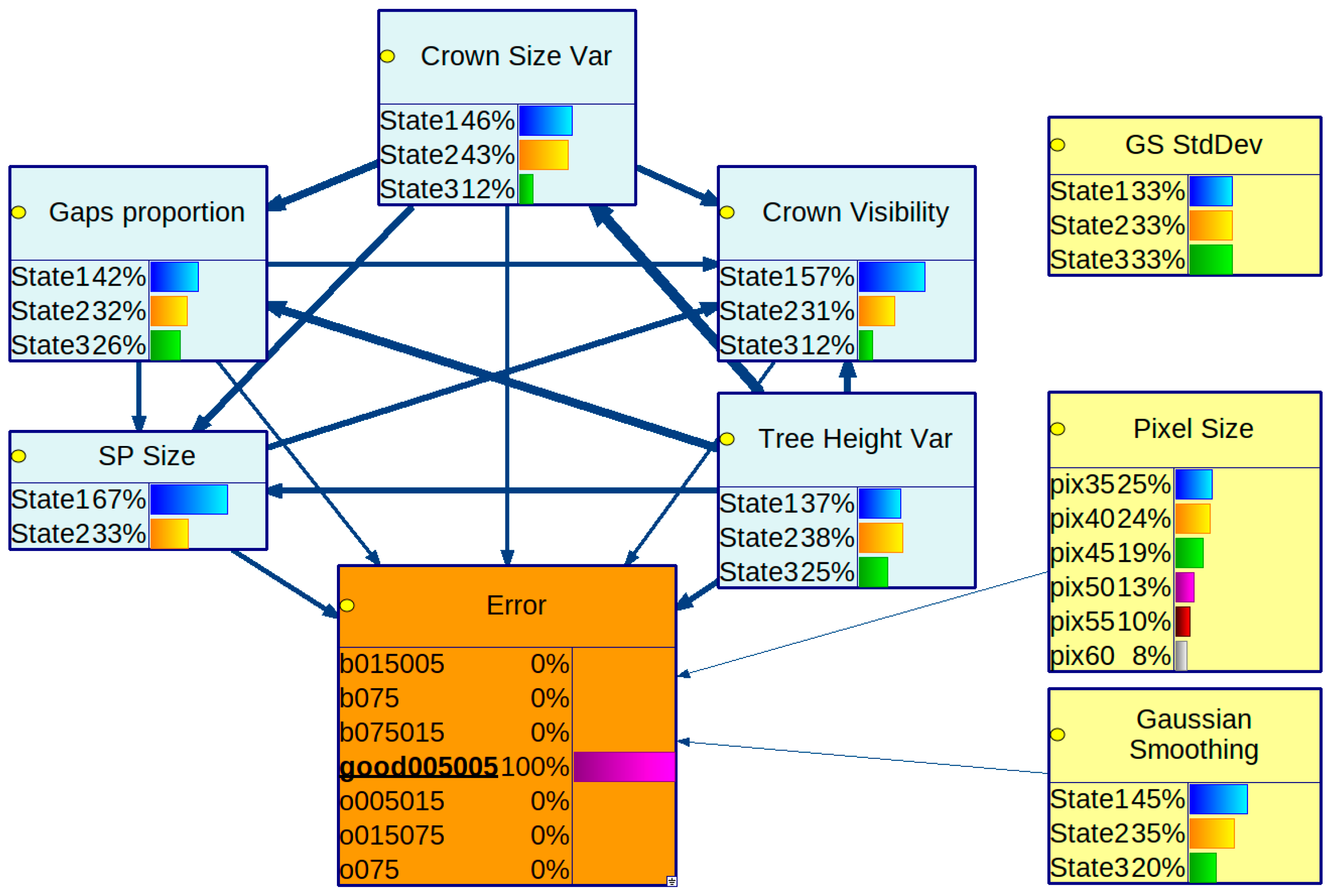
3.1. Obtained Bayesian Networks
3.2. Strength of Influence
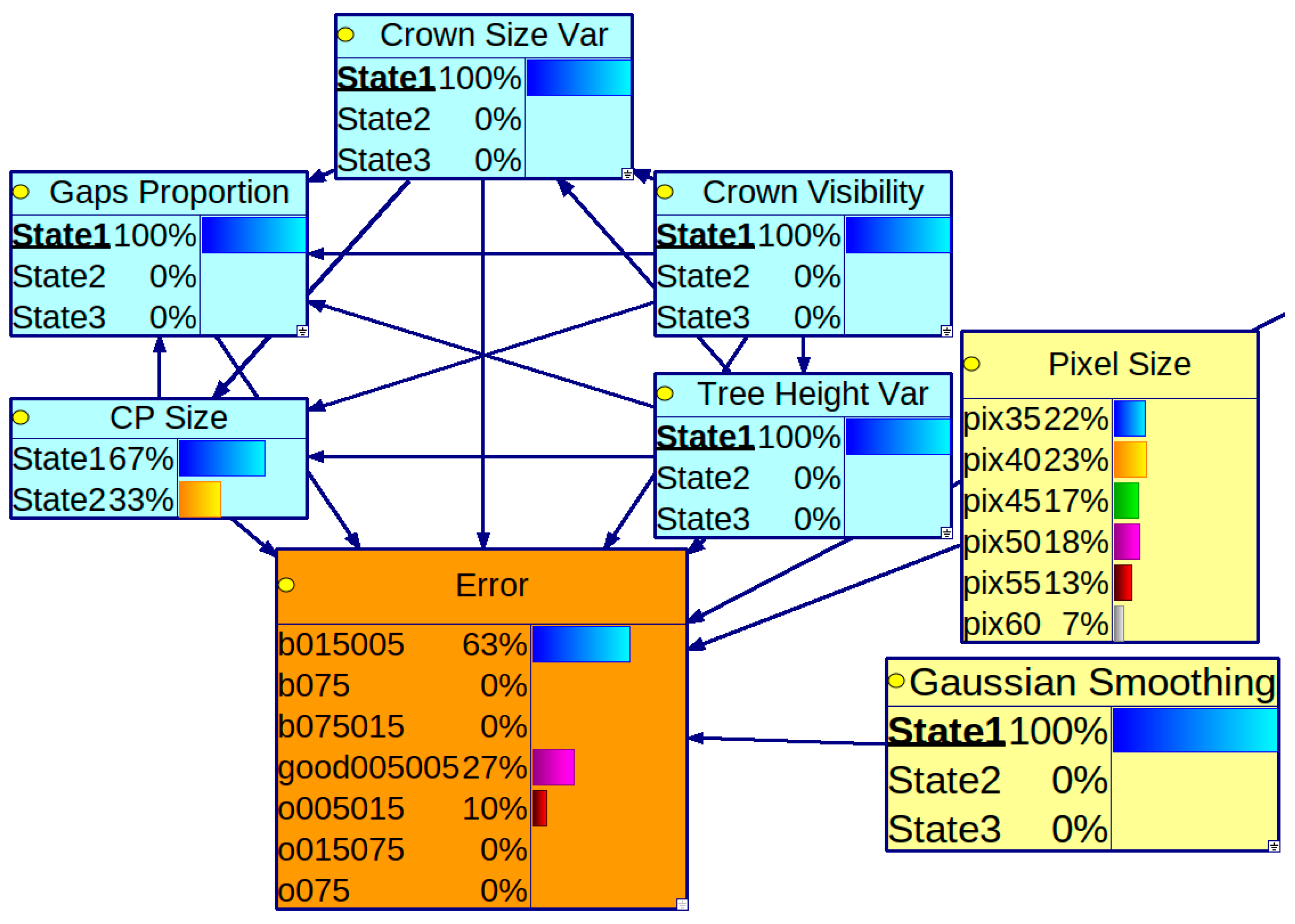
3.3. Conditional Probability Distribution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panagiotidis, D.; Abdollahnejad, A.; Slavík, M. Assessment of Stem Volume on Plots Using Terrestrial Laser Scanner: A Precision Forestry Application. Sensors 2021, 21, 301. [Google Scholar] [CrossRef] [PubMed]
- Moskal, L.M.; Erdody, T.; Kato, A.; Richardson, J.; Zheng, G.; Briggs, D. Lidar applications in precision forestry. In Proceedings of the Silvilaser 2009, College Station, TX, USA, 14–16 October 2009; pp. 154–163. [Google Scholar]
- Kovácsová, P.; Antalová, M. Precision forestry–definition and technologies. Šumarski List 2010, 134, 603–610. [Google Scholar]
- Dyck, B. Precision forestry—The path to increased profitability. In Proceedings of the Second International Precision Forestry Symposium, University of Washington, Seattle, WA, USA, 15–17 June 2003; Volume 2003, pp. 3–8. [Google Scholar]
- Fardusi, M.J.; Chianucci, F.; Barbati, A. Concept to practice of geospatial-information tools to assist forest management and planning under precision forestry framework: A review. Ann. Silvic. Res. 2017, 41, 3–14. [Google Scholar]
- Instytut Badawczy Leśnictwa (Forest Research Institute). Comprehensive Monitoring of Stand Dynamics in Białowieza Forest Supported with Remote Sensing Techniques (ForBioSensing). 2014. Available online: http://www.forbiosensing.pl/about-project (accessed on 1 November 2024).
- Goodbody, T.R.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest inventorypurposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef]
- Koch, B.; Kattenborn, T.; Straub, C.; Vauhkonen, J. Segmentation of Forest to Tree Objects BT—Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies. In Forestry Applications of Airborne Laser Scanning. Managing Forest Ecosystems; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 89–112. ISBN 978-94-017-8663-8. [Google Scholar]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Kolendo, Ł.; Kozniewski, M.; Ksepko, M.; Chmur, S.; Neroj, B. Parameterization of the Individual Tree Detection Method Using Large Dataset from Ground Sample Plots and Airborne Laser Scanning for Stands Inventory in Coniferous Forest. Remote Sens. 2021, 13, 2753. [Google Scholar] [CrossRef]
- Xu, X.; Iuricich, F.; De Floriani, L. A topology-based approach to individual tree segmentation from airborne LiDAR data. GeoInformatica 2023, 27, 759–788. [Google Scholar] [CrossRef]
- Yu, K.; Hao, Z.; Post, C.J.; Mikhailova, E.A.; Lin, L.; Zhao, G.; Tian, S.; Liu, J. Comparison of Classical Methods and Mask R-CNN for Automatic Tree Detection and Mapping Using UAV Imagery. Remote Sens. 2022, 14, 295. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using Lidar and Multispectral Data Fusion with Local Filtering and Variable Window Size for Estimating Tree Height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, D.; Fu, S.; Mathiopoulos, P.T.; Sui, M.; Na, J.; Peethambaran, J. Segmentation of Individual Tree Points by Combining Marker-Controlled Watershed Segmentation and Spectral Clustering Optimization. Remote Sens. 2024, 16, 610. [Google Scholar] [CrossRef]
- Li, Y.; Xie, D.; Wang, Y.; Jin, S.; Zhou, K.; Zhang, Z.; Li, W.; Zhang, W.; Mu, X.; Yan, G. Individual tree segmentation of airborne and UAV LiDAR point clouds based on the watershed and optimized connection center evolution clustering. Ecol. Evol. 2023, 13, e10297. [Google Scholar] [CrossRef] [PubMed]
- Ma, K.; Chen, Z.; Fu, L.; Tian, W.; Jiang, F.; Yi, J.; Du, Z.; Sun, H. Performance and Sensitivity of Individual Tree Segmentation Methods for UAV-LiDAR in Multiple Forest Types. Remote Sens. 2022, 14, 298. [Google Scholar] [CrossRef]
- Yang, Q.; Su, Y.; Jin, S.; Kelly, M.; Hu, T.; Ma, Q.; Li, Y.; Song, S.; Zhang, J.; Xu, G.; et al. The Influence of Vegetation Characteristics on Individual Tree Segmentation Methods with Airborne LiDAR Data. Remote Sens. 2019, 11, 2880. [Google Scholar] [CrossRef]
- Nemmaoui, A.; Aguilar, F.J.; Aguilar, M.A. Benchmarking of Individual Tree Segmentation Methods in Mediterranean Forest Based on Point Clouds from Unmanned Aerial Vehicle Imagery and Low-Density Airborne Laser Scanning. Remote Sens. 2024, 16, 3974. [Google Scholar] [CrossRef]
- Jensen, F.V.; Nielsen, T.D. Bayesian Networks and Decision Graphs; Springer: New York, NY, USA, 2007. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Dyrekcja Generalna Lasów Państwowych (General Directorate of the State Forests). Raport o Stanie Lasów W Polsce 2019 [Raport on the State of Forests in Poland 2019]; Centrum Informacyjne Lasów Państwowych: Warsaw, Poland, 2020. (In Polish) [Google Scholar]
- Kolendo, Ł.; Ksepko, M. Selection of optimal tree top detection parameters in a context of effective forest management. Ekon. Sr. 2019, 68, 67–85. [Google Scholar]
- Myszkowski, M.; Ksepko, M.; Gajko, K. Detekcja liczby drzew na podstawie danych lotniczego skanowania laserowego. Arch. Inst. Inżynierii Lądowej 2009, 6, 63–72. [Google Scholar]
- American Society for Photogrammetry and Remote Sensing. LAS Specification. Version 1.2. 2008. Available online: https://www.asprs.org/wp-content/uploads/2010/12/asprs_las_format_v12.pdf (accessed on 1 November 2024).
- Stereńczak, K.; Kraszewski, B.; Mielcarek, M.; Piasecka, Ż.; Lisiewicz, M.; Heurich, M. Mapping individual trees with airborne laser scanning data in an European lowland forest using a self-calibration algorithm. Int. J. Appl. Earth Obs. Geoinf. 2020, 93, 102191. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation: Chicago, IL, USA, 2009. [Google Scholar]
- Roussel, J.R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Véga, C.; Renaud, J.P.; Durrieu, S.; Bouvier, M. On the interest of penetration depth, canopy area and volume metrics to improve Lidar-based models of forest parameters. Remote Sens. Environ. 2016, 175, 32–42. [Google Scholar] [CrossRef]
- Druzdel, M.J.; Van Der Gaag, L.C. Building probabilistic networks: “Where do the numbers come from?”. IEEE Trans. Knowl. Data Eng. 2000, 12, 481–486. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Spirtes, P.; Glymour, C. An algorithm for fast recovery of sparse causal graphs. Soc. Sci. Comput. Rev. 1991, 9, 62–72. [Google Scholar] [CrossRef]
- Koiter, J.R. Visualizing Inference in Bayesian Networks. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Ratnapinda, P.; Druzdzel, M.J. An empirical evaluation of costs and benefits of simplifying Bayesian networks by removing weak arcs. In Proceedings of the 27th International Florida Artificial Intelligence Research Society Conference, FLAIRS 2014, Pensacola Beach, FL, USA, 21 May 2014; pp. 508–511. [Google Scholar]
- Oniśko, A.; Druzdzel, M.J. Impact of bayesian network model structure on the accuracy of medical diagnostic systems. In Artificial Intelligence and Soft Computing, Proceedings of the 13th International Conference, ICAISC 2014, Zakopane, Poland, 1–5 June 2014; Proceedings, Part II 13; Springer International Publishing: Cham, Switzerland, 2014; pp. 167–178. [Google Scholar]
- Hellinger, E. Die Orthogonalinvarianten Quadratischer Formen Von Unendlich Vielen Variablen. Ph.D. Thesis, University of Gottingen, Gottingen, Germany, 1907. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Johnson, D.H.; Sinanovic, S. Symmetrizing the kullback-leibler distance. IEEE Trans. Inf. Theory 2001, 1, 1–10. [Google Scholar]
- Knapp, N.; Huth, A.; Fischer, R. Tree Crowns Cause Border Effects in Area-Based Biomass Estimations from Remote Sensing. Remote Sens. 2021, 13, 1592. [Google Scholar] [CrossRef]
- Pascual, A. Using tree detection based on airborne laser scanning to improve forest inventory considering edge effects and the co-registration factor. Remote Sens. 2019, 11, 2675. [Google Scholar] [CrossRef]
- Packalen, P.; Strunk, J.L.; Pitkänen, J.A.; Temesgen, H.; Maltamo, M. Edge-tree correction for predicting forest inventory attributes using area-based approach with airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1274–1280. [Google Scholar] [CrossRef]
- Parkitna, K.; Krok, G.; Miścicki, S.; Ukalski, K.; Lisańczuk, M.; Mitelsztedt, K.; Magnussen, S.; Markiewicz, A.; Stereńczak, K. Modelling growing stock volume of forest stands with various ALS area-based approaches. For. Int. J. For. Res. 2021, 94, 630–650. [Google Scholar] [CrossRef]
- Stereńczak, K.; Miścicki, S. Crown delineation influence on standing volume calculations in protected area. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 441–445. [Google Scholar] [CrossRef]
- Lisiewicz, M.; Kamińska, A.; Kraszewski, B.; Stereńczak, K. Correcting the Results of CHM-Based Individual Tree Detection Algorithms to Improve Their Accuracy and Reliability. Remote Sens. 2022, 14, 1822. [Google Scholar] [CrossRef]


| E [%] | D [m] | C [m2] | B [%] | A [m] | Category |
|---|---|---|---|---|---|
| 0–10 [46] | 0–2 [35] | 0–100 [48] | 0–20 [50] | ≤12.62 [75] | 1 |
| 10–20 [45] | 2–5 [35] | 100–250 [43] | 20–30 [34] | >12.62 [37] | 2 |
| >20 [21] | >5 [42] | >250 [21] | 30–100 [28] | - | 3 |
| Airborne Laser Scanning Features | Value |
|---|---|
| Airing date | 30 August 2017 |
| Scanning density [pts/m2] | 6.7 |
| Point cloud density [pts/m2] | 19.64 |
| Density of single point returns [pts/m2] | 4.06 |
| Flight Altitude (AGL) [m] | 520 |
| Flight Altitude (MSL) [m] | 687–713 |
| Scanning coverage | 25% |
| Number of strips | 19 |
| Length of strips [km] | 186 |
| Data coverage area [km2] | 70 |
| Scanning angle (FOV) | 60° |
| Type | Number of Possible Values | Description | Variable Name |
|---|---|---|---|
| Sample plot feature | 2 | Radius size of the circular plot (A) 1 | SP Size |
| Tree stands feature | 3 | Proportion of gaps in the circular pot (B) 1 | Gaps proportion |
| Tree stands feature | 3 | Variance of the area of the rectangular projection of the crown in the circular plot (C) 1 | Crown Size Var |
| Tree stands feature | 3 | Variance of the height of the trees in the sample plot (D) 1 | Tree Height Var |
| Tree stands feature | 3 | Proportion of the number of trees with apex partial visibility to full visibility (E) 1 | Crown Visibility |
| Optimization parameter | 14 | Threshold describing minimal proportion of the returns to be intersected with the circular plot to count the tree segment in as detected in the tree count | SP member |
| ITCD parameter | 6 | Size of pixel of canopy height model | Pixel Size |
| ITCD parameter | 3 | Radius of window (mask) of Gaussian smoothing applied to CHM before running ITCD algorithm in pixels | Gaussian Smoothing |
| ITCD parameter | 3 | Standard deviation of Gaussian function used as mask in smoothing applied to CHM before running ITCD algorithm in pixels | GS StdDev |
| Target information | 7 | Percentage error of ITCD method | Error |
| Maximum | Average | Influencing Variable |
|---|---|---|
| 0.804846 | 0.250066 | Tree Height Var |
| 0.83973 | 0.236435 | Crown Size Var |
| 0.75 | 0.207426 | SP Size |
| 0.827431 | 0.198224 | Crown Visibility |
| 0.847462 | 0.164218 | Gaps Proportion |
| 0.9 | 0.0631768 | Pixel Size |
| 0.8 | 0.0552013 | Gaussian Smoothing |
| Maximum | Average | Influencing Variable |
|---|---|---|
| 0.75923 | 0.268126 | Tree Height Var |
| 0.79081 | 0.253597 | Crown Size Var |
| 0.78625 | 0.220884 | SP Size |
| 0.781293 | 0.212671 | Crown Visibility |
| 0.801939 | 0.179083 | Gaps Proportion |
| 0.83666 | 0.068304 | Pixel Size |
| 0.777412 | 0.0589087 | Gaussian Smoothing |
| Maximum | Average | Influencing Variable |
|---|---|---|
| 0.798391 | 0.238439 | Tree Height Var |
| 0.841084 | 0.223915 | Crown Size Var |
| 0.846235 | 0.19196 | SP Size |
| 0.825058 | 0.186933 | Crown Visibility |
| 0.841664 | 0.15368 | Gaps Proportion |
| 0.871302 | 0.0606175 | Pixel Size |
| 0.821108 | 0.0490628 | Gaussian Smoothing |
| Pixel Size = 0.45 | Pixel Size = 0.4 | |||||
|---|---|---|---|---|---|---|
| SP Size State2 | SP Size State1 | SP Size Not Set | SP Size State2 | SP Size State1 | SP Size Not Set | Error |
| 1.92% | 1.93% | 1.92% | 1.92% | 1.93% | 1.92% | ≤−0.75 |
| 46.24% | 47.69% | 47.21% | 33.25% | 34.89% | 34.35% | (−0.75, −0.15] |
| 25.06% | 20.39% | 21.94% | 31.61% | 19.10% | 23.23% | (−0.15, −0.05] |
| 20.19% | 6.61% | 11.10% | 22.48% | 14.53% | 17.15% | (−0.05, 0.05] |
| 2.75% | 14.32% | 10.50% | 6.07% | 16.42% | 13.00% | (0.05, 0.15] |
| 1.92% | 7.13% | 5.41% | 2.75% | 11.21% | 8.42% | (0.15, 0.75] |
| 1.92% | 1.93% | 1.92% | 1.92% | 1.93% | 1.92% | >0.75 |
| Pixel Size = pix45 | Pixel Size = pix40 | ||
|---|---|---|---|
| Crown Visibility = State3 | Crown Visibility = State2 | Crown Visibility = State1 | Error |
| 2.54% | 2.23% | 1.34% | <=−0.75 |
| 61.23% | 38.99% | 16.92% | (−0.75, −0.15] |
| 17.71% | 24.09% | 31.22% | (−0.15, −0.05] |
| 2.54% | 12.39% | 22.80% | (−0.05, 0.05] |
| 10.90% | 15.15% | 15.05% | (0.05, 0.15] |
| 2.54% | 4.91% | 11.33% | (0.15, 0.75] |
| 2.54% | 2.23% | 1.34% | >0.75 |
| SP Size | |||
|---|---|---|---|
| State2 | State1 | Not Set | Pixel Size |
| 20.69% | 23.33% | 22.47% | pix35 |
| 20.69% | 24.47% | 23.24% | pix40 |
| 20.69% | 15.33% | 17.08% | pix45 |
| 18.50% | 17.62% | 17.90% | pix50 |
| 14.11% | 11.91% | 12.63% | pix55 |
| 5.33% | 7.34% | 6.68% | pix60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozniewski, M.; Kolendo, Ł.; Chmur, S.; Ksepko, M. Impact of Parameters and Tree Stand Features on Accuracy of Watershed-Based Individual Tree Crown Detection Method Using ALS Data in Coniferous Forests from North-Eastern Poland. Remote Sens. 2025, 17, 575. https://doi.org/10.3390/rs17040575
Kozniewski M, Kolendo Ł, Chmur S, Ksepko M. Impact of Parameters and Tree Stand Features on Accuracy of Watershed-Based Individual Tree Crown Detection Method Using ALS Data in Coniferous Forests from North-Eastern Poland. Remote Sensing. 2025; 17(4):575. https://doi.org/10.3390/rs17040575
Chicago/Turabian StyleKozniewski, Marcin, Łukasz Kolendo, Szymon Chmur, and Marek Ksepko. 2025. "Impact of Parameters and Tree Stand Features on Accuracy of Watershed-Based Individual Tree Crown Detection Method Using ALS Data in Coniferous Forests from North-Eastern Poland" Remote Sensing 17, no. 4: 575. https://doi.org/10.3390/rs17040575
APA StyleKozniewski, M., Kolendo, Ł., Chmur, S., & Ksepko, M. (2025). Impact of Parameters and Tree Stand Features on Accuracy of Watershed-Based Individual Tree Crown Detection Method Using ALS Data in Coniferous Forests from North-Eastern Poland. Remote Sensing, 17(4), 575. https://doi.org/10.3390/rs17040575







