Highlights
- This review systematically summarizes and compares both classical and AI-based satellite clock bias prediction models, providing a comprehensive reference for model selection in real-time high-precision GNSS applications.
- We propose generalized modeling frameworks for classical and AI-driven approaches and analyze error sources from systematic, data, and applicability perspectives to enhance prediction robustness.
- This review identifies that AI models (e.g., LSTM, Transformer) outperform in complex nonlinear scenarios, whereas classical models (e.g., polynomial, Kalman) excel under short-term or stable conditions.
- We outline promising research directions including multi-source data fusion, integration of short- and long-term prediction, and enhanced model generalizability to advance next-generation GNSS timing services.
Abstract
As foundational infrastructure for spatiotemporal information, the Global Navigation Satellite System (GNSS) delivers high-precision positioning, navigation, and timing (PNT) services worldwide. However, satellite atomic clock drift causes satellite clock bias, degrading PNT service quality. Compared to post-processed clock bias products and real-time estimation, satellite clock bias prediction offers a key advantage: it provides high-precision real-time clock bias even in scenarios with limited real-time data or poor communication. Through analysis and summarization of error sources in prediction models, this paper proposed generalized modeling frameworks for both classical and AI-based approaches. We reviewed current research on classical mathematical models—including polynomial, grey, Kalman filter, and time series models—and AI-based models such as machine learning (ML), multilayer perceptron (MLP), recurrent neural networks (RNN), and Transformer architectures. Technical characteristics, applicability, and limitations of each model were discussed. While AI-based models demonstrate superior flexibility and adaptability in complex scenarios compared to classical approaches, they require extensive datasets and computational resources. In conclusion, we summarized the advantages, disadvantages, and future research directions, offering insights for developing next-generation real-time high-precision GNSS PNT services.
1. Introduction
As fundamental infrastructure for spatiotemporal information, the Global Navigation Satellite System (GNSS) provides high-precision global positioning, navigation, and timing (PNT) services. It is extensively utilized in transportation logistics, agriculture, environmental monitoring, scientific research, and military applications, delivering critical foundational support for developing information-based intelligent societies [1,2,3,4]. With technological advancements, emerging high-precision applications—including autonomous driving, unmanned aerial vehicle (UAV) collaborative operations, smart grids, and communication networks—increasingly demand real-time GNSS positioning accuracy at the centimeter level and timing precision at the nanosecond level. These requirements impose heightened demands on next-generation GNSS real-time high-precision PNT services. Consequently, real-time precise satellite clock bias prediction has become a prerequisite for achieving high-precision GNSS time synchronization and PNT services, establishing it as a key research focus in the GNSS field.
Autonomous GNSS navigation and sustained high-precision PNT services require precise satellite clock bias products. GNSS ground control centers establish and maintain the navigation system’s time reference using high-performance atomic clock ensembles. These centers continuously monitor and periodically correct clock deviations—termed satellite clock bias—between GNSS satellite atomic clocks and ground-system time references. For example, the US GPS system conducts satellite-to-ground time comparisons via a global network of ground stations performing continuous 24-h GPS satellite observations [5]. Similarly, China’s BeiDou System (BDS) employs inter-satellite and satellite-to-ground links for real-time monitoring of on-orbit satellite clock bias [6,7]. However, disruptions to ground stations or communication links may permit natural onboard atomic clock drift to induce clock bias, potentially degrading PNT service quality. Notably, a satellite clock bias of merely 1 nanosecond (10−9 s) can introduce pseudo-range errors up to 30 cm [8]. Achieving centimeter-level positioning thus demands clock bias products with sub-nanosecond accuracy. User Range Error (URE), a key determinant of positioning accuracy, quantifies errors in measured satellite-to-user ranges caused by orbital and clock bias inaccuracies. Current GNSS open service performance indicates average UREs (95% reliability) of 1.0 m for BDS, 7.8 m for GPS, 7.0 m for Galileo, and 18.0 m for GLONASS [9].
Currently, precise satellite clock bias is primarily obtained from four sources: broadcast ephemeris clock bias, post-processed precise products from data analysis centers, real-time estimation, and prediction [10]. GNSS broadcast clock bias satisfies real-time requirements but exhibits limited accuracy, typically around 5 ns. Post-processed precise products achieved tens of picoseconds accuracy, yet suffer from significant latency—often released hours to days after observation. The International GNSS Service (IGS) final products currently provided 75 ps accuracy but require 12–18 days for availability. To address this, IGS offered ultra-rapid products comprising a 48-h arc: the first 24-h observed segment achieves <0.15 ns accuracy with 3–9 h latency, while the subsequent 24-h predicted segment attains only ~3 ns accuracy. This marginally exceeded broadcast ephemeris performance but remains substantially below the IGS-recommended 0.3 ns threshold for real-time high-precision positioning [11]. Domestically, Wuhan University’s WUM products demonstrate consistency with IGS final products. When referenced against IGS final GPS solutions, WUM achieves daily average RMS and STD values of 154.9 ps and 55.1 ps, respectively, though requiring 2–3 days for release [12].
Real-time satellite clock bias prediction employs a global network of GNSS observation stations, utilizing efficient data communication and rapid processing to generate clock bias in real time. This approach provides near-real-time precise solutions with significantly enhanced accuracy compared to broadcast products, forming the foundation for contemporary high-precision positioning services. In 2013, the International GNSS Service (IGS) launched its comprehensive Real-Time Service (RTS) through collaboration with Natural Resources Canada (NRCan), the German Federal Agency for Cartography and Geodesy (BKG), and ESA’s European Space Operations Centre (ESOC). Supported by 160+ globally distributed stations, multiple data centers, and 10 analysis centers, RTS delivered products with 0.300 ns accuracy at ~25 s latency [13]. Nevertheless, practical implementations may encounter service interruptions, clock bias anomalies (errors/jumps), and network failures [14].
Satellite clock bias prediction involves predicting future clock bias variations over a certain period by establishing mathematical models or employing deep learning methods. Compared to post-processed precise clock bias products and real-time estimation, clock bias prediction offers the advantage of providing real-time high-precision clock bias services even in scenarios lacking real-time data or under poor communication conditions. This capability is particularly critical in specific applications, such as environments with limited ground stations, poor data transmission conditions, or strict mission planning requirements. Due to these advantages, extensive research on satellite clock bias prediction has been conducted both domestically and internationally. However, the field currently lacks a systematic and comparative review that synthesizes the diverse modeling approaches—from classical mathematical methods to modern artificial intelligence techniques—and evaluates their performance, applicability, and limitations under varying operational conditions. This gap hinders the optimization and selection of appropriate prediction strategies for emerging high-stakes applications. Therefore, the primary motivation of this review is to comprehensively summarize and analyze existing satellite clock bias prediction models, clarify their theoretical foundations and practical challenges, and provide a clear reference for future research and operational deployments. This paper summarizes the factors influencing the errors of prediction models and presents generalized modeling flowcharts for classical prediction models and artificial intelligence-based prediction models. It reviews the research progress, technical characteristics, and limitations of satellite clock bias prediction models from both classical mathematical and artificial intelligence perspectives, while also outlining future research directions for reference by researchers in related fields worldwide.
2. Model Error Analysis
Errors in clock bias prediction models mainly arise from model construction methods, data quality, and applicability constraints. As illustrated in Figure 1, we analyze these errors through three dimensions: systematic model errors, input data error propagation, and scenario-specific applicability limitations.
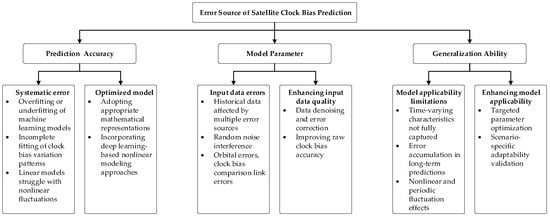
Figure 1.
Error analysis of satellite clock bias.
Systematic errors in clock bias prediction models originate from inherent design limitations, primarily determined by whether the mathematical formulation accurately captures variation patterns. Current mainstream models include time series methods (e.g., Autoregressive Integrated Moving Average, Kalman filtering) and machine learning approaches (e.g., Support Vector Machines, Long Short-Term Memory networks). Time series models typically assume autocorrelation and trend characteristics in clock bias data. However, empirical clock signals often exhibit nonlinear fluctuations that models cannot fully characterize, introducing systematic errors. For example, in a study predicting the clock bias of BDS satellites, the ARIMA model exhibited an average prediction error of approximately 3.5 ns over 6 h due to unmodeled periodic variations and thermal-induced fluctuations [15]. Although machine learning models excel at handling complex data, their dependence on historical datasets creates vulnerabilities: insufficient training data or suboptimal feature selection frequently causes overfitting or underfitting, degrading prediction accuracy [16]. When using LSTM for Galileo satellite clock error prediction, model performance degraded significantly during solar radiation periods because the training set lacked sufficient examples of space weather-induced anomalies [17].
Input data error propagation constitutes another major error source in clock bias prediction models. Historical clock bias data—essential for model training—contain inherent inaccuracies from acquisition and processing stages [18]. Errors originating from onboard atomic clocks and post-processed products directly propagate into prediction models, compromising prediction precision. Satellite orbit inaccuracies and signal propagation delays, for example, introduce additional noise that degrades data integrity. A notable case is the error amplification observed in BeiDou-3 satellites: orbital determination errors of 20 cm resulted in additional clock bias prediction inaccuracies of up to 1.8 ns over a 12-h prediction horizon [19]. Since models train on historical data, both systematic and random errors affect parameter estimation, propagating into future predictions. Furthermore, satellite clock bias exhibits random noise characteristics, particularly power-law noise components (e.g., frequency random walk, phase flicker noise) [20], which destabilize data and reduce predictability, further diminishing prediction accuracy. Experimental support comes from a study on clocks of Compass constellations where ignoring noise type mismatches (e.g., treating flicker noise as white noise) increased prediction RMS error by 40% compared to noise-adaptive filtering methods [21].
Model applicability limitations constitute a third significant error source in clock bias prediction. The generalization ability of the prediction model depends on multiple factors, including the time-varying nature of clock variations and complex environmental influences. During operation, satellite clock bias is affected not only by onboard atomic clock performance but also by periodic orbital perturbations, attitude variations, and space environmental conditions. These factors exhibit nonlinear periodic fluctuations that challenge model adaptability [22]. Failure to accurately capture such dynamics induces error accumulation, particularly in long-term predictions. For instance, during geomagnetic storms, the prediction error of a quadratic polynomial model for GPS clocks increased by 230% due to unmodeled ionospheric delay variations and increased atomic frequency instability [23]. Consequently, adaptive validation across satellites and timeframes, coupled with dynamic parameter adjustments, becomes essential for enhancing model robustness and accuracy in diverse scenarios.
In summary, clock bias prediction model errors originate from three primary sources: inherent systematic errors in model design, propagated input data inaccuracies, and scenario-specific applicability limitations. Mitigating these errors requires not only judicious model parameter selection and optimization during the modeling phase but also rigorous input data preprocessing through noise reduction and error correction techniques to enhance prediction accuracy and reliability.
3. Classical Prediction Models
Classical prediction models rely on precise mathematical formulations for modeling, achieving forecasts through data feature extraction and fitting. Figure 2 illustrates the general modeling process of these models, demonstrating sequential relationships between stages and incorporating a closed-loop feedback mechanism to support continuous optimization and improvement.
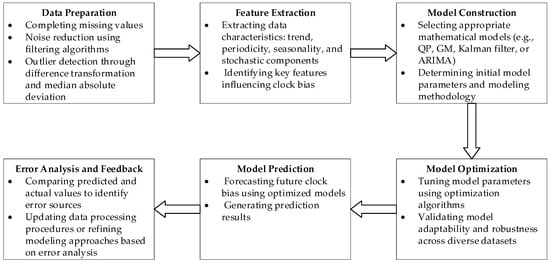
Figure 2.
General modeling flow of a classical prediction model.
This section will introduce the following four categories of classical prediction models: Polynomial Model (PM), Grey Model (GM), Kalman Filter Model (KFM), and Autoregressive Integrated Moving Average model (ARIMA).
3.1. Polynomial Model
The polynomial model for satellite clock bias prediction originates from studies on the operational behavior of onboard atomic clocks. Its primary objective is to forecast clock bias variations using mathematical modeling techniques, thereby improving the accuracy of navigation systems. The earliest implementation of such a model was proposed by developers of the U.S. GPS system, where clock bias variations were represented using a quadratic polynomial. This method characterizes clock bias changes through three parameters: clock bias, frequency bias, and frequency drift [24,25]. The mathematical formulation is presented in Equation (1).
where represents the clock bias at epoch , is the reference time, denotes the residual error of the clock bias at epoch , , and are the parameters representing clock bias, frequency bias, and frequency drift, respectively.
To more accurately capture the characteristics of onboard atomic clocks, the periodic variations of satellite clocks should also be taken into account. Spectral analysis techniques can be applied to identify significant periodic components within the data sequence. By incorporating these components into the quadratic polynomial model, a spectral analysis–based model can be derived [26], whose mathematical formulation is presented in Equation (2).
where represents the number of main periodic functions, , and denote the amplitude, frequency, and phase of corresponding periodic terms, respectively. Other parameters maintain the same meaning as in Equation (1).
Recent research has introduced numerous enhancements to polynomial models for satellite clock bias prediction. Han et al. [24] combined IGS precise orbit data with clock bias observations from IGS tracking stations in 2001 to predict post-processed precise clock bias at 30-s intervals, achieving an accuracy of 0.1 ns. Bernier et al. [25] investigated the characteristics of new passive hydrogen masers in 2005 using standardized quadratic difference prediction algorithms, obtaining results second only to those of energy spectrum noise models. In 2008, Panfilo et al. [26] conducted targeted research on noise components in onboard atomic clock bias, extracting random walk noise and developing a prediction model that produced objective results. Allan et al. [27], in their 2018 study, analyzed optimal estimation methods for onboard atomic clocks under five common noise conditions, deriving extrapolation expressions for these noise models and providing corresponding prediction confidence levels and trends. Lei et al. [28] employed polynomial fitting based on the physical characteristics of onboard atomic clocks to extract clock bias trend terms, followed by phase space reconstruction and Gaussian process prediction for the fitting residuals. For processing random terms in polynomial models, Wang et al. [29] adopted robust least-squares collocation methods, whereas Liao et al. [30] proposed iterative approaches for random error correction and modeling, achieving a 1-day RMS accuracy of 0.57 ns and a maximum deviation of 1 ns.
Polynomial models exhibit strong data-fitting capabilities and are effective for short-term clock bias prediction; however, they face challenges in capturing complex nonlinear variations and generally perform poorly in extrapolation. While these models can provide basic fitting and prediction of clock bias, their accuracy deteriorates markedly over time. Therefore, regularly updating the polynomial model parameters in navigation messages is essential for maintaining prediction precision.
3.2. Grey Model
The grey model was first applied to GPS satellite clock bias prediction in the 1990s. A grey prediction system is a prediction framework that operates with partially known and partially unknown information, representing an incompletely certain system. Based on grey models, it generates new data sequences by accumulating or differencing the original series, and then models these sequences to more objectively capture useful information. Atomic clocks onboard navigation satellites are highly sensitive to both external and internal factors, making it challenging to characterize their complex and detailed variation patterns. These characteristics closely correspond to the principles of grey system theory.
Among grey system models, the GM(1,1) model is the most commonly used grey model, with its expression shown in Equation (3).
where represents the original clock bias sequence, denotes the grey coefficient, indicates the grey action quantity, is a natural number.
A comprehensive review of literature from the past decade reveals substantial research efforts aimed at improving the prediction accuracy of grey models from multiple perspectives. In clock bias data processing, Liang et al. [31] employed difference sequences, whereas Mei et al. [32] proposed ratio sequences for clock bias modeling. Jiang Yu et al. [33] applied a power function transformation to clock bias data, and Yu et al. [34] implemented Vondrák filtering for preprocessing. Regarding coefficient determination and optimization, Zheng et al. [35] analyzed the relationship between prediction accuracy, GM exponential coefficients, and different sampling intervals, and compared the results with those from polynomial models. Yu et al. [36] improved the grey prediction model by employing least absolute deviation to enhance performance under abrupt-change conditions. Yu Ye et al. [37] developed a particle swarm optimization–weighted grey regression hybrid model, achieving average 24-h prediction residuals below 5.71 ns. Li et al. [38] proposed an adaptive twin-subpopulation improved particle swarm optimization algorithm (TS-IPSO), whereas Yang et al. [39] optimized grey model parameters using the Levenberg–Marquardt algorithm. Yuan et al. [40] introduced an enhanced firefly algorithm (SAFA-FD), achieving 3–6 h prediction errors below 1 ns and 9–12 h errors under 2 ns. Additionally, Zhao et al. [41] developed a dynamic grey model that continuously updates by discarding outdated data and incorporating new observations, thereby improving the whiteness of prediction intervals. Tan et al. [42] optimized the initial conditions of grey models by deriving them from components of the original clock bias sequence.
The grey model demonstrates effective prediction capability with limited samples, low data requirements, and fast modeling speed, yet exhibits instability in long-term predictions, making it suitable for monotonic data but less effective for highly fluctuating datasets.
3.3. Kalman Filter Model
The Kalman filter, introduced by Rudolf E. Kalman in 1960, is a recursive optimal estimation algorithm originally developed for navigation systems. The National Institute of Standards and Technology (NIST) employed the Kalman filter algorithm to establish Atomic Time. However, due to the incomplete observability of the system during the filtering process, the error covariance matrix diverged continuously, leading to unbounded growth in the clock bias estimates. Additionally, the Kalman filter’s estimation of clock offset relied on the long-term stability of atomic clocks while overlooking their short-term stability. To address these limitations, several improved Kalman filter algorithms were proposed. For instance, Davis et al. [43] introduced two distinct methods to reduce the estimation error covariance matrix and demonstrated the optimality of the reduced Kalman scale. Greenhall et al. [44] developed an approach that combined the Kalman filter with a weighted average algorithm, along with a method for modeling flicker noise, to constrain the divergence in the estimated clock error covariance matrix.
Kalman filter enables real-time computation of satellite clock bias, frequency bias, and frequency drift, thereby functioning as both a clock bias prediction model and an estimation model. In this framework, the current state prediction depends on the previous state estimate and the latest observations. The state equation of the Kalman filter for onboard atomic clocks is presented in Equation (4) [45].
where: represents the sampling interval; , and denote the clock bias, frequency bias, and frequency drift parameters of the onboard clock, respectively. , and are random errors with zero mean.
The key to constructing a Kalman filter model lies in determining the process noise covariance matrix and the measurement noise covariance matrix. Current approaches include the Hadamard total variance method proposed by Guo and Yang [46], the Allan variance introduced by Howe et al. [47], and the variance recursion method developed by Hutsell et al. [48]. Further research indicates that Davis J. et al. [49] implemented a Kalman filter–based prediction algorithm capable of achieving near-optimal performance, maintaining prediction errors at the 1-nanosecond level for next-generation Block IIR and IIF satellites over a one-day prediction horizon. Pihlajasalo et al. [50] used grid search to identify optimal noise parameters, selecting those that minimized prediction errors in experimental tests. Pratt et al. [51] incorporated both satellite-to-ground and satellite-to-satellite measurement data into a Kalman filter framework to estimate each Iridium satellite’s clock bias, with typical results showing a current filter accuracy within 200 ns, consistently meeting the original system specification of 0.5 µs. Various improvements to the Kalman filter model have been proposed: Zhang et al. [52] integrated prediction penalties and amplitude variation constraints into clock bias estimation, while Wang et al. [53] applied wavelet denoising to clock bias observations and proposed a linearly weighted combination Kalman filter model.
The Kalman filter model can update predictions in real-time and is suitable for clock bias prediction in dynamic environments. However, its performance may degrade for nonlinear systems or when noise distributions deviate from Gaussian assumptions, as it strictly requires accurate noise statistical characteristics—prediction quality decreases with inaccurate noise models, and demands prior knowledge of both system models and noise statistics.
3.4. Autoregressive Integrated Moving Average Model
The autoregressive integrated moving average (ARIMA) model, proposed by Box and Jenkins in 1970, is a widely used time series analysis method applied in fields such as economics, meteorology, and engineering for prediction purposes. ARIMA modeling and prediction rely on analyzing the characteristics of the time series data to determine an appropriate model type and select suitable orders. The ARIMA model, which incorporates differencing, is denoted as ARIMA , where and represent the autoregressive and moving average orders, respectively, and denotes the number of differencing operations. When , the ARIMA model reduces to the autoregressive moving average (ARMA) model, whose formulation is given in Equation (5) [54].
where: and represent the autoregressive and moving average parameters to be estimated; denotes the white noise sequence, and is the white noise variance; when and equal 0, respectively, the model becomes an MA model and an AR model correspondingly.
Mutaz et al. [54] applied time series models to predict and correct time-delay errors in precise point positioning (PPP) single-point solutions, achieving a 28% improvement in prediction accuracy. Zhou et al. [55] optimized the ARIMA model by introducing a novel fitting approach and refined criteria for determining the and orders, applying it to short-term satellite clock bias prediction, with most GPS rubidium clocks exhibiting prediction errors below 0.6 ns for 6-h forecasts and below 0.25 ns for 1-h forecasts. Jiang et al. [56] evaluated the performance of ARIMA models under varying data-fitting lengths and prediction horizons. Several enhancements to ARIMA models have been reported: Yan et al. [57] applied sparsity theory to autoregressive model parameters to mitigate the influence of redundant parameters; Gonzalez et al. [58] incorporated seasonal components into prediction residuals, achieving nanosecond-level root-mean-square errors (RMSE) throughout the day; Kim et al. [59] integrated neural networks with ARIMA models for predicting IGS real-time service corrections, where the ARIMA coefficients were determined via neural networks. In addition, time series models are widely employed for detecting and correcting AO-type outliers in clock bias data. Han et al. [60] developed an algorithm for detecting AO-type outliers in autoregressive (AR) models, effectively addressing masking and swamping issues in clustered outlier detection. Ma et al. [61] proposed a variance-inflation model based on ARIMA for anomaly detection in BDS satellite clock bias, employing likelihood ratio methods to identify outliers in BDS clock bias time series. Zhang et al. [62] introduced a method that combines ARMA time series modeling with Bayesian statistics for both precise satellite clock bias prediction and historical anomaly detection.
The ARIMA model effectively captures temporal dependencies and autocorrelations in clock bias data, making it suitable for long-term prediction with solid theoretical foundations and broad applicability. However, parameter selection and order determination can be complex, often requiring substantial prior knowledge, and while the model works well for linear variations, its performance degrades with nonlinear data patterns.
3.5. Summary of Classical Models
Classical mathematical modeling approaches rely on explicitly defined mathematical formulas and parameters, where the predictive accuracy is strongly influenced by the trend, periodicity, stochastic characteristics, and noise properties of the clock bias data. However, such models encounter challenges when addressing complex nonlinear relationships and typically impose stringent requirements on parameter selection and prior knowledge. As the prediction horizon extends, errors tend to accumulate progressively, thereby constraining the models’ capability for long-term prediction. Moreover, the inherent linear assumptions and fixed parameter configurations in classical methods reduce their adaptability to the dynamic variations and intricate noise patterns frequently observed in satellite clock behavior—particularly over extended horizons, where error propagation becomes increasingly significant. These limitations have driven researchers to investigate more advanced modeling techniques, such as machine learning approaches, to more effectively capture nonlinear dynamics and enhance the long-term prediction stability of satellite clock bias.
4. Artificial Intelligence Prediction Models
The general modeling workflow for artificial intelligence (AI)-based prediction models is illustrated in Figure 3. Compared with classical mathematical modeling approaches, the AI prediction framework places greater emphasis on model complexity and the importance of iterative optimization. At present, AI models applied to satellite clock bias time series prediction can be broadly classified into four categories: machine learning (ML)-based models, multilayer perceptron (MLP)-based models, recurrent neural network (RNN)-based models, and Transformer-based models that employ self-attention mechanisms.
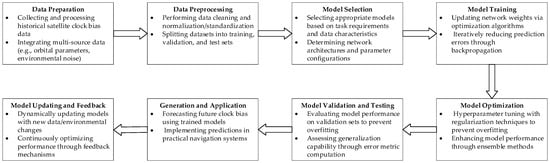
Figure 3.
General modeling process for AI predictive models.
4.1. ML-Based Models
Classical machine learning algorithms have well-established theoretical foundations, providing strong mathematical interpretability and reliable performance guarantees. These conventional models depend on manual feature extraction and generally adopt relatively simple architectures with fewer layers, which enable faster training and make them particularly suitable for small- to medium-sized datasets.
In Support Vector Machine (SVM) prediction models, the radial basis function (RBF) is commonly employed as the kernel function, enabling nonlinear mapping of input variables into a high-dimensional feature space where linear optimization functions are constructed for prediction. Xiao et al. [63] developed a refined quadratic polynomial prediction algorithm based on Particle Swarm Optimization–SVM (PSO-SVM), which performs rolling predictions by modeling residuals during the fitting stage. He et al. [64] proposed an enhanced approach that integrates spectral analysis models (SAM) with least squares support vector machines (LS-SVM). As illustrated in Figure 4, their satellite clock bias data processing framework demonstrated that the improved model can maintain prediction deviations within ±1.0 ns for most Medium Earth Orbit (MEO) satellites over 3-h prediction periods. Zhu et al. [65] introduced a least squares support vector machine (LSSVM) prediction algorithm for hydrogen atomic clocks, achieving improvements in prediction accuracy of 50% and 29% compared with linear prediction algorithms and standard SVM prediction algorithms, respectively.
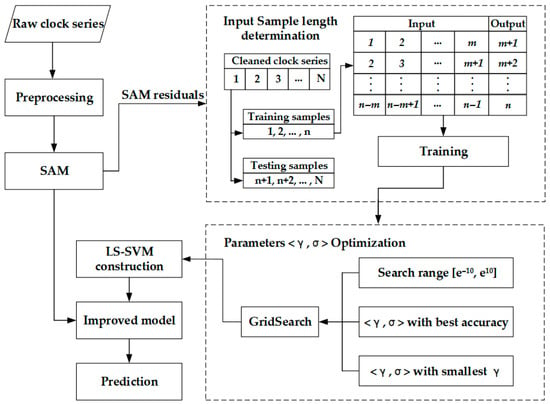
Figure 4.
Clock bias data processing flowchart using an improved SVM model [56].
The Extreme Learning Machine (ELM), proposed by Huang and colleagues in 2004, is a single-hidden-layer feedforward neural network distinguished from classical neural networks by its random initialization of input weights and hidden layer biases, which remain fixed during training, while the output weights are computed directly via least squares methods. This design significantly accelerates the training process. He et al. [66] developed an enhanced clock prediction method by integrating spectral analysis models with ELM, demonstrating that prediction accuracy remains consistently high, with errors below 1.0 ns as the prediction horizon extends from 0 to 18 h. Lei et al. [67] proposed an ELM network structure design based on Adaptive Resonance Theory (ART) networks, leveraging ART’s superior self-organizing classification capabilities. Ya et al. [68] implemented a Sparrow Search Algorithm (SSA)-optimized ELM prediction model that utilizes 12-h historical satellite clock bias data to forecast the subsequent 6-h bias. The SSA-ELM model achieved improvements of 53.16% and 52.09% over QP models, and 40.66% and 46.38% over GM models, respectively, as illustrated in Figure 5.
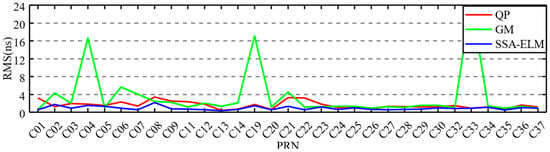
Figure 5.
Predicting BDS Satellite Clock Bias Accuracy for the Next 6 Hours Based on Historical 12-Hour Satellite Clock Bias Data [60].
SVMs are well-suited for small sample sizes and have strong theoretical foundations; however, they face challenges in parameter selection and exhibit high computational complexity. ELMs offer advantages such as rapid training speeds and fewer tunable parameters, facilitating relatively straightforward implementation. Nonetheless, ELMs suffer from limited generalization capability and comparatively poor robustness to noise and anomalous data. Moreover, classical machine learning methods may encounter computational and storage limitations when processing large-scale datasets, restricting their applicability in scenarios that require real-time processing of massive GNSS observation data.
4.2. MLP-Based Models
The Multilayer Perceptron (MLP) is a feedforward neural network consisting of multiple fully connected layers. Input data is processed through successive layers of linear transformations followed by nonlinear activation functions, resulting in hierarchical feature extraction. In time series prediction tasks, historical values of the time series are typically employed as inputs, allowing the MLP to learn underlying patterns and trends for prediction purposes [69]. The MLP demonstrates strong adaptability, robustness, and associative memory capabilities, rendering it especially effective in capturing complex nonlinear relationships within satellite clock bias data.
Du et al. [70] employed empirical mode decomposition combined with backpropagation neural networks to predict GNSS receiver clock biases, demonstrating excellent performance in predicting receiver clock bias time series. However, MLP models are susceptible to becoming trapped in local optima during backpropagation training and exhibit slow convergence rates, which ultimately affect final convergence accuracy. To optimize MLP neural network weights and thresholds while enhancing prediction accuracy and convergence speed, numerous scholars have proposed various optimization algorithms, including genetic algorithms [71], mind evolutionary algorithms [72,73], sparrow search algorithms [69], whale optimization algorithms [74], beetle antennae search algorithms [75], and improved particle swarm optimization algorithms [76]. These optimized models demonstrate varying degrees of improvement in prediction accuracy compared to classical MLP models and conventional prediction methods. Specifically, Bai et al. [73] achieved a 12-h prediction accuracy of 1.56 ns using mind evolutionary algorithm optimization, while Lyu et al. [76] attained average prediction accuracies better than 0.15 ns for 20-min and 60-min forecasts with their improved particle swarm optimization model, representing approximately 85% improvement over conventional models. Building upon the MLP neural network framework, researchers have further enhanced hidden layer neural units by replacing standard activation functions with wavelet basis functions or radial basis functions, resulting in wavelet neural networks [77,78,79] and radial basis function neural networks [80,81], both of which provide notable improvements in clock bias prediction accuracy.
MLP neural networks exhibit strong adaptability in modeling complex nonlinear relationships; however, their training processes require multiple iterations and are time-consuming, with a propensity to converge to local optima. Wavelet neural networks leverage the multiscale analysis capabilities of wavelet transforms to more effectively capture time-frequency characteristics in clock bias data, as wavelet transforms can compress data efficiently and enhance computational performance. Nevertheless, these networks involve complex architectural designs and wavelet basis function selections, necessitating substantial training data and computational resources. RBF neural networks offer rapid training speeds suitable for real-time prediction and demonstrate strong generalization abilities; however, they are highly dependent on sample quality and present challenges in parameter selection. Each of these neural network approaches presents distinct advantages and limitations in satellite clock bias prediction, with their relative efficacy contingent upon specific operational requirements, available computational resources, and desired prediction horizons within GNSS.
4.3. RNN-Based Models
Recent research on clock bias prediction has increasingly focused on Recurrent Neural Networks (RNNs), which possess inherent “memory” capabilities that differentiate them from conventional Multilayer Perceptron (MLP) networks. Designed specifically for sequential data processing, RNNs are characterized by their recurrent connections, which enable the retention of historical information. At each time step, RNNs incorporate the hidden state from the previous step, allowing them to capture temporal dependencies within sequential data. Long Short-Term Memory (LSTM) networks and Gated Recurrent Unit (GRU) networks represent enhanced variants of RNNs, addressing the vanishing gradient problem via more sophisticated and more streamlined gating mechanisms, respectively, thereby improving their capacity to model long-term dependencies. The architectures of these three models are depicted in Figure 6 [82], illustrating their progressive complexity and efficiency in handling time series data. The Tanh function maps any real-valued number to a value between −1 and 1. The Sigma function is a mathematical function that maps any real-valued number to a value between 0 and 1. In a standard RNN cell, the Tanh function is typically used to activate the combined input and hidden state to produce the new hidden state. The Sigma function is not used in the simplest RNN cells but becomes crucial in gated architectures like LSTMs to manage information flow over long sequences.
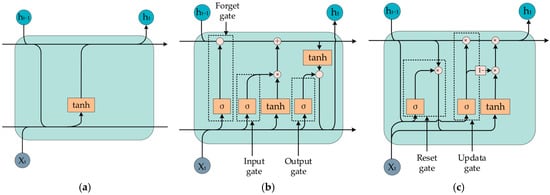
Figure 6.
Three Typical Recurrent Neural Network Models. (a) The Basic RNN Model Architecture. (b) The LSTM Model Architecture. (c) The GRU Model Architecture.
Piotr et al. [82] employed LSTM models for real-time clock bias prediction of GPS satellites, achieving results superior to current state-of-the-art methods. Huang et al. [83] proposed a supervised learning LSTM network (SL-LSTM) that separately models the periodic and random components of clock bias data, demonstrating improved prediction accuracy and stability in long-term prediction. He et al. [84] utilized LSTM models to predict BDS-3 satellite clock biases, attaining short-term (0–6 h) prediction accuracies of 0.5 ns and 0.3 ns for IGSO and MEO satellites, respectively. For long-term clock bias prediction, the LSTM model exhibited improvements of 72.0% and 64.0% over ARIMA and QP models, respectively. Cai et al. [85] developed an integrated LSTM-attention neural network incorporating self-attention mechanisms, as illustrated in Figure 7, which effectively balances global attention with local feature extraction, achieving 62.51% improvement over standard LSTM models in 12-h prediction tasks and 71.16% enhancement in 24-h prediction.
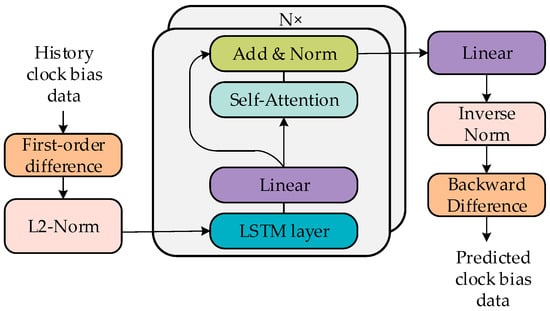
Figure 7.
The LSTM-Attention Neural Network Model [77].
Yang et al. [86] employed a sparsely sampled LSTM network algorithm to enhance the long-term prediction accuracy of clock biases for space-based time scales, achieving onboard frequency stabilities of 1.35 × 10−15, 3.37 × 10−16, and 2.81 × 10−16 at sampling intervals of 300 s, 8.64 × 104 s, and 1 × 106 s, respectively. Liu et al. [87] developed a BDS-3 satellite clock bias prediction model using GRU neural networks, implementing an improved Sparrow Search Algorithm (SSA)-GRU hybrid model (ITSSA-GRU) that demonstrates superior generalization capability and prediction performance across three types of satellite clocks. Additionally, Liang et al. proposed the Nonlinear Autoregressive Exogenous (NARX) neural network in 2021 [88], an enhanced recurrent neural network variant capable of incorporating feedback from output neurons, and introduced the Elman neural network in 2022 [89], which incorporates a “context layer” to memorize previous states, rendering it particularly effective for time series processing and dynamic system modeling.
RNN-based models excel at capturing long-term dependencies and are well-suited for time series prediction. By employing gating mechanisms to regulate information flow, these models demonstrate strong memory capabilities for extended sequential data. However, they require lengthy training periods, involve complex training procedures, and demand careful tuning of network architectures and parameters. Despite these challenges in practical implementation, RNN-based models outperform conventional approaches in capturing the intricate temporal patterns of satellite clock behavior.
4.4. Transformer-Based Models
The Transformer neural network model, first proposed by Vaswani et al. [90] in 2017 was illustrated in Figure 8. It was originally designed to address sequence modeling challenges in natural language processing (NLP) and to overcome the limitations of classical sequence models such as RNNs and LSTMs in capturing long-range dependencies. The core innovation of the Transformer is the self-attention mechanism, which fundamentally differs from the recurrent structures of RNNs and LSTMs by processing input sequences entirely through attention mechanisms. This design enables effective modeling of long-distance dependencies and allows parallel data processing, resulting in higher computational efficiency. The Transformer architecture comprises two main components: an encoder and a decoder, each consisting of multiple identical layers.
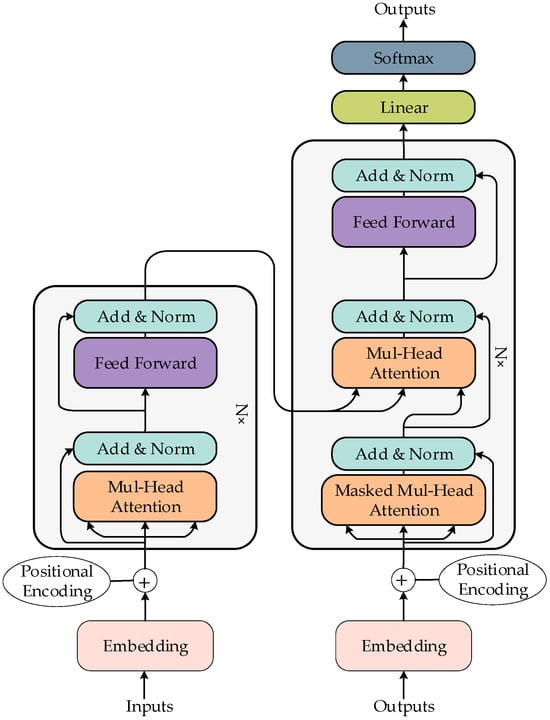
Figure 8.
The Transformer Model Architecture [82].
Syam et al. [8] developed a Transformer-based deep neural network for ML time series modeling, providing fast and reliable clock bias correction predictions for single-frequency receivers with an accuracy of less than 2 ns and maximum prediction horizons up to 2 h. This model demonstrated a 50% improvement in prediction performance compared to other clock bias prediction methods, as illustrated in Figure 9. Pan et al. [91] proposed a sequence-to-sequence neural network model (Informer) based on optimized self-attention mechanisms, which effectively leverages dependencies within clock bias data to achieve deep latent feature extraction and parallel computation, exhibiting high accuracy and stability in short-term clock bias prediction.
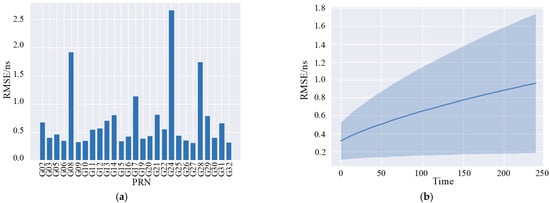
Figure 9.
Clock Bias Prediction Results for two hours Based on the Transformer Model [8]. (a) RMSE of PRN Clock Bias Prediction. (b) RMSE of Clock Bias Prediction for the Next.
The Transformer deep learning model utilizes parallel computation via its self-attention mechanism, enabling efficient training and superior capability in capturing global features of sequence data, particularly excelling in handling long sequences. However, it requires substantial computational resources and memory, performing optimally with large-scale datasets but exhibiting relatively poorer performance than classical RNNs, LSTMs, or convolutional neural networks when data or computational resources are limited. The Informer model, specifically designed for long-term time series prediction, offers enhanced capabilities for modeling lengthy sequences and achieves greater computational efficiency compared to conventional Transformer architectures. Nevertheless, its complex structure imposes stringent hardware and algorithmic requirements, and its performance heavily depends on abundant training data; insufficient data volume may hinder the model from reaching its full potential.
4.5. Summary of AI Models
Satellite atomic clocks are vulnerable to external environmental factors and possess inherently complex characteristics, causing their clock bias to exhibit pronounced nonlinear behavior that challenges classical models in accurately describing these variations [84]. In contrast, artificial neural networks exhibit strong sensitivity to nonlinear dynamics and can overcome the limitations of conventional models, rendering them particularly suitable for modeling within big data environments. By leveraging extensive historical data through deep learning and optimization techniques, these networks automatically extract salient features from the data, making them well-suited for various complex time series prediction tasks.
5. Conclusions
The clock bias prediction models introduced above each possess distinct characteristics in practical applications, all capable of achieving relatively good prediction results under certain conditions. An analysis and summary of the advantages and disadvantages of current major clock bias prediction models are presented in Table 1.

Table 1.
Advantages and disadvantages of satellite clock bias prediction model.
Classical mathematical models rely on well-defined formulas and parameters, employing specific algorithms that make them suitable for scenarios characterized by strong regularity or short-term predictions. These conventional models demonstrate higher efficiency with linear and regular data patterns, exhibit better applicability for small sample sizes, and incur low computational costs, rendering them appropriate for short-term, regular predictions or resource-constrained environments.
Artificial intelligence prediction models leverage neural networks and deep learning techniques to automatically extract data features and adapt to complex nonlinear characteristics, proving particularly effective in big data contexts. While AI models excel at handling nonlinear features and complex data patterns, they require substantial data volume and computational resources, making them more appropriate for large-scale datasets and predictions involving intricate dynamics. Despite these advances, the fundamental trade-off between model complexity and interpretability remains a inherent limitation of many state-of-the-art AI systems.
Table 2 systematically reviews both classical and recent representative studies in the field, compiling key performance metrics (e.g., RMSE, MAE) reported across different research works on official datasets. This approach allows for evidence-based extraction from existing literature, objectively illustrating the relative performance of various models and providing a well-founded basis for our comparative analysis.

Table 2.
The accuracy of each model from classical and recent representative studies.
Table 3 provides a decision-making framework for the practical application of different models in real-world scenarios. Model selection is not merely a benchmarking exercise based on performance rankings, but rather a trade-off process constrained by practical considerations. While academic research often prioritizes State-of-the-Art (SOTA) results and tends to favor complex AI models such as Transformers, real-world industrial applications are typically governed by critical factors including robustness, interpretability, computational cost, and maintenance overhead. It is considered best practice to begin with a simple model to establish a strong baseline. More complex deep learning models should only be introduced when simpler approaches prove insufficient and the anticipated benefits clearly justify the additional complexity and cost.

Table 3.
Decision-making reference framework for model application.
The future of satellite clock bias prediction will depend on the integrated optimization of classical mathematical and artificial intelligence models, advancements in real-time data acquisition and processing technologies, and efficient utilization of computational resources. Through multifaceted innovation and refinement, the accuracy, robustness, and adaptability of clock bias prediction will be significantly enhanced, thereby better supporting the advancement of navigation and positioning systems. Considering the critical importance of satellite clock bias prediction and the limitations of existing research, several promising research directions and their associated key technologies are proposed:
- Multi-source data fusion and processing
Satellite clock bias data come from diverse sources, including ground observation data, measured atomic clock data, inter-satellite link data, and satellite orbit parameters, with coupled relationships existing between clock bias data and orbit parameter determination. Future research could explore multi-source data fusion methods to improve the accuracy and stability of prediction models by integrating data from different sources.
- 2.
- Integration of short-term and long-term prediction
Current satellite clock bias prediction models mostly focus on either short-term or long-term prediction while neglecting their complementary nature. Short-term prediction models typically rely on recent data and can quickly respond to short-term variations but are susceptible to sudden events and noise; long-term prediction focuses on global trends and better captures stable long-term variation patterns but responds relatively slowly to dynamic changes. Future research should emphasize the combination of short-term and long-term prediction to achieve accurate full-cycle prediction of satellite clock bias.
- 3.
- Improving model generalization capability and robustness
Although existing models perform well in specific scenarios, their generalization capability and robustness across different satellites and environments still need improvement. Future research could focus on cross-satellite and cross-constellation adaptability studies to enhance prediction capability in complex environments. Further improvements could also be made to existing models by incorporating actual physical characteristics of onboard clocks, such as considering more complex periodic and random terms, and applying more advanced algorithms. Deep learning techniques could be further utilized to improve the capture of complex nonlinear clock bias variations, while optimizing neural network architectures and parameter tuning strategies to obtain higher-precision prediction results.
- 4.
- Emphasizing real-time performance and computational efficiency
As application scenarios of satellite navigation systems become increasingly complex, the real-time requirements for clock bias prediction are also growing. Future research could focus on improving computational efficiency by applying parallel and distributed computing technologies to enhance model training and prediction efficiency, particularly for processing long time series data. Hardware acceleration devices such as GPUs and TPUs could be utilized to improve the training speed and prediction efficiency of deep learning models.
- 5.
- Innovating deep learning model architectures
Future research could also explore how to integrate these new deep learning models with existing models to form a multi-model ensemble system. By combining the advantages of different models and optimizing ensemble strategies, the robustness and accuracy of satellite clock bias prediction could be further improved. Such innovative deep learning architectures are expected to break through current bottlenecks of prediction models and provide more reliable clock bias prediction support for future satellite navigation systems.
Author Contributions
Conceptualization, Y.L. and Z.M.; Methodology, Y.L.; Software, G.W.; Validation, Y.L., M.L. and E.Y.; Formal Analysis, Y.L.; Investigation, Y.L.; Resources, Z.M.; Data Curation, G.W.; Writing—Original Draft Preparation, Y.L.; Writing—Review & Editing, Z.M. and G.W.; Visualization, M.L.; Supervision, Z.M.; Project Administration, Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The experimental data in the manuscript are all public data and can be downloaded from https://cddis.nasa.gov/archive (accessed on 7 September 2025).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hadas, T.; Kazmierski, K.; Kudłacik, I.; Marut, G.; Madraszek, S. Galileo High Accuracy Service in Real-Time PNT, Geoscience and Monitoring Applications. IEEE Geosci. Remote Sens. Lett. 2024, 21, 8000905. [Google Scholar] [CrossRef]
- Sun, R.; Yang, Y.; Chiang, K.-W.; Duong, T.-T.; Lin, K.-Y.; Tsai, G.-J. Robust IMU/GPS/VO Integration for Vehicle Navigation in GNSS Degraded Urban Areas. IEEE Sens. J. 2020, 20, 10110–10122. [Google Scholar] [CrossRef]
- Lutwak, R. Micro-Technology for Positioning, Navigation, and Timing towards PNT Everywhere and Always. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (INERTIAL), Laguna Beach, CA, USA, 25–26 February 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Iannucci, P.A.; Humphreys, T.E. Economical Fused LEO GNSS. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 426–443. [Google Scholar] [CrossRef]
- Zhai, W.; Wu, J.; Sun, C. Real Time Precision Clock Difference Determination and Accuracy Evaluation Based on iGMAS/IGS Orbit. In Proceedings of the 9th China Satellite Navigation Conference (CSNC), Harbin, China, 23–25 May 2018; pp. 5, 31–35. [Google Scholar]
- Breakiron, L.A.; Smith, A.L.; Fonville, B.C.; Powers, E.; Matsakis, D.N. The Accuracy of Two-Way Satellite Time Transfer Calibrations. In Proceedings of the 36th Annual Precise Time and Time Interval Systems and Applications Meeting, Washington, DC, USA, 7–9 December 2004. [Google Scholar]
- Yang, Y.; Mao, Y.; Sun, B. Basic Performance and Future Developments of BeiDou Global Navigation Satellite System. Satell. Navig. 2020, 1, 1. [Google Scholar] [CrossRef]
- Syam, W.P.; Priyadarshi, S.; Roqué, A.A.G.; Conesa, A.P.; Buscarlet, G.; Orso, M.D. Transformer Deep Learning for Accurate Orbit Corrections in Real-Time. In Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023), Denver, CO, USA, 11–15 September 2023; pp. 159–174. [Google Scholar] [CrossRef]
- Chen, Q.; Yi, T. Brief analysis on global four major navigation satellite systems. J. Navig. Position. 2020, 8, 115–120. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–Achievements, Prospects and Challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Nie, Z.; Gao, Y.; Wang, Z.; Ji, S.; Yang, H. An Approach to GPS Clock Prediction for Real-Time PPP during Outages of RTS Stream. GPS Solut. 2017, 22, 14. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Yin, Q.; Lou, Y.; Yi, W. Comparison and analysis of igs real-time products. J. Geod. Geodyn. 2012, 32, 1671–5942. [Google Scholar]
- Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of Precise Orbit and Clock Products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, G.; Fu, W.; Chen, X. A Real-Time Linear Prediction Algorithm for Detecting Abnormal BDS-2/BDS-3 Satellite Clock Offsets. Remote Sens. 2023, 15, 1831. [Google Scholar] [CrossRef]
- Han, Z.; Zhao, J.; Leung, H.; Ma, K.F.; Wang, W. A Review of Deep Learning Models for Time Series Prediction. IEEE Sens. J. 2021, 21, 7833–7848. [Google Scholar] [CrossRef]
- Hassan, T.; Hassan, A. Employing artificial intelligence in Galileo orbital error prediction for real-time offline positioning. GPS Solut. 2025, 29, 135. [Google Scholar] [CrossRef]
- Mei, G.; Zhao, F.; Qi, F.; Zhong, D.; An, S. Characteristics of the space-borne rubidium atomic clocks for the BeiDou III navigation satellite system. Sci. Sin.-Phys. Mech. Astron. 2021, 51, 118–124. [Google Scholar] [CrossRef]
- Zhang, H.; JU, B.; GU, D.; Liu, Y. Precise orbit determination for TH02-02 satellites based on BDS3 and GPS observations. Chin. J. Aeronaut. 2023, 36, 475–485. [Google Scholar] [CrossRef]
- Jiao, Y.; Kou, Y. Analysis, modeling and simulation of GPS satellite clock errors. Sci. Sin. Phys. Mech. Astron. 2011, 41, 596. [Google Scholar] [CrossRef]
- Liu, L.; Du, L.; Zhu, L.; Han, C. Satellite clock parameter short-term prediction using piece-wise adaptive filter with state noise compensation. In China Satellite Navigation Conference (CSNC) 2012 Proceedings, Proceedings of the CSNC2012, Guanzhou, China, 15–19 May 2012; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 160, pp. 527–538. [Google Scholar] [CrossRef]
- Xie, X. Precise Orbit and Clock Determination for BDS-3 Satellites Using Inter-Satellite Link Observations. Ph.D. Dissertation, Wuhan University, Wuhan, China, 2020. [Google Scholar] [CrossRef]
- Ding, S.; Yang, H.; Yang, X.; Zhang, Z. Influence of the second-order ionospheric delay on GPS PPP time transfer. Xi’an Dianzi Keji Daxue Xuebao/J. Xidian Univ. 2021, 48, 50–56, 82. [Google Scholar] [CrossRef]
- Han, S.C.; Kwon, J.H.; Jekeli, C. Accurate Absolute GPS Positioning through Satellite Clock Error Estimation. J. Geod. 2001, 75, 33–43. [Google Scholar] [CrossRef]
- Jiang, M.; Dong, S.; Wu, W. Research on Time Scale Algorithm Based on Hydrogen Masers. IEEE Instrum. Meas. Mag. 2020, 23, 35–40. [Google Scholar] [CrossRef]
- Panfilo, G.; Tavella, P. Atomic Clock Prediction Based on Stochastic Differential Equations. Metrologia 2008, 45, S108–S116. [Google Scholar] [CrossRef]
- Allan, D.W.; Levine, J. A Historical Perspective on the Development of the Allan Variances and Their Strengths and Weaknesses. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2016, 63, 513–519. [Google Scholar] [CrossRef]
- Lei, Y.; Cai, H.; Zhao, D. A Novel Method for Satellite Clock Bias Prediction Based on Phase Space Reconstruction and Gaussian Processes. Acta Metrol. Sin. 2016, 37, 318–322. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, Z.; Wang, N.; Li, L. Prediction of Navigation Satellite Clock Bias Considering Clock’s Stochastic Variation Behavior with Robust Least Square Collocation. Acta Geod. Cartogr. Sin. 2016, 45, 646–655. [Google Scholar] [CrossRef]
- Liao, J.; Zhang, Y. Satellite Clock Error Prediction of Improved Polynomial and Periodic Model. GNSS World China 2018, 43, 91–95. [Google Scholar] [CrossRef]
- Liang, Y.; Ren, C.; Yang, X.; Pang, G.; Lan, L. A Grey Model Based on First Differences in the Application of Satellite Clock Bias Prediction. Chin. Astron. Astrophys. 2016, 40, 79–93. [Google Scholar] [CrossRef]
- Mei, C.; Huang, H.; Jiang, K.; Xia, L.; Pan, X. Application of Discrete Grey Model Based on Stepwise Ratio Sequence in the Satellite Clock Offset Prediction. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1154–1160. [Google Scholar] [CrossRef]
- Jiang, Y. Application research of GM(1,1) model of power function transform in BDS satellite clock bias prediction. GNSS World China 2020, 45, 49–54. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, H.; Li, X.; Xiao, B. Prediction Method of Satellite Clock Bias Based on Grey Model of First-order Difference of Vondrfik Filter. Acta Astron. Sin. 2018, 59, 75–84. [Google Scholar] [CrossRef]
- Zheng, Z.; Lu, X.; Chen, Y. Improved Grey Model and Application in Real-Time GPS Satellite Clock Bias Prediction. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; Volume 2, pp. 419–423. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, M.; Duan, T.; Wang, C.; Hu, R. Enhancing Satellite Clock Bias Prediction Accuracy in the Case of Jumps with an Improved Grey Model. Math. Probl. Eng. 2020, 2020, 81–86. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, M.; Duan, T.; Wang, C.; Hu, R. Satellite clock bias prediction based on particle swarm optimization and weighted grey regression combined model. J. Harbin Inst. Technol. 2020, 52, 144–151, 182. [Google Scholar] [CrossRef]
- Li, C.; Chen, X.; Liu, J.; Wu, W.; Liu, Z. Predicting Satellite Clock Errors Using Grey Model Optimizedby Adaptive TS-IPSO. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 854–859. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Z.; Xu, X. Application of L-M Algorithm Optimized Gray Model in GPS Satellite Clock Error Predication. J. Henan Polytech. Univ. 2020, 39, 47–52. [Google Scholar] [CrossRef]
- Yuan, D.; Zhang, J.; Zhang, Z.; Wei, S. BDS Clock Error Prediction Based on SAFA-FDGM(1,1) Model. J. Geod. Geodyn. 2021, 41, 672–675. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, Z.; Chen, M.; Yang, W. Application and Accuracy Analysis of Dynamic Grey Model in Satellite Clock Error Prediction. Explor. Sci. Technol. 2016, 1, 23–25, 36. [Google Scholar] [CrossRef]
- Tan, X.; Xu, J.; Li, F.; Wu, M.; Chen, D.; Liang, Y. Improved GM (1,1) Model by Optimizing Initial Condition to Predict Satellite Clock Bias. Math. Probl. Eng. 2022, 2022, 3895884. [Google Scholar] [CrossRef]
- Davis, J.; Greenhall, C.; Stacey, P. A Kalman filter clock algorithm for use in the presence of flicker frequency modulation noise. Metrologia 2005, 42, 1–10. [Google Scholar] [CrossRef]
- Greenhall, C. Forming stable timescales from the Jones-Tryon Kalman filter. Metrologia 2003, 40, S335–S341. [Google Scholar] [CrossRef]
- Guo, H. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navi-gation Satellites. Ph.D. Dissertation, PLA Information Engineering University, Zhengzhou, China, 2006. [Google Scholar]
- Guo, H.; Yang, Y.; He, H.; Xu, T. Determination of Covariance Matrix of Kalman Filter Used for Time Prediction of Atomic Clocks of Navigation Satellites. Acta Geod. Cartogr. Sin. 2010, 39, 146–150. [Google Scholar]
- Howe, D.; Beard, R.; Greenhall, C.; Vernotte, F.; Riley, B. A Total Estimator of the Hadamard Function Used for GPS Operations. In Proceedings of the 32nd Annual Precise Time and Time Interval (PTTI) Meeting, Reston, VA, USA, 28–30 November 2000. [Google Scholar]
- Hutseil, T. Relating the hadamard variance to MCS kalman filter clock estimation. In Proceedings of the 27th Annual Precise Time and Time Interval Systems and Applications Meeting, San Diego, CA, USA, 1–29 November 1995. [Google Scholar]
- Davis, J.; Bhattarai, S.; Ziebart, M. Development of a Kalman Filter Based GPS Satellite Clock Time-Offset Prediction Algorithm. In Proceedings of the 2012 European Frequency and Time Forum, Gothenburg, Sweden, 23–27 April 2012; pp. 152–156. [Google Scholar] [CrossRef]
- Pihlajasalo, J.; Leppäkoski, H.; Kuismanen, S.; Ali-Löytty, S.; Piché, R. Methods for Long-Term GNSS Clock Offset Prediction. In Proceedings of the 2019 International Conference on Localization and GNSS (ICL-GNSS), Nuremberg, Germany, 4–6 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Pratt, J.; Axelrad, P.; Larson, K.M.; Lesage, B.; Gerren, R.; DiOrio, N. Satellite Clock Bias Estimation for iGPS. GPS Solut. 2013, 17, 381–389. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, L. Improved Kalman filter for the rubidium atomic clock error prediction. J. Xi’an Univ. Posts Telecommun. 2019, 24, 1–5. [Google Scholar] [CrossRef]
- Wang, J.; Hu, Y.; He, Z.; Yang, H. Clock Bias Prediction Based on Linear Weighted Combination Kalman Filter. Acta Astron. Sin. 2012, 53, 213–221. [Google Scholar] [CrossRef]
- Qafisheh, M.; Martín, A.; Capilla, R.M.; Anquela, A.B. SVR and ARIMA Models as Machine Learning Solutions for Solving the Latency Problem in Real-Time Clock Corrections. GPS Solut. 2022, 26, 85. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, C.; Song, S.; Chen, Q.; Liu, Z. Characteristic Analysis and Short-Term Prediction of GPS/BDS Satellite Clock Correction. In China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume III, Proceedings of the CSNC2016, Changsha, China, 18–20 May 2016; Springer Nature: Berlin/Heidelberg, Germany, 2016; Volume 390, pp. 187–200. [Google Scholar] [CrossRef]
- Jiang, S.; Li, B. Application of ARIMA Model in Short-Term Satellite Clock Error Prediction. J. Navig. Position. 2019, 7, 118–124. [Google Scholar] [CrossRef]
- Yan, K.; Chang, G.; Zhou, T.; Zhao, Z. Sparse auto-regressive modeling for satellite clock offsets prediction. Hydrogr. Surv. Charting 2021, 41, 28–32, 37. [Google Scholar] [CrossRef]
- González, S.G. Advanced ARIMA Model for Clock Bias Prediction. Master’s Thesis, Technical University of Madrid, Madrid, Spain, 2018. [Google Scholar]
- Kim, M.; Kim, J. Predicting IGS RTS Corrections Using ARMA Neural Networks. Math. Probl. Eng. 2015, 2015, 851761. [Google Scholar] [CrossRef]
- Han, S.; Zhang, G.; Zhang, N.; Zhu, J. New algorithm for detecting AO outliers in AR model and its application in the prediction of GPS satellite clock errors. Acta Geod. Cartogr. Sin. 2019, 48, 1225–1235. [Google Scholar] [CrossRef]
- Ma, Z.; Li, G.; Zhang, Q.; Li, X. Likelihood Ratio Method for Outlier Detection and Estimation in BeiDou Satellite Clock Offset. J. Geomat. Sci. Technol. 2019, 36, 221–226. [Google Scholar] [CrossRef]
- Zhang, G.; Han, S.; Ye, J.; Hao, R.; Zhang, J.; Li, X.; Jia, K. A Method for Precisely Predicting Satellite Clock Bias Based on Robust Fitting of ARMA Models. GPS Solut. 2022, 26, 3. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, S. Short-term prediction of satellite clock bias based on PSO-SVM refined QP model. J. Guilin Univ. Technol. 2019, 39, 893–898. [Google Scholar] [CrossRef]
- He, L.; Zhou, H.; Liu, Z.; Wen, Y.; He, X. Improving Clock Prediction Algorithm for BDS-2/3 Satellites Based on LS-SVM Method. Remote Sens. 2019, 11, 2554. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, X.; Gao, Y.; Zhang, J.; Wang, S. Hydrogen Atomic Clock Difference Prediction Based on the LSSVM. J. Eng. 2019, 2019, 9017–9021. [Google Scholar] [CrossRef]
- He, L.; Zhou, H.; Zhu, S.; Zeng, P. An Improved QZSS Satellite Clock Offsets Prediction Based on the Extreme Learning Machine Method. IEEE Access 2020, 8, 156557–156568. [Google Scholar] [CrossRef]
- Lei, Y.; Guo, J. A network structure design method for ELM and its application to prediction of satellite clock bias. J. Time Freq. 2015, 38, 209–215. [Google Scholar] [CrossRef]
- Ya, S.; Zhao, X.; Liu, C.; Chen, J.; Liu, C. Improved BDS-2/3 Satellite Ultra-Fast Clock Bias Prediction Based with the SSA-ELM Model. Sensors 2023, 23, 2453. [Google Scholar] [CrossRef]
- Sun, W.; Zou, Y. Short Term Load Forecasting Based on BP Neural Network Trained by PSO. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; Volume 5, pp. 2863–2868. [Google Scholar] [CrossRef]
- Du, L.; Chen, H.; Yuan, Y.; Song, L.; Meng, X. Global Navigation Satellite System Receiver Positioning in Harsh Environments via Clock Bias Prediction by Empirical Mode Decomposition and Back Propagation Neural Network Method. Sensors 2024, 24, 2342. [Google Scholar] [CrossRef]
- Sun, P.; Wei, D.; Sun, B. Genetic Algorithm Optimization in the Prediction of Satellite Clock Bias by BP Neural Network. Acta Astron. Sin. 2020, 61, 92–104. [Google Scholar] [CrossRef]
- Lv, D.; Ou, J.; Yu, S. Prediction of the satellite clock bias based on MEA-BP neural network. Acta Geod. Cartogr. Sin. 2020, 49, 993–1003. [Google Scholar] [CrossRef]
- Bai, H.; Cao, Q.; An, S. Mind Evolutionary Algorithm Optimization in the Prediction of Satellite Clock Bias Using the Back Propagation Neural Network. Sci. Rep. 2023, 13, 2095. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Wu, D.; Lei, Y. Neural Network Satellite Clock Bias Prediction Based on the Whale Optimization Algorithm. Adv. Nat. Comput. Fuzzy Syst. Knowl. Discov. 2022, 89, 1152–1160. [Google Scholar] [CrossRef]
- Ya, S.; Zhao, X.; Liu, C.; Chen, J.; Liu, C.; Hu, H. Enhancing Short-Term Prediction of BDS-3 Satellite Clock Bias Based with BSO Optimized BP Neural Network. Int. J. Aerosp. Eng. 2022, 2022, 1–18. [Google Scholar] [CrossRef]
- Lv, D.; Liu, G.; Ou, J.; Wang, S.; Gao, M. Prediction of GPS Satellite Clock Offset Based on an Improved Particle Swarm Algorithm Optimized BP Neural Network. Remote Sens. 2022, 14, 2407. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Z.; Qu, Y.; Li, L.; Wang, N. Improving Prediction Performance of GPS Satellite Clock Bias Based on Wavelet Neural Network. GPS Solut. 2017, 21, 523–534. [Google Scholar] [CrossRef]
- Wang, X.; Chai, H.; Wang, C. A High-Precision Short-Term Prediction Method with Stable Performance for Satellite Clock Bias. GPS Solut. 2020, 24, 105. [Google Scholar] [CrossRef]
- Ai, Q.; Xu, T.; Li, J.; Xiong, H. The Short-Term Forecast of BeiDou Satellite Clock Bias Based on Wavelet Neural Network. In China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume I, Proceedings of the CSNC2016, Changsha, China, 18–20 May 2016; Sun, J., Liu, J., Fan, S., Wang, F., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2016; Volume 388, pp. 145–154. [Google Scholar] [CrossRef]
- Zhang, J. Research of Satellites Clock Error Prediction Based on Neural Networks. Comput. Eng. Des. 2014, 35, 3254–3257. [Google Scholar]
- Wang, R.; Cai, H.; Pan, Z. Satellite Clock Bias Prediction Algorithm with Multi System Based on RBF Neural Network. J. Ocean Technol. 2019, 38, 56–61. [Google Scholar] [CrossRef]
- Gnyś, P.; Przestrzelski, P. Application of long short term memory neural networks for GPS satellite clock bias prediction. TASK Q. 2021, 25, 381–395. [Google Scholar] [CrossRef]
- Huang, B.; Ji, Z.; Zhai, R.; Xiao, C.; Yang, F.; Yang, B.; Wang, Y. Clock Bias Prediction Algorithm for Navigation Satellites Based on a Supervised Learning Long Short-Term Memory Neural Network. GPS Solut. 2021, 25, 80. [Google Scholar] [CrossRef]
- He, S.; Liu, J.; Zhu, X.; Dai, Z.; Li, D. Research on Modeling and Predicting of BDS-3 Satellite Clock Bias Using the LSTM Neural Network Model. GPS Solut. 2023, 27, 108. [Google Scholar] [CrossRef]
- Cai, C.; Liu, M.; Li, P.; Li, Z.; Lv, K. Enhancing Satellite Clock Bias Prediction in BDS with LSTM-Attention Model. GPS Solut. 2024, 28, 92. [Google Scholar] [CrossRef]
- Yang, S.; Yi, X.; Dong, R.; Wu, Y.; Shuai, T.; Zhang, J.; Ren, Q.; Gong, W. Long-Term Autonomous Time-Keeping of Navigation Constellations Based on Sparse Sampling LSTM Algorithm. Satell. Navig. 2024, 5, 15. [Google Scholar] [CrossRef]
- Liu, H.; Liu, F.; Kong, Y.; Yang, C. Improved SSA-Based GRU Neural Network for BDS-3 Satellite Clock Bias Forecasting. Sensors 2024, 24, 1178. [Google Scholar] [CrossRef]
- Liang, Y.F.; Xu, J.N.; Li, F.N.; Jiang, P.F. Nonlinear Autoregressive Model With Exogenous Input Recurrent Neural Network to Predict Satellites’ Clock Bias. IEEE Access 2021, 9, 24416–24424. [Google Scholar] [CrossRef]
- Liang, Y.; Xu, J.; Wu, M. Elman Neural Network Based on Particle Swarm Optimization for Prediction of GPS Rapid Clock Bias. In China Satellite Navigation Conference (CSNC 2022) Proceedings, Proceedings of the CSNC 2022, Beijing, China, 25–27 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; Volume 910, pp. 361–371. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Pan, X.; Zhao, W.; Huang, W.; Zhang, S.; Jin, L. Short-term prediction of satellite clock bias based on improved self-attention model. J. Chin. Inert. Technol. 2023, 31, 1092–1101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).