Abstract
Lidar technology plays a pivotal role in lunar exploration, particularly in terrain mapping, 3D topographic surveying, and velocity measurement, which are crucial for guidance, navigation, and control. This paper reviews the current global research and applications of lidar technology in lunar missions, noting that existing efforts are primarily focused on 3D terrain mapping and velocity measurement. The paper also discusses the detailed system design and key results of the laser altimeter, laser ranging sensor, laser 3D imaging sensor, and laser velocity sensor used in the Chang’E lunar missions. By comparing and analyzing similar foreign technologies, this paper identifies future development directions for lunar laser payloads. The evolution towards multi-beam single-photon detection technology aims to enhance the point cloud density and detection efficiency. This manuscript advocates that China actively advance new technologies and conduct space application research in areas such as multi-beam single-photon 3D terrain mapping, lunar surface water ice measurement, and material composition analysis, to elevate the use of laser pay-loads in lunar and space exploration.
1. Introduction
The Moon, as the closest celestial body to Earth, has become one of the primary targets for astronomical and space exploration activities. The essential requirements for lunar exploration include powerful high-thrust launch capabilities, sophisticated precision guidance and navigation systems, and robust long-range communication infrastructure. These challenges are intricately linked to the enduring aspirations of aerospace technology’s advancement. Lunar exploration is a pivotal gateway and catalyst for the rigorous testing and innovative advancement of these technologies. On 12 September 1959, the Soviet Union achieved a historic milestone by successfully launching Luna 2, the first spacecraft to make a hard landing on the lunar surface [1]. This event heralded the dawn of direct human engagement with the Moon and sparked an intense, 18-year-long rivalry between the United States and the Soviet Union in the realm of lunar exploration. Throughout this era, a succession of pioneering lunar exploration missions achieved groundbreaking milestones, including circumlunar flights, hard and soft landings, the deployment of lunar rovers, and the historic human landing. These accomplishments laid a solid foundation for various spacefaring nations to formulate plans for a return to the Moon in the 1990s. Furthermore, these ventures offered invaluable insights that significantly influenced the inception of China’s lunar exploration initiatives in the early 21st century, most notably the renowned Chang’E Program [2].
The Chang’E Program is meticulously structured into three stages: ‘Unmanned Lunar Exploration’, ‘Human Lunar Landing’, and ‘Establishment of a Lunar Base’. Eminent academician Ouyang Ziyuan has underscored the importance of initially concentrating on the ‘Unmanned Lunar Exploration’, which itself is delineated into three technological milestones: (1) Lunar Orbital Exploration; (2) Lunar Soft Landing Exploration and Automatic Surveying and Mapping; and (3) Lunar Surface Automatic Sampling and Return. Ouyang Ziyuan has delineated 14 pivotal lunar scientific inquiries, encompassing the composition and genesis of the lunar atmosphere, its dynamical evolution, the lunar ionosphere, and the diverse topographical and geomorphological features of the Moon. He also addresses the lunar and surface environment, the provenance and distribution of lunar regolith, the principal rock types and their lunar distribution, the enigma of lunar water ice, the geological stratification of the lunar surface, the Moon’s internal structural layering and its formative processes, the heterogeneity of the Moon’s internal material distribution, the evolution of the Moon’s global intrinsic dipole magnetic field, the Moon’s internal energy and material evolution, key events in lunar history, and the origins of the Moon and the Earth–Moon system [3]. Notably, laser technology plays a dual role in lunar exploration: it aids in precision guidance, navigation, and control; and serves as a vital detection tool for investigating scientific questions such as the lunar atmosphere’s composition and lunar topography. Table 1 encapsulates the significant laser payloads utilized in lunar exploration from 1970 to 2023.

Table 1.
The significant laser payloads utilized in lunar exploration from 1970 to 2023 [4].
With the successful implementation of the Chang’E-5 mission, China has achieved the three developmental milestones of lunar exploration missions: lunar orbiting, lunar surface landing/roving, and lunar surface sampling and return. Throughout these missions, laser payloads have played a crucial role in precise guidance, navigation, and control. With the Chang’E Program entering a new stage of ‘Human Lunar Landing’, the significance of laser technology is set to escalate further. Therefore, summarizing the current laser technology used in lunar exploration both domestically and internationally, and forecasting the future trends of laser technology development, can provide references for the implementation of tasks in the new phase of crewed lunar exploration.
Integrating the laser technologies employed in these lunar missions, they can be broadly classified into three categories: (1) laser altimeters and rangefinders that serve in topographic mapping and distance measurement; (2) laser 3D imaging sensors designed for terrain mapping and obstacle avoidance systems; and (3) laser velocity sensors for the autonomous navigation and hazard evasion capabilities of landing modules. Presently, the lunar-based laser payloads are mainly lidar systems. The following discussion will provide a detailed overview of the instrumentation and operational status of each lidar payload within the Chang’E lunar exploration initiative.
2. Altimeters for Chang’E-1 and Chang’E-2
The Chang’E series of lunar missions is outfitted with advanced laser-ranging sensors that fulfill pivotal roles at different stages of lunar exploration. Chang’E-1 and Chang’E-2 focus on accurately measuring the satellite’s proximity to the Moon’s surface, a task essential for creating detailed topographic maps of the Moon’s entirety. Meanwhile, the later missions, from Chang’E-3 to Chang’E-5, prioritize the use of these sensors during the lunar landing phase, where they are instrumental in measuring the satellite’s altitude relative to the surface, ensuring a precise and secure touchdown. The Chang’E-1 spacecraft, launched on 24 October 2007, from the Xichang Satellite Launch Center, stands as a testament to the precision achievable with laser altimetry in lunar missions. It operated in lunar orbit for 495 days, from its launch until its controlled lunar impact on 1 March 2009, successfully executing a variety of scientific exploration tasks. A highlight of Chang’E-1’s payload was China’s first laser altimeter in a satellite configuration, which provided critical topographic data by measuring the altitude of the lunar surface directly beneath the satellite. These data were then integrated with the satellite’s orbital elements and the celestial coordinates of the Earth and the Moon through an intricate data processing procedure in conjunction with ground systems, culminating in the acquisition of detailed lunar topographic information.
2.1. Instrument
2.1.1. Hardware Configuration
The Chang’E-1 lunar mission features an advanced laser altimeter system, elegantly divided into two core components: an optical probe and an electronic circuit box, with key equipment specifications outlined in Table 2 [5]. The device’s primary function is to meticulously record the precise distance between the satellite and the lunar surface target, thereby contributing invaluable data to our understanding of the Moon’s topography. The laser altimeter operates on a refined measurement principle. It emits a pulsed laser beam toward the lunar surface, and the optical system captures the light that is scattered back. A photoelectric detector then converts a portion of the emitted pulse and the reflected laser signal into an electric signal. This conversion simultaneously initiates and halts the timing mechanism of the ranging counter, which measures the light pulse’s round-trip flight time. The distance to the lunar surface is subsequently calculated using the formula , where c is the vacuum speed of light and is the round-trip time of the laser pulse, providing an accurate measurement of the satellite’s altitude above the Moon.

Table 2.
Main parameters of Chang’E-1 satellite laser altimeter.
The laser altimeter is precisely synchronized to a timing sequence generated by its onboard computer. At the behest of the total synchronization pulse, the laser dispatches a pulse once per second, initiating the time measurement circuit with a main wave start signal. The returning signal, once detected, is amplified, and processed to produce an output pulse that signals the time measurement circuit to halt its count. The onboard computer then retrieves the count, utilizing these data to calculate the precise distance from the altimeter to the lunar surface. In parallel, the computer engages with the payload data management system to receive data injections, thereby executing monitoring and control tasks for the laser altimeter’s principal operational parameters. The system’s architecture is comprehensively detailed in the block diagram presented in Figure 1.
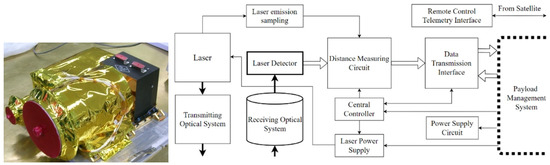
Figure 1.
The photo and diagram of the laser altimeter [5].
The laser altimeter’s system diagram highlights its core components: a laser assembly and an accompanying laser beam expander. This laser system marks the first application of Chinese laser technology in space, realized through innovative technical pathways: (1) diode-pumped solid-state Nd: YAG laser; (2) a resonant cavity and linear structure formed by right-angle prisms and plane mirrors; and (3) active electro-optic Q-switching for precise pulse emission. To address the substantial distance measurements required by the spaceborne laser altimeter, the laser pulses are engineered for high instantaneous power and a tightly controlled divergence angle. They undergo a refinement process within the beam expander, which is essential for collimating the beam and compressing its divergence to an even finer degree. Specifically, the beam expander is designed to increase the beam diameter by five, resulting in an ultra-precise divergence angle of 0.6 milliradians for the expanded beam. The principal performance metrics of the laser emitting system are detailed in Table 3.

Table 3.
Main parameters of laser emitting system.
The receiving system of the laser altimeter consists of a receiving telescope and a receiving circuit. The telescope is used to efficiently converge the light reflected from the target onto the detector. Considering the long detection distance required by the onboard equipment and the limited resources of the platform, the laser altimeter adopts a large aperture and a compact double aspherical reflective Cassegrain telescope design. The telescope is followed by a set of relay mirrors to converge the light collected by the telescope onto the detector, in which a front cut-off filter and a narrow-band filter are inserted to suppress the background noise.
The laser altimeter operates at a wavelength of 1064 nm, using a domestically produced SPD-0522 near-infrared enhanced avalanche photodiode as its detector. This avalanche photodiode converts the optical signal into an electrical signal, which is then amplified by a matching amplifier. A threshold detector comparator subsequently processes the amplified signal, which detects the target signal and triggers the time-counting circuit to stop timing. Additionally, the laser altimeter includes a signal peak sampling circuit. This circuit samples the peak value of the lidar signal returned from the lunar surface, providing a measure of the reflected intensity of the laser energy from the lunar surface. The key performance parameters of the receiving system are presented in Table 4.

Table 4.
Main parameters of laser receiving system.
The operational environment of the Chang’E-1 satellite is inherently complex, characterized by factors such as solar irradiation, ultraviolet radiation, vacuum conditions, extreme temperatures, plasma, and charged-particle radiation. These environmental conditions can significantly impact the satellite’s system performance. Therefore, the influence of the space environment on the system’s structural integrity, optical components, and circuitry has been thoroughly considered. Space-adaptive design strategies have been implemented, and a series of environmental simulation experiments have been conducted to ensure the hardware performance and reliability of the system under these harsh conditions.
2.1.2. Critical Technologies
The primary function of the laser altimeter is to perform ranging operations at an altitude of 200 km from the lunar surface. However, the direct measurement of its operational capability on the ground is not feasible. Consequently, it is essential to calibrate its ranging accuracy and maximum range through indirect methods on the ground to verify its capability. The ground-based calibration of the laser altimeter, such as ranging uncertainty and maximum range, is crucial as it directly influences the final performance [6]. This calibration process is therefore considered a vital technology in ensuring the effectiveness of the altimeter for its intended lunar mission.
Ranging uncertainty encompasses several components: the quantization error due to counting time resolution , errors arising from the instability of the timing crystal , distortions in the lidar ranging signal , and systematic residual errors from calibration . The first three of these four error components are independent random events, while the fourth is a fixed systematic error. Therefore, the total uncertainty δ of the laser altimeter can be expressed using the formula . These components can be tested and calibrated on the ground. The quantization error due to counting time resolution includes the errors in both the main wave start time and the lidar return stop time. With the system’s counting crystal frequency of 155.2 MHz, the quantization ranging error can be calculated to be approximately 0.422 m. The error arising from the instability of the timing crystal is . The laser altimeter employs a temperature-compensated crystal with a time-base stability of of 1.5 × 10−6, resulting in a counting uncertainty of 0.3 m at an altitude R of 200 km. The ranging error due to the distortion of the ranging signal and the jitter of the rising edge are primarily attributed to the time delay differences caused by changes in the return signal amplitude, signal pulse width, and noise. The cumulative ranging error from these sources does not exceed 0.66 m. The systematic ranging residual error is the remaining error after the laser altimeter’s calibration to correct systematic errors. Measurements show this error does not exceed 1 m. According to the formula, the ranging uncertainty of the altimeter can be calculated, yielding a value of m.
The maximum range can be calibrated using an extinction ratio simulation test in the external field, or a target return signal simulator. According to the formula , the maximum range is related to the laser emission power , the optical system efficiency , the two-way atmospheric transmittance , the target reflectivity , the system receiving aperture , and the system’s minimum detection power . The maximum range of the laser altimeter can be calibrated by determining the system’s minimum detection power and incorporating the target and environmental characteristics. The outfield extinction ratio simulation test involves simulating the target ranging under known environmental conditions, distances, and target characteristics. The received target echo is matched to the system detection sensitivity to determine the required extinction ratio, thereby projecting the laser altimeter’s maximum range under specified conditions. For a known distance and reflectivity of the surface target, an optical attenuation sheet is placed in the laser receiving path to reduce the probability of detection to 95%. The amount of optical attenuation in the laser receiving path at this point is referred to as the extinction ratio (ER). The minimum detection power is calculated using the formula , where is the known target distance. Target return signal simulation for direct detection involves determining the detection sensitivity of the laser altimeter when all other parameters have been established. This is achieved using specialized equipment, after which the maximum range of the system can be calculated using a distance formula. For the Chang’E-1 laser altimeter, a dedicated simulator has been developed, and its diagram is presented in Figure 2.
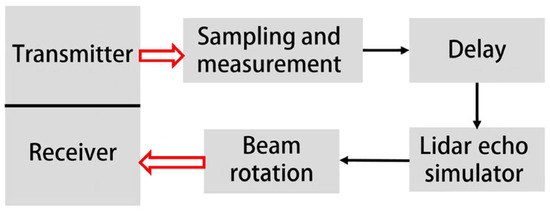
Figure 2.
The diagram of target return signal simulator [6].
The maximum ranges of the Chang’E-1 laser altimeter, as measured using these two methods, are 279.773 km and 308.09 km, respectively.
2.1.3. Algorithm Description
The laser altimeter directly converts the time elapsed between the transmission and reception of the laser pulse during satellite orbit into a distance value. This distance information is used to create a digital elevation model (DEM) of the lunar surface. The process involves several steps, including the elimination of invalid data, system corrections, geometric localization, elevation calculation, data filtering, and interpolation and mapping of the data [7].
To make the distance information obtained by the laser altimeter meaningful, it must be accurately mapped to a specific spatial position, a process known as geometric localization. Geometric localization involves constructing and solving observation equations based on various parameters, including satellite orbit data, satellite attitude data, instrument geometric parameters, instrument mounting parameters, and lunar rotation, and pointing data at the time of data acquisition. The Chang’E-1 orbit data are referenced in the geocentric J2000 coordinate system, the attitude is provided in the orbital coordinate system, and the geometric parameters of the altimeter mounting are defined in the satellite body coordinate system. All measurements from these different coordinate systems are uniformly transformed into the lunar-fixed coordinate system to compute the geometric position of the laser footprint. Subsequently, the lunar-fixed coordinate data of the footprint on the lunar surface are converted to the lunar geodetic coordinate system to obtain the corresponding geographic coordinates and elevation values. The lunar geodetic system employs a spherical lunar-fixed coordinate system, with a reference ellipsoid defined as a sphere of radius 1737.400 km. The prime meridian is aligned with the apparent center of the lunar near side, and latitude and longitude are defined like Earth.
Due to errors in instrument system noise, lunar surface topography, and satellite orbit and attitude measurements, the raw data inevitably contain inaccuracies. These errors propagate and may be amplified during the processing from raw data to the DEM, leading to significant elevation anomalies or even severe distortions in the altimetry data. Since random noise cannot be fully removed during preprocessing, further filtering is required. The effectiveness of the filtering process is directly related to the terrain’s degree of relief. To efficiently filter out anomalous elevation data, the lunar surface can be divided into four regions: the South Pole (60°S to 90°S), the North Pole (60°N to 90°N), the mid-latitude lunar mare (70°S to 70°N, 95°W to 95°E), and the mid-latitude lunar highlands (70°S to 70°N, 180°W to 85°W, and 85°E to 180°E). Different elevation thresholds are applied for filtering in each region. The filtering process consists of two stages: single-track filtering and regional filtering. In single-track filtering, a geostatistical approach is used, where the mean and standard deviation of each elevation point and its neighboring data points are calculated. Points where the difference from the mean exceeds a certain threshold are identified as outliers and excluded. The threshold is region-specific; for example, two times the standard deviation might be used for relatively flat lunar mare regions, while four times the standard deviation might be appropriate for areas with significant terrain variation. After single-track filtering, the elevation data are merged and subjected to regional filtering using a moving surface fitting method. First, for each DEM grid point, the elevation points within a certain radius are used to determine an initial fitting surface using the least-squares method. The fitted elevation value and the standard deviation of the initial fitting surface are calculated, and points where the difference between the actual and fitted elevation exceeds a given threshold are filtered out. The remaining points are then used to determine a least-squares quadratic surface, and the process is repeated. The thresholds for regional filtering are set similarly to those used in single-track filtering.
After data filtering, the anomalies in the laser altimetry data are eliminated. To generate a global elevation model on a regular grid, it is necessary to interpolate the elevation data at different resolutions. Commonly used interpolation algorithms include the Kriging method [8,9], radial basis function method [10], minimum curvature method [11], nearest neighbor method [12], triangular section method with linear interpolation [13], and others. Li et al. conducted experiments and comparisons on various interpolation algorithms, including internal consistency accuracy, elevation rendering maps, and topographic profiles. The results indicated that the Kriging method achieved the highest internal consistency accuracy of within 200 m and demonstrated the optimal application effect on Chang’E-1 satellite data [14]. In the Kriging method, the elevation at the interpolation point is estimated as a linear combination of the elevations at the nearby sampled points, expressed as . The Kriging method ensures that this estimate is unbiased and minimizes the estimation variance by determining the appropriate weighting coefficients for each point. However, the interpolation process cannot indefinitely enhance the spatial resolution of the global lunar DEM. Experimental evaluations of elevation data measurement errors and DEM accuracy at different grid sizes have shown that selecting a 3 km grid size for global DEM mapping meets the required elevation measurement accuracy. When generating the global DEM, we continued to use the regional filtering strategy applied during the data filtering process. The final 3 km spatial resolution global DEM model was obtained by mosaicking the four regions, as shown in Figure 3 [14].
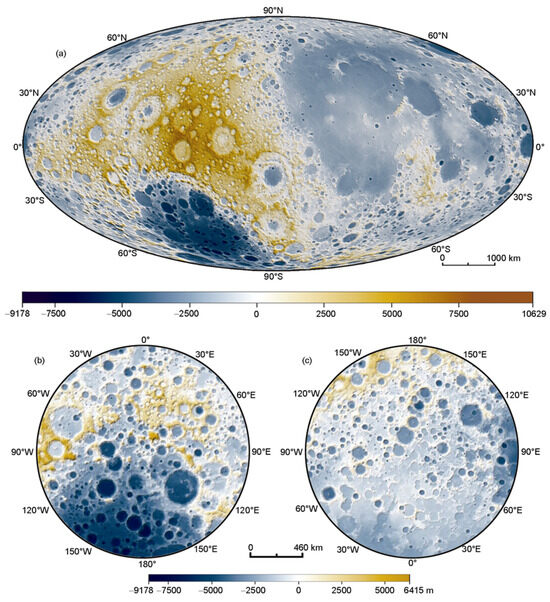
Figure 3.
The DEM model was generated from the Chang’E-1 laser altimeter elevation data [14]. (a) A Digital Elevation Model (DEM) of the entire lunar surface created using data from the CE-1 satellite laser altimeter. (b) A DEM model of the lunar surface in the region of the South Pole, spanning from 60°S to 90°S latitude. (c) A DEM model of the lunar surface in the region of the North Pole, spanning from 60°N to 90°N latitude.
It is worth mentioning that the radial topographic error of the obtained DEM is related not only to the ranging uncertainty mentioned earlier but also to a variety of factors, including orbital altitude errors, star tracker errors, timing measurement errors, and so on. Moreover, due to the divergence angle of the laser, the laser spot projected onto the rugged lunar surface is effectively a circular surface. The divergence angle of the Chang’E-1 laser altimeter is 0.6 mrad, and with an operational altitude of approximately 200 km, the laser footprint has a diameter of about 200 m. Therefore, each laser ranging measurement represents the average elevation of a 200 m diameter circular area on the lunar surface.
2.1.4. Results
The raw data for this DEM model were collected between 28 November 2007 and 4 December 2008, totaling approximately 9.12 million soundings. These data cover the entire lunar surface, ranging from 180°W to 180°E and between 90°S and 90°N latitudes. The projection used is a Mollweide equal-area pseudo-cylindrical projection [15] with a central meridian at 270°W, where the left half represents the far side of the Moon and the right half represents the near side. The lunar coordinate system is based on the selenocentric homopolar axis system, with the elevation reference surface defined as a sphere with a radius of 1737.4 km centered at the Moon’s center of mass. The spatial resolution of the DEM is 3 km. The global maximum elevation difference on the Moon is 19.807 km. The highest point is located on the uplift structure between the Korolev and Dirichlet–Jackson basins (158.656°W, 5.441°N, +10.629 km), while the lowest point is within the South Pole-Aitken Basin (172.413°W, 70.368°S, −9.178 km). The two subplots illustrate the DEM models of the lunar polar regions derived from the laser altimeter data. The left subplot depicts the DEM model of the lunar surface in the region from 60°S to 90°S at the Moon’s south pole, while the right subplot shows the DEM model of the region from 60°N to 90°N at the north pole. Both subplots use a polar-spherical isotropic projection centered on the pole, with the 70° latitude line as the isotropic deformation line. The lunar coordinate system, elevation reference plane, and reference origin are consistent with those used for the global DEM images, and both have a spatial resolution of 3 km.
2.2. Introduction to International Progress
Similar laser-ranging sensors have been deployed on several missions, including the Apollo 15 to 17 missions, the Clementine lunar orbiter, the Lunar Reconnaissance Orbiter (LRO) launched by the United States in 2009, India’s Chandrayaan series of satellites, and Japan’s SELENE (or Kaguya) satellite. Notably, the LRO carries a Lunar Orbiter Laser Altimeter (LOLA), which has produced the highest density measurement data to date, resulting in a detailed three-dimensional topographic map of the lunar surface [16].
LOLA leverages a Neodymium-doped yttrium aluminum garnet (Nd: YAG) laser for its light source, coupled with a unique five-beam emission capability. This configuration significantly enhances both the data acquisition rate and the horizontal resolution of the measurements. LOLA’s system architecture includes a diffractive optical element (DOE) that is instrumental in achieving the multi-beam laser emission. The DOE is the core of the system, dividing a single laser beam into five distinct beams. To capture the return signals from these beams, five detectors are strategically positioned at the focal plane, allowing for the simultaneous detection of all five beams.
This innovative design yields a dual benefit: it not only provides denser elevation data but also captures valuable insights into the lunar surface’s slope and roughness. The arrangement of the five beams in a plane enables the system to discern the relative positions of the beam spots, offering a more comprehensive understanding of the lunar terrain. In essence, LOLA’s sophisticated setup transforms the way we gather and interpret lunar topographical data, paving the way for more detailed and accurate lunar mapping.
The method of LOLA for deriving lunar surface elevation is analogous to that used by the Chang’E-1 altimeter. By using the lunar surface elevation as a reference, the slope can be further determined. Employing the principle that three points can form a plane, the least-squares plane fitting method applied to collections of 4–10 points enables differential slope measurements. Lunar surface roughness measurements are derived from the temporal broadening of the backscattered signal. It has been observed that surface-reflected echoes, with a 30 cm (rms) variation in height, exhibit a significant broadening of the echo pulse width when compared to those reflected from flat ground. The relationship between signal broadening and surface roughness is established during pre-launch calibration. LOLA is capable of estimating surface roughness down to 1 m by monitoring the pulse width at the threshold crossing of the backscattered pulse. The instrument’s function for measuring lunar surface reflectivity was primarily designed to detect lunar surface ice. This is achieved by calculating the ratio of the reflected echo pulse to the transmitted pulse energy to determine the surface reflectance at that laser wavelength. Since the instrument was not designed for in-flight self-calibration, the relative measurements of lunar surface reflectance are based on pre-launch calibration data.
To illustrate the performance of the Chang’E-1 laser altimeter, a comparative analysis was conducted on the DEM results obtained from different instruments near the launch year, as shown in Table 5.

Table 5.
Comparison of results obtained from different lunar altimeters.
3. Laser 3D Imaging Sensor for Chang’E-3, Chang’E-4, and Chang’E-5
3.1. Instrument
The Chang’E-3 probe is China’s first soft-landing mission on an extraterrestrial body and the world’s first successfully realized autonomous obstacle avoidance for soft-landing on an extraterrestrial body using laser three-dimensional imaging technology. Since the launch of the Chang’E-3 mission, the Chang’E series of landers have been equipped with laser 3D imaging sensors (L3DIS). The L3DIS is an important payload carried by the Chang’E lander, which is used to obtain an accurate 3D mapping of the landing area in the field of view within a very short imaging time during the soft landing, hovering, and obstacle avoidance sections, thus completing the precise obstacle avoidance during the descending hovering section of the lander and guaranteeing a highly reliable and safe soft landing on the lunar surface of the lander.
3.1.1. Hardware Configuration
The L3DIS mainly consists of laser emission, laser deflection, laser reception, and time measurement units, as shown in Figure 4 [19,20]. The laser emission is composed of the laser control and drive, the laser source, and the DOE. A semiconductor laser is driven by a laser driver to emit a short pulse, which is beam-split into two parts. One part is received by the main wave detector, which starts the time measurement unit and records the start time of the laser pulse; the other part is formed into a 16-channel laser after DOE splitting, which is emitted out of the system through the laser deflection structure.
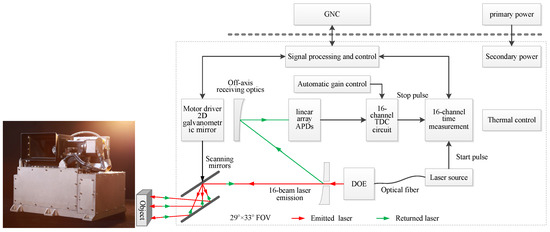
Figure 4.
The diagram of the L3DIS [19,20]: the red and green arrows represent the emitted and returned laser.
The laser deflection system consists of a horizontal galvanometer, a vertical galvanometer, and a driving motor, which is a two-axis scanning mechanism. The galvanometer adopts a dynamic magnetic structure, which is small, easy to dissipate heat, has good frequency characteristics, and can achieve rapid oscillation. The laser incident on the galvanometer is a 16-beam equirectangularly spaced line array laser after beam splitting, and the far-field spots are shown in Figure 5b. The installation of the double galvanometer is shown in Figure 5a (only showing the rotation axis and double galvanometer). The installation axes of the two mirror motors are perpendicular. The lower scanning mirror is recorded as the X scanning mirror, and the upper scanning mirror is recorded as the Y scanning mirror. The scanner body coordinate system follows the right-hand Cartesian coordinate system. The initial position of the X and Y scanning mirror is at an angle of 45° to the XOZ plane, and the scanning mirror can swing along its axis. The angular spacing of the emitted 16 beams is 2 mrad, and the direction of the 16 beams is arranged parallel to the X mirror. Ideally, the line laser will be incident on the axis of the X mirror, and after reflection, it will be refracted again by the Y mirror before being irradiated onto the imaging target. The X mirror achieves sinusoidal reciprocating oscillation, while the Y mirror achieves unidirectional motion from a negative maximum angle to a positive maximum angle, thereby achieving two-dimensional scene coverage. The entire field of view of the scanner can achieve 29° × 33° with the help of dual mirrors.
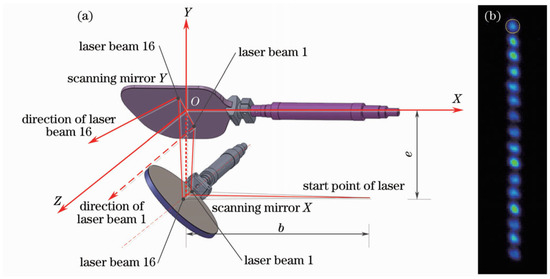
Figure 5.
Schematic diagram of double galvanometers: (a) dual mirrors with rotation axis; (b) 16-beam spots in far-field [19,20].
The returned laser pulse is reflected by the target surface, which is collected by a coaxial telescope, and the echo signals of multiple laser channels are detected by a highly sensitive line array avalanche photodiode (APD), and the end time of this pulse is recorded through the analog-to-digital conversion of the shaping circuit. A time interval measurement is then performed, and the ranging values of different channels are obtained. Using the ranging values of the multiple channels measured, combined with the angular measurements of the double galvanometers, the 3D point cloud can be computed by the geometric model of the L3DIS.
3.1.2. Algorithm Description
Compared to single-beam laser scanning, the geometric model of multi-beam laser 3D scanning is more complex, mainly involving two processes: the measured 3D point cloud is computed in the scanner coordinate system and transformed from the scanner coordinate system coordinates to the user coordinate system.
Figure 6 illustrates the geometric model of the L3DIS. The 3D point cloud can be computed using the raw observation of the horizontal and vertical angles and ranges of the 16 channels. The origin of coordinate O is set as the laser emission origin. OX and OY are the centers of the dual mirrors. θk is the angle between OS and OOX. S’ is the intersection of the second mirror and the reflection of the beam. O’ is the symmetry point of the lower mirror of O, while O” is the symmetry point of the top mirror of O’. P is laser spots on a target’s surface. Then, we can define the geometric model of the scanner as OY-XYZ, and the user coordinate system as O’-XYZ. R is the length of the PS’. According to the geometric relationship, the raw observations (R, θx, θy) can be calculated to the coordinates of point P (XP, YP, ZP) in the scanner coordinate system [21], shown as Equation (1), where e is the distance between the centers of the two galvanometric mirrors.
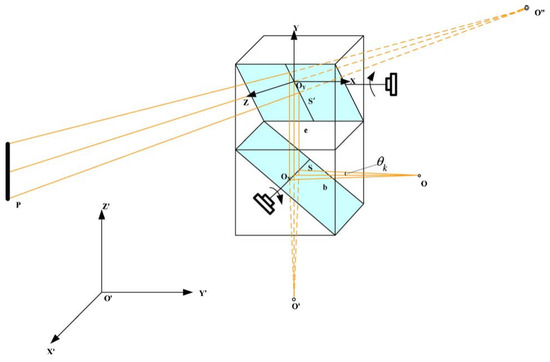
Figure 6.
The geometric model of the L3DIS [21].
The coordinates of point P in the user coordinate system can be transformed through from Equation (2) to Equation (6), where (, , ) is the translation matrix and M is the rotation matrix calculated using three rotations about X, Y, and Z axis (i.e., ω, φ, and κ).
For 3D lidar with complex structures, errors in the design and manufacture of the instrument will lead to measurement errors, such as the physical characteristics of laser ranging, the laser beam divergence angle, the detector sensitivity, and the asynchrony between the scanning mechanism and the rangefinder. The measurement accuracy of 3D laser scanning is greatly affected by systematic errors, mainly in the measurement of the distance and horizontal and vertical angle of the main factors affecting the measurement, including random errors and systematic errors. For the distance, this involves the deviation of the starting position in laser emission due to electronic and mechanical errors, single channel ranging errors, and inter-channel ranging deviations; while for the angle, it involves the angle measurement error of the motors, the synchronization accuracy of the two motors, the installation error of the two galvanometers, and the incomplete perpendicularity of the two motor axes. For a multi-beam lidar with two galvanometers, the axial error and synchronization problem of the two galvanometers are the main influencing factors, which lead to horizontal deviation and vertical alignment between the scanned strips. Referring to terrestrial laser scanners [22], the distance and angular error terms of multi-beam lidar can be modeled with additional parameters having constant offset error and scale factor error to model the system error [21].
For the systematic errors of the multi-beam lidar, plane-based self-calibration can optimally estimate both systematic error parameters and planar feature parameters, and then accurately correct for significant systematic errors. It was first used by Rietdorf for the calibration of terrestrial 3D laser scanners [23]. It has the advantage of providing highly redundant observations in the plane, making it easier to find and extract planar objects, which are more suitable for multi-beam laser scanning [24]. Based on the point-on-plane condition [25], the point i on the plane k in a scanning position j can be computed using a rigid-body transformation between the scanner coordinate system and the user coordinate system, as shown in Equation (7), where the normal parameter of the plane can be obtained using least-squares plane fitting, as shown in Equation (9).
where is the coordinates of point i in the scanning position j and is the center of the scanner position j. The least-squares method is then used to minimize the distance from the point to the plane. This method requires laying some planar targets in the calibration field and obtaining high-precision reference data, which we used to accurately calibrate the lidar [7,21].
3.1.3. Results
To achieve a soft landing of the Chang’E lander, an L3DIS was installed on the lander. When the Chang’E-3 lander hovers at a height of approximately 100 m above the Moon’s surface, the L3DIS obtains a 3D point cloud of the landing area below the lander to avoid obstacles and accurately land in a flat area. The payload adopts 16 beamlets split from a laser beam and scanned using a two-axis galvanometric mirror to achieve a 3D terrain with a rate of 4 frames/s. The energy of a single laser beam is 5 μJ. The laser repetition frequency is 50 kHz and the receiving system diameter is 33 mm. The ranging accuracy is better than 0.15 m and the scanning field of view reaches 29° × 33°. Figure 7 shows a 3D map detected during the final stage of the Chang’E-3 soft landing. The final landing point was selected in a relatively flat area.
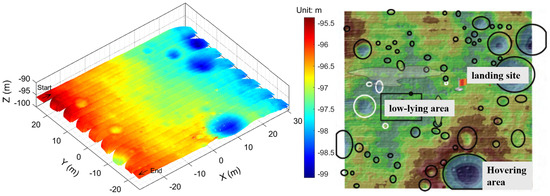
Figure 7.
The measurement results of the L3DIS during the landing process of Chang’E-3 [21]: the white circles represent low-lying areas and black shapes represent craters.
3.2. Introduction to International Progress
In the early 1990s, NASA Johnson Space Center (NASA-JSC) conducted research on using lidar to scan and image the landing area for obstacle detection and avoidance [26], and the Jet Propulsion Laboratory (JPL) [27,28] further investigated the use of lidar for autonomous obstacle avoidance and safe landing on Mars and verified it through mathematical simulations. Meanwhile, Lafontaine et al. [29,30,31,32] from the Sherbrooke University in Canada also studied the navigation and obstacle avoidance of planetary autonomous landing using 3D laser imaging. In 2006, NASA initiated the Autonomous Landing and Hazard Avoidance Technology (ALHAT) project to meet the requirements for autonomous landing of probes on the Moon, Mars, and even asteroids [33]. Lidar-based terrain-relative navigation is one of the core technologies of ALHAT. NASA has specially developed a flash-lidar for ALHAT and has conducted extensive testing and validation of precise landing with this sensor [34,35,36]. Finally, closed-loop flight tests have shown that the ALHAT system based on this lidar has reached or even exceeded NASA’s Level 6 Technology Readiness Level (TRL) [37]. The “Peregrine Falcon” lunar probe launched by the United States in 2024 is equipped with this new 3D imaging system.
The flash-lidar uses a two-dimensional detector array to detect laser pulses returning from the target. The detector’s Readout Integrate Circuit (ROIC) simultaneously measures the time of the laser pulse as each pixel arrives. Therefore, each flash of the laser generates a 3D image of the target illuminated by the laser, which can provide a higher image frame rate, eliminate the need for fast laser beam scanning, and mitigate the effects of platform motion. The system integrates a 3D imaging camera based on an indium gallium arsenide avalanche photodiode and novel microelectronics technology, with a 128 × 128 pixel array that operates at a rate of 20 frames per second. The system is also equipped with a high-pulse energy 1.06 μm Nd:YAG laser; a remote laser safety termination system; high-performance transmitter and receiver optics with 1° and 5° fields of view (FOVs), respectively; an enhanced in-built thermal control; and a set of compact and self-contained support electronics packaged in a box and built around a PC-104 architecture for autonomous operation. The key technical parameters of the system are shown in the Table 6.

Table 6.
Main parameters of Gen 2.2 Flash Lidar.
Based on the developed flash-lidar, Roback et al. carried out experimental validation on a ground orbit, a helicopter, and a rocket propulsion Vertical Test Bed (VTB) vehicle. All large features, such as craters and rocks, were clearly shown on the obtained DEM and located in the same position as they are on the real DEM. By comparing the diameters and heights of the six small features (rocks) with those measured in the real DEM, five of these six rocks can be identified, and the one target that cannot be identified is under the threshold of less than 30 cm [36].
5. Key Technological Development Trends
Laser detection technology for lunar and space applications will continue to be widely used due to its advantages in distance, angular resolution, and spectral detection capabilities. A higher spatiotemporal resolution and an increased detection efficiency and accuracy will be important development directions for future space laser payloads. Through an analysis of the current research status at home and abroad, combined with the demand for new types of data from applied research institutions, this paper summarizes several key technological development trends as follows.
5.1. Novel Space Laser
The laser system is a critical component of space laser payloads, and its specific technological routes generally fall into two categories: high-energy, low-repetition-rate laser technology; and low-energy, high-repetition-rate laser technology. Among them, laser payloads based on low-energy, narrow-pulse, high-repetition-rate laser technology have advantages such as large observation data volume, high ranging accuracy, and high density of standard point data. This matches well with the high-density point cloud data required for three-dimensional detection and has become a development trend in laser ranging technology both domestically and internationally. High-repetition-rate laser ranging aims not only to increase the success rate of echo detection in single-range measurements, but also to increase the amount of detection data by improving the ranging frequency, thereby enhancing the measurement accuracy. Additionally, using lasers with high repetition rates, picosecond-level pulse widths, and low single-pulse energy also offers advantages such as high reliability, small size, and low maintenance costs, making them suitable for space applications.
5.2. Near-Infrared Single-Photon Detection
The two major systems of existing space laser detection technology, linear and single-photon detection technology, can both achieve a centimeter-level ranging resolution. However, single-photon detection technology has lower requirements for single-pulse energy. Under the same laser average power limitation, it can increase laser repetition rates and the number of beams, thereby increasing the density of ground points along and across the track. Taking the ICESat-2 Earth mapping satellite as an example, its photon-counting laser radar payload ATLAS has achieved nearly continuous observations along the track direction using a single-photon detector with a single-pulse laser energy of only 40–170 μJ. Considering that ATLAS is still based on a 532 nm laser emission wavelength, under the same single-pulse energy, longer wavelengths result in more photons. For laser ranging and three-dimensional terrain detection, using longer-wavelength laser emissions can reduce the single-beam emission energy, and increase laser repetition rates, or the number of beams. Moreover, the most widely used Nd:YAG laser in space applications emits fundamental light at 1064 nm, which is in the near-infrared band. Using the same laser technology can further reduce energy losses in frequency-doubling processes. Therefore, breakthroughs in high-efficiency near-infrared single-photon detection technology are important technical approaches to further improve the efficiency of space laser ranging and three-dimensional measurement payloads, especially for the 1064 nm band. Alternative technologies include superconducting nanowire single-photon detection technology, quantum upconversion single-photon detection technology, InP-based single-photon detector technology, and mercury cadmium telluride single-photon detector technology, among others.
5.3. Multi-Beam Transmit–Receive Three-Dimensional Detection
Three-dimensional terrain detection aims for large-angle and high-resolution ranges to obtain more detailed terrain information about the measured object. In the future, three-dimensional terrain detection laser radar will inevitably evolve towards continuously distributed multi-beam directions. Taking the ICESat-2 Earth mapping satellite as an example again, although its photon-counting laser radar payload ATLAS has achieved nearly continuous detection along the track direction, for the across-track direction, due to the limited number of beams, the swath is still relatively sparse. To enhance the mapping density, NASA has proposed a new initiative known as the Lidar Surface Topography (LIST) program, which expands upon the six-beam photon-counting lidar technology of ICESat-2. Utilizing a push-broom approach with 1000 beams in the across-track direction, LIST aims to conduct single-photon detection with a horizontal resolution of 5 m over a 5 km swath. If successfully implemented, this could enable true laser-based three-dimensional imaging and detection of the Earth’s surface. This method is particularly effective for lunar and other space applications, where proximity allows for even better results.
5.4. Novel Laser Detection
According to the reflectance data of LRO payloads, the lunar permanently shadowed regions may contain water ice and other volatile substances on the surface, but this finding has not been definitively confirmed [42,43]. Understanding the composition, quantity, distribution, and morphology of water ice and other volatile substances related to lunar permanently shadowed regions is of great significance for future human exploration of the Moon, the utilization of lunar resources, and research into cosmic evolution, and has been identified as a strategic knowledge gap in NASA’s human exploration activities. Therefore, in December 2022, NASA launched a CubeSat small satellite to execute the Lunar Flashlight mission. This is the first planetary mission to explore water ice using active multi-frequency laser reflection technology. Lunar Flashlight operates four lasers with 1-millisecond pulse intervals, interspersing a millisecond without laser illumination to illuminate the permanently shadowed regions of the Moon and measure the surface reflectance at specific wavelengths absorbed by water ice. It distinguishes water ice from dry regolith in two ways: (1) spatial variations in reflectance, as differences in surface reflectance in different regions can help identify water ice; and (2) the ratio of reflectance between absorption and continuum spectral channels by comparing the reflectance in absorption and non-absorption bands of water ice (water ice and dry soil can be further distinguished). The mission will map the depth of water ice bands to distinguish compositional differences between permanently shadowed regions and sunlit terrains. In May 2023, due to propulsion system issues, the technology could not undergo on-orbit testing and verification.
Laser-Induced Breakdown Spectroscopy (LIBS) uses high-energy lasers focused onto the surface of the sample to ablate the sample and generate plasma, which is then collected using a device and transferred to a spectrometer for spectral analysis. The spectral data obtained using photodetectors can analyze the elemental composition and content of the sample in the computer based on the wavelength and intensity of the plasma emission spectrum. This technology has advantages such as simple sampling and rapid, in situ, remote, and synchronous analysis of all elements, and has important application prospects in coal detection, metallurgical analysis, biomedical applications, water quality testing, and other fields. The Mars rover “Curiosity”, part of the United States’ NASA Mars Science Laboratory (MSL), and China’s “Tianwen-1” Mars exploration mission, which carried the “Zhurong” rover, were both equipped with Laser-Induced Breakdown Spectroscopy (LIBS) analyzers to detect the surface mineral compositions on Mars. In lunar exploration missions, India’s Chandrayaan-2 mission also carried a rover named “Pragyan”, which was equipped with a Laser-Induced Breakdown Spectrometer (LIBS) for analyzing the material composition of the lunar surface. Unfortunately, the “Pragyan” rover failed to land as planned and conduct on-site exploration.
6. Conclusions
Lidar technology plays a crucial role in various stages of lunar exploration missions, particularly in terrain mapping, 3D topographic surveying, and velocity measurement, which are essential for guidance, navigation, and control applications. Both domestic and international efforts have yielded significant advancements in the application of lidar technology in these areas. This paper primarily analyzed the current state of lidar technology research in lunar exploration missions worldwide, highlighting that existing payload applications are mainly focused on the 3D terrain mapping and velocity measurement of the Moon. To enhance the point cloud density and detection efficiency, 3D terrain mapping is evolving towards multi-beam single-photon detection technology. By reviewing the current payload technologies, this paper suggests that China should actively pursue new technological advancements and space application research in areas such as multi-beam single-photon 3D terrain mapping, lunar surface water ice measurement, and lunar surface material composition analysis. This would elevate the application level of laser payloads in China’s lunar and space exploration missions.
Author Contributions
G.H.: writing—original draft, conceptualization, methodology, investigation; W.X.: writing—review and editing, conceptualization, methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (42241169, 62205361), the Shanghai Sailing Program (23YF1455100), the Youth Innovation Promotion Association, the Chinese Academy of Sciences (2021234), Shanghai Rising-Star Program (22QA1410500), the Shanghai Municipal Science and Technology Major Project of Science and Technology Commission of Shanghai Municipality (2019SHZDZX01), and the Innovation Program for Quantum Science and Technology (2021ZD0300304).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Slyuta, E. The Luna program. In Sample Return Missions; Elsevier: Amsterdam, The Netherlands, 2021; pp. 37–78. [Google Scholar]
- Zheng, Y.; Ouyang, Z.; Li, C.; Liu, J.; Zou, Y. China’s Lunar Exploration Program: Present and future. Planet. Space Sci. 2008, 56, 881–886. [Google Scholar] [CrossRef]
- Li, C.; Wang, C.; Wei, Y.; Lin, Y. China’s present and future lunar exploration program. Science 2019, 365, 238–239. [Google Scholar] [CrossRef]
- Rong, S.; Genghua, H.; Wei, K. Development and review of space-based laser altimetry technology. Infrared Laser Eng. 2020, 49, 20201047-1. [Google Scholar] [CrossRef]
- Jianyu, W.; Rong, S.; Weibiao, C.; Jianjun, J.; Genghua, H.; Binyong, W.; Xia, H. Chang’E-1 Satellite-Borne Laser Altimeter. Sci. China-Phys. Mech. Astron. 2010, 40, 1063–1070. [Google Scholar]
- Huang, G.; Wang, B.; Shu, R. Ground-based calibration and performance verification of the lunar observation laser altimeter. Infrared Laser Eng. 2006, 35, 375–377. [Google Scholar]
- Cai, Z.-C.; Liang, Y.-Y.; Li, J.; Tang, Z.-S.; Qi, D.-X. Digital elevation model of the Moon from the Chang’E-1 Laser altimeter. Prog. Geophys. 2010, 25, 1153–1160. [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Kleijnen, J. Kriging: Methods and Applications. CentER Discussion Paper Series No. 2017-047. 2017. Available online: https://ssrn.com/abstract=3075151 (accessed on 12 September 2024).
- Zhang, Y.; Cao, J.; Zhang, B.; Zheng, X.; Chen, W. A comparative study of different radial basis function interpolation algorithms in the reconstruction and path planning of γ radiation fields. Nucl. Eng. Technol. 2024, 56, 2806–2820. [Google Scholar] [CrossRef]
- Sawaryn, S.J.; Thorogood, J.L. A Compendium of Directional Calculations Based on the Minimum Curvature Method. SPE Drill. Complet. 2005, 20, 24–36. [Google Scholar] [CrossRef]
- Xing, Y.; Song, Q.; Cheng, G. Benefit of Interpolation in Nearest Neighbor Algorithms. SIAM J. Math. Data Sci. 2022, 4, 935–956. [Google Scholar] [CrossRef]
- Watson, D.F.; Philip, G.M. Triangle based interpolation. J. Int. Assoc. Math. Geol. 1984, 16, 779–795. [Google Scholar] [CrossRef]
- Li, C.; Ren, X.; Liu, J.; Zou, X.; Mu, L.; Wang, J.; Shu, R.; Zou, Y.; Zhang, H.; Lü, C. Laser altimetry data of Chang’E-1 and the global lunar DEM model. Sci. China Earth Sci. 2010, 53, 1582–1593. [Google Scholar] [CrossRef]
- Snyder, J.P. Map Projections: A Working Manual; US Government Printing Office: Washington, DC, USA, 1987; Volume 1395. [Google Scholar]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W., III; Duxbury, T.H. Initial observations from the lunar orbiter laser altimeter (LOLA). Geophys. Res. Lett. 2010, 37, L18204. [Google Scholar] [CrossRef]
- Archinal, B.A.; Rosiek, M.R.; Kirk, R.L.; Redding, B.L. The Unified Lunar Control Network 2005; US Geological Survey: Sunrise Valley Drive Reston, VA, USA, 2006. [Google Scholar]
- Araki, H.; Tazawa, S.; Noda, H.; Ishihara, Y.; Goossens, S.; Sasaki, S.; Kawano, N.; Kamiya, I.; Otake, H.; Oberst, J.; et al. Lunar Global Shape and Polar Topography Derived from Kaguya-LALT Laser Altimetry. Science 2009, 323, 897–900. [Google Scholar] [CrossRef]
- Weiming, X.; Jun, L.; Ziqing, J.; Kuifeng, L.; Rong, S. Scanning Property Analysis and System Error Calibration of Dual Galvanometers Based Multi-Points Parallel Scanning Imaging Lidar. Chin. J. Lasers 2014, 41, 214002. [Google Scholar] [CrossRef]
- Liu, X.; Xu, W.; Xie, H.; Luan, K.; Zhang, Z.; Wang, F.; Jiang, Z.; Li, M.; Jiang, H.; Tong, P. Calibration and validation of a multi-beam LiDAR onboard China Chang’e lunar probe for landing obstacle avoidance. Opt. Laser Technol. 2025, 181, 111579. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Luan, K.; Xu, W.; Shu, R. Plane-based self-calibration and improvement of three-dimensional multi-beam laser scanning with two-axis-mirror. Meas. Sci. Technol. 2022, 33, 115015. [Google Scholar] [CrossRef]
- Lichti, D.D. Error modelling, calibration and analysis of an AM–CW terrestrial laser scanner system. ISPRS J. Photogramm. Remote Sens. 2007, 61, 307–324. [Google Scholar] [CrossRef]
- Rietdorf, A.; Gielsdorf, F.; Gruendig, L. A concept for the calibration of terrestrial laser scanners. In Proceedings of the INGEO 2004 and FIG Regional Central and Eastern European Conference of Engineering Surveying, Bratislava, Slovakia, 11–13 November 2004; p. 13. [Google Scholar]
- Glennie, C.; Lichti, D.D. Static Calibration and Analysis of the Velodyne HDL-64E S2 for High Accuracy Mobile Scanning. Remote Sens. 2010, 2, 1610–1624. [Google Scholar] [CrossRef]
- Lichti, D.D.; Chow, J.C. Inner constraints for planar features. Photogramm. Rec. 2013, 28, 74–85. [Google Scholar] [CrossRef]
- Wang, D.; Xu, C.; Huang, X. Overview of autonomous navigation based on sequential images for planetary landing. J. Harbin Inst. Technol. 2016, 48, 1–12. [Google Scholar]
- Johnson, A.; Klumpp, A.; Collier, J.; Wolf, A. Lidar-based hazard avoidance for landing on mars. In Proceedings of the AAS/AIAA Space Flight Machanics Meeting, Santa Barbara, CA, USA, 19–23 January 2025; p. 11. [Google Scholar]
- Wong, E.C.; Singh, G.; Masciarelli, J.P. Guidance and control design for hazard avoidance and safe landing on Mars. J. Spacecr. Rocket. 2006, 43, 378–384. [Google Scholar] [CrossRef]
- De Lafontaine, J.; Gueye, O. Autonomous Planetary Landing using a LIDAR sensor: The navigation function. Spacecr. Guid. Navig. Control. Syst. 2003, 516, 147. [Google Scholar]
- De Lafontaine, J.; Neveu, D.; Lebel, K. Autonomous planetary landing with obstacle avoidance: The quartic guidance revisited. In 14th AAS. In Proceedings of the AAIA Space Flight Mechanics Conference, Austin, TX, USA, 15–19 January 2023. [Google Scholar]
- De Lafontaine, J.; Neveu, D.; Lebel, K. Autonomous planetary landing using a lidar sensor: The closed-loop system. In Proceedings of the Guidance, Navigation and Control Systems, Loutraki, Greece, 17–20 October 2005. [Google Scholar]
- DE Lafontaine, J.; Ulitsky, A.; Tripp, J.W.; Richards, R.; Daly, M.; Sallaberger, C. LAPS: The development of a scanning lidar system with GNC for autonomous hazard avoidance and precision landing. In Proceedings of the Spaceborne Sensors, Orlando, FL, USA, 1 September 2004; pp. 81–93. [Google Scholar]
- Striepe, S.A.; Epp, C.D.; Robertson, E.A. Autonomous precision landing and hazard avoidance technology (ALHAT) project status as of May 2010. In Proceedings of the International Planetary Probe Workshop 2010 (IPPW-7), Barcelona, Spain, 14–18 June 2010. [Google Scholar]
- Keim, J.A.; Mobasser, S.; Da, K.; Yang, C.; Ivanov, T.; Johnson, A.E.; Goldberg, H.R.; Khanoyan, G.; Natzic, D.B. Field test implementation to evaluate a flash LIDAR as a primary sensor for safe lunar landing. In Proceedings of the 2010 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010; pp. 1–14. [Google Scholar]
- Johnson, A.E.; Keim, J.A.; Ivanov, T. Analysis of flash lidar field test data for safe lunar landing. In Proceedings of the 2010 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010; pp. 1–11. [Google Scholar]
- Roback, V.E.; Bulyshev, A.; Amzajerdian, F.; Brewster, P.; Barnes, B.; Kempton, K.; Reisse, R.A. Helicopter flight test of a compact, real-time 3-D flash lidar for imaging hazardous terrain during planetary landing. In Proceedings of the AIAA SPACE 2013 Conference and Exposition, San Diego, CA, USA, 12 September 2013; p. 5383. [Google Scholar]
- Epp, C.; Robertson, E.; Carson, J.M. Real-time hazard detection and avoidance demonstration for a planetary lander. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 12 September 2013; p. 4312. [Google Scholar]
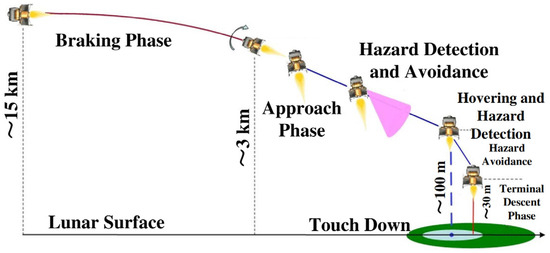
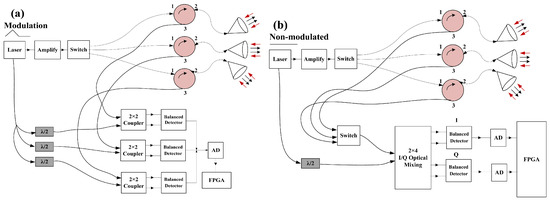
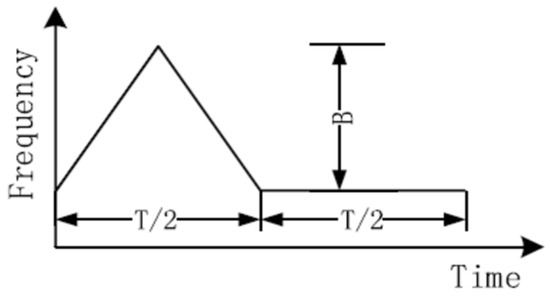
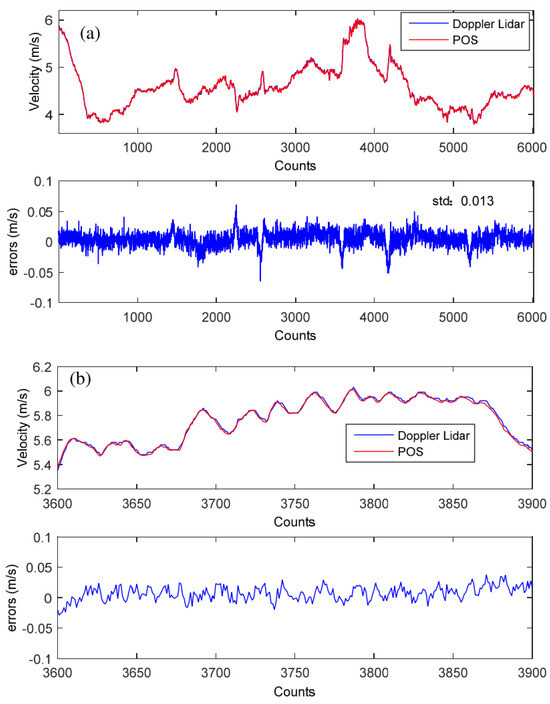
- Xu, W.; Hongxuan, Y.; Jiang, H.; Tong, P.; Kuang, Y.; Li, M.; Shu, R. Navigation Doppler lidar sensor for precision landing of China’s Chang’E-5 lunar lander. Appl. Opt. 2020, 59, 8167–8174. [Google Scholar] [CrossRef]
- Ahn, T.-J.; Kim, D.Y. Analysis of nonlinear frequency sweep in high-speed tunable laser sources using a self-homodyne measurement and Hilbert transformation. Appl. Opt. 2007, 46, 2394–2400. [Google Scholar] [CrossRef]
- Gragossian, A.; Pierrottet, D.F.; Estes, J.; Barnes, B.W.; Amzajerdian, F.; Hines, G.D. Navigation Doppler Lidar performance analysis at high speed and long range. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0369. [Google Scholar]
- Amzajerdian, F.; Vanek, M.; Petway, L.; Pierrottet, D.; Busch, G.; Bulyshev, A. Utilization of 3D imaging flash lidar technology for autonomous safe landing on planetary bodies. In Proceedings of the Quantum Sensing and Nanophotonic Devices VII, San Francisco, CA, USA, 24–28 January 2010; pp. 685–695. [Google Scholar]
- Sanin, A.; Mitrofanov, I.; Litvak, M.; Malakhov, A.; Boynton, W.; Chin, G.; Droege, G.; Evans, L.; Garvin, J.; Golovin, D. Testing lunar permanently shadowed regions for water ice: LEND results from LRO. J. Geophys. Res. Planets 2012, 117, E00H26. [Google Scholar] [CrossRef]
- Hayne, P.O.; Hendrix, A.; Sefton-Nash, E.; Siegler, M.A.; Lucey, P.G.; Retherford, K.D.; Williams, J.-P.; Greenhagen, B.T.; Paige, D.A. Evidence for exposed water ice in the Moon’s south polar regions from Lunar Reconnaissance Orbiter ultraviolet albedo and temperature measurements. Icarus 2015, 255, 58–69. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).