Abstract
A modified regional algorithm to quantify the coccolithophore concentration in the northeastern part of the Black Sea under conditions of intense bloom is presented. To modify the algorithm, the data of in situ measurements of coccolithophore Emiliania huxleyi abundance performed in June 2017 and 2022 (when the maximum values were 9 × 106 and 13 × 106 Cells L−1, respectively), as well as the data from hydro-optical and satellite measurements, were used. In addition, the ratio between the number of detached coccoliths and coccolithophore cells was taken into account. Based on the expanded array of in situ data, the optimal values of the regional algorithm parameters were obtained. The modified algorithm makes it possible to obtain more accurate results in areas of high coccolithophore concentrations and takes into account the contribution of coccoliths. To test the sensitivity of the algorithm to variations in bio-optical characteristics, model calculations were performed using Hydrolight software. The updated algorithm is significantly less sensitive to variations in chlorophyll concentration and CDOM absorption coefficient than its previous version.
1. Introduction
Phytoplankton in the world ocean play an important role in the regulation of the planet’s climate. They contain almost half of all carbon assimilated [1,2]. The ocean is the main depositor of absorbed atmospheric carbon; it has 50 times more carbon than the atmosphere [3,4,5]. The flow of carbon dioxide at the ocean–atmosphere boundary, its biological assimilation into the ocean water, and the further transfer of carbon in organic form from the upper layers to the deep ocean and to the ocean floor is carried out through a process called the ‘carbon pump’ [6,7]. Due to this, carbon pump global carbon export occurs, and it is currently estimated at between 5 and 15 × 1015 g of carbon per year [8,9]. At the ocean–atmosphere interface, the transport of CO2 molecules takes place. Its speed and direction depend on the difference in the partial pressures of carbon dioxide in the atmosphere and in the ocean surface layer.
In water, phytoplankton convert dissolved carbon into organic form through photosynthetic reactions, and this process is called the ‘organic pump’, while some researchers suggest the term ‘soft tissue pump’ [10]. Diatoms are mainly responsible for the operation of the organic pump in the ocean [11]. The concentration of chlorophyll is an indicator reflecting the functioning of the organic pump [12].
However, in the ocean, evolution has proposed another biological way of fixing dissolved carbon. Calcite is a mineral formed by calcium carbonate (CaCO3). It is also formed in the ocean in addition to organic carbon. This type of carbon assimilation process is called the ‘carbonate pump’; the main contributors to its work are coccolithophores, which have one important property of forming a calcite cell shell [13,14,15]. This shell consists of separate plates—coccoliths. The release of a CO2 molecule, as a result of the formation of a single calcite molecule, is important for the functioning of the carbonate pump. In other words, if the organic pump reduces the partial pressure of carbon dioxide in water, the carbonate pump, in contrast, increases it. Therefore, during the coccolithophore bloom (CB), the concentration of carbon dioxide in the water increases and, as a result, there is a significant decrease in its flow into the water or even its release into the atmosphere [16,17,18]. Therefore, the ratio of diatoms and coccolithophores is a fundamental indicator characterizing the state of the carbonate system [19].
Emiliania huxleyi is the main phytoplankton species that determines the functioning of the carbonate pump in the ocean. This species is widespread throughout the Northern and Southern Hemispheres, but its blooms are recorded mainly in high latitudes [20,21,22,23,24]. In the Black Sea, the intensive growth in coccolithophore abundance was noted in the 1950s [25]. In the beginning of this century, their role in the phytoplankton structure increased, as was noted in field observations [26,27,28]. Long-term observations of the phytoplankton structure in the northeastern part of the Black Sea have established that in the end of May and beginning of June, an intensive growth of Emiliania huxleyi is observed almost annually, and the abundance of this species exceeds 106 Cells L−1 [28].
The method of field observations does not allow creation of a unified picture of coccolithophore bloom distributions. Such capabilities are provided by ocean remote sensing, which allows blooms to be studied in a wide range of spatial and temporal scales. Only remote sensing methods give an opportunity to obtain the data necessary for the creation of carbon export global models from the upper layers to the deep ocean [9]. Coccolithophores differ from other phytoplankton species in terms of strong low-selective light scattering, which makes it possible to observe bloom according to satellite ocean color scanner data [15,29,30,31,32,33]. Satellite data are used to observe the CB in the Black Sea, starting with the SeaWiFS ocean color data [34]. The results of observations show that during late spring and early summer, extensive bloom areas are observed, covering most of the sea [29,35,36,37,38,39,40].
Previously, a regional algorithm for the northeastern part of the Black Sea based on bio-optical measurements from 2004–2008 was developed to evaluate the coccolithophore concentration [29]. Using this algorithm, monthly average maps and diagrams for the period 1998–2018 were drawn, and were presented in the Atlas of Bio-optical Characteristics of the Ocean Optics Laboratory at the Shirshov Institute of Oceanology of the Russian Academy of Sciences (SIO RAS) [41]. However, the coccolithophore concentrations obtained in the expeditions, using the results of which this algorithm was created, did not exceed 2.5 × 106 Cells L−1 in most cases. They are significantly lower than the values that can be observed during the period of intense blooms. For example, according to the regional algorithm, the monthly average concentration of coccolithophores in June 2017 exceeded 6 × 106 Cells L−1 [41]. Such a significant difference in the range of values used for the algorithm development with the results of its application requires verification and appropriate modification of the regional algorithm.
Specifically, the purpose of this work is the development of a new algorithm for high coccolithophore and coccolith concentrations using the latest data from in situ and simultaneous satellite measurements.
2. Materials and Methods
For our purpose, the data from in situ and simultaneous satellite measurements in the northeastern part of the Black Sea near Gelendzhik (44.56°N, 38.08°E) in June 2017 and 2022, obtained during the period of intense coccolithophore blooms, were used. In situ measurements included both a complex of hydrooptical works and laboratory measurements of coccolithophore plated cell and detached coccolith abundance. The median coccolithophore concentration in the upper mixed layer according to direct measurements in those years was 7 and 5.4 × 106 Cells L−1. Along with the expansion of the field measurements dataset, model data obtained using Hydrolight 6.0 software [42] were used to modify the algorithm.
2.1. Study Area and Bio-Optical Measurements
The complex optical measurements were performed in June 2017 and 2022 on the small research vessel Ashamba on the transect from the Blue Bay (near Gelendzhik) to the center of the sea (Figure 1a) with simultaneous ocean color satellite observations accompanied by hydrological and biogeochemical studies. Favorable weather conditions provided good-quality remote sensing data.
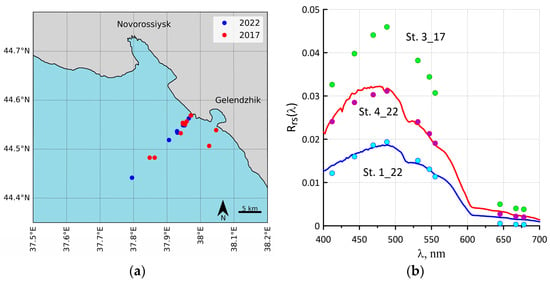
Figure 1.
(a) Map of stations. (b) Examples of Rrs(λ) spectra measured using the floating spectroradiometer PRO-1 (solid lines) and calculated from MODIS data (circles).
For a number of stations in 2022, the spectra of the remote sensing reflectance Rrs(λ) were obtained using the floating spectroradiometer PRO-1 [43]. The floating spectroradiometer was developed at SIO RAS and allows the measurement of spectral values of the surface downwelling irradiance Ed(λ,0+) and the upwelling radiance below the sea surface L(λ,0−). From the obtained values the water, radiance reflectance ρ(λ) is calculated, which then is converted to Rrs(λ), using the following formula [44]:
PRO-1 works in the spectral range of 390–700 nm with a spectral resolution of 2.5 nm; its accuracy is about 5%.
Rrs(λ) = 0.165 ρ(λ)/[1 − 0.497 ρ(λ)].
Figure 1b shows examples of Rrs(λ) values measured with the help of the floating spectroradiometer PRO-1 in comparison with satellite data for two stations from June 11, 2022. The observed difference in spectra is explained well by the distinction in the intensity of CB at these stations; according to direct measurements, the coccolithophore concentration at station 1_22 was 4.8 × 106 Cells L−1, and at station 4_22 it was 9.3 × 106 Cells L−1.
A submerged transmissometer PUM-200 developed at SIO RAS [45] was used to measure vertical profiles of the beam attenuation coefficient at a 530 nm wavelength c(530). These profiles are quite valuable, as the c(530) profile depicts the vertical distribution of the coccolithophore layer. PUM-200 measurements made it possible to determine the thickness of the coccolithophore layer Zcoc.
2.2. Sampling
At the stations (Figure 1a), water samples were taken from different depths for laboratory determination of the spectral absorption coefficient of colored dissolved organic matter (CDOM) ag(λ), the concentration of chlorophyll a (Chl), and the species composition of phytoplankton. Water samples were taken using 5-L Niskin bathometers mounted on a Rosette sampler.
An integrated cavity absorption meter (ICAM) was used to measure the absorption spectra of seawater, filtrates, and suspended particles [46,47]. The difference between the values of the filtrate and pure water absorption coefficients allowed the estimation of the CDOM absorption coefficient ag(λ). The biogeochemical parameters also included the concentrations of chlorophyll a and pheophytin a measured using a fluorometric method [48,49].
Samples for determining the species composition of phytoplankton were fixed using neutralized formaldehyde (final concentration 0.8–1.0%). Sample settling was the main method of cell concentration. The identification of the species and counting of the cells were carried out using a light microscope at 16 × 10 and 16 × 40 magnifications. Identification was based on the described morphology [50,51] (http://www.algaebase.org, accessed on 18 April 2022, and http://www.marinespecies.org, accessed on 18 April 2022). The nano- and microplankton cells were counted using 0.05 mL Nageotte and 1 mL Naumann counting chambers [27]. The small flagellates (2–4, 4–6, and 6–8 μm fractions) and coccoliths were counted using a Finuchs–Rosenthal counting chamber. A method based on the geometric shape of cells was used to calculate biomass [52,53]. The number of coccolithophores equal to 1 × 106 Cells L−1 was taken as the bloom threshold concentration [24].
In our study, we used the results of determining the concentration of coccolithophore cells Ncc and separated coccoliths Ncl. Light scattering occurs both on coccolithophore cells and on detached coccoliths. According to the work presented in [54], the values of the specific backscattering coefficients for a coccolith are, on average, 50 times lower than for a coccolithophore cell, that is, the contribution to the backscattering of 50 coccoliths and one cell is approximately the same. Therefore, according to direct measurements, the value of Ncc_cl was calculated as
while the average values for the two upper depths were used (the first one was 0 m, the second was 5–11 m).
Ncc_cl = Ncc + Ncl/50,
2.3. Satellite Data
We used the Level 2 data of the satellite spectroradiometers Moderate-Resolution Imaging Spectroradiometer (MODIS)-Aqua and MODIS-Terra, Visible Infrared Imaging Radiometer Suite (VIIRS)-SNPP and VIIRS-JPSS, available through the NASA website [55]. Satellite data processing was performed using the SMCS 1.9 software package developed at the SIO Ocean Optics Laboratory [56].
The spectra of the remote sensing reflectance Rrs(λ) in the pixel closest to the station were selected for the stations. Two satellite datasets were selected: in the first, shipboard and satellite measurements were performed on the same day, and in the second, satellite data were added on the previous and subsequent days. Thus, in the first dataset, the time difference between shipboard and satellite measurements did not exceed 8 h, and in the second 32 h. Examples of the comparison of satellite (from the first dataset) and in situ Rrs(λ) for two stations in 2022 are shown in Figure 1b. It also shows an example of the MODIS spectrum for station 3_17 in 2017 with laboratory estimates of Ncc_cl = 11.6 × 106 Cells L−1.
2.4. Regional Algorithm 2014
Based on field measurements of coccolithophore concentration Ncoc performed in 2004–2008, a regional algorithm for estimating Ncoc from satellite data in the Black Sea was created [29]. According to this algorithm, the backscattering coefficient is determined by three components:
where bbp_bg is its background value, bbp_riv is the backscattering coefficient due to terrigenous suspended matter brought by river runoff, and bbp_coc is responsible for the presence of coccolithophores and coccoliths in seawater. The value of bbp_bg was selected as the lowest monthly means of bbp = 0.0025 m−1, derived from satellite data over the period 2003–2010. To account for the contribution of terrigenous suspension, the following formula was used:
where ag and ag_bg are the absorption coefficients of CDOM at the wavelength 440 nm. The first is determined in the algorithm [29] as a result of solving the inverse problem of obtaining two unknown model parameters (ag and Ncoc) from the Rrs spectra for two wavelengths. The second is determined similarly to bbp_bg based on the minimum values of satellite ag estimates for 2003–2010, and is equal to 0.047 m−1. We used the following expression for coccolithophore suspension:
bbp = bbp_bg + bbp_riv + bbp_coc,
bbp_riv = Kriv (ag − ag_bg),
bbp_coc = Kcoc Ncoc.
The following values of Kcoc and Kriv were obtained: Kcoc = 2.74 × 10−3 and Kriv = 0.157 [29].
To find two parameters of the model, the use of two spectral MODIS bands is proposed: 488 and 555 nm. In the case of VIIRS, we used close bands: 489 and 556 nm for JPSS, and 486 and 551 nm for SNPP. For model Rrs spectra obtained using Hydrolight, we used bands 488 and 551 nm.
The error estimation results for the in situ and satellite Rrs spectra for the obtained algorithm turned out to be close (standard errors 1.15 and 0.99 × 106 Cells L−1). The differences are due to the different dataset used for these estimates. Moreover, in both cases, the average concentration of Ncoc according to the results of direct measurements did not exceed 1.5 × 106 Cells L−1 and only a few spectra related to the case of Ncoc > 5 × 106 Cells L−1. When deriving the algorithm, differences in Ncl/Ncc for different years were not taken into account. However, it was possible to identify a set of data for which the bbp correlated well with the ag coefficient (R2 = 0.82). This allowed us to reliably take into account the contribution of terrigenous suspension and not show ‘false’ coccolithophore blooms in the area of strong influence of river runoff.
In our work, we used the approach of the algorithm presented in [29], but tried to use other values for its parameters Kcoc, Kriv, and bbp_bg in order to improve its accuracy in conditions of intense coccolithophore bloom, which was observed in 2017 and 2022.
For the 2017 and 2022 dataset, the coefficient of determination R2 for the linear correlation between bbp and ag is 0.60, which indicates less influence of terrigenous suspended matter in these years. Therefore, reduction by multiple times was considered for the Kriv and bbp_bg parameters.
2.5. Error Assessment
To evaluate the accuracy of the Ncoc algorithm and remote sensing reflectance values, the root mean square error (RMSE) and mean absolute percentage error (MAPE) were calculated as
where yi and yim are the calculated and measured values of coccolithophore concentrations or remote sensing reflectance.
The regional Ncoc estimation algorithm uses two spectral bands in the range of 486–489 and 551–556 nm. For the 2022 stations, when in situ measurements of Rrs(λ) were carried out, estimates of the correspondence of satellite and in situ Rrs values in spectral bands from the considered spectral ranges were made. For a set with satellite data on the same day (16 pairs in total), the maximum difference for MODIS and VIIRS-JPSS for both bands did not exceed 8%, and MAPE was equal to 4%. With an increase in the permissible time difference between satellite and shipboard measurements to 32 h (37 pairs), the maximum difference reached 60%, and MAPE turned out to be equal to 15% for MODIS and 8–9% for VIIRS-JPSS. Our estimates of the differences between satellite and in situ Rrs values during the CB period are even slightly better than those obtained in earlier work [57], where for the VIIRS-JPSS band 556 nm, MAPE = 9.3%, and for the 555 nm band of two MODIS sensors, MAPE was equal to 10.3 and 12.3%, respectively. It is worth noting that [57] used a dataset with more spectra and a time difference between in situ and satellite measurements less than 2 h, as waters were strongly influenced by river runoff.
The acceptable difference between the satellite and in situ Rrs allowed us to use the combined set of satellite and in situ Rrs spectra to modify the regional Ncoc estimation algorithm.
2.6. Tuning of the Hydrolight Model
Hydrolight software was used to calculate the light field parameters. We used the case 2 water model, where inherent optical properties were determined for 4 components [58]. The parameters of pure water absorption and scattering were taken from [59,60].
The optical properties of the component associated with Chl were parameterized through its concentration. The result of field measurements of the concentration of Chl at the depths of 1–10 m shows insignificant (5–10%) changes, so the concentration was set as a constant with depth. Absorption and scattering parameters were introduced using standard models available in Hydrolight [61,62]. The parameters of the scattering phase function represent the Morel model for “large particles” [63].
The CDOM component was considered to be non-scattering. The absorption of CDOM was calculated relatively to the absorption value at wavelength 443 nm ag(443) [56]. This value and CDOM spectral slope were specified using the results of laboratory ICAM measurements, or through the GIOP Rrs(λ) decomposition algorithm [64].
The mineral suspension component was set, assuming that the suspension is represented only by coccolithophore cells and detached coccoliths, which corresponds to more than 99% of the biomass during intense blooms, according to in situ measurements. The absorption properties of coccolithophores and coccoliths were neglected, as they are several times less than those of Chl and CDOM. We used the typical coccolithophore bloom backscattering ratio value bb/b = 0.02 [65], and the spectral scattering coefficient b(λ) was assigned as
b(λ) = b0 (550/λ)m.
The parameters b0 and m were determined to spectrum bb(λ) and matched the results of the decomposition of the Rrs spectra using GIOP. The depth of a homogeneous surface layer with coccolithophores Zcoc was also specified, below which coccolithophore concentration was set to zero.
Figure 2a shows the comparison of the scattering parameters b0 and m calculated using GIOP from satellite and in situ Rrs (λ) spectra. In this case, all available satellite spectra were used. The coefficient of determination R2 of the linear correlation was 0.49, which made it possible to determine the parameter m based on the value b0:
m = 1.274 − 0.067·b0
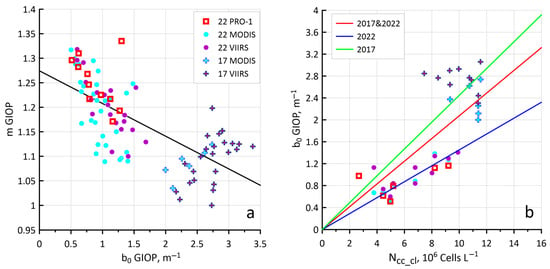
Figure 2.
Comparison of scattering parameters and concentration of coccolithophores: (a) parameters b0 and m for coccolithophore backscattering, calculated by GIOP; (b) coefficient b0 and concentration Ncc_cl. Solid straight lines are linear regressions.
Parameter b0 correlates well with the concentration of Ncc_cl according to direct measurements (b0 = 0.207·Ncc_cl, R2 = 0.62, Figure 2b). Only satellite spectra with a measurement time difference of less than 8 h were used here. If we expand the array of satellite data by increasing the time interval to 32 h, then R2 will decrease to 0.49, and the correlation equation will change slightly: b0 = 0.212·Ncc_cl. However, as can be seen in Figure 2b, there is a significant difference in the location of the data for 2017 and 2022 relative to the regression line for the general dataset, which can be explained by the different phases of blooms recorded according to in situ measurements over these years. If we calculate the regression separately for each year, then for 2017, we will obtain b0 = 0.245·Ncc_cl, and for 2022, it will be b0 = 0.145·Ncc_cl.
3. Results
3.1. Coccolithophore Concentrations in the Northeastern Part of the Black Sea in 2017 and 2022
In 2017, intense coccolithophore bloom represented by one species Emiliania huxleyi was observed at all stations from the shelf to stations above the depth of 1500 m. The maximum number of coccolithophores exceeded 9 × 106 Cells L−1 (Table S1), and their contribution to the total phytoplankton biomass was above 99%. Coccolithophore bloom was observed mainly in the upper mixed layer. The median concentration of coccolithophore cells for all sampling depths was equal to 6 × 106 Cells L−1, and for the two upper ones was 7 × 106 Cells L−1.
In 2022, coccolithophore bloom was generally less intense, although the abnormally high value of 13 × 106 Cells L−1 was obtained at one station (Table S2). Bloom also occurred at all stations of the continental shelf and slope, and it was recorded in the upper mixed layer. The median concentration of coccolithophore cells for all sampling depths was equal to 4 × 106 Cells L−1, and for the two upper ones was 5.4 × 106 Cells L−1.
The median value for the Ncl/Ncc ratio for all sampling depths in 2017 was 11.5, and for the two upper ones was 15.0; in 2022, for all depths it was 1.3, and for the two upper ones was 2.2. Such a strong difference in the value of Ncl/Ncc, apparently, occurs due to the difference in the bloom phase for those two years. In June 2022, the bloom was in an earlier phase, when significantly fewer detached coccoliths were observed; in June 2017, measurements were performed near the end of bloom, so the abundance of detached coccoliths exceeded the abundance of placed coccolithophore cells.
3.2. Sensitivity of the Ncoc Algorithm to Variations in Bio-Optical Characteristics
Figure 3 shows a comparison of the measured and model Rrs(λ) spectra using the examples of station 1_22 (11.06.2022, 44.56N, 37.96E) and station 3_17 (08.06.2017, 44.48N, 37.85E). For station 1_22, the model spectra are compared with the field-measured Rrs(λ), and for station 3_17, with the spectrum according to MODIS Terra data. The concentration of Ncc_cl according to direct measurements for station 1_22 was 5.2 × 106 Cells L−1, and for station 3_17 was 11.6 × 106 Cells L−1. In this case, for station 1_22, the best agreement of the model spectrum with the measured one was achieved for Zcoc = 10 m, while in the case of more intense bloom at the station 3_17, the spectrum matched for Zcoc = 5 m. For both stations, the value of Zcoc* was calculated, when all model spectra with Zcoc > Zcoc* hardly differed from the one obtained with Zcoc*. This indicates that the Rrs(λ) spectrum is formed by the upper layer of a water column with a thickness of Zcoc*. For the stations shown in Figure 3, the Zcoc* was 15 and 10 m.
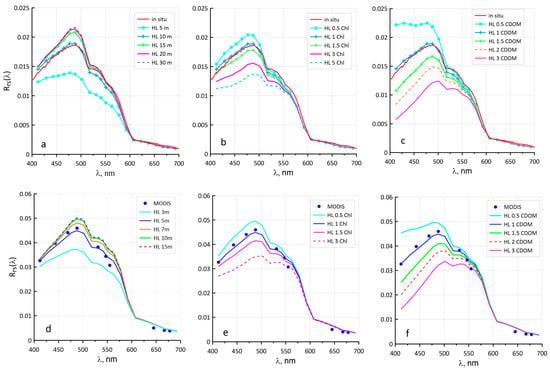
Figure 3.
The results of modeling the Rrs(λ) spectra with Hydrolight software with a change in the values of Zcoc (a,d), Chl (b,e), and CDOM (c,f) using data from stations 1_22 (upper row) and 3_17 (bottom row). The notation Chl/CDOM ‘X’ refers to the case of an X-fold increase in the concentration of Chl or ag(443).
To test the stability of the regional coccolithophore concentration algorithm to variations in the Chl concentration and the CDOM content, additional model calculations were carried out (Figure 3 in the center and right column). These variations were set using a multiplier X to the initial values of Chl and ag(443), for which the best agreement was obtained with the measured Rrs spectra. The effect on the Rrs spectrum of the change in CDOM is more noticeable than the change in Chl (Figure 3). The reason for this is that the CDOM-related absorption is usually significantly greater than the phytoplankton absorption in the northeastern part of the Black Sea. When the Chl value changes by 50%, there is only a slight change in the Rrs(λ) spectra, while the same relative decrease in CDOM brings not only a significant increase in Rrs, but also a noticeable change in the shape of the spectrum. This shape is typical for coccolithophore bloom spectra in the Barents Sea [66], where the content of CDOM is significantly lower than in the Black Sea. Only with such a low content of CDOM or with a significant increase in Chl (3–5 times) is the effect of the maximum absorption by phytoplankton near 450 nm noticeable in the shape of a small deflection of the Rrs(λ) spectrum near this wavelength.
Table 1 shows the sensitivity of the regional Ncoc algorithm [29] to variations in the Zcoc, Chl, and the absorption of CDOM values. In addition to the Ncoc values for different model spectra (Figure 3), their difference (Δ, %) from the Ncoc* values calculated from the measured spectra (Ncoc* = 3.1 and 13.4 × 106 Cells L−1 for station 1_22 and 3_17, respectively) is shown. A decrease in Zcoc by 2 times leads to underestimation of Ncoc estimates by almost 2 times for station 1_22, where the bloom is not so intense. For station 3_17, with a decrease in Zcoc, there is also a significant decrease in Ncoc (by more than 3 × 106 Cells L−1, ~26%). The increase in Zcoc does not play such a significant role, since the spectrum of upwelling radiation is formed by the surface layer of the water column—Zcoc*. In fact, a greater relative variability of Ncoc estimates in response to changes in modeling parameters was observed for station 1_22, with a less intense CB than for station 3_17. The Ncoc for station 1_22 changes particularly noticeably when the CDOM absorption changes. For station 3_17, in an intense CB area, the response to changes in CDOM and Chl is approximately the same, as the absorption of Chl becomes comparable to the absorption of CDOM for the 488 nm spectral band used in the Ncoc algorithm. The higher concentration of Chl (0.47 in comparison to 0.2 mg L−1) proves it, while the value of CDOM for station 3_17 is only 26% higher than station 1_22.

Table 1.
The values of Ncoc (106 Cells L−1) according to the 2014 algorithm [29] and their difference Δ (%) from the values of Ncoc* calculated from the measured spectra, depending on the parameters of the Hydrolight model with an example for stations 1_22 and 3_17. Columns highlighted in bold refer to calculations with the set of parameters when the best match between the measured and calculated Rrs spectra was obtained.
3.3. New Values of Kcoc as a Result of Hydrolight Modeling
Using a customized bio-optical model, Rrs calculations were carried out for five values of Ncc_cl 2, 4, 7, 10, and 15 × 106 Cells L−1. For each value of the concentration of Ncc_cl, the values of Chl (0.3, 0.5, and 0.8 mg L−1) and CDOM (0.03, 0.05, and 0.08 m−1) were varied to cover the most likely range of changes in these optically active components (OAC), typical for the northeastern part of the Black Sea [55,67]. The calculations were carried out under the assumption of a homogeneous distribution of coccolithophores in the layer 15 m deep, which generally corresponds to the results of the performed field measurements of the vertical profiles of the beam attenuation coefficient c(530).
Thus, 45 Rrs spectra were obtained, to which the regional algorithm was applied to estimate the Ncoc concentration. The comparison of the Ncc_cl input values used in Hydrolight calculations and obtained Ncoc estimates is shown in Figure 4. If we use the values of the parameters Kcoc, Kriv, and bbp_bg defined in the article [29], then the Ncoc estimates (shown in pink circles) vary visibly in response to changes in the content of the OAC. Simultaneously, overestimated Ncoc evaluations are obtained for Ncc_cl = 15 × 106 Cells L−1, and underestimated ones (in a number of cases even negative) for Ncc_cl = 2 × 106 Cells L−1. This result arises from the fact that in our Hydrolight model, the contribution of terrigenous suspended matter is not taken into account. The origin of this matter is associated with river runoff, as well as with the bbp background amount, which is parametrized through the bbp_bg value. Therefore, Ncoc estimates were calculated for the case of Kriv = 0 and bbp_bg = 0 (blue circles in Figure 4). In this case, the influence of the OAC practically disappears, but for all Ncc_cl data, overestimated Ncoc values are obtained, and this overestimation increases in direct proportion to Ncc_cl, which indicates an incorrect Kcoc value. For the best correspondence of the initial values Ncc_cl with the results of Ncoc estimates, the value 4.36 × 10−3 is used (red circles in Figure 4).
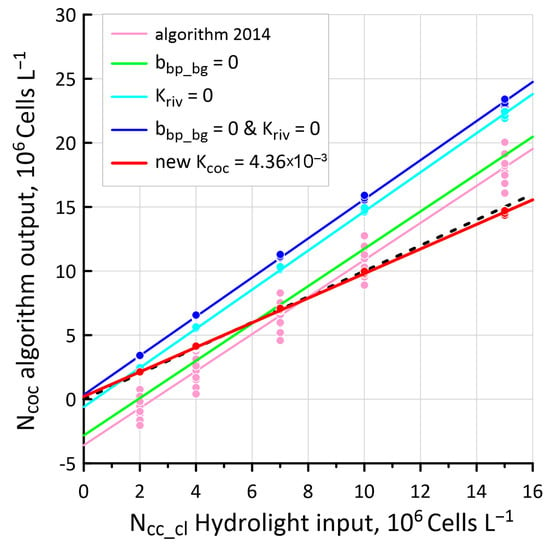
Figure 4.
Comparison of Ncc_cl input values used in Hydrolight calculations and the Ncoc estimates obtained depending on the regional algorithm parameters. The circles show individual calculations, solid lines show linear regressions, and the dotted line shows a perfect 1:1 correspondence.
Figure 4 also shows Ncoc estimates for the cases of Kriv = 0 (in blue) and bbp_bg = 0 (in green). The results obtained in these cases are close to the variants of Kriv = 0 and bbp_bg = 0 and the original algorithm [29], respectively, showing that the influence of the value of bbp_bg on the algorithm results is significantly less than the influence of Kriv.
As was previously noted (Section 2.4), there are noticeable differences for the data we use depending on the year. Therefore, similar calculations of Rrs spectra arrays were performed, but using the coupling equations between b0 and Ncc_cl obtained separately for 2017 and 2022 data. These arrays allowed us to obtain two more variants of the Kcoc value: 5.13 × 10−3 for 2017 and 3.10 × 10−3 for 2022. Additionally, if the first Kcoc value is almost two times higher than the previous Kcoc estimate [29], then the second one is very close to it. The use of these Kcoc values is discussed in Section 3.4 and Section 4.5.
3.4. Configuring Other Model Parameters
As long as the results of the Hydrolight calculations were obtained without taking into account the terrigenous suspended matter, the presence of which is quite possible when using real data, the data of in situ and satellite measurements of Rrs were used to adjust two parameters of the Ncoc algorithm related to the terrigenous suspended matter (Kriv and bbp_bg) for stations where the in situ measurements of Ncc_cl were completed. The difference in measurement time between satellite and shipboard data did not exceed 8 h. In total, 41 corresponding spectra were selected for 2017 and 2022.
We set the value of Kriv and bbp_bg as a fraction of their values defined in the previous work [29], leaving values from the original algorithm or decreasing them. For example, the notation ‘0.25_0.5’ means that Kriv = 0.25 × 0.157 = 0.03926 and bbp_bg = 0.5 × 0.0025 = 0.00125.
For the Kcoc parameter, both previous values 2.74 × 10−3 and three new variants, 3.10, 4.36, and 5.13 × 10−3, obtained in Section 3.3 were used. As there is a rather large difference between the variants of the Kcoc 3.10 and 4.36 × 10−3, two more intermediate ones were used: 3.52 and 3.94 × 10−3. Table 2 shows the RMSE and MAPE values of the Ncoc estimates obtained relative to the measured Ncc_cl for the selected dataset and depending on the three parameters values of the algorithm: Kcoc, Kriv, and bbp_bg.

Table 2.
The RMSE (106 Cells L−1) and MAPE values of Ncoc estimates relative to the measured Ncc_cl for the selected dataset and depending on the value of the parameters of the algorithm Kcoc, Kriv, and bbp_bg.
If we focus on the RMSE and MAPE values, the best correspondence between the calculated Ncoc and the measured Ncc_cl is obtained in the case of 0.1_0.1 and Kcoc = 3.52 × 10−3. In fact, it is the option of reducing the contribution of terrigenous suspended matter to 10% of the initial one, almost regardless of the Kcoc value, that leads to a decrease in RMSE and MAPE and, therefore, to an improvement in compliance. Comparison graphs of Ncoc vs. Ncc_cl show that the discrepancy in the variants with different values of the algorithm parameters are no longer so noticeable (Figure 5). The best option, “10%” (Figure 5b), does not differ much from the original “algorithm 2014” (Figure 5a); it even has less difference from the intermediate “50%” option (Figure 5c), although the values of RMSE and MAPE are noticeably different for all given versions.
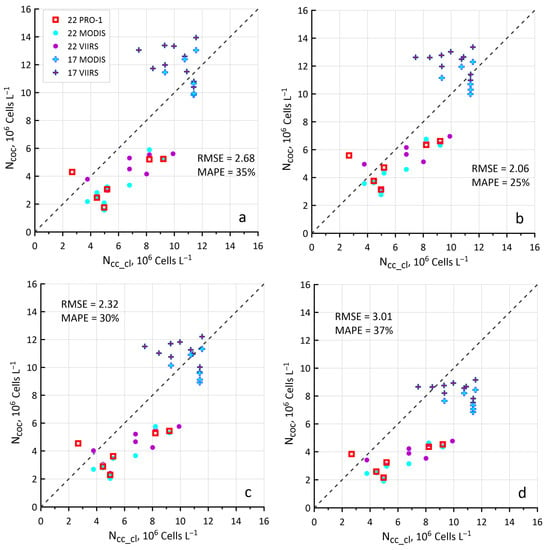
Figure 5.
Comparison of the coccolithophore concentration Ncoc calculated from Rrs(λ) with different parameters of the regional algorithm Kcoc, Kriv, and bbp_bg, and measured Ncc_cl: (a) algorithm 2014 (1.0_1.0, Kriv = 2.74 × 10−3); (b) option “10%” (0.1_0.1, Kriv = 3.52 × 10−3); (c) option “50%” (0.5_0.5, Kriv = 3.52 × 10−3); (d) option “10% 2017” (0.1_0.1, Kriv = 5.13 × 10−3). Notations are the same as in Figure 2.
Figure 5d shows the variant 0.1_0.1 and Kcoc = 5.13 × 10−3, as it was the value of Kcoc obtained in the Hydrolight calculations with the focus on 2017 data and the corresponding best option for terrigenous suspended matter was selected from Table 2. However, even if we only pay attention to the data for 2017, the “50%” option suits them much better (Figure 5c). Thus, model calculations do not always allow us to find the best variant of the algorithm parameters that works with real satellite data, because atmospheric correction errors begin to contribute to the accuracy of the latter [57,68], as well as errors associated with the time difference between in situ and satellite measurements. In addition, the error is caused by the discrepancy between the spatial resolution of shipboard and satellite data and the interannual dynamics of phytoplankton communities.
Furthermore, we will consider the “10%” option (0.1_0.1 and Kcoc = 3.52 × 10−3) to be the best one for the conditions of intensive CB in the northeastern part of the Black Sea. We will denote it as ‘algorithm 2023’. The algorithm code (MATLAB script) for both algorithms (2014 and 2023) is available in the Supplementary Materials.
4. Discussion
4.1. Coccolithophore Blooms in the Black Sea
Coccolithophore blooms are an almost annual phenomena in the Black Sea, but in 2017 and 2022, these blooms reached their maximum intensity in comparison to previous years [28]. The maximum concentration of Emiliania huxleyi was registered in 2022, and it has been the maximum for all the years of research since the beginning of this century. Coccolithophore blooms grow in the upper mixed layer with high stability of the water column [22]. In the northeastern part of the Black Sea, weak SE winds dominate in late and early spring, and wind forcing during this period is minimal [28,69]. This contributes to the development of a sharp seasonal thermocline, the presence of which is a necessary condition for the bloom [22,24,28,70].
Typical features of the blooms of 2017 and 2022 are the presence of a large number of detached coccoliths (Tables S1 and S2). In 2017, the number of detached coccoliths per Emiliania huxleyi plated cell reached 600. In 2022, this number was lower, but still high. This suggests that the bloom was in late phase and the number of destroyed cells accumulated. One of the possible mechanisms for the appearance of a large number of detached coccoliths during the bloom is the intensive consumption of living cells by species of a higher trophic level [71].
Due to a large number of plated cells and detached coccoliths in the upper mixed layer, a kind of optical medium is created to generate optimal conditions for the growth of coccolithophore cells, and does not allow other species in competition to win [65]. However, it is not yet clear why intense coccolithophore blooms grow. There is a hypothesis that the intensity of blooms is related to the nature of winters, as after cold winters, there are usually more intense blooms [70,72]. However, the details of this connection remain unclear.
4.2. Sensitivity of the New Ncoc Algorithm
Table 3 shows the sensitivity test results of the 2023 regional algorithm to determine Ncoc with the example of the 1_22 and 3_17 stations (just as in Table 1). Firstly, the new algorithm has allowed us to obtain Ncoc* estimates from the measured spectra that better correspond to the data of direct measurements of Ncc_cl. For the station 1_22, Ncoc* = 4.7 × 106 Cells L−1, and for 3_17 it is 12.3 × 106 Cells L−1, which is much closer to the estimates of Ncc_cl: 5.2 and 11.6 × 106 Cells L−1, respectively. Secondly, the new algorithm has become significantly less sensitive to Chl and CDOM value changes, which is a consequence of a reduction in the contribution of terrigenous suspended matter to the total suspension matter backscattering. With a 50% change in Chl and CDOM, the Ncoc estimates for both stations now hardly change. The influence of the Zcoc layer thickness has somewhat decreased, but the mechanism of this influence remains the same.

Table 3.
The values of Ncoc (106 Cells L−1) according to the algorithm “10%” and their difference Δ (%) from the value of Ncoc* calculated from the measured spectra, depending on the parameters of the HydroLight model for the stations 1_22 and 3_17. Columns highlighted in bold refer to calculations with a set of the parameters when the best match between the measured and calculated Rrs spectra was obtained.
4.3. Comparison of Ncoc Distributions for 2014 and 2023 Algorithms
Figure 6 shows a comparison of the distributions of Ncoc concentration estimates calculated with the old [29] and the new 2023 algorithms for the entire Black Sea. For this figure, we used data from two VIIRS overpasses for 12 June 2017 and 17 June 2022, which gives us an opportunity to see almost the entire Black Sea water area and relate to the time of the expeditions in those years. For both images, the comparison of the two algorithms shows that the main difference between their results arises primarily in areas affected by river runoff: for example, near the mouth of the Danube River or in the Sea of Azov. There are also noticeable differences in the area of low Ncoc concentrations. This is especially noticeable for 2022 in the central part of the sea, where according to the 2014 algorithm, there was no CB; However, the modified algorithm indicates its presence (Ncoc > 106 Cells L−1).
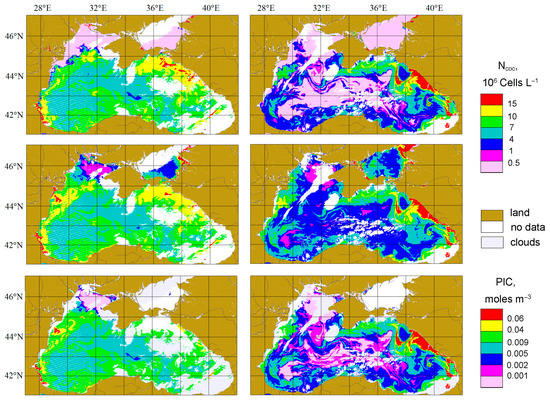
Figure 6.
Spatial distributions of Ncoc in the Black Sea, calculated with 2014 and 2023 algorithms (upper and middle rows), and PIC (lower row). On the left are VIIRS data from 12 June 2017, and on the right are VIIRS data from 17 June 2022.
In addition, Figure 6 shows the differences in CB in the studied years. In 2017, intensive CB with Ncoc > 4 × 106 Cells L−1 covers almost the entire Black Sea area (with the exception of the northwestern shelf area). In 2022, extremely high values of Ncoc > 15 × 106 Cells L−1 were observed near the northeastern coast, but for the rest of the Black Sea, the CB was less intensive or absent.
Since the modification of the Ncoc algorithm in conditions of intense CB has been carried out on the basis of field measurement data in a fairly small area in the northeastern part of the Black Sea, the new algorithm may not be suitable for the entire sea. The informative MODIS Terra data from 8 June 2017 were selected to see the differences between the two algorithms’ performance in the eastern part of the sea (Figure 7). Note that a different scale was chosen. As there are no rivers as large as the Danube or Dnieper in the eastern part of the sea, the differences between the two algorithms appear only in the area of relatively small Ncoc values. In addition, it is worth noting that despite a very intense CB near the northeast coast in 2022, satellite Ncoc values were clearly lower in the sampling area near Gelendzhik than those from 2017. Thus, the differences for satellite estimates of the CB near Gelendzhik are consistent with the field measurement data.
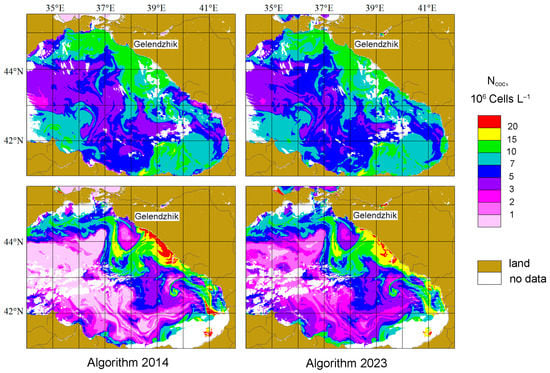
Figure 7.
Comparison Ncoc spatial distributions in the eastern part of the Black Sea, calculated with the 2014 and the new 2023 algorithms. Upper row: MODIS Terra data from 6 August 2017, lower row: VIIRS data from 17 June 2022.
Thus, the new algorithm gives more accurate estimates in conditions of intense CB and the absence of strong influence of terrigenous suspended matter. However, for areas affected by significant river runoff and in areas of weak CB (Ncoc < 3 × 106 Cells L−1), it seems that the previous version of the algorithm should be used. To set up a regional algorithm in such waters, it is necessary to conduct complex expedition studies, including in situ determination of the coccolithophore concentration. Note that spectral variations of the remote sensing reflectance during coccolithophore blooms in the western part of the Black Sea, affected by river runoff, were carried out in [57] according to AERONET-OC. Nevertheless, the authors did not have in situ data on the coccolithophore concentration, although it is typical for a number of other works [73,74,75,76,77], due to the complexity of such measurements.
4.4. The Comparison with PIC Product
The standard satellite data processing product particle inorganic carbon (PIC) is widely used for CB intensity and calcite (CaCO3) concentration assessments [78,79]. In the work [29], an equation of the relationship between Ncoc and PIC with a correlation coefficient of 0.61 was obtained. The comparison of the distributions of Ncoc and PIC for two satellite overpasses with intensive CB in June 2017 and 2022 is shown in Figure 6. It can be seen that, in fact, the Ncoc and PIC distributions are visually similar. Note that for PIC values in areas affected by river runoff (for example, near the mouth of the Danube River) the data are masked, while the 2014 algorithm yields low Ncoc estimates in these areas. Moreover, sometimes, areas where the algorithm for Ncoc shows an intense CB are hidden in PIC distribution map, as was the case near the Kerch Strait (45N, 37E) for the 2017 image, for example.
According to the 8 June 2017 MODIS Terra data in the eastern part of the Black Sea (Figure 7 upper image), the pixel-by-pixel comparison of PIC and Ncoc values was performed for both Ncoc algorithms. The proportionality coefficients between Ncoc and PIC transpired to be 252 and 250, which is quite consistent with the previous value of 223 [29]. It is of interest to make comparisons under non-typical Saharan dust transfer conditions, for which additional data correction is recommended [80].
4.5. The Effect of the Bloom Phase (The Difference for Two Years)
To select the best algorithm for estimating Ncoc in conditions of intensive CB in the north-eastern part of the Black Sea, we focused on the correspondence of the measured and calculated Ncoc values for the total dataset for two years. Moreover, it was seen that, on the whole, the data in these years have their own peculiarities (see Figure 5). In addition, according to direct measurements, a different ratio was recorded for them between the concentrations of placed coccolithophore cells Ncc and detached coccoliths Ncl, which may be the result of a different bloom phase during field measurements. In order to select the best algorithm for each year separately, the statistical parameters (RMSE and MAPE) of the calculated Ncoc and measured Ncc_cl are presented separately for each year (Table 4).

Table 4.
The RMSE (106 Cells L−1) and MAPE values of the Ncoc estimates relative to the measured Ncc_cl for the 2017 and 2022 data separately and depending on the value of the parameters of the algorithm Kcoc, Kriv, and bbp_bg.
As in the case of a general data array, the smallest difference between the measured and calculated values was obtained with the smallest fraction of terrigenous suspension (option 0.1_0.1). Although the Kcoc = 3.94 × 10−3 value suits 2017 better, for 2022, it should be changed to 2.74 × 10−3. However, this choice is rather arbitrary as for other parameters of the algorithm almost the same compliance estimates were obtained. For example, for the 2017 data, RMSE = 1.79 and MAPE = 15% in the case of the 0.1_0.1 option and Kcoc = 3.94 × 10−3, while for the 0.5_0.5 option and Kcoc = 3.52 × 10−3, we obtain almost the same difference parameters: RMSE = 1.86 and MAPE = 16%. This means that although the regional algorithm can be customized for specific bloom phases, the algorithm without taking into account the bloom phase will give almost the same Ncoc estimations equally well, which should certainly be attributed as one of its advantages. A number of previously developed optical methods can be used to detect different bloom phases [81,82].
4.6. Influence of the Spectral Index m Values for the Suspended Matter on the Rrs Spectra
To determine the parameter m of the spectral dependence of backscattering by suspended matter in HydroLight calculations, we used Equation (9) with a low coefficient of determination value (R2 = 0.49). The value of m could vary in the range 1.0–1.3 (Figure 2). To check what effect the m value has on the model Rrs(λ) spectrum, HydroLight calculations for station 3_17 with different values of m (Figure 8) were performed. It can be seen that even for extreme values of 1.0 and 1.3, the model spectra differ only very slightly. For the 551 nm band, they coincide and for 488 nm, the difference is 3%. That is, in the HydroLight calculation model, in order to improve the Ncoc estimation algorithm, it is possible to use Equation (9) or a fixed m value from the range 1.0–1.3 with good accuracy.
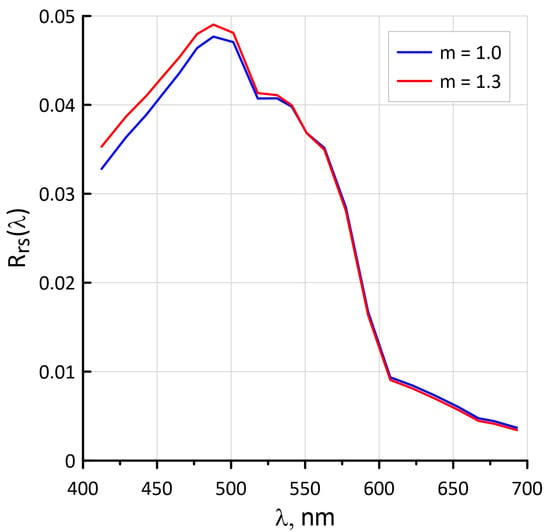
Figure 8.
The results of modeling the Rrs(λ) spectra using the Hydrolight software with changes in the m value—the parameter of the spectral dependence of suspended matter backscattering—at station 3_17.
5. Conclusions
A modified regional algorithm to quantify the concentration of coccolithophores in the northeastern part of the Black Sea under conditions of intense bloom is presented. Compared to the data underlying the previous version of the algorithm, over recent years, it has been possible to significantly expand the accumulated dataset of in situ coccolithophore and coccolith concentration determinations. In addition, the ratio between the number of detached coccoliths and plated coccolithophore cells was taken into account. The undoubted advantages of the new algorithm include its lower sensitivity to variations in the values of chlorophyll concentration and CDOM absorption, which are not associated with coccolithophorid blooms. In the future, much attention should be paid to the Western part of the Black Sea, where the problem of separating the contribution of the Danube and Dnieper rivers into the remote sensing reflectance signal arises, as well as developing an algorithm for quantifying the concentration of coccolithophorids during winter blooms. This means that it will be necessary to carry out extended expeditionary studies for the mentioned region and season, including direct determinations of the concentration of coccolithophorids. In general, the proposed approach with the separation of particulate matter into two components (terrigenous and coccolithophore) can be used to create regional or seasonal algorithms for estimating the concentration of coccolithophores in any region of the world ocean during any period. It is only necessary to have the data of field measurements of coccolithophore concentration and simultaneous shipboard or satellite measurements of the remote sensing reflectance for the selected region and period.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15092219/s1; Table S1. Abundance and biomass of Emiliania huxleyi, total phytoplankton biomass, and coccoliths abundance in 2017. Table S2. Abundance and biomass of Emiliania huxleyi, total phytoplankton biomass, and coccoliths abundance in 2022; MATLAB Script S1: Ncoc_BlackSea_regional.
Author Contributions
Conceptualization, S.V. and D.G.; methodology, S.V., D.D., V.S. and L.P.; software, S.V. and D.D.; validation, S.V.; formal analysis, S.V. and D.G.; investigation, S.V., D.D., D.G., V.S. and L.P.; writing, S.V., V.S., D.D. and D.G.; visualization, S.V.; project administration, D.G.; funding acquisition, D.G. All authors have read and agreed to the published version of the manuscript.
Funding
Shipboard data retrieval was carried out as part of the state assignment of SIO RAS (theme No. FMWE-2021-0001). Hydrooptical modeling of coccolithophore blooms was funded by the Russian Science Foundation (project No. 21-77-10059). Field sampling and analyses of coccolithophores abundance data were supported by the Russian Science Foundation (project No. 22-17-00066). Ocean color data processing was sponsored under the project funded by the Russian Hydrometeorological Service (contract agreement No. 169-15-2023-002).
Data Availability Statement
The data of in situ measurements of coccolithophore Emiliania huxleyi abundance and the algorithm code (MATLAB script) are available in the Supplementary Materials.
Acknowledgments
We are grateful to the GSFC NASA for the MODIS and VIIRS data. We are also grateful to V.A. Artemyev, A.V. Grigoriev, and A.N. Khrapko for help with optical measurements and to S.V. Sheberstov for help with satellite data processing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Falkowski, P.G.; Raven, J.A. Aquatic Photosynthesis: Second Edition; Princeton University Press: Princeton, NJ, USA, 2013; ISBN 978-1-4008-4972-7. [Google Scholar]
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Keppler, L.; Landschützer, P.; Gruber, N.; Lauvset, S.K.; Stemmler, I. Seasonal Carbon Dynamics in the Near-Global Ocean. Glob. Biogeochem. Cycles 2020, 34, e2020GB006571. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Bakker, D.C.E.; Hauck, J.; Le Quéré, C.; Peters, G.P.; Peters, W.; Pongratz, J.; et al. Global Carbon Budget 2021. Earth Syst. Sci. Data 2022, 14, 1917–2005. [Google Scholar] [CrossRef]
- Volk, T.; Hoffert, M.I. Ocean Carbon Pumps: Analysis of Relative Strengths and Efficiencies in Ocean-Driven Atmospheric CO2 Changes. In Geophysical Monograph Series; Sundquist, E.T., Broecker, W.S., Eds.; American Geophysical Union: Washington, DC, USA, 2013; pp. 99–110. ISBN 978-1-118-66432-2. [Google Scholar]
- Sarmiento, J.L.; Gruber, N. Ocean Biogeochemical Dynamics; Princeton University Press: Princeton, NJ, USA, 2006; ISBN 978-0-691-01707-5. [Google Scholar]
- Henson, S.A.; Sanders, R.; Madsen, E.; Morris, P.J.; Le Moigne, F.; Quartly, G.D. A Reduced Estimate of the Strength of the Ocean’s Biological Carbon Pump: BIOLOGICAL CARBON PUMP STRENGTH. Geophys. Res. Lett. 2011, 38, L04606. [Google Scholar] [CrossRef]
- Siegel, D.A.; Buesseler, K.O.; Doney, S.C.; Sailley, S.F.; Behrenfeld, M.J.; Boyd, P.W. Global Assessment of Ocean Carbon Export by Combining Satellite Observations and Food-Web Models. Glob. Biogeochem. Cycles 2014, 28, 181–196. [Google Scholar] [CrossRef]
- Legendre, L.; Rivkin, R.B.; Weinbauer, M.G.; Guidi, L.; Uitz, J. The Microbial Carbon Pump Concept: Potential Biogeochemical Significance in the Globally Changing Ocean. Prog. Oceanogr. 2015, 134, 432–450. [Google Scholar] [CrossRef]
- Tréguer, P.J.; De La Rocha, C.L. The World Ocean Silica Cycle. Annu. Rev. Mar. Sci. 2013, 5, 477–501. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011; ISBN 978-0-521-15175-7. [Google Scholar]
- Milliman, J.D. Production and Accumulation of Calcium Carbonate in the Ocean: Budget of a Nonsteady State. Glob. Biogeochem. Cycles 1993, 7, 927–957. [Google Scholar] [CrossRef]
- Poulton, A.J.; Adey, T.R.; Balch, W.M.; Holligan, P.M. Relating Coccolithophore Calcification Rates to Phytoplankton Community Dynamics: Regional Differences and Implications for Carbon Export. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2007, 54, 538–557. [Google Scholar] [CrossRef]
- Balch, W.M. The Ecology, Biogeochemistry, and Optical Properties of Coccolithophores. Annu. Rev. Mar. Sci. 2018, 10, 71–98. [Google Scholar] [CrossRef]
- Kondrik, D.V.; Pozdnyakov, D.V.; Johannessen, O.M. Satellite Evidence that E. huxleyi Phytoplankton Blooms Weaken Marine Carbon Sinks. Geophys. Res. Lett. 2018, 45, 846–854. [Google Scholar] [CrossRef]
- Kondrik, D.V.; Kazakov, E.E.; Pozdnyakov, D.V.; Johannessen, O.M. Satellite evidence for enhancement of columnal mixing ratio of atmospheric CO2 over E. huxleyi blooms. Trans. Karelian Res. Cent. Russ. Acad. Sci. 2019, 9, 125–135. [Google Scholar] [CrossRef]
- Morozov, E.A.; Kondrik, D.V.; Chepikova, S.S.; Pozdnyakov, D.V. Atmospheric columnar CO2 enhancement over E. huxleyi blooms: Case studies in the North Atlantic and Arctic waters. Trans. Karelian Res. Cent. Russ. Acad. Sci. 2019, 3, 28–33. [Google Scholar] [CrossRef]
- Cermeño, P.; Dutkiewicz, S.; Harris, R.P.; Follows, M.; Schofield, O.; Falkowski, P.G. The Role of Nutricline Depth in Regulating the Ocean Carbon Cycle. Proc. Natl. Acad. Sci. USA 2008, 105, 20344–20349. [Google Scholar] [CrossRef]
- Holligan, P.M.; Fernández, E.; Aiken, J.; Balch, W.M.; Boyd, P.; Burkill, P.H.; Finch, M.; Groom, S.B.; Malin, G.; Muller, K.; et al. A Biogeochemical Study of the Coccolithophore, Emiliania huxleyi, in the North Atlantic. Glob. Biogeochem. Cycles 1993, 7, 879–900. [Google Scholar] [CrossRef]
- Young, J. Functions of coccoliths. In Coccolithophores; Winter, A., Siesser, W.G., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 63–82. [Google Scholar]
- Iglesias-Rodríguez, M.D.; Brown, C.W.; Doney, S.C.; Kleypas, J.; Kolber, D.; Kolber, Z.; Hayes, P.K.; Falkowski, P.G. Representing key phytoplankton functional groups in ocean carbon cycle models: Coccolithophorids. Glob. Biogeochem. Cycles 2002, 16, 47-1–47-20. [Google Scholar] [CrossRef]
- Paasche, E. A Review of the Coccolithophorid Emiliania huxleyi (Prymnesiophyceae), with Particular Reference to Growth, Coccolith Formation, and Calcification-Photosynthesis Interactions. Phycologia 2001, 40, 503–529. [Google Scholar] [CrossRef]
- Tyrrell, T.; Merico, A. Emiliania huxleyi: Bloom Observations and the Conditions That Induce Them. In Coccolithophores; Thierstein, H.R., Young, J.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 75–97. ISBN 978-3-642-06016-8. [Google Scholar]
- Morozova-Vodyanitskaya, N.V.; Belogorskaya, E.V. On the Significance of Coccolithophores and, Especially, Pontosphere in the Black Sea Plankton. Tr. Sev. Biol. Stantsii. 1957, 9, 14–21. (In Russian) [Google Scholar]
- Pautova, L.A.; Mikaelyan, A.S.; Silkin, V.A. Structure of Plankton Phytocoenoses in the Shelf Waters of the Northeastern Black Sea during the Emiliania huxleyi Bloom in 2002–2005. Oceanology 2007, 47, 377–385. [Google Scholar] [CrossRef]
- Mikaelyan, A.S.; Silkin, V.A.; Pautova, L.A. Coccolithophorids in the Black Sea: Their Interannual and Long-Term Changes. Oceanology 2011, 51, 39–48. [Google Scholar] [CrossRef]
- Silkin, V.A.; Pautova, L.A.; Giordano, M.; Chasovnikov, V.K.; Vostokov, S.V.; Podymov, O.I.; Pakhomova, S.V.; Moskalenko, L.V. Drivers of Phytoplankton Blooms in the Northeastern Black Sea. Mar. Pollut. Bull. 2019, 138, 274–284. [Google Scholar] [CrossRef]
- Kopelevich, O.; Burenkov, V.; Sheberstov, S.; Vazyulya, S.; Kravchishina, M.; Pautova, L.; Silkin, V.; Artemiev, V.; Grigoriev, A. Satellite Monitoring of Coccolithophore Blooms in the Black Sea from Ocean Color Data. Remote Sens. Environ. 2014, 146, 113–123. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Burenkov, V.I.; Vazyulya, S.V.; Sheberstov, S.V. Problems of detection of coccolithophore blooms from satellite data. Mod. Probl. Remote Sens. Earth Space 2012, 9, 241–250. [Google Scholar]
- Churilova, T.; Moncheva, S.; Suslin, V.; Kryvenko, O. Intensity, area extent and frequency of coccolithophores Emiliania huxleyi blooms in the Black Sea: Application of remote sensing approach. Int. Multidiscip. Sci. GeoConference SGEM 2017, 17, 871–879. [Google Scholar] [CrossRef]
- Pozdnyakov, D.V.; Pettersson, L.H.; Korosov, A.A. Exploring the Marine Ecology from Space; Springer Remote Sensing/Photogrammetry; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-30074-0. [Google Scholar]
- Pozdnyakov, D.V.; Gnatiuk, N.V.; Davy, R.; Bobylev, L.P. The Phenomenon of Emiliania huxleyi in Aspects of Global Climate and the Ecology of the World Ocean. GES 2021, 14, 50–62. [Google Scholar] [CrossRef]
- Cokacar, T.; Kubilay, N.; Oguz, T. Structure of Emiliania huxleyi Blooms in the Black Sea Surface Waters as Detected by SeaWIFS Imagery. Geophys. Res. Lett. 2001, 28, 4607–4610. [Google Scholar] [CrossRef]
- Kideys, A.E. Fall and Rise of the Black Sea Ecosystem. Science 2002, 297, 1482–1484. [Google Scholar] [CrossRef]
- Karabashev, G.S.; Sheberstov, S.V.; Yakubenko, V.G. The June maximum of normalized radiance and its relation to the hydrological conditions and coccolithophorid bloom in the Black Sea. Oceanology 2006, 46, 305–317. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Burenkov, V.I.; Sheberstov, S.V.; Vazulya, S.V.; Sahling, I.V. Coccolithophore Blooms in the North-Eastern Black Sea. In Proceedings of the Twelfth International Conference on the Mediterranean Coastal Environment, Varna, Bulgaria, 6–10 October 2015; MEDCOAST, Mediterranean Coastal Foundation: Dalyan, Turkey, 2015; Volume 1, pp. 363–374. [Google Scholar]
- Karabashev, G.S.; Evdoshenko, M.A. Manifestations of the rim current, coccolithophore blooms, and continental runoff in the long-term monthly mean distributions of satellite reflectance coefficients of the Black Sea. Oceanology 2015, 55, 36–46. [Google Scholar] [CrossRef]
- Karabashev, G.S. On the mesoscale structure of the Black Sea satellite images during coccolithophorid bloom. Remote Sens. Earth Space 2018, 15, 183–190. [Google Scholar] [CrossRef]
- Vostokov, S.V.; Vostokova, A.S.; Vazyulya, S.V. Seasonal and Long-Term Variability of Coccolithophores in the Black Sea According to Remote Sensing Data and the Results of Field Investigations. JMSE 2022, 10, 97. [Google Scholar] [CrossRef]
- Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Yushmanova, A.V. Atlas of Bio-Optical Characteristics of the Russian Seas According to Satellite Ocean Color Scanners. Available online: http://optics.ocean.ru/ (accessed on 18 April 2023).
- Hedley, J.D.; Mobley, C.D. Hydrolight 6.0 Ecolight 6.0 Technical Documentation; Numerical Optics Ltd.: Tiverton, UK, 2019; Available online: https://scholar.google.com/scholar_lookup?title=HYDROLIGHT+6.0+ECOLIGHT+6.0+Technical+Documentation&author=Hedley,+J.D.&author=Mobley,+C.D.&publication_year=2019 (accessed on 18 April 2023).
- Artemiev, V.A.; Burenkov, V.I.; Vortman, M.I.; Grigoriev, A.V.; Kopelevich, O.V.; Khrapko, A.N. Sea-truth measurements of ocean color: A new floating spectroradiometer and its metrology. Oceanology 2000, 40, 139–145. [Google Scholar]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral Remote Sensing for Shallow Waters. I. A Semianalytical Model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef]
- Burenkov, V.I.; Sheberstov, S.V.; Artemiev, V.A.; Taskaev, V.R. Estimation of Measurement Error of the Seawater Beam Attenuation Coefficient in Turbid Water of Arctic Seas. Light Eng. 2019, 27, 103–111. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Sheberstov, S.V.; Kopelevich, O.V.; Zaytseva, A.F.; Pogosyan, S.I. Measuring the sea water absorption factor using integrating sphere. Light Eng. 2018, 26, 120–126. [Google Scholar] [CrossRef]
- Yushmanova, A.V.; Kopelevich, O.V.; Vazyulya, S.V.; Sahling, I.V. Inter-annual variability of the seawater light absorption in surface layer of the northeastern Black Sea in connection with hydrometeorological factors. J. Mar. Sci. Eng. 2019, 7, 326. [Google Scholar] [CrossRef]
- Holm-Hansen, O.; Riemann, B. Chlorophyll a Determination: Improvements in Methodology. Oikos 1978, 30, 438–447. [Google Scholar] [CrossRef]
- Arar, E.J.; Collins, G.B. Method 445.0 In Vitro Determination of Chlorophyll a and Pheophytin in Marine and Freshwater Algae by Fluorescence; United States Environmental Protection Agency: Washington, DC, USA, 1997.
- Tomas, C.R. Identifying Marine Phytoplankton; Academic Press: New York, NY, USA, 1997; p. 858. [Google Scholar]
- Throndsen, J.; Hasle, G.R.; Tangen, K.I. Phytoplankton of Norwegian Coastal Waters; Almater Forlorlag AS: Oslo, Norway, 2007; ISBN 978-82-7858-037-0. [Google Scholar]
- Hillebrand, H.; Dürselen, C.-D.; Kirschtel, D.; Pollingher, U.; Zohary, T. Biovolume Calculation for Pelagic and Benthic Microalgae. J. Phycol. 1999, 35, 403–424. [Google Scholar] [CrossRef]
- Moncheva, S.; Parr, B. Manual for Phytoplankton Sampling and Analysis in the Black Sea. Phytoplankton Manual, UP-GRADE Black Sea Scene Project, FP7. 2010, p. 67. Available online: http://blacksea-commission.org/Downloads/Phytoplankton_%20Mannual-Final-1.pdf (accessed on 3 April 2023).
- Voss, K.J.; Balch, W.M.; Kilpatrick, K.A. Scattering and Attenuation Properties of Emiliania huxleyi Cells and Their Detached Coccoliths. Limnol. Oceanogr. 1998, 43, 870–876. [Google Scholar] [CrossRef]
- NASA’s OceanColor Web, Level 1&2 Brouser. Available online: https://oceancolor.gsfc.nasa.gov/cgi/browse.pl (accessed on 18 April 2023).
- Sheberstov, S.V. A system of batch processing of oceanological satellite data. Curr. Probl. Remote Sens. Earth Space 2015, 12, 154–161. Available online: http://jr.rse.cosmos.ru/article.aspx?id=1447&lang=eng (accessed on 18 April 2023).
- Cazzaniga, I.; Zibordi, G.; Mélin, F. Spectral Variations of the Remote Sensing Reflectance during Coccolithophore Blooms in the Western Black Sea. Remote Sens. Environ. 2021, 264, 112607. [Google Scholar] [CrossRef]
- Mobley, C.; Stramski, D.; Bissett, W.; Boss, E. Optical Modeling of Ocean Waters: Is the Case 1–Case 2 Classification Still Useful? Oceanography 2004, 17, 60–67. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption Spectrum (380–700 Nm) of Pure Water II Integrating Cavity Measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Röttgers, R.; McKee, D.; Utschig, C. Temperature and Salinity Correction Coefficients for Light Absorption by Water in the Visible to Infrared Spectral Region. Opt. Express 2014, 22, 25093–25108. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994; ISBN 978-0-12-502750-2. [Google Scholar]
- Loisel, H.; Morel, A. Light Scattering and Chlorophyll Concentration in Case 1 Waters: A Reexamination. Limnol. Oceanogr. 1998, 43, 847–858. [Google Scholar] [CrossRef]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional Reflectance of Oceanic Waters: Accounting for Raman Emission and Varying Particle Scattering Phase Function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized Ocean Color Inversion Model for Retrieving Marine Inherent Optical Properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef]
- Tyrrell, T.; Holligan, P.M.; Mobley, C.D. Optical Impacts of Oceanic Coccolithophore Blooms. J. Geophys. Res. 1999, 104, 3223–3241. [Google Scholar] [CrossRef]
- Kopelevich, O.; Sheberstov, S.; Vazyulya, S. Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column. JMSE 2020, 8, 456. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2017; VASh FORMAT, OOO: Moscow, Russia, 2018. [Google Scholar]
- Glukhovets, D.; Kopelevich, O.; Yushmanova, A.; Vazyulya, S.; Sheberstov, S.; Karalli, P.; Sahling, I. Evaluation of the CDOM Absorption Coefficient in the Arctic Seas Based on Sentinel-3 OLCI Data. Remote Sens. 2020, 12, 3210. [Google Scholar] [CrossRef]
- Arkhipkin, V.S.; Gippius, F.N.; Koltermann, K.P.; Surkova, G.V. Wind Waves in the Black Sea: Results of a Hindcast Study. Nat. Hazards Earth Syst. Sci. 2014, 14, 2883–2897. [Google Scholar] [CrossRef]
- Mikaelyan, A.S.; Pautova, L.A.; Chasovnikov, V.K.; Mosharov, S.A.; Silkin, V.A. Alternation of Diatoms and Coccolithophores in the North-Eastern Black Sea: A Response to Nutrient Changes. Hydrobiologia 2015, 755, 89–105. [Google Scholar] [CrossRef]
- Drits, A.V.; Nikishina, A.B.; Sergeeva, V.M.; Solov’ev, K.A. Feeding, Respiration, and Excretion of the Black Sea Noctiluca Scintillans MacCartney in Summer. Oceanology 2013, 53, 442–450. [Google Scholar] [CrossRef]
- Burenkov, V.I.; Kopelevich, O.V.; Rat’kova, T.N.; Sheberstov, S.V. Satellite Observations of the Coccolithophorid Bloom in the Barents Sea. Oceanology 2011, 51, 766–774. [Google Scholar] [CrossRef]
- Kubryakov, A.A.; Mikaelyan, A.S.; Stanichny, S.V. Summer and Winter Coccolithophore Blooms in the Black Sea and Their Impact on Production of Dissolved Organic Matter from Bio-Argo Data. J. Mar. Syst. 2019, 199, 103220. [Google Scholar] [CrossRef]
- Kubryakov, A.A.; Mikaelyan, A.S.; Stanichny, S.V. Extremely Strong Coccolithophore Blooms in the Black Sea: The Decisive Role of Winter Vertical Entrainment of Deep Water. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2021, 173, 103554. [Google Scholar] [CrossRef]
- Kubryakova, E.A.; Kubryakov, A.A.; Mikaelyan, A.S. Winter Coccolithophore Blooms in the Black Sea: Interannual Variability and Driving Factors. J. Mar. Syst. 2021, 213, 103461. [Google Scholar] [CrossRef]
- Vostokov, S.V.; Lobkovskiy, L.I.; Vostokova, A.S.; Solov’ev, D.M. Seasonal and Interannual Variability of Phytoplankton in the Black Sea on the Basis of Remote Sensing Data and In Situ Measurements of Chlorophyll-a. Dokl. Earth Sci. 2019, 485, 293–297. [Google Scholar] [CrossRef]
- Vostokova, A.; Vostokov, S.; Saling, I. Regional Features of Seasonal Variability of Phytoplankton in the Black Sea Studied by Remote Sensing Data. In Proceedings of the 28th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Tomsk, Russia, 4–8 July 2022; Romanovskii, O.A., Matvienko, G.G., Eds.; SPIE: Tomsk, Russia, 2022; p. 281. [Google Scholar] [CrossRef]
- Gordon, H.R.; Balch, W.M. MODIS Detached Coccolith Concentration Algorithm Theoretical Basis Document, Version 4, Algorithm Theoretical Basis Document. 1999; p. 27. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod23.pdf (accessed on 3 April 2023).
- Gordon, H.R.; Boynton, G.C.; Balch, W.M.; Groom, S.B.; Harbour, D.S.; Smyth, T.J. Retrieval of Coccolithophore Calcite Concentration from SeaWiFS Imagery. Geophys. Res. Lett. 2001, 28, 1587–1590. [Google Scholar] [CrossRef]
- Kalinskaya, D.V.; Papkova, A.S. Why Is It Important to Consider Dust Aerosol in the Sevastopol and Black Sea Region during Remote Sensing Tasks? A Case Study. Remote Sens. 2022, 14, 1890. [Google Scholar] [CrossRef]
- Konyukhov, I.V.; Glukhovets, D.I. A set of optical methods for studying marine phytoplankton. Oceanology 2017, 57, 419–423. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Goldin, Y.A. Express method for chlorophyll concentration assessment. J. Photochem. Photobiol. 2021, 8, 100083. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).