Abstract
Plastic-covered greenhouse (PCG) segmentation represents a significant challenge for object-based PCG mapping studies due to the spectral characteristics of these singular structures. Therefore, the assessment of PCG segmentation quality by employing a multiresolution segmentation algorithm (MRS) was addressed in this study. The structure of this work is composed of two differentiated phases. The first phase aimed at testing the performance of eight widely applied supervised segmentation metrics in order to find out which was the best metric for evaluating image segmentation quality over PCG land cover. The second phase focused on examining the effect of several factors (reflectance storage scale, image spatial resolution, shape parameter of MRS, study area, and image acquisition season) and their interactions on PCG segmentation quality through a full factorial analysis of variance (ANOVA) design. The analysis considered two different study areas (Almeria (Spain) and Antalya (Turkey)), seasons (winter and summer), image spatial resolution (high resolution and medium resolution), and reflectance storage scale (Percent and 16Bit formats). Regarding the results of the first phase, the Modified Euclidean Distance 2 (MED2) was found to be the best metric to evaluate PCG segmentation quality. The results coming from the second phase revealed that the most critical factor that affects MRS accuracy was the interaction between reflectance storage scale and shape parameter. Our results suggest that the Percent reflectance storage scale, with digital values ranging from 0 to 100, performed significantly better than the 16Bit reflectance storage scale (0 to 10,000), both in the visual interpretation of PCG segmentation quality and in the quantitative assessment of segmentation accuracy.
1. Introduction
Recently, the agricultural areas using plastic-covered greenhouses (PCG) have expanded rapidly as the food demand increases with the population growth, since the intensification of agriculture production is a promising alternative. Nevertheless, PCG activities are subject to various environmental concerns in addition to their contribution to agricultural development [1,2]—for example: contamination of aquifers [3], deterioration of soils due to plastic film residues [4], invasion of protected areas [5], or transformation of primary land use and land cover [6]. In this way, it is necessary to understand and monitor the distribution of these structures worldwide to develop efficient management strategies. Nowadays, remote sensing technology has proven to be a suitable approach to obtain information on the distribution of PCG, as it provides monitoring in a wide geographical area and has an extensive temporal archive [6,7]. However, PCG mapping from remote sensing images remains challenging due to the unique spectral characteristics of greenhouses [6,8].
Once remotely sensed images have been acquired, they have to be processed to extract meaningful information. Among available image processing methods, object-based image analysis (OBIA) has been widely utilized in PCG mapping, since its ability to model contextual information, including shape, texture, and topological relationships between groups of pixels (segments), reduces confusion in the classification process [9]. In this sense, the first and one of the most crucial steps in OBIA workflow is image segmentation, which largely determines the accuracy of subsequent classification [10], thus constituting a basic intermediate step for many applications [11]. Image segmentation divides the input image into relatively homogeneous and semantically significant groups of pixels representing real land cover depending on color, spectral characteristics, texture, or shape of objects [12]. The reader can find a detailed meta-analysis on remote sensing image segmentation advances during the last two decades in Kotaridis and Lazaridou [13].
Although there are different image segmentation algorithms developed in the fields of image processing and computer vision, the multiresolution segmentation (MRS) algorithm, available through eCognition software (Trimble, Munich, Germany), has been widely used and successfully employed in various remote sensing applications. For instance, Ma et al. [14] reported that up to 80.9% of the 254 case studies analyzed in their work had adopted eCognition software to carry out the segmentation stage. It is important to note that this image segmentation algorithm has also been used effectively in object-based PCG mapping studies from different input data [9,15,16,17,18].
The MRS outputs depend on three tuning parameters (scale, shape, and compactness) specified by the user. The optimal value of these parameters depends largely on the intended application, which is mainly related to the target land cover and the characteristics of the input image. The main reason for this is that land objects or segments have different spectral and structural variability, which means that the parameters that reach optimal segmentation may vary for different land objects [10,19,20,21]. Nonetheless, deciding the most suitable segmentation is not an easy task, since it may be impossible to achieve an optimal segmentation for even a single land object due to image noise, fuzzy borders, or hierarchical details of the objects [22]. In this case, it is necessary to create a framework in which segmentation quality can be evaluated to ensure the generalization of image segmentation. Consequentially, segmentation quality can be assessed iteratively on the image until the most suitable segmentation is produced [20].
However, how does one assess segmentation quality? Numerous empirical methods have been proposed to evaluate the accuracy of image segmentation, and these are categorized as supervised and unsupervised [23,24]. Supervised evaluation methods rely on the discrepancy between a set of reference polygons and their corresponding image segments generated by the tested algorithm [25]. On the other hand, unsupervised approaches measure segmentation goodness by analyzing the inter-class heterogeneity and intra-class homogeneity [20,24]. Chen et al. [26] stated that the supervised evaluation methods are more appropriate for the artificial target recognition task since these methods take more into account the accuracy of geometric boundaries. Accordingly, supervised evaluation methods can be used efficiently to choose the optimal segmentation algorithm or to decide the most appropriate segmentation parameters for a specific segmentation algorithm [26]. Regarding unsupervised evaluation methods, it is worth noting that intra-class homogeneity within a single PCG segment can be affected by factors such as the presence of plants inside the PCG or roof whitewashing activities. Furthermore, inter-class heterogeneity may be influenced in study areas where PCG are densely concentrated. Such reasons may result in unsupervised evaluation methods being ineffective in evaluating the accuracy of PCG segmentation.
Several empirical studies have focused on assessing segmentation quality through supervised evaluation metrics [20,25,27,28]. For instance, a well-documented review reported by Clinton et al. [25] assessed several segmentation evaluation metrics for measuring under-segmentation and over-segmentation, or both. In addition, a recent study by Jozdani and Chen [20] compared the under-segmentation, over-segmentation, and combined supervised segmentation evaluation metrics, finally providing a general overview on the selection of supervised evaluation metrics for buildings extraction.
Although the segmentation outputs on satellite imagery obtained through the MRS algorithm are highly dependent on the selected scale parameter, they may also be affected by the acquisition date (note that the spectral signature of greenhouses changes over time), shape parameter, and image spatial resolution [11,29].
Aguilar et al. [29] reported the first finding to determine the optimal WorldView-3-derived image data source to perform the MRS algorithm on PCG. They found that the multispectral WorldView-3 atmospherically corrected orthoimage was the most suitable image data source to achieve the best PCG segmentation. This image product presented a geometric resolution of 1.2 m and digital values expressed as ground reflectance ranging from 0 to 100 (percentage values).
Finally, and to the best of authors’ knowledge, no study has experimentally analyzed the direct effect and interactions of all the variables that can potentially affect PCG segmentation quality so far. Thus, in the light of the examined literature, a two-stage experimental research was designed in this study to tackle PCG segmentation through applying the MRS algorithm. In this way, the first objective of this paper is to evaluate the performance of eight supervised segmentation metrics for estimating PCG segmentation quality. The second objective aims at statistically unraveling the influence of several factors (reflectance storage scale, image spatial resolution, shape parameter, study area, and image capture date or season) and their interactions on PCG segmentation quality through a full factorial analysis of variance (ANOVA) design.
2. Study Areas
Two square areas of 3 km per side located in Almería (Spain) and Antalya (Turkey) were selected as the study areas in this work (Figure 1).
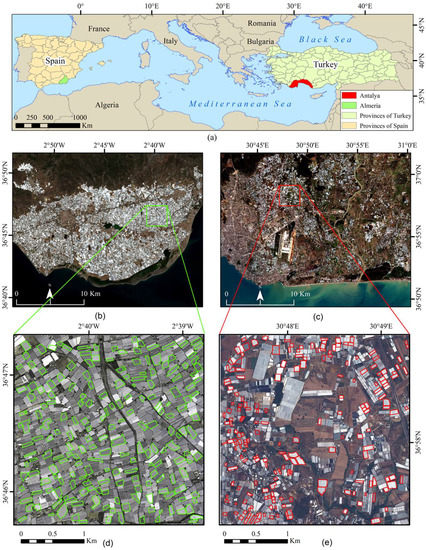
Figure 1.
(a) Global location of the Almería and Antalya study sites; (b) general overview of the PCG in Almería, and (c) Antalya; (d) study area in Almería and (e) Antalya. Note: those polygons depicted in (d,e) are the manually digitized reference polygons used for segmentation quality assessment.
The study area of Almería, southeast of Spain, was centered on the geographic coordinates (WGS84) 2.668°W and 36.777°N. There is a dense concentration of PCG in this region dedicated to the intensive production of horticultural crops such as tomato, pepper, cucumber, aubergine, melon, and watermelon [30,31]. It is worth noting that the spectral signatures of PCG change over time due to both the phenological development of the growing crops [18] and frequent roof whitewashing performed to mitigate excess radiation and lower the temperature inside the greenhouse [7].
The second study area was located in the Aksu district of Antalya, Turkey, centered on the geographic coordinates (WGS84) 30.805°E and 36.968°N. This region is one of the provinces where greenhouse production is most intense in Turkey, mainly dedicated to the cultivation of vegetables, cut flowers, ornamental plants, and saplings. The most common covering material for the greenhouse structures located at this study area is plastic, although there are also some glass greenhouses. The distribution of PCG in Antalya looks more isolated and dispersed than in Almería (Figure 1).
3. Datasets and Pre-Processing
Eight cloud-free satellite images corresponding to Almería (two images from WorldView-3 and two from Sentinel-2) and Antalya (two images from SPOT-7 and two from Sentinel-2) study sites were used in this work. The image acquisition dates were chosen based on data availability and with the intention of trying to cover two different seasons, since the spectral signature of PCG changes substantially between the winter and summer seasons due mainly to the whitewashing of greenhouse roofs, which is more frequent in summer.
3.1. WorldView-3
WorldView-3 (WV3) is a high-spatial-resolution optical satellite launched in 2014 and operated by DigitalGlobe Inc. (currently Maxar). The two WV3 images covering the Almería study area were taken on 11 June 2020 (summer image) and 25 December 2020 (winter image). Both images, taken in Ortho Ready Standard Level-2A (ORS2A) format, included the multispectral (MS) image composed of eight visible and near-infrared bands with a spatial resolution of 1.24 m [32]. The WV3 images were acquired with off-nadir angles of 27.6° and 1.5° for the summer and winter images, respectively. The final MS product presented a ground sample distance (GSD) of 1.2 m. The delivered products were ordered with a dynamic range of 11 bits (without dynamic range adjustment).
According to Aguilar et al. [31], the MS WV3 orthoimages were obtained using the coordinates of seven ground control points (GCPs) and a sensor model based on rational functions refined by a zero-order transformation (RPC0). A medium resolution 10 m grid spacing DEM was used to carry out the orthorectification process by using Catalyst v. 2222.0.5 software (PCI Geomatics, Richmond Hill, ON, Canada).
The MS WV3 orthoimages were atmospherically corrected with the ATCOR module based on the MODTRAN (MODerate resolution atmospheric TRANsmission) radiative transfer code [33] implemented in Catalyst. The WV3 ATCOR MS orthoimages were computed in two ways to investigate the effect of reflectance digital storage scale on segmentation accuracy: (i) 16Bit Reflectance: computing the output in reflectance units ranging from 0 to 10,000 integer values stored in a 16-bit signed integer format (hereinafter referred to as 16Bit reflectance). (ii) Percent Reflectance: computing the output in reflectance units from zero to 100 real values stored in a float32 single-precision floating-point format (hereinafter referred to as Percent reflectance).
3.2. SPOT-7
SPOT-7 was launched by AIRBUS Defense & Space in 2014, acquiring MS images including four bands (red, green, blue, and NIR) with 6 m GSD. It also counts on a panchromatic (PAN) image with a spatial resolution of 1.5 m. The radiometric resolution of SPOT-7 imagery is 12 bits. The two SPOT-7 images used to cover the Antalya study area were Orthorectified products, being taken on 5 February 2019 (winter season) and 4 July 2019 (summer season) with off-nadir angles of 9.3° and 20.6°, respectively.
SPOT-7 pan-sharpened images (1.5 m GSD with four spectral bands) were obtained from the SPOT-7 PAN and MS images using the PANSHARP module of Catalyst. Next, atmospherically corrected SPOT-7 pan-sharpened orthoimages (both in 16Bit reflectance and Percent reflectance formats) were produced with the ATCOR module following the methodology previously described for WV3 imagery.
3.3. Sentinel-2
Sentinel-2 (S2) is a satellite system designed for simultaneous global and continuous monitoring of land and coastal areas made up of two identical satellites, namely Sentinel-2A (S2A) and Sentinel-2B (S2B). The MultiSpectral Instrument (MSI) sensors on-board S2A and S2B satellites provide up to 13 spectral bands with different GSD, ranging from 10 m to 60 m. In this research, four S2 Level-2A (Orthorectified product providing Bottom-Of-Atmosphere reflectance, L2A) images for Almería and Antalya study sites were downloaded from the Copernicus Open Access Hub (https://scihub.copernicus.eu/dhus/#/home; accessed on 1 November 2022). The radiometric resolution of S2 is 12 bits [34], although S2 L2A reflectance products are provided as 16 bits integers. In the case of the Almería study area, a winter season S2A image taken on 26 December 2020 (just one day later than the corresponding image from WV3) and a summer season S2B image taken on 14 June 2020 (three days later) were acquired from the orbit number R051. This orbit, which leaves the sun behind the sensor, was recommended by Aguilar et al. [30] to avoid sun glint effects on the plastic sheets of greenhouse roofs. Regarding the Antalya study area, two S2 images taken as close as possible to their corresponding SPOT-7 orthoimages (i.e., on 1 February 2019 (S2B) and 6 July 2019 (S2A)) were acquired from the orbit number R064 to avoid sun glint effects.
The original L2A S2 images were co-registered with their corresponding High Resolution (HR) images (WV3 and SPOT-7) using the AROSICS library available through python programming language [35].
Finally, the co-registered S2 images downloaded as L2A format (0–10,000 integer values of reflectance units) were equivalent to the aforementioned 16Bit reflectance format of WV3 and SPOT-7. In order to obtain a format equivalent to Percent reflectance (i.e., 0–100 real values of reflectance units), it used a python script that simply divided pixel values by 100 to transform the digital values from 0–10,000 (16-bit signed integer format) to 0–100 (float32 single-precision floating-point format).
4. Methods
A two-step methodology was devised to quantitatively assess image segmentation quality over PCG land cover and investigate some factors (and interactions between them) that could explain its variability.
4.1. First Phase: Supervised Metrics Assessment
Regarding the first phase, eight supervised evaluation metrics (see Section 4.1.1) were tested to determine which performs better on estimating PCG segmentation quality on a wide range of segmentations (see Section 4.1.2).
4.1.1. Segmentation Quality Assessment Metrics
Supervised metrics for segmentation quality assessment rely on reference polygons (usually manually digitized) to estimate the goodness of image segmentation [22,29]. Metrics usually measure under-segmentation error, over-segmentation error, or the type of error where both are combined [22]. In fact, Jozdani and Chen [20] tested up to 21 over-segmentation, under-segmentation, and combined types of metrics. They reported that both over-segmentation and under-segmentation metrics showed distinct disadvantages. Therefore, only the combined metrics have been considered in this research.
According to the notation given by Clinton et al. [25] and Costa et al. [22], let be the reference data set composed of n reference polygons and be the segmentation dataset consisting of m segments. Moreover, the describes the geometric intersection of the reference object xi and the segment yj. In this way, the following notations are used to describe the different supervised metrics:
- -
- is the set of all yj objects that intersect reference object xi
- -
- -
- -
- -
- -
- -
The first supervised segmentation metric evaluated in this research is Area Fit Index (AFI), proposed by Lucieer and Stein [36]. AFI (Table 1, metric 1) is calculated as the mean of all AFIij values. If the overlap ratio between the reference dataset and the segments is 100%, then AFI equals zero, which means perfect fit. AFI > 0.0 would indicate over-segmentation, whereas AFI < 0.0 would mean under-segmentation.
Regarding the Quality Rate (QR) (Table 1, metric 2) [37], it ranges from 0 to 1. The ideal segmentation value would mean that QR = 0. Global metric QR would be the mean of all QRij.
Clinton et al. [25] described Index D (D-index) (Table 1, metric 3) as the “closeness” to an ideal segmentation result for a predefined reference polygons dataset. This index was originally proposed by Levine and Nazif [38] by combining over-segmentation (OS) and under-segmentation (US) measures. The D-index ranges from 0 to 1, with the ideal segmentation corresponding to a D-index = 0.
The fourth metric is Match (M) (Table 1, metric 4), introduced by Janssen and Molenaar [39]. M is the mean of all Mij values. It presents values ranging from 0 to 1. M = 1 means a perfect match between the reference dataset and segmentation objects, whereas M = 0 corresponds to the no matching scenario.
Fitness Function (FF) (Table 1, metric 5), devised by Costa et al. [22], quantifies both over-segmentation and under-segmentation. Global metric F is the mean of all summed Fij over all yj. This index results in zero for a perfect fit, whereas larger values mean an over-segmentation or under-segmentation scenario.
The F measure (Table 1, metric 6) was proposed by Zhang et al. [40]. It is based on the widely known precision and recall metrics. The precision metric is computed by comparing reference polygons to corresponding segments, whereas the recall measure is calculated by comparing segments to each reference object. This metric uses the weight argument (α) that takes values between 0.0 and 1.0, taking the value of 0.5 in this research. The F measure ranges from 0 to 1, considering the value of 1 as optimal. In order to describe the Modified Euclidean Distance 2 (MED2) (Table 1, metric 7), let us suppose that the intersection area between a reference polygon (xi) and a candidate segment (yj) is more than half the area of either the reference polygon or the candidate segment. In that case, a candidate segment can be defined as a corresponding segment [25,41]. Based on the corresponding segments, Liu et al. [41] proposed the Euclidean Distance 2 (ED2) to evaluate both geometric discrepancy (difference between the reference polygon and the corresponding segment polygon) and arithmetic discrepancy (the difference between the total number of reference polygons and the total number of corresponding segments). In this way, the ED2 metric evaluates the segmentation quality in a two-dimensional Euclidean space composed of two components: the Potential Segmentation Error (PSE) and the Number-of-Segments Ratio (NSR) [41]. However, it is important to note that when the number of reference polygons rises, there are often reference polygons without any corresponding segment. In those cases, the number of employed reference polygons will be less than the original. The original ED2 index does not consider this, so it calculates biased values of both PSE and NSR. To solve this problem, Novelli et al. [18] proposed the modified ED2 (MED2) based on a new formulation of PSE and NSR (now PSEnew and NRSnew). In fact, the new formulations of PSEnew and NRSnew consider the number of reference polygons to be m; v is the number of corresponding segments; n is the number of excluded reference polygons; is the maximum over-segmented area found for a single reference polygon; vmax is the maximum number of corresponding segments that can be found for one single reference polygon; and computes the total area of the m-n reference polygons. A MED2 value equal to zero means a perfect match between the reference dataset and the segmentation objects, whereas a higher MED2 value would point to important arithmetic and/or geometric discrepancies.
Finally, the Euclidean Distance 3 (ED3) (Table 1, metric 8) was proposed by Yang et al. [42] and is based on OS2 and US2 (Table 1). ED3 integrates both geometric and arithmetic discrepancies with values ranging from 0 to 1. The ideal value for the perfect match would be 0.
In this research, AFI, QR, D-index, M, FF, ED3, and F measure were calculated using the segmetric library (https://CRAN.R-project.org/package=segmetric; accessed on 1 November 2022), which is available through the R programming language. In addition, the MED2 metric was computed automatically through the free access command-line tool named AssesSeg tool (https://w3.ual.es/Proyectos/SentinelGH/index_archivos/links.htm; accessed on 1 November 2022), developed by Novelli et al. [18,43].

Table 1.
Combined metrics evaluated in the research.
Table 1.
Combined metrics evaluated in the research.
| Metric | Formula | Range | Optimal Value | Reference |
|---|---|---|---|---|
| , | [−∞, ∞] | 0 | [25,36] |
| , | [0, 1] | 0 | [25,37] |
| , where , , | [0, 1] | 0 | [25,38] |
| [0, 1] | 1 | [39] | |
| [0, ∞] | 0 | [22] | |
| , where , , , | [0, 1] | 1 | [40] |
| [0, ∞] | 0 | [18] | |
| , where , , | [0, 1] | 0 | [42] |
4.1.2. Image Segmentation—MRS
The multiresolution segmentation algorithm (MRS), available through eCognition v.10.1 software, was used in this research. MRS is based on the Fractal Net Evolution Approach [44]. This segmentation approach consists of a bottom-up region-merging technique starting with one-pixel objects. In numerous iterative steps, smaller image objects are merged into larger ones. MRS is an optimization procedure that, for a given number of image objects, minimizes the average heterogeneity and maximizes their respective homogeneity [44]. Three parameters determine the MRS outcome: scale, compactness, and shape. Scale parameter defines the maximum heterogeneity for the created segment, whereas compactness represents the weight of the smoothness criteria. Finally, shape parameter determines the weight of the color and shape criteria [21]. In addition to these parameters, the bands involved in the calculation of the segmentation and their weights must be set up.
Novelli et al. [18] reported that the blue-green-NIR combination for S2 and the blue-green-NIR2 combination for WorldView-2 images yielded the best segmentation results for PCG detection. Therefore, the segmentation stage was conducted in this study using the equally weighted blue-green-NIR2 bands of WV3 imagery and blue-green-NIR bands of S2 and SPOT-7 data.
Next, a significant number of segmentations over agricultural greenhouses areas were generated from different image sources, including a wide variety of cases (over-segmentation, under-segmentation, and cases which fit quite well with reality). Four factors (i.e., experimental levels of explanatory variables) were considered: two study sites (Almería and Antalya), two seasons (summer and winter), two reflectance digital storage scales (16Bit and Percent), and two different image spatial resolutions such as High Resolution (HR) (WV3 and SPOT-7) and Medium Resolution (MR) (S2) (Figure 2). Ten segmentations were extracted for each image source with a different MRS scale parameter (shape and compactness parameters were kept constant at 0.5 during this initial stage). In this way, 160 segmentation datasets were generated at this first phase (2 study sites × seasons × 2 image spatial resolutions × 2 reflectance storage scales × 10 segmentations with different MRS scale parameter = 160. See Figure 2).
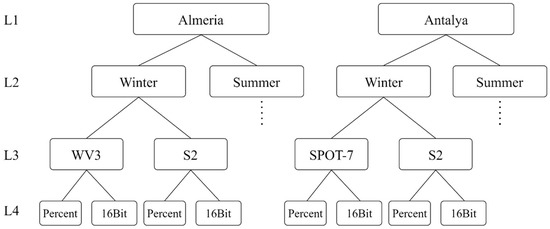
Figure 2.
Simplified draft showing the factorial design made up of four factors such as L1 (study site), L2 (season), L3 (image spatial resolution), and L4 (reflectance storage scale).
4.1.3. Reference Polygons
To calculate all the eight supervised metrics tested on the aforementioned 160 segmentations, a reference dataset (vector layer) composed of 200 polygons representing individual PCG was manually digitized for each study site. Aguilar et al. [29] already recommended this number of reference polygons for assessing segmentation accuracy on PCG. The WV3 MS orthoimage dated 25 December 2020 and the SPOT-7 pan-sharpened orthoimage taken on 5 February 2019 were used as reference images for on-screen digitizing in the Almería and Antalya study sites, respectively. Note that these images were used as reference because their low off-nadir angle. Figure 1d shows in green the 200 reference polygons digitized on Almería study site, whereas Figure 1e depicts in red the 200 reference polygons digitized on Antalya.
4.1.4. Visual Inspection and Metrics Assessment
Six experienced interpreters visually inspected the ten segmentation datasets generated for each of the sixteen image sources, scoring and ranking those datasets from best to worst. Note that the scale parameter corresponding to each segmentation file was hidden from the interpreters to assure a fair visual interpretation of the segmentation quality. The 10 segmentation files for each image source were named randomly, requesting the 6 interpreters to rank them from 1 (the best PCG segmentation) to 10 (the worst PCG segmentation) according to their visual quality. It is important to highlight that segmentation visual quality is understood in this experiment as the match between image segments and geo-objects (i.e., PCG in our case) visually appreciated by the interpreter. Summing up, each experienced interpreter evaluated the segmentation quality of each dataset by considering the segmentation file (vector layer), the reference polygons, and the background satellite image from which segmentation files were derived by applying the MRS algorithm. Jozdani and Chen [20] already used a similar methodology, also choosing the most optimal segmentation scale by visually inspecting their segmentation results, although they did not give details about the number of interpreters used.
To better understand the visual interpretation process, Table 2 shows, as an example (see Tables S1–S8 in Supplementary Materials for all other datasets), the results for the ten segmentations computed from the S2 Percent orthoimage taken on 25 December 2020 at the Almería study site.

Table 2.
Example of optimal segmentations determined through visual inspections for Almería study site, winter season, and S2 Percent orthoimage. Note that the corresponding scale parameter remained hidden from the interpreters during visual evaluation.
Next, the segmentation rankings provided by the panel of the six interpreters and the values computed on the reference polygons from applying the eight supervised evaluation metrics tested were compared to find out the best metrics for each of the sixteen image sources. Each one of the ten segmentation files was labeled with an individual score value computed as the median (robust estimator) of the scores granted by the six interpreters. In the same way, every segmentation file presented a value computed for each one of the eight tested segmentation quality metrics, thus determining the optimal values for each metric and image source.
For each image source, the three better (i.e., lower) median values granted by the visual interpreters were selected and grouped into three categories (gold, silver, and bronze medals). The results were evaluated based on the match between the three best median values determined for each image source and the optimal values provided by the calculated metrics. Consequently, the metric that matched the best median value (that is, the metric located in the same row as the smallest median value) was assigned three points, followed by two points assigned to the metric that coincided with the second-best value of the median. Finally, one point was awarded to the metric that coincided with the third-best value of the median. Note that it is possible to have more than one metric associated with each of the three categories. In fact, this would be the case of a tie between metrics associated with the minimum values of medians (see the example shown in Table 3). In this case, all matching metrics would be assigned the same score. Additionally, no points would be assigned if any of the three best median values did not match the optimal values for the calculated metrics.

Table 3.
Computed segmentation accuracy metrics and median values of visual rankings for the S2 Percent image taken at the Almería study site on 25 December 2020. Optimal values for each metric are indicated within parenthesis, whereas optimal values among the ten segmentations for each metric are shown in bold. The best three categories for the median scores are highlighted.
An example of the computed segmentation metrics and the median values for each segmentation file calculated from the visual evaluation rankings can be seen in Table 3 for Almería winter S2 Percent orthoimage (see Tables S9–S16 in Supplementary Materials for all other datasets). The metrics with the best visual score (smallest median) were associated to the gold category, thus receiving three points (MED2 in Table 3). The metrics corresponding to the silver category received two points (AFI, D-index, ED3, and QR in Table 3). Finally, the metrics associated to the bronze category got only one point (F measure in Table 3). The scores for each metric were summed for all image sources in order to determine which metrics performed better overall.
4.1.5. Statistical Analysis
In the first phase of the study, a factorial ANOVA was performed to quantify the contribution of the studied factors (i.e., study site, season, image spatial resolution, and reflectance storage scale) and their two-way interactions in explaining the variation of the median values for the visual ranking as the dependent variable. Only the best 16 segmentations having the best median value (i.e., one for each image source investigated) were selected and analyzed through ANOVA. For statistical significance, values of p < 0.05 were considered. The Kolmogorov-Smirnov test was used as an indicator of goodness of fit to a standard normal distribution.
4.2. Second Phase: Experimental Design
The second phase was headed up to analyze the influence of several factors on PCG segmentation quality using the MRS algorithm. For this, a full factorial ANOVA design was implemented. Segmentation quality was quantitatively estimated using the best metric determined during the first phase. In this sense, this metric played the role of the dependent variable in the statistical analysis.
In this second phase, thousands of segmentations were computed using the MRS algorithm implemented in eCognition software, varying scale parameter (step of one) and shape parameter (ranging from 0.1 to 0.9 with a step of 0.1). The compactness parameter was set again to 0.5, taking into account that this parameter usually has little influence on the segmentation results [45,46].
The independent factors considered in the ANOVA were study site (Almería and Antalya), season (winter and summer), spatial resolution (MR and HR), reflectance storage scale (Percent and 16Bit reflectance), and shape parameter (0.1 to 0.9). The shape parameter was grouped into three categories: low (0.1, 0.2, 0.3), medium (0.4, 0.5, 0.6), and high (0.7, 0.8, 0.9) shape values. Additionally, the partial eta squared (partial η2) was calculated to measure the effect sizes in factorial designs [47].
Lastly, 144 combinations corresponding to the factors (2 × 2 × 2 × 2 × 9 = 144) were analyzed through ANOVA to determine the possible factors and interactions between them that could significantly influence segmentation accuracy.
5. Results
5.1. First phase: Supervised Metrics Assessment
Figure 3 depicts some sample segmentations located in the study sites of Almería and Antalya corresponding to the MRS scale parameters that produced over-segmentation (first column), near-optimal segmentation (second column), and under-segmentation (third column). Note that the actual boundaries of the greenhouses can also be seen in Figure 3 through the background orthoimages. The MRS segmentation outputs of the images that store reflectance values as integers ranging from 1 to 10,000 (16Bit digital scale) produced noisier and shakier greenhouse segments edges than those storing reflectance values in a float32 single-precision floating-point format ranging from 0 to 100 (Percent digital scale), mainly when using high spatial resolution images (Figure 3).
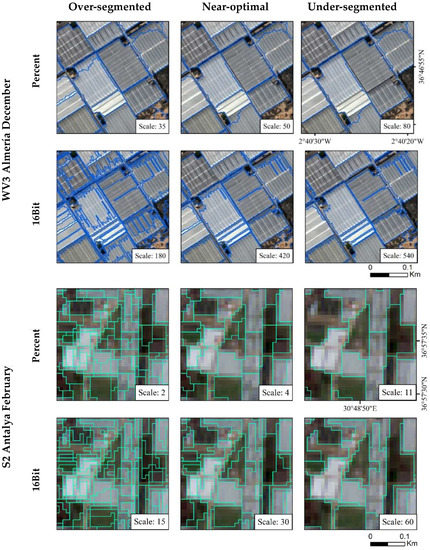
Figure 3.
Some sample areas of the Almería and Antalya study sites corresponding to over-segmentation (left), near-optimal segmentation (center), and under-segmentation (right).
Table 4 shows the overall scores granted by the interpreters for all segmentations carried out in Almería and Antalya. In Almería, MED2 was the highest scored metric (19 points), followed by ED3 (15 points) and M (12 points). Again, in Antalya, MED2 achieved the best score (23 points), followed by D-index and QR (13 points), and finally ED3 (10 points). According to the overall scoring results, it was clear that the metric with the highest score was MED2, with 42 points. In the second place, ED3 reached 25 points. Finally, the third position was shared by QR and D-index metrics, both with 22 points. Based on these results, it can be clearly stated that the MED2 metric turned out to be the most successful among the tested metrics to quantitatively assess the quality of PCG land cover segmentation. Without any doubt, this was the most important finding attained in this first phase.

Table 4.
Overall scores (points granted by experienced interpreters) of each one of the tested metrics given by the sum of the scores of all segmentation data sets in Almería and Antalya.
A similar test was carried out to evaluate the capacity of the tested metrics for detecting the worst segmentations. In this case, the gold, silver, and bronze medals were given to the worst datasets following the interpreters’ scores (see Tables S17 and S18 in Supplementary Materials). Overall, the metrics that stood out as the ones that best pointed out the worst segmentation datasets were: MED2 was first (45 points); ED3, D-index, and QR reached the second position (42 points); finally, FF (39) occupied the third position.
Regarding the ANOVA of the visual ranking scores, computed as the lowest median values, it is important to underline that the population of this dependent variable fit a normal distribution according to Kolmogorov-Smirnov test. The ANOVA results (Table 5) revealed that the factor reflectance storage scale (RSS) (16Bit and Percent) was highly significant (p-value = 0.00). In this sense, the mean value of the dependent variable (median of scores) for 16Bit format took a value of 2.250, significantly higher (i.e., worse) than the value of 1.563 provided by Percent format. This significant difference between interpreters’ ability to appreciate the quality of segmentation indicates that they felt more comfortable when evaluating images in Percent than in 16Bit format, probably because MRS segmentation in Percent format seemed less artificial and smoother than 16Bit. As can be seen in Figure 3, noisy and jittery segment edges are more common in 16Bit segmentation outputs than in Percent outputs. Thus, it can be concluded that this effect, associated with the RSS format, significantly affected the interpreter’s visual perception.

Table 5.
Summary of the ANOVA results (N = 16) for the visual ranking scores (median value). The factors and interactions written in bold were statistically significant (p < 0.05).
It was also noticed that the spatial resolution (SR) (p-value = 0.06) and season (p-value = 0.06) were not statistically significant (p < 0.05), although they were close to it. It meant that spatial resolution did not significantly affect the interpreter’s visual perception concerning segmentation quality. However, the interaction between SR and RSS result was statistically significant (p-value = 0.01), meaning that this interaction turned out to be an essential factor in determining the best scale parameter for the visual evaluation of segmentation quality. In this sense, the mean value of the dependent variable for the Percent format and HR images was 1.125, whereas the value was significantly worse (2.375) in the case of 16Bit format and HR images. Based on this result, it can be concluded that there was more agreement in the interpreters regarding the best segmentation when they evaluated segmentations on HR images and Percent format rather than HR images and 16Bit. The study site factor and other two-way interactions between factors did not show significant results at a significance level of p < 0.05.
5.2. Second Phase: Evaluating Factors Affecting Segmentation Accuracy
Up to 4000 segmentation datasets were generated through the MRS algorithm in this second phase, using the 16 image sources, varying both scale and shape parameters, and always keeping compactness fixed at 0.5. The accuracy of the segmentation outputs focused on PCG was tested by calculating their MED2 metric since, according to the first phase, this metric was clearly the best at pointing out both the best and the worst segmentations. A total of 144 samples corresponding to the optimal MED2 values determined for each shape parameter were considered to examine the variation in segmentation accuracy as a function of the different factors investigated. In order to facilitate the reader’s understanding of the obtained results, Figures S1–S4 in Supplementary Materials depict the best achieved segmentation based on MED2 for each of the 16 cases studied. In these additional figures, the reader can see the image sources used in Almería and Antalya (summer and winter), showing the 200 reference polygons (green in Almería and red in Antalya). The scale and shape parameters, as well as the corresponding MED2 value, are shown for each case.
Figure 4 presents the aforementioned 144 MED2 values against the corresponding scale parameters, also grouping the different studied factors. According to Figure 4, and focusing on the results obtained from 16Bit orthoimages, it was observed that, for each spatial resolution, the lower the scale parameter, the lower the value of MED2 (i.e., segmentation accuracy increased). It was also found that as the shape parameter increased, and, regardless of image spatial resolution, the optimal scale parameter and the MED2 value decreased, thus attaining better segmentations.
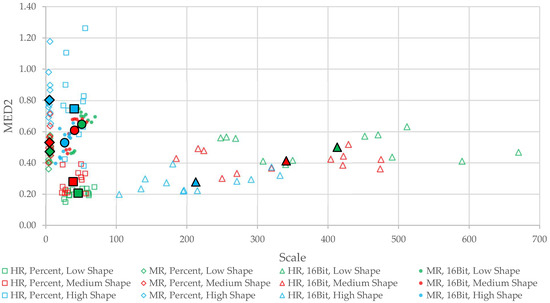
Figure 4.
Scale parameter vs. MED2 graph showing the results for each spatial resolution (HR and MR), reflectance storage scale (16Bit and Percent), and shape parameter category (Low Shape, Medium Shape, and High Shape). Note: average values of each reflectance storage scale and shape category are depicted in a solid and larger symbol.
With respect to Percent orthoimages, it was observed that segmentation accuracy decreased as the shape parameter increased. Furthermore, the optimal scale parameter was close to each other for each shape parameter category, thus forming dense and clustered groups (Figure 4). In fact, the distribution of optimal scale parameters for 16Bit format images presented a greater dispersion of values (from 14 to 670) than those calculated on Percent format images (from 4 to 70).
To analyze the effect of the factors studied on segmentation accuracy, quantitatively expressed in terms of the values of MED2 metric, a statistical analysis was carried out over a set of 144 samples. Previously, we tested that the MED2 values fit a normal distribution. The ANOVA model presented an adjusted coefficient of determination (R2 adjusted) of 0.768, meaning that the explanatory variables or factors were able to explain up to 76.8% of the variance of the optimal MED2 metric (i.e., segmentation accuracy).
Table 6 summarizes the significant outcomes of ANOVA for MED2 metric. In fact, it quantifies the relationships between MRS segmentation accuracy (optimal MED2 values) and the studied factors, also including their interactions. Table 6 also shows the partial eta squared statistic and its associated effect size for each factor. Note that both the factors and their interactions are ordered from highest to lowest based on their partial η2 value.

Table 6.
Summary of the ANOVA results (N = 144) indicating those significant factors and interactions (p < 0.05) together with their associated partial η2. Notes: reflectance storage scale (RSS); shape parameter category (Shp); spatial resolution (SR); study site (SS).
The overall statistical results reported that the ANOVA model was statistically very significant (F = 11.096, p = 0.000), which means that the variation of the optimal values of MED2 (segmentation quality) can be reasonably explained by the factors and interactions tested in this study. In fact, most of the factors and interactions (double and triple interactions) were found to significantly explain the variance of optimal MED2 values (p < 0.05) (Table 6). On the contrary, the ANOVA results yielded no statistically significant four-way and five-way interactions among factors.
The factors and interactions that had the largest effect size on segmentation quality based on partial η2 values were the interaction between the factors RSS and shape parameter category (Shp) (partial η2 = 0.714), the SR factor (partial η2 = 0.584), and the Shp factor (partial η2 = 0.362). Note that the partial η2 values represent the explained variance of the dependent variable after partially removing the effects of other factors or interactions. In this sense, it can be stated that the effect of the interaction RSS × Shp on segmentation quality was approximately twice as strong as the Shp factor, whereas the effect of the factor SR on segmentation quality was 1.61 times stronger than that of Shp (Table 6).
To illustrate the reasons behind the strong effect on segmentation accuracy attributed to the interaction RSS × Shp, the estimated marginal means of optimal MED2 as a function of RSS and the shape parameter values were calculated (Figure 5). What is striking in Figure 5 is the general pattern of both RSS types (Percent and 16Bit formats) against the shape parameter. Indeed, the plot of the aforementioned marginal means brought out a completely opposite effect on MRS segmentation quality depending on RSS type. Whereas segmentation accuracy was improved with the increasing shape parameter for 16Bit RSS, segmentation accuracy consistently decreased with the decreasing shape parameter for the Percent RSS.
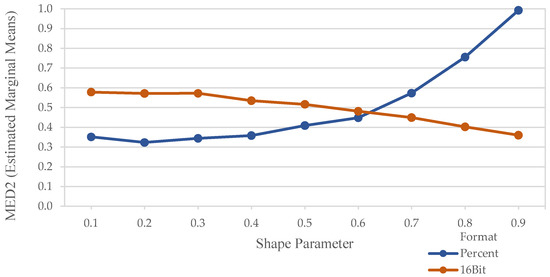
Figure 5.
Estimated marginal means of optimal MED2 as a function of reflectance storage scale (Percent or 16Bit formats) and shape parameter.
Figure 5 shows a completely different pattern for 16Bit and Percent orthoimages with respect to the shape parameter. The highest values for MED2 come from segmentations calculated on Percent orthoimages using the highest shape parameters. This finding demonstrates the crucial role of choosing an appropriate MRS shape parameter for achieving the best segmentation accuracy depending on the RSS format of the input images.
Overall, Antalya, with a mean MED2 value of 0.478, achieved slightly better segmentations than Almería, with a mean MED2 value of 0.525. In addition, HR images presented a mean MED2 value of 0.404, whereas MR images took a value of 0.599, evidencing that HR images achieved higher segmentation accuracy.
In order to evaluate the influence of RSS on MED2 more in depth, the worst Shp categories for each RSS type (i.e., High Shape for Percent and Low Shape for 16Bit) were removed from the ANOVA. In this case, the mean MED2 value for Percent orthoimages (0.373) was much better than for 16Bit orthoimages (0.458) and was statistically significant, demonstrating the superiority of the Percent RSS format for conducting PCG segmentation using MRS.
In detail, the Percent orthoimages belonging to the Almería study site had a mean MED2 value of 0.390, whereas a value of 0.478 was attained from the 16Bit orthoimages. Likewise, the mean MED2 value for Percent orthoimages (0.355) was lower than for 16Bit orthoimages (0.437) in the Antalya study site. When the results were based on only high spatial resolution images, it was observed that the Percent orthoimages had a mean MED2 value of 0.243, whereas the 16Bit orthoimages took a value of 0.346. Similarly, the Percent orthoimages with the medium spatial resolution achieved lower mean MED2 values. In summary, it can be concluded that Percent orthoimages achieved better PCG segmentation accuracy than 16Bit orthoimages, which suggests that this would be the recommended RSS to obtain the best MRS segmentation results in PCG areas.
6. Discussion
6.1. Evaluation of Supervised Segmentation Metrics
The selection of the best combination of MRS parameters to produce optimal segmentations over PCG areas is very challenging due to many factors mainly related to the spectral reflectance of PCG. This is the reason why it is essential to count on metrics capable of quantitatively evaluating image segmentation quality. This point is addressed in the first phase of this research. According to the results provided by the first phase, the MED2 metric could be stated as the best to assess PCG segmentation quality, whereas the other metrics tested in this study showed some deficiencies. Witharana and Civco [48] reported that the original ED2 metric proposed by Liu et al. [41] is not always able to produce optimal segmentation results properly. They tested images from QuickBird MS (2.44 m GSD), WorldView-2 MS (2 m GSD), GeoEye-1 pan-sharpened (0.5 m GSD), and EO-1 ALI MS (30 m GSD) on different land covers (shelters, water, pasture, houses, and sport fields), pointing out that the main weakness of ED2 occurred when using high values of scale parameter. In fact, the lack of applying normalization in the formulation of PSE and NSR can erroneously increase the sensitivity of ED2 to over-segmentation at smaller scales [42].
On the other hand, Jozdani and Chen [20] tested several supervised metrics for assessing segmentation quality over buildings land cover using 100 manually digitized buildings as reference polygons, finding that the hypothetically optimal scale parameter proposed by the MED2 metric led to an over-segmentation scenario. Considering the results provided by these authors, it is mandatory to highlight that the results obtained in this work about MED2 are applicable only to PCG land cover.
The worst segmentation accuracy given by F measure metric coincided for almost all the datasets with the highest scale parameter tested (i.e., maximum under-segmentation). In the case of FF metric, the lowest scale parameter tested (i.e., maximum over-segmentation) consistently performed the worst segmentation results. On the contrary, FF always reached the best segmentation results for those datasets in which the highest scale parameter was used (i.e., maximum under-segmentation). Although the worst scale parameter could be determined in some cases by matching the median values obtained from the visual evaluations with this metric, it was unsuccessful in determining the best scale parameter. Jozdani and Chen [20] also found that FF proposed optimal scale parameters, leading to under-segmentation results. In addition, they claimed that both the MED2 and F metrics produced over-segmented results in the case of buildings segmentation. However, our results show that the MED2 metric proposed optimal scale parameters that generated the best segmentations (visual evaluation) over PCG land cover for all case studies (see Tables S9–S16 in Supplementary Materials). It is important to underline here that our experimental design covered different patterns and types of PCG with different crops, along with consideration of different image spatial resolutions. Furthermore, the F measure did not always achieve the optimal segmentation with the over-segmented scale parameter, although the optimal scale parameter obtained with this metric always resulted in over-segmentation compared to MED2.
With respect to the metrics D-index and ED3, which were ranked as the best metrics after MED2, their biggest drawback is that their range of variation for the scale parameters investigated is too small. Therefore, deciding on the optimal scaling parameter could be challenging when applying these metrics.
It is worth noting that new research lines are being proposed in the field of segmentation in different fields. In recent works, image super-resolution technology has been applied to image segmentation, for example in medical researches [49]. Deep learning was used to create a dense nested attention network (DNANet) by Li et al. [50] that was specially designed to detect small infrared targets and retained the characteristics of small targets in the deep network. Finally, Liu et al. [51] proposed an interesting algorithm for detecting small targets from the subtle level, focusing on strengthening the edge of small targets, improving the separation between small targets and the background, and expanding the number of target pixels.
6.2. Factors Affecting the PCG Segmentation
6.2.1. Reflectance Storage Scale
The RSS factor stood out as an important factor affecting segmentation quality in both stages of this study. Regarding the first phase, the ANOVA results regarding visual evaluation revealed that the six experienced interpreters agreed more when assessing the Percent orthoimages than the 16Bit ones, which is probably related to the visual differences between the segmented objects for both reflectance storage formats. According to Aguilar et al. [29], the ventilation roof windows of PCG were ignored with WV3 MS ATCOR Percent orthoimages, whereas segmentation outputs from original 11 bits orthoimages (from 0 to 2048 digital values) commonly presented strip-shaped segments. This statement was also confirmed in our study. Even in the under-segmented scenario, in which the scale parameter took a value of 540 for WV3 16Bit orthoimage, these strips can be made out in the segmentation output (Figure 3). Although these strips are unlikely to appear in S2 orthoimages due to their lower spatial resolution, over-segmentation can be appreciated for the ideal S2 16Bit orthoimage using a scale parameter of 30 in Figure 3.
In fact, it was observed that image segmentation quality was also improved with Percent orthoimages compared to 16Bit ones for the MED2 metric. The computed estimated marginal means of MED2 values according to spatial resolution and study area showed that the Percent orthoimages achieved better segmentation accuracy than the 16Bit ones. Aguilar et al. [29] already achieved better MED2 values (i.e., lower values) working on PCG using WV3 MS ATCOR Percent orthoimages than with the original 11 bits orthoimages.
However, what is behind the better MRS segmentation results provided by images that store reflectance values in percentage format, compared to 16Bit ones? First, it should be remembered that the main goal of any image segmentation algorithm is to minimize the heterogeneity embodied in each individual fusion of two smaller objects. That is, an image object will merge with another adjacent image object as long as a minimal increase in heterogeneity occurs [44]. In order to quantify this heterogeneity, the MRS algorithm uses the heterogeneity function, f, given by the formulation shown in Equation (1).
where wcolor and wshape represent the weights of the spectral heterogeneity increment (∆hcolor) and spatial heterogeneity increment (∆hshape). Note that both weights have to add up to one (i.e., wcolor + wshape = 1). Furthermore, wcolor ϵ [0,1] and wshape ϵ [0,1]. These weight parameters allow the definition of heterogeneity to be adapted to each specific application.
In this sense, the decision rule followed by the MRS algorithm works like this. Let object 1 and object 2 be two neighboring objects in an image. These objects will be merged in a larger object if the heterogeneity (f), given by Equation (1), turns out to be less than a certain threshold related to the so-called scale parameter. This scale parameter is the stopping criterion for the optimization process. Before merging two adjacent objects, the resulting increase in heterogeneity f is calculated. If this resulting increase exceeds a threshold determined by the scale parameter, then no further merging occurs, and segmentation stops [52].
The increment in spectral heterogeneity when merging two neighboring objects (∆hcolor) is given by Equation (2).
where nmerge, nobj1, and nobj2 are the number of pixels in the merged object, object 1 and object 2, respectively. The terms σcmerge, σcobj1, and σcobj2 represent the standard deviations corresponding to the merged object, object 1 and object 2, respectively, whereas c refers to the spectral band of weight wc. Note that each band or spectral channel may have different weights.
On the other hand, spatial heterogeneity (∆hshape) is given by the following Equations (3)–(6).
where l is the perimeter of the object, b is the perimeter of the object’s bounding box, and ∆hcomp and ∆hsmooth are the compactness and smoothness metrics, which depend on the shape of the object. It is important to underline that an increase in the edge tortuosity of the merged object above the selected threshold (scale parameter) will cause the MRS algorithm to stop the merge procedure if the weight of spatial heterogeneity is significant (see Equation (1)).
Based on the above formulations, it seems clear that downscaling the reflectance storage from the 16Bit format (1–10,000) to Percent format (1–100) translates into a noticeable decrease in the standard deviation of the objects to merge (σcobj1, σcobj2). Therefore, the spectral heterogeneity (∆hcolor) also decreases, leading to the decrease in the value of the heterogeneity function (Equation (1)) when the shape weight is kept small. In this way, the higher values in which the reflectance is stored in the case of the 16Bit format would work as a true “resonance box” due to the multiplicative numerical effect of calculating the standard deviations of the neighboring objects and the merged object on the basis of a greater range of variation. Considering that the MRS algorithm stops merging objects when the function f for the two neighboring objects exceeds a threshold determined by the scale parameter, this would explain the lower scale parameters found for Percent format images compared to 16Bit ones.
The aforementioned “resonance box” effect, associated with increasing values of standard deviations (spectral heterogeneity) within objects in 16Bit format images, would also increase segmentation instability. It leads to elongated and strip shapes provoked by the remarkable spectral heterogeneity of some greenhouses roof features, such as the roof windows, seams between plastic sheets or different crops growing under the roof, and shifting reflections along greenhouse support structures. This effect associated to RSS scale was also observed by Aguilar et al. [29]; when working on WV3 MS ATCOR Percent format product, they reporting that increasing heterogeneity, measured through standard deviation of neighboring objects, can be expected when dealing with images presenting higher relative differences in pixel content values (i.e., greater range of reflectance storage values). These authors stated that WV3 MS ATCOR Percent format achieved a more realistic segmentation of the individual greenhouses, avoiding the over-segmentation due to the existence of roof windows on the plastic sheets.
6.2.2. Shape Parameter
The results provided by Figure 5 have shown that selecting a right value for the shape parameter of the MRS algorithm plays a crucial role in the quality of the segmentations produced, allowing to obtain a good segmentation accuracy for images with different reflectance storage scales. Aguilar et al. [29], also using MED2 and 200 reference polygons, reported 0.3 as the optimal shape parameter when working on a WV3 MS ATCOR Percent orthoimage, whereas the shape parameter took a value of 0.5 (the maximum value that they tested) when working on the original 11 bits WV3 MS orthoimage. In that same work, the optimal scale values were 68 and 220 for the WV3 MS ATCOR Percent and the original WV3 MS 11 bits orthoimages, respectively. Some authors such as Yao and Wang [11,53] investigated the effects of image heterogeneity on PCG segmentation using fixed shape and compactness parameters. In this sense, and at least when working on PCG segmentation using MRS, the shape parameter should not be kept fixed but allowed to vary in order to achieve the best possible segmentation together with the scale parameter.
6.2.3. Image Spatial Resolution
The results of ANOVA for the second phase pointed out that image spatial resolution significantly affects PCG segmentation. In detail, a higher segmentation accuracy was obtained from the HR images than from the MR ones. Mesner and Oštir [54] also reported that down-sampling the original image spatial resolution from 0.5 to 2.5, 5, 10, 20, and 50 m GSD greatly reduced segmentation quality. This effect can also be appreciated if we look at the lowest observed MED2 value of 0.150 depicted in Figure 4, which is associated to WV3 MS orthoimages with 1.2 m GSD (HR images) and Percent RSS. This MED2 value turns out to be slightly higher than the value of 0.112 reached by Aguilar et al. [29] when also working on PCG and using 1.2 m GSD WV3 MS orthoimages but only employing 100 reference polygons as reference. The slightly worse MED2 metric of 0.198 was reported by Novelli et al. [18] when working on 2 m GSD WorldView-2 MS orthoimage, likely because they used lower spatial resolution images. In the last work, MED2 values of 0.319 and 0.424 were achieved working on S2 (10 m GSD) and Landsat 8 (30 m GSD) orthoimages, respectively.
6.2.4. Study Area
The estimated marginal means of the optimal MED2 revealed that the segmentation accuracy achieved in the Antalya study site was better than that obtained in Almería. This fact is explained because the dissemination of greenhouses is greater in Antalya, whereas they appear more concentrated and closer to each other in the case of Almería. This high concentration of PCG in Almería causes the segmentation to mistakenly merge two or more greenhouses into the same object because there are almost no boundaries (background) between them. In that sense, Aguilar et al. [16] reported MED2 values of 0.213 and 0.299 for Antalya and Almería study sites, respectively, when working with 1 m GSD Deimos-2 pan-sharpened orthoimages.
7. Conclusions
This study analyzed several supervised metrics to assess PCG image segmentation quality and some potentially influential factors such as study site, image capture date (season), image spatial resolution, and reflectance storage scale. The following conclusions can be drawn from this work:
Among the eight supervised metrics examined, the MED2 was found to be the most successful metric for evaluating PCG segmentation quality. AssesSeg, a free command-line tool for computing MED2, provides the evaluation of multiple segmentation files easily and independently from any software. In addition, it can be concluded that FF and F metrics performed poorly in determining the optimal scale parameter and thus in assessing the quality of PCG segmentation.
The ANOVA devised to quantify the influence of some factors on the visual interpretation of MRS segmentation quality revealed that reflectance storage scale significantly impacted interpreter’s visual perception for estimating the best optimal scale parameter, i.e., segmentation quality. Moreover, the statistical analysis reported that the segmentations generated from satellite orthoimages with Percent reflectance scale values (single-precision floating-point values ranging from 0 to 100) turned out to be more comfortable for the interpreter in order to assess segmentation quality.
Optimal MRS scale parameters were clustered (small ranges of variation) in orthoimages with Percent reflectance storage scale, whereas scale parameters were more unstable (large ranges of variation) for 16Bit orthoimages. This indicates that Percent format can make it easier to determine the optimal scale parameter for PCG segmentation.
Reflectance storage scale and shape parameter had a crucial impact on the quality of PCG segmentation. Moreover, the general pattern of segmentation accuracy for Percent and 16Bit reflectance storage scales were quite different regarding the shape parameter selected. In fact, segmentation accuracy increased as shape parameter decreased for the Percent format. On the other hand, segmentation accuracy decreased as shape parameter decreased for the 16Bit format. Thus, reflectance storage scale of the input images should be taken into account whentra selecting the optimal MRS parameters.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15020494/s1, Figures S1–S4: High and Medium resolution image sources used in Almería and Antalya showing the 200 reference polygons and the best segmentation based on MED2 for each case; Tables S1–S8: Optimal segmentations determined through visual inspections; Tables S9–S16: Computed segmentation accuracy metrics and median values of visual rankings; Tables S17 and S18: Total points (best and worst cases) for each supervised metrics in Antalya and Antalya study sites.
Author Contributions
G.S., M.A.A. and F.J.A. proposed the methodology, designed and conducted the experiments and contributed extensively to manuscript writing and revision. G.S. collected the input data and performed the experiments; A.N. and C.G. made significant contributions to the research design and manuscript preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been carried out during Gizem Senel’s fellowship as a visiting researcher at the University of Almería. This scholarship was supported by TUBITAK (Turkish Scientific and Technological Research Council) [grant number: 2214a-1059B142100454]. Gizem Senel also acknowledges the Council of Higher Education (CoHE) 100/2000 and TUBITAK 2211-A scholarships. This research was funded by Spanish Ministry for Science, Innovation and Universities (Spain) and the European Union (European Regional Development Fund, ERDF) funds, grant number RTI2018-095403-B-I00.
Data Availability Statement
The AssesSeg Tool is publicly available at: https://w3.ual.es/Proyectos/SentinelGH/index_archivos/links.htm (accessed on 1 November 2022). The data that support the findings of this study are available on request from the corresponding author (Manuel A. Aguilar: email: maguilar@ual.es).
Acknowledgments
We also thank Rafael Jiménez-Lao for his collaboration in the visual interpretation phase. Finally, this study takes part in the general research lines promoted by the Agrifood Campus of International Excellence ceiA3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, D.; Chen, J.; Zhou, Y.; Chen, X.; Chen, X.; Cao, X. Mapping plastic greenhouse with medium spatial resolution satellite data: Development of a new spectral index. ISPRS J. Photogramm. Remote Sens. 2017, 128, 47–60. [Google Scholar] [CrossRef]
- Zhang, P.; Du, P.; Guo, S.; Zhang, W.; Tang, P.; Chen, J.; Zheng, H. A novel index for robust and large-scale mapping of plastic greenhouse from Sentinel-2 images. Remote Sens. Environ. 2022, 276, 113042. [Google Scholar] [CrossRef]
- Lu, L.; Di, L.; Ye, Y. A Decision-Tree Classifier for Extracting Transparent Plastic-Mulched Landcover from Landsat-5 TM Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4548–4558. [Google Scholar] [CrossRef]
- Picuno, P.; Tortora, A.; Capobianco, R.L. Analysis of plasticulture landscapes in Southern Italy through remote sensing and solid modelling techniques. Landsc. Urban Plan. 2011, 100, 45–56. [Google Scholar] [CrossRef]
- Agüera, F.; Aguilar, M.A.; Aguilar, F.J. Detecting greenhouse changes from QuickBird imagery on the Mediterranean coast. Int. J. Remote Sens. 2006, 27, 4751–4767. [Google Scholar] [CrossRef]
- Jiménez-Lao, R.; Aguilar, F.; Nemmaoui, A.; Aguilar, M. Remote Sensing of Agricultural Greenhouses and Plastic-Mulched Farmland: An Analysis of Worldwide Research. Remote Sens. 2020, 12, 2649. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Vallario, A.; Aguilar, F.J.; García Lorca, A.; Parente, C. Object-Based Greenhouse Horticultural Crop Identification from Multi-Temporal Satellite Imagery: A Case Study in Almeria, Spain. Remote Sens. 2015, 7, 7378–7401. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Bianconi, F.; Aguilar, F.J.; Fernández, I. Object-based greenhouse classification from GeoEye-1 and WorldView-2 stereo imagery. Remote Sens. 2014, 6, 3554–3582. [Google Scholar] [CrossRef]
- Tarantino, E.; Figorito, B. Mapping Rural Areas with Widespread Plastic Covered Vineyards Using True Color Aerial Data. Remote Sens. 2012, 4, 1913–1928. [Google Scholar] [CrossRef]
- Hossain, M.D.; Chen, D. Segmentation for Object-Based Image Analysis (OBIA): A review of algorithms and challenges from remote sensing perspective. ISPRS J. Photogramm. Remote Sens. 2019, 150, 115–134. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, S. Evaluating the Effects of Image Texture Analysis on Plastic Greenhouse Segments via Recognition of the OSI-USI-ETA-CEI Pattern. Remote Sens. 2019, 11, 231. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Kotaridis, I.; Lazaridou, M. Remote sensing image segmentation advances: A meta-analysis. ISPRS J. Photogramm. Remote Sens. 2021, 173, 309–322. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Aguilar, F.J.; García-Lorca, A.; Guirado, E.; Betlej, M.; Cichon, P.; Nemmaoui, A.; Vallario, A.; Parente, C. Assessment of Multiresolution Segmentation for Extracting Greenhouses from Worldview-2 Imagery. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B7, 145–152. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Jiménez-Lao, R.; Ladisa, C.; Aguilar, F.J.; Tarantino, E. Comparison of spectral indices extracted from Sentinel-2 images to map plastic covered greenhouses through an object-based approach. GISci. Remote Sens. 2022, 59, 822–842. [Google Scholar] [CrossRef]
- Bektas Balcik, F.; Senel, G.; Goksel, C. Object-Based Classification of Greenhouses Using Sentinel-2 MSI and SPOT-7 Images: A Case Study from Anamur (Mersin), Turkey. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 2769–2777. [Google Scholar] [CrossRef]
- Novelli, A.; Aguilar, M.A.; Nemmaoui, A.; Aguilar, F.J.; Tarantino, E. Performance evaluation of object based greenhouse detection from Sentinel-2 MSI and Landsat 8 OLI data: A case study from Almería (Spain). Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 403–411. [Google Scholar] [CrossRef]
- Hay, G.J.; Blaschke, T.; Marceau, D.J.; Bouchard, A. A comparison of three image-object methods for the multiscale analysis of landscape structure. ISPRS J. Photogramm. Remote Sens. 2003, 57, 327–345. [Google Scholar] [CrossRef]
- Jozdani, S.; Chen, D. On the versatility of popular and recently proposed supervised evaluation metrics for segmentation quality of remotely sensed images: An experimental case study of building extraction. ISPRS J. Photogramm. Remote Sens. 2020, 160, 275–290. [Google Scholar] [CrossRef]
- Tian, J.; Chen, D.M. Optimization in multi-scale segmentation of high-resolution satellite images for artificial feature recognition. Int. J. Remote Sens. 2007, 28, 4625–4644. [Google Scholar] [CrossRef]
- Costa, H.; Foody, G.M.; Boyd, D.S. Supervised methods of image segmentation accuracy assessment in land cover mapping. Remote Sens. Environ. 2018, 205, 338–351. [Google Scholar] [CrossRef]
- Zhang, Y.J. A survey on evaluation methods for image segmentation. Pattern Recognit. 1996, 29, 1335–1346. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. Image segmentation evaluation: A survey of unsupervised methods. Comput. Vis. Image Underst. 2008, 110, 260–280. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Chen, G.; Weng, Q.; Hay, G.J.; He, Y. Geographic object-based image analysis (GEOBIA): Emerging trends and future opportunities. GISci. Remote Sens. 2022, 55, 159–182. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 67–75. [Google Scholar] [CrossRef]
- Tong, H.; Maxwell, T.; Zhang, Y.; Dey, V. A Supervised and Fuzzy-based Approach to Determine Optimal Multi-resolution Image Segmentation Parameters. Photogramm. Eng. Remote Sens. 2012, 78, 1029–1044. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Novelli, A.; Nemamoui, A.; Aguilar, F.J.; García-Lorca, A.; González-Yebra, O. Optimizing Multiresolution Segmentation for Extracting Plastic Greenhouses from Worldview-3 Imagery. In Proceedings of the International Conference on Intelligent Interactive Multimedia Systems and Services, Vilamoura, Portugal, 21–23 June 2017; Springer: Berlin/Heidelberg, Germany, 2018; pp. 31–40. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Jiménez-Lao, R.; Nemmaoui, A.; Aguilar, F.J.; Koc-San, D.; Tarantino, E.; Chourak, M. Evaluation of the Consistency of Simultaneously Acquired Sentinel-2 and Landsat 8 Imagery on Plastic Covered Greenhouses. Remote Sens. 2020, 12, 2015. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Jiménez-Lao, R.; Aguilar, F.J. Evaluation of Object-Based Greenhouse Mapping Using WorldView-3 VNIR and SWIR Data: A Case Study from Almería (Spain). Remote Sens. 2021, 13, 2133. [Google Scholar] [CrossRef]
- DigitalGlobe. Worldview-3 Data Sheet. 2014. Available online: http://satimagingcorp.s3.amazonaws.com/site/pdf/WorldView3-DS-WV3-Web.pdf (accessed on 20 September 2022).
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN Cloud and Multiple Scattering Upgrades with Application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
- ESA. Sentinel-2 Products Specification Document. 2021. Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2-Products-Specification-Document (accessed on 21 September 2022).
- Scheffler, D.; Hollstein, A.; Diedrich, H.; Segl, K.; Hostert, P. AROSICS: An Automated and Robust Open-Source Image Co-Registration Software for Multi-Sensor Satellite Data. Remote Sens. 2017, 9, 676. [Google Scholar] [CrossRef]
- Lucieer, A.; Stein, A. Existential uncertainty of spatial objects segmented from satellite sensor imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2518–2521. [Google Scholar] [CrossRef]
- Weidner, U. Contribution to the assessment of segmentation quality for remote sensing applications. In Proceedings of the 21st Congress for the International Society for Photogrammetry and Remote Sensing, Beijing, China, 3–11 July 2008. [Google Scholar]
- Levine, M.D.; Nazif, A. An experimental rule-based system for testing low level segmentation strategies. In Multicomputers and Image Processing: Algorithms and Programs; Academic Press: New York, NY, USA, 1982; pp. 149–160. [Google Scholar]
- Janssen, L.L.F.; Molenaar, M. Terrain objects, their dynamics and their monitoring by the integration of GIS and remote sensing. IEEE Trans. Geosci. Remote Sens. 1995, 33, 749–758. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Xiao, P.; He, G.; Zhu, L. Segmentation quality evaluation using region-based precision and recall measures for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2015, 102, 73–84. [Google Scholar] [CrossRef]
- Liu, Y.; Bian, L.; Meng, Y.; Wang, H.; Zhang, S.; Yang, Y.; Shao, X.; Wang, B. Discrepancy measures for selecting optimal combination of parameter values in object-based image analysis. ISPRS J. Photogramm. Remote Sens. 2012, 68, 144–156. [Google Scholar] [CrossRef]
- Yang, J.; Li, P.; He, Y. A multi-band approach to unsupervised scale parameter selection for multi-scale image segmentation. ISPRS J. Photogramm. Remote Sens. 2014, 94, 13–24. [Google Scholar] [CrossRef]
- Novelli, A.; Aguilar, M.A.; Aguilar, F.J.; Nemmaoui, A.; Tarantino, E. AssesSeg—A Command Line Tool to Quantify Image Segmentation Quality: A Test Carried Out in Southern Spain from Satellite Imagery. Remote Sens. 2017, 9, 40. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, M. Multiresolution Segmentation—An Optimization Approach for High Quality Multi-Scale Image Segmentation. In Angewandte Geographische Informations-Verarbeitung XII.; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Drǎguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef]
- Liu, D.; Xia, F. Assessing object-based classification: Advantages and limitations. Remote Sens. Lett. 2010, 1, 187–194. [Google Scholar] [CrossRef]
- Richardson, J.T.E. Eta squared and partial eta squared as measures of effect size in educational research. Educ. Res. Rev. 2011, 6, 135–147. [Google Scholar] [CrossRef]
- Witharana, C.; Civco, D.L. Optimizing multi-resolution segmentation scale using empirical methods: Exploring the sensitivity of the supervised discrepancy measure Euclidean distance 2 (ED2). ISPRS J. Photogramm. Remote Sens. 2014, 87, 108–121. [Google Scholar] [CrossRef]
- Wang, H.; Lin, L.; Hu, H.; Chen, Q.; Li, Y.; Iwamoto, Y.; Han, X.H.; Chen, Y.W.; Tong, R. Patch-Free 3D Medical Image Segmentation Driven by Super-Resolution Technique and Self-Supervised Guidance. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; Springer: Cham, Switzerland, 2021; pp. 131–141. [Google Scholar]
- Li, B.; Xiao, C.; Wang, L.; Wang, Y.; Lin, Z.; Li, M.; An, W.; Guo, Y. Dense nested attention network for infrared small target detection. arXiv 2021, arXiv:2106.00487. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Chen, P.; Woźniak, M. Image Enhancement-Based Detection with Small Infrared Targets. Remote Sens. 2022, 14, 3232. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, S. Effects of Atmospheric Correction and Image Enhancement on Effective Plastic Greenhouse Segments Based on a Semi-Automatic Extraction Method. ISPRS Int. J. Geo-Inf. 2022, 11, 585. [Google Scholar] [CrossRef]
- Mesner, N.; Oštir, K. Investigating the impact of spatial and spectral resolution of satellite images on segmentation quality. J. Appl. Remote Sens. 2014, 8, 083696. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).