Coseismic Gravity Changes and Crustal Deformation Induced by the 2018 Fiji Deep-Focus Earthquake Observed by GRACE and GRACE-FO Satellites

Abstract

Earthquakes at depths of ≥300 km are generally called deep-focus earthquakes. Only two deep-focus earthquakes with Mw 8.0 or more have occurred in this century—the 2013 Okhotsk earthquake (Mw 8.3) and the 2018 Fiji earthquake (Mw 8.2) on 19 August 2018. However, the 2018 Fiji earthquake was only reported on seismographs, and the related crustal deformations were not observed by the Global Navigation Satellite System because the observation network did not exist around the epicenter. This study analyzed the time series of gravity data observed by the Gravity Recovery And Climate Experiment (GRACE) and its successor, GRACE Follow-On, and detected the spatial distribution of coseismic gravity changes mainly due to crustal deformation by the 2018 Fiji earthquake. The results in this study were not consistent with the numerical calculation of gravity changes when using the fault parameters estimated by the data of seismic waves. Thus, numerical calculations were used to construct a uniform slip rectangle fault model to explain coseismic gravity changes and provide a spatial distribution map of crustal deformation. However, this fault model is only based on gravity changes; thus, new research combining satellite gravimetry and seismic wave data will be necessary in the future.

1. Introduction

More than 60% of deep-focus earthquakes worldwide occur in the Fiji–Tonga subduction zone [1]. The largest local deep-focus earthquake of this century occurred on 19 August 2018 (Mw 8.2) at a depth of approximately 600 km, followed by another earthquake on 6 September 2018 (Mw 7.9) at a depth of approximately 650–670 km. These earthquakes occurred at the Tonga Trench and have been observed and reported by several groups [1,2], and complex physical processes of fault ruptures have been suggested. The United States Geological Survey (USGS) provides finite fault models based on seismological analysis in their earthquake catalog (https://earthquake.usgs.gov/earthquakes/eventpage/us1000gcii/finite-fault) (accessed on 10 January 2023). In addition, Global Navigation Satellite System (GNSS) data were used to reveal the ionospheric anomalies possibly related to the Fiji earthquake by focusing on Total Electron Content (TEC) [3]. However, the crustal deformation distribution was not well resolved by GNSS because of the small number of observation stations, as shown in Figure 1 of Mitsui et al. [4].

The spatial distribution of the three-dimensional crustal deformation of deep-focus earthquakes was first observed by Shestakov et al. [5] in the 2013 Okhotsk deep-focus earthquake (Mw 8.3) at a depth of approximately 600 km by the GNSS observation network on the Kamchatka Peninsula. This earthquake was the first deep-focus earthquake with a Mw of ≥8.0 after the launch of the Gravity Recovery And Climate Experiment (GRACE) satellites in 2002. Tanaka et al. [6] showed the distribution of coseismic gravity changes related to crustal vertical deformation of the Okhotsk earthquake by analyzing GRACE satellite data. However, it was difficult to extract the signals of coseismic gravity changes in the region completely because permafrost in and around the Kamchatka Peninsula contributes to gravity changes.

In contrast to the 2013 Okhotsk deep-focus earthquake, the 2018 Fiji earthquake (Mw 8.2) occurred in the Pacific Ocean area, including only small islands without strong land-water effects such as permafrost signals. The moment magnitude of this earthquake (Mw 8.2) was similar to that of the 2013 Okhotsk earthquake (Mw 8.3). This suggests that the signal of a coseismic gravity change can be clearly detected. However, the second 2018 Fiji deep-focus earthquake (Mw 7.9), which occurred only 18 days after the largest earthquake (6 September 2018), was slightly smaller, and the time interval from the first event was too short. Therefore, it is difficult to distinguish the two events from the monthly GRACE observation data [6].

Thus, in this study, I investigated the two-dimensional coseismic gravity changes of the 2018 double Fiji deep-focus earthquakes by analyzing GRACE and its successor GRACE Follow-On (GRACE-FO, GFO) observation data. The Mw 8.2 earthquake was the second deep-focus earthquake with a Mw > 8.0 after the launch of the GRACE satellites. I also present the physical modeling results of the observed signal and show crustal deformation maps of both the land and ocean bottom areas.

2. Materials and Methods

GRACE and GFO data were downloaded from the International Centre for Global Earth Models (ICGEM) website, and monthly “Release 06” gravity field data were provided by the Center for Space Research at the University of Texas. The unfiltered data of spherical harmonic coefficients for the periods from April 2002 to July 2016 (GRACE) and from March 2019 to January 2022 (GFO) were downloaded, with degrees and orders up to 60. A fan filter (a two-dimensional Gaussian filter used for spatial smoothing) of 400 km radius [7] was then applied to the data after the C₂₀ and C₃₀ coefficients were replaced with those obtained by the Satellite Laser Ranging (SLR) technique, as these long-wavelength components are measured more accurately by high-altitude SLR satellites than by low-altitude satellites, such as GRACE. The SLR data were downloaded from the ICGEM website. The radius of the filter was set according to the parameters in Tanaka et al. [6] to reduce short-wavelength noise. The principal spatial wavelength of the coseismic gravity change of a deep-focus earthquake is sufficiently long and is not removed by the filter.

The coefficients were converted into gravity as outlined by Wahr et al. [8] for the coefficients of degrees and orders from 2 to 60. These components are gravity anomalies that have no offsets between the GRACE and GFO data. I produced time series data from the monthly data at each 1 (deg) × 1 (deg) grid point for longitudes from 165E to 200E (160W) and latitudes from 35S to the equator, and modeled the resultant time variable gravity (TVG), ∆g, with the following formula by the least squares method:

$$\Delta g\left(t\right)=a_1+a_{2}t+a_3\sin 2\pi t+a_4\cos 2\pi t+a_5\sin 4\pi t+a_6\cos 4\pi t+a_{7}H\left(t-t_0\right)$$

(1)

where the coefficients a_i (i = 1–7) are constants estimated by the least squares, the first term is the overall bias, the second term is the secular trend, the third–sixth terms represent annual and semi-annual variations, t₀ is the time (in years) at the occurrence of the 2018 Fiji largest earthquake, and H(t − t₀) denotes the Heaviside step function, which provides 0 when t − t₀ < 0, otherwise it provides 1. In this equation, the estimated a₇ values indicate coseismic gravity jumps at given locations; thus, the spatial distribution of the coseismic gravity change is shown by mapping these values. The standard deviation (1 sigma) was estimated at the same time. Here, I used only one Heaviside step function because it was impossible to separate the two earthquakes based on the time series with only a one-month temporal resolution. In addition, post-seismic components were considered to be zero because post-seismic gravity changes are probably negligible for the first several years after deep-focus earthquakes [9].

All numerical calculations in this study are based on the work of Sun et al. [10]. These numerical calculations provide coseismic gravity changes and crustal deformations by providing fault parameters based on the Preliminary Reference Earth Model (PREM). By correcting the contributions of sea-water movements by ocean bottom crustal deformations to gravity changes and filtering the calculation results in the same way as the observation data, the calculation results can be compared with the observation results. The sea-water correction follows the Bouguer correction with density contrasts.

3. Results

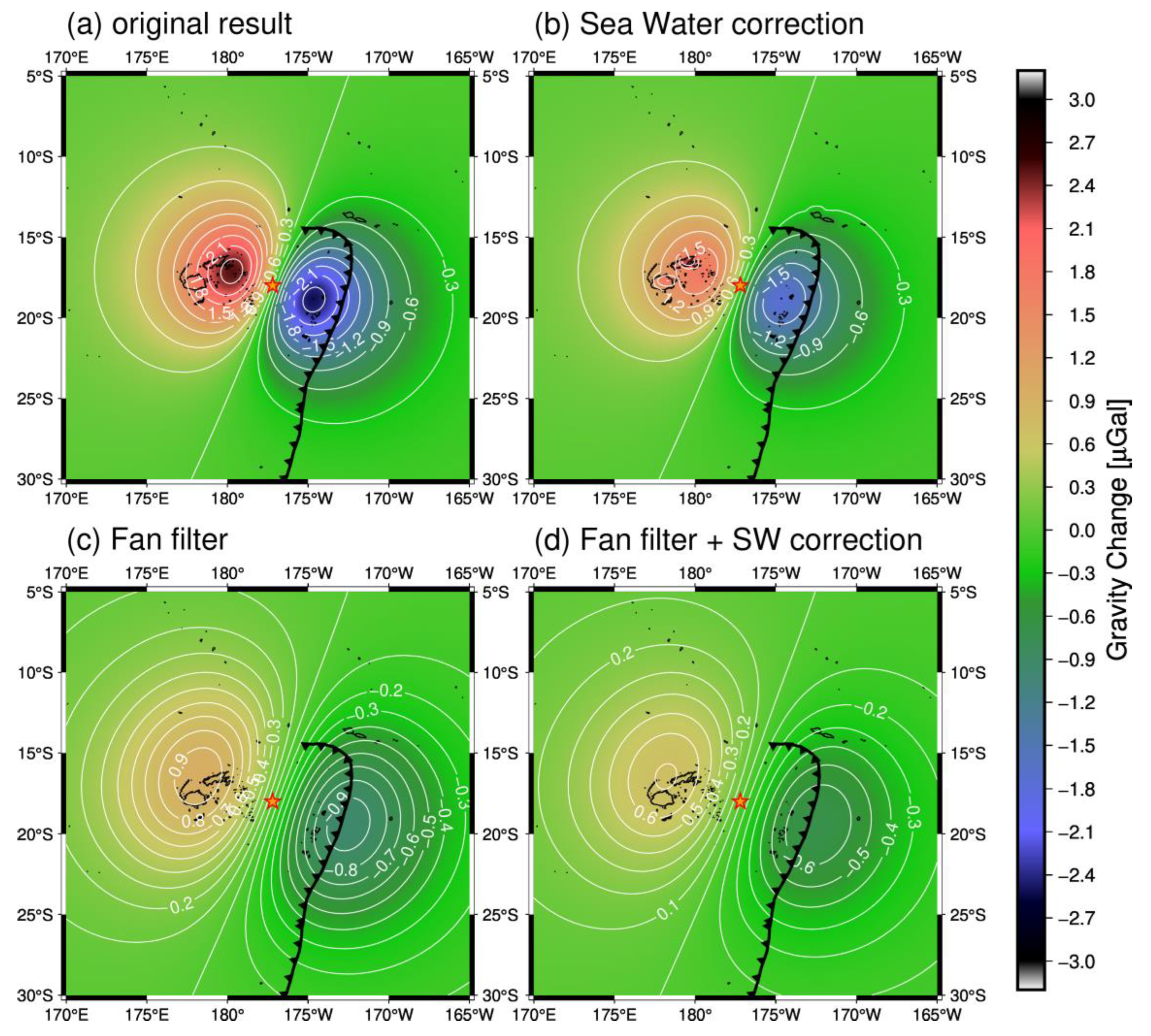
Figure 1 shows the calculation results of the coseismic gravity changes of the two 2018 Fiji deep-focus earthquakes after filtering and correcting the sea-water contributions. The faults used in these calculations are simplified uniform slip rectangular fault models with reference to the USGS Centroid Moment Tensor (CMT) solutions (details are provided in Section S1 of Supplementary Materials).

Figure 1a,b shows the calculated coseismic gravity changes of the 19 August 2018, and 6 September 2018, deep-focus earthquakes, respectively. The first earthquake generated gravity increases and decreases at maximum amplitudes of approximately +0.2 μGal and −0.4 μGal (Figure 1a). The amplitudes of the calculated gravity changes of the first earthquake were sufficiently large for GRACE and GFO detections. These amplitudes were slightly amplified by the second earthquake shown in Figure 1b. As a result, the two earthquakes caused the gravity changes as shown in Figure 1c. However, the amplitudes of the calculated coseismic gravity change of the second earthquake were well below the level of the GRACE and GFO observation errors (<0.1 μGal), and the first earthquake was dominant for the spatial pattern of the gravity change. Thus, the contributions of the second earthquake to the total gravity change were considered negligible for the observational analysis.

I analyzed the GRACE and GFO data with the expectation that the observed results would be similar to the calculated results. However, the observation results in Figure 2a contradict the calculation results. The observation results revealed two significant differences. First, a gravity increase and decrease appeared clearly on both sides of the trench. The other is that the calculation results shown in Figure 1 suggest that the amplitude of the coseismic gravity decrease is larger than that of the increase, but the maximum amplitudes of the increase and decrease are approximately 0.7 μGal and −0.6 μGal, respectively, which are twice as large as the standard deviations as shown in Figure 2a,b.

This also suggests that the second earthquake may not be negligible for the GRACE and GFO observations. However, the contribution of the second earthquake is considered small relative to the first earthquake because of its smaller moment magnitude and the deeper source (650–670 km). The temporal resolution of the GRACE and GFO observations is also not sufficient to separate the two 2018 Fiji deep-focus earthquakes; thus, I determined the parameters of a single uniform slip rectangular fault by numerical calculation. According to the finite fault model provided by the USGS, the depth of the geometric center of the fault is assumed to be 590 km. The shape of the fault is set at 100 × 100 km² because there is a tradeoff between the lengths, widths, and amounts of the slips (Section S2 in Supplementary Materials). A square of 100 km on a side is a simplified shape with reference to the USGS infinite fault model. Based on these assumptions, the grid search method was used to estimate the longitude, latitude, rake/strike/dip angles, and amount of slip of the fault to coincide with the observation results.

The fault parameters were estimated based on these observations. First, the rake, strike, and dip angles were determined to satisfy three features of the observation result (Figure 2a): (1) the gravity increase and decrease appear on either side of the trench, (2) the absolute value of the gravity increase is larger than that of the gravity decrease, and (3) the centers of the gravity increase and decrease are located at the latitudes of 16S and 20S, respectively. Further details are provided in Section S3 of the Supplementary Materials. At the same time, the latitude and longitude were determined so that the locations of the peaks of the gravity increase and decrease coincided with the observed results. Finally, the amount of slip was determined according to the maximum amplitudes of the observed gravity increases and decreases. The details are presented in Sections S3 and S4 of the Supplementary Materials. The calculation to estimate the parameters was performed every 10° of rake, dip, and strike angles, every 0.2° of longitude and latitude, and every 0.1 m of the amount of the slip. Thus, estimation errors are 5° for rake/dip/strike angles and 0.5 m for the amount of the slip. However, the spatial resolution of the GRACE and GFO data is limited (spherical harmonic coefficients of degrees and orders up to 60, where a two-dimensional Gaussian filter with a radius of 400 km is applied); therefore, the longitudes and latitudes may not be determined accurately.

Figure 2c shows the calculation results based on the estimated optimum fault parameters listed in

Table 1. The fault parameters.

Latitude	Longitude	Slip	Rake	Depth	Strike	Dip	Length	Width
18.0S	177.2W	3.7 m	270	590 km *	20	90	100 km *	100 km *

Marks of * indicate that the parameters are provided artificially rather than being estimated. The latitude and longitude coordinates represent the geometric center of the fault. The latitude, longitude, rake angle, strike angle, and dip angle are all measured in degrees. The moment magnitude of this fault is Mw 8.4.

. The calculation was filtered in the same manner as that for the observation data. The moment magnitude of the estimated fault was 8.4. The residuals between the observation and calculation were smaller than the standard deviations over the entire target area (Figure 2b,d); therefore, this fault model likely represents the source fault. The remaining difference was likely caused by the contributions of the second earthquake, the assumption that PREM was used, and the uncertainty of the GRACE/GFO observations. The target area has a complex structure with a curved and subducted Pacific slab; therefore, PREM may not be ideal.

Figure 2e shows a comparison along the latitudes of 16S and 20S for a more detailed comparison of the observation and calculation. The amplitudes of the gravity increase, and decrease are very consistent, and the spatial patterns are the same. Figure 2f,g are TVG and modeled functions after removing offsets, secular trends, and seasonal variations. The coseismic gravity jumps appeared in the 2018 Fiji earthquake.

One significant feature of the observed result (Figure 2a) was that the absolute value of the maximum increase was larger than that of the decrease. This was probably because of the following effects. The coseismic gravity changes caused by deep-focus earthquakes mainly stem from crustal deformations, especially surface uplift and subsidence [6,11], but those caused by ocean bottom deformations are weakened by sea-water movement. Thus, if surface uplift and subsidence occur at the same amplitude at a dip angle of 90°, the absolute values of coseismic gravity changes become larger in island areas than in ocean areas. The coseismic gravity increase is mainly due to the crustal uplift of the 2018 Fiji deep-focus earthquake overlapping the island area in Figure 2a, so the gravity increase can become larger than the gravity decrease, as shown in Figure 3. The amplitudes of the gravity increase and decrease in Figure 3a are the same because of the vertical dip angle, but the gravity increase becomes larger than the decrease by correcting the sea-water contributions in Figure 3b. The amplitudes become smaller by filtering, as shown in Figure 3c,d and the final result Figure 3d shows the signal observed by the GRACE and GFO satellites.

Coseismic crustal deformations were also calculated based on the fault parameters listed in Table 1. The calculated surface deformations of solid Earth are shown in Figure 4. Filters were not applied to these results.

I have also provided calculation results for coseismic gravity changes caused by the Moho deformation and the uplift and subsidence of the Moho in Section S5 of Supplementary Materials and the land–sea mask used in this study in Section S6 of the Supplementary Materials for reference.

4. Discussion

The spatial pattern of the coseismic gravity changes detected by GRACE and GFO data analysis in this study differs from that of the 2013 Okhotsk deep-focus earthquake [6]. Gravity increase and decrease appeared on either side of the trench in the 2018 Fiji earthquake, but only gravity decrease around the Kamchatka Peninsula was observed in the 2013 Okhotsk earthquake. This difference is probably caused by the differences in dip angles and distributions of land and ocean; the estimated dip angle of the 2018 Fiji earthquake is 90°, but that of the 2013 Okhotsk earthquake is approximately 10–20°, and the distributions of land and ocean areas around these two earthquakes are completely different, which leads to different ocean water effects.

Previous studies estimated the dip angles of the 2018 Fiji largest earthquake at approximately 60–80° [1,2] and the strike angle estimated by the USGS was 12.9°. These solutions were derived from seismic wave data, and the spatial patterns of coseismic gravity changes observed by GRACE and GFO were not provided by these parameters. The heterogeneity of the physical conditions at depth and the geometric complexity of the tectonics of this region may explain this difference. This suggests that identifying the physical processes of deep-focus earthquakes from only one type of data is difficult.

The data of the GNSS observation station near the fault was provided by the International GNSS Service (IGS; ID, FINA00WLF; location [14.308S, 178.121E]). However, the signal-to-noise ratio of the displacement time series at the station, was low (the “position time series” is available at https://igs.org/imaps/station.php?id=FTNA00WLF (accessed on 10 January 2023)), thus small signals were difficult to detect. Large signals did not appear at the earthquake occurrence according to the position time series, which does not conflict with the calculation result (Figure 4), but suggests that the data of the GNSS observation stations are not sufficiently available to research the 2018 Fiji deep-focus earthquakes. The GRACE and GFO data present unique tools to detect local two-dimensional crustal deformation.

The observation results of GRACE and GFO may differ because they reflect the sum of the coseismic gravity changes of the two 2018 Fiji deep-focus earthquakes. Because the calculation results in Figure 1 are different from the observation results in Figure 2, the second earthquake may also not be negligible, and the fault parameters of the two earthquakes in previous studies were either not sufficiently estimated or included large uncertainties. More detailed estimations of the physical processes of these two earthquakes may be necessary to explain both the seismic waves and gravity changes. The strict reason for this difference is still unclear, but the GRACE and GFO satellites observe both land and ocean areas two-dimensionally; thus, the results of this study provide new and significant insights into the research of deep-focus earthquakes.