Abstract
In linear inverse scattering, the performance of the imaging system is sometimes evaluated in terms of its resolution, i.e., its capability to reconstruct a point-like scatterer. However, there is still a lack of analytical studies on the achievable resolution. To address this, we consider the point spread function (PSF) evaluation of the scattered near field for the single frequency and multi-view/multi-static case in homogeneous medium. Instead of numerically computing the PSF, we propose and discuss an approximate closed form under series expansions according to the angular ranges of both source and receiver location. In order to assess the effectiveness of the proposed approximation, we consider two cases including both full and limited view angles for the incident field and observation ranges. In addition, we provide a localization application to show the usefulness of the theoretical discussion. Numerical results confirmed the analytical investigations.
1. Introduction
In the inverse electromagnetic scattering problem, the goal is to determine the permittivity and permeability of an unknown scatterer and identify its shape and location. This is achieved by using information about the scattered field, obtained through the illumination of the scatterer with a known incident field. This problem is of great interest because of its applications in various areas of physics and engineering; for instance, radar imaging [1], synthetic-aperture radar (SAR) imaging [2,3], remote sensing [4,5], ground penetrating radar (GPR) [6,7], civil engineering applications of GPR [8], geophysics application of GPR [9], and medical imaging [10,11,12]. The near or far field can be considered in terms of the favorite application.
When considering objects with significant differences in dielectric properties, such as strong contrasts, or objects that are very large in terms of the wavelength, multiple scattering becomes a significant factor to take into account. Therefore, the problem becomes strongly non-linear and requires the use of iterative approaches for its solution. Then, solution algorithms are based on the minimization of an error function. Stochastic methods are applicable when the number of unknowns is very low due to their heavy computational burden. On the other hand, iterative and gradient based approaches may converge to false solutions, according to the choice of the starting point. Therefore, all these methods do not allow consideration of the mathematical features of the operator to be inverted so as to predict their ultimate results. On the contrary, linear approximations allow investigation of their results and their limitations. To this end, it is common to consider the pertinent so-called point spread function (PSF) in tomographic approaches in order to appreciate the resolution of the algorithm. In this paper, we attempt to find a closed form expression for the PSF in the case of single frequency excitation and to validate it numerically.
Linear scattering models also arise in iterative non-linear method such as the Born iterative method (BIM) [13] and the distorted Born iterative (DBI) [14,15]. Therefore, an accurate analysis of the linear inverse scattering problem deserves attention in order to understand the best expected performances in connection with the source and receiver locations. Hereafter, we consider the Born approximation.
We need to introduce two mathematical tools for our analysis. When the operator is linear and compact, the singular value decomposition (SVD) of the relevant operator can be applied to introduce the number of degrees of freedom (NDF) and PSF. For the operators of which we are interested in this paper, the compact operators whose singular values exponentially decay to 0, when the singular values exhibit a step-like behavior, NDF can then be estimated as the number of significant singular values before the knee or exponential decay. This number can be assumed as an estimate of the maximum achievable resolution, meaning the number of independent point-like scatterers that can be accurately reconstructed. However, determining the NDF in closed form is often a difficult task, except for specific geometries like linear, circumference, and circular geometries. For all other cases, one can attempt to derive an estimate or upper bound for the NDF through numerical means.
The NDF evaluation of scattered fields was addressed in [16] for strip geometries, where it was found that the length of the strip matters in computing the NDF and the NDF of two linear scatterers can be computed by the matrix approach which is equal to the summation of the NDF of each strip when they are far apart. In [17] it was shown that the NDF of a full 2D square source is equivalent to the NDF of a void square source, which is provided by summing the NDF of each side of the square. An analytical evaluation of the NDF of the radiated/scattered fields was provided in [18] for circumference geometries and two concentric circumferences were considered to show that the NDF of two geometries is equal to the NDF of the outer circumference in the inverse source. Whereas in inverse scattering, the total NDF is the sum of each circumference.
The PSF represents the impulse response of the cascade formed by the operator and its regularized inverse. It provides the impulse response of a linear imaging system to a point-like object. Therefore, the width of its main lobe is related to the achievable resolution by the inversion process. This means that the response produced by any object can be represented as the convolution of the response due to a point-like scatterer with the spatial variation of the object itself. Using this method makes it possible to quickly and reliably reconstruct images of objects of good quality. The PSF is a fast and significant approach to computing the achievable image quality of the objects.
In addition, it is feasible to represent the regularized solution to the inverse problem using a truncated SVD (TSVD) by using an expansion in the right singular functions. Thus, in the reconstruction, the truncation index allows excluding from the reconstruction the components corresponding to small singular values, which eliminates the noise components. The behavior of the exact PSF is related to the truncation index that can be adapted in terms of the NDF, which means the unknown can be reconstructed reliably by an imaging algorithm, even when there are uncertainties present in the data. Nevertheless, the analytical form of the PSF is not always available when using TSVD inversion, and its determination may require a numerical approach.
The PSF concept was used in [19] to perform holographic imaging of dielectric media. In [20], the imaging resolutions of the time-reversal and back-projection algorithms were compared by analyzing their PSFs with numerical studies, and it was shown that both algorithms had the same imaging resolutions, whether in the free space or the layered media.
Earlier research in [21] presented an approximate evaluation of the resolution for strip source/scattering geometries, assuming full data availability. The evaluation demonstrates that the approximation can effectively predict the resolution. Furthermore, the resolution is spatially invariant in the full-view case. The same analysis is available in [18] for circumference source/scattering geometries. For the limited view case, a good approximation of the resolution was evaluated in [22] for curve geometries and in [23] for the full 2D geometries, and the studies found that a spatially variant of the resolution was achieved.
This paper addresses the evaluation of the PSF of the scattered field to estimate the achievable resolution for a single frequency and multi-view in the homogeneous medium in the near zone. In fact, there is no analytical evaluation of the exact PSF, and it should be determined numerically. To overcome these limitations, we propose an analytical approximation of the exact PSF. Our analysis covers two cases: the full-view case, where the incident field and observation ranges cover full angles, and the aspect-limited case, where the incident field and observation ranges are limited to a certain range of angles. In this analysis, we adopt a circumference geometry for the sensing system. While the analytical estimation of the NDF is known in [23,24] for the far field, we extend this approach to compute the NDF in the near field. We discuss how the NDF in both far and near fields is equal by providing a comparison between them for each case. Numerical simulations are provided for each case to confirm the analytical discussions. Finally, we show how to use analytical discussions for a localization application.
In this paper, we focus on the linear approximation of the scattering equations for dielectric objects in free space, specifically the Born approximation. However, the entire approach and the results can also be extended to other linear approximations of scattering. For instance, for a perfectly electric conducting object, the physical optics (PO) approximation [25], arising from the radiation of equivalent approximate currents in free space, provides a linear approximation of the scattering operator very similar to the one considered hereafter. The PO approximation has been also extended to the scattering of a strong dielectric object so that it can be also invoked in the remote sensing of the Earth’s surface. In addition, we consider near field conditions, which are common in subsurface prospection by ground penetrating radars. Finally, the observation and the excitation domains are assumed to lay on an arc of the circumference, as it allows a closed form evaluation of some of the functions relevant in the chosen approach. However, in the aspect-limited case, a chord and circumference can approximate the arc. Therefore, the results can be expected to hold approximately for linear domains as well.
The following is the structure of the paper. In Section 2, the problem statement and the approximate evaluation of the resolution for a general scattering geometry are presented. Section 3 provides various numerical examples to support the theoretical discussions. Section 4 provides a numerical application of the theoretical discussions. Finally, in Section 5, conclusions and discussions are provided.
2. Statement of the Problem
In this section, we first provide some mathematical preliminaries and notations used in the following sections. Second, we recall the definition of the exact PSF and provide the evaluation of the approximated PSF.
Figure 1 shows the general geometry of the problem in the near field. An unknown scatterer is located in a homogeneous domain referred to as the investigation domain (ID). The position vectors of the scattering object, the source point(transmitter), and the observation point (receiver) are denoted by , and , respectively, where and are constant. The incident field and observations angular domains are supposed to be limited so that and .
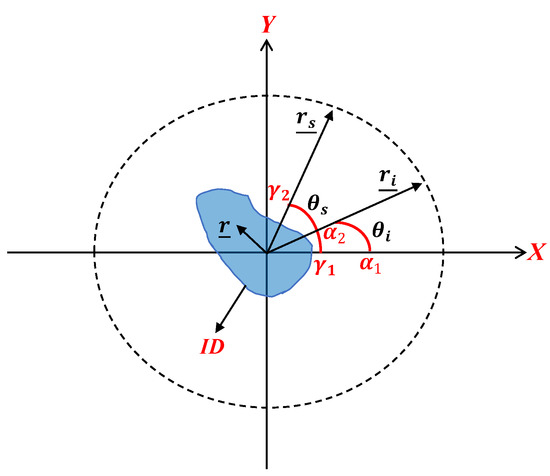
Figure 1.
The general geometry of the problem.
The scattered field is defined by
where is the Hankel function of the second kind and zero-th order. and are contrast function and pertinent linear operator for the multi-view and single frequency scattering configuration of our interest. is equal to , where is the relative permittivity of the scatterer. We suppose that the scatterer is located in the free space as a homogenous background. Furthermore, the wavenumber and wavelength are indicated by and , respectively.
Approximate Evaluation of the Resolution
The achievable resolution in the inverse scattering problem may be impacted by factors such as the shape of the scattering geometry and the ranges of the incident field and observation domains. To assess the performance of the reconstruction algorithm and demonstrate its effectiveness in achieving resolution, the PSF concept is used. In this subsection, to provide a clear view of the mathematical details leading to the main analytical results of the paper, we present the individual steps as a numbered list.
- The definition of the exact PSF. In the scatterer domain, the impulse response of an imaging system to a point-like scatterer is defined by the PSF concept and can be expressed by the cascade of the , i.e., the regularized inverse operator of and the direct operator. The PSF is observed at when the point-like scatterer is located at . In other words, the response of the system to a Dirac delta function is the PSF of the system. Mathematically, the exact PSF is defined by
Then, the SVD is applied to (1) because the operator is linear and compact. Its singular system consists of , where and are the singular functions, which span the data and the scatterer contrast function spaces, respectively, and expresses the singular values by arranging them under a decreasing order [26]. To define the TSVD inversion [26], we can express (2) using the truncated completeness relation involving singular functions . In this way, we can obtain the minimum-norm solution to the inverse scattering problem requiring the projection of the actual contrast function onto the singular function that possesses singular values that are not zero. Then, it can be shown as follows:
where the symbol (*) denotes the conjunction operation. Equation (3) expresses that the exact PSF depends on the number of retained singular values. The truncation index is related to the accuracy of the solution and can be adopted in terms of the NDF.
- 2.
- The introduction of the approximated PSF. To derive the closed-form expression of (3), it is necessary to have information about the singular functions, which cannot be calculated in closed form in general. However, according to [18,21,22], the adjoint operator can approximate the inverse operator in (2) if the singular values of the relevant operator exhibit a nearly constant behavior before the knee of its curve. Therefore, if this condition is satisfied, we can substitute the inversion operator in (2) with the adjoint operator to build a good approximation of the PSF, which can overcome the aforementioned limitation. The goal is to provide an analytical evaluation of the approximated PSF to predict the resolution, while the approximated is defined as follows:
- 3.
- The analytical evaluation of (4). The adjoint operator of (1) is provided by
Then, the spectral theorem is applied to , which is a compact self-adjoint operator.
whose kernel is as below:
- 4.
- The addition theorem for the Hankel functions. This is invoked as a series representation as, for instance below:where is the Bessel function of the first kind and n-th order and is the Hankel function of the second kind and n-th order.
By using (8) four times and interchanging the integrals with the summations, (7) becomes a four-fold summation, which can be factored as the product of two symmetrical functions with different arguments:
and are concerned with the observation and incident field, respectively.
- 5.
- Residual closed form integration. The function can be written as a double summation:
By performing the simple closed form integration in (11)b, the computation of gives the following:
where .
At the same time, the function can be written as (10):
where , and are now the following:
By performing the simple closed form integration in (14)b, the computation of gives now the following:
- 6.
- Final result. We can rewrite explicitly Equation (9) as below:thus, providing the analytical expression of the approximated . The summations can be safely truncated to , as is the maximum integer, due to asymptotic exponentially decay of the Bessel functions for indices larger than its argument, when are smaller than .
It should be noted that while the exact PSF depends on the truncation value of the TSVD algorithm, which depends on the NDF of the problem, the is independent of it. Therefore, to assess the performance of the , it is important to estimate the NDF pertinent to the scattering geometry and use this information to truncate the SVD. This will allow for a fair comparison between the approximate and exact PSFs. In the Appendix A, a discussion is provided on how to estimate the NDF in the case of aspect limited data in the near field.
3. Numerical Validation
This section provides numerical examples to validate the analytical discussions and to demonstrate the effectiveness of the approximated PSF. Specifically, a circle ID with a radius of is considered. As far as the numerical inversion of the integral Equation (1) is concerned, in order to achieve a good approximation of the continuous operator, the simple choice of a sufficiently polar dense grid to achieve a step on both arc and radial variables is adopted. The SVD of the resulting matrix equation is computed in the MATLAB environment. In this way, we may obtain the exact PSF by truncating the SVD to the exact NDF.
In the following numerical examples, and are both equal to . Moreover, only the main lobe of the PSF is considered to highlight its focusing properties, and the amplitudes of both PSFs are normalized to 1.
In order to compute the NDF of the considered ID, we use the analytical result provided in [23,24] for the far scattered field concerning the evaluation of the NDF for the double Fourier transform operator. In fact, for far zone observation, the scattering operator (1) can be cast as such by an appropriate change of variables form the angular to the spectral ones. Then, a closed form value of the NDF is known in the literature and employed here: it requires only to know the measure of the ID and of the spectral domain area. In turn this depends on the ranges of excitation and observation angles. Therefore, the NDF for the far scattered field is provided by the following:
where for the considered ID. More detailed information is available for computing in [23].
First, numerical examples are presented for the full-view case in Section 3.1. Then, different examples are provided for the aspect-limited case in Section 3.2.
3.1. Full-View Case
In this subsection, we consider the full view case where the angular ranges of the excitation and observation directions are wide. This means that and are equal to , whereas and are .
First, we compare the NDF of both the far and near scattered field and compute them numerically by referring to the pertinent far zone operator [23,24] and to (1), respectively. Figure 2 provides a comparison of the behaviours of their normalized singular values. The expected NDF of the far field from (17) is equal to NDF = , as and the numerical results confirm that the NDF in the near field is equal to the NDF of the far field. This result can be expected in virtue of the equivalence theorem, as for each source the corresponding near scattered field has the same NDF of the corresponding far field.
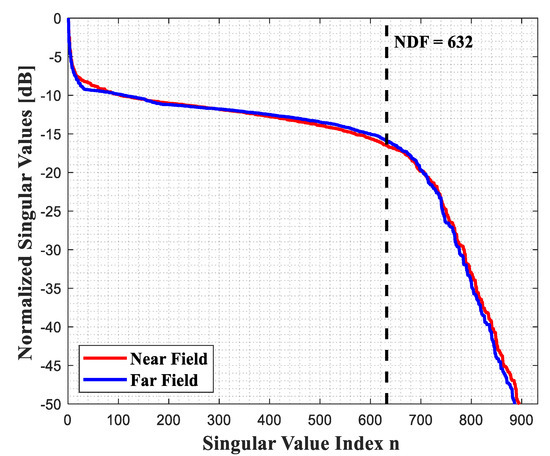
Figure 2.
Comparison of the behaviors of the normalized singular values of the linearized inverse scattering for the full view case in the near and far fields.
In order to assess the performance of the in achieving the resolution, a comparison is made between the normalized amplitude of the exact and approximated PSFs cut along in Figure 3. The results are presented for three point-like scatterers when . The findings demonstrate that the resolution remains space-invariant and confirm a significant overlap between the and the exact PSF in the main lobes. This reliable prediction of the achievable resolution applies to every point-like scatterer.
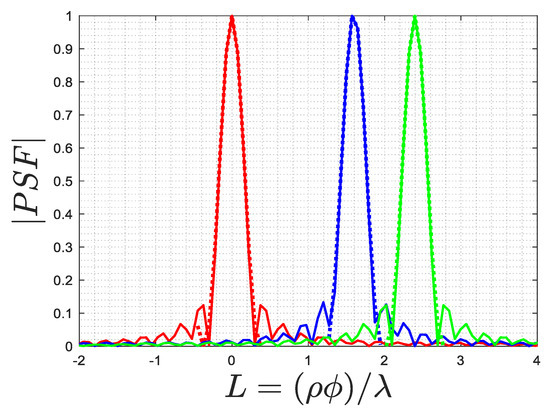
Figure 3.
Comparison of the normalized amplitude of the actual (solid lines) and approximated (dashed lines) PSFs for (red lines), (blue lines), and (green lines), when .
Next, we compare both PSFs for -cut when , as illustrated in Figure 4. As observed, the space invariance is once again achieved and the approximated also performs well.
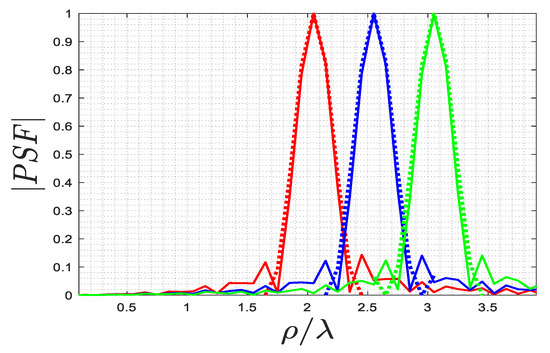
Figure 4.
Comparison of the normalized amplitude of the actual (solid lines) and approximated (dashed lines) PSFs for (red lines), (blue lines), and (green lines), when .
3.2. Aspect-Limited Observation and Excitation
In this subsection, we consider the aspect limited case when the system is in reflection mode where the angular ranges of the excitation and observation directions are wide. This means that and are equal to , while and are . The spectral domain area is computed in [23] for this angular range, which is . Hence, the NDF of the far field can be analytically derived from (17), which is . Figure 5 displays the behavior of the computed singular values of the pertinent operators for the near and far fields. It is observed once again that both NDFs are approximately the same, although their behaviors are different. (See Appendix A for an explanation of this result for the present scenario).
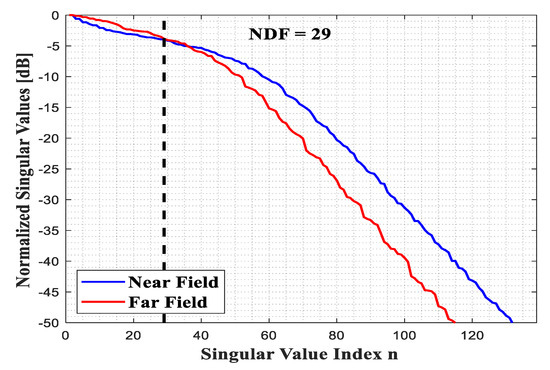
Figure 5.
The behavior of the normalized singular values of the linearized inverse scattering in near and far fields.
Figure 6 presents a comparison between the normalized amplitude of both PSFs along -cut, achieved for different values. We considered that three different point-like scatterers are positioned within the angular domain. Along the the PSF exhibits a narrow main lobe width at the center of the angular range (indicated by the red lines). However, as the point-like scatterer moves from the center towards the edge, the main lobe width increases. Conversely, for the three points located well inside the ID (), the main lobe width appears broader, and as increases, the width becomes narrower. These results demonstrate that the proposed approximation accurately predicts the achievable resolution for each point-like scatterer.
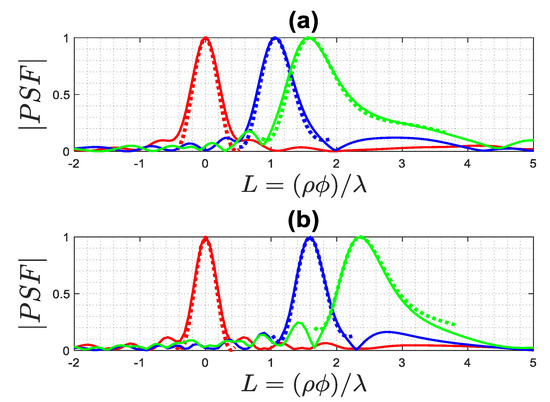
Figure 6.
Comparison of the normalized amplitude of the actual (solid lines) and approximated (dashed lines) PSFs for (red lines), (blue lines), and (green lines): (a) , (b) .
The previous example is replicated here for (red lines), (blue lines), and (green lines) along -cut for different values, as shown in Figure 7. Once again, it is observed that , for the point-like scatterer located within the angular range, the main lobe width of their respective PSFs varies as their positions change. However, for , which lies outside the angular range, the width of its main lobe becomes wide. Similarly, the width of the main lobe appears broad for three points situated at the depth of ID (). Furthermore, increasing the value results in a narrower main lobe width. These results once again verify that the approximation is acceptable for every point-like scatterer.
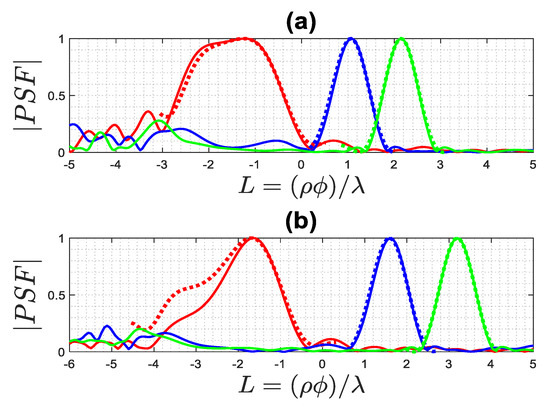
Figure 7.
Comparison of the normalized amplitude of the actual (solid lines) and approximated (dashed lines) PSFs for (red lines), (blue lines), and (green lines). (a): , (b): .
Figure 8 presents a comparison of two PSFs along the -cut, aiming to evaluate the performance of the and observe the achievable resolution. In Figure 8a, the PSFs exhibit a wide main lobe width when , while in Figure 8b, the main lobe width is smaller when . Along the -cut, the resolution of the considered point-like scatterers remains constant but it varies as changes. These results once again validate the effectiveness of the proposed , which closely overlaps with the exact PSF for each point-like scatterer.
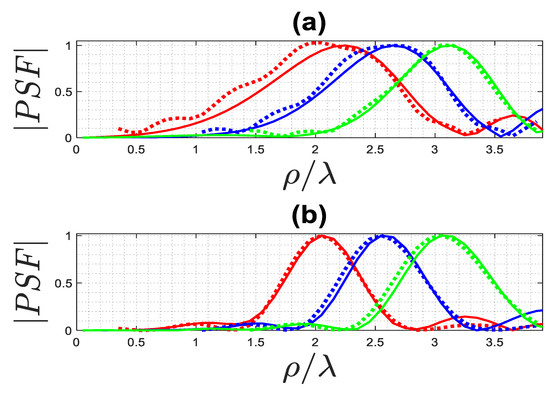
Figure 8.
Comparison of the normalized amplitude of the actual (solid lines) and approximated (dashed lines) PSFs for (red lines), (blue lines), and (green lines). (a): , (b): .
4. Application to Localization of Point-Like Scatterers
This section provides a localization application related to the theoretical discussions. The application concerns localizing some point-like scatterers. We consider a 2D full square dielectric object as an ID, where and , with and are equal to . The ranges , and other parameters are the same as in the previous section. As mentioned earlier, the NDF for this ID is not available in the close form for the near scattered field. However, as discussed above and in the Appendix A, the NDF can be expected to be approximately the same as the far scattered fields, which can be analytically derived from (17), and is given by . Figure 9 shows the normalized behaviors of singular values of relevant operators in the near and far fields and confirms that the NDF in the near field is approximately equal to the NDF in the far field for the same angular ranges of the position of sources and receivers.
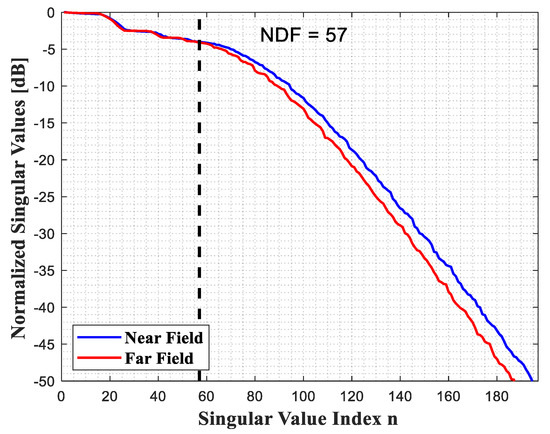
Figure 9.
The behaviors of the normalized singular values of the relevant operator for a 2D full square in near and far fields.
To implement our proposed application, it is necessary to determine the achievable resolution. For this purpose, a comparison between the exact and approximated PSFs is now provided along both the x-cut and y-cut, as depicted in Figure 10. The results reveal that the main lobe width of the PSF along the x-cut is wider compared to the width of the main lobe in the y-cut. Consequently, the space-variant behaviour of the PSF is only observed when the scatterer moves from one cut line to another. In other words, the resolution remains unchanged along each cut. Additionally, the PSF results confirm that the approximated PSF can work well. We define the resolution, denoted as , as half of the width of the main lobe of the PSF. Hence, the resolution is determined as along the x-cut, while the resolution is measured as along the y-cut.
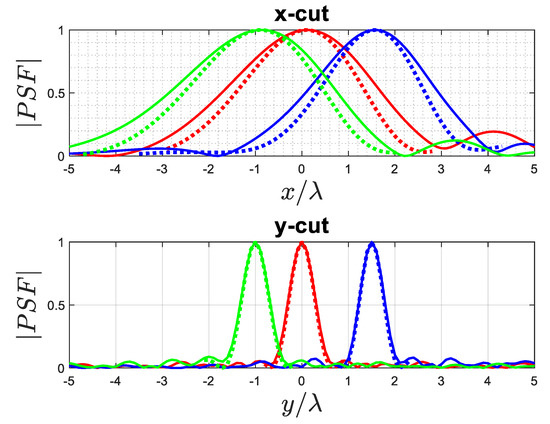
Figure 10.
Comparison of the normalized amplitude of the actual (solid lines) and approximated (dashed lines) PSFs: (x-cut) for (green lines), (red lines), and (blue lines) when , (y-cut) for (green lines), (red lines), and (blue lines) when .
In this application, we consider the scenario where five point-like scatterers are positioned along an oblique line within the ID, which can mimic a localization problem along the separation between media with very different permittivities so that the PO approximation holds as sometimes in remote sensing. The reconstructed result of these point-like scatterers is displayed in Figure 11. Figure 11a validates that the considered scatterers are effectively resolved and can be distinguished from each other when they are spaced according to the resolution distance . However, if the scatterers are located closer than the resolution distance , as depicted in Figure 11b, the reconstruction appears as two merged points instead of separate individual points.
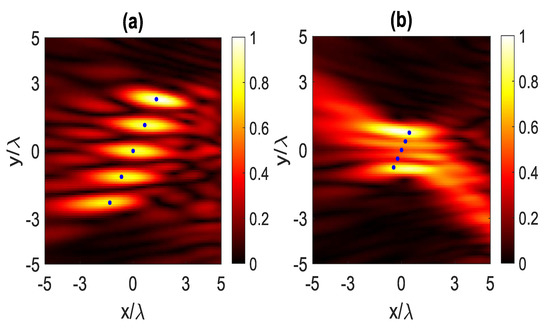
Figure 11.
The reconstructed image of five point-like scatterers when: (a) the distance between them is equal to the resolution, (b) the distance between them is less than the resolution. The blue dots indicate the position of the scatterers.
Since the resolution does not depend on the shape of the ID and as shown in the previous example is large, therefore, we consider a rectangular geometry with and to reconstruct five point-like scatterers located on an oblique line within ID. In this case, the NDF is equal to 68 (which is computed by the equation provided in the previous example). Figure 12 shows the reconstructed image of the considered points. When the distance between points is equal to the resolution , they can be resolved well, as shown in Figure 12a. On the other hand, if they are positioned at a distance less than the resolution, they appear as a line rather than separable points, as shown in Figure 12b.
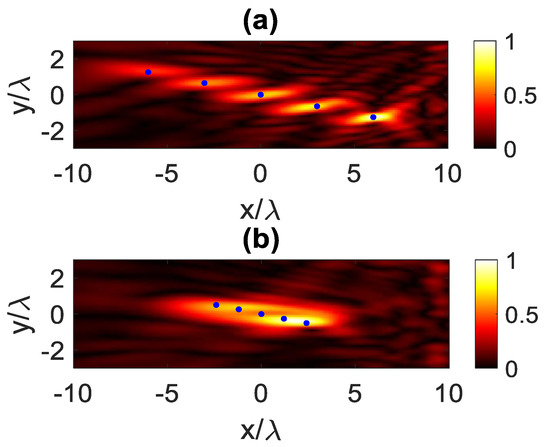
Figure 12.
The reconstructed image of five point-like scatterers: (a) the distance between them is equal to the resolution, (b) the distance between them is less than the resolution. The blue dots indicate the position of the scatterers.
In conclusion, the defocusing effect of the PSF can be appreciated by the fact that the correct reconstruction of the same number of point-like scatterers can be achieved only when they are sufficiently spaced away, due to the width of the main lobe of the PSF according to observation and source locations. Additionally, this effect varies along different directions.
5. Conclusions and Discussion
The PSF evaluation of scattered fields was addressed to estimate the resolution in the near field for both full view and aspect-limited cases. The main goal of evaluation was to introduce an analytical approximated PSF, overcoming the limitations due to the need of a numerical evaluation of the exact PSF. Circle geometry was considered as an ID. We computed the NDF for near and far fields in both full and limited cases. The results demonstrated that the NDF of the near field is approximately equal to that of the far field. The specially invariant PSF is achieved along both and for the full-view case, while the resolution is different along each cut for the aspect-limited case. In the aspect-limited case, the main lobe width of the PSF is wide along for a point-like scatterer located outside of the angular range, whereas inside it is smaller. Additionally, the main lobe width of the PSF is also large for horizontal and small for vertical. We also showed that the NDF of a full square is the same for both fields in the aspect-limited case, and the space-variance is achieved only when the point-like scatterer moves from one side to the other.
The results confirmed that the approximation works well in both cases. An application was introduced to reconstruct some point-like scatterers along an oblique line, which may mimic a localization problem along a part of the Earth’s surface. It showed that the considered scatterers can be reconstructed quite correctly if they are spaced in terms of the resolution space. This occurs because the approximate evaluation by the adjoint operator still allows quite well the prediction of the main lobe of the PSF. On the other side, in order to examine the resolution of isolated point-like scatterers, taking into account the main lobe is sufficient. Instead, when many point-like scatterers are present in the scattering scenario, their reconstruction is affected by the sidelobes of the PSF and use of the approximated one might be questionable. The proposed approximation may provide a valuable tool to imaging systems for close remote sensing for the possibility of predicting achievable resolution in advance by analytical means from the geometrical features of the sensing system, once the source and observations ranges are assigned over circumferences in close proximity to the investigation domain.
Author Contributions
Conceptualization, G.L.; methodology, G.L.; software, E.A.S.; validation, E.A.S. and G.L.; formal analysis, E.A.S. and G.L.; investigation, E.A.S. and G.L.; resources, E.A.S.; data curation, E.A.S.; writing—original draft preparation, E.A.S.; writing—review and editing, G.L. and E.A.S.; visualization, G.L.; supervision, G.L.; project administration, G.L.; funding acquisition, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data supporting reported results were generated during the study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Hereafter: we present an explanation about the evaluation of the NDF in the near field when the source points and the observation points scan a limited angle over the respective circumference geometry. We make use of some arguments in [27] to provide an overestimate of the NDF of the scattered field in the near field, which is then linked to the aspect-limited available data.
Let us first consider the far field case with a single impinging plane wave and a circumference ID of radius a. In this circumstance, based on the Born approximation, the scattered field coincides with the field radiated by the equivalent source provided by the induced currents within the ID due to the presence of the scatterer. For this problem, the pertinent analytical SVD is available [28], which provides , where , for NDF and Fourier harmonics as right singular functions. Consequently, the scattered field can be represented by a finite Fourier series as follows:
At the same time, the finite Fourier series, being a periodic function, can be equivalently converted into a sampling series as below:
where is the n-th sample position and is the Dirichlet sampling function of degree .
By the reciprocity theorem , which means that each sample can be viewed as the file scattered by the object in the direction when a plane wave is impinging from the direction. Therefore, the previous discussion can be repeated leading to the following:
Putting everything together the double finite series can be obtained as follows:
where the samples of the scattered field over the whole observation angles for all incidence angles are involved. (Note that , again because of the reciprocity theorem, so that only samples are actually independent).
When we consider a limited angular observation domain, only the scattered field samples belonging to that domain become relevant in representing the scattered field as a rough estimate. Similarly, when the impinging plane waves travel from a limited angular set, only a limited number of scattered field samples are necessary to evaluate the scattered field within the same angular domains. This suggests that a similar proportionality argument holds for the NDF (indeed this is the case discussed in [23]), where the number of necessary scattered field samples is proportional to the angular domains of observations and incidence.
When we consider both the source and the observation points located over a circumference in the near field, the previous discussion only needs to be adjusted in terms of the SVD of the scattered field under a single excitation source. Once again, it coincides with the field radiated by the equivalent source created by the induced currents within the ID, and the corresponding SVD is analytically known. This yields , with , NDF (if the transmitters and receivers are a few wavelengths apart form the ID) and, again, Fourier harmonics as right singular functions. Therefore, we can repeat the entire discussion regarding the sampling representation of the scattered field, and the same arguments about the significance of a limited number of samples to roughly evaluate the scattered field over the limited incident field and observation angular domains hold true. Consequently, it can be expected that also the NDF of the problem scales with the available angular domains when and .
References
- Gennarelli, G.; Soldovieri, F. A linear inverse scattering algorithm for radar imaging in multipath environments. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1085–1089. [Google Scholar] [CrossRef]
- Solimene, R.; Catapano, I.; Gennarelli, G.; Cuccaro, A.; Dell’Aversano, A.; Soldovieri, F. SAR imaging algorithms and some unconventional applications: A unified mathematical overview. IEEE Signal Process. Mag. 2014, 31, 90–98. [Google Scholar] [CrossRef]
- Munson, D.C.; Visentin, R.L. A signal processing view of strip-mapping synthetic aperture radar. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 2131–2147. [Google Scholar] [CrossRef]
- Kagiwada, H.; Kalaba, R.; Timko, S.; Ueno, S. Associate memories for system identification: Inverse problems in remote sensing. Math. Comput. Model. 1990, 14, 200–202. [Google Scholar] [CrossRef]
- Wang, Y. Regularization for inverse models in remote sensing. Prog. Phys. Geogr. 2012, 36, 38–59. [Google Scholar] [CrossRef]
- Daniels, D.J. Ground Penetrating Radar; IET: Edison, NJ, USA, 2001; Volume 1. [Google Scholar]
- Soldovieri, F.; Hugenschmidt, J.; Persico, R.; Leone, G. A linear inverse scattering algorithm for realistic GPR applications. Near Surf. Geophys. 2007, 5, 29–41. [Google Scholar] [CrossRef]
- Benedetto, A.; Pajewski, L. Civil Engineering Applications of Ground Penetrating Radar; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Davis, J.L.; Annan, A. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy 1. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Semenov, S. Microwave tomography: Review of the progress towards clinical applications. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 3021–3042. [Google Scholar] [CrossRef]
- Caorsi, S.; Massa, A.; Pastorino, M. Numerical assessment concerning a focused microwave diagnostic method for medical applications. IEEE Trans. Microw. Theory Tech. 2000, 48, 1815–1830. [Google Scholar]
- Larsen, L.E.; Jacobi, J.H. Medical Applications of Microwave Imaging; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 1985. [Google Scholar]
- Wang, Y.; Chew, W. An iterative solution of the two-dimension electrom, agnetic in-verse scattering problem. Int. J. Syst. Technol. 1989, 1, 100–108. [Google Scholar] [CrossRef]
- Chew, W.; Wang, Y. Reconstruction of two-dimensional permittivity distribution using the distorted born iterative method. IEEE Trans. Med. Imag. 1990, 9, 218–225. [Google Scholar] [CrossRef] [PubMed]
- Noritake, K.; Kidera, S. Boundary extraction enhanced distorted born iterative method for microwave mammography. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 776–780. [Google Scholar] [CrossRef]
- Akbari Sekehravani, E.; Leone, G.; Pierri, R. NDF of scattered fields for strip geometries. Electronics 2021, 10, 202. [Google Scholar] [CrossRef]
- Sekehravani, E.A.; Leone, G.; Pierri, R. NDF of the far zone field radiated by square sources. In Proceedings of the XXXIVth General Assembly and Scientific Symposium of the International Union of Radio Science, Rome, Italy, 28 August–4 September 2021; pp. 1–4. [Google Scholar]
- Sekehravani, E.A.; Leone, G.; Pierri, R. NDF and PSF analysis in inverse source and scattering problems for circumference geometries. Electronics 2021, 10, 2157. [Google Scholar] [CrossRef]
- Amineh, R.K.; McCombe, J.J.; Khalatpour, A.; Nikolova, N.K. Microwave holography using point-spread functions measured with calibration objects. IEEE Trans. Instrum. Meas. 2014, 64, 403–417. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, X.; Fang, G. Comparison of the imaging resolutions of time reversal and back-projection algorithms in EM inverse scattering. IEEE Geosci. Remote Sens. Lett. 2012, 10, 357–361. [Google Scholar] [CrossRef]
- Sekehravani, E.A.; Leone, G.; Pierri, R. PSF Analysis of the inverse source and scattering problems for strip geometries. Electronics 2021, 10, 754. [Google Scholar] [CrossRef]
- Sekehravani, E.A.; Leone, G.; Pierri, R. Resolution of born scattering in curve geometries: Aspect-Limited observations and excitations. Electronics 2021, 10, 3089. [Google Scholar] [CrossRef]
- Sekehravani, E.A.; Leone, G.; Pierri, R. Performance of the Linear Model Scattering of 2D Full Object with Limited Data. Sensors 2022, 22, 3868. [Google Scholar] [CrossRef]
- Gori, F.; Guattari, G. Shannon number and degrees of freedom of an image. Opt. Commun. 1973, 7, 163–165. [Google Scholar] [CrossRef]
- Pierri, R.; Liseno, A.; Soldovieri, F. Shape reconstruction from PO multifrequency scattered fields via the singular value decomposition approach. IEEE Trans. Antennas Propag. 2001, 49, 1333–1343. [Google Scholar] [CrossRef]
- Bertero, M.; Boccacci, P. Introduction to Inverse Problems in Imaging; Institute of Physics: Bristol, UK, 1998. [Google Scholar]
- Bucci, O.M.; Isernia, T. Electromagnetic inverse scattering: Retrievable information and measurement strategies. Radio Sci. 1997, 32, 2123–2137. [Google Scholar] [CrossRef]
- Devaney, A.J. Mathematical Foundations of Imaging, Tomography and Wavefield Inversion; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).