Spatial-Convolution Spectral-Transformer Interactive Network for Large-Scale Fast Refined Land Cover Classification and Mapping Based on ZY1-02D Satellite Hyperspectral Imagery
Abstract
1. Introduction
- In the face of high spectral variability, convolution operations cannot reasonably address sequential features and long-distance dependent features in spectral signals [27]. The category information of ground objects is mainly reflected by the spectral sequence curve in the HSI. However, the convolution kernel with a fixed size is restricted to extracting features in the local scope and ignores the global sequence relationship between bands;
- The computational expense affects the application of CNN-based deep learning methods in large-scale HSI classification. The limited convolution kernel size requires the CNN model to increase the depth to improve its feature extraction ability [34], which leads to a high computational cost and longer training and inference times. Especially for 3D-CNN, the hyperspectral 3D data structure significantly increases the sliding number and size of the convolution kernel, thereby increasing the running time;
- Simple feature fusion methods inadequately utilize the spatial-spectral characteristics within the HSI patches. The spatial and spectral features extracted by CNN are generally combined by simple addition or connection at the end of the network, which may weaken the integration of these features.
- As an early attempt, a new Spatial-Convolution Spectral-Transformer Interactive Network (SCSTIN) is proposed for large-scale fast refined land cover classification and mapping using ZY1-02D satellite hyperspectral imagery. The CNN and Transformer are innovatively integrated as dual-branch architectures to efficiently perform hyperspectral image classification tasks;
- To extract spatial context characteristics and spectral sequence features of HSI according to the data organization format, 2D-CNN and Transformer are performed in the spatial branch and the spectral branch, respectively. This design can make full use of the respective strengths of CNN and the Transformer to extract spatial and spectral semantic information, respectively;
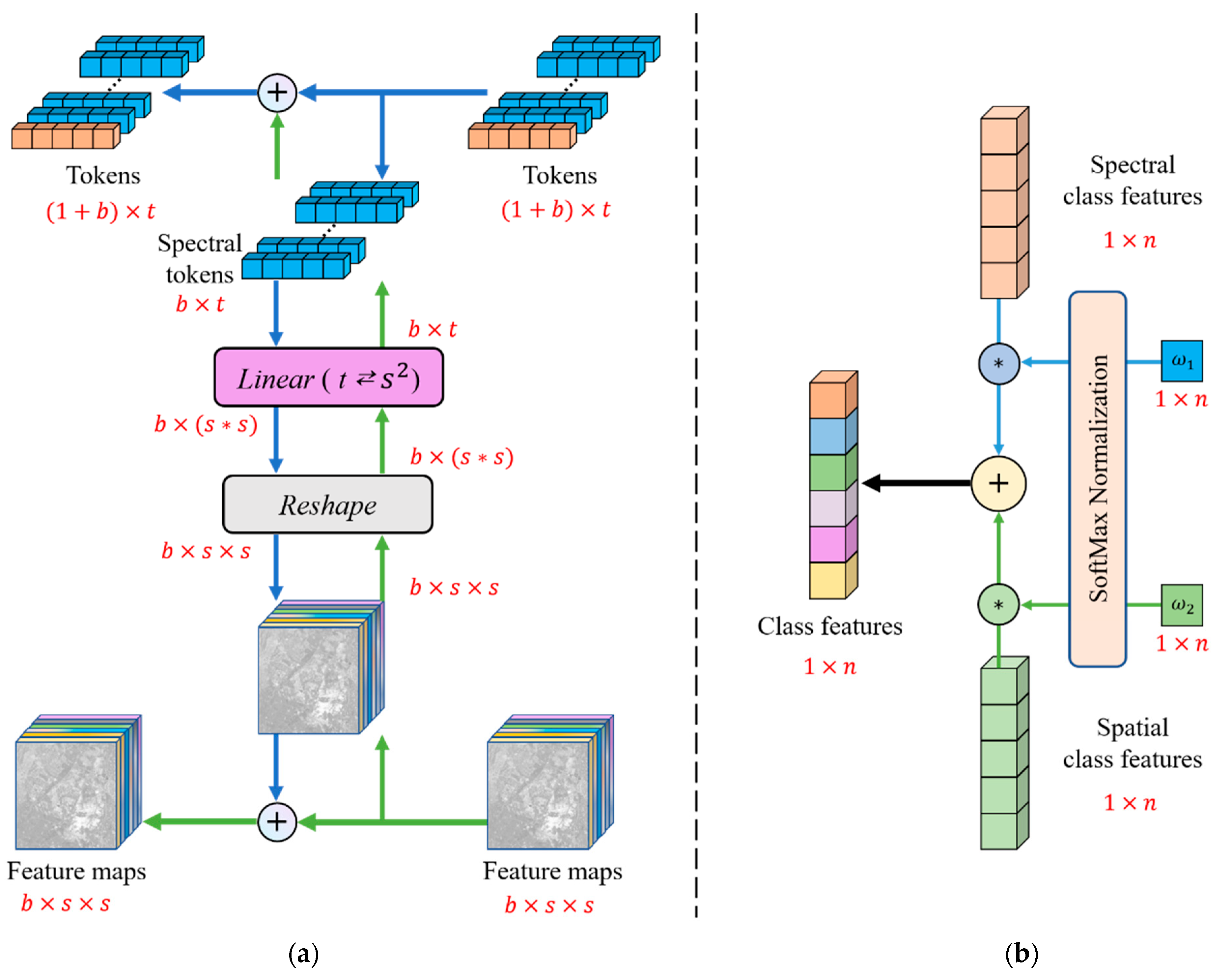
- Two blocks, including SSIF and CAW, are designed to effectively fuse spatial and spectral features at different stages of SCSTIN. In the process of extracting features from two different branches, SSIF fuses two types of features continuously and interactively. Before the two types of discriminative features are fed into the classifier, the CAW is used to apply adaptive weights to the features for further fusion;
- The superiority of the proposed SCSTIN framework is experimentally verified and compared with other advanced algorithms on the large-scale eastern foothills of the Helan Mountains (EFHLM) dataset, which covers about 8800 km2 with 16 types of ground objects (the largest dataset to our knowledge). The spatial distribution patterns of ground objects in the EFHLM region are also shown and analyzed. In addition, extended experiments on the EFHLM dataset and two benchmark datasets (i.e., Indian Pines and Botswana) demonstrate that the proposed SCSTIN can achieve satisfactory classification performance with low complexity and high efficiency.
2. Data and Materials
2.1. Study Area
2.2. ZY1-02D Hyperspectral Imagery and Preprocessing
2.3. EFHLM Dataset
3. Methodology
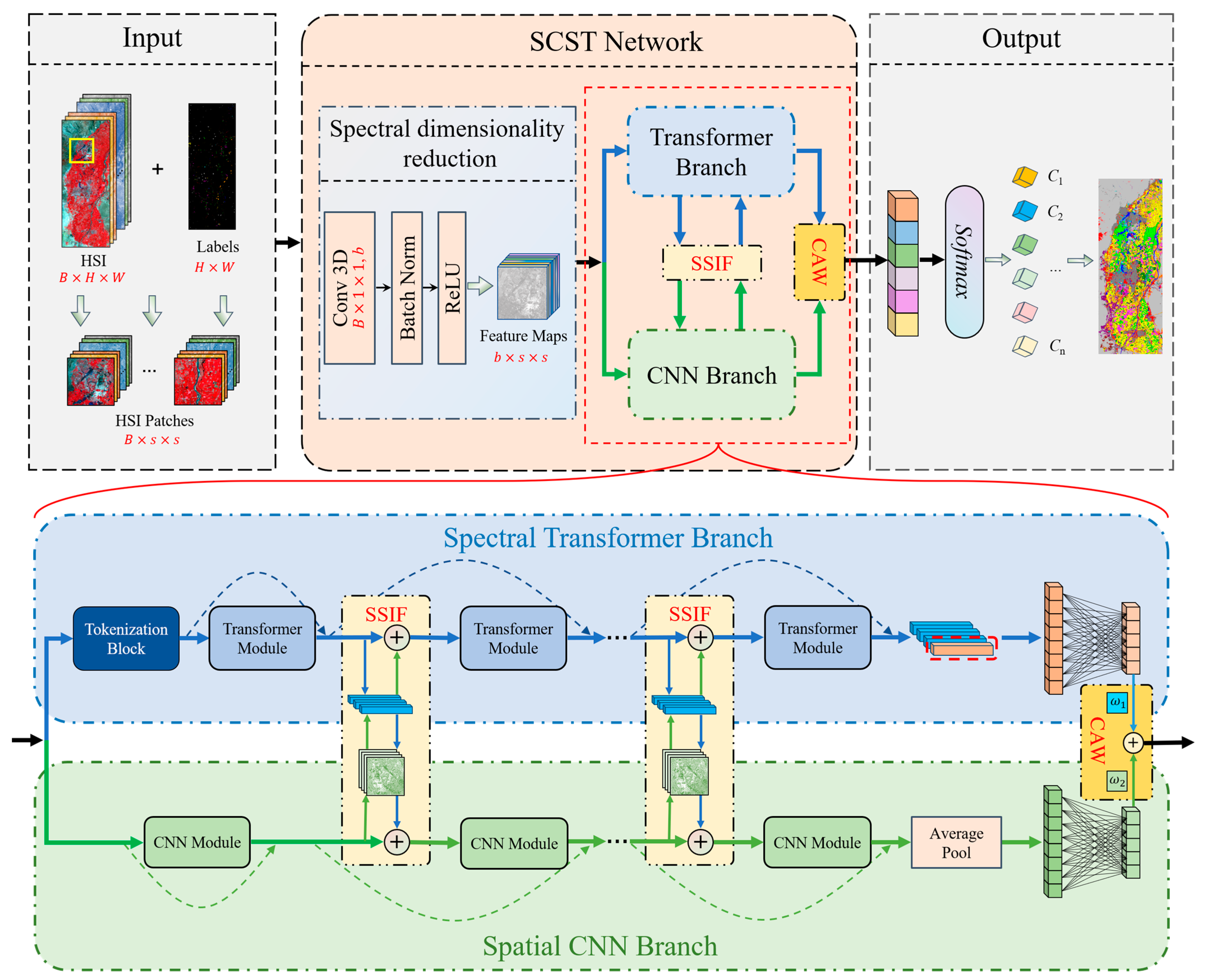
3.1. Overview of the SCSTIN
3.2. Spectral Transformer Branch
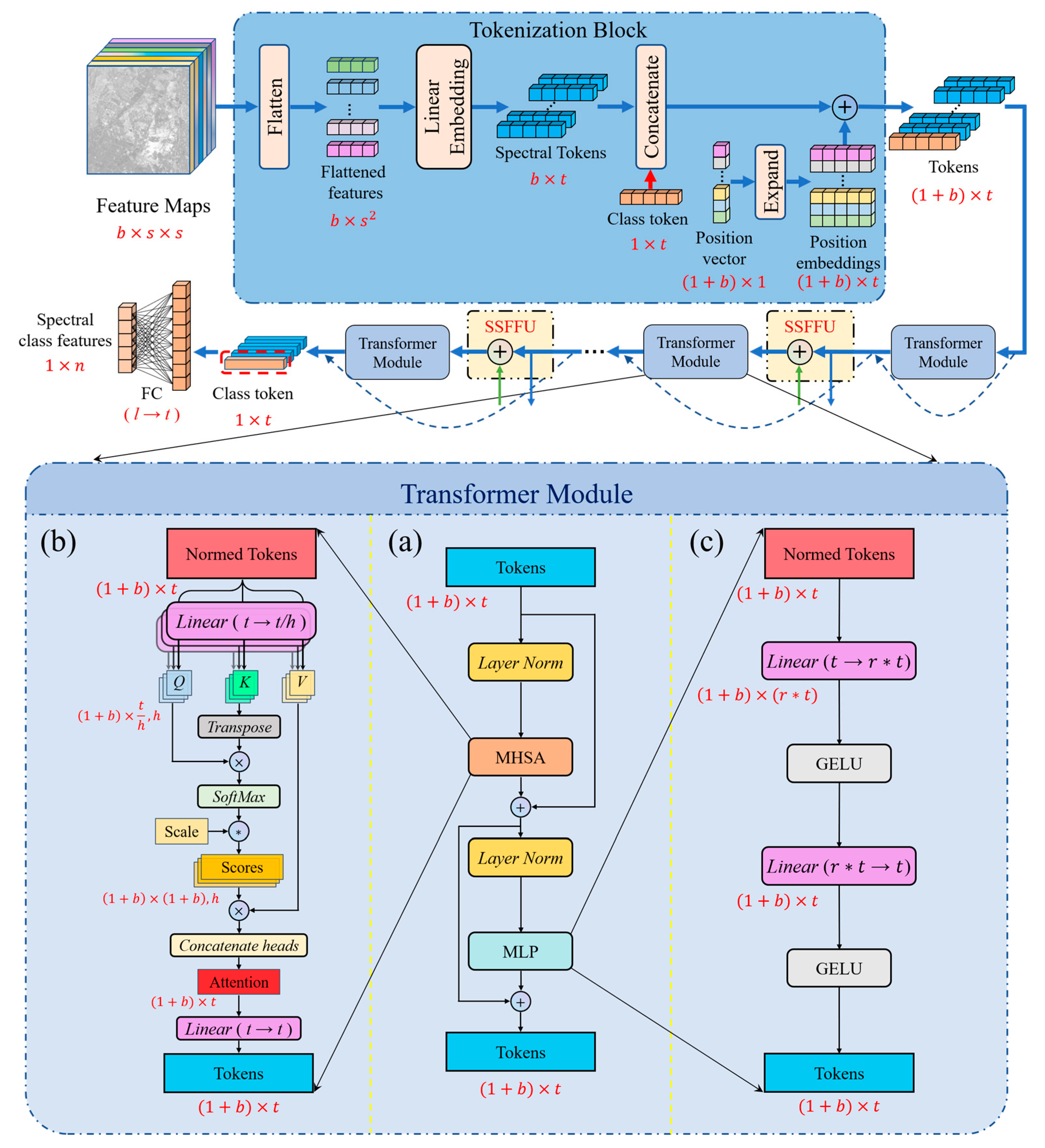
3.2.1. The Tokenization Block
3.2.2. The Transformer Module
3.3. Spatial CNN Branch
3.4. Feature Fusion Method
4. Results
4.1. Experimental Settings
4.1.1. The SCSTIN Framework Parameter Setting
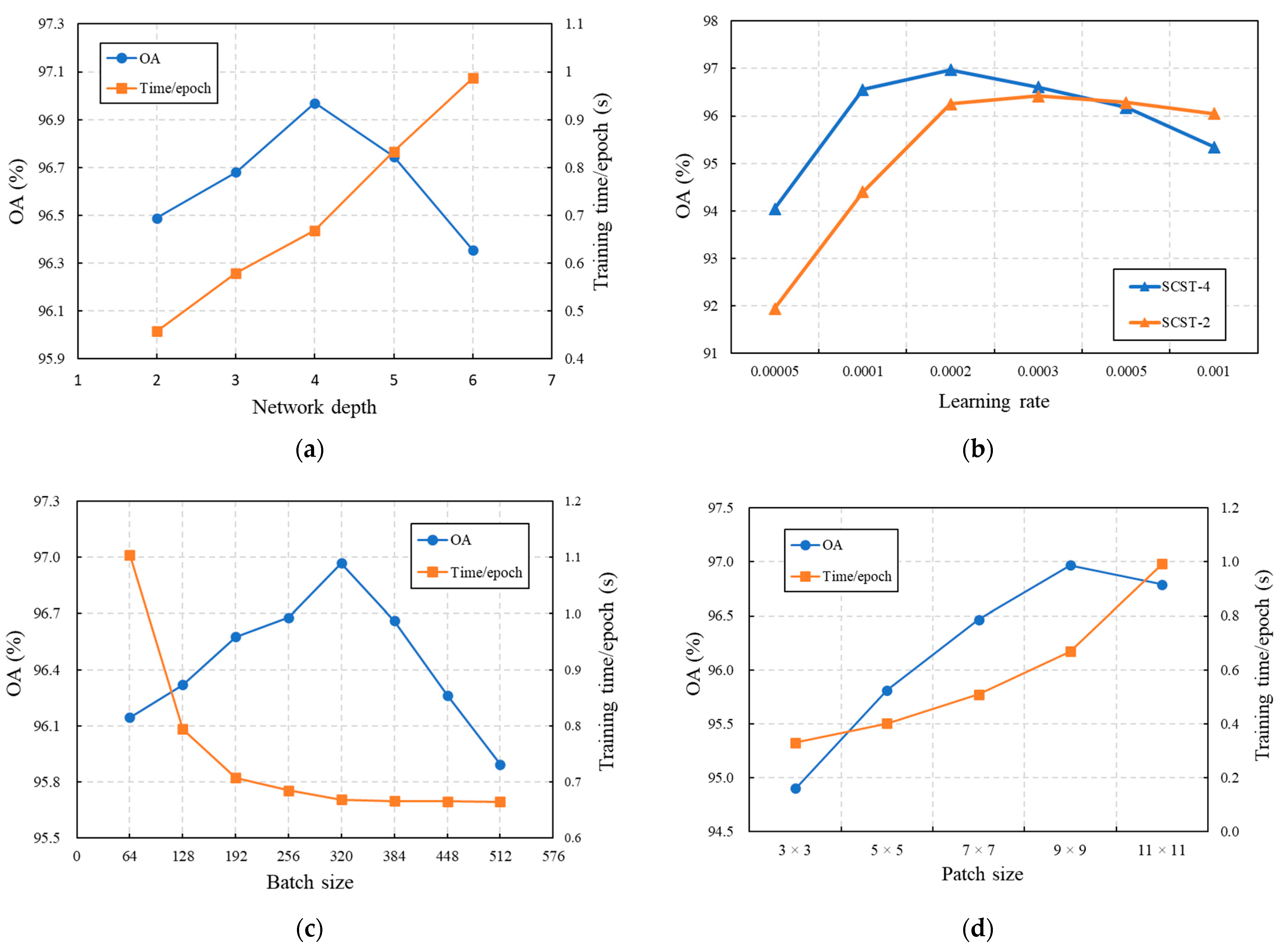
- Depth of the SCSTIN framework
- Learning Rate
- Training Batch Size
- Input patch size
4.1.2. Comparison Algorithms
4.2. EFHLM Classification Results
4.2.1. Classification Accuracy Comparison
4.2.2. Mapping Time Comparison
4.3. EFHLM Mapping Results and Distribution Analysis
5. Discussions
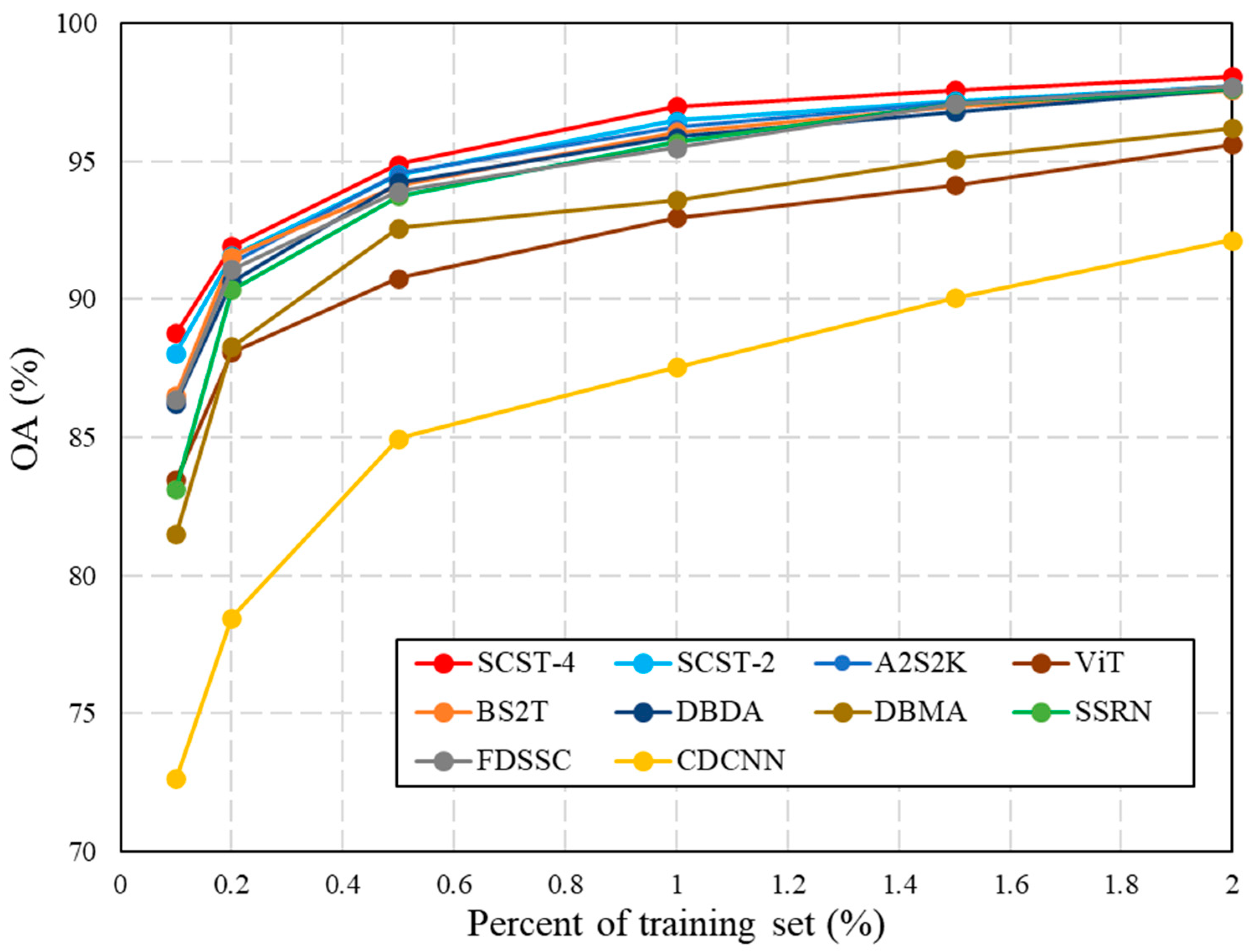
5.1. Analysis of the Training Sample Proportion
5.2. Ablation Study on Module
5.3. Model Complexity
5.4. Model Generalization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Beeri, O.; Peled, A. Geographical model for precise agriculture monitoring with real-time remote sensing. ISPRS J. Photogramm. Remote Sens. 2009, 64, 47–54. [Google Scholar] [CrossRef]
- Pott, L.P.; Amado, T.J.C.; Schwalbert, R.A.; Corassa, G.M.; Ciampitti, I.A. Satellite-based data fusion crop type classification and mapping in Rio Grande do Sul, Brazil. ISPRS J. Photogramm. Remote Sens. 2021, 176, 196–210. [Google Scholar] [CrossRef]
- Karpatne, A.; Jiang, Z.; Vatsavai, R.R.; Shekhar, S.; Kumar, V. Monitoring Land-Cover Changes: A Machine-Learning Perspective. IEEE Geosci. Remote Sens. Mag. 2016, 4, 8–21. [Google Scholar] [CrossRef]
- Li, J.; Pei, Y.; Zhao, S.; Xiao, R.; Sang, X.; Zhang, C. A Review of Remote Sensing for Environmental Monitoring in China. Remote Sens. 2020, 12, 1130. [Google Scholar] [CrossRef]
- Tan, K.; Ma, W.; Chen, L.; Wang, H.; Du, Q.; Du, P.; Yan, B.; Liu, R.; Li, H. Estimating the distribution trend of soil heavy metals in mining area from HyMap airborne hyperspectral imagery based on ensemble learning. J. Hazard. Mater. 2021, 401, 123288. [Google Scholar] [CrossRef]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake Damage Assessment of Buildings Using VHR Optical and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite imaging reveals increased proportion of population exposed to floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Zhong, Y.; Jia, T.; Wang, X.; Xu, Y.; Shu, H.; Zhang, L. Spectral-spatial classification of hyperspectral imagery with cooperative game. ISPRS J. Photogramm. Remote Sens. 2018, 135, 31–42. [Google Scholar] [CrossRef]
- Xue, Z.; Du, P.; Li, J.; Su, H. Sparse graph regularization for robust crop mapping using hyperspectral remotely sensed imagery with very few in situ data. ISPRS J. Photogramm. Remote Sens. 2017, 124, 1–15. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 1120012. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Wang, S.; Zhang, L. Advances in spaceborne hyperspectral remote sensing in China. Geo-Spat. Inf. Sci. 2021, 24, 95–120. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Hu, X.; Wang, X.; Zhong, Y.; Zhang, L. S3ANet: Spectral-spatial-scale attention network for end-to-end precise crop classification based on UAV-borne H2 imagery. ISPRS J. Photogramm. Remote Sens. 2022, 183, 147–163. [Google Scholar] [CrossRef]
- Su, H.; Yao, W.; Wu, Z.; Zheng, P.; Du, Q. Kernel low-rank representation with elastic net for China coastal wetland land cover classification using GF-5 hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2021, 171, 238–252. [Google Scholar] [CrossRef]
- Wei, D.; Liu, K.; Xiao, C.; Sun, W.; Liu, W.; Liu, L.; Huang, X.; Feng, C. A Systematic Classification Method for Grassland Community Division Using China’s ZY1-02D Hyperspectral Observations. Remote Sens. 2022, 14, 3751. [Google Scholar] [CrossRef]
- Datta, D.; Mallick, P.K.; Bhoi, A.K.; Ijaz, M.F.; Shafi, J.; Choi, J. Hyperspectral Image Classification: Potentials, Challenges, and Future Directions. Comput. Intell. Neurosci. 2022, 2022, 3854635. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; Cao, X.; Huang, C.; Liu, E.; Qian, S.; Liu, X.; Wu, Y.; Dong, F.; Qiu, C.W.; et al. Artificial intelligence: A powerful paradigm for scientific research. Innovation 2021, 2, 100179. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ham, J.; Yangchi, C.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Bera, S.; Shrivastava, V.K.; Chandra Satapathy, S. Advances in Hyperspectral Image Classification Based on Convolutional Neural Networks: A Review. Comput. Model. Eng. Sci. 2022, 133, 219–250. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N.; Zhan, Y. Semi-Supervised Locality Preserving Dense Graph Neural Network With ARMA Filters and Context-Aware Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification With Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Jaiswal, G.; Sharma, A.; Yadav, S.K. Critical insights into modern hyperspectral image applications through deep learning. WIREs Data Min. Knowl. Discov. 2021, 11, e1426. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, P.; Benediktsson, J.A. Automatic Design of Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper With Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Z.; Zheng, K.; Hong, D.; Yang, H.; Song, M. MSTNet: A Multilevel Spectral–Spatial Transformer Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Ashish, V.; Noam, S.; Niki, P.; Jakob, U.; Llion, J.; Aidan, N.; Gomez; Lukasz, K.; Illia, P. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- He, X.; Chen, Y.; Lin, Z. Spatial-Spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral Image Transformer Classification Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Zhang, J.; Tao, D. ViTAE: Vision Transformer Advanced by Exploring Intrinsic Inductive Bias. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Online, 6–14 December 2021. [Google Scholar]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Song, R.; Feng, Y.; Cheng, W.; Mu, Z.; Wang, X. BS2T: Bottleneck Spatial–Spectral Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Guo, X.; Wang, N.; Geng, K.; Li, D.; Wang, Z. Comparison of Methoxypyrazine Content and Expression Pattern of O-Methyltransferase Genes in Grape Berries and Wines from Six Cultivars (Vitis vinifera L.) in the Eastern Foothill of the Helan Mountain. Plants 2022, 11, 1613. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Gong, Z.; Liang, Y.; Liang, S. Retrieval of Chlorophyll-a Concentrations of Class II Water Bodies of Inland Lakes and Reservoirs Based on ZY1-02D Satellite Hyperspectral Data. Remote Sens. 2022, 14, 1842. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Liu, K.; Sun, W.; Shao, Y.; Liu, W.; Yang, G.; Meng, X.; Peng, J.; Mao, D.; Ren, K. Mapping Coastal Wetlands Using Transformer in Transformer Deep Network on China ZY1-02D Hyperspectral Satellite Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3891–3903. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Aleissaee, A.A.; Amandeep, K.; Anwer, R.M.; Salman, K.; Hisham, C.; Xia, G.; Khan, F.S. Transformers in Remote Sensing A Survey. Remote Sens. 2023, 15, 1860. [Google Scholar] [CrossRef]
- He, J.; Yuan, Q.; Li, J.; Xiao, Y.; Liu, X.; Zou, Y. DsTer: A dense spectral transformer for remote sensing spectral super-resolution. Int. J. Appl. Earth Obs. Geoinf. 2022, 109. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, D.; Sha, J.; Gao, L.; Liu, L.; Zhang, Y.; Rong, X. Spectral–Spatial–Temporal Transformers for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Ghosh, P.; Roy, S.K.; Koirala, B.; Rasti, B.; Scheunders, P. Hyperspectral Unmixing Using Transformer Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Rao, W.; Gao, L.; Qu, Y.; Sun, X.; Zhang, B.; Chanussot, J. Siamese Transformer Network for Hyperspectral Image Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–19. [Google Scholar] [CrossRef]
- Alexey, D.; Lucas, B.; Alexander, K.; Dirk, W.; Zhai, X.; Thomas; Unterthiner; Mostafa, D.; Matthias, M.; Georg, H.; et al. An image is worth 16 × 16 words. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Keskar, N.S.; Mudigere, D.; Nocedal, J.; Smelyanskiy, M.; Tang, P.T.P. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral–Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef]
- Ma, W.; Yang, Q.; Wu, Y.; Zhao, W.; Zhang, X. Double-Branch Multi-Attention Mechanism Network for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1307. [Google Scholar] [CrossRef]
- Roy, S.K.; Manna, S.; Song, T.; Bruzzone, L. Attention-Based Adaptive Spectral–Spatial Kernel ResNet for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7831–7843. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Liu, W.; Zhang, X.; He, F.; Xiong, Q.; Zan, X.; Liu, Z.; Sha, D.; Yang, C.; Li, S.; Zhao, Y. Open-air grape classification and its application in parcel-level risk assessment of late frost in the eastern Helan Mountains. ISPRS J. Photogramm. Remote Sens. 2021, 174, 132–150. [Google Scholar] [CrossRef]
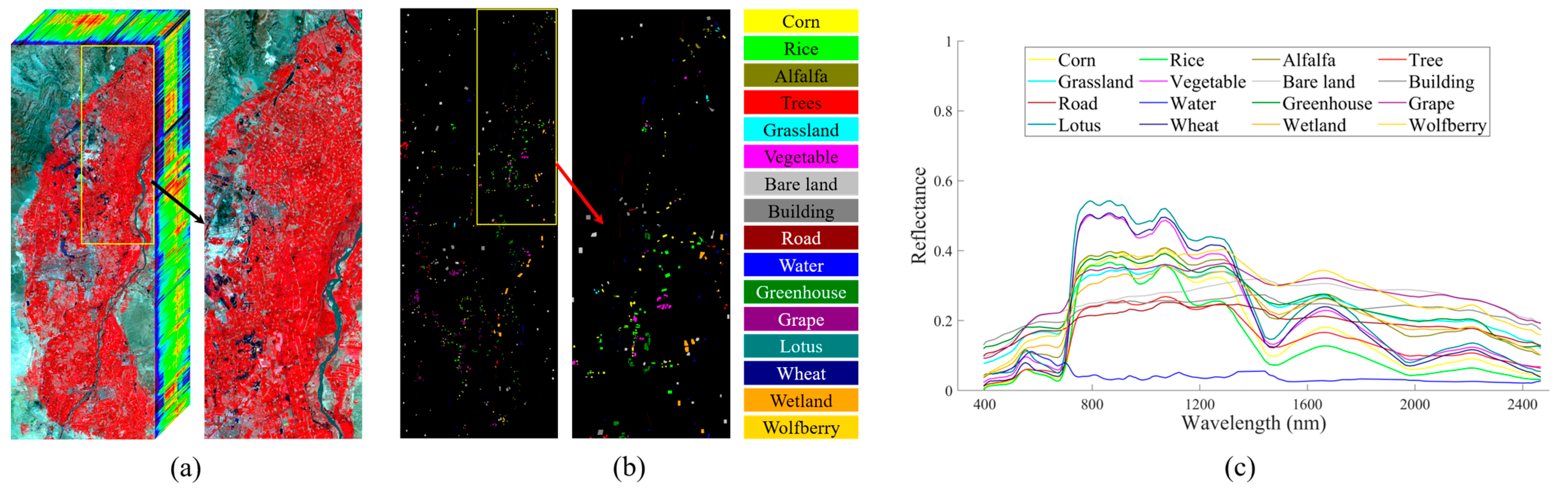




| Configurations | ZY1-02D AHSI | |
|---|---|---|
| VNIR | SWIR | |
| Wavelength | 400–1040 nm | 1005–2500 nm |
| Spectral resolution | 10 nm | 20 nm |
| Spatial resolution | 30 m | 30 m |
| Bands | 76 | 90 |
| Swath width | 60 km | 60 km |
| Class Number | Ground Object | Number of Samples |
|---|---|---|
| 1 | Corn | 13,686 |
| 2 | Rice | 13,241 |
| 3 | Alfalfa | 3480 |
| 4 | Trees | 9658 |
| 5 | Grassland | 2103 |
| 6 | Vegetable | 10,383 |
| 7 | Bare land | 26,306 |
| 8 | Building | 23,291 |
| 9 | Road | 4689 |
| 10 | Water | 7823 |
| 11 | Greenhouse | 14,368 |
| 12 | Grape | 13,113 |
| 13 | Lotus | 1545 |
| 14 | Wheat | 2413 |
| 15 | Wetland | 13,691 |
| 16 | Wolfberry | 825 |
| Total | 160,615 |
| Stage | CNN Branch | SSIF | Transformer Branch |
|---|---|---|---|
| Input | |||
| Spectral dimension reduction | Three-dimensional Conv [ Batch Norm ReLU | ||
| Output | |||
| Tokenization | Tokenization block | -- | -- |
| Output | -- | ||
| Depth 1 | Layer Norm MHSA-4 Layer Norm MLP-4 | -- | Two-dimensional Conv [] Batch Norm ReLU |
| Output | 16 ⇄ | ||
| Depth 2 | Layer Norm MHSA-4 Layer Norm MLP-4 | -- | Two-dimensional Conv [] Batch Norm ReLU |
| … | … | … | … |
| Output | 16 ⇄ | ||
| Depth m | Layer Norm MHSA-4 Layer Norm MLP-4 | -- | Two-dimensional Conv [] Batch Norm ReLU |
| Output | -- | ||
| Last Layer | Class token | Two-dimensional average pool | |
| CAW | |||
| Output | |||
| Class | Training Samples | CNN-Based Models | Attention-Based Models | Transformer-Based Models | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CDCNN | SSRN | FDSSC | DBMA | DBDA | A2S2K | ViT | BS2T | SCSTIN-2 | SCSTIN-4 | ||
| Corn | 136 | 97.39 | 98.18 | 97.98 | 97.37 | 98.73 | 98.76 | 98.76 | 98.75 | 99.00 ** | 98.84 * |
| Rice | 132 | 93.47 | 96.69 | 96.86 | 95.31 | 97.24 | 97.95 * | 95.19 | 97.58 | 96.40 | 98.06 ** |
| Alfalfa | 34 | 61.38 | 85.83 | 90.34 * | 82.63 | 88.44 | 87.80 | 82.02 | 89.74 | 89.63 | 91.45 ** |
| Trees | 96 | 79.03 | 91.49 | 92.26 | 88.75 | 92.20 | 92.29 | 88.79 | 91.67 | 95.96 ** | 95.64 * |
| Grassland | 21 | 23.22 | 82.10 * | 82.03 | 75.49 | 80.54 | 79.15 | 69.68 | 80.90 | 79.76 | 82.12 ** |
| Vegetable | 103 | 88.01 | 95.49 | 95.50 | 92.13 | 95.55 | 95.99 ** | 87.71 | 95.58 * | 94.82 | 95.26 |
| Bare land | 263 | 89.47 | 94.80 | 95.77 | 94.52 | 96.89 | 96.64 | 92.40 | 96.11 | 97.08 * | 97.39 ** |
| Building | 232 | 93.07 | 97.28 | 97.15 | 96.81 | 97.55 | 98.03 ** | 95.92 | 97.89 | 97.72 | 97.97 * |
| Road | 46 | 68.72 | 74.03 | 70.17 | 63.06 | 69.64 | 73.41 | 80.08 | 75.60 | 82.47 ** | 82.35 * |
| Water | 78 | 94.43 | 95.15 | 94.66 | 92.69 | 95.05 | 97.02 | 96.96 | 95.46 | 97.13 * | 97.53 ** |
| Greenhouse | 143 | 96.95 | 98.10 | 98.24 | 98.30 | 98.91 | 99.20 * | 98.48 | 99.29 ** | 98.98 | 99.14 |
| Grape | 131 | 92.02 | 97.61 | 97.66 | 95.76 | 98.09 | 98.34 * | 93.97 | 97.93 | 98.04 | 98.47 ** |
| Lotus | 15 | 46.89 | 89.19 | 91.39 * | 86.42 | 91.01 | 89.14 | 84.46 | 90.72 | 88.28 | 92.18 ** |
| Wheat | 24 | 10.50 | 96.57 | 98.33 * | 90.33 | 97.84 | 97.40 | 63.02 | 98.03 | 92.15 | 98.91 ** |
| Wetland | 136 | 92.22 | 96.60 | 98.76 * | 96.64 | 98.56 | 98.04 | 97.11 | 98.42 | 98.53 | 98.85 ** |
| Wolfberry | 8 | 9.88 | 94.63 | 94.35 | 89.39 | 93.72 | 93.65 | 71.12 | 95.82 * | 92.21 | 96.00 ** |
| OA (%) | 89.54 | 95.19 | 95.50 | 93.60 | 95.89 | 96.24 | 92.95 | 96.06 | 96.49 * | 96.98 ** | |
| AA (%) | 71.04 | 92.73 | 93.21 | 89.73 | 93.12 | 93.30 | 87.23 | 93.72 * | 93.67 | 95.01 ** | |
| Kappa | 86.18 | 94.78 | 95.13 | 92.92 | 95.45 | 95.84 | 92.19 | 95.64 | 96.11 * | 96.65 ** | |
| Mapping Time (min) | 6.80 ** | 21.57 | 26.53 | 32.61 | 31.77 | 28.68 | 55.00 | 75.79 | 9.49 * | 15.72 | |
| Models | Parameters | FLOPs (MMac) | Training Time/Epoch (s) |
|---|---|---|---|
| CDCNN | 2,181,136 | 15.00 | 0.30 |
| SSRN | 284,296 | 116.30 | 0.88 |
| FDSSC | 915,490 | 129.75 | 1.28 |
| DBMA | 449,309 | 211.42 | 2.80 |
| DBDA | 294,836 | 99.69 | 1.72 |
| A2S2K | 289,661 | 125.98 | 1.16 |
| ViT | 3,576,976 | 291.85 | 1.53 |
| BS2T | 282,904 | 78.19 | 2.86 |
| SCSTIN-2 | 193,522 | 15.68 | 0.46 |
| SCSTIN-4 | 372,212 | 30.32 | 0.67 |
| Models | Botswana | Indiana Pines | ||||||
|---|---|---|---|---|---|---|---|---|
| OA | AA | Kappa | Training Time/Epoch (s) | OA | AA | Kappa | Training Time/Epoch (s) | |
| CDCNN | 75.61 | 76.23 | 73.64 | 0.05 | 67.39 | 50.38 | 62.18 | 0.11 |
| SSRN | 91.91 | 91.80 | 91.23 | 0.11 | 94.58 | 93.42 | 93.82 | 0.42 |
| FDSSC | 93.99 | 93.75 | 93.49 | 0.12 | 95.58 | 90.06 | 94.95 | 3.00 |
| DBMA | 95.88 | 95.89 | 95.54 | 0.12 | 89.99 | 88.99 | 88.59 | 1.29 |
| DBDA | 95.86 | 95.79 | 95.51 | 0.13 | 96.07 | 95.92 | 95.53 | 0.73 |
| A2S2K | 92.63 | 92.71 | 92.01 | 0.11 | 93.74 | 90.28 | 92.85 | 0.50 |
| ViT | 91.99 | 92.38 | 91.32 | 0.14 | 86.65 | 87.28 | 84.74 | 0.52 |
| BS2T | 95.97 | 96.20 | 95.63 | 0.38 | 95.65 | 94.40 | 95.03 | 1.29 |
| SCSTIN-2 | 95.84 | 95.74 | 95.50 | 0.07 | 95.84 | 93.73 | 95.25 | 0.12 |
| SCSTIN-4 | 96.54 | 96.56 | 96.25 | 0.09 | 96.32 | 95.99 | 95.80 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, X.; Huang, C.; Qi, W.; Wang, J.; Yang, X.; Ding, S.; Tao, S. Spatial-Convolution Spectral-Transformer Interactive Network for Large-Scale Fast Refined Land Cover Classification and Mapping Based on ZY1-02D Satellite Hyperspectral Imagery. Remote Sens. 2023, 15, 3269. https://doi.org/10.3390/rs15133269
Wang Y, Zhang X, Huang C, Qi W, Wang J, Yang X, Ding S, Tao S. Spatial-Convolution Spectral-Transformer Interactive Network for Large-Scale Fast Refined Land Cover Classification and Mapping Based on ZY1-02D Satellite Hyperspectral Imagery. Remote Sensing. 2023; 15(13):3269. https://doi.org/10.3390/rs15133269
Chicago/Turabian StyleWang, Yibo, Xia Zhang, Changping Huang, Wenchao Qi, Jinnian Wang, Xiankun Yang, Songtao Ding, and Shiyu Tao. 2023. "Spatial-Convolution Spectral-Transformer Interactive Network for Large-Scale Fast Refined Land Cover Classification and Mapping Based on ZY1-02D Satellite Hyperspectral Imagery" Remote Sensing 15, no. 13: 3269. https://doi.org/10.3390/rs15133269
APA StyleWang, Y., Zhang, X., Huang, C., Qi, W., Wang, J., Yang, X., Ding, S., & Tao, S. (2023). Spatial-Convolution Spectral-Transformer Interactive Network for Large-Scale Fast Refined Land Cover Classification and Mapping Based on ZY1-02D Satellite Hyperspectral Imagery. Remote Sensing, 15(13), 3269. https://doi.org/10.3390/rs15133269








