Abstract
This paper investigates the design of waveforms for multiple-input multiple-output (MIMO) radar systems that can exploit multipath returns to enhance target detection performance. By making reasonable use of multipath information in the waveform design, MIMO radar can effectively improve the signal-to-interference and noise ratio (SINR) of the receiver under a constant modulus (CM) constraint. However, optimizing the waveform design under these constraints is a challenging non-linear and non-convex problem that cannot be easily solved using traditional methods. To overcome this challenge, we proposed a novel waveform design method for MIMO radar in multipath scenarios based on deep learning. Specifically, we leveraged the powerful nonlinear fitting ability of neural networks to solve the non-convex optimization problem. First, we constructed a deep residual network and transform the CM constraint into a phase sequence optimization problem. Next, we used the constructed waveform optimization design problem as the loss function of the network. Finally, we used the adaptive moment estimation (Adam) optimizer to train the network. Simulation results demonstrated that our proposed method outperformed existing methods by achieving better SINR values for the receiver.
1. Introduction
Radar systems often encounter multipath effects when detecting low-altitude targets. In such scenarios, the received returns consist not only of the backscattered line-of-sight (LOS) component, but also of the multipath returns component [1,2,3]. However, the presence of multipath returns can cause the received echo signal to fluctuate and even cancel, which will reduce the performance of target detection and parameter estimation. The early research has been devoted to suppressing the multipath returns [4,5,6,7]. In [4], multipath returns are regarded as clutter and suppressed.
However, the principle of multipath generation suggests that both the direct and multipath returns are coherent and contain target energy [8]. If the energy of the multipath returns can be accurately estimated and accumulated, it can improve the detection and tracking performance of the target [9,10,11].
Multiple-input multiple-output (MIMO) radar is a new type of radar system in which the transmitting antennas can transmit mutually independent signals [12,13,14,15,16]. By adaptively adjusting the MIMO radar transmission waveform for different tactical needs, the radar detection performance can be significantly improved in complex environments [17,18].
MIMO channel models can be broadly categorized into two types based on the methods used for their establishment. The first type is deterministic channel models [19,20,21], where precise information about the channel is obtained, and the wireless propagation is deemed as a deterministic process. This enables the determination of the spatio-temporal characteristics of any point in space. One study [19] employed a multilayer artificial neural network method to predict channel characteristics, thereby overcoming the low computational efficacy of traditional deterministic channel models. In contrast, the other type is statistical channel models [22,23,24,25], wherein the channel is regarded as a stochastic process, and a probability distribution is used to describe its temporal and spatial changes.
Depending on the specific application requirements of the radar, the waveform optimization design criteria for MIMO radar can be divided into four types. The first type of optimization criterion aims to maximize the signal-to-interference and noise ratio (SINR) [26,27,28,29]. Through appropriate waveform design, MIMO radar can maximize the SINR to improve target detection performance. In [29], an optimization design problem for maximizing the SINR based on constant modulus, similarity, and spectrum constraints was presented, and a semi-definite programming method was used to solve the problem. The second type of optimization criterion aims to maximize mutual information [30,31]. By maximizing the amount of mutual information between the corresponding target and the received waveform, the echo can exhibit more target characteristics. The third type of optimization criterion is the pattern matching problem [32,33]. The goal of this type of problem is to concentrate the transmitted beam energy of the MIMO radar in a specified airspace while minimizing the transmitted energy of the side lobes. The last type of optimization criterion is the orthogonal waveform design problem [34,35,36]. By reducing the correlation between the transmitted waveforms, the performance of matched filtering can be improved.
Combining high degrees of freedom in the MIMO radar waveform design with multipath exploitation [37,38,39] has shown great potential for further improving target detection performance. Most existing waveform design methods using multipath returns focus on slow time domain weight optimization for fixed waveform. In [37], the authors proposed to improve the detection performance of moving targets in multipath scenarios by optimizing the weights between different coherent processing intervals (CPIs), which they performed by using the orthogonal frequency division multiplexing (OFDM) waveform. On the other hand, in [38], the authors proposed an OFDM MIMO adaptive waveform design algorithm based on the mutual information criteria, thus aiming to select the best OFDM waveform by maximizing the mutual information between the state and measurement vectors. This particular type of slow time domain MIMO radar waveform can present challenges in scenarios that demand low range domain sidelobes, due to its high range domain sidelobes. Additionally, complex signal processing algorithms are required for slow time domain waveforms, which can increase system cost and overall complexity.
In recent years, there has been an increasing interest among radar technicians in exploring fast time domain waveform design methods that make use of multipath information. In [40], the transmit waveform and receive filter of a MIMO radar system were jointly designed to maximize the SINR of the receiver for multipath exploitation. In [41], the robust joint design of MIMO radar transmit waveform and receive filter banks was considered under the uncertainty of multipath returns information. This method addressed the limitation of requiring accurate prior knowledge of the multipath returns information in the method presented in [40]. The optimization problem discussed in the literature is non-convex and, therefore, cannot be solved directly. Existing research primarily relies on algorithms such as semi-definite relaxation algorithms to solve non-convex problems indirectly by relaxing the objective function or the constraint to a more tractable form. Oftentimes, these methods experience degradation in performance due to the relaxation process.
The constant modulus (CM) constraint is a common requirement for MIMO radar waveform design to avoid distortion of the transmit signal in near-saturated operating modes of the high frequency amplifier [42]. The objective of MIMO radar waveform design for multipath exploitation is to maximize the SINR of the receiver while adhering to the CM constraint of the transmit waveform. However, this problem is non-linear and non-convex, thereby making it difficult to solve with traditional optimization algorithms.
Deep learning, as a natural non-linear system [43], can effectively solve such problems. In this paper, we proposed a method to design MIMO radar fast time domain waveforms for multipath exploitation using deep learning. We used a residual neural network to directly solve the non-convex optimization problem, rather than indirectly solving it by relaxing the CM constraint or SINR function. Firstly, we transformed the CM constraint problem into an unconstrained phase optimization problem and took a random phase sequence as the input of the network. Next, the reciprocal of the SINR function of the received signal model in the multipath scenario was used as the loss function of the network. After training the network using an adaptive moment estimation (Adam) optimizer, the output of the network became the phase sequence of the designed waveform.
The simulation results demonstrated that the proposed algorithm made full use of the multipath energy, thus resulting in the waveform with higher SINR performance and detection probability compared to existing methods.
In summary, the main contributions of this article can be summarized as follows:
- A MIMO radar signal model was constructed for multipath scenarios;
- The MIMO radar waveform design problem for multipath exploitation was modeled as a maximizing SINR problem with the constant modulus constraint on the transmit waveform;
- Our proposed MIMO radar waveform design algorithm employed deep learning that utilized the non-linear fitting ability of neural networks to directly solve the non-convex waveform optimization problem.
The remainder of this paper is organized as follows. In Section 2, the multipath signal model for the MIMO radar is established. In Section 3, the MIMO radar waveform optimization design problem is formulated, and the waveform design algorithm based on deep learning is presented. Section 4 provides the simulation results to demonstrate the effectiveness of the proposed algorithm and the superiority of the designed waveform. Finally, Section 5 draws the conclusions.
Notations: In this paper, we use italic letters for scalars, bold italic lowercase letters for vectors, and bold italic uppercase letters for matrices. The superscripts , and denote the transpose, conjugate transpose, and conjugate, respectively. denotes the sets of complex matrices. denotes stacking the matrix by column. The symbol ⊗ denotes the Kronecker product. represents the calculation expectation, and denotes the trace of a square matrix. denotes the Frobeneous norm. and denote the real part and imaginary part of the vector , respectively.
2. Signal Model
A colocated MIMO radar consisting of transmitting antennas and receiving antennas was considered in the multipath scenario. The transmit waveform of the lth snapshot can be expressed as
where , L denotes the number of samples in the fast time domain. The transmit signal matrix can be represented by
It is assumed that the unit spacing in the transmitting antenna array and the receiving antenna array is set at half wavelength, that is, . The synthetic signal of the lth snapshot at the azimuth can be expressed as
where denotes the transmit steering vector.
The signal received by the MIMO radar receiver of the lth snapshot can be modeled as
where is the complex reflection coefficient, and denotes the receive steering vector .
As shown in Figure 1, it is assumed that there is a reflective surface in the scenario that results in multipath returns. When the radar system transmits signals to detect a target, the returns received by the radar array include not only direct returns, but also multipath returns from the reflector. The transmit–receive path of direct returns is . Multipath returns include the multipath of the transmission process and the multipath of the reception process, namely, and . In addition, there are returns from the clutter area, namely . The received signal model is given by
where , , , and represent the direct returns, multipath returns, clutter returns, and noise, respectively.
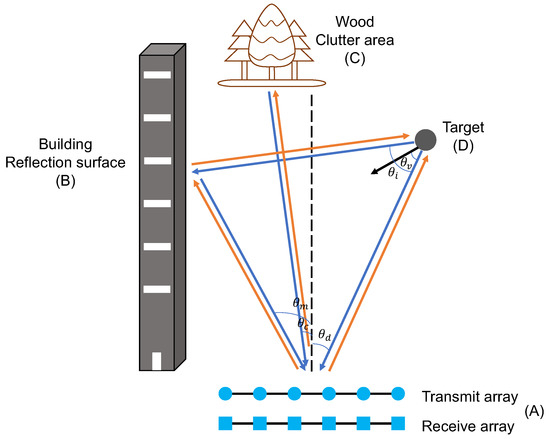
Figure 1.
Multipath scenario diagram.
2.1. Direct Returns Model
Assuming that the target velocity and the angle between the target motion direction and LOS are v and , respectively, the Doppler frequency of the direct returns can be expressed as
where is the wavelength of the transmit waveform. The shift matrix is defined as , which is represented as
The direct returns model of the pth pulse can be expressed as
where is the complex scattering coefficient of the target, and and denote the transmit steering vector and receive steering vector in the target azimuth , respectively.
Assuming that the radar transmits P pulses in a CPI, we have
where . The direct return model vector can be expressed as
where , .
2.2. Multipath Returns Model
The Doppler frequency of the multipath returns can be given by
where is the angle between and .
For the multipath returns, the transmit steering vector and the receive steering vector will point in different azimuths due to the reflective surface. Taking into account both the receiving and transmitting multipath, the received signal model of the pth pulse can be represented as
where and are the complex reflection coefficient of the surface and the arrival azimuth of multipath returns, respectively, and is the relative fast time delay of the multipath path with respect to the direct path.
Considering the CPI, the multipath returns model can finally be expressed as
where .
2.3. Clutter
In radar operations, there will inevitably be reflections from other objects in the scene that are not desired, which will have a noticeable effect on the received returns. The clutter returns of the pth pulse can be expressed as
where is the complex backscattering coefficient of the clutter area, is the azimuth of the clutter area, and is the relative fast time delay of the clutter path with respect to the direct path. The clutter signal model can be further expressed as
where denotes a row unit vector of length P.
2.4. Noise
There is also signal-independent interference in the received data, which is caused by system noise. Typically, signal-independent noise is modeled as a Gaussian distribution.
3. Methods
3.1. Problem Formulation
The SINR is a commonly used optimization criterion that is closely related to target detection and parameter estimation performance. In our approach, we maximized the SINR in multipath scenarios to optimize the waveform design. Unlike common methods that treat multipath returns as clutter and suppress them, we leveraged the information from the multipath returns to improve the SINR of the output.
In order to calculate the SINR, the signal power of the received direct returns, multipath returns, clutter, and noise should be calculated separately and expressed as , , , and .
Based on the direct returns model, the signal power of the direct returns can be expressed as
where .
The signal power of the multipath returns consists of two parts, namely, the signal power of the transmitting multipath returns and the signal power of the receiving multipath returns, which can be expressed as
where , , and
.
The signal power of the clutter is given by
where .
The noise power can be expressed as
where represents the variance of Gaussian white noise.
To sum up, the output SINR can be expressed as
where , , and .
The aim of this paper was to optimize the waveform design by maximizing the output SINR with the constant modulus constraint. Therefore, the waveform optimization problem in this paper can be summarized as
3.2. The Proposed Design Method
The problem of optimizing MIMO radar waveform to maximize SINR with a CM constraint is challenging due to the non-convex nature of both the SINR function and the CM constraint. This is a high-dimensional and non-convex problem that cannot be solved optimally using conventional methods. However, deep learning models are highly suitable for solving this problem, since they are high-dimensional and non-linear systems.
As the residual network can effectively tackle the issues of gradient disappearance and explosion while increasing the number of network layers [44], we constructed a deep residual network to use its non-linear fitting ability to solve the nonconvex problem of maximizing SINR with the CM constraint. The optimized training network designed in this paper is displayed in Figure 2 and comprises five modules: input, forward propagation, output, loss function, and Adam optimizer.
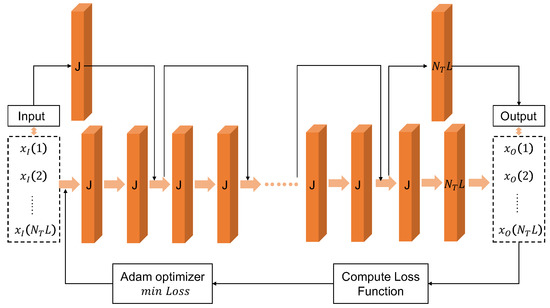
Figure 2.
Constructed residual network.
3.2.1. Input and Output
A randomly generated normalized phase sequence of length was used as the input of the network and can be represented as
where .
The output of the network is a normalized phase sequence and can be represented as
where .
3.2.2. Forward Propagation Module
The constructed residual network consists of 10 residual blocks, each comprising two fully connected neural network layers. The first layer of the first residual block is a neural network with weight matrix dimension of , where the number of neurons is J. The second layer is a neural network with weight matrix dimension of and J neurons.
The first layer of the last residual block is a neural network with weight matrix dimension of , with J neurons. The second layer is a neural network with weight matrix dimension of , with J neurons.
To achieve dimension matching of the residual network, there is a network with weight matrix dimension of and J neurons between the input and output of the first residual block, and there is a network with weight matrix dimension of and J neurons between the input and output of the last residual block.
The other residual blocks in between consist of two layers of neural networks with weight matrix dimension of and J neurons.
3.2.3. Loss Function
The output of forward propagation is a normalized phase sequence . Assuming , the original signal from one forward propagation output can be expressed as . By the inverse process of vectorizing the waveform columns, an output signal matrix of dimension can be obtained, where the lth column is the signal of the lth snapshot.
As the residual network cannot directly handle complex problems, an algebraic transformation of the original objective function is necessary. Assuming and , the synthetic signal of the lth snapshot of MIMO radar in azimuth can be expressed as
The direct returns, multipath returns, and clutter of the lth snapshot of the pth pulse can be expressed as
Considering the delay of multipath returns and clutter relative to direct returns, the direct returns, multipath returns, and clutter of the pth pulse can be expressed as
where denotes a column zero vector of length L. Taking into account the coherent pulse interval P, the direct returns, multipath returns, and clutter can be finally expressed as
The signal power of the direct returns, multipath returns, clutter, and noise can be given by
The loss function of the network is set to be the inverse of the objective function in the above optimization problem and can be expressed as
3.2.4. Adam Optimizer
The optimizer is a tool to guide the neural network for parameter updates. After the neural network achieves forward propagation once and calculates the loss function, the optimizer is needed to perform backward propagation to achieve the update of the network parameters. Adam optimizer is a classical deep learning optimizer based on gradient descent algorithm, combining the ideas of momentum method and adaptive learning rate, with the advantage of adaptively adjusting the learning rate to adapt to different data and models.
The Adam optimizer computes first-order moment estimates and second-order moment estimates of the gradient in each iteration, thus updating the learning rate and network parameters.
The gradient parameter of the loss function at the tth iteration with respect to the network weights can be expressed as
The first-order moments and second-order moments of the network weights in the tth iteration can be expressed as
where and are two hyperparameters of the Adam optimizer, usually set to and .
At the beginning of the iteration, there is a deviation of and to the initial value, so it is necessary to correct the deviation of the first-order moments and second-order moments. The corrected first-order moments and second-order moments can be expressed as
We iterate over the network weights, and the network weight parameters can be updated and represented as follows
where refers to a small constant used for numerical stabilization, usually set to .
We summarize the proposed algorithm in Algorithm 1.
| Algorithm 1: Proposed algorithm. |
Input: Random normalized phase sequence , learning rate of Adam , number of iterations E. Output: Desired waveform phase sequence . Set , Adam learning rate set to ; 1: Construct forward propagation module according to Figure 2; 2: Input to the forward propagation module to obtain output ; 5: Optimizing loss function with Adam optimizer; 6: If , stop and output the result. Otherwise, update e, i.e., , and back to the step 2. |
3.2.5. Complexity Analysis
To evaluate the complexity of our proposed model, we measured its time complexity using floating-point arithmetic, FLOPs, and its spatial complexity using parameter quantities, Params. Assuming that the input of the network is a sequence with a length of 320, the complexity of the proposed model is shown in Table 1.

Table 1.
The complexity of the proposed model.
4. Results and Discussion
In this section, a series of simulations were conducted to verify the effectiveness of the proposed algorithm and the superiority of the designed waveform. All simulations were analyzed on a PC with a i7-12700H CPU and a GTX3080 GPU and 16 GB RAM. The neural network in this article was processed with Python 3.7 and pytorch 1.12 and ran on GPU.
The MIMO radar employed a transceiver co-array that consisted of a uniform line array with half-wavelength spacing and a wavelength of . The simulation parameters shown in Table 2 were used in the subsequent simulations.

Table 2.
Simulation Parameters.
4.1. Convergence
This section analyzes the convergence of the proposed algorithm. The learning rate of the network was , and the number of iterations was . The number of optimized signals was , and the number of snapshots for each signal was .
As illustrated in Figure 3, the curve of the loss function gradually decreased as the number of training iterations increased. Particularly, during the first 10 training sessions, the loss function decreased rapidly. After 20 training sessions, the loss function started to converge and eventually approached zero, thus indicating that the proposed algorithm can converge to the global optimal solution.
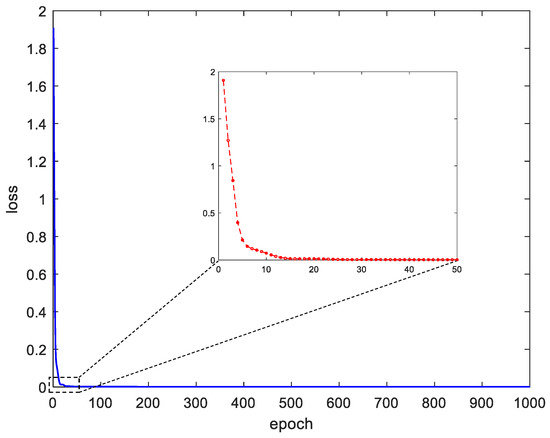
Figure 3.
Loss function curve.
4.2. SINR Performance
In this section, the learning rate of the network and the number of iterations were and . The number of optimized signals was , and the number of snapshots for each signal was . The interference-to-noise ratio was . The set of SNR were [−20 dB, −15 dB, −10 dB, −5 dB, 0 dB, 5 dB, 10 dB, 15 dB, 20 dB].
To evaluate the SINR performance of the waveform designed by the proposed algorithm, we compared it with the SINR performance of the waveforms designed using the multipath suppression algorithm [4] and the CAN algorithm [34] at different SNR conditions, as shown in Figure 4. It can be seen that the proposed algorithm achieved a higher SINR at both low SNR and high SNR. The SINR performance of the proposed algorithm was more than 2 dB higher than that of the multipath suppression algorithm at different SNR conditions. Because the purpose of the CAN algorithm is to generate orthogonal waveforms, the SINR performance of the generated waveform was much worse than that of the proposed algorithm and the multipath suppression algorithm.
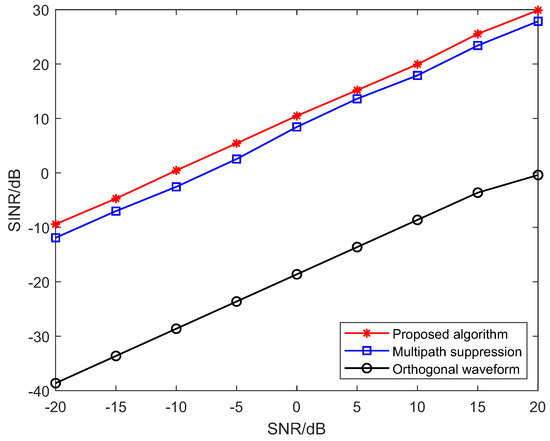
Figure 4.
Output SINR versus the SNR.
To further highlight the superiority of the SINR performance of the waveform generated by the proposed algorithm, we conducted a comparative analysis assuming SNR = 20 dB and . Specifically, we compared the SINR performance of the proposed algorithm against an existing multipath exploitation algorithm [40] and a multipath suppression algorithm under these conditions. As shown in Table 3, the SINR performance of the proposed algorithm was higher than that of the multipath exploitation algorithm and multipath suppression algorithm.

Table 3.
SINR performance of the proposed algorithm, existing multipath exploitation algorithm, and multipath suppression algorithm.
4.3. Transmit Beampattern
In this section, we set the learning rate of the network to , and we set the number of iterations to . The number of optimized signals was , and the number of snapshots for each signal was . The signal-to-noise ratio was SNR = 20 dB, and the interference-to-noise ratio was INR = 20 dB. The azimuth ofthe target, multipath, and clutter were , , and . The azimuth ranged from to with a grid point spacing of .
Figure 5 shows a comparison between the transmit beampattern generated by the proposed algorithm and the multipath suppression algorithm. As can be observed from the figure, the transmit beampattern generated by the proposed algorithm forms peaked in the target and multipath azimuths, while creating a deep notch in the clutter azimuth. In contrast, the multipath suppression algorithm treated the multipath returns as clutter, thus resulting in deep notches in both the multipath azimuth and clutter azimuth. It is evident from the transmit beampattern generated by the proposed algorithm and the multipath suppression algorithm that the multipath suppression algorithm achieved a suppression level of approximately −40 dB for both multipath returns and clutter. On the other hand, the proposed algorithm achieved a significantly superior suppression level of −70 dB for clutter energy.
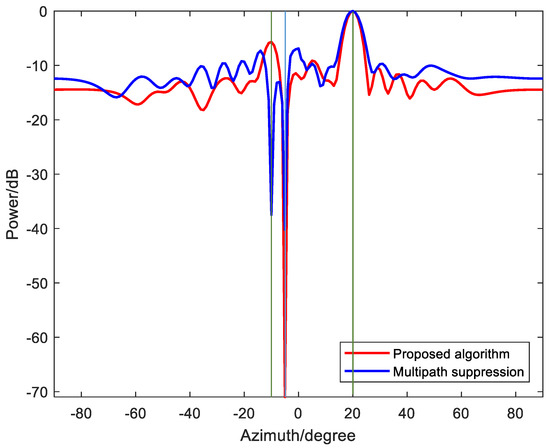
Figure 5.
The transmit beampattern.
4.4. Detection Probability
In this section, we compared the detection performance of the waveforms generated by the proposed algorithm and multipath suppression algorithm under different specular reflection coefficients. The learning rate of the network was , and the number of iterations was . The number of optimized signals was , and the number of snapshots for each signal was . The set of SNR were [−20 dB, −15 dB, −10 dB, −5 dB, 0 dB, 5 dB, 10 dB, 15 dB, 20 dB], and the interference-to-noise ratio was INR = 20 dB. The set of specular reflection coefficients included the values of 0.7, 0.8, and 0.9.
The corresponding detection probabilities can be calculated by
where denotes the Marcum-Q function [45], and denotes the false alarm probability.
Assuming the false alarm probability , the simulation results are shown in Figure 6. The proposed algorithm exhibited superior detection probability performance compared to the multipath suppression algorithm under the same input of SNR, as is evidenced by its higher value.
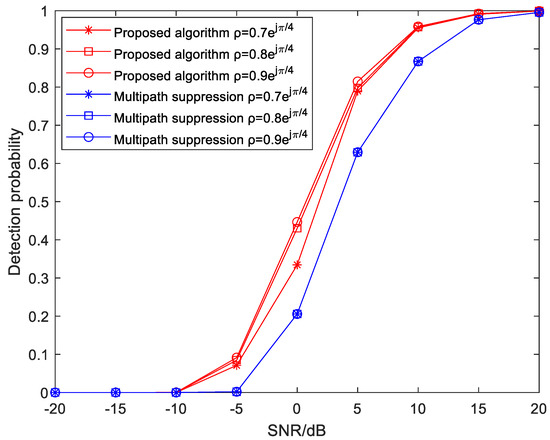
Figure 6.
Comparisons of the detection probability.
Regarding the proposed algorithm for multipath exploitation, the detection probability increased with the increase in multipath reflection intensity. In contrast, for the multipath suppression algorithm, the detection probability was not significantly affected by the multipath reflection intensity, as the multipath returns were treated as clutter and were suppressed by the algorithm.
To confirm the impact of the false alarm probability on the detection probability performance of the proposed algorithm, we evaluated and compared the detection probability performance of the proposed algorithm with existing and multipath exploitation algorithm and a multipath suppression algorithm under different false alarm probabilities. We set the signal-to-noise ratio to and the number of optimized signals to . As shown in Table 4, the detection probability of the proposed algorithm was higher than that of the multipath exploitation algorithm and multipath suppression algorithm under different false alarm probabilities.

Table 4.
The detection probability performance under different false alarm probabilities.
4.5. Effect of Initial Input
In this section, we set the learning rate of the network to and the number of iterations to . The number of optimized signals was , and the number of snapshots for each signal was . The signal-to-noise ratio was , and the interference-to-noise ratio was .
We compared the SINR performance of the proposed algorithm using two different initial inputs: a random normalized phase sequence and a sequence optimized by the CAN algorithm. As shown in Figure 7, the proposed algorithm was insensitive to the initial input. For both cases, where the initial input was a random normalized sequence and a sequence optimized by the CAN algorithm, the SINR performance of the proposed algorithm had an acceptable error at the beginning of training and tended to become consistent with the increase in training iterations.

Figure 7.
SINR of different initial inputs.
4.6. Effect of Number of Transmitting Antennas
In this section, we compared the SINR performance of the proposed algorithm with different numbers of transmit antennas. We set the learning rate of the network to , and the number of iterations to . The number of snapshots for each signal was . The signal-to-noise ratio was , and the interference-to-noise ratio was . The set of the number of transmit antennas were [4, 8, 12, 16, 20, 24, 28].
As shown in Figure 8, the SINR performance of the proposed algorithm increased with the number of transmit array antennas . This is because the increase in the number of transmit antennas provided higher degrees of freedom (DOFs), which enabled the algorithm to exploit the multipath reflections better and achieve a higher SINR. This implies that augmenting the number of transmit antennas in the proposed algorithm leads to a better detection performance of the MIMO radar. Nonetheless, the increase in the number of transmit antennas may also escalate the cost and computational complexity of MIMO radar systems, thereby necessitating a comprehensive consideration in choosing an appropriate number of transmit antennas for practical applications.
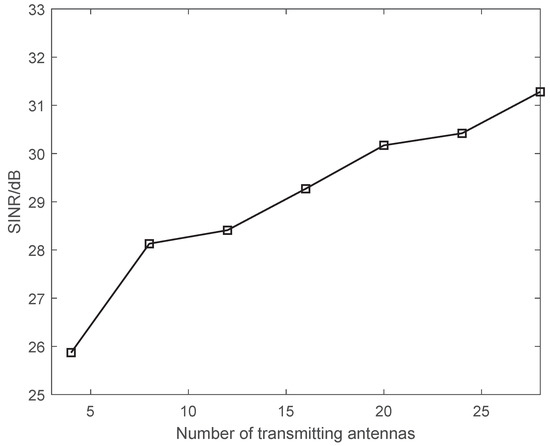
Figure 8.
SINR with different numbers of transmitting antennas.
4.7. The Phase of the Waveform
In this section, we plotted the phase of the waveform optimized by the proposed algorithm under different numbers of transmit antennas. We set the learning rate of the network to and the number of iterations to . The number of snapshots for each signal was . The signal-to-noise ratio was , and the interference-to-noise ratio was .
As shown in Figure 9, the phase of the waveform optimized by the proposed algorithm varied between 0 and 2 for different numbers of transmit antennas. This result demonstrates the effectiveness of the algorithm in optimizing the transmission waveform.
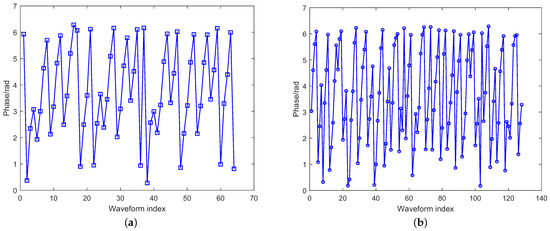
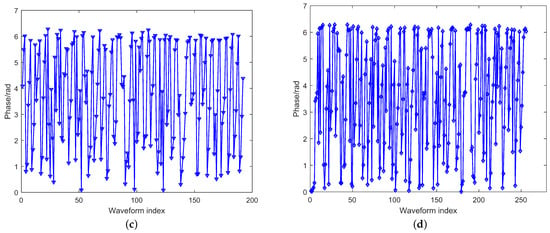
Figure 9.
Phase of the optimized waveform with different numbers of transmit antennas. (a) , (b) , (c) , (d) .
5. Conclusions
In conclusion, this paper presents a novel approach for designing transmit waveforms for multipath exploitation using deep learning. We established the MIMO radar signal model for scenarios where a multipath exists and proposes an optimization objective that maximizes the receiver’s SINR with a CM constraint. To solve this non-convex problem, we developed a deep residual optimization training network that directly and optimally solved the problem without relaxation.
Our simulation results demonstrate that the proposed algorithm effectively utilized the energy of multipath reflections, thus outperforming existing methods in terms of SINR performance and detection probability. We also showed that the proposed algorithm was robust to different initial inputs and benefited from the increased degrees of freedom provided by additional transmit antennas.
Overall, our research has important implications for MIMO radar applications, where optimizing waveform design can significantly impact the accuracy and reliability of target detection. Future work could explore the generalization of our approach to more complex scenarios, such as those with unknown multipath information or multi-target situations.
Author Contributions
Conceptualization, Z.Z. and Y.Z.; methodology, Y.Z.; software, Z.Z.; validation, Z.Z., Y.Z. and X.P.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Y.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z., X.P., H.X. and Y.Z.; visualization, J.M., J.C. and Y.S.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant U2133216.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barton, D.K. Low-angle radar tracking. Proc. IEEE 1974, 62, 687–704. [Google Scholar] [CrossRef]
- White, W.D. Low-Angle Radar Tracking in the Presence of Multipath. IEEE Trans. Aerosp. Electron. Syst. 1974, 10, 835–852. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Kumar, A.; Blair, W.D.; Groves, G.W. Tracking low elevation targets in the presence of multipath propagation. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 973–979. [Google Scholar] [CrossRef]
- Hickman, G.; Krolik, J.L. MIMO GMTI radar with multipath clutter suppression. In Proceedings of the 2010 IEEE Sensor Array and Multichannel Signal Processing Workshop, Jerusalem, Israel, 4 October 2010; pp. 65–68. [Google Scholar]
- Xin, J.; Sane, A. Linear prediction approach to direction estimation of cyclostationary signals in multipath environment. IEEE Trans. Signal Process. 2001, 49, 710–720. [Google Scholar] [CrossRef]
- Xin, J.; Sane, A. Direction estimation of coherent narrowband signals using spatial signature. In Proceedings of the 2002 IEEE Sensor Array and Multichannel Signal Processing Workshop, Rosslyn, VA, USA, 6 August 2002; pp. 523–527. [Google Scholar]
- Yu, J.; Krolik, J. MIMO adaptive beamforming for nonseparable multipath clutter mitigation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2604–2618. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Foglia, G.; Orlando, D. Diffuse Multipath Exploitation for Adaptive Radar Detection. IEEE Trans. Signal Process. 2015, 63, 1268–1281. [Google Scholar] [CrossRef]
- Hayvaci, H.T.; De Maio, A.; Erricolo, D. Improved detection probability of a radar target in the presence of multipath with prior knowledge of the environment. IET Radar Sonar Navig. 2013, 7, 36–46. [Google Scholar] [CrossRef]
- Rong, Y.; Aubry, A.; De Maio, A.; Tang, M. Automatically tunable AMF for radar detection in diffuse multipath. In Proceedings of the 2020 IEEE Sensor Array and Multichannel Signal Processing Workshop, Hangzhou, China, 8 June 2020; pp. 1–5. [Google Scholar]
- Yilmaz, S.H.G.; Hayvaci, H.T. Multipath exploitation radar with adaptive detection in partially homogeneous environments. IET Radar Sonar Navig. 2020, 14, 1475–1482. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference, Philadelphia, PA, USA, 29 April 2004; pp. 71–78. [Google Scholar]
- Sun, H.; Brigui, F.; Lesturgie, M. Analysis and comparison of MIMO radar waveforms. In Proceedings of the 2014 International Radar Conference, Lille, France, 13 October 2014; pp. 1–6. [Google Scholar]
- Stoica, P.; Li, J.; Xie, Y. On Probing Signal Design For MIMO Radar. IEEE Trans. Signal Process. 2007, 55, 4151–4161. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; Xu, L.; Roberts, W. On Parameter Identifiability of MIMO Radar. IEEE Signal Process. Lett. 2007, 14, 968–971. [Google Scholar]
- Yu, X.; Qiu, H.; Yang, J.; Wei, W.; Cui, G.; Kong, L. Multi-spectrally constrained MIMO radar beampattern design via sequential convex approximation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2935–2949. [Google Scholar] [CrossRef]
- Raei, E.; Alaee-Kerahroodi, M.; Shankar, M.B. Spatial-and range-ISLR trade-off in MIMO radar via waveform correlation optimization. IEEE Trans. Signal Process. 2021, 69, 3283–3298. [Google Scholar] [CrossRef]
- Qian, J.Y.; Zheng, G.X.; Saleem, A. Channel modeling based on multilayer artificial neural network in metro tunnel environments. ETRI J. 2022, 1–13. [Google Scholar] [CrossRef]
- Jia, M.H.; Zheng, G.X.; Ji, W.L. A new model for predicting the characteristic of RF propagation in rectangular tunnel. In Proceedings of the 2008 IEEE International Conference on Personal Wireless Communications Conference Proceedings, Dalian, China, 10 September 2008; pp. 1–4. [Google Scholar]
- Kermani, M.H.; Kamarei, M. A ray-tracing method for predicting delay spread in tunnel environments. In Proceedings of the 2000 IEEE International Conference on Personal Wireless Communications Conference Proceedings, Hyderabad, India, 17 December 2000; pp. 538–542. [Google Scholar]
- Zhao, X.W.; Du, F.; Geng, S.Y.; Sun, N.Y.; Zhang, Y.; Fu, Z.H.; Wang, G.J. Neural network and GBSM based time-varying and stochastic channel modeling for 5G millimeter wave communications. China Commun. 2019, 16, 80–90. [Google Scholar] [CrossRef]
- Sun, N.; Geng, S.; Li, S.; Zhao, X.; Wang, M.; Sun, S. Channel modeling by RBF neural networks for 5G Mm-wave communication. In Proceedings of the 2018 IEEE/CIC International Conference on Communications in China, Beijing, China, 12 August 2018; pp. 768–772. [Google Scholar]
- Ertel, R.B.; Reed, J.H. Angle and time of arrival statistics for circular and elliptical scattering model. IEEE J. Sel. Areas Commun. 1999, 17, 1829–1840. [Google Scholar] [CrossRef]
- Petrus, P.; Rappaport, T.S. Geometrical-based statistical macrocell channel model for mobile environments. IEEE Trans. Commun. 2002, 50, 495–502. [Google Scholar] [CrossRef]
- Li, J.; Guerci, J.R.; Xu, L. Signal Waveform’s Optimal Under Restriction Design for Active Sensing. In Proceedings of the 2006 IEEE Sensor Array and Multichannel Signal Processing Workshop, Waltham, MA, USA, 12 July 2006; pp. 382–386. [Google Scholar]
- Tang, B.; Li, J.; Liang, J. Alternating direction method of multipliers for radar waveform design in spectrally crowded environments. Signal Process. 2018, 142, 398–402. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Kong, L.; Li, J.; Gui, G. Constrained Waveform Design for Colocated MIMO Radar With Uncertain Steering Matrices. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 356–370. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Piezzo, M.; Farina, A. Radar waveform design in a spectrally crowded environment via nonconvex quadratic optimization. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1138–1152. [Google Scholar] [CrossRef]
- Yang, Y.; Blum, R.S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 330–343. [Google Scholar] [CrossRef]
- Naghsh, M.M.; Modarres-Hashemi, M.; Shahbazpanahi, S. Unified Optimization Framework for Multi-Static Radar Code Design Using Information-Theoretic Criteria. IEEE Trans. Signal Process. 2013, 61, 5401–5416. [Google Scholar] [CrossRef]
- Yu, X.; Cui, G.; Zhang, T. Constrained Transmit Beampattern Design for Colocated MIMO Radar. Signal Process. 2017, 144, 145–154. [Google Scholar] [CrossRef]
- Wang, Y.C.; Wang, X.; Liu, H. On the Design of Constant Modulus Probing Signals for MIMO Radar. IEEE Trans. Signal Process. 2012, 60, 4432–4438. [Google Scholar] [CrossRef]
- Stoica, P.; He, H.; Li, J. New Algorithms for Designing Unimodular Sequences with Good Correlation Properties. IEEE Trans. Signal Process. 2009, 57, 1415–1425. [Google Scholar] [CrossRef]
- He, H.; Stoica, P.; Li, J. Designing Unimodular Sequence Sets with Good Correlations—Including an Application to MIMO Radar. IEEE Trans. Signal Process. 2009, 57, 4391–4405. [Google Scholar] [CrossRef]
- Li, Y.; Vorobyov, S.A. Fast Algorithms for Designing Unimodular Waveform(s) with Good Correlation Properties. IEEE Trans. Signal Process. 2018, 66, 1197–1212. [Google Scholar] [CrossRef]
- Sen, S.; Hurtado, M.; Nehorai, A. Adaptive OFDM radar for detecting a moving target in urban scenarios. In Proceedings of the 2009 International Waveform Diversity and Design Conference, Kissimmee, FL, USA, 8 February 2009; pp. 268–272. [Google Scholar]
- Sen, S.; Nehorai, A. OFDM MIMO radar with mutual-information waveform design for low-grazing angle tracking. IEEE Trans. Signal Process. 2010, 58, 3152–3162. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. Adaptive OFDM radar for target detection in multipath scenarios. IEEE Trans. Signal Process. 2011, 59, 78–90. [Google Scholar] [CrossRef]
- Xu, Z.; Fan, C.; Huang, X. MIMO Radar Waveform Design for Multipath Exploitation. IEEE Trans. Signal Process. 2021, 69, 5359–5371. [Google Scholar] [CrossRef]
- Fan, C.; Xie, Z.; Wang, J.; Xu, Z.; Huang, X. Robust MIMO Waveform Design in the Presence of Unknown Mutipath Return. Remote Sens. 2023, 14, 4356. [Google Scholar] [CrossRef]
- Imani, S.; Ghorashi, S.A. Sequential quasi-convex-based algorithm for waveform design in colocated multiple-input multiple-output radars. IET Signal Process. 2023, 10, 309–317. [Google Scholar] [CrossRef]
- Hertz, J.A. Introduction to the Theory of Neural Computation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27 June 2016; pp. 770–778. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw Hill: New York, NY, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).