Spatial Probability Characteristics of Waves Generated by Polar Lows in Nordic and Barents Seas
Abstract
1. Introduction
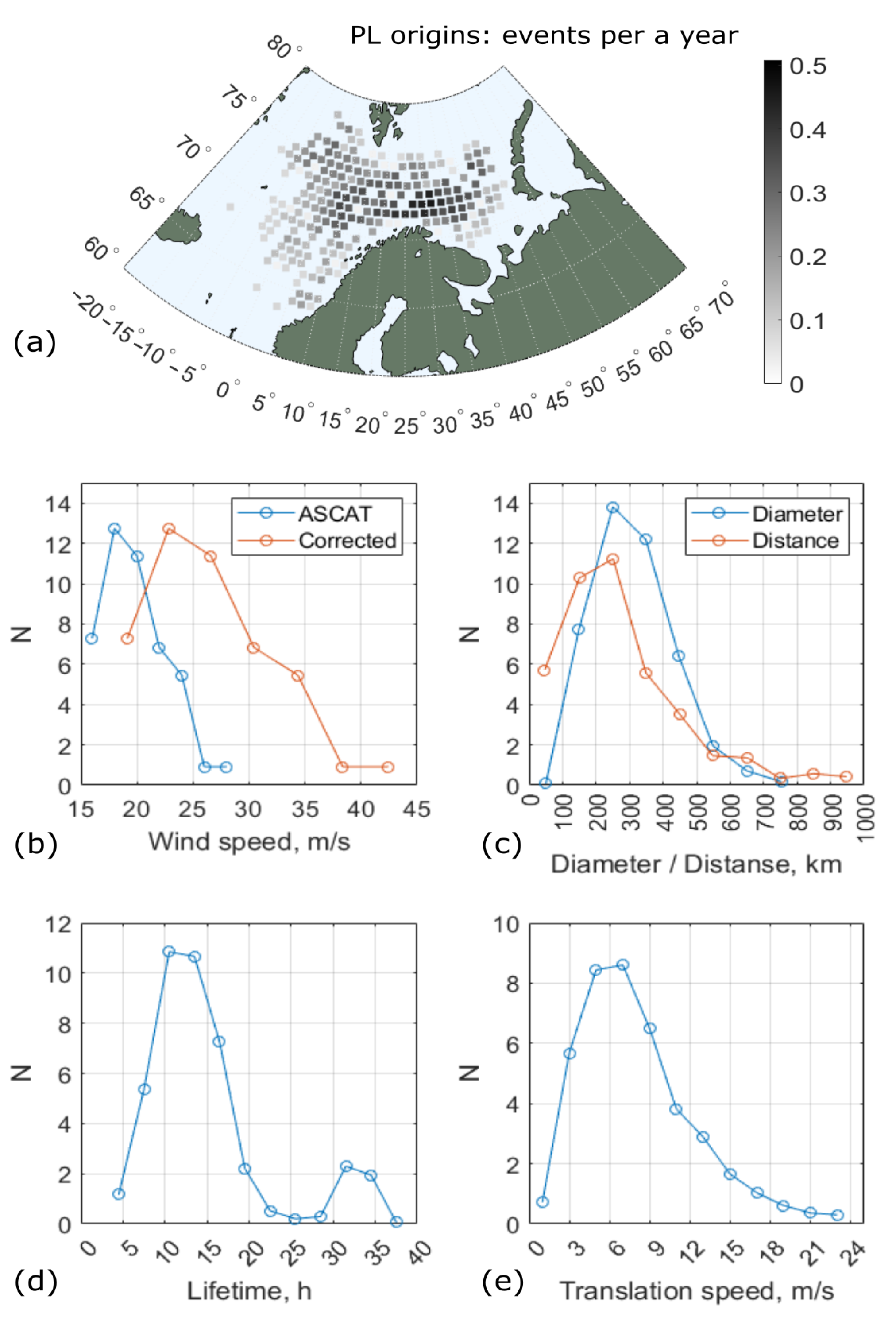
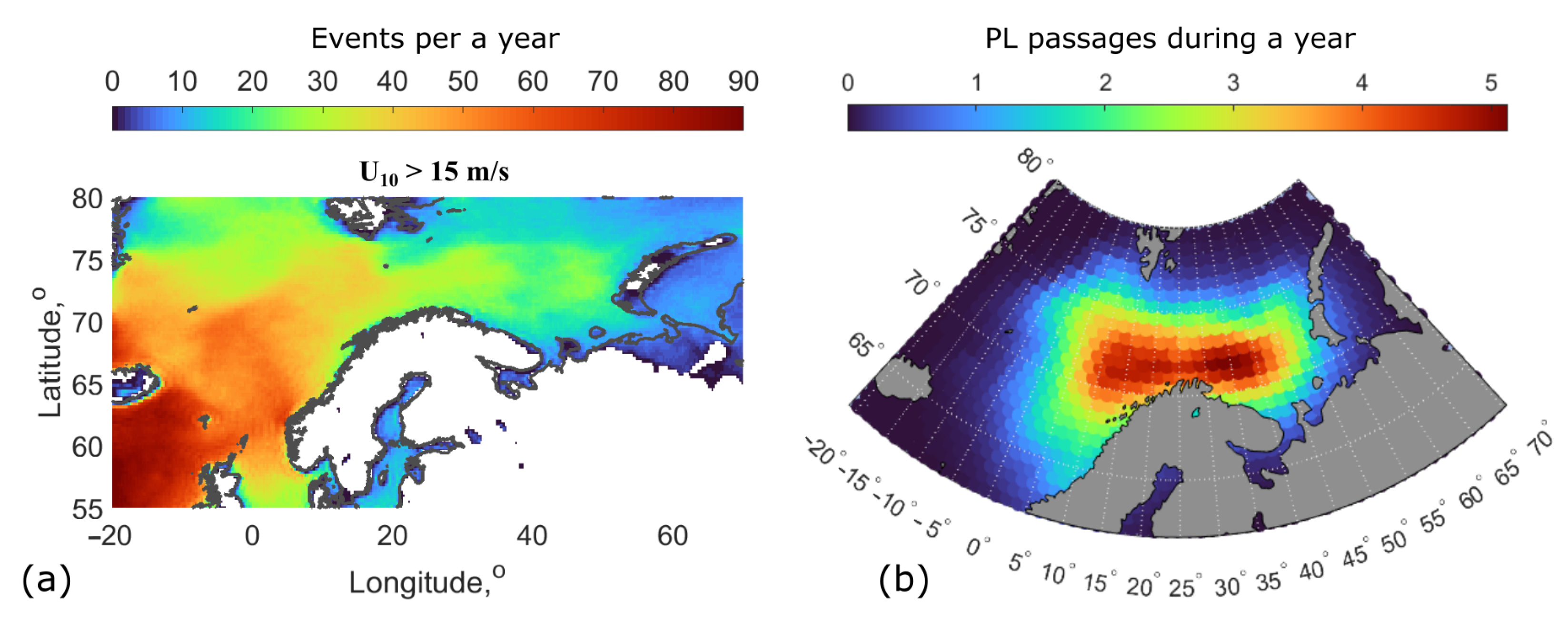
2. Data: PL Climatology
3. Method
3.1. Model of Wave Evolution
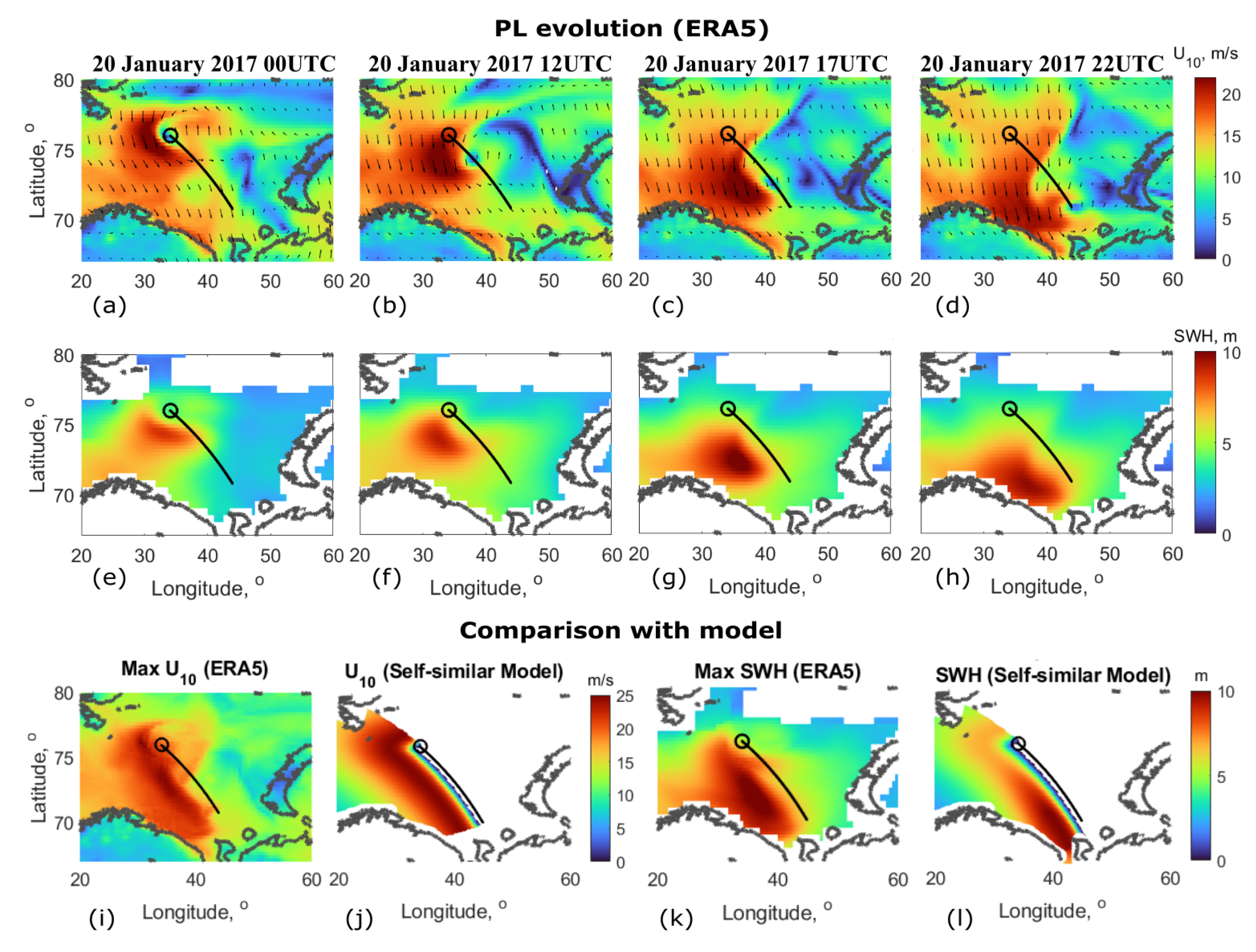
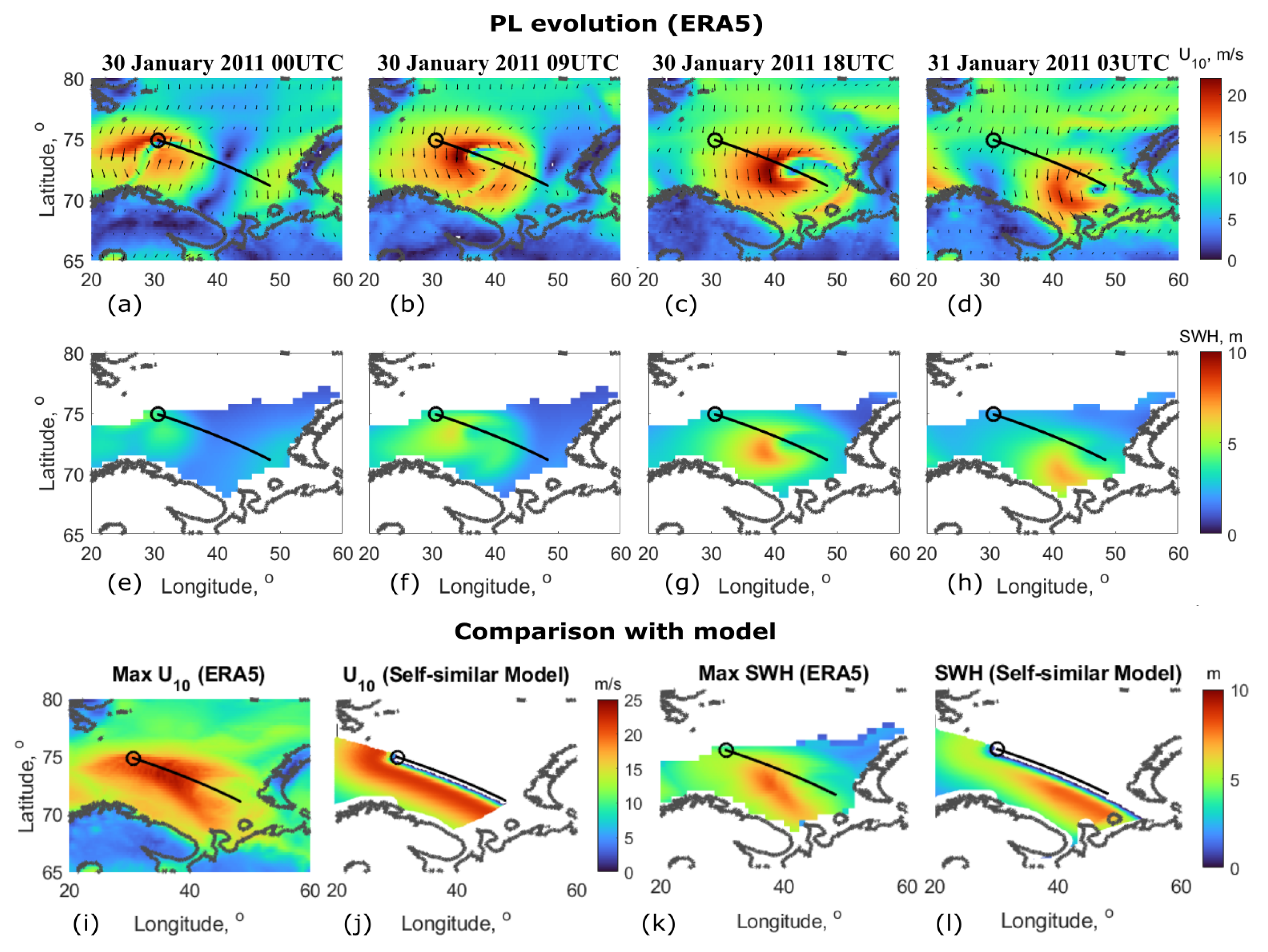
3.2. Examples of Model Performance
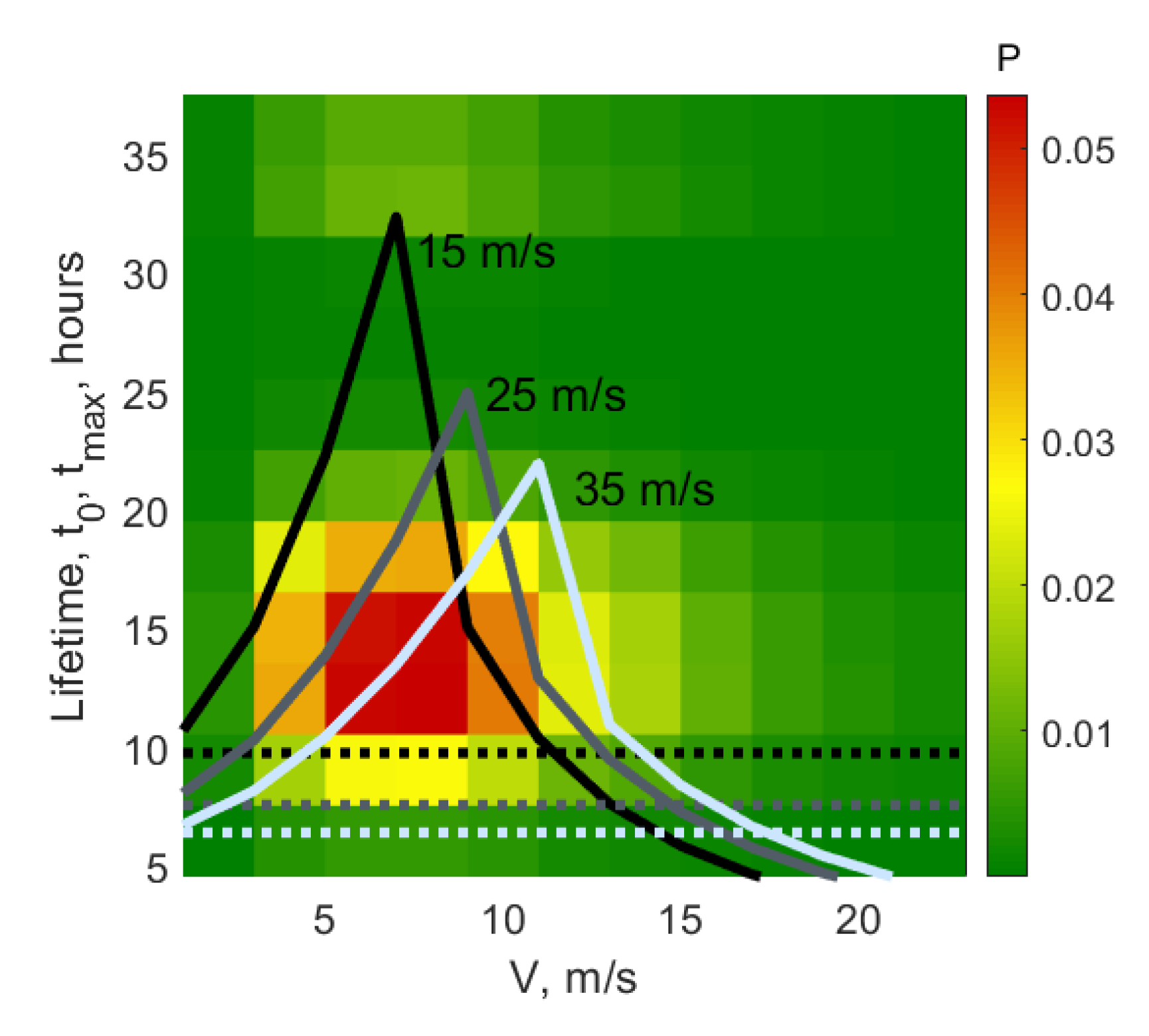
3.3. Calculation Procedure
- If the distance traveled by the PL, , is less than the distance D adjusted for (as mentioned above, the area covered by the most developed waves has a scale of approximately ): , then the waves reach the point as swell with parameters prescribed by Equation (8), with and , obtained at .
- If the PL track is masked by the land, the term () is set to zero (ice coverage is not considered in present study).
- The result of wave parameter calculation at each iteration is compared with each of the specified threshold values in the range from 2 to 15 m for SWH and from 100 to 500 m for wavelength. If H or L exceeds a given threshold, the respective number of events, (), is summarized with the number accumulated at earlier iterations for this threshold.
- Finally, the total annual numbers of cases of occurrence the waves with SWH and wavelength exceeding specified levels are obtained for each of the 75 × 75 km grid points .
4. Results
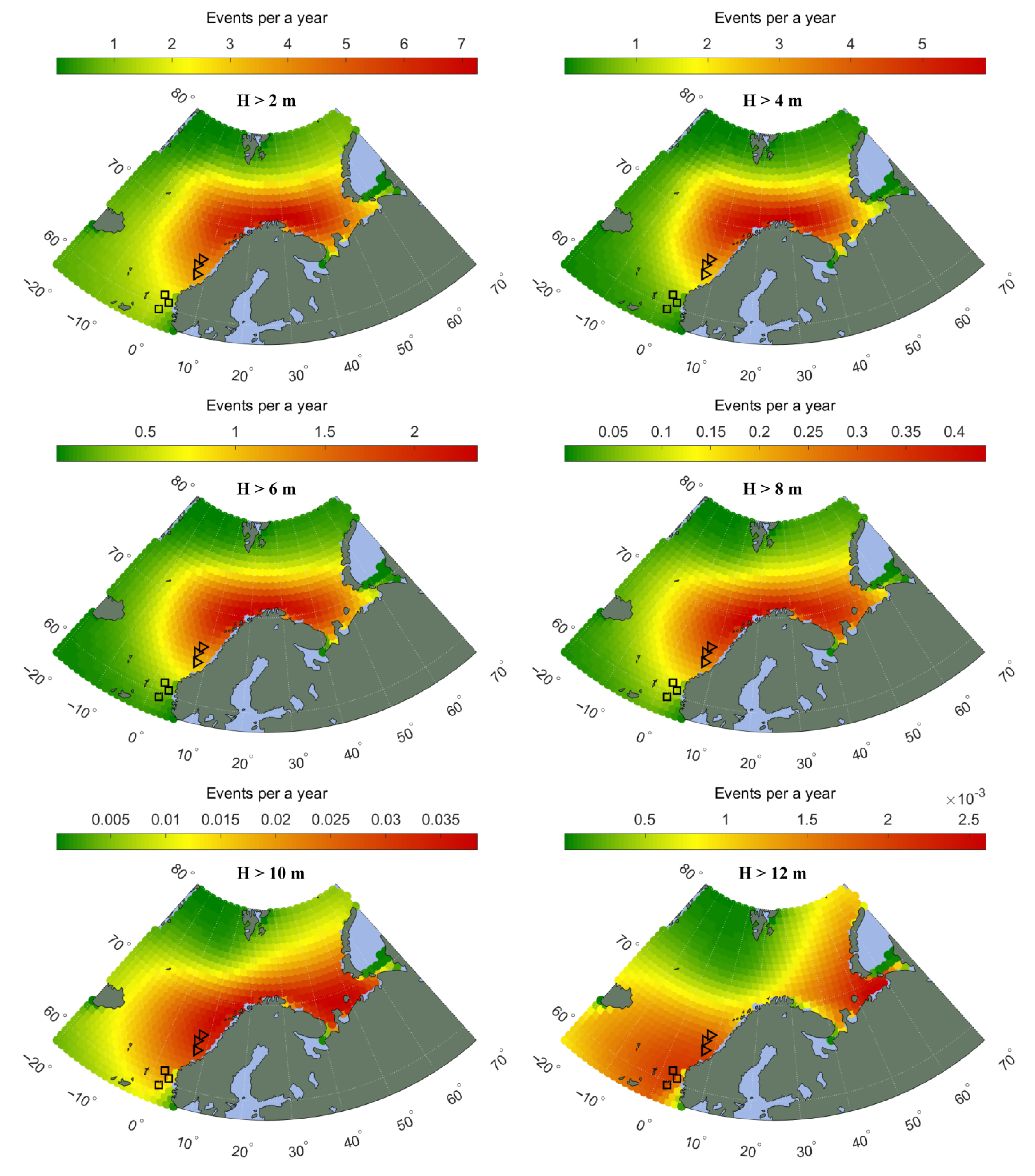
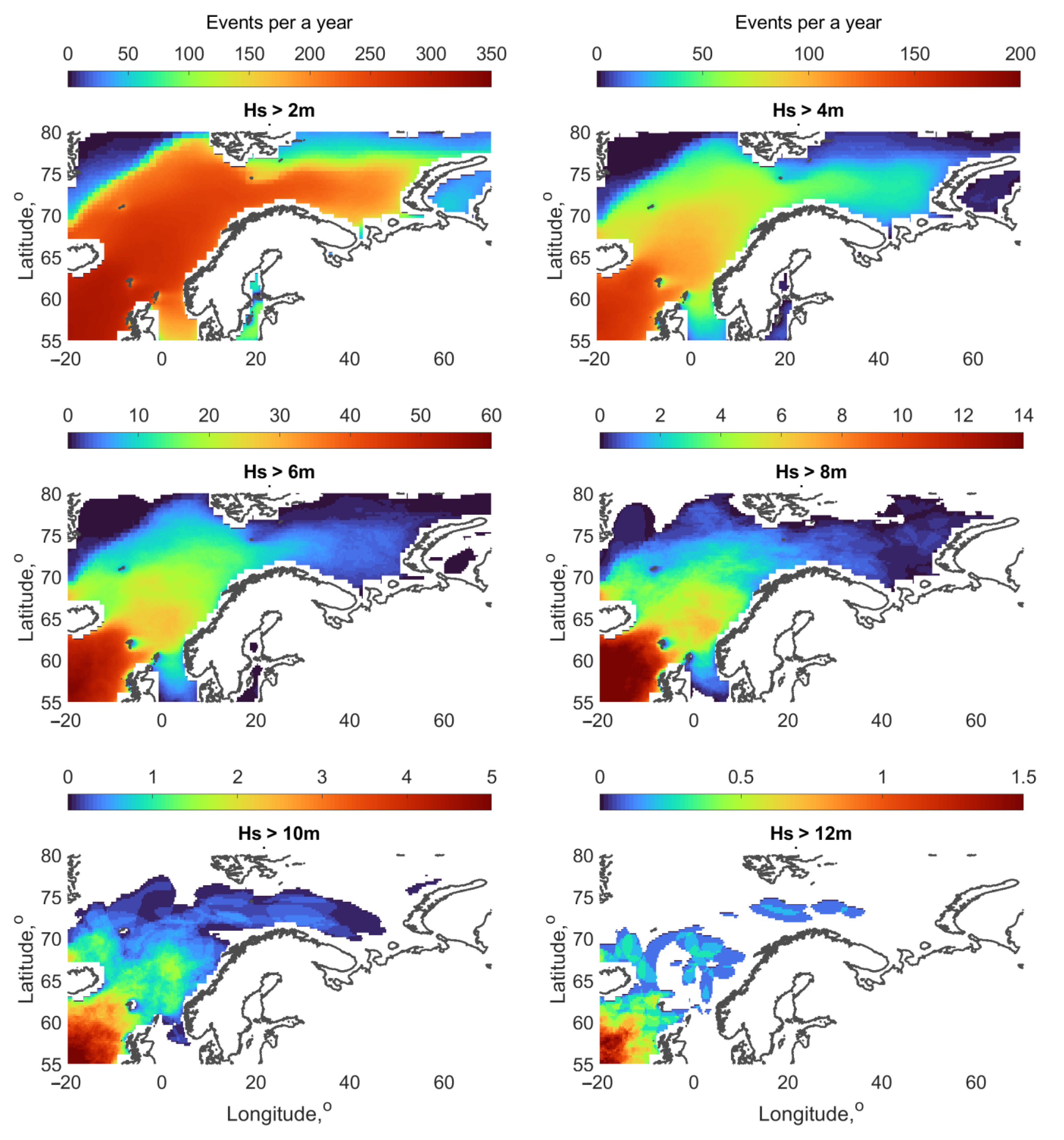
4.1. Significant Wave Height Probability Distributions
4.2. Comparison with Observations
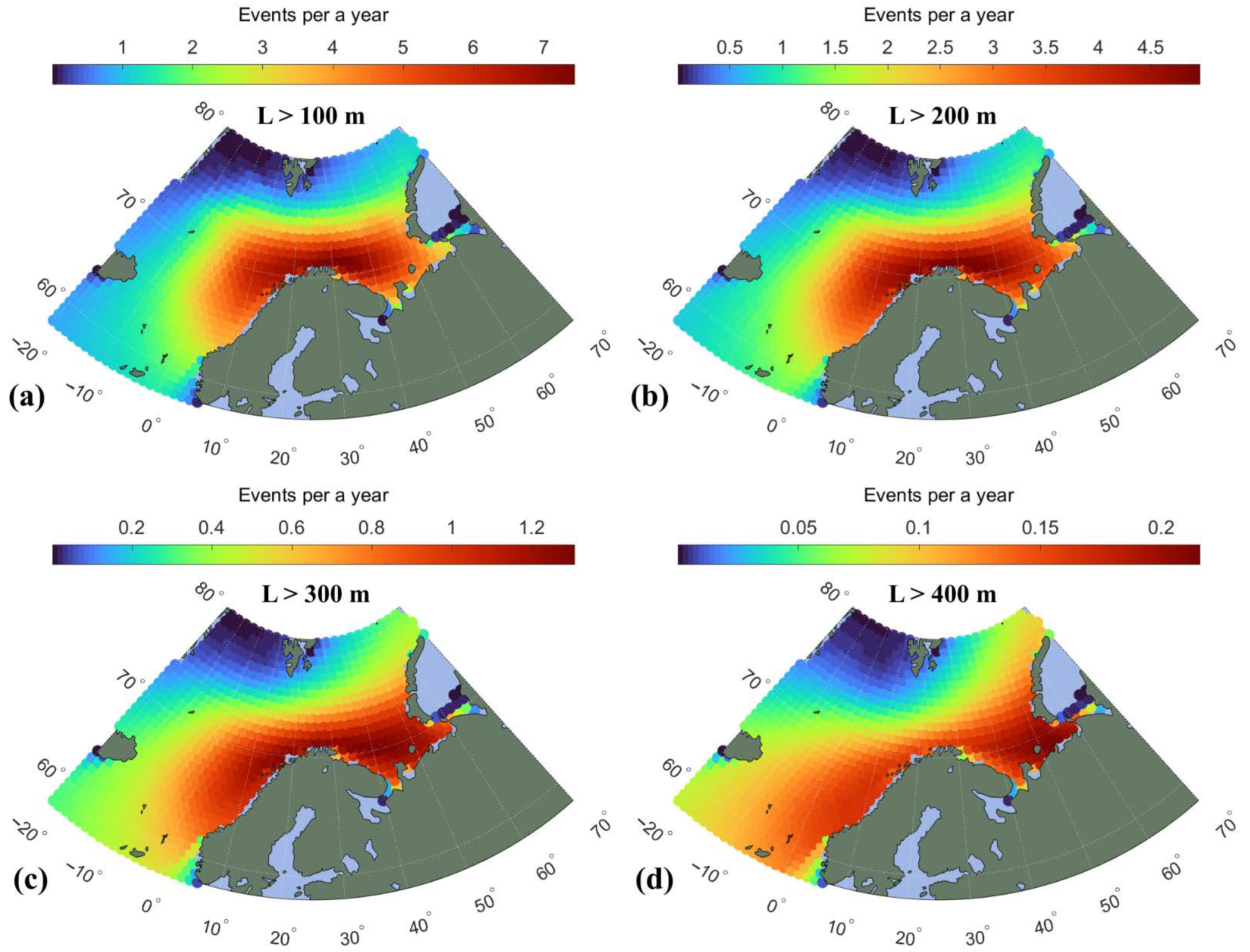
4.3. Wavelength Probability Distributions
5. Discussion
5.1. Accuracy of Predictions
5.2. Waves Not Associated with PLs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Renfrew, I. Polar lows. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Ed.; Academic Press: Oxford, UK, 2003; pp. 1761–1768. [Google Scholar] [CrossRef]
- Heinemann, G.; Claud, C. “Report of a Workshop on Theoretical and Observational Studies of Polar Lows” of the European Geophysical Society Polar Lows Working Group. Bull. Am. Meteorol. Soc. 1997, 78, 2643–2658. [Google Scholar] [CrossRef]
- Smirnova, J.E.; Golubkin, P.A.; Bobylev, L.P.; Zabolotskikh, E.V.; Chapron, B. Polar low climatology over the Nordic and Barents Seas based on satellite passive microwave data. Geophys. Res. Lett. 2015, 42, 5603–5609. [Google Scholar] [CrossRef]
- Rojo, M.; Claud, C.; Mallet, P.E.; Noer, G.; Carleton, A.M.; Vicomte, M. Polar low tracks over the Nordic Seas: A 14-winter climatic analysis. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 24660. [Google Scholar] [CrossRef]
- Gachon, P.; Laprise, R.; Zwack, P.; Saucier, F.J. The effects of interactions between surface forcings in the development of a model-simulated polar low in Hudson Bay. Tellus A Dyn. Meteorol. Oceanogr. 2003, 55, 61–87. [Google Scholar] [CrossRef]
- Diansky, N.; Panasenkova, I.; Fomin, V. Investigation of the Barents Sea Upper Layer Response to the Polar Low in 1975. Phys. Oceanogr. 2019, 26, 467–483. [Google Scholar] [CrossRef]
- Condron, A.; Renfrew, I. The impact of polar mesoscale storms on northeast Atlantic Ocean circulation. Nat. Geosci. 2003, 6, 34–37. [Google Scholar] [CrossRef]
- Stoll, P.J.; Graversen, R.G.; Noer, G.; Hodges, K. An objective global climatology of polar lows based on reanalysis data. Q. J. R. Meteorol. Soc. 2018, 144, 2099–2117. [Google Scholar] [CrossRef]
- Fletcher, J.; Mason, S.; Jakob, C. The Climatology, Meteorology, and Boundary Layer Structure of Marine Cold Air Outbreaks in Both Hemispheres. J. Clim. 2016, 29, 1999–2014. [Google Scholar] [CrossRef]
- Moreno-Ibáñez, M.; Laprise, R.; Gachon, P. Recent advances in polar low research: Current knowledge, challenges and future perspectives. Tellus A Dyn. Meteorol. Oceanogr. 2021, 73, 1–31. [Google Scholar] [CrossRef]
- Yanase, W.; Niino, H.; Ichi, I.; Watanabe, S.; Hodges, K.; Zahn, M.; Spengler, T.; Gurvich, I.A. Climatology of Polar Lows over the Sea of Japan Using the JRA-55 Reanalysis. J. Clim. 2016, 29, 419–437. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Bromwich, D.H.; Wilson, A.B.; Bai, L.; Liu, Z.; Barlage, M.; Shih, C.F.; Maldonado, S.; Hines, K.M.; Wang, S.H.; Woollen, J.; et al. The Arctic System Reanalysis, Version 2. Bull. Am. Meteorol. Soc. 2018, 99, 805–828. [Google Scholar] [CrossRef]
- Noer, G.; Saetra, O.; Lien, T.; Gusdal, Y. A climatological study of polar lows in the Nordic Seas. Q. J. R. Meteorol. Soc. 2011, 137, 1762–1772. [Google Scholar] [CrossRef]
- Wilhelmsen, K. Climatological study of gale-producing polar lows near Norway. Tellus A Dyn. Meteorol. Oceanogr. 1985, 37, 451–459. [Google Scholar] [CrossRef]
- Laffineur, T.; Claud, C.; Chaboureau, J.P.; Noer, G. Polar Lows over the Nordic Seas: Improved Representation in ERA-Interim Compared to ERA-40 and the Impact on Downscaled Simulations. Mon. Weather Rev. 2014, 142, 2271–2289. [Google Scholar] [CrossRef]
- Zappa, G.; Shaffrey, L.; Hodges, K. Can Polar Lows be Objectively Identified and Tracked in the ECMWF Operational Analysis and the ERA-Interim Reanalysis? Mon. Weather Rev. 2014, 142, 2596–2608. [Google Scholar] [CrossRef]
- Smirnova, J.; Golubkin, P. Comparing Polar Lows in Atmospheric Reanalyses: Arctic System Reanalysis versus ERA-Interim. Mon. Weather Rev. 2017, 145, 2375–2383. [Google Scholar] [CrossRef]
- Michel, C.; Terpstra, A.; Spengler, T. Polar Mesoscale Cyclone Climatology for the Nordic Seas Based on ERA-Interim. J. Clim. 2018, 31, 2511–2532. [Google Scholar] [CrossRef]
- Young, I.R. Parametric Hurricane Wave Prediction Model. J. Waterw. Port Coast. Ocean Eng. 1988, 114, 637–652. [Google Scholar] [CrossRef]
- Bowyer, P.J.; MacAfee, A.W. The Theory of Trapped-Fetch Waves with Tropical Cyclones—An Operational Perspective. Weather Forecast. 2005, 20, 229–244. [Google Scholar] [CrossRef]
- Young, I.R. A Review of Parametric Descriptions of Tropical Cyclone Wind-Wave Generation. Atmosphere 2017, 8, 194. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Golubkin, P.; Chapron, B. A simplified wave enhancement criterion for moving extreme events. J. Geophys. Res. Ocean. 2015, 120, 7538–7558. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Yurovskaya, M.; Chapron, B. Self Similarity of Surface Wave Developments Under Tropical Cyclones. J. Geophys. Res. Oceans 2021, 126, e16916. [Google Scholar] [CrossRef]
- Dysthe, K.B.; Harbitz, A. Big waves from polar lows? Tellus A Dyn. Meteorol. Oceanogr. 1987, 39, 500–508. [Google Scholar] [CrossRef]
- Orimolade, A.P.; Furevik, B.R.; Noer, G.; Gudmestad, O.T.; Samelson, R.M. Waves in polar lows. J. Geophys. Res. Ocean. 2016, 121, 6470–6481. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Cheshm Siyahi, V.; Yurovskaya, M.; Chapron, B. On Surface Waves in Arctic Seas. Bound.-Layer Meteorol. 2022, 187, 267–294. [Google Scholar] [CrossRef]
- Rojo, M.; Claud, C.; Noer, G.; Carleton, A.M. In Situ Measurements of Surface Winds, Waves, and Sea State in Polar Lows Over the North Atlantic. J. Geophys. Res. Atmos. 2019, 124, 700–718. [Google Scholar] [CrossRef]
- Cavaleri, L.; Barbariol, F.; Benetazzo, A.; Bertotti, L.; Bidlot, J.R.; Janssen, P.; Wedi, N. The Draupner wave: A fresh look and the emerging view. J. Geophys. Res. Ocean. 2016, 121, 6061–6075. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Zabolotskikh, E.; Chapron, B. Abnormal Wind Waves in the Arctic: Probability of Occurrence and Spatial Distribution. Russ. Meteorol. Hydrol. 2019, 44, 268–275. [Google Scholar] [CrossRef]
- Golubkin, P.; Smirnova, J.; Bobylev, L. Satellite-Derived Spatio-Temporal Distribution and Parameters of North Atlantic Polar Lows for 2015–2017. Atmosphere 2021, 12, 224. [Google Scholar] [CrossRef]
- Polverari, F.; Portabella, M.; Lin, W.; Sapp, J.W.; Stoffelen, A.; Jelenak, Z.; Chang, P.S. On High and Extreme Wind Calibration Using ASCAT. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Gille, S.T.; Bitz, C.; Carlson, D.; Cerovecki, I.; Clayson, C.A.; Cronin, M.F.; Drennan, W.M.; Fairall, C.W.; Hoffman, R.N.; et al. High-Latitude Ocean and Sea Ice Surface Fluxes: Challenges for Climate Research. Bull. Am. Meteorol. Soc. 2013, 94, 403–423. [Google Scholar] [CrossRef]
- Lin, W.; Portabella, M.; Stoffelen, A.; Vogelzang, J.; Verhoef, A. ASCAT wind quality under high subcell wind variability conditions. J. Geophys. Res. Ocean. 2015, 120, 5804–5819. [Google Scholar] [CrossRef]
- Kitaigorodski, S. Applications of the theory of similarity to the analysis of wind-generated wave motion as a stochastic process. Bull. Acad. Sci. USSR Geophys. Ser. 1962, 1, 105–117. [Google Scholar]
- Babanin, A.V.; Soloviev, Y.P. Field Investigation of Transformation of the Wind Wave Frequency Spectrum with Fetch and the Stage of Development. J. Phys. Oceanogr. 1998, 28, 563–576. [Google Scholar] [CrossRef]
- Badulin, S.I.; Babanin, A.V.; Zakharov, V.E.; Resio, D. Weakly turbulent laws of wind-wave growth. J. Fluid Mech. 2007, 591, 339–378. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Badulin, S.I.; Geogjaev, V.V.; Pushkarev, A.N. Weak-Turbulent Theory of Wind-Driven Sea. Earth Space Sci. 2019, 6, 540–556. [Google Scholar] [CrossRef]
- Dulov, V.; Kudryavtsev, V.; Skiba, E. On fetch- and duration-limited wind wave growth: Data and parametric model. Ocean Model. 2020, 153, 101676. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Yurovskaya, M.; Chapron, B. 2D Parametric Model for Surface Wave Development Under Varying Wind Field in Space and Time. J. Geophys. Res. Oceans 2021, 126, e16915. [Google Scholar] [CrossRef]
- Yurovskaya, M.; Kudryavtsev, V.; Mironov, A.; Mouche, A.; Collard, F.; Chapron, B. Surface Wave Developments under Tropical Cyclone Goni (2020): Multi-Satellite Observations and Parametric Model Comparisons. Remote Sens. 2022, 14, 2032. [Google Scholar] [CrossRef]
- Yurovskaya, M.; Kudryavtsev, V.; Chapron, B. A self-similar description of the wave fields generated by tropical cyclones. Ocean Model. 2023, 183, 102184. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horanyi, A.; Munoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1940 to present. Copernic. Clim. Chang. Serv. (C3s) Clim. Data Store CDS 2023, 10. [Google Scholar] [CrossRef]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Myslenkov, S.; Platonov, V.; Kislov, A.; Silvestrova, K.; Medvedev, I. Thirty-Nine-Year Wave Hindcast, Storm Activity, and Probability Analysis of Storm Waves in the Kara Sea, Russia. Water 2021, 13, 648. [Google Scholar] [CrossRef]
- Merrill, R.T. A Comparison of Large and Small Tropical Cyclones. Mon. Weather Rev. 1984, 112, 1408–1418. [Google Scholar] [CrossRef]
- Kimball, S.K.; Mulekar, M.S. A 15-Year Climatology of North Atlantic Tropical Cyclones. Part I: Size Parameters. J. Clim. 2004, 17, 3555–3575. [Google Scholar] [CrossRef]
- Wu, L.; Tian, W.; Liu, Q.; Cao, J.; Knaff, J.A. Implications of the Observed Relationship between Tropical Cyclone Size and Intensity over the Western North Pacific. J. Clim. 2015, 28, 9501–9506. [Google Scholar] [CrossRef]
- Kim, H.J.; Moon, I.J.; Oh, I. Comparison of Tropical Cyclone Wind Radius Estimates between the KMA, RSMC Tokyo, and JTWC. Asia-Pac. J. Atmos. Sci. 2022, 58, 563–576. [Google Scholar] [CrossRef]
- Romero, R.; Emanuel, K. Climate Change and Hurricane-Like Extratropical Cyclones: Projections for North Atlantic Polar Lows and Medicanes Based on CMIP5 Models. J. Clim. 2017, 30, 279–299. [Google Scholar] [CrossRef]
- Gebhardt, C.; Bidlot, J.R.; Gemmrich, J.; Lehner, S.; Pleskachevsky, A.; Rosenthal, W. Wave observation in the marginal ice zone with the TerraSAR-X satellite. Ocean Dyn. 2016, 66, 839–852. [Google Scholar] [CrossRef]
- Ardhuin, F.; Stopa, J.; Chapron, B.; Collard, F.; Smith, M.; Thomson, J.; Doble, M.; Blomquist, B.; Persson, O.; Collins, C.O.; et al. Measuring ocean waves in sea ice using SAR imagery: A quasi-deterministic approach evaluated with Sentinel-1 and in situ data. Remote Sens. Environ. 2017, 189, 211–222. [Google Scholar] [CrossRef]
- Shen, H.; Perrie, W.; Hu, Y.; He, Y. Remote Sensing of Waves Propagating in the Marginal Ice Zone by SAR. J. Geophys. Res. Ocean. 2018, 123, 189–200. [Google Scholar] [CrossRef]
- Collard, F.; Marié, L.; Nouguier, F.; Kleinherenbrink, M.; Ehlers, F.; Ardhuin, F. Wind-Wave Attenuation in Arctic Sea Ice: A Discussion of Remote Sensing Capabilities. J. Geophys. Res. Ocean. 2022, 127, e2022JC018654. [Google Scholar] [CrossRef]
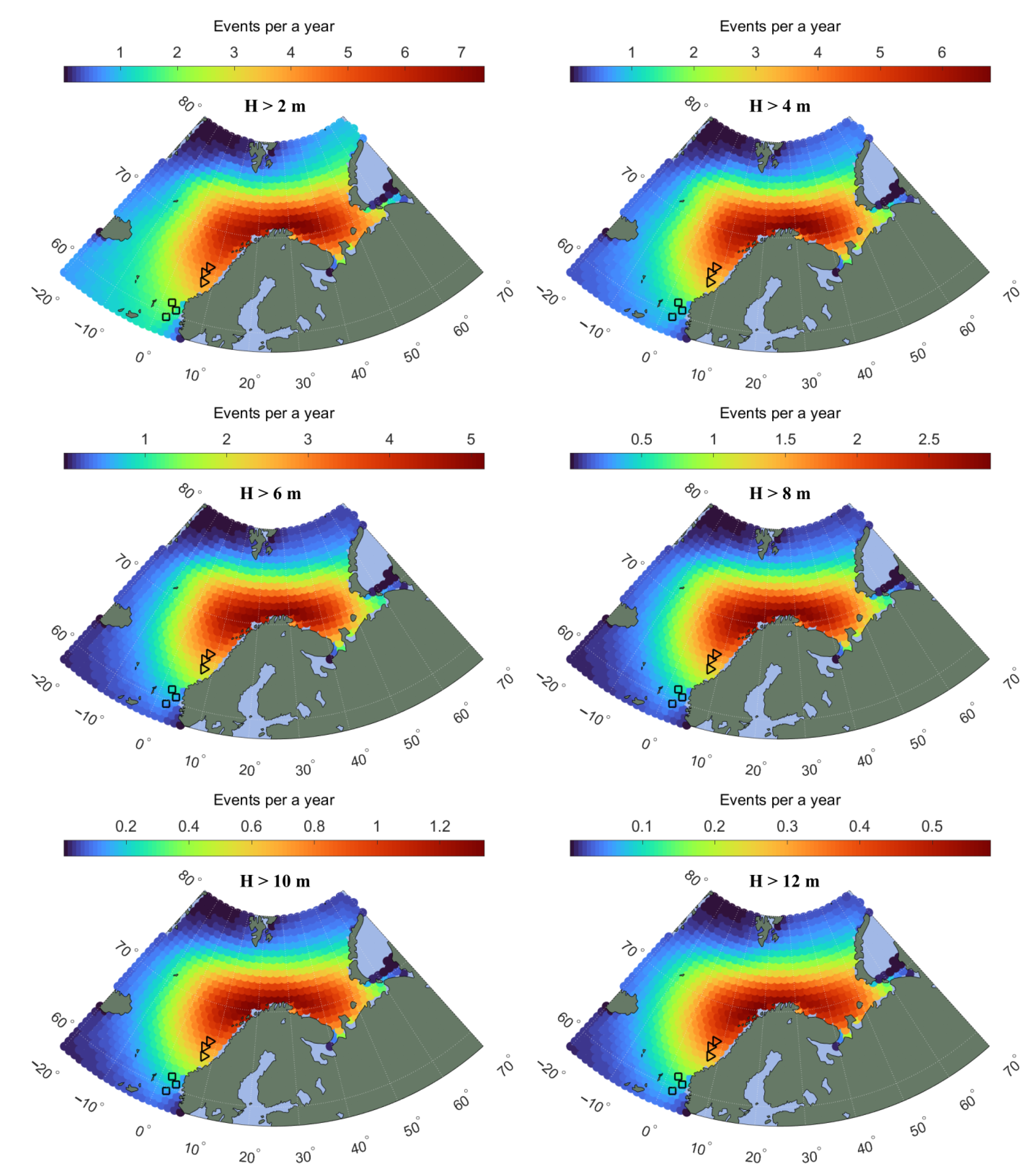
| Stations 76,925, 76,928, 76,930 | Stations 76,923, 76,931, 76,932 | |||
|---|---|---|---|---|
| SWH Threshold | Total Number of Events | Annual Number of Events | Total Number of Events | Annual Number of Events |
| >2 m | 22 | 1.6 | 6 | 0.43 |
| >4 m | 20 | 1.4 | 6 | 0.43 |
| >6 m | 12 | 0.86 | 4 | 0.29 |
| >8 m | 5 | 0.36 | 1 | 0.07 |
| >10 m | 1 | 0.07 | 1 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yurovskaya, M.; Kudryavtsev, V.; Chapron, B. Spatial Probability Characteristics of Waves Generated by Polar Lows in Nordic and Barents Seas. Remote Sens. 2023, 15, 2729. https://doi.org/10.3390/rs15112729
Yurovskaya M, Kudryavtsev V, Chapron B. Spatial Probability Characteristics of Waves Generated by Polar Lows in Nordic and Barents Seas. Remote Sensing. 2023; 15(11):2729. https://doi.org/10.3390/rs15112729
Chicago/Turabian StyleYurovskaya, Maria, Vladimir Kudryavtsev, and Bertrand Chapron. 2023. "Spatial Probability Characteristics of Waves Generated by Polar Lows in Nordic and Barents Seas" Remote Sensing 15, no. 11: 2729. https://doi.org/10.3390/rs15112729
APA StyleYurovskaya, M., Kudryavtsev, V., & Chapron, B. (2023). Spatial Probability Characteristics of Waves Generated by Polar Lows in Nordic and Barents Seas. Remote Sensing, 15(11), 2729. https://doi.org/10.3390/rs15112729








