Abstract
The estimation of characteristic parameters such as diameter at breast height (DBH), aboveground biomass (AGB) and stem volume (V) is an important part of urban forest resource monitoring and the most direct manifestation of the ecosystem functions of forests; therefore, the accurate estimation of urban forest characteristic parameters is valuable for evaluating urban ecological functions. In this study, the height and density characteristic variables of canopy point clouds were extracted as Scheme 1 and combined with the canopy structure variables as Scheme 2 based on unmanned aerial vehicle lidar (UAV-Lidar). We analyzed the spatial distribution characteristics of the canopies of different tree species, and multiple linear regression (MLR), support vector regression (SVR), and random forest (RF) models were used to estimate the DBH, AGB, and V of urban single trees. The estimation accuracy of different models was evaluated based on the field-measured data. The results indicated that the model accuracy of coupling canopy structure variables (R2 = 0.69–0.85, rRMSE = 9.87–24.67%) was higher than that of using only point-cloud-based height and density characteristic variables. The comparison of the results of different models shows that the RF model had the highest estimation accuracy (R2 = 0.76–0.85, rRMSE = 9.87–22.51%), which was better than that of the SVR and MLR models. In the RF model, the estimation accuracy of AGB was the highest (R2 = 0.85, rRMSE = 22.51%), followed by V, with an accuracy of R2 = 0.83, rRMSE = 18.51%, and the accuracy of DBH was the lowest (R2 = 0.76, rRMSE = 9.87%). The results of the study provide an important reference for the estimation of single-tree characteristic parameters in urban forests based on UAV-Lidar.
1. Introduction
Urban forests are an important part of urban ecosystems, and they are the foundation and guarantee of urban sustainable development [1,2]. They can effectively reduce the urban heat island effect and improve air quality and other environmental conditions as well as ecosystem services [3,4]. The single tree is the basic unit of the forests [5]; their characteristic parameters such as tree height (H), diameter at breast height (DBH), crown width, aboveground biomass (AGB), and tree volume (V) can effectively reflect the growth status, spatial distribution, and structural characteristics of forest resources, which are important elements of forest resource investigation and reliable diversity indicators of forest succession stages [6], as well as being the focus of research on urban ecosystems and their functions [7].
Single trees in cities are highly fragmented and unevenly distributed in urbanized areas with high population densities and high concentrations of artificial landscapes [8], so it is time-consuming and labor-intensive to obtain information on the characteristic parameters of urban single trees through traditional forest resource investigation methods [9]. Remote sensing technology has rapidly developed and can be used to quickly and accurately obtain multiscale and multitemporal information on forest structure characteristics, effectively making up for the shortcomings of traditional forest resource monitoring methods and greatly improving the work efficiency [10]. However, passive remote sensing technology only provides spectral and textural information of the forest canopy surface, which is susceptible to atmospheric conditions and other factors, and it is difficult to obtain the three-dimensional structure of the vegetation canopy [11,12].
Light detection and ranging (LiDAR) is an active remote sensing technology that obtains the distance between a sensor and a target by calculating the time difference between the laser pulse emitted by the sensor and the received echo pulse. Because LiDAR has strong penetration into the forest, it can accurately obtain the three-dimensional structure information of forest tree height and canopy [13,14,15], thus realizing the leap from two-dimensional to three-dimensional forest canopy structure information, resulting in the emergence of canopy parameters extracted from lidar data as a hot research topic globally. Previous studies have shown that LiDAR-based estimation of diameter at breast height, biomass, stock volume, and forest distribution mapping can be effective [16,17,18,19]. For example, Cao et al. [20] used full-waveform unmanned aerial vehicle (UAV) lidar data to extract point cloud metrics and waveform metrics calculated based on voxel-based methods to estimate the single tree AGB of plantation forests in the coastal region of east China. The results indicated that full-waveform lidar data can effectively estimate the AGB of single trees. Liu et al. [21] used the constant allometric ratio model to estimate the forest single tree biomass based on UAV lidar data to obtain single tree canopy characteristic parameters (tree height, crown width, canopy projection area, and canopy volume) and achieved a good fit and high prediction accuracy. Qin et al. [22] used UAV lidar to estimate the subtropical single tree carbon stock in Shenzhen, southern China, and the results indicated that the height variable can explain the variation of tree carbon stock and estimate the single tree carbon stock well. Therefore, it is important to examine the application of UAV lidar for estimating single tree characteristic parameters in urban areas.
Forest canopy structure includes the horizontal and vertical directions of branches and leaves, canopy width and height, and canopy light transmission [23,24]. The canopy width and cross-sectional area can be used to measure the horizontal extension size of the canopy. The vertical structure of the canopy is mainly the spatial distribution and hierarchical characteristics of the forest vegetation, and the performance is comparatively complex [25,26,27]. To quantify the three-dimensional structure of the forest canopy, Lefsky et al. proposed a voxel-based canopy volume model (CVM) to characterize the differences in the volume and vertical spatial distribution of the canopy [28]. The basic principle of the CVM model is reflecting the spatial heterogeneity of the forest structure arising from the difference in the light environment within the canopy by dividing the canopy into two parts, the photosynthetically active zone and the inactive zone, to realize the spatial arrangement of elements within the canopy structure and the distinction of volume structure [29,30,31,32]. Therefore, the CVM model is an important method for obtaining the parameters of tree canopy structure.
In summary, the estimation of DBH, AGB, and stem volume of trees is an important element of urban forest resource monitoring and the most direct manifestation of the ecosystem functions of forests, and lidar is an advanced technical tool for detecting the three-dimensional structure of forests. Therefore, in this study, three urban tree species, Ginkgo (Ginkgo biloba L.), Cinnamomum camphora (Cinnamomum camphora (Linn.) Presl), and Metasequoia glyptostroboides (Metasequoia glyptostroboides Hu et Cheng) were used as examples. UAV-Lidar data were used to obtain the canopy point clouds of the three kinds of single trees, coupled with point clouds and canopy structure variables, and three methods, multiple linear regression (MLR), support vector regression (SVR) and random forest (RF), were used to establish models for estimating the DBH, AGB, and V of single trees in urban forests based on UAV-Lidar data. The model and estimation results were validated using ground-measured data. This provides an important technical tool for rapid and accurate monitoring of single tree parameters in urban forests.
2. Materials and Methods
2.1. Study Area
The study area is in Lin’an (29°56′ to 30°23′N latitude and 118°51′ to 119°52′E longitude) (Figure 1), Hangzhou City, Zhejiang Province. Lin’an belongs to the subtropical monsoon climate with warm and humid conditions, abundant light and rainfall, and four distinct seasons. The average annual temperature is 16.4 °C, the frost-free period is 237 days, the sunshine time is 1847.3 h, and the annual precipitation is 1613.9 mm. The area is dominated by hills and mountains, the terrain inclines from northwest to southeast, and the three-dimensional climate is obvious. The climax vegetation is subtropical evergreen broad-leaved forest, and the main tree species planted in the urban area of Lin’an City include Metasequoia glyptostroboides (M. glyptostroboides), Ginkgo biloba (G. biloba), Cinnamomum camphora (C. camphora), etc.
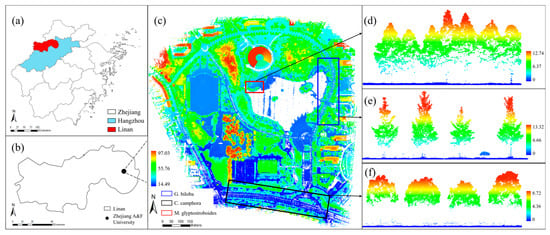
Figure 1.
Overview of the study area: (a) location of Lin’an, (b) location of the study area, (c) UAV-Lidar point clouds of the study area, (d) Metasequoia glyptostroboides point cloud profile, (e) Ginkgo biloba point cloud profile, (f) Cinnamomum camphora point cloud profile.
2.2. Field Measurements
In July 2021, the DBH, tree height, crown height, and crown width of 64 stems of G. biloba, 74 stems of C. camphora, and 55 stems of M. glyptostroboides in the study area were measured in detail, as shown in Figure 1. The single trees were positioned with Huace Smart Real Time Kinematic. The AGB consisted of stem biomass (WS), branch biomass (WB), and foliage biomass (WF). In this study, the biomass of each component was calculated according to the biomass allometric equations of different tree species and summed to obtain the AGB of a single tree [33,34,35], as shown in Table 1. The stem volume was calculated according to the single-entry stem volume table of Zhejiang Province and the measured single tree DBH data [36]. Table 2 shows the statistical characteristics of the parameters of the three tree species.

Table 1.
Biomass allometric equations for each biomass component of the three tree species.

Table 2.
Summary of information on measured characteristics parameters of the three tree species.
2.3. Lidar Data
The DJI Matrice 600 Pro six-rotor UAV with a lightweight Velodyne Puck LITE™ laser scanner was used to acquire the original lidar point clouds in the study area (Figure 2). The flight height of the UAV is 60 m above ground level, with a flight speed of 8 m/s, a route spacing of 25 m, and a lateral overlap rate of data sampling of 50%. The sensor records the first echo information of the laser pulse with a wavelength of 903 nm, a maximum scanning angle of ±15°, a scanning frequency of 20 Hz, and a scanning speed of 300,000 points/s. The final average point cloud density obtained is approximately 230 points/m2.
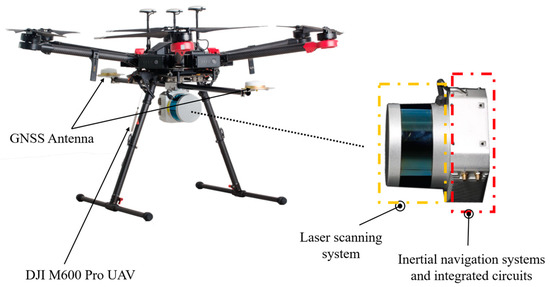
Figure 2.
UAV and LiDAR system.
2.3.1. Lidar Data Preprocessing
The original lidar point cloud data were denoised using the height thresholding method, and the point cloud data after noise removal were filtered and separated into ground points and nonground points. First, the ground points were extracted by filtering with the improved progressive TIN densification algorithm [37]. Then, the height average of the laser points within a cell was calculated via the inverse distance weighting method to obtain a digital elevation model (DEM) with a spatial resolution of 0.5 m. Finally, the DEM was used to normalize the point cloud data to obtain the normalized point cloud data. In this study, the point cloud segmentation algorithm was used to segment individual trees based on normalized point cloud data [38,39]. This algorithm identified single trees via region growing combined with thresholding, and then identified the top of the tree to determine the distance between the surrounding points and the vertex, and expanded the region to segment the first tree. Successive iterations were made on this basis until all trees were segmented. The characteristic variables of a single tree were extracted based on the segmented single tree point cloud.
2.3.2. Lidar Metrics
The characteristic variables based on the lidar data can be used to estimate the forest characteristic parameters, and the point cloud characteristics extracted from the first returns have a remarkable correlation with the height, which is more suitable for estimating the forest characteristic parameters [13,40]. Of course, to reduce the influence of low ground vegetation on the data, the data after filtering the point clouds below 2 m were used as the crown point clouds, and characteristic variables were extracted from the first returns of the lidar point cloud [41,42]. In this study, the lidar data characteristic variables included: height-based metrics (HB) describing the parameters related to the lidar point cloud height; density-based metrics (DB) describing the canopy return density variable, which is the ratio of the number of height percentile point clouds to the total number of point clouds; the canopy area (S), which is the projected area of the canopy point cloud calculated based on the two-dimensional convex packet algorithm; the crown diameter (CD), which is the average of the east–west and north–south crown diameters of the point clouds. The canopy volume variables include OG, CG, EV, and OV. The metrics and descriptions are shown in Table 3.
2.3.3. Calculation of the Volume of Single Tree Canopy
Urban trees are frequently pruned and truncated, [43], making the crown of the pruned single tree change, often with a special crown shape. Therefore, canopy volume was extracted as a metric for single tree characteristic parameter estimation, as shown in Table 3. As shown in Figure 3, in this study, the voxel-based canopy volume method was used to calculate the canopy volume metrics for lidar point clouds of tree crowns:
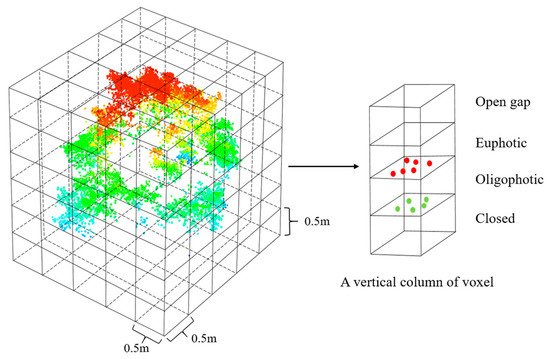
Figure 3.
Illustration of the voxel-based canopy volume model.
The space where the canopy point clouds was located was divided into 0.5 × 0.5 × 0.5 m voxels [44], which were divided into vertical columns, and each column was further layered into four canopy structures. First, each voxel was classified as “filled” or “empty” according to whether there was a point cloud in the voxel, that is, the volume in unit area (m3/m2).

Table 3.
Description of metrics derived from lidar data.
Table 3.
Description of metrics derived from lidar data.
| Metrics | Description | Reference | |
|---|---|---|---|
| Height-based metrics(HB) | Height percentiles (H5, H25, H50, H75, H95, and H99) | The percentiles of the canopy height distribution (5th, 25th, 50th, 75th, 95th, and 99th) of first returns | [25,45,46] |
| The coefficient of variation of height (Hcv) | The coefficient of variation of heights of all first returns | ||
| Maximum height (Hmax) | Maximum height above ground of all first returns | ||
| Variance of height (Hva) | The variation in heights of all first returns | ||
| Standard deviation of height (Hstd) | The standard deviation of heights of all first returns | ||
| Median height (Hmed) | Median height above ground of all first returns | ||
| Mean height (Hmean) | Mean height above ground of all first returns | ||
| Interquartile distance of height (HIQ) | The interquartile distance of height of all first returns | ||
| Root mean square of height (Hsq) | The root mean square of height of all first returns | ||
| Cube mean of height (Hcm) | The cube mean of height of all first returns | ||
| Density-based metrics(DB) | Canopy return density (D3, D5, D7, D9) | The proportion of points above the quantiles (30th, 50th, 70th and 90th) to total number of points | [47] |
| Canopy structure metrics(CS) | Canopy projection area (S) | Canopy projection area calculated using two-dimensional convex hull algorithm | [21] |
| Crown diameter (CD) | Average diameter of crown point cloud | ||
| Open gap volume (OG) and closed gap volume (CG) of CVM | The volume of empty voxels located above and below the filled canopy, respectively | [32] | |
| Euphotic volume (EV) and oligophotic volume (OV) of CVM | The volume of filled voxels located 65% above and 35% below of all filled grid cells of that column |
Then, according to the distribution of the filled position, the upper 65% of the filled zone was defined as “euphotic”, in every column of voxels, and the remaining 35% was defined as “oligophotic”. According to the spatial distribution and location of the empty voxel, in each voxel column, the empty voxels between the top of the canopy and the first filled voxels were defined as the “open gap”, and the empty voxels between the filled voxels and the ground were called the “closed gap”. The three-dimensional canopy volume distribution was converted into a two-dimensional canopy volume profile (CVP) according to the percentage of the volume of the four classified canopy volume characteristics in each height interval. The canopy volume distribution indicated the distribution of elements arranged in the vertical spatial extent of the canopy [30].
2.4. Model Construction Methods and Scheme
In this study, three modeling methods, MLR, SVR and RF, were used to construct the estimation models of urban single tree characteristic parameters based on the obtained lidar data characteristic variables. To study the influence of canopy structure on the accuracy of single tree characteristic parameters, the models were constructed in two schemes. The model excluding canopy structure variables is referred to as “Scheme 1”, and the model including canopy structure variables is referred to “Scheme 2”.
2.4.1. MLR Model
MLR is the most commonly used parameterization method for estimating forest characteristic parameters from remote sensing information, and can quickly establish a linear relationship between two or more independent variables and dependent variables to achieve parameter estimation. The MLR is generally expressed as follows:
where a0 is the constant term; a1, a2, …, an are regression coefficients representing the degree of contribution of the respective variables to the dependent variable; and x1, x2, …, xn are the independent variables, which are the characteristic variables shown in Table 3. Y is the dependent variable, which is the estimated characteristic parameter of this study. In this study, all possible combinations of variables were evaluated using “all subsets” regression, and the best combination of variables was selected to build the MLR model to estimate the three characteristic parameters [48].
2.4.2. SVR Model
SVR is a machine learning model that uses support vector machines to perform regression analysis [49,50]. It applies classification methods to solve regression problems with finite samples, mainly based on a given sample data set, by seeking a function to fit all sample points so that the total variance of sample points from the hyperplane is minimized [51]. SVR transforms the nonlinear problem into a linear problem in high-dimensional space via kernel functions for nonlinear separable samples in low-dimensional input space, replacing the inner product operation in high-dimensional space, and ensuring good generalization ability [52]. Therefore, the SVR model has high accuracy, good ability to handle high-dimensional and small sample data, good generalization ability, and robustness. In this study, four kernel function models, including linear, polynomial, radial basis function (RBF), and multilayer perceptron (Sigmoid), were used, and the best penalty coefficient (C) with gamma value (g) was selected via grid search cross-validation to construct the SVR model to estimate the three characteristic parameters.
2.4.3. RF Model
The random forest algorithm is another commonly used machine learning method. The algorithm is based on modified nonparametric modeling of decision trees [53], and constructs a decision tree by bootstrapping from the original sample set with put-back randomly selected N samples to predict the results. The RF algorithm has good noise resistance and can handle high-dimensional data with relatively high prediction accuracy. An unbiased estimate of the error can be generated during the RF calculation, and the importance of each variable involved in the model can be evaluated. There are three important parameters in the estimation of single tree characteristic parameters using the RF algorithm: Mtry is the number of variables used randomly at the nodes of each tree, and Ntree is the number of regression trees in the RF. Nodesize is the minimum number of terminal nodes in the regression analysis, and the default value is 5 [54,55]. In this study, three characteristic parameters estimation models are developed based on the optimization of RF parameters.
2.5. The Flow Chart and Accuracy Validation
The flow chart of this study is shown in Figure 4. First, field measurements, lidar data processing, and characteristic variable extraction were conducted. Second, two-thirds of all measured samples were selected into training samples, and one-third were divided into test samples. Finally, three modeling methods, MLR, SVR and RF, were used to construct single tree characteristic estimation models according to Scheme 1 and Scheme 2, and the accuracy of the models was evaluated.
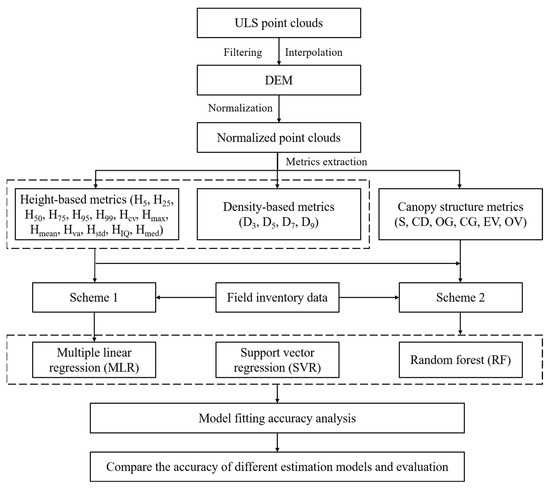
Figure 4.
The flow chart of this study.
The model accuracy evaluation metrics include the determination coefficient (R2), root mean square error (RMSE), and relative root mean square error (rRMSE). Generally, higher values of R2 and lower values of RMSE and rRMSE indicate better performance of the model. R2, RMSE, and rRMSE are calculated as follows:
where n is the number of samples, is the measured value of the sample canopy characteristic parameters, is the mean value of the sample canopy characteristic parameters, and is the predicted value of the sample canopy characteristic parameters.
3. Results
3.1. Canopy Volume and Profile Analysis
The canopy volume profile can directly show the spatial heterogeneity of the forest canopy structure and the distribution and change in elements in the vertical direction. Comparing the canopy volumes and profiles of the three species, the euphotic volume was significantly larger than the oligophotic volume in the filled volume of the G. biloba canopy (Figure 5); the closed gap volume was larger than the open gap volume in the empty volume, and the closed gap volume occupied the largest volume. The canopy distribution of C. camphora was consistent with that of G. biloba (Figure 6), and the euphotic volume was greater than the oligophotic volume; the closed gap volume was larger than the open gap volume in the empty volume, and the closed gap volume occupied the largest volume. In the canopy distribution of M. glyptostroboides (Figure 7), the euphotic volume was close to the oligophotic volume; the closed gap volume was slightly larger than the open gap volume in the empty volume.
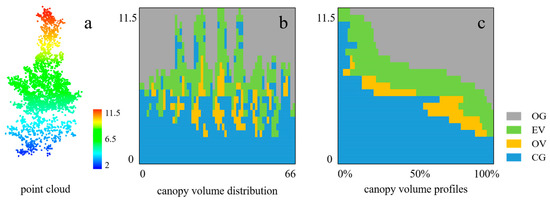
Figure 5.
(a) G. biloba point cloud, (b) canopy volume distribution, which shows the distribution of canopy structure classes after the expansion of all columns in the panel; and (c) canopy volume profile, which shows the volume percentage of each class of total volume in each height interval.
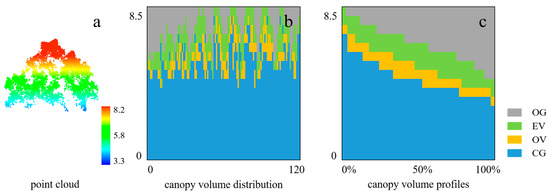
Figure 6.
(a) C. camphora point cloud, (b) canopy volume distribution, which shows the distribution of canopy structure classes after the expansion of all columns in the panel, and (c) canopy volume profile, which shows the volume percentage of each class of total volume in each height interval.
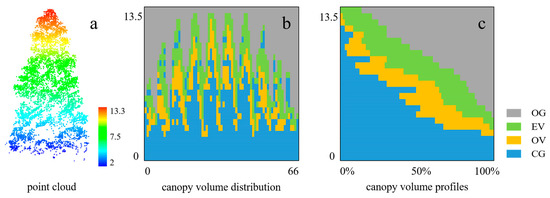
Figure 7.
(a) M. glyptostroboides point cloud, (b) canopy volume distribution, which shows the distribution of canopy structure classes after the expansion of all columns in the panel; and (c) canopy volume profile, which shows the volume percentage of each class of total volume in each height interval.
3.2. Variable Importance Analysis
In this study, the point cloud characteristic variables extracted from lidar data were run 100 times using the RF model according to two modeling schemes. Figure 8 and Figure 9 show the importance scores of Scheme 1 and Scheme 2 input variables, respectively. As shown in Figure 8, the importance score of the height characteristic variable in Scheme 1 is significantly higher than that of the density characteristic variable. Among the three single tree characteristic parameter models, Hcv was the largest in DBH and AGB, with values of 27.89 and 44.05, respectively; Hsq was the largest in V, with a value of 21.12. As shown in Figure 9, the three parameters with the highest importance in Scheme 2 were all canopy structure variables. In the DBH and V models, CG had the highest influence, with 31.96 and 28.97, respectively, and in the AGB model, CD had the highest influence, with 40.57. The results show that the canopy structure variable was significantly more important than other variables and was the key variable in the estimation of single tree structure parameters.
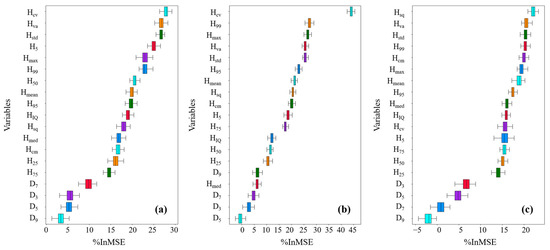
Figure 8.
Importance of input variables based on Scheme 1 (%InMSE: the percentage increase in the mean square error, ((a): DBH, (b): AGB, (c): V)).
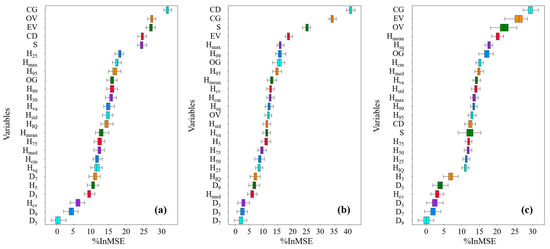
Figure 9.
Importance of input variables based on Scheme 2 (%InMSE: the percentage increase in the mean square error, ((a): DBH, (b): AGB, (c): V)).
Figure 10 shows the path coefficients (absolute values) calculated using the structural equations for the direct effect of the three characteristic variables of height characteristics, density characteristics, and canopy structure on the characteristic parameters. As shown in Figure 10, CS had the largest direct effect on DBH and AGB, while HD had the largest direct effect on V, and DB had the smallest effect on characteristic parameters. For DBH, the path coefficient values, in order, were as follows: CS (0.647) > HD (0.318) > DB (−0.095). For AGB, the path coefficient values were as follows: CS (0.871) > HD (0.116) > DB (−0.101). For V, the path coefficient values were as follows: HD (0.593) > CS (0.389) > DB (0.038). The canopy structure variables had important influence on the estimation of the three single tree characteristics parameters.
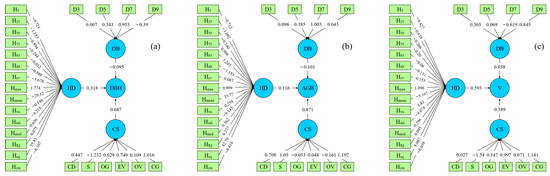
Figure 10.
Relative importance of input variables to characteristic parameters based on Scheme 2 ((a): DBH, (b): AGB, (c): V).
3.3. Model Construction and Evaluation
3.3.1. MLR Estimation Results
To evaluate the accuracy of the established prediction models of single tree characteristic parameters, three independent variables were selected to construct the MLR models in this study (Table 4). Among all the metrics selected in the MLR model of Scheme 1, the height percentiles (Hcv, Hmean, Hsq, Hstd, H99, and Hvar) were frequently selected by the models. Among all the metrics selected by the MLR model in Scheme 2, height percentile (Hcm, H95, Hcv and Hvar), canopy structure variables (CD, CG, EV) were frequently selected by the models. The accuracy value R2 of the models was improved after coupling the canopy structure variables. The canopy structure variables played an important role in the construction of the model, indicating that these variables are sensitive in estimating forest structure.

Table 4.
The MLR prediction models and their accuracy assessment under different schemes.
Figure 11 and Figure 12 show the correlations between the predicted and field-measured values of characteristic parameters estimated using the MLR models of Scheme 1 and Scheme 2, respectively. As shown in Figure 11, the R2 values of the model training accuracy for single tree DBH, AGB, and V in Scheme 1 were 0.76, 0.78, and 0.83, respectively, with rRMSE = 9.67 to 27.23%; the R2 values of the model testing accuracy were 0.64, 0.69, and 0.62, respectively, with rRMSE = 11.02 to 39.01%. As shown in Figure 12, the training and testing accuracy of Scheme 2 single tree characteristic parameters were improved. The R2 values of the model training accuracy of DBH, AGB, and V were 0.78, 0.85, and 0.84, respectively, with rRMSE = 9.33 to 30.82%. The R2 values of the model testing accuracy were 0.69, 0.82, and 0.80, respectively, with rRMSE = 10.41–24.67%. The comparison of the results shows that the R2 values of the estimation accuracy of the characteristic parameters of Scheme 2 were all improved after adding the canopy structure variable. Among them, the estimation accuracy of V improved by 29.0%, which was the greatest improvement, followed by AGB with an accuracy improvement of 18.8% and DBH with an accuracy improvement of 7.8%. In addition, the rRMSE values of the AGB and V estimation results also decreased by 36.8% and 27.7%, respectively, which were large decreases.
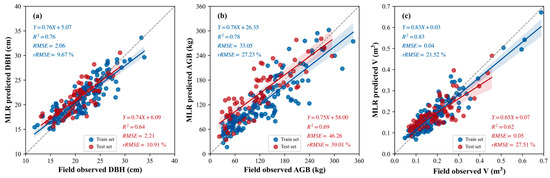
Figure 11.
Correlation between measured and estimated values of single tree DBH (a), AGB (b), and V (c) of the MLR model based on Scheme 1.
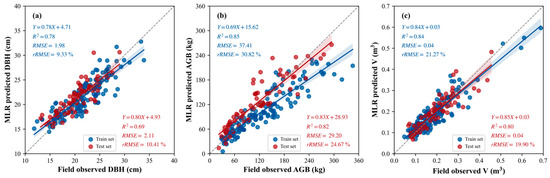
Figure 12.
Correlation between measured and estimated values of single tree DBH (a), AGB (b), and V (c) of the MLR model based on Scheme 2.
3.3.2. SVR Estimation Results
Figure 13 shows the comparison of the R2 values of the estimated characteristic parameters for the four kernel function SVR models under the two modeling schemes. As shown in Figure 13, the R2 values of the single tree characteristic parameters in both Scheme 1 and Scheme 2 were the highest for the SVR model with RBF as the kernel function. Therefore, the RBF kernel function was chosen to construct the SVR model in this study.
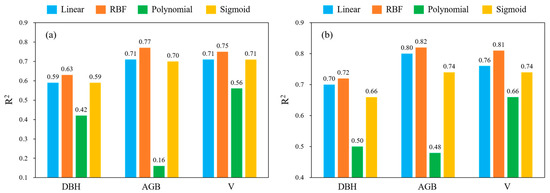
Figure 13.
Results of single tree characteristic parameters using different kernel functions ((a): Scheme 1, (b): Scheme 2).
Figure 14 and Figure 15 show the correlations between the predicted and field-measured values of characteristic parameters estimated using the SVR models of two modeling schemes, respectively. As shown in Figure 14, the R2 values of the model training accuracy for single tree DBH, AGB, and V in Scheme 1 were 0.83, 0.84, and 0.85, respectively, with rRMSE = 8.14 to 24.10%; the R2 values of the model testing accuracy were 0.67, 0.77, and 0.75, respectively, with rRMSE = 10.76 to 26.78%. As shown in Figure 15, the R2 values of the model testing accuracy of DBH, AGB, and V were 0.72, 0.82, and 0.81, respectively, with rRMSE = 10.24 to 23.37%. The comparison of the results shows that the R2 values of the training and testing accuracy of single tree characteristic parameters of the SVR model were all improved by adding canopy structure variables in Scheme 2. Among them, the estimation accuracy of V improved by 8%, which was the greatest improvement, followed by DBH with an accuracy improvement of 7.4% and AGB with an accuracy improvement of 6.5%. In addition, the rRMSE values of the AGB and V estimation results also decreased by 12.7% and 11.6%, respectively, which were large decreases, indicating that coupling canopy parameters can improve the estimation accuracy of urban single tree parameters.
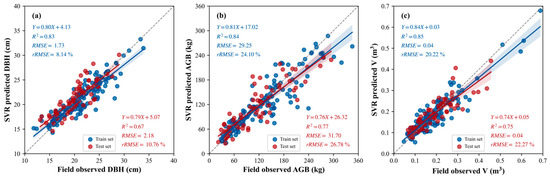
Figure 14.
Correlation between measured and estimated values of single tree DBH (a), AGB (b), and V (c) of the SVR model based on Scheme 1.
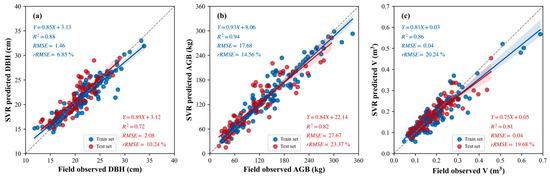
Figure 15.
Correlation between measured and estimated values of single tree DBH (a), AGB (b), and V (c) of the SVR model based on Scheme 2.
3.3.3. RF Estimation Results
The training data were input into the random forest model to traverse all variable values and eventually obtain the optimal parameters. Figure 16 shows Mtry, which was used to determine the minimum variable for each tree in the RF model, and the minimum Mtry value was required when the model error was minimal. As shown in Figure 17, the RMSE of the model error tended to be stable after Ntree reached 1500. Therefore, the values of Ntree in the optimized random forest model were set to 1500 in this study. Table 5 lists the specific settings for different parameter values for the two schemes.
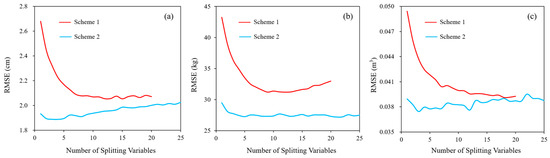
Figure 16.
Influence of Mtry on model error ((a): DBH, (b): AGB, (c): V).
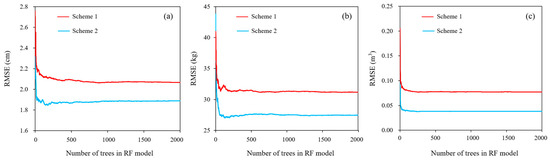
Figure 17.
Influence of Ntree on model error ((a): DBH, (b): AGB, (c): V).

Table 5.
Results of the optimization of model parameters for different schemes.
Figure 18 and Figure 19 show the correlations between the predicted and field-measured values of characteristic parameters estimated using the RF models of Scheme 1 and Scheme 2, respectively. As shown in Figure 18, the R2 values of the model training accuracy for single tree DBH, AGB, and V in Scheme 1 were 0.74, 0.80, and 0.81, respectively, with rRMSE = 10.46 to 26.36%; the R2 values of the model testing accuracy were 0.67, 0.74, and 0.76, respectively, with rRMSE = 10.95 to 29.69%. As shown in Figure 19, the training and testing accuracy of Scheme 2 single tree characteristic parameters were improved. The R2 values of the model training accuracy of DBH, AGB, and V were 0.80, 0.89, and 0.86, respectively, with rRMSE = 8.9 to 20.77%. The R2 values of the model testing accuracy were 0.76, 0.85, and 0.83, respectively, with rRMSE = 9.87–22.51%. Comparing the RF model results, the R2 values of the estimation accuracy of the characteristic parameters of Scheme 2 were all improved after adding the canopy structure variable. Among them, the estimation accuracy of AGB improved by 14.9%, which was the greatest improvement, followed by DBH with an accuracy improvement of 13.4% and V with an accuracy improvement of 9.2%. In addition, the rRMSE values of the AGB and V estimation results also decreased by 24.2% and 15.2%, respectively, which were large decreases.
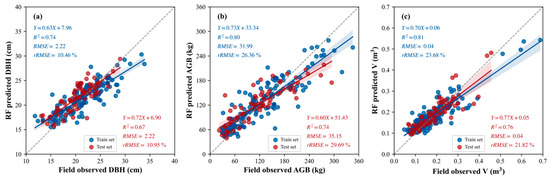
Figure 18.
Correlation between measured and estimated values of single tree DBH (a), AGB (b), and V (c) of the RF model based on Scheme 1.
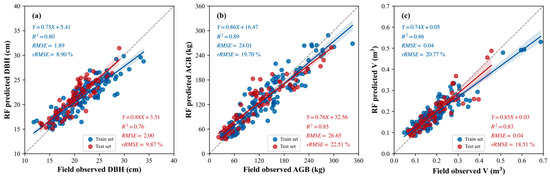
Figure 19.
Correlation between measured and estimated values of single tree DBH (a), AGB (b), and V (c) of the RF model based on Scheme 2.
3.4. Comparison of Model Results
Table 6 shows the summary of the field measured data and the estimation results of different model characteristic parameters. Compared with the field-measured data, the estimated CV values of MLR, SVR, and RF models range from 16.6 to 18.11%, the estimated CVs of AGB range from 49.15 to 54.22%, and the estimated CVs of V range from 44.67 to 46.55%, with smaller variations and mean values closer to the measured values. Appendix A (Table A1) shows the comparison of the model training accuracy and testing accuracy of three models for estimating three single tree parameters in two schemes. An analysis of the results in Appendix A (Table A1) shows that all models of the two schemes achieved higher accuracy estimation of single tree parameters in urban forests. Figure 20 shows the distribution of the normalized residuals for the testing phase of the characteristic parameters for different models. The normalized residuals of the characteristic parameters of the testing samples of the three models were in the range of −2 to 2, indicating that all models had good stability and reliability in predicting the characteristic parameters of a single tree.

Table 6.
Summary of information on measured and predicted characteristic parameters of the samples.
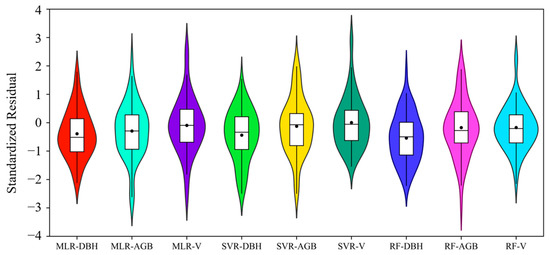
Figure 20.
Distribution of normalized residuals for the testing phase of characteristic parameters for different models.
However, for the two schemes, the model accuracy and testing accuracy of the single tree parameters for all models of Scheme 2 were improved, and the error was decreased compared with Scheme 1, indicating that the coupled canopy parameters could improve the estimation accuracy of the urban single tree parameter. In addition, from the three models, the performance of the two machine learning models was better than that of the MLR model, where the training accuracy of single tree characteristic parameters of the SVR model was slightly higher than that of the RF model, but the testing accuracy of single tree characteristic parameters of the RF model was better than that of the SVR model.
4. Discussion
The forest canopy is a key component of forests that affects ecosystem processes and functions [56], and the quantification and analysis of canopy distribution is one of the methods used to characterize the spatial structure of forests. In this study, voxel-based canopy volume was used to characterize the canopy spatial structure of different urban trees, and the canopy volume profile was derived to more intuitively reflect the spatial heterogeneity of the canopy structure and the variation in the arrangement of elements within the canopy. As shown in Figure 5, Figure 6 and Figure 7, the open gap volume of G. biloba was the largest, while the closed gap volume of C. camphora was larger than that of both G. biloba and M. glyptostroboides. First, this had a direct influence on the structure and shape of the canopy, which was relatively regular for C. camphora and M. glyptostroboides, while the canopy shape of G. biloba was more complex and the distribution of branches and leaves was more dispersed, resulting in a larger volume share in the open gap of G. biloba. In addition, closed gap volume was also strongly related to proper pruning in cities, which causes higher crown base height [43], thus leading to a larger percentage of closed gap volume. On the other hand, coniferous trees allow more light penetration into the lower canopy compared to broadleaved trees [57], and M. glyptostroboides belongs to the coniferous species, thus allowing M. glyptostroboides to form more areas of oligophotic zone.
Lidar data can provide parameter information directly connected to forest canopy structure, and the estimation of forest characteristic parameters using different regression methods can produce satisfactory prediction results [58]. The results of this study show that the estimation accuracy of single tree characteristic parameters with coupled canopy structural variables was improved compared to using only height and density characteristic variables. The model accuracy was higher than the prediction accuracy of stand stock and aboveground biomass in urban broadleaf forest areas estimated using ALS data [59]. This is due to the fact that high-density ULS data had richer canopy structure information. Therefore, high-density lidar data were more advantageous in estimating stand volume and aboveground biomass.
This research shows that the performance of the SVR and RF machine learning models was better than that of the MLR model. As a statistical regression model, MLR is not suitable for representing the complexity of high data and is sensitive to noise, and the MLR model is often prone to underfitting, making the model performance poor. SVR seeks linear regression hyperplanes and solves nonlinear problems in low-dimensional spaces by mapping kernel functions from low to high dimensions. Although the SVR model fits the training data well, there may be overfitting of the model. In addition, the SVR model also needs to find the optimal penalty coefficient and gamma value to obtain the optimal model [60,61]. The RF was able to handle high-dimensional data and had good noise resistance. During the model operations, unbiased estimates of errors can be obtained, and the importance of each variable can be evaluated in the RF model [62]. The accuracy of training the single tree characteristic parameters of the SVR model in this study was slightly higher than that of the RF model, but the validation accuracy was not as good as that of the RF model in the study, which may be caused by this reason.
Related studies around the world also indicate that RF has good predictive ability in forest parameter estimation [58,60,63]. For example, Zhou et al. [64] used a RF model to estimate the AGB of urban single trees based on UAV lidar data and achieved high estimation accuracy. Zhang et al. [65] combined lidar and high-resolution remote sensing images by comparing different models (SLR, LNN, BPNN, SVR, RF) for the quantitative estimation and inversion of biomass, and the results indicated that the RF model had the highest fitting accuracy. Cao et al. [63] indicated that the accuracy of the RF model was higher than that with SVR, backpropagation neural networks, k-nearest neighbor, and the generalized linear mixed model in the remote sensing estimation of forest biomass based on satellite remote sensing. Peng Xi et al. [66] established different models for estimating the s characteristic parameters of tropical forests in China based on UAV lidar data, and the study indicated that the RF model had good accuracy in estimating forest characteristic parameters. Although this study provides a reference for the application of UAV lidar in urban forest characteristic parameter estimation, there are still some limitations. The urban forest is unevenly distributed, and the estimation of large-scale urban forest characteristic parameters using UAV lidar is still a challenge.
5. Conclusions
In this study, we used UAV lidar to obtain three kinds of single tree canopy point clouds coupled with point cloud and canopy structure variables. MLR, SVR, and RF models were used to estimate the characteristic parameters of DBH, AGB, and V of single trees in urban forests based on UAV-Lidar data. The results indicate that canopy volume profiles can visualize the spatial heterogeneity of forest canopy structure and the distribution and variation of elements in the vertical direction, and canopy structure variables such as CG, OV, EV, S, and CD had important effects on single tree characteristic parameters. The model training accuracy and testing accuracy of the single tree parameters of the MLR, SVR, and RF models were improved by incorporating canopy structure variables. In comparison, the two machine learning models, SVR and RF, outperformed MLR, but the testing accuracy of single tree characteristic parameters of the RF model was better than that of the SVR model. The results of the study provide an important reference for the estimation of single tree characteristic parameters in urban forests based on UAV-Lidar data, which is necessary and useful for urban managers to understand the functions and values of urban forests and to maximize the environmental benefits of urban forests.
Author Contributions
Conceptualization, H.D.; methodology, B.Z.; validation, B.Z.; formal analysis, B.Z. and Z.H.; investigation, B.Z., L.Z., J.X., Y.G. and C.C.; data curation, B.Z.; writing—original draft preparation, B.Z.; writing—review and editing, X.L., F.M., G.Z. and H.D.; visualization, B.Z.; supervision, H.D. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the support of the National Natural Science Foundation of China (U1809208, 32171785), the Key Research and Development Program of Zhejiang Province (2021C02005), and the State Key Laboratory of Subtropical Silviculture (No. ZY20180201).
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge the support of various foundations. The authors are grateful to the editor and anonymous reviewers whose comments have contributed to improving the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Accuracy evaluation of the parametric model of a single tree characteristic for different schemes.
Table A1.
Accuracy evaluation of the parametric model of a single tree characteristic for different schemes.
| Model | Scheme | DBH | AGB | V | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | rRMSE (%) | R2 | RMSE | rRMSE (%) | R2 | RMSE | rRMSE (%) | |||
| Train | MLR | Scheme 1 | 0.76 | 2.06 | 9.67 | 0.78 | 33.05 | 27.23 | 0.83 | 0.04 | 21.52 |
| Scheme 2 | 0.78 | 1.98 | 9.33 | 0.85 | 37.41 | 30.82 | 0.84 | 0.04 | 21.27 | ||
| SVR | Scheme 1 | 0.83 | 1.73 | 8.14 | 0.84 | 29.25 | 24.10 | 0.85 | 0.04 | 20.22 | |
| Scheme 2 | 0.88 | 1.46 | 6.85 | 0.94 | 17.68 | 14.56 | 0.86 | 0.04 | 20.24 | ||
| RF | Scheme 1 | 0.74 | 2.22 | 10.46 | 0.80 | 31.99 | 26.36 | 0.81 | 0.04 | 23.68 | |
| Scheme 2 | 0.80 | 1.89 | 8.90 | 0.89 | 24.01 | 19.70 | 0.86 | 0.04 | 20.77 | ||
| Test | MLR | Scheme 1 | 0.64 | 2.21 | 10.91 | 0.69 | 46.26 | 39.01 | 0.62 | 0.05 | 27.51 |
| Scheme 2 | 0.69 | 2.11 | 10.41 | 0.82 | 29.20 | 24.67 | 0.80 | 0.04 | 19.90 | ||
| SVR | Scheme 1 | 0.67 | 2.18 | 10.76 | 0.77 | 31.70 | 26.78 | 0.75 | 0.04 | 22.27 | |
| Scheme 2 | 0.72 | 2.08 | 10.24 | 0.82 | 27.67 | 23.37 | 0.81 | 0.04 | 19.68 | ||
| RF | Scheme 1 | 0.67 | 2.22 | 10.95 | 0.74 | 35.15 | 29.69 | 0.76 | 0.04 | 21.82 | |
| Scheme 2 | 0.76 | 2.00 | 9.87 | 0.85 | 26.65 | 22.51 | 0.83 | 0.04 | 18.51 | ||
References
- Baumeister, C.F.; Gerstenberg, T.; Plieninger, T.; Schraml, U. Exploring cultural ecosystem service hotspots: Linking multiple urban forest features with public participation mapping data. Urban For. Urban Green. 2020, 48, 126561. [Google Scholar] [CrossRef]
- Cheng, W.; Chunju, C.; Kanghua, T. The Concept, Range and Researh Area of Urban Forest. World For. Res. 2004, 17, 23–27. [Google Scholar] [CrossRef]
- Escobedo, F.J.; Nowak, D.J. Spatial heterogeneity and air pollution removal by an urban forest. Landsc. Urban Plan 2009, 90, 102–110. [Google Scholar] [CrossRef]
- Liu, L.; Coops, N.C.; Aven, N.W.; Pang, Y. Mapping urban tree species using integrated airborne hyperspectral and LiDAR remote sensing data. Remote Sens. Environ. 2017, 200, 170–182. [Google Scholar] [CrossRef]
- Zengyuan, L.; Qingwang, L.; Yong, P. Review on forest parameters inversion using LiDAR. Natl. Remote Sens. Bull. 2016, 20, 1138–1150. [Google Scholar]
- Jones, M.S.D. Characterizing forest ecological structure using pulse types and heights of airborne laser scanning. Remote Sens. Environ. 2010, 114, 1069–1076. [Google Scholar]
- Li, X.; Liu, J.; Jiang, S.; Jia, B. Analysis of the urban tree canopy and community structure of hospitals in urban areas of Beijing. Acta Ecol. Sin. 2019, 39, 12. [Google Scholar]
- Wang, C.; Peng, Z.; Tao, K. Characteristics and development of urban forest in China. Chin. J. Ecol. 2004, 23, 5. [Google Scholar]
- Gao, L.; Chai, G.; Zhang, X. Above-Ground Biomass Estimation of Plantation with Different Tree Species Using Airborne LiDAR and Hyperspectral Data. Remote Sens. 2022, 14, 2568. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Nsset, E.; Gobakken, T. LiDAR sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Hirata, Y.; Furuya, N.; Saito, H.; Pak, C.; Leng, C.; Sokh, H.; Ma, V.; Kajisa, T.; Ota, T.; Mizoue, N. Object-Based Mapping of Aboveground Biomass in Tropical Forests Using LiDAR and Very-High-Spatial-Resolution Satellite Data. Remote Sens. 2018, 10, 438. [Google Scholar] [CrossRef]
- Torres de Almeida, C.; Gerente, J.; Rodrigo dos Prazeres Campos, J.; Caruso Gomes Junior, F.; Providelo, L.A.; Marchiori, G.; Chen, X. Canopy Height Mapping by Sentinel 1 and 2 Satellite Images, Airborne LiDAR Data, and Machine Learning. Remote Sens. 2022, 14, 4112. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Sun, Y.; Ruan, H.; Wang, G.; Dai, J.; She, G. Estimating canopy structure and biomass in bamboo forests using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 114–129. [Google Scholar] [CrossRef]
- Yin, T.; Cook, B.D.; Morton, D.C. Three-dimensional estimation of deciduous forest canopy structure and leaf area using multi-directional, leaf-on and leaf-off airborne lidar data. Agric. For. Meteorol. 2022, 314, 108781. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Wang, Y.; Zheng, Z.; Zheng, S.; Zhao, D.; Bai, Y. UAV-based individual shrub aboveground biomass estimation calibrated against terrestrial LiDAR in a shrub-encroached grassland. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102358. [Google Scholar] [CrossRef]
- Jiang, X.; Li, G.; Lu, D.; Chen, E.; Wei, X. Stratification-Based Forest Aboveground Biomass Estimation in a Subtropical Region Using Airborne Lidar Data. Remote Sens. 2020, 12, 1101. [Google Scholar] [CrossRef]
- Lin, W.; Lu, Y.; Li, G.; Jiang, X.; Lu, D. A comparative analysis of modeling approaches and canopy height-based data sources for mapping forest growing stock volume in a northern subtropical ecosystem of China. GIScience Remote Sens. 2022, 59, 568–589. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jones, S.D.; Soto-Berelov, M.; Haywood, A.; Hislop, S. Monitoring aboveground forest biomass dynamics over three decades using Landsat time-series and single-date inventory data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101952. [Google Scholar] [CrossRef]
- Zhao, K.; Suarez, J.C.; Garcia, M.; Hu, T.; Wang, C.; Londo, A. Utility of multitemporal lidar for forest and carbon monitoring: Tree growth, biomass dynamics, and carbon flux. Remote Sens. Environ. 2018, 204, 883–897. [Google Scholar] [CrossRef]
- Cao, L.; Gao, S.; Li, P.; Yun, T.; Shen, X.; Ruan, H. Aboveground Biomass Estimation of Individual Trees in a Coastal Planted Forest Using Full-Waveform Airborne Laser Scanning Data. Remote Sens. 2016, 8, 729. [Google Scholar] [CrossRef]
- Liu, H.; Fan, W.; Xu, Y.; Lin, W. Single tree biomass estimation based on UAV LiDAR point cloud. J. Cent. South Univ. For. Technol. 2021, 41, 8. [Google Scholar]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Estimating Aboveground Carbon Stock at the Scale of Individual Trees in Subtropical Forests Using UAV LiDAR and Hyperspectral Data. Remote Sens. 2021, 13, 4969. [Google Scholar] [CrossRef]
- Hao, L.; Zhengnan, Z.; Lin, C. Estimating forest stand characteristics in a coastal plain forest plantation based on vertical structure profile parameters derived from ALS data. Natl. Remote Sens. Bull. 2018, 22, 17. [Google Scholar]
- McElhinny, C.; Gibbons, P.; Brack, C.; Bauhus, J. Forest and woodland stand structural complexity: Its definition and measurement. For. Ecol. Manag. 2005, 218, 1–24. [Google Scholar] [CrossRef]
- Camarretta, N.; Ehbrecht, M.; Seidel, D.; Wenzel, A.; Zuhdi, M.; Merk, M.S.; Schlund, M.; Erasmi, S.; Knohl, A. Using Airborne Laser Scanning to Characterize Land-Use Systems in a Tropical Landscape Based on Vegetation Structural Metrics. Remote Sens. 2021, 13, 4794. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q. Review of forest vertical structure parameter inversion based on remote sensing technology. Natl. Remote Sens. Bull. 2013, 17, 20. [Google Scholar]
- Zheng, J.; Zhang, C.; Zhou, J.; Zhao, X.; Yu, X.; Qin, Y. Study on Vertical Structue of Forest Communities in Yunmengshan. For. Res. 2007, 20, 7. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating canopy structure of Douglas-fir forest stands from discrete-return LiDAR. Trees 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, Z.; Cao, L.; Coops, N.C.; Wu, X. Assessment of approaches for monitoring forest structure dynamics using bi-temporal digital aerial photogrammetry point clouds. Remote Sens. Environ. 2021, 255, 112300. [Google Scholar] [CrossRef]
- Hilker, T.; Leeuwen, M.V.; Coops, N.C.; Wulder, M.A.; Newnham, G.J.; Jupp, D.; Culvenor, D.S. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; She, G. Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
- Cao, Z. Biomass and Distribution Pattern of Cinnamomum camphora in Yangzhou. For. Sci. Technol. 2020, 10, 69–71. [Google Scholar]
- Liu, K.; Cao, L.; Wang, G.; Cao, F. Biomass allocation patterns and allometric models of Ginkgo biloba. J. Beijing For. Univ. 2017, 39, 12–20. [Google Scholar] [CrossRef]
- Zhuang, H.; Becuwe, X.; Xiao, C.; Wang, Y.; Wang, H.; Yin, S.; Liu, C. Alometric Equation-Based Estimation of Biomass Carbon Sequestration in Metasequoia glyptostroboides Plantations in Chongming lsland, Shanghai. J. Shanghai Jiaotong Univ. (Agric. Sci.) 2012, 30, 8. [Google Scholar]
- Xingan, L. Mathematical Model of Tree Volume Table in Zhejiang Province. J. Zhejiang For. Sci. Technol. 1986, 4, 25–30. [Google Scholar]
- Zhao, X.q.; Guo, Q.h.; Su, Y.j.; Xue, B.l. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, T.; Zhu, J.; Wu, F.; Li, X.; Lu, D.; Yu, F. Individual Tree Segmentation and Tree Height Estimation Using Leaf-Off and Leaf-On UAV-LiDAR Data in Dense Deciduous Forests. Remote Sens. 2022, 14, 2787. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Kim, Y.; Yang, Z.; Cohen, W.B.; Pflugmacher, D.; Lauver, C.L.; Vankat, J.L. Distinguishing between live and dead standing tree biomass on the North Rim of Grand Canyon National Park, USA using small-footprint lidar data. Remote Sens. Environ. 2009, 113, 2499–2510. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F.; She, G.; Cao, L. Extrapolation Assessment for Forest Structural Parameters in Planted Forests of Southern China by UAV-LiDAR Samples and Multispectral Satellite Imagery. Remote Sens. 2022, 14, 2677. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Z. Inversion of biomass components of the temperate forest using airborne Lidar technology in Xiaoxing’ an Mountains, Northeastern of China. Chin. J. Plant Ecol. 2012, 36, 1095–1105. [Google Scholar] [CrossRef]
- Dong, Y.H.; Li, Y.Q.; Sun, D.; Li, P.P.; Fan, H.L. Street Tree Information Extraction and Dynamic Analysis Based on Vehicle-Borne LiDAR Data. Geogr. Geo-Inf. Sci. 2018, 34, 46–51+82. [Google Scholar]
- Zięba-Kulawik, K.; Skoczylas, K.; Węzyk, P.; Teller, J.; Mustafa, A.; Omrani, H. Monitoring of urban forests using 3D spatial indices based on a LiDAR point clouds and voxel approach. Urban For. Urban Green. 2021, 65, 127324. [Google Scholar] [CrossRef]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Estimating forest structural attributes using UAV-LiDAR data in Ginkgo plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Estornell, J.; Hadas, E.; Martí, J.; López-Cortés, I. Tree extraction and estimation of walnut structure parameters using airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102273. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J. A Review of Tree Species Classification Based on Airborne LiDAR Data and Applied Classifiers. Remote Sens. 2021, 13, 353. [Google Scholar] [CrossRef]
- Lumley, T.; Miller, A. Leaps: Regression Subset Selection. EMBO J. 2009, 12, 4657–4666. [Google Scholar]
- Ding, J.; Huang, W.; Liu, Y.; Hu, Y. Estimation of Forest Aboveground Biomass in Northwest Hunan Province Based on Machine Learning and Multi-Source Data. Sci. Silvae Sin. 2021, 57, 36–48. [Google Scholar]
- Poorazimy, M.; Shataee, S.; McRoberts, R.E.; Mohammadi, J. Integrating airborne laser scanning data, space-borne radar data and digital aerial imagery to estimate aboveground carbon stock in Hyrcanian forests, Iran. Remote Sens. Environ. 2020, 240, 111669. [Google Scholar] [CrossRef]
- Zhao, X. Research on Forest Aboveground Biomass Estimation Based on Airborne LiDAR Data; Xi’an University of Science and Technology: Xi’an, China, 2020. [Google Scholar]
- Xiao, Y. Research on Estimation Method of Forest Volume Wangyedian Forest Farm Based on Multi-Source Remote Sensing Data; Central South University of Forestry and Technology: Changsha, China, 2021. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Dong, L.; Du, H.; Han, N.; Li, X.; He, S. Application of Convolutional Neural Network on Lei Bamboo Above-Ground-Biomass (AGB) Estimation Using Worldview-2. Remote Sens. 2020, 12, 958. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Fan, W.; Xu, X.; Liu, Y.; Cui, L. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms—ScienceDirect. Agric. For. Meteorol. 2018, 256, 445–457. [Google Scholar] [CrossRef]
- Leiterer, R.; Torabzadeh, H.; Furrer, R.; Schaepman, M.E.; Morsdorf, F. Towards Automated Characterization of Canopy Layering in Mixed Temperate Forests Using Airborne Laser Scanning. Forests 2015, 6, 4146–4167. [Google Scholar] [CrossRef]
- Ishii, H. The role of crown architecture in promoting complementary use of light among coexisting species in temperate forests. Ecol. Res. 2010, 25, 715–722. [Google Scholar] [CrossRef]
- Almeida, C.; Galvo, L.S.; Sato, Y.; Lopes, A.P.; Longo, M. Combining LiDAR and hyperspectral data for aboveground biomass modeling in the Brazilian Amazon using different regression algorithms. Remote Sens. Environ. 2019, 232, 111323. [Google Scholar] [CrossRef]
- Giannico, V.; Lafortezza, R.; John, R.; Sanesi, G.; Chen, J. Estimating Stand Volume and Above-Ground Biomass of Urban Forests Using LiDAR. Remote Sens. 2016, 8, 339. [Google Scholar] [CrossRef]
- Gao, Y.; Dengsheng, L.; Guiying, L.; Guangxing, W.; Qi, C.; Lijuan, L.; Dengqiu, L. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Shen, B.; Ding, L.; Ma, L.; Li, Z.; Pulatov, A.; Kulenbekov, Z.; Chen, J.; Mambetova, S.; Hou, L.; Xu, D.; et al. Modeling the Leaf Area Index of Inner Mongolia Grassland Based on Machine Learning Regression Algorithms Incorporating Empirical Knowledge. Remote Sens. 2022, 14, 4196. [Google Scholar] [CrossRef]
- Chen, M.; Qiu, X.; Zeng, W.; Peng, D. Combining Sample Plot Stratification and Machine Learning Algorithms to Improve Forest Aboveground Carbon Density Estimation in Northeast China Using Airborne LiDAR Data. Remote Sens. 2022, 14, 1477. [Google Scholar] [CrossRef]
- Cao, L.; Pan, J.; Li, R.; Li, J.; Li, Z. Integrating Airborne LiDAR and Optical Data to Estimate Forest Aboveground Biomass in Arid and Semi-Arid Regions of China. Remote Sens. 2018, 10, 532. [Google Scholar] [CrossRef]
- Zhou, L.; Li, X.; Zhang, B.; Xuan, J.; Gong, Y.; Tan, C.; Huang, H.; Du, H. Estimating 3D Green Volume and Aboveground Biomass of Urban Forest Trees by UAV-Lidar. Remote Sens. 2022, 14, 5211. [Google Scholar] [CrossRef]
- Zhang, Y.; Shao, Z. Assessing of Urban Vegetation Biomass in Combination with LiDAR and High-resolution Remote Sensing Images. Int. J. Remote Sens. 2021, 42, 964–985. [Google Scholar] [CrossRef]
- Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H.; Wang, J.; Li, H. Comparison of Modeling Algorithms for Forest Canopy Structures Based on UAV-LiDAR: A Case Study in Tropical China. Forests 2020, 11, 1324. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).