Error in Figure
In the original article [1], there was a mistake in Figure 4 as published. The annotation of Equation (5) was incorrect. The corrected Figure 4 appears below.
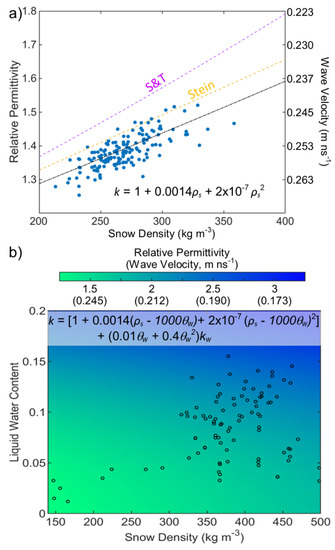
Figure 4.
Results of in situ data comparisons for (a) dry snow with Sihvola and Tiuri [31] (S and T) and Stein et al. [47] shown for comparison to our regression line; and (b) for calorimeter-based liquid water content observations.
Text Correction
There was an error in the original article. There was a typographical error in Equation (5) where a constant was not included.
A correction has been made to Section 3. Results, 3.2. Wet Snow Observations, paragraph 1:
The snow pit observations at the Sandia Mountains and Cameron Pass sites resulted in 92 observations with LWC present and isothermal conditions (necessary for appropriate application of Equation (3). The values of ranged from 147–498 kg m−3, observations of ranged from approximately 0.01 to 0.16, and measurements from 1.15 to 2.83. A regression analysis of as a function of and resulted in a r2 value of 0.37 with a RMSE of 0.22 and a standard deviation of 0.21. In terms of deviations from , this regression results in an RMSE of 0.030 and a standard deviation of 0.032 (Figure 4b). This regression equation for as a function of and is
where is the relative permittivity of liquid water at 0 °C (~87.9) and the bracketed portion of the equation is the background effect of dry snow permittivity, described using Equation (4).
The authors apologize for any inconvenience caused and state that the scientific conclusions are unaffected. The original article has been updated.
Reference
- Webb, R.W.; Marziliano, A.; McGrath, D.; Bonnell, R.; Meehan, T.G.; Vuyovich, C.; Marshall, H.-P. In Situ Determination of Dry and Wet Snow Permittivity: Improving Equations for Low Frequency Radar Applications. Remote Sens. 2021, 13, 4617. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).