Abstract
Downgoing/upgoing P/S-wave decomposition of ocean-bottom seismic (OBS) multicomponent data can help suppress the water-layer multiples and cross-talks between P- and S-waves, and therefore plays an important role in seismic migration and construction of P- and S-wave velocity models. We proposed novel composite calibration filters by introducing an additional dimension to the calibration of the particle velocity components, extending the wave-equation-based adaptive decomposition method. We also modified the existing workflow by jointly using primary reflections at near-to-medium offsets and ocean-bottom refractions at far offsets in the calibration optimization. The decomposition scheme with the novel calibration filters yielded satisfactory results in a deep-water OBS field data decomposition example. Expected decomposition effects, such as the enhancement of primary reflections and the attenuation of water-layer multiple events, can be observed in the decomposed upgoing wavefields. An experiment illustrated the effectiveness of composite calibration filters that compensated for unexpected velocity errors along the offset dimension.
1. Introduction
With the rapid development of ocean-bottom seismic (OBS) acquisition technologies in the last few decades, multicomponent seismology, which was originally exploited in large-scale geophysical research, has revealed its superiority in ocean-bottom seismic prospecting applications over traditional mono-component (acoustic pressure) methods [1,2]. The additional elastic information carried by the geophone-recorded orthogonal particle velocity components can be exploited to acquire shear wave-related properties. Another advantage of ocean-bottom acquisition is the capability of time-lapse reservoir monitoring (4D survey), realized by the almost permanent deployment of seabed instruments [3,4,5].
Based on multicomponent OBS observations, combined P- and S-wave data permit more effective estimations of the elasticity and physical properties of subsurface media, and improve the accuracy of geological structure imaging and petroleum reservoir characterization. For multicomponent OBS data processing, the decomposition procedure separates the acquired seismic data into downgoing and upgoing P- and S-waves, in preparation for subsequent velocity estimation and respective migration imaging processes [6], or other analyses such as amplitude variation with offset (AVO) [7]. White [8] pointed out that water-layer multiples can be attenuated by summing the pressure component recorded by the hydrophone and the vertical velocity component recorded by the geophone. Early practices of this technique did not involve the horizontal velocity component (also called dual-sensor summation or PZ summation), and the acoustic decomposition of downgoing and upgoing waves occurs solely at a depth level just above the seafloor [9]. Based on these early attempts at multicomponent summation, Schalkwijk et al. [10,11,12] and Muijs et al. [13,14] structured the wave-equation-based quint-stage/quad-step scheme. This adaptive method sequentially carries out decomposition just above and just below the seafloor. What makes the adaptive decomposition method stand out is that no a priori knowledge of the medium parameters of the seabed in the immediate vicinity of the geophones is needed, and all the seabed elastic parameters required by the decomposition of P- and S-waves are given by optimization procedures. Some subsequent studies proposed adjustments in the selection of optimization cost functions or refinement of seabed property estimation in the scheme [15], whereas the basic structure of adaptive decomposition remained identical. Acoustic decomposition is common prior to elastic decomposition. Separated downgoing waves are essential for the velocity calibration steps after acoustic decomposition. The up–down separated pressure just above the ocean bottom can also serve as the input data for mirror migration, which improves the illumination of shallower structures, and up–down deconvolution, which further eliminates the free-surface multiples [16,17,18,19,20,21]. The decomposed wavefields (particularly upgoing S-wave potential) can improve the resolution of imaging, ameliorate the “gas chimney” problem and provide support for predicting oil and gas reservoirs or the gas hydrate stability zone (GHSZ) [22,23,24]. These advantages of the adaptive scheme have made the application of the ocean-bottom decomposition method even more practical compared with the decomposition of land seismic data. Other technical routes for elastic decomposition also exist, such as those that take advantage of polarization characteristics often carried out in the ray-parameter domain and decomposition schemes developed for downhole data [25,26,27,28,29].
This study focuses on the crucial steps of geophone component calibration that would severely affect the reliability of P- and S-wave separation [30,31,32], especially for field data. Our modified adaptive decomposition scheme has incorporated practical techniques using far-offset windows rather than sole near-offset windows containing primary reflections in the optimization procedures [33,34]. The 1D calibration filters in traditional schemes can only perform an overall adjustment to the velocity data and cannot precisely calibrate data from each trace. To solve this problem, we add another dimension to the calibration of the velocity components in the ω-x (angular frequency–offset) domain, and present novel calibration filters called “composite calibration filters”. In later sections, the corresponding optimization procedures of our novel ω-x domain composite calibration filters are discussed in detail for the vertical and horizontal velocities, respectively. The verification of our method was demonstrated by its application to a deep-water OBS dataset acquired in the South China Sea.
2. Methods
First, we briefly review some characteristics of the multicomponent seismic recordings acquired from the ocean bottom. Figure 1 shows a schematic diagram of ocean-bottom seismic data acquisition. As shown in the bottom left of the figure, a typical multicomponent ocean-bottom seismic receiver comprises hydrophone and orthogonal geophone sensors such that acoustic information and elastic motion information can be faithfully recorded simultaneously. Hydrophone and geophone sensors are not significantly separated in space in field data acquisition. The so-called “just above the seafloor” and “just below the seafloor” terms are theoretical expressions that indicate the depth level of the acoustic decomposition steps (i.e., Stage 1 in our practice) and the elastic decomposition steps (i.e., Stage 2 to Stage 4 in our practice). Because only P-waves can propagate in the water layer, all S-waves are generated at the solid–fluid and subsurface interfaces. Downgoing P-waves in the water layer are either waves directly emitted from the seismic source near the free surface or waves reflected from the free surface. The waves related to free-surface reflections are often categorized as water-layer multiples and are commonly considered noise in seismic imaging. Upgoing P-waves in the water layer consist of transmitted waves propagating through the seafloor and reflections from the ocean bottom. The motion information of the waves mentioned above is recorded by hydrophones, which are commonly assumed to be perfectly coupled to seawater. However, orthogonal geophone sensors need to be calibrated with respect to the hydrophone to compensate for their imperfect coupling to the seabed and response differences. The components recorded by geophones consist of P-wave constituents and S-wave constituents simultaneously. Downgoing waves just below the seafloor consist of transmitted waves propagating down from the water layer and reflections caused by the solid–fluid interface. Upgoing waves just below the seafloor are considered the seismic data of interest, containing P- and S-waves reflected from the subsurface structures. S-waves are generated at the solid-fluid and subsurface interfaces during propagation. These converted S-waves can also be converted back into P-waves. The ocean-bottom refractions that travel along the solid-fluid interface are also recorded by hydrophones and geophones. The reflection from the seabed unavoidably affects the upgoing pressure and particle velocity separated by the acoustic decomposition equations (see Appendix A), regardless of the seismic data quality. Therefore, it is normal to witness direct events in the upgoing pressure and some level of subsurface-reflected events in downgoing stress or downgoing potentials. Detailed discussions on the seafloor interface effect and free surface-related effects can be found in the work of Edme and Singh [35].

Figure 1.
Schematic diagram of ocean-bottom multicomponent seismic data acquisition. Triangles represent ocean-bottom receivers. Waves received by seawater-coupled hydrophones are marked blue while waves received by seabed-coupled geophones are marked red. Ocean-bottom refractions that propagate horizontally are neglected in this figure for clarity. The black horizontal line denotes the fluid–solid interface. The horizontal dashed lines above and below the seafloor line respectively denote the depth level of acoustic decomposition and the depth level of elastic decomposition.
An adaptive decomposition scheme usually includes four stages [13,34]:
- P/vz calibration.
- Seabed property estimation.
- P/vx calibration.
- P-/S-wavefield decomposition.
Figure 2 shows the detailed workflow of our modified scheme with the composite calibration steps. Some general decomposition equations are presented in Appendix A.
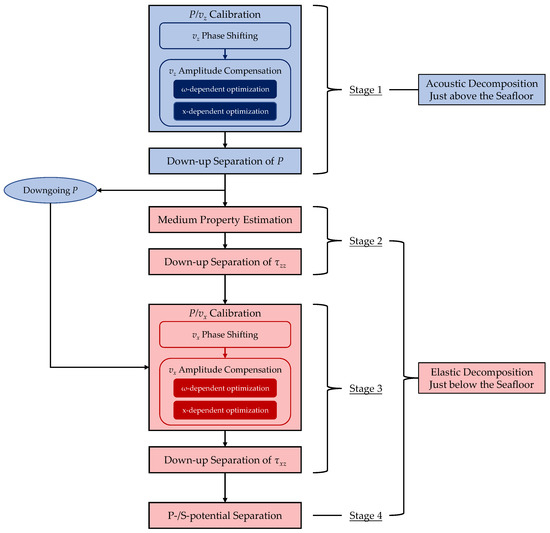
Figure 2.
The workflow of our modified adaptive decomposition scheme with composite calibration filters. Steps related to acoustic decomposition above the seafloor are painted blue, and steps related to elastic decomposition below the seafloor are painted red.
2.1. Stage 1: P/vz Calibration
In this stage, primary reflections are usually chosen for optimal processing in conventional decomposition schemes; however, primary events are often relatively weak and difficult to isolate from direct events at far offsets. Therefore, the velocity-calibration optimization is often dominated by data from near offsets, causing a leakage phenomenon in the decomposition results at far offsets. We believe broadening the choice of waves adopted in the optimization is necessary to ameliorate the existing problem, especially at far offsets. Considering the calibration accuracy for both near and far offsets, we decided to jointly use the primary reflections and ocean-bottom refractions (i.e., a combination of the methods from Schalkwijk et al. [10] and Liu et al. [34]). The contribution of critically-refracted waves can effectively expand the offset range suitable for decomposition processing. Particularly, for our composite calibration method, it is important to ensure that the selected data window effectively covers every trace such that the offset-dependent optimization can run with sufficient input data. Therefore, the supplement of critically-refracted waves at far offsets plays an especially important role in our scheme.
In our method, the phase and amplitude spectra of the composite calibration filters were obtained in sequence, not simultaneously. The complete composite calibration filter for the vertical particle velocity can be expressed as
where is the composite calibration filter in the ω-x domain, is the 2D phase-shifting filter, and is the composite amplitude compensation filter, that is, the amplitude spectrum of the composite calibration filter for the vertical velocity component. The 2D phase-shifting filter can be further expressed by a 2D phase spectrum using Euler’s formula. The composite amplitude compensation filter can be further divided into a frequency-dependent filter and an offset-dependent filter .
The ocean-bottom refractions and primary reflections selected by the time window in the pressure and vertical velocity components should be summed destructively in the calculation of the downgoing waves. In other words, deriving from the acoustic decomposition equation (Equation (A1)), the ideal calibration of the vertical velocity ensures that the wave energy is zeroed in the refracted and reflected areas of the calculated downgoing pressure:
where P represents acoustic pressure, represents the vertical particle velocity, superscript . denotes the selected refracted and reflected data window, is the vertical slowness for acoustic waves propagating in the immediate vicinity of the hydrophone (see Appendix A), and is the ideal calibration filter that is assumed to be able to eliminate ocean-bottom refractions and primary reflections in downgoing waves separated just above the seafloor. The expression indicates that the calculations in the braces are carried out in the ray-parameter domain, and the results are then transformed to the ω-x domain. In contrast, the expression indicates that the calculations in the square brackets are directly carried out in the ω-x domain. Based on Equation (2), a rough estimate of the vertical velocity calibration filter can be obtained by directly performing point-to-point division on the processed pressure and vertical velocity:
where denotes the rough estimate of the vertical velocity calibration filter in the ω-x domain without smoothing or optimization. The phase angle information of that rough estimate is directly adopted as the phase spectrum of our novel composite calibration filter for the vertical velocity component:
is used to obtain the argument (principal value) of . We abandoned the amplitude information of , rather than adopting it as the amplitude compensation filter, as we did to the phase angle information. This is because the principal value of the argument is self-limited to between −π and π, and no drastic outlier would ever occur in the phase spectrum. This simple operation is sufficiently stable and robust for phase-spectrum obtainment, and any complicated optimization procedure can therefore be avoided. In contrast, point-to-point division can easily generate dramatic outliers in the amplitude spectrum of which would severely degrade calibration robustness, caused by local imperfections such as noises and signal losses. Therefore, a stable optimization strategy customized for calibration in the ω-x domain must be designed, and the modulus of is rejected.
For the optimization of composite amplitude composition filters, one reasonable choice is to imitate the optimization procedure in the classical scheme. An alternate optimization method that sequentially uses data by rows and then by columns in the ω-x domain was then developed and adopted. In practice, frequency-dependent optimization (involving data from one frequency row at a time) is carried out as for the classical method. Then, a similar algorithm is performed along the offset axis (involving data from one offset column at a time) to obtain the additional calibration values we intend to add to our composite calibration method. We use the word “composite” when referring to the calibration filter that is obtained by composing these two sequentially-obtained 1D-form filters. The cost functions of the two sub-steps of the amplitude compensation optimization are
where and respectively denote the cost functions of the ω-dependent optimization and the x-dependent optimization. Note that the output of the first sub-step (i.e., ) is applied to the velocity data prior to the optimization along the second dimension, therefore, those two sub-steps are sequential, not parallel. Parameter n can be selected empirically. We let n = 2 in our practice.
The first sub-step of optimization along frequency can be seen as a replicate of the optimization procedure presented in classical schemes. Because of that, our composite method is at least comparable to the older methods. The significance of the velocity component calibration against pressure is based on the observation that geophone-acquired data are vulnerable to various internal and external interferences, including subtle differences in sensor responses and seabed coupling degrees. Because these factors are uncontrollable and unpredictable, it is understandable that seismic data acquired under different temporal and spatial circumstances may require varying degrees of calibration. Our practice of introducing composite calibration can reduce the residual disorders left by classical 1D calibration. We arrange this second dimension of calibration in the ω-x domain rather than in the ω-k (angular frequency–wavenumber) domain or the ω-p (angular frequency–horizontal slowness) domain as follows: 1. Seismic data are more evenly distributed in the ω-x domain, which can help increase the precision and efficiency of the filter calculation; in the ω-k domain, low-frequency data are too concentrated in the near-zero-k area, and in the ω-p domain, high-frequency data are too concentrated in the near-zero-p area; 2. For ω-x domain calibration, adding the second dimension of optimization can be understood as fitting the need of each trace. In contrast, the physical meaning of wavenumber-dependent or slowness-dependent optimization is less intuitive.
The application of the phase and amplitude calibration to the vertical velocity component can be expressed as
where denotes the calibrated vertical velocity in the ω-x domain. With well-calibrated vertical velocity data, separation of the downgoing and upgoing acoustic pressure can then be performed:
2.2. Stage 2: Seabed Property Estimation
Seabed properties can be estimated by performing a minimization operation on the zero-lag cross-correlation between the upgoing stress separated just below the seafloor and the downgoing waves obtained by the summation of pressure and the calibrated vertical velocity just above the seafloor [13]. This means that those events (e.g., direct and water-layer multiple events) that appear in the downgoing velocity just above the seafloor should not appear in the upgoing stress just below the seafloor. From this stage, the downgoing waves separated just above the seafloor (here, we use the scaled downgoing vertical velocity) act as the needed data window or as a “weighting function”. The cost function of the optimization in this stage is
with the weighting function
where represents seawater density. Parameter n was set to 1 in our practice. The parameter used in the parentheses above is the intercept time, and p is the horizontal slowness. The transformation between the t-x (time-offset) domain and the τ-p domain is realized by the forward/inverse Radon transform. The desired estimates of the seabed elastic properties can be obtained by least-squares curve fitting as follows:
where is the density of the seabed, is the vertical slowness of P-waves propagating in the immediate vicinity of the geophone, and is a dimensionless factor related to seabed properties (see Appendix A). More details of property estimation can be found in the Section 3.
After the estimation of seabed properties, separation of downgoing and upgoing normal stress just below the seafloor can be performed:
where and represent the downgoing and upgoing normal stress just below the seafloor, respectively.
2.3. Stage 3: P/vx Calibration
This calibration step was performed similarly to Stage 1. The composite calibration filter for the horizontal particle velocity can be expressed as
where is the composite calibration filter in the ω-x domain, is the 2D phase-shifting filter, and is the composite amplitude compensation filter, that is, the amplitude spectrum of the composite calibration filter for the horizontal velocity component, and , , and are the 2D phase spectrum, ω-dependent amplitude filter and x-dependent amplitude filter for P/vx calibration, correspondingly.
Events that appear in the downgoing pressure separated just above the seafloor should not appear in the upgoing stress just below the seafloor. In other words, deriving from Equation (A3), the ideal calibration of the horizontal velocity ensures that the cross-correlation is zeroed between the downgoing pressure separated by acoustic decomposition and the calculated upgoing horizontal stress:
where represents horizontal particle velocity, is the ideal calibration filter that is assumed to be able to eliminate the cross-correlation between the downgoing pressure separated by acoustic decomposition and the calculated upgoing horizontal stress, is a dimensionless factor related to seabed properties (see Appendix A), the superscript denotes the weighted versions of components using the separated downgoing acoustic pressure obtained just above the seafloor, following the expressions
The expression represents that the calculations in the braces are carried out in the ray-parameter domain, and the results are then transformed to the t-x domain. A rough estimate of the horizontal velocity calibration filter can then be obtained:
where denotes the rough estimate of horizontal velocity in the ω-x domain. The phase angle of the rough estimate is taken as the phase spectrum of the composite calibration filter for the horizontal velocity component:
The cost functions of composite amplitude calibration optimizations are
where and respectively denote the cost functions of the ω-dependent optimization and the x-dependent optimization. We let n = 2 in our practice.
The application of the phase and amplitude calibration to the horizontal velocity component can be expressed as
Here, denotes the calibrated horizontal velocity in the ω-x domain. With well-calibrated horizontal velocity data, separation of downgoing and upgoing shear stress just below the seafloor can then be performed:
where and represent downgoing and upgoing shear stress just below the seafloor, respectively, and is the vertical slowness of S-waves propagating in the immediate vicinity of the geophone (see Appendix A).
2.4. Stage 4: P-/S-Wavefield DECOMPOSITION
P/S decomposition can be performed using Equation (A7) with the normal and shear stress obtained in Stages 2 and 3. The reliability of the decomposition results of the downgoing and upgoing potentials relies on the successful separation of the downgoing and upgoing stress.
3. Decomposition Results
The OBS dataset used in this study was acquired at a water depth of approximately 1000 m in the South China Sea. The sampling interval of the OBS was 0.001 s. We adopted 550 traces in our application of decomposition, and the corresponding offset range was approximately 13,725 m in total.
Before the first stage of decomposition, multicomponent OBS data must undergo preprocessing, including OBS relocation [36] and OBS orientation [37,38]. The raw data were severely affected by noise, especially the water column-related low-frequency noises in the pressure data recorded by hydrophones. Therefore, we applied a trapezoid band-pass filter of 9–10–90–100 Hz to eliminate low-frequency and high-frequency noise. Subsequent filter optimization in the frequency domain is correspondingly limited to 9–100 Hz. We believe that the selected frequency range is sufficiently wide to preserve the meaningful information needed for ocean-bottom seismic exploration. Figure 3 shows the critically-refracted and primary-reflected waves selected for Stage 1 of decomposition. In the adopted case, critically refracted events are much clearer within ±5000 m and the signal-to-noise ratio degrades quickly beyond ±6000 m, particularly in the negative-offset area.
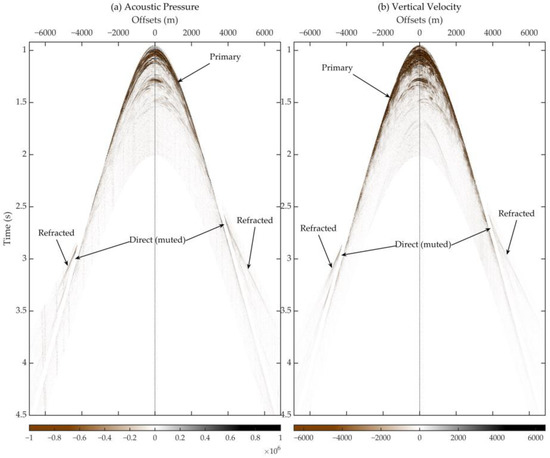
Figure 3.
Critically-refracted and primary-reflected waves selected by data windows in the (a) acoustic pressure and (b) vertical velocity components. As implied by the gaps between refracted and reflected events, direct waves have been excluded.
3.1. Composite P/vz Calibration Filters and the Separated Pressure
The 2D phase spectrum of the composite calibration filter for vertical velocity is shown in Figure 4. It is both frequency- and offset-dependent (or trace-dependent). Although there appear to be intensive burrs, some patterns can be observed. The low-frequency near-offset area tends to be bluer, which means that the frequency components of the vertical velocity from this area are more likely to be negatively shifted in phase. However, the frequency components from the high-frequency far-offset areas do not exhibit evident tendencies.
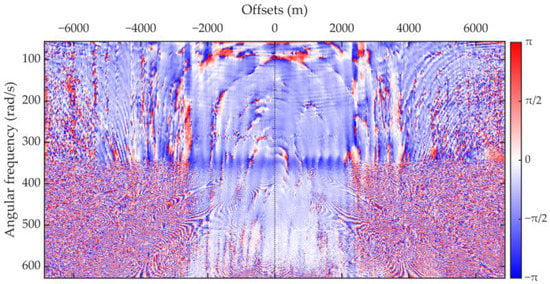
Figure 4.
2D phase spectrum of composite P/vz calibration filter. To fully fit the definition of the ω domain, here we use angular frequency as the y-axis, and the unit of the left-hand labels is rad/s, not Hz. The phase angle is denoted by radian, not degree. A slight outlier-removal algorithm is applied to the 2D phase spectrum.
A demonstration of the composite amplitude compensation filter optimized for the vertical velocity component is shown in Figure 5. The curvy shape of the additional amplitude calibration filter along the offset axis shown in Figure 5b is a proof of its own meaningfulness because, if the traditional 1D filter is capable of simultaneously satisfying calibration objectives of all traces from the velocity component by itself, the optimization algorithm along the offset axis would describe a perfectly straight line, not a curve. Regarding the overall variation of the classical-type ω-dependent filter (Figure 5a), we found a decreasing trend along the positive direction of frequency, partly because we performed preliminary band-pass filtering, so the calibration itself does not need to take responsibility for bubble-noise energy damping in the low-frequency area.

Figure 5.
Demonstration of amplitude calibration for vertical particle velocity data. (a) The classical-type frequency-dependent amplitude calibration filter optimized following traditional methods. (b) The additional calibration along the offset axis introduced after applying classical calibration by our novel method. (c) The composite amplitude compensation filter (i.e., the full amplitude spectrum of composite calibration filter) for the vertical velocity component. Blue curves are plotted using the directly optimized value, while the orange curves are the smoothed ones after two rounds of optimization. Average levels of the smoothed curves are presented using black dashed lines. The composite filter shares the frequency axis with the frequency-dependent calibration filter on the left side and shares the offset axis with the offset-dependent calibration filter on the upper side. Note that the unit of frequency labels used in the demonstration of the classical-type frequency-dependent filter has been converted to Hz for convenient comparison with amplitude spectra displayed in other studies.
Figure 6 displays the calibrated (Figure 6c) and not-yet-calibrated (Figure 6b) vertical velocity component together with the hydrophone-acquired acoustic pressure component (Figure 6a), in the ω-x domain. The low-frequency far-offset areas are much brighter after applying the composite calibration filter, which is consistent with the color variation observed in the demonstration of the composite calibration (Figure 5c). Longitudinally, high-frequency components above 500 rad/s (about 80 Hz) are noticeably suppressed, and wave energy is more concentrated at the dominant frequency near 375 rad/s (about 60 Hz). In the low-frequency area, the energy of the vertical particle velocity is more evenly distributed. Such adjustments in the lateral distribution cannot be realized by applying classical 1D filters. We also transformed the velocity data back to the t-x domain, and a comparison of the vertical velocity component before and after calibration is shown in Figure 7. The refracted events are more discernible in the calibrated vertical velocity.
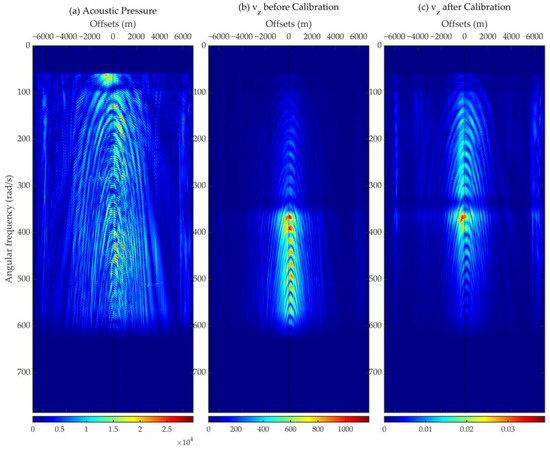
Figure 6.
Comparison of the (a) acoustic pressure component, and vertical particle velocity component (b) before and (c) after calibration, in the ω-x domain.
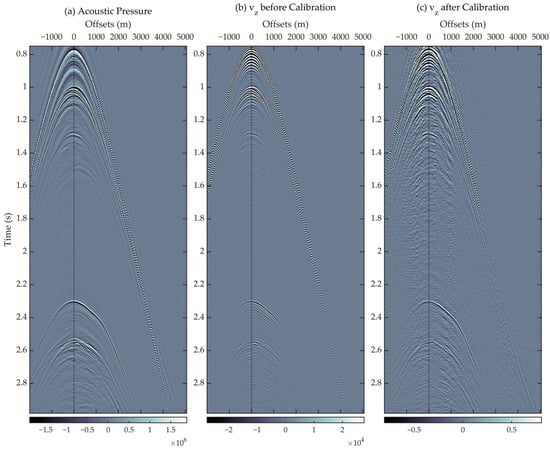
Figure 7.
Comparison of the (a) acoustic pressure component, and vertical particle velocity component (b) before and (c) after calibration, in the t-x domain. Because of the relatively wide display range, we use a blue–grey colormap to avoid visual interferences brought by high-contrast colors.
Figure 8 displays the downgoing (Figure 8a) and upgoing (Figure 8b) acoustic pressure separated just above the seafloor using Equation (8). As indicated by the arrows, the critically-refracted and primary-reflected waves are suppressed in the downgoing pressure, while they are well preserved and noticeably enhanced in the upgoing pressure. These contrasts demonstrate the successful application of composite velocity calibration and downgoing–upgoing separation of acoustic pressure. Direct and water-layer multiple events are partly attenuated in the upgoing pressure. The separated downgoing wave data can be used in the following stages.
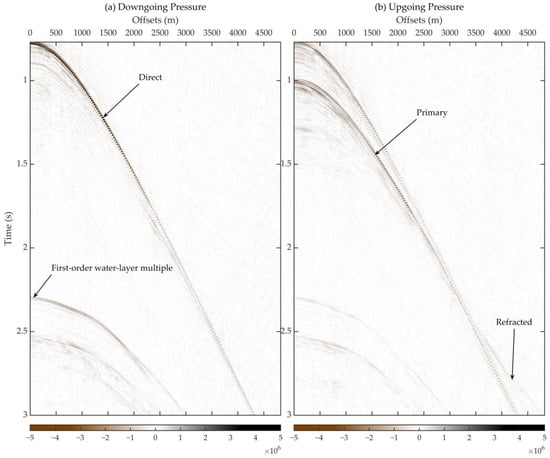
Figure 8.
The (a) downgoing and (b) upgoing acoustic pressure separated just above the seafloor in the t-x domain. The colormaps have been unified. The direct wave and the first-order water-layer multiple in downgoing pressure and critically refracted and primary reflected waves in upgoing pressure are indicated by the black arrows.
3.2. Seabed Property Estimates and the Separated Normal Stress
The data directly obtained from the optimization (blue) and the calculated curve (orange) using the estimated elastic parameters are shown in Figure 9. A moderate outlier removal algorithm removes overlarge values (mostly between 4.5 × 10−4 and 6.0 × 10−4 s/m). The inverted elastic properties (density, P-wave velocity, and S-wave velocity) were , , and .
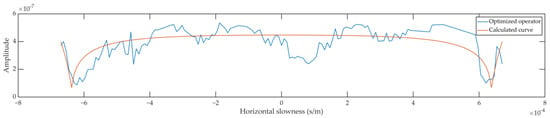
Figure 9.
Property estimation by least-squares curve-fitting. The blue curve denotes the values directly given by the optimization procedure (some outlier removal algorithms are applied). The orange curve denotes the fitted curve calculated using the inverted elastic parameters.
Figure 10 shows the downgoing and upgoing normal stress separated just below the seafloor using the estimated medium parameters. As indicated by the arrows, first-order water-layer multiple events are well suppressed and almost eliminated in the upgoing normal stress, demonstrating the successful application of property inversion and normal stress separation. Primary reflected events have been noticeably enhanced in the upgoing normal stress.
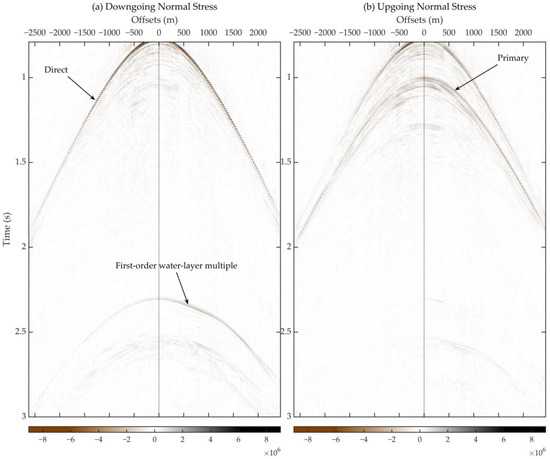
Figure 10.
The (a) downgoing and (b) upgoing normal stress separated just below the seafloor. The colormaps of both sides have been unified. The direct wave and the first-order water-layer multiple in downgoing stress and primary events in upgoing stress are indicated by the black arrows.
3.3. Composite P/vx Calibration Filters
The 2D phase spectrum obtained for horizontal velocity calibration is shown in Figure 11. Compared with the phase spectrum of the vertical velocity calibration filter (Figure 4), the phase spectrum for the horizontal velocity is more focused on positively shifting the frequency components from the low-frequency near-offset area.
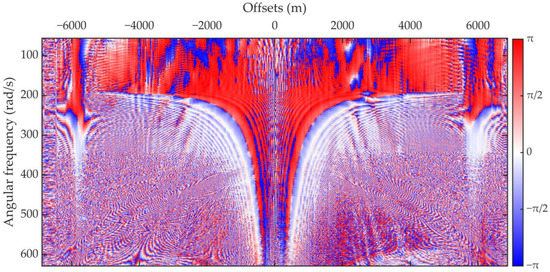
Figure 11.
2D phase spectrum of composite P/vx calibration filter.
A demonstration of the composite amplitude calibration optimized for the horizontal velocity component is shown in Figure 12. Generally, the frequency-dependent filter (Figure 12a) follows a similar decreasing trend as the frequency-dependent filter for vertical velocity (Figure 5a). The additional calibration filter along the offset axis fluctuates at far offsets, which is suspected to be caused by the relatively low signal-to-noise ratio of the horizontal velocity data at the corresponding far offsets. The offset range we chose is slightly wider than the range in which the signal-to-noise ratio is sufficiently large so that the limits and stability of our novel calibration method can be tested. The calibration filters remain stable at near offsets with high-quality data, and satisfactory decomposition results can be obtained.
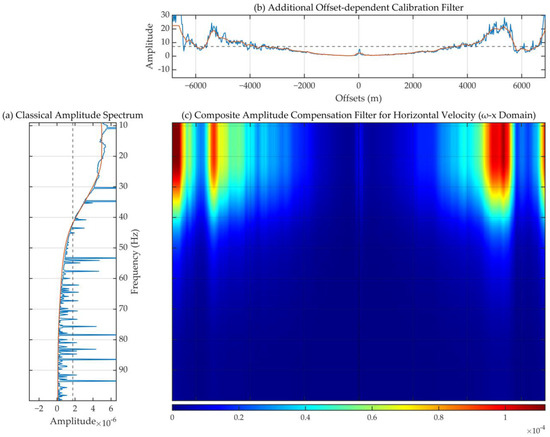
Figure 12.
Demonstration of amplitude calibration for horizontal particle velocity data. (a) The classical-type frequency-dependent amplitude calibration filter optimized following traditional methods. (b) The additional calibration along the offset axis introduced after applying classical calibration by our novel method. (c) The composite amplitude compensation filter (i.e., the full amplitude spectrum of composite calibration filter) for the horizontal velocity component. Blue curve—optimized operator, orange curves—calculated curve.
Figure 13 displays the calibrated (Figure 13c) and not-yet-calibrated (Figure 13b) horizontal velocity component together with the hydrophone-acquired acoustic pressure component (Figure 13a), in the the ω-x domain. The high-frequency components are more severely suppressed than the calibration of the vertical velocity. The low-frequency energy is more evenly distributed. Figure 14 shows the comparison in the t-x domain.
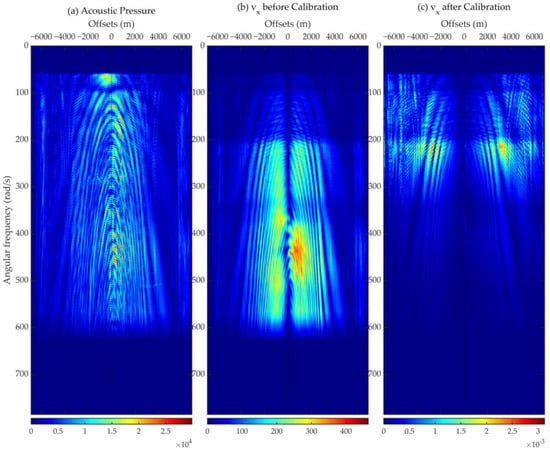
Figure 13.
Comparison of the (a) acoustic pressure component, and horizontal particle velocity component (b) before and (c) after calibration, in the ω-x domain.
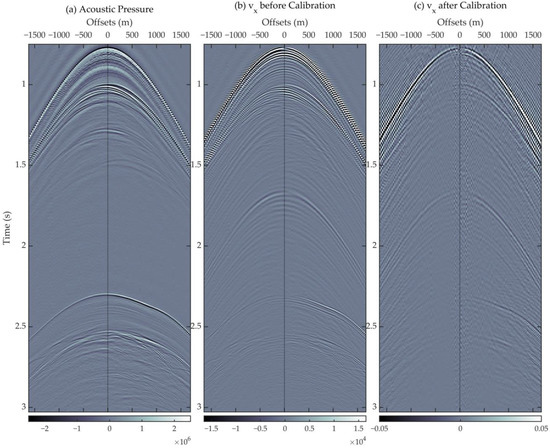
Figure 14.
Comparison of the (a) acoustic pressure component, and horizontal particle velocity component (b) before and (c) after calibration, in the t-x domain.
3.4. Decomposed Downgoing and Upgoing P- and S-Wave Potentials
For comparison, we transformed the decomposed downgoing and upgoing P- and S-wave potentials calculated in the ray-parameter domain to the t-x domain (Figure 15). Water-layer multiples, although commonly existing as acoustic waves propagating in the water, can also present as S-wave events because of the existence of a fluid–solid interface. Therefore, first-order multiple events are noticeable both in the downgoing P-wave potential (Figure 15a), and the downgoing S-wave potential (Figure 15c) decomposed just below the seafloor. As indicated by the black arrows in Figure 15, water-layer multiple events are notably suppressed, and primary reflections are well preserved in upgoing wave potentials (Figure 15b,d), both for P-wave potentials (Figure 15a,b) and S-wave potentials (Figure 15c,d). Figure 16 shows an enlarged view of the near-offset area. The enhancement of the primary events in the upgoing wave potentials (Figure 16b,d) is more clearly shown. Some residuals of primary reflections in the downgoing potentials (Figure 16a,c) are acceptable because the decomposition of this stage is carried out just below the seafloor and is unavoidably affected by reflections from the solid–fluid interface. To clearly show the amplitude differences, data from the 300th trace (approximately 612.5 m if expressed by offset value) are selected and displayed in Figure 17. The primary reflections in the upgoing wave potentials (Figure 17b,d) and the peak of the water-layer multiple in the downgoing wave potentials (Figure 17a,c) are indicated by the arrows. These satisfactory decomposition results illustrate the successful application of the novel composite calibration method.
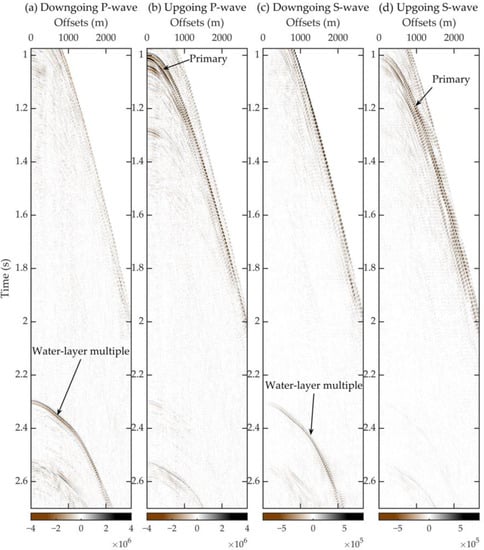
Figure 15.
The (a) downgoing P-potential, (b) upgoing P-potential, (c) downgoing S-potential and (d) upgoing S-potential decomposed just below the seafloor (mostly positive-offset areas between primary events and the first-order water-layer multiple events). The colormaps for (a,b) P-potential and (c,d) S-potential are respectively unified. The direct wave and the first-order water-layer multiple in (a,c) downgoing potentials and primary events in (b,d) upgoing potentials are indicated by the black arrows.
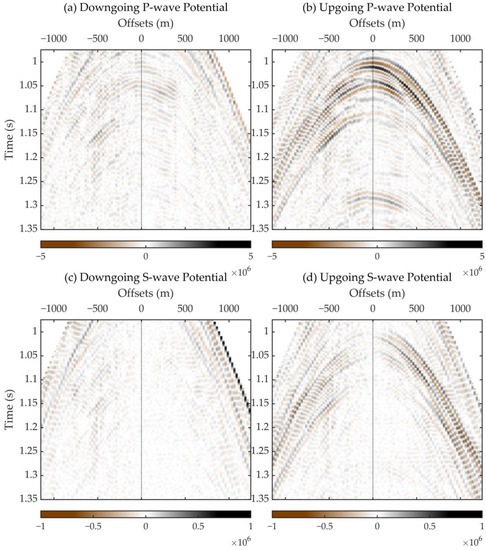
Figure 16.
Enlarged views of the (a) downgoing P-potential, (b) upgoing P-potential, (c) downgoing S-potential, and (d) upgoing S-potential decomposed just below the seafloor (mostly focused on the area containing primary events).
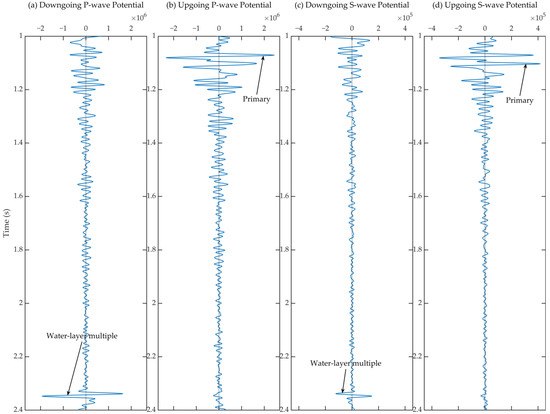
Figure 17.
One-trace samples (the 300th trace, about 612.5 m in offsets) from the (a) downgoing P-potential, (b) upgoing P-potential, (c) downgoing S-potential, and (d) upgoing S-potential decomposed just below the seafloor. Black arrows indicate representative peaks.
4. Discussion
4.1. Polarization Analysis of Particle Velocity before and after Calibration
We performed a polarization analysis of the particle velocity components before and after calibration using data from the 276th trace (Figure 18a,d), 288th trace (Figure 18b,e), and 320th trace (Figure 18c,f). It is evident that after calibration, the trend of the particle velocity transforming from vertical polarization to horizontal polarization is reinforced. This means that, in this deep-water case, the horizontal velocity component underwent stronger enhancement at far offsets during calibration than the vertical velocity component.
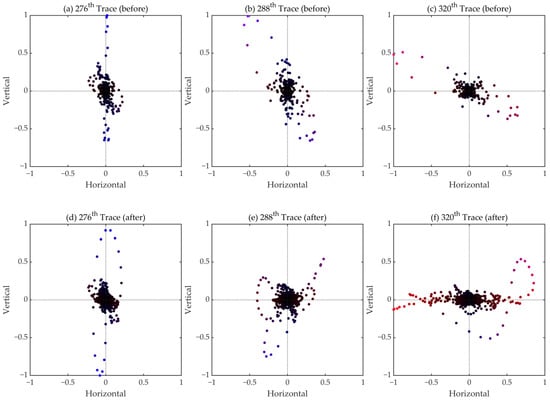
Figure 18.
Polarization analysis of particle velocity before (the upper panel) and after (the lower panel) calibrations using data from (a,d) the 276th trace, (b,e) the 288th trace, and (c,f) the 320th trace. The horizontal velocity component determines the projection position of the data points on the x-axis. In contrast, the projection positions of the data points on the y-axis are determined by the vertical velocity component. Note that both axes have been normalized by the maximum value, so the labels between −1 to 1 do not represent the absolute values of particle velocity data. The data points dominated by vertical polarization mode are painted bluer, and the data points dominated by horizontal polarization mode are painted redder.
4.2. Redistribution of P-Wave Energy
We transformed the decomposed upgoing P-wave potential and the original hydrophone-acquired acoustic pressure to the ω-k domain (Figure 19b,d). The corresponding analysis of changes in the energy distribution can be performed. As shown in Figure 19a, the energy distribution of the hydrophone-acquired pressure near zero-wavenumber is saddle-shaped, with an evident falling-off around 300 rad/s (about 47 Hz); while in Figure 19c, wave energies of upgoing P-wave potentials near zero-wavenumber trace are more normally distributed with a dominant frequencies between 350 rad/s to 390 rad/s.
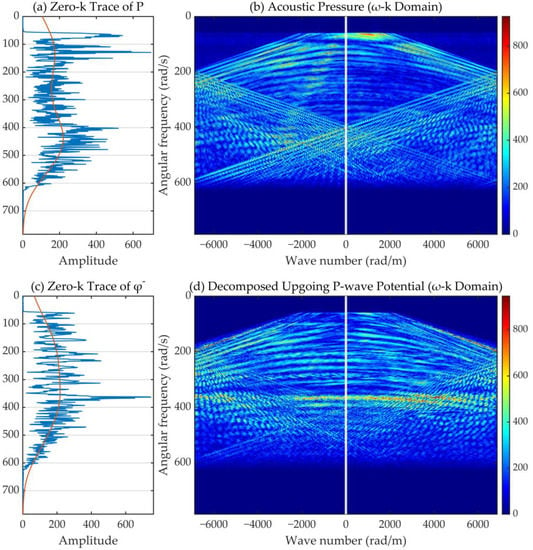
Figure 19.
Demonstration of (b) the original acoustic pressure recording (the slashes from the boundary are caused by spatial aliasing) and (d) the upgoing P-potential decomposed just below the seafloor in the ω-k domain. The corresponding zero-k trace samples (denoted by the white vertical lines), (a) for pressure, and (c) for upgoing P-potential are displayed on the left side. The blue curves with burrs are the zero-k data obtained by obtaining geometric mean of the two traces with the minimum absolute value of wavenumber. The orange curves are the trend curves obtained by executing outlier removal and smoothing algorithms to the blue curve.
4.3. Experiment Using Errored Velocity Data
We conducted a simple numerical experiment to test the feasibility of our method by illustrating the response of the introduced horizontal amplitude calibration to the potential energy loss of the acquired velocity components. We cut the amplitudes of the vertical velocity of several traces (the 293rd to 307th) around the 300th trace to one-fifth of its original value to mimic accidental errors in field acquisition. First, we used the traditional 1D calibration method in the decomposition workflow and obtained the results (also the 300th trace) as shown in Figure 20. The degradation of the decomposition effects was evident. The unwanted water-layer multiple residuals in the upgoing potentials (Figure 20c,d) and the over-strong primary residuals in the downgoing potentials (Figure 20a,b) are marked by black dotted ellipses. Then, we applied our composite calibration method to the same errored dataset. The response of the composite calibration filter to the introduced energy loss is illustrated in Figure 21. A bright stripe (in Figure 21c) corresponds to the additional compensation for the amplitude loss. The final decomposition results displayed in Figure 22 are satisfactory and are barely affected by the introduced errors when compared to the decomposition results of the original data.
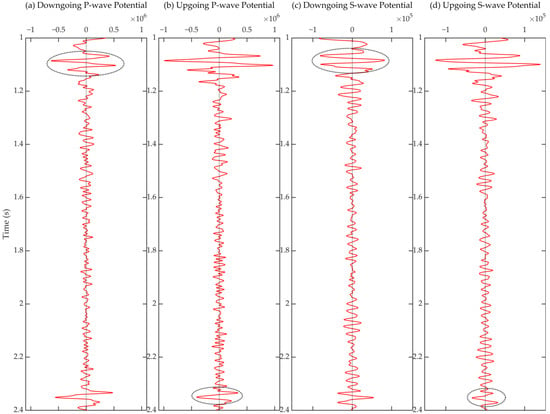
Figure 20.
One-trace samples (the 300th trace, about 612.5 m in offsets) from the (a) downgoing P-potential, (b) upgoing P-potential, (c) downgoing S-potential, and (d) upgoing S-potential decomposed just below the seafloor using the classical method with errored vertical velocity data. The degradations in the results are indicated by black dotted ellipses.
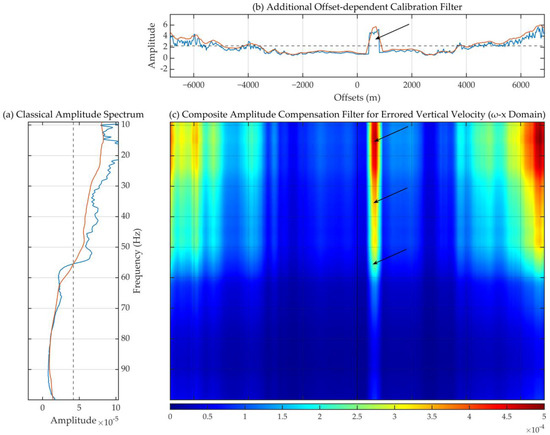
Figure 21.
Amplitude calibration optimized for the errored vertical velocity component. (a) The classical-type frequency-dependent amplitude calibration filter optimized following traditional methods. (b) The additional calibration along the offset axis introduced after applying classical calibration by our novel method. (c) The composite amplitude compensation filter (i.e., the full amplitude spectrum of composite calibration filter) for errored vertical velocity. The corresponding responses of the horizontal and composite calibration filters to the deliberately introduced errors are indicated by the arrows. Blue curve—optimized operator, orange curves—calculated curve.

Figure 22.
One-trace samples (the 300th trace, about 612.5 m in offsets) from the (a) downgoing P-potential, (b) upgoing P-potential, (c) downgoing S-potential, and (d) upgoing S-potential decomposed just below the seafloor using our composite calibration method with errored vertical velocity data. No evident degradation in the results has been observed.
5. Conclusions
According to the suppression effect of water-layer multiple events demonstrated in the field OBS data decomposition results, our novel composite calibration method is stable, valid, and compatible with the adaptive wavefield decomposition scheme. The new decomposition workflow can successfully decompose downgoing/upgoing P-/S-wave potentials. Test results of decomposition methods applying to seismic data with energy loss in particular traces show that our new method can correctly respond to errors varying along the spatial direction, which are usually neglected by traditional methods. With the modifications proposed in the present study, the adaptive decomposition of ocean-bottom seismic data can be performed more precisely.
The optimized composite filters revealed some underlying patterns in the geophone data calibration and wave separation. One common characteristic illustrated by calibration filters for vertical component and horizontal component is that far-offset seismic data usually need to be relatively amplified compared to near-offset area. Polarization analysis showed that the composite calibration also emphasized the polarization shifting of the particle velocity from the vertical vibration mode to the horizontal vibration mode with an increase of offset value. The wave energy of the decomposed upgoing P-wave potential is more normally distributed in the frequency range compared to the directly acquired acoustic pressure in the deep-water case.
Author Contributions
Conceptualization, M.C. and P.Y.; methodology, M.C.; software, M.C.; validation, M.C. and P.Y.; formal analysis, M.C.; investigation, M.C. and P.Y.; resources, P.Y.; data curation, M.C. and P.Y.; writing—original draft preparation, M.C.; writing—review and editing, M.C. and P.Y.; visualization, M.C.; supervision, P.Y.; project administration, P.Y.; funding acquisition, P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 42074149), Natural Science Foundation of Jiangsu Province (grant number BK20201318), and Fundamental Research Funds for the Central Universities (grant number B210202133).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Wave-Equation-Based Adaptive Decomposition
We present some general equations that are commonly used in wave-equation-based adaptive decomposition schemes. The equations listed in this appendix are all theoretical expressions derived for ideal cases and do not contain any type of component calibration or optimization. These decomposition equations are based on the eigenvalue decomposition of wave equations in the special case of seismic waves propagating in the x-z plane (the wavenumber in the y-direction is set to be zero). Although the derivations of these decomposition equations are based on the assumption of horizontally layered media, the algorithm still performs well in the presence of dipping interfaces.
Upgoing and downgoing separation above the seafloor uses the following expression [39]:
in which is the vertical slowness for seawater
represents acoustic pressure, represents vertical particle velocity, and superscripts + and − respectively symbolize downgoing and upgoing, is the density of water, is the acoustic velocity in the water layer, and is the horizontal slowness. In classical methods, the summation and subtraction of pressure and velocity data are normally performed in the ray-parameter domain. Water-layer multiple events tend to concentrate in areas with small slowness.
The separation of downgoing and upgoing normal and shear stress just below the seafloor uses the following expression [10]:
in which
represents shear stress, represents normal stress, , and are seabed properties in the immediate vicinity of the geophone, respectively denoting density, P-wave velocity and S-wave velocity, the subscript 1 is used to denote the geophone-coupled elastic medium, is the corresponding vertical slowness for P-wave, is the corresponding vertical slowness for S-waves just below the seafloor, and and are two dimensionless factors that would respectively degrade to 1 and −1 when transferred to acoustic cases.
Decomposition of the downgoing and upgoing P- and S-wave potentials just below the seafloor uses the following expression [10,40]:
with and denoting the P-wave and S-wave potentials, respectively.
References
- Davis, T.L. Multicomponent seismology—The next wave. Geophysics 2001, 66, 49. [Google Scholar] [CrossRef]
- Gaiser, J.; Moldoveanu, N.; Macbeth, C.; Michelena, R.; Spitz, S. Multicomponent technology: The players, problems, applications, and trends: Summary of the workshop sessions. Lead. Edge 2001, 20, 974–977. [Google Scholar] [CrossRef]
- Granger, P.; Manin, M.; Boelle, J.; Ceragioli, E.; Lefeuvre, F.; Crouzy, E. Autonomous 4C Nodes used in infill areas to complement streamer data, deepwater case study. In SEG Technical Program Expanded Abstracts 2005, Proceedings of the 2005 SEG Annual Meeting, Houston, TX, USA, 6–11 November 2005; Society of Exploration Geophysicists: Houston, TX, USA, 2005; pp. 84–87. [Google Scholar]
- Eggenberger, K.; Pedersen, Å.S.; Thompson, M.; Solheim, O.A.; Amundsen, L.; van Manen, D.-J.; Andersson, F.; Robertsson, J.O.A. High-productivity seabed time-lapse seismic data acquisition using simultaneous sources enabled by seismic apparition: A synthetic-data study. Lead. Edge 2016, 35, 894–904. [Google Scholar] [CrossRef]
- Yang, D.; Liu, F.; Morton, S.; Malcolm, A.; Fehler, M. Time-lapse full-waveform inversion with ocean-bottom-cable data: Application on Valhall field. Geophysics 2016, 81, R225–R235. [Google Scholar] [CrossRef]
- Berkhout, A.J.; Wapenaar, C.P.A. Delphi: Delft philosophy on acoustic and elastic inversion, Part 1. Lead. Edge 1990, 9, 30–33. [Google Scholar] [CrossRef]
- DeVault, B.; Davis, T.L.; Tsvankin, I.; Verm, R.; Hilterman, F. Multicomponent AVO analysis, Vacuum field, New Mexico. Geophysics 2002, 67, 701–710. [Google Scholar] [CrossRef][Green Version]
- White, J.E. Seismic Waves: Radiation, Transmission, and Attenuation. Phys. Today 1967, 20, 74–75. [Google Scholar] [CrossRef]
- Ball, V.; Corrigan, D. Dual-sensor summation of noisy ocean-bottom data. In SEG Technical Program Expanded Abstracts 1996, Proceedings of the 1996 SEG Annual Meeting, Denver, CO, USA, 10–15 November 1996; Society of Exploration Geophysicists: Houston, TX, USA, 1996; pp. 28–31. [Google Scholar]
- Schalkwijk, K.M.; Wapenaar, C.P.A.; Verschuur, D.J. Application of two-step decomposition to multicomponent ocean-bottom data: Theory and case study. J. Seism. Explor. 1999, 8, 261–278. [Google Scholar]
- Schalkwijk, K.M. Decomposition of Multicomponent Ocean-Bottom Data into P- and S-Waves. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2001. [Google Scholar]
- Schalkwijk, K.M.; Wapenaar, C.P.A.; Verschuur, D.J. Adaptive decomposition of multicomponent ocean-bottom seismic data into downgoing and upgoing P- and S-waves. Geophysics 2003, 68, 1091–1102. [Google Scholar] [CrossRef]
- Muijs, R.; Robertsson, J.O.A.; Holliger, K. Data-driven adaptive decomposition of multicomponent seabed recordings. Geophysics 2004, 69, 1329–1337. [Google Scholar] [CrossRef]
- Muijs, R.; Robertsson, J.O.A.; Holliger, K. Data-driven adaptive decomposition of multicomponent seabed seismic recordings: Application to shallow-water data from the North Sea. Geophysics 2007, 72, V133–V142. [Google Scholar] [CrossRef]
- Eggenberger, K.; Muijs, R.; Robertsson, J.; van Manen, D.-J.; Holliger, K. Estimation of inelastic seismic material properties of a surficial sea-bed from multi-component marine seismic data. Near Surf. Geophys. 2010, 8, 459–465. [Google Scholar] [CrossRef]
- Muijs, R.; Robertsson, J.O.; Holliger, K. Prestack depth migration of primary and surface-related multiple reflections: Part I—Imaging. Geophysics 2007, 72, S59–S69. [Google Scholar] [CrossRef]
- Muijs, R.; Robertsson, J.O.; Holliger, K. Prestack depth migration of primary and surface-related multiple reflections: Part II—Identification and removal of residual multiples. Geophysics 2007, 72, S71–S76. [Google Scholar] [CrossRef]
- Grion, S.; Exley, R.; Manin, M.; Miao, X.; Pica, A.L.; Wang, Y.; Granger, P.; Ronen, S. Mirror imaging of OBS data. First Break 2007, 25, 37–42. [Google Scholar] [CrossRef]
- Dash, R.; Spence, G.; Hyndman, R.; Grion, S.; Wang, Y.; Ronen, S. Wide-area imaging from OBS multiples. Geophysics 2009, 74, Q41–Q47. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Bale, R.; Grion, S.; Holden, J. The ups and downs of ocean-bottom seismic processing: Applications of wavefield separation and up-down deconvolution. Lead. Edge 2010, 29, 1258–1265. [Google Scholar] [CrossRef]
- Eggenberger, K.; Robertsson, J.O.A.; Andersson, F.; van Manen, D.; Pedersen, Å.S.; Amundsen, L.; Haavik, K.; Thompson, M.; Solheim, O. PZ Processing of a Signal-Apparition Triple-Source Field Test in the North Sea. In Proceedings of the 80th EAGE Conference and Exhibition 2018, Copenhagen, Denmark, 11–14 June 2018. [Google Scholar]
- Caldwell, J. Marine multicomponent seismology. Lead. Edge 1999, 18, 1274–1282. [Google Scholar] [CrossRef]
- Wapenaar, K.; Slob, E.; Snieder, R. Seismic and electromagnetic controlled-source interferometry in dissipative media. Geophys. Prospect. 2008, 56, 419–434. [Google Scholar] [CrossRef]
- Chabert, A.; Minshull, T.A.; Westbrook, G.K.; Berndt, C.; Thatcher, K.E.; Sarkar, S. Characterization of a stratigraphically constrained gas hydrate system along the western continental margin of Svalbard from ocean bottom seismometer data. J. Geophys. Res. 2011, 116, B12102. [Google Scholar] [CrossRef]
- Cho, W.H.; Spencer, T.W. Estimation of polarization and slowness in mixed wavefields. Geophysics 1992, 57, 805–814. [Google Scholar] [CrossRef]
- Wang, Y.; Singh, S.C.; Barton, P.J. Separation of P- and SV-wavefields from multi-component seismic data in the domain. Geophys. J. Int. 2002, 151, 663–672. [Google Scholar] [CrossRef]
- Wang, Y.; Singh, S.C. Separation of P- and S-wavefields from wide-angle multicomponent OBC data for a basalt model: Separation of P- and S-wavefields. Geophys. Prospect. 2003, 51, 233–245. [Google Scholar] [CrossRef]
- Daoli, L.; Tianyue, H.; Yanbin, W. Separation of P-and SV-wavefields from multi-component seismic data. Appl. Geophys. 2006, 3, 163–168. [Google Scholar] [CrossRef]
- van der Neut, J.; Thorbecke, J.; Mehta, K.; Slob, E.; Wapenaar, K. Controlled-source interferometric redatuming by crosscorrelation and multidimensional deconvolution in elastic media. Geophysics 2011, 76, SA63–SA76. [Google Scholar] [CrossRef]
- Soubaras, R. Ocean bottom hydrophone and geophone processing. In SEG Technical Program Expanded Abstracts 1996, Proceedings of the 1996 SEG Annual Meeting, Denver, CO, USA, 10–15 November 1996; Society of Exploration Geophysicists: Houston, TX, USA, 1996; pp. 24–27. [Google Scholar]
- Soubaras, R. PEG-LEG Attenuation in Ocean Bottom Acquisitions. In Proceedings of the 60th EAGE Conference and Exhibition, Leipzig, Germany, 8–12 June 1998; European Association of Geoscientists & Engineers: Leipzig, Germany, 1998. [Google Scholar]
- Soubaras, R. Multiple attenuation and P-S decomposition of multicomponent ocean-bottom data. In SEG Technical Program Expanded Abstracts 1998, Proceedings of the 1998 SEG Annual Meeting, New Orleans, LA, USA, 13–18 September 1998; Society of Exploration Geophysicists: Houston, TX, USA, 1998; pp. 1336–1339. [Google Scholar]
- Wang, Y.; Grion, S. PZ calibration in shallow waters: The Britannia OBS example. In SEG Technical Program Expanded Abstracts 2008, Proceedings of the 70th EAGE Conference and Exhibition Incorporating SPE EUROPEC 2008, Rome, Italy, 9–12 June 2008; Society of Exploration Geophysicists: Houston, TX, USA, 2008; pp. 1088–1092. [Google Scholar]
- Liu, X.; Cheng, J.; Wang, T.; Geng, J.; Liu, Y. Wavefield decomposition of ocean bottom multi-component seismograms with low signal-to-noise ratio. Chin. J. Geophys. 2021, 64, 684–699. [Google Scholar] [CrossRef]
- Edme, P.; Singh, S.C. Receiver function decomposition of OBC data: Theory. Geophys. J. Int. 2009, 177, 966–977. [Google Scholar] [CrossRef]
- Creager, K.C.; Dorman, L.M. Location of instruments on the seafloor by joint adjustment of instrument and ship positions. J. Geophys. Res. 1982, 87, 8379. [Google Scholar] [CrossRef]
- Olofsson, B.; Massacand, C.; Millington, M. Determining 3-C geophone orientation from a single seismic shot. In SEG Technical Program Expanded Abstracts 2007, Proceedings of the 2007 SEG Annual Meeting, San Antonio, TX, USA, 23–26 September 2007; Society of Exploration Geophysicists: Houston, TX, USA, 2007; pp. 970–974. [Google Scholar]
- Jeong, W.; Almubarak, M.S.; Tsingas, C. Quality control for the geophone reorientation of ocean bottom seismic data using k-means clustering. Geophys. Prospect. 2021, 69, 1487–1502. [Google Scholar] [CrossRef]
- Amundsen, L. Wavenumber-based filtering of marine point-source data. Geophysics 1993, 58, 1335–1348. [Google Scholar] [CrossRef]
- Amundsen, L.; Reitan, A. Decomposition of multicomponent sea-floor data into upgoing and downgoing P- and S-waves. Geophysics 1995, 60, 563–572. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).