Immunized Token-Based Approach for Autonomous Deployment of Multiple Mobile Robots in Burnt Area

Abstract

Collaborative exploration, sensing and communication in previously unknown environments with high network latency, such as outer space, battlefields and disaster hit areas are promising in multi-agent applications. When disasters such as large fires or natural disasters occur, previously established networks might be destroyed or incapacitated. In these cases, multiple autonomous mobile robots (AMR) or autonomous unmanned ground vehicles carrying wireless devices and/or thermal sensors can be deployed to create an end-to-end communication and sensing coverage to support rescue efforts or access the severity of damage. However, a fundamental problem is how to rapidly deploy these mobile agents in such complex and dynamic environments. The uncertainties introduced by the operational environment and wide range of scheduling problem have made solving them as a whole challenging. In this paper, we present an efficient decentralized approach for practical mobile agents deployment in unknown, burnt or disaster hit areas. Specifically, we propose an approach that combines methods from Artificial Immune System (AIS) with special token messages passing for a team of interconnected AMR to decide who, when and how to act during deployment process. A distributed scheme is adopted, where each AMR makes its movement decisions based on its local observation and a special token it receives from its neighbors. Empirical evidence of robustness and effectiveness of the proposed approach is demonstrated through simulation.

1. Introduction

Multi-agent systems consisting of autonomous mobile robots have gained significant attention in various strategic real-world applications such as reconnaissance and surveillance [1,2,3,4], search and rescue operations [5,6], etc. This is as a result of progress made in the development of autonomous systems technology. Among their many applications, rapid deployment in high network latency areas is a key functionally that is attracting attention from researchers and industry players. In order to complete certain missions, multi-agent systems consisting of autonomous systems need to spread out from an initial drop off point in unknown areas to achieve some fixed configurations such as forming a temporal ad hoc network or provide a complete map of the environment. We use the term deployment to describe this phase. The study on AMR deployment and mobility problems is an important research field, which is significant for both military and civilian applications. In hazardous areas such as fire burnt areas, toxic urban regions, disaster hit areas, or remote planets and battlefields, human operations sometimes become impossible or dangerous. Hence, unmanned systems can be deployed in those challenging areas to replace or facilitate human work such as gathering information in search and rescue, provide communication support or perform target tracking and surveillance. In these regards, AMR provides greater practicality and shows robust performance in recent studies. The fundamental problem is an approach of how to rapidly perform the deployment optimally in these environments.

The tremendous potential offered by AMR for possible applications such as these, stem from the fact that using multi-AMR in general can lead to increased flexibility and redundancy, resulting in an overall increase in reliability. Moreover, multi-AMR working as a team can perform an exploration, mapping and localization, surveillance task or any other group mission more effectively and efficiently compared to a single agent [7,8]. Besides covering wider area, the deployment of a multi-AMR systems in general, would provide greater benefits regarding area-coverage, mission duration and optimized task sharing and execution between participating agents. For complex tasks that would often require a certain level of cooperation, each system within the team might need to have a compatible messaging interface to enable the exchange of messages with other teammates and/or with command centers within its communication range. The resulting network of the team can be used to facilitate the task performance of the team within the environment [9,10].

This paper analyzes the characteristics and requirements of deploying AMR or unmanned vehicles to provide remote sensing, mapping and coverage of burnt areas and proposes a network deployment and adjustment algorithm that can facilitate operations in various situations such as during fire outbreaks and post fire management. For instance, when disasters such as large fires occur, previously established networks might be destroyed or incapacitated. In scenarios such as these, autonomous systems carrying wireless devices can be deployed to create an end-to-end communication network to support rescue efforts or access the severity of damage. The networks deployed in these situations can guide human firefighters and responders to potential targets for rescue and to areas that require attention while warning them of dangerous areas along the way. In these application settings, the robots team or mobile agents might be deployed from a single or multiple accessible drop of points to coordinate detection of environmental information by spreading out as much as possible to traverse and detect the given area in order to collect enough information to assist the execution of tasks while keeping connected. State-of-the-art approaches of deployment of mobile agents for communication support or area exploration and mapping often employ one of three different management strategies to manage and control such systems including centralized, decentralized or distributed strategies [11]. In the centralized approach, each entity or robot communicates with every other entity in the systems, and the decision-making process of the entire team or swarm is centralized or executed by a single decision maker. In a distributed approach, each entity in the task environment communicates its information and coordinates its actions with others, while in the decentralized approaches, agents rely only on the available local information. In this case, the exchange of information may not be required among the different entities and coordination between entities may be achieved through shared global variable(s).

Based on these strategies, some deployment approaches such as Voronoi-inspired algorithms [12,13] assume that the global information of the unexplored area can be previously obtained by humans, thus potential locations for deployment can be calculated. During the deployment, robots already have knowledge about the pre-calculated locations they should go to. For other approaches, such as the virtual-force [14] based algorithm, the capability of gaining real-time information and knowledge is assumed, therefore the AMR team can interact with low network latency and perform actions in a synchronized way. However, those assumptions are sometimes infeasible in unexplored areas. For example, in some areas, such as disaster hit areas, outer space, battlefields, etc., humans may only have access to limited information. In an area after an earthquake or fire burnt areas, where the roads and buildings are damaged and destroyed, the structure may be significantly changed. Thus, a pre-calculated approach maybe be rendered ineffective or useless. In disaster hit areas or remote planets, where the network latency is unpredictable, robots will take an extremely long time to communicate. Thus, an accurate synchronization cannot be achieved by the team and real-time information cannot be updated instantly.

In this paper, we present a decentralized deployment strategy for robot teams taking into account the above issues. The main idea underlies that, the multiple AMR team deployment problem is a multi-agent coordination problem. Through coordination, the asynchronous robots are coupled and they can decide how to cooperatively complete their mission. In order to reduce the communication cost in a large scale team, a decentralized approach is proposed. This proposed approach has three advantages. Firstly, this approach does not require any previously known information about the deploying area, in other words, robots only need to gain the knowledge about the environment when they are situated in the environment. Secondly, decentralized approach does not need a powerful system to achieve global observation, information or states of the whole team, as each mobile robot only has local observation. Thirdly, an AMR team applying a decentralized approach needs only to communicate with physically local neighbors through message exchange, resulting in simple protocols and cheap communication resource consumption among the AMR team.

On the other hand, the technological advancement in land, aerial and marine robotics as purpose-built systems are making the use of multi-agent teams to support various operations and missions by deploying several mobile agents for area coverage and temporal communication networks formation in recent years possible. This is attributed to the fact that multi-agent teams can outperform a single agent for the same task while enabling flexibility, reduced operational cost and efficiency. Multi-agent teams can be used in a variety of complex missions and operations such as: surveillance and communication in unknown and dynamic environments (i.e., disaster hit areas, remote planets), environmental monitoring (i.e., deployment and monitoring in remote planet, forests, and disaster areas) and operations in law enforcement missions such as border patrols, etc. Several approaches have been proposed in the literature to tackle the mobile robots/sensor deployment for operations support and optimal area coverage and mapping using a team of mobile agents. These have resulted in various solutions ranging from machine learning to bio-inspired approaches. Our approach is inspired by the working mechanism of the biological immune system to perform deployment and coverage using tokens by deciding who, when and how to act during deployment process to ensure robust connectivity and coverage of the team.

The artificial immune system (AIS) is a typical multi-agent and decentralized information processing system inspired by the working mechanisms exhibited by the biological immune system [15,16], which is adaptive. The advantages of high parallelism, distributed operation, strong adaptability, and self-organization exhibited by the biological immune system has inspired various theories and models that represent the different aspects proposed under the artificial immune system, such as the immune network [17] and danger theory [18], and several applications have been demonstrated based on these theories [19].

The immune network theory is a critical theory of the artificial immune system that exhibits characteristics of adaptiveness of the immune system. The immune network theory proposed by Jerne [17] suggests that the immune system is capable of achieving immunological memory by the presence of a mutually reinforcing network of B-Cells that produces an interaction mechanism between network cells. Jerne’s theory stipulates that this network would be self-regulating through stimulatory and suppressive interaction. This interaction is as a result of the idiotope of one antibody being recognized by the paratope of another antibody with or without the presence of an antigen that possesses an epitope. The recognized antibody is suppressed while the recognizer antibody is simulated. In the robotics domain, a computational model of Jerne’s idiotypic network theory has been proposed in [16] as a means of inducing adaptive behavior mediation and has demonstrated some encouraging results. In these idiotypic networks, competence modules are mapped to both environmental stimuli (antigens) and to each other, leading to the formation of a dynamic chain of stimulation and suppression that influence their concentration levels globally.

On the other hand, the concept of danger theory [18] stipulates that, in other to properly contain attacks, the immune system responds to harmful and dangerous events that causes damage to cells. This danger signals from the damaged cells forms a danger zone that attracts the attention of the concerned immune cells. The attracted cells get stimulated and undergo clonal expansion to contain the attack. Consequently, the danger theory assumes that the immune system is activated by danger signals that are emitted by damaged cells, i.e., cells affected by foreign agents or with mechanical damage.

Comparatively, the multi-agent deployment coordination control is similar in characteristics with those in the biological immune system since both require coordination and adaptive control of agent’s behaviors in a dynamic or unknown environment. In our approach, we combined immune-based methods with token-based approach to find an appropriate amount of suppression and simulation of behaviors to response to situations during agents deployment, in addition to adapting the internal mechanism of each agent so that agents are adaptive to situations in the environment. The robots decisions for providing efficient mobility support are achieved with an intersection of token messages exchange, immune network theory and danger theory. We show that, deployment problem can be solved through multi-agent decentralized coordination, implementing coupling of asynchronous robots. The proposed approach enables individual agents of the team to consider theirs situational information and tokens from other agents to improve movement decisions such as the direction and distances to moved. In addition, as the communication cost of the large-scale agent team is expensive, if token message can be passed optimally, it can reach the destination with minimum distance and the overall communication cost of for agents’ coordination can be minimized. The concept of danger theory and immune network is used to minimize the overall communication cost by determining an adaptive token generation and passing in the the agent team.

The remainder of this paper is organized as follows: In Section 2, we discussed the background of decentralized coordination and related deployment approaches from the literature. Section 3 introduces the problem description and scenario. In Section 4, we provide our decentralized coordination approach for deployment where the modeling of the deployment problem and our decentralized algorithm is proposed. Next, in Section 5, the empirical analysis to evaluate the performance of the proposed algorithm is presented through experiments. Finally, Section 6 and Section 7 discuss and summarizes the main contributions of this work.

2. Related Work

Mobile systems deployment and coverage maximization approaches have been widely studied in the literature for different application scenarios. In the study of improving the efficiency and connectivity in mobile wireless sensors and robotics networks, a relevant functional requirement is to maximize the coverage while maintaining connectivity with other nodes of the network and/or with a base station in the region of interest by employing proper deployment of sensors. By adopting a centralized approach, energy efficient deployment algorithms based on multi-objective immune algorithm were presented in [20,21]. In the first approach, the authors present an immune-based node deployment algorithm that takes into consideration mobility and coverage cost. While in their second approach, voronoi diagram was introduced to complement the immune-based approach by using it to adjust sensing nodes. However, despite considering energy efficiency, mobility and redundant coverage, this approaches is centralized and might suffer from usual problems of centralized approaches. In [22], a distributed movement assisted sensor deployment algorithm is presented to enhance area coverage in a distributed mobile sensor network. The Edge Based Centroid algorithm adopted in their work moves sensor nodes towards the centroid of the local Voronoi polygon from the initial deployment position. A dispersion movement algorithm for multi-robot systems that uses the number of communication links of each individual robot for movement control is proposed in [23]. Reference [24] presents a holistic connectivity controller (HCC) to regulate and restore inter-agent connections during the dispersion of the mobile network. In [25], a dispersion algorithm based on wireless signal intensities is proposed. The signal intensities are modeled by employing a sampling technique, which takes into consideration both the distance and relative orientations of the wireless sensor. Similar approaches that use the strength of the robots’ radio signals and the gradient descent algorithm to achieve a swarm dispersion are presented in [26,27].

Further more, authors in [28] studied the coverage of specific zones of interest that can change dynamically over time by using a swarm of flying robots. The mobility of the flying devices is achieved through particle swarm optimization and virtual forces algorithm. In this approach, flying robots only require the local information from the neighbors to update their velocity and trajectory. A collaborative complete coverage and path planning approach for single robot and multi-robot systems where the coverage from a robot movement is maximized by a a novel cost function and goal selection function to facilitate collaborative exploration for a multi-robot system is proposed in [29]. The proposed method is able to optimize the overall coverage efficiency by considering local gains from individual robots and the global gain by the goal selection function. A decentralized deployment process for wireless mobile sensor networks focused on deployment efficiency, connectivity maintenance and network reparation is discussed in [30]. In [31], a novel distributed algorithm for deploying multiple robots in an unknown two-dimensional (2D) area to achieve complete blanket coverage is presented. A redeployment scheme based an artificial immune systems for wireless mobile sensor nodes initially deployed randomly is proposed in [32]. The authors employ artificial immune systems inspired approach to calculate the appropriate positions for sensors to redeploy. A comprehensive review of various evolutionary algorithms employed for deploying sensor nodes at optimized positions in wireless sensor networks is presented [33].

In this paper, we treat the mobile robot deployment problem as multi-agent coordination problem and approach it from a perspective which differ from previous work. Our coordination approach implements the coupling of the asynchronous agents, addressing three problems of the previous work. The first problem of some previous studies is that deployed robots focus on their own observations and knowledge to make decision and then act (e.g., calculate neighbor’s and obstacle’s locations and orientations then choose a position to move). However, some trivial but essential information for the teams is ignored. For example, if one robot observes that it is situated in a location that is blocked by obstacles, then its best choice is to inform other vehicles about this fact, and thus prevent other agents unnecessarily accessing this corner, rather than just leave this corner itself. That information can be obtained and shared through coordination and the whole team will get more useful information for deployment, and thus helps the team make more efficient and useful decisions.

Another problem is the connectivity loss problem, this is because robots have no extra information about others’ potential actions. When robots start to execute a moving action, they have no idea of the consequent configuration of the network. In a connected network, for example, even if only two neighboring robots move simultaneously, the resulting connected network may lead to two separated components. However, those two robots may not notice the fact because they still maintain the connection with some other robots. Another example in simultaneous moving strategy is that if robots observe that there is no connected neighbor, it may try to move back to the previous location to find neighbors. However, due to the location changes of other vehicles, it might be difficult to find a neighbor. Through coordination, robots can get information from other robots, which provides knowledge (local network topology, others’ neighbor lists, etc.) for making more sensible decisions. For example, based on this information, robots can decide to choose the suitable robots to move or a suitable distance and direction to move in order to eliminate the possibility of connectivity loss. Similarly, during the movement of some robots, other robots can decide to stay in the current locations to wait for the feedback of the moving robots, thus even when an agent observes the connectivity loss, it can relocate to the previous locations to connect with those staying robots to prevent the connectivity loss.

An individual robot also may not be able predict the utility brought to the whole team after some actions, leading to energy waste because those actions actually bring no utility improvement to the whole team. This is because of their limited local observation. In a swarm-inspired algorithm for deployment, for example, obviously the utility can be significantly improved by the location changes of the boundary robots, but in existing approaches such as [14], the boundary robots and inner robots are based on the same rules to move. After several periods of the location adjustment, some inner robots’ locations remain approximately unchanged, but they have consumed some resources trembling between the original location. By coordinating, it is practical for the robot team to decide and act more feasibly, such as which robots is more appropriate to move, or where and how to move in order to increase the team’s utility.

3. Multi-Robot Network Deployment Problem

At the initial step, there is a team $A=\{a_1,a_2,a_3...,a_n\}$ of mobile agents, placed at initial drop off point in an unexplored or surveillance region ∪, do be dispersed to cover a task area such as burnt region, outer space, or battlefields. ∪ may contain a set $E=\{e_1,e_2,e_3...,e_n\}$ of different entities or no go areas. The first kind of entity is areas where agent should not move into (e.g., burning area, collapsed structures, holes in the roads), which is called risked or dangerous areas. Agents are not willing to enter those areas as they may lead to unpredictable damage to agents. The second kind of entity are obstacles which agents cannot pass through (e.g., buildings, stones). Certain entities will have some impacts on robots. For example, a metallic wall situated between two robots will weaken the wireless signal strength. If a robot enters a trap region, it may be damaged and no longer be useful or movable. The goal of the team is to gradually adjust their locations through moving, and finally achieve some fixed configuration. An ad hoc network will be formed by the team, which can be utilized or provide support for other operations. We use the term deployment to describe this adjustment phase of the team.

After the multi-robot team finishes deployment and finally forms an ad hoc network or a surveillance map, the performance of the system can be evaluated based on three factors. The first factor is the energy consumption $EnergyCost$ of the team. Energy is used to move, communicate, sense and afterwards apply. If a robot spends too much energy for deployment, then it will not have sufficient energy for later application or actual task execution. The second factor is the time consumption, $TimeCost$. Time is often essential in some emergent cases, such as search and rescue in large disasters. The third factor that needs to be taken into account is the quality of the final ad hoc network Q, which can be evaluated by two key factors. The first being the total coverage of the ad hoc network, where the coverage is defined as the joint areas covered by the whole team. In supporting rescue teams and firefighters, for example, the robots’ goal will be to maximize the coverage area in order to increase the probability to detect victims or identify danger to first responders. Another factor is the connectivity of the network. Basically, we require the deployed systems must be connected, if there are several components, some pairs of the agents might loose connection. In a communication system for example, this lost of connection might splits the whole network into many separate parts. Thus, leading to disastrous outcomes (e.g., the communication system is no longer serviceable). We also need network’s robustness to evaluate connectivity, as the network with bad robustness will lead to expensive communication energy consumption. For example, if one network is formed like a straight line then the communication cost is undesirable high. However, there is always a trade-off between coverage and connectivity.

The goal of the deployed systems is to maximize communication or sensing coverage while maintaining connectivity within limited communication and movement energy. Every robot hopes to keep connection with at least $m_c$ agents for robustness. So, we define team’s weighted utility function and the evaluating terms for utility function as shown in Equation (1);

$$\begin{array}{c}\hfill Utility=\alpha \ast Cov-\beta \ast con{n}_{loss}-\gamma \ast R_{loss}\end{array}$$

(1)

$$\begin{array}{c}\hfill R_{loss}=\sum _{i=1}^{n}max(m_c-\left|N\left(a_i\right)\right|,0)\end{array}$$

(2)

$Cov=\cup Cov$ is defined as the joint communication coverage of the whole robot team, a robot $a_i$’s communication coverage is a circle with center in position of $a_i$ and radius $r_c$. On the other hand, $con{n}_{loss}=N_{comp}-1$, represents the connectivity loss penalty while the $N_{comp}$ is the numbers of component of the formed ad hoc network. For example, if there is only a component then the penalty is zero (0). $R_{loss}$ is sum of the robustness loss penalty of all the robots while the robustness penalty for a robot $a_i$ is described as the difference between $m_c$ and its neighbor’s size $N\left(a_i\right)$ as shown in Equation (2). If its neighbor’s size is greater then $m_c$, then the robustness penalty is zero. Here, $m_c$ is a robustness factor defined as the minimum number of neighbors robot $a_i$ should keep connection with. Based on our problem definition, we set $\alpha$ to 1, and $\gamma$ to a factor $\in [0,1]$ according to the specific scenario. We set $\beta$ to ∞ $\varpi$ (such that $\gamma <\varpi >\alpha$) because the aim is to obtain a connected network.

4. Multi-Robot Deployment Control Approach

The proposed deployment approach presented in this section is derived from the working mechanism of the biological immune system. The approach employs tokens and danger signals that trigger movement response from agents in the team. Figure 1 shows a simplified block diagram of the software system of the deployment control approach. The proposed algorithm is implemented on the coordination control and navigation module. With the absence or access to GPS, robots can only perform local localization by sending hello messages out and estimate its neighbor size and relative locations based on the responses it get in return. This mechanism is a key requirement that can facilitate robots’ deployment when services are incapacitated during disasters. Next, we present the details of our modeling and algorithmic execution in our approach.

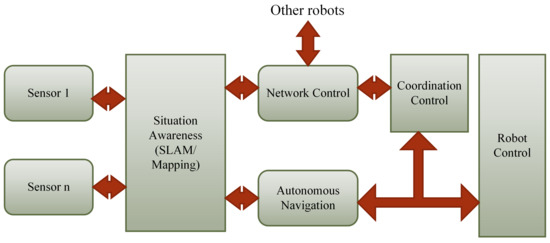
Figure 1. Simplified block diagram of the software system of the deployment control approach. The proposed algorithm is implemented on the coordination control and navigation module.

4.1. AIS Based Agent and Team Model

In this work, mobile agents or robots have computational, communication, and detection capabilities. We model a robot as B-Cell agent. An agent contains body and embedded controller, where the embedded controller has computational capability such as calculation, information processing and object recognition. Body includes sensor (receptors) and effector (B-cell operations), for communication, detection and movement. Sensor equipment are used for communicating and detecting. For example, robots may be equipped with wireless communication device to detect other robots within its communication range by sending ’hello’ messages and evaluating the responses. Furthermore, robots can be installed with isotropic radial sensors to detect surrounding environments. Effector consists of devices for movement and communication. For example, effector may contain message receiving and delivering devices to exchange messages with other robots in the team. In the immune system, an action of a B-cell may involve a change in shape of its receptors. However, in this paper, an agent’s action include changing location by choosing appropriate direction and distance, generating or forwarding a token. At each time step, agents update their local information through their sensors in addition to any received information through other agents that determines their goal. In this model, robots response to danger signals by performing an adjustment or send tokens. Antigens are obstacles or other robots’ information in the environment. In these case, the characteristics or information vector of these entities can be seen as epitopes of antigens. While state and information of the individual B-cell agents becomes the paratopes. We describe agents’ capabilities as septuple form:

$$⟨B_{ID},r_c,t{h}_{signal},r_d,di{r}_{set},co{m}_{battery},mov{e}_{battery}⟩.$$

where $r_c$ and $r_d$ are communication and sensory neighborhood of B-cell agents, $t{h}_{signal}$ is a signal affinity threshold, a value of signal strength describing the communication capability. A robot can communicate with another robot if and only if the distance between the two robots is less than $r_c$ and signal strength $\lambda$ is greater than a threshold $t{h}_{signal}$. Here, we base on a COST Hata model to calculate signal strength $\lambda$. Agents can also gain the approximate signal strengths and orientations of others. When $\lambda$ is too high or too low, then the affected robot becomes distressed triggering a danger signal that generates a token to initiate an adjustment process. We use $B_{ID}$ to identify different agents. While $di{r}_{set}$ is a set of directions to describe agents’ orientation ability, in other words, the precision of orientation an agent can obtain is similar to shape changing of the B-cell. We add two constraints, $co{m}_{battery}$ and $mov{e}_{battery}$, to agents to limit the battery consumption for communication and movement, which corresponds to the death rate of B-cells in Jerne’s network. To simplify the model, we do not consider the speed capability of vehicles, but this is a straightforward extension.

The agent team forms an ad hoc network which is equivalent to the immune network (Jerne’s network) of the AIS. The immune network is a network of B-cells agents, A, that can simulate and suppress each other. Hence, for $a_i,a_j\in A$, $a_i$ and $a_j$ are considered neighbors if they have stimulatory and suppressive effects on each other. Neighbors are pair of agents which can send and receive message from each other.

Similar to danger theory that assumes that the immune system is activated by dangers signals that are emitted by damaged cells, we also abstract these signals as tokens and distressed situations that trigger a response mechanism from the Jerne’s network of B-Cells’ agents. A danger signal establishes a danger zone based on $r_c$ and $t{h}_{signal}$ determines the activation of B-cells agents’ within the zone (communication neighborhood). In this model, tokens received from distress agents or self-generated tokens in the network are sent and received through the wireless link between agents. We assume each token is an information vector $\mathsf{\Omega }=⟨T,P,{\lambda }_{Aff},L⟩$, where T indicates the type of token (role or information token), which in the work determines coordination type, P records the information of agents who have received the token, ${\lambda }_{Aff}$ is an affinity threshold that corresponds to the control information for resource and role for the type of token which is not required for information tokens, while L is a decay rate of a signal corresponding to the time length a token is allowed to exist in the network. During the deployment process, the dynamics of the Jerne’s network of agents due to location changes will cause a corresponding topology structure change of the ad hoc network formed by the agents.

4.2. Deployment Algorithm Design

In this proposed decentralized adaptive deployment approach, to control the robots, we design two kinds of behaviors based on the model presented above. These behaviors are based on the type of tokens sent/received to control teams’ adjustment. These include; self-adjust tokens, ${\mathsf{\Omega }}_{self}$ and boundary tokens, ${\mathsf{\Omega }}_{boundary}$. They are both role tokens implying two types of role for self local adjustment and local boundary adjustment, respectively. When a token is received by an agent in the team, agents who received the signal decide whether to act according to the information encapsulated in the signal. This approach allows efficient and low-cost coordination, without gaining the global knowledge of the team. The proposed adaptive deployment is achieved in two phases.

4.2.1. Phase I

This phase involves the generation and sending of danger signals in a form of tokens for activation of appropriate robots to perform adjustments or dissemination of information. Specifically, we define a function DiffuseSignal($\lambda ,S,O$) to determine whether a token (danger signal) should be emanated and sent by agent a across its neighbors. Danger signals are modeled as information vector or tokens [34] as shown in Section 4.1 where each token is an information vector. The tokens’ type is determine by the observation 0, signal intensity, $\lambda$, received from neighbors, and state S of the agent. The lifespan of a token wane at each hop across the robot/agent that emanated it. Agents are capable of gaining the approximate signal strengths and orientations of others through observation and use it together with its own situation to determine the type of signal/token to send out. Heuristically, agents at the boundary will mostly diffuse/send self-adjust signals/tokens while agents within high dense regions will generate boundary tokens to trigger adjustment of agents on the boundary of the network. On the other hand when a robot is trapped in a hole and unable to escape it diffuse a danger signal to all neighbors (i.e., an information token is send to neighbors). On the other hand, when the signal intensity $\lambda$ is too high or low, an appropriate role token is sent out. The process of execution of Phase I is shown in Algorithm 1.

$$\begin{array}{c}\hfill {\tau }_f=F_v=\frac{1}{N\left(a\right)}\ast \sum _{i=1}^{N\left(a\right)}\frac{\overrightarrow{l_a}-\overrightarrow{l_i}}{\overrightarrow{l_a}-\overrightarrow{l_i}\ast {(\overrightarrow{l_a}-\overrightarrow{l_i})}^2}\ast ϵ\end{array}$$

(3)

where, $l_a$ represents the relative location of robot a, whose activation is being determined, $l_i$ is the positions of other robots, $a_i$. While $\overrightarrow{l_a}-\overrightarrow{l_i}$ is the orientation from a to $a_i$ and $ϵ\in [0,1]$ is a factor that indicates if obstacles are located in the direction $F_v$.

$$\begin{array}{c}\hfill B_{act}=({\tau }_f+\epsilon \ast {\tau }_{f_j})-({\tau }_{f_j}+\rho \ast {\tau }_f)\end{array}$$

(4)

A received token results in two behaviors if the type of token is a role token. These include; self-adjust behavior and boundary behavior. The self-adjust behavior is a behavior that an agent exhibits when it receives a token classified as self-adjust token, ${\mathsf{\Omega }}_{self}$. The ${\mathsf{\Omega }}_{self}$ is a type of token that asks robots in the Jerne’s network who receive the token to adjust their position according to their own knowledge and information encapsulated in the information vector of the token. In this type of token, ${\lambda }_{Aff}$ describes the affinity threshold to activate or stimulate the robot to generate appropriate move actions. When agent $a_i$ receives ${\mathsf{\Omega }}_{self}$, it first calculates its activation value with respect to its neighbor set, $N\left(a_j\right)$, based on the intensity of its virtual force. The virtual force can be calculated using Equation (3).

The activation of the agent is therefore calculated using Equation (4). In this equation, the first term is the stimulation effect of the current agent, the second represents the suppressive effects of its neighbors. Where ${\tau }_f$ and ${\tau }_{f_j}$ are the affinity of the current agent with respect to its neighbors $N\left(a_j\right)$ states and vice versa, respectively, $\epsilon$ and $\rho$ are both scaling factors. If $B_{act}$ is greater than ${\lambda }_{Aff}$, the agent is activated to change its location, otherwise the agent forwards the token. However, before executing the moving action, an agent must choose a direction from $di{r}_{set}$ and decide a certain distance d to move straightly taking into consideration other information tokens it has received. This process corresponds to the antibodies production of the B-cells. When detecting the orientations of entities and signal of other agents, agents will obtain the direction in $di{r}_{set}$.

On the other hand, the boundary behavior is executed based on a received boundary token ${\mathsf{\Omega }}_{boundary}$. This behavior is exhibited by an agent who observes that its situation is on the boundary of the whole team. When agent $a_i$ receives ${\mathsf{\Omega }}_{boundary}$, it first calculates its activation level with respect to its neighbor agents set, $N\left(a_j\right)$, by observing the orientations of all the neighbors and calculates the respective relative angles. The activation function for the boundary signal is calculated using a modified version of Equation (4).

$$\begin{array}{c}\hfill B_{act}=(\psi +\epsilon \ast {\psi }_j)-{\psi }_j+\rho \ast \psi )\end{array}$$

(5)

where $\psi =max({\theta }_i-{\theta }_{i+1})$ and ${\theta }_i$ is the relative angle between agent heading and neighbor i direction and ${\psi }_j$ is the vice versa. Similarly, if $B_{act}$ is greater than ${\lambda }_{Aff}$, the agent is activated to change its location by performing boundary oriented movement. Here, ${\lambda }_{Aff}$ is set between $\frac{5\pi }{6}$ and $\frac{5\pi }{2}$.

Algorithm 1 Algorithmic execution of phase I of the proposed approach executing on each agent.

4.2.2. Phase II

In this phase, the process of agents taking adjusting actions and selecting the corresponding antibodies according the binding affinity after agents are activated in phased I is described. Base on the immune network concepts, antibodies produced by B-cells in response to foreign antigens induce an anti-idiotypic antibodies that proceed to regulate further production of anti-idiotypic antibodies keeping the immune system in balance. Here, the binding affinity is determined by the interactions between the produced antibodies (selected moving distance and direction) and the agents environment. The execution of phase I may leads to the activation of h agents who meet the activation threshold to change their locations based on their situation. This adjustment is executed in h rounds determined by L. An agent is qualified to perform movement according to the value of $B_{act}$, i.e., agents with $B_{act}$ that is higher than the threshold set on the token information vector perform the necessary adjustment.

To execute movement behavior, an agent must decide the distance and directions that maximize the utility function in Equation (1).

$$\begin{array}{c}\hfill A{b}_{aff}\left(a\right)=\frac{\phi }{m_c}\ast (F_v^{{}^{\prime }}-F_v^{{}^{\prime }})\end{array}$$

(6)

$$\begin{array}{c}\hfill B_{act}\left(a\right)=(\varrho \ast \sum _{j=1}^J{(F_v^{{}^{\prime }}\left(a\right)+F_v^{{}^{\prime }}\left(j\right))}^{-d_{aj}}+A{b}_{aff}\left(a\right)-k_a+)\ast \Gamma \end{array}$$

(7)

Algorithm 2 Algorithmic Execution of phase II of the proposed approach.

During adjustment action, agents have to ensure connectivity after its adjustment. Hence, when the agent first selects or generates candidate antibodies (direction and distance) as the candidate antibodies, the agent checks whether there is connectivity loss risk using Equation (6). Antibodies with less connectivity loss undergo stimulation and suppression to select action and direction with maximum activation taking into account $co{m}_{battery}$ and $mov{e}_{battery}$ of the agent base on Equation (7). In this equation, $\varrho ={(co{m}_{battery}\ast mov{e}_{battery})}^{-1}$, $F_v^{{}^{\prime }}$ and $F_v^{{}^{\prime }}$ are the virtual forces with respect to one and two-hops neighbors of the current agent with respect to a newly computed position by the agent, $k_a$ is the degradation rate of a solution and $\Gamma$ is scaling factor. In addition, in Equation (6), $m_c$ is a heuristic value used to define a minimum set of agents that the moving agent must keep in connection with when executing a movement action. Adjustment decisions that maximize the utility function are cloned and distributed to neighbor agents. By so doing, agents are capable of sharing knowledge and adapting to environment and situation mapping from others. The process for phase II is described in Algorithm 2.

5. Experiments and Results

In this section, we first present the simulation setup along with the most important simulation settings. Next, we describe a centralized token based approach and other approaches that have been used in our comparative analysis.

In order to illustrate the performance of the proposed approach, we design a java based simulation environment to simulate a mobile network of robots to test deployment models in sparse and dense environments. In the framework of the simulation, the AMR team is deployed in a bounded rectangular area containing an unknown number and type of obstacles. The environment is meshed by user-designed equal sized square cells that are at least large enough to contain a robot so as to avoid collisions. The robots move in discrete time intervals of a second modeled according to the maximum speed of the robots. In each iteration, a robot’s travel distance at its maximum allowed speed is assumed to always be smaller than its obstacle sensor range. Some obstacles are assumed to weaken the communication signal strength between robots, i.e., they shorten the original communication range. At each iteration, each robot can analyze the environment with its sensor(s) and detect obstacles around it. To present a realistic experiment, simple rules-based collision avoidance is implemented on each robot agent for collision avoidance. We compare the performance of our approach with some deployment algorithms, which are RD [31] and CBS [35] approaches in addition to the heuristic approaches designed for comparison.

5.1. Experiment Setup

Each robot is configured with communication range $r_c$ and operational coverage (e.g., sensor) $r_d$ range of 200 m and 100 m, respectively. The size of the area of interest is defined as a rectangular shape consisting of tall rise buildings with no moving obstacles except the robots composing the team. In this work, we simulate two types obstacles. Obstacles such as buildings and walls are simulated as static obstacles that can be avoided by mobile agents. We also simulate traps that robots can run/fall into that will cause a robot to be immobile or degrade its performance. For example, holes on the ground, which robots must not fall into, or flames, which can damage vehicles. In addition, we set the signal strength of the robots’ wireless connection by taking into account the attenuation of signal free propagation and the attenuation of obstacles, and use the COST Hata model to calculate robots’ signal strength. The affinity threshold ${\lambda }_{Aff}$ is set to $\frac{5\pi }{6}$. The speed of a robot is arbitrarily set at 5 m/s. The maximum distance a robot can decide to move is 30 m. Base on this value, the robot can choose a distance from the set $mov{e}_{dis}=⟨10,20,30⟩$. We further define nine choices including eight moving directions and staying in place that a robot can choose from, i.e., $di{r}_{Set}$ = ⟨ NORTH, NORTHEAST, EAST, SOUTHEAST, SOUTH, SOUTHWEST, WEST, NORTHWEST, STAY ⟩. For a robot not to be considered isolated, the connectivity number of neighbors of the robot is set to $m_c=3$ during the simulation. A simulation lasts for 250 s and with update frequency of 5 ms. Figure 2 shows an example initial setup of a deployment scenario.

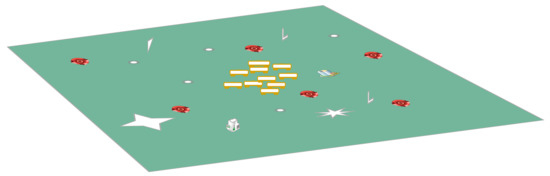
Figure 2. Example of initial setup with 10 robots at a drop-off point to be deployed in the task environment.

5.2. Results and Analysis

To properly evaluate the performance of the approach, we adopt two scenarios (region with obstacles and region without obstacles) for 50 robots, which is enough to cover the task region. In both scenarios (Scene 1 and Scene 2), respectively, we simulate two initial deployment strategies where agents are deployed from a single location or multiple locations (ThreePoints). Figure 4 shows robots’ dynamic deployment process in a region with obstacles with single point initialization of robots. Here, the yellow circles show communication range, dark blue represents static objects and trap/ditches areas are represented by the other shapes. Figure 3a,b show the coverage rate of Scene 1 and 2, respectively, of the task region. As can be seen from the two graphs, the coverage rate in an obstacle free region is higher compared to the region with obstacles. Furthermore, the convergence rate for multiple location deployment is faster compared to deployment from a single location. It can be seen from Figure 4 that, as the simulation progresses, the coverage increases while the entire robot team remains connected in a single network. Figure 3 depicts the coverage rate of the task area during simulation, where the coverage is defined as the joint areas covered by the whole robot team.

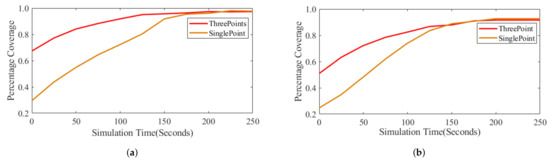
Figure 3. The average coverage rate during simulation time. (a) Deployment in obstacle free region. (b) Deployment in obstacle rich region.

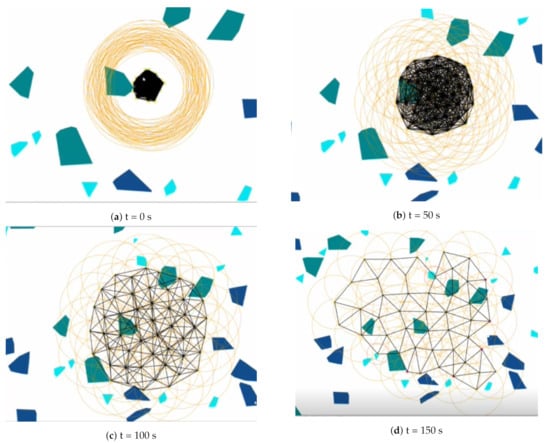
Figure 4. Dynamic Deployment process of robots. (a) shows the initial state, (b) after 30 s, (c) just around a minute, and (d) after 90 s.

Next, among the important performance metrics is the cost and robustness of the final ad hoc network of the team. These can partially be measure by the connectivity constraints and traveled distances of the agent team after the deployment has completed. Figure 5a shows the number of agents satisfying the connectivity constraints of 3 neighbors during deployment. While Figure 5b depicts the moving distances of all agents during deployment. In Figure 5a, it can be realized that the presence of obstacles affects agents’ ability to satisfy the connectivity requirement until the final configuration is realized. Similarly, agents’ moving distance turns to increase more with the presents of obstacles.

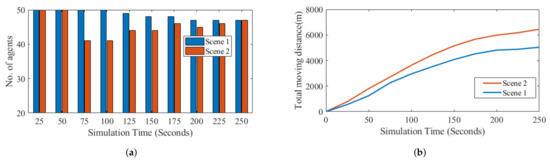
Figure 5. The total moving distance of all agents and number of agents satisfying connectivity constraint. (a) Number of agents satisfying degree constraint. (b) Moving distance of agent team.

Most of recent approaches consider deployment with specific distribution without considering robots failure, traps and information sharing. Hence, to provide a somewhat balanced comparison, we also consider the coverage and network connectivity for comparison with the other approaches. Figure 6a shows the performance of different algorithms with minimum of 3 neighbors during deployment. On the other hand, Figure 6b depicts the coverage performances of the three algorithms. As can be seen from the graphs, our approach does much better in satisfying the constraint of at least 3 neighbors while still providing good coverage.

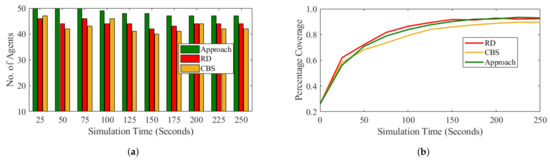
Figure 6. Performance of different algorithms on coverage and connectivity constraint satisfaction. (a) Connectivity constraint satisfaction of different algorithms. (b) Coverage rate of different algorithms.

Furthermore, we provide centralized and random heuristic algorithms to compare with our decentralized algorithm. In the centralized approach, in each round, the centralized agent will gather the global information of all agents, then randomly choose an agent with high virtual force (such as, top 10%) to adjust their location and an agent situated on the boundary to carry out boundary adjustment. The control process is implemented by sending tokens. The agents who receive the token will never send tokens to others, but send feedback to the centralized agent. The random approach employs a similar mechanism, but instead sends move commands to randomly selected agents. In both heuristic approaches, when an agent receives a move command, it selects a random direction closer to a direction of the virtual force and distance of its detection range to move. Table 1 shows the performance comparisons of these approaches.

Table 1. Performance comparison with heuristic algorithms.

Time in Seconds		t = 40	t = 80	t = 120	t = 160	t = 200	t = 240
Random	Effective robots	50	50	50	46	39	35
	Effective Coverage	0.10	0.30	0.41	0.48	0.59	0.70
	Total Distance	1174.13	2324.73	3045.68	3996.47	5264.24	6206.98
Centralized	Effective robots	50	50	50	45	44	43
	Effective Coverage	0.17	0.43	0.67	0.76	0.84	0.88
	Total Distance	1451.32	2961.25	3923.34	4965.11	5809.69	6559.34
Our Approach	Effective robots	50	50	48	47	47	47
	Effective Coverage	0.20	0.50	0.77	0.90	0.94	0.96
	Total Distance	1741.86	3436.26	4735.13	5687.22	6242.31	6711.38

6. Discussion

The fundamental problem of mobile agents deployment for coverage with connectivity constraints is how to establish decentralized coordination among the multiple agents team and how to control their movement and behavior to achieve a desired configuration. This becomes more challenging with the absence of GPS for positions and navigation. With the absence or access to GPS, robots can only perform local localization by sending hello messages out and estimate their neighbor size and relative locations based on the responses they get in return. This mechanism is a key requirement that can facilitate robots deployment when services are incapacitated during disasters.

The approach presented in this paper enabled the successful deployment of mobile robots to achieve maximum coverage while meeting a connectivity constraints. While the approach presented in this work achieved similar coverage with the approach presented in [35] and better coverage than the one presented in [31], our approach outperforms both in terms of the connectivity constraints satisfaction of the mobile robots during and after the final configuration is achieved.

Comparing the centralized and random approach with the approach presented in this work, the two algorithms have more robot losses, less coverage and less moving distance. The less moving distance achieved by both heuristic centralized and random approaches can be attributed to the significant number of ineffective robots. Total moving distance and connectivity of robots during deployment is affected by the complexity and difficulty level of the environments. Generally, the cumulative distance of the system increases with higher complexity and uncertainty levels of the operating environment. This distance determines the amount energy consumed by the robots during deployments. Furthermore, about $10\%$ to $15\%$ more robots fail to satisfy the connectivity constraints in the obstacle rich environments as compared to deployment in obstacle free environments. Ultimately, there is no significant difference in the robustness and coverage as more robots meet the connectivity constraints of the final configuration in both settings.

While the requirement of the decentralized approach is for robots to exchange information, which may increase the amount of message exchange and energy consumption, the information exchange is essential for efficient deployment and reduce robots loss as shown in Table 1. By sending out information tokens, our approach was able to reduce number of ineffective robots and achieve higher effective coverage.

7. Conclusions

This work presents a decentralized robots deployment framework for coverage in unknown and dynamic environments such as disaster hit areas and remote planets that combines the working mechanism of the biological immune system and token-based approach for coordination to decide who, when and how to act during the deployment process to ensure robust connectivity and coverage of the team. The robots’ decisions for providing efficient mobility support are realized with an intersection of immune network theory and danger theory, which can be classified as a decentralized adaptive technique. The proposed approach enables individual agents of the team to consider their local information and tokens from other agents to improve movement decisions such as the direction and distances to move based on observed states. We conduct several simulations to evaluate the performance of the proposed approach. The results of simulation show that the approach can achieve a high coverage ratio while satisfying a connectivity constraint that guarantees robustness compared with other approaches with more effective robots. In comparison with the two heuristic approaches, the other two algorithms have more robot losses and less coverage, but less moving distance.