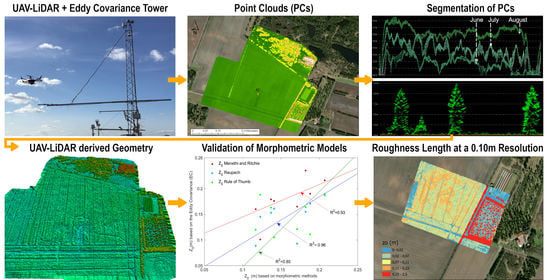
Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR
Abstract
1. Introduction
- An evaluation of the performance of three segmentation approaches (i.e., a morphological filter (MF), a progressive triangulated irregular network densification filter (TIN), and a combination of MF and TIN) to reliably partition the UAV-LiDAR-derived point cloud data into bare earth and vegetation and, consequently, to generate CHMs at centimeter resolution.
- A discussion of the challenges and further potential of UAV-LiDAR in precision agriculture and related applications.
2. Materials and Methods
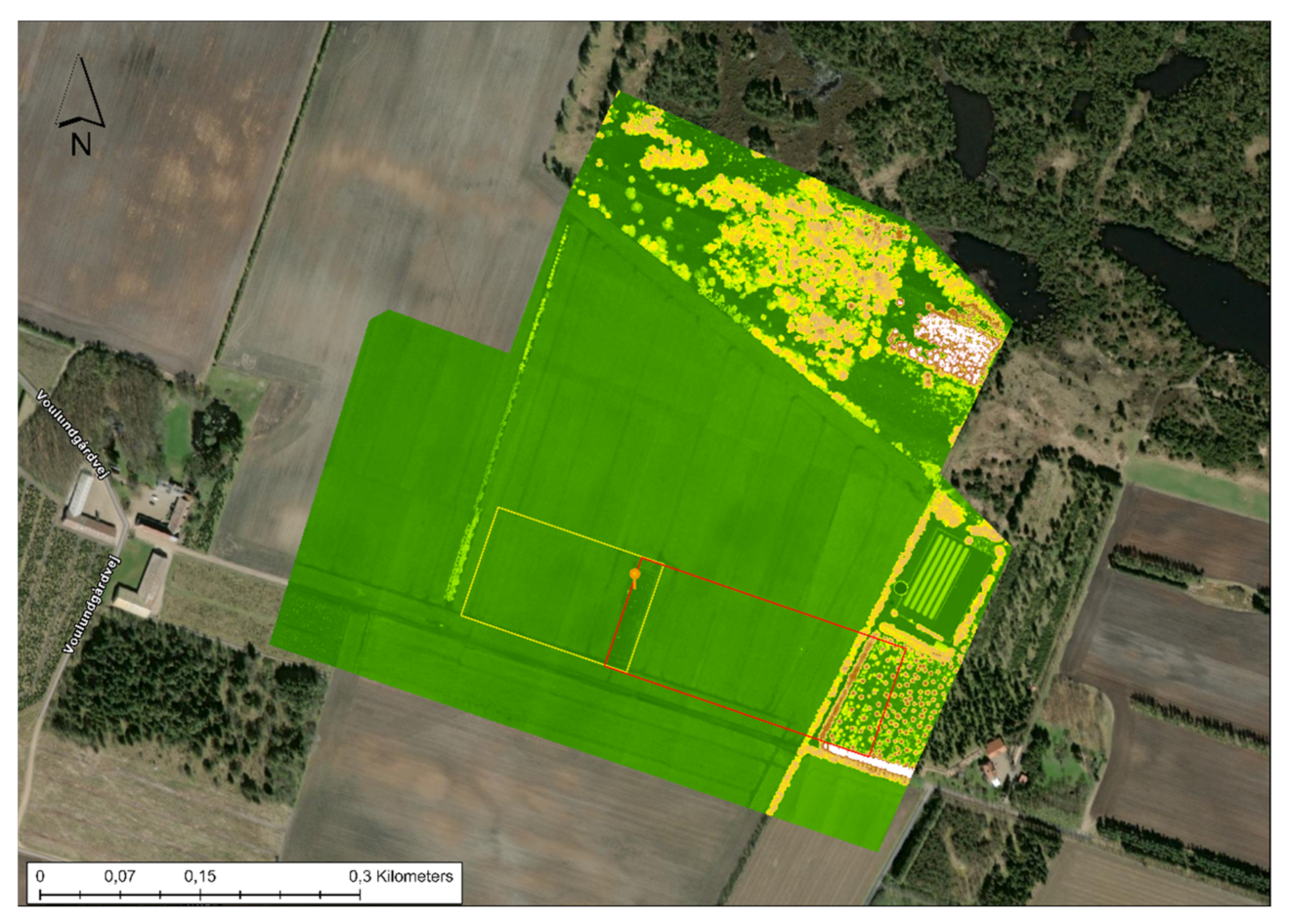
2.1. Site Description
2.2. Data Collection
2.3. Evaluation Procedure
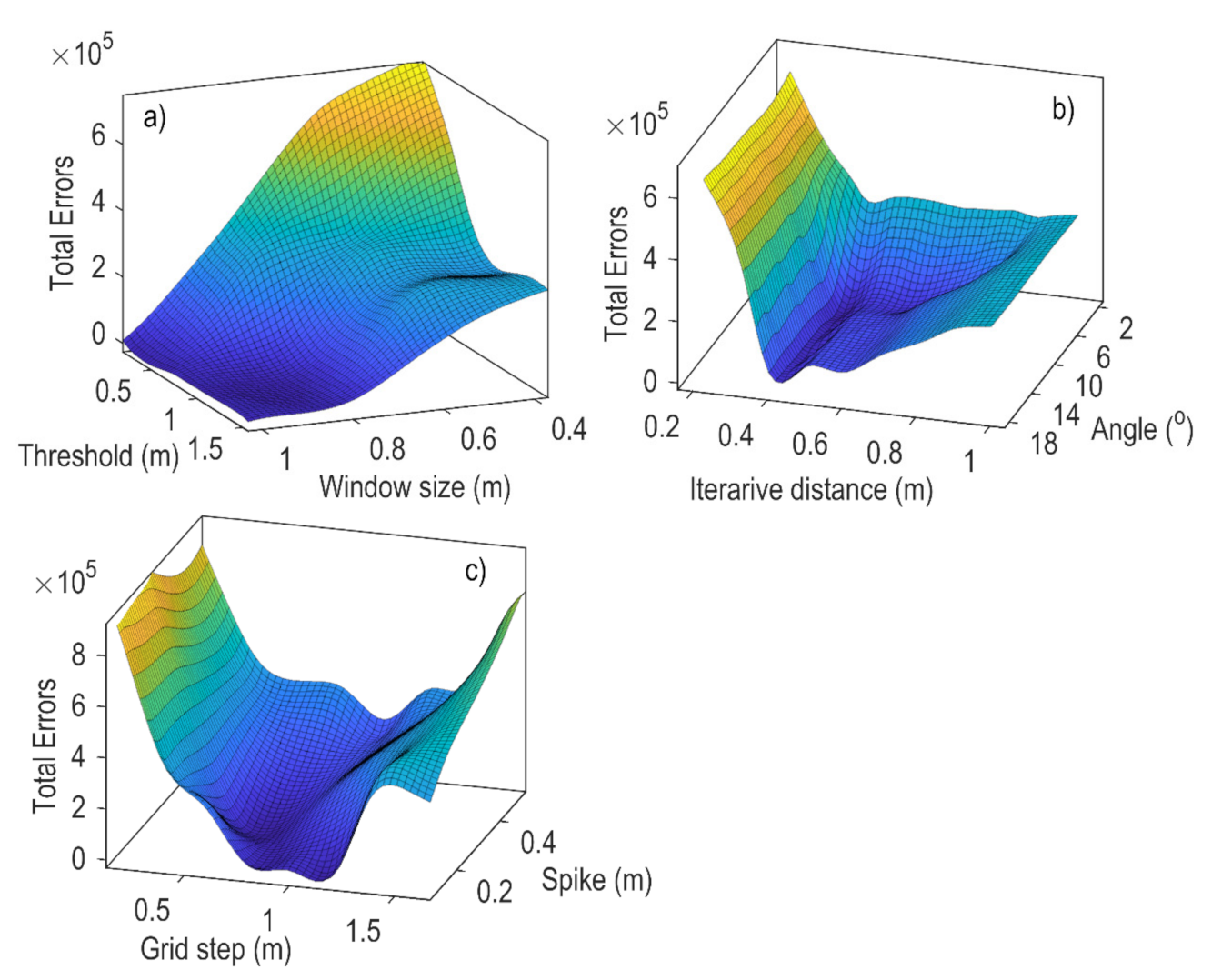
2.4. Point Cloud Processing
2.5. Description of Morphometric Methods
2.5.1. Roughness Length Based on Vegetation Height
2.5.2. Roughness Length Based on Vegetation Geometry and Wind Conditions
u*/U = min [(cs + cr fai)0.5, (u*/U)max]
2.5.3. Roughness Length Based on Vegetation Height Variability
2.6. Description of the Anemometric Method
3. Results
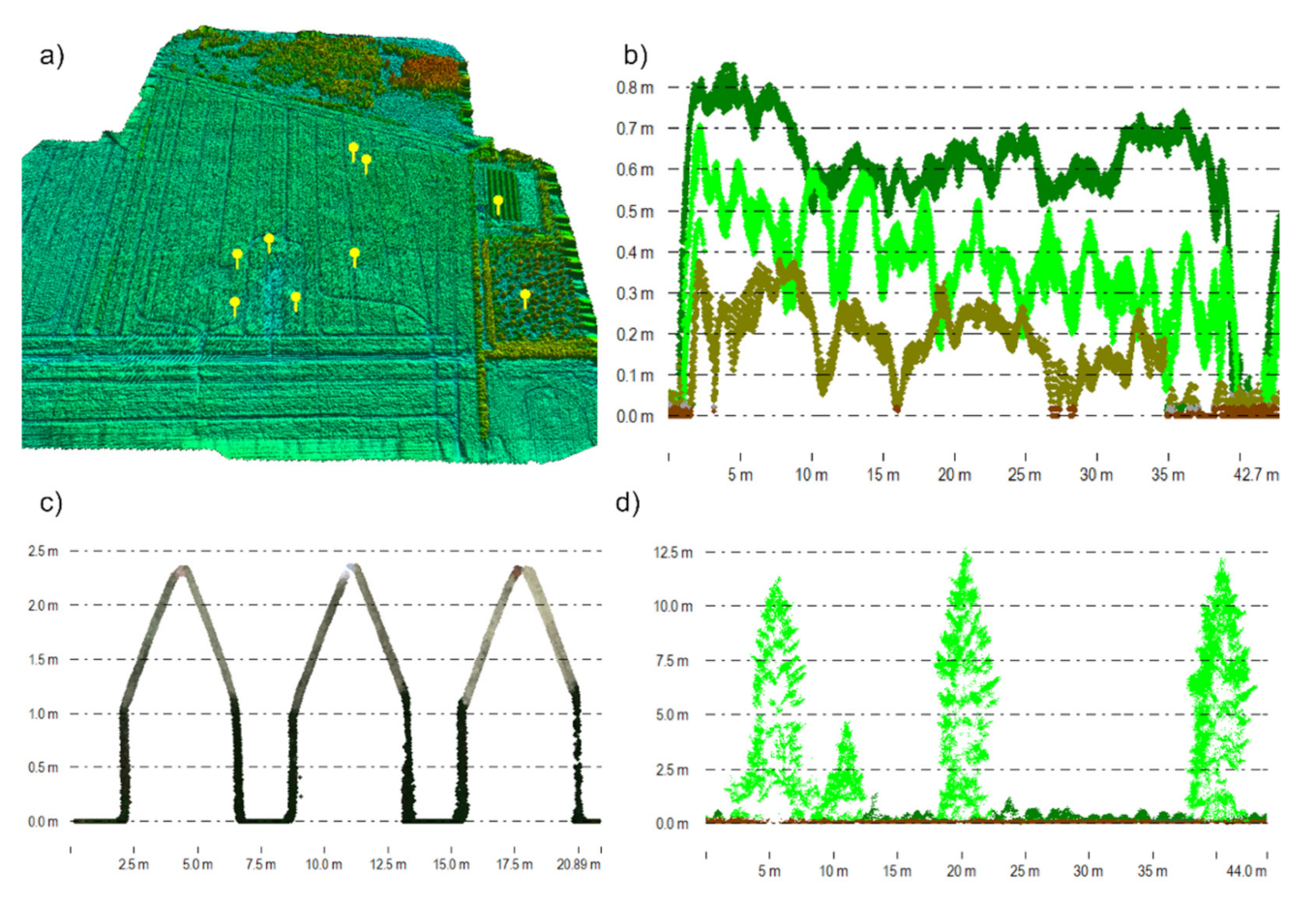
3.1. Segmentation of Point Cloud Data
3.2. Validation of Canopy Height Models
3.3. Source Turbulent Areas Using Morphometric Models
3.4. Comparison of Methods to Derive Roughness Length
3.5. Influence of Wind Orientation for Deriving Roughness Length
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; p. 670. [Google Scholar]
- Minvielle, F.; Marticorena, B.; Gillette, D.A.; Lawson, R.E.; Thompson, R.; Bergametti, G. Relationship between the Aerodynamic Roughness Length and the Roughness Density in Cases of Low Roughness Density. Environ. Fluid Mech. 2003, 3, 249–267. [Google Scholar] [CrossRef]
- Dickinson, R.E. Land surface processes and climate surface albedos and energy balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)–model. J. Irrig. Drain. Eng. ASCE 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL), 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Roerink, G.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes at scales ranging from a point to a continent. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Massman, W.J. A model study of kBH-1 for vegetated surfaces using ‘localized near-field’ Lagrangian theory. J. Hydrol. 1999, 223, 27–43. [Google Scholar] [CrossRef]
- Blumel, K.B. A simple formula for estimation of the roughness length for heat transfer over partly vegetated surfaces. J. Appl. Meteorol. 1999, 38, 814–829. [Google Scholar] [CrossRef]
- Su, Z.; Schmugge, T.; Kustas, W.P.; Massman, W.J. An evaluation of two models for estimation of the roughness height for heat transfer between the land surface and the atmosphere. J. Appl. Meteorol. 2001, 40, 1933–1951. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Li, F. Utility of radiometric–aerodynamic temperature relations for heat flux estimation. Bound.-Layer Meteorol. 2007, 122, 167–187. [Google Scholar] [CrossRef]
- Macdonald, R.; Griffiths, R.; Hall, D. An improved method for the estimation of surface roughness of obstacle arrays. Atmos. Environ. 1998, 32, 1857–1864. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Kustas, W.P.; Choudhury, B.J.; Moran, M.S.; Reginato, R.J.; Jackson, R.D.; Gay, L.W.; Weaver, H.L. Determination of sensible heat flux over sparse canopy using thermal infrared data. Agric. For. Meteorol. 1989, 44, 197–216. [Google Scholar] [CrossRef]
- Garratt, J. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1992; p. 336. [Google Scholar]
- Borak, J.S.; Jasinski, M.; Crago, R. Time series vegetation aerodynamic roughness fields estimated from modis observations. Agric. For. Meteorol. 2005, 135, 252–268. [Google Scholar] [CrossRef]
- Schaudt, K.J.; Dickinson, R.E. An approach to deriving roughness length and zero-plane displacement height from satellite data, prototyped with BOREAS data. Agric. For. Meteorol. 2000, 104, 143–155. [Google Scholar] [CrossRef]
- Tian, X.; Li, Z.Y.; Van der Tol, C.; Su, Z.; Li, X.; He, Q.; Bao, Y.; Chen, E.; Li, L. Estimating zero-plane displacement height and aerodynamic roughness length using synthesis of LiDAR and SPOT-5 data. Remote Sens. Environ. 2011, 115, 2330–2341. [Google Scholar] [CrossRef]
- Yilmaz, V.; Konakoglu, B.; Serifoglu, C.; Gungor, O.; Gökalp, E. Image classification-based ground filtering of point clouds extracted from UAV-based aerial photos. Geocarto Int. 2018, 33, 310–320. [Google Scholar] [CrossRef]
- Paul-Limoges, E.; Christen, A.; Coops, N.C.; Black, T.A.; Trofymow, J.A. Estimation of aerodynamic roughness of a harvested Douglas-fir forest using airborne LiDAR. Remote Sens. Environ. 2013, 136, 225–233. [Google Scholar] [CrossRef]
- Floors, R.; Enevoldsen, P.; Davis, N.; Arnqvist, J.; Dellwik, E. From LiDAR scans to roughness maps for wind resource modelling in forested areas. Wind Energ. Sci. 2018, 3, 353–370. [Google Scholar] [CrossRef]
- Holland, D.E.; Berglund, J.A.; Spruce, J.P.; McKellip, R.D. Derivation of effective aerodynamic surface roughness in urban areas from airborne LiDAR terrain data. J. Appl. Meteorol. Clim. 2008, 47, 2614–2626. [Google Scholar] [CrossRef]
- Colin, J.; Faivre, R. Aerodynamic roughness length from very high-resolution LIDAR observation. Hydrol. Earth Syst. Sci. 2010, 14, 2661–2669. [Google Scholar] [CrossRef]
- Brown, O.W.; Hugenholtz, C.H. Estimating aerodynamic roughness (zo) in mixed grassland prairie with airborne LiDAR. Can. J. Remote Sens. 2012, 37, 422–428. [Google Scholar] [CrossRef]
- Li, A.; Zhao, W.; Mitchell, J.J.; Glenn, N.F.; Germino, M.J.; Sankey, J.B.; Allen, R.G. Aerodynamic Roughness Length Estimation with Lidar and Imaging Spectroscopy in a Shrub-Dominated Dryland. Photogramm. Eng. Remote S. 2017, 83, 415–427. [Google Scholar] [CrossRef][Green Version]
- Hopkinson, C.; Chasmer, L.E.; Gabor, S.; Creed, I.F.; Sitar, M.; Kalbfleisch, W.; Treitz, P. Vegetation class dependent errors in LiDAR ground elevation and canopy height estimates in a boreal wetland environment. Can. J. Remote Sens. 2005, 13, 191–206. [Google Scholar] [CrossRef]
- Rosso, P.H.; Ustin, S.L.; Hastings, A. Use of LiDAR to study changes associated with Spartina invasion in San Francisco Bay marshes. Remote Sens. Environ. 2006, 100, 295–306. [Google Scholar] [CrossRef]
- Wang, C.; Menenti, M.; Stoll, M.P.; Feola, A.; Belluco, E.; Marani, M. Separation of ground and low vegetation signatures in LiDAR measurements of salt-marsh environments. IEEE Trans. Geosci. Remote 2009, 47, 2014–2023. [Google Scholar] [CrossRef]
- Kellner, J.R.; Armston, J.; Birrer, M.; Cushman, K.; Duncanson, L.; Eck, C.; Falleger, C.; Imbach, B.; Král, K.; Krůček, M.; et al. New Opportunities for Forest Remote Sensing Through Ultra-High-Density Drone LiDAR. Surv. Geophys. 2019, 40, 959–977. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.J.; Glenn, N.F.; Sankey, T.T.; Derryberry, D.R.; Anderson, M.O.; Hruska, R.C. Small-footprint LiDAR estimations of sagebrush canopy characteristics. Photogramm. Eng. Remote S. 2011, 77, 521–530. [Google Scholar] [CrossRef]
- Resop, J.P.; Lehmann, L.; Hession, W.C. Drone Laser Scanning for Modeling Riverscape Topography and Vegetation: Comparison with Traditional Aerial LiDAR. Drones 2019, 3, 35. [Google Scholar] [CrossRef]
- Sankey, T.T.; McVay, J.; Swetnam, T.L.; McClaran, M.P.; Heilman, P.; Nichols, M. UAV hyperspectral and LiDAR data and their fusion for arid and semi-arid land vegetation monitoring. Remote Sens. Ecol. Con. 2018, 4, 20–33. [Google Scholar] [CrossRef]
- Bates, J.S.; Montzka, C.; Schmidt, M.; Jonard, F. Estimating Canopy Density Parameters Time-Series for Winter Wheat Using UAS Mounted LiDAR. Remote Sens. 2021, 13, 710. [Google Scholar] [CrossRef]
- Rogers, S.R.; Manning, I.; Livingstone, W. Comparing the spatial accuracy of digital surface models from four unoccupied aerial systems: Photogrammetry versus LiDAR. Remote Sens. 2020, 12, 2806. [Google Scholar] [CrossRef]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and digital aerial photogrammetry point clouds for estimating forest structural attributes in subtropical planted forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
- Sofonia, J.; Shendryk, Y.; Phinn, S.; Roelfsema, C.; Kendoul, F.; Skocaj, D. Monitoring sugarcane growth response to varying nitrogen application rates: A comparison of UAV SLAM LiDAR and photogrammetry. Int. J. Appl. Earth Observ. Geoinform. 2019, 82, 101878. [Google Scholar] [CrossRef]
- Duan, T.; Zheng, B.; Guo, W.; Ninomiya, S.; Guo, Y.; Chapman, S.C. Comparison of ground cover estimates from experiment plots in cotton, sorghum and sugarcane based on images and ortho-mosaics captured by UAV. Funct. Plant. Biol. 2017, 44, 169–183. [Google Scholar] [CrossRef]
- Shendryka, Y.; Sofonia, J.; Garrardc, R.; Rista, Y.; Skocajd, D.; Thorburn, P. Fine-scale prediction of biomass and leaf nitrogen content in sugarcane using UAV LiDAR and multispectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102177. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Gano, B.; Dembele, J.S.B.; Ndour, A.; Luquet, D.; Beurier, G.; Diouf, D.; Audebert, A. Using UAV Borne, Multi-Spectral Imaging for the Field Phenotyping of Shoot Biomass, Leaf Area Index and Height of West African Sorghum Varieties under Two Contrasted Water Conditions. Agronomy 2021, 11, 850. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering airborne laser scanning data with morphological methods. Photogram. Eng. Remote Sens. 2007, 73, 175–185. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound.-Lay. Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Menenti, M.; Ritchie, J.C. Estimation of effective aerodynamic roughness of Walnet Gulch watershed with laser altimeter measurements. Water Resour. Res. 1994, 5, 1329–1337. [Google Scholar] [CrossRef]
- Jensen, R.; Herbst, M.; Friborg, T. Direct and indirect controls of the interannual variability in atmospheric CO2 exchange of three contrasting ecosystems in Denmark. Agric. For. Meteor. 2017, 233, 12–31. [Google Scholar] [CrossRef]
- Chang, C.; Habib, F.; Lee, C.; Yom, H. Automatic classification of lidar data into ground and nonground points. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 463–468. [Google Scholar]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogram. Remote Sens. 2000, 33, 111–118. [Google Scholar]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing non-ground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Hutton, C.; Brazier, R. Quantifying riparian zone structure from airborne LiDAR: Vegetation filtering, anisotropic interpolation, and uncertainty propagation. J. Hydrol. 2012, 442–444, 36–45. [Google Scholar] [CrossRef]
- Blue Marble Geographics. 2020. Available online: https://www.bluemarblegeo.com/ (accessed on 19 January 2021).
- LAStools. 2015. Available online: https://rapidlasso.com/lastools/ (accessed on 14 February 2021).
- GreenValley International Ltd. LiDAR360 Suite Software. 2019. Available online: https://greenvalleyintl.com (accessed on 7 April 2021).
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogram. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA; 1968; pp. 517–524. [Google Scholar]
- Krayenhoff, E.; Santiago, J.; Martilli, A.; Christen, A.; Oke, T. Parametrization of drag and turbulence for urban neighbourhoods with trees. Bound.-Layer Meteorol. 2015, 156, 157–189. [Google Scholar] [CrossRef]
- De Vries, A.C.; Kustas, W.P.; Ritchie, J.C.; Klaassen, W.; Menenti, M.; Rango, A.; Prueger, J.H. Effective aerodynamic roughness estimated from airborne laser altimeter measurements of surface features. Int. J. Remote Sens. 2003, 24, 1545–1558. [Google Scholar] [CrossRef]
- Lindberg, F.; Grimmond, C.S.B.; Gabey, A.; Huang, B.; Kent, C.W.; Sun, T.; Theeuwes, N.E.; Järvi, L.; Ward, H.C.; Capel-Timms, I.; et al. Urban Multi-scale Environmental Predictor (UMEP): An integrated tool for city-based climate services. Environ. Model. Softw. 2018, 99, 70e87. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2017. Available online: http://www.qgis.org/ (accessed on 23 May 2021).
- Vickers, D.; Mahrt., L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Nakai, T.; Van Der Molen, M.K.; Gash, J.H.C.; Kodama, Y. Correction of sonic anemometer angle of attack errors. Agric. For. Meteorol. 2006, 136, 19–30. [Google Scholar]
- Schotanus, P.; Nieuwstadt, F.T.M.; De Bruin, H.A.R. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound.-Lay. Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.A.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Foken, T.; Göockede, M.; Mauder, M.; Mahrt, L.; Amiro, B.; Munger, W. Post-field data quality control. In Handbook of Micrometeorology; Lee, X., Massman, W., Law, B., Eds.; Atmospheric and Oceanographic Sciences Library, Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Tennekes, H.; Lumley, J.L. Wall-bounded shear flows. In A First Course in Turbulence, 16th ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Högström, U. Review of some basic characteristics of the atmospheric surface € layer. Bound.-Layer Meteorol. 1996, 28, 215–246. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model. Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Arya, P. Thermally stratified surface layer. In Introduction to Micrometeorology, 2nd ed.; Academic Press: San Diego, CA, USA, 2001; p. 420. [Google Scholar]
- Shaw, R.H.; Pereira, A.R. Aerodynamic roughness of a plant canopy: A numerical experiment. Agric. Meteorol. 1982, 26, 51–65. [Google Scholar] [CrossRef]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]
- Jimenez-Berni, J.A.; Deery, D.M.; Rozas-Larraondo, P.; Condon, A.G.; Rebetzke, G.; James, R.; Bovill, W.; Furbank, R.; Sirault, X. High Throughput Determination of Plant Height, Ground Cover, and Above-Ground Biomass in Wheat with LiDAR. Front. Plant. Sci. 2018, 9, 237. [Google Scholar] [CrossRef]
- Walter, J.D.C.; Edwards, J.; McDonald, G.; Kuchel, H. Estimating Biomass and Canopy Height with LiDAR for Field Crop Breeding. Front. Plant. Sci. 2019, 10, 1145. [Google Scholar] [CrossRef] [PubMed]
- Streutker, D.R.; Glenn, N.F. LiDAR measurement of sagebrush steppe vegetation heights. Remote Sens. Environ. 2006, 102, 135145. [Google Scholar] [CrossRef]
- Su, J.G.; Bork, E.W. Characterization of diverse plant communities in Aspen Parkland rangeland using LiDAR data. Appl. Veg. Sci. 2007, 10, 407–416. [Google Scholar] [CrossRef]
- Wang, D.; Xin, X.; Shao, Q.; Brolly, M.; Zhu, Z.; Chen, J. Modeling Aboveground Biomass in Hulunber Grassland Ecosystem by Using Unmanned Aerial Vehicle Discrete Lidar. Sensors 2017, 17, 180. [Google Scholar] [CrossRef] [PubMed]
- Maas, H.G.; Vosselman, G. Two algorithms for extracting building models from raw laser altimetry data. ISPRS J. Photogramm. Remote Sens. 1999, 54, 153–163. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Wang, S.; Garcia, M.; Bauer-Gottwein, P.; Jakobsen, J.; Zarco-Tejada, P.J.; Bandini, F.; Paz, V.S.; Ibrom, A. High spatial resolution monitoring land surface energy, water and CO2 fluxes from an Unmanned Aerial System. Remote Sens. Environ. 2019, 229, 14–31. [Google Scholar] [CrossRef]
- Colin, J.; Menenti, M.; Rubio, E.; Jochum, A. Accuracy vs. operability: A case study over barrax in the context of the idots. In Proceedings of the AIP Conference Proceedings, Naples, Italy, 10–11 November 2005; Volume 852, pp. 75–83. [Google Scholar]
- Yang, X.; Yu, Y.; Fan, W.A. A method to estimate the structural parameters of windbreaks using remote sensing. Agrofor. Syst. 2017, 91, 37–49. [Google Scholar] [CrossRef]
- Kent, C.W.; Grimmond, S.; Gatey, D. Aerodynamic roughness parameters in cities: Inclusion of vegetation. J. Wind Eng. Ind. Aerod. 2017, 169, 168176. [Google Scholar] [CrossRef]
- Millward-Hopkins, J.; Tomlin, A.; Ma, L.; Ingham, D.; Pourkashanian, M. Estimating aerodynamic parameters of urban-like surfaces with heterogeneous building heights. Bound.-Layer Meteorol. 2011, 141, 443–465. [Google Scholar] [CrossRef]


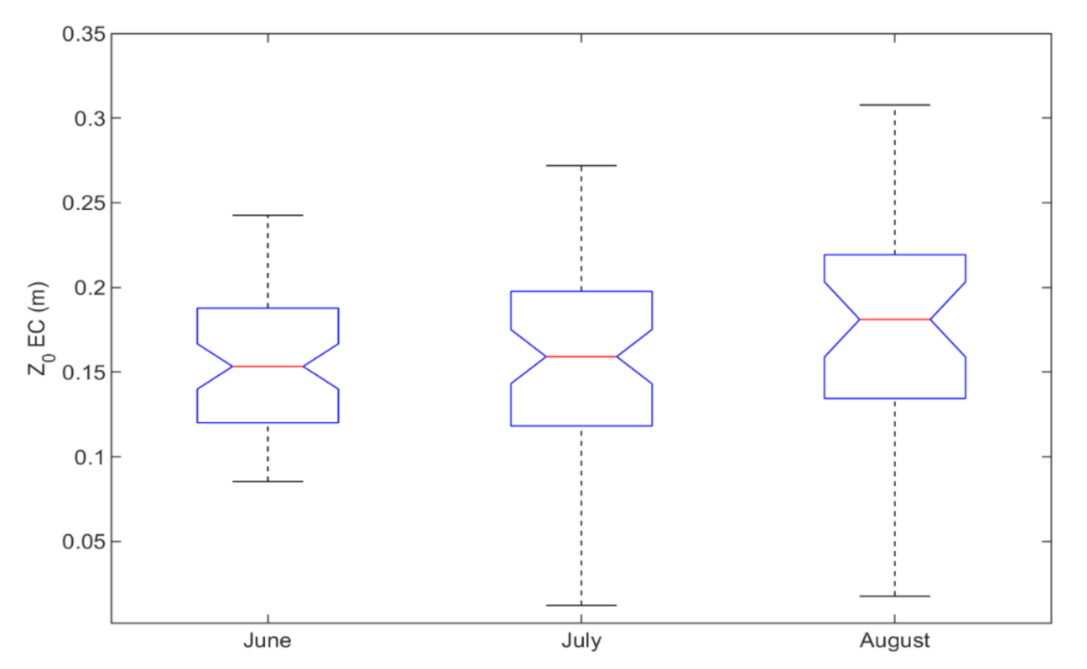

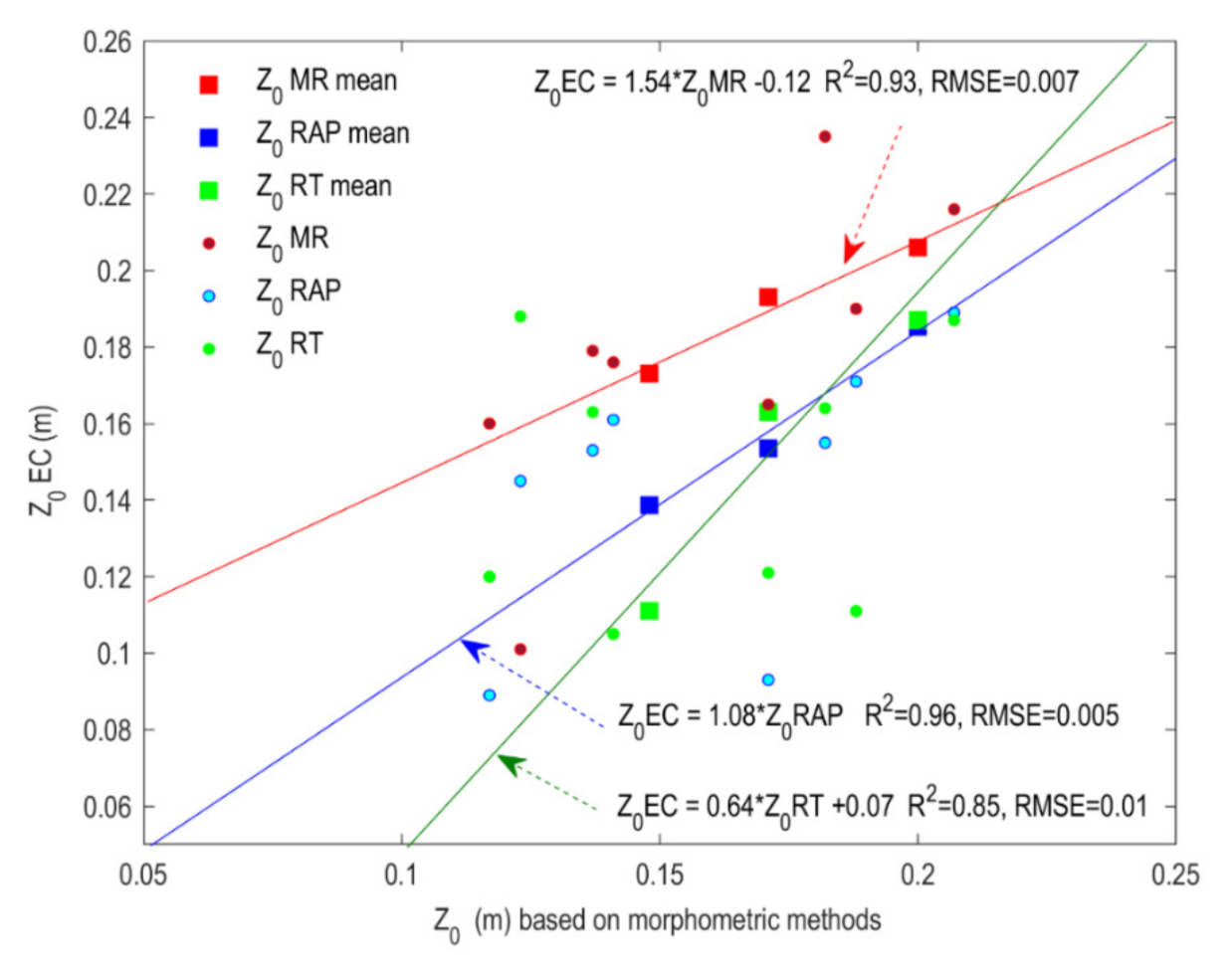

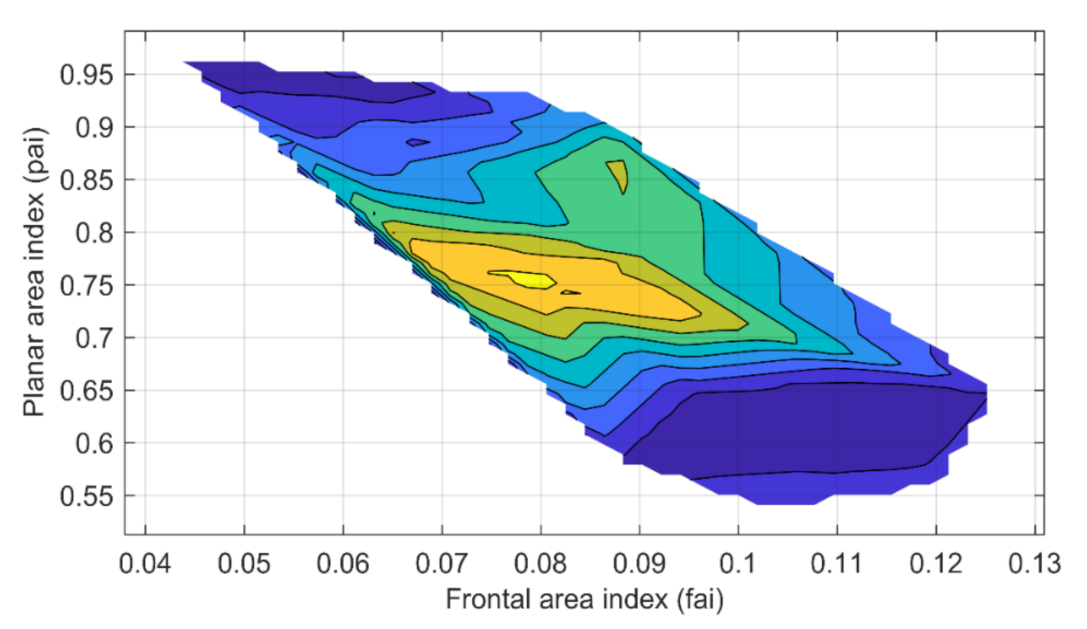

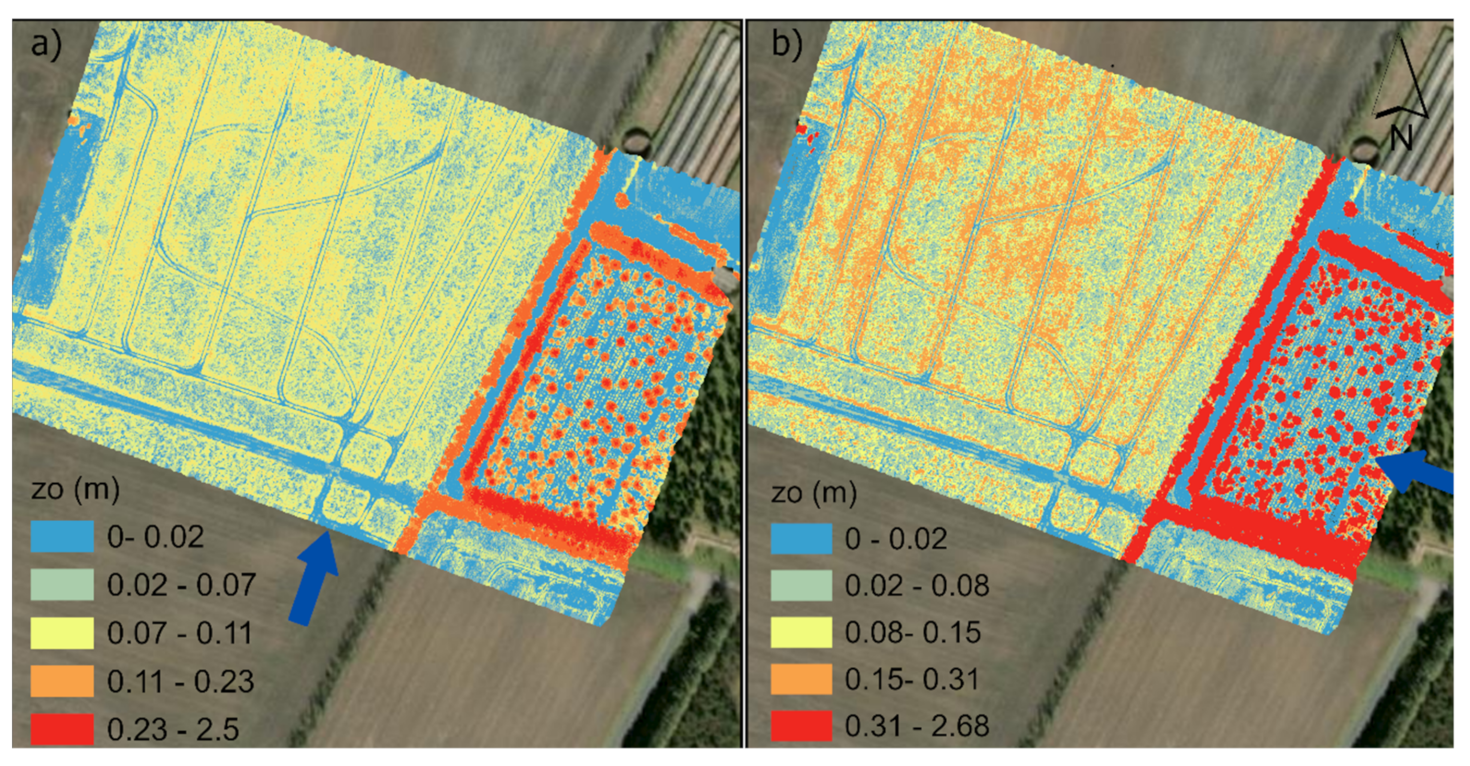
| Methods | Parameter Set | |||||
|---|---|---|---|---|---|---|
| Window Size (m) | Elevation Threshold (m) | Iterative Distance (m) | Iterative Angle (°) | Grid Size (m) | Spike (m) | |
| MF | 1 | 1 | ||||
| PTD | 0.4 | 4 | ||||
| TIN | 0.8 | 0.2 | ||||
| Subscene/Date | PTD | TIN | MF |
|---|---|---|---|
| Plot 1/26 June | 15.57 | 26.38 | 9.27 |
| Plot 1/14 July | 28.75 | 46.10 | 18.28 |
| Plot 1/12 August | 23.84 | 40.56 | 16.36 |
| Plot 2/26 June | 14.75 | 34.73 | 19.62 |
| Plot 2/14 July | 18.32 | 37.46 | 25.65 |
| Plot 2/12 August | 16.84 | 32.39 | 20.52 |
| Mean Error | 19.67 | 36.27 | 18.28 |
| Date | Field h (m) | LiDAR h (m) |
|---|---|---|
| 26 June | 0.52 | 0.44 |
| 14 July | 0.71 | 0.56 |
| 12 August | 0.78 | 0.72 |
| Date | Mean h (m) | Mode h (m) | Standard Deviation h (m) | Increase in Vegetation (%) |
|---|---|---|---|---|
| 26 June | 0.61 | 0.60 | 0.11 | |
| 14 July | 0.76 | 0.75 | 0.16 | 30.25 |
| 12 August | 0.91 | 1.00 | 0.15 | 44.36 |
| Z0_RAP | Z0_RT | Z0_MR | Z0_EC | fai | |
|---|---|---|---|---|---|
| Differences to Z0_EC | |||||
| June (n = 63) | 0.009 | 0.037 | −0.025 | 0.148 | 0.048 |
| July (n = 62) | 0.018 | 0.008 | −0.023 | 0.171 | 0.048 |
| August (n = 36) | 0.015 | 0.013 | −0.006 | 0.200 | 0.058 |
| Average | 0.014 | 0.013 | −0.019 | ||
| Standard deviation | 0.031 | 0.042 | 0.022 | ||
| Unstable conditions Plot 1 | |||||
| June (n = 8) | 0.028 | −0.003 | −0.043 | 0.117 | 0.039 |
| July (n = 46) | −0.016 | −0.026 | −0.042 | 0.137 | 0.045 |
| August (n = 3) | −0.022 | −0.065 | 0.022 | 0.123 | 0.042 |
| Neutral conditions Plot 1 | |||||
| June (n = 13) | 0.078 | 0.05 | 0.006 | 0.171 | 0.041 |
| July (n = 16) | 0.027 | 0.018 | −0.053 | 0.182 | 0.042 |
| August (n = 33) | 0.018 | 0.02 | −0.009 | 0.207 | 0.060 |
| Unstable conditions Plot 2 | |||||
| June (n = 36) | −0.020 | 0.036 | −0.035 | 0.141 | 0.054 |
| Neutral conditions Plot 2 | |||||
| June (n = 6) | 0.017 | 0.077 | −0.002 | 0.188 | 0.046 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trepekli, K.; Friborg, T. Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR. Remote Sens. 2021, 13, 3538. https://doi.org/10.3390/rs13173538
Trepekli K, Friborg T. Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR. Remote Sensing. 2021; 13(17):3538. https://doi.org/10.3390/rs13173538
Chicago/Turabian StyleTrepekli, Katerina, and Thomas Friborg. 2021. "Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR" Remote Sensing 13, no. 17: 3538. https://doi.org/10.3390/rs13173538
APA StyleTrepekli, K., & Friborg, T. (2021). Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR. Remote Sensing, 13(17), 3538. https://doi.org/10.3390/rs13173538