Abstract
Onboard target detection of hyperspectral imagery (HSI), considered as a significant remote sensing application, has gained increasing attention in the latest years. It usually requires processing huge volumes of HSI data in real-time under constraints of low computational complexity and high detection accuracy. Automatic target generation process based on an orthogonal subspace projector (ATGP-OSP) is a well-known automatic target detection algorithm, which is widely used owing to its competitive performance. However, ATGP-OSP has an issue to be deployed onboard in real-time target detection due to its iteratively calculating the inversion of growing matrices and increasing matrix multiplications. To resolve this dilemma, we propose a novel fast implementation of ATGP (Fast-ATGP) while maintaining target detection accuracy of ATGP-OSP. Fast-ATGP takes advantage of simple regular matrix add/multiply operations instead of increasingly complicated matrix inversions to update growing orthogonal projection operator matrices. Furthermore, the updated orthogonal projection operator matrix is replaced by a normalized vector to perform the inner-product operations with each pixel for finding a target per iteration. With these two major optimizations, the computational complexity of ATGP-OSP is substantially reduced. What is more, an FPGA-based implementation of the proposed Fast-ATGP using high-level synthesis (HLS) is developed. Specifically, an efficient architecture containing a bunch of pipelines being executed in parallel is further designed and evaluated on a Xilinx XC7VX690T FPGA. The experimental results demonstrate that our proposed FPGA-based Fast-ATGP is able to automatically detect multiple targets on a commonly used dataset (AVIRIS Cuprite Data) at a high-speed rate of 200 MHz with a significant speedup of nearly 34.3 times that of ATGP-OSP, while retaining nearly the same high detection accuracy.
1. Introduction
Hyperspectral imaging sensors can acquire images with hundreds of contiguous spectral channels [1,2]. As a benefit from such rich spectral information, hyperspectral images (HSIs) have unique advantages for classification, detection, and recognition [3,4,5,6]. Real-time target detection aiming to find timely interesting targets has drawn much attention because of its significance in military and civilian applications [7,8,9]. Although the presence of targets in HSI provides critical information in data analysis, it is rather rare and may be difficult to find because many of HSI-detected targets are relatively small and weak, such as anomalies [10]. Consequently, real-time target detection in HSI presents a great challenge and has become increasingly important.
Currently, many algorithms have been developed for target detection in HSI, such as unsupervised fully constrained least squares (UFCLS) [11], automatic target-generation process based on an orthogonal subspace projector (ATGP-OSP) [12], and Reed-Xiaoli (RX) detector [13]. Among them, the performance of ATGP performs well in terms of detection accuracy and computational complexity according to the quantitative and comparative assessments [14,15]. However, despite the fact that automatic target detection has received increasing attention [16,17,18], two problems with real-time onboard applications need to be addressed. One is to continuously increase the scale of operations in the process of automatically iterating to update currently being found targets, which complicates the process of updating operator matrix. The other one is a large-scale matrix multiplication problem when projecting HSI data onto the direction specified by the operator matrix, which consumes most of the time and resources and makes ATGP-OSP realize inefficiently. To mitigate the aforementioned problems, Fast-ATGP is proposed to solve the increasingly complicated operation problem and to replace the update of the operator matrix with a normalized vector.
Owing to the complexity and dimensionality of HSI, ATGP is still computationally intensive [19]. This often leads to the requirement of hardware accelerators to speed up computations [20]. The algorithm could be implemented on one of the widely used platforms like CPUs [16], GPUs [21], and field-programmable gate array (FPGAs) [22]. Among them, FPGAs have significant advantages in efficiently processing HSIs due to the following three main reasons. First, FPGAs are able to provide much more competent levels of performance closing to those offered by GPUs with much lower power consumption. Another is that FPGA devices with increased levels of tolerance to ionizing radiation in space are widely used as the solution for onboard processing at earth observation satellites. Last but not least, is the fact that FPGAs have the inherent ability to change their functionality through partial or full reconfiguration. In the past, there have been several developments toward the implementation of target detection algorithms on FPGAs [23]. Specifically, Yang et al. [24] utilized Streaming Background Statistics (SBS) structure with an idea of continuously updating the inverse of the correlation matrix on FPGA. Recently, Gonzalez et al. [17] developed an FPGA implementation of ATGP-OSP using the pseudoinverse operation with superior hardware implementation. Unfortunately, the Gauss-Jordan elimination method for updating the inverse matrix still suffers higher computational complexity and resource utilization.
Although FPGAs gain much attention, it is still not easy to apply them to accelerate those algorithms which still have high computational complexity [25,26]. The primary reason is that the conventional development technique of FPGA uses hardware description language (HDL) at the register-transfer level (RTL), which is a massive time-consumed process and lacks portability and flexibility compared to those based on C/C++ for CPUs or GPUs. As a promising alternative, FPGA vendors and developers begin to take advantage of high-level synthesis (HLS) to develop FPGA applications [27]. HLS is a relatively mature design methodology [28], which allows high-level abstraction languages such as C/C++ to be synthesized into VHDL/Verilog HDL for RTL-level circuit design [29,30]. Specifically, there have been some studies on using HLS for HSI applications, such as classification [31], unmixing [32], and compression [33]. The merit of HLS is validated in our previous work [34] that the deep pipelined background statistics (DPBS) structure is developed for real-time target detection. In addition, Domingo et al. [29] proposed an HSI spatial-spectral classifier accelerator using Intel FPGA SDK for OpenCL. Guo et al. [35] introduced the pixel purity index (PPI) to extract endmembers in HSI described in Vivado HLS.
In this paper, a Fast-ATGP algorithm is developed and implemented on FPGA using HLS for real-time target detection. Like ATGP-OSP, the orthogonal projection operator is gradually updated using pseudoinverse operation [17]. Different from the traditional target update with an increasing scale of calculation, Fast-ATGP optimizes the Gram Schmidt orthogonal vector projection (GSOVP) method to update the operator matrix. As for the issue of calculating large-scale matrix multiplication when the operator projected on HSI, a normalized vector is proposed to perform vector multiplications instead of matrix multiplications. As a result, an extremely fast version of ATGP can be further proposed, which has an extraordinary performance improvement resulting from a significant reduction in the amount of computations. Experiments performed on two real hyperspectral data sets prove the effectiveness of the proposed algorithm in terms of detection accuracy and speed performance. More specifically, our architecture has the capability of operating at a high-speed rate of 200 MHz with a significant speedup of near 34.3 times ATGP-OSP in the AVIRIS Cuprite data set with nearly the same detection accuracy.
The contributions of this paper can be summarized as follows.
- A solution is derived to remove traditional complex inversion in ATGP-OSP by a simple method. The proposed method is capable of achieving real-time detection without sacrificing target quality at a fixed scale of operation.
- A novel effectively update structure for orthogonal projection operator is proposed to accelerate Fast-ATGP. A normalized vector is adopted to replace the classical operator to complete the projection process.
- The proposed architecture can greatly balance speedup factors and resources by combining the serial-parallel structure and multiplex technique, which is optimal for processing wealthy HSI information in terms of real-time hardware implementation.
- The approach can be simply reconstructed by adjusting several parameters in HLS. As a consequence, the framework is able to support HSI with different sizes and spectral bands and conforms to multiple amounts of processing element (PE) to achieve different levels of parallelism.
The remainder of this paper is organized as follows. Section 2 briefly describes the principle of ATGP-OSP and analyzes its problems when it is implemented on FPGAs. The proposed Fast-ATGP is introduced in Section 3. The FPGA implementation of Fast-ATGP is presented in Section 4. Section 5 conducts a detailed performance analysis via extensive experiments. Finally, conclusions along with some remarks are drawn in Section 6.
2. Background
In this section, we briefly describe ATGP-OSP and analyze its problems when it is implemented in practical applications.
2.1. ATGP-OSP Algorithm
The original ATGP is based on OSP concepts and will be referred to hereinafter as ATGP-OSP [17]. The basic concept of OSP is to project each pixel vector onto a subspace which is orthogonal to the obtained signatures [14]. It is an iterative process in which orthogonal projections are applied to find a set of spectrally distinct pixels [12]. ATGP-OSP method is summarized in Algorithm 1, where is a matrix of spectral signatures, is the transpose of it, and is the identity matrix. It should be emphasized that the ATGP-OSP primarily comes from a need of finding targets of interest in HSI only with the prior knowledge of t, where t denotes the number of targets to be detected. In general, the value of t can be obtained by the virtual dimensionality (VD) developed in [22].
In ATGP-OSP, denote an HSI with pixels and L spectral bands. The ATGP-OSP algorithm begins by an orthogonal projection operator specified by the following expression:
Orthogonal projection operator has the same structure with the orthogonal complement projector, where is the pseudoinverse of . The operator is first applied to the original image, with , where is an initial target signature (i.e., the pixel vector with maximum length). It then finds a target signature , with the maximum projection in , where is the orthogonal projection operator composed with by step 4 in Algorithm 1. is the orthogonal complement space linearly spanned by . The following target signature is obtained by another with and selected by the maximum projection in . Then the procedure above is repeated until the target pixels are detected.
| Algorithm 1 Pseudocode of ATGP-OSP |
| 1: Inputs: , and t; % denotes an n-dimensional hyperspectral image with r pixels, and t denotes the number of targets to be detected 2: ; % is the initial target signature with maximum length in 3: for to do 4: ; % is a vector orthogonal to the subspace spanned by the columns of 5: ; % is projected onto the direction indicates by 6: ; % The maximum projection value is found, where r denotes the total number of pixel in the hyperspectral image and the operator “:” denotes “all elements” 7: ; % The target matrix is updated 8: end for i 9: Outputs: ; |
2.2. Analysis
According to Algorithm 1, the target detection process can be summarized in three stages. The first stage updates the orthogonal subspace projector (step 4 of Algorithm 1). The next stage is the orthogonal projection process (step 5 of Algorithm 1). The last stage mainly finds the target pixel with maximum length in (step 6 of Algorithm 1). In addition, the number of computations for each stage is shown in Table 1 when detecting the i-th target, where . Although ATGP-OSP achieves considerable detection performance [36], it is computationally expensive because of the complexity and dimensionality of HSI, which limits the possibility of utilizing this approach in time-critical applications. In the above three stages, the tightest bottleneck in the detecting process can be inducted as following two problems.

Table 1.
Computations for each stage when detecting the i-th target in automatic target generation process based on an orthogonal subspace projector (ATGP-OSP).
2.2.1. Increasing Operation Problem
The traditional ATGP-OSP requires inverting a matrix to eliminate the effect of the obtained targets [37]. However, as shown in Table 1, one of the most important issues with ATGP-OSP method is of high complexity in matrix inversion. ATGP-OSP needs time-slots every time when updating the operator . Though i is much smaller than L, it is still unusually difficult for hardware to design because the complicated process of matrix inversion is required. Besides, when the number of targets keeps increasing, which is indeed the case of hyperspectral data, ATGP-OSP will become slower due to the growing size of inverting matrices. In other words, high complexity makes it much more difficult to be realized on hardware like FPGAs.
To deal with this problem, Song et al. [38] developed a simple and new type of OSP without computing matrix inversion, referred to as GSOVP, which is also based on orthogonal projection. The purpose of using the GSOVP method in combination with ATGP is to orthogonalize a set of linearly independent vectors in an inner product space, usually the space in which the original hyperspectral image is defined. GSOVP theory, shown in Equation (2), can be described as follows: Suppose that there is a set of orthogonal base corresponding to the original signature vectors . The vector obtained by the Gram Schmidt theory is orthogonal to all the vectors included in . It is found in the orthogonal complement subspace to the space linearly spanned by by
where , .
The method above, which is much less complicated, makes use of consecutive inner product operations to achieve the purpose of eliminating the inversion of a matrix. However, according to Equation (2), the orthogonal vector in must be operated with in sequence, in which redundant multiplications are required. In addition, as the number of iterations i increasing, more repetitive operations need to be processed. Therefore, it is critical to convert this kind of increasing operations into regularized operations.
2.2.2. Huge Matrix Multiplication Problem
We test on a large number of HSIs and finding that stage 2 in Table 1 consumes the most of the time and resources because of the wealth of spectral information in . As shown in Table 1, after all of the target signatures are obtained, multiplications need to be performed, where r is about tens of thousands. It is also expected that, in the future, hyperspectral sensors will continue increasing their spatial, spectral, and temporal resolutions [39]. Therefore, HSI makes stage 2 have a typical huge matrix multiplication problem, which may cause a significant slow process to extraction the target signatures.
To reduce large-scale matrix multiplications, Bernabe et al. [18] utilized the normalized vectors generated by orthonormal set to update the orthogonal projector . In their implementation, is an arbitrary n-dimensional vector. Unfortunately, the method utilizes the operator repeatedly every time when extracting a next new signature, resulting in a large number of redundant and repetitive operations. What is more, the update of by orthogonal set is another process with redundant matrix multiplications. In conclusion, stage 2 overhead would be the major bottleneck of ATGP-OSP in data computation performance.
3. The Proposed Approach
To solve the aforementioned problems, an optimized algorithm, called Fast-ATGP, is proposed in this section in detail. The two main solutions are proposed to reduce computational complexity while realizing it in parallel. The Fast-ATGP calculates the orthogonal projection without using the pseudoinverse operation and updates the operator in one step, which is described in Algorithm 2.
| Algorithm 2 Pseudocode of Fast-ATGP |
| 1: Input: , and t; % denotes an n-dimensional hyperspectral image with r pixels and t denotes the number of targets to be detected 2: Initialized: , , ; % is the identity matrix and L denotes spectral bands of HSI, and are the initialized orthogonal projection operators 3: for to do 4: ; % HSI data is projected onto the direction indicates by 5: ; % The maximum projection value is found, where r denotes the total number of pixels 6: ; % The target is detected and the target matrix is updated, where the operator “:” denotes “all elements” 7: % , used for updating the operator and , is a vector obtained by the target signature projected onto the direction indicated by 8: % The projection operator of matrix is updated 9: ; % The projection operator of vector is updated 10: end for i 11: Output: ; |
3.1. The Principle of Fast-ATGP
3.1.1. Fixed Scale of Operation
In classical ATGP-OSP, the operator projects the pixel vector into the orthogonal complement of the signatures when executing the i-th iteration. To reduce unnecessary complex calculations like matrix inversion when updating the operator , GSOVP algorithm utilizes another way to obtain the orthogonal vector. But it inevitably performs more complicated operations as the number of targets increases, and each operation requires all the previous pixels to participate, instead of updating it in real time based on existed results. To solve the increasing operation problem, a fixed scale of operation can be applied to update the . In our implementation, the update of orthogonal set is changed into a matrix form by performing matrix operations. Instead of , operator still acts as the orthogonal subspace to project the image like ATGP-OSP. The Fast-ATGP algorithm extracts the orthogonal projection operator by
At this time, only a single update of matrix is needed rather than i-times vector operations when attaining the orthogonal projection vector . In addition, the first target may be a priori vector in ATGP-OSP. But when is unknown, the calculation process is different from the other targets so that when implementing the ATGP algorithm in hardware, an extra and separate module needs to be designed. In this paper, the orthogonal projection operator is initialized to an identity matrix, and the processing module of the first target combined with the others shown in Algorithm 2. The update of can be described as follows:
where the initial matrix is .
3.1.2. Update Operator in One Step
As mentioned above, significant resources and time are consumed in stage 2 of Table 1. To reduce this cost, we propose a projector which can be utilized to project on HSI and it is also orthogonal to all vectors in . It is worth emphasizing that the L components of the orthogonal projector could be initialized to any values since it would not affect its orthogonality. In this paper, the is initialized as , which is suited for hardware and updated by
where is fixed to .
The pseudocode for Fast-ATGP is provided in Algorithm 2. In addition, it is important to emphasize that steps 7 and 9 in Algorithm 2 are unnecessary to be performed when . During the last two iterations, step 8 also can be neglected.
3.2. Parallel Strategy
According to Algorithm 2, the detection process of Fast-ATGP can be summed up in another three new stages: Updating projector, performing orthogonal projection, and finding targets. The number of computations is listed in Table 2 for the ith iteration (). According to stage 1 in Table 1, the number of computations will increase exponentially as i increases, while there exists a strong data dependency problem. In our implementation, Fast-ATGP completes this stage with a fixed L-scale operation through parallel operations. It can also be clearly seen from Table 1 and Table 2, Fast-ATGP saves nearly L times of operations in the latter two stages, which reduce a considerable amount of computation.

Table 2.
Computations for each stage when detecting the i-th target in Fast-ATGP.
In previous work, it has been reported that data-parallel approaches, in which the hyperspectral data is partitioned among different PEs, are particularly effective for parallel processing in the high-performance computing systems like FPGA [40,41]. So, it is crucial to choose a satisfactory strategy for partitioning the HSI data in stage 2. Since the processing between pixels in Fast-ATGP is independent, a spatial-domain decomposition approach can be adopted for data partition, and the neighboring pixels can be processed in parallel. Previous experiments also indicate that spatial-domain partitioning can significantly reduce inter-processor communication, resulting from the fact that a single pixel vector is never partitioned and communications are not needed at the pixel level [42].
The parallel-based version of Fast-ATGP consists of the following steps,
- (1)
- The master divides the HSI data into spatial-domain partitions according to the number of PEs, and sends partitions and operator to all parallel processing units.
- (2)
- Each processing unit finds the pixel vector with maximum length in its local partition. Specifically, performing the dot-product operation in step 4 of Algorithm 2, and completing the comparison and target selection process in step 5 of Algorithm 2. It is worth noting that the above two steps can be implemented using HLS in parallel. In other words, the local brightest pixel vector can be selected while operating dot-product simultaneously. Then, each unit sends the spatial location and maximum length of the pixel to master respectively.
- (3)
- The master finds the global pixel vector () with the maximum length. Then, the pixel vector is serially projected into the orthogonal subspace (step 7 of Algorithm 2). Finally, the master updates the orthogonal projection operators and , and broadcasts to all units.
- (4)
- Repeat from step 2 to step 3 until a set of t target pixels are extracted from the original cube.
4. FPGA Implementation
This section describes the detailed implementation of Fast-ATGP. An overall hardware structure of Fast-ATGP is given in Section 4.1. Section 4.2 describes the microscopic hardware architecture.
4.1. Overall Hardware Architecture of Fast-ATGP
As shown in Figure 1, the hardware architecture of Fast-ATGP has been implemented in OpenCL framework, which mainly consists of two components including an off-chip memory (DDR3 SDRAM) and a processor core. The off-chip memory is utilized to cache the HSI data. And the processor core of Fast-ATGP is mainly responsible for the data processing, which involves three modules. The first module is Target Searcher, dedicated to processing the HSI and finding the locations of the target pixel. The second module is Sub-space Projector, applied to calculate the projection vector of the target . The last module is Updater, utilized to update the orthogonal projection operator and the orthogonal projector .
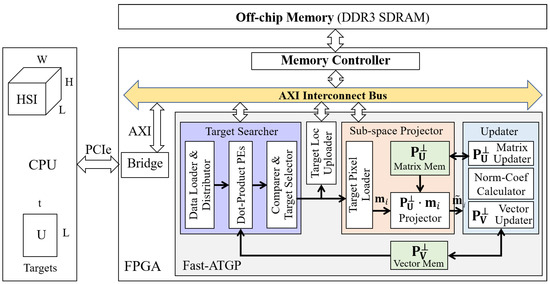
Figure 1.
Overall hardware structure of Fast-automatic target generation process (Fast-ATGP).
4.2. Microscopic Hardware Architecture of Fast-ATGP
4.2.1. Target Searcher
As described in Figure 2, the Target Searcher contains three processing stages for finding the location information of the target. This module is the center of parallel optimization to improve the processing speed.
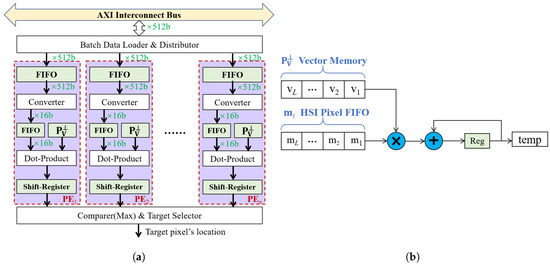
Figure 2.
(a) Hardware structure of Target Searcher; (b) Hardware circuit of Dot-Product ( represents the the result of dot-product).
The batch Data Loader and Distributor reads HSIs from the DDR3 SDRAM through the AXI interconnect bus and loads pixel vectors for Dot-Product PEs in parallel. In order to provide enough data for Dot-Product PEs, the data width of DDR3 SDRAM is set to 512 bits, which is the maximum bit-width of the device available to use. Specifically, given an HSI with a pixel width of 16 bits, 32 successive bands of a pixel vector at each address can be saved. In other words, when the number of PEs is set to 32, the processing unit can make full use of the bandwidth of DDR3 SDRAM.
Multiple PEs work in parallel, which can efficiently accomplish dot-product operations of with each pixel in HSI. Moreover, a task-level pipeline structure is adopted in each PE. As described in Figure 2a, each PE first stores a pixel derived from batch Data Loader and Distributor into FIFO with bit-width of 512. Then, the 512 bits data in FIFO is split into single band pixel data by the converter and stored in FIFO with bit-width of 16. Finally, the inner product of pixel vector and in FIFO is completed by dot-product calculator, and the result is passed to the next stage through shift-register.
Comparer and Target Selector can get the new projection value by comparing 32 results from Multiple PEs. When the new value obtained, comparing if it is greater than the currently stored value. If yes, the position information of a target pixel will be updated and the new value will be stored. In this way, after completing an iteration process, the position information of a new target pixel with maximum length can be obtained, which is transmitted to the off-chip memory through Target Loc Updater and used as input to Sub-space Projector.
Figure 2b shows the specific calculations of dot-product. In order to reduce the consumption of computing resources, we only instantiate a multiply add accumulator and realize the operation in serial.
4.2.2. Sub-Space Projector
Figure 3 shows the specific hardware circuit of Sub-space Projector. This module, which has two inputs including the matrix from the Updater and the vector from the Target Pixel Loader, is used to calculate the product . It is worth noting that should be set to the identity matrix when the system is initialized. In order to improve the capability of parallel computation with fewer logic resources, L multipliers are allocated to realize the parallel matrix calculation.
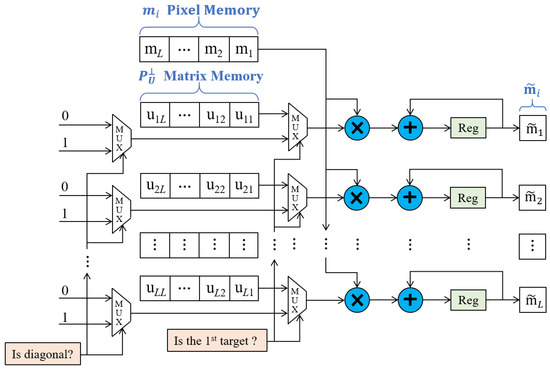
Figure 3.
Hardware circuit of Sub-space Projector.
4.2.3. Updater
The Updater module consists of three sub-modules, including Matrix Updater, Norm-Coefficient Calculator, and Vector Updater. The Updater is mainly optimized for reducing on-chip resources, which is similar to the Sub-space Projector.
Figure 4 describes the Norm-Coefficient Calculator, which is used to calculate and that are respectively applied to update and . To begin with, it can be seen that both and are intermediate variables. is the sum of squared elements of target pixel , which makes it the denominator of the fraction by referring to Equation (4). Therefore, , the negative reciprocal of , is the subtrahend of Equation (4). Then is computed using the product of and , the sum of all the element of . According to Equation (5), the fraction is equal to . Computing occupied only one multiply add accumulator and uses one accumulator.
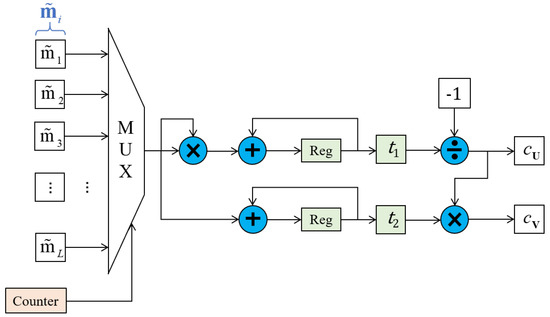
Figure 4.
Hardware circuit of Norm-Coefficient.
Figure 5 shows the architecture of Matrix Updater. Because is the same as the denominator of the fraction Equation (4), Equation (4) can be converted to Equation (6), which is shown by the equation above. So that we can reuse the architecture to finish the complicated calculation in two steps. The first step is to work out one column in outer product of , and store the results in registers. The next step starts with multiplying the first step results with , then it adds these products to the element of in order. When the writing enable signal is valid, the members of will be stored in the given BRAM. The two steps form the pipeline for figuring out matrix every time, thus improving the performance in terms of throughput.
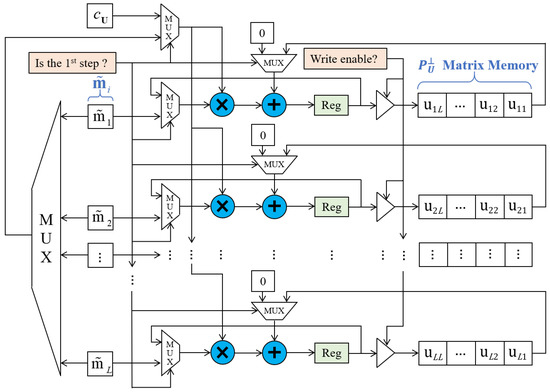
Figure 5.
Hardware circuit of the updater by using and .
In the proposed system, each member of the same column in is processed and updated in parallel. As a result, it can be inferred that the instantiation of L-element multiply accumulates is necessary for Matrix Updater.
Figure 6 shows the architecture of Vector Updater, which implements the updating of . When it comes to , usually initialized as all ones, the new is equal to the old one plus the product of and . There exists only one multiply accumulate for the sake of cutting down resources consumption.
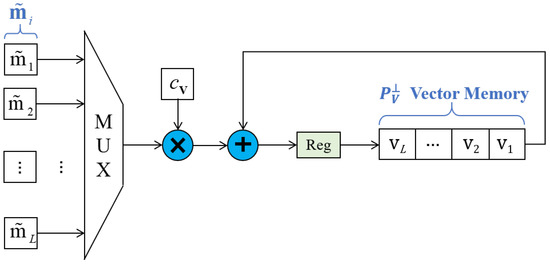
Figure 6.
Hardware circuit of the updater.
Besides, it is worth noting that the following design optimization strategies play an important role in improving the performance of the FPGA implementation.
- (1)
- The data type of input data is 16 bits unsigned fixed-point (15 bits fractional part), while the majority of data types of intermediate data are not easy to assign. To better balance the trade-off between detection accuracy and resource consumption, different data types are used in different intermediate data. For example, as shown in Figure 2, the variable and are respectively set to 38 bits signed fixed-point type (10 bits integer part, 18 bits fractional part) and 36 bits signed fixed-point type (5 bits integer part, 31 bits fractional part). The elements of are 36 bits signed fixed-point type (10 bits integer part, 26 bits fractional part). All the other intermediate data are also assigned to the appropriate data type.
- (2)
- The elements of and are continuously updated and become smaller, so more bits should be assigned to the fractional part for avoiding data overflow. However, the fixed bit-width of and are recommended to be applied in order to reduce the resource consumption as much as possible. Considering the circumstances, we have done a lot of tests in HSIs and found that the variation trend of elements in was approximate to the inverse proportion function, so the values of elements were enlarged in a certain proportion in our implementation to ensure the variation trend constrained to a fixed interval. In this way, the risk of data overflow could be effectively avoided.
5. Experimental Results and Discussion
5.1. Experimental Environment
The hardware architecture described in Section 4 has been implemented in OpenCL framework for the specification of Fast-ATGP [43]. The communication between CPUs and FPGAs in the full framework is completed using SDAccel, which can support standard OpenCL APIs. Moreover, HLS tool is used to achieve the kernel of Fast-ATGP in Vivado HLS 2017.3. In our implementation, an Alpha-Data ADM-PCIE-7V3 board (configured with Virtex-7 XC7VX690T FPGA) is chosen as our development platform, which features two independent channels of DDR3 memory capable of 1333 MT/s (fitted with two 8 GB SODIMMs). To better compare the performance of our proposed algorithm on FPGA with software implementation on a computer, the computer simulation is performed by MATLAB in Windows 7 operating system where the computer hardware specification is specified by Intel Core™ quad CPU@3.2 GHz and 4 GB main memory.
5.2. Hyperspectral Image Data Set
5.2.1. Cuprite Data
Cuprite, as shown in Figure 7a, is the most benchmarked dataset for the hyperspectral detection research that covers the Cuprite in Las Vegas, NV, USA. The well-known AVIRIS Cuprite dataset is considered as a reference within the hyperspectral remote sensing research field, which is available on the website http://aviris.jpl.nasa.gov/. This scene is composed by 250 × 191 pixels and 224 spectral bands distributed between 0.4 and 2.5 m, with a spectral resolution of 10 nm. As a result, a total of 188 bands were used for experiments after removing the noisy channels (1–2 and 221–224) and water absorption channels (104–113 and 148–167) [44]. Reference ground-signatures of the above minerals (see Figure 7b), available in the form of a U.S. Geological Survey library (USGS), will be used to assess Fast-ATGP algorithm in this paper.
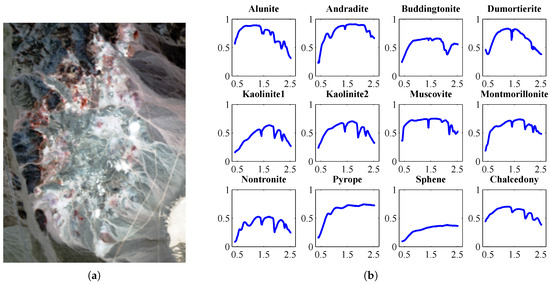
Figure 7.
(a) False color composition of the AVIRIS hyperspectral over the Cuprite mining district in Nevada; (b) U.S. Geological Survey mineral spectral signatures used for validation purposes.
5.2.2. Urban Data
Urban Data, available at http://www.tec.army.mil/Hypercube, is one of the most widely used hyperspectral data set for target detection [45,46]. It was recorded by the Hyperspectral Digital Imagery Collection Experiment (HYDICE) in October 1995, whose location is an urban area at CA, USA. As shown in Figure 8a, there are 307 × 307 pixels with 210 bands in this image, ranging from 400 nm to 2500 nm. After the bands 1–4, 76, 87, 101–111, 136–153, and 198–210 are removed (due to dense water vapor and atmospheric effects), 162 bands remained in this data.
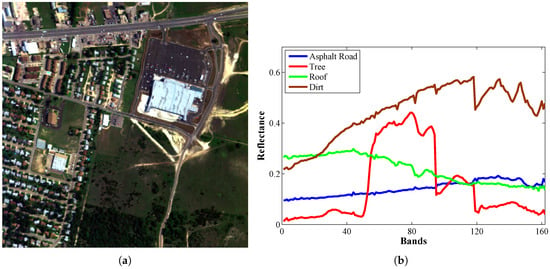
Figure 8.
(a) False color composition of an HYDICE hyperspectral image collected on October 1995 over an urban area at CA, USA; (b) Four signatures: Asphalt Road, Tree, Roof, and Dirt.
5.3. Analysis of Target Detection Accuracy
In this section, we evaluate the detection accuracy of the proposed implementation of Fast-ATGP by using the real hyperspectral data sets which ground-truth information is available. ATGP-OSP is evaluated together with our approach. It is worthwhile to emphasize that our hardware version of Fast-ATGP provides exactly the same results as a software version of the same algorithm, implemented using the Intel C/C++ compilers.
Figure 9 shows the location and sequence information of the detected targets in two datasets, where the number of targets is calculated by the VD algorithm. Specifically, the red circles indicate the targets detected in HSI, with the numbers next to the circles indicating the order of the targets being detected. Figure 9a displays the detection result of AVIRIS Cuprite Data and Figure 9b is the detection result of HYDICE Urban Data.

Figure 9.
Detection results on two different images, where the red circles indicate the targets detected in hyperspectral imagery (HSI), with the numbers next to the circles indicating the order of the targets being detected. (a) AVIRIS Cuprite scene; (b) HYDICE Urban scene.
The detection accuracy can be evaluated via spectral angle mapper (SAM) [47] values (in degrees) between the detected target and the reference spectral signature, which reflects the similarity of pixels in an HSI. The SAM between two pixel vectors and is defined by the following expressions,
It should be noted that SAM is invariant in the presence of illumination interferes, which can provide advantages in terms of target detection in complex backgrounds.
5.3.1. Results for the AVIRIS Cuprite Scene
Table 3 shows the SAM values (in degrees) between the most similar target pixels detected by two different versions of ATGP (ATGP-OSP and Fast-ATGP) at the known target positions in the AVIRIS Cuprite image. In addition, the number of target pixels to be detected was set to t = 19 after calculating the VD. As shown by Table 3, again ATGP-OSP and Fast-ATGP extracted targets were similar, spectrally, to the known ground-truth targets.

Table 3.
Spectral angle mapper values (in degrees) between the target pixels extracted by ATGP-OSP and Fast-ATGP and the known ground targets in the AVIRIS Cuprite scene.
5.3.2. Results with the HYDICE Urban Scene
Table 4 tabulates the SAM values (in degrees) between the most similar target pixels detected by the two considered versions: ATGP-OSP and Fast-ATGP in the HYDICE Urban image. In addition, the number of target pixels to be detected was set to t = 15 after calculating the VD. As shown by Table 4, Fast-ATGP extracted targets which were slightly similar (on average) to the ground references than those provided by ATGP-OSP for 4 targets in HYDICE Urban image [48]. This indicates that the proposed Fast-ATGP optimization does not penalize ATGP-OSP in terms of target detection accuracy.

Table 4.
Spectral angle mapper values (in degrees) between the target pixels extracted by ATGP-OSP and Fast-ATGP and the known ground targets in the HYDICE Urban scene.
5.4. Performance Evaluation
Two different platforms have been used in our experiments. The first one is the C++ environment on CPU, and the second one is the Virtex7 FPGA. As shown in Table 5, the processing time of Fast-ATGP implemented on FPGA has achieved a speedup of 5282.5× on average faster than our software version, where it detects 19 targets in Cuprite data and 15 targets in Urban data.

Table 5.
Processing time measured for Fast-ATGP methods in C++ and field programmable gate array (FPGA) implementations.
Table 6 tabulates the processing time obtained for the FPGA implementation of ATGP-OSP and Fast-ATGP for the AVIRIS Cuprite scene. It should be noted that the FPGA implementation of ATGP-OSP corresponds to an architecture described in [17], while Fast-ATGP is described in this paper. As shown by Table 6, not only the maximum frequency of Fast-ATGP with 32 PEs are higher than that of ATGP-OSP, but also the clock periods occupied by Fast-ATGP are fewer than ATGP-OSP. Overall, the processing time consumed by ATGP-OSP is about 34.3 times that required by Fast-ATGP.

Table 6.
Processing time of the AVIRIS Cuprite scene measured for ATGP-OSP and Fast-ATGP on FPGAs.
It is also remarkable that the processing time achieved by the FPGA implementation of Fast-ATGP is strictly in real-time for the Cuprite data. This is because the data acquisition ratio by the AVIRIS sensor is known and we have used this information to determine if the proposed hardware implementation could be applied at the same time as the data are collected without delaying the collection procedure at the sensor. Specifically, the cross-track line scan time in AVIRIS, a push-broom instrument, is quite fast (8.3 to collect 512 full-pixel vectors). This introduces the need to process the Cuprite scene in 0.77 s to fully achieve real-time performance. As noted in Table 5, all out implementation of Fast-ATGP are well below 0.05 s in processing times, including loading times and the data transfer times from CPU to FPGA device. This represents a significant improvement with regard to previous FPGA implementations of ATGP-OSP.
Table 7 shows the hardware resource utilization corresponding to ATGP-OSP and Fast-ATGP algorithm with 32 PEs. Our hardware design is implemented on an FPGA, which has a total of 1470 block RAMs, 3600 DSP48E1s, 433,200 slice look-up tables (LUTs), and 866,400 slice registers. As Table 7 illustrates, because of the optimal architecture we have adopted, the resources such as block RAMs, DSP48E1s and slice LUTs are obviously reduced compared to the ATGP-OSP. Although the usage of slice registers is increased, the proposed hardware structure occupies fewer resources than ATGP-OSP in general.

Table 7.
Resource utilization measured for ATGP-OSP and Fast-ATGP on FPGAs after processing the AVIRIS Cuprite scene.
5.5. Design Space Exploration and Potential Analysis
Computation and communication are two principal constraints in system throughput optimization. An implementation can be either computation-bounded or memory-bounded. To find the optimal architecture configuration for a specific FPGA device, a design space exploration methodology [49] is introduced to relate system performance to off-chip memory traffic and the peak performance provided by the hardware platform.
For Fast-ATGP, a straightforward way to improve the system performance is to increase the number of PEs. However, increasing the number of PEs indicates that the consumption of memory bandwidth and resources are also increased. Figure 10 shows the change trends of speedup and resource consumption at different number of PEs. It is worth mentioning that the trends remain the same for any other datasets regardless of their spatial and spectral resolutions. This is because the speedup linearly goes up with the increase of the number of PEs as shown in Figure 10a, as long as the maximum memory bandwidth provided by the FPGA device is not consumed out. In this paper, the memory bandwidth is limited to 512 bits per clock cycle by the FPGA platform we selected. It means that a maximum of 32 spectral pixels can be processed simultaneously per clock cycle if the data type of the pixel is set to 16 bits unsigned fixed-point. As a result, the maximum number of PEs required to accelerate is 32 since each PE is dedicated to handling one of the spectral pixels respectively. Figure 10b illustrates that the main computing resource consumption is not obviously raised as the increase of PEs. Even when the number of PEs is 32, the computing resource utilization rate has not reached half of the resource capacity. However, further increasing parallelism will not improve the performance of the system because of the memory bandwidth limitation.
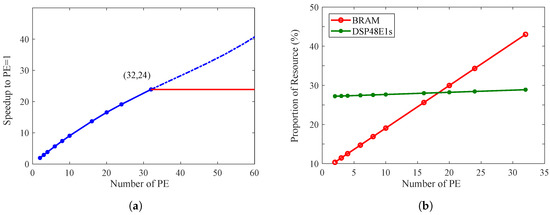
Figure 10.
(a) The changing trend of the processing time speedup as the number of processing elements (PEs) increases; (b) The variation trend of resource utilization relative to the number of PEs.
Predictably, when the hardware platform is replaced with larger memory bandwidth, the speedup of the proposed implementation will continue to increase. Fast-ATGP can choose the appropriate number of PEs according to computational roof and I/O bandwidth roof for different platforms, which fully reflects its flexibility and adaptability.
6. Conclusions
In this paper, a novel approach to HSI target detection, referred to as Fast-ATGP, is implemented on FPGA using HLS, which has never been explored in the past. Through analyzing calculations of ATGP-OSP, an increasing operation problem occurs during growing matrix inversion process and a huge matrix multiplication problem also arises in the OSP process. For the first problem, a fixed operation scale is introduced to replace the continuously increasing computations when updating the OSP operator matrix, which ensures that the consumption of hardware resources does not change as the number of detected targets increases. Moreover, a vectorization approach is also developed for the operator matrix to avoid the latter problem, which updates the operator in a vector form only by one step and decreases computation to a great extent. The experimental results, conducted on a Virtex-7 XC7VX690T FPGA, demonstrate that our implementation makes advanced use of FPGA architecture including balancing the serial-parallel structure and multiplex technique, detection accuracy, and computation performance. Under the same conditions, the detection speed of our proposed Fast-ATGP is about 34.3 times faster than that of ATGP-OSP on AVIRIS Cuprite data when detecting multiple targets. Finally, a design space exploration method based on our architecture is leveraged for the optimal configuration in arbitrary FPGA device. In the future, we will exploit unsupervised deep learning method like deep belief network (DBN) and autoencoder (AE) for feature extraction and dimension reduction, and combine them with Fast-ATGP to gain performance improvement in detection accuracy and speed.
Author Contributions
J.L. provided conceptualization; L.W. performed the experiments and analyzed the result data; Y.L. designed the methodology; W.X. investigated related work; C.-I.C. provided suggestions on algorithm optimization and paper revision; J.Z. and B.H. contributed software and resources; J.L. wrote the paper.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China (Nos. 61801359, 61571345, 91538101, 61501346, 61502367 and 61701360) and the 111 project (B08038)). It was also partially supported by Yangtse Rive Scholar Bonus Schemes, Ten Thousand Talent Program, the Fundamental Research Funds for the Central Universities JB180104, the Natural Science Basic Research Plan in Shaanxi Province of China (Nos. 2016JQ6023, 2016JQ6018) and General Financial Grant from the China Postdoctoral Science Foundation (No. 2017M620440).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HSI | Hyperspectral imagery |
| FPGA | Field programmable gate array |
| ATGP | Automatic target generation process |
| HLS | High-level synthesis |
| PE | Processing element |
References
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection algorithms in hyperspectral imaging systems: An overview of practical algorithms. IEEE Signal Process. Mag. 2014, 31, 24–33. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J. Advances in hyperspectral image and signal processing: A comprehensive overview of the state of the art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Xie, W.; Shi, Y.; Li, Y.; Jia, X.; Lei, J. High-quality spectral-spatial reconstruction using saliency detection and deep feature enhancement. Pattern Recognit. 2019, 88, 139–152. [Google Scholar] [CrossRef]
- Sun, W.; Yang, G.; Du, B.; Zhang, L.; Zhang, L. A sparse and low-rank near-isometric linear embedding method for feature extraction in hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4032–4046. [Google Scholar] [CrossRef]
- Li, Y.; Xie, W.; Li, H. Hyperspectral image reconstruction by deep convolutional neural network for classification. Pattern Recognit. 2017, 63, 371–383. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Sun, W.; Tian, L.; Xu, Y.; Du, B.; Du, Q. A randomized subspace learning based anomaly detector for hyperspectral imagery. Remote Sens. 2018, 10, 417. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Sun, W.; Ma, J.; Yang, G.; Du, B.; Zhang, L. A Poisson nonnegative matrix factorization method with parameter subspace clustering constraint for endmember extraction in hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2017, 128, 27–39. [Google Scholar] [CrossRef]
- Chen, S.Y.; Ouyang, Y.C.; Lin, C.; Chen, H.M.; Gao, C.; Chang, C.-I. Progressive endmember finding by fully constrained least squares method. In Proceedings of the Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Tokyo, Japan, 2–5 June 2015; pp. 1–4. [Google Scholar]
- Ren, H.; Chang, C.-I. Automatic spectral target recognition in hyperspectral imagery. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1232–1249. [Google Scholar]
- Zhao, L.; Lin, W.; Wang, Y.; Li, X. Recursive local summation of rx detection for hyperspectral image using sliding windows. Remote Sens. 2018, 10, 103. [Google Scholar] [CrossRef]
- Yu, C.; Lee, L.C.; Chang, C.-I.; Xue, B.; Song, M.; Chen, J. Band-Specified Virtual Dimensionality for Band Selection: An Orthogonal Subspace Projection Approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2822–2832. [Google Scholar] [CrossRef]
- Chang, C.-I.; Chen, S.Y.; Li, H.C.; Chen, H.M.; Wen, C.H. Comparative study and analysis among ATGP, VCA, and SGA for finding endmembers in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4280–4306. [Google Scholar] [CrossRef]
- Chang, C.-I.; Li, Y. Recursive band processing of automatic target generation process for finding unsupervised targets in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5081–5094. [Google Scholar] [CrossRef]
- Gonzalez, C.; Bernabe, S.; Mozos, D.; Plaza, A. FPGA implementation of an algorithm for automatically detecting targets in remotely sensed hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4334–4343. [Google Scholar] [CrossRef]
- Bernabe, S.; Lopez, S.; Plaza, A.; Sarmiento, R. GPU implementation of an automatic target detection and classification algorithm for hyperspectral image analysis. IEEE Geosci. Remote Sens. Lett. 2013, 10, 221–225. [Google Scholar] [CrossRef]
- Chang, C.-I.; Gao, C.; Chen, S.Y. Recursive Automatic Target Generation Process in Subpixel Detection. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1848–1852. [Google Scholar] [CrossRef]
- Plaza, A.J. Special issue on architectures and techniques for real-time processing of remotely sensed images. J. Real Time Image Process. 2009, 4, 191–193. [Google Scholar] [CrossRef]
- Li, X.; Huang, B.; Zhao, K. Massively parallel GPU design of automatic target generation process in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2862–2869. [Google Scholar] [CrossRef]
- Gonzalez, C.; Lopez, S.; Mozos, D.; Sarmiento, R. A novel FPGA-based architecture for the estimation of the virtual dimensionality in remotely sensed hyperspectral images. J. Real Time Image Process. 2018, 15, 297–308. [Google Scholar] [CrossRef]
- Chang, C.-I.; Li, Y.; Wang, Y. Progressive Band Processing of Fast Iterative Pixel Purity Index for Finding Endmembers. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1464–1468. [Google Scholar] [CrossRef]
- Yang, B.; Yang, M.; Plaza, A.; Gao, L.; Zhang, B. Dual-mode FPGA implementation of target and anomaly detection algorithms for real-time hyperspectral imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2950–2961. [Google Scholar] [CrossRef]
- Vellas, S.; Lentaris, G.; Maragos, K.; Soudris, D.; Kandylakis, Z.; Karantzalos, K. FPGA acceleration of hyperspectral image processing for high-speed detection applications. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Pei, S.; Wang, R.; Zhang, J.; Jin, Y. FPGA-based Acceleration for Hyperspectral Image Analysis. In Proceedings of the IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 24–26 March 2017; pp. 324–327. [Google Scholar]
- Nane, R.; Sima, V.M.; Pilato, C.; Choi, J.; Fort, B.; Canis, A.; Anderson, J. A survey and evaluation of FPGA high-level synthesis tools. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2016, 35, 1591–1604. [Google Scholar] [CrossRef]
- Cong, J.; Liu, B.; Neuendorffer, S.; Noguera, J.; Vissers, K.; Zhang, Z. High-level synthesis for FPGAs: From prototyping to deployment. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2011, 30, 473–491. [Google Scholar] [CrossRef]
- Domingo, R.; Salvador, R.; Fabelo, H.; Madronal, D.; Ortega, S.; Lazcano, R. High-level design using Intel FPGA OpenCL: A hyperspectral imaging spatial-spectral classifier. In Proceedings of the International Symposium on Reconfigurable Communication-centric Systems-on-Chip (ReCoSoC), Madrid, Spain, 12–14 July 2017; pp. 1–8. [Google Scholar]
- Desai, P.; Aslan, S.; Saniie, J. FPGA Implementation of Gram-Schmidt QR Decomposition Using High Level Synthesis. In Proceedings of the IEEE International Conference on Electro Information Technology (EIT), Lincoln, NE, USA, 14–17 May 2017; pp. 482–487. [Google Scholar]
- Ma, S.; Shi, X.; Andrews, D. Parallelizing maximum likelihood classification (MLC) for supervised image classification by pipelined thread approach through high-level synthesis (HLS) on FPGA cluster. Big Earth Data 2018, 1–15. [Google Scholar] [CrossRef]
- Guerra, R.; López, S.; Sarmiento, R. A FPGA implementation for linearly unmixing a hyperspectral image using OpenCL. In High-Performance Computing in Geoscience and Remote Sensing VII; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; p. 104300D. [Google Scholar]
- Santos, L.; Berrojo, L.; Moreno, J.; Lopez, J.F.; Sarmiento, R. Multispectral and hyperspectral lossless compressor for space applications (HyLoC): A low-complexity FPGA implementation of the CCSDS 123 standard. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 757–770. [Google Scholar] [CrossRef]
- Lei, J.; Li, Y.; Zhao, D.; Xie, J.; Chang, C.I.; Wu, L. A Deep Pipelined Implementation of Hyperspectral Target Detection Algorithm on FPGA Using HLS. Remote Sens. 2018, 10, 516. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Liu, K.; Lei, J.; Wang, K. Fast FPGA Implementation for Computing the Pixel Purity Index of Hyperspectral Images. J. Circuits Syst. Comput. 2018, 27, 1850045. [Google Scholar] [CrossRef]
- Chang, C.-I.; Wu, C.C.; Tsai, C.T. Random N-finder (N-FINDR) endmember extraction algorithms for hyperspectral imagery. IEEE Trans. Image Process. 2011, 2011, 641–656. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Chang, C.-I. Recursive automatic target generation process for unsupervised hyperspectral target detection. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, QC, Canada, 13–18 July 2014; pp. 3598–3601. [Google Scholar]
- Song, M.; Li, H.C.; Chang, C.-I.; Li, Y. Gram-Schmidt orthogonal vector projection for hyperspectral unmixing. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, QC, Canada, 13–18 July 2014; pp. 2934–2937. [Google Scholar]
- Geng, X.; Yang, W.; Ji, L.; Ling, C.; Yang, S. A Piecewise Linear Strategy of Target Detection for Multispectral/Hyperspectral Image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 951–961. [Google Scholar] [CrossRef]
- Xu, F.; Lv, Y.; Xu, X.; Dinavahi, V. FPGA-Based real-time wrench model of direct current driven magnetic levitation actuator. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Hahne, C.; Lumsdaine, A.; Aggoun, A.; Velisavljevic, V. Real-time refocusing using an FPGA-based standard plenoptic camera. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Guerra, R.; Martel, E.; Khan, J.; Lopez, S.; Athanas, P.; Sarmiento, R. On the Evaluation of Different High-Performance Computing Platforms for Hyperspectral Imaging: An OpenCL-Based Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4879–4897. [Google Scholar] [CrossRef]
- Zhu, F.; Wang, Y.; Xiang, S.; Fan, B.; Pan, C. Structured sparse method for hyperspectral unmixing. ISPRS J. Photogramm. Remote Sens. 2014, 88, 101–118. [Google Scholar] [CrossRef]
- Guo, Q.; Pu, R.; Gao, L.; Zhang, B. A novel anomaly detection method incorporating target information derived from hyperspectral imagery. Remote Sens. Lett. 2016, 7, 11–20. [Google Scholar] [CrossRef]
- Roussel, G.; Weber, C.; Briottet, X.; Ceamanos, X. Comparison of two atmospheric correction methods for the classification of spaceborne urban hyperspectral data depending on the spatial resolution. Int. J. Remote Sens. 2018, 39, 1593–1614. [Google Scholar] [CrossRef]
- Panda, A.; Pradhan, D. Hyperspectral image processing for target detection using Spectral Angle Mapping. In Proceedings of the IEEE International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 1098–1103. [Google Scholar]
- Dumke, I.; Nornes, S.M.; Purser, A.; Marcon, Y.; Ludvigsen, M.; Ellefmo, S.L. First hyperspectral imaging survey of the deep seafloor: High-resolution mapping of manganese nodules. Remote Sens. Environ. 2018, 209, 19–30. [Google Scholar] [CrossRef]
- Chang, C.-I. A review of virtual dimensionality for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).