Abstract
Arctic sea ice concentration (SIC) has been studied extensively using passive microwave (PM) remote sensing. This technology could be used to improve navigation along vessel cruise paths; however, investigations on this topic have been limited. In this study, shipborne photographic observation (P-OBS) of sea ice was conducted using oblique-oriented cameras during the Chinese National Arctic Research Expedition in the summer of 2016. SIC and the areal fractions of open water, melt ponds, and sea ice (Aw, Ap, and Ai, respectively) were determined along the cruise path. The distribution of SIC along the cruise path was U-shaped, and open water accounted for a large proportion of the path. The SIC derived from the commonly used PM algorithms was compared with the moving average (MA) P-OBS SIC, including Bootstrap and NASA Team (NT) algorithms based on Special Sensor Microwave Imager/Sounder (SSMIS) data; and ARTIST sea ice, Bootstrap, Sea Ice Climate Change Initiative, and NASA Team 2 (NT2) algorithms based on Advanced Microwave Scanning Radiometer 2 (AMSR2) data. P-OBS performed better than PM remote sensing at detecting low SIC (< 10%). Our results indicate that PM SIC overestimates MA P-OBS SIC at low SIC, but underestimates it when SIC exceeds a turnover point (TP). The presence of melt ponds affected the accuracy of the PM SIC; the PM SIC shifted from an overestimate to an underestimate with increasing Ap, compared with MA P-OBS SIC below the TP, while the underestimation increased above the TP. The PM algorithms were then ranked; SSMIS-NT and AMSR2-NT2 are the best and worst choices for Arctic navigation, respectively.
1. Introduction
Arctic sea ice cover has undergone substantial changes in recent decades, such as reductions in sea ice thickness [1,2] and extent [3,4], loss of sea ice volume [5] and multiyear ice coverage [6,7], and a rapid decline in sea ice concentration (SIC) in summer and early autumn [8,9]. These changes have made the Arctic more accessible, which has led to numerous studies of sea ice along the Arctic Passage in the fields of remote sensing, engineering, and geoscience. SIC is one of the main parameters, not only for Arctic sea surface albedo [10] and climate change [11], but also for ice resistance and the safety of ships during Arctic navigation [12].
Passive microwave (PM) remote sensing is a powerful approach to detect SIC at a pan-Arctic scale. This method is widely used because of its relatively low sensitivity to atmospheric conditions, such as clouds and humidity, and because it is independent of daylight hours. In addition, PM has also been adopted to investigate the snow properties such as snow water equivalent [13,14]. PM Arctic sea ice information has been available since the launch of the Scanning Multichannel Microwave Radiometer (SMMR) in 1978, followed by the Special Sensor Microwave/Imager (SSM/I) and the Special Sensor Microwave Imager/Sounder (SSMIS) in 1987. Later, more useful PM information on Arctic sea ice has been provided by the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and its successor, the Advanced Microwave Scanning Radiometer 2 (AMSR2), launched in 2002 and 2012, respectively. Several algorithms have been developed to estimate Arctic SIC based on PM data, such as NASA Team (NT) and its enhanced version (NASA Team 2, NT2), Bootstrap, Arctic radiation and turbulence interaction study (ARTIST) sea ice (ASI), and the European Space Agency (ESA) Sea Ice Climate Change Initiative (SICCI) algorithms. Based on these algorithms, more variability and unknown aspects of the SIC in the Northern Polar Region have been revealed [15,16,17].
However, the accuracy of the SIC derived from PM algorithms is limited. Each algorithm uses a set of brightness temperatures for ice-free ocean (SIC = 0) and closed ice cover (SIC = 100%) to retrieve SIC [18], which represents the radiometric characteristics of different polar sea surface types [19]. The brightness temperature of sea ice depends on the real temperature and emissivity, which in turn depends on the phase (ice/water) and salinity [20]. In summer, the real temperature is at the melting point, but the phase and salinity experience high variability. Therefore, the brightness temperature of summer sea ice varies considerably in time and space, and the PM algorithms have large uncertainties [21]. Inter-comparison of SIC algorithms has shown that there are differences between the SIC retrieved from different PM algorithms [21,22,23,24]. Ivanova et al. [25] also showed that the differences between the PM SIC algorithms are greater in summer than in winter.
Due to the potential errors in the PM SIC, field measurements are essential to obtain SIC at higher resolution and to validate PM SIC measurements. Several methods are available for shipborne observations. The visual observation (V-OBS) aboard a vessel is a direct way to record SIC along the cruise transect, according to the protocol of the Antarctic Sea Ice Processes and Climate program (ASPeCt) or the Arctic Shipborne Sea Ice Standardization Tool (ASSIST) standard, and V-OBS has been carried out extensively on expeditions in the Polar Regions [26,27,28,29,30]. Ozsoy-Cicek et al. [31] compared NT2 and Bootstrap SIC based on AMSR-E data with V-OBS SIC in Antarctica, and found that in general the NT2 algorithm produces slightly higher SIC measurements than the Bootstrap algorithm. Beitsch et al. [19] found that Bootstrap and ASI SIC based on AMSR-E data were in better agreement with V-OBS SIC than the SIC based on SSM/I data using the same algorithms. Pang et al. [32] found that AMSR2-ASI SIC matched better with V-OBS SIC at the Arctic ice edge than AMSR2-Bootstrap SIC.
However, because human subjectivity during V-OBS cannot be avoided [33], instruments, such as digital cameras, have been applied. Hall et al. [34] used an oblique-oriented camera to capture the ice conditions on a scientific cruise to the Greenland Sea. When retrieving SIC, they only used a sub-scene close to the ship without a geometric correction of the images. To promote the use of photographs and retrieval accuracy, algorithms have been developed to retrieve SIC from oblique-captured photographs that have been processed with image partitioning and geometric orthorectification. Band thresholding, the simplest classification method for pixel extraction, has been used extensively for image partitioning [27,35,36,37]. Other methods, such as the K-means technique, has also been employed [38,39]. For geometric orthorectification, Weissling et al. [38] used a Delauney Triangulation method, which needs a considerable number of ground control points, stating that this method was just an ad hoc solution. A more general method of geometric correction for oblique-view photographs was developed by Lu and Li [40] based on photogrammetric theory, in which the actual image pixel size can be calculated using the camera system parameters. Using the shipborne photographic observation (P-OBS) method enables the recording of small-scale ice features that cannot be detected by PM.
With the development of commercial activities in the Arctic, ice management requires more small-scale SIC information along the ship routes to guide navigation. In fact, vessels are always directed to the areas with wide leads [41]. However, as the most widely used method to detect sea ice condition, PM observations are deficient in detecting SIC at small scales due to its coarse grid. Therefore, the performances of PM SIC algorithms need to be evaluated to validate their agreements with the SIC along the vessel routes from the perspective of navigation. Furthermore, ranking of the PM SIC algorithms is necessary for choosing an optimal option to guide ice navigation. Although a few studies have reported the differences between PM and shipborne SIC along a cruise path in the Arctic [28,29,30,42], very few ones have adopted an objective method, such as P-OBS.
In order to achieve the present objective, a shipborne sea ice P-OBS program was carried out on the icebreaker R/V Xuelong as it sailed in the sea ice zone within the Pacific Arctic sector during the Chinese National Arctic Research Expedition (CHINARE) in the summer of 2016. Based on the P-OBS SIC, the performances of several most commonly used PM SIC algorithms (including Bootstrap and NT SIC based on SSMIS data and ASI, Bootstrap, SICCI, and NT2 SIC based on AMSR2 data) were evaluated. The text is divided as follows: Section 2 provides details of the P-OBS method and image processing. Section 3 presents the distribution of SIC along the cruise path by P-OBS and the comparisons between PM SIC and P-OBS SIC. In Section 4, we discuss the potential factors influencing the differences in the SIC derived from the two sources, the effects of melt ponds, and an inter-comparison of SIC from 2010 to 2016. Finally, these PM algorithms are ranked in Section 5.
2. Data and Methods
2.1. Overview of Ice Navigation
The cruise path of R/V Xuelong in the Pacific sector of the Arctic Ocean in summer 2016 is shown by the black line in Figure 1. The cruise was restricted by the ice-breaking ability of the vessel, local ice conditions, and the locations of ice and oceanographic stations. Furthermore, the vessel’s captain tended to navigate to regions with wide leads. Sea ice was first encountered at around 71.7°N on 25 July. After entering into the sea ice zone, the vessel sailed northward to 82.7°N on 7 August for a long-term ice camp (nine days), and then drifted back to 82.2°N. The southward navigation began on 15 August and lasted until 23 August, when the vessel sailed out of the sea ice zone at around 74.7°N. The cruise passed through Chukchi Sea, Beaufort Sea, and the Central Arctic, all of which are important seas along the Arctic Passage. Shipborne P-OBS was initiated once sea ice was first encountered and suspended temporarily during the long-term ice camp. When the southward navigation began, P-OBS was resumed and finally terminated as the vessel sailed out of the sea ice zone. A threshold of 60% SIC was used to define the boundary between the marginal ice zone (MIZ) and the pack ice zone (PIZ) [43]. The region north of 82°N on the northward leg was taken as the PIZ (see Section 3.1). In the PIZ, surface wave actions were weak because they were largely constrained by sea ice. In the MIZ, waves were enhanced with large open water areas present. While it was found that the wavelengths were less than the size of most floes, so that sea ice seldom fluctuated with waves [44]. The weather conditions were recorded every minute by the shipborne weather instruments. During ice navigation, air temperature varied between −5.2 °C and 7.3 °C, 82% of the time in the range of from −3 to 0 °C. Wind velocity was normally distributed approximately with the average and standard deviation of 8.0 m/s and 4.0 m/s, respectively. Relative humidity ranged between 77% and 100%, and exceeded 98% in half of the sailing duration.
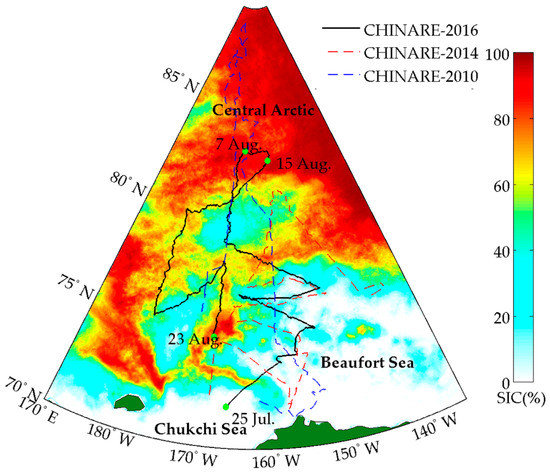
Figure 1.
The cruise path of R/V Xuelong (black solid line) during Chinese National Arctic Research Expedition (CHINARE)-2016 with mean sea ice concentration (SIC) derived using the AMSR2-ASI (Advanced Microwave Scanning Radiometer 2-Arctic radiation and turbulence interaction study sea ice) algorithm between 25 July 2016 and 23 August 2016 shown in the background. Also included are the dates of the main turning points (green dots), and the cruise tracks of CHINARE-2014 (red dashed line) [43] and CHINARE-2010 (blue dashed line) [30] with ice observations in the same sector.
2.2. Shipborne Photographic Observations
The shipborne P-OBS was carried out using oblique-oriented cameras to automatically capture the sea surface. Two digital cameras were mounted on the port and starboard sides of the R/V Xuelong to observe the surface morphology during the cruise. Each camera was installed in a plastic box inlaid with a glass window at the front to protect it from snow and wind (the portside example is shown in Figure 2). The boxes were attached to the ship’s hull firmly, so that cameras could only shake with the vessel motion. To gain a wide view, the cameras were placed on the bridge deck (27.3 m above the sea surface) and oriented obliquely at an angle of 25° to the horizon to ensure that the view encompassed the range from shipside to the skyline. The focal length of the cameras was fixed throughout the cruise. The cameras worked automatically with a time interval of 1 min and their time format was set to the Coordinated Universal Time, which was adopted in the shipborne Global Position System, so that the locations of the photographs could be determined from the moment of capture.

Figure 2.
The camera used to observe the sea surface (a) on the portside of the R/V Xuelong (b).
The first step to derive P-OBS SIC from oblique-oriented pictures is image partitioning. We used the band-thresholding method, which has been adopted in several investigations in Arctic [27,35,36,45,46]. The accuracy of this method has been assessed by Li et al. [46] using the confusion matrix, and the results showed that the overall accuracy and kappa coefficient were 87%–91% and 0.80–0.86, respectively. We used the same assessment method as Li et al. [45] in this study and the overall accuracy and kappa coefficient turned out to be 94% and 0.91, respectively, which indicates high reliability. As shown in Figure 3a, melt ponds can be distinguished from the surrounding ice because they look bluish, and because of its lower reflectance, open water can be identified by its darker appearance [47]. According to these criteria, sea surface morphology can be partitioned into three categories: sea ice, melt ponds, and open water, by selecting red, green, and blue thresholds based on the color distribution histograms within each picture, as shown in Figure 3b. Because the color of these sea surface categories varies depending on the weather conditions (sunlight or cloud cover) and viewing angle, it was impossible to select common thresholds for the whole image set. Therefore, the threshold level for each surface category in each image was independently determined by hand. Especially, melt ponds were usually misidentified during image partitioning. Manual intervention was a necessary procedure to check the boundary of melt ponds based on the threshold calculated by computer and justified by naked eyes. Then the targets mistaken as melt ponds could be excluded and corrected.

Figure 3.
An original oblique-oriented picture (a) and its corresponding image after partitioning (b) in which the white, red, and blue parts are sea ice, open water, and melt ponds, respectively.
In oblique-oriented cameras, unless the image is rectified, geometric distortion can cause errors in the areal fractions of the sea surface categories. Therefore, the second step in deriving P-OBS SIC is geometric orthorectification. The simplified method proposed by Lu and Li [40] was adopted in this study. In this method, the actual image pixel size is calculated using camera height H, camera tilt α, and focal length f. H and α were obtained during camera installation, and f could be obtained from image information. The ship motion, especially the roll of vessel, influences the geometric distortion. While the error can be effectively controlled by setting an upper limit of the viewing angle. To maintain the balance between the avoidance of large errors and the full utilization of the image, the upper limit of the viewing angle was set to 85°. The relative error induced per degree of the ship’s roll was, therefore, less than 30%, and approximately 78% of the image could be used.
After the above two steps, the areal fractions of open water, melt ponds, and sea ice were determined by dividing the area of the pixels of each sea surface category by the total area of the pixels. The results are denoted as Aw, Ap, and Ai, respectively, for open water, melt ponds and sea ice. SIC is the sum of Ap and Ai. Of the total 53,200 pictures captured, 19.7% were not processed due to poor visibility caused by heavy fog or precipitation. Photographs from both port and starboard sides were selected at 10-min intervals to reduce our workload, and a total of 4792 pictures were used for the analysis in this study. The average of the areal fractions obtained from both sides at the same location was used as the local value. In all, we obtained the sea ice conditions at 2396 locations along the cruise path.
2.3. Passive Microwave Data
The PM data used in this work are from SSMIS launched onboard the Defense Meteorological Satellite Program satellites and AMSR2 launched onboard the Global Change Observation Mission 1st-Water satellite. These satellites are on sun-synchronous, near-circular polar orbits and cover the Polar Regions every day. The SSMIS sensor is a 24-channel PM radiometer with frequencies ranging from 19.4 to 183.3 GHz, and the AMSR2 sensor is a 7-channel PM radiometer with frequencies ranging from 6.9 to 89.0 GHz. We selected several commonly used algorithms at their highest spatial resolution, including Bootstrap and NT algorithms based on SSMIS data and ASI, Bootstrap, SICCI, and NT2 algorithms based on AMSR2 data (Table 1).

Table 1.
Information on the passive microwave (PM) SIC used in the study. NT: NASA Team; NT2: NASA Team 2; SICCI: Sea Ice Climate Change Initiative.
2.4. Auxiliary Data
Alongside CHINARE-2016 data, shipborne V-OBS SIC data from CHINARE-2010 and shipborne P-OBS data from CHINARE-2014 were used to characterize the interannual variability of SIC in the Central Arctic Passage. During CHINARE-2010, V-OBS was conducted from the bridge deck of R/V Xuelong at time intervals of half an hour [30]. The main information related to SIC, floe size, ice type, melt pond coverage, and ice and snow thickness were recorded according to the ASSIST standard; we used SIC for this work. During CHINARE-2014, P-OBS was carried out using the same method as in this study to measure SIC [43], and these SIC data were therefore also used for comparison.
3. Results
3.1. Sea Ice Concentration Derived from Shipborne Photographic Observations
The SIC distribution along the cruise path is presented in Figure 4a. P-OBS was suspended temporarily during the long-term ice camp (nine days) and also for a short time when the instruments were repaired, as shown by the discontinued sections of the curve with colored points on the northward and southward legs. P-OBS shows that there were two ice belts at the beginning of the northward leg between 71.7° and 72.6°N and between 73.0° and 73.7°N, with a mean SIC of 70.3% and 95.7%, respectively. The sea surface in these ice belts was mainly covered by small floes with melt ponds and melt holes spreading onto the ice surface (Figure 4b). There was not much open water present, but leads were found between small floes. In the 73.7°–78.1°N region, SIC decreased rapidly with an average of 10.4%. Although the sea ice still appeared mainly as small floes, a lot of open water area was observed (Figure 4c). Sailing northward, the open water area diminished, and floe size increased with a mean SIC of 53.5% between 78.1° and 82.7°N (Figure 4d,e). Within the high-latitude part of the southward leg, 80.0°–82.2°N, the latitude 81°N appeared to be a demarcation point. The SIC between 81.0° and 82.2°N was less than that in the same latitude on the northward leg; while the SIC between 80.0° and 81.0°N was similar to that in the same latitude on the northward leg. SIC decreased abruptly with a mean value of 7.6% moving southward and large open water areas reappeared with small floes and brash ice (Figure 4f).
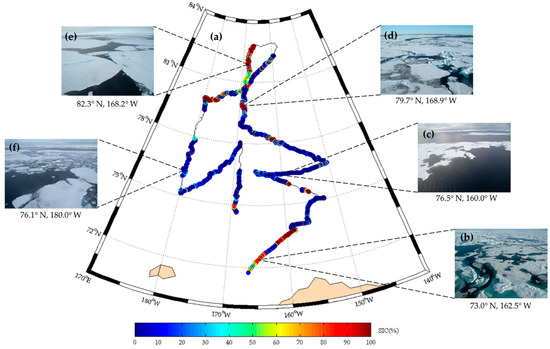
Figure 4.
The distribution of sea ice concentration (SIC) (colored points) derived from shipborne photographic observation along the cruise track (black line) in 2016 (a) with photographs of typical ice conditions and corresponding locations (b–f).
The frequency distribution of SIC along the cruise path is shown in Figure 5, with a 10% bin size. SIC was not normally distributed, but bimodal, and tended to show an approximate U-shape. Because the cruise path was biased towards wide leads, most data were in the 0%–10% bin with a frequency of 0.55. The frequency in the 90%–100%-bin was the second highest, with a value of 0.19. In the other bins, the frequencies in the low SIC class interval (10%–30%-bin) were marginally more than those in the high interval (30%–90%-bin), with frequencies of approximately 0.02.
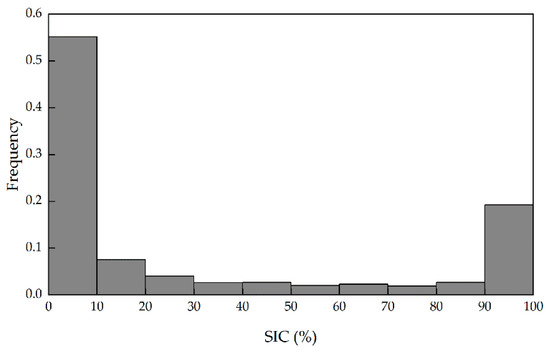
Figure 5.
Histogram of the frequency distribution of sea ice concentration (SIC) along the cruise path with a 10% bin size.
3.2. Sea Surface Categories Distribution along the Cruise Path
Figure 6 presents the distribution of each sea surface category (open water, melt ponds, and sea ice) along the cruise path. There were three regions with a small amount of water along the cruise track (Figure 6a): 72.0°–73.7°N (mean Aw = 39.8%) and 80.6°–82.7°N (mean Aw = 15.8%) on the northward leg and 79.9°–80.1°N (mean Aw = 11.9%) on the southward leg. In most of the other regions, open water accounted for the largest fraction. Observations also showed that along the whole cruise path, Ap fluctuated within a relatively narrow range from 0% to 39.8% with an average of 1.2%. The distribution of Ai was the opposite of Aw; the three regions with small Aw mentioned above all had large Ai, with mean Ai values of 60.0%, 82.9%, and 85.6%, respectively.
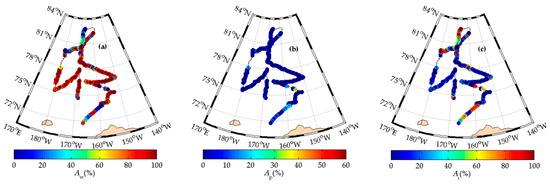
Figure 6.
The distribution of areal fractions of open water (Aw) (a), melt ponds (Ap) (b), and sea ice (Ai) (c) (colored points) along the cruise path (black line) based on the photographic observation data.
To better depict the spatial variability in the sea ice conditions, the mean fractional coverage of the sea surface categories and SIC on the northward and southward legs at each latitude are shown in Figure 7. On the northward leg (Figure 7a), the mean Aw was approximately 60% at the southern edge of the sea ice zone (< 74°N), and increased to more than 90% in the 74°–77°N latitude bands. The mean Aw decreased with a slope of 14.8% per degree of latitude in the 78°–82°N latitude bands, although there was a peak at 80°N. The spatial variability of Ai and SIC on the northward leg showed similar trends that were opposite to the Aw. Both the mean Ai and SIC decreased from approximately 35% and 40%, respectively, to 7% as the latitude increased from 72°–73°N to 74°–77°N, and then increased by 14.8% per degree of latitude between 78° and 82°N. Overall, the mean Ap remained fairly small, measuring only 5% for 72°–73°N, and then decreased to less than 2.5% for 74°–82°N. On the southward leg (Figure 7b), the spatial variability of the sea ice conditions was similar to that on the northward cruise track, but at 81°N the mean Aw was higher and the mean Ai and SIC were lower. The mean Ap was never more than 1.8% on the southward leg.
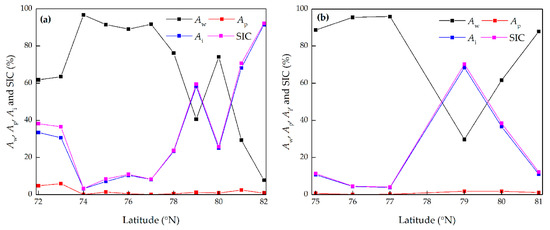
Figure 7.
Average areal fractions of open water, melt ponds, and sea ice (Aw, Ap, and Ai, respectively) and sea ice concentration (SIC) on the northward (a) and southward (b) legs along the cruise path.
3.3. Comparison of Sea Ice Concentration Derived from Two Sources
Because of the fixed PM data grid, there is a large difference in the spatial resolution between PM SIC and P-OBS SIC. According to the equipment installation parameters (H and α) and the upper limit angle set in the image process algorithm, the actual P-OBS area is a 624-m-wide strip along the cruise track. Furthermore, the average sailing speed of R/V Xuelong in the ice zone was 4.47 knots (8.28 km/h), and therefore, the ship advanced a distance of 1.38 km in each 10-min interval. It is therefore questionable whether a direct comparison between PM SIC and P-OBS SIC is viable given the different resolutions [27]. However, a moving average (MA) method was adopted to provide a better comparison. The PM SIC of the same day as the P-OBS was interpolated to each image location using the value of the closest grid point. The displacement between the locations of two adjoining P-OBS images was calculated to determine the average window, which was close to but no more than the corresponding PM resolution (Table 1). The P-OBS SIC within the average window was then averaged. Finally, the SIC derived from the two sources with different resolutions were compared. The standard deviation of the MA P-OBS SIC was calculated. It was found that in areas with MA P-OBS SIC < 50%, the standard deviation increased from 0 to approximate 40% with SIC increasing from 0 to 50%; while in areas with MA P-OBS SIC ≥ 50%, the standard deviation decreased from approximate 40% to 0 with SIC increasing from 50% to 100%.
However, a number of uncertainties regarding spatial and temporal differences also warrant discussion before moving onto the comparison. First, because the P-OBS area is only a 624-m-wide strip along the cruise path, and although it is averaged, the result does not exactly match the PM pixels of 3.125–25 km in both dimensions. With the objective to evaluate the performances of PM algorithms in estimating SIC along ship routes, it was assumed that the ice conditions were isotropic and homogeneous on the scale of the PM grid cells [40]. Second, P-OBS SIC is instantaneous while PM SIC is a daily average. An error is introduced due to the temporal difference, which can be divided into two main components: the varied sea ice surface condition due to dynamic and thermodynamic processes and the varied sea ice position due to drift. The former component is difficult to estimate because of the varying dynamic-thermodynamic sea ice processes in Arctic summer, while the latter can be estimated qualitatively. Considering that the drift speed of Arctic sea ice is generally no more than 0.1 m/s [48,49,50], the influence caused by sea ice drift is expected to have minor effects on the comparison of PM SIC with sparser resolutions such as 12.5 km and 25 km. Above all, the error in the comparison is objective because of the distinct resolutions and sampling time of the data. In fact, this issue occurs when comparing the PM SIC with any field observations, not only P-OBS as in our study, but also SIC from aerial observations [27,46] and visual surveys [19,42]. To the authors’ best knowledge, a good solution to this issue is absent so far. Maybe improving the field observation technique is a possible way to access the problem in the future.
The comparison between PM SIC and the corresponding MA P-OBS SIC for different resolutions along the cruise path are shown in Figure 8. All the PM SIC series exhibited similar characteristics. PM SIC fluctuated at the start of the northward leg (distance < 1000 km), followed by a peak at a distance of approximately 1000 km (region A). Between 1000 and 2000 km the PM SIC series again fluctuated and reached a peak at approximately 2000 km (region B). Next, all the PM SIC series decreased abruptly, except for AMSR2-NT2 SIC (red circle), and then increased up to approximately 100% when the ship arrived at the long-term ice camp. At the start of the southward leg, all the PM SIC series fluctuated between 3000 and 4000 km, followed by a gradual decline, and again increased abruptly in region C and at the end of the cruise.
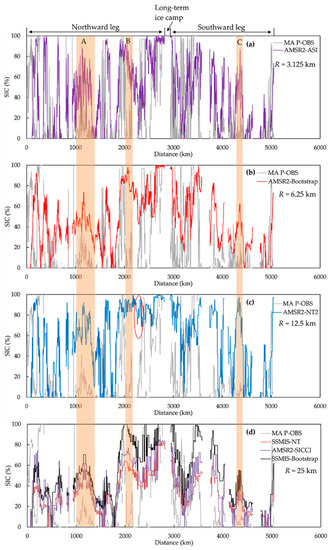
Figure 8.
Comparison between passive microwave (PM) sea ice concentration (SIC) and moving average (MA) photographic observation (P-OBS) SIC along the cruise path for each algorithm (a–d). The orange columns represent the regions with a large difference between PM SIC and MA P-OBS SIC, and R denotes the spatial resolution. The sections of the northward leg, long-term ice camp, and southward leg are also indicated.
Compared with the MA P-OBS SIC, the PM SIC series showed similar variability. There were three regions (A, B, and C shown in Figure 8) where the PM SIC data were much higher than the corresponding MA P-OBS SIC. AMSR2-NT2 SIC had the largest bias with respect to MA P-OBS SIC in these three regions, reaching 60.6%, 79.8%, and 72.5% for regions A, B, and C, respectively. Examining the image set, the three regions showed similar ice conditions, where open water covered almost the whole sea surface with only a few floes in the far range of the image.
The results of the frequency distributions between PM SIC and MA P-OBS SIC are shown in Figure 9. In general, the frequencies of low SIC derived from PM data were much less than those observed by P-OBS, while the opposite occurred for high SIC. This demonstrates that it is difficult for PM to detect low levels of SIC. AMSR2-ASI, AMSR2-Bootstrap, SSMIS-NT, AMSR2-SICCI, and SSMIS-Bootstrap all underestimated the SIC frequency in the < 20%-bin, and AMSR2-NT2 underestimated the SIC frequency in the < 40%-bin. In the middle section (40%–80%-bin for AMSR2-NT2 and 20%–80%-bin for the others), the frequencies were higher for PM SIC than for MA P-OBS SIC. In the > 80%-bin, individual differences occurred. SSMIS-NT and AMSR2-SICCI did not detect SIC beyond 90%, and only SSMIS-NT SIC had a lower frequency than the MA P-OBS SIC in the 80–90%-bin. Apart from SSMIS-NT, the other PM SIC data showed higher frequencies than MA P-OBS SIC in the > 80%-bin.
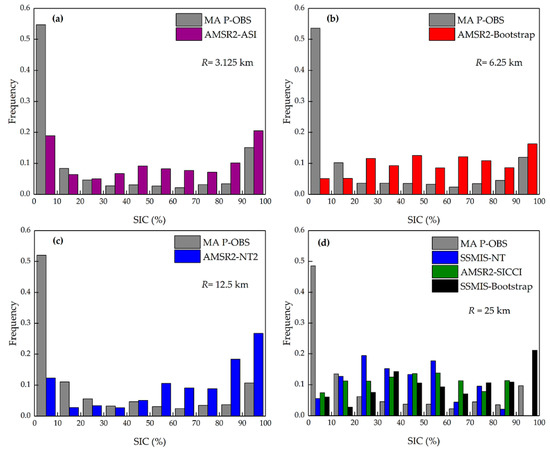
Figure 9.
Comparison of the frequency distributions between passive microwave (PM) sea ice concentration (SIC) and moving average (MA) photographic observation (P-OBS) SIC for each algorithm (a–d), where R denotes the spatial resolution.
As MA P-OBS SIC reflects the true situation in the field, the difference between PM SIC and MA P-OBS is due to an error in the PM algorithms. To further evaluate the agreement of the SIC derived from PM algorithms with the SIC along a ship cruise path, we calculated the mean error and the root-mean-square-error (RMSE) between MA P-OBS SIC and PM SIC. Figure 10 shows the comparison of the mean error and RMSE. The PM algorithms with lower resolutions do not always have poorer accuracy, e.g., PM SIC with a resolution of 25 km did not perform the worst in the comparisons. SSMIS-NT (mean = 10.3%, RMSE = 32.0%) and AMSR2-SICCI (mean = 15.3%, RMSE = 35.9%) were the best two and even better than AMSR2-ASI (mean = 22.1%, RMSE = 47.9%), which had the highest resolution. AMSR2-Bootstrap had a slightly larger mean error than AMSR2-ASI, whereas it had a lower RMSE. SSMIS-Bootstrap and AMSR2-NT2 had the poorest performance, and AMSR2-NT2 (mean = 34.7%, RMSE = 54.9%) was worse than SSMIS-Bootstrap (mean = 30.2%, RMSE = 45.4%). AMSR2-ASI, AMSR2-Bootstrap, AMSR2-NT2, and SSMIS-Bootstrap obtained SIC values between 0 and 100%. However, for SSMIS-NT the upper limits were 64% in the regime with MA P-OBS SIC < 64%, and 82% in the regime with MA P-OBS SIC > 64%, and for AMSR2-SICCI the upper limit was 83.8% in the whole SIC regime; and the lower limit of PM SIC was 0 for both algorithms.
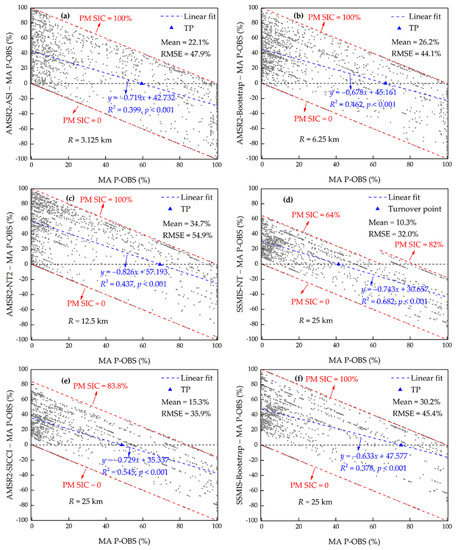
Figure 10.
The difference in passive microwave (PM) sea ice concentration (SIC) with respect to moving average (MA) photographic observation (P-OBS) SIC for each algorithm (a–f). The gray dashed lines represent a difference equal to 0. The blue dashed lines represent the linear fit line of the difference. The red dashed lines represent the upper and lower limits of the PM SIC. The blue triangles represent the turnover points (TPs) of SIC. Also shown are the mean error, root-mean-square-error (RMSE), equations of linear fit, coefficient of determination R2, and the significance level p.
The linear fit as shown in Figure 10 can be used to further describe the general variation of the mean error; the over- and underestimation of the PM SIC compared with MA P-OBS SIC can be seen clearly. In general, with increasing SIC, PM SIC shifts from an overestimate to an underestimate compared with P-OBS SIC. For example, for AMSR2-ASI (Figure 10a), the linear fit turned from positive to negative at SIC = 59.4%, i.e., an overestimate at SIC < 59.4% and an underestimate at SIC ≥ 59.4%. The turnover point (TP) of the SIC for each PM algorithm is listed in Table 2. SSMIS-NT and SSMIS-Bootstrap had the lowest and highest TP values, respectively. Each PM algorithm performed differently in the SIC regimes below and above the TP. Table 3 summarizes the mean error and RMSE of each PM algorithm in these two SIC regimes. Almost all algorithms had a higher mean error below the TP than the absolute value of the mean error above the TP. This result was also seen in the RMSE. The exception was SSMIS-NT, where the mean error below the TP was slightly less than the absolute value of the mean error above the TP. For SSMIS-NT and AMSR2-SICCI, the RMSE values below the TP were 8.8% and 0.8% less than above the TP, respectively. It is noteworthy that the TP values can be used to statistically determine the over- and underestimation of the PM algorithms, while it does not mean that the SIC derived from the PM measurement must be greater or less than that derived from P-OBS in the SIC regime below or above the TP.

Table 2.
The turnover point (TP) of the sea ice concentration (SIC) from an overestimate to an underestimate for the passive microwave (PM) algorithms compared with moving average photographic observation SIC.

Table 3.
The mean error and root-mean-square-error (RMSE) of the passive microwave (PM) sea ice concentration (SIC) with respect to moving average photographic observation SIC below and above the turnover point (TP) of the SIC.
4. Discussion
4.1. Factors Influencing the Difference of Sea Ice Concentration Derived from Two Sources
The resolution of the PM data and the physical properties of summer sea ice and snow are the two contributing factors responsible for the difference between the shipborne observed and PM SIC [27]. On the one hand, because vessel cruise paths are typically biased towards areas with leads and isotropic ice conditions are assumed, P-OBS always underestimates the mean regional SIC. It is difficult to detect leads from PM measurements because the spatial resolution is much coarser than the lead scale, which has resulted in overestimates by the PM SIC algorithms in regions with leads compared with P-OBS data. On the other hand, sea ice and snow cover become saturated and flooded with liquid water during the melting season, and hence their physical properties, especially emissivity, change and the surface appears as a mixture of ice and open water to the PM sensors. This causes an underestimate of PM SIC [19].
As shown in Figure 10, PM SIC shifts from an overestimate to an underestimate compared with P-OBS SIC. Therefore, different factors play major roles in the SIC regimes below and above the TP. The coarse resolution dominates mainly below the TP, because more open water leads exist in areas with low SIC. With increasing SIC, less leads occur, and overestimation of the PM SIC decreases. However, the physical properties of summer sea ice and snow dominate above the TP. In areas with high SIC, the sea surface is mostly covered by sea ice and fewer leads are present. In these areas the bias is controlled by the physical properties of wet ice and snow, which results in an underestimate of PM SIC. Similar observations were reported by Knuth and Ackley [27], who compared the SIC derived from the SSM/I-NT algorithm (25 km) with V-OBS SIC in the summer and fall in the Antarctic, respectively. In the summer, there is a similar trend whereby PM SIC shifts from an overestimate to an underestimate compared with V-OBS SIC with a TP of approximately 57%. In the fall, however, PM SIC underestimates V-OBS data at any SIC.
In addition to PM resolution and physical properties of snow and ice, there are several other factors influencing the difference between MA P-OBS SIC and PM SIC, such as the inherent characteristics (e.g., channels and their sensitivities to atmospheric conditions and tie-points) of PM algorithms. Of the investigated algorithms, NT2 and ASI algorithms based on the AMSR2 sensor are very sensitive to atmospheric effects because of using the 89 GHz channel. The cloud liquid water and water vapor can reduce the polarization difference over open water and near ice edge [21]. NT algorithm shows some sensitivity to wind-roughened ocean surface [21]. Algorithms based solely on the 19 and 37 GHz vertically polarized channels display the smallest sensitivity to the atmospheric conditions [22]. Each algorithm uses a set of tie-points to retrieve SIC, while the brightness temperature may have a range of variability for the same ice type or open water due to varying emissivity, atmospheric conditions, and the temperature of the emitting layer, which in turn affects the retrieval accuracy. To compare the superiority of the PM algorithms without the influence of resolution, we selected the algorithms with the same resolution of 25 km, i.e., SSMIS-Bootstrap, SSMIS-NT, and AMSR2-SICCI. Comparison in Figure 10 shows that although the SSMIS-Bootstrap had the smallest sensitivity to the atmospheric conditions, its performance was still lower than SSMIS-NT which accuracy is affected by wind, indicating that the selection of tie-points has heavier effects on Bootstrap algorithm than NT algorithm. SICCI algorithm was suggested as a good choice for SIC retrieval [21], and it is found from the comparison that the performance of AMSR2-SICCI was better than most of other algorithms, but was slightly poorer than SSMIS-NT. The characteristics of SSMIS and AMSR2 sensors may be the causes of the differences. While a thorough study on the characteristics of PM algorithms and sensors is beyond the scope of the current work, as this research has paid more attention to the application of PM SIC algorithms in guiding Arctic navigation. Systemic evaluation can be seen in Ivanova et al. [21] and Andersen et al. [22].
4.2. Melt Pond Effects on the Mean Error of Passive Microwave Sea Ice Concentration
Melt ponds are known to be an important source of error for PM algorithms in detecting Arctic summer SIC, and thus, have attracted much attention [21,51,52]. The previous works provide a qualitative understanding of the melt pond effects; however, to the authors’ best knowledge, only very limited studies have quantified the melt pond effects. Only Kern et al. [53] presented that AMSR-E algorithms underestimated MODIS SIC by 20–30% in areas with a high melt pond fraction of 50%. To explore the melt pond effects in a quantitative way, the data shown in Figure 10 were analyzed further. The MA AP of each data point was first determined, and then the MA Ap range was divided at 1% intervals. The mean error at each interval was defined using the average difference of the PM SIC with respect to MA P-OBS SIC. The variations of the mean error versus MA Ap are shown in Figure 11.
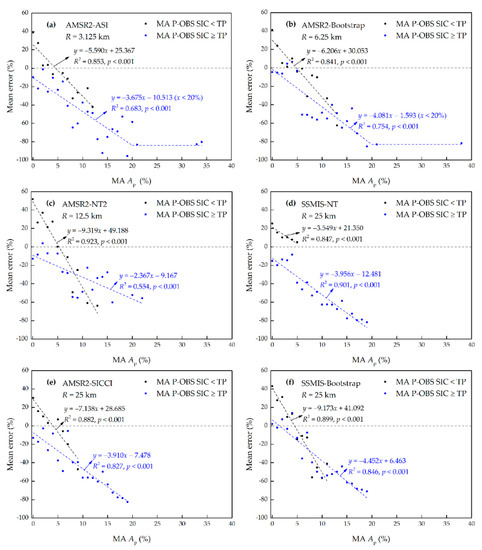
Figure 11.
The mean error of the passive microwave (PM) sea ice concentration (SIC) with respect to moving average (MA) photographic observation (P-OBS) SIC with the MA areal fraction of melt ponds (Ap) for each algorithm (a–f), where R denotes the spatial resolution. The gray dashed lines represent the mean error equal to 0. The black and blue dashed lines represent the linear fit line of the mean error below and above the turnover point (TP) for each PM SIC algorithm. Also shown are the equations of the linear fit, the coefficient of determination R2, and the significance level p.
Below the TP, all the PM SIC methods overestimated the MA P-OBS SIC when the MA AP was approximately less than 5%, mainly because the PM measurement has difficulty in detecting leads due to the coarser spatial resolution. As the MA Ap exceeded 5%, the PM SIC shifted from an overestimate to an underestimate. Because of the similar microwave radiometric nature between open water and melt ponds (the presence of liquid water) as well as the limited penetration depth of microwave radiation into liquid water, melt ponds are easily interpreted as open water by PM measurements [21]. The MA Ap regime below the TP for SSMIS-NT was only 0%–5%, while according to the trend shown in Figure 11d, SSMIS-NT SIC could also underestimate the MA P-OBS SIC if the MA Ap exceeded 5%. Above the TP, almost all PM SIC underestimated the MA P-OBS SIC when the MA AP varied between approximately 0 and 20%, and the underestimation increased with increasing MA Ap. The exception was SSMIS-Bootstrap, where the mean error was positive with a value of 2.0% when MA Ap was 0. For AMSR2-ASI and AMSR2-Bootstrap above the TP, when the MA Ap exceeded 20%, the mean error was independent of Ap and reached the lower limit, as the horizontal curves show in Figure 11a,b. We also assumed that there are critical values of Ap for the other PM algorithms in the SIC regime above the TP and all the PM algorithms in the SIC regime below the TP, above which the mean error of PM SIC reaches the lower limit, at least –100%, and is independent of Ap.
The trends of the mean error with the MA Ap in the observed Ap regime below and above the TP of SIC were quantitatively described using linear regression (Figure 11). The results show a good linear relationship between the mean error and MA Ap. The slope of the linear fit indicates the influence level of Ap on the mean error. The influence level of Ap below the TP was greater than that above the TP for most PM SIC, with the ratio ranging between 1.5 and 3.9. Only SSMIS-NT had a relatively smaller Ap influence level below the TP than that above the TP. Among these PM algorithms, AMSR2-NT2 had both the highest and lowest influence level of Ap below and above the TP, respectively. SSMIS-NT had the lowest Ap influence level below the TP and SSMIS-Bootstrap had the highest Ap influence level above the TP.
4.3. An Inter-Comparison of Sea Ice Concentration from 2010 to 2016
Shipborne observations of SIC were also conducted during CHINARE-2010 [30] and CHINARE-2014 [43]. The expedition areas covered 178.8°E–152.5°W, 75.6°–88.5°N in 2010 and 139.0°–169.0°W, 72.3°–82.7°N in 2014 (Figure 1); both were similar to the area covered in 2016. The observations were carried out from 21 July–28 August 2010 and from 2 August–1 September 2014, similar to the duration of the observation in 2016. Therefore, the comparison of SIC between these three expeditions can be helpful to depict the variation of summer sea ice in the Central Arctic Passage.
The results show that there were clear differences in SIC between 2010, 2014, and 2016. The boundary between PIZ and MIZ was clear in 2010 and 2014: the area north of 75°N on the northward leg and north of 80°N on the southward leg can be defined as the PIZ in 2010. For 2014, PIZ covered the area north of 76°N on both of the northward and southward legs. It was difficult to identify the boundary between MIZ and PIZ in 2016 due to the dramatically varying SIC, and only the region north of 82°N on the northward leg could be taken as the PIZ. Therefore, the boundary was farther north in 2016 than in 2010 and 2014. In 2010, the mean SIC in the PIZ was 66% for the northward leg and 71% for the southward leg, and the mean SIC in the MIZ was 30% (Table 4). The numbers were slightly higher in 2014: the mean SIC was 76% in the PIZ and 48% in the MIZ. The mean SIC in the MIZ decreased to 20% in 2016. However, in the PIZ, the SIC remained at a similar level to that in 2010 and 2014, with an average of 70%.

Table 4.
The mean sea ice concentration along the cruise path in marginal ice zone (MIZ), pack ice zone (PIZ), Chukchi Sea, Beaufort Sea, and Central Arctic in 2010, 2014, and 2016, respectively.
Based on the Arctic Sea area division provided by the National Snow and Ice Data Center, the SIC in the R/V Xuelong cruise region covered parts of the Chukchi Sea, Beaufort Sea, and the Central Arctic. Therefore, the SIC in these seas can be compared, while due to a lack of detailed information, the SIC in 2010 was not included in the following comparison. Our results show that the SIC in Chukchi Sea and Beaufort Sea were similar in 2014, with averages of 56% and 59%, respectively, while there were larger areas of open water in these two seas in 2016. The mean SIC was only 21% in the Chukchi Sea and even less in the Beaufort Sea (8%). In the Central Arctic, the sea surface in 2014 was almost fully covered with sea ice (or ponded sea ice), with a mean SIC of 98%, while in 2016 the mean SIC was only 56%.
5. Conclusions
With the objective to perform a detailed evaluation on the performances of PM algorithms in estimating SIC along the vessel routes from the perspective of guiding Arctic navigation, a shipborne photographic observation (P-OBS) program was conducted as a part of the Chinese National Arctic Research Expedition in the summer of 2016. When sailing in the sea ice zone, the vessel’s cruise path was biased towards wide ice leads. P-OBS was performed using two cameras mounted obliquely to map the sea surface along a strip beside the ship’s track. The sea ice concentration (SIC) and areal fractions of open water, melt ponds, and sea ice (Aw, Ap, and Ai, respectively) along the strip were calculated based on the collected images, which were processed using image partitioning and geometric orthorectification. Using these P-OBS data, we compared several commonly used passive microwave (PM) SIC algorithms, including Bootstrap (25 km resolution) and NASA Team (NT) (25 km) algorithms based on the Special Sensor Microwave Imager/Sounder (SSMIS) data and Arctic radiation and turbulence interaction study (ARTIST) sea ice (ASI) (3.125 km), Bootstrap (6.25 km), Sea Ice Climate Change Initiative (SICCI) (25 km), and NASA Team 2 (NT2) (12.5 km) algorithms based on the Advanced Microwave Scanning Radiometer 2 (AMSR2) data.
The observations showed that the distribution of SIC along the cruise path was U-shaped, where the SIC in the SIC classes 0%–10% and 90%–100% accounted for a large proportion of the probability mass. PM SIC mainly underestimated the proportion of SIC in the 0%–10%-bin and overestimated the proportion of SIC in the 90%–100%-bin, indicating that PM measurements have difficulties in detecting very low SIC values. Observations also showed that there were only three areas with small Aw values along the whole cruise track, while in the other parts of the cruise, open water accounted for the largest proportion of the sea surface. Throughout the whole cruise track, Ap fluctuated within a relatively narrow range from 0 to 39.8% with an average of 1.2%.
To provide an optimal option for guiding Arctic navigation, the PM SIC algorithms investigated in this paper were ranked based on the agreement compared with the MA P-OBS SIC (mean error and root-mean-square-error, RMSE). SSMIS-NT produces the smallest mean error and RMSE, and thus performs best out of the chosen algorithms. AMSR2-SICCI produces a slightly larger mean error and RMSE than SSMIS-NT, and is the second best. AMSR2-ASI and AMSR2-Bootstrap have similar performances, while AMSR2-ASI exhibits a lower mean error and ranks as the third choice. The relatively high mean error makes the performance of AMSR2-Bootstrap poorer than that of AMSR2-ASI. Both SSMIS-Bootstrap and AMSR2-NT2 perform worse; AMSR2-NT2 has a larger mean error and RMSE, and is therefore ranked as the last.
The moving average (MA) P-OBS SIC is considered to reflect the true situation, and the difference between PM SIC and MA P-OBS is due to an error in the PM algorithms. A turnover point (TP) in the SIC was determined using the variations in the PM SIC error. Below the TP, PM SIC overestimated P-OBS SIC due to the much coarser PM resolution, whereas it underestimated P-OBS SIC above the TP because the emissivity of the saturated and flooded sea ice and snow cover made the surface signatures appear as a mixture of ice and open water to the PM sensors. The effects of melt ponds on the mean error of PM SIC were analyzed quantitatively. Below the TP, the mean error shifted from positive to negative with increasing Ap. Above the TP, the underestimation of PM SIC increased as Ap increased from 0% to 20%. A linear trend was found for the mean error varying with MA Ap, which was used to quantify the effects of melt ponds on PM SCI.
Arctic sea ice is changing rapidly, which results in increased ship traffic on the Arctic ship routes. Therefore, there will be a greater need for information on the sea ice conditions along ship cruise paths for Arctic ice management. The present research focused on to evaluate the performances of PM algorithms in estimating SIC along the ship routes. Thus, the results will facilitate navigation in the Polar Regions in which only PM satellite data are available. In addition, more factors influencing the accuracy of PM SIC retrieval, such as weather conditions, will be evaluated further in future. Field observation technique also needs improvement to diminish the error caused by temporal and spatial differences in comparisons.
Author Contributions
Conceptualization, Q.W.; Methodology, P.L. and Z.L.; Formal analysis, Q.W. and Y.Z.; Investigation, Q.W.; Writing—original draft preparation, Q.W.; Writing—review and editing, P.L., M.L. and G.Z.
Funding
This research was funded by the National Major Research High Resolution Sea Ice Model Development Program of China (grant number 2018YFA0605903), the National Key Research and Development Program of China (grant number 2017YFE0111400), the National Natural Science Foundation of China (grant numbers 41876213, 51639003 and 51579028), the High Technology of Ship Research Project of the Ministry of Industry and Information Technology (grant number 350631009), the National Postdoctoral Program for Innovative Talent (grant number BX20190051), and the Academy of Finland (grant number 325363).
Acknowledgments
In this study, both AMSR2-ASI and AMSR2-Bootstrap SIC were downloaded from the archive provided by the University of Bremen (https://seaice.uni-bremen.de/start/data-archive/). The SSMIS-Bootstrap, SSMIS-NT, and AMSR2-NT2 SIC were downloaded from the archive provided by the National Snow and Ice Data Center (https://nsidc.org). The AMSR2-SICCI SIC was downloaded from the archive provided by the University of Hamburg (http://icdc.cen.uni-hamburg.de/1/projekte/esa-cci-sea-ice-ecv0.html). The Arctic sea area division was provided by the National Snow and Ice Data Center (https://nsidc.org/data/masie). We also wish to acknowledge the crews of the R/V Xuelong for their assistance during the shipborne observations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Renner, A.H.H.; Gerland, S.; Haas, C.; Spreen, G.; Beckers, J.F.; Hansen, E.; Nicolaus, M.; Goodwin, H. Evidence of Arctic sea ice thinning from direct observations. Geophys. Res. Lett. 2014, 41, 5029–5036. [Google Scholar] [CrossRef]
- Lindsay, R.; Schweiger, A. Arctic sea ice thickness loss determined using subsurface, aircraft, and satellite observations. Cryosphere 2015, 9, 269–283. [Google Scholar] [CrossRef]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Kattsov, V.; Barrett, A.; Serreze, M.; Pavlova, T.; Holland, M.; Meier, W.N. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 2012, 39, L16502. [Google Scholar] [CrossRef]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C.; et al. CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F. Contribution of melt in the Beaufort Sea to the decline in Arctic multiyear sea ice coverage: 1993−2009. Geophys. Res. Lett. 2010, 37, 79–93. [Google Scholar] [CrossRef]
- Comiso, J.C. Large decadal decline of the Arctic multiyear ice cover. J. Clim. 2012, 25, 1176–1193. [Google Scholar] [CrossRef]
- Deser, C.; Teng, H. Evolution of Arctic sea ice concentration trends and the role of atmospheric circulation forcing, 1979–2007. Geophys. Res. Lett. 2008, 35, L02504. [Google Scholar] [CrossRef]
- Lei, R.; Xie, H.; Wang, J.; Leppäranta, M.; Jónsdóttir, I.; Zhang, Z. Changes in sea ice conditions along the Arctic Northeast Passage from 1979 to 2012. Cold Reg. Sci. Technol. 2015, 119, 132–144. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, T.; Zheng, L. The characteristics of surface albedo change trends over the Antarctic sea ice region during recent decades. Remote Sens. 2019, 11, 821. [Google Scholar] [CrossRef]
- Serreze, M.C.; Barry, R.G. Processes and impacts of Arctic amplification: A research synthesis. Glob. Planet. Chang. 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Takimoto, T.; Kanada, S.; Shimoda, H.; Wako, D.; Uto, S.; Izumiyama, K. Field measurements of local ice load on a ship hull in pack ice of the southern Sea of Okhotsk. In Proceedings of the OCEANS 2008-MTS/IEEE Kobe Techno-Ocean, Kobe, Japan, 8–11 April 2008. [Google Scholar]
- Langlois, A.; Barber, D.G.; Hwang, B.J. Development of a winter snow water equivalent algorithm using in situ passive microwave radiometry over snow-covered first-year sea ice. Remote Sens. Environ. 2007, 106, 75–88. [Google Scholar] [CrossRef]
- Langlois, A.; Barber, D.G. Advances in seasonal snow water equivalent (SWE) retrieval using in situ passive microwave measurements over first-year sea ice. Int. J. Remote Sens. 2008, 29, 4781–4802. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K.; Cho, J.; Kang, Y.; Yoon, H.; Lee, Y. Satellite-based prediction of Arctic sea ice concentration using a deep neural network with multi-model ensemble. Remote Sens. 2019, 11, 19. [Google Scholar] [CrossRef]
- Strong, C.; Golden, K. Filling the polar data gap in sea ice concentration fields using partial differential equations. Remote Sens. 2016, 8, 442. [Google Scholar] [CrossRef]
- Comiso, J.C.; Meier, W.N.; Gersten, R. Variability and trends in the Arctic sea ice cover: Results from different techniques. J. Geophys. Res. Oceans 2017, 122, 6883–6900. [Google Scholar] [CrossRef]
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89-GHz channels. J. Geophys. Res. 2008, 113, C02S03. [Google Scholar] [CrossRef]
- Beitsch, A.; Kern, S.; Kaleschke, L. Comparison of SSM/I and AMSR-E sea ice concentrations with ASPeCt ship observations around Antarctica. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1985–1996. [Google Scholar] [CrossRef]
- Rees, G. Remote Sensing of Snow and Ice; Taylor & Francis: London, UK, 2006. [Google Scholar]
- Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef]
- Andersen, S.; Tonboe, R.; Kern, S.; Schyberg, H. Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using numerical weather prediction model fields: An intercomparison of nine algorithms. Remote Sens. Environ. 2006, 104, 374–392. [Google Scholar] [CrossRef]
- Comiso, J.C.; Cavalieri, D.J.; Parkinson, C.L.; Per, G. Passive microwave algorithms for sea ice concentration: A comparison of two techniques. Remote Sens. Environ. 1997, 60, 357–384. [Google Scholar] [CrossRef]
- Heygster, G.; Wiebe, H.; Spreen, G.; Kaleschke, L. AMSR-E geolocation and validation of sea ice concentrations based on 89 GHz data. J. Remote Sens. Soc. Jpn. 2009, 29, 226–235. [Google Scholar]
- Ivanova, N.; Johannessen, O.M.; Pedersen, L.T.; Tonboe, R.T. Retrieval of Arctic sea ice parameters by satellite passive microwave sensors: A comparison of eleven sea ice concentration algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7233–7246. [Google Scholar] [CrossRef]
- Worby, A.P.; Allison, I. A technique for making ship-based observations of Antarctic sea ice thickness and characteristics, Part I: Observational techniques and results. In Antarctic CRC Research Report; Antarctic CRC: Hobart, Australia, 1999; Volume 14, pp. 1–23. [Google Scholar]
- Knuth, M.A.; Ackley, S.F. Summer and early-fall sea-ice concentration in the Ross Sea: Comparison of in situ ASPeCt observations and satellite passive microwave estimates. Ann. Glaciol. 2006, 44, 303–309. [Google Scholar] [CrossRef][Green Version]
- Lei, R.; Li, Z.; Li, N.; Lu, P.; Cheng, B. Crucial physical characteristics of sea ice in the Arctic section of 143°−180°W during August and early September 2008. Acta Oceanol. Sin. 2012, 31, 65–75. [Google Scholar] [CrossRef]
- Lei, R.; Tian-Kunze, X.; Li, B.; Heil, P.; Wang, J.; Zeng, J.; Tian, Z. Characterization of summer Arctic sea ice morphology in the 135°−175°W sector using multi-scale methods. Cold Reg. Sci. Technol. 2017, 133, 108–120. [Google Scholar] [CrossRef]
- Xie, H.; Lei, R.; Ke, C.; Wang, H.; Li, Z.; Zhao, J.; Ackley, S.F. Summer sea ice characteristics and morphology in the Pacific Arctic sector as observed during the CHINARE 2010 cruise. Cryosphere 2013, 7, 1057–1072. [Google Scholar] [CrossRef]
- Ozsoy-Cicek, B.; Ackley, S.F.; Worby, A.; Xie, H.; Lieser, J. Antarctic sea-ice extents and concentrations: Comparison of satellite and ship measurements from International Polar Year cruises. Ann. Glaciol. 2011, 52, 318–326. [Google Scholar] [CrossRef]
- Pang, X.; Pu, J.; Zhao, X.; Ji, Q.; Qu, M.; Cheng, Z. Comparison between AMSR2 sea ice concentration products and pseudo-ship observations of the Arctic and Antarctic sea ice edge on cloud-free days. Remote Sens. 2018, 10, 317. [Google Scholar] [CrossRef]
- Worby, A.P.; Comiso, J.C. Studies of the Antarctic sea ice edge and ice extent from satellite and ship observations. Remote Sens. Environ. 2004, 92, 98–111. [Google Scholar] [CrossRef]
- Hall, R.J.; Hughes, N.; Wadhams, P. A systematic method of obtaining ice concentration measurements from ship-based observations. Cold Reg. Sci. Technol. 2002, 34, 97–102. [Google Scholar] [CrossRef]
- Perovich, D.K.; Tucker, W.B., III; Ligett, K.A. Aerial observations of the evolution of ice surface conditions during summer. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Inoue, J.; Curry, J.A.; Maslanik, J.A. Application of Aerosondes to melt-pond observations over Arctic sea ice. J. Atmos. Ocean. Technol. 2008, 25, 327–334. [Google Scholar] [CrossRef]
- Lu, P.; Li, Z.; Cheng, B.; Lei, R.; Zhang, R. Sea ice surface features in Arctic summer 2008: Aerial observations. Remote Sens. Environ. 2010, 114, 693–699. [Google Scholar] [CrossRef]
- Weissling, B.; Ackley, S.; Wagner, P.; Xie, H. EISCAM—Digital image acquisition and processing for sea ice parameters from ships. Cold Reg. Sci. Technol. 2009, 57, 49–60. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Q.; Lubbad, R.; Loset, S.; Skjetne, R. A shipborne measurement system to acquire sea ice thickness and concentration at engineering scale. In Proceedings of the Arctic Technology Conference, St. John’s, NL, Canada, 24–26 October 2016. [Google Scholar]
- Lu, P.; Li, Z. A method of obtaining ice concentration and floe size from shipboard oblique sea ice images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2771–2780. [Google Scholar] [CrossRef]
- Worby, A.P.; Geiger, C.A.; Paget, M.J.; Van Woert, M.L.; Ackley, S.F.; DeLiberty, T.L. Thickness distribution of Antarctic sea ice. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Alekseeva, T.A.; Frolov, S.V. Comparative analysis of satellite and shipborne data on ice cover in the Russian Arctic seas. Izv. Atmos. Ocean. Phys. 2013, 49, 879–885. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Lu, P.; Lei, R.; Cheng, B. 2014 summer Arctic sea ice thickness and concentration from shipborne observations. Int. J. Digit. Earth 2018, 1–17. [Google Scholar] [CrossRef]
- Mcgovern, D.J.; Bai, W. Experimental study on kinematics of sea ice floes in regular waves. Cold Reg. Sci. Technol. 2014, 103, 15–30. [Google Scholar] [CrossRef]
- Huang, W.; Lu, P.; Lei, R.; Xie, H.; Li, Z. Melt pond distribution and geometry in high Arctic sea ice derived from aerial investigations. Ann. Glaciol. 2016, 57, 105–118. [Google Scholar] [CrossRef]
- Li, L.; Ke, C.; Xie, H.; Lei, R.; Tao, A. Aerial observations of sea ice and melt ponds near the North Pole during CHINARE2010. Acta Oceanol. Sin. 2017, 36, 64–72. [Google Scholar] [CrossRef]
- Lu, P.; Leppäranta, M.; Cheng, B.; Li, Z.; Istomina, L.; Heygster, G. The color of melt ponds on Arctic sea ice. Cryosphere 2018, 12, 1331–1345. [Google Scholar] [CrossRef]
- Martin, T.; Augstein, E. Large-scale drift of Arctic Sea ice retrieved from passive microwave satellite data. J. Geophys. Res. Oceans 2000, 105, 8775–8788. [Google Scholar] [CrossRef]
- Sumata, H.; Kwok, R.; Gerdes, R.; Kauker, F.; Karcher, M. Uncertainty of Arctic summer ice drift assessed by high-resolution SAR data. J. Geophys. Res. Oceans 2015, 120, 5285–5301. [Google Scholar] [CrossRef]
- Leppäranta, M. The Drift of Sea Ice, 2nd ed.; Springer-Praxis: Heidelberg, Germany, 2011. [Google Scholar]
- Cavalieri, D.J.; Onstott, R.G.; Burns, B.A. Investigation of the effects of summer melt on the calculation of sea ice concentration using active and passive microwave data. J. Geophys. Res. 1990, 95, 5359–5369. [Google Scholar] [CrossRef]
- Comiso, J.C.; Kwok, R. Surface and radiative characteristics of the summer Arctic sea ice cover from multisensor satellite observations. J. Geophys. Res. 1996, 101, 28397–28416. [Google Scholar] [CrossRef]
- Kern, S.; Rösel, A.; Pedersen, L.T.; Ivanova, N.; Saldo, R.; Tonboe, R.T. The impact of melt ponds on summertime microwave brightness temperatures and sea-ice concentrations. Cryosphere 2016, 10, 2217–2239. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).