Abstract
This study focuses on the crustal deformation and interseismic fault coupling along the strike-slip Kunlun fault, northern Tibet, whose western segment ruptured in the 2001 Mw 7.8 Kokoxili earthquake. We first integrated published Global Positioning System (GPS) velocity solutions and calculated strain rate fields covering the Kunlun fault. Our results show abnormally high post-earthquake strain rate values across the ruptures; furthermore, these exceed those in pre-earthquake data. Together with two tracks of interferometric synthetic aperture radar (InSAR) observations (2003–2010) and position time-series data from two continuous GPS sites, we show that the postseismic deformation of the Kokoxili earthquake may continue up to 2014; and that the postseismic transients of the earthquake affect the 2001–2014 GPS velocity solutions. We then processed the GPS data observed in 2014–2017 and obtained a dense interseismic velocity field for the northern Tibet. Using a fault dislocation model in a Bayesian framework, we estimated the slip rates and fault coupling on the Kunlun fault in 1991–2001 and 2014–2017. Results show an increase of slip rates and eastward migration of high fault coupling on the Kunlun fault after 2001. We propose the temporal variations are a result of the eastward accelerating movement, as a whole, of the Bayanhar block, whose boundaries were decoupled by several large earthquakes since 1997. Moreover, our results show the accumulated elastic strains along the Alake Lake-Tuosuo Lake segments could be balanced by an Mw 7.4–7.7 earthquake.
1. Introduction
The collision and continued convergence of India and Eurasia since the Eocene epoch (~55 Ma) has resulted in the formation of the Tibetan Plateau, where strong and active crustal deformation extends thousands of kilometers northwards from the Himalayan orogenic belt to the Mongolian platform (e.g., [1,2]). Probing the crustal deformation of the Tibetan Plateau has long represented a significant research focus [3,4,5,6]. Over the last 30 years, modern geodetic observations (i.e., Global Positioning System (GPS) and interferometric synthetic aperture radar (InSAR)) provided abundant data and sufficient precision to investigate the large-scale surface deformation of the Tibetan Plateau [7,8,9,10,11,12,13,14,15]; and the interseismic, coseismic and postseismic faulting behaviors of large crustal faults in and around the Tibet, including the Main Himalaya Thrust [16,17], the Longmenshan fault system [9,18,19], the Xianshuihe-Xiaojiang fault system [20], and the Altyn Tagh-Haiyuan fault system [5,21,22]. However, relatively few studies have focused on the regions along the Kunlun fault (Figure 1), owing to insufficient coverage of GPS sites [7,9,11,12], which is the focus of this study.
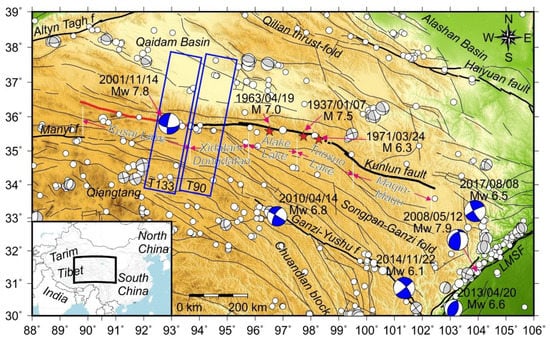
Figure 1.
Regional tectonic map of the northern Tibetan Plateau. Bold black lines represent the main faults. Thin black lines indicate active secondary faults. Blue focal mechanism solutions (Mw > 6, 1999–2018) and grey focal mechanism solutions (Mw ≤ 6, 1976–2018) are from the Global Centroid Moment Tensor (GCMT). White circles represent earthquakes with magnitudes of larger than 5.0 from 1960 to 2018 (United States Geological Survey (USGS)). Red stars show the epicenters of historical earthquakes with magnitudes larger than 6.0. Thin white lines mark the segmentation of the Kunkun fault. Blue rectangles show the coverage of InSAR data. LMSF denotes the Longmenshan fault. The inset map shows the regional position of study area.
The Kunlun fault is a left-lateral strike-slip fault in the northern Tibet that accommodates for both the northeastward shortening and the eastward extrusion of Tibet; it marks the northern boundary of the Bayanhar block (Figure 1) [4,23]. Several large earthquakes have occurred in mainland China and Tibet since 2000, including the 2001 Mw 7.8 Kokoxili earthquake, the 2008 Mw 7.9 Wenchuan earthquake, the 2010 Mw 6.8 Yushu earthquake, the 2013 Mw 6.9 Lushan earthquake, and the 2017 Mw 6.5 Jiuzhaigou earthquake, with all of them ruptured on the boundaries of the Bayanhar block [24], leaving the (eastern) Kunlun fault to be a potentially ‘seismic gap.’ Of those, the 2001 Mw 7.8 Kokoxili earthquake and 2008 Mw 7.9 Wenchuan earthquakes generated large-scale (several hundred kilometers), long-lasting (several years) postseismic crustal deformation (Figure 1) [10,25,26,27,28,29]. Consequently, a fundamental issue is, to study the interseismic crustal deformation behavior along the Kunlun fault, we require GPS sites velocities that are not perturbed by the postseismic transients of these two large earthquakes. Unfortunately, GPS stations were sparse across the Kunlun fault before the 2001 Mw 7.8 Kokoxili earthquake [7,8,30,31,32]; while additional GPS benchmarks were constructed across the fault after the earthquake, the impact from postseismic displacements was not investigated [9,11,12,33]. Furthermore, there is a need to investigate the temporal variations in crustal deformation following the 2001 large earthquake. For instance, the fault slip rate and fault coupling along the Kunlun fault, with implications for both seismic hazards and regional tectonic [17,19].
There also remains a need to investigate the seismic hazard along the Kunlun fault, whose westernmost segments ruptured (426 km) during the 2001 Mw 7.8 Kokoxili earthquake, but whose eastern segments remain unruptured (Figure 1) [34]. Studies of Coulomb stress triggering reported that both the 2001 Mw 7.8 Kokoxili earthquake and the 2008 Mw 7.9 Wenchuan earthquakes imposed a stress load along the Maqin-Maqu segment, eastern Kunlun fault, bringing the fault segment closer to rupture [35,36]. Interpreting the seismic potential along the Kunlun fault requires interseismic fault coupling estimates, which provide information for building future large earthquakes scenarios [19,37]. Recently, Li et al. [38] and Zhu et al. [39] reported heterogeneous fault coupling along the Kunlun fault. However, both of them used the GPS velocity solutions (data span 2001–2014) that might been perturbed by the postseismic transients of the 2001 Kokoxili earthquake, with potentially biased block rotation and fault coupling estimates. Furthermore, they used the block modeling approach, which is implemented under the frame of least squares [40], with limitations in characterizing the uncertainties of parameter estimates. Consequently, investigating the fault coupling along the Kunlun fault using a secular interseismic GPS velocity solution is necessary, and using a Bayesian approach could provide robust fault coupling estimates, with implications for seismic hazards.
In this study, we first collected published GPS velocity solutions for northern Tibet and calculated the strain rate across the Kunlun fault, together with two tracks of InSAR data and long-term GPS position time series data, to investigate the effects of postseismic transients from the 2001 Mw 7.8 Kokoxili earthquake on GPS site velocities. We then processed the GPS data measured in 2014–2017 and obtained a dense interseismic GPS velocity field for northern Tibet. Using a finite fault dislocation model, which is implemented in the frame of Bayesian, we estimated the slip rate and interseismic fault coupling (ISC) on the eastern Kunlun fault before (1991–2001) and after (2014–2017) the 2001 Mw 7.8 Kokoxili earthquake. Lastly, we explored the elastic strain accumulation and the corresponding seismic potential along the Kunlun fault.
2. Geodetic Data and Model
2.1. Geodetic Data
Several GPS velocity solutions using GPS data collected before the 2001 Mw 7.8 Kokoxili earthquake have been published [7,8,30,31,32]. Those GPS data were collected between 1991 and 2002, with stations across the Kunlun fault in place before November 2001. Despite subtle differences in processing strategies and reference frames between the different solutions [41], the GPS site velocities represent the secular interseismic crustal deformation of the Tibetan Plateau before the 2001 Kokoxili earthquake. To combine them, we solved for the Euler vector between two solutions by minimizing the velocity residuals within common sites [22]. We choose the Zhang et al. [32] solution as the master solution and translated the other velocity solutions into it. To compensate for the sparseness of GPS sites along the middle segments of the Kunlun fault (approximately 97–99°E), we also compiled the GPS velocity solution from Diao et al. [42]. The number of common sites and the Root Mean Square (RMS) of the velocity residuals are shown in Table 1. The final Eurasia-fixed GPS sites velocities are shown in Figure 2a.

Table 1.
The number of co-located sites and the Root Mean Square (RMS) of velocity residuals.
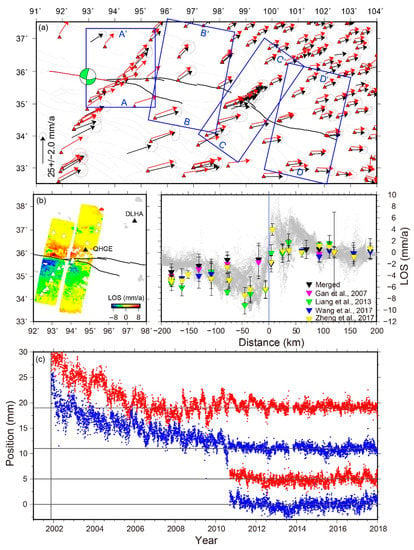
Figure 2.
(a) Global Positioning System (GPS) velocity solutions for northern Tibet under a Eurasia-fixed reference frame. Red triangles show the GPS site position. Black arrows represent the merged GPS site velocities (1991–2001). Red arrows represent the GPS site velocities in 2014–2017. Note that the site positions are shifted to avoid overlapping. The green focal mechanism of the 2001 Kokoxili earthquake comes from GCMT. Blue rectangles show the location of GPS velocity profiles in Figure 5. (b) InSAR velocity across the Kunlun fault; triangles show the location of GPS stations. The right panel show the comparisons between InSAR and GPS. (c) Position time-series of two continuous GPS sites, DLHA (2001–2018) and QHGE (2011–2018), with the northern components in red and eastern components are in blue. The solid line in black indicates the time of the 2001, Mw 7.8 Kokoxili earthquake.
After the 2001 Mw 7.8 Kokoxili earthquake, additional GPS benchmarks were constructed in mainland China and Tibet; the subsequently published GPS velocity solutions have denser GPS sites [9,11,12,33]. Between 2001 and 2017, several destructive earthquakes occurred in mainland China and Tibet, including the 2001 Mw 7.8 Kokoxili earthquake and the 2008 Mw 7.9 Wenchuan earthquake, both of which generated significant postseismic deformation [10,25,26,27,28,29]. To avoid the impact of postseismic transients from the 2008 Mw 7.9 Wenchuan earthquake, GPS data from near the rupture were excluded after May 2008. However, it is ambiguously explained how the impact of postseismic transients from the 2001 Mw 7.8 Kokoxili earthquake were considered in the data processing. Consequently, we did not include the GPS velocity solutions from 2001–2014 into our study. We give it further discussion in Section 4.1.
We also collected and processed the CMONOC (Crustal Movement Observation Network of China) GPS data measured between 2001 and 2017 in northern Tibet, in order to get the velocity solution of 2014–2017 and position time series data for two continues sites (DLHA and QHGE) near the 2001 Kokoxili rupture. A total of 345 sites, with 24 continuous, and 321 campaign-mode stations were included. Continuous GPS data were observed from November 2001 to January 2018. During that time span, we propose that the GPS velocity solution from 2014–2017 represents the secular interseismic crustal movements after the 2001 Kokoxili earthquake, and we show evidence below. Therefore, we selected the campaign-mode GPS data observed between January 2014 and January 2018. During this time period, GPS sites were measured in 2015, 2016 and 2017, with at least 72 hours of continuous observation in each campaign. With reference to the GPS data processing strategies of Li et al. [22], we used the GAMIT/GLOBK 10.6 software to process the raw GPS data [43]. We used IGS’s precise orbits and Earth orientation parameters, absolute antenna phase center calibrations, and the FES2004 ocean tide-loading model to derive loosely constrained daily solutions, which were then expressed in the International Terrestrial Reference Frame (ITRF2008) using a standard 7-parameter transformation. The time series for each station was carefully checked to exclude outliers. Finally, the site’s velocities, in 2014–2017, were transformed into a Eurasia-fixed reference frame (Figure 2a) [44].
Meanwhile, we obtained the position time series data of DLHA and QHGE sites. Using the time series polynomial fitting function [45], we removed the offsets caused by antenna movement, equipment replacement and coseismic deformation. The annual and semi-annual periodic fluctuations were also removed. The final results are shown in Figure 2c. Small fluctuations remain in the data of DLHA site (2002–2012). We attribute the fluctuations to data quality or other unmodeled signals. Despite this, our results in this study were not affected.
We compiled two tracks of InSAR velocities (ENVISAT/ASAR, data span: 2003 to 2010; Figure 2b) covering the GPS stations from Zhao et al. [29]. The raw synthetic aperture radar (SAR) data were processed using GAMMA software, and subsequent post-processing, including orbital and atmospheric error corrections, was applied. Both tracks of InSAR observations show significant postseismic deformation following the 2001 Mw 7.8 Kokoxili earthquake. We used the InSAR result to compare with GPS results in order to verify the existence of postseismic transients in the GPS velocity solutions. Since the GPS and InSAR data are under different reference frames, to do a comparison, we first projected the GPS horizontal velocities (vertical components were ignored due to their small magnitudes and large uncertainties) into the Light of Sight (LOS) direction. Then a constant value, which represented the differences in reference frames, was removed from the GPS-in-LOS. Here the constant value was estimated from the averaged LOS differences, between InSAR-LOS and GPS-in-LOS, of the four GPS sites that are more than 100 km north of the Kunlun fault (Figure 2b).
2.2. Strain Rate and Fault Dislocation Model
Strain rate is the spatial differentiation of velocity; it is independent of reference frames and thus can be used for general comparison between different GPS velocity solutions [46]. Following the method of Wang and Wright [47], we first constructed a continuous triangle mesh (dimension of ~1°) covering the Kunlun fault. Assuming a constant strain rate for each triangle, we used an L-curve method to interpolate the velocities at triangle vertices. Using the differential relationship between displacement and strain [46], the strain rate vectors were derived; these were then used to calculate the second invariant of the strain rate tensors.
Considering the facts that limited GPS stations were within the Bayanhar block before the 2001 Kokoxili earthquake, and there were potential postseismic transients in the GPS velocity solution after the event, we did not use the conventional elastic block model, as in Li et al. [38] and Zhu et al. [39]. We introduced a finite fault dislocation model to investigate the interseismic fault coupling along the Kunlun fault. Our basic hypothesis is that the GPS observed displacements along a strike-slip fault are a result of deep dislocation and shallow fault locking:
where Vd represents the surface displacements related to the deep slip motion (below the seismogenic depth) of the fault, Vs represents the slip on the shallow fault plane (above the seismogenic depth) and G is the Green’s function [48]. With reference to the back-slip routines [49], the interseismic fault coupling on the fault should be . Our inversion includes two steps:
First, we introduced the conventional 2-D arctangent model to estimate the deep fault slip rate [50]. For a displacement V(x) at a perpendicular distance x from the fault, . We used a Bayesian approach to derive the posterior probability density function (PDF) of the model parameters [51]; p(m|d) is defined as: , with d and p vectors containing the observations and model predictions, C−1 being the inverse of the covariance matrix of the data, and p(m), the prior PDF of the model parameters. In our inversion, we set the seismogenic depth to be 20 km, consistent with the result from coseismic inversion [52], owning to extremely sparse GPS sites across the fault, along the Kunlun fault.
Secondly, the deep slip rate was fixed and slips on the shallow fault plane were estimated in a Bayesian framework. We used the approach proposed by Amey et al. [53], which adopts fractal properties of fault slips as a form of regularization, instead of Laplacian smoothing. We will not introduce the detailed theories regarding the method; we propose that the readers refer to Amey et al. [53]. In our inversion, the Kunlun fault was modeled as vertical fault with pure strike-slip motion; such an assumption is reasonable for the strike-slipping faults, as the case for the Haiyuan fault [54]. We discretize the fault plane to be small patches with a 40 km long strike and a 5 km along dip. Note that in our model, we assume the GPS observed displacements are only related to the fault motion. To minimize the systematic motion caused by block rotations, and to avoid the impact from adjacent large faults, we only used the GPS sites within 100 km (5 times the depth of the fault locking depth) on either sides of the Kunlun fault.
We conducted a resolution test to investigate the ability of the GPS network to determine variations of ISC on the Kunlun fault. We first ran a forward model to predict the horizontal velocities at all GPS sites under a given ISC distribution (Figure 3a). We added a white noise characteristic of the estimated uncertainties to the predicted velocities, and then inverted these data to estimate the ISC distribution from the ‘noisy’ data. The results showed that, for our current model, the ISCs could be recovered along the strike and below a depth of 10 km, especially along the Alake Lake-Tuosuo Lake segment, where with relatively dense GPS stations (Figure 3b).
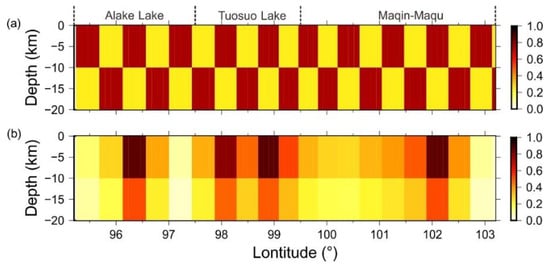
Figure 3.
Resolution test for locking on the Kunlun fault interface. (a) Assumed locking distribution for the forward model; (b) locking distribution recovered by the inversion of ‘noisy’ data generated by the forward model.
3. Results
3.1. Strain Rate
Using GPS velocities from before and after the 2001 Kokoxili Mw 7.8 earthquake, we obtained the second invariant of the strain rate tensors across the Kunlun fault (Figure 4a). The first-order characteristics of the strain rate field are the relatively small values and smooth gradients of strain rates across the Kunlun fault before the 2001 Kokoxili earthquake. The smooth gradients of strain rates across the ruptured segments indicates a locked fault before the 2001 event. Note that the strain rate result (Figure 4b) from the velocity solution of Gan et al. [9] is consistent with that from the pre-earthquake velocity solution. This is because they only used the GPS data across the Kunlun fault that was measured before the 2001 event [32].
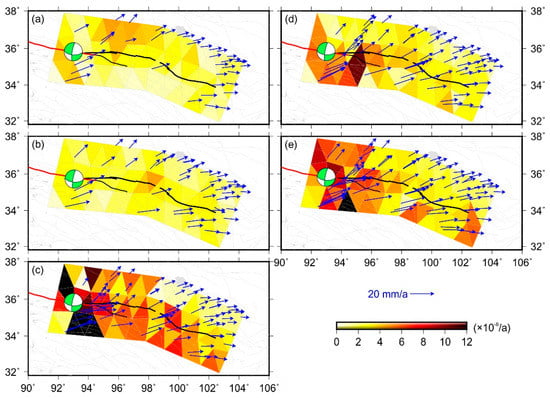
Figure 4.
Second invariant of the strain rate tensor fields across the Kunlun fault. Input GPS site velocities for each panel are shown. GPS site velocities from (a) the merged velocity before the 2001 Kokoxili earthquake, (b) Gan et al. [9], (c) Liang et al. [11], (d) Wang et al. [33], and (e) Zheng et al. [12]. Green focal mechanism of the 2001, Mw 7.8 Kokoxili earthquake comes from GCMT.
Another notable characteristic is the abnormally high strain rate tensor values across the ruptured Kunlun fault (Figure 4c–e). Those results were calculated from the GPS velocity solutions after the 2001 Kokoxili earthquake; the strain rate values were about 2–3 times of those derived from the pre-2001 GPS site velocities (Figure 4a). This comparison may indicate the effects of the postseismic transients of the 2001 Mw 7.8 Kokoxili earthquake on GPS site velocities. Note that although the velocity interpolation method may impact the strain rate results to some extent, we propose that the calculation results are robust, due to relatively dense GPS sites in the abnormally high-value strain rate tensor regions.
3.2. Slip Rate and Fault Coupling
We quantified the fault slip rate (below the seismogenic depth) of the Kunlun fault using a 2-D dislocation model; the results are shown in Figure 5 and Figure 6a. Before the 2001 Mw 7.8 Kokoxili earthquake, a geodetic fault slip rate of 7.2 ± 2.2 mm/a was achieved along the Xidatan-Dongdatan segment, overlapping the 8–14 mm/a estimates from previous studies [7,8,32]. To the east, an obvious increase of left-lateral slip rate (10.0 ± 1.4 mm/a) was estimated on the Alake Lake segment, and decreased further eastward to a relatively uniform slip rate of roughly 5 mm/a along the Tuosuo Lake segment (4.9 ± 1.2 mm/a) and the Maqin-Maqu segment (5.0 ± 1.4 mm/a). In 2014–2017, after the 2001 Mw 7.8 Kokoxili earthquake, a significant increase of slip rate (17.4 ± 1.2 mm/a) was recorded along the Xidatan-Dongdatan segment. Eastward along the other segments, while not obvious, slip rates show a 2 mm/a increase compared with that before the 2001 Kokoxili event, with a 10.7 ± 1.0 mm/a, 6.2 ± 1.0 mm/a, and 6.1 ± 1.0 mm/a increase along the Alake Lake segment, the Tuosuo Lake segment and the Maqin-Maqu segment, respectively. In general, despite some discrepancies, our slip rate results are consistent with that from geodetic [32,42] and geological [23,55,56,57,58] studies. We present more details in the discussion section.
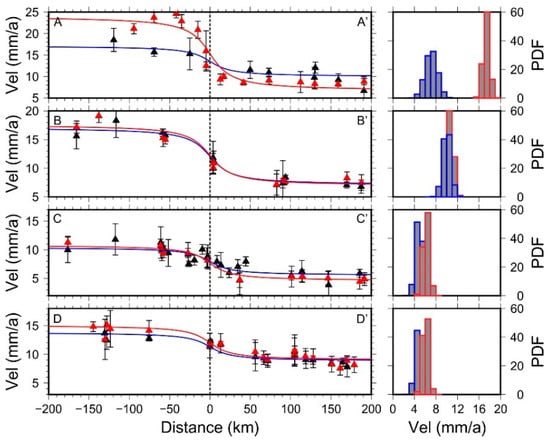
Figure 5.
Observed and calculated fault-parallel velocities across the Kunlun fault. Black and red diamonds with 1σ uncertainty error bars show the fault-parallel velocity component of the GPS velocities before (1991–2001) and after (2014–2017) the 2001 Kokoxili earthquake, respectively. Black and red solid lines represent best fitting curves. The right panels show posterior marginal probability density functions (PDFs) of slip rate estimates.
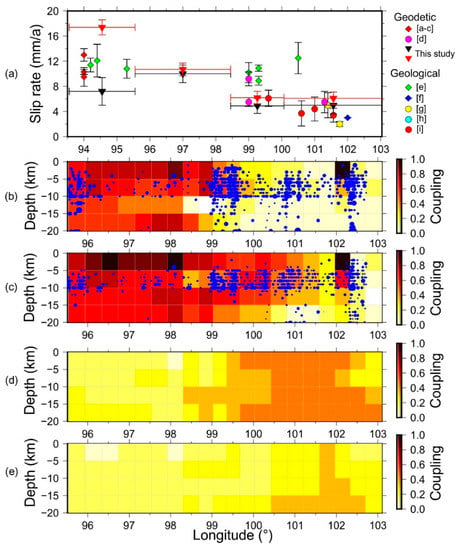
Figure 6.
Slip rates and fault coupling along the Kunlun fault. (a) The data are from [a] Wang et al. [30]; [b] Chen et al. [8]; [c] Zhang et al. [32]; [d] Diao et al. [42]; [e] Van Der Woerd et al. [23]; [f] Lin and Guo [57]; [g] Kirby et al. [55]; [h] Harkins and Kirby [56]; [i] Harkins et al. [58]. (b) The fault coupling along the Kunlun fault in 1991–2001. Blue dots represent the epicenters of microseismicity (1970–2001). (c) Fault coupling along the Kunlun fault in 2014–2017, with microseismicity in 2014–2017. (d,e) show the 1σ uncertainty of fault coupling estimates in 1991-2001 and 2014–2017 respectively.
Considering that there were only a limited number of GPS sites across the Xidatan-Dongdatan segment, and the potentially postseismic transients along this segment, we only focused on the eastern segments of the Kunlun fault. Our results show heterogeneous ISC distributions on the Kunlun fault. Before the 2001 Mw 7.8 Kokoxili earthquake, the Alake Lake segment shows strong coupling, with locking depths of approximate 20 km and ISCs larger than 0.6. The Tuosuo Lake segment also shows strong coupling to a depth of 10 km (Figure 6b). However, the Maqin-Maqu segment shows relatively weak fault coupling, implying scarcely elastic strain accumulation and thus low possibility of seismic rupture. From the resolution test result (Figure 3), we are confident that the above fault coupling features are robust. In 2014–2017, after the 2001 Mw 7.8 Kokoxili earthquake, a striking variation in the fault coupling was the strong coupling along the Maqin-Maqu segment, with a fault locking depth of 10–15 km (Figure 6c). We present more discussions below. The fault coupling uncertainties are shown in Figure 6c–d; an overall uncertainty value of 0.3 was obtained. The ISC distribution, together with the estimated slip rate, was integrated to quantitatively calculate the seismic moment accumulation rate on the fault plane, and thus assess the seismic hazard on the Kunlun fault [22,37], which we also present in the discussion section.
4. Discussion
4.1. Postseismic Transients of the 2001 Mw 7.8 Kokoxili Earthquake
Postseismic deformation of continental earthquakes (Mw > 8), especially lower crust viscoelastic relaxation-driven deformation, can last from several months to several decades, covering areas of several tens of kilometers, or even hundreds of kilometers [59]. For instance, postseismic transients were found to affect regions of 140 km across after the 1992 Mw 7.3 Landers and 1999 Mw 7.1 Hector Mine earthquakes in the Mojave Desert, Southern California [60]. Liu et al. [60] also found 2–3 mm/a excess right-lateral shear across earthquake ruptures in velocity solutions of the Southern California Earthquake Center’s Crustal Motion Map, Version 4; the Plate Boundary Observatory, the Scripps Orbit, and the Permanent Array Center’s GPS. If the postseismic transients are disregarded as interseismic deformation, then we would probably get biased understanding of crustal deformation, with implications for both seismic hazards and region tectonics. Consequently, there was a need to investigate how postseismic transients of the 2001 Mw 7.8 Kokoxili earthquake affected the CMONOC velocity solutions [11,12,33].
After the 2001, Mw 7.8 Kokoxili earthquake, more than a dozen GPS stations were installed across the eastern section of the surface rupture (94°E). Shen et al. [61] processed 6 months of GPS data after the earthquake and found both afterslip and viscoelastic relaxation in a weak lower crustal layer. Ren and Wang [62] used 1 year of GPS data from the same stations as Shen et al. [61], and obtained a 129 mm relative surface displacement across the eastern section of the surface rupture. They noted that 47% of the total surface deformation occurred in the two weeks immediately following the earthquake, implying rapidly decreasing deformation. Ryder et al. [25] processed InSAR data (from 2003 to 2007) covering almost the entire ruptured fault length to measure the surface deformation (Figure 1); they proposed that the most likely mechanism of postseismic stress relaxation is time-dependent distributed creep of viscoelastic material in the lower crust. Subsequently, Wen et al. [26] introduced InSAR data for longer spans (from 2003 to 2008) to investigate the surface deformation; their results showed an up to 8 cm of peak of trough deformation 15 km from the fault trace; the surface displacements could be modeled by an afterslip on a discrete fault plane, or relaxation of a Maxwell viscoelastic medium, or a combination of both. More recently, Zhao et al. [29] used 5 tracks of InSAR data (2003–2010) to investigate postseismic surface deformation across the Kunlun fault and obtained results similar to those of Wen et al. [26], despite of subtle differences. In summary, previous studies revealed both significant and long-lasting postseismic deformation that could introduce perturbations to GPS sites velocities across surface ruptures. Here, the key issue is whether the postseismic transients of the 2001 event exist in the GPS velocity solutions [11,12,33]. We discuss the issue from three aspects:
(1) The temporal variations of strain rate across the ruptured Kunlun fault. Our strain rate results show a value of 2.0 × 10−8/a across the Kunlun fault (94°E; Figure 4a,b) before 2001, implying a velocity gradient of 20 mm/a (triangle dimension of 100 km). However, after the 2001 Mw 7.8 Kokoxili earthquake, despite subtle differences between different velocity solutions (Figure 4c–e), strain rate values were as high as 6–10 × 10−8/a, implying a velocity gradient of 60–100 mm/a, and an excess velocity of 40–80 mm/a. Such an excess velocity is unlikely caused by non-tectonic movements; it more likely reflects the postseismic transients of the Kokoxili earthquake.
(2) We compare the InSAR data, which contain postseismic deformation, with the CMONOC GPS velocities. As shown in Figure 2b, GPS sites’ velocities that were obtained before the 2001 Kokoxili event show smooth gradients across the Kunlun fault, an indication of a locked fault. However, the site velocities that were obtained after 2001 show sharp gradients across the fault, which is in accordance with the postseismic deformation behavior for strike-slip faults [63].
(3) We showed the position time series of two continuous GPS sites that are located near the 2001 Kokoxili surface rupture (Figure 2c). It is striking that, despite of 350 km from the surface rupture, the DLHA site recorded significant a postseismic signal following the 2001 Kokoxili earthquake, and it continued up to 2014, with a duration of 13 years. The other GPS site, QHGE, is located 150 km from the surface rupture and started to operate at the end of 2010. The position time-series results also show clear postseismic decay between 2011 and 2014. In general, we learn from the GPS position time-series that the postseismic deformation of the 2001 Mw 7.8 Kokoxili earthquake continued for 13 years, with an area of at least 350 km from the surface rupture affected.
In summary, the above analyses suggest that postseismic transients affected the CMONOC velocity solutions [11,12,33] across the ruptured Kunlun fault. However, the amplitude and extent of the postseismic transients of the 2001 Kokoxili earthquake remain unsolved, due to lack of continuous geodetic observations near the surface ruptures after the event. Our present study emphasizes the need for better quantification of the temporal and spatial behaviors of postseismic transients using large-scale sequential InSAR observations.
4.2. Geodetic Slip Rate and Fault Coupling Variations along the Kunlun Fault
We showed the estimated fault slip rate in Figure 6a. For quantitative comparisons, we only selected the geodetic results from before the 2001 Mw 7.8 Kokoxili earthquake. Wang et al. [30] processed early GPS data (1991–2001) from mainland China and Tibet, and reported a slip rate of 12–14 mm/a across the Kunlun fault (94°E) by analyzing GPS velocity profiles. Subsequently, Chen et al. [8] used a 2-D screw dislocation model to fit the GPS velocities (1991–2001) across the Kunlun fault (94°E) by assuming a fault locking depth of 15 km and got a slip rate of 10.3 ± 0.4 mm/a. Zhang et al. [32] introduced more GPS data (1998–2002) and obtained similar results (8–11 mm/a) by analyzing GPS velocity profiles. The above slip rate results are slightly larger than those derived from our 2-D screw dislocation model (7.2 ± 2.2 mm/a) at the same location, but within the uncertainties. We propose that these minor discrepancies are due to the different number of GPS sites and the assumed fault locking depth.
Geological studies have reported Quaternary slip rates for the Kunlun fault. Van der Woerd et al. [64] measured two terrace risers’ offsets and ages on the Xidatan segment of the Kunlun fault (94.4°E), and obtained a long-term slip rate of 12.1 ± 2.6 mm/a. Subsequently, they measured the displacements of alluvial surfaces along the Kunlun fault and reported slip rates of 11.7 ± 1.5 mm/a (94°E), 10 mm/a (99°E), and 12.5 ± 2.5 mm/a (100°E) for three different segments; their results suggest uniform long-term slip along the Kunlun Fault [23]. However, Lin and Guo [57] proposed an average Holocene slip rate of only 3 mm/a on the Maqin-Maqu segment (102°E). Kirby et al. [55] and Harkins and Kirby [56] reported an eastward decrease in the long-term slip rate along the Kunlun fault, from 5.0 ± 2.0 mm/a (101.4°E) to 1.0 mm/a (103.1°E). In summary, our results are consistent with Van der Woerd et al. [23,64] in the western segments (94–98°E), but only half of those in the eastern segment (99–103°E). Besides, our estimated slip rates are in agreement with that from Kirby et al. [55] and Harkins and Kirby [56] along the Maqin-Maqu segment, but larger than the 3 mm/a slip rate proposed by Lin and Guo [57]. We attribute the above discrepancies between geological and geodetic to different spatial locations. Understanding the slip-rate discrepancies requires denser GPS observations across the Kunlun fault.
To our knowledge, there have two published studies on the fault coupling along the Kunlun fault. However, both Li et al. [38] and Zhu et al. [39] used the GPS velocity solutions in 2001–2014. As we present in the above discussion, postseismic deformation of the 2001 Mw 7.8 Kokoxili earthquake continued up to 2014 and impacted regions at least 350 km from the surface rupture. Consequently, we do not compare our fault coupling results with these from Li et al. [38] and Zhu et al. [39]. We show the background seismicity along the Kunlun fault in Figure 6b,c. Regional earthquakes were selected from within 15 km width-wise on either side of the fault. Despite the uncertainty of location, especially for their depths, most of these minor earthquakes appear to occur around the transition areas between locked and slipping zones. The correspondence of seismicity and the edge of the locked zone has also been observed for the main Himalayan thrust [65].
One intriguing issue is the temporal variation of the slip rate and fault coupling on the Kunlun fault (Figure 6). We attribute the variations to the eastward accelerating movements, as a whole, of the Bayanhar block. There have been several large (Mw > 7) earthquakes which have occurred in mainland China and Tibet since 1995, with all of them having occurred along the boundaries of the Bayanhar block, as shown in the Figure 7a. At least part of the western boundary of the Bayanhar block ruptured in the 2008 Mw 7.1 Yutian earthquake, and the 2014 Mw 6.9 Yutian earthquake. Along the southern boundary, there occurred the 1997 Mw 7.5 Manyi earthquake (surface rupture length of 130 km), the 2010 Mw 6.9 Yushu earthquake (surface rupture length of 61 km) and the 2014 Mw 6.1 Kangding earthquake. Along the eastern boundary, the 2008 Mw 7.9 Wenchuan earthquake, the 2013 Mw 6.6 Lushan earthquake and the 2017 Mw 6.5 Jiuzhaigou earthquake resulted in almost full decoupling of the Longmenshan fault [19]. The northern boundary of the Bayanhar block had ruptured to a length of 426 km by the 2001 Mw 7.8 Kokoxili earthquake. In summary, the decoupling of the block boundaries leads to an eastward accelerating movement of the Bayanhar block, as evidenced by the GPS velocity profile, especially the western area (93°E) and the eastern area (101–104°E; Figure 7b). Such accelerating movement not only results in the increase of slip rates along the Kunlun fault, but also the increase of shear stress on the fault plane, which in turn leads to the eastward migration of strong fault coupling along the fault.
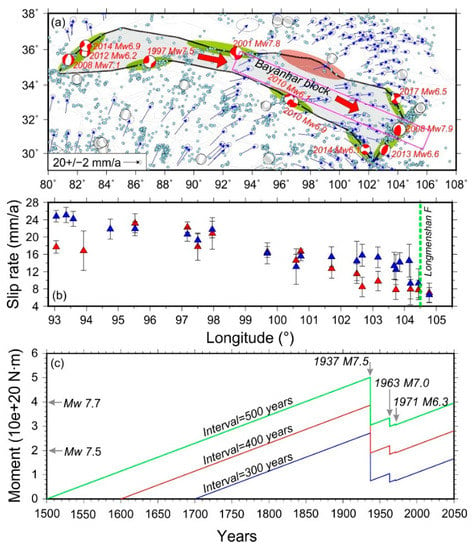
Figure 7.
(a) The Bayanhar block and earthquake distributions. Bold black lines show the block boundaries. Focal mechanisms (Mw > 6, 1995–2017) are from GCMT. Light blue circles represent earthquakes with magnitudes smaller than 6 in 1995–2017 (USGS). Blue arrows show the GPS velocities that are come Zhang et al. [32]. Ellipses in green show the approximately fault ruptures of large earthquakes, and the dark red ellipse represents the fault segments with high seismic hazard that proposed in this study. Magenta rectangle shows the location of GPS velocity profile in Figure 7b. Red arrows indicate the movement of the Bayanhar block. (b) Total magnitudes of GPS velocities. Diamonds with 1σ uncertainties in red and blue are from Zhang et al. [32], and our obtained velocity solution in 2014–2017, respectively, representing the GPS site velocities before and after the 2001 Mw 7.8 Kokoxili earthquake. (c) Cumulative moment deficit corrected from large earthquakes moment along the Alake Lake-Tuosuo Lake segments.4.3. Implications for Seismic Potential along the Kunlun Fault.
Previous studies have shown that the interaction between earthquakes is realized through earthquake triggering by the changes in the Coulomb failure stress (ΔCFS); that is, positive ΔCFS brings a fault closer to failure (and thus earthquake occurrence), while negative ΔCFS retards subsequent events [66]. Under a framework of earthquake triggering, Xiong et al. [36] studied the evolution of the Coulomb stress field along the Kunlun fault by analyzing a sequence of five strong earthquakes (Mw ≥ 7) since 1937; they reported high levels of stress accumulated on the Xidatan-Dongdatan segment and on the Maqin-Maqu segment. As a result, these areas have high seismic potential. Moreover, the coseismic rupture of the 2008 Mw 7.9 Wenchuan earthquake also increased the Coulomb stress on the Maqin-Maqu segment, implying an increased earthquake probability in the region [35].
Our dislocation model provides an independent reference to assess the seismic hazard along the Kunlun fault. We first focus on the Maqin-Maqu segment, where weak fault coupling was obtained before 2001, thus implying little elastic strain accumulation along this segment and relatively low possibilities of seismic rupture. Moreover, the cluster of microseismicity along this segment implies the elastic strain might be released aseismically.
Another focus is the Alake Lake–Tuosuo Lake segments, where it is assumed to be highly coupled across the geodetic observation span. Previous geological studies reported a long-term slip rate of 10 mm/a along this segment [64,67], which is in agreement with the present-day geodetic estimates, implying time invariant slip behaviors. We suppose that the interseismic strain is time invariant and purely elastic along this segment, and considering the earthquake recurrence time of 300–500 years [64,67], we obtained the cumulative moment deficit corrected by the large seismic moments release (Figure 7c). Here we assumed a constant shear modulus of μ = 30 GPa and obtained a seismic moment accumulation rate of 1.15 × 1018 N∙m/a along the segments. At the estimated moment deficit rate, we could reach the equivalent of earthquake with moment magnitude at 7.4–7.7 by the year 2050. Our calculation highlights the relatively high seismic potential along the Alake Lake-Tuosuo Lake segments.
5. Conclusions
We investigated the crustal deformation and fault coupling along the Kunlun fault before and after the 2001 Kokoxili earthquake using geodetic data. First, we compiled the published GPS velocity solutions for northern Tibet and used them to calculate strain rate fields, and to investigate how postseismic transients of the 2001 Mw 7.8 Kokoxili earthquake affected GPS site velocities. Our results showed abnormally high strain rate values across the coseismic ruptures after the earthquake; these strain rate values are about 2–3 time those derived from pre-earthquake GPS velocities. Together with two tracks of InSAR data and the position time-series data of two continuous GPS sites, we show that the postseismic deformation of the 2001 Mw 7.8 Kokoxili earthquake lasted about 13 years, and we propose that the postseismic transients of the 2001 Mw 7.8 Kokoxili earthquake affected the 2001–2014 CMONOC velocity solutions. Secondly, we processed the GPS data measured in 2014–2017 and obtained a dense interseismic GPS velocity field for northern Tibet. Using a finite fault dislocation model, we inverted the slip rate and ISC on eastern segments of the Kunlun fault before and after the 2001 Kokoxili event. Our results show an increase of slip rates and eastward migration of strong fault coupling along the Kunlun fault after the Kokoxili earthquake. We attribute the temporal variations to the eastward accelerating movements, as a whole, of the Bayanhar block, due to the decoupling of block boundaries by large earthquakes. Thirdly, our results highlighted a seismic potential of Mw 7.4–7.7 along the Alake Lake-Tuosuo Lake segments, and a low seismic hazard along the Maqin-Maqu segment.
Author Contributions
Y.L. processed the GPS data and conducted the fault model inversions. X.S. and C.Q. participated in interpreting the results. All authors contributed to editing the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number 41631073, 41872229).
Acknowledgments
We are grateful to all the colleagues who constructed the CMONOC sites and collected measurements. We show our appreciation to the two anonymous reviewers for their constructive comments, which improved the quality of this manuscript. Parts of our inversions were implemented by the slipBERI code (https://github.com/ruthamey/slipBERI). All figures were generated using the Generic Mapping Tools (GMT) software (https://gmt.soest.hawaii.edu).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Molnar, P.; Tapponnier, P. Cenozoic tectonics of Asia: Effects of a continental collision. Science 1975, 189, 419–426. [Google Scholar] [CrossRef] [PubMed]
- Rowley, D.B. Age of initiation of collision between India and Asia: A review of stratigraphic data. Earth Planet. Sci. Lett. 1996, 145, 1–13. [Google Scholar] [CrossRef]
- Avouac, J.P.; Tapponnier, P. Kinematic model of active deformation in central Asia. Geophys. Res. Lett. 1993, 20, 895–898. [Google Scholar] [CrossRef]
- Tapponnier, P.; Zhiqin, X.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Jingsui, Y. Oblique stepwise rise and growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
- Wright, T.J.; Parsons, B.; England, P.C.; Fielding, E.J. InSAR observations of low slip rates on the major faults of western Tibet. Science 2004, 305, 236–239. [Google Scholar] [CrossRef] [PubMed]
- Thatcher, W. Microplate model for the present-day deformation of Tibet. J. Geophys. Res. 2007, 112, B01401. [Google Scholar] [CrossRef]
- Shen, Z.K.; Wang, M.; Li, Y.; Jackson, D.D.; Yin, A.; Dong, D.; Fang, P. Crustal deformation along the Altyn Tagh fault system, western China, from GPS. J. Geophys. Res. 2001, 106, 30607–30621. [Google Scholar] [CrossRef]
- Chen, Q.; Freymueller, J.T.; Wang, Q.; Yang, Z.; Xu, C.; Liu, J. A deforming block model for the present-day tectonics of Tibet. J. Geophys. Res. 2004, 109, B01403. [Google Scholar] [CrossRef]
- Gan, W.; Zhang, P.; Shen, Z.K.; Niu, Z.; Wang, M.; Wan, Y.; Zhou, D.; Cheng, J. Present-day crustal motion within the Tibetan Plateau inferred from GPS measurements. J. Geophys. Res. 2007, 112, B08416. [Google Scholar] [CrossRef]
- Garthwaite, M.C.; Wang, H.; Wright, T.J. Broadscale interseismic deformation and fault slip rates in the central Tibetan Plateau observed using InSAR. J. Geophys. Res. 2013, 118, 5071–5083. [Google Scholar] [CrossRef]
- Liang, S.; Gan, W.; Shen, C.; Xiao, G.; Liu, J.; Chen, W.; Ding, X.; Zhou, D. Three-dimensional velocity field of present-day crustal motion of the Tibetan Plateau derived from GPS measurements. J. Geophys. Res. 2013, 118, 5722–5732. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, H.; Wright, T.J.; Lou, Y.; Zhang, R.; Zhang, W.; Shi, C.; Huang, J.; Wei, N. Crustal deformation in the India-Eurasia collision zone from 25 years of GPS measurements. J. Geophys. Res. 2017, 122, 9290–9312. [Google Scholar] [CrossRef]
- Reigber, C.; Michel, G.W.; Galas, R.; Angermann, D.; Klotz, J.; Chen, J.Y.; Papschec, A.; Arslanov, R.; Tzurkov, V.E.; Ishanov, M.C. New space geodetic constraints on the distribution of deformation in Central Asia. Earth Planet. Sci. Lett. 2001, 191, 157–165. [Google Scholar] [CrossRef]
- Farolfi, G.; Del Ventisette, C. Monitoring the Earth’s ground surface movements using satellite observations: Geodinamics of the Italian peninsula determined by using GNSS networks. In Proceedings of the 2016 IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016; pp. 479–483. [Google Scholar]
- Feng, W.; Samsonov, S.; Almeida, R.; Yassaghi, A.; Li, J.; Qiu, Q.; Li, P.; Zheng, W. Geodetic Constraints of the 2017 Mw 7.3 Sarpol Zahab, Iran Earthquake, and Its Implications on the Structure and Mechanics of the Northwest Zagros Thrust-Fold Belt. Geophys. Res. Lett. 2018, 45, 6853–6861. [Google Scholar] [CrossRef]
- Bilham, R.; Larson, K.; Freymueller, J. GPS measurements of present-day convergence across the Nepal Himalaya. Nature 1997, 386, 61–64. [Google Scholar] [CrossRef]
- Elliott, J.R.; Jolivet, R.; González, P.J.; Avouac, J.P.; Hollingsworth, J.; Searle, M.P.; Stevens, V.L. Himalayan megathrust geometry and relation to topography revealed by the Gorkha earthquake. Nat. Geosci. 2016, 9, 174–180. [Google Scholar] [CrossRef]
- Shen, Z.K.; Sun, J.; Zhang, P.; Wan, Y.; Wang, M.; Bürgmann, R.; Zeng, Y.; Gan, W.; Liao, H.; Wang, Q. Slip maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake. Nat. Geosci. 2009, 2, 718–724. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, G.; Shan, X.; Liu, Y.; Wu, Y.; Liang, H.; Qu, C.; Song, X. GPS-Derived Fault Coupling of the Longmenshan Fault Associated with the 2008 Mw 7.9 Wenchuan Earthquake and Its Tectonic Implications. Remote Sens. 2018, 10, 753. [Google Scholar] [CrossRef]
- Shen, Z.K.; Lü, J.; Wang, M.; Bürgmann, R. Contemporary crustal deformation around the southeast borderland of the Tibetan Plateau. J. Geophys. Res. 2005, 110, B11409. [Google Scholar] [CrossRef]
- Daout, S.; Doin, M.P.; Peltzer, G.; Lasserre, C.; Socquet, A.; Volat, M.; Sudhaus, H. Strain Partitioning and Present-Day Fault Kinematics in NW Tibet from Envisat SAR Interferometry. J. Geophys. Res. 2018, 123, 2462–2483. [Google Scholar] [CrossRef]
- Li, Y.; Shan, X.; Qu, C.; Liu, Y.; Han, N. Crustal Deformation of the Altyn Tagh Fault Based on GPS. J. Geophys. Res. 2018, 123, 10309–10322. [Google Scholar] [CrossRef]
- Van Der Woerd, J.; Tapponnier, P.; Ryerson, F.J.; Meriaux, A.S.; Meyer, B.; Gaudemer, Y.; Finkel, R.; Caffee, M.; Zhao, G.; Xu, Z. Uniform postglacial slip-rate along the central 600 km of the Kunlun Fault (Tibet), from 26Al, 10Be, and 14C dating of riser offsets, and climatic origin of the regional morphology. Geophys. J. Int. 2002, 148, 356–388. [Google Scholar] [CrossRef]
- Deng, Q.; Cheng, S.; Ma, J.; Du, P. Seismic activities and earthquake potential in the Tibetan Plateau. Chin. J. Geophys. 2014, 57, 2025–2042. [Google Scholar]
- Ryder, I.; Bürgmann, R.; Pollitz, F. Lower crustal relaxation beneath the Tibetan Plateau and Qaidam Basin following the 2001 Kokoxili earthquake. Geophys. J. Int. 2011, 187, 613–630. [Google Scholar] [CrossRef]
- Wen, Y.; Li, Z.; Xu, C.; Ryder, I.; Bürgmann, R. Postseismic motion after the 2001 Mw 7.8 Kokoxili earthquake in Tibet observed by InSAR time series. J. Geophys. Res. 2012, 117, B08405. [Google Scholar] [CrossRef]
- Huang, M.H.; Bürgmann, R.; Freed, A.M. Probing the lithospheric rheology across the eastern margin of the Tibetan Plateau. Earth Planet. Sci. Lett. 2014, 396, 88–96. [Google Scholar] [CrossRef]
- Diao, F.; Wang, R.; Wang, Y.; Xiong, X.; Walter, T.R. Fault behavior and lower crustal rheology inferred from the first seven years of postseismic GPS data after the 2008 Wenchuan earthquake. Earth Planet. Sci. Lett. 2018, 495, 202–212. [Google Scholar] [CrossRef]
- Zhao, D.; Qu, C.; Shan, X.; Bürgmann, R.; Gong, W.; Zhang, G. Spatiotemporal Evolution of Postseismic Deformation Following the 2001 Mw7. 8 Kokoxili, China, Earthquake from 7 Years of Insar Observations. Remote Sens. 2018, 10, 1988. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, P.; Freymueller, J.; Bilham, R.; Larson, K.; Lai, X.; You, X.; Niu, Z.; Wu, J.; Li, Y.; et al. Present-day crustal deformation in China constrained by global positioning system measurements. Science 2001, 294, 574–577. [Google Scholar] [CrossRef]
- Chen, Z.H.; Burchfiel, B.C.; Liu, Y.; King, R.W.; Royden, L.H.; Tang, W.; Wang, E.; Zhao, J.; Zhang, X. Global Positioning System measurements from eastern Tibet and their implications for India/Eurasia intercontinental deformation. J. Geophys. Res. 2000, 105, 16215–16227. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Shen, Z.K.; Wang, M.; Gan, W.; Bürgmann, R.; Molnar, P.; Wang, Q.; Niu, Z.; Sun, J.; Wu, J.; et al. Continuous deformation of the Tibetan Plateau from global positioning system data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
- Wang, W.; Qiao, X.; Yang, S.; Wang, D. Present-day velocity field and block kinematics of Tibetan Plateau from GPS measurements. Geophys. J. Int. 2017, 208, 1088–1102. [Google Scholar] [CrossRef]
- Xu, X.; Yu, G.; Klinger, Y.; Tapponnier, P.; Van Der Woerd, J. Reevaluation of surface rupture parameters and faulting segmentation of the 2001 Kunlunshan earthquake (Mw 7.8), northern Tibetan Plateau, China. J. Geophys. Res. 2006, 111, B05316. [Google Scholar]
- Toda, S.; Lin, J.; Meghraoui, M.; Stein, R.S. 12 May 2008 M = 7.9 Wenchuan, China, earthquake calculated to increase failure stress and seismicity rate on three major fault systems. Geophys. Res. Lett. 2008, 35, L17305. [Google Scholar] [CrossRef]
- Xiong, X.; Shan, B.; Zheng, Y.; Wang, R. Stress transfer and its implication for earthquake hazard on the Kunlun Fault, Tibet. Tectonophysics 2010, 482, 216–225. [Google Scholar] [CrossRef]
- Bürgmann, R.; Schmidt, D.; Nadeau, R.M.; d’Alessio, M.; Fielding, E.; Manaker, D.; McEvilly, T.V.; Murray, M.H. Earthquake potential along the northern Hayward fault, California. Science 2000, 289, 1178–1182. [Google Scholar] [CrossRef]
- Li, Q.; Tan, K.; Zhao, B.; Zhang, C.; Lu, X.; Wang, D.; Yu, J. Slip rate change of East Kunlun fault and its stress effect on 2017 Jiuzhaigou earthquake. Chin. J. Geophys. 2019, 62, 912–922. [Google Scholar]
- Zhu, L.; Ji, L.; Jiang, F. Variations in Locking Along the East Kunlun Fault, Tibetan Plateau, China, Using GPS and Leveling Data. Pure Appl. Geophys. 2019, 1–17. [Google Scholar] [CrossRef]
- McCaffrey, R.; Qamar, A.I.; King, R.W.; Wells, R.; Khazaradze, G.; Williams, C.A.; Stevens, C.A.; Vollick, J.J.; Zwick, P.C. Fault locking, block rotation and crustal deformation in the Pacific Northwest. Geophys. J. Int. 2007, 169, 1315–1340. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P.; Rothacher, M. A new data processing strategy for huge GNSS global networks. J. Geodesy 2016, 80, 199–203. [Google Scholar] [CrossRef]
- Diao, F.; Xiong, X.; Wang, R.; Walter, T.R.; Wang, Y.; Wang, K. Slip rate variation along the Kunlun Fault (Tibet): Results from new GPS observations and a viscoelastic earthquake-cycle deformation model. Geophys. Res. Lett. 2019, 46, 2524–2533. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McCluskey, S.C. Introduction to GAMIT/GLOBK, Release 10.6; Massachusetts Institue of Technology: Cambridge, MA, USA, 2016. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geodesy 2011, 85, 457–473. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2004. [Google Scholar]
- Savage, J.C.; Gan, W.; Svarc, J.L. Strain accumulation and rotation in the Eastern California Shear Zone. J. Geophys. Res. 2001, 106, 21995–22007. [Google Scholar] [CrossRef]
- Wang, H.; Wright, T.J. Satellite geodetic imaging reveals internal deformation of western Tibet. Geophys. Res. Lett. 2012, 39, L07303. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Savage, J.C. A dislocation model of strain accumulation and release at a subduction zone. J. Geophys. Res. 1983, 88, 4984–4996. [Google Scholar] [CrossRef]
- Savage, J.C.; Burford, R.O. Geodetic determination of relative plate motion in central California. J. Geophys. Res. 1973, 78, 832–845. [Google Scholar] [CrossRef]
- Minson, S.E.; Simons, M.; Beck, J.L. Bayesian inversion for finite fault earthquake source models I—Theory and algorithm. Geophys. J. Int. 2013, 194, 1701–1726. [Google Scholar] [CrossRef]
- Lasserre, C.; Peltzer, G.; Crampé, F.; Klinger, Y.; Van Der Woerd, J.; Tapponnier, P. Coseismic deformation of the 2001 Mw = 7.8 Kokoxili earthquake in Tibet, measured by synthetic aperture radar interferometry. J. Geophys. Res. 2005, 110, B12408. [Google Scholar] [CrossRef]
- Amey, R.M.J.; Hooper, A.; Walters, R.J. A Bayesian Method for Incorporating Self-Similarity into Earthquake Slip Inversions. J. Geophys. Res. 2018, 123, 6052–6071. [Google Scholar] [CrossRef]
- Jolivet, R.; Lasserre, C.; Doin, M.P.; Peltzer, G.; Avouac, J.P.; Sun, J.; Dailu, R. Spatio-temporal evolution of aseismic slip along the Haiyuan fault, China: Implications for fault frictional properties. Earth Planet. Sci. Lett. 2013, 377, 23–33. [Google Scholar] [CrossRef]
- Kirby, E.; Harkins, N.; Wang, E.; Shi, X.; Fan, C.; Burbank, D. Slip rate gradients along the eastern Kunlun fault. Tectonics 2007, 26, TC2010. [Google Scholar] [CrossRef]
- Harkins, N.; Kirby, E. Fluvial terrace riser degradation and determination of slip rates on strike-slip faults: An example from the Kunlun fault, China. Geophys. Res. Lett. 2008, 35, L05406. [Google Scholar] [CrossRef]
- Lin, A.; Guo, J. Nonuniform slip rate and millennial recurrence interval of large earthquakes along the eastern segment of the Kunlun fault, northern Tibet. Bull. Seismol. Soc. Am. 2008, 98, 2866–2878. [Google Scholar] [CrossRef]
- Harkins, N.; Kirby, E.; Shi, X.; Wang, E.; Burbank, D.; Chun, F. Millennial slip rates along the eastern Kunlun fault: Implications for the dynamics of intracontinental deformation in Asia. Lithosphere 2010, 2, 247–266. [Google Scholar] [CrossRef]
- Thatcher, W. Nonlinear strain buildup and the earthquake cycle on the San Andreas Fault. J. Geophys. Res. 1983, 88, 5893–5902. [Google Scholar] [CrossRef]
- Liu, S.; Shen, Z.K.; Bürgmann, R. Recovery of secular deformation field of Mojave Shear Zone in Southern California from historical terrestrial and GPS measurements. J. Geophys. Res. 2015, 120, 3965–3990. [Google Scholar] [CrossRef]
- Shen, Z.K.; Zeng, Y.; Wang, M.; Wang, Q.; Wang, Q.L.; Wan, Y.; Gan, W.; Zhang, Z. Postseismic deformation modeling of the 2001 Kokoxili earthquake, western China. In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003. [Google Scholar]
- Ren, J.; Wang, M. GPS measured crustal deformation of the Ms 8.1 Kunlun earthquake on November 14th, 2001 in Qinghai-Xizang plateau. Quat. Sci. 2005, 25, 34–44. [Google Scholar]
- Meade, B.J.; Hager, B.H. Block models of crustal motion in southern California constrained by GPS measurements. J. Geophys. Res. 2005, 110, B03403. [Google Scholar] [CrossRef]
- Van Der Woerd, J.; Ryerson, F.J.; Tapponnier, P.; Gaudemer, Y.; Finkel, R.; Mériaux, A.S.; Caffee, M.; Zhao, G.; He, Q. Holocene left-slip rate determined by cosmogenic surface dating on the Xidatan segment of the Kunlun fault (Qinghai, China). Geology 1998, 26, 695–698. [Google Scholar] [CrossRef]
- Stevens, V.L.; Avouac, J.P. Interseismic coupling on the main Himalayan thrust. Geophys. Res. Lett. 2015, 42, 5828–5837. [Google Scholar] [CrossRef]
- Stein, R.S.; Barka, A.A.; Dieterich, J.H. Progressive failure on the North Anatolian fault since 1939 by earthquake stress triggering. Geophys. J. Int. 1997, 128, 594–604. [Google Scholar] [CrossRef]
- Li, H.; Van der Woerd, J.; Tapponnier, P.; Klinger, Y.; Xuexiang, Q.; Jingsui, Y.; Yintang, Z. Slip rate on the Kunlun fault at Hongshui Gou, and recurrence time of great events comparable to the 14/11/2001, Mw~7.9 Kokoxili earthquake. Earth Planet. Sci. Lett. 2005, 237, 285–299. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).