1. Introduction
Soil moisture is a key variable in weather forecast and climate research because it plays a role in both the energy and water cycles [
1,
2,
3,
4]. It controls how much water returns to the atmosphere via land-atmosphere interactions and it also carries the energy in terms of the latent heat flux when evaporated to reshape the atmospheric circulation. Therefore, availability of accurate and near real-time global soil moisture is critical for the improvement of weather forecast and climate projection skills [
5,
6,
7].
Since the 1970s, satellite remote sensing has been used to estimate global soil moisture with microwave frequencies and more recently focus has been on L-band (1400–1427 MHz), which is sensitive to the dielectric constant as well as is a protected radio astronomy band with minimum radio frequency interference (RFI). Both the Soil Moisture and Ocean Salinity (SMOS) [
8] and the Soil Moisture Active Passive (SMAP) [
9] missions operate at L-band for providing the brightness temperature and soil moisture data products. With the efforts from SMOS and SMAP missions, abundant data have been produced and applied in various studies [
10,
11,
12,
13,
14].
However L-band radiometry for monitoring soil moisture is strongly affected by the soil temperature and soil moisture [
15,
16], which usually leads to questions on where the satellite is exactly sensing [
17,
18,
19]. Corresponding to the satellite missions, plenty of in situ soil moisture monitoring networks have been established to calibrate and validate (Cal/Val) L-band brightness temperature (
) or soil moisture data [
20]. Usually, the soil moisture and soil temperature sensors are installed at certain depths (e.g., 2.5 cm, 5 cm, 10 cm or deeper) based on experiences or to match numerical simulations of soil moisture and soil temperature. However, such in situ defined depths do not precisely match the satellite sensing depths, at which the
Tb or soil moisture data are retrieved. Hence errors may arise because the Cal/Val data are not correspondingly sampled, in other words, are not comparable to the satellite observations. Additionally, different satellite soil moisture products may have different sensing depths, as different frequencies are used. As such, the various satellite soil moisture products may lack consistency and generate ambiguity in Cal/Val and their applications [
21].
In regard to the dielectric constant and the soil effective temperature, the SMOS/SMAP sensors may measure soil moisture deeper over the dry soil than over the wet soil. Even for the same region, the sensing depths may vary in a certain range, depending on the soil moisture and soil temperature profiles [
19,
22]. For that reason, different satellite soil moisture products can be only made inter-comparable, after defining exactly the sensing depths. Furthermore, data assimilation approach has been deemed as the most feasible method for estimating the soil moisture profile [
22,
23], by extrapolating the remotely sensed surface information to lower depths in the soil via a coupled heat and moisture flow model. It is, therefore, critical to understand which depth is sensed by a satellite sensor for a sound retrieval and use of soil moisture and soil temperature profile information. The exact sensing depth strongly affects the accuracy of the soil moisture and soil temperature profile retrieval, as the soil moisture and soil temperature near the land surface has strong gradients and can be varying dramatically. One way to infer soil moisture sensing depth is by correlating brightness temperature and in-site soil moisture time-series so that the soil moisture layer that corresponds best with brightness temperature is considered to be the sensing layer [
24,
25]. To get soil moisture at different depth, this method always requires precise and vertically dense soil profile measurement or simulation. Another way is to use models to compute the sensing depth according to its definition [
26,
27] or an empirical model [
26,
28]. However, these methods need either vertically dense profile information or relay on prior knowledge, which is hard to acquire in practice. Besides soil, it should be noted that vegetation also has an impact on the penetration depth. The attenuation by vegetation is mainly due to the vegetation water content. Usually, the penetration depth only focuses on soil because comparatively, the influence of atmospheric attenuation at L-band is almost negligible.
As the penetration depth (henceforth we use penetration depth synonymously with sensing depth and emission depth) is defined by energy attenuation, it is possible to infer it from
Teff. In general, all current two-layer
schemes use a weighting function for the soil temperature between upper layer and deeper layer. Such weighting function can be a constant [
29], a fitting function [
30,
31], or an exponential function [
15,
16]. The weighting function is supposed to reflect the impact of soil moisture on the soil effective temperature. However, there is no variable of depth contained in Choudhury’s [
29], Wigneron’s [
30] or Holmes’ [
31]
schemes. As indicated by the integral scheme, the weighting function would be more representative if it considers the influence of both soil moisture and soil temperature. However, it is difficult to quantify its effect on soil effective temperature, because soil temperature also affects soil moisture (e.g., as in dielectric constant models). In other words,
is a weighted mean of the soil temperature along the vertical profile. Therefore, it must be
(if
, e.g., non-uniform profile which is always the case for a land surface subject to radiative heating and cooling). Considering the diurnal variation and a semi unbounded soil column,
Tmax and
usually appear at the surface skin or the deep layer where the soil temperature is almost constant. When the above condition is satisfied the sample layer covers the variation of
. This also means as the soil temperature profile is continuous, there must be a layer where its soil temperature equals to
.
In order to investigate the relationship between the penetration depth and
, in terms of
calculation, we first review the hypotheses of the coherent/incoherent microwave radiative transfer models and the definition of satellite sensing depth (
Section 2). We then analytically quantify the relationship between the penetration depth and
(
Section 3). Next, we use the field soil moisture and soil temperature observation at Maqu Network to verify the developed approach and demonstrate its application to SMAP (
Section 4). Finally, we discuss the uncertainties of the developed method (
Section 5) and conclude with some final thoughts for future work (
Section 6).
2. Theoretical Background
In this section, we first review the default assumption in zeroth-order incoherent model in which there is only one emissivity for all layers and then reformulate the Lv’s scheme in terms of the optical depth and clarify the definition of penetration depth.
2.1. Microwave Radiative Transfer Model
The SMOS and SMAP soil moisture retrieval algorithms are based on the following equation
where
is the brightness temperature detected by the radiometer,
is the unique emissivity in the zeroth-order incoherent microwave radiative transfer model (e.g., based on Fresnel reflectivity equation) and
is the soil effective temperature which utilizes the net radiative energy affected by the soil moisture/temperature gradient in the profile [
32]. Equation (1) implies that
ε does not contain depth information. Meanwhile
Teff is expressed in terms of soil physical temperature of different layers, usually of two layers as
where
represents the soil temperature at 0–5 cm and
is for 40–80 cm or even deeper depending on the soil texture. The
and
are weighting function which are mainly affected by soil moisture, wavelength and slightly by soil temperature [
16,
33] (Note: All specific variables in this study are listed in
Table 1). The sum of weighting function should satisfy:
In the above equations, the unique emissivity is a variable to simplify the coherent microwave radiative transfer model, assuming that the dielectric and temperature properties of the soil are uniform throughout the emitting layer.
Combining Equations (2) and (3) leads to following expressions:
As we know, if . The opposite case is also possible as if . For a special case, when (or ), the only possible solution is (or ). is the necessary and sufficient condition for .
In the following, we will prove that the soil temperature at one time of the optical depth equals to with linear soil temperature gradient assumption. The accuracy of this inference depends on whether the linear assumption is satisfied which is basically the case if more layers are observed (e.g., via the use of Lv’s multilayer scheme).
2.2. Soil Effective Temperature
The concept of soil effective temperature
is developed to describe the emissive capacity of a soil column. According to the Rayleigh-Jeans approximation, in the microwave domain the emitted energy from the soil is proportional to the thermodynamic temperature [
35] as shown in Equation (1), where the
is the emissivity that is strongly related to soil moisture, while
is the effective temperature and is formulated by [
36] as:
where
. Equation (5) states that
at the soil surface is a superposition of the intensities emitted at various depths within the soil.
An accurate computation of
is thus critical for obtaining relevant values of soil emissivity from brightness temperature measurements. It follows that soil moisture can be retrieved from the estimate of soil emissivity [
35]. However, the soil moisture and soil temperature profile information is usually limited in a field experiment, because discrete observation sensors are usually installed empirically at limited vertical intervals. Recently, a new scheme (hereafter, Lv’s scheme, [
16,
33]) has been derived directly from Equation (5) as
in which
, a parameter related to wavelength
, to soil moisture through the dielectric constant (
—real part,
—imaginary part), and to sampling depth
for each layer. Comparing to other two-layer schemes, Lv’s scheme uses an exponential function to distribute the weight among different layers. In Equation (6),
depicts the mean soil temperature of the
th layer, with
indicating its weight in the calculation of
. Parameter
is the key variable for Lv’s scheme, and is a function of
. While
is fixed for any specified sensor and the dielectric constant is varying with soil moisture and temperature,
is the only remaining variable which needs to be determined.
As stated in Lv et al. (2016b),
could be determined by considering
as a function of
and the integral exponential function
,
where
is calculated using the depth where the first layer sensors are installed (
). With Equation (7),
can be determined as well as the Δ
x1 used in Equation (6). The physical meaning of
could be inferred from Equation (6) that
matches the layer-averaged soil temperature integrated from the surface to the sampling depth
, which is used for calculating
. It is to note that
(i.e., the bulk sampling layer thickness) is different from
(i.e., the exact installation depth). Therefore, the soil moisture and soil temperature detected at
represents average values from surface to
, so that
will be called the representative depth for the first layer. The representative depth is computed from the known installation depth for soil moisture and soil temperature sensors and has no relation to the deeper layers below. Let
(noting
for the first layer). Since soil depth at
ith layer can be expressed as
, it follows
. Hence,
monotonically increases with soil column depth
. With
instead of
we can compute the correlation coefficient (
) along the profile.
2.3. Penetration Depth
For the non-isothermal case, Njoku and Entekhabi (1996) defined the penetration depth (e.g., the temperature sensing depth, hereafter as PD1) as the depth, which satisfies the following condition:
The equals to one time of the optical thickness (or optical depth, Napierian absorbance) with the linear assumption and is the natural logarithm of the ratio of incident to transmitted radiant intensity through soil at L-band. The optical thickness gives a measurement about the attenuation of radiation through the medium (e.g., soil in this study). According to Equation (8), the penetration depth will be affected by those factors influencing the soil effective temperature, including soil temperature, soil moisture, and wavelength
[
36]. For SMOS and SMAP missions, the wavelength is a given constant,
cm. The impact of soil moisture and soil temperature on the soil effective temperature is functional through the dielectric models, while the soil moisture’s influences dominate over the soil temperature one. When soil temperature is neglected and wavelength is fixed, a monotonic relationship between the soil moisture and the penetration depth (
) could be founded. However, it is not clearly stated how the change in penetration depth is related to the in situ observation.
is a characteristic length, the value of which is somewhat arbitrary and could not be computed without knowing detailed soil moisture and soil temperature profiles [
37].
Meanwhile, there is another definition of the penetration depth (PD2) [
32]. The radiative transfer theory has shown that while the thickness of the emitting layer may actually exceed 1 m for low-frequency radiation, the magnitude of its contribution becomes infinitesimal after a comparatively shallow depth (e.g., compared to 1 m layer). This comparatively shallow depth, which provides most of the measurable energy contribution, is also called the penetration depth (PD2) [
38]. Nevertheless, the PD2 is somewhat less quantitative since the magnitude of its contribution cannot be quantified. Hence, the penetration depth in this study refers to only PD1, e.g.,
.
4. Results
In this section, the penetration depth is first calculated according to Equation (10) for SMOS/SMAP at 1.4 GHz. The result is intended to give a broad view on how penetration depth is affected by soil moisture and soil temperature theoretically. After that, Equation (8) and Equation (11) are applied at Maqu Center Station, where a dedicated penetration depth time series is generated for further analysis. With the penetration depth acquired at Maqu Center Station, we then can select accordingly the soil moisture and soil temperature observation to compare with the integral soil effective temperature by Equation (12).
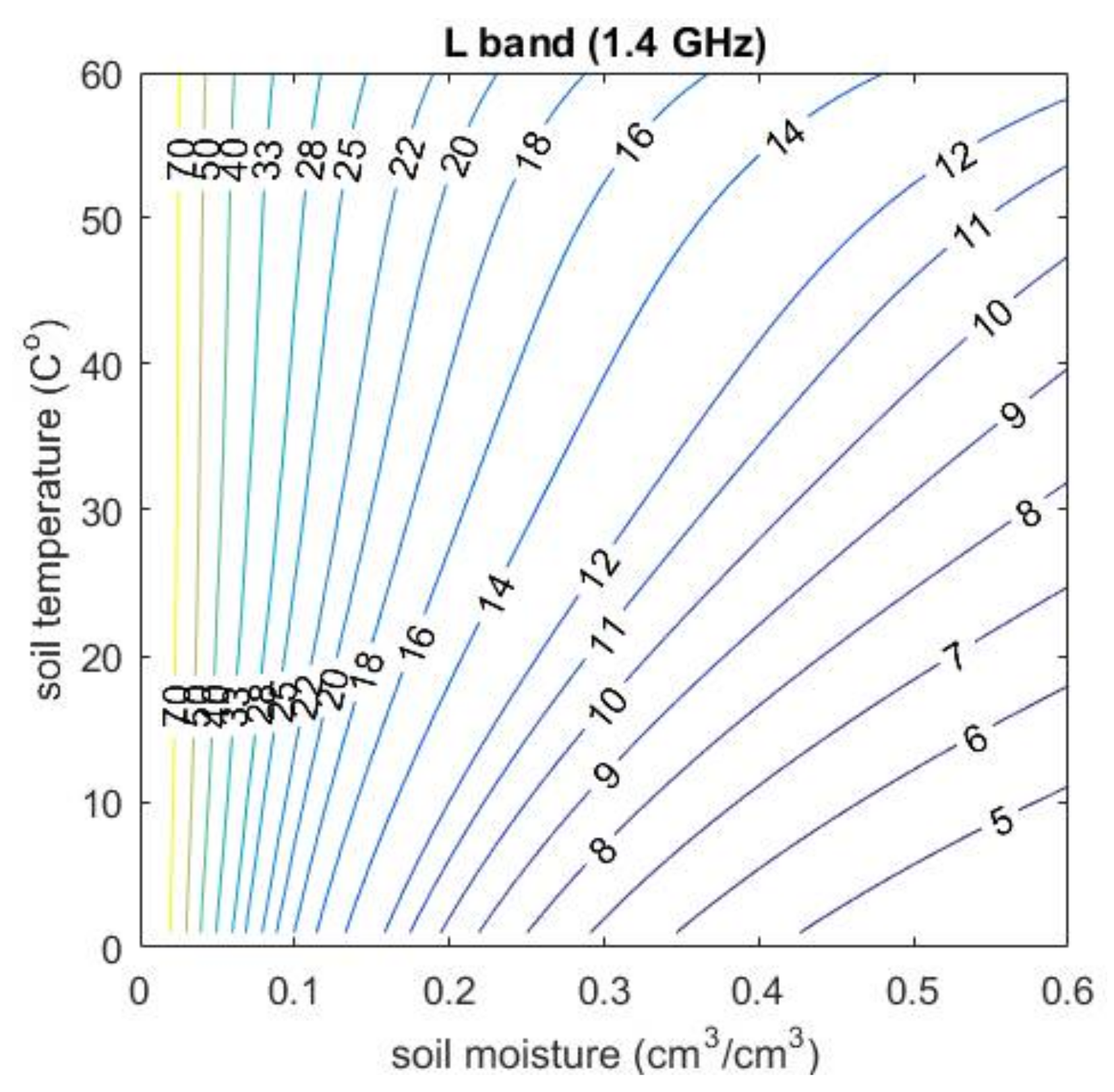
Figure 3 uses the operational channel of SMOS/SMAP (L-band, 1.4 GHz) as examples to show how the soil moisture and soil temperature affect the penetration depth. It is clear that soil moisture is the dominant factor in affecting the penetration depth when the soil is dry, while soil temperature has more impact on the penetration depth for the wet soil. With the range of soil moisture of 0.01–0.6 cm
3 cm
−3 and soil temperature of 0–60 °C, the penetration depth ranges from 3–70 cm for L-band. When the soil is very dry (i.e., soil moisture is less than 0.01 cm
3 cm
−3), the penetration depth is the greatest. Generally, the penetration depth would be 12 cm for L-band at 0.3 cm
3 cm
−3 and 30 °C. If the soil is not so dry, the effect of soil temperature needs to be considered. For instance, in
Figure 3, the penetration depth could be 11 cm when soil moisture is 0.55 cm
3 cm
−3 and soil temperature is 50 °C. Nevertheless, the same penetration depth is also associated with soil moisture of 0.2 cm
3 cm
−3 and soil temperature of 10 °C. However, an error of soil temperature both in measurement and model simulation larger than 10 °C is rare and soil moisture dominate the penetration depth especially for dry soil. In this case, although the calculation of the penetration depth strongly depends on the dielectric constant model but the difference can be ignored. If the layers configuration were too sparse, the estimation would not be so precise in practice as in
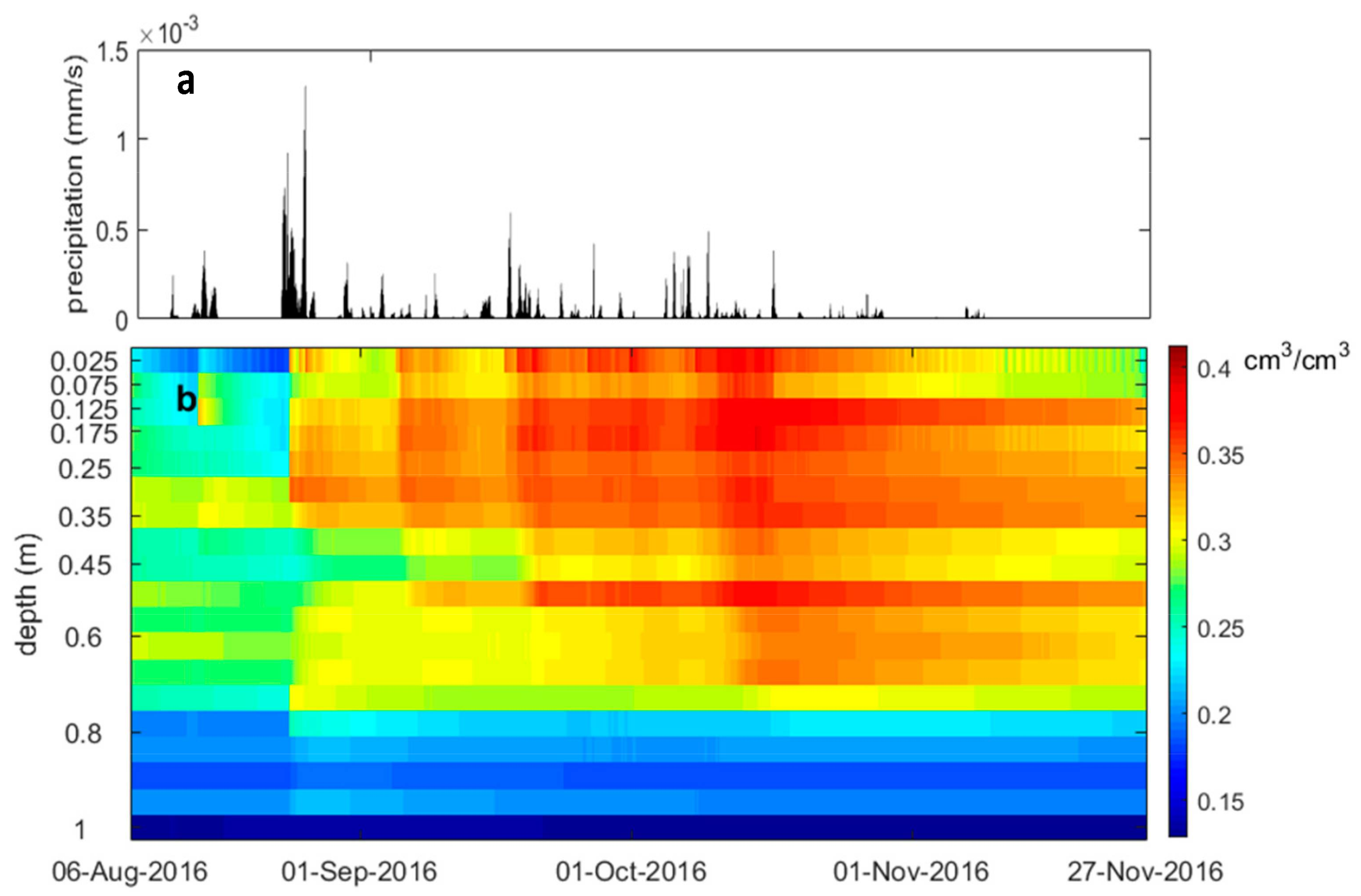
Figure 3. This is partly the reason why a vertically dense soil moisture and soil temperature profile was mounted at the Maqu Center Site with dense layers (19 layers within the top one meter). Such intensive layering would greatly minimize the uncertainty introduced by the dielectric models.
Figure 4 shows the time series of the penetration depth (Blue) and correlation coefficient (Red) between the soil temperature at the penetration depth and the corresponding soil effective temperature. With vertically dense soil moisture/temperature profile measurement at Maqu Center Station, the penetration depth in
Figure 4 is computed by Equations (8) and (12). While soil moisture ranges from 0.15 to 0.45 cm
3 cm
−3, the penetration depth varies from 6 to 10 cm at the center site. The average penetration depth is about 9 cm for the time before August 25 and 7 cm for the rest. As can be seen the penetration depth is strongly correlated with soil moisture which explains the variation in the period. Meanwhile, the penetration depth has its diurnal changes (around 1 cm) and is affected dominantly by soil temperature.
From the foregoing we highlighted the essence of
Teff as the mid-level of soil temperature profile in terms of Equations (1), (5) and (12) which could represent the average soil temperature of the soil column. Similarly, the soil moisture detected by satellites are also supposed to be the average soil moisture of the soil column in the view of emission depth. With
Teff computed from MERRA-2 and global soil moisture map acquired from SMAP,
Figure 5 illustrates a global distribution of the penetration depth by Equation (10).
The minimum cases (
Figure 5a,b) reflect the penetration depth especially after the rainfall when the soil moisture is then higher. If there is a sufficient rain event, the surface soil layer would be fully moist even the soil column would be dry. Therefore, the penetration depth would be less than 0.1 m or even 0.05 m around the globe. In comparison, the cases for maximum penetration depth (
Figure 5c,d) occur after a long drying period when the soil moisture has drawn down from the surface to deeper layers. This situation depends on how dry the soil could be so such regions coincide with the arid regions like central Asia, Australia and Sahara where the penetration depth is over 0.3 m. The annual mean value of penetration depth (
Figure 5e,f) is from 0.05 to 0.2 m except the extremely dry regions. According to Equation (7) in Lv’s scheme, the soil moisture/temperature sampled at 0.05 m represents the radiative contribution from 0 m to more than 0.1 m (depending on the specific profile) so 0.05 m samples may match with the satellite signal in most regions. In general, there is not too much difference between 6 a.m. and 6 p.m. while the latter may have deeper penetration depth of a few centimeters because
Teff is higher.
5. Discussion
Because the penetration depth is defined as the depth at which the intensity of the radiation inside the medium reduces to (about 37%) of its original value at the surface (or from its source origin to the surface from a sensing point of view), it means there are about 37% signal comes beneath the penetration depth. To characterize the penetration depth, several factors (see below) need to be considered and their uncertainties quantified, among which the validity of the assumption of linear temperature gradient is of most significance which we will briefly discuss as follows.
Several factors influence the characteristics of penetration depth which means that for Cal/Val the satellite soil moisture product, it is very important to know the overpassing time, because the penetration depth can vary diurnally. On the other hand, Equations (12) and (19) are derived based on the linear assumption (i.e., ). If the soil moisture and soil temperature profiles are complex or have great gradients, the remotely sensed soil moisture may not be at the penetration depth as calculated by Equation (12).
To which extent the linear assumption could be satisfied is quantified by the absolute value of correlation coefficient
between the soil temperature profile and the optical depth profile at Maqu Center Station.
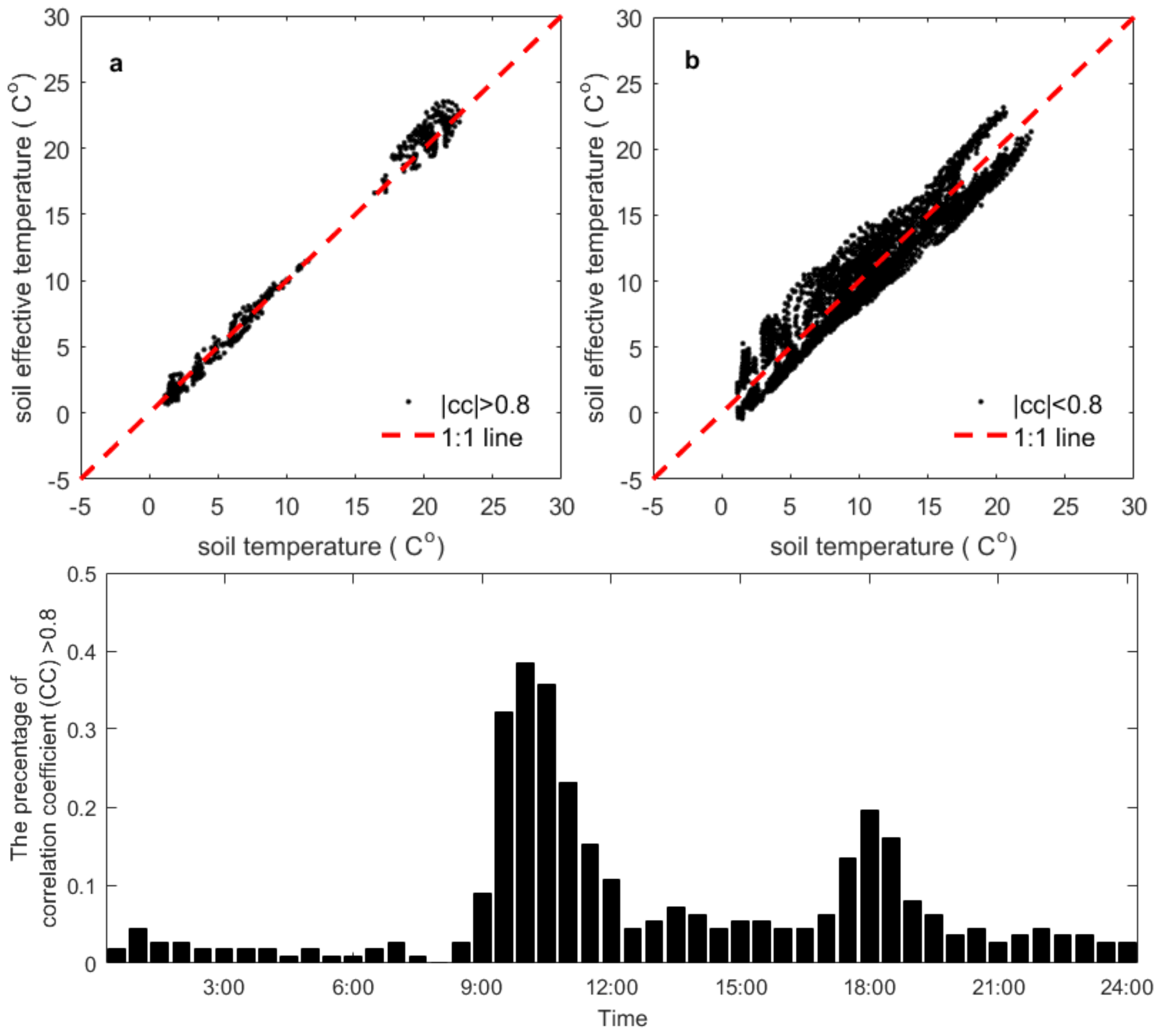
Figure 6 gives a glance about the validity of the linear assumption. It could be seen that the best accuracy was achieved when the assumption is valid if the data satisfy (
), which accounts for 10.89% during the experiment period. The
appears mainly around 10:00 o’clock (local time) and about 40% of the observation period. The second occurrence peak is around 18:00 o’clock (local time) which coincides with SMOS/SMAP descending/ascending overpassing time. Other than the validity of the liner assumption, the assumption of
in Equation (18) can affect the correlation coefficient as well.
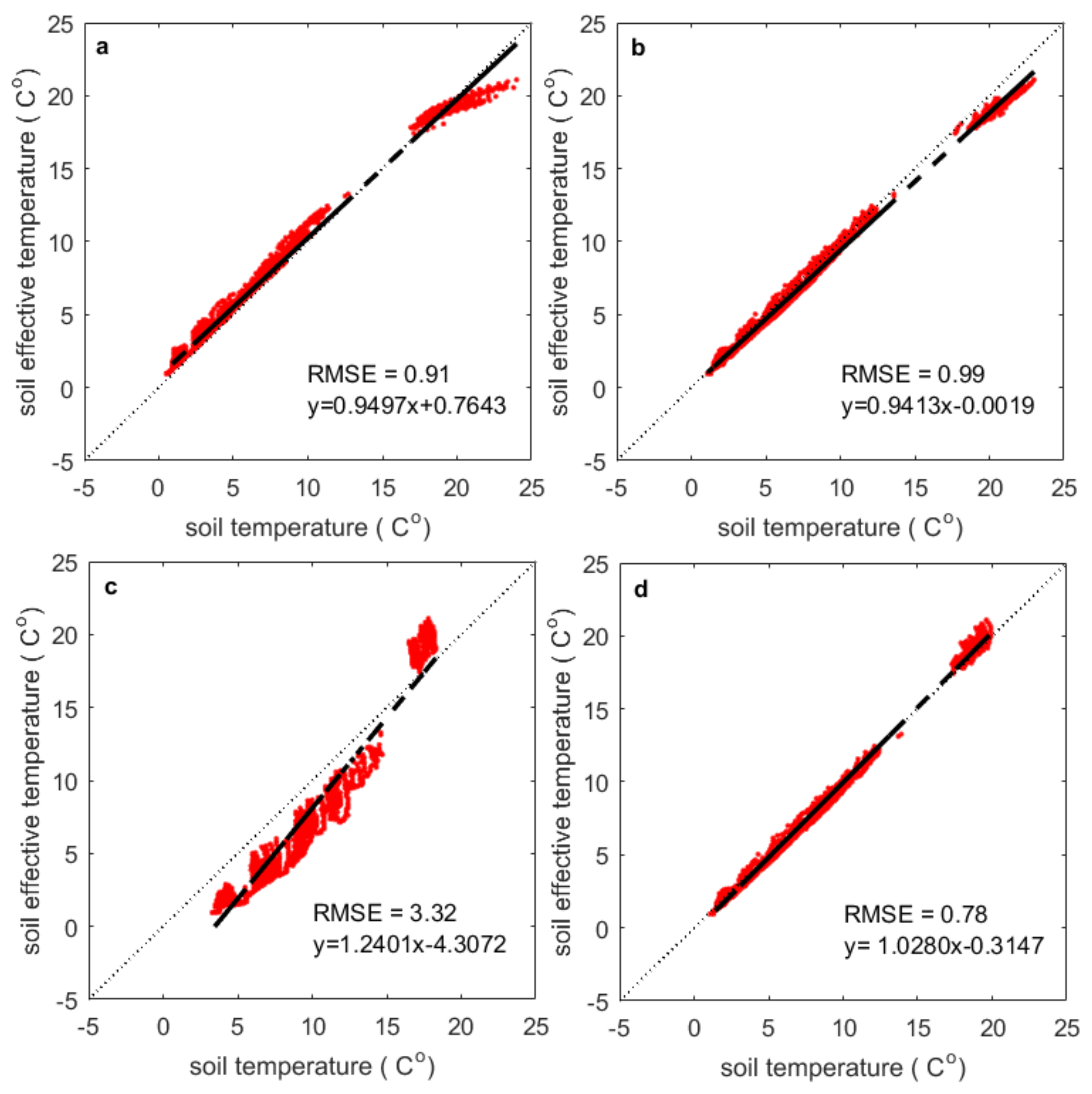
Equation (19) indicates that the soil temperature value at one certain depth could represent the soil temperature profile in terms of soil effective temperature (e.g., Lv’s two-layer scheme vs. Wilheit’s integral scheme) and that depth is the penetration depth. The soil temperature observed at 5 cm, 10 cm, 40 cm and the penetration depth in
Figure 4 are compared with the soil effective temperature calculated by Wilheit’s scheme in
Figure 7. It is seen that the soil temperature variation at 2.5 cm (
Figure 7a) has a slight underestimation bias and the distribution of points is much scattered than at the penetration depth (
Figure 7d). For the soil temperature approximately between 15 and 20 °C, the difference can reach about 5 °C. When the soil temperature is out of that temperature range, the difference become relatively smaller. The variation range of soil temperature at 10 cm (
Figure 7b) matches better but is still worse than that at the penetration depth. From
Figure 4, it is known that the average penetration depth is about 7 cm after 20 August. Therefore the relatively similar accuracy is reasonable between
Figure 7b,d. The soil temperature at 40 cm (
Figure 7c) has a positive/negative bias after/before 20 August. RMSE reaches 3.32 °C. Obviously 40 cm cannot represent the soil profile (
Figure 7c) to calculate
Teff.
For those data with
(i.e.,
) (see
Figure 6), the soil temperature at the penetration depth is very close to as expected by Equation (19). The penetration depth contains all the factors which affect the soil effective temperature, such that the soil effective temperature varies with the penetration depth.
6. Conclusions
The concept of penetration depth in microwave radiometry was published more than four decades ago and its importance has long been realized by the microwave remote sensing community. The penetration depth is a characteristic length in the soil column which should be considered as a dynamic whole instead of just a few centimeters at the surface layer and becomes especially important with the increased wavelength for the dedicated soil moisture mission SMOS/SMAP. Because the penetration depth is defined based on the integral effective soil temperature, it leaves a gap between the simple two-layer schemes (e.g., commonly used in the operational soil moisture retrieval) and the integral one. Nevertheless, the implication behind the penetration depth has so far not been fully investigated and explained. The casually referred 1/e residual is just a “qualitative” number and how it is linked with satellite soil moisture sensing depth has not been analytically determined.
In this study, with rigorous mathematical derivations based on Lv’s scheme, we have proved that the penetration depth is not only a “qualitative” number but a characteristic depth which synthesizes emitting behavior of a soil column in microwave radiometry. In Lv’s scheme, the optical depth appears in and thus unifies the radiative transfer processes in atmosphere, vegetation and soil. More specifically, quantifies the attenuation of radiation transfer in a medium, being the air dielectric properties in the atmosphere, vegetation optical thickness (mainly the water content in leaves) in vegetation, as well as soil dielectric properties (e.g., mainly soil moisture) in the soil. The use of the integral instead of soil depth is proposed in this study for the first time and with appearing in the formula, we can determine essential characteristics in . By means of , it is proved that the penetration is not just the depth where the energy is reduced to 1/e of its original value but it is also the median value of soil temperature in the soil column. The penetration depth is strongly related to soil moisture but also has diurnal variation which may have an amplitude of several centimeters at the center station of Maqu network.
The question of at which depth L-band soil moisture monitoring satellites such as SMOS/SMAP measure has confused the soil moisture community at large. As stated in introduction, the sensitive layer is supposed to be the depth where these satellites are sensing in previous studies. In SMAP retrieval [
46], vegetation and soil surface roughness are accounted in terms of emissivity calibration. The final soil moisture product is derived from a smooth emission model. A precise estimation of vegetation and roughness is critical before determining the penetration depth. Particularly, the global map of penetration depth in
Figure 5 depends on a correct vegetation calibration. Therefore, the penetration depth over dense vegetation zone, for instance the tropics may be even smaller. In contrast, in the dessert area with few or no vegetation, the penetration depth is usually large and vegetation calibration is not so important except after rainfall events. The conclusion in this study would be most useful to the transition zone where soil moisture variation is larger and affects climate/hydro-process more intensively. Different to the sensitive layer view, we proposed in this study a median value view and found the soil temperature median value under the linear assumption. From the hypothesis of zeroth-order incoherent microwave transfer frame, the median soil temperature layer represents not only
but also provides the depth information contained in this frame. The soil moisture retrieved from microwave (e.g., L-band) observation should be the average radiative emission capacity of the soil column and there should be a median soil moisture depth as well. This study has successfully developed such a new method to find this median soil moisture depth by relating the penetrating depth in terms of temperature to radiative energy attenuation. This is done by building up a
relationship with median theory in which a median value of
could be found at the penetration depth with certain condition. The method is verified with in situ data from the Maqu observation site and the conclusion is valid whenever the field condition satisfies the assumption. This is critical to the application of SMOS/SMAP soil moisture product because a difference of several centimeters between the depth of in situ measurement and the satellite sensing depth will lead to systematic bias in evaluating the satellite products. Based on an application of the developed method to SMAP passive L3 soil moisture product and the corresponding soil effective temperature calculated from MERRA-2 for 2016, it may be concluded that it is appropriate to use 5 cm depth of soil moisture measurement as a ground reference to calibrate and validate satellites soil moisture product because 5 cm captures the main signal source on average. However, for some extreme cases like arid region or the region after a long drought event, 5 cm may not represent the dominant emission layer. In other words, it means that even though the satellite product is precise, we may still get biased conclusion, if the ground measurement is inappropriately organized, and the comparability between satellite and in situ measurement is not established [
47]. The developed method should also be beneficial to the Earth surface modelling in improving the consistency in the dynamics of the soil moisture processes and satellite observations.