Estimating AADT Using Statewide Traffic Data Programs: Missing Data Impact
Abstract
1. Introduction
2. Literature Review
3. Study Motivation
- At least one daily volume is necessary for each day of the week (DOW) within a month.
- A minimum of 19 hourly observations must be recorded for each daily volume.
- The daily traffic volume should fall within 20% of the average for that specific day of the week in the month.
4. Study Approach
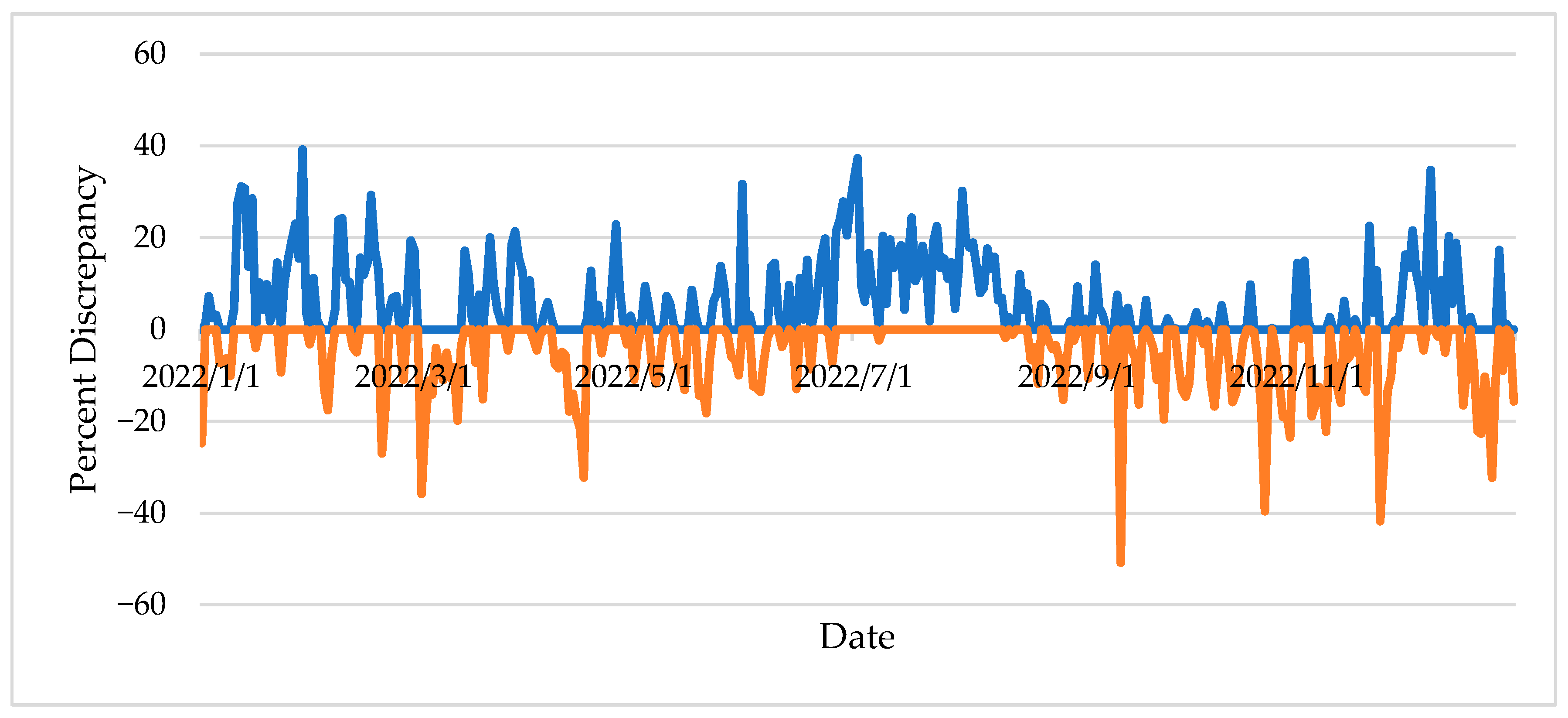
- Sampling technique I: In this technique, random days within a specific month are selected to represent the level of available (or missing) data. For instance, one week of available data would include one Monday, one Tuesday, one Wednesday, etc., all selected randomly within the month.
- Sampling technique II: In this technique, the duration of the available data (one, two, or three weeks) is selected randomly within the month as a continuous period of time. This sampling approach seems more realistic, as periods when ATRs or WIMs are down or malfunctioning tend to be continuous within any given month.
5. Data Collection
6. Analysis and Results
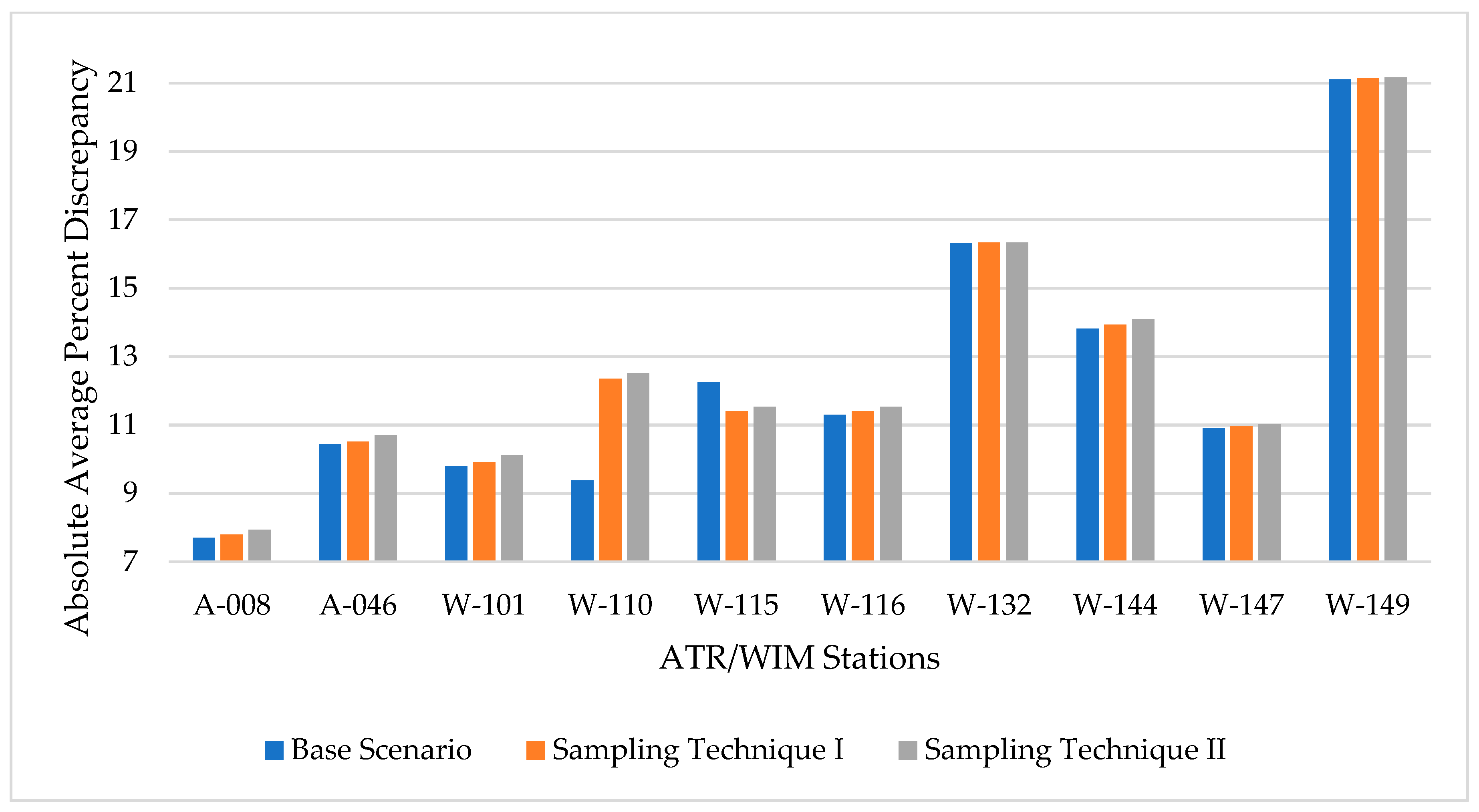
6.1. Base Condition (No Missing Data)
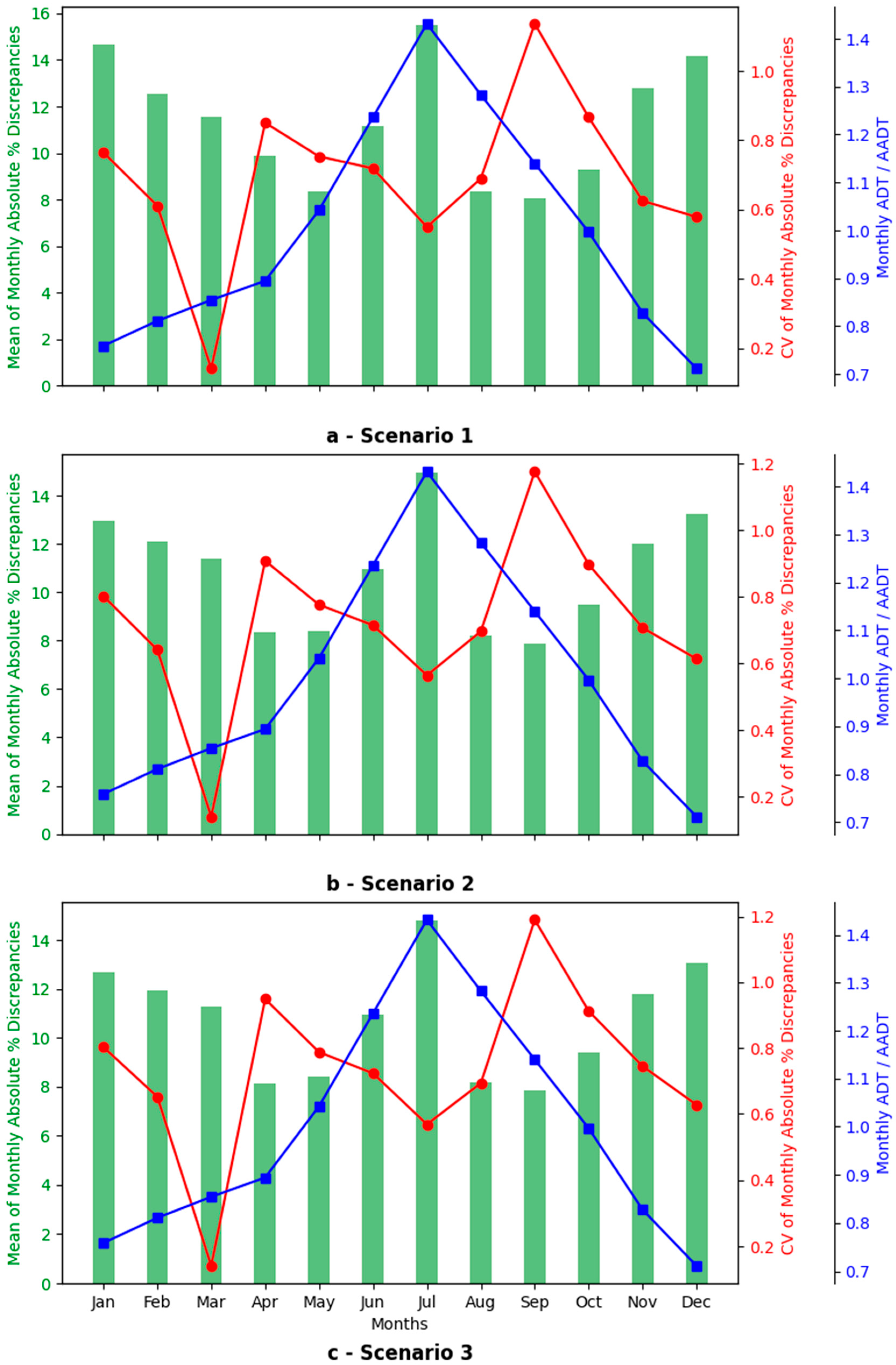
6.2. Scenario 1 (Permanent Stations with One Week of Data per Month)
6.3. Scenario 2 (Permanent Stations with Two Weeks of Data per Month)
6.4. Scenario 3 (Permanent Stations with Three Weeks of Data per Month)
7. Summary and Conclusions
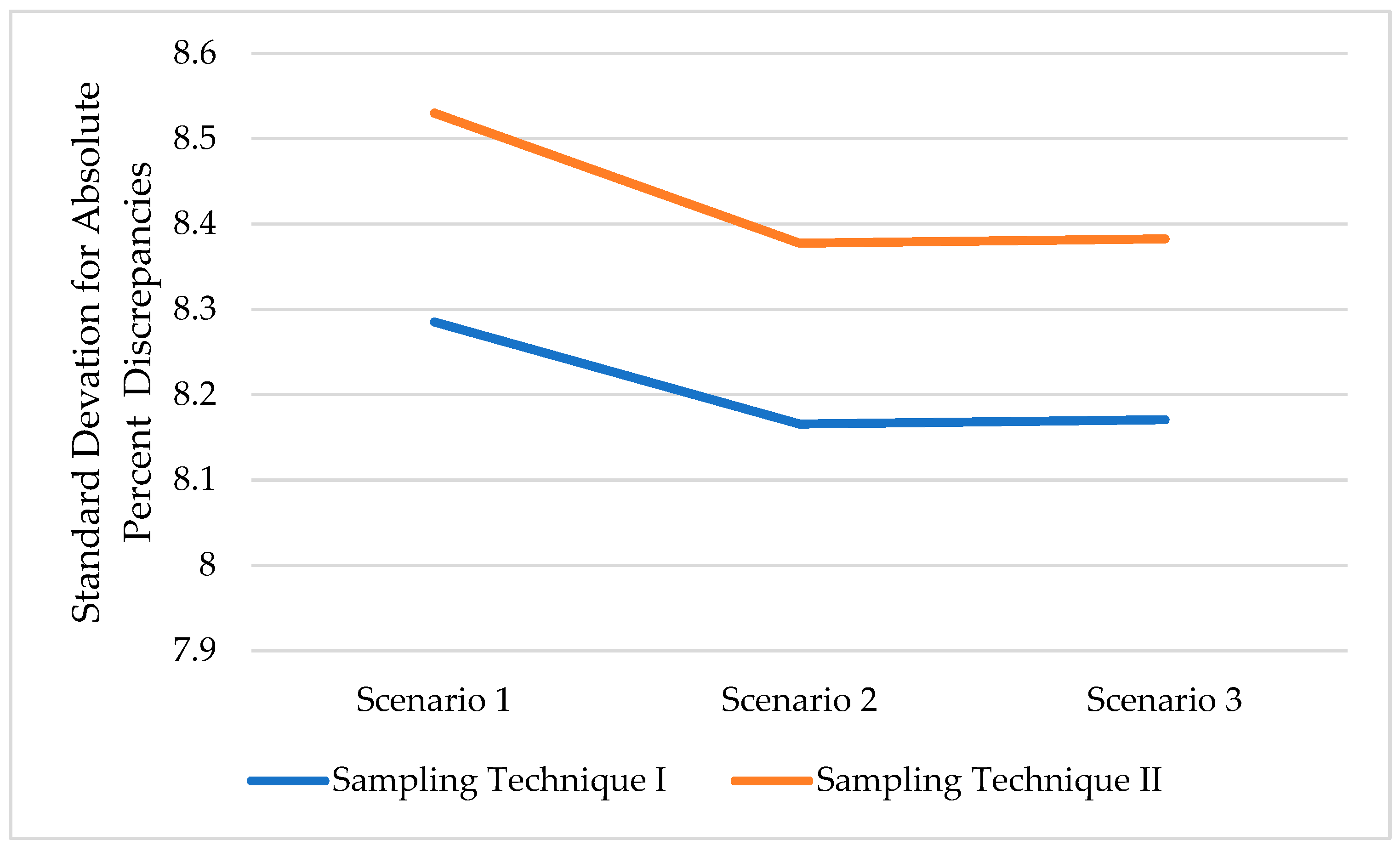
- Study results clearly show that the missing data has a consistent effect on the accuracy of AADT estimation, measured using the absolute percent discrepancy between the actual and estimated AADT. This finding supports the research hypothesis that the greater the amount of missing data, the less accurate the AADT estimation. However, this effect was not statistically significant using a two-way ANOVA at the 95% confidence level.
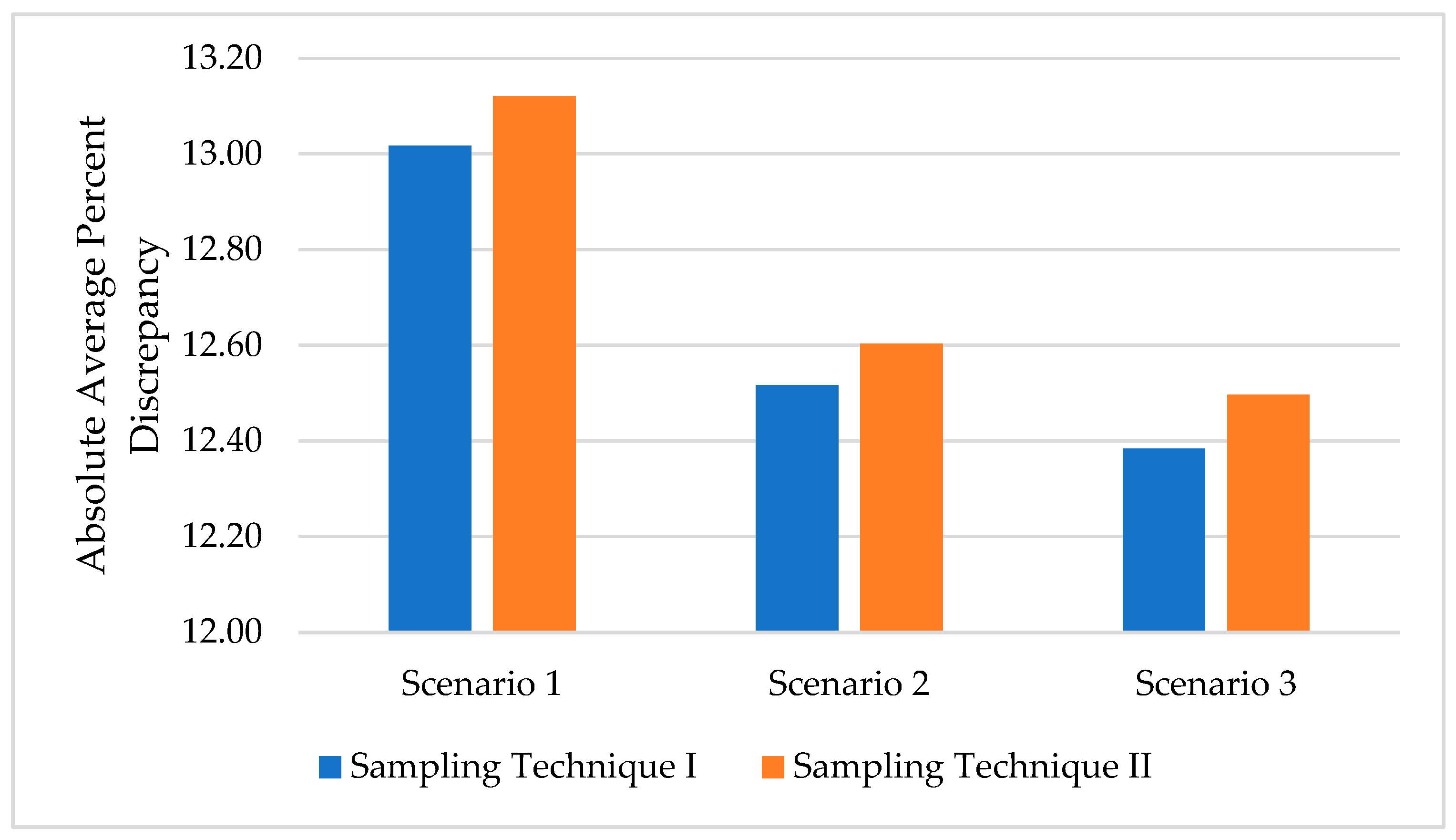
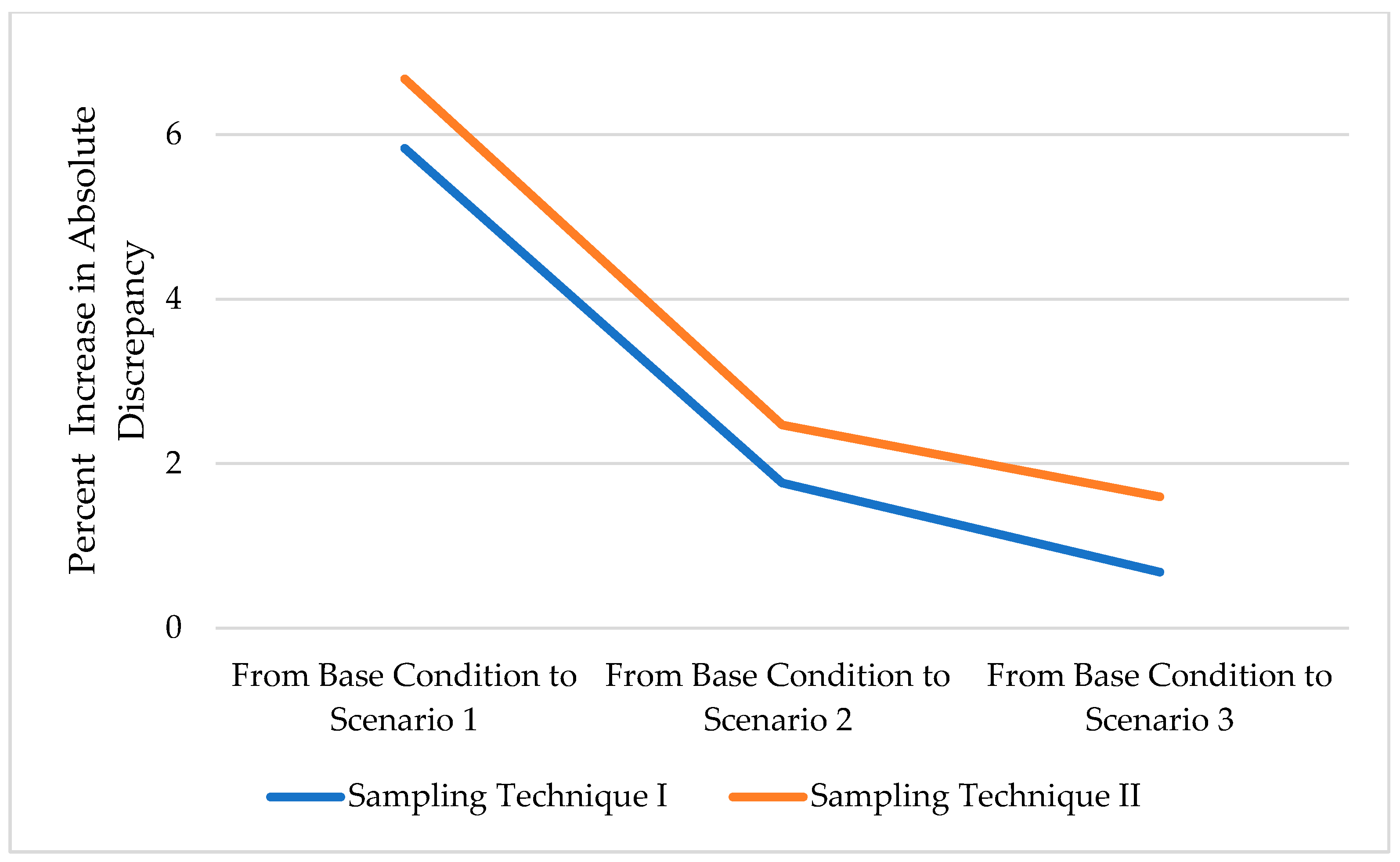
- The increase in % discrepancy for AADT estimation was not linearly proportional to the increase in the amount of missing data. Despite the dramatic scenarios of missing data used in the analysis (31% to 77%), the change in the AADT estimation error between the highest and lowest levels of missing data was in the order of 6%.
- Given the extreme scenarios of missing data used in the study (all permanent stations missing significant amounts of data simultaneously) and the relatively low effect on % discrepancy in AADT estimation (less than 7% discrepancy for the most extreme scenario), it is reasonable to conclude that the current practice in treating missing data does not involve an important compromise in the accuracy of AADT estimation. This increase remains within the ±10% error tolerance commonly referenced in FHWA’s Traffic Monitoring Guide for planning-level AADT estimation, though such discrepancies may be more critical in design or safety applications [8]. The finding also suggests that data containing at least one day of the week for each month can be used to develop daily and seasonal adjustment factors (i.e., MDOW factors) without the need to impute missing data. Based on the results, at least DOW per month appears to be the minimum acceptable threshold for reliable AADT estimation. This level of data coverage maintains accuracy within acceptable limits while capturing the necessary traffic pattern. Below this threshold, the reliability of AADT estimates may diminish, especially for design and safety-related applications that require higher precision.
- Sampling technique I of selecting random days within the month was associated with a lower % discrepancy in AADT estimation compared with sampling technique II of selecting a random period within the month (one, two, or three weeks).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AADT | Annual Average Daily Traffic |
| MDOW | Monthly Day of the Week |
| MDT | Montana Department of Transportation |
| FHWA | Federal Highway Administration |
| ATR | Automatic Traffic Recorder |
| WIM | Weigh-in-Motion |
References
- Sharma, S.C.; Lingras, P.; Liu, G.X.; Xu, F. Estimation of Annual Average Daily Traffic on Low-Volume Roads: Factor Approach Versus Neural Networks. Transp. Res. Rec. J. Transp. Res. Board 2000, 1719, 103–111. [Google Scholar] [CrossRef]
- Zhao, F.; Chung, S. Contributing Factors of Annual Average Daily Traffic in a Florida County: Exploration with Geographic Information System and Regression Models. Transp. Res. Rec. J. Transp. Res. Board 2001, 1769, 113–122. [Google Scholar] [CrossRef]
- Sun, X.; Das, S. Estimating Annual Average Daily Traffic for Low-Volume Roadways: A Case Study in Louisiana. In Proceedings of the 12th International Conference on Low-Volume Roads, Kalispell, MT, USA, 15–18 September 2019; Available online: https://trid.trb.org/View/1689977 (accessed on 15 February 2025).
- Robichaud, K.; Gordon, M. Assessment of Data-Collection Techniques for Highway Agencies. Transp. Res. Rec. J. Transp. Res. Board 2003, 1855, 129–135. [Google Scholar] [CrossRef]
- Albright, D. History of estimating and evaluating annual traffic volume statistics. Transp. Res. Rec. J. Transp. Res. Board 1991, 1305, 103–107. [Google Scholar]
- Fekpe, E.; Gopalakrishna, D.; Middleton, D. Highway Performance Monitoring System Traffic Data for High-Volume Routes: Best Practices and Guidelines; Final Report; Office of Highway Policy Information Federal Highway Administration U.S. Department of Transportation: Washington, DC, USA, 2004. [Google Scholar]
- Vandervalk-Ostrander, A.; American Association of State Highway and Transportation Officials; United States Federal Highway Administration; National Cooperative Highway Research Program. AASHTO Guidelines for Traffic Data Programs; PB-American Association of State Highway and Transportation Officials: Washington, DC, USA, 2009; Volume 1, Available online: http://dl1.wikitransport.ir/book/AASHTO_Guidelines_for_Traffic_Data_Programs_2009.pdf (accessed on 10 December 2024).
- Federal Highway Administration (FHWA). Traffic Monitoring Guide. 2022. Available online: https://rosap.ntl.bts.gov/view/dot/74643 (accessed on 10 December 2024).
- Macioszek, E.; Kurek, A. Road Traffic Distribution on Public Holidays and Workdays on Selected Road Transport Network Elements. Transp. Probl. 2021, 16, 127–138. [Google Scholar] [CrossRef]
- Zhong, M.; Sharma, S.; Liu, Z. Assessing Robustness of Imputation Models Based on Data from Different Jurisdictions: Examples of Alberta and Saskatchewan, Canada. Transp. Res. Rec. J. Transp. Res. Board 2005, 1917, 116–126. [Google Scholar] [CrossRef]
- Albright, D. 1990 Survey of Traffic Monitoring Practices Among State Transportation Agencies of the United States. 1990. Available online: https://api.semanticscholar.org/CorpusID:168276711 (accessed on 20 January 2025).
- Albright, D. An imperative for, and current progress toward, national traffic monitoring standards. ITE J.-Inst. Transp. Eng. 1991, 61. Available online: https://api.semanticscholar.org/CorpusID:107206642 (accessed on 20 January 2025).
- Khan, Z.; Khan, S.M.; Dey, K.; Chowdhury, M. Development and Evaluation of Recurrent Neural Network-Based Models for Hourly Traffic Volume and Annual Average Daily Traffic Prediction. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 489–503. [Google Scholar] [CrossRef]
- Jia, X.; Dong, X.; Chen, M.; Yu, X. Missing data imputation for traffic congestion data based on joint matrix factorization. Knowl.-Based Syst. 2021, 225, 107114. [Google Scholar] [CrossRef]
- Shafique, M.A. Imputing Missing Data in Hourly Traffic Counts. Sensors 2022, 22, 9876. [Google Scholar] [CrossRef] [PubMed]
- Roll, J. Daily Traffic Count Imputation for Bicycle and Pedestrian Traffic: Comparing Existing Methods with Machine Learning Approaches. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 1428–1440. [Google Scholar] [CrossRef]
- Mendenhall, W. Introduction to Probability and Statistics [Internet], 14th ed.; Duxbury Press: Duxbury, MA, USA, 1986; Available online: https://books.google.com/books/about/Introduction_to_Probability_and_Statisti.html?id=fQsKAAAAQBAJ (accessed on 28 December 2024).
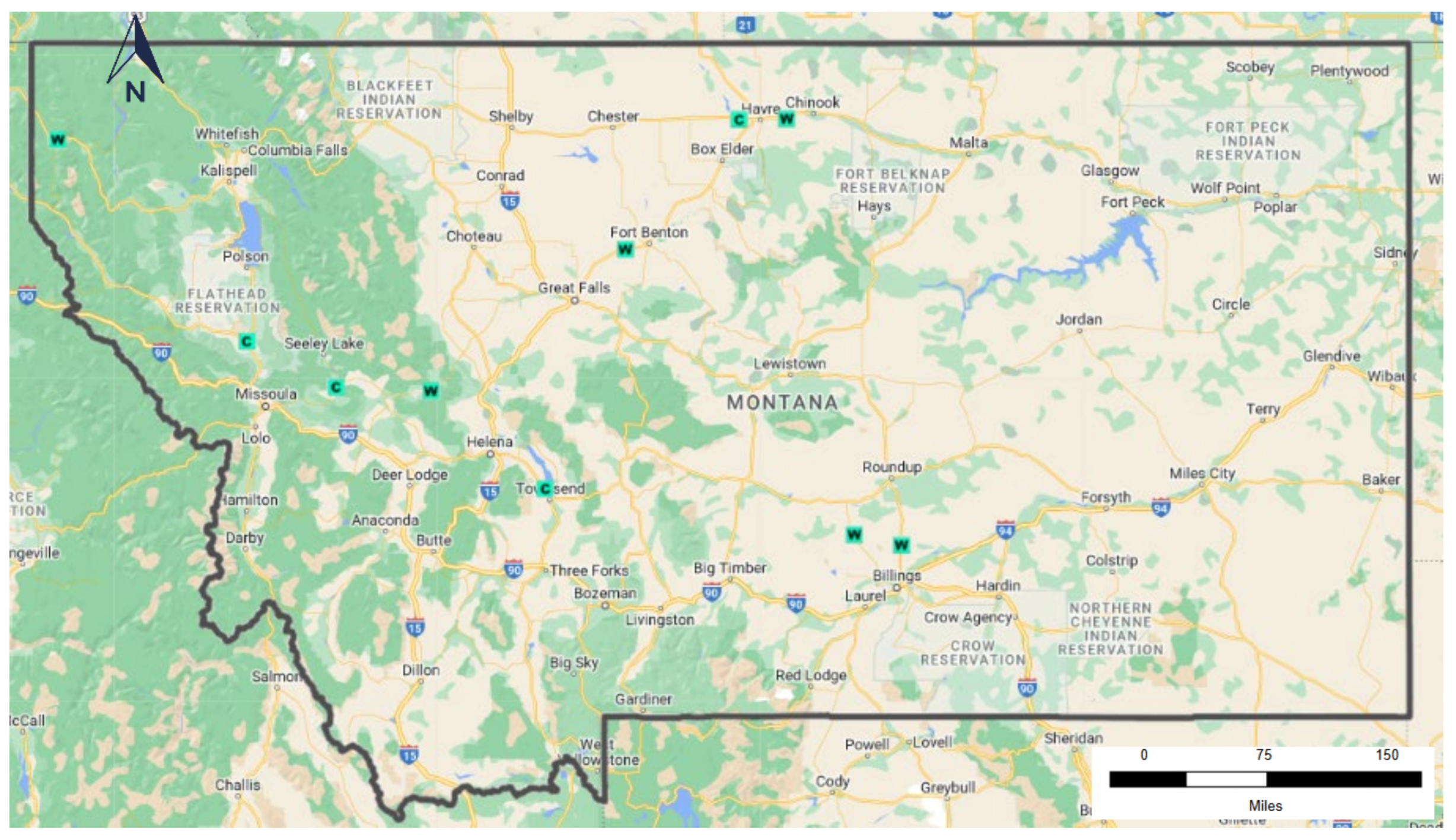


| Station | Road | County | No. of Lanes | Lane Width (ft) |
|---|---|---|---|---|
| A-008 | US 89 | Cascade | 4 | 12 |
| A-046 | US 2 | Hill | 2 | 12 |
| W-101 | US 287/US 12 | Broadwater | 2 | 12 |
| W-110 | MT Hwy 3 | Broadwater | 2 | 12 |
| W-115 | US 87 | Chouteau | 2 | 12 |
| W-116 | US 2 | Hill | 3 | 12 |
| W-132 | MT 200 | Missoula | 2 | 12 |
| W-144 | US 87 | Yellowstone | 2 | 12 |
| W-147 | US 2 | Lincoln | 2 | 12 |
| W-149 | MT 200 | Lewis and Clark | 2 | 12 |
| Stations | A-008 | A-046 | W-101 | W-110 | W-115 | W-116 | W-132 | W-144 | W-147 | W-149 |
|---|---|---|---|---|---|---|---|---|---|---|
| Absolute Average Percent Discrepancy | 7.71 | 10.43 | 9.79 | 9.37 | 12.26 | 11.30 | 16.31 | 13.82 | 10.90 | 21.11 |
| One-Tailed t-Test | Two-Tailed t-Test | ||
|---|---|---|---|
| Stations | Base Condition vs. Sampling Technique I | Base Condition vs. Sampling Technique II | Sampling Technique I vs. Sampling Technique II |
| A-008 | 0.030 | 0.019 | 0.818 |
| A-046 | 0.108 | 0.071 | 0.802 |
| W-101 | 0.078 | 0.043 | 0.759 |
| W-110 | 0.111 | 0.085 | 0.877 |
| W-115 | 0.135 | 0.104 | 0.879 |
| W-116 | 0.096 | 0.079 | 0.911 |
| W-132 | 0.469 | 0.470 | 0.997 |
| W-144 | 0.146 | 0.104 | 0.836 |
| W-147 | 0.112 | 0.123 | 0.955 |
| W-149 | 0.497 | 0.515 | 0.963 |
| One-Tailed t-Test | Two-Tailed t-Test | ||
|---|---|---|---|
| Stations | Base Condition vs. Sampling Technique I | Base Condition vs. Sampling Technique II | Sampling Technique I vs. Sampling Technique II |
| A-008 | 0.317 | 0.213 | 0.737 |
| A-046 | 0.374 | 0.263 | 0.752 |
| W-101 | 0.321 | 0.231 | 0.783 |
| W-110 | 0.341 | 0.331 | 0.978 |
| W-115 | 0.365 | 0.319 | 0.891 |
| W-116 | 0.334 | 0.305 | 0.934 |
| W-132 | 0.505 | 0.516 | 0.978 |
| W-144 | 0.361 | 0.311 | 0.889 |
| W-147 | 0.358 | 0.395 | 0.923 |
| W-149 | 0.507 | 0.527 | 0.959 |
| One-Tailed t-Test | Two-Tailed t-Test | ||
|---|---|---|---|
| Stations | Base Condition vs. Sampling Technique I | Base Condition vs. Sampling Technique II | Sampling Technique I vs. Sampling Technique II |
| A-008 | 0.427 | 0.327 | 0.788 |
| A-046 | 0.449 | 0.333 | 0.758 |
| W-101 | 0.427 | 0.310 | 0.754 |
| W-110 | 0.444 | 0.395 | 0.901 |
| W-115 | 0.449 | 0.365 | 0.827 |
| W-116 | 0.441 | 0.375 | 0.866 |
| W-132 | 0.551 | 0.527 | 0.948 |
| W-144 | 0.448 | 0.369 | 0.839 |
| W-147 | 0.453 | 0.490 | 0.926 |
| W-149 | 0.594 | 0.536 | 0.928 |
| Absolute Average % Discrepancies | |||
|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | |
| % Missing Data | 76.98 | 53.97 | 30.95 |
| Sampling Technique I | 13.017 [5.83] * | 12.517 [1.76] | 12.383 [0.68] |
| Sampling Technique II | 13.121 [6.67] | 12.603 [2.46] | 12.496 [1.59] |
| DF | Sum Sq | Mean Sq | F Value | Pr (>F) | |
|---|---|---|---|---|---|
| Missing Data Scenario | 2 | 181 | 90.47 | 1.302 | 0.272 |
| Sampling Technique | 1 | 21 | 20.64 | 0.297 | 0.586 |
| Sampling Technique: Scenario | 2 | 0 | 0.03 | 0 | 1 |
| Residuals | 2184 | 151,815 | 69.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qureshi, M.F.R.; Al-Kaisy, A. Estimating AADT Using Statewide Traffic Data Programs: Missing Data Impact. Sustainability 2025, 17, 9896. https://doi.org/10.3390/su17219896
Qureshi MFR, Al-Kaisy A. Estimating AADT Using Statewide Traffic Data Programs: Missing Data Impact. Sustainability. 2025; 17(21):9896. https://doi.org/10.3390/su17219896
Chicago/Turabian StyleQureshi, Muhammad Faizan Rehman, and Ahmed Al-Kaisy. 2025. "Estimating AADT Using Statewide Traffic Data Programs: Missing Data Impact" Sustainability 17, no. 21: 9896. https://doi.org/10.3390/su17219896
APA StyleQureshi, M. F. R., & Al-Kaisy, A. (2025). Estimating AADT Using Statewide Traffic Data Programs: Missing Data Impact. Sustainability, 17(21), 9896. https://doi.org/10.3390/su17219896






