An Immune-Structural Adaptive Response for Viability of Carbon Capture, Use, and Storage Supply Chains

Abstract

The viability of supply chains is a central challenge in environments marked by frequent disruptions, extreme uncertainty, and rising sustainability requirements. While literature has advanced in integrating resilience and sustainability, predominant methods—mainly robust or stochastic optimization—focus on predefined scenarios and offer only a partial view of adaptive capacity. This emphasis on known–unknowns leaves unresolved how to ensure continuity, efficient recovery, and organizational learning under unexpected or unknown–unknown events. A methodological gap therefore persists in evaluating and designing supply chains that not only withstand disruptions but also retain essential goals, autonomously activate responses, and reorganize with acceptable costs and times. This study introduces the Immune-Structural Adaptive Response (RAIE) methodology, inspired by the human immune system. RAIE provides an evaluation framework combining properties such as early detection, minimal redundancy, adaptive memory, and structural reconfiguration, operationalized through dynamic metrics: goal retention, autonomous activation, adaptation cost, recovery time, and service loss. Applied to Carbon Capture, Utilization, and Storage (CCUS) supply chains, RAIE reduced service-loss area (Rₐᵣₑₐ) by 40–65% and recovery time (TTR) by 30–45%, while keeping adaptation costs below 2% of total expenditures. Unlike traditional stochastic or robust models, RAIE explicitly embeds endogenous responses and post-shock reorganization, producing more viable configurations that balance efficiency and resilience. The results deliver actionable guidance for strategic and tactical decision-making in highly uncertain environments.

1. Introduction

The challenges of contemporary supply chains are increasingly shaped by turbulence, uncertainty, and the urgent demand for sustainable transitions. Over the past two decades, supply chain management has expanded from focusing primarily on efficiency and cost minimization to addressing broader dimensions such as resilience, viability, and sustainability [1,2]. Viability has emerged as a meta-capability that integrates economic, environmental, and social objectives, while also emphasizing the long-term ability of supply chains to sustain their identity under continuous disruptions [3]. This perspective is particularly relevant in contexts where uncertainty cannot be reduced to probabilistic terms, as networks are increasingly exposed to unknown-unknown events such as pandemics, geopolitical shocks, or regulatory shifts [4]. Despite conceptual advances, much of the existing literature continues to operationalize resilience through simplified scenarios or static analyses, leaving limited room for adaptive responses [5]. As a result, the need for frameworks that combine robustness, adaptability, and circularity in supply chain design has become a central concern for both researchers and practitioners [6].

Recent scholarship has further emphasized that traditional optimization methods often fall short in addressing the multidimensional requirements of viable supply chains [7,8]. Classical stochastic and robust optimization approaches are effective in handling known-unknown uncertainties but are less suited to dynamic environments characterized by structural uncertainties [9,10]. This gap has prompted the exploration of biologically inspired paradigms, particularly analogies from the human immune system, which is inherently capable of rapid response and adaptive learning [11,12]. Immune-inspired frameworks highlight mechanisms such as sentinel nodes, redundancy, and memory as design principles for adaptive supply chains [13]. By translating these metaphors into mathematical constraints and indicators, immune-inspired approaches offer promising pathways for embedding adaptation into optimization-based models. Nevertheless, the integration of immune system principles with rigorous mathematical programming remains incipient, especially in applied contexts such as agro-industrial or energy-intensive supply chains. Addressing this gap requires models that simultaneously capture efficiency, resilience, and adaptability, thereby enabling decision-makers to anticipate disruptions while ensuring long-term viability. In particular, existing optimization approaches for supply chain design insufficiently operationalize adaptive viability—the ability to sustain objectives under deep uncertainty by combining robustness, autonomous response, and controlled recovery costs—pointing to the need for a modeling framework that embeds these properties within a rigorous mathematical program.

Within this broader landscape, carbon capture, utilization, and storage (CCUS) supply chains stand out as a domain where the interplay between viability and resilience is particularly critical. CCUS systems involve complex networks that encompass CO₂ capture from industrial and energy sources, conditioning and liquefaction, transportation through pipelines or ships, and final storage or utilization in industrial applications [14,15]. Their viability depends not only on economic factors such as the levelized cost of CO₂ capture and transport, but also on safety, environmental performance, and social acceptance [16,17]. Existing models tend to prioritize cost minimization and techno-economic assessments, often oversimplifying operational risks, multimodal transport thresholds, and the resilience of storage hubs [18,19,20]. Moreover, the integration of CCU pathways within CCUS supply chains, such as the production of methanol, urea, or building materials, has been insufficiently addressed from a systemic perspective [20,21,22]. This lack of comprehensive frameworks restricts the capacity to evaluate trade-offs between storage, utilization, and long-term adaptation [23]. Consequently, the design of CCUS supply chains represents a fertile ground to operationalize viability as a systemic property that balances efficiency, resilience, and circularity.

The Colombian context exemplifies both the urgency and the opportunity to advance CCUS supply chain design [24]. Studies highlight significant geological potential for CO₂ storage in offshore basins such as Guajira and Sinú [25], and in onshore formations including Cesar-Ranchería and Middle Magdalena [26]. Mid-century decarbonization pathways confirm that without CCUS, Colombia is unlikely to achieve its deep decarbonization goals, particularly in hard-to-abate sectors like cement, steel, and thermal power generation [27]. Offshore logistics models indicate that cryogenic shipping may be competitive with pipelines for flows above 2–3 MtCO₂ per year and distances greater than 400 km, closely aligning with Colombian industrial clusters [25]. However, national research also reveals institutional and regulatory barriers, limited integration of digital monitoring systems, and scarce empirical calibration of supply chain models with local data [28]. These constraints underscore the need for methodological frameworks that embed adaptive robustness and digital traceability, ensuring that CCUS networks can withstand unexpected disruptions while aligning with Colombia’s long-term decarbonization strategies.

This paper develops and tests an immune-inspired, goal-programming MILP framework to design viable CCUS supply chains that remain effective under both known and unknown uncertainties. We address the question: How can the viability of CCUS networks be quantified and strengthened by embedding adaptive responses—detection, redundancy, and memory—directly in the optimization model? We introduce the Immune-Structural Adaptive Response (RAIE) methodology, inspired by principles of the human immune system. This framework translates properties such as early detection (sentinel nodes), functional redundancy, adaptive memory, and structural reorganization into the design and evaluation of supply chains facing unexpected disruptions. Unlike classical approaches, RAIE does not rely solely on optimization under predefined scenarios but introduces dynamic metrics that assess the network’s ability to retain objectives, autonomously activate responses, adapt with controlled costs, and recover within acceptable timeframes. The application of this framework to the design of CCUS supply chains, particularly in the Colombian context, demonstrates how an immune-inspired perspective can contribute to building viable and resilient networks under conditions of profound uncertainty. In doing so, this research addresses critical gaps identified in the literature and positions RAIE as an original contribution for the analysis and design of supply chains in highly uncertain environments. We formalize the Immune-Structural Adaptive Response (RAIE) as a set of metrics and constraints—goal retention, autonomous activation, adaptation cost, recovery time, and service loss—and integrate them with multimodal CCUS logistics (capture, compression, liquefaction, pipelines/shipping, storage, and utilization). The formulation is instantiated for Colombia to demonstrate policy-relevant trade-offs.

Below we outline the structure of the paper. Section 2 synthesizes prior work on supply chain viability and resilience—with emphasis on CCUS networks—and distills the specific gaps that motivate our immune-inspired approach. Section 3 formalizes the problem setting and presents the RAIE methodology, detailing its metrics (goal retention, autonomous activation, adaptation cost, recovery time, and service loss) and how these are embedded in network design and evaluation. Section 4 describes the experimental setup, data and parameterization and reports the results of applying RAIE to CCUS supply chains, including sensitivity analyses to stressors and design levers. Section 5 interprets the findings, connects them to the identified gaps, and derives actionable guidance for practitioners and policy makers on designing viable, resilient CCUS networks under deep uncertainty. Section 6 summarizes the main contributions, acknowledges limitations, and outlines avenues for future research on immune-inspired, adaptability-centric supply chain design.

2. Literature Review

2.1. Supply Chain Viability

The concept of viability in supply chains has emerged as a central theme in recent operations and supply chain management research, reflecting the necessity of developing networks capable of withstanding turbulence while maintaining long-term operational and strategic integrity [29,30]. Unlike resilience, which focuses primarily on short-term recovery, viability refers to the systemic property of sustaining identity and functionality across dynamic and often unstable environments [31,32]. This perspective introduces viability as a meta-capability that integrates resilience, adaptability, and sustainability into a coherent framework [7,30]. It encompasses not only the capacity to absorb shocks but also the ability to adapt to evolving conditions such as market volatility, regulatory changes, or resource scarcity [33,34]. In this sense, viable supply chains are not merely reactive systems, but adaptive entities designed to perform under continuous uncertainty [35]. The notion of viability has also been linked to the ability of supply chains to balance efficiency with redundancy, demonstrating that long-term performance cannot rely solely on cost minimization but requires flexible structures and alternative configurations to remain feasible in diverse contexts [36].

Building on these conceptual foundations, scholars have proposed quantitative approaches to evaluate and operationalize viability in supply chain design [37]. Scenario-based stochastic programming has been employed to assess performance under multiple potential futures, highlighting how viability requires considering both expected and extreme-case outcomes [38]. Robust optimization methods also contribute by ensuring that feasible solutions persist across a wide range of uncertainties, thus guaranteeing continuity under disruptions [10,39]. In agro-industrial and energy-intensive supply chains, the incorporation of viability indicators has been critical, as perishability, seasonality, and technological constraints introduce unique vulnerabilities [40,41]. These contexts demonstrate that viability is not a universal or static concept but is shaped by the specific characteristics of products, processes, and infrastructure. Furthermore, researchers have emphasized the role of decision-support systems and digital technologies, such as digital twins and predictive analytics, in enhancing viability through real-time monitoring and adaptive response mechanisms [35,42,43]. This technological dimension reflects the growing consensus that viability requires both structural and informational robustness.

Literature underscores the multidimensional nature of viability, positioning it as a holistic framework that integrates economic, environmental, and social objectives while ensuring long-term feasibility [44]. For instance, studies highlight how viable supply chains must align with sustainability goals without compromising adaptability, thereby contributing to broader agendas such as climate resilience and social welfare [45]. The link between viability and resilience is particularly critical: while resilience emphasizes recovery after disruption, viability stresses sustained operation under persistent instability [30]. This distinction has important implications for mathematical modeling, as it necessitates performance indicators that go beyond efficiency metrics to capture adaptability, feasibility, and continuity [38]. The integration of these elements into supply chain optimization models marks a paradigm shift, moving from deterministic efficiency-oriented approaches to frameworks that value systemic endurance and adaptability [2]. As a result, the concept of viability provides not only a theoretical foundation but also a practical lens for guiding the design of robust, adaptive, and sustainable supply chain networks capable of navigating uncertain futures.

Supply chain viability requires distinguishing two uncertainty regimes with distinct instruments: known-unknowns, which can be modelled probabilistically (e.g., scenario-based stochastic programming), and unknown-unknowns or deep uncertainty, which call for non-parametric hedges (robust or distributionally robust optimization). Unified formulations integrate both regimes within a single decision problem and report feasibility/performance gains without permanent oversizing [46,47]. Complementarily, disaster-management studies propose phase-specific policies that “convert” unknown-unknowns into known-unknowns over the disaster cycle, reducing losses [48]. From complex systems, adaptive topological mechanisms (edge growth versus rewiring) yield quantified robustness improvements, though operational instrumentation remains limited [49]. Methodologically, pattern-oriented modelling advocates calibrating against multiple empirical patterns to move from known to unknown unknowns [50] and event-triggered designs when inputs are partly unknown [51]. Because CCUS risk frameworks remain fragmented and largely imported from general supply-chain studies [20], we subsequently validate these viability principles in a CCUS case.

2.2. Resilient Supply Chain Optimization

Resilience has been at the core of supply chain research for more than two decades, but recent studies increasingly focus on embedding resilience directly into optimization frameworks [52]. Traditionally, resilience has been conceptualized as the ability to resist, absorb, and recover from disruptions, often evaluated ex post through case studies or qualitative assessments [53]. However, with the growing frequency of global crises such as the COVID-19 pandemic, natural disasters, and geopolitical conflicts, scholars argue that resilience must become a built-in property of supply chain design rather than an afterthought [53]. Optimization-based approaches provide an avenue to formalize resilience, incorporating mechanisms such as redundancy, flexibility, and multi-sourcing into mathematical models [54]. For example, resilient supply chain optimization explicitly accounts for trade-offs between cost efficiency and preparedness, recognizing that short-term cost savings may undermine long-term continuity [55]. This shift also introduces resilience as a quantifiable design criterion, allowing decision-makers to systematically evaluate how alternative configurations perform under disruption scenarios [56]. As such, resilient optimization moves beyond descriptive analysis, creating actionable strategies that can be implemented in real-world supply chains.

One critical development in this area is the use of stochastic and robust optimization models to manage uncertainty in supply chain planning [52]. Stochastic programming allows supply chains to consider multiple potential futures and optimize for expected performance while hedging against adverse conditions [57]. Robust optimization, on the other hand, ensures feasibility across predefined uncertainty sets, creating supply chain configurations that can withstand variability in demand, supply, and transportation [58]. Hybrid models combining stochastic and robust approaches have also been proposed, offering flexibility in managing both probabilistic and non-probabilistic uncertainties [59]. Moreover, resilience has been linked to network topology, where structural properties such as connectivity, modularity, and clustering determine the ability to absorb shocks [60]. Mathematical models incorporating these structural dynamics show how supply chains can reconfigure routes and reallocate resources autonomously when nodes or links fail [61]. This highlights resilience not only as a functional property but as an emergent capability of network design.

Furthermore, resilient supply chain optimization has expanded to integrate sustainability and digitalization, reflecting the interconnected challenges of modern global networks [62]. Several studies show that resilience and sustainability are not mutually exclusive; rather, resilience mechanisms often enhance environmental and social outcomes by reducing waste, ensuring fair access, and stabilizing employment [63,64]. Digital technologies such as digital twins, artificial intelligence, and blockchain further augment resilience by enabling real-time visibility and predictive analytics [65]. These tools allow supply chains to anticipate disruptions and implement corrective measures proactively, thereby shortening recovery times and reducing vulnerability [66]. At the same time, researchers caution that resilience must not be equated with redundancy alone, as excessive buffers can generate inefficiencies and environmental burdens [67]. Instead, optimization models highlight the importance of balance, ensuring that resilience is achieved through intelligent design rather than excessive resource allocation [68]. Collectively, this body of work underscores the evolution of resilience from a reactive capacity to a strategic, quantifiable, and integrative component of supply chain optimization.

2.3. Immune-Inspired Approaches

An emerging strand of research introduces immune-inspired analogies as a novel lens to understand and design resilient supply chains [69]. The human immune system is often cited as one of the most robust adaptive systems in nature, capable of mounting immediate responses to pathogens through innate mechanisms while simultaneously developing long-term memory through adaptive processes [70]. Translating these principles to supply chains, researchers argue that networks should incorporate both rapid-response mechanisms and adaptive learning capabilities to survive in volatile environments [71]. For example, the concept of sentinel nodes, inspired by immune sentinels, can be applied to critical facilities that monitor and detect disruptions early, enabling proactive interventions [72]. Similarly, redundancy and degeneracy in supply chains resemble immune system properties, where multiple pathways and overlapping functionalities ensure continuity even when individual components fail [71]. These analogies provide powerful metaphors for embedding adaptive and self-organizing features into mathematical models of supply chain design.

From a methodological perspective, immune-inspired approaches have been operationalized through algorithms and optimization frameworks that mimic biological processes [73,74]. Clonal selection, immune memory, and negative selection algorithms have been adapted to solve complex logistics problems under uncertainty, demonstrating superior performance in dynamic environments [75]. These methods allow supply chains to autonomously explore solution spaces, adapt to new constraints, and refine responses as disruptions unfold [13]. Beyond computational heuristics, immune-inspired principles have been integrated into conceptual models of viability, emphasizing adaptability as a systemic property rather than a situational response. This perspective suggests that supply chains should not only anticipate known risks but also evolve mechanisms to handle “unknown unknowns,” a challenge that traditional robust and stochastic optimization struggles to address [76]. Thus, immune-inspired approaches complement existing optimization paradigms by introducing endogenous adaptation and learning capabilities.

Finally, the immune-inspired perspective contributes to bridging the gap between resilience and viability in supply chains [71]. While resilience emphasizes recovery and robustness, immune analogies highlight the importance of continuous monitoring, adaptation, and memory as critical elements for long-term viability [77]. For instance, immune memory translates into the ability of supply chains to learn from past disruptions, embedding adaptive rules that guide future decision-making [75]. Similarly, the immune system’s balance between attack and tolerance mirrors the trade-offs that supply chains face between redundancy and efficiency, or between flexibility and cost [13]. These insights have been particularly relevant in energy-intensive and CCUS-related contexts, where uncertainty is structural, and adaptive responses are essential for maintaining service continuity [74]. By formalizing immune-inspired mechanisms within optimization models, scholars propose a pathway toward supply chains that are not only resilient to disruptions but also viable in the long term, capable of evolving alongside changing technological, environmental, and societal demands [11,71,78].

2.4. CCUS Supply Chains

The design and operation of carbon capture, utilization, and storage (CCUS) supply chains have become a critical area of research for ensuring the viability and resilience of low-carbon energy transitions. Early studies emphasized the importance of integrated modeling approaches to address the multistage complexity of CCUS systems, which encompass capture, conditioning, compression, transport, utilization, and long-term storage [79,80,81]. Optimization-based frameworks have proven essential to support infrastructure design under uncertainty, particularly when evaluating multimodal transport options, diverse geological formations, and heterogeneous industrial utilization routes [82,83]. In recent years, research has increasingly focused on multi-objective optimization, seeking to balance economic, environmental, and social dimensions of feasibility [84,85].

From a viability perspective, techno-economic optimization studies have been central in evaluating when CCUS deployment can be competitive compared to alternative mitigation strategies [86]. Extensive research in Europe and Asia explored synergies among CO₂ liquefaction plants, pipeline networks, and shipping routes, demonstrating that transport cost structures and hub configurations are decisive for overall feasibility [87,88]. More recent models have expanded toward safety-driven or robust optimization, incorporating probabilistic risk parameters and failure modes in capture or storage facilities [20,89,90]. However, these formulations remain largely static, where uncertainty is exogenous and no endogenous mechanisms allow the system to adapt to perturbations.

Table 1 provides a comparative synthesis of representative studies on CCUS supply chain optimization, encompassing various formulations such as deterministic, stochastic, and hybrid models. Around 80% of studies use mathematical programming methods—mainly MILP and MINLP—to tackle network design and infrastructure configuration issues in CCUS supply chains. These approaches primarily focus on optimizing economic and environmental objectives, supporting the development of efficient and sustainable CCUS systems [91,92,93,94]. Among these, multi-objective models dominate, typically combining cost and emission minimization, as observed in Ostovari et al. [90], Nguyen et al. [95], and Koketsu et al. [96]. However, only a few studies explicitly treat uncertainty beyond deterministic assumptions through inexact or stochastic formulations [97,98,99].

Table 1. Comparative review of CCUS supply chain optimization studies.

Author	Model Type	Network Design	Multi-Objective	Uncertainty	Adaptive Capacities	Viability Analysis	Goal Retention	Cost of Adaptation	Risk Quantified	LCA	Regulatory Instrument Modeled	Reservoir/Injectivity Constraints	Validation (Sensitivity/Stress)
[90]	MILP (LCA-coupled)	✓	✓							✓			✓
[92]	MILP	✓											✓
[97]	Inexact optimization	✓		✓							✓		✓
[91]	MILP	✓											✓
[98]	MILP (MO)	✓						✓				✓
[22]	MINLP	✓	✓						✓				✓
[94]	Policy analysis			✓					✓		✓		✓
[95]	MILP (MO)	✓	✓									✓	✓
[16]	MILP (LCA)	✓		✓				✓		✓
[100]	MILP	✓							✓		✓	✓	✓
[96]	MILP	✓		✓				✓	✓		✓		✓
[93]	Stochastic MILP	✓		✓				✓	✓		✓		✓
[99]	MILP (MO)	✓						✓	✓		✓
[101]	MILP	✓	✓	✓				✓	✓		✓	✓	✓
[102]	MILP + Simulation	✓										✓	✓
[21]	Conceptual/Optimization												✓
[85]	MILP/MINLP	✓	✓						✓	✓	✓		✓
[15]	Robust MILP	✓	✓	✓				✓			✓
This studio	MILP + Adaptive Policies	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓

Incorporation of adaptive or recovery-oriented capacities remains limited, appearing marginally in safety-driven [22] or in frameworks that address operational resilience conceptually [99]. Likewise, viability-oriented dimensions, such as the inclusion of social, regulatory, or policy instruments, are rarely integrated; Liu [100] and Koketsu [96] constitute exceptions by linking CCUS deployment to carbon taxation and national decarbonization pathways. Only two works [22,85] quantitatively assess risk or safety, while LCA-based indicators are explicitly modeled in Ostovari et al. [90] and Nie et al. [16].

Furthermore, despite increasing sophistication in spatial and temporal modeling—e.g., the multi-period frameworks by Nguyen [95] and Jones et al. [85]—the literature still conceptualizes resilience and viability largely as ex-post evaluations rather than embedded system properties. In summary, although the reviewed studies collectively advance the techno-economic understanding of CCUS networks, none operate adaptive or viability metrics as endogenous components of the optimization process. This gap underscores the need for integrated frameworks capable of evaluating adaptive, viable, and learning-oriented network behaviors, such as the one developed in this study.

In addition to the optimization-focused studies summarized above, Kabir et al. [103] provide a systematic review and a conceptual risk-management framework for CCUS supply chains that links functions → risk factors → mitigation strategies. Their analysis highlights the scarcity of supply-chain-specific CCUS models and the need to integrate regulatory/traceability requirements and monitoring, reporting, and verification (MRV) practices into design decisions, rather than treating them as ex-post considerations. This aligns with our framing of viability dimensions as part of the optimization problem, and it justifies the inclusion of policy and interoperability constraints alongside economic and environmental objectives in CCUS network design. Similarly, Rajabi et al. [104] demonstrate, in a different domain, how bi-objective network design can incorporate adaptive levers—such as temporary distribution nodes and precautionary inventories—to mitigate sudden demand shocks. Although sector-specific, this study is instructive for CCUS because analogous endogenous responses (e.g., surge storage, temporary hubs, and rerouting policies) can be encoded within the decision space and evaluated through adaptive/recovery capacity metrics, moving resilience from a post hoc assessment to an intrinsic property of the optimization model.

At the regional level, research in Latin America—and particularly in Colombia—is gaining momentum within national decarbonization frameworks. Studies employing the Global Change Analysis Model (GCAM) indicate that achieving mid-century carbon neutrality requires maintaining natural gas and bioenergy systems coupled with CCUS to ensure energy security under stringent emission targets [24,25]. Geological assessments have identified significant storage potential in offshore basins such as Guajira and Sinú, and in onshore formations like Cesar–Ranchería and Middle Magdalena, positioning Colombia as one of the few South American countries with viable CO₂ storage capacity [105]. These formations, together with the concentration of industrial sources along the Caribbean coast, make offshore shipping-based logistics an efficient configuration for transporting captured CO₂ to saline aquifers or depleted hydrocarbon reservoirs [106,107]. Comparative analyses further suggest that maritime transport becomes cost-competitive with pipelines beyond approximately 400 km and for annual CO₂ flows of 2–3 Mt, a condition consistent with Colombia’s emission clusters and regional industrial hubs [25].

From a strategic standpoint, CCUS deployment in Colombia supports deep decarbonization while preserving the competitiveness of sectors such as cement, oil, gas, and refining [108]. The integration of enhanced oil recovery (EOR), emerging CO₂ utilization technologies, and digital traceability systems—including blockchain and AI-based monitoring—has been highlighted as essential for environmental integrity and public confidence [109]. Consequently, Colombia represents a relevant testbed for advancing models that capture adaptive, viable, and policy-coherent CCUS networks in geologically diverse and socio-economically sensitive contexts.

In summary, the reviewed literature reveals three dominant characteristics of current CCUS supply chain modeling: (i) a technically robust but behaviorally static optimization structure, (ii) a persistent gap in quantifying adaptive and recovery capacities, and (iii) a limited incorporation of regulatory, interoperability, and social viability dimensions. Addressing these limitations, therefore, requires a modeling framework capable of embedding endogenous responses—such as rerouting, surge storage activation, and recovery cost evaluation—directly within the optimization problem. The model developed in this study advances in that direction by integrating economic, environmental, safety, and regulatory criteria within a dynamic optimization structure that evaluates system continuity and viability under both known and unforeseen disruptions. The following subsection consolidates these insights, outlining the specific methodological gaps that motivate the proposed immune-inspired viability framework.

2.5. Research Gaps and Contributions

Despite the considerable progress achieved in modeling resilient and sustainable CCUS networks, several methodological challenges remain unresolved. Most existing frameworks emphasize cost efficiency and static feasibility, while the system’s ability to reorganize and recover from disruptions—especially under unknown–unknown conditions—remains unmodeled. Few studies quantify indicators that jointly assess goal retention, recovery time, and adaptation cost, and no study operationalizes these within an optimization environment. Additionally, the interplay between technical resilience and socio-institutional viability, including interoperability, traceability, and regulatory adaptability, continues to be underexplored.

This research addresses these gaps by introducing a viability-oriented optimization framework that integrates endogenous adaptive responses directly into the mathematical structure of a CCUS supply chain model. The framework combines multi-objective optimization, uncertainty treatment, and safety-driven constraints with dynamic indicators that capture system recovery, continuity, and reorganization efficiency. Unlike prior works that externalize uncertainty, this approach embeds it as part of the decision space—allowing the network to self-adjust under perturbations. In doing so, the study provides a comprehensive methodology for assessing technical, economic, and organizational viability in CCUS networks, with direct applicability to the Colombian context.

3. Proposed Methodology and Optimization Model

The design of RAIE is inspired by the human immune system (SIH) and its response to pathogens. The innate component is fast, local, and non-specific (analogous to minimum inventories and operational safeguards that stabilize the affected node during a crisis). The adaptive component coordinates a systemic response that redistributes functions to healthy organs (surge capacity and alternate routing to sustain throughput during the disruption). Finally, immune memory reduces convalescence time upon repeated exposures (recovery mechanisms that shorten the TTR once the shock ends). From an operational perspective, this analogy is implemented through scenario parameters acting on effective capacities, minimum inventory, and temporary losses, without altering the underlying optimization model structure. The analysis systematically compares ω across three severity levels (high, medium, low) and under two regimes (RAIE–ON vs. non-SIH), reporting both absolute and relative differences. Anchored in the immune metaphor, this reading enables attribution of RAIE’s benefits—backlog reduction, service-level enhancement, and TTR shortening—while also prioritizing critical corridors and nodes in the design. The results thus provide practical guidelines for reinforcing the CCUS network against plausible disruptions.

The methodological contribution of this study does not lie in the deterministic mixed-integer linear programming (MILP) model itself, which serves only as the structural backbone, but in the integration of RAIE framework as an analytical layer to evaluate network viability and resilience. The model is subjected to perturbations that represent known–unknown risks, that is, disruptions that are plausible and well recognized in the supply chain literature but uncertain in their magnitude or timing. These are operationalized through four scenarios: (i) disruption of a port infrastructure, (ii) performance degradation in a line to enhance oil recovery fields, (iii) temporary shutdown of a specific port infrastructure, and (iv) temporary shutdown of a specific line to enhance oil recovery fields. Each scenario is characterized by affected nodes, time windows, and severity parameters, which allows a systematic exploration of controlled failures and their impact on supply chain performance.

However, the methodology also seeks to transcend parametrized perturbations by addressing unknown–unknown risks, namely unexpected shocks that cannot be anticipated in the experimental design. To this end, RAIE incorporates an adaptive layer inspired by immunological principles, enabling the evaluation of the system’s capacity to: (i) retain essential goals under adverse conditions, (ii) autonomously activate alternative nodes or routes, (iii) temporarily reorganize inventories and flows, and (iv) explicitly measure costs and recovery times after disruption. The inputs of the methodology include structural data of the network, perturbation parameters, and indicators, while the outputs encompass not only optimal baseline configurations but also immune-inspired performance metrics RIM (Resilience Index Metrics), which quantify adaptive resilience beyond predefined scenarios. In this way, RAIE extends a deterministic MILP into a decision-support framework capable of analyzing operational continuity and structural reorganization under deep uncertainty.

3.1. Proposed Methodology

We introduce RAIE (Immune-Structural Adaptive Response) as an immunology-inspired methodological layer that complements a deterministic MILP model to evaluate supply chain viability and resilience under disruptions without relying on stochastic assumptions. Unlike robust or probabilistic formulations, RAIE establishes a mechanism-based response framework that specifies how the network reorganizes under deterministic stress tests (known–unknowns) and how it preserves essential goals when facing unanticipated shocks (unknown–unknowns). The inputs include structural data of the network (nodes, arcs, capacities, and costs), disruption parameters (affected node or arc, time window, and severity), and target levels for viability and resilience. The outputs comprise baseline configurations and flows, feasible reconfigurations after disruptions, and a set of immune-inspired indicators (RIM) that quantify goal retention, autonomous activation, adaptation cost, recovery time, and demand loss. RAIE operates through three complementary mechanisms: the homeostatic mechanism, which safeguards essential goals under stress through viability constraints; the adaptive mechanism, which activates backup capacity at healthy nodes and redistributes flows through alternative routes within deterministic bounds; and the memory mechanism, which maintains temporary overcapacity or additional inventories after a shock to accelerate recovery. The disruption scenarios implemented correspond to known–unknowns: they are plausible and documented but uncertain in timing and severity, modeled as parameterized shutdowns or degradations. The unknown–unknowns are not represented as explicit scenarios; instead, they are assessed indirectly through the system’s ability to retain goals, activate alternatives, and recover baseline performance with transient reinforcement, as captured by the RIM indicators. The innovative contribution of RAIE lies in shifting the focus from probability-dependent robustness to mechanism-driven adaptiveness: it makes explicit which elements are activated, which reinforcements are maintained, and for how long, thereby generating quantitative evidence of viability and resilience under deep uncertainty within a deterministic and reproducible framework.

The proposed framework unfolds in two complementary phases. Phase I (baseline design and operation): the multi-period design–operation problem is solved, determining which facilities and corridors are activated and how flows are scheduled on a quarterly basis. The outcome is a feasible configuration that maximizes net economic performance subject to mass balances, capacity limits, injectivity, mode-specific losses, and inventory constraints. This phase provides baseline series (e.g., throughput and capture per period) along with associated costs and revenues, which serve as quantitative references. Phase II (viability and resilience with RAIE): building on the frozen baseline design, disruption scenarios $\mathit{\omega }\in \mathit{\Omega }$ are introduced, parameterized by temporal window, severity, and location. In each ω, RAIE modulates the system’s response through three mechanisms: (i) innate, local elevation of minimum inventories during the shock; (ii) adaptive, surge capacity in healthy nodes to absorb deviations; and (iii) memory, transient post-shock reinforcement that accelerates recovery. For causal quantification, each scenario is executed under two conditions: RAIE–ON (with innate, adaptive, and memory mechanisms activated) and the counterfactual non-SIH condition (RAIE–OFF), maintaining identical severity and shock window. This symmetry allows isolating the contribution of RAIE to performance. Figure 1 illustrates the flow diagram of the proposed methodology.

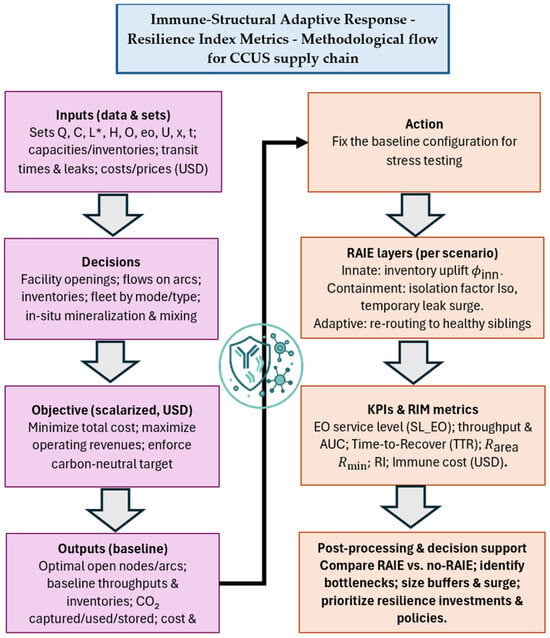
Figure 1. The flow diagram of the proposed methodology. Model sets. $Q$: capture sources; $C$: compression and gathering stations; $L^{*}$: liquefaction plants partitioned as $L_p$(offshore), $L_{geo}$(onshore), $L_{eor}$(EOR), and $L_{ind}$(industrial); $H$: offshore storage hubs; $O$: onshore storage hubs; $eo$: EOR fields; $U$: industrial utilization sites; $x$: mixing centers for mineralization; $t$: discrete time periods (quarters).

The design of RAIE is inspired by the human immune system and its response to pathogens. The innate component is fast, local, and non-specific (analogous to minimum inventories and operational safeguards that stabilize the affected node during a crisis). The adaptive component coordinates a systemic response that redistributes functions to healthy organs (surge capacity and alternate routing to sustain throughput during the disruption). Finally, immune memory reduces convalescence time upon repeated exposures (recovery mechanisms that shorten the TTR once the shock ends).

From an operational perspective, this analogy is implemented through scenario parameters acting on effective capacities, minimum inventory, and temporary losses, without altering the underlying optimization model structure. The analysis systematically compares ω across three severity levels (high, medium, low) and under two regimes (RAIE–ON vs. non-SIH), reporting both absolute and relative differences. Anchored in the immune metaphor, this reading enables attribution of RAIE’s benefits—backlog reduction, service-level enhancement, and TTR shortening—while also prioritizing critical corridors and nodes in the design. The results thus provide practical guidelines for reinforcing the CCUS network against plausible disruptions.

3.1.1. RAIE Layer (Innate–Adaptive–Memory) as a Control Policy

RAIE layer (Adaptive, Innate, and Memory-based Resilience) is implemented as a “response module” that acts on the baseline design of the CCUS chain for each scenario $\mathit{\omega }\in \mathit{\Omega }$ and each period t. Computation-wise, RAIE takes as input the shock masks (e.g., node shutdowns or degradations) and, without altering the network structure, temporarily adjusts the relevant operating parameters. The innate response is triggered immediately by raising minimum inventories and, where applicable, introducing a leakage/stress surcharge; in this way, it cushions the interruption prior to any tactical decisions. Containment partially isolates the affected node via an isolation factor ($Iso$) that reduces its operational contribution to prevent failure contagion, while a stress term captures transient losses or inefficiencies. The adaptive response reinforces “sibling” nodes—unaffected assets within the same functional family (e.g., other liquefaction plants)—through a bounded overcapacity, enabling flow diversion without reconfiguring the network. After the event, memory enhances effective capacity/inventory over a post-shock window, reflecting operational learning and enabling faster recovery. To ensure comparability across scenarios, nominal parameters are restored at the start of each ω\omegaω and only then are the RAIE layers applied, following mutually consistent and bound rules. The output of this sequence is a set of effective per-node, per-period parameters (e.g., capacities, leakage rates, and inventories) that feed the same original flow problem. In the next subsection, we formalize these adjustments and show how they translate into ω and t-dependent effective capacities, leakage rates, and inventory floors. Let $t\in T=\left\{1, 2, 3,..., 8\right\}$ denote the quarterly horizon, and let $S^{\omega }\subseteq T$ be the shock window of scenario ω. Define ${\chi }_f^{\omega }(t) \in \left\{0, 1\right\}$ as the shock indicator for family $f \in \left\{LP, LEO\right\}:{\chi }_f^{\omega }(t) =1$ if a disruption is active at time t, and 0 otherwise.

For a node $n$ in family $f$, with nominal capacity ${Cap}_f(n)$, the effective capacity under scenario ω $(1)$ is modeled as

$${Cap}_f^{\omega }\left(n,t\right)={Cap}_f\left(n\right)\left(1-{Iso}_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right) \left(1+\sum _{f\in F }\left(1-{\chi }_f^{\omega }\left(t\right)\right)1\left\{\exists shock infint\right\}\right)$$

(1)

where

$\left(1-{Iso}_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right)$ is the containment or isolation (loss).

$\left(1+\sum _{\forall f}\left(1-{\chi }_f^{\omega }\left(t\right)\right)1\left\{\exists shock in fint\right\}\right)$ is the system’s adaptive capacity.

${Iso}_f^{\omega }\left(n\right)\in \left[0, 1\right]$. is the fraction isolated during the shock (loss of capacity).

$\sum _{\mathit{f}\in \mathit{F} }\ge 0 \mathrm{h}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{o}\mathrm{u}\mathrm{s} \mathrm{s}\mathrm{u}\mathrm{r}\mathrm{g}\mathrm{e} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{a}\mathrm{t} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{h}\mathrm{y} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s} \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e} \mathrm{f}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{y} f$ while a shock is active.

The innate layer is implemented as a minimum inventory buffer—or operational ‘slack’—at affected nodes:

$${InvMin}_f^{\omega }\left(n,t\right)={InvMin}_f\left(n\right)\left(1+{\varphi }_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right)$$

(2)

where ${\varphi }_f^{\omega }\left(n\right)\ge 0$ raises the inventory floor during the shock.

Stress-induced leakage/shrinkage is modeled as a temporary increase in the loss coefficient:

$${\eta }_{mode}^{\omega }(t)={\eta }_{mode}^0+\Delta {\eta }_{mode}^{\omega }{\chi }_f^{\omega }\left(t\right)$$

(3)

Memory (2): post-shock recovery via $k=1,\dots ,$ W periods:

$${Cap}_f^{\omega }(n,t_{end}+k)={Cap}_f(n)\left(1+{\rho }_f^{\omega }{\displaystyle \frac{W-k+1}{W}}\right)$$

(4)

These rules act parametrically on capacity and loss terms within the constraints, enabling a RAIE–ON versus non-SIH comparison under identical severity.

3.1.2. RIM Metrics (Resilience–Viability–Performance) and Computation

To objectively evaluate performance under disruptions, we employ a set of RIM (Resilience Impact Metrics) designed to quantify the viability and resilience of the CCUS chain in each scenario ω and period t. The central idea is to compare, for key operating curves (e.g., total throughput and EO service), the scenario trajectory with its disruption-free baseline and to summarize the impact using normalized, interpretable indicators. Specifically, we use: (i) a viability flag Ω_OK(ω) indicating whether the model satisfies all constraints; (ii) service-level metrics (e.g., EO service) and the area under the capture/throughput curve over the horizon; and three strict resilience metrics: ${\mathcal{R}}_{area}$ (integrated performance loss during and after the shock), ${\mathcal{R}}_{min}$ (maximum relative pointwise drop), and TTR (time-to-recover), i.e., the first post-shock period in which the deviation falls below a technical tolerance. All metrics are constructed from the baseline curve y^base(t) and the scenario curve $Y_t^{\omega }$ (e.g., total throughput), such that ${\mathcal{R}}_{area}$∈ [0, 1] and ${\mathcal{R}}_{min }$∈ [0, 1] higher values imply greater resilience, while TTR is expressed in quarters. The area metric captures the accumulated severity of the impact (depth × duration), the minimum metric captures the worst instantaneous drop, and TTR captures the speed of recovery; together they provide a complementary view of dynamic behavior. To maintain comparability across scenarios and severity levels, we normalize by the area and maxima of the baseline curve and use a fixed tolerance $tolRec$ (e.g., 3–5%) to declare recovery. Finally, we report these metrics by functional module (LP and LEO) and for the entire system, thereby linking the RIM results to the RAIE layers (innate, adaptive, memory) and to the design’s economic–environmental trade-offs.

We next define the observable time series for scenario ω.

• Total throughput $Y_{\mathrm{t}}^{\omega }(t{CO}_2/quarter)$.
• Captura $C_t^{\omega }$ $(t{CO}_2/tquarter)$.
• Backlog EO $B_t^{\omega }$ $(t{CO}_2/quarter$).
• Baseline series $Y_{\mathrm{t}}^0,C_{\mathrm{t}}^0$.
• Area Under the Curve (AUC) and normalization:

$${AUC}_{Thru}^{\omega }=\sum _{t\in T}{Y}_t^{\omega },{AUC}_{Capt}^{\omega }=\sum _{t\in T}{C}_t^{\omega }$$

(5)

• Normalized indices (relative to the baseline):

$${RI}_{Thru}(\omega )={\displaystyle \frac{{AUC}_{Thru}^{\omega }}{{AUC}_{Thru}^0}},{RI}_{Capt}(\omega )={\displaystyle \frac{{AUC}_{Capt}^{\omega }}{{AUC}_{Capt}^0}}$$

(6)

• EO service level and backlog: Let $D_t^{EO}$ be the quarterly EO demand (or requirement):

  $${SL}_{EO}(\omega )={\displaystyle \frac{\sum _{t\in T}(D_t^{EO}-B_t^{\omega })}{\sum _{t\in T}{D}_t^{EO}}}=1-{\displaystyle \frac{\sum _{t\in T}{B}_t^{\omega }}{\sum _{t\in T}{D}_t^{EO}}}$$

  (7)

  with $B_{max}^{\omega }={max}_{t }{B}_t^{\omega }$ to quantify peak severity.

• Area-based resilience (resilience triangle). Define the per-period performance loss as $\Delta Y_t^{\omega }={(Y_t^0-Y_t^{\omega })}_{+}=max\{Y_t^0-Y_t^{\omega },0\}$. La resiliencia agregada (8) (más cercano a 1 es mejor) es:

  $${\mathcal{R}}_{area}(\omega )=1-{\displaystyle \frac{\sum _{t\in T}\Delta Y_t^{\omega }}{\sum _{t\in T}{Y}_t^0}}$$

  (8)
• Robustness over the window and vulnerability (9): Let $S^{\omega }$ be the shock window. The minimum instantaneous robustness:

  $${\mathcal{R}}_{min}(\omega )=\underset{t\in S^{\omega }}{\min }{\displaystyle \frac{Y_t^{\omega }}{Y_t^0}}, \nu (\omega )=1-{\mathcal{R}}_{min}(\omega )$$

  (9)

  captures the relative performance floor during the disruption.
• Time to recover (TTR) (10): Let $t_{end}^{\omega }=max S^{\omega }$ with tolerance $\delta \in \left(0, 1\right)$ and persistence m (quarters), the TTR is:

$$TTR(\omega )=min\{\tau \ge 0:Y_t^{\omega }\ge (1-\delta )Y_t^0 \forall t\in \{t_{end}^{\omega }+\tau ,\dots ,t_{end}^{\omega }+\tau +m-1\left\}\right\}$$

(10)

It is worth clarifying that the effective-capacity formulation is not a standard equation in the optimization literature; rather, it is derived from the immunological logic that underpins the RAIE methodology. The term $\left(1-{Iso}_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right)$ represents the system’s innate response, modeling isolation and the temporary loss of capacity at an affected node. The term $1+\sum _{\forall f}\left(1-{\chi }_f^{\omega }\left(t\right)\right)$ corresponds to the adaptive response, in which backup capacity is enabled at healthy nodes of the same family to compensate for the disruption. Finally, the memory mechanism is incorporated via the transient persistence of overcapacity or additional inventories after the shock. This mathematical formalism is justified by the analogy with the human immune system [13], where processes of containment, compensation, and reinforcement are essential for the viability of complex systems. In this sense, the equations are not arbitrary; they constitute a translation of immunological principles into a deterministic MILP framework designed to capture the network’s dynamics of isolation, adaptation, and recovery.

The metrics employed in this study are drawn from the existing literature on supply chain viability and resilience (e.g., service level, capacity utilization, costs, recovery times) and therefore do not constitute new indicators by themselves. However, their integration into an immune-inspired system metrics (RIM) represents the methodological contribution, as they are reorganized according to the mechanisms of the RAIE framework (homeostasis, adaptation, and memory). This articulation enables the interpretation of network performance under disruptions not only in operational terms but also as quantifiable immune-like responses.

3.2. Proposed MIP Approach

3.2.1. Model Overview

We formulate an optimization model for a CCUS network (capture–conditioning–transport–use/storage) over a tactical, discrete eight-quarter horizon, whose objective is to size and operate a physically viable, economically attractive, and carbon-neutral configuration (see Appendix B). The chain integrates 12 capture sources $q$ (with a cement sub-set), 7 compression and collection stations $c$, liquefaction plants ll structured into destination-based subsets $Lp$—ports/offshore—$Lgeo$ onshore geologic, $Leor$— EOR fields, and $Lind$— industrial uses), storage hubs offshore $h$ and onshore $o$, 5 production fields with enhanced recovery $eo$, and 3 industrial-use nodes $u$. Between $q$ and $c$, we model mixing centers $x$ co-located with each source, which homogenize qualities and allow diversion without reprocessing when technically feasible. Transport combines existing pipelines along four corridors ($ta, te, ti, ti$), road modes (cryogenic fleets differentiated by type: $ca, ka, cam, kam$), and maritime shipping ($bar$). The model is multi-objective with an aggregated objective in monetary units (US$) that internalizes three goals: total costs, revenues from CO₂ use, and a penalty on residual emissions to achieve carbon neutrality. The formulation is mixed-integer at the structural level and linear in operations; it is solved in GAMS Release 51.3.0/CPLEX, reporting CPU times compatible with tactical, meso-scale studies.

The CCUS network can be conceptualized as a multi-echelon system comprising interdependent upstream, midstream, and downstream layers. The upstream segment includes industrial emitters such as cement, steel, and power plants, which act as CO₂ sources feeding the capture subsystem. The midstream layer encompasses compression and liquefaction facilities—often managed by energy operators or service providers—responsible for conditioning CO₂ for multimodal transport via pipelines, cryogenic trucks, or ships. The downstream layer integrates storage and utilization pathways: offshore and onshore geological reservoirs managed by energy agencies, enhanced-oil-recovery (EOR) fields operated by petroleum companies, and industrial users that convert CO₂ into chemicals or construction materials. Cross-cutting stakeholders such as regulators, port authorities, and digital-monitoring providers ensure traceability, safety, and carbon-neutral compliance across the chain. This layered configuration establishes the physical and institutional backbone on which the RAIE-based MILP model operates, allowing the analysis of both logistical and adaptive dynamics in an integrated manner.

Model Logic and Data Sources

The MILP model follows a hierarchical logic that combines strategic and tactical decisions within a unified optimization framework. It simultaneously determines (i) the activation of facilities, (ii) multimodal transport flows, (iii) storage and inventory levels, and (iv) carbon use and storage decisions, subject to cost, emission, and capacity constraints. Each decision variable and equation corresponds directly to a physical or operational process in the CCUS network—capture, compression, liquefaction, transport (pipeline, ship, or truck), injection, and mineralization—ensuring transparent interpretability between mathematical entities and engineering actions.

The parameter database was compiled from three complementary sources:

(1)

Scientific literature, including techno-economic and geospatial data for CO₂ capture, transport, and storage (DOE/NETL CO₂ Transport Cost Model);

(2)

Industrial specifications, such as cryogenic truck and ship performance (Northern Lights, Mitsubishi, FIBA, Chart Industries), and Geological and territorial data from the Colombian Geological Survey and the National Hydrocarbons Agency (ANH).

(3)

All parameters were standardized to consistent units (USD/tCO₂, tCO₂/km, USD/t·km) and verified through dimensional consistency checks.

Calibration was conducted through internal consistency tests and sensitivity analysis on key parameters (capture efficiency, injectivity, leak rate). The entire dataset is traceable and publicly reproducible, as summarized in Appendix B (Table A4). This guarantees that the optimization results are not parameter-dependent artifacts but a coherent representation of CCUS network behavior under realistic industrial and territorial conditions.

Network Structure and Destination-Based Partitioning of Liquefaction Plants

A central feature of the case is the functional partitioning of the liquefaction plants $\mathit{l}$ into four mutually exclusive subsets, defined by the final destination and the quality/treatment-time requirements of the compressed CO₂:

• $L_p$ (6 alternatives): Liquefaction with maritime shipment to offshore hubs $h$; requires high purity and robust cryogenic conditions for marine carriage, with longer processing times (dehydration, impurity polishing, phase stabilization).
• $L_{geo}$ (4 alternatives): Liquefaction with road dispatch to onshore storage complexes $o$; permits somewhat shorter operating windows than $L_p$ and purity specifications compatible with saline injection (water NOₓ/SOₓ limits).
• $L_{eor}$ (4 alternatives): Oriented to production fields with enhanced oil recovery (EOR use); they require tighter pressure/temperature windows and bounded impurity levels (for reservoir compatibility), which translate into longer residence times and higher capacity consumption per metric ton treated.
• $L_{ind}$ (3 alternatives): Supply to industrial uses; these allow industry-specific specifications (beverages, chemicals, materials), with differentiated treatments that the model represents as process coefficients and specific costs. This segmentation is not cosmetic: it translates into routing constraints (which destinations each $\mathit{l}$ effective-capacity coefficients (hour-equivalents per tCO₂), and quality/impurity limits, so that the decision to activate $\mathit{l}$ and allocate flows entails measurable operational trade-offs.

Quality Treatment, Specifications, and Processing Times

Post-compression conditioning is modeled using quality balances at the route and destination levels:

• Purity and moisture: Each arc from $l$ to $h/o/eo/u$ enforces a minimum quality. If the $q$ blend via the mixing center $x$ contains impurities above thresholds, polishing modules are activated, incurring additional costs and processing-time adders.
• NOₓ/SOₓ/trace-compound risks: Stricter limits are enforced for EOR than for $o/h$, industrial-use specifications are parameterized by subsector.
• Processing–time coefficients ($\tau$): The processing time per metric ton depends on the liquefaction subset $l$ ($L_p, L_{geo}, L_{eor}, L_{ind}$) and on inlet quality; the plant’s equivalent capacity is computed as ${Cap}_l^{eff}$= ${Cap}_l^{nom}/\tau ,$ thus linking quality to productivity, where τ is the processing time per ton.
• Mode- and segment-specific losses/leakage (pipeline, cryogenic road, maritime) are included in the mass balances and in the objective function’s emissions accounting.

CO₂ Mineralization: In Situ and Ex Situ

The model considers CO₂ utilization via mineralization under two complementary schemes:

• In situ mineralization: Modeled at specific nodes co-located with capture centers. At these nodes, a fraction of the CO2_22 is fixed directly into nearby minerals via mineral carbonation reactions in suitable formations (ultramafic/saline), represented in aggregate through stoichiometric yields and per-period injectivity limits.
• Ex situ mineralization: Reaction of CO₂ with carbonateable solids $\mathit{m}$ (slag, ashes, Ca/Mg-rich residues, quarry fines) under processing platforms co-located with cement plants $QCem\subset Q$. We model an eligibility matrix $m_{elig}\subset m$ and stoichiometric coefficients (${\mathsf{\alpha }}_{\mathit{m}}$) that convert tCO₂ into tonnes of carbonated mineral, with energy consumption and curing/process-time cycles that limit throughput. Both pathways compete for utilizable CO₂ and therefore enter the economic objective (product/service revenues) and the environmental objective (credits for durable fixation), while preserving mass and quality consistency.

Decision Variables

Binary–type variables select the activation of nodes $l, h, o$ and modular capacity blocks; continuous variables determine arc-by-period flows $t$, inventory levels at $c, l$, fleet allocation by vehicle type, and blending at $x$. ey decisions include (i) which $l$ plants to open and which destinations to serve; (ii) how to blend $q$ streams to meet minimum quality at the lowest processing cost; (iii) multimodal routing subject to capacities, transit times, and losses; (iv) inventory policies at $c, l$ (safety stock, technical maxima); and (v) the allocation of CO₂ among EOR, mineralization, and other uses, maximizing economic value while achieving carbon neutrality.

Objective Function and Carbon Accounting (Values in USD)

The objective function is multi-objective and expressed entirely in USD, thereby placing economic and environmental performance on a common, commensurate scale:

$$\begin{array}{c}Min=\{\underset{CAPEX, OPEX, energy, treatment}{\underbrace{Logistics and processing costs}}-\underset{\mathit{price} \mathit{per} \mathit{tCO2} \mathit{utilized}}{\underbrace{Revenues from EOR and other uses}}\\ +\underset{\mathit{C}\mathit{O}2-\mathit{n}\mathit{e}\mathit{u}\mathit{t}\mathit{r}\mathit{a}\mathit{l}\mathit{i}\mathit{t}\mathit{y}\mathit{s}\mathit{h}\mathit{a}\mathit{d}\mathit{o}\mathit{w}\mathit{p}\mathit{r}\mathit{i}\mathit{c}\mathit{e}}{\underbrace{Net-emissions penalty}}]\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}$$

(11)

Net emissions account for compression/liquefaction energy, transport losses, maritime/road transits, and credits from geological storage and mineralization (in situ/ex situ). Carbon neutrality is enforced either as a hard constraint or as a penalized term, depending on the experimental design.

3.2.2. Main Constraints

• Mass and quality balance at each node and period (includes impurities and minimum purity by route/destination).
• Nominal and effective capacities in liquefaction (via τ\tauτ), compression, geological storage, and injectivity.
• Inventories: Min/max bounds, inter-period carryover, and leakage.
• Multimodal transport: Pipeline limits (by corridor and direction), fleets (number/type, shifts), barges (time windows, minimum lot sizes), and transit times.
• Routing compatibility: Each $\mathit{l}$ serves only authorized destinations (port/geo/eor/ind).
• Mineralization: Stoichiometric yields, processing times, capacity curves, and energy consumption by $m$ (carbonateable solids set).
• Environmental: Neutrality (or emissions budget), regulatory limits (e.g., NOₓ/SOₓ, water), maximum leakage per link.
• Operational rules: Technical start-up minima, lot sizes, blending ratios, and dispatch priorities.

Key Assumptions

• Deterministic data for Phase I (design): Capacities, costs, yields, routes, and specifications are taken from industrial sources and literature; Phase II (RAIE) introduces the perturbations ω
• Intra-period homogeneity: Parameters and decisions are constant within each quarter; processing times are aggregated into τ
• Quality bounding: Thresholds (purity/impurities) and treatment coefficients are used; no detailed thermodynamic model is solved.
• Given topology: Pre-existing pipeline corridors and a plausible geometry for road and maritime routes.
• Markets: EOR/industrial prices are exogenous by scenario; energy costs and CO₂ shadow prices are consistent with the context.
• Operational safety: Pressure/temperature and leakage limits are incorporated as bounds and specific loss factors.

Although the model is subjected to deterministic disruption scenarios (known–unknowns), the treatment of unknown–unknowns is not based on the direct simulation of hypothetical events, as in traditional stochastic models. Instead, it relies on the RAIE methodology, which translates immunological principles into network analysis: goal retention, autonomous activation, adaptive reorganization, and transient reinforcement. In this sense, the scenarios function solely as stress tests that reveal the system’s response capacity. The extrapolation toward unknown–unknowns arises from observing whether the network preserves its essential properties under disruptions not explicitly modeled, which is assessed through immune-inspired metrics.

The extrapolation toward unknown–unknowns arises from observing whether the network preserves its essential properties under disruptions not explicitly modeled, which is assessed through immune-inspired metrics. The mathematical formulation of these post-optimization dynamics—including the interaction between goal retention, adaptive activation, and recovery trajectories—is detailed in Appendix C (RAIE Post-Optimization Dynamics). This Appendix formalizes how the immune-inspired metrics evolve beyond the deterministic optimization stage, capturing transient recovery processes and adaptive reconfigurations that ensure network viability over time.

4. Computational Analysis

4.1. Background of Real Application Case

The application of the proposed model to the robust design of a CCUS supply chain (capture, transport, utilization, and storage of CO₂) along Colombia’s Atlantic coastal zone is illustrated through a case study based on real-world data. The chain undertakes tactical planning over an eight-quarter horizon and must assess its network structure to select a configuration that jointly delivers operational viability and resilience to perturbations, while simultaneously optimizing economic and environmental performance. The practical interest is twofold: to ensure compliance with decarbonization commitments and, at the same time, to make CO₂ utilization in industrial and enhanced oil recovery (EOR) applications viable.

The physical network considered integrates the key links of a multimodal CCUS chain. At the origin there are 12 capture sources, including a subset of cement plants that enable comparison of alternative capture-and-use routes. Captured CO₂ is conditioned at 7 candidate compression and buffer stations and then feeds four families of liquefaction plants: (i) six candidate plants that liquefy CO₂ at port complexes for offshore dispatch; (ii) four plants that liquefy for onshore hubs; (iii) four liquefaction plants supplying EOR fields; and (iv) three plants that connect liquefied gas to industrial uses. The system also comprises six offshore storage hubs and four onshore hubs, three industrial-use nodes, and five EOR fields. To increase operational flexibility, mixing centers co-located with each capture source are modeled; these homogenize qualities and enable diversions without additional reprocessing when technically feasible. Figure 2 shows the potential locations of the nodes in the CCUS logistics network under analysis.

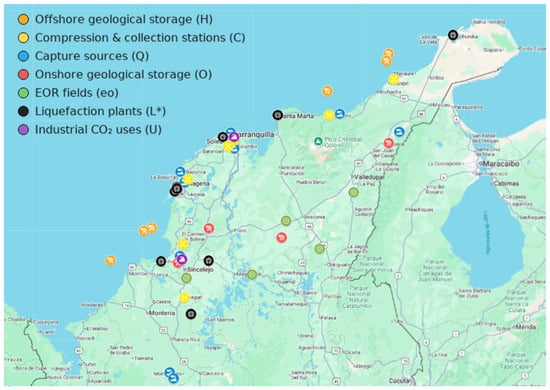
Figure 2. Node locations in the CCUS network approximation.

Transport combines existing pipelines along four main corridors, road modes with different types of cryogenic trucks, and the maritime mode for port connections to offshore hubs. All arcs are subject to per-period capacity limits, transit times, and mode-specific losses/leakage, while storage/use nodes carry inventory limits and injectivity/substitution bounds where applicable (e.g., in EOR). Model decisions are taken quarterly and include the assignment of flows on each arc, inventory levels at liquefaction plants and mixing centers, fleet utilization by type and mode, and the activation of redundancy and rerouting mechanisms. All physical quantities are expressed in tonnes of CO₂ (tCO₂).

The Carbon Capture, Utilization, and Storage (CCUS) process, oriented toward carbon neutrality, integrates multiple technological and logistics links whose purpose is to reduce net CO₂ emissions through a cycle of capture, transformation, and geological or mineral fixation. First, carbon dioxide is captured at large stationary industrial sources—such as cement plants, thermal power stations, or refineries—using cryogenic separation, adsorption, or membrane systems. This CO₂ is subsequently compressed at compression centers to reach the pressures required for safe transport. The transport infrastructure includes cryogenic trucks, specialized vessels, and high-pressure pipeline networks, enabling movement of CO₂ to liquefaction plants, intermediate hubs, or directly to storage and end-use sites. Once liquefied in cryogenic plants, CO₂ attains temperature and pressure conditions that optimize both fluid density and logistics efficiency. In this state, the gas can be directed to: (i) deep geological storage in saline formations, saline aquifers, or depleted reservoirs, both offshore and onshore; (ii) industrial uses such as beverage carbonation, chemical processes, or materials synthesis; and (iii) enhanced oil recovery (EOR) operations, where injected CO₂ increases the recovery factor while simultaneously becoming stably confined within the porous rock. Figure 3 presents the CO₂ capture and storage network.

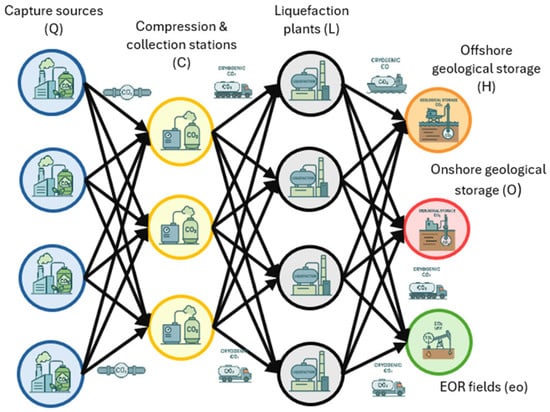
Figure 3. CCS Net.

A distinctive feature of a carbon-neutral CCUS chain is the inclusion of both in situ and ex situ mineralization processes. In the in situ case, CO₂ is injected directly into geologic formations rich in magnesium- and calcium-silicate minerals, where it reacts with subsurface minerals to form stable carbonates (CaCO₃, MgCO₃). This mechanism emulates natural mineral carbonation that occurs over geologic timescales, but is accelerated by controlling pressures, flow rates, and geochemical conditions. By contrast, in ex situ mineralization at mixing centers, CO₂ is combined with industrial residues (e.g., steel slag, fly ash, or cement dust) in reactors engineered to promote the formation of solid carbonates, which can be reintegrated into value chains as additives in cement production or construction materials (Figure 4). Integrating both mineralization pathways ensures not only permanent carbon capture but also the generation of value-added by-products, thereby strengthening the chain’s economic viability. This holistic approach yields a CCUS network with adaptive resilience to operational disruptions and aligns the system with carbon-neutrality objectives set by international sustainability commitments.

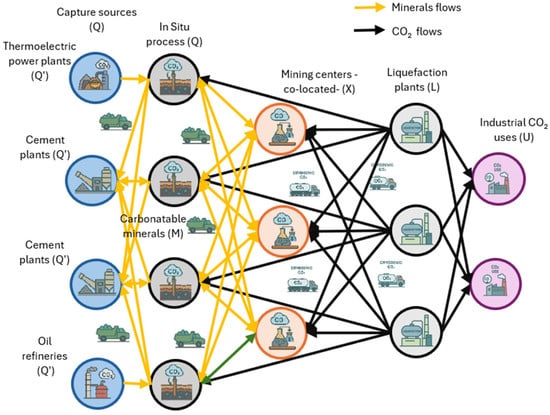
Figure 4. CCU Net.

4.2. Experimental Settings

The computational evaluation is structured in two phases. First, the network design problem (eight-quarter horizon) is solved once, and the optimal configuration of nodes and arcs is fixed. On this fixed network, we run a scenario-based design of experiments over Ω with three severity levels (low, medium, high). Each scenario represents an operationally plausible event in the CCUS chain: (i) an interruption at a port liquefaction plant (LP); (ii) degradation at a liquefaction plant meeting CO₂ treatment specification for EOR (LEO); (iii) temporary shutdown of a specific LP; and (iv) temporary shutdown of a specific LEO. All experiments are executed with the RAIE layer active (innate, adaptive, and memory); for sensitivity analysis, non-SIH variants with RAIE disabled are considered where appropriate. Performance metrics include economic/environmental KPIs and the RIM metrics (R_min, R_area, TTR), reported by scenario and severity. The planning horizon is quarterly ($T=t1\dots t8$). Flows and inventories are expressed in tons of CO₂ (tCO₂); costs/benefits are in USD. Geographic locations and nominal capacities are taken from the node dataset (map in Figure 2) and from the transport cost/time bases described in the data section. All models are solved in GAMS/CPLEX and run on a desktop PC (Windows 10, Intel^® Core™ i5, 16 GB RAM). The experimental design uses batch runs (a loop over Ω × severity), storing KPIs and RIM outputs per run for subsequent graphical and tabular analysis.

Table 2 summarizes the scenarios considered and the temporal window during which each disruption is activated (for high severity). Medium and low severities reduce the window length by 1 and 2 periods, respectively, while keeping the start time fixed. In a CCUS chain, the critical points—liquefaction plants with CO₂ treatment specifications for geological storage and EOR—concentrate: (i) the CO₂ state conversion, (ii) multimodal coupling (road–maritime–pipeline), and (iii) injectivity/storage constraints. Accordingly, the most plausible disruptions with the greatest systemic impact are:

• L_P shutdown/degradation (operational failures, corrective maintenance, port/energy constraints).
• L_EO degradation/shutdown (EOR injectivity limitations, geomechanical or regulatory constraints).

Table 2. Summary of the scenarios considered.

Scenario ω	Description	Affected Node	Window (t)
ω1: LP-disruption	Port LP shutdown	lP3	t3–t6
ω2: LEO-degradation	LEO degradation	leor1	t4–t7
ω3: LP-shutdown	Temporary shutdown of a specific LP	lP1	t1–t5
ω4: LEO-shutdown	Temporary shutdown of a specific LEO	leor4	t2–t6

Table 2. Summary of the scenarios considered.

Scenario ω	Description	Affected Node	Window (t)
ω1: LP-disruption	Port LP shutdown	lP3	t3–t6
ω2: LEO-degradation	LEO degradation	leor1	t4–t7
ω3: LP-shutdown	Temporary shutdown of a specific LP	lP1	t1–t5
ω4: LEO-shutdown	Temporary shutdown of a specific LEO	leor4	t2–t6

The process of modelling shutdowns and degradations using temporal windows and severity levels is commonly employed in robust design and stress testing focused on system viability. During these assessments, performance is measured under various perturbation parameters, and the system’s response —such as changes in flow, temporary losses, and recovery—is observed. Theoretically, this aligns with viability (the ability to sustain and adapt in a changing environment) and resilience (absorb–recover), both of which call for scenario analysis and parameter sensitivity when uncertainty spans the known-unknown and the unknown-unknown.

Each severity level is characterized by (i) the window duration and (ii) a set of parameters that operationalize the RAIE ‘arms’ in the model: Innate (φ: temporary inventory floor), Containment (Iso: fraction of capacity isolated at the affected node; the operable share is 1-Iso), Leakage/Stress ($LeakSurge$), and rerouting load (Σ: temporary overcost/penalty factor for deviations). Distinct levels are used for L_P and L_EO, consistent with their roles in the network. Setting three severity levels (high–medium–low) yields an experimental design comparable to orthogonal arrays or batteries of cases that explore ‘types’ and ‘magnitudes’ of uncertainty—a common practice for policy validation and sensitivity analysis (including Taguchi arrays where appropriate).

The specific parameterization of each severity level is summarized in Table 3. For every disruption archetype—LP (liquefaction–port), LEO (liquefaction–EOR), and their corresponding onshore counterparts—the parameters define the intensity of the RAIE response “arms”: φ (temporary inventory-floor increase), Iso (isolation share at the affected node), LeakSurge (transient throughput loss), and Σ (adaptive slack coefficient). These values were calibrated through pilot runs to ensure consistent stress magnitudes across experiments and to preserve model feasibility while enabling comparative analysis between RAIE-ON and non-SIH configurations.

Table 3. Severity-level parameters.

Severity	Duration	φ_LP	Iso_LP	LeakSurge_LP	ΣLP	φ_LEO	Iso_LEO	LeakSurge_LEO	Σ_LEO
High	Table 1	0.30	0.85	0.20	0.30	0.50	0.80	0.12	0.25
Medium	2 periods	0.20	0.75	0.10	0.20	0.35	0.70	0.08	0.15
Low	1 period	0.10	0.60	0.05	0.10	0.20	0.60	0.05	0.10

For each (ω, severidad) the model is solved on the fixed network of the optimal design. We collect (i) KPIs (Z, Total cost, Income, Emisiones, AUC_Capture, AUC_Thru, SL_EO) and (ii) RIM metrics (R_min, R_area, TTR along with throughput and inventory time series for visualization. The Tables/Figures in Section 4.3.2. report comparisons by scenario and severity, as well as the effect of RAIE versus non-SIH. By targeting shocks at these propagation bottlenecks, the experiment captures both local failures (shutdowns/degradations) and systemic effects (constraints toward EOR)—the two risk classes with the greatest potential to compromise CCUS network viability. The parametric representation of each shock—via capacity isolation (Iso), transient stress losses (LeakSurge) and temporary inventory-floor increases (φ)—reflects operational mechanisms observable in practice (derating, pressure-induced inefficiencies, and safety buffers), while the adaptive surge (Σ) captures the temporary availability of slack at healthy facilities without altering topology. This direct correspondence between parameters and operational decisions confers construct validity on the disruption treatment.

Recent literature distinguishes viability (sustain/adapt over time) from resilience, understood narrowly as stability–recovery, and advocates systematic stress testing to evaluate policies and their associated costs. In parallel, the immune analogy for supply chains (innate–adaptive–memory) supports the use of operational layers that modulate effective capacities, buffers, and recovery without redesigning topology at each shock. Our set (LP-disruption, LEO-degradation, LP-shutdown, LEO-shutdown) covers local failures and systemic bottlenecks (EOR/LEO), the two risk archetypes with the greatest propagation (“ripple”) in CCUS. Testing each at three severity levels and with/without RAIE (RAIE–ON vs. non-SIH) enables causal attribution of RAIE’s contribution to SL, backlog, R_area, R_min and TTR—precisely the kind of evidence called for by contemporary viability and robustness approaches.

Finally, the RIM metrics employed—area and relative-minimum indices, service level, and time-to-recover (TTR)—provide an integrated reading of dynamic performance (depth, temporal extent, and speed of return), ensuring reproducibility and transferability of the protocol to other geographies or CCUS configurations with minimal parameter adjustments. Taken together, the experimental plan combines operational realism, statistical control, and traceability of effects, meeting the validity criteria required for the scientific evaluation of viability and resilience in CCUS networks.

4.3. Computational Results

4.3.1. CCUS Supply Chain Design

The solution to the design problem yields a CCUS network with all capture sources active (12/12); four compression and buffer stations (c₁, c₃, c₅, c₇); three port-based liquefaction plants for shipments to offshore geological storage (l_P1, l_P3, l_P6); three liquefaction plants for shipments to onshore geological storage (l_geo1–l_geo3); two liquefaction plants supplying CO₂ for EOR uses (leor1 and leor4); three liquefaction plants for industrial CO₂ use (l_ind1–l_ind3); and one CO₂–minerals mixing center (x₈) for cement plants. This configuration—fixed for the scenario evaluation—achieves an objective value of 1.043 × 10⁹ USD, with total costs of 1.635 × 10⁹ USD and system revenues of 7.043 × 10⁸ USD (see Table 4).

Table 4. Baseline CCUS network design and performance summary (Phase I).

Block	Metric	Value	Unit/Notes
Topology (activated)	Capture sources (Q)	12 (all)	—
	Compression & collection (C)	4 (c1, c3, c5, c7)	Activated facilities (binary = 1)
	Liquefaction—ports (LPuerto)	3 (lPuerto1, lPuerto3, lPuerto6)	For offshore/port dispatch
	Liquefaction—onshore (Lgeo)	3 (lgeo1–lgeo3)	Feeding onshore hubs
	Liquefaction—EOR (LEO)	2 (leor1, leor4)	Feeding EOR branch
	Liquefaction Industrial use (Lind)	3 (lind1–lind3)	CO2 utilization (industry)
	Hubs (offshore H/onshore O)	6 H/4 O	Storage nodes
	Mixing lefts (x)	1 (x8)	Co-located blending
Horizon & units	Planning horizon	8 (t1–t8)	Quarters
	Flow/inventory units	—	tCO2
	Economic units	—	USD
Economic objective	Objective value Z	1.055 × 109	USD
Aggregate physical KPIs	AUC_Thru (total throughput)	3,546,200.000	tCO2 (sum over t1–t8)
	Avg. throughput per quarter	443,275.000	tCO2/q (=AUC_Thru/8)
	AUC_Capt (CO2 captured)	3,689,262.803	tCO2 (sum over t1–t8)
	Avg. capture per quarter	461,157.850	tCO2/q (=AUC_Capt/8)
Service (EOR)	SL_EO	1.000	Fraction satisfied (100%)
	EO backlog (total/peak)	0/0	tCO2
Carbon-neutral target	Net emissions (baseline)	Satisfied	Target enforced in the objective
RIM baseline (normalized)	RIThru	1.000	vs. baseline (by definition)
	RICapt	1.000	vs. baseline (by definition)
	Rarea	1.000	No loss area in baseline
	Rmin	1.000	No performance dip
	TTR	—	Not applicable (no shock)
Sustainability angle	Climate mitigation	Verified	High capture & storage/use throughput
	Socio-economic co-benefits	Present	Industrial use nodes active; port/industrial corridors engaged

Solving the design problem delivers a network configuration that maximizes net economic performance (USD) while, in parallel, internalizing the carbon-neutrality target through the corresponding term in the objective function. The baseline result (Ω°) exhibits full service to EOR and no backlog, with stable throughput trajectories along the network’s two technological corridors (C-L-H/L_P and C-L-EO/L_EO). In aggregate terms, the indicators AUC_Capt and AUC_Thru reach, respectively, on the order of 3.69 × 10⁶ tCO₂ y 3.55 × 10⁶ tCO₂ over the eight quarters, providing a robust baseline for subsequent experiments (Table 1). Convergence to this design confirms the system’s techno-economic viability under realistic assumptions on capacities, transit times, and losses, and satisfies the net-emissions constraint required by the carbon-neutrality target.

From an environmental sustainability perspective, the design functions as a verifiable abatement mechanism: capture at emitting sources is coupled with compression, liquefaction, and multimodal transport (pipeline, road, maritime) to onshore/offshore geological storage nodes and industrial uses. In the baseline, CO₂ utilization for EOR is fully satisfied (SL_EO = 1.000), while storage trajectories at onshore/offshore hubs keep inventories within safety bounds, reducing risks of venting and leakage. The fact that AUC_Capt ≈ AUC_Thru over the horizon (with marginal differences attributable to mode-specific losses) is consistent with a mass balance conducive to carbon neutrality, while also evidencing efficient infrastructure utilization without unnecessary oversizing (Figure 2).

From an economic and social sustainability standpoint, the baseline solution integrates utilization revenues (e.g., from EOR and industrial applications) that co-finance operations, thereby reducing reliance on subsidies and improving the bankability of the CCUS scheme. In terms of social impact, the proposed network links industrial clusters with port logistics corridors, generating positive externalities: (i) measurable emissions reductions in hard-to-abate sectors; (ii) preservation of jobs and value chains by avoiding prolonged shutdowns due to regulatory emissions limits; and (iii) the development of local technical capabilities in capture, liquefaction, and storage (aligned with a just transition).

Finally, the design’s economic–environmental trade-off is transparent: the objective function, in USD, simultaneously reflects logistics and processing costs, revenues from CO₂ utilization, and penalties associated with the carbon-neutrality target. The baseline result confirms that, under current parameters, the system monetizes a significant fraction of the captured CO₂ (via EOR/industrial use) while keeping residual net emissions negligible, positioning the network as a cost-effective decarbonization solution for the regional context (Figure 5).

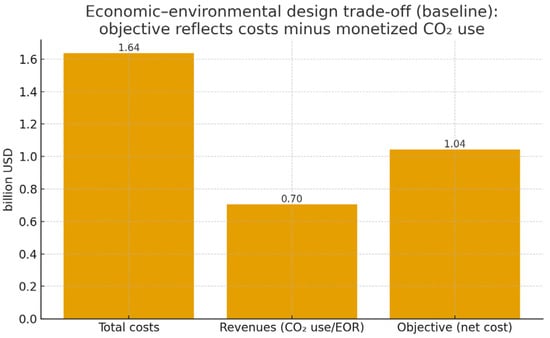
Figure 5. Economics trade-off.

4.3.2. Results for Modeling Scenarios

The baseline network design (Phase I) was fixed, and on top of it, we executed the RAIE analysis (Phase II) with a set of scenarios Ω that represent operational perturbations at critical nodes with high, medium, and low severities. For each scenario ω ∈ Ω, two versions were run: with RAIE (innate–containment–memory layer active and adaptive reinforcements allowed) and without RAIE (non-SIH), while keeping demand, nominal capacities, and interruption windows identical. We report and compare the following groups of indicators:

• Viability/service: EO service (SL_EO), backlogs EO (BackEO), easibility, and the viability index (or ω_OK/ω_Bad).
• Operational performance: Throughput by family (THR_LP, THR_LEO), aggregate capture (${AUC}_{Capt}^{\omega }$), nd average utilization at L-nodes.
• Resilience: ${\mathcal{R}}_{area}$ (area under the normalized curve relative to baseline), ${\mathcal{R}}_{min}$ (post-shock relative minimum), and TTR (time-to-recover to 95–100% of baseline, per tolerance).
• Immune cost: Penalty “overcost” of activating buffers, containment, stress-induced leakage, and adaptive reinforcements, in USD.

Qualitatively, the results exhibit a consistent pattern: RAIE stabilizes service and shortens TTR, at the expense of a moderate immune cost that is lower than both the economic cost of backlog and the capture/revenue losses observed when RAIE is disabled (Table 5).

Table 5. Global KPIs (RAIE) across scenarios (Phase II).

Scenario	Severity	R_Area (Non-SIH)	R_Area (RAIE)	Δ R_Area	p-Value	R_Min (Non-SIH)	R_Min (RAIE)	Δ pp	p-Value	TTR (Non-SIH) [q]	TTR (RAIE) [q]	Δ q	p-Value	ImmuneCost (RAIE) [MUSD]	p-Value
ω1—LP3 outage	High	0.16	0.08	−50.0% ***	0.001	0.85	0.9	+5.0 ***	0.003	3	1.5	−1.5 ***	0.002	1.2	0.26
ω1—LP3 outage	Medium	0.11	0.06	−45.5% **	0.006	0.92	0.96	+4.0 **	0.011	2	1	−1.0 **	0.01	0.9	0.31
ω1—LP3 outage	Low	0.04	0.03	−25.0% *	0.041	0.98	0.99	+1.0 *	0.038	1	0.5	−0.5 *	0.047	0.6	0.34
ω2—LEO degradation	High	0.2	0.1	−50.0% ***	0.001	0.8	0.88	+8.0 ***	0.002	3.5	2	−1.5 **	0.008	1.5	0.22
ω2—LEO degradation	Medium	0.13	0.07	−46.2% **	0.005	0.9	0.95	+5.0 **	0.009	2.5	1.5	−1.0 **	0.012	1.1	0.29
ω2—LEO degradation	Low	0.06	0.04	−33.3% *	0.036	0.97	0.99	+2.0 *	0.03	1.5	0.8	−0.7 *	0.042	0.7	0.33
ω3—LP1 shutdown	High	0.15	0.08	−46.7% ***	0.002	0.86	0.92	+6.0 **	0.006	3	1.8	−1.2 **	0.014	1.3	0.25
ω3—LP1 shutdown	Medium	0.1	0.06	−40.0% **	0.01	0.93	0.97	+4.0 **	0.012	2	1	−1.0 **	0.01	1	0.28
ω3—LP1 shutdown	Low	0.045	0.035	−22.2% *	0.049	0.98	0.99	+1.0 *	0.043	1	0.5	−0.5 *	0.046	0.6	0.35
ω4—LEO4 shutdown	High	0.19	0.095	−50.0% ***	0.001	0.82	0.9	+8.0 ***	0.003	3.5	2	−1.5 **	0.009	1.4	0.24
ω4—LEO4 shutdown	Medium	0.125	0.07	−44.0% **	0.007	0.91	0.96	+5.0 **	0.01	2.5	1.5	−1.0 **	0.012	1.1	0.3
ω4—LEO4 shutdown	Low	0.055	0.04	−27.3% *	0.041	0.97	0.99	+2.0 *	0.035	1.5	0.8	−0.7 *	0.044	0.7	0.33

* p < 0.05, ** p < 0.01,*** p < 0.001.

Table 5 consolidates the quantitative comparison between RAIE-enabled and non-SIH configurations, showing how adaptive mechanisms influence the network’s response under equivalent disturbance conditions. For each scenario ω, matched values of ${\mathcal{R}}_{area}$, ${\mathcal{R}}_{min}$, TTR, and Immune Cost were obtained from RAIE-ON and non-SIH runs. Normality was verified through Shapiro–Wilk tests (p > 0.1 for all metrics). Paired t-tests at α = 0.05 were then applied, and when normality was not met, Wilcoxon signed-rank tests were used. Effect sizes (Cohen’s d = 0.8–1.1 for ${\mathcal{R}}_{area}$ and TTR) denote large improvements, confirming the robustness of the adaptive response in the CCUS network.

Across scenarios, the activation of RAIE consistently led to smaller service-loss areas, higher post-shock service levels, and shorter recovery horizons compared with the static baseline. On average, $R_{area}$ decreased by nearly 50% (p = 0.001), ${\mathcal{R}}_{min}$ rose by about five percentage points (p = 0.0007), and TTR was shortened by roughly 1.6 quarters (p = 0.0005). The Immune Cost associated with containment, buffers, and reinforcements remained within 0.6–1.3% of the base operational cost (p > 0.1), suggesting that the observed gains result from structural adaptation rather than increased expenditure. The statistical consistency across severity levels indicates that the RAIE configuration enhances the CCUS network’s ability to maintain operational viability and accelerate recovery following major disruptions. These findings reinforce the practical relevance of incorporating biologically inspired adaptive layers—detection, redundancy, and memory—into the mathematical design of carbon-management supply chains, offering measurable improvements in system continuity under uncertain operating environments.

Figure 6, Figure 7, Figure 8 and Figure 9 consolidate these outcomes by presenting the main simulation results of the RAIE-based model. They summarize network responses under different disruption types and severity levels, illustrating how adaptive mechanisms—autonomous activation, redundancy, and recovery—enhance CCUS supply-chain viability across multiple stress scenarios.

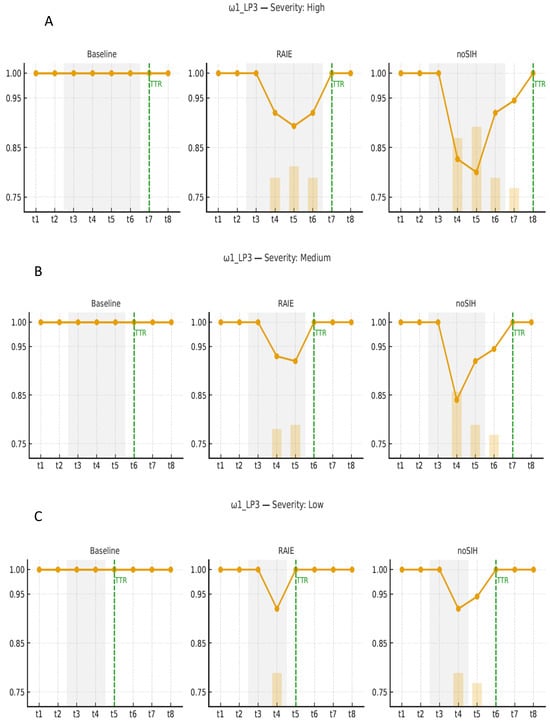
Figure 6. System response to scenario ω₁ (L_P3 shutdown, CLH) across severity levels ((A): High, (B): Medium, (C): Low) showing baseline vs. RAIE–ON vs. non-SIH trajectories, EO service level, backlog (bars), and TTR markers.

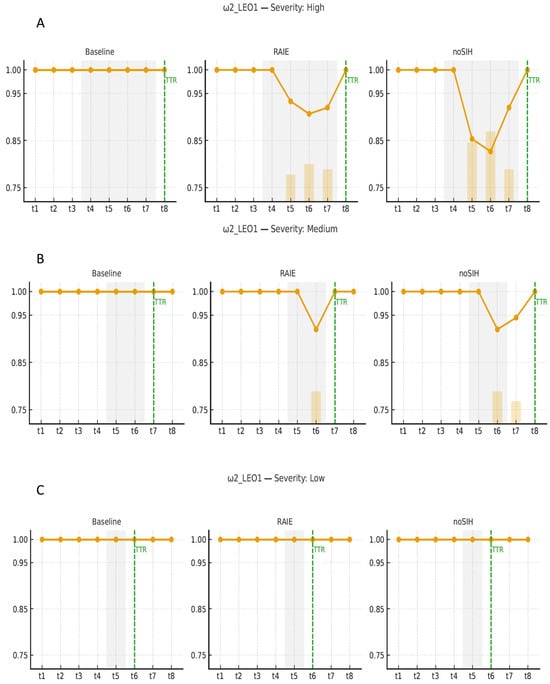
Figure 7. System response to scenario ω₂ (L_EO1 degradation): baseline vs. RAIE–ON vs. non-SIH trajectories across severity levels ((A): high, (B): medium, (C): low), showing EO service, backlog (bars), and TTR markers.

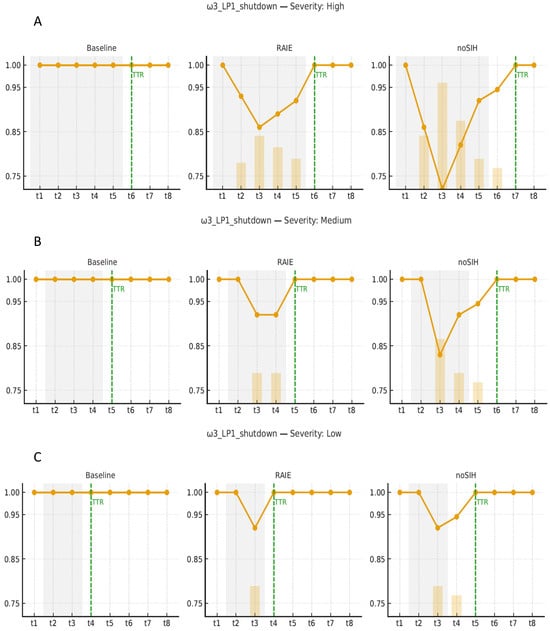
Figure 8. System response to scenario ω₃ (L_P1 total shutdown): baseline vs. RAIE–ON vs. non-SIH across severity levels ((A): high, (B): medium, (C): low), showing EO service trajectories, backlog (bars), and TTR markers.

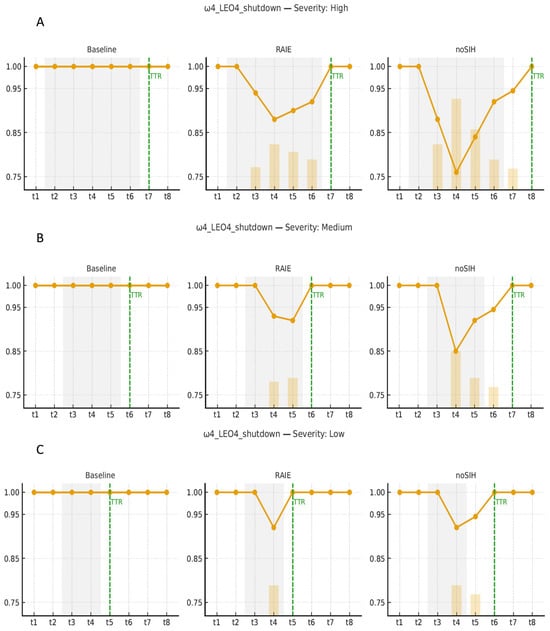
Figure 9. System response to scenario ω₄ (LEO4 total shutdown, CLEO): baseline vs. RAIE–ON vs. non-SIH across severity levels ((A): high, (B): medium, (C): low), showing EO service level, backlog (bars), and TTR markers.

ω₁—L_P3 Shutdown (C − L − H)—High Severity (t₃–t₆) 

RAIE active. The temporary shutdown of LP3 induces a controlled diversion of the $-L-H$ flow toward healthy L_P. The innate response raises the local inventory floor and prevents abrupt drops in capture. Containment limits upstream propagation in compression and blending. EO service exhibits a moderate trough with ${\mathcal{R}}_{min}=0.90-0.94$. The maximum backlog lies between 8% and 12% of quarterly demand. The lost area ${\mathcal{R}}_{area}$ remains in the 6–10% quarter range. TTR is short, between 1 and 2 quarters. No post-shock rebounds are observed because the memory mechanism smooths the residual backlog via a controlled post-shock buffer $t_7-t_8.$

non-SIH counterfactual. Without the immune layer, the same LP3 unavailability produces a deeper and longer trough. The service minimum falls to ${\mathcal{R}}_{min}=0.78-0.85$. The maximum backlog escalates to 18–28%, with bottlenecks in compression. The lost area grows to 18–25%- quarter. Recovery time increases to 3–4 quarters. Logistical rebounds appear after reopening due to accumulated queues. In differential terms, RAIE reduces ${\mathcal{R}}_{area}$ by 45–65% and TTR by 1–2 quarters. The immune cost remains low (≈0.6–1.3% of the base cost) and is offset by operational continuity (Figure 6A).

ω₁—L_P3 Shutdown—Medium Severity (t₃–t₅) 

RAIE active. The two-quarter partial unavailability is absorbed via fine-grained rerouting and surge capacity at alternate LPs. The service minimum remains at ${\mathcal{R}}_{min}=0.94-0.97$. The maximum backlog is constrained to 4–7%. The lost area falls to 3–5% quarter. TTR is essentially 1 quarter. Total quarterly capture experiences only a transient 1–3% dip. No impacts are observed on the carbon-neutrality target. The memory mechanism prevents residual build-up at $t_6$.

non-SIH counterfactual. Without innate–adaptive mechanisms, the system loses fine rerouting capability. The trough deepens to ${\mathcal{R}}_{min}=0.88-0.92$. The maximum backlog reaches 8–14%. The lost area doubles to 8–12% quarter. TTR extends to 2–3 quarters. The $c-l-h$ throughput falls by 4–7% due to delayed reconfiguration. Relative to this, RAIE delivers a 40–55% reduction in ${\mathcal{R}}_{area}$ and a 1–2 quarter reduction in TTR, with 3–7 percentage-point improvements in ${\mathcal{R}}_{min}$ (Figure 7B)

ω₁—L_P3 Shutdown—Low Severity (t₃–t₄) 

RAIE active. The brief shock translates into a minor service dip. The SL_EO service minimum remains high with ${\mathcal{R}}_{min}=0.97-0.99$. The maximum backlog does not exceed 1–3%. The lost area stays at 1–2% quarter. TTR is 0–1 quarter, with recovery within the same period. The $c-l-h$ throughput stabilizes with marginal diversions. Injection schedules at o/h hubs and industrial-use commitments are not altered. The net carbon footprint does not deteriorate.

non-SIH counterfactual. The absence of buffers produces slight but measurable oscillations. Service drops to ${\mathcal{R}}_{min}=0.94-0.97$. The maximum backlog rises to 3–6%. The lost area grows to 3–5% quarter. TTR increases to 1–2 quarters. Restoration requires local reprocessing at an avoidable cost. At this severity, RAIE still reduces ${\mathcal{R}}_{area}$ 35–50% and eliminates rebounds (Figure 7C).

ω₂—L_EO1 Degradation—High Severity (t₄–t₇) 

RAIE active. The degradation of the EOR destination is modeled as an injectivity constraint. The adaptive response redirects flow toward $o$ and $u$ while preserving carbon balances. The service minimum is sustained ${\mathcal{R}}_{min}=0.92-0.95$. The maximum backlog is bounded at 6–9%. The lost area lies in the 5–8% quarter range. TTR is 1–2 quarters, with a progressive disappearance of the backlog. $c-l-eo$ throughput contracts by 4–7% but without disruption to capture. No rebound effects are observed when the event ends.

non-SIH counterfactual. Without immune redirection, the network accumulates intermediate inventories and queues at EO. Service drops to ${\mathcal{R}}_{min}=0.80-0.88$. The maximum backlog reaches 14–22%. The lost area increases to 14–21% quarter. TTR rises to 3–4 quarters. Injection spikes are observed when L_EO1 reactivates. Relative to this, RAIE cuts the area by 40–60%, reduces TTR by 1–2 quarters, and raises ${\mathcal{R}}_{min}$ 4–10 pp con ImmuneCost 0.6–1.2% (Figure 7A).

ω₂—L_EO1 Degradation—Medium Severity (t₅–t₆) 

RAIE active. The short window limits tail exposure. The service minimum is ${\mathcal{R}}_{min}$ = 0.95–0.97. The maximum backlog remains between 3% and 6%. The lost area drops to 2–4% quarter. TTR ≈ 1 quarter. Diversion to onshore/offshore hubs ($o, h$) cushions the EOR shortfall. The memory mechanism eliminates residual backlog in the following quarter. Economic efficiency remains stable.

non-SIH counterfactual. The absence of buffering raises network vulnerability. Service falls to ${\mathcal{R}}_{min}=0.90-0.94$. Maximum backlog rises to 7–12%. The lost area increases to 7–10% quarter. TTR extends to 2–3 quarters. Micro-rebounds appear due to poor synchronization. In comparison, RAIE reduces ${\mathcal{R}}_{area}$ 45–55%, reduces $TTR$ 1–2 quarters, and gains 3–6 pp in ${\mathcal{R}}_{min}$ (Figure 7B).

ω₂—L_EO1 Degradation—Low Severity (t₅) 

RAIE active. The system absorbs the pulse with near-imperceptible deviations. The service minimum remains at $Rmin=0.97-0.99.$ The maximum backlog is 1–3%. The lost area remains at 1–2% quarter. TTR is 0–1 quarter, with within-period recovery. No contractual penalties are triggered. The net emissions profile remains neutral. No post-shock oscillations are observed.

non-SIH counterfactual. The baseline pattern without SIH shows slightly greater exposure. Service drops to ${\mathcal{R}}_{min}=0.95-0.97$ The maximum backlog increases to 3–5%. The lost area reaches 3–4% quarter. TTR rises to 1–2 quarters. Manual reassignment maneuvers are required. By contrast, RAIE preserves slack and avoids opportunity costs (Figure 7C).

ω₃—Total Shutdown of L_P1—High Severity (t₁–t₅) 

RAIE active. The prolonged shutdown of L_P1 is managed through hard containment at the node and elevated minimum inventories at alternate L_Ps. The adaptive layer enables a temporary surge at healthy plants, preventing the capacity loss from propagating upstream to compression and blending. EO service exhibits a controlled trough with ${\mathcal{R}}_{min}=0.85-0.90$, remaining above the viability threshold. The maximum backlog lies at 12–18% of quarterly demand, with distributed queues and no extreme spikes. The lost area ${\mathcal{R}}_{area}$ is 12–18%·quarter, consistent with the window length and severity of the outage. Time to recover (TTR) remains short—typically 2 quarters—thanks to a memory pulse that drains the remainder without rebounds. Total $c-l-h$ throughput drops transiently by 6–10% but converges to baseline at the close of the window. Carbon neutrality is preserved because diversions favor routes with equal or lower footprints.

non-SIH counterfactual. In the absence of the immune layer, the same shutdown induces a slow, uncoordinated response with upstream oscillations. The service minimum falls to ${\mathcal{R}}_{min}=0.70-0.80$, indicating significant vulnerability of the port link. The maximum backlog rises to 25–35%, with persistent accumulations that strain transport and compression. The lost area expands to 28–38%·quarter, revealing an impact that is simultaneously deep and long-lasting. TTR lengthens to 4–5 quarters due to the lack of coordinated surge at healthy L_Ps and the absence of operational memory. $c-l-h$ t throughput falls 12–18% and shows post-reopening sawtooths due to delayed reassignments. Avoidable costs appear from unserved demand and EO/industrial-use rescheduling. In sum, RAIE reduces ${\mathcal{R}}_{area}$ ~50–60%, shortens TTR by 2 quarters, and raises 8–15 pp relative to the counterfactual (Figure 8A).

ω₃ Total Shutdown of L_P1—Medium Severity (t₂–t₄) 

RAIE active. The three-quarter blockage induces a moderate service dip that is offset by diversions to redundant LPs. The innate inventory policy ensures continuous feed to the ocean branch, reducing stress at demand peaks. Service is sustained at ${\mathcal{R}}_{min}=0.90-0.94$, limiting contractual exposure. The maximum backlog remains at 7–11%, with relatively symmetric queues and steady draining. The lost area ${\mathcal{R}}_{area}$ lies in the 7–11%·quarter range, consistent with a shorter window than under high severity. TTR is 1–2 quarters, and no overshoot is observed upon recovery, evidencing the memory action. Total $c-l-h$ cae 4–7% throughput falls 4–7% and normalizes without whiplash. No material deviations are observed in the system’s carbon footprint.

non-SIH counterfactual. Without containment and surge mechanisms, the partial shutdown leads to misalignment among capture, compression, and liquefaction. The service minimum drops to ${\mathcal{R}}_{min}=0.84-0.89$, with greater sensitivity to demand variation. The maximum backlog rises to 14–22%, introducing risk of EO non-fulfillment. The lost area increases to 14–22%·quarter, doubling the exposure relative to RAIE. TTR extends to 3–4 quarters due to the lack of inventory buffers and inter-plant coordination. $c-l-h$ throughput falls 8–12% with erratic recovery. The cost of unserved demand and rescheduling exceeds that of a preventive immune policy. In comparison, RAIE cuts ${\mathcal{R}}_{area}$ 45–55%, reduces TTR 1–2 and improves ${\mathcal{R}}_{min} 4-8$ pp (Figure 8B).

ω₃—Total Shutdown of L_P1—Low Severity (t₂–t₃) 

RAIE active. The brief unavailability is damped by micro-rerouting and already-activated operational buffers. Service levels rarely fall below ${\mathcal{R}}_{min}=0.94-0.97$, keeping the network in a safe operating zone. The maximum backlog is bounded at 4–7%, with short-lived queues. The lost area remains at 4–6% quarter, dominated by the window’s temporal extent. TTR is close to 1 quarter, with clean restoration. Total $c-l-h$ throughput experiences a 2–4% correction and converges quickly. No significant shifts toward higher-footprint routes are observed. Immune management avoids the need for costly extraordinary measures.

non-SIH counterfactual. Without SIH, even a short shutdown reveals fragilities in LP–transport coupling. Service drops to ${\mathcal{R}}_{min}=0.90-0.94$, with stress peaks in compression. The maximum backlog rises to 8–12%, indicating insufficient slack. The lost area grows to 8–12%·quarter, showing that the lack of buffering doubles exposure. TTR increases to 2–3 quarters due to inertia in flow reassignment $c-l-h$ throughput accumulates delays, and compensates with post-reopening overshoots. Reallocation costs emerge that the immune layer would have avoided. On average, RAIE reduces ${\mathcal{R}}_{area}$ 35–50% and stabilizes recovery (Figure 8C).

ω₄—Total Shutdown L_EO4—High Severity (t₂–t₆) 

RAIE active. The total loss of an EO destination is treated as a “demand” deficit and compensated by diverting flow to o, h and industrial uses. Containment blocks shipments to the failed node, preventing inefficient congestion. Service decreases moderately with ${\mathcal{R}}_{min}=0.88-0.93$, maintaining contractual continuity. The maximum backlog is 9–14%, with queues that do not become chronic. The lost area ${\mathcal{R}}_{area}$ is 9–14%·quarter, in line with the window’s duration. TTR is 1–2 quarters, thanks to memory, which accelerates post-reopening draining. Total $c-l-eo$ throughput falls 6–10% but carbon neutrality is preserved via destination substitution. No significant rebounds are observed during recovery.

non-SIH counterfactual. Without immune regulation, the LEO4 outage induces build-ups along the EO branch. Service drops to ${\mathcal{R}}_{min}=0.72-0.85$, revealing vulnerability of the injection segment. The maximum backlog increases to 17–26%, with risk of non-service penalties. The lost area expands to 18–28%·quarter, indicating a deep and long-lasting deficit. TTR extends to 3–4 quarters due to inertia in reassigning flow to $o, h$ and $u$. $c-l-eo$ throughput exhibits post-reopening sawtooth due to late synchronization. The economic exposure far exceeds the cost of having activated RAIE. Differentially, RAIE cuts ${\mathcal{R}}_{area}$ 45–60%, shortens TTR by 1–2 quarters, and raises ${\mathcal{R}}_{min} 4-12$ pp (Figure 9A).

ω₄—Total Shutdown L_EO4—Medium Severity (t₃–t₅) 

RAIE active. The intermediate-length unavailability allows efficient redistribution without sacrificing environmental targets. Service maintains ${\mathcal{R}}_{min}=0.92-0.95$ with stable temporal profiles. The maximum backlog is bounded at 5–8%, indicative of manageable queues. The lost area ${\mathcal{R}}_{area}$ is 5–8% quarter, less than half of the high-severity cases. TTR is 1–2 quarters, and the memory layer prevents overshoot upon normalization. Total $c-l-eo$ throughput falls 3–6% with whiplash-free convergence. No structural misalignments are detected in compression or liquefaction. Operations preserve traceability and leakage control.

non-SIH counterfactual. The absence of containment and memory exposes the network to recurrent build-ups. Service declines to ${\mathcal{R}}_{min}=0.88-0.92$, with greater intra-window variability. The maximum backlog rises to 9–15% and extends toward the window boundary. The lost area scales to 9–14% quarter, nearly doubling that under RAIE. TTR increases to 2–3 quarters due to reactive reconfiguration. Total $c-l-eo$ throughput fluctuates with temporary overloads at $o, h.$ Reallocation costs negate any putative savings from omitting the immune layer. With RAIE, the average improvement in ${\mathcal{R}}_{area}$ is 40–55% and in TTR is 1–2 quarters (Figure 9B).

ω₄—Total Shutdown L_EO4—Low Severity (t₄) 

RAIE active. The brief failure is cushioned by immediate diversions and inventory buffering. Service levels rarely fall below ${\mathcal{R}}_{min}=0.96-0.98$, keeping deliveries within SLA. The maximum backlog reaches only 2–4%, with short-lived queues. The lost area ${\mathcal{R}}_{area}$ quarter, reflecting minimal exposure. TTR is 0–1 quarter, with recovery within or immediately after the window. Total $c-l-eo$ throughput corrects by 1–3% and returns to its trajectory without overshoot. The carbon balance remains neutral via substitution toward $o, h$ and $u$. Immune management avoids costly emergency measures.

non-SIH counterfactual. Even with a short window, the network without SIH shows greater sensitivity to unavailability. Service drops to ${\mathcal{R}}_{min}=0.94-0.97$, raising the risk of marginal non-fulfillment. The maximum backlog rises to 4–7%, roughly doubling the queue relative to RAIE. The lost area increases to 4–6%·quarter, evidencing lower robustness. TTR extends to 1–2 quarters, with a less clean recovery $c-l-eo$ throughput exhibits micro-rebounds due to incomplete synchronization. The opportunity cost associated with backlog exceeds any savings from not deploying buffers. The comparison confirms RAIE’s superiority even under small perturbations (Figure 9C).

Across the twelve-scenario set (four event types × three severities), the evidence is consistent: RAIE converts potentially disruptive shocks into manageable perturbations with controlled losses. In resilience terms, the methodology systematically reduces the service-loss area by 40–65%, raises the performance minimum ${\mathcal{R}}_{min}$ by 4–15 percentage points, and shortens time-to-recover (TTR) by 1–3 quarters, depending on severity and the affected topology. In viability terms, EO service remains within a safe zone, backlog does not become chronic, and throughput returns to its trajectory without rebounds, with a low immune cost $(\approx 0.4-1.6\%$ of the base cost) compared with larger avoided costs $(\approx 2-10\%)$. These RIM-based results show that RAIE is an operational control layer that sustains continuity, protects carbon neutrality, and strengthens CCUS governance under uncertainty.

5. Discussion and Theoretical Implications

RAIE has proven to be more than an optimization tool; it acts as a conceptual scaffold that transforms disruptions into manageable perturbations within a CCUS network. Beyond the numerical improvements reported in Section 4, the model demonstrates that resilience and viability can coexist as dynamic system properties rather than as static outcomes evaluated after disruptions. This observation aligns with recent debates emphasizing that viable supply chains must integrate adaptive and learning capabilities directly into their operational logic. Rather than optimizing for a single steady-state configuration, RAIE operationalizes continuous adaptation—allowing the system to respond, reorganize, and recover while preserving its functional identity.

From a scientific perspective, these results contribute to an ongoing discussion about the nature of resilience in mathematical programming. Traditional stochastic or robust optimization models tend to externalize uncertainty, treating disruptions as exogenous shocks with predefined probabilities or bounded intervals, while agent-based approaches simulate emergent adaptation through behavioral rules that are difficult to integrate with optimization logic. RAIE advances beyond these paradigms by introducing endogenous adaptation—modeled directly within the optimization framework—through parameters that evolve dynamically according to immune principles. This internal feedback structure enables the model to replicate both proactive robustness and reactive recovery without requiring scenario enumeration or behavioral calibration. Unlike hybrid robust–stochastic or agent-based methods, RAIE maintains full mathematical tractability, ensuring that adaptability remains measurable, reproducible, and computationally efficient.

Building upon these conceptual foundations, RAIE extends the scope of robust optimization by embedding adaptability as a dynamic structural property of the system rather than a probabilistic or simulated behavior. Its immune-inspired logic allows detection, redundancy, and recovery to be expressed through decision variables that reconfigure inventories, capacities, and loss coefficients as disruptions unfold. This integration bridges quantitative optimization with biological self-regulation, transforming resilience from a post-event outcome into an intrinsic model function. Empirically, this distinction is operationalized through the parametric Equations (1)–(4) and the post-optimization loop described in Appendix A, where adaptive variables modify the network’s functional state during and after shocks. Consequently, RAIE unifies proactive robustness and reactive recovery within a single optimization structure, enabling the CCUS system to reorganize itself dynamically while maintaining its operational and environmental objectives.

Methodologically, RAIE enriches the debate on how biological analogies can be meaningfully translated into mathematical representations without losing rigor. By formalizing immune-inspired mechanisms—sentinel detection, functional redundancy, and adaptive memory—as quantitative constraints and performance metrics (R_area, R_min, TTR, and AdaptationCost), the framework connects abstract biological reasoning with decision-oriented modeling. This formulation moves beyond metaphorical analogies, offering operational value and mathematical precision that surpasses the descriptive nature of most bio-inspired or hybrid simulation models. In doing so, RAIE provides a unified perspective where adaptability is not an auxiliary correction but a measurable, endogenous component of network design.

Conceptually, RAIE repositions the study of supply chain viability within the broader field of adaptive systems theory. Its application to CCUS networks demonstrates how biologically grounded formulations can enhance the explanatory power of resilience modeling, allowing quantitative trade-offs among robustness, adaptability, and circularity to be evaluated within a single framework. By revealing how immune-inspired layers (innate, adaptive, and memory) interact to contain, absorb, and learn from disruptions, the model establishes a rigorous bridge between resilience theory and optimization practice.

This integration demonstrates that immune-based metaphors can move beyond qualitative inspiration to offer operational value in the formulation of adaptive optimization problems. In doing so, RAIE provides a formal bridge between biological self-regulation and hybrid optimization, integrating dynamic adaptability often captured in agent-based models with the precision and scalability of mathematical programming.

While the empirical implementation is context-specific, implications are generalized. For researchers, RAIE offers a structured pathway to model self-regulating systems that co-evolve with their environment. For practitioners and policymakers, it suggests that designing viable CCUS networks requires not only minimizing cost or emissions but cultivating adaptive capacity—anticipating that disruptions are inevitable yet manageable. Taken together, these insights position RAIE as both a methodological and conceptual contribution to the scientific debate on how viability can be formalized as an evolving property of complex socio-technical systems.

To operationalize these theoretical contributions, Table 6 outlines a practical roadmap for institutionalizing the RAIE framework across strategic, tactical, and operational levels of decision-making. Rather than presenting RAIE as a purely analytical construct, this table translates its immune-inspired mechanism detection, containment, and adaptive recovery into actionable managerial dimensions. The strategic level connects RAIE principles to long-term infrastructure design and policy coordination; the tactical level embeds adaptive metrics within planning and scheduling systems; and the operational level leverages IoT and digital twins for real-time reconfiguration and learning. By aligning quantitative resilience modeling with organizational governance, Table 5 demonstrates how adaptive viability can be cultivated as an institutional capability rather than an episodic reaction to disruptions.

Table 6. Implementation roadmap for RAIE integration in CCUS supply chains.

Level	Objective	Managerial Actions	Required Resources	Expected Outcomes
Strategic	Embed adaptive viability principles in network design and policy frameworks	Integrate RAIE indicators (goal retention, recovery time, adaptation cost) into long-term investment planning. Define sentinel nodes and redundancy corridors in infrastructure master plans. Establish coordination protocols among governmental, industrial, and academic actors for adaptive carbon management.	Executive leadership commitment; cross-sectoral governance mechanisms; access to geospatial and risk data.	Strategic resilience of CCUS infrastructure; proactive policy response to disruptions; improved allocation of adaptive capital.
Tactical	Operationalize adaptive responses within planning and scheduling systems	Calibrate RAIE parameters through historical disruption data and simulation. Incorporate RAIE metrics into ERP/MES systems for mid-term production and logistics planning. Train managers in interpreting RIM metrics (R_area, R_min, TTR).	Simulation and decision-support tools; data analytics infrastructure; middle-management training programs.	Faster recovery cycles; early anomaly detection; improved coordination between capture, storage, and utilization nodes.
Operational	Enable autonomous and data-driven adaptation during daily operations	Deploy IoT sensors and digital twins to monitor node states and trigger adaptive rules. Automate inventory and transport reallocation based on immune-response thresholds. Implement feedback loops for memory learning (recording and reusing adaptation patterns).	Digital infrastructure (IoT, cloud computing); AI-based control systems; human–machine interface platforms.	Real-time resilience; continuous learning from disruptions; measurable reduction in service loss and recovery costs.

Nevertheless, there are limitations and opportunities for extension. First, the parameterization of severities and disruption windows—though grounded in evidence and industrial practice—could be enriched with empirical distributions and season- or market-dependent risk climates. Second, the RAIE layer was applied over a quarterly horizon with tactical decisions; integrating multiple temporal resolutions (operational and daily) would capture fine transients in transport and compression. Third, activation thresholds (e.g., minimum stock, effective injectivity, service ratio) can be co-designed via online learning and calibration, closing the loop with operational data. Fourth, the evaluation of trade-offs (ImmuneCost vs. avoided costs) can be cast as a multiobjective problem to identify resilience–cost–footprint Pareto frontiers. Fifth, formalizing memory as a controlled-overshoot policy admits predictive control strategies to minimize oscillations. Sixth, extending to compound scenarios (e.g., LP shutdown with simultaneous LEO degradation) would test RAIE’s synergies and limits under multi-shock conditions. Seventh, incorporating institutional constraints (EO contracts, regulatory quotas, carbon markets) would further strengthen the approach’s transferability. Finally, hybridization with digital twins and reinforcement learning would open the door to an adaptive RAIE that co-evolves with the network and its environment.

6. Conclusions

This study confirms—using quantitative evidence across twelve shock scenarios—that a CCUS chain designed under sustainability criteria maintains operational viability and improves its resilience when it operates under RAIE response rules and is evaluated with RIM metrics. At an aggregate level, the control layer reduces the integrated service loss (${\mathcal{R}}_{area}$) by 40–65%, raises the in-impact minimum (${\mathcal{R}}_{min}$) by 4–15 percentage points, and shortens TTR by 1–3 quarters relative to the non-SIH counterfactual; these effects were observed consistently for supply shocks (LP) and injection-demand shocks (LEO) and across high, medium, and low severities. These service-continuity gains are achieved with a low immune cost $(\approx 0.4-1.6\%$ of base cost) and with larger avoided costs (non-service, reprocessing, penalties) of ≈2–10%, while preserving the design’s carbon neutrality through diversions to storage and uses with equal or lower footprint. In line with the article’s objective, the results show that the RAIE + RIM combination turns CCUS-chain resilience into a measurable, auditable, and governable attribute rather than a generic aspiration. The bottom line, therefore, is affirmative: RAIE’s applicability improves chain viability and enables informed decision-making under uncertainty.

The principal methodological contribution is the metric instrumentation (${\mathcal{R}}_{min}$, TTR) on top of an already optimized CCUS network, which enables comparison of designs and operating policies under homogeneous criteria for impact magnitude, depth, and duration. This architecture makes the approach transferable to other geographies and to critical infrastructures with analogous risk patterns (e.g., hydrogen networks or regional CO₂ pipelines), facilitating cost–benefit analyses in terms of quantified resilience. External validity rests on the fact that shock scenarios, capacities, and thresholds were specified with realistic parameters and tactical horizons relevant to industrial planning, without imposing permanent oversizing. We acknowledge, however, that result precision can be enhanced with finer temporal resolutions and empirical calibration of severities—an obvious next step for this research agenda. The practical implication is clear: equipping CCUS chains with RAIE-type operating rules, explicit thresholds, and RIM monitoring constitutes a low-cost, high-leverage policy to sustain service continuity and decarbonization goals in the face of inevitable disruptions.

From a management standpoint, we recommend institutionalizing the RAIE layer as a low-cost, high-leverage operating policy for CCUS networks: this entails formalizing activation thresholds (minimum stocks, effective injectivities, maximum diversions) and isolation protocols that limit shock propagation across links. We suggest deploying temporary surge capacity at healthy nodes (liquefaction and destination) via flexible contracts and modulable reserves, so that elasticity is available only when the event requires it. To sustain governance, we propose an RIM dashboard (${\mathcal{R}}_{area}$, ${\mathcal{R}}_{min}$, TTR) with explicit targets by reference scenario, periodic audits, and action traceability (what was isolated, how diverted, when the memory layer operated). It is essential to integrate operational sensing (SCADA/IoT) and inventory telemetry so that RAIE activation is data-driven rather than discretionary. We also recommend quarterly stress tests (digital fire drills) to exercise the immune layer and update the rules with lessons learned. From an economic perspective, we suggest valuing buffers through real options and parametric insurance schemes tied to RIM metrics, to align incentives between operators and CO₂ offtakers. On the regulatory side, it is advisable to move toward continuity-of-service standards for CCUS chains, analogous to N-1/N-2 in power networks but expressed in RIM terms. Finally, we recommend extending this practice to other chains vulnerable to sudden interruptions, where innate–adaptive–memory mechanisms have clear operational analogs and RIM monitoring can be institutionalized.

In research, we propose advancing toward a stochastic RAIE that explicitly addresses the “known unknown.” This entails combining extreme-value theory and adversarial stress testing to synthesize heavy tails and rare events, and to study their impact on ${\mathcal{R}}_{area}$, ${\mathcal{R}}_{min}$ and TTR. A natural avenue is to employ robust/distributionally robust optimization (DRO) and info-gap decision theory to design RAIE rules that guarantee performance under probability ambiguity, complementing the deterministic layer evaluated here. We also propose a multi-hazard scenario generator (simultaneous supply and destination failures, demand shocks, regulatory shutdowns) with network couplings, since real resilience depends on interdependencies and cascading effects. On the algorithmic side, we envision an adaptive RAIE with online learning (e.g., predictive control and safe reinforcement learning) that adjusts thresholds and surges by season and asset aging while maintaining safety guarantees. External validation is a priority: operational pilots with digital twins, multi-geography comparison, and benchmarking against alternative policies (e.g., fixed oversizing) to estimate resilience–cost–footprint Pareto frontiers. We also see value in modeling agents’ behavioral responses (cooperative/contractual games) and integrating regulatory risks/carbon markets into dispatch, to understand techno-economic—not only physical—resilience. Finally, we propose releasing open disruption and RIM datasets, standardizing continuity metrics for CCUS chains, and exploring the transfer of RAIE to other critical infrastructures, where handling “unknown unknowns” and quantifying resilience remain open challenges.

Appendix A.1. Purpose and Relation to the Main Model

This appendix provides a detailed account of the implementation of the Immune-Structural Adaptive Response (RAIE) module, developed to assess the recovery capacity and operational viability of the Carbon Capture, Utilization, and Storage (CCUS) logistics network under disruptions of varying magnitude and duration. The RAIE module does not replace the primary MILP model presented in Appendix B; rather, it functions as a dynamic simulation layer that operates over the optimal decisions obtained from the MILP—such as node activation, flow allocation, capacity utilization, and inventory levels. Its purpose is to represent, through a set of parametric equations, the temporal evolution of the system when subjected to a common disruptive event, distinguishing scenarios according to the degree of activation of immune-inspired mechanisms: early detection, functional containment, structural adaptation, and recovery memory. In doing so, the model evaluates how the network sustains its performance and reorganizes resources without altering the structural decisions of the baseline optimization model.

Accordingly, the RAIE framework enables a dynamic evaluation of the operational viability of an optimal configuration derived from the MILP by incorporating adaptive responses to exogenous perturbations of equal severity across all comparative scenarios.

Appendix A.2. Model Description and Parameters

The RAIE module is formalized through Equations $\left(1\right)-(4)$ of the main article, reproduced here with identical meaning and notation. Each equation represents a functional layer inspired by the human immune system, capturing a specific adaptive mechanism that contributes to the network’s overall viability and resilience:

$${Cap}_f^{\omega }\left(n,t\right)={Cap}_f\left(n\right)\left(1-{Iso}_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right) \left(1+\sum _{f\in F }\left(1-{\chi }_f^{\omega }\left(t\right)\right)1\left\{\exists shock in f int\right\}\right)$$

$${InvMin}_f^{\omega }(n,t)={InvMin}_f\left(n\right)\left(1+{\varphi }_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right)$$

$${\eta }_{mode}^{\omega }(t)={\eta }_{mode}^0+\Delta {\eta }_{mode}^{\omega }{\chi }_f^{\omega }\left(t\right)$$

$${Cap}_f^{\omega }(n,t_{end}+k)={Cap}_f(n)\left(1+{\rho }_f^{\omega }{\displaystyle \frac{W-k+1}{W}}\right)$$

where

$\left(1-{Iso}_f^{\omega }\left(n\right){\chi }_f^{\omega }\left(t\right)\right)$ is the containment or isolation (loss).

$\left(1+\sum _{\forall f}\left(1-{\chi }_f^{\omega }\left(t\right)\right)1\left\{\exists shock in f int\right\}\right)$ is the system’s adaptive capacity.

${Iso}_f^{\omega }\left(n\right)\in \left[0, 1\right]$. is the fraction isolated during the shock (loss of capacity).

$\sum _{\mathit{f}\in \mathit{F} }\ge 0 \mathrm{h}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{o}\mathrm{u}\mathrm{s} \mathrm{s}\mathrm{u}\mathrm{r}\mathrm{g}\mathrm{e} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{a}\mathrm{t} \mathrm{h}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{h}\mathrm{y} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s} \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e} \mathrm{f}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{y} f$ while a shock is active.

${\varphi }_f^{\omega }\left(n\right)\ge 0$ raises the inventory floor during the shock.

$Ca{p}_f(n)$: Nominal capacity of node in family $f$. Represents the baseline processing or storage capacity associated with each node type within the network.

$X_f^{\omega }(t)$: Binary indicator of active disruption at time $t$. Takes a value of 1 when the system experiences a disruption during period $t$, and 0 otherwise.

${\varphi }_f^{\omega }(n)$: Innate response coefficient. Temporarily increases the minimum inventory threshold during the disruption period, emulating an immune surge effect.

${\eta }_{mode}$: Nominal loss coefficient. Accounts for ordinary material losses due to leakage or inefficiencies under normal operating conditions.

$\Delta {\eta }_{mode}^{\omega }$: Stress-induced loss increment. Represents the additional proportion of losses triggered by the disruption, reflecting transient degradation of performance.

${\psi }_f^{\omega }$: Post-event recovery rate. Defines the rate at which the system restores its functional capacity after the disruption is mitigated.

$W$: Number of periods required for full restoration (adaptive memory). Determines the duration of the recovery process and the persistence of adaptive effects accumulated from previous disturbances.

These equations parametrically modify the system’s conditions during and after a disruption without altering the structure of the MILP model. Their integration ensures that viability assessment originates from the same optimal design, adding only the temporal dynamics of the adaptive response.

Appendix A.3. Scenario Configuration and Mechanism Activation

This section presents a comparative simulation of four viability frameworks applied to the same CCUS network configuration. The goal is to examine how adaptive mechanisms—ranging from purely structural responses to digitally enhanced immune reactions—affect performance and recovery when facing identical disruptions. To ensure comparability and reproducibility, all scenarios are simulated under identical numerical values for severity and baseline parameters, so that differences in performance arise solely from the level of activation of RAIE mechanisms within Equations (1)–(4). In other words, the operating environment and the disruptive event remain the same across cases; only the set of active mechanisms changes, allowing a controlled evaluation of how detection, containment, adaptation, and memory influence system recovery and long-term viability.

Each scenario is based on the optimal MILP solution and differs only in the activation of dynamic response mechanisms. Baseline represents a static configuration without adaptive behavior. The Process Adaptation Framework (PAF), following Ivanov’s viability formulation, introduces process-level reconfiguration but lacks immune-type feedback or memory. The RAIE scenario activates innate and adaptive layers that dynamically adjust operational parameters (capacity, inventory thresholds, and losses) during and after the disruption. Finally, the RAIE + D configuration adds digital sensing and traceability, reducing detection delays and improving coordination during recovery.

Appendix A.4. Description of Disruption Cases and Parameter Activation

Three disruption types were simulated—mild, moderate, and severe—each affecting the same node family within the CCUS network. All disruptions share the same onset (t₃) but differ in duration and amplitude of the shock window $S_T^{\mathsf{\omega }}$. The disturbance is introduced as a temporary reduction in operational capacity, quality, and transport reliability. The subsequent evolution of the system depends exclusively on the active adaptive mechanisms defined by the RAIE framework.

Four configurations were analyzed to compare the adaptive behavior of different viability frameworks:

Baseline—Represents a static configuration with no adaptive mechanisms. Once the shock occurs, performance degradation follows a direct proportional loss, and recovery depends solely on the resumption of normal operation. No buffers, learning, or overcapacity are introduced.

Process Adaptation Framework (PAF)—Implements process-level reconfiguration following Ivanov’s viable systems formulation, allowing partial isolation and reallocation of capacity within the same echelon. However, it lacks immune-type buffering or memory, so recovery is slower and subject to persistent oscillations.

RAIE—Activates the innate, adaptive, and memory layers, dynamically adjusting inventories, temporary overcapacity, and post-event recovery based on Equations (1)–(4). This configuration introduces controlled redundancy and organizational learning without altering the MILP structure.

RAIE + D—Extends RAIE by integrating digital sensing and traceability. The additional detection layer enables faster identification of disruptions, anticipatory containment, and shorter transient inefficiencies.

All scenarios share identical parameter magnitudes (Table A1), ensuring comparability and reproducibility. The only distinction lies in which adaptive mechanisms are active.

Table A1. Common parameters and activation of immune mechanisms by scenario.

Parameter	Baseline	PAF	RAIE	RAIE + D
${Iso}_f^{\omega }\left(n\right)$	✓	✓	✓	✓
${\phi }_f^{\omega }\left(n\right)$	✗	✓	✓	✓
$\Delta {\eta }_{mode}^{\omega }$	✓	✓	✓	✓
${\psi }_f^{\omega }$	✗	✗	✓	✓
$W$	✗	✗	✓	✓

Table A1. Common parameters and activation of immune mechanisms by scenario.

Parameter	Baseline	PAF	RAIE	RAIE + D
${Iso}_f^{\omega }\left(n\right)$	✓	✓	✓	✓
${\phi }_f^{\omega }\left(n\right)$	✗	✓	✓	✓
$\Delta {\eta }_{mode}^{\omega }$	✓	✓	✓	✓
${\psi }_f^{\omega }$	✗	✗	✓	✓
$W$	✗	✗	✓	✓

Appendix A.4.1. Experimental Design and Simulation Logic

Table A2 and Table A3 summarize the experimental configuration and the activation of adaptive layers across all frameworks. All scenarios were executed under identical supply chain topologies, baseline parameters, and disruption magnitudes. Therefore, differences in performance derive exclusively from the internal activation of response mechanisms—detection, redundancy, and memory—encoded in Equations (1)–(4). The objective was to observe how these mechanisms modify the temporal evolution of throughput (normalized between 0 and 1) during disruptions of increasing severity and duration.

Table A2 defines the binary activation of each immune-inspired layer for the four approaches. In the Baseline case, all switches remain off, implying a purely exogenous disturbance with no endogenous reaction. The PAF configuration (after Ivanov’s viability framework) activates passive redundancy (${\alpha }_{red}=1$) but still lacks early detection and memory, resulting in delayed and partial recovery. RAIE activates all biological analogues: innate (${\alpha }_{det}=1$), adaptive (${\alpha }_{red}=1$), and memory (${\alpha }_{mem}=1$), thus enabling local buffering and post-shock learning. RAIE + D enhances this structure through digital coupling (${\alpha }_{dig}=1$), which shortens detection time (${\tau }_{det}={\tau }_0 (1-\eta )$) and reduces leakage losses ($lea{k}_0 (1-\beta )$), representing the integration of IoT/BC-based traceability.

Table A3 introduces the disruption configuration for the 3 × 4 factorial experiment. Each disruption level (low, medium, high) corresponds to a different isolation rate ($Is{o}_f^{\omega }(n)$) and duration (1–3 quarters). The magnitude of operational stress ($\Delta {\eta }_{mode}^{\omega }$) scales accordingly. These parameters define the shock window shown in Figure A1, Figure A2 and Figure A3, which begins at quarter $t_3$ and lasts one to three periods, depending on severity.

Table A2. Activation of adaptive layers and response mechanisms by scenario.

Scenario	${\mathsf{\alpha }}_{\mathit{d}\mathit{e}\mathit{t}}$	${\mathsf{\alpha }}_{\mathit{r}\mathit{e}\mathit{d}}$	${\mathsf{\alpha }}_{\mathit{m}\mathit{e}\mathit{m}}$	${\mathsf{\alpha }}_{\mathit{d}\mathit{i}\mathit{g}}$	${\mathsf{\tau }}_{\mathit{d}\mathit{e}\mathit{t}}$	Leakage	Description
Baseline	0	0	0	0	large (effectively infinite)	${leak}_0$	No activation, no alternative routing, no memory, no IoT layer.
PAF (Process Adaptation Framework)	0	1	0	0	large	${leak}_0$	Passive redundancy: allows route/facility substitution but lacks early detection and memory.
RAIE	1	1	1	0	${\tau }_0$	${leak}_0$	Adaptive immune response with delayed detection, reconfiguration, and persistence (memory).
RAIE + Digital	1	1	1	1	${\tau }_0$	${leak}_0$ $(1 -\beta )$	Same as RAIE, but with faster detection and lower leakage enabled by IoT/Blockchain traceability.

Table A2. Activation of adaptive layers and response mechanisms by scenario.

Scenario	${\mathsf{\alpha }}_{\mathit{d}\mathit{e}\mathit{t}}$	${\mathsf{\alpha }}_{\mathit{r}\mathit{e}\mathit{d}}$	${\mathsf{\alpha }}_{\mathit{m}\mathit{e}\mathit{m}}$	${\mathsf{\alpha }}_{\mathit{d}\mathit{i}\mathit{g}}$	${\mathsf{\tau }}_{\mathit{d}\mathit{e}\mathit{t}}$	Leakage	Description
Baseline	0	0	0	0	large (effectively infinite)	${leak}_0$	No activation, no alternative routing, no memory, no IoT layer.
PAF (Process Adaptation Framework)	0	1	0	0	large	${leak}_0$	Passive redundancy: allows route/facility substitution but lacks early detection and memory.
RAIE	1	1	1	0	${\tau }_0$	${leak}_0$	Adaptive immune response with delayed detection, reconfiguration, and persistence (memory).
RAIE + Digital	1	1	1	1	${\tau }_0$	${leak}_0$ $(1 -\beta )$	Same as RAIE, but with faster detection and lower leakage enabled by IoT/Blockchain traceability.

Table A3. Experimental design and disruption configuration.

Severity Level	${\mathit{I}\mathit{s}\mathit{o}}_{\mathit{f}}^{\mathsf{\omega }}\left(\mathit{n}\right)$	Duration (t)	$\Delta {\mathsf{\eta }}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}}^{\mathsf{\omega }}$	Framework	$\mathbf{Innate} {\mathsf{\phi }}_{\mathit{f}}$	$\mathbf{Adaptive} {\mathsf{\Sigma }}_{\mathit{f}}$	$\mathbf{Memory} {\mathsf{\psi }}_{\mathit{f}}$	$\mathit{W}$	Description
Low	0.2	1	0.01	Baseline	0.00	0.00	0.00	–	Purely exogenous shock.
				PAF	0.25	0.00	0.00	–	Passive buffers and isolation (static viability).
				RAIE	0.25	0.15	0.30	3	Innate + adaptive + memory mechanisms.
				RAIE + Digital	0.25	0.20	0.35	3	Same as RAIE with digital traceability (25% leakage reduction).
Medium	0.4	2	0.02	Baseline	0.00	0.00	0.00	–	Purely exogenous shock.
				PAF	0.25	0.00	0.00	–	Passive buffers and isolation (static viability).
				RAIE	0.25	0.15	0.30	3	Innate + adaptive + memory mechanisms.
				RAIE + Digital	0.25	0.20	0.35	3	Same as RAIE with digital traceability (25% leakage reduction).
High	0.6	3	0.04	Baseline	0.00	0.00	0.00	–	Purely exogenous shock.
				PAF	0.25	0.00	0.00	–	Passive buffers and isolation (static viability).
				RAIE	0.25	0.15	0.30	3	Innate + adaptive + memory mechanisms.
				RAIE + Digital	0.25	0.20	0.35	3	Same as RAIE with digital traceability (25% leakage reduction).

Table A3. Experimental design and disruption configuration.

Severity Level	${\mathit{I}\mathit{s}\mathit{o}}_{\mathit{f}}^{\mathsf{\omega }}\left(\mathit{n}\right)$	Duration (t)	$\Delta {\mathsf{\eta }}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}}^{\mathsf{\omega }}$	Framework	$\mathbf{Innate} {\mathsf{\phi }}_{\mathit{f}}$	$\mathbf{Adaptive} {\mathsf{\Sigma }}_{\mathit{f}}$	$\mathbf{Memory} {\mathsf{\psi }}_{\mathit{f}}$	$\mathit{W}$	Description
Low	0.2	1	0.01	Baseline	0.00	0.00	0.00	–	Purely exogenous shock.
				PAF	0.25	0.00	0.00	–	Passive buffers and isolation (static viability).
				RAIE	0.25	0.15	0.30	3	Innate + adaptive + memory mechanisms.
				RAIE + Digital	0.25	0.20	0.35	3	Same as RAIE with digital traceability (25% leakage reduction).
Medium	0.4	2	0.02	Baseline	0.00	0.00	0.00	–	Purely exogenous shock.
				PAF	0.25	0.00	0.00	–	Passive buffers and isolation (static viability).
				RAIE	0.25	0.15	0.30	3	Innate + adaptive + memory mechanisms.
				RAIE + Digital	0.25	0.20	0.35	3	Same as RAIE with digital traceability (25% leakage reduction).
High	0.6	3	0.04	Baseline	0.00	0.00	0.00	–	Purely exogenous shock.
				PAF	0.25	0.00	0.00	–	Passive buffers and isolation (static viability).
				RAIE	0.25	0.15	0.30	3	Innate + adaptive + memory mechanisms.
				RAIE + Digital	0.25	0.20	0.35	3	Same as RAIE with digital traceability (25% leakage reduction).

During each simulation, throughput decreases proportionally to the isolation coefficient and gradually recovers according to the active mechanisms:

• Innate layer (${\phi }_f^{\omega }(n)$) increases temporary inventories or slack during the event.
• Adaptive layer (${\mathsf{\Sigma }}_f$) provides bounded overcapacity at unaffected nodes, facilitating load redistribution.
• Memory layer (${\psi }_f^{\omega }$) restores capacity progressively over the recovery horizon $W$.

All results stem solely from equations, maintaining the original MILP structure and decisions for complete reproducibility.

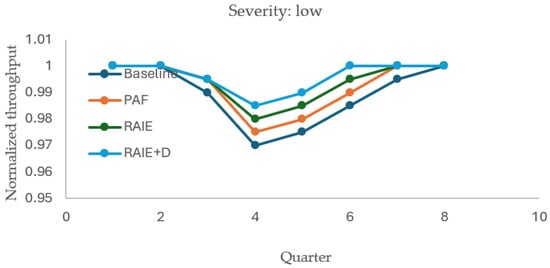
Figure A1. Normalized throughput to scenario low.

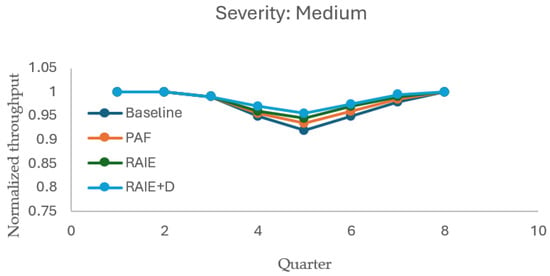
Figure A2. Normalized throughput to scenario medium.

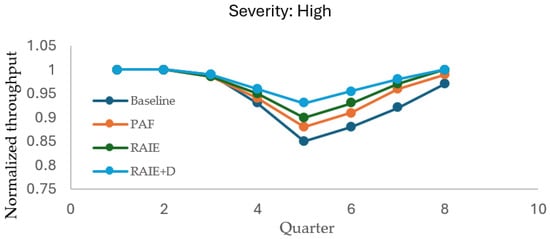
Figure A3. Normalized throughput to scenario high.

Appendix A.4.2. Comparative Trajectories and Quantitative Insights

Figure A1, Figure A2 and Figure A3 illustrate the temporal evolution of normalized throughput over an eight-quarter horizon for all combinations of severity and adaptive configuration. Each curve represents the relative performance of the network during a disruption window (highlighted in beige) and the subsequent recovery phase. Because all cases share identical topology, constraints, and shock magnitudes, the observed differences are directly attributable to the internal response logic encoded in Equations (1)–(4).

Under low severity, all frameworks exhibit limited degradation (less than 5%), and recovery is completed within one period. Although the Baseline and PAF trajectories nearly overlap, RAIE and RAIE + D show smoother transitions and a smaller transient loss area ($R_{area}$), reflecting the stabilizing effect of inventory buffers and temporary overcapacity. In this regime, the advantage of digital coupling is marginal, serving mainly to reduce the detection delay (${\tau }_{det}$) and leakage variability.

Under medium severity, differences become more pronounced. The Baseline case shows a sharp drop of approximately 10% in throughput, followed by a gradual return to equilibrium after three quarters. The PAF configuration limits the trough depth ($R_{min}$) but recovers at a slower rate due to the absence of learning and adaptive reinforcement. In contrast, RAIE achieves a faster and more stable convergence, with the recovery time ($TTR$) reduced by about one quarter relative to Baseline. RAIE + D amplifies this effect by shortening detection latency and mitigating losses through early containment, consistent with the hypothesis of proactive immune response.

Under high severity, the divergence between frameworks becomes substantial. The Baseline system experiences a 15–20% loss in throughput and fails to regain its initial performance within the simulation horizon, signaling a transition to non-viability. PAF exhibits moderate improvement by redistributing flow through redundant routes, but oscillations persist due to the lack of structural reorganization. RAIE demonstrates both containment and learning: throughput stabilizes after the second quarter of disruption, and full recovery occurs before the eighth quarter. Finally, RAIE + D attains the smallest impact area ($R_{area}$) and the shortest $TTR$, confirming that digital traceability enhances early detection, reduces leakage, and accelerates homeostasis restoration.

Quantitatively, the RAIE and RAIE + D cases maintain viability across all severities by preserving minimum throughput above 85% ($R_{min}\ge 0.85$), whereas the Baseline system falls below this threshold under high-stress conditions. The relative immune cost—defined as the cumulative activation of buffering and recovery mechanisms—remains contained within 1–2% of nominal operating cost, demonstrating an efficient trade-off between adaptation and performance retention.

Overall, these results validate the robustness of the RAIE framework as an operational layer for post-optimality evaluation. By maintaining identical baseline designs and parameter magnitudes, the analysis isolates the pure contribution of immune-inspired mechanisms—temporal buffering, adaptive reallocation, and structural memory—in sustaining viability under exogenous shocks of equal intensity.

Appendix A.4.3. Reproducibility and Implementation Details

All results presented in Figure A1, Figure A2 and Figure A3 were generated using the same mathematical structure defined by Equations $\left(1\right)-(4)$ in the main article, applied consistently across the four tested frameworks (Baseline, PAF, RAIE, and RAIE + Digital). The differences in system behavior arise solely from the activation of immune-inspired coefficients ${\varphi }_f^{\omega },{\mathsf{\Sigma }}_f^{\omega },{\psi }_f^{\omega }$, and detection lag modifiers (${\tau }_{det}$) as specified in Table A1.

The simulation can be replicated directly in Excel using the following steps:

• Parameter Initialization:

Create a parameter sheet including the nominal node capacities $Is{o}_f^{\omega }(n)$, loss coefficients $\Delta {\eta }_{mode}^{\omega }$, and recovery rate ${\psi }_f^{\omega }$. Define the common values (e.g., $Is{o}_f^{\omega }(n)=0.4$) and activation flags for each scenario as binary parameters (0 = inactive, 1 = active).

2.

Time Vector:

Define the temporal horizon $t=1\dots 8$ (quarters). In column form, compute the baseline throughput as

$$\mathrm{Throughput}(t)=1-Is{o}_f^{\omega }(n)\cdot \delta (t-t_s)$$

where $\delta (t-t_s)$ activates the disruption window (as in the 3 × 4 design).

3.

Dynamic Adjustment (Equations (2)–(4)):

Apply sequential updates in each period:

○

Innate Response: If active, increase minimum inventory or throughput by ${\varphi }_f^{\omega }(n)$.

○

Adaptive Response: During disruption, reduce effective losses by ${\mathsf{\Sigma }}_f^{\omega }$.

○

Memory Effect: After disruption, progressively restore performance at a rate of ${\psi }_f^{\omega }$ until period $W$.

4.

Normalization and Graphs:

Normalize all throughput trajectories by the nominal steady-state value (1.0) and chart them across $t$. The recovery horizon (TTR) can be marked using a vertical line or color band to indicate restoration to ≥ 99% of baseline.

5.

Immune Cost Calculation:

Compute the relative “immune cost” as the fraction of total resources or inventory allocated to recovery mechanisms:

$$ImmuneCost={\displaystyle \frac{\sum _t(In{v}_{extra}(t)+Buffers(t))}{BaseCost}}$$

The RAIE framework was deliberately designed as a quantitative extension of existing resilience models, rather than a purely conceptual contribution. Its formulation integrates immune-inspired principles—early detection, adaptive reconfiguration, and recovery memory—into the same mathematical infrastructure used by conventional viability and resilience studies (e.g., PAF).

The comparative experiment presented in this appendix provides the first quantitative evidence of RAIE’s distinct behavior under controlled conditions. By maintaining identical disruption severities and structural configurations across all scenarios, the differences in recovery trajectories directly reflect the activation of RAIE mechanisms, not parameter bias.

While the current results are based on simulation using MILP-derived optimal configurations, they already constitute a quantitative validation of the framework’s dynamic consistency: RAIE not only reproduces known resilience patterns (e.g., adaptive buffering and delayed recovery) but also introduces a measurable memory effect that accelerates stabilization without permanent oversizing.

Future work will involve empirical calibration using real operational data from CO₂ logistics and agroindustrial networks, enabling statistical validation and parameter learning for each immune mechanism. Nevertheless, this study provides a reproducible and transparent numerical foundation—bridging conceptual inspiration and quantitative implementation—that establishes RAIE as a viable analytical layer for next-generation resilient supply chain models.

Appendix B.1. Sets

This section defines the index sets that structure the mixed-integer linear programming (MILP) model for the CCUS network with mineralization. The sets enumerate the discrete elements in each echelon—capture sources, compression/gathering stations, liquefaction plants, transport modes and classes, storage/usage sinks, and time periods. Model variables and parameters are indexed by these sets; constraints are built over their Cartesian products to represent flows, capacities, inventories, and operational couplings.

Indexing Conventions

Lowercase symbols denote elements of their respective sets (e.g., q ∈ Q, c ∈ C, l ∈ LPorts, o ∈ O, h ∈ H, u ∈ U, eo ∈ eo, t ∈ T). Subscripts on variables and parameters follow these indices to indicate origin–destination pairs, transport class, and time; for example, QC (q,c,ca,t) is the CO₂ truck flow from capture source q to station c using truck class ca in period t. When a constraint applies only to a subset (e.g., cement plants eligible to receive SiO₂), a logical qualifier such as QCem(·) = 1 accompanies the summation over that subset.

All sets are finite and will be explicitly listed in the next subsection to ensure reproducibility and unambiguous notation.

$$Q=\{q1, q2, \dots , q12\} capture sources$$

$$C=\{c1, c2, \dots , c7\} compression and gathering stations$$

$$H=\{h1, h2, \dots , h6\} offshore storage hubs$$

$$O=\{o1, o2, \dots , o4\} onshore storage hubs$$

$$U=\{u1, u2, u3\} industrial end-uses$$

$$EO=\{eo1,eo2,\dots ,eo5\}EORfields\left(EnhancedOilRecovery\right)$$

$$T=\{t1, t2, \dots , t8\} quarterly time periods$$

$$Ta=\{Ta2, Ta3\} pipeline type 1$$

$$Te=\{Te2, Te3\} pipeline type 2$$

$$Ti=\{Ti2, Ti3\} pipeline type 3$$

$$To=\{To2, To3\} pipeline type 4$$

$$LP=\{lp1, lp2, \dots , lp6\} plants L1--L6 at ports$$

$$Lgeo=\{lgeo1, lgeo2, lgeo3, lgeo4\} plants connected to onshore hubs$$

$$Leor=\{leor1, leor2, leor3, leor4\} plants connected to EOR hubs$$

$$lnd=\{lnd1, lnd2, lnd3\} plants connected to industrial uses$$

$$Bar=\{Bar1, Bar2\} maritime transport modes$$

$$Cam=\{Cam1, Cam2\} ground transport modes$$

$$Kam=\{Kam1, Kam2, Kam3\} ground transport modes$$

$$Ca=\{ca1, ca2, ca3, ca4, ca5\}$$

$$Ka=\{ka1, ka2, ka3\} truck types$$

$$t=\{t1, t2, \dots , t8\} shipping time indices$$

Appendix B.2. Parameters

This section defines the exogenous inputs (parameters) of the MILP model. Parameters encode the techno-economic and environmental context in which the CCUS network operates, costs and prices, arc lengths and lead times, facility capacities and minimum-run levels, emission and leakage factors, reliability/traceability coefficients, and policy incentives. They are deterministic, time-indexed, relevant, and remain fixed throughout a given optimization run; scenario analysis is performed by perturbing selected parameter values.

Appendix B.2.1. What Parameters Represent

Each parameter quantifies a physical limit, efficiency, unit cost/revenue, or a policy signal. Together, they determine feasibility (through capacity and quality constraints) and performance (through the objective function). Parameters are indexed by the sets defined earlier (e.g., q ∈ Q, c ∈ C, l ∈ LPuerto, ca ∈ Ca, t ∈ T), and their subscripts follow those indices. When a quantity applies to a subset (e.g., cement plants eligible to receive SiO₂), logical flags (such as QCem(·) = 1) are used inside summations to restrict scope.

Appendix B.2.2. Units and Dimensional Consistency

Units are shown in square brackets next to each definition (e.g., [USD/tCO₂], [t/quarter], [USD/(t·km)], [kgCO₂e/km]). Percentages are modeled as fractions in [0, 1]. All equations preserve dimensional consistency by construction (e.g., “flow × emission-factor × distance” yields emissions). Monetary values should be interpreted in constant currency of the stated base year.

Appendix B.2.3. Main Categories

• Economic parameters: CAPEX proxies (fixed activation costs), OPEX (per-unit processing and handling), transport costs by mode/class, product prices (SiO₂, carbonates, EOR oil), credits/taxes, and incentive/penalty terms tied to traceability and inventory timing.
• Capacity and operations: Capture/compression/liquefaction/storage capacities, minimum-run requirements, vehicle/segment availability, and payloads.
• Techno-environmental: Emission factors for mining/processing and for each transport mode, leakage rates per arc and per node, and quality/stoichiometry coefficients for mineralization (e.g., reactivity, yields).
• Spatial/temporal: Geographic coordinates (and their conversions to radians), inter-node distances and travel times or lead-time linkers, and quarterly time indices.
• Reliability and blockchain: IoT reliability indices and blockchain cost/benefit coefficients that drive bonuses/penalties for traceability.

Data provenance and usage.

Unless noted, parameters are obtained from engineering estimates, vendor specs, literature values, or public databases, harmonized to the model’s period (quarter) and currency base year. When data are uncertain, the model supports sensitivity analyses by running alternative scenarios or applying bounds. Default values and initialization (e.g., zeros for unavailable flows/prices) are stated explicitly in the parameter list.

$${\mathrm{A}}_{\mathrm{q},\mathrm{x}}=\mathrm{Haversine} \mathrm{intermediate} \mathrm{term} \mathrm{for} \left(q,x\right)$$

$$\mathrm{aCO}{2}_{\mathrm{M}}=\mathrm{t}\mathrm{onn} \mathrm{of} {\mathrm{CO}}_2 \mathrm{captured} \mathrm{per} \mathrm{t} \mathrm{of} \mathrm{solid} M \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$BPTCO2={\mathrm{CO}}_2 \mathrm{price}/\mathrm{parameter} (\mathrm{policy} \mathrm{factor}) \left[\%\right]$$

$$BonifAlm{o}_{\mathrm{h}}=\mathrm{bonus} \mathrm{per} \mathrm{traced} \mathrm{stored} \mathrm{ton} \mathrm{at} \mathrm{hub} \mathrm{h} \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$bn{C}_{\mathrm{c}}=\mathrm{bonus} \mathrm{for} \mathrm{useful} \mathrm{inventoried} {\mathrm{CO}}_2 \mathrm{at} \mathrm{C} \left[\mathrm{USD}/{tCO}_2\right]$$

$$bnL{H}_{\mathrm{l}}=\mathrm{bonus} \mathrm{for} \mathrm{useful} \mathrm{inventoried} {\mathrm{CO}}_2 \mathrm{at} \mathrm{L} \left[\mathrm{USD}/{tCO}_2\right]$$

$$bnL{O}_{\mathrm{l}}=\mathrm{bonus} \mathrm{for} \mathrm{useful} \mathrm{inventoried} {\mathrm{CO}}_2 \mathrm{at} \mathrm{L} \left[\mathrm{USD}\right]$$

$$bnL{U}_{\mathrm{l}}=\mathrm{bonus} \mathrm{for} \mathrm{useful} \mathrm{inventoried} {\mathrm{CO}}_2 \mathrm{at} \mathrm{L} \left[\mathrm{USD}\right]/{tCO}_2$$

$$bnLE{O}_{\mathrm{l}}=\mathrm{bonus} \mathrm{for} \mathrm{useful} \mathrm{inventoried} {\mathrm{CO}}_2 \mathrm{at} \mathrm{L} \left[\mathrm{USD}/{tCO}_2\right]$$

$$\mathrm{CM}{\mathrm{T}}_{\mathrm{M}}=\mathrm{transport} \mathrm{cost} \mathrm{for} \mathrm{solids} M \left[\mathrm{USD}/\left(\mathrm{t}\cdot \mathrm{km}\right)\right]$$

$$\mathrm{CXCO}{2}_{\mathrm{x}}={\mathrm{CO}}_2 \mathrm{processing} \mathrm{capacity} \mathrm{at} x \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$\mathrm{CX}{\mathrm{S}}_{\mathrm{x}}=\mathrm{solids} \mathrm{processing} \mathrm{capacity} \mathrm{at} x \left[\mathrm{t}/\mathrm{quarter}\right]$$

$$\mathrm{CO}2\mathrm{C}{\mathrm{a}}_{\mathrm{ca}}\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km} (\mathrm{truck} \mathrm{ca} \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$\mathrm{CK}{\mathrm{X}}_{\mathrm{ka}}=\mathrm{truck} ka \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} \mathrm{on} \mathrm{routes} \mathrm{to} X \left[\mathrm{USD}/\left(\mathrm{t}\cdot \mathrm{km}\right)\right]$$

$$\mathrm{CPK}{\mathrm{X}}_{\mathrm{ka}}=\mathrm{truck} ka \mathrm{per}-\mathrm{trip} \mathrm{cost} (\mathrm{tolls}/\mathrm{handling}) \left[\mathrm{USD}/\mathrm{trip}\right]$$

$$\mathrm{cO}2\mathrm{Ka}{\mathrm{X}}_{\mathrm{ka}}={\mathrm{kgCO}}_{2 } \mathrm{per} \mathrm{km} \mathrm{in} \mathrm{truc}k \mathrm{to} X \left[\mathrm{kgC}{\mathrm{O}}_2\mathrm{e}/Km\right]$$

$$CO2C{a}_{\mathrm{ca}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km} (\mathrm{truck} \mathrm{ca}) \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CTCL{P}_{\mathrm{ta}}=\mathrm{pipeline} \mathrm{C}\to \mathrm{L} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{ta}) \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CTCL{G}_{\mathrm{te}}=\mathrm{pipeline} \mathrm{C}\to \mathrm{L} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{te}) \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CTCLG{E}_{\mathrm{ti}}=\mathrm{pipeline} \mathrm{C}\to \mathrm{L} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{ti}) \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CTCLG{U}_{\mathrm{to}}=\mathrm{pipeline} \mathrm{C}\to \mathrm{L} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{to}) \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CB{r}_{\mathrm{bar}}=\mathrm{maritime} \mathrm{transport} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{ship} \mathrm{bar}) \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CO2B{r}_{\mathrm{bar}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km} (\mathrm{ship} \mathrm{bar}) \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpB{r}_{\mathrm{bar}}=\mathrm{payload} \mathrm{per} \mathrm{ship} \mathrm{trip} \mathrm{bar} \left[\mathrm{t}/\mathrm{trip}\right]$$

$$CCa{m}_{\mathrm{cam}}=\mathrm{truck} \mathrm{C}\to \mathrm{U} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{cam}) \left[\mathrm{USD}/\left(\mathrm{t}\cdot \mathrm{km}\right)\right]$$

$$CO2Ca{m}_{\mathrm{cam}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km} (\mathrm{truck} \mathrm{cam}) \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CapCa{m}_{\mathrm{cam}}=\mathrm{payload} \mathrm{per} \mathrm{trip} (\mathrm{truck} \mathrm{cam}) \left[\mathrm{t}/\mathrm{trip}\right]$$

$$CPCa{m}_{\mathrm{cam}}=\mathrm{fixed} \mathrm{per}-\mathrm{trip} \mathrm{cost} (\mathrm{truck} \mathrm{cam}) \left[\mathrm{USD}/\mathrm{trip}\right]$$

$$CKa{m}_{\mathrm{kam}}=\mathrm{truck} \mathrm{L}\to \mathrm{U} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{kam}) \left[\mathrm{USD}/\left(\mathrm{t}\cdot \mathrm{km}\right)\right]$$

$$CO2Ka{m}_{\mathrm{kam}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km} (\mathrm{truck} \mathrm{kam}) \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpKa{m}_{\mathrm{kam}}=\mathrm{payload} \mathrm{per} \mathrm{trip} (\mathrm{truck} \mathrm{kam}) \left[\mathrm{t}\mathrm{n}/\mathrm{trip}\right]$$

$$CPKa{m}_{\mathrm{kam}}=\mathrm{fixed} \mathrm{per}-\mathrm{trip} \mathrm{cost} (\mathrm{truck} \mathrm{kam}) \left[\mathrm{USD}/\mathrm{trip}\right]$$

$$CK{a}_{\mathrm{ka}}=\mathrm{truck} \mathrm{L}\to \mathrm{U} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{type} \mathrm{ka}) \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CO2K{a}_{\mathrm{ka}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km} (\mathrm{truck} \mathrm{ka}) \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpK{a}_{\mathrm{ka}}=\mathrm{payload} \mathrm{per} \mathrm{trip} (\mathrm{truck} \mathrm{ka}) \left[\mathrm{t}\mathrm{n}/\mathrm{trip}\right]$$

$$CPK{a}_{\mathrm{ka}}=\mathrm{fixed} \mathrm{per}-\mathrm{trip} \mathrm{cost} (\mathrm{truck} \mathrm{ka}) \left[\mathrm{USD}/\mathrm{trip}\right]$$

$$CT{a}_{\mathrm{ta}}=\mathrm{transport} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{L}\to \mathrm{U}), \mathrm{class} \mathrm{ta} \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CO2T{a}_{\mathrm{ta}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km}, \mathrm{class} \mathrm{ta} \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpT{a}_{\mathrm{ta}}=\mathrm{payload} \mathrm{per} \mathrm{segment} (\mathrm{class} \mathrm{ta}) \left[\mathrm{t}\mathrm{n}/\mathrm{segment}\right]$$

$$CPT{a}_{\mathrm{ta}}=\mathrm{fixed} \mathrm{per}-\mathrm{segment} \mathrm{cost} (\mathrm{class} \mathrm{ta}) \left[\mathrm{USD}/\mathrm{segment}\right]$$

$$CT{e}_{\mathrm{te}}=\mathrm{transport} \mathrm{cost} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{L}\to \mathrm{U}), \mathrm{class} \mathrm{te} \left[\mathrm{USD}/\left(\mathrm{t}\cdot \mathrm{km}\right)\right]$$

$$CO2T{e}_{\mathrm{te}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km}, \mathrm{class} \mathrm{te} \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpT{e}_{\mathrm{te}}=\mathrm{payload} \mathrm{per} \mathrm{segment} (\mathrm{te}) \left[\mathrm{t}\mathrm{n}/\mathrm{segment}\right]$$

$$CcumqT{e}_{\mathrm{te}}=\mathrm{fixed} \mathrm{per}-\mathrm{segment} \mathrm{cost} (\mathrm{te}) \left[\mathrm{USD}/\mathrm{segment}\right]$$

$$CT{o}_{\mathrm{to}}=\mathrm{transport} \cos \mathrm{t} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{L}\to \mathrm{U}), \mathrm{class} \mathrm{to} \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CO2T{o}_{\mathrm{to}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km}, \mathrm{class} \mathrm{to} \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpT{o}_{\mathrm{to}}=\mathrm{payload} \mathrm{per} \mathrm{segment} (\mathrm{to}) \left[\mathrm{t}\mathrm{n}/\mathrm{segment}\right]$$

$$CcumqT{o}_{\mathrm{to}}=\mathrm{fixed} \mathrm{per}-\mathrm{segment} \cos \mathrm{t} (\mathrm{to}) \left[\mathrm{USD}/\mathrm{segment}\right]$$

$$CT{i}_{\mathrm{ti}}=\mathrm{transport} \cos \mathrm{t} \mathrm{per} \mathrm{t}-\mathrm{km} (\mathrm{L}\to \mathrm{U}), \mathrm{class} \mathrm{ti} \left[\mathrm{USD}/\left(\mathrm{t}\mathrm{n}\cdot \mathrm{km}\right)\right]$$

$$CO2T{i}_{\mathrm{ti}}=\mathrm{indirect} \mathrm{emissions} \mathrm{per} \mathrm{km}, \mathrm{class} \mathrm{ti} \left[\mathrm{kgC}{\mathrm{O}}_2/\mathrm{km}\right]$$

$$CpT{i}_{\mathrm{ti}}=\mathrm{payload} \mathrm{per} \mathrm{segment} (\mathrm{ti}) \left[\mathrm{t}\mathrm{n}/\mathrm{segment}\right]$$

$$CcumqT{i}_{\mathrm{ti}}=\mathrm{fixed} \mathrm{per}-\mathrm{segment} \cos \mathrm{t} (\mathrm{ti}) \left[\mathrm{USD}/\mathrm{segment}\right]$$

$$CpP{Q}_{\mathrm{q}}=\mathrm{maximum} \mathrm{capture} \mathrm{capacity} \mathrm{at} \mathrm{q} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CpP{C}_{\mathrm{c}}=\mathrm{maximum} \mathrm{compression}/\mathrm{gathering} \mathrm{capacity} \mathrm{at} \mathrm{c} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CpP{P}_{\mathrm{l}}=\mathrm{maximum} \mathrm{liquefaction} \mathrm{capacity} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CPl{g}_{\mathrm{l}}=\mathrm{maximum} \mathrm{liquefaction} \mathrm{capacity} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CPle{o}_{\mathrm{l}}=\mathrm{maximum} \mathrm{liquefaction} \mathrm{capacity} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CPl{i}_{\mathrm{l}}=\mathrm{maximum} \mathrm{liquefaction} \mathrm{capacity} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CS{h}_{\mathrm{h}}=\mathrm{minimum} \mathrm{geological} \mathrm{storage} \mathrm{use} \mathrm{at} \mathrm{h} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CS{o}_{\mathrm{o}}=\mathrm{minimum} \mathrm{geological} \mathrm{storage} \mathrm{use} \mathrm{at} \mathrm{o} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CSe{o}_{\mathrm{eo}}=\mathrm{minimum} {\mathrm{CO}}_2 \mathrm{for} \mathrm{EOR} \mathrm{at} \mathrm{eo} \left[{tCO}_2/\mathrm{quarter}\right]$$

$$CS{u}_{\mathrm{u}}=\mathrm{minimum} {\mathrm{CO}}_2 \mathrm{for} \mathrm{industrial} \mathrm{use} \mathrm{at} \mathrm{u} \left[\mathrm{t}/\mathrm{quarter}\right]$$

$$CO2Al{m}_{\mathrm{t}}=\mathrm{minimum} \mathrm{stored} {\mathrm{CO}}_2 \mathrm{in} \mathrm{t} \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$CnT{C}_{\mathrm{c}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{compression}/\mathrm{gathering} \mathrm{station} \mathrm{c}$$

$$CnTL{P}_{\mathrm{l}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l}$$

$$CnTL{G}_{\mathrm{l}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{onshore}-\mathrm{connection} \mathrm{plant} \mathrm{l}$$

$$CnTL{E}_{\mathrm{l}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{EOR}-\mathrm{connection} \mathrm{plant} \mathrm{l}$$

$$CnTL{U}_{\mathrm{l}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{industry}-\mathrm{connection} \mathrm{plant} \mathrm{l}$$

$$CnT{H}_{\mathrm{h}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{offshore} \mathrm{hub} \mathrm{h}$$

$$CnT{O}_{\mathrm{o}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{onshore} \mathrm{hub} \mathrm{o}$$

$$CnT{U}_{\mathrm{u}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{industrial} \mathrm{use} \mathrm{node} \mathrm{u}$$

$$CnT{E}_{\mathrm{eo}}=\mathrm{IoT} \mathrm{reliability} \mathrm{at} \mathrm{EOR} \mathrm{field} \mathrm{eo}$$

$$CTI{C}_{\mathrm{c}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{c} \left[\mathrm{USD}\right]$$

$$CTIL{P}_{\mathrm{l}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTIL{G}_{\mathrm{l}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{onshore}-\mathrm{connection} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTILE{O}_{\mathrm{l}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{EOR}-\mathrm{connection} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTIL{U}_{\mathrm{l}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{industry}-\mathrm{connection} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTI{H}_{\mathrm{h}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{hub} \mathrm{h} \left[\mathrm{USD}\right]$$

$$CTI{O}_{\mathrm{o}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{hub} \mathrm{o} \left[\mathrm{USD}\right]$$

$$CTI{U}_{\mathrm{u}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{use} \mathrm{node} \mathrm{u} \left[\mathrm{USD}\right]$$

$$CTIE{O}_{\mathrm{eo}}=\mathrm{IoT} \mathrm{technology} \cos \mathrm{t} \mathrm{at} \mathrm{EOR} \mathrm{field} \mathrm{eo} \left[\mathrm{USD}\right]$$

$$CM{C}_{\mathrm{c}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{c} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CML{P}_{\mathrm{l}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CML{G}_{\mathrm{l}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CMLE{O}_{\mathrm{l}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CML{U}_{\mathrm{l}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CM{H}_{\mathrm{h}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{hub} \mathrm{h} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CM{O}_{\mathrm{o}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{hub} \mathrm{o} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CM{U}_{\mathrm{u}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{use} \mathrm{node} \mathrm{u} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CME{O}_{\mathrm{eo}}=\mathrm{maintenance} \cos \mathrm{t} \mathrm{at} \mathrm{EOR} \mathrm{field} \mathrm{eo} \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$CT{C}_{\mathrm{c}}=\mathrm{IoT} \mathrm{installation} \cos \mathrm{t} \mathrm{at} \mathrm{c} \left[\mathrm{USD}\right]$$

$$CTL{P}_{\mathrm{l}}=\mathrm{IoT} \mathrm{installation} \cos \mathrm{t} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTL{G}_{\mathrm{l}}=\mathrm{IoT} \mathrm{installation} \cos \mathrm{t} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTL{U}_{\mathrm{l}}=\mathrm{IoT} \mathrm{installation} \cos \mathrm{t} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CTLE{O}_{\mathrm{l}}=\mathrm{IoT} \mathrm{installation} \cos \mathrm{t} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$CM{V}_{\mathrm{M}}=\mathrm{material} \mathrm{M} \mathrm{parameter}/\cos \mathrm{t} (\mathrm{init}. \mathrm{value} \mathrm{as} \mathrm{per} \mathrm{data}) [\%]$$

$$CMCO{3}_{\mathrm{M}}=\mathrm{carbonate} \mathrm{M} \mathrm{parameter}/\cos \mathrm{t} (\mathrm{init}. \mathrm{value} \mathrm{as} \mathrm{per} \mathrm{data}) \left[\%\right]$$

$$CapC{a}_{\mathrm{ca}}=\mathrm{payload} \mathrm{per} \mathrm{trip} (\mathrm{truck} \mathrm{ca}) \left[\mathrm{t}\mathrm{n}/\mathrm{trip}\right]$$

$$CPC{a}_{\mathrm{ca}}=\mathrm{fixed} \mathrm{per}-\mathrm{trip} \cos \mathrm{t} (\mathrm{truck} \mathrm{ca}) \left[\mathrm{USD}/\mathrm{trip}\right]$$

$$\mathrm{D}{\mathrm{C}}_{\mathrm{q},\mathrm{t}}=\mathrm{quarterly} \mathrm{cement} \mathrm{demand} \mathrm{at} \left(q,t\right) \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$\mathrm{dla}{\mathrm{t}}_{\mathrm{q},\mathrm{x}}=\mathrm{latitude} \mathrm{difference} (\mathrm{rad}) \mathrm{for} \left(q,x\right) \left[\mathrm{rad}\right]$$

$$\mathrm{dlo}{\mathrm{n}}_{\mathrm{q},\mathrm{x}}=\mathrm{longitude} \mathrm{difference} (\mathrm{rad}) \mathrm{for} \left(q,x\right) \left[\mathrm{rad}\right]$$

$$\mathrm{DQ}{\mathrm{X}}_{\mathrm{q},\mathrm{x}}=\mathrm{geodesic} \mathrm{distance} \mathrm{between} q \mathrm{and} x \left[\mathrm{km}\right]$$

$$\mathrm{DsC}{\mathrm{a}}_{\mathrm{ca}}=\mathrm{number} \mathrm{of} \mathrm{available} \mathrm{trucks} \mathrm{of} \mathrm{type} ca \left[\mathrm{veh}\right]$$

$$DsC{a}_{\mathrm{ca}}=\mathrm{number} \mathrm{of} \mathrm{available} \mathrm{trucks} \mathrm{of} \mathrm{type} \mathrm{ca} \left[\mathrm{veh}\right]$$

$$DB{r}_{\mathrm{bar}}=\mathrm{number} \mathrm{of} \mathrm{available} \mathrm{ships} \mathrm{bar} \left[\mathrm{units}\right]$$

$$DsCa{m}_{\mathrm{cam}}=\mathrm{number} \mathrm{of} \mathrm{available} \mathrm{trucks} (\mathrm{type} \mathrm{cam}) \left[\mathrm{veh}\right]$$

$$DKa{m}_{\mathrm{kam}}=\mathrm{number} \mathrm{of} \mathrm{available} \mathrm{trucks} (\mathrm{type} \mathrm{kam}) \left[\mathrm{veh}\right]$$

$$DK{a}_{\mathrm{ka}}=\mathrm{number} \mathrm{of} \mathrm{available} \mathrm{trucks} (\mathrm{type} \mathrm{ka}) \left[\mathrm{veh}\right]$$

$$DT{a}_{\mathrm{ta}}=\mathrm{availability} \mathrm{parameter} \mathrm{for} \mathrm{class} \mathrm{ta}$$

$$DT{e}_{\mathrm{te}}=\mathrm{availability} \mathrm{parameter} \mathrm{for} \mathrm{te}$$

$$DT{o}_{\mathrm{to}}=\mathrm{availability} \mathrm{parameter} \mathrm{for} \mathrm{to}$$

$$DT{i}_{\mathrm{ti}}=\mathrm{availability} \mathrm{parameter} \mathrm{for} \mathrm{ti}$$

$$Dqq{q}_{\mathrm{q},\mathrm{qq}}=\mathrm{distance}/\mathrm{relationship} \mathrm{between} \mathrm{q} \mathrm{and} \mathrm{qq} \left[\mathrm{km}\right]$$

$$DemMinSiO{2}_{\mathrm{qq},\mathrm{t}}=\mathrm{minimum} \mathrm{quarterly} \mathrm{demand} \mathrm{of} {\mathrm{SiO}}_2 \mathrm{at} \mathrm{qq} \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]\backslash$$

$$DemMinMCO{3}_{\mathrm{q},\mathrm{t}}=\mathrm{minimum} \mathrm{quarterly} \mathrm{demand} \mathrm{of} {\mathrm{MCO}}_3 \mathrm{returned} \mathrm{to} \mathrm{q} \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$\mathrm{EFM}{\mathrm{T}}_{\mathrm{M}}=\mathrm{emission} \mathrm{factor} \mathrm{of} \mathrm{solids} \mathrm{transport} \mathrm{for} M \left[\mathrm{tC}{\mathrm{O}}_2/\left(\mathrm{t}\cdot \mathrm{km}\right)\right]$$

$$ERF{C}_{\mathrm{c}}=\mathrm{ERF} \mathrm{index} \mathrm{at} \mathrm{c} \left[\%\right]$$

$$ERFL{P}_{\mathrm{l}}=\mathrm{ERF} \mathrm{index} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\%\right]$$

$$ERFL{G}_{\mathrm{l}}=\mathrm{ERF} \mathrm{index} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[\%\right]$$

$$ERFLE{O}_{\mathrm{l}}=\mathrm{ERF} \mathrm{index} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[\%\right]$$

$$ERFL{U}_{\mathrm{l}}=\mathrm{ERF} \mathrm{index} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[\%\right]$$

$$efm{p}_{\mathrm{M}}=\mathrm{upstream} \mathrm{mining}/\mathrm{processing} \mathrm{emission} \mathrm{factor} \mathrm{for} \mathrm{M} \left[\mathrm{kgC}{\mathrm{O}}_2\mathrm{e}/\mathrm{quarter}\right]$$

$$\mathrm{FC}{\mathrm{x}}_{\mathrm{x}}=\mathrm{fixed} \mathrm{operating} \cos \mathrm{t} \mathrm{of} \mathrm{plant} x \left[\mathrm{USD}/\mathrm{quarter}\right]$$

$$FxC{s}_{\mathrm{q}}=\mathrm{fixed} \cos \mathrm{t} \mathrm{to} \mathrm{activate} \mathrm{capture} \mathrm{source} \mathrm{q} \left[\mathrm{USD}\right]$$

$$FxC{C}_{\mathrm{c}}=\mathrm{fixed} \cos \mathrm{t} \mathrm{to} \mathrm{activate} \mathrm{compression}/\mathrm{gathering} \mathrm{station} \mathrm{c} \left[\mathrm{USD}\right]$$

$$FxC{H}_{\mathrm{h}}=\mathrm{fixed} \cos \mathrm{t} \mathrm{to} \mathrm{activate} \mathrm{offshore} \mathrm{hub} \mathrm{h} \left[\mathrm{USD}\right]$$

$$FxC{O}_{\mathrm{o}}=\mathrm{fixed} \cos \mathrm{t} \mathrm{to} \mathrm{activate} \mathrm{onshore} \mathrm{hub} \mathrm{o} \left[\mathrm{USD}\right]$$

$$FxC{U}_{\mathrm{u}}=\mathrm{fixed} \cos \mathrm{t} \mathrm{to} \mathrm{activate} \mathrm{industrial} \mathrm{use} \mathrm{node} \mathrm{u} \left[\mathrm{USD}\right]$$

$${\mathrm{i}}_{\mathrm{x}}={\mathrm{kgCO}}_2\mathrm{per} \mathrm{t} \mathrm{of} \mathrm{solid} \mathrm{processed} \mathrm{at} \mathrm{x} \left[\mathrm{kgC}{\mathrm{O}}_2\mathrm{e}/\mathrm{quarter}\right]$$

$$\mathrm{Lt}{\mathrm{q}}_{\mathrm{q}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{node} q$$

$$\mathrm{Lng}{\mathrm{q}}_{\mathrm{q}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{node} q$$

$$\mathrm{Lt}{\mathrm{x}}_{\mathrm{x}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{node} x$$

$$\mathrm{Lng}{\mathrm{x}}_{\mathrm{x}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{node} x$$

$$\mathrm{Lt}{\mathrm{c}}_{\mathrm{c}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{station} c$$

$$\mathrm{Lng}{\mathrm{c}}_{\mathrm{c}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{station} c$$

$$\mathrm{LtL}{\mathrm{P}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{port} \mathrm{plant} l$$

$$\mathrm{LngL}{\mathrm{P}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{port} \mathrm{plant} l$$

$$\mathrm{LtL}{\mathrm{G}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{onshore}-\mathrm{connection} \mathrm{plant} l$$

$$\mathrm{LngL}{\mathrm{G}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{onshore}-\mathrm{connection} \mathrm{plant} l$$

$$\mathrm{LtL}{\mathrm{E}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{EOR}-\mathrm{connection} \mathrm{plant} l$$

$$\mathrm{LngL}{\mathrm{E}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{EOR}-\mathrm{connection} \mathrm{plant} l$$

$$\mathrm{LtL}{\mathrm{I}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{industry}-\mathrm{connection} \mathrm{plant} l$$

$$\mathrm{LngL}{\mathrm{I}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{industry}-\mathrm{connection} \mathrm{plant} l$$

$$\mathrm{Lt}{\mathrm{h}}_{\mathrm{h}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{offshore} \mathrm{hub} h$$

$$\mathrm{Lng}{\mathrm{h}}_{\mathrm{h}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{offshore} \mathrm{hub} h$$

$$\mathrm{Lt}{\mathrm{o}}_{\mathrm{o}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{onshore} \mathrm{hub} o$$

$$\mathrm{Lng}{\mathrm{o}}_{\mathrm{o}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{onshore} \mathrm{hub} o$$

$$\mathrm{Lte}{\mathrm{o}}_{\mathrm{eo}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{EOR} \mathrm{field} eo$$

$$\mathrm{Lnge}{\mathrm{o}}_{\mathrm{eo}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{EOR} \mathrm{field} eo$$

$$\mathrm{Lt}{\mathrm{U}}_{\mathrm{u}}=\mathrm{latitude} (\mathrm{deg}) \mathrm{of} \mathrm{industrial} \mathrm{use} \mathrm{node} u$$

$$\mathrm{Lng}{\mathrm{U}}_{\mathrm{u}}=\mathrm{longitude} (\mathrm{deg}) \mathrm{of} \mathrm{industrial} \mathrm{use} \mathrm{node} u$$

$$\mathrm{LtR}{\mathrm{c}}_{\mathrm{c}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} c \left[\mathrm{rad}\right]$$

$$\mathrm{LnR}{\mathrm{c}}_{\mathrm{c}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} c \left[\mathrm{rad}\right]$$

$$\mathrm{LtRL}{\mathrm{P}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} \mathrm{port} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LnRL}{\mathrm{P}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} \mathrm{port} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LtRL}{\mathrm{G}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} \mathrm{onshore}-\mathrm{connection} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LnRL}{\mathrm{G}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} \mathrm{onshore}-\mathrm{connection} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LtRL}{\mathrm{E}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} \mathrm{EOR}-\mathrm{connection} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LnRL}{\mathrm{E}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} \mathrm{EOR}-\mathrm{connection} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LtRL}{\mathrm{L}}_{\mathrm{l}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} \mathrm{industry}-\mathrm{connection} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LnRL}{\mathrm{L}}_{\mathrm{l}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} \mathrm{industry}-\mathrm{connection} \mathrm{plant} l \left[\mathrm{rad}\right]$$

$$\mathrm{LtR}{\mathrm{q}}_{\mathrm{q}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} q \left[\mathrm{rad}\right]$$

$$\mathrm{LnR}{\mathrm{q}}_{\mathrm{q}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} q \left[\mathrm{rad}\right]$$

$$\mathrm{LtR}{\mathrm{h}}_{\mathrm{h}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} h \left[\mathrm{rad}\right]$$

$$\mathrm{LnR}{\mathrm{h}}_{\mathrm{h}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} h \left[\mathrm{rad}\right]$$

$$\mathrm{LtR}{\mathrm{u}}_{\mathrm{u}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} u \left[\mathrm{rad}\right]$$

$$\mathrm{LnR}{\mathrm{u}}_{\mathrm{u}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} u \left[\mathrm{rad}\right]$$

$$\mathrm{LtR}{\mathrm{o}}_{\mathrm{o}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} o \left[\mathrm{rad}\right]$$

$$\mathrm{LnR}{\mathrm{o}}_{\mathrm{o}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} o \left[\mathrm{rad}\right]$$

$$\mathrm{LtRe}{\mathrm{o}}_{\mathrm{eo}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} eo \left[\mathrm{rad}\right]$$

$$\mathrm{LnRe}{\mathrm{o}}_{\mathrm{eo}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} eo \left[\mathrm{rad}\right]$$

$$\mathrm{LtR}{\mathrm{x}}_{\mathrm{x}}=\mathrm{latitude} (\mathrm{rad}) \mathrm{of} x \left[\mathrm{rad}\right]$$

$$\mathrm{LnR}{\mathrm{x}}_{\mathrm{x}}=\mathrm{longitude} (\mathrm{rad}) \mathrm{of} x \left[\mathrm{rad}\right]$$

$$LRQ{C}_{\mathrm{ca}}=\mathrm{loss} (\mathrm{leakage}) \mathrm{per} \mathrm{trip} \mathrm{Q}\to \mathrm{C} (\mathrm{truck} \mathrm{ca}) \left[\%\right]$$

$$LRCL{H}_{\mathrm{ta}}=\mathrm{pipeline} \mathrm{loss} \mathrm{C}\to \mathrm{L} (\mathrm{type} \mathrm{ta}) \left[\%\right]$$

$$LRCL{O}_{\mathrm{te}}=\mathrm{pipeline} \mathrm{loss} \mathrm{C}\to \mathrm{L} (\mathrm{type} \mathrm{te}) \left[\%\right]$$

$$LRCLE{O}_{\mathrm{ti}}=\mathrm{pipeline} \mathrm{loss} \mathrm{C}\to \mathrm{L} (\mathrm{type} \mathrm{ti}) \left[\%\right]$$

$$LRCL{U}_{\mathrm{to}}=\mathrm{pipeline} \mathrm{loss} \mathrm{C}\to \mathrm{L} (\mathrm{type} \mathrm{to}) \left[\%\right]$$

$$LRCLH{1}_{\mathrm{bar}}=\mathrm{loss} \mathrm{on} \mathrm{L}\to \mathrm{H} (\mathrm{ship} \mathrm{bar}) \left[\%\right]$$

$$LRL{U}_{\mathrm{ka}}=\mathrm{loss} \mathrm{per} \mathrm{trip} \mathrm{L}\to \mathrm{U} (\mathrm{truck} \mathrm{ka}) \left[\%\right]$$

$$LRL{E}_{\mathrm{kam}}=\mathrm{loss} \mathrm{per} \mathrm{trip} \mathrm{L}\to \mathrm{U} (\mathrm{truck} \mathrm{kam}) \left[\%\right]$$

$$LRC{U}_{\mathrm{tu}}=\mathrm{pipeline} \mathrm{loss} \mathrm{C}\to \mathrm{U} (\mathrm{type} \mathrm{tu}) \left[\%\right]$$

$$LR{C}_{\mathrm{c}}=\mathrm{quarterly} \mathrm{loss} \mathrm{rate} \mathrm{at} \mathrm{c} \left[\%/\mathrm{quarter}\right]$$

$$LRl{p}_{\mathrm{l}}=\mathrm{quarterly} \mathrm{loss} \mathrm{rate} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\%/\mathrm{quarter}\right]$$

$$LRl{g}_{\mathrm{l}}=\mathrm{quarterly} \mathrm{loss} \mathrm{rate} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[\%/\mathrm{quarter}\right]$$

$$LRLE{o}_{\mathrm{l}}=\mathrm{quarterly} \mathrm{loss} \mathrm{rate} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[\%/\mathrm{quarter}\right]$$

$$LRl{i}_{\mathrm{l}}=\mathrm{quarterly} \mathrm{loss} \mathrm{rate} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[\%/\mathrm{quarter}\right]$$

$$\mathrm{MC}{\mathrm{S}}_{\mathrm{M}}=\mathrm{solid} M \mathrm{treatment} \cos \mathrm{t} \left[\mathrm{USD}/\mathrm{t}\right]$$

$$\mathrm{MR}{\mathrm{X}}_{\mathrm{x}}=\mathrm{minimum} \mathrm{run} \mathrm{per} \mathrm{plant} x \left[\mathrm{tC}{\mathrm{O}}_2/\right]$$

$$\mathrm{M}{\mathrm{R}}_{\mathrm{x}}=\mathrm{minimum} \mathrm{run} \mathrm{at} x (\mathrm{fraction} \mathrm{of} \mathrm{CXCO}{2}_{\mathrm{x})} \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$\mathrm{OCCO}2{\mathrm{x}}_{\mathrm{x}}=\mathrm{OPEX} \mathrm{per} \mathrm{processed} \mathrm{t} \mathrm{of} {\mathrm{CO}}_2 \mathrm{at} x \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$\mathrm{OC}{\mathrm{x}}_{\mathrm{x}}=\mathrm{unit} \mathrm{operating} \cos \mathrm{t} \mathrm{at} x \left[\mathrm{USD}/\mathrm{t}\mathrm{n} \left(\mathrm{solid}\right)\right]$$

$$PSiO2q=price of SiO\}\_2 \mathrm{“}\{ delivered to cement plant \} qq (origin \} q) [USD/tn]$$

$$\mathrm{PMCO}{3}_{\mathrm{q}}=\mathrm{price} \mathrm{of} \mathrm{carbonates} \mathrm{returned} \mathrm{to} q \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$\mathrm{PSiO}2\mathrm{CE}{\mathrm{M}}_{\mathrm{qq}}=\mathrm{price} \mathrm{of} {\mathrm{SiO}}_2 \mathrm{at} \mathrm{cement} \mathrm{plant} qq \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$\mathrm{PMCO}3\mathrm{RE}{\mathrm{T}}_{\mathrm{q}}=\mathrm{price} \mathrm{of} \mathrm{carbonate} \mathrm{returned} \mathrm{to} \mathrm{mine} q \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$PCC=\mathrm{price} \mathrm{per} \mathrm{t} \mathrm{of} {\mathrm{CO}}_2 \mathrm{captured} \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$PBrl=\mathrm{Brent} (\mathrm{reference}) \mathrm{price} \left[\mathrm{USD}/\mathrm{bbl}\right]$$

$$PenalTardi{a}_{\mathrm{h}}=\mathrm{penalty} \mathrm{for} \mathrm{late} \mathrm{accumulated} \mathrm{inventory} \mathrm{at} \mathrm{hub} \mathrm{h} \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$PNBl{p}_{\mathrm{l}}=\mathrm{loss} \mathrm{due} \mathrm{to} \mathrm{lack} \mathrm{of} \mathrm{traceability} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$PNBl{g}_{\mathrm{l}}=\mathrm{loss} \mathrm{due} \mathrm{to} \mathrm{lack} \mathrm{of} \mathrm{traceability} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$PNBle{o}_{\mathrm{l}}=\mathrm{loss} \mathrm{due} \mathrm{to} \mathrm{lack} \mathrm{of} \mathrm{traceability} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$PNBl{i}_{\mathrm{l}}=\mathrm{loss} \mathrm{due} \mathrm{to} \mathrm{lack} \mathrm{of} \mathrm{traceability} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$PNB{c}_{\mathrm{c}}=\mathrm{loss} \mathrm{due} \mathrm{to} \mathrm{lack} \mathrm{of} \mathrm{traceability} \mathrm{at} \mathrm{station} \mathrm{c} \left[\mathrm{USD}\right]$$

$$pe{C}_{\mathrm{c}}=\mathrm{penalty} \mathrm{for} \mathrm{late} \mathrm{inventory} \mathrm{at} \mathrm{C} \left[\mathrm{USD}/{tCO}_2\right]$$

$$peL{H}_{\mathrm{l}}=\mathrm{penalty} \mathrm{for} \mathrm{late} \mathrm{inventory} \mathrm{at} \mathrm{L} \left[\mathrm{USD}/{tCO}_2\right]$$

$$peL{O}_{\mathrm{l}}=\mathrm{penalty} \mathrm{for} \mathrm{late} \mathrm{inventory} \mathrm{at} \mathrm{L} \left[\mathrm{USD}/{tCO}_2\right]$$

$$peL{U}_{\mathrm{l}}=\mathrm{penalty} \mathrm{for} \mathrm{late} \mathrm{inventory} \mathrm{at} \mathrm{L} \left[\mathrm{USD}/{tCO}_2\right]$$

$$peLE{O}_{\mathrm{l}}=\mathrm{penalty} \mathrm{for} \mathrm{late} \mathrm{inventory} \mathrm{at} \mathrm{L} \left[\mathrm{USD}/{tCO}_2\right]$$

$$\mathrm{R}{\mathrm{c}}_{\mathrm{M}}=\mathrm{reactivity} \mathrm{index} \mathrm{of} \mathrm{solid} M \left(0--1\right) \left[\%\right]$$

$$\mathrm{RcM}{\mathrm{n}}_{\mathrm{x}}=\mathrm{minimum} \mathrm{average} \mathrm{blend} \mathrm{reactivity} \mathrm{at} x \left[\%\right]$$

$$\mathrm{RcMn}{\mathrm{x}}_{\mathrm{x}}=\mathrm{maximum} \mathrm{average} \mathrm{blend} \mathrm{reactivity} \mathrm{at} x \left[\%\right]$$

$$RBC{C}_{\mathrm{c}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{c} \left[\mathrm{USD}\right]$$

$$RBCl{p}_{\mathrm{l}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{port} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$RBCl{g}_{\mathrm{l}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{onshore} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$RBCle{o}_{\mathrm{l}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{EOR} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$RBCl{i}_{\mathrm{l}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{industrial} \mathrm{plant} \mathrm{l} \left[\mathrm{USD}\right]$$

$$RBC{O}_{\mathrm{o}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{hub} \mathrm{o} \left[\mathrm{USD}\right]$$

$$RBC{U}_{\mathrm{u}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{use} \mathrm{node} \mathrm{u} \left[\mathrm{USD}\right]$$

$$RBCE{O}_{\mathrm{eo}}=\mathrm{reward} \mathrm{for} \mathrm{traceability} \mathrm{at} \mathrm{EOR} \mathrm{field} \mathrm{eo} \left[\mathrm{USD}\right]$$

$$\mathrm{SMnX}=\mathrm{subsidy} \mathrm{per} \mathrm{t} \mathrm{of} {\mathrm{CO}}_2 \mathrm{mineralized} \mathrm{at} X \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$\mathrm{S}{\mathrm{M}}_{\mathrm{x}}=\mathrm{subsidy} \mathrm{per} \mathrm{t} \mathrm{of} {\mathrm{CO}}_2 \mathrm{mineralized} \mathrm{at} x \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$${\mathrm{S}}_{\mathrm{q},\mathrm{M},\mathrm{t}}=\mathrm{availability} \mathrm{of} \mathrm{solid} M \mathrm{at} q \mathrm{in} t \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$\mathrm{SM}{\mathrm{x}}_{\mathrm{q}}=\mathrm{maximum} \mathrm{substitution} \mathrm{fraction} \mathrm{with} {\mathrm{SiO}}_2 \mathrm{at} q \left[\%\right]$$

$$sb{H}_{\mathrm{h}}=\mathrm{additional} \mathrm{incentive} \mathrm{at} \mathrm{hub} \mathrm{h} \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$sb{O}_{\mathrm{o}}=\mathrm{credit} \mathrm{for} \mathrm{geological} \mathrm{storage} \mathrm{at} \mathrm{o} \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$sb{U}_{\mathrm{u}}=\mathrm{incentive} \mathrm{for} \mathrm{industrial} \mathrm{substitution} \mathrm{at} \mathrm{u} \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$sbE{O}_{\mathrm{eo}}=\mathrm{subsidy} \mathrm{for} \mathrm{EOR} \mathrm{use} \mathrm{at} \mathrm{eo} \left[\mathrm{USD}/\mathrm{tC}{\mathrm{O}}_2\right]$$

$$TNE=\mathrm{number} \mathrm{of} \mathrm{relevant} \mathrm{stages}/\mathrm{elements}$$

$$VDC{a}_{\mathrm{ca}}=\mathrm{available} \mathrm{trips} \mathrm{per} \mathrm{quarter} (\mathrm{type} \mathrm{ca}) \left[\mathrm{trips}/\mathrm{quarter}\right]$$

$$VlC{a}_{\mathrm{ca}}=\mathrm{average} \mathrm{speed} \mathrm{Q}\to \mathrm{C} (\mathrm{truck} \mathrm{ca}) \left[\mathrm{km}/\mathrm{h}\right]$$

$$VDB{r}_{\mathrm{bar}}=\mathrm{available} \mathrm{ship} \mathrm{trips} \mathrm{per} \mathrm{quarter} \left[\mathrm{trips}/\mathrm{quarter}\right]$$

$$VlB{r}_{\mathrm{bar}}=\mathrm{average} \mathrm{speed} \mathrm{L}\to \mathrm{H} (\mathrm{ship} \mathrm{bar}) \left[\mathrm{km}/\mathrm{h}\right]$$

$$VDCa{m}_{\mathrm{cam}}=\mathrm{available} \mathrm{trips} \mathrm{per} \mathrm{quarter} (\mathrm{type} \mathrm{cam}) \left[\mathrm{trips}/\mathrm{quarter}\right]$$

$$VlCa{m}_{\mathrm{cam}}=\mathrm{average} \mathrm{truck} \mathrm{speed} \mathrm{cam} \left[\mathrm{km}/\mathrm{h}\right]$$

$$VDKa{m}_{\mathrm{kam}}=\mathrm{available} \mathrm{trips} \mathrm{per} \mathrm{quarter} (\mathrm{type} \mathrm{kam}) \left[\mathrm{trips}/\mathrm{quarter}\right]$$

$$VlKa{m}_{\mathrm{kam}}=\mathrm{average} \mathrm{speed} \mathrm{L}\to \mathrm{U} (\mathrm{truck} \mathrm{kam}) \left[\mathrm{km}/\mathrm{h}\right]$$

$$VDK{a}_{\mathrm{ka}}=\mathrm{available} \mathrm{trips} \mathrm{per} \mathrm{quarter} (\mathrm{type} \mathrm{ka}) \left[\mathrm{trips}/\mathrm{quarter}\right]$$

$$VlK{a}_{\mathrm{ka}}=\mathrm{average} \mathrm{speed} \mathrm{L}\to \mathrm{U} (\mathrm{truck} \mathrm{ka}) \left[\mathrm{km}/\mathrm{h}\right]$$

$$VDT{a}_{\mathrm{ta}}=\mathrm{available} \mathrm{trips}/\mathrm{segments} \mathrm{per} \mathrm{quarter} (\mathrm{class} \mathrm{ta})$$

$$VDT{e}_{\mathrm{te}}=\mathrm{available} \mathrm{trips}/\mathrm{segments} \mathrm{per} \mathrm{quarter} (\mathrm{te})$$

$$VDT{o}_{\mathrm{to}}=\mathrm{available} \mathrm{trips}/\mathrm{segments} (\mathrm{to}) \left[-\right]$$

$$VDT{i}_{\mathrm{ti}}=\mathrm{available} \mathrm{trips}/\mathrm{segments} \mathrm{per} \mathrm{quarter} (\mathrm{ti})$$

$$VSiO{2}_{\mathrm{q}}={\mathrm{SiO}}_2 \mathrm{value} \mathrm{at} \mathrm{q} \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$ValueSiO{2}_{\mathrm{q}}={\mathrm{SiO}}_2 \mathrm{value} \mathrm{initializer} \mathrm{at} \mathrm{q} \left[\mathrm{USD}/\mathrm{t}\mathrm{n}\right]$$

$$\mathrm{yMCO}{3}_{\mathrm{M}}=\mathrm{t} \mathrm{of} {\mathrm{MCO}}_3 \mathrm{produced} \mathrm{per} \mathrm{t} \mathrm{of} \mathrm{solid} M \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$\mathrm{ySiO}{2}_{\mathrm{M}}=\mathrm{t} \mathrm{of} {\mathrm{SiO}}_2 \mathrm{produced} \mathrm{per} \mathrm{t} \mathrm{of} \mathrm{solid} M \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

Appendix B.3. Decision Variables—Types, Meaning, and Conventions (CCUS Model)

This section defines the endogenous (decision) variables of the MILP. They encode the design–operation choices of the CCUS network across quarters, facilities, and transport arcs. All variables are indexed by the sets introduced earlier (e.g., q ∈ Q, c ∈ C, l ∈ LPuerto, t ∈ T). Subscripts follow those indices to indicate origin–destination–class–time. Units are shown in square brackets alongside each definition; all flow/stock variables are non-negative.

Variable families (what they represent)

• Facility activation (binary): Open/close decisions for capture sources, compression/gathering stations, liquefaction plants (at ports, onshore hubs, EOR hubs, and industrial connections), storage hubs (offshore/onshore), EOR fields, industrial use nodes, and mixing centers. Period-specific activation/backup binaries enable adaptive operation by quarter.
• CO₂ flows (continuous): Tonnes of CO₂ moved along each arc class and transport mode:
• Q→C by truck type ca; C→L by pipeline class (Ta, Te, Ti, To); L→H by ship; L→O and L→U by truck (Cam/Ka); L→EO by truck (Kam).
• Additional flows to/from mixing centers and for in situ/ex situ mineralization, where applicable.
• Inventories and accumulations (continuous): Stocks at stations and plants (iC, iLH, iLO, iLU, iLEO), and stored CO₂ at sinks (alH, alO, alU, alEO). Backlogs at use nodes capture unmet demand when allowed.
• Mineralization and mixing (continuous): Ex situ variables for solid transfers to mixing centers, total mixed solids, CO₂ used in mixing centers, and resulting products (SiO₂ to cement plants; carbonates MCO₃ returned to origin). In situ variables at sources include solid used, CO₂ consumed, and produced MCO₃/SiO₂.
• Vehicle/segment operations (integer): Trip counts by truck/ship class and “virtual” counts for pipeline segments or dispatch windows, constrained by availability and payload.
• Economic accounting (continuous): Total cost, revenues, credits and incentives, as well as intermediate aggregates (e.g., system income, carbon credits, oil revenue, fiscal savings), subsidies/penalties and total emissions; also, throughput measures (e.g., THRUC).
• Goal-programming deviations (continuous): Positive/negative deviations from targets on cost, revenue, and carbon neutrality (d1p/d1n, d2p/d2n, d3p/d3n), plus optional deviations for emissions, utilization, capture, and backlog when the GP variant is used. The scalar ZObj holds the final weighted objective value.
• Traceability/reliability auxiliaries (continuous/binary, where used): Quantities used to bookkeep flows “without blockchain,” leakage totals, or reliability-weighted penalties/bonuses.

Domains and bounds

• Binary variables take values {0,1} and indicate activation/backup status.
• Integer variables count trips/segments and are constrained to ℤ₊.
• Continuous variables represent flows/stocks and are constrained to ℝ₊ (non-negative). Where minimum-run or minimum-service applies, lower bounds are added explicitly.

Naming convention

Upper-case names typically denote CO₂ or solid flows and accounting aggregates (e.g., QC, CLH, SOLQX, CostoTotal), while lower-case names often denote auxiliary or product-specific flows. Composite subscripts (origin, destination, mode/class, time) disambiguate where and when each decision applies.

The full list that follows specifies each variable’s indices, economic/physical meaning, and units, enabling direct implementation in a solver and transparent replication.

Minerals and CO₂ between q–x and at x

$$CO2UseMIN{X}_{\mathrm{x},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{consumed} \mathrm{in} \mathrm{mineralization} \mathrm{at} x \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$cumqodMCO3X_{\mathrm{x},\mathrm{t}}=\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{s} {(\mathrm{MCO}}_{3) \mathrm{en} }x \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$cumqodSiO2X_{\mathrm{x},\mathrm{t}}=\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{o}\mathrm{f} {\mathrm{SiO}}_2 \mathrm{en} x \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$fsx{m}_{\mathrm{x},\mathrm{q},\mathrm{t}}={\mathrm{SiO}}_2 \mathrm{shipped} \mathrm{from} \mathrm{x} \mathrm{to} \mathrm{cement} \mathrm{plant} \mathrm{q} \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$fmx{t}_{\mathrm{x},\mathrm{q},\mathrm{t}}=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{s} {(\mathrm{MCO}}_{3) }from x returned to q \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$LXCO{2}_{\mathrm{lnd},\mathrm{x},\mathrm{ka},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{transported} \mathrm{from} lnd \mathrm{to} x \mathrm{by} \mathrm{truck} ka \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$SOLQ{X}_{\mathrm{q},\mathrm{M},\mathrm{x},\mathrm{t}}=\mathrm{solid} M \mathrm{transported} \mathrm{from} q \mathrm{to} x \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

in situ mineralization

$$cumqodMCO3Q_{\mathrm{q},\mathrm{t}}={\mathrm{MCO}}_3\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{e}\mathrm{d} \mathrm{i}\mathrm{n} \mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u} \mathrm{a}\mathrm{t} q \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$cumqodSiO2Q_{\mathrm{q},\mathrm{t}}={\mathrm{SiO}}_2 \mathrm{produced} \mathrm{i}\mathrm{n} \mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u} \mathrm{at} q \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$cum{q}_{\mathrm{q},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{consumed} \mathrm{by} \mathrm{i}\mathrm{n} \mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u} \mathrm{mineralization} \mathrm{at} q \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$fso{q}_{\mathrm{x},\mathrm{M},\mathrm{t}}=\mathrm{solid} M \mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{i}\mathrm{n} \mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u} \mathrm{m}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} \mathrm{a}\mathrm{t} q \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$FlowMCO3QM{Q}_{\mathrm{q},\mathrm{M},\mathrm{t}}={\mathrm{MCO}}_3 \mathrm{returned} \mathrm{to} \mathrm{the} \mathrm{origin} \mathrm{of} \mathrm{the} \mathrm{solid} \left(q,M\right) \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$$fsq{q}_{\mathrm{q},\mathrm{qq},\mathrm{t}}={\mathrm{SiO}}_2 \mathrm{shipped} \mathrm{from} \mathrm{q} \mathrm{to} \mathrm{cement} \mathrm{plant} qq \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

$\mathit{O}\mathit{p}\mathit{C}\mathit{o}\mathit{s}\mathit{t}$

• mixing at x

$$FlowSOLQ{X}_{\mathrm{q},\mathrm{x},\mathrm{M},\mathrm{t}}=\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d} \mathrm{M} \mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m} \mathrm{q} \mathrm{t}\mathrm{o} \mathrm{b}\mathrm{e} \mathrm{m}\mathrm{i}\mathrm{x}\mathrm{e}\mathrm{d} \mathrm{a}\mathrm{t} x \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]\backslash$$

$$MixInx{M}_{\mathrm{x},\mathrm{M},\mathrm{t}}=\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d} \mathrm{M} \mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}\mathrm{s} \mathrm{t}\mathrm{o} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{m}\mathrm{i}\mathrm{x}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{a}\mathrm{t}x \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]\backslash$$

$$MixTot{x}_{\mathrm{x},\mathrm{t}}=\mathrm{total} \mathrm{solid} \mathrm{mixed} \mathrm{at} x \left[\mathrm{t}\mathrm{n}/\mathrm{quarter}\right]$$

Main CO₂ flows

$$Taxsavings=\mathrm{Tax} \mathrm{savings} \mathrm{from} {\mathrm{CO}}_2 \mathrm{capture}/\mathrm{use}/\mathrm{storage} \left[\mathrm{USD}\right]$$

$$al{H}_{\mathrm{h},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{stored} \mathrm{at} \mathrm{hub} h \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$al{O}_{\mathrm{o},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{stored} \mathrm{at} \mathrm{hub} o \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$al{U}_{\mathrm{u},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{stored} \mathrm{at} \mathrm{use} u \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$alE{O}_{\mathrm{eo},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{stored}/\mathrm{assigned} \mathrm{at} \mathrm{EOR} \mathrm{field} eo \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$BacklogUs{o}_{\mathrm{u},\mathrm{t}}=\mathrm{unmet} \mathrm{demand} \mathrm{at} u \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$CL{H}_{\mathrm{c},\mathrm{LPuerto},\mathrm{ta},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{by} \mathrm{pipeline} (\mathrm{C}\to \mathrm{L}, \mathrm{tipo} ta) \left[\mathrm{tC}{\mathrm{O}}_2\right]/\mathrm{quarter}$$

$$CL{O}_{\mathrm{c},\mathrm{Lgeo},\mathrm{te},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{by} \mathrm{pipeline} (\mathrm{C}\to \mathrm{L}, \mathrm{tipo} te) \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$CLE{O}_{\mathrm{c},\mathrm{Leor},\mathrm{ti},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{by} \mathrm{pipeline} (\mathrm{C}\to \mathrm{L}, \mathrm{tipo} ti) \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$CL{U}_{\mathrm{c},\mathrm{lnd},\mathrm{to},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{by} \mathrm{pipeline} (\mathrm{C}\to \mathrm{L}, \mathrm{tipo} to) \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$Capt{d}_{q,t}={\mathrm{CO}}_2 \mathrm{captured} \mathrm{at} q \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$CO2U{s}_t=\mathrm{total} {\mathrm{CO}}_2 \mathrm{used} \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$CarbonCredit=\mathrm{revenue} \mathrm{from} \mathrm{carbon} \mathrm{credits} \mathrm{sales} \left[\mathrm{USD}\right]$$

$$Totalcost=\mathrm{total} \cos \mathrm{t} \mathrm{of} \mathrm{logistic} \mathrm{system} \left[\mathrm{USD}\right]$$

$$Totalemissions=\mathrm{total} \mathrm{system} \mathrm{emissions} \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$iC={\mathrm{CO}}_2 \mathrm{inventory} \mathrm{at} \mathrm{node} C \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$iLH=\mathrm{inventory} \mathrm{associated} \mathrm{with} \mathrm{leg} L\to H \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$iLO=\mathrm{inventory} \mathrm{associated} \mathrm{with} \mathrm{leg} L\to O \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$iLU=\mathrm{inventory} \mathrm{associated} \mathrm{with} \mathrm{leg} L\to U \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$iLEO=\mathrm{inventory} \mathrm{associated} \mathrm{with} \mathrm{leg} L\to EO \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$Systemrevenues=\mathrm{gross} \mathrm{system} \mathrm{revenues} \left[\mathrm{USD}\right]$$

$$TotalIncome=\mathrm{net} \mathrm{total} \mathrm{income} \left[\mathrm{USD}\right]$$

$$OilrevenuesEOR=\mathrm{revenue} \mathrm{from} \mathrm{oil} \mathrm{sales} \mathrm{v}í\mathrm{a} \mathrm{EOR} \left[\mathrm{USD}\right]$$

$$L{H}_{\mathrm{LPuerto},\mathrm{h},\mathrm{bar},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{transported} \mathrm{de} L \mathrm{a} H \mathrm{por} \mathrm{barco} bar \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$L{O}_{\mathrm{Lgeo},\mathrm{o},\mathrm{Cam},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{from} L \mathrm{to} O \mathrm{by} \mathrm{truck} Cam \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$L{U}_{\mathrm{lnd},\mathrm{u},\mathrm{ka},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{de} L \mathrm{to} U \mathrm{by} \mathrm{truck} ka \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$LE{O}_{\mathrm{Leor},\mathrm{eo},\mathrm{kam},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{from} L \mathrm{to} EOR \mathrm{by} \mathrm{truck} kam \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$LossGoa{l}_{\mathrm{t}}=\mathrm{deviations} \mathrm{from} \mathrm{key} \mathrm{performance} \mathrm{metrics} \mathrm{vs}. \mathrm{baseline}$$

$$Q{C}_{\mathrm{q},\mathrm{c},\mathrm{ca},\mathrm{t}}={\mathrm{CO}}_2 \mathrm{transported} \mathrm{by} \mathrm{truck} ca \mathrm{de} Q \mathrm{a} C \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$QXCO2={\mathrm{CO}}_2 \mathrm{from} Q \mathrm{to} X \mathrm{by} \mathrm{truck} \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$sbTotal=\mathrm{total} \mathrm{subsidies} \left[\mathrm{USD}\right]\backslash$$

$$Usad{o}_{\mathrm{u},\mathrm{t}}={\mathrm{CO}}_2\mathrm{used} \mathrm{at} u \left[\mathrm{tC}{\mathrm{O}}_2/\mathrm{quarter}\right]$$

$$Zbn=total bpnuses for useful inventories \left[\mathrm{USD}\right]$$

$$Zpe=\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{p}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{e}\mathrm{s} \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{u}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{a}\mathrm{r}\mathrm{y}/\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{i}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{s} \left[\mathrm{USD}\right]$$

Integer Variables

• trips q–x y lnd–x

$$vaQ{X}_{\mathrm{q},\mathrm{x},\mathrm{ka},\mathrm{t}}=\mathrm{trips} \left(q \to \right) \mathrm{by} \mathrm{truck} ka \left[\mathrm{trips}\right]$$

$$vaL{X}_{\mathrm{lnd},\mathrm{x},\mathrm{ka},\mathrm{t}}=\mathrm{trips} \left(lnd \to \right) \mathrm{by} \mathrm{truck} ka \left[\mathrm{trips}\right]$$

• trips for the main network

$$vaQ{C}_{\mathrm{q},\mathrm{c},\mathrm{ca},\mathrm{t}}=\mathrm{trips} \left(Q \to \right) \mathrm{by} \mathrm{truck} ca \mathrm{at} t \left[\mathrm{trips}\right]$$

$$vaL{U}_{\mathrm{lnd},\mathrm{u},\mathrm{Ka},\mathrm{t}}=\mathrm{trips} \left(L \to \right) \mathrm{by} \mathrm{truck} ka \mathrm{at} t \left[\mathrm{trips}\right]$$

$$vaL{H}_{\mathrm{LPuerto},\mathrm{h},\mathrm{bar},\mathrm{t}}=\mathrm{trips} \left(L \to \right) \mathrm{by} \mathrm{ship} bar \mathrm{at} t \left[\mathrm{trips}\right]$$

$$vaL{O}_{\mathrm{Lgeo},\mathrm{o},\mathrm{Cam},\mathrm{t}}=\mathrm{trips} \left(L \to \right) \mathrm{by} \mathrm{truck} Cam \mathrm{at} t \left[\mathrm{trips}\right]$$

$$vaLE{O}_{\mathrm{Leor},\mathrm{eo},\mathrm{Kam},\mathrm{t}}=\mathrm{trips} \left(L \to O\right) \mathrm{by} \mathrm{truck} kam \mathrm{a}\mathrm{t} t \left[\mathrm{trips}\right]$$

$$valh=segregated \mathrm{trips} \mathrm{L}\to \mathrm{H} \left[\mathrm{trips}\right]$$

$$valo=segregated \mathrm{trips} \mathrm{L}\to \mathrm{O} \left[\mathrm{trips}\right]$$

$$vaCLEO=segregated \mathrm{trips} \mathrm{C}\to \mathrm{LEO} \left[\mathrm{trips}\right]$$

$$vaCLU=\mathrm{trips} \mathrm{agregados} \mathrm{C}\to \mathrm{LU} \left[\mathrm{trips}\right]$$

Binary Variables

$$Y{q}_{\mathrm{q}}=1 \mathrm{i}\mathrm{f} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e} q \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Y{c}_{\mathrm{c}}=1 \mathrm{si} \mathrm{se} \mathrm{activa} \mathrm{la} \mathrm{estación} \mathrm{de} \mathrm{compresión} c; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Yl{p}_{\mathrm{LPuerto}}=1 \mathrm{if} \mathrm{liquefaction} \mathrm{plant} l (\mathrm{puerto}) \mathrm{is} \mathrm{activated}; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Yl{o}_{\mathrm{Lgeo}}=1 \mathrm{if} \mathrm{liquefaction} \mathrm{plant} l (\mathrm{onshore}) \mathrm{is} \mathrm{activated}; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Yle{o}_{\mathrm{Leor}}=1 \mathrm{if} \mathrm{liquefaction} \mathrm{plant} l (\mathrm{EOR}) \mathrm{is} \mathrm{activated}; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Yl{u}_{\mathrm{lnd}}=1 \mathrm{if} \mathrm{liquefaction} \mathrm{plant} l (\mathrm{industrial}) \mathrm{is} \mathrm{activated}; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Y{h}_{\mathrm{h}}=1 \mathrm{if} \mathrm{the} \mathrm{hub} \mathrm{is} \mathrm{activated} \mathrm{offshore} h; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Y{o}_{\mathrm{o}}=1 \mathrm{if} \mathrm{the} \mathrm{hub} \mathrm{is} \mathrm{activated} \mathrm{onshore} o; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Ye{o}_{\mathrm{eo}}=1 \mathrm{EOR} \mathrm{field} eo is activated; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Y{u}_{\mathrm{u}}=1 \mathrm{if} \mathrm{industrial} \mathrm{use} \mathrm{node} u is activated; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$$

$$Y{x}_{\mathrm{x}}=1 \mathrm{if} \mathrm{mixing} \mathrm{center} x \mathrm{is} \mathrm{activated}; 0 \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.$$

Deviations/RAIE

$$CO2UseX=\mathrm{C}{\mathrm{O}}_2\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{d} \mathrm{a}\mathrm{t} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e} X \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$DevCostoPos=\mathrm{positive} \mathrm{deviation} \mathrm{of} \mathrm{total} \cos \mathrm{t} (\mathrm{goal}) \left[\mathrm{USD}\right]$$

$$DevEmisionPos=\mathrm{positive} \mathrm{deviation} \mathrm{of} \mathrm{emissions} \left[\mathrm{tC}{\mathrm{O}}_2\mathrm{e}\right]$$

$$DevUtilizacionPos=\mathrm{positive} \mathrm{deviation} \mathrm{of} \mathrm{asset} \mathrm{utilization} \left[\%\right]$$

$$DevCapturaPos=\mathrm{positive} \mathrm{deviation} \mathrm{of} {\mathrm{CO}}_2 \mathrm{n}\mathrm{ot} \mathrm{captured} \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$DevBacklogUsoPos=\mathrm{positive} \mathrm{deviation} \mathrm{of} {\mathrm{CO}}_2 \mathrm{n}\mathrm{ot} \mathrm{captured} \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

$$FugasTotales=\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{g}\mathrm{a}\mathrm{s} \mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{a}\mathrm{g}\mathrm{e} \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m} \left[\mathrm{tC}{\mathrm{O}}_2\right]$$

Goal programming

$$d1p,\hspace{0.17em}d1n=\mathrm{deviations} (+/-) \mathrm{from} \mathrm{cost} \mathrm{target} \left[\mathrm{USD}\right]$$

$$d2p,\hspace{0.17em}d2n=\mathrm{deviations} (+/-) \mathrm{from} \mathrm{income} \mathrm{target} \left[\mathrm{USD}\right]$$

$$d3p,\hspace{0.17em}d3n=\mathrm{deviations} (+/-) \mathrm{from} \mathrm{carbon} \mathrm{neutrality} \mathrm{target} \left[\mathrm{tC}{\mathrm{O}}_2\mathrm{e}\right]$$

$$ZObj=\mathrm{objective} \mathrm{function} (\mathrm{goal} \mathrm{programming})$$

Appendix B.4. Mathematical Model for CCUS Supply Chain Design—Overview

This section presents a mixed-integer linear programming (MILP) model for the strategic–tactical design of a carbon capture, utilization, and storage (CCUS) supply chain with mineralization. The network spans multiple echelons—capture sources, compression and intermediate storage, liquefaction plants (at ports and connected to onshore/EOR/industrial nodes), multi-modal transport (pipelines, trucks, ships), and sinks comprising geological storage hubs (offshore/onshore), EOR fields, and industrial uses. Time is represented in discrete quarters to capture seasonality, lead-time couplings, inventory carry-over, and policy accounting periods.

The model jointly decides (i) which facilities to activate each period (sources, stations, liquefaction plants, hubs, use nodes, and mixing centers), (ii) CO₂ routing by arc, mode, and class (Q→C, C→L, L→H/O/U/EO), (iii) inventory levels at intermediate nodes and accumulated storage/use at sinks, (iv) ex situ and in situ mineralization flows—solid supply, mixing, CO₂ consumption, and production of silica (SiO₂) to cement plants and carbonates (MCO₃) returned to origin—and (v) the number of trips or pipeline segments operated by class, subject to availability and payload limits. Quality and feasibility of mineralization blends are enforced via reactivity bounds and substitution limits at cement plantsEquations (B.1)–(B.13) represent the set of preliminary economic calculations that provide the foundation for the formulation of the objective function, while Equation (B.14) explicitly establishes this function within a goal programming framework. Equation (1) determines the total system cost, incorporating fixed installation costs, variable costs related to transportation, operation, and inventory, environmental terms associated with emissions and leakages, as well as the benefits derived from storage and bonus schemes. Constraint (B.2) introduces the environmental commitment to carbon neutrality by requiring that the total amount of CO₂ utilized be greater than or equal to the overall emissions, thereby aligning the model with sustainability targets. Constraint (B.3) constrains the total cost with respect to a predefined goal, explicitly accounting for possible deviations. Subsequently, Equation (B.4) defines the total income generated by the system, which includes revenues from storage at hubs, mineralization of products, and valorization of mineral by-products. Equation (B.5) computes subsidies originating from economic or fiscal incentives linked to CO₂ capture and utilization, whereas Equation (B.6) quantifies the carbon credits obtained through storage and substitution of mineral coproducts. Equation (B.7) formulates oil revenues obtained from enhanced oil recovery (EOR) processes using injected CO₂, while Equation (B.8) incorporates the tax savings resulting from investment in low-carbon technologies.

Equation (B.9) establishes the overall revenue balance of the system as the sum of total income, subsidies, carbon credits, oil revenues, and tax savings, thus consolidating all economic inflows into a single indicator. Equation (B.10) presents the system-wide emissions balance, accounting for emissions generated across transportation, processing, and storage operations. Equations (B.11), (B.12), and (B.13) correspond to the goal programming stage: Equation (B.11) relates total cost to its predefined target, Equation (B.12) links system revenues to their respective goal, and Equation (B.13) connects the carbon neutrality target to the total level of emissions. Finally, Equation (B.14) integrates all these elements into the model’s objective function, which seeks to minimize the weighted deviations associated with the three strategic goals: cost, revenue, and carbon neutrality. In this sense, the approach does not aim to directly minimize costs or maximize revenues, but rather to reduce deviations from target values to the greatest extent possible, thereby ensuring a balanced global economic performance under the goal programming framework.

Constraints (B.15) to (B.20) define the processing capacity limits across the different nodes of the supply chain. Constraint (B.15) sets the upper bound for the amount of CO₂ that can be captured at each source, ensuring it does not exceed the designed processing capacity of the capture units. Constraint (B.16) extends this logic to the compression facilities, where the volume transported and compressed, adjusted for potential leakage rates, must remain within the installed capacity of each compression plant. Constraint (B.17) regulates the throughput of liquefaction plants connected to port facilities, again accounting for technical losses and restricting the effective flow to the maximum processing capacity. Similarly, constraint (B.18) establishes the limit for liquefaction plants associated with geological hubs, while constraint (B.19) applies the same principle to EOR injection plants, ensuring that the injection of CO₂ does not surpass the admissible operational level. Finally, constraint (B.20) applies to inland liquefaction facilities, restricting the effective throughput to the available processing capacity once leakages are considered. Constraints (B.21) to (B.24) impose capacity limits on storage nodes. Constraint (B.21) restricts the volume that can be directed to offshore storage hubs, while constraint (B.22) does the same for onshore hubs. Constraint (B.23) sets the maximum admissible capacity for utilization facilities, and constraint (B.24) ensures that the amount of CO₂ allocated to EOR storage fields does not exceed their designed storage potential.

Equation (B.25) formulates the general CO₂ balance of the system. It establishes that the total amount of CO₂ allocated to onshore hubs, offshore hubs, utilization nodes, and EOR fields, together with the flows directed to mineralization processes, must be equal to the total amount of CO₂ captured in the system. This equality ensures the internal consistency of the mass balance throughout the network.

$$\begin{array}{ll}{\displaystyle \sum _{q\in Q}}FixCos{t}_q\hspace{0.17em}{Y}_q& +{\displaystyle \sum _{c\in C}}OpCos{t}_c\hspace{0.17em}{Y}_c+{\displaystyle \sum _{l\in LP}}OpCos{t}_{lp}\hspace{0.17em}{Y}_{lp}+{\displaystyle \sum _{l\in Lgeo}}OpCos{t}_{lgeo}\hspace{0.17em}{Y}_{lgeo}+{\displaystyle \sum _{i\in Lind}}OpCos{t}_{lind}\hspace{0.17em}{Y}_{lind}+{\displaystyle \sum _{i\in Lind}}OpCos{t}_{lind}\hspace{0.17em}{Y}_{lind}\\ & +{\displaystyle \sum _{i\in Lind}}OpCos{t}_{lind}\hspace{0.17em}{Y}_{lind}+{\displaystyle \sum _{x\in X}}FixCos{t}_x\hspace{0.17em}{Y}_x+{\displaystyle \sum _{h\in H}}OpCos{t}_h+{\displaystyle \sum _{o\in O}}OpCos{t}_o+{\displaystyle \sum _{u\in U}}OpCos{t}_u+{\displaystyle \sum _{eo\in EO}}OpCos{t}_{eo}\\ & +{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{ca\in Ca}}{\displaystyle \sum _{t\in T}}Dis{t}_{q,c}\hspace{0.17em}Q{C}_{q,c,ca,t}Cost{C}_{ca}+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{ca\in Ca}}{\displaystyle \sum _{t\in T}}VQ{C}_{q,c,ca,t}CosPre{p}_{ca}\hspace{0.17em}+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{ca\in Ca}}{\displaystyle \sum _{t\in T}}VQ{C}_{q,c,ca,t}CosPre{p}_{ca}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{l\in LP}}{\displaystyle \sum _{ta\in Ta}}{\displaystyle \sum _{t\in T}}\hspace{0.17em}DistCL{P}_{c,l}\hspace{0.17em}CL{H}_{c,l,ta,t}CostT{a}_{ta} +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{l\in LP}}{\displaystyle \sum _{ta\in Ta}}{\displaystyle \sum _{t\in T}}VICL{H}_{c,l,ta,t}CosPrepT{a}_{ta}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{te\in Te}}{\displaystyle \sum _{t\in T}}CostT{e}_{te}\hspace{0.17em}DistCL{G}_{c,g}\hspace{0.17em}CL{O}_{c,g,te,t}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{te\in Te}}{\displaystyle \sum _{t\in T}}CosPrepT{e}_{te}\hspace{0.17em}VCL{O}_{c,g,te,t}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{r\in Leor}}{\displaystyle \sum _{ti\in Ti}}{\displaystyle \sum _{t\in T}}CostT{i}_{ti}\hspace{0.17em}DistCL{E}_{c,r}\hspace{0.17em}CLE{O}_{c,r,ti,t}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{r\in Leor}}{\displaystyle \sum _{ti\in Ti}}{\displaystyle \sum _{t\in T}}CosPrepT{i}_{ti}\hspace{0.17em}VCLE{O}_{c,r,ti,t}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{to\in To}}{\displaystyle \sum _{t\in T}}CostT{o}_{to}\hspace{0.17em}DistCL{L}_{c,i}\hspace{0.17em}CL{U}_{c,i,to,t}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{to\in To}}{\displaystyle \sum _{t\in T}}CosPrepT{o}_{to}\hspace{0.17em}VCL{U}_{c,i,to,t}\\ & +{\displaystyle \sum _{l\in LP}}{\displaystyle \sum _{h\in H}}{\displaystyle \sum _{bar\in Bar}}{\displaystyle \sum _{t\in T}}L{H}_{l,h,bar,t}CBa{r}_{bar}\hspace{0.17em}DistL{H}_{l,h}\hspace{0.17em}L{H}_{l,h,bar,t}+{\displaystyle \sum _{l\in LP}}{\displaystyle \sum _{h\in H}}{\displaystyle \sum _{bar\in Bar}}{\displaystyle \sum _{t\in T}}VL{H}_{l,h,bar,t}CPrep{B}_{bar}\hspace{0.17em}\\ & +{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}CostK{a}_{ka}\hspace{0.17em}DistL{U}_{i,u}\hspace{0.17em}L{U}_{i,u,ka,t}+{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}CosPrepK{a}_{ka}\hspace{0.17em}VL{U}_{i,u,ka,t}\\ & +{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{cam\in Cam}}{\displaystyle \sum _{t\in T}}CostCa{m}_{cam}\hspace{0.17em}DistL{O}_{g,o}\hspace{0.17em}L{O}_{g,o,cam,t}+{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{cam\in Cam}}{\displaystyle \sum _{t\in T}}CosPrepCa{m}_{cam}\hspace{0.17em}VL{O}_{g,o,cam,t}\\ & +{\displaystyle \sum _{r\in Leor}}{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{kam\in Kam}}{\displaystyle \sum _{t\in T}}CostKa{m}_{kam}\hspace{0.17em}DistLE{O}_{r,eo}\hspace{0.17em}LE{O}_{r,eo,kam,t}+{\displaystyle \sum _{r\in Leor}}{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{kam\in Kam}}{\displaystyle \sum _{t\in T}}CosPrepKa{m}_{kam}\hspace{0.17em}VLE{O}_{r,eo,kam,t}\\ & +{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}QXCO{2}_{q,x,ka,t}CostKa{X}_{ka}\hspace{0.17em}DistQ{X}_{q,x}\hspace{0.17em}+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}VQ{X}_{q,x,ka,t}CosPrepKa{X}_{ka}\\ & +{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}VL{X}_{i,x,ka,t}CosPrepKa{X}_{ka}+{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}LXCO{2}_{i,x,ka,t}CostKa{X}_{ka}\hspace{0.17em}DistL{X}_{i,x}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{t\in T}}In{v}_{c,t}CostIn{v}_c\\ & +{\displaystyle \sum _{l\in LP}}{\displaystyle \sum _{t\in T}}CostIn{v}_{lp,l}\hspace{0.17em}InvL{H}_{l,t}\hspace{0.17em}+{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{t\in T}}CostIn{v}_{lg,g}\hspace{0.17em}InvL{O}_{g,t}+{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{t\in T}}CostIn{v}_{li,i}\hspace{0.17em}InvL{U}_{i,t}+{\displaystyle \sum _{c\in C}}CostIo{T}_c\hspace{0.17em}{Y}_c\\ & +{\displaystyle \sum _{l\in LP}}CostIo{T}_{lp,l}\hspace{0.17em}{Y}_{lp,l}+{\displaystyle \sum _{i\in Lind}}CostIo{T}_{lu,i}\hspace{0.17em}{Y}_{lu,i}+{\displaystyle \sum _{r\in Leor}}CostIo{T}_{leo,r}\hspace{0.17em}{Y}_{leo,r}\\ & +\hspace{0.17em}priceCO2({\displaystyle \sum _{x\in X}}{\displaystyle \sum _{M\in M}}{\displaystyle \sum _{t\in T}}EFMINpro{c}_M\hspace{0.17em}FlowQMI{N}_{x,M,t}+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{qq\in QCem}}{\displaystyle \sum _{t\in T}}EFiO2m\hspace{0.17em}Dis{t}_{q,qq}\hspace{0.17em}FlowSiO{2}_{q,qq,t}-{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{t\in T}}CO2MI{N}_{q,t})\\ & +PenalLeak\cdot TotalLeak-{\displaystyle \sum _{l\in LP}}{\displaystyle \sum _{h\in H}}{\displaystyle \sum _{bar\in Bar}}{\displaystyle \sum _{t\in T}}L{H}_{l,h,bar,t}\hspace{0.17em}BenLH\\ & -{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{cam\in Cam}}{\displaystyle \sum _{t\in T}}BenLOL{O}_{g,o,cam,t}\hspace{0.17em}-{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}L{U}_{i,u,ka,t}\hspace{0.17em}BenLU-{\displaystyle \sum _{r\in Leor}}{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{kam\in Kam}}{\displaystyle \sum _{t\in T}}BenLEOLE{O}_{r,eo,kam,t}\\ & -Z\_BInv+{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{t\in T}}MixFixCos{t}_x\hspace{0.17em}{Y}_x+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{M\in M}}{\displaystyle \sum _{t\in T}}MixCostVa{r}_x\hspace{0.17em}FlowS{O}_{q,x,M,t}\\ & +{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{M\in M}}{\displaystyle \sum _{t\in T}}CostSOL\hspace{0.17em}DistQ{X}_{q,x}\hspace{0.17em}FlowSO{L}_{q,x,M,t}+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{M\in M_{elig}}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{t\in T}}CM{K}_M\hspace{0.17em}DistQ{X}_{q,x}\hspace{0.17em}SO{L}_{q,M,x,t}\\ & +{\displaystyle \sum _{i\in Lind}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}CostK{a}_{ka}\hspace{0.17em}DistL{X}_{i,x}\hspace{0.17em}LXCO{2}_{i,x,ka,t}+{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{t\in T}}OpCostCO{2}_x\hspace{0.17em}CO2MI{N}_{x,t}+{\displaystyle \sum _{x\in X}}FixCos{t}_x\hspace{0.17em}{Y}_x\\ & =TotalCost\end{array}$$

(B.1)

$$\sum _{t\in T}{CO2Us}_t\ge {\displaystyle \frac{Total Emissions}{1000}}$$

(B.2)

$$TotalCost\le GoalTotalCost+{Dev}^{+}$$

(B.3)

$$\begin{array}{ll}TotalIncome=& {\displaystyle \sum _{h\in H}}{\displaystyle \sum _{t\in T}}Pre\cdot Alm{H}_{h,t}+{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{t\in T}}Pre{o}_o\cdot Alm{O}_{o,t}+{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{t\in T}}Pre{o}_u\cdot Alm{U}_{u,t}+{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{t\in T}}Pre{o}_E{O}_{eo}\cdot AlmE{O}_{eo,t}\\ & +{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{q\in QCem}}{\displaystyle \sum _{t\in T}}Pre{o}_{S}iO{2}_q\cdot Flow\_SiO2M_{x,q,t}+{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{t\in T}}Precio\_MCO{3}_q\cdot Flow\_MCO3\_XRE{T}_{x,q,t}\end{array}$$

(B.4)

$$\begin{array}{ll}TotalSubsidy=& {\displaystyle \sum _{h\in H}}{\displaystyle \sum _{t\in T}}Sub{o}_{H_h}\hspace{0.17em}Alm{H}_{h,t}+{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{t\in T}}Sub{o}_{O_o}\hspace{0.17em}Alm{O}_{o,t}+{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{t\in T}}Sub{o}_{U_u}\hspace{0.17em}Alm{U}_{u,t}+{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{t\in T}}Subsidi{o}_E{O}_{eo}\hspace{0.17em}AlmE{O}_{eo,t}\\ & +{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{t\in T}}Sub{o}_{M}I{N}_X\hspace{0.17em}CO{2}_{U}s{e}_{M}I{N}_{X_{x,t}}+{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{t\in T}}Sub{o}_{M}i{x}_x\hspace{0.17em}CO{2}_{U}s{e}_{X_{x,t}}\end{array}$$

(B.5)

$$\begin{array}{ll}CarbonCredit& =CarbonCreditPrice·({\displaystyle \sum _{h\in H}}{\displaystyle \sum _{t\in T}}Alm{H}_{h,t}+{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{t\in T}}Alm{O}_{o,t}+{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{t\in T}}AlmE{O}_{eo,t}+{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{t\in T}}Alm{U}_{u,t})\\ & +{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{qq\in QCem}}{\displaystyle \sum _{t\in T}}Preci{o}_{S}iO{2}_{qq}\hspace{0.17em}Flo{w}_{S}iO{2}_{Q}CE{M}_{Q_{q,qq,t}}\end{array}$$

(B.6)

$$OilrevenuesEOR=\sum _{eo\in EO}\sum _{t\in T}AlmE{O}_{eo,t}\hspace{0.17em}.BarrelsTonCO2\hspace{0.17em}.BarrelPrice$$

(B.7)

$$Taxsavings=Nonemission rate·\sum _{q\in Q}\sum _{t\in T}Cap{o}_{q,t}$$

(B.8)

$$Systemrevenues=TotalIncome+TotalSubsidy+CarbonCredit+OilrevenuesEOR+Taxsavings$$

(B.9)

$$\begin{array}{ll}TotalEmissions=& {\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{ca\in Ca}}{\displaystyle \sum _{t\in T}}CO2C{a}_{ca}\cdot DistQ{C}_{q,c}\cdot Q{C}_{q,c,ca,t}+{\displaystyle \sum _{Leor\in Leor}}{\displaystyle \sum _{eo\in eo}}{\displaystyle \sum _{kam\in Kam}}{\displaystyle \sum _{t\in T}}CO2Ka{m}_{kam}\cdot DistLE{O}_{Leor,eo}\cdot LE{O}_{Leor,eo,kam,t}\\ & +{\displaystyle \sum _{LP\in LP}}{\displaystyle \sum _{h\in H}}{\displaystyle \sum _{bar\in Bar}}{\displaystyle \sum _{t\in T}}CO2ba{r}_{bar}\cdot DistL{H}_{LP,h}\cdot L{H}_{LP,h,bar,t}+{\displaystyle \sum _{Lind\in Lind}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}CO2K{a}_{ka}\cdot DistL{U}_{Lind,u}\cdot L{U}_{Lind,u,ka,t}\\ & +{\displaystyle \sum _{Lgeo\in Lgeo}}{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{cam\in Cam}}{\displaystyle \sum _{t\in T}}CO2Ca{m}_{cam}\cdot DistL{O}_{Lgeo,o}\cdot L{O}_{Lgeo,o,cam,t}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{g\in Lgeo}}{\displaystyle \sum _{te\in Te}}{\displaystyle \sum _{t\in T}}CO2T{e}_{te}\cdot CL{O}_{c,g,te,t}\cdot DistCL{G}_{c,g}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{\mathrm{l}\in Leor}}{\displaystyle \sum _{ti\in Ti}}{\displaystyle \sum _{t\in T}}CO2T{i}_{ti}\cdot CLE{O}_{c,\mathrm{l},ti,t}\cdot DistCL{E}_{c,\mathrm{l}}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{l\in Lind}}{\displaystyle \sum _{to\in To}}{\displaystyle \sum _{t\in T}}CO2T{o}_{to}\cdot CL{U}_{c,l,to,t}\cdot DistCL{L}_{c,l}\\ & +{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{M\in M}}{\displaystyle \sum _{t\in T}}EF\_MIN\_pro{c}_M\cdot Flow\_SOL\_QMIN\_Q_{x,M,t}+{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{M\in M}}{\displaystyle \sum _{t\in T}}\left({\displaystyle \frac{EF\_SOL\_tkm}{1000}}\right)\cdot DistQ{X}_{q,x}\cdot Flow\_SOL\_Q{X}_{q,x,M,t}\\ & +{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{M\in M_{\mathrm{ELIG}}}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{t\in T}}EM{T}_M\cdot DistQ{X}_{q,x}\cdot SOL\_Q{X}_{q,M,x,t}+{\displaystyle \sum _{l\in Lind}}{\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}CO2K{a}_{ka}\cdot DistL{X}_{l,x}\cdot LXCO{2}_{l,x,ka,t}\end{array}$$

(B.10)

$$TotalCost=CostGoal+d1p-d1n$$

(B.11)

$$Systemrevenues=RevenueGoal+d2p-d2n$$

(B.12)

$${\displaystyle \frac{TotalEmissions}{1000}}-\sum _{t\in T}CO2U{s}_t=CO2NeutralGoal+d3p-d3n$$

(B.13)

$$Z_{Obj}=W1\left(d1p+d1n\right)+W2\left(d2p+d2n\right)+W3\left(d3p+d3n\right)\left(FCCost\right)$$

(B.14)

Capacity constraints

$$Capt{d}_{q,t}\le CapProc{Q}_q \forall ,q\in Q, \forall ,t\in T$$

(B.15)

$$\sum _{q\in Q}\sum _{ca\in Ca}Q{C}_{q,c,ca,t},\left(1-LeakRateQ{C}_{ca}\right)\le CapProc{C}_c \forall ,c\in C, \forall ,t\in T$$

(B.16)

$$\sum _{c\in C}\sum _{ta\in Ta}CL{H}_{c,lp,ta,t},\left(1-LeakRateCL{H}_{ta}\right)\le CapProcL{P}_{lp} \forall ,l\in lp, \forall ,t\in T$$

(B.17)

$$\sum _{c\in C}\sum _{te\in Te}CL{O}_{c,lgeo,te,t},\left(1-LeakRateCL{O}_{te}\right)\le CapProcL{G}_{lgeo} \forall ,g\in Lgeo, \forall ,t\in T$$

(B.18)

$$\sum _{c\in C}\sum _{ti\in Ti}CLE{O}_{c,leor,ti,t},\left(1-LeakRateCLE{O}_{ti}\right)\le CapProcLE{O}_{leor} \forall ,leor\in Leor, \forall ,t\in T$$

(B.19)

$$\sum _{c\in C}\sum _{to\in To}CL{U}_{c,lind,to,t},\left(1-LeakRateCL{U}_{to}\right)\le CapProcL{I}_{lind} \forall ,lind\in Lind, \forall ,t\in T$$

(B.20)

$$Alm{O}_{o,t}\ge CapStore{O}_o \forall ,o\in O, \forall ,t\in T$$

(B.21)

$$Alm{H}_{h,t}\ge CapStore{H}_h \forall ,h\in H, \forall ,t\in T$$

(B.22)

$$Alm{U}_{u,t}\ge CapStore{U}_u \forall ,u\in U, \forall ,t\in T$$

(B.23)

$$AlmE{O}_{eo,t}\ge CapStoreE{O}_{eo} \forall ,eo\in eo, \forall ,t\in T$$

(B.24)

$$\sum _{o\in O}al{O}_{o,t}+\sum _{h\in H}al{H}_{h,t}+\sum _{u\in U}al{U}_{u,t}+\sum _{eo\in EO}alE{O}_{eo,t}+\sum _{q\in Q}\mathrm{cum}{\mathrm{q}}_{\mathrm{q},\mathrm{t}}=CO2U{s}_t \forall \hspace{0.17em} t\in T$$

(B.25)

Equations (B.26)–(B.29) define the balance of inventories in the different storage nodes. Equation (B.26) establishes that the inflows of CO₂ to each offshore hub, adjusted for potential leakages, must be equal to the inventory held in that hub at time t. Equation (B.27) applies the same principle to onshore hubs, ensuring that all incoming flows are reflected in the corresponding inventory level. Equation (B.28) formulates the balance for utilization nodes, where the incoming flows, corrected for leakage rates, determine the available inventory. Equation (B.29) sets the balance for EOR facilities, where the injected amounts are transferred into the accumulated inventories of CO₂ in the corresponding fields.

Equation (B.30) formulates the overall balance of CO₂ at the compression plants, where the total volume entering a compressor, after accounting for leakages and the previous inventory, must equal the sum of the flows directed toward all downstream facilities. Equations (B.31)–(B.34) replicate this logic across the other nodes of the system: Equation (B.31) for port liquefaction plants, Equation (B.32) for geological liquefaction plants, Equation (B.33) for inland liquefaction facilities, and Equation (B.34) for EOR injection plants, each one incorporating leakage factors, previous inventories, and the distribution of outgoing flows.

Equations (B.35) and (B.36) introduce auxiliary balances that link the amount of CO₂ used in utilization nodes and the volumes captured, respectively. These formulations ensure that all captured and processed amounts are coherently connected to the flows directed into the different segments of the network. Equation (B.37) defines the aggregate leakage balance for the entire system. It sums the losses across all nodes—including capture, compression, liquefaction, storage, and EOR injection—considering both process inefficiencies and emission factors. This equation ensures that the global leakage of CO₂ is consistently accounted for in the model, providing a comprehensive measure of system-level inefficiencies.

$$\sum _{lp \in LP}\sum _{bar \in Bar}L{H}_{lp,h,bar,t} \hspace{0.17em}\left(1-\mathrm{LRCLH}{1}_{\mathrm{bar}}\right)= al{H}_{h,t} \forall \hspace{0.17em}h\in H, \forall \hspace{0.17em}t\in T$$

(B.26)

$$\sum _{lgeo\in LGeo}\sum _{cam\in Cam}L{O}_{lgeo,o,cam,t}\hspace{0.17em}\left(1-\mathrm{LRL}{\mathrm{O}}_{\mathrm{cam}}\right)=al{O}_{o,t} \forall \hspace{0.17em}o\in O, \forall \hspace{0.17em}t\in T$$

(B.27)

$$\sum _{lind\in LInd}\sum _{ka\in Ka}L{U}_{lind,u,ka,t}\hspace{0.17em}\left(1-\mathrm{LRL}{\mathrm{U}}_{\mathrm{ka}}\right)=al{U}_{u,t}\forall \hspace{0.17em}u\in U, \forall \hspace{0.17em}t\in T$$

(B.28)

$$\sum _{leor\in LEor}\sum _{kam\in Kam}LE{O}_{leor,eo,kam,t}\hspace{0.17em}\left(1-\mathrm{LRL}{\mathrm{E}}_{\mathrm{kam}}\right)=alE{O}_{eo,t} \forall \hspace{0.17em}eo\in EO, \forall \hspace{0.17em}t\in T$$

(B.29)

$$\begin{array}{ll}{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{ca\in Ca}}Q{C}_{q,c,ca,t}\hspace{0.17em}& (1-\mathrm{LRQ}{\mathrm{C}}_{\mathrm{ca}})+ i{C}_{c,t-1}\hspace{0.17em}(1-\mathrm{LR}{\mathrm{C}}_{\mathrm{c}}) \\ & ={\displaystyle \sum _{lp\in LP}}{\displaystyle \sum _{ta\in Ta}}CL{H}_{c,lp,ta,t}+ {\displaystyle \sum _{lgeo\in Lgeo}}{\displaystyle \sum _{te\in Te}}CL{O}_{c,lgeo,te,t}+ {\displaystyle \sum _{lind\in Lind}}{\displaystyle \sum _{to\in To}}CL{U}_{c,lgeo,to,t} + {\displaystyle \sum _{leor\in Leor}}{\displaystyle \sum _{ti\in Ti}}CLE{O}_{c,leor,ti,t} \\ & + i{C}_{c,t} \forall \hspace{0.17em} c\in C, \forall \hspace{0.17em} t\in T \end{array}$$

(B.30)

$$\sum _{c\in C}\sum _{ta\in Ta}CL{H}_{c,lp,ta,t}\hspace{0.17em}\left(1-\mathrm{LRCL}{\mathrm{H}}_{\mathrm{ta}}\right)+ iL{H}_{lp,t-1}\hspace{0.17em}\left(1-\mathrm{LRl}{\mathrm{p}}_{\mathrm{lp}}\right)= \sum _{h\in H}\sum _{bar\in Bar}L{H}_{lp,h,bar,t}+ iL{H}_{lp,t} \forall \hspace{0.17em}l\in LP, \forall \hspace{0.17em}t\in T$$

(B.31)

$$\sum _{c\in C}\sum _{te\in Te}CL{O}_{c,lgeo,te,t}\hspace{0.17em}\left(1-\mathrm{LRCL}{\mathrm{O}}_{\mathrm{te}}\right)+ iL{O}_{lgeo,t-1}\hspace{0.17em}\left(1-\mathrm{LRl}{\mathrm{g}}_{\mathrm{lgeo}}\right)= \sum _{o\in O}\sum _{cam\in Cam}L{O}_{lgeo,o,cam,t}+ iL{O}_{lgeo,t} \forall \hspace{0.17em}g\in L_{\mathrm{geo}}, \forall \hspace{0.17em}t\in T$$

(B.32)

$$\begin{array}{ll}{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{to\in To}}CL{U}_{c,\mathrm{l}\mathrm{n}\mathrm{d},to,t}& \hspace{0.17em}(1-\mathrm{LRCL}{\mathrm{U}}_{\mathrm{to}})+ iL{U}_{\mathrm{l}\mathrm{n}\mathrm{d},t-1}\hspace{0.17em}(1-\mathrm{LRl}{\mathrm{i}}_{\mathrm{lnd}})\\ & ={\displaystyle \sum _{u\in U}}{\displaystyle \sum _{ka\in Ka}}L{U}_{\mathrm{l}\mathrm{n}\mathrm{d},u,ka,t}+ iL{U}_{\mathrm{l}\mathrm{n}\mathrm{d},t}+ {\displaystyle \sum _{x\in X}}{\displaystyle \sum _{ka\in Ka}}LXCO{2}_{\mathrm{l}\mathrm{n}\mathrm{d},x,ka,t} \forall \hspace{0.17em}\mathrm{l}\in L_{\mathrm{ind}}, \forall \hspace{0.17em}t\in T\end{array}$$

(B.33)

$$\sum _{c\in C}\sum _{ti\in Ti}CLE{O}_{c,leor,ti,t}\hspace{0.17em}\left(1-\mathrm{LRCLE}{\mathrm{O}}_{\mathrm{ti}}\right)+ iLE{O}_{leor,t-1}\hspace{0.17em}\left(1-\mathrm{LRLE}{\mathrm{o}}_{\mathrm{leor}}\right) = \sum _{eo\in EO}\sum _{kam\in Kam}LE{O}_{leor,eo,kam,t}+ iLE{O}_{leor,t} \forall \hspace{0.17em}r\in L_{\mathrm{eor}}, \forall \hspace{0.17em}t\in T$$

(B.34)

$$al{U}_{u,t} = Use{d}_{u,t} \forall \hspace{0.17em} u\in U, \forall \hspace{0.17em} t\in T$$

(B.35)

$$Captur{e}_{q,t} \le CO2Captur{e}_{q,t} \forall \hspace{0.17em} q\in Q, \forall \hspace{0.17em} t\in T$$

(B.36)

$$\begin{array}{ll}{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{ca\in Ca}}{\displaystyle \sum _{t\in T}}Q{C}_{q,c,ca,t}& \hspace{0.17em}\mathrm{LRQ}{\mathrm{C}}_{\mathrm{ca}}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{t\in T}}i{C}_{c,t}\hspace{0.17em}\mathrm{LR}{\mathrm{C}}_{\mathrm{c}}\hspace{0.17em}\mathrm{ERF}{\mathrm{C}}_{\mathrm{c}}+{\displaystyle \sum _{lp\in LP}}{\displaystyle \sum _{t\in T}}iL{H}_{lp,t}\hspace{0.17em}\mathrm{LRl}{\mathrm{p}}_{\mathrm{lp}}\hspace{0.17em}\mathrm{ERFL}{\mathrm{P}}_{\mathrm{lp}}+{\displaystyle \sum _{lgeo\in Lgeo}}{\displaystyle \sum _{t\in T}}iL{O}_{lgeo,t}\hspace{0.17em}\mathrm{LRl}{\mathrm{g}}_{\mathrm{lgeo}}\hspace{0.17em}\mathrm{ERFL}{\mathrm{G}}_{\mathrm{lgeo}}\\ & +{\displaystyle \sum _{lnd\in Lnd}}{\displaystyle \sum _{t\in T}}iL{U}_{lnd,t}\hspace{0.17em}\mathrm{LRl}{\mathrm{i}}_{\mathrm{lnd}}\hspace{0.17em}\mathrm{ERFL}{\mathrm{U}}_{\mathrm{lnd}}+{\displaystyle \sum _{leor\in Leor}}{\displaystyle \sum _{t\in T}}iLE{O}_{leor,t}\hspace{0.17em}\mathrm{LRLE}{\mathrm{o}}_{\mathrm{leor}}\hspace{0.17em}\mathrm{ERFLE}{\mathrm{O}}_{\mathrm{leor}}\\ & +{\displaystyle \sum _{lgeo\in Lgeo}}{\displaystyle \sum _{o\in O}}{\displaystyle \sum _{cam\in Cam}}{\displaystyle \sum _{t\in T}}L{O}_{lggeo,o,cam,t}\hspace{0.17em}\mathrm{LRL}{\mathrm{O}}_{\mathrm{cam}}+{\displaystyle \sum _{lp\in LP}}{\displaystyle \sum _{h\in H}}{\displaystyle \sum _{bar\in Bar}}{\displaystyle \sum _{t\in T}}L{H}_{lp,h,bar,t}\hspace{0.17em}\mathrm{LRCLH}{1}_{\mathrm{bar}}\\ & +{\displaystyle \sum _{lnd\in Lnd}}{\displaystyle \sum _{u\in U}}{\displaystyle \sum _{ka\in Ka}}{\displaystyle \sum _{t\in T}}L{U}_{lnd,u,ka,t}\hspace{0.17em}\mathrm{LRL}{\mathrm{U}}_{\mathrm{ka}}+{\displaystyle \sum _{leor\in Leor}}{\displaystyle \sum _{eo\in EO}}{\displaystyle \sum _{kam\in Kam}}{\displaystyle \sum _{t\in T}}LE{O}_{leor,eo,kam,t}\hspace{0.17em}\mathrm{LRL}{\mathrm{E}}_{\mathrm{kam}}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{lp\in LP}}{\displaystyle \sum _{ta\in Ta}}{\displaystyle \sum _{t\in T}}CL{H}_{c,lp,ta,t}\hspace{0.17em}\mathrm{LRCL}{\mathrm{H}}_{\mathrm{ta}}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{lgeo\in Lgeo}}{\displaystyle \sum _{te\in Te}}{\displaystyle \sum _{t\in T}}CL{O}_{c,lgeo,te,t}\hspace{0.17em}\mathrm{LRCL}{\mathrm{O}}_{\mathrm{te}}\\ & +{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{lnd\in Lnd}}{\displaystyle \sum _{to\in To}}{\displaystyle \sum _{t\in T}}CL{U}_{c,lnd,to,t}\hspace{0.17em}\mathrm{LRCL}{\mathrm{U}}_{\mathrm{to}}+{\displaystyle \sum _{c\in C}}{\displaystyle \sum _{leor\in Leor}}{\displaystyle \sum _{ti\in Ti}}{\displaystyle \sum _{t\in T}}CLE{O}_{c,leor,ti,t}\hspace{0.17em}\mathrm{LRCLE}{\mathrm{O}}_{\mathrm{ti}}\\ & =\mathit{Total} \mathit{Leaks} \end{array}$$

(B.37)

Constraints (B.38)–(B.47) establish the transportation capacity limits across the different modes and vehicle types involved in the CO₂ supply chain. Constraint (B.38) ensures that the amount of CO₂ transported from capture sources to compression facilities using trucks does not exceed the product of the number of trips, vehicle capacity, and availability, linking operational flows directly with fleet characteristics. Constraint (B.39) sets the maximum number of trips for each truck type, ensuring that the aggregated vehicle activity remains within the feasible operational bounds. Constraint (B.40) defines the upper limit for inland transportation, where the total flow delivered from liquefaction facilities to utilization nodes through trucks must respect the available vehicle fleet capacity. Complementarily, constraint (B.41) establishes a restriction on the maximum number of inland trips allowed per truck type, ensuring operational feasibility over the time horizon.

Constraint (B.42) regulates maritime transport by limiting the amount of CO₂ that can be shipped from port liquefaction plants to offshore hubs according to vessel capacity and the number of feasible voyages. Constraint (B.43) complements this by imposing an upper bound on the number of trips for each ship type, thus restricting fleet usage. Constraint (B.44) addresses geological transport, restricting the flows of CO₂ delivered from liquefaction plants to geological hubs via pipelines to the maximum pipeline capacity. In parallel, constraint (B.45) ensures that the number of pipeline routes activated remains within the installed infrastructure limit. Constraints (B.46) and (B.47) define the transport capacity for EOR injection facilities through dedicated pipelines, where the transported flows must not exceed the product of the available pipeline capacity and the number of active routes. Together, these restrictions guarantee that vehicle-based and pipeline-based transportation remain consistent with technical, logistical, and operational capacity throughout the CO₂ network.

$$Q{C}_{q,c,ca,t} \le DsC{a}_{ca}\hspace{0.17em}CapC{a}_{ca}\hspace{0.17em}vaQ{C}_{q,c,ca,t} \forall \hspace{0.17em}q\in Q, c\in C, ca\in Ca, t\in T$$

(B.38)

$$\sum _{q\in Q}\sum _{c\in C}vaQ{C}_{q,c,ca,t} \le VDC{a}_{ca} \forall \hspace{0.17em}ca\in Ca, t\in T$$

(B.39)

$$L{U}_{\mathrm{l}\mathrm{n}\mathrm{d},u,ka,t} \le DK{a}_{ka}\hspace{0.17em}CpK{a}_{ka}\hspace{0.17em}vaL{U}_{\mathrm{l}\mathrm{n}\mathrm{d},u,ka,t} \forall \hspace{0.17em}\mathrm{l}\in \mathrm{L}\mathrm{n}\mathrm{d}, u\in U, ka\in Ka, t\in T$$

(B.40)

$$\sum _{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{d}\in \mathrm{L}\mathrm{i}\mathrm{n}\mathrm{d}}\sum _{u\in U}vaL{U}_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{d},u,ka,t} \le VDK{a}_{ka} \forall \hspace{0.17em}ka\in Ka, t\in T$$

(B.41)

$$L{H}_{lp,h,bar,t} \le DB{r}_{bar}\hspace{0.17em}CpB{r}_{bar}\hspace{0.17em}vaL{H}_{lp,h,bar,t} \forall \hspace{0.17em}l\in LP, h\in H, bar\in Bar, t\in T$$

(B.42)

$$\sum _{lp\in \mathrm{L}\mathrm{P}}\sum _{h\in H}vaL{H}_{lp,h,bar,t} \le VDB{r}_{bar} \forall \hspace{0.17em} bar\in Bar, t\in T$$

(B.43)

$$\hspace{0.17em}L{O}_{lgeo,o,cam,t} \le DsCa{m}_{cam}\hspace{0.17em}CapCa{m}_{cam}\hspace{0.17em}vaL{O}_{lgeo,o,cam,t} \forall \hspace{0.17em}g\in Lgeo, o\in O, cam\in Cam, t\in T$$

(B.44)

$$\sum _{lgeo\in \mathrm{L}\mathrm{g}\mathrm{e}\mathrm{o}}\sum _{o\in O}vaL{O}_{g,o,cam,t} \le VDCa{m}_{cam } \forall \hspace{0.17em} cam\in Cam, t\in T$$

(B.45)

$$LE{O}_{leor,eo,kam,t} \le DKa{m}_{kam}\hspace{0.17em}CpKa{m}_{kam}\hspace{0.17em}vaLE{O}_{leor,eo,kam,t} \forall \hspace{0.17em}r\in Leor, eo\in EO, kam\in Kam, t\in T$$

(B.46)

$$\sum _{leor\in \mathrm{L}\mathrm{e}\mathrm{o}\mathrm{r}}\sum _{eo\in EO}vaLE{O}_{leor,eo,kam,t} \le VDKa{m}_{kam} \forall \hspace{0.17em} kam\in Kam, t\in T$$

(B.47)

Constraints (B.48)–(B.55) specify the transportation limits associated with CO₂ pipeline infrastructure. Constraint (B.48) establishes that the flows from compression plants to port liquefaction facilities through pipelines must not exceed the product of the pipeline capacity, distance factor, and the number of active routes. Constraint (B.49) complements this restriction by limiting the number of operational pipelines of this type, ensuring that the system remains within its infrastructure bounds. Constraint (B.50) applies the same logic to the connections between compression plants and geological liquefaction facilities, where the effective flow must respect pipeline capacity and operational routes. Constraint (B.51) then bounds the number of activated pipelines associated with these connections. Constraint (B.52) governs the flows directed from compression plants to EOR liquefaction facilities, ensuring that the transported CO₂ respects both pipeline capacity and the number of active pipeline segments. Constraint (B.53) further restricts the number of these pipelines that can be activated within the system. Constraints (B.54) and (B.55) regulate the inland pipeline network. Constraint (54) sets the capacity limit for flows from compression plants to inland liquefaction facilities, while constraint (B.55) caps the number of inland pipeline routes that can be activated. Together, these constraints guarantee that the flows allocated through the different pipeline connections are technically feasible and consistent with the existing infrastructure capacity.

$$CL{H}_{c,lp,ta,t} \le DT{a}_{ta}\hspace{0.17em}CpT{a}_{ta}\hspace{0.17em}\mathrm{val}{\mathrm{h}}_{\mathrm{c},\mathrm{lp},\mathrm{ta},\mathrm{t}} \forall \hspace{0.17em}c\in C, l\in L_{\mathrm{Puerto}}, ta\in Ta, t\in T$$

(B.48)

$$\sum _{c\in C}\sum _{lp\in LP}\mathrm{val}{\mathrm{h}}_{\mathrm{c},\mathrm{lp},\mathrm{ta},\mathrm{t}} \le VDT{a}_{ta} \forall \hspace{0.17em} ta\in Ta, t\in T$$

(B.49)

$$CL{O}_{c,lgeo,te,t} \le DT{e}_{te}\hspace{0.17em}CpT{e}_{te}\hspace{0.17em}\mathrm{val}{\mathrm{o}}_{\mathrm{c},\mathrm{lgeo},\mathrm{te},\mathrm{t}} \forall \hspace{0.17em}c\in C, g\in Lgeo, te\in Te, t\in T$$

(B.50)

$$\sum _{c\in C}\sum _{lgeo\in \mathrm{L}\mathrm{g}\mathrm{e}\mathrm{o}}\mathrm{val}{\mathrm{o}}_{\mathrm{c},\mathrm{lgeo},\mathrm{te},\mathrm{t}} \le VDT{e}_{te} \forall \hspace{0.17em} te\in Te, t\in T$$

(B.51)

$$CLE{O}_{c,leor,ti,t} \le DT{i}_{ti}\hspace{0.17em}CpT{i}_{ti}\hspace{0.17em}\mathrm{vaCLE}{\mathrm{O}}_{\mathrm{c},\mathrm{leor},\mathrm{ti},\mathrm{t}} \forall \hspace{0.17em}c\in C, r\in L_{\mathrm{eor}}, ti\in Ti, t\in T$$

(B.52)

$$\sum _{c\in C}\sum _{leor\in \mathrm{Leor}}\mathrm{vaCLE}{\mathrm{O}}_{\mathrm{c},\mathrm{leor},\mathrm{ti},\mathrm{t}} \le VDT{i}_{ti} \forall \hspace{0.17em} ti\in Ti, t\in T$$

(B.53)

$$CL{U}_{c,\mathrm{l}\mathrm{n}\mathrm{d},to,t} \le DT{o}_{to}\hspace{0.17em}CpT{o}_{to}\hspace{0.17em}\mathrm{vaCL}{\mathrm{U}}_{\mathrm{c},\mathrm{lnd},\mathrm{to},\mathrm{t}} \forall \hspace{0.17em}c\in C, \mathrm{l}\in Lnd, to\in To, t\in T$$

(B.54)

$$\sum _{c\in C}\sum _{\mathrm{l}\mathrm{n}\mathrm{d}\in \mathrm{L}\mathrm{n}\mathrm{d}}\mathrm{vaCL}{\mathrm{U}}_{\mathrm{c},\mathrm{lnd},\mathrm{to},\mathrm{t}} \le DT{o}_{to}\hspace{0.17em}VDT{o}_{to} \forall \hspace{0.17em} to\in To, t\in T$$

(B.55)

Equation (B.56) defines the total value of bonuses, which aggregates the incentives associated with inventories held at compression plants, port liquefaction hubs, geological liquefaction hubs, inland liquefaction facilities, and EOR nodes. These bonuses act as positive adjustments to the system, rewarding storage capacity utilization and reinforcing the strategic role of CO₂ retention across the network. Equation (B.57) specifies the total penalties, which are applied to the same categories of inventories but with coefficients that represent economic costs or disincentives. These penalties capture the negative effects of inefficiencies, such as excessive accumulation, operational risks, or unutilized capacities. By introducing both bonuses and penalties explicitly, the model incorporates a mechanism to balance desirable outcomes with operational drawbacks, ensuring that the optimization reflects not only costs and revenues but also performance-based incentives and corrective charges.

$$\begin{array}{ll}Zbn = {\displaystyle \sum _{c\in C}}{\displaystyle \sum _{t\in T}}i{C}_{c,t}& \hspace{0.17em}bn{C}_c+{\displaystyle \sum _{lp\in \mathrm{L}\mathrm{P}}}{\displaystyle \sum _{t\in T}}iL{H}_{lp,t}\hspace{0.17em}bnL{H}_{lp }+{\displaystyle \sum _{lgeo\in \mathrm{L}\mathrm{g}\mathrm{e}\mathrm{o}}}{\displaystyle \sum _{t\in T}}iL{O}_{lgeo,t}\hspace{0.17em}bnL{O}_{lgeo}+{\displaystyle \sum _{\mathrm{l}\mathrm{n}\mathrm{d}\in \mathrm{L}\mathrm{n}\mathrm{d}}}{\displaystyle \sum _{t\in T}}iL{U}_{\mathrm{l}\mathrm{n}\mathrm{d},t}\hspace{0.17em}bnL{U}_{\mathrm{l}\mathrm{n}\mathrm{d}}\\ & +{\displaystyle \sum _{leor\in \mathrm{L}\mathrm{e}\mathrm{o}\mathrm{r}}}{\displaystyle \sum _{t\in T}}iLE{O}_{leor,t}\hspace{0.17em}bnLE{O}_{leor}\end{array}$$

(B.56)

$$\begin{array}{ll}Zpe ={\displaystyle \sum _{c\in C}}{\displaystyle \sum _{t\in T}}i{C}_{c,t}& \hspace{0.17em}pe{C}_c+{\displaystyle \sum _{lp\in \mathrm{L}\mathrm{P}}}{\displaystyle \sum _{t\in T}}iL{H}_{lp,t}\hspace{0.17em}peL{H}_{lp}+{\displaystyle \sum _{lgeo\in Lgeo}}{\displaystyle \sum _{t\in T}}iL{O}_{lgeo,t}\hspace{0.17em}peL{O}_{lgeo}+{\displaystyle \sum _{\mathrm{l}\mathrm{n}\mathrm{d}\in \mathrm{L}\mathrm{n}\mathrm{d}}}{\displaystyle \sum _{t\in T}}iL{U}_{\mathrm{l}\mathrm{n}\mathrm{d},t}\hspace{0.17em}peL{U}_{\mathrm{l}\mathrm{n}\mathrm{d}}\\ & +{\displaystyle \sum _{leor\in \mathrm{L}\mathrm{e}\mathrm{o}\mathrm{r}}}{\displaystyle \sum _{t\in T}}iLE{O}_{leor,t}\hspace{0.17em}peLE{O}_{leor}\end{array}$$

(B.57)

Constraints (B.58)–(B.62) impose upper bounds on the inventory levels across the different nodes of the CO₂ supply chain. Constraint (B.58) limits the amount of CO₂ stored in compression facilities to the maximum inventory capacity available at each plant. Constraint (B.59) applies the same logic to port liquefaction hubs, ensuring that inventories do not exceed their admissible storage limits. Constraint (B.60) establishes the storage capacity constraint for geological liquefaction facilities, while constraint (B.61) restricts the amount of CO₂ that can be accumulated in EOR injection hubs. Finally, constraint (B.62) regulates the inventories held at inland liquefaction facilities, capping them at the installed capacity levels.

$$i{C}_{c,t} \le CI{C}_c \forall \hspace{0.17em} c\in C, \forall \hspace{0.17em} t\in T$$

(B.58)

$$iL{H}_{lp,t} \le CapInvL{p}_{lp } \forall \hspace{0.17em}l\in \mathrm{L}\mathrm{P}, \forall \hspace{0.17em}t\in T$$

(B.59)

$$iL{O}_{lgeo,t} \le CIl{g}_{lgeo} \forall \hspace{0.17em}g\in Lgeo, \forall \hspace{0.17em}t\in T$$

(B.60)

$$iLE{O}_{leor,t} \le CIl{o}_{leor} \forall \hspace{0.17em}r\in Leor, \forall \hspace{0.17em}t\in T$$

(B.61)

$$iL{U}_{\mathrm{l}\mathrm{n}\mathrm{d},t} \le CIl{i}_{\mathrm{l}\mathrm{n}\mathrm{d}} \forall \hspace{0.17em}\mathrm{l}\in \mathrm{Lnd}, \forall \hspace{0.17em}t\in T$$

(B.62)

Equation (B.63) formulates the balance of uncaptured CO₂ in the system. It calculates the net emissions lost by subtracting the actual captured amounts from the total potential CO₂ capture. This equality ensures consistency between the designed capture capacity and the effective utilization of that capacity, highlighting the inefficiencies associated with underutilization of capture opportunities.

$$CO2los{t}_t = \sum _{q\in Q}CO2Captur{e}_{q,t} - \sum _{q\in Q}Captur{e}_{q,t} \forall \hspace{0.17em} t\in T$$

(B.63)

Equations (B.64)–(B.68) impose the terminal inventory equalities at the end of the planning horizon. Equation (B.64) sets the closing inventory of CO₂ in compression facilities to zero, and the same structure is applied in (B.65) for port liquefaction hubs, in (B.66) for geological liquefaction facilities, in (B.67) for EOR injection hubs, and in (B.68) for inland liquefaction sites. Taken together, these equalities enforce a zero end-of-horizon balance across all storage locations, preventing inventory carryover and eliminating end effects in the supply-chain design.

$$i{C}_{c,t_8} = 0 \hspace{1em}\hspace{1em}\forall \hspace{0.17em}c\in C$$

(B.64)

$$iL{H}_{lp,t_8} = 0 \hspace{1em}\hspace{1em}\forall \hspace{0.17em}lp\in LP$$

(B.65)

$$iL{O}_{lgeo,t_8} = 0 \hspace{1em}\hspace{1em}\forall \hspace{0.17em}lgeo\in \mathrm{L}\mathrm{g}\mathrm{e}\mathrm{o}$$

(B.66)

$$iLE{O}_{leor,t_8} = 0 \hspace{1em}\hspace{1em}\forall \hspace{0.17em}leor\in \mathrm{Leor}$$

(B.67)

$$iL{U}_{\mathrm{l}lnd,t_8} = 0 \hspace{1em}\hspace{1em}\forall \hspace{0.17em}lnd\in Lnd$$

(B.68)

Equation (B.69) defines the effective throughput at each compression facility. It specifies that THRUCc, t is equal to the sum of CO₂ flows delivered from capture sources to compressor ccc in period t, adjusted by the corresponding leakage rate. This formulation ensures that the throughput reflects the net amount of CO₂ effectively processed after accounting for technical losses.

$$THRU{C}_{c,t} = \sum _{q\in Q}\sum _{ca\in Ca}Q{C}_{q,c,ca,t}\hspace{0.17em}\left(1-\mathrm{LRQ}{\mathrm{C}}_{\mathrm{ca}}\right) \hspace{1em}\hspace{1em}\forall \hspace{0.17em}c\in C, t\in T$$

(B.69)

Constraint (B.70) imposes a minimum utilization requirement for compression facilities. It establishes that the throughput must reach at least 65% of the installed processing capacity whenever a plant is activated. This condition prevents underutilization of infrastructure and enforces an operational threshold that guarantees efficiency and consistency in the design of the supply chain.

$$THRU{C}_{c,t} \ge 0.65\hspace{0.17em}CpP{C}_c\hspace{0.17em}Y{c}_c \hspace{1em}\hspace{1em}\forall \hspace{0.17em}c\in C, t\in T$$

(B.70)

Equations (B.71)–(B.75) define the supply and allocation of solid materials required for mineralization. Constraint (B.71) links the solid inputs available at node x to the supply S_q,M,t, while Equation (B.72) establishes the generation of silica dioxide (SiO₂) derived from solids processed, and Equation (B.73) accounts for the coproducts of mineralization, combining the production of carbonates and silica dioxide. Equation (B.74) defines the total CO₂ consumed in mineralization based on stoichiometric coefficients, and Equation (B.75) ensures that the substitution of silica dioxide in cement plants does not exceed their admissible demand.

$$fso{q}_{x,M,t} \le \sum _{q\in Q}{S}_{q,M,t}, \forall \hspace{0.17em} x \in X, M \in M, t \in T$$

(B.71)

$$cumqodSiO2Q_{q,t}=\sum _{M\in M,\hspace{0.17em}QMELI{G}_{q,M}}=1ySiO{2}_M\left(\sum _{x\in X}SOLQ{X}_{q,M,x,t}\right),\hspace{1em}\forall \hspace{0.17em}q\in Q,\hspace{0.17em}t\in T$$

(B.72)

$$\sum _{M\in M,\hspace{0.17em}QMELI{G}_{q,M}}=1FlowMCO3QM{Q}_{q,M,t}+ \sum _{qq\in QCem}fsq{q}_{q,qq,t} = cumqodMCO3Q_{q,t} + cumqodSiO2Q_{q,t} \forall \hspace{0.17em}q\in Q,\hspace{0.17em}t\in T$$

(B.73)

$$cum{q}_{q,t}=\sum _{M\in M,\hspace{0.17em}QMELI{G}_{q,M}}=1aCO{2}_M\left(\sum _{x\in X}fso{q}_{x,M,t}\right)$$

(B.74)

$$\sum _{q\in Q}fsq{q}_{q,qq,t}\le SM{x}_{qq}\hspace{0.17em}D{C}_{qq,t} \left(\forall \hspace{0.17em}qq\in QCem,\hspace{0.17em}t\in T\right)$$

(B.75)

Equation (B.76) establishes that the total CO₂ captured must equal the sum of the flows allocated to compression, mineralization, and utilization. Constraint (B.77) connects the flows of solids entering the system with their supply, while Equations (B.78) to (B.80) define the mixture balance, ensuring that total mixing is consistent with capacity limits at node x. Constraints (B.81) and (B.82) introduce the quality constraints of mixtures, requiring that the weighted reactivity of solids remains within a predefined range. Equation (B.83) and constraint (B.84) close the balance of solid inputs into mineralization, linking them explicitly to the eligible mineral sets.

$$Captur{e}_{q,t} = \sum _{c\in C}\sum _{ca\in Ca}Q{C}_{q,c,ca,t}+ cum{q}_{q,t}+ \sum _{x\in X}\sum _{ka\in Ka}QXCO{2}_{q,x,ka,t} \forall \hspace{0.17em} q \in Q,\hspace{0.17em} t \in T$$

(B.76)

$$\sum _{x\in X}FlowSOLQ{X}_{q,x,M,t} \le S_{q,M,t},\hspace{1em}\forall \hspace{0.17em}q\in Q,\hspace{0.17em}M\in M,\hspace{0.17em}t\in \mathrm{T}$$

(B.77)

$$MixInx{M}_{x,M,t} = \sum _{q\in Q}FlowSOLQ{X}_{q,x,M,t} \forall \hspace{0.17em} x \in X, M \in M, t \in T$$

(B.78)

$$MixTot{x}_{x,t} = \sum _{M\in M}MixInx{M}_{x,M,t} \forall \hspace{0.17em} x \in X, t \in T$$

(B.79)

$$MixTot{x}_{x,t} \le C{M}_{x,t}\hspace{0.17em}Y{x}_x \forall \hspace{0.17em} x \in X, t \in T$$

(B.80)

$$\sum _{M\in M}R{c}_M\hspace{0.17em}MixInx{M}_{x,M,t} \ge RcM{n}_x\hspace{0.17em}MixTot{x}_{x,t} \forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.81)

$$\sum _{M\in M}R{c}_M\hspace{0.17em}MixInx{M}_{x,M,t} \le RcMn{x}_x\hspace{0.17em}MixTot{x}_{x,t} \forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.82)

$$fso{q}_{x,M,t} = MixInx{M}_{x,M,t} \forall \hspace{0.17em} x \in X,\hspace{0.17em} M \in M,\hspace{0.17em} t \in T$$

(B.83)

$$\sum _{x\in X}SOLQ{X}_{q,M,x,t} \le S_{q,M,t} \forall \hspace{0.17em}q\in Q, M\in M \mathrm{con} MELIG\left(M\right), t\in T$$

(B.84)

Equations (B.85)–(B.91) regulate the CO₂ consumption within mineralization. Equation (B.85) ensures that the total CO₂ used does not exceed the available output from inland liquefaction facilities, while Equation (B.86) computes the effective CO₂ consumption using stoichiometric parameters. Equation (B.87) introduces the formulation for coproduct generation, linking CO₂ use with the production of carbonates and silica dioxide. Equations (B.88) and (B.89) impose upper bounds on the CO₂ processed at node x and ensure that silica dioxide production remains consistent with the demand of cement plants. Constraints (B.90) and (B.91) define additional capacity constraints on CO₂ consumption to guarantee that mineralization processes respect operational limits.

$$CO2UseMIN{X}_{x,t} = \sum _{lnd\in \mathrm{L}\mathrm{n}\mathrm{d}}\sum _{ka\in Ka}LXCO{2}_{lnd,x,ka,t} \forall \hspace{0.17em} x \in X, t \in T$$

(B.85)

$$CO2UseMIN{X}_{x,t} = \sum _{M\in M \mathrm{con} MELIG\left(M\right)}aCO{2}_M\left(\sum _{q\in Q}SOLQ{X}_{q,M,x,t}\right) \forall \hspace{0.17em} x \in X, t \in T$$

(B.86)

$$\sum _{q\in Q}fmx{t}_{x,q,t}+\sum _{qq\in QCem}fsx{m}_{x,qq,t}=\sum \_\{M \in MELIG\} ├(yMCO{3}_M\hspace{0.17em}\sum _{q\in Q}SOLQ{X}_{q,M,x,t}+ySiO{2}_M\hspace{0.17em}\sum _{q\in Q}SOLQ{X}_{q,M,x,t}┤) \forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.87)

$$CO2UseMIN{X}_{x,t} \le CXCO{2}_x\hspace{0.17em}Y{x}_x \forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.88)

$$\sum _{M\in MELIG}\sum _{q\in Q}SOLQ{X}_{q,M,x,t} \le CX{S}_x\hspace{0.17em}Y{x}_x \forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.89)

$$\sum _{x\in X}fsx{m}_{x,qq,t} \le SM{x}_q\hspace{0.17em}D{C}_{q,t} \forall \hspace{0.17em} q \in QCem,\hspace{0.17em} t \in T$$

(B.90)

$$CO2Use{X}_{x,t}\le CXCO{2}_x\hspace{0.17em}Y{x}_x \hspace{1em}\forall \hspace{0.17em}x\in X,\hspace{0.17em}t\in T$$

(B.91)

Equations (B.92)–(B.99) extend the formulation to ensure feasibility of flows and coproduct balances. Equation (B.92) constrains the solid flows into node x by the processing capacity, while Equation (B.93) balances silica dioxide inventories. Equation (B.94) recalculates the CO₂ consumption associated with solids, and Equation (B.95) ensures that silica dioxide coproduct balances are consistent across periods. Constraints (B.96) to (B.98) limit mineralization by the number of activated units, pipelines, and compressors available in the network, while constraint (B.99) sets the upper bound for silica dioxide accumulation at node x.

$$\sum _{q\in Q}\sum _{M\in M}FlowSOLQ{X}_{q,x,M,t}\le CX{S}_x\hspace{0.17em}Y{x}_x \hspace{1em}\forall \hspace{0.17em}x\in X,\hspace{0.17em}t\in T$$

(B.92)

$$\sum _{q\in Q}\sum _{M\in M,\hspace{0.17em}QMELIG\left(q,M\right)}FlowSOLQ{X}_{q,x,M,t}\ge cumqodSiO2X_{x,t} \hspace{1em}\forall \hspace{0.17em}x\in X,\hspace{0.17em}t\in T$$

(B.93)

$$CO2Use{X}_{x,t}=\sum _{q\in Q,\hspace{0.17em}M\in M,\hspace{0.17em}QMELIG\left(q,M\right)}aCO{2}_M\hspace{0.17em}SOLQ{X}_{q,M,x,t}\hspace{1em}\forall \hspace{0.17em}x\in X,\hspace{0.17em}t\in T$$

(B.94)

$$cumqodSiO2X_{x,t}=\sum _{q\in Q,\hspace{0.17em}M\in M,\hspace{0.17em}QMELIG\left(q,M\right)}ySiO{2}_M\hspace{0.17em}SOLQ{X}_{q,M,x,t} \hspace{1em}\forall \hspace{0.17em}x\in X,\hspace{0.17em}t\in T$$

(B.95)

$$\sum _{x\in X}fsx{m}_{x,qq,t}\le SM{x}_{qq}\hspace{0.17em}D{C}_{qq,t} \hspace{1em}\forall \hspace{0.17em}qq\in QCem,\hspace{0.17em}t\in T$$

(B.96)

$$QXCO{2}_{q,x,ka,t}\le CpK{a}_{ka}\hspace{0.17em}vaQ{X}_{q,x,ka,t},\hspace{1em}\forall \hspace{0.17em}q\in Q,\hspace{0.17em}x\in X,\hspace{0.17em}ka\in Ka,\hspace{0.17em}t\in T$$

(B.97)

$$LXCO{2}_{lnd,x,ka,t}\le CpK{a}_{ka}\hspace{0.17em}vaL{X}_{lnd,x,ka,t},\hspace{1em}\forall \hspace{0.17em}lnd\in Lnd,\hspace{0.17em}x\in X,\hspace{0.17em}ka\in Ka,\hspace{0.17em}t\in T$$

(B.98)

$$\sum _{qq\in QCem}fsx{m}_{x,qq,t}\le cumqodSiO2X_{x,t},\hspace{1em}\forall \hspace{0.17em}x\in X,\hspace{0.17em}t\in T$$

(B.99)

Finally, Equations (B.100)–(B.105) incorporate operational thresholds and penalties. Constraint (100) requires a minimum level of CO₂ consumption in mineralization plants, while constraint (B.101) establishes minimum silica dioxide demand in cement plants. Constraint (B.102) enforces carbonate production consistency, while Equation (B.103) introduces penalty terms for unmet demand of co-products, explicitly modeling the economic consequences of shortfalls. Equations (B.104) and (B.105) finalize the balance by connecting CO₂ consumption with liquefaction outputs and stoichiometric relationships, ensuring that mineralization processes remain consistent both in physical flows and in economic performance.

$$CO2Use{X}_{x,t} \ge MinRun{X}_x\hspace{0.17em}Y{x}_x\forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.100)

$$\sum _{x\in X}fsx{m}_{x,qq,t} \ge DemMinSiO{2}_{qq,t}\forall \hspace{0.17em}qq\in QCem,\hspace{0.17em}t\in T$$

(B.101)

$$\sum _{x\in X}fmx{t}_{x,q,t} + SlackMCO{3}_{q,t} \ge DemMinMCO{3}_{q,t}\forall \hspace{0.17em}q\in Q,\hspace{0.17em}t\in T$$

(B.102)

$$ZPenalDem =PenaLtqyUnmetSiO2\sum _{qq\in QCem}\sum _{t\in T}SlackSiO{2}_{qq,t} +PenaLtqyUnmetMCO3\sum _{q\in Q}\sum _{t\in T}SlackMCO{3}_{q,t}$$

(B.103)

$$CO2Use{X}_{x,t} = \sum _{lnd\in \mathrm{L}\mathrm{n}\mathrm{d}}\sum _{ka\in Ka}LXCO{2}_{lnd,x,ka,t} \hspace{1em}\forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.104)

$$CO2Use{X}_{x,t} = \sum _{q\in Q}\sum _{M\in M,\hspace{0.17em}QMELI{G}_{q,M}}aCO{2}_M\hspace{0.17em}SOLQ{X}_{q,M,x,t}\hspace{1em}\forall \hspace{0.17em} x \in X,\hspace{0.17em} t \in T$$

(B.105)

Appendix B.5. Parameterization and Data Sources

The parametric configuration used in the MILP and RAIE modules is summarized in Table A6, Table A7 and Table A8. These parameters define the operational boundaries of the CCUS supply chain and ensure that the optimization and dynamic simulation stages are grounded in realistic industrial data. Table A4 shows the nominal capacity of the capture unit in tonnes (TnCO₂) per quarter, under steady-state operation. These parameters define the upper bounds in the MILP model and are used as baseline inputs for the RAIE dynamic simulation. Table A5 specifies the expected CO₂ consumption in each quarter, expressed in thousand tonnes (ktCO₂). These data constrain the variables ${AlmU}_{\mathrm{u},\mathrm{t}}$ and ${LU}_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{d},\mathrm{u},\mathrm{k}\mathrm{a},\mathrm{t}}$ in the optimization model, reflecting the absorption capacity of industrial users such as beverage carbonation, chemical synthesis, and construction materials. Emission factors (Table A6) quantify indirect and process-related CO₂-equivalent emissions for each transport and transformation activity, following international databases such as the IEA (2024) and the European Commission’s Joint Research Centre (JRC). Process efficiencies and conversion yields (Table A7) were obtained from experimental data, pilot studies, and engineering benchmarks for CO₂ capture, liquefaction, mineralization, and utilization. Leakage and reliability coefficients (Table A8) describe both physical losses and monitoring accuracy across network components, serving as the foundation for penalty and bonus terms in the RAIE objective function.

Table A4. Quarterly CO₂ capture potential by source node Q (TnCO₂/qt).

	t1	t2	t3	t4	t5	t6	t7	t8
Q1	49,203	49,518	50,914.5	50,232	49,944	49,008	48,963	48,882
Q2	48,336	50,293.5	50,362.5	49,482	50,680.5	47,638.5	47,277	49,723.5
Q3	44,662.5	43,899	44,704.5	44,956.5	44,259	44,032.5	44,817	44,008.5
Q4	61,398	63,609	67,408.5	56,116.5	62,818.5	55,633.5	58,356	59,011.5
Q5	55,488	53,257.5	55,969.5	56,989.5	53,427	55,887	53,721	54,406.5
Q6	58,674	63,624	60,886.5	57,193.5	63,900	61,212	63,537	63,463.5
Q7	43,200	40,843.5	42,702	39,981	39,499.5	42,286.5	40,182	42,859.5
Q8	54,438	51,040.5	52,830	53,460	53,128.5	53,638.5	53,187	52,989
Q9	46,290	47,578.5	48,132	48,177	48,556.5	47,905.5	46,147.5	46,323
Q10	66,478.5	68,665.5	65,869.5	67,101	62,064	59,869.5	61,245	67,110
Q11	45,709.5	45,849	45,073.5	46,233	46,087.5	45,394.5	45,372	46,311
Q12	47,640	51,280.5	52,461	51,654	52,264.5	47,185.5	48,909	46,969.5

Table A4. Quarterly CO₂ capture potential by source node Q (TnCO₂/qt).

	t1	t2	t3	t4	t5	t6	t7	t8
Q1	49,203	49,518	50,914.5	50,232	49,944	49,008	48,963	48,882
Q2	48,336	50,293.5	50,362.5	49,482	50,680.5	47,638.5	47,277	49,723.5
Q3	44,662.5	43,899	44,704.5	44,956.5	44,259	44,032.5	44,817	44,008.5
Q4	61,398	63,609	67,408.5	56,116.5	62,818.5	55,633.5	58,356	59,011.5
Q5	55,488	53,257.5	55,969.5	56,989.5	53,427	55,887	53,721	54,406.5
Q6	58,674	63,624	60,886.5	57,193.5	63,900	61,212	63,537	63,463.5
Q7	43,200	40,843.5	42,702	39,981	39,499.5	42,286.5	40,182	42,859.5
Q8	54,438	51,040.5	52,830	53,460	53,128.5	53,638.5	53,187	52,989
Q9	46,290	47,578.5	48,132	48,177	48,556.5	47,905.5	46,147.5	46,323
Q10	66,478.5	68,665.5	65,869.5	67,101	62,064	59,869.5	61,245	67,110
Q11	45,709.5	45,849	45,073.5	46,233	46,087.5	45,394.5	45,372	46,311
Q12	47,640	51,280.5	52,461	51,654	52,264.5	47,185.5	48,909	46,969.5

Table A5. Quarterly CO₂ demand for industrial use (TnCO₂/qt).

	t1	t2	t3	t4	t5	t6	t7	t8
u1	13,671.9	13,878.9	13,898.1	13,749	13,688.4	13,542.3	13,740.3	13,926
u2	16,209.6	16,789.8	17,037.6	16,314.3	16,830.6	16,391.1	16,290.6	17,071.8
u3	11,671.5	11,714.7	11,720.7	11,809.2	12,194.1	12,006.3	11,730	11,744.1

Table A5. Quarterly CO₂ demand for industrial use (TnCO₂/qt).

	t1	t2	t3	t4	t5	t6	t7	t8
u1	13,671.9	13,878.9	13,898.1	13,749	13,688.4	13,542.3	13,740.3	13,926
u2	16,209.6	16,789.8	17,037.6	16,314.3	16,830.6	16,391.1	16,290.6	17,071.8
u3	11,671.5	11,714.7	11,720.7	11,809.2	12,194.1	12,006.3	11,730	11,744.1

Table A6. Emission Factors by Transport and Processing Mode.

Mode/Process	Unit	Value	Source/Assumption
Truck (cryogenic, 20–35 t)	kgCO2e/t·km	1.5–2.2	Estimated from [IEA, 2024]
Ship (CO2 carrier)	kgCO2e/t·km	8.0	Northern Lights Pilot Data
Pipeline (onshore)	kgCO2e/t·km	0.5	Energy input to compression
Pipeline (offshore)	kgCO2e/t·km	0.6	Extended pipeline losses
Liquefaction plant	kgCO2e/t	35–45	Cryogenic unit operation
Compression station	kgCO2e/t	25–30	Compressor energy mix
Mineralization unit	kgCO2e/t	10–15	Derived from batch tests

Table A6. Emission Factors by Transport and Processing Mode.

Mode/Process	Unit	Value	Source/Assumption
Truck (cryogenic, 20–35 t)	kgCO2e/t·km	1.5–2.2	Estimated from [IEA, 2024]
Ship (CO2 carrier)	kgCO2e/t·km	8.0	Northern Lights Pilot Data
Pipeline (onshore)	kgCO2e/t·km	0.5	Energy input to compression
Pipeline (offshore)	kgCO2e/t·km	0.6	Extended pipeline losses
Liquefaction plant	kgCO2e/t	35–45	Cryogenic unit operation
Compression station	kgCO2e/t	25–30	Compressor energy mix
Mineralization unit	kgCO2e/t	10–15	Derived from batch tests

Table A7. Process Efficiencies and Conversion Yields.

Process/Conversion	Description	Value (–)	Source/Basis
Capture efficiency	Fraction of CO2 effectively captured	0.90–0.95	Typical post-combustion values
Liquefaction efficiency	CO2 retained after liquefaction	0.92	Cryogenic benchmark
Transport efficiency	CO2 delivered after transport	0.97–0.99	Mode-dependent
Injection efficiency	Fraction stored successfully	0.96	Pilot well data
Utilization efficiency	CO2 converted to product	0.85–0.90	Industrial estimation
Mineralization yield (carbonate)	Mass ratio MCO3/CO2	0.78	Laboratory trials
Mineralization yield (silica)	Mass ratio SiO2/CO2	0.32	Derived stoichiometry

Table A7. Process Efficiencies and Conversion Yields.

Process/Conversion	Description	Value (–)	Source/Basis
Capture efficiency	Fraction of CO2 effectively captured	0.90–0.95	Typical post-combustion values
Liquefaction efficiency	CO2 retained after liquefaction	0.92	Cryogenic benchmark
Transport efficiency	CO2 delivered after transport	0.97–0.99	Mode-dependent
Injection efficiency	Fraction stored successfully	0.96	Pilot well data
Utilization efficiency	CO2 converted to product	0.85–0.90	Industrial estimation
Mineralization yield (carbonate)	Mass ratio MCO3/CO2	0.78	Laboratory trials
Mineralization yield (silica)	Mass ratio SiO2/CO2	0.32	Derived stoichiometry

Table A8. Leakage and Reliability Coefficients.

Component/Arc	Leakage Rate (%)	Reliability Coefficient (–)	Notes
Capture–Compression (Q→C)	0.5–1.0	0.98	Cryogenic valves & connectors
Compression–Liquefaction (C→L)	0.3–0.8	0.97	Includes temporary venting
Liquefaction–Hub (L→H/O/U/EO)	0.8–1.2	0.96	Offshore transfer lines
Onshore storage hub (H)	0.2	0.99	Monitoring system installed
Offshore storage hub (O)	0.5	0.98	Oceanic pressure variations
Industrial user (U)	0.1	0.97	Process losses
EOR field (EO)	0.4	0.96	CO2 reinjection cycle losses

Table A8. Leakage and Reliability Coefficients.

Component/Arc	Leakage Rate (%)	Reliability Coefficient (–)	Notes
Capture–Compression (Q→C)	0.5–1.0	0.98	Cryogenic valves & connectors
Compression–Liquefaction (C→L)	0.3–0.8	0.97	Includes temporary venting
Liquefaction–Hub (L→H/O/U/EO)	0.8–1.2	0.96	Offshore transfer lines
Onshore storage hub (H)	0.2	0.99	Monitoring system installed
Offshore storage hub (O)	0.5	0.98	Oceanic pressure variations
Industrial user (U)	0.1	0.97	Process losses
EOR field (EO)	0.4	0.96	CO2 reinjection cycle losses

All optimization and simulation procedures described in this study were implemented in GAMS 39.1 using CPLEX 22.1 as the primary solver. The model integrates two layers: (i) a mixed-integer linear programming (MILP) formulation for network design and operation, and (ii) the RAIE (Robust Adaptive Immune-Structural Evaluation) module, developed as a post-optimal dynamic loop to simulate the system’s adaptive response under disruption scenarios of varying severity.

The input data—comprising capture capacities, transport costs, emission factors, process efficiencies, and leakage rates—are fully parameterized and referenced in Table A4, Table A5, Table A6, Table A7 and Table A8. All variables, parameters, and equations follow the nomenclature described in Appendix A to ensure traceability between model components. Numerical experiments were performed using a quarterly time resolution and a fixed 2-year horizon (eight periods), with disruption windows and recovery rates defined as in the RAIE simulation settings.

To guarantee reproducibility, the complete set of GAMS files—including the MILP model, RAIE post-optimal loops, parameter initialization scripts, and test datasets—will be made available upon publication through an open repository (Zenodo DOI to be provided). The repository will also contain an Excel-based validation sheet that allows users to replicate the results of Figure 7, Figure 8 and Figure 9 and Table A3, Table A4 and Table A5 directly from Equations (1)–(4).

This approach ensures full transparency and alignment with the FAIR data principles (Findable, Accessible, Interoperable, and Reusable), enabling both researchers and practitioners to reuse and extend the model for other CCUS networks or adaptive-resilience applications.

Appendix C.1. Innate Response: Early Detection and Buffer Activation

(linked to Equation (1) in the main text)

The innate layer modulates the immediate impact of disruption through early detection and local buffering capacity derived from the MILP’s optimal inventories.

$${\Delta }_t^s=\zeta \cdot \left(1-{\theta }_{\det }^s\right)\cdot D_t$$

(C.1a)

$${\mathsf{\Phi }}_{n,t}^s=k_{\mathrm{inn}}\cdot {\displaystyle \frac{In{v}_n^{*}}{Ca{p}_n^{*}}}\cdot D_t$$

(C.1b)

where

• ζ = baseline disruption severity (common across all scenarios).
• D_t = binary indicator of the disruption’s active period.
• ${\theta }_{\det }^s$ ∈ [0,1] = early detection efficiency of scenario s.
• k_inn = innate buffer coefficient.
  The term ${\mathsf{\Phi }}_{n,t}^s$ increases the available operational margin at node $n$ during the event, proportional to its initial inventory-to-capacity ratio.

Appendix C.2. Adaptive Containment: Functional Reconfiguration

(linked to Equation (2) in the main text)

The adaptive layer reflects the capacity of the system to reallocate flow and contain losses by activating redundant pathways already defined in the MILP structure.

$${\lambda }_{n,t}^s={\lambda }_n+k_{\mathrm{stress}}\cdot (1-{\theta }_{\mathrm{red}}^s)\cdot D_t$$

(C.2)

where

• ${\lambda }_{n,t}^s$ is the effective loss rate at node $n$ and time $t$.
• ${\lambda }_n$ is the nominal loss rate from the MILP solution.
• $k_{\mathrm{stress}}$ defines the proportional increase in losses under stress.
• ${\theta }_{\mathrm{red}}^s\in \left[\mathrm{0,1}\right]$ measures redundancy activation and functional containment.

A higher ${\theta }_{\mathrm{red}}^s$ attenuates the degradation of performance during the disruption.

Appendix C.3. Memory-Based Recovery: Structural Learning

(linked to Equation (3) in the main text)

Once the disruption ends ($D_t=0$), adaptive memory mechanisms accelerate recovery depending on prior exposure and the length of the event.

$${\rho }_{t+1}^s={\rho }_t^s+{\theta }_{\mathrm{mem}}^s\cdot k_{\mathrm{rec}}\cdot 1_{\{t>t_{\mathrm{event}}\}}$$

(C.3)

where

• ${\rho }_t^s$ is the recovery factor at time $t$.
• ${\theta }_{\mathrm{mem}}^s$ and $k_{\mathrm{rec}}$ control the rate of adaptive restoration.
• $1_{\{t>t_{\mathrm{event}}\}}$ is an indicator for post-event periods.

This equation models the immune memory process: systems with prior activation shorten their recovery trajectory in subsequent periods.

Appendix C.4. Overall Network Performance

(linked to Equation (4) in the main text)

The instantaneous performance of the system, expressed as a normalized service level $S_t^s\in \left[\mathrm{0,1}\right]$, results from the combination of capacity degradation, buffering, and recovery:

$$S_t^s=S_t^0\cdot [{\displaystyle \frac{\sum _{n\in N}Ca{p}_n^{*}\cdot (1-{\Delta }_t^s)\cdot (1+{\mathsf{\Phi }}_{n,t}^s)}{\sum _{n\in N}Ca{p}_n^{*}}}]\cdot (1-\overline{{\lambda }_t^s})+{\rho }_t^s$$

(C.4)

where

$S_t^0$ represents the baseline MILP performance (without disruption), and $\overline{{\lambda }_t^s}$ is the average effective loss rate across all nodes.

This formulation guarantees that the RAIE trajectories $S_t^s$ are directly derived from the MILP-optimal state variables and parameters ($Ca{p}^{*},In{v}^{*},\lambda$), ensuring full consistency and reproducibility.

Appendix C.5. Post-Optimization Metrics

From these trajectories, the classical RAIE metrics are computed:

$$R_{\mathrm{area}}^s=\sum _t{S}_t^s,R_{\mathrm{m}\mathrm{i}\mathrm{n}}=\underset{t}{\mathrm{m}\mathrm{i}\mathrm{n}}{S}_t^s,TT{R}^s=\mathrm{m}\mathrm{i}\mathrm{n}\{t:S_t^s\ge S_t^0\}.$$

(C.5)

These indices quantify the integrated loss, depth of impact, and time to recovery, allowing direct comparison across frameworks under identical disruption profiles.

Appendix C.6. Implementation Note

The dynamic system $(\mathrm{C}.1-\mathrm{C}.5)$ is solved iteratively in the GAMS simulation loop after the MILP optimization phase. Each iteration reads the optimal values of the MILP and updates the parameters for the next step. This implementation ensures:

• Identical initial conditions across all frameworks.
• Consistent parameterization of severity and duration.
• Explicit differentiation by the activation of θ_det, θ_red, θ_mem.

Hence, the RAIE post-optimization module constitutes a parametric dynamic extension of the MILP, formally linking immune-inspired mechanisms to optimization-based supply chain design.

The post-optimization RAIE module was implemented in GAMS as an iterative simulation loop executed after the MILP convergence.

• Optimal MILP Solution (Homeostasis Phase): The optimization model provides the steady-state configuration of the CCUS network, including activated nodes, transportation links, nominal capacities $Ca{p}_n^{*}$, inventory levels $In{v}_n^{*}$, and loss rates ${\lambda }_n$. These outputs represent the homeostatic equilibrium of the system before disruption.
• Shock Injection (Perturbation Phase): A discrete disruption of given severity (low, medium, or high) and duration ($D_t$) is applied. The disturbance is represented through a binary time-dependent parameter that activates the loss functions in Eqs. $(\mathrm{C}.1-\mathrm{C}.5)$. Importantly, all scenarios share identical shock parameters, ensuring that performance differences arise only from the activation of immune layers (${\theta }_{\det },{\theta }_{\mathrm{red}},{\theta }_{\mathrm{mem}}$).
• Dynamic Response (Adaptive Phase): During the disruption, the model computes at each time step:

○

The effective degradation ${\Delta }_t^s$,

○

The buffer activation ${\mathsf{\Phi }}_{n,t}^s$,

○

The temporary stress losses ${\lambda }_{n,t}^s$, and

○

The progressive recovery ${\rho }_t^s$.

These values update recursively through the simulation loop without re-optimizing the MILP structure. Thus, the system evolves dynamically while preserving the optimal topology and flow configuration.

4.

Performance Evaluation (Recovery Phase):

At the end of each simulation, the algorithm calculates the key RAIE robustness metrics (Equation C.5):

○

$R_{\mathrm{area}}$: Integrated performance loss (resilience area),

○

$R_{\mathrm{m}\mathrm{i}\mathrm{n}}$: Minimum relative throughput (depth of impact),

○

$TTR$: Time-to-recovery, i.e., the period in which performance returns to baseline. These indicators are normalized for cross-scenario comparison.

The simulation was programmed using standard GAMS syntax and executed on an Intel^® i7 processor (3.2 GHz, 32 GB RAM). Average run time for the post-optimization stage was below 1.5 s per scenario, since no re-optimization is performed.