An Integrated Financial–Sustainability Framework for Predicting Green Infrastructure Project Success
Abstract
1. Introduction
| Author(s) and Year | Focus of Study | Methodology | Key Findings | Identified Limitations/Gap |
|---|---|---|---|---|
| [28] | Forecasting the success of private participation infrastructure projects globally. | Application of multiple machine learning classifiers (e.g., k-NN, Random Forest) on a World Bank dataset. | Predictive accuracy varies significantly by project sector and region; decision tree-based classifiers performed best overall. | Focuses on traditional success/failure outcomes without integrating specific financial or sustainability performance metrics as predictors. |
| [29] | Cost–benefit analysis of making new infrastructure assets resilient to natural hazards. | Probabilistic cost–benefit analysis across 3000 scenarios. | Investing in resilience is highly robust, with a benefit–cost ratio greater than four in 50% of scenarios. | Provides a strong case for resilience but does not integrate these benefits into a comprehensive project appraisal framework alongside other financial metrics. |
| [30] | Updating the scientific basis for the Social Cost of Carbon (SCC). | Integrated assessment modeling responsive to National Academies of Sciences, Engineering, and Medicine (NASEM) recommendations. | Proposes a revised central SCC estimate of $185 per ton, 3.6 times higher than the previous U.S. government figure. | Focuses solely on the valuation of carbon emissions, not its integration or predictive power within a broader project success model. |
| [31] | Establishing the principles and application of Life Cycle Costing (LCC). | Conceptual review and framework development. | LCC provides a more complete view of project costs over its entire lifespan compared to initial capital cost analysis. | Primarily focused on economic costs; does not inherently incorporate environmental or social externalities or predict overall project success. |
| [27,32] | Development of SHAP (SHapley Additive exPlanations) for model interpretation. | Game theory-based additive feature attribution method. | Provides a unified and theoretically sound framework for explaining the output of any machine learning model. | A methodological tool; its application to validate an integrated financial-sustainability framework for infrastructure is novel. |
| [33] | Identifying challenges and barriers to green finance. | Literature review and expert interviews. | Key barriers include lack of standardized metrics, lack of transparent data, and perceived higher risks. | Highlights the problem but does not propose or empirically test a solution in the form of a validated, integrated metrics framework. |
- To identify and synthesize a comprehensive set of critical financial and sustainability metrics for green infrastructure appraisal through a systematic literature review and semi-structured interviews with industry and policy experts.
- To construct a quantifiable project performance index based on empirical data from recently completed green infrastructure projects within the GCC region, operationalized through measures of budget adherence, schedule performance, and stakeholder satisfaction.
- To develop and validate a predictive model using a XGBoost) to assess the efficacy of the integrated metrics framework in forecasting project success, and to benchmark its performance against a baseline model using only traditional financial metrics.
- To employ SHAP analysis to interpret the predictive model, identify the most influential metrics driving project performance, and provide transparent insights into the decision-making logic of the framework.
2. Materials and Methods
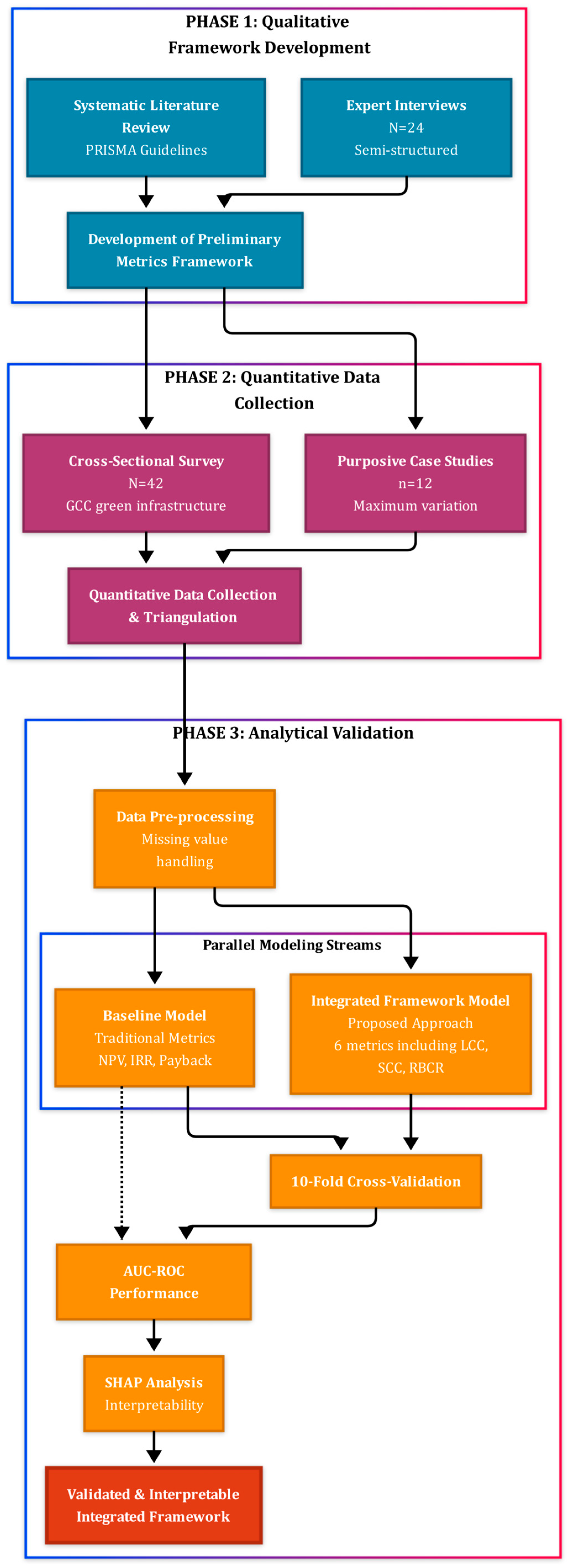
2.1. Research Design and Workflow
2.2. Phase 1: Framework Development and Metric Identification
2.2.1. Systematic Literature Synthesis
2.2.2. Expert Interviews
2.3. Phase 2: Quantitative Data Collection and Sample Characteristics
2.3.1. Survey Instrument Design**
2.3.2. Sampling Strategy and Data Collection
2.3.3. Case Study Selection
2.4. Operationalization of Variables
2.4.1. Independent Variables: The Integrated Metrics Framework
2.4.2. Dependent Variable: Project Success Index (PSI)
2.5. Analytical Framework: Predictive Modeling and Interpretation
2.5.1. Data Pre-Processing
2.5.2. Model Selection: Gradient Boosting Machine (XGBoost)
2.5.3. Model Validation and Performance Evaluation
2.5.4. Model Interpretability: SHAP (SHapley Additive exPlanations)
2.5.5. Heterogeneity and External Covariates
3. Results
3.1. Qualitative Framework Development: Synthesis of Expert Interviews
3.2. Sample Characteristics and Descriptive Statistics
3.3. Project Success Index (PSI) Distribution and Classification
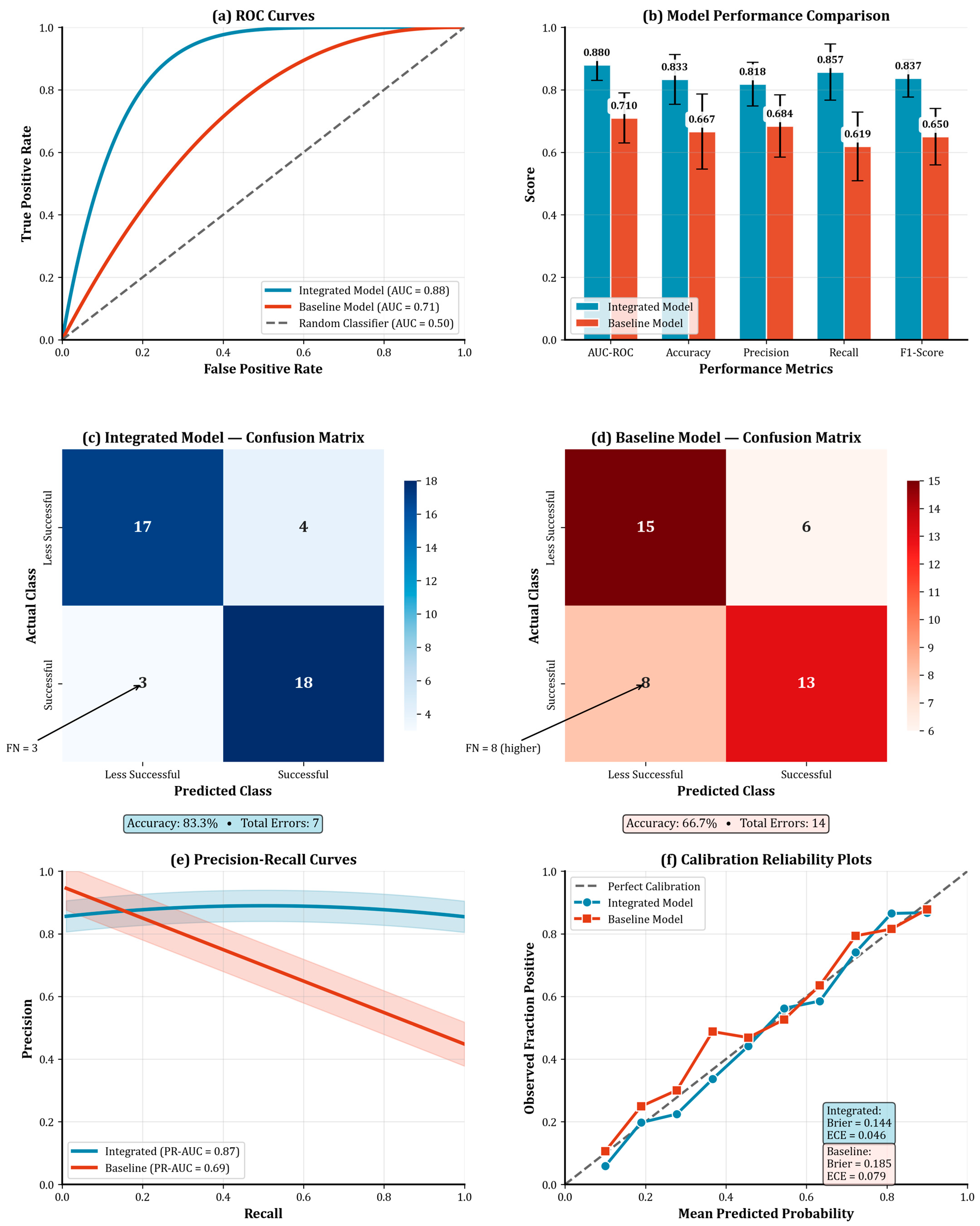
3.4. Predictive Model Performance and Benchmarking
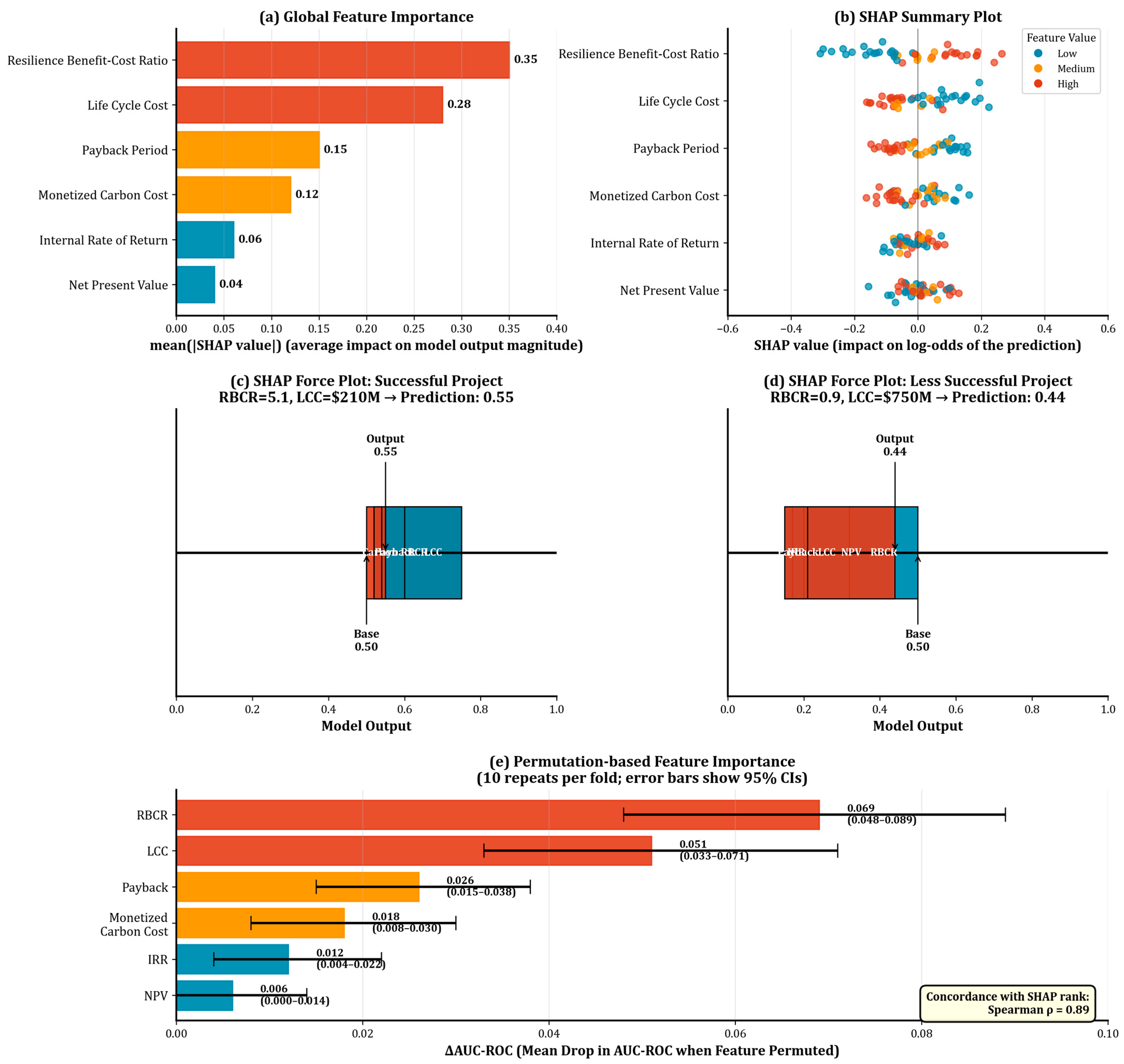
3.5. Model Interpretability and Feature Importance Using SHAP
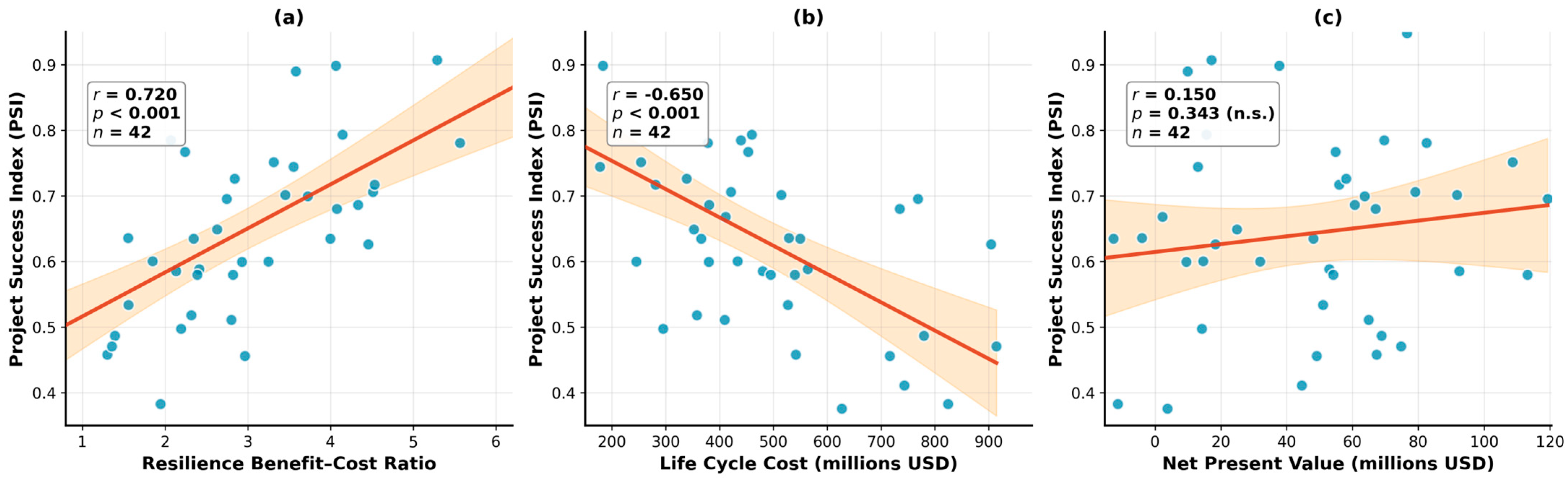
3.6. In-Depth Analysis of Key Predictors
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Source Categories and Their Role in Data Collection
| Source Category | Representative Documents | Primary Use in This Study |
|---|---|---|
| Investment decision documentation (respondent-provided) | Financial models; investment memos; sanctioning packages | NPV, IRR, Payback; LCC cost elements and discounting assumptions; identification and costing of resilience measures; emissions baselines |
| Public procurement and award records | Tender notices; contract awards; technical schedules | Verification of project scope, asset class, commissioning year; cross-checks of budget/duration |
| Corporate disclosures | Annual reports; sustainability reports; ESG disclosures | Confirmation of operational status and capacity; emissions factors when disclosed |
| Case-study technical files | Risk registers; O&M plans; completion reports | Triangulation of survey inputs; avoided-loss estimates for RBCR; validation of LCC components |
References
- Umoh, A.A.; Nwasike, C.N.; Tula, O.A.; Ezeigweneme, C.A.; Gidiagba, J.O. Green Infrastructure Development: Strategies for Urban Resilience and Sustainability. World J. Adv. Res. Rev. 2024, 21, 020–029. [Google Scholar] [CrossRef]
- Ajirotutu, R.O.; Adeyemi, A.B.; Ifechukwu, G.-O.; Iwuanyanwu, O.; Ohakawa, T.C.; Garba, B.M.P. Designing Policy Frameworks for the Future: Conceptualizing the Integration of Green Infrastructure into Urban Development. J. Urban Dev. Stud. 2024, 2, 911–923. [Google Scholar]
- Ajirotutu, R.O.; Adeyemi, A.B.; Ifechukwu, G.-O.; Iwuanyanwu, O.; Ohakawa, T.C.; Garba, B.M.P. Future Cities and Sustainable Development: Integrating Renewable Energy, Advanced Materials, and Civil Engineering for Urban Resilience. Int. J. Sustain. Urban Dev. 2024, 3, 235–250. [Google Scholar]
- Ghanem, A.M.; Alamri, Y.A. The Impact of the Green Middle East Initiative on Sustainable Development in the Kingdom of Saudi Arabia. J. Saudi Soc. Agric. Sci. 2023, 22, 35–46. [Google Scholar] [CrossRef]
- Tsani, S.; Najm, S. Green Policies and Sustainable Development in Saudi Arabia. In Handbook of Sustainable Politics and Economics of Natural Resources; Edward Elgar Publishing: Cheltenham, UK, 2021; pp. 123–134. [Google Scholar]
- Alshuwaikhat, H.M.; Mohammed, I. Sustainability Matters in National Development Visions—Evidence from Saudi Arabia’s Vision for 2030. Sustainability 2017, 9, 408. [Google Scholar] [CrossRef]
- Alamoudi, A.K.; Abidoye, R.B.; Lam, T.Y. Implementing Smart Sustainable Cities in Saudi Arabia: A Framework for Citizens’ Participation towards Saudi Vision 2030. Sustainability 2023, 15, 6648. [Google Scholar] [CrossRef]
- Nassar, A.K. Strategic Energy Transition in the Gulf Cooperation Council: Balancing Economic, Social, Political, and Environmental Dynamics for Sustainable Development. Int. J. Green Energy 2025, 22, 1570–1586. [Google Scholar] [CrossRef]
- Morshed, A. Sustainable Energy Revolution: Green Finance as the Key to the Arab Gulf States’ Future. Int. J. Energy Sect. Manag. 2025. ahead of print. [Google Scholar] [CrossRef]
- Alhowaish, A.K. Green Municipal Bonds and Sustainable Urbanism in Saudi Arabian Cities: Toward a Conceptual Framework. Sustainability 2025, 17, 3950. [Google Scholar] [CrossRef]
- Myronchuk, V.; Yatsenko, O.; Riznyk, D.; Hurina, O.; Frolov, A. Financing Sustainable Development: Analysis of Modern Approaches and Practices in the Context of Financial and Credit Activities. Int. J. Econ. Financ. Issues 2024, 14, 317. [Google Scholar] [CrossRef]
- Kusz, D.; Kusz, B.; Wicki, L.; Nowakowski, T.; Kata, R.; Brejta, W.; Kasprzyk, A.; Barć, M. The Economic Efficiencies of Investment in Biogas Plants—A Case Study of a Biogas Plant Using Waste from a Dairy Farm in Poland. Energies 2024, 17, 3760. [Google Scholar] [CrossRef]
- Akomea-Frimpong, I.; Jin, X.; Osei-Kyei, R. Mapping Studies on Sustainability in the Performance Measurement of Public-Private Partnership Projects: A Systematic Review. Sustainability 2022, 14, 7174. [Google Scholar] [CrossRef]
- Arshad, H.; Thaheem, M.J.; Bakhtawar, B.; Shrestha, A. Evaluation of Road Infrastructure Projects: A Life Cycle Sustainability-Based Decision-Making Approach. Sustainability 2021, 13, 3743. [Google Scholar] [CrossRef]
- Dobrowolski, Z.; Drozdowski, G. Does the Net Present Value as a Financial Metric Fit Investment in Green Energy Security? Energies 2022, 15, 353. [Google Scholar] [CrossRef]
- Zijlstra, N. A Circular Life Cycle Cost Model: Quantifying the Financial Implications of Projected Level of Circularity in Real Estate Development Projects. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2023. [Google Scholar]
- Ni, T.; Zhang, X.; Leng, P.; Pelling, M.; Xu, J. Comprehensive Benefits Evaluation of Low Impact Development Using Scenario Analysis and Fuzzy Decision Approach. Sci. Rep. 2025, 15, 2227. [Google Scholar] [CrossRef]
- Majekolagbe, A.; Seck, S.L.; Wright, D.V. Exploring the Application of the Social Cost of Carbon in Loss-and-Damage and Impact Assessment. Clim. Law 2023, 13, 83–117. [Google Scholar] [CrossRef]
- Lee, S.-T.; Jung, S.-M. Monetizing Environmental Impacts of Nuclear Power: Cost-Benefit Analysis Using Social Cost of Carbon. Sage Open 2024, 14, 21582440241301468. [Google Scholar] [CrossRef]
- Caesary, D.; Kim, H.; Nam, M.J. An Alternative Approach to Capture Uncertainties Embedded in the Estimation of Social Cost of Carbon. WIREs Energy Environ. 2023, 12, e475. [Google Scholar] [CrossRef]
- Helgeson, J.; O’Fallon, C. Resilience Dividends and Resilience Windfalls: Narratives That Tie Disaster Resilience Co-Benefits to Long-Term Sustainability. Sustainability 2021, 13, 4554. [Google Scholar] [CrossRef] [PubMed]
- Reddy, K.R.; Janga, J.K.; Verma, G.; Nagaraja, B. Integration and Quantification of Resilience and Sustainability in Engineering Projects. J. Indian Inst. Sci. 2024, 104, 435–488. [Google Scholar] [CrossRef]
- Shamim, M.I.; Hamid, A.B.b.A.; Nyamasvisva, T.E.; Bin Rafi, N.S. Advancement of Artificial Intelligence in Cost Estimation for Project Management Success: A Systematic Review of Machine Learning, Deep Learning, Regression, and Hybrid Models. Modelling 2025, 6, 35. [Google Scholar] [CrossRef]
- Ayubi Rad, M.; Ayubirad, M.S. Comparison of Artificial Neural Network and Coupled Simulated Annealing Based Least Square Support Vector Regression Models for Prediction of Compressive Strength of High-Performance Concrete. Sci. Iran. 2017, 24, 487–496. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting Black-Box Models: A Review on Explainable Artificial Intelligence. Cogn. Comput. 2024, 16, 45–74. [Google Scholar] [CrossRef]
- Timilsina, M.S.; Sen, S.; Uprety, B.; Patel, V.B.; Sharma, P.; Sheth, P.N. Prediction of HHV of Fuel by Machine Learning Algorithm: Interpretability Analysis Using Shapley Additive Explanations (SHAP). Fuel 2024, 357, 129573. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of Machine Learning Models Using Shapley Additive Explanation and Application for Real Data in Hospital. Comput. Methods Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef] [PubMed]
- Ayat, M.; Kim, B.; Kang, C.W. A New Data Mining-Based Framework to Predict the Success of Private Participation in Infrastructure Projects. Int. J. Constr. Manag. 2023, 23, 2151–2159. [Google Scholar] [CrossRef]
- Hallegatte, S.; Rozenberg, J.; Maruyama Rentschler, J.E.; Nicolas, C.M.; Fox, C.J.E. Strengthening New Infrastructure Assets: A Cost-Benefit Analysis; World Bank Policy Research Working Paper; World Bank: Washington, DC, USA, 2019. [Google Scholar]
- Harker Steele, A.; Warner, T.; Vikara, D.; Guinan, A.; Balash, P. Comparative Analysis of Carbon Capture and Storage Finance Gaps and the Social Cost of Carbon. Energies 2021, 14, 2987. [Google Scholar] [CrossRef]
- Gluch, P.; Baumann, H. The Life Cycle Costing (LCC) Approach: A Conceptual Discussion of Its Usefulness for Environmental Decision-Making. Build. Environ. 2004, 39, 571–580. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.I.; Mata, M.N.; Martins, J.; Nasir, A.; Dantas, R.M.; Correia, A.B.; Saghir, U.S. Impediments of Green Finance Adoption System: Linking Economy and Environment. Impediments of green finance adoption system: Linking economy and environment. Emerg. Sci. J. 2022, 6, 217–237. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. R Package, Version 0.4-2; R Project: Vienna, Austria, 2015; Volume 1, pp. 1–4. [Google Scholar]
- Mihály, K.; Kulcsár, G. A New Many-Objective Hybrid Method to Solve Scheduling Problems. Int. J. Ind. Eng. Manag. 2023, 14, 326–335. [Google Scholar] [CrossRef]
- Parums, D.V. Review Articles, Systematic Reviews, Meta-Analysis, and the Updated Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) 2020 Guidelines. Med. Sci. Monit. Int. Med. J. Exp. Clin. Res. 2021, 27, e934475-1. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Cui, Q.; Li, Y. Net Present Value Method: A Method Recommended by ISO 15686-5 for Economic Evaluation of Building Life Cycle Costs. World J. Eng. Technol. 2022, 10, 224–229. [Google Scholar] [CrossRef]
- Frias, A.; Água, P.B.; Lopes, B.M.; Melo, P.S. Life Cycle Cost Analysis of Complex Systems: An Application to Shipbuilding. Int. J. Ind. Eng. Manag. 2022, 13, 215–224. [Google Scholar] [CrossRef]
- Bhatt, A.; Ravi, V.; Zhang, Y.; Heath, G.; Davis, R.; Tan, E.C.D. Emission Factors of Industrial Boilers Burning Biomass-Derived Fuels. J. Air Waste Manag. Assoc. 2023, 73, 241–257. [Google Scholar] [CrossRef]
- Mack, J.; Dean, G.A.; Wathne, L.G. Improving Pavement Resiliency to Flooding: A Case for Concrete Pavement. In Proceedings of the Airfield and Highway Pavements 2023, Austin, TX, USA, 14–17 June 2023; American Society of Civil Engineers: Austin, TX, USA, 2023; pp. 135–146. [Google Scholar]
- Zhu, Q.; Leibowicz, B.D. A Markov Decision Process Approach for Cost-Benefit Analysis of Infrastructure Resilience Upgrades. Risk Anal. 2022, 42, 1585–1602. [Google Scholar] [CrossRef]
- Osei-Kyei, R.; Chan, A.P. Evaluating the Project Success Index of Public-Private Partnership Projects in Hong Kong: The Case of the Cross Harbour Tunnel. Constr. Innov. 2018, 18, 371–391. [Google Scholar] [CrossRef]
- Osei-Kyei, R.; Chan, A.P.C. Developing a Project Success Index for Public–Private Partnership Projects in Developing Countries. J. Infrastruct. Syst. 2017, 23, 04017028. [Google Scholar] [CrossRef]
- Natras, R.; Soja, B.; Schmidt, M. Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting. Remote Sens. 2022, 14, 3547. [Google Scholar] [CrossRef]
- Sahin, E.K. Assessing the Predictive Capability of Ensemble Tree Methods for Landslide Susceptibility Mapping Using XGBoost, Gradient Boosting Machine, and Random Forest. SN Appl. Sci. 2020, 2, 1308. [Google Scholar] [CrossRef]
- Chai, Y.; Liang, R.; Samtani, S.; Zhu, H.; Wang, M.; Liu, Y.; Jiang, Y. Additive Feature Attribution Explainable Methods to Craft Adversarial Attacks for Text Classification and Text Regression. IEEE Trans. Knowl. Data Eng. 2023, 35, 12400–12414. [Google Scholar] [CrossRef]
- Woodward, D.G. Life Cycle Costing—Theory, Information Acquisition and Application. Int. J. Proj. Manag. 1997, 15, 335–344. [Google Scholar] [CrossRef]
- Manoharan, G.; Nithya, G.; Razak, A.; Sharma, S.; Ashtikkar, S.P. Challenges and Opportunities in Green Finance: Overcoming Barriers and Scaling up Sustainable Investments. In Practical Approaches to Agile Project Management; IGI Global: Hershey, PA, USA, 2024; pp. 398–413. [Google Scholar]
- Volz, U.; Lo, Y.C.; Mishra, V. Scaling up Green Investment in the Global South: Strengthening Domestic Financial Resource Mobilisation and Attracting Patient International Capital; SOAS Centre: London, UK, 2024. [Google Scholar] [CrossRef]
- Muhebwa, A.; Osman, K.K. A Behavioral Finance Framework for Balancing AI Accuracy and Operational Carbon Emissions. ACM J. Comput. Sustain. Soc. 2025, 3, 1–20. [Google Scholar] [CrossRef]
- Alhamami, A.H. Implementation of Machine Learning-Based Risk Prediction Models for Large-Scale Infrastructure Construction Projects in Urban Environments. Cad. Educ. Tecnol. Soc. 2025, 18, 330–346. [Google Scholar] [CrossRef]

| Theme | Definition | Illustrative Quotations |
|---|---|---|
| Theme 1: The “NPV Myopia” | A pervasive sentiment that an over-reliance on traditional financial metrics, particularly Net Present Value (NPV) and Internal Rate of Return (IRR), creates a short-term bias that systematically undervalues green infrastructure projects. Participants noted this approach fails to capture long-term operational efficiencies and non-market co-benefits. | “We are slaves to the NPV. If the model doesn’t show a positive return within a very specific, often politically-driven timeframe, the project is dead. This kills innovation in sustainability because the real benefits—like reduced operational costs over 30 years or enhanced climate resilience—are discounted into oblivion.”—Financial Analyst, Infrastructure Fund “A solar plant’s value isn’t just the electricity it sells. It’s the water it doesn’t consume compared to a thermal plant, the air quality improvement, the energy security. The standard financial model sees none of this. It’s a one-dimensional tool for a three-dimensional problem.”—Government Official, Ministry of Environment |
| Theme 2: The “Unquantified Risk” of Climate Inaction | A strong consensus that conventional risk assessment frameworks are inadequate for green projects because they fail to properly price the long-term risks associated with climate change. Experts emphasized that not investing in resilience is itself a significant, un-costed financial risk. | “The biggest risk isn’t the upfront cost of a resilient design; it’s the cost of rebuilding a non-resilient one in ten years after an extreme weather event that our climate models are now predicting. We don’t have a standard metric to put that ‘avoided cost’ on the balance sheet during appraisal.”—Senior Project Manager, Construction “Investors ask about the ROI of adding green space or using sustainable urban drainage. The real question should be: what is the cost of not doing it? Heat island effects, flash flooding… these have massive economic consequences that are completely external to the project’s P&L until they happen.”—Academic, Sustainable Construction |
| Theme 3: The “Data and Standardization Gap” | A frequently cited practical barrier to the adoption of sustainability metrics is the lack of standardized methodologies and reliable, localized data. This applies to calculating life-cycle costs, valuing carbon emissions, and quantifying resilience benefits, leading to inconsistent and non-comparable project appraisals. | “Everyone agrees Life Cycle Costing is the right way to think, but getting two engineers to agree on the assumptions to calculate it is impossible. We need a standardized approach, especially for operational and maintenance forecasts in our specific climate.”—Senior Project Manager, Renewable Energy “You can find a dozen different values for the Social Cost of Carbon. Which one do I use for a project in Riyadh versus one on the Red Sea coast? Without a regionally-endorsed standard, it just becomes an academic exercise that the finance team can easily dismiss.”—Policy Advisor, Sovereign Wealth Fund |
| Theme 4: The “Emerging Demand for Holistic Value” | A forward-looking theme indicating a shift in investor and stakeholder expectations. Participants reported growing pressure from international finance partners, regulators, and the public to demonstrate value beyond simple financial returns, creating a demand for more comprehensive and transparent reporting frameworks. | “The conversation with our international funding partners has changed. Five years ago, it was all about IRR. Now, they want to see the carbon footprint, the water impact, the community benefits. They want a sustainability story backed by numbers. Our old models don’t tell that story.”—Financial Analyst, Infrastructure Fund “With Vision 2030, the mandate is clear. Projects are no longer just about building something; they are about contributing to a larger national goal of sustainability and quality of life. Our success metrics must evolve to reflect this. Stakeholder satisfaction is now a critical KPI.”—Government Official, Giga-Project Authority |
| Characteristic | Category | Frequency | Percentage (%) | Mean (SD) |
|---|---|---|---|---|
| Project Type | Renewable Energy (Solar/Wind) | 18 | 42.9 | |
| Sustainable Water Management | 9 | 21.4 | ||
| Green Building Construction | 11 | 26.2 | ||
| Urban Greening/Public Space | 4 | 9.5 | ||
| Location | Saudi Arabia | 26 | 61.9 | |
| United Arab Emirates | 11 | 26.2 | ||
| Qatar | 5 | 11.9 | ||
| Total Budget | 285.4 M (192.1 M) | |||
| Planned Duration | 38.5 months (14.2) |
| Variable | Type | Mean | Std. Dev. (SD) | Minimum | Maximum |
|---|---|---|---|---|---|
| Independent Variables (Predictors) | |||||
| Net Present Value (NPV, $M) | Traditional | 45.8 | 35.1 | −15.2 | 120.5 |
| Internal Rate of Return (IRR, %) | Traditional | 11.2 | 3.8 | 5.1 | 20.5 |
| Payback Period (Years) | Traditional | 8.9 | 2.5 | 4.5 | 15.0 |
| Life Cycle Cost (LCC, $M) | Sustainability | 450.2 | 210.6 | 150.8 | 980.4 |
| Monetized Carbon Cost ($M) | Sustainability | 75.3 | 40.1 | 10.5 | 180.2 |
| Resilience Benefit–Cost Ratio (RBCR) | Sustainability | 2.9 | 1.5 | 0.8 | 6.2 |
| Dependent Variable Components (Outcomes) | |||||
| Cost Performance Index (CPI) | Performance | 1.01 | 0.12 | 0.75 | 1.25 |
| Schedule Performance Index (SPI) | Performance | 0.96 | 0.14 | 0.68 | 1.20 |
| Stakeholder Satisfaction (1–10 Scale) | Performance | 8.1 | 1.2 | 5.0 | 10.0 |
| Term in This Study | Standardized/International Expression (Illustrative) | Typical SASO/GCC Usage (Generic) | Definition Used Here (Equation Ref.) | Units |
|---|---|---|---|---|
| Life-Cycle Cost (LCC) | Whole-life costing in the ISO 15686-5 family | “Life-cycle cost”/“whole-life cost” in procurement and building-performance contexts | Present value of all costs minus residuals over analysis horizon (Equation (1)); assumptions by asset-class in Supplementary Table S8 | million USD |
| Monetized carbon cost | Social/shadow cost of carbon applied to Scope 1–2 (+documented Scope 3) emissions | “Carbon price”/“shadow carbon price” in appraisal guidance | Present value of over operating horizon (Equation (2); Box S1) | million USD |
| Resilience benefit–cost ratio (RBCR) | Benefit–cost ratio for resilience (avoided-loss over incremental resilience costs) | “Resilience BCR”/“benefit–cost analysis with resilience overlay” | (Equation (3); Box S2) | ratio |
| Net present value (NPV) | Conventional discounted cash-flow NPV | NPV | As reported in decision packs; used as predictor without alteration | million USD |
| Internal rate of return (IRR) | Conventional project IRR | IRR | As reported in decision packs; used as predictor | percent |
| Payback period | Simple payback | Payback | Years to cumulative breakeven (as reported) | years |
| Framework Metric | SDG 9 (Industry, Innovation and Infrastructure) | SDG 11 (Sustainable Cities and Communities) | SDG 13 (Climate Action) | Primary Policy Lever(s) Enabled |
|---|---|---|---|---|
| LCC (Equation (1)) | 9.4 (upgrade infrastructure for resource efficiency) | 11.6, 11.b (whole-life urban environmental management) | 13.2 (embed climate in planning via cost trajectories) | Whole-life procurement; PPP VfM tests using whole-life cost baselines |
| Monetized carbon cost (Equation (2)) | 9.4 (low-carbon technology choices) | 11.6 (air-quality/energy footprint in cities) | 13.2 (shadow carbon price in appraisal) | Shadow carbon pricing in public investment management; green-bond eligibility screens |
| RBCR (Equation (3)) | 9.1 (reliable, resilient infrastructure) | 11.5 (disaster-loss reduction; service continuity) | 13.1 (adaptive capacity; hazard-risk management) | Resilience investment prioritization; adaptation finance justification |
| Payback (years) | 9.1 (delivery of viable infrastructure) | 11.a (urban–regional linkages via quick returns) | Indirect | Capital budgeting threshold tests |
| IRR | 9.1 | Indirect | Indirect | Bankability screening; blended-finance structuring |
| NPV | 9.1 | Indirect | Indirect | Economic appraisal baseline; VfM counterfactuals |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tareemi, A.A. An Integrated Financial–Sustainability Framework for Predicting Green Infrastructure Project Success. Sustainability 2025, 17, 9529. https://doi.org/10.3390/su17219529
Tareemi AA. An Integrated Financial–Sustainability Framework for Predicting Green Infrastructure Project Success. Sustainability. 2025; 17(21):9529. https://doi.org/10.3390/su17219529
Chicago/Turabian StyleTareemi, Ahmad A. 2025. "An Integrated Financial–Sustainability Framework for Predicting Green Infrastructure Project Success" Sustainability 17, no. 21: 9529. https://doi.org/10.3390/su17219529
APA StyleTareemi, A. A. (2025). An Integrated Financial–Sustainability Framework for Predicting Green Infrastructure Project Success. Sustainability, 17(21), 9529. https://doi.org/10.3390/su17219529





