Water Consumption Prediction Based on Improved Fractional-Order Reverse Accumulation Grey Prediction Model
Abstract
1. Introduction
2. Literature Review
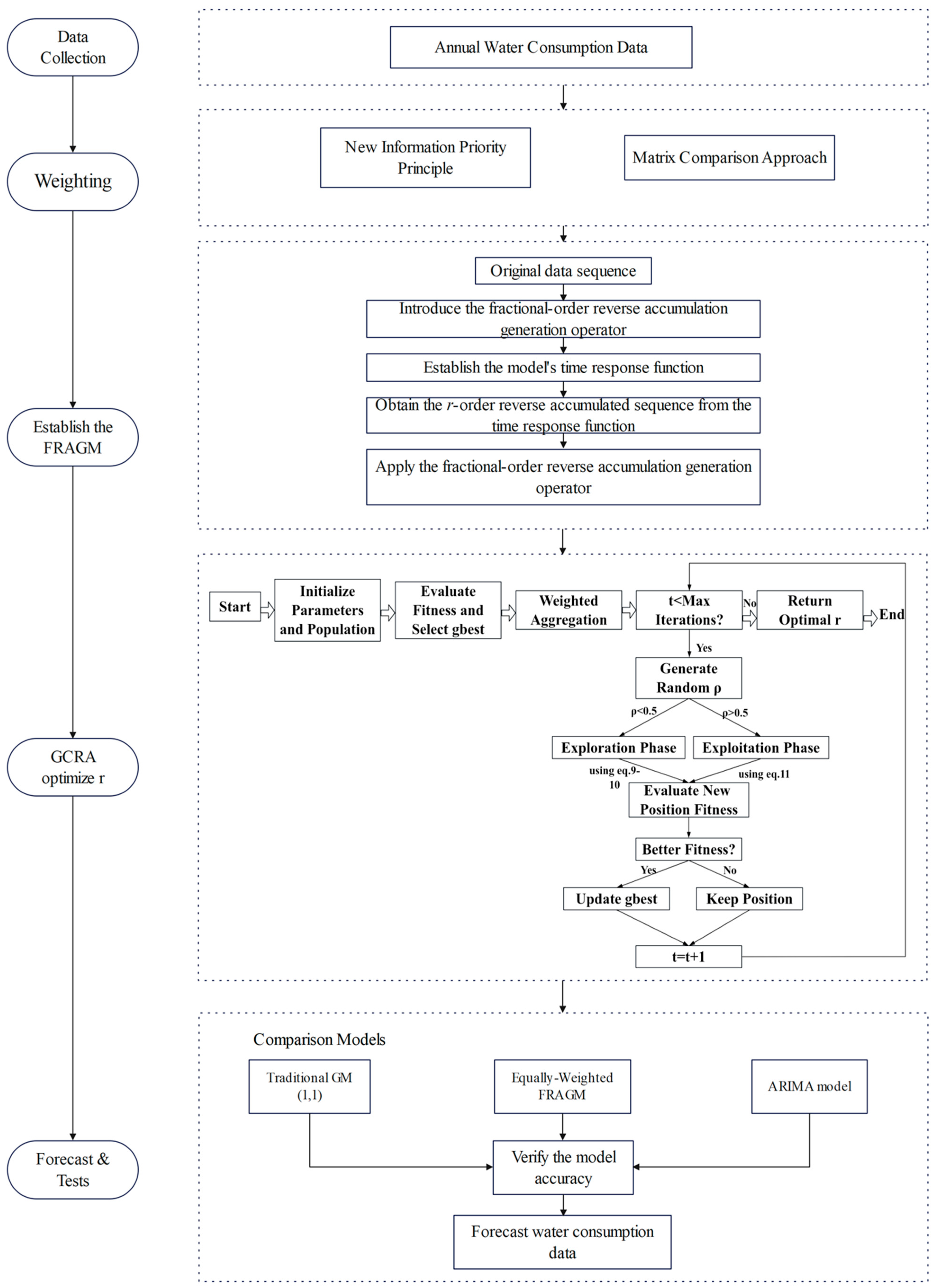
3. Methodology
3.1. Calculation of Yearly Data Weights Based on the New Information Priority Principle
3.2. Model Formulation of the FRAGM
3.3. GCRA-Based Optimization of the FRAGM
- Step 1
- Step 2
- Step 3
- Step 4
- Step 5
- Step 6
3.4. Comparison Models
- (1)
- Traditional GM (1,1)
- (2)
- Equally Weighted FRAGM
- (3)
- ARIMA model
3.5. Comparing Metrics
3.6. Model Performance Assessment Methods
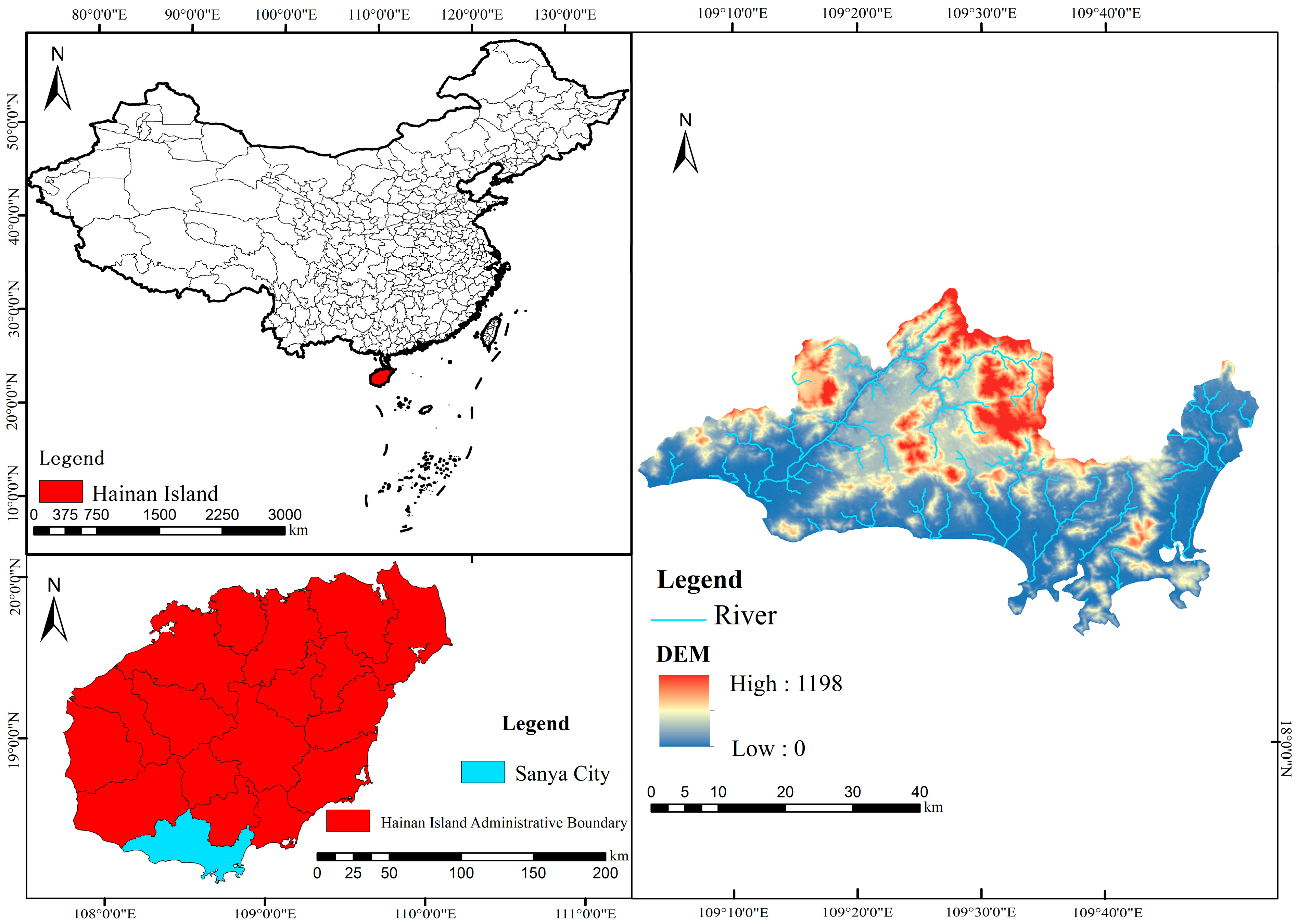
4. Case Study
5. Model Application and Results
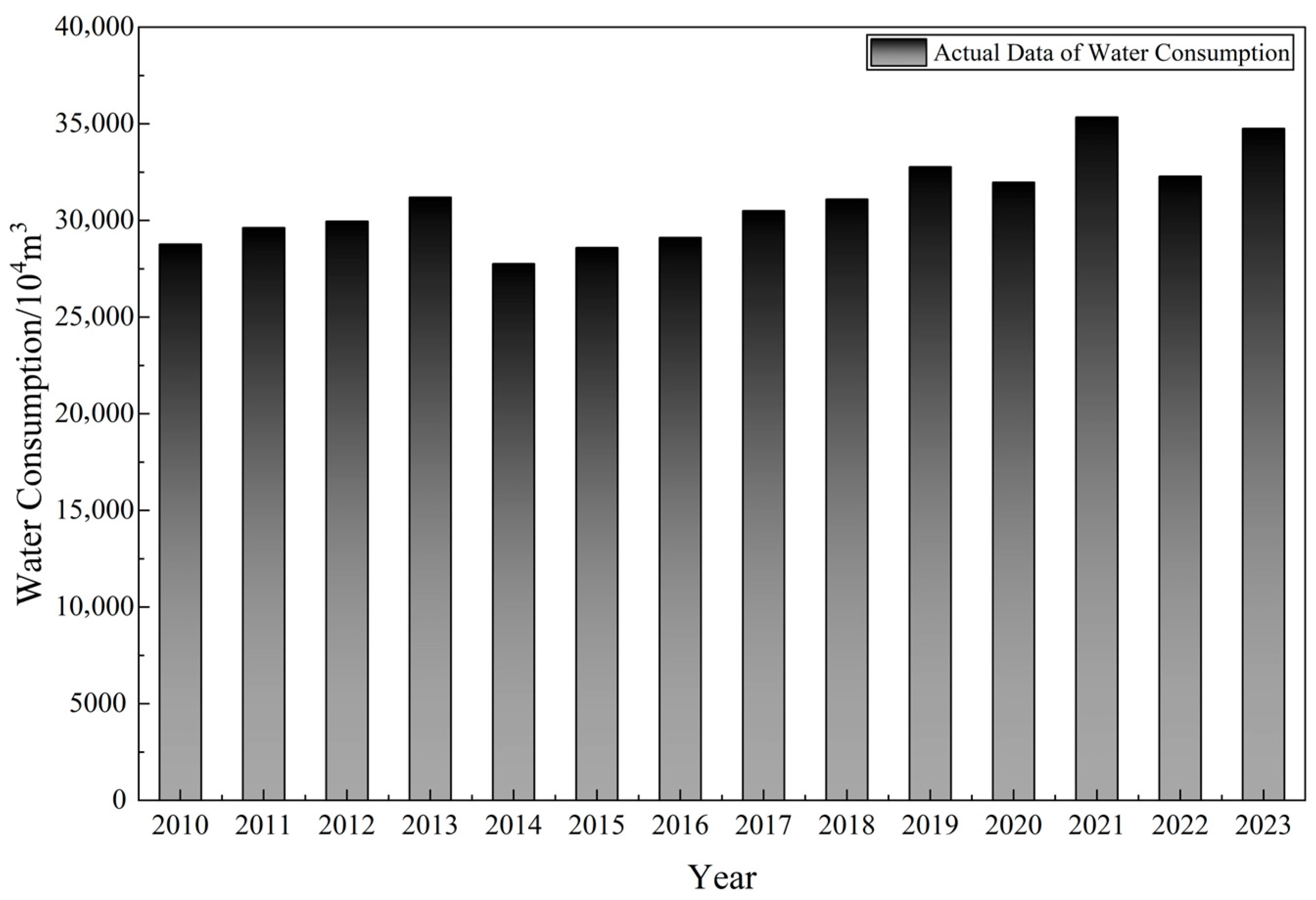
5.1. Data Preprocessing
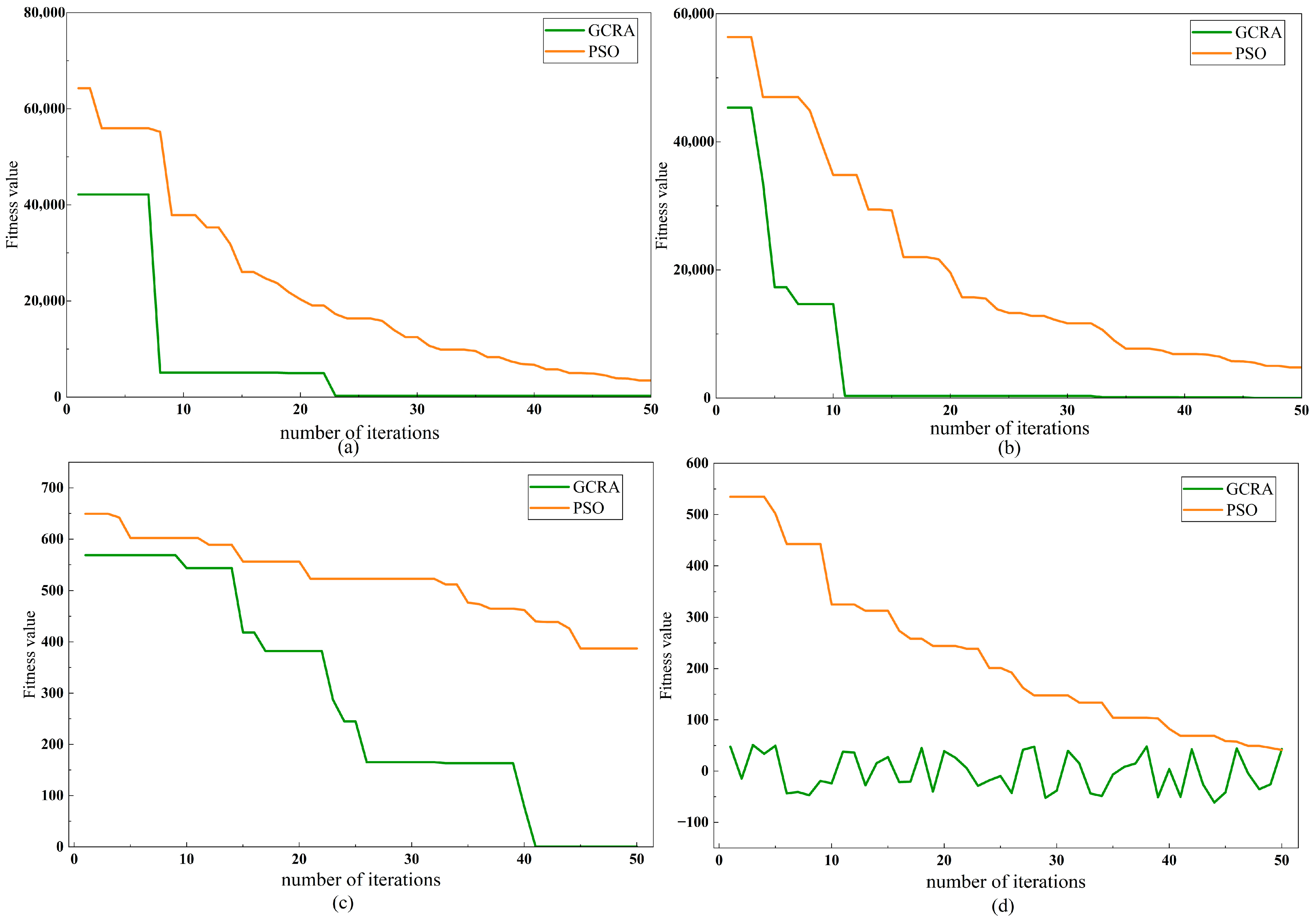
5.2. Algorithm Performance Evaluation
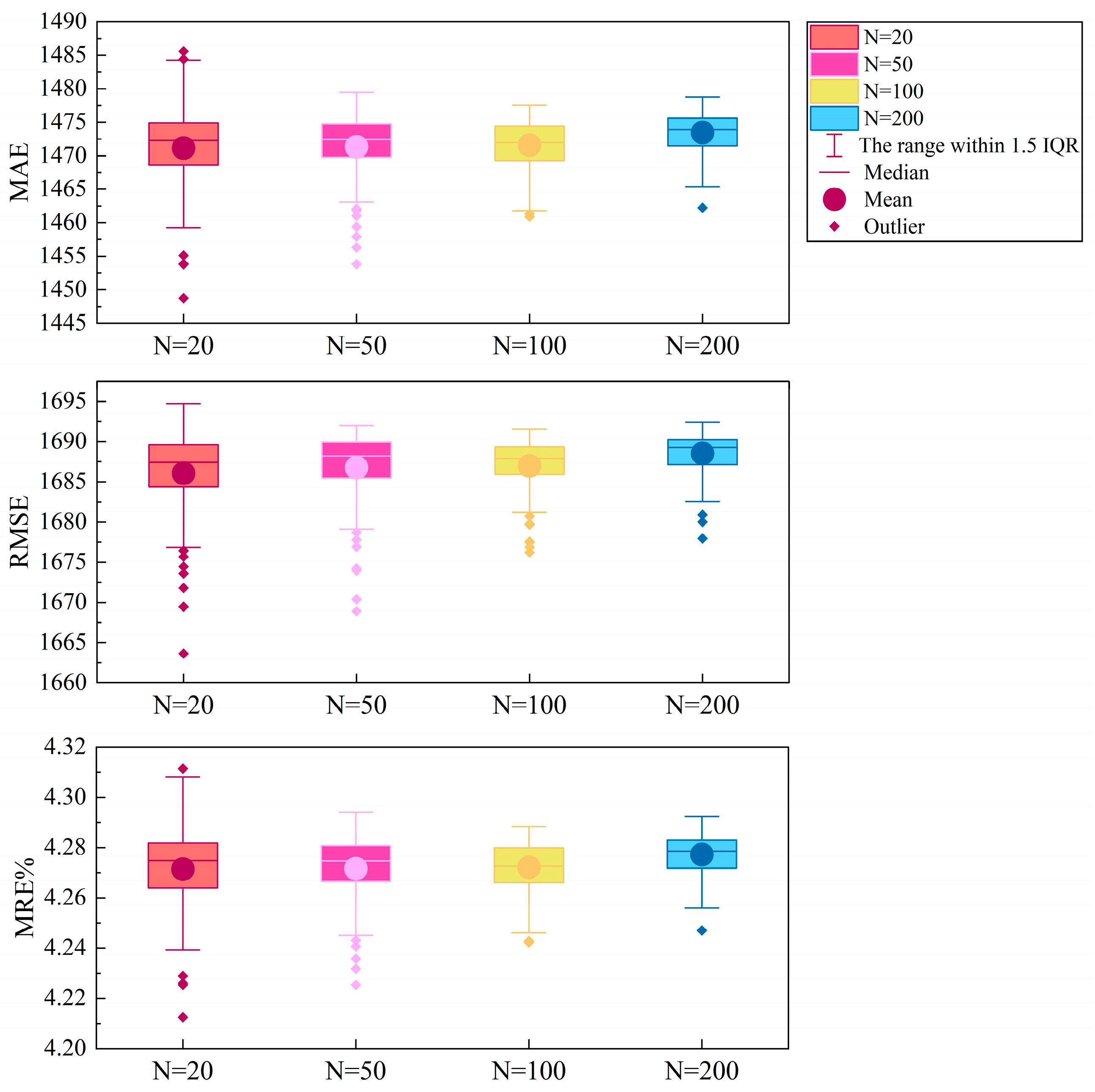
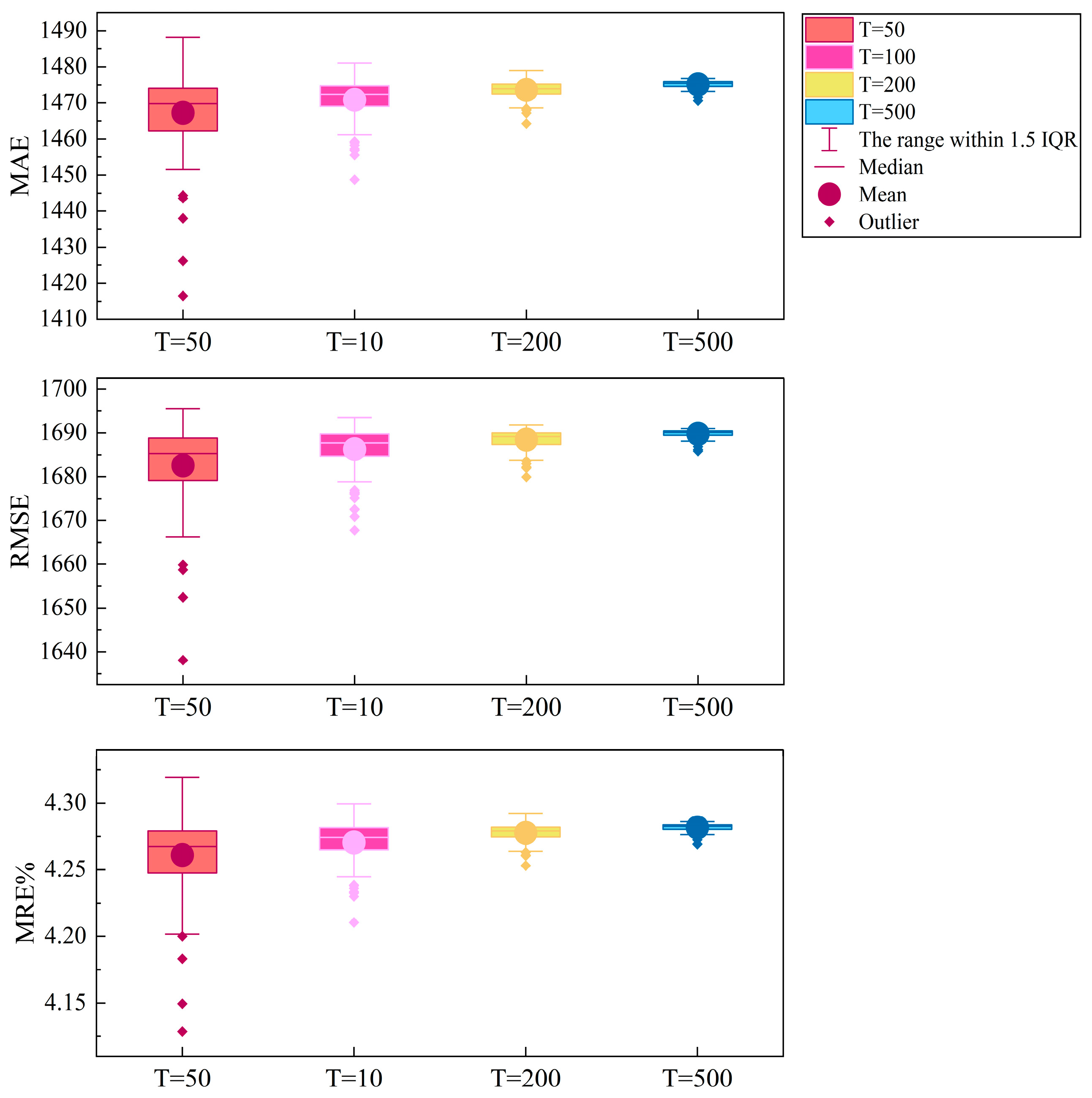
5.3. Parameter Sensitivity Analysis
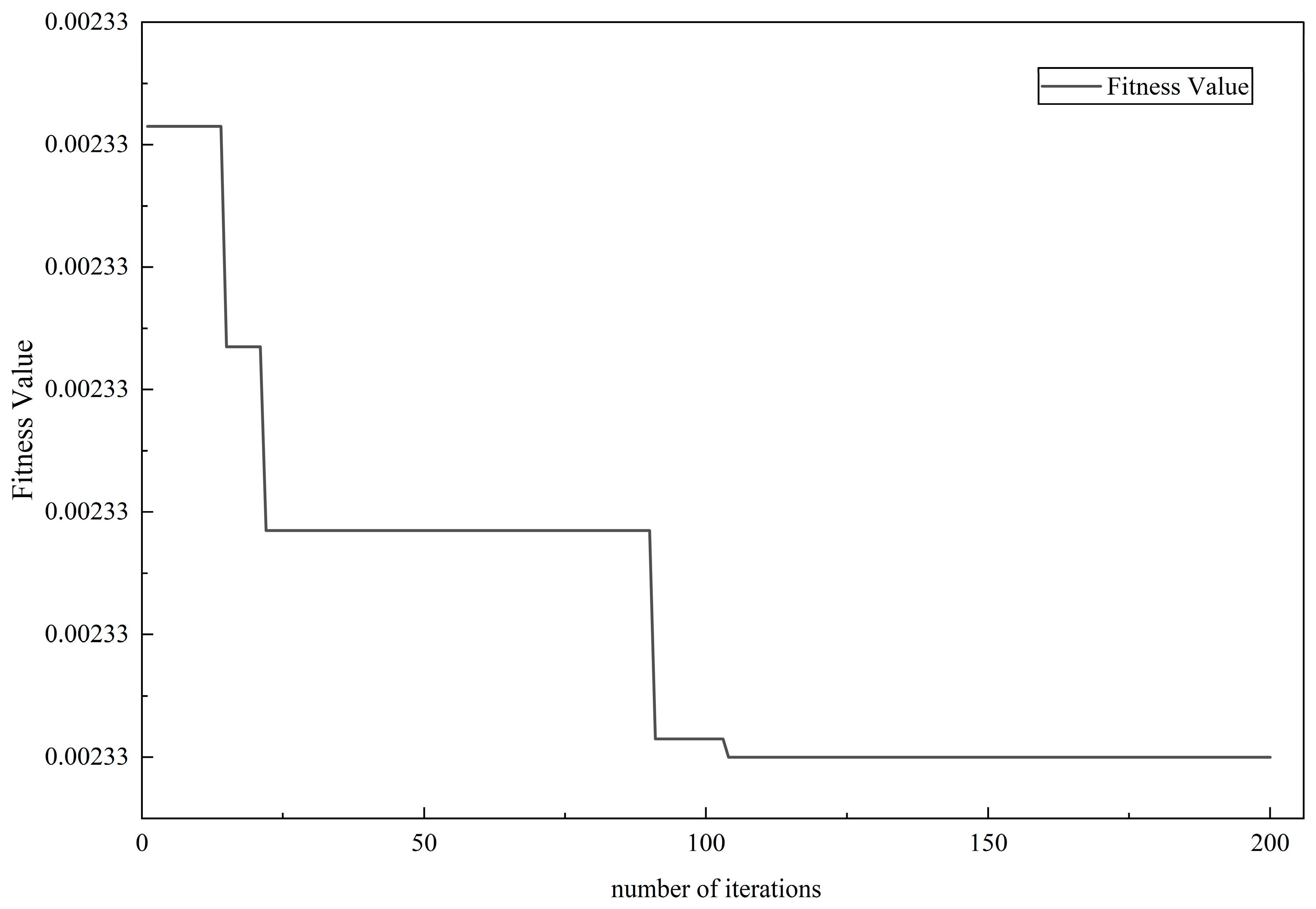
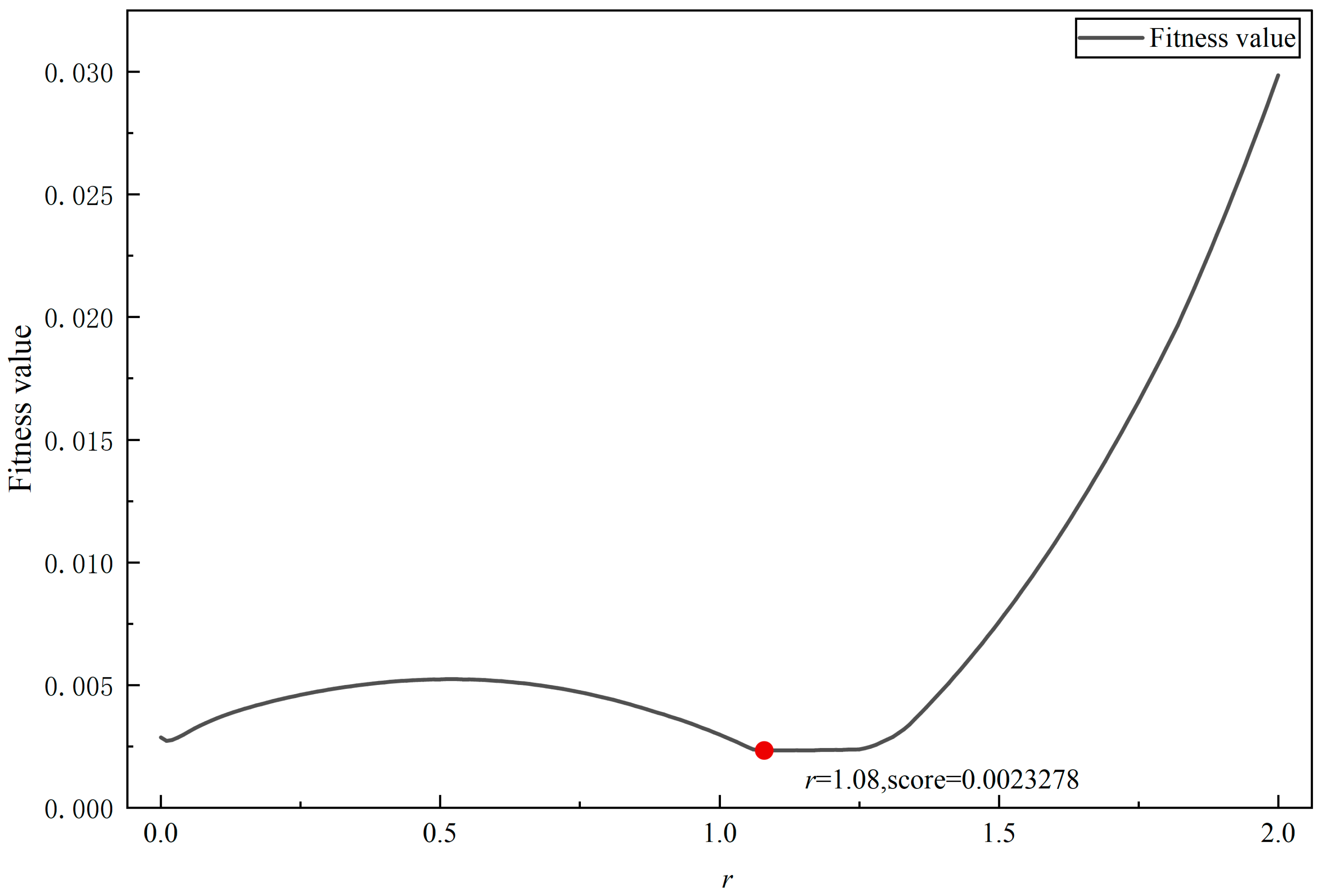
5.4. Optimal Order Determination via GCRA
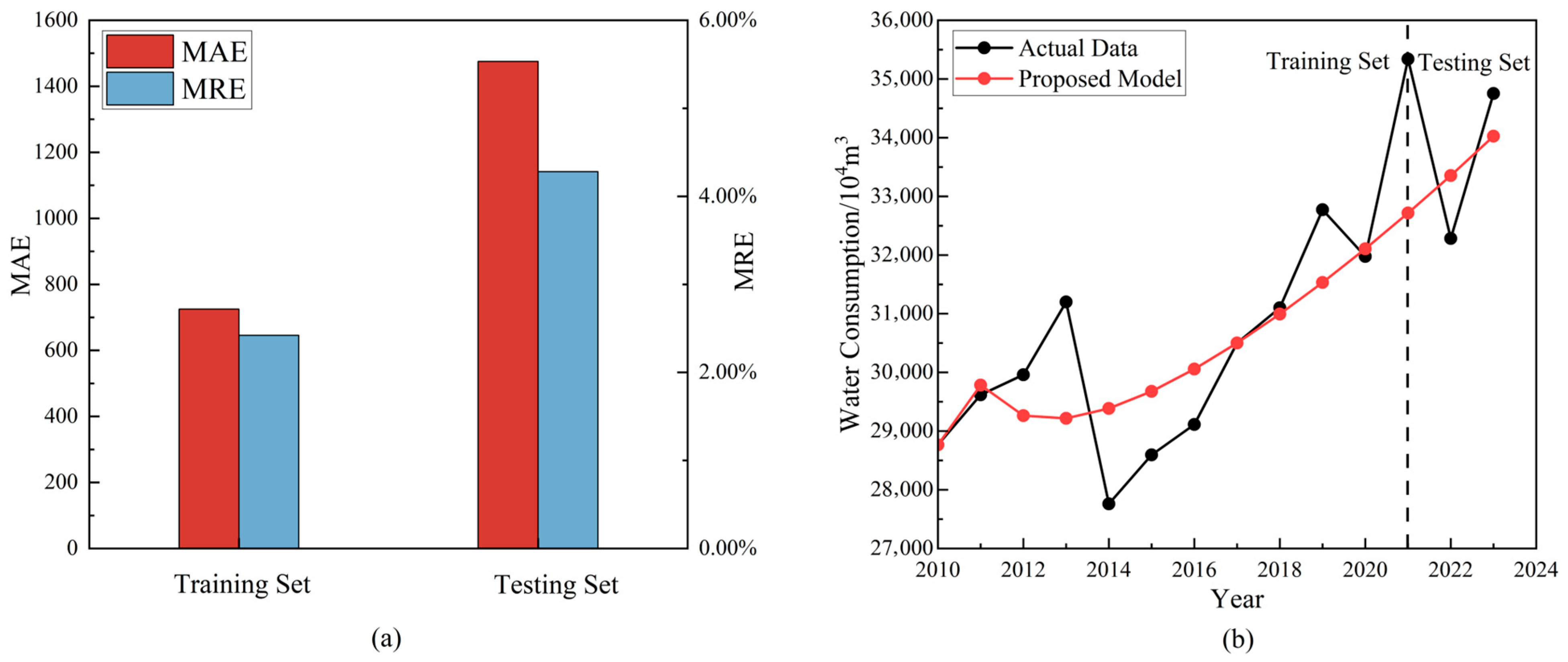
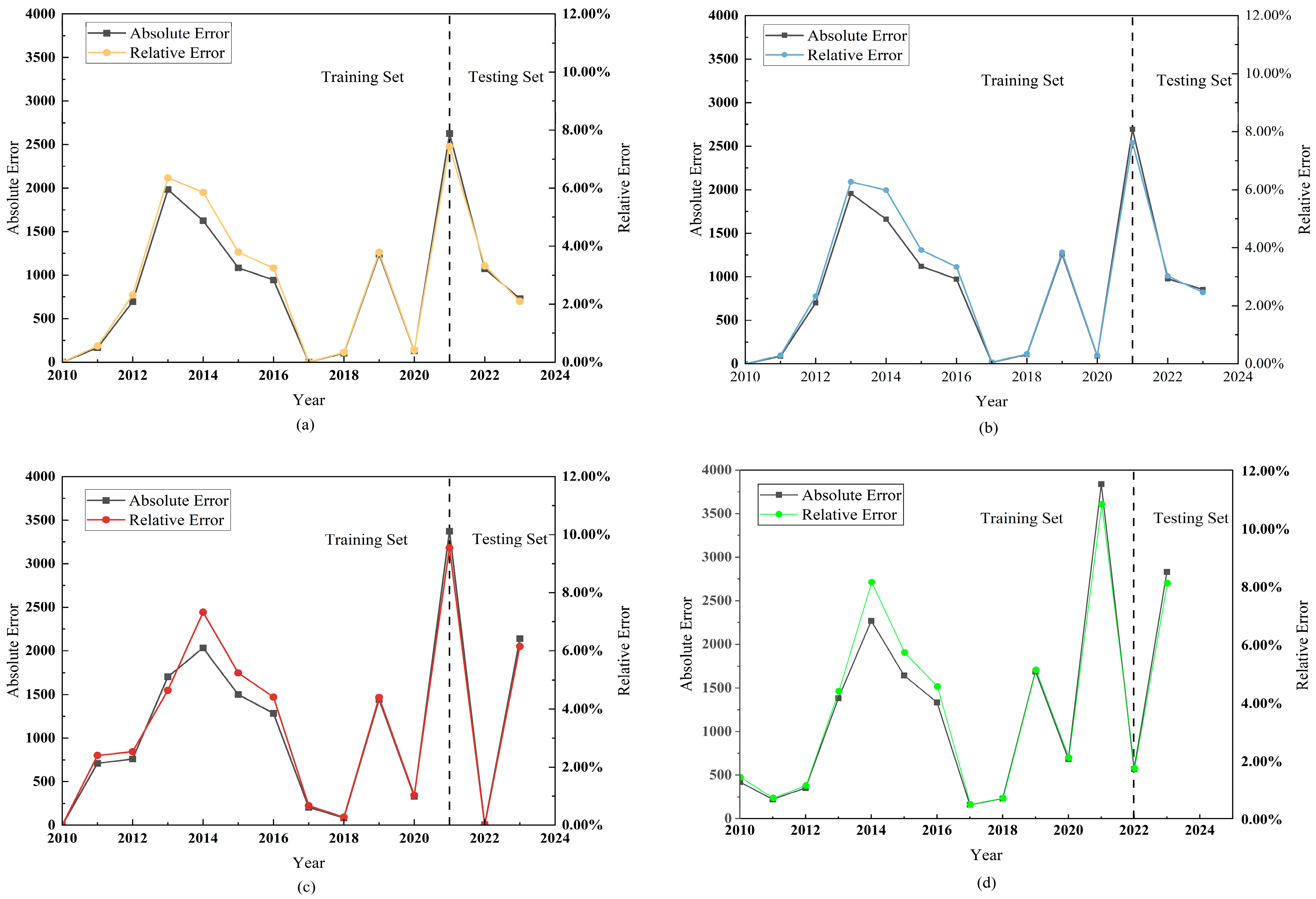
5.5. Analysis of Training and Testing Set Prediction Results
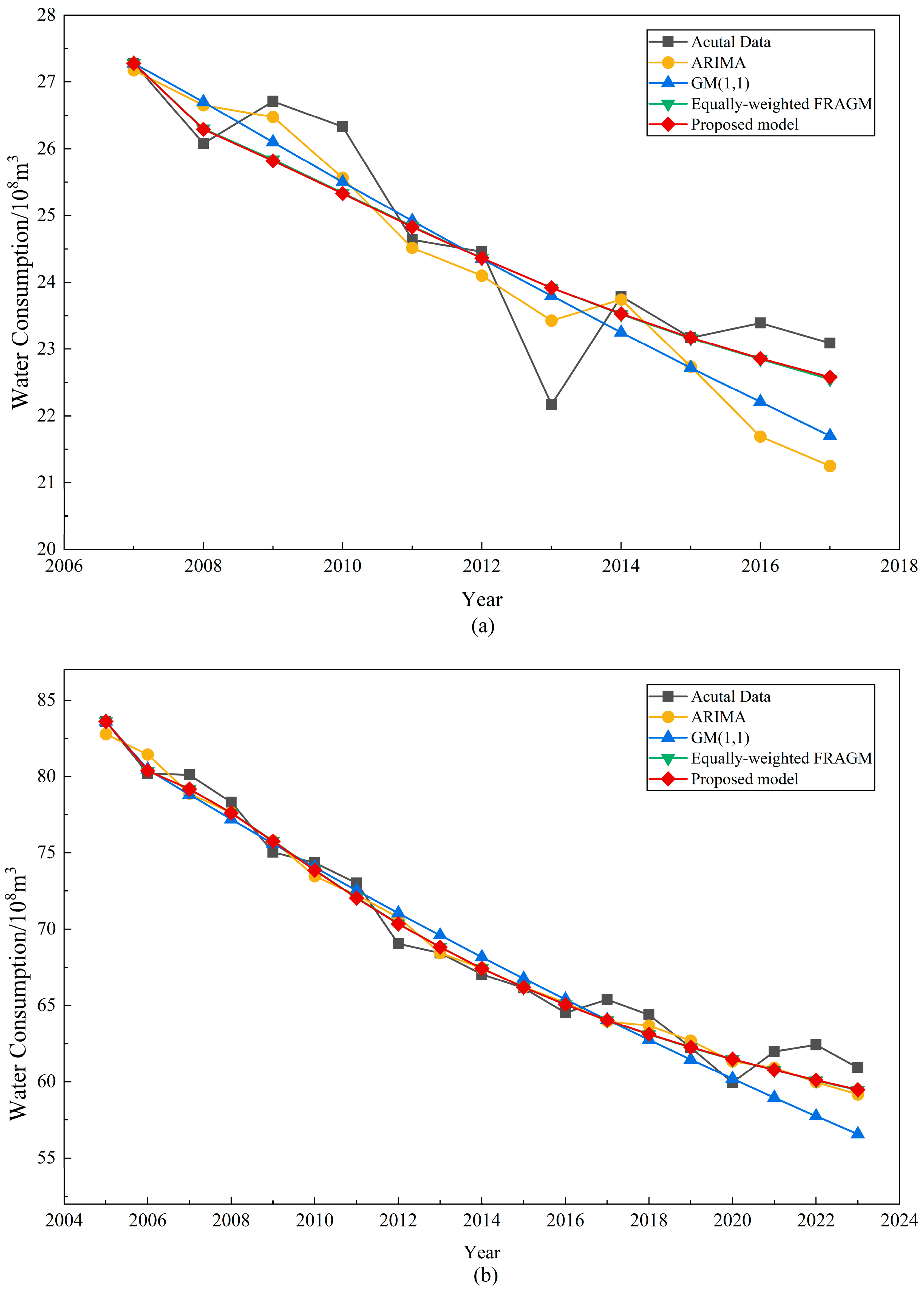
5.6. Model Comparison and Validation
5.7. External Validity Verification
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FRAGM | Fractional-order Reverse Accumulation Grey Model |
| GCRA | Greater Cane Rat Algorithm |
| PSO | Particle Swarm Optimization |
| DM | Diebold and Mariano |
References
- Bunn, S.M.; Reynolds, L. The energy-efficiency benefits of pump-scheduling optimization for potable water supplies. IBM J. Res. Dev. 2009, 53, 1–13. [Google Scholar] [CrossRef]
- Bakker, K. Neoliberal versus postneoliberal water: Geographies of privatization and resistance. Ann. Assoc. Am. Geogr. 2013, 103, 253–260. [Google Scholar] [CrossRef]
- Giacomello, C.; Kapelan, Z.; Nicolini, M. Fast hybrid optimization method for effective pump scheduling. J. Water Resour. Plan. Manag. 2013, 139, 175–183. [Google Scholar] [CrossRef]
- Qi, C.; Chang, N. System dynamics modeling for municipal water demand estimation in an urban region under uncertain economic impacts. J. Environ. Manag. 2011, 92, 1628–1641. [Google Scholar] [CrossRef]
- Reschenhofer, E. Modification of autoregressive fractionally integrated moving average models for the estimation of persistence. J. Appl. Stat. 2000, 27, 113–118. [Google Scholar] [CrossRef]
- Yang, P.; Wu, C.; Guo, Y.; Liu, H.; Huang, H.; Wang, H.; Zhan, S.; Tao, B.; Mu, Q.; Wang, Q. Parameter estimation in exponential models by linear and nonlinear fitting methods. Front. Inf. Technol. Electron. Eng. 2017, 18, 434–444. [Google Scholar] [CrossRef]
- Wu, H.; Zeng, B.; Zhou, M. Forecasting the water demand in Chongqing, China using a grey prediction model and recommendations for the sustainable development of urban water consumption. Int. J. Environ. Res. Public Health 2017, 14, 1386. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Lin, K.; Huang, L.; Yao, Z.; Bai, X.; Chen, Z. Assessing the vulnerability of water resources system using VSD-SD coupling model: A case of pearl river delta. Water 2022, 14, 1103. [Google Scholar] [CrossRef]
- Tetko, I.V.; Livingstone, D.J.; Luik, A.I. Neural network studies. 1. Comparison of overfitting and overtraining. J. Chem. Inf. Comput. Sci. 1995, 35, 826–833. [Google Scholar] [CrossRef]
- Spiridonakos, M.D.; Fassois, S.D. Non-stationary random vibration modelling and analysis via functional series time-dependent ARMA (FS-TARMA) models–A critical survey. Mech. Syst. Signal Process. 2014, 47, 175–224. [Google Scholar] [CrossRef]
- Huang, X.; Kang, S.; Wang, J. A preliminary study on predicting method for the demand of irrigation water resource. J. Irrig. Drain. 2004, 23, 13–15. [Google Scholar]
- Deng, J. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Yanju, L.; Yu, H.; Hua, B.; Genzhong, X.; Minghu, Z. Analysis on the Impact of Tourism Water Use in Cities of Hainan Province. Trop. Geogr. 2010, 30, 200–204. [Google Scholar]
- Li, J.; Song, S.; Kang, Y.; Wang, H.; Wang, X. Prediction of urban domestic water consumption considering uncertainty. J. Water Resour. Plan. Manag. 2021, 147, 05020028. [Google Scholar] [CrossRef]
- Mao, S.; Gao, M.; Xiao, X.; Zhu, M. A novel fractional grey system model and its application. Appl. Math. Model. 2016, 40, 5063–5076. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Yao, L.; Yan, S.; Liu, D. Grey system model with the fractional order accumulation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1775–1785. [Google Scholar] [CrossRef]
- Xiao, X.; Guo, H.; Mao, S. The modeling mechanism, extension and optimization of grey GM (1, 1) model. Appl. Math. Model. 2014, 38, 1896–1910. [Google Scholar] [CrossRef]
- Che, X.; Luo, Y.; He, Z. Grey new information GOM (1,1) model based on opposite-direction accumulated generating and its application. Appl. Mech. Mater. 2013, 364, 207–210. [Google Scholar]
- Liao, D.; Luo, Y. Grey new information GOM (1,1) model and its application based on opposite-direction accumulated generating and background value optimization. Adv. Mater. Res. 2011, 321, 33–36. [Google Scholar]
- Xiong, P.; Shi, J.; Pei, L.; Ding, S. A novel linear time-varying GM (1,N) model for forecasting haze: A case study of Beijing, China. Sustainability 2019, 11, 3832. [Google Scholar] [CrossRef]
- Zeng, L. Non-Equidistant GM (1,1) models based on fractional-order reverse accumulation and the application. Appl. Math. Mech. 2018, 39, 841–854. [Google Scholar]
- Wang, H.; Li, Y. A novel seasonal grey prediction model with fractional order accumulation for energy forecasting. Heliyon 2024, 10, e29960. [Google Scholar] [CrossRef]
- Xu, J.; Wu, W.; Liu, C.; Xie, W.; Zhang, T. An extensive conformable fractional grey model and its application. Chaos Solitons Fractals 2024, 182, 114746. [Google Scholar] [CrossRef]
- Zheng, J.; Huang, M.; Zhang, J. An innovative nonlinear grey system model with generalized fractional operators and its application. Alex. Eng. J. 2025, 125, 463–479. [Google Scholar] [CrossRef]
- Wu, W.; Xu, J.; Xie, W.; Zhang, T. An innovative fractional grey system model and its application. Math. Comput. Simul. 2025, 230, 68–79. [Google Scholar] [CrossRef]
- Huang, R.; Fu, X.; Pu, Y. A novel fractional accumulative grey model with GA-PSO optimizer and its application. Sensors 2023, 23, 636. [Google Scholar] [CrossRef] [PubMed]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L.; Abd Elaziz, M. Migration-based moth-flame optimization algorithm. Processes 2021, 9, 2276. [Google Scholar] [CrossRef]
- Salehizadeh, S.M.A.; Yadmellat, P.; Menhaj, M.B. Local optima avoidable particle swarm optimization. In Proceedings of the 2009 IEEE Swarm Intelligence Symposium, Nashville, TN, USA, 30 March–2 April 2009; pp. 16–21. [Google Scholar]
- Raß, A.; Schmitt, M.; Wanka, R. Explanation of stagnation at points that are not local optima in particle swarm optimization by potential analysis. In Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 11–15 July 2015; pp. 1463–1464. [Google Scholar]
- Zamani, H.; Nadimi-Shahraki, M.H.; Mirjalili, S.; Soleimanian Gharehchopogh, F.; Oliva, D. A critical review of moth-flame optimization algorithm and its variants: Structural reviewing, performance evaluation, and statistical analysis. Arch. Comput. Methods Eng. 2024, 31, 2177–2225. [Google Scholar] [CrossRef]
- Bala, I.; Karunarathne, W.; Mitchell, L. Optimizing Feature Selection by Enhancing Particle Swarm Optimization with Orthogonal Initialization and Crossover Operator. Comput. Mater. Contin. 2025, 84, 727–744. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E.; Saha, A.K.; Pal, J.; Abualigah, L.; Mirjalili, S. Greater cane rat algorithm (GCRA): A nature-inspired metaheuristic for optimization problems. Heliyon 2024, 10, e31629. [Google Scholar] [CrossRef]
- Li, J. A flood season division model considering uncertainty and new information priority. Water Resour. Manag. 2024, 38, 3755–3784. [Google Scholar] [CrossRef]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A novel algorithm for global optimization: Rat Swarm Optimizer. J. Ambient Intell. Humaniz. Comput. 2021, 12, 8457–8482. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Alan Roberson, J. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Zhou, J.; Li, H.; Zhong, W. A modified Diebold–Mariano test for equal forecast accuracy with clustered dependence. Econ. Lett. 2021, 207, 110029. [Google Scholar] [CrossRef]
- Geng, R.; Li, M.; Sun, M.; Wang, Y. Comparing methods of imputation for time series missing values. In IoT and Big Data Technologies for Health Care; Springer: Berlin/Heidelberg, Germany, 2021; pp. 333–340. [Google Scholar]
- Dhawan, D.; Singh, R. Performance Evaluation of Nature Inspired Meta-Heuristic Algorithms using Rosenbrock, Rastrigin and Sphere Test Function for Optimization. Int. J. Recent Technol. Eng. 2019, 8, 1157–1163. [Google Scholar]
- Huang, Y.; Li, J.; Wang, P. Unusual phenomenon of optimizing the Griewank function with the increase of dimension. Front. Inf. Technol. Electron. Eng. 2019, 20, 1344–1360. [Google Scholar] [CrossRef]
- Li, J.; Song, S. Urban water consumption prediction based on CPMBNIP. Water Resour. Manag. 2023, 37, 5189–5213. [Google Scholar] [CrossRef]

| MRE (%) | Prediction Accuracy |
|---|---|
| <5 | Outstanding |
| 5–15 | Acceptable |
| 15–50 | Moderate |
| >50 | Unsatisfactory |
| Test Function | Domain | Optimal Value |
|---|---|---|
| [−100, 100] | 0 | |
| [−100, 100] | 0 | |
| [−5.12, 5.12] | 0 | |
| [−600, 600] | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhang, B.; Li, J. Water Consumption Prediction Based on Improved Fractional-Order Reverse Accumulation Grey Prediction Model. Sustainability 2025, 17, 9417. https://doi.org/10.3390/su17219417
Zhu Y, Zhang B, Li J. Water Consumption Prediction Based on Improved Fractional-Order Reverse Accumulation Grey Prediction Model. Sustainability. 2025; 17(21):9417. https://doi.org/10.3390/su17219417
Chicago/Turabian StyleZhu, Yuntao, Binglin Zhang, and Jun Li. 2025. "Water Consumption Prediction Based on Improved Fractional-Order Reverse Accumulation Grey Prediction Model" Sustainability 17, no. 21: 9417. https://doi.org/10.3390/su17219417
APA StyleZhu, Y., Zhang, B., & Li, J. (2025). Water Consumption Prediction Based on Improved Fractional-Order Reverse Accumulation Grey Prediction Model. Sustainability, 17(21), 9417. https://doi.org/10.3390/su17219417






