Abstract
The transition to a circular economy has increased the significance of reusable plastic container (RPC) pooling systems in green logistics. These systems are third-party reliant; selecting an appropriate service provider becomes crucial, particularly when measured against Environmental, Social, and Governance (ESG) principles. This study proposes a novel decision-making paradigm that incorporates ESG considerations into the evaluation process of RPC pooling service providers through an SF-RANCOM-ARLON (Spherical Fuzzy Sets-Ranking Comparison-Alternative Ranking Using Two-Step Logarithmic Normalization) hybrid method. A real-world case study involving multiple RPC service providers is presented to ensure that the proposed framework is appropriate. It determined 13 sub-criteria under 4 essential headings in the direction of assessing. Not only does this approach provide decision-makers with a methodical and unbiased approach for selecting the leading RPC pooling service provider within an uncertain environment, but it also helps in determining the necessary criteria for RPC pooling service provider selection. Based on rankings, the most critical criteria for service provider selection are delivery reliability, service flexibility, and customer relationship management, while less emphasis is placed on information disclosure. This research contributes to the emerging discourse on ESG-integrated supplier selection and offers a decision-support tool adaptable for sustainability-oriented supply chain networks.
1. Introduction
With increasing environmental concerns, cost pressures, and supply chain complications, businesses are increasingly turning to reusable packaging solutions to achieve sustainability as well as efficiency. Of these, Reusable Plastic Containers (RPCs) are a strategic solution that addresses both the dual needs of reducing the environmental footprint as well as logistical performance. Unlike single-use packaging, RPCs are reusable, which offers long-term cost savings, standardized handling, and better protection of the contents, particularly in fresh produce, retail, and fast-moving consumer goods industries. Supply chain-wise, RPCs are instrumental in maximizing reverse logistics efficiency, space usage, and product tracing. As companies move to build stronger and more circular supply chains, the deployment of RPC systems becomes not just a cost-driven initiative, but a necessary enabler of sustainable supply chain planning.
The RPC pooling system is a holistic packaging management model that supports environmental, economic and operational sustainability in the supply chain. However, the success of this system is directly related to the effectiveness of the logistics infrastructure, user behavior, hygiene practices and compliance with legal regulations.
Moreover, pooling systems, which are considered within the framework of the sharing economy, enable the collective use of logistics infrastructure and support the development of a collaborative economic model [1]. The success of the RPC system depends not only on its technical performance but also on the selection of the appropriate service provider.
While the sharing economy contributes to sustainable development with more efficient use of resources, reduction in waste and access-oriented consumption models, the Environmental, Social, and Governance (ESG) framework strengthens the governance and social responsibility foundations of this transformation. Practices such as reducing environmental impacts (e.g., car sharing or shared office use), increasing community-based economic participation and transparent and accountable management of platforms are directly related to all dimensions of ESG. In addition, studies emphasize that the sharing economy brings with it governance issues such as ethical algorithm design, data privacy, labor rights and digital inclusion [2,3]. In this context, ESG criteria have become decisive, especially in supply chain processes. Reference [4] emphasized that traditional supplier evaluation criteria do not fully comply with ESG regulations and therefore a new evaluation system focused on ESG is needed.
The primary motivation of this study is to develop a robust decision support system for the selection of RPC pooling service providers, which is recognized as a complex multi- criteria decision-making (MCDM) problem. To address this challenge, a Multi-Attribute Group Decision Making (MAGDM) approach has been adopted, enabling the integration of expert opinions under uncertainty and the evaluation of multiple conflicting criteria simultaneously.
Accordingly, the SF (Spherical Fuzzy)–Yager–RANCOM (Ranking Comparison)–ARLON (Alternative Ranking Using Two-Step Logarithmic Normalization) hybrid method is proposed as a novel solution framework for the RPC pooling service provider selection problem. In this hybrid method, expert weights are determined using Spherical Fuzzy Sets (SF sets) [5], while criterion weights are calculated via the SF-RANCOM method [6], which incorporates an aggregation operator based on Yager t-norm and t-conorm operations to effectively process uncertain and imprecise data. The Yager t-norm and t-conorm, depending on their parameter, can behave more strictly, approaching the minimum value, or more tolerantly. Like min–max operators, they provide results with a higher degree of determinacy. Consequently, the Yager t-norm and t-conorm offer greater adaptability and contribute to standardization in the aggregation of information compared to other t-norm and t-conorm operators. The final ranking of alternatives is conducted using the SF-ARLON method [7], which ensures a reliable prioritization of service providers by integrating expert evaluations.
The applicability and reliability of the proposed SF-Yager-RANCOM-ARLON hybrid method are validated through a comprehensive case study. Additionally, the robustness of the method is supported by conducting three sensitivity analysis scenarios and comparative analyses with alternative methodologies. This ensures the consistency, stability, and practical utility of the proposed decision-making approach in real-world RPC pooling service provider selection contexts.
1.1. Aims of the Study
The primary objective of this study is to develop a robust and comprehensive decision support system for the selection of RPC pooling service providers under uncertainty. The specific aims of the research are as follows:
- To design and propose a novel hybrid decision-making method named SF-Yager-RANCOM-ARLON, which integrates spherical fuzzy sets, advanced aggregation operators, and ranking models.
- To employ linguistic variables and convert them into SF numbers to effectively handle vagueness and subjectivity in expert evaluations during the decision-making process.
- To utilize the SFYWA aggregation operator, which is based on Yager’s t-norm and t-conorm, for aggregating expert judgments and scoring alternatives more flexibly and accurately.
- To adapt and extend the RANCOM method to the spherical fuzzy environment (SF-RANCOM) for determining the weights of criteria based on expert evaluations using SF numbers.
- To apply the SF-ARLON method for ranking the RPC pooling service provider alternatives under uncertainty, leveraging the benefits of spherical fuzzy modeling in the alternative evaluation process.
- To implement the proposed hybrid method in a real-world case study involving eight experts, thirteen decision criteria, and five RPC pooling service providers, and to identify the most suitable service provider.
- To perform comprehensive sensitivity analysis through three different scenarios to evaluate the robustness of the proposed hybrid method against parameter changes and model variations.
- To compare the results of the proposed method with those obtained from established MCDM methods (e.g., ALWAS, AROMAN, ARTASI, MABAC, RAM, SAW, TOPSIS, WASPAS) to assess the consistency and reliability of the proposed approach.
- To offer theoretical contributions to the literature on fuzzy MCDM methodologies and practical recommendations for decision-makers in logistics and service provider selection contexts.
1.2. Contributions of the Study
This study provides significant theoretical and practical contributions to the field of decision-making under uncertainty, particularly in the context of RPC pooling service provider selection. The major contributions are outlined as follows:
- This study introduces a novel hybrid multi-criteria decision-making method, SF-Yager-RANCOM-ARLON, which integrates spherical fuzzy logic, advanced aggregation operators, and robust ranking methodologies. By extending the classical RANCOM and ARLON methods to a spherical fuzzy environment and employing the SFYWA operator, the model enhances the accuracy of linguistic assessments and strengthens the theoretical development of fuzzy MCDM approaches.
- A comprehensive case study with eight experts, thirteen decision criteria, and five RPC pooling service provider alternatives demonstrates the model’s applicability in real-world logistics. The results reveal Delivery Reliability as the most influential criterion, providing valuable managerial insights for logistics and supply chain decision-makers.
- The proposed model’s reliability is confirmed through sensitivity analyses and comparative evaluation against established MCDM methods (TOPSIS, SAW, MABAC, RAM, WASPAS, ALWAS, AROMAN, and ARTASI), showing its stability and generalizability under varying conditions.
2. Conceptual Framework and Literature Review
2.1. Sharing Economy
The sharing economy, an economic model based on temporary access rather than ownership of products, services, or assets among individuals and organizations [8], is grounded in the idea of utilizing underused or unused resources more efficiently and making them accessible to broader audiences through digital tools [9]. Unlike the traditional notion of ownership, the sharing economy promotes new consumption patterns that are access-based and community-oriented. As one can witness in the case of Airbnb and Uber, information and communication technologies enabled these models to scale and evolve into global platforms that move beyond local relations [10].
The sharing economy typically encompasses three basic components: a platform provider (e.g., Uber, Airbnb), a resource provider (a person or an organization), and a user (the person or the organization consuming the product or service) [11]. These structures operate not only in business to consumer contexts, but also increasingly in business to business (B2B) settings. B2B sharing economy models enable firms to optimize their resources by providing temporary access to assets they do not own. Particularly, the temporary sharing of physical resources such as infrastructure, production capacity, storage, or transportation offers significant cost advantages and contributes to environmental sustainability [12].
Closely linked to the concept of sustainability, the sharing economy helps reduce resource waste, minimize waste generation, and create new consumption habits that positively impact the environment [10,13]. However, the sharing economy may also lead to rebound effects, such as shortening product lifespans and increasing carbon emissions in transportation [14]. From a social perspective, the sharing economy enhances interaction among individuals while also introducing new forms of employment and income models. The gig economy (task-based work) and on-demand service models are concrete manifestations of this transformation [15,16].
In essence, the sharing economy has emerged as a new economic paradigm driven by digital transformation—one that prioritizes access over ownership, is flexible and user-centric, and considers environmental impacts. Nevertheless, it is critically important to evaluate this model comprehensively in terms of its social, economic, and ethical consequences, and to support it with sustainable policy frameworks [9,13,17].
2.2. ESG-Based Reusable Plastic Container Pooling
Reusable Plastic Container Pooling (RPC Pooling) is a sustainable and circular packaging system in which plastic containers used for the transportation and storage of goods are not owned by the user but by a service provider (pooler), and are repeatedly used within the logistics cycle by being rented to producers, distributors, and retailers, then collected, cleaned, and redistributed after a certain number of uses [18,19]. This system is distinctive in the food, automotive, and retail sectors through its capacity to reduce environmental footprints, enhance the efficiency of resource usage, and lower operational costs. Adhering to circular economy principles, it aims to reduce packaging waste and maximize the efficient utilization of resources [20,21].
According to life cycle analyses, RPC systems have a lower greenhouse gas emission, lower waste generation, and lower energy consumption compared to single-use cardboard or plastic packaging. RPCs also offer savings opportunities, courtesy of their strength, their reuse, and lower waste management costs. However, these environmental benefits can only be achieved after achieving a certain use level. For example, RPCs are environmentally friendly after around 15 uses [22,23,24].
Moreover, reverse logistics activities such as centralized washing, repair, and redistribution of the containers can significantly influence the overall environmental performance of the system [23,25]. In pooling models managed through centralized washing and return systems, reductions in carbon footprint of up to 83% have been observed [22]. In addition to their environmental benefits, RPC systems also involve food safety risks that must be carefully managed. Studies have shown that in the absence of adequate cleaning and sanitation, pathogens such as Salmonella and Listeria can survive on the surfaces of RPCs and cause cross-contamination [26]. Microorganisms tend to adhere to and from biofilms on food contact surfaces, with a higher propensity observed on plastic materials [27]. Therefore, RPC systems must be disinfected in compliance with national and international hygiene standards.
RPC systems involve complex structures in terms of reverse logistics infrastructure, washing capacity, and inventory management. This complexity necessitates coordinated information sharing and decision support systems among suppliers, retailers, and pool operators. Reference [22] has shown that uncertainties in RPC applications within the food sector—such as when and where empty containers will be collected—can significantly impact overall system costs. RPC systems provide not only economic and environmental but also social benefits. Ergonomic improvements in packaging operations enhance employee health and safety, while the more conscious use of resources and the prevention of waste contribute to promoting sustainability awareness across society [28].
The European Union and many other countries are promoting reusable packaging systems such as RPCs within the framework of regulations aimed at banning or reducing single-use plastic packaging. Reusable packaging is expected to become mandatory in the retail and ready-to-eat food sectors as part of the 2030 and 2040 sustainability targets [29]. In this context, RPC systems are considered a strategic solution not only for their environmental benefits but also for their alignment with regulatory expectations.
ESG became an evolving sustainability standard in sizes measuring the effects a firm has on the environment, social responsibilities, and company governance mechanisms. The concept was first introduced into the literature through the ‘Who Cares Wins’ report, supported by the United Nations Global Compact in 2004. This report advocated for the integration of environmental, social, and governance factors into investors’ decision-making processes [30,31].
The environmental dimension focuses on how companies consume natural resources, manage carbon emissions, reduce waste, and take measures against environmental risks. Reference [32] points out that ESG has a significant contribution towards environmental sustainability, particularly in green supply chain management. When integrated with technologies such as the Industrial Internet of Things (IIoT) and blockchain, ESG practices can enable the development of more transparent, traceable, and accountable supply chains.
The social dimension encompasses a company’s responsibilities toward its employees, customers, suppliers, and society. These involve such aspects as occupational health and safety, diversity, fair compensation, and community engagement. Reference [33] observes that the social component of ESG, when combined with circular economic principles, plays a significant role in transforming businesses into more long-term oriented, equitable, and resilient structures.
The governance dimension constitutes a multi-dimensional structure of corporate responsibility that goes beyond financial performance and shareholder relations. It encompasses elements such as transparency in operational processes, internal audit procedures, management of information technology, ethical practices in supply chains, and risk management. Current studies suggest that governance is also closely associated with financial sustainability, operational efficiency, effective use of resources, and transparency in strategic decision-making [34,35]. Furthermore, the adoption of good governance practices enhances investor confidence, not only, but also contributes positively to a firm’s market value, resistance to crises, and long-run sustainable growth opportunities [36]. ESG goes beyond traditional financial performance metrics by encompassing a company’s environmental impact (e.g., carbon foot-print, energy efficiency, and waste management), social responsibilities (e.g., labor rights, diversity and inclusion, and customer health and safety), and corporate governance structures (e.g., board independence, transparency, and anti-corruption practices) [37].
ESG principles are inherently consistent with the circular economy model, which promotes the reuse of resources, reduction in waste, and extension of product lifecycles. When ESG is integrated with circular economic strategies, it leads to a range of benefits—not only in terms of environmental impact, but also through improved social outcomes and stronger governance practices [33]. The strategic significance of ESG extends beyond investment decisions, having an impact on customer preferences and brand reputation too. A study conducted in the e-commerce sector revealed that consumers tend to favor companies with strong ESG awareness, and that implementing ESG practices within logistics operations can enhance a firm’s competitive edge [38].
In conclusion, ESG has evolved beyond being merely a reporting tool—it has become an integral part of corporate strategies for sustainable growth, stakeholder engagement, and social responsibility. Strong ESG performance enables companies to align financial returns with social accountability, making them more resilient and better positioned for long-term sustainability [39].
2.3. Literature Review on MCDM
This study introduces a novel solution framework for the selection of RPC pooling service providers by employing a hybrid approach that integrates the SF (Spherical Fuzzy), Yager, RANCOM (Ranking Comparison), and ARLON (Alternative Ranking Using Two-Step Logarithmic Normalization) methods.
The Spherical Fuzzy Set (SFS) theory represents a refined extension of traditional fuzzy set models, designed to express expert opinions under uncertainty, contradiction, and hesitation within a three-dimensional structure. Unlike classical fuzzy sets, which define uncertainty solely through a membership degree, the SFS model introduces a more comprehensive representation by incorporating membership, non-membership, and hesitancy degrees, all constrained within a unit sphere [5]. This geometric constraint enables a richer and more balanced expression of uncertainty, making it particularly suitable for multi-criteria decision-making (MCDM) scenarios where both individual and group perspectives must be accounted for. Studies in the literature demonstrate that methods developed under the SFS framework—such as extensions of AHP, TOPSIS, VIKOR, and ELECTRE—offer a robust approach to managing ambiguity in the evaluation of decision criteria [40,41]. These integrations provide a more nuanced interpretation of expert judgments and contribute to the generation of more consistent and reliable decision outcomes in complex environments.
RANCOM (Ranking Comparison) is a contemporary subjective weighting approach tailored for multi-criteria decision-making processes, where the importance of criteria is derived solely from the order assigned by experts. Unlike conventional techniques that often require pairwise comparisons or complex evaluations, RANCOM simplifies the task by demanding only a ranked list of criteria, thus reducing cognitive load and increasing tolerance to expert inconsistencies. This streamlined structure makes it particularly effective in scenarios with numerous evaluation factors, offering more stable and reproducible outcomes than traditional models such as AHP [6]. The method has been applied successfully across various domains including blockchain platform evaluation [42], user-centered product selection [43], and sustainable development assessments in agri-food logistics [44].
ARLON (Alternative Ranking using Two-Step Logarithmic Normalization) is a new alternative ranking method used in multi-criteria decision-making (MCDM) issues, originally developed within the field of logistics performance measurement [7]. ARLON was later extended to uncertain decision-making problems, such as sustainable brand equity measurement, using the T2NN-ARLON (Type-2 Neutrosophic Numbers) version [45]. In graphical alternative decision-making systems, such as AI-assisted logo selection, it was used with the PF-ARLON (Picture Fuzzy) version [46]. In more specialized domains such as human resources management, namely for authentication system selection, IF-ARLON (Intuitionistic Fuzzy) was applied to prioritize alternatives based on expert opinions, with weights of criteria determined with the IF-CIMAS approach [47]. Most significantly, in the case of transport policy decision-making for Russia’s Northern Sea Route (NSR), the IF-SIWEC-ARLON model was suggested, where weights of criteria were calculated by a simplified variance-based method (SIWEC) and alternatives were ranked by IF-ARLON. This was the foundation for developing a robust decision support system that can consider geographic, environmental, and geopolitical factors simultaneously [48]. These diverse applications of ARLON sufficiently demonstrate its flexibility, capacity to handle uncertainty, and adaptability to support decision-making across various sectors.
3. Methodology Framework
In this study, the SF-Yager-RANCOM-ARLON hybrid method is proposed for the selection of RPC pooling service providers. This hybrid method consists of three stages, each of which includes several sub-steps. In Stage-1, the weights of the experts are determined using SF sets. These sets are essential for capturing the linguistic preferences of the experts. In Stage-2, the criterion weights are calculated using the SF-RANCOM method, which incorporates spherical fuzzy logic to handle uncertainties in the decision-making process. In Stage-3, the alternative rankings are established using the SF-ARLON method, which facilitates the ranking of alternatives based on expert assessments and fuzzy criteria.
Figure 1 presents the overall structure of the SF-Yager-RANCOM-ARLON hybrid method, illustrating the various stages and sub-steps involved. The first step is the application of SF sets, followed by the integration of Yager t-norm and t-conorm operators to handle fuzzy operations effectively. The aggregation process is then carried out using the SFYWA aggregation operator, ensuring that the results are robust and reliable. The final rankings of the service providers are determined through the SF-Yager-RANCOM-ARLON hybrid method, which integrates all the previous steps into a coherent decision-making framework.
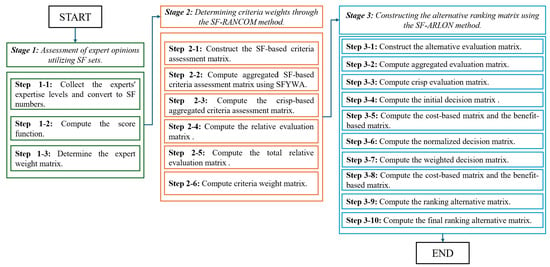
Figure 1.
The SF-Yager-RANCOM-ARLON hybrid method.
This method provides a systematic and comprehensive approach to the RPC pooling service provider selection problem by combining the strengths of spherical fuzzy logic, the RANCOM method for criterion weight determination, and the ARLON method for alternative ranking. The proposed hybrid method is designed to handle complex decision-making scenarios, incorporating expert knowledge and addressing uncertainty in a structured manner. The next section delves into the detailed implementation steps and the application of this hybrid method in the context of RPC pooling service provider selection.
3.1. Preliminaries of Spherical Fuzzy Sets with Yager t-Norm and t-Conorm
Definition 1.
Reference [5] have provided a detailed explanation of a concise representation of SF sets, referred to as , applied within a substantial domain , as follows: wherein for every element within the domain . , and indicate the degree of the membership, the degree of the non-membership and degree of the indeterminacy, respectively. In addition, each function can provide this constraint: . In SF sets, SF numbers represent as follows: .
Definition 2.
Consider a SF set as within the universal set G, the score function is computed using Equation (1) for obtaining crisp values [49]:
Definition 3.
Consider two SF sets as and , within the universal set . For calculation of the score functions for , interrelationships between score functions can be characterized following the structure outlined in the proposed framework by [49]
| (i) | If > , then , |
| (ii) | If < , then , |
| (iii) | If = , then . |
Definition 4.
The Yager t-norm and t-conorm, identified by Equation (2) and Equation (3), respectively [50], are as follows:
Wherein, and refer the t-norm and t-conorm, respectively. Also, .
Definition 5.
Consider two SF numbers defined within the universal set : and . The interaction principles between two SF numbers, based on the Yager t-norm and t-conorm, are specified as follows [51]:
| (i) | , |
| (ii) | , |
| (iii) | |
| (iv) |
Definition 5 must be expected to provide the following set of requirements [51]:
| (i) | |
| (ii) | |
| (iii) | |
| (iv) | |
| (v) | |
| (vi) |
Definition 6.
Consider a collection of SF numbers defined within the universal set
: . The SF-Yager Weighted Arithmetic Mean (SFYWA) aggregation operator is calculated using Equation (4) as introduced by [51].
In this context, the indicates the weight vector relation with , characterized by and . The proof was performed by [51].
3.2. The SF-Yager-RANCOM-ARLON Hybrid Method
In this study, a hybrid method named SF-Yager-RANCOM-ARLON is proposed to address the RPC pooling service providers selection problem. In this hybrid approach, SF set operations are conducted based on Yager operations. The SF-RANCOM method is employed for criteria weighting, while the SF-ARLON method is used for ranking the RPC pooling service providers. Experts’ evaluations based on linguistic variables are aggregated using the SFYWA aggregation operator. The inputs of the hybrid method are defined as the expert group , the set of criteria , and the set of alternatives representing the RPC pooling service providers. The definitions of the notations are provided in the Notation Section. The steps of the SF-Yager-RANCOM-ARLON hybrid method are as follows:
Stage 1: Assessment of expert opinions utilizing SF sets [5].
Step 1-1: The experts are characterized in accordance with their levels of experience, which are evaluated through a set of predefined linguistic variables as outlined in Table 1, allowing for a qualitative representation of expertise within the decision-making framework. Following this, an expert definition matrix is developed by utilizing the SF numbers corresponding to the linguistic variables presented in Table 1, thereby enabling a structured and quantifiable representation of the experts’ experience matrix within the evaluation process.

Table 1.
Linguistic variables [52].
Step 1-2: Defuzzification is carried out using the score function defined in Equation (5), resulting in the computation of a crisp-valued expert experience matrix .
Step 1-3: The weights of the experts are derived from the crisp-valued expert experience matrix, reflecting the experience of the experts. Thus, the expert weight matrix , representing the individual importance of each expert, is obtained through the application of Equation (6).
Herein, the expert weight matrix can be shown , wherein each and .
Stage 2: Determining criteria weights through the SF-RANCOM method [6].
Step 2-1: The evaluation of the criteria is carried out by the experts using linguistic variables defined in Table 2, resulting in the formation of a criteria evaluation matrix composed of linguistic expressions. These linguistic assessments are then systematically transformed into their corresponding SF numbers, as specified in Table 2, thereby producing an SF-based criteria assessment matrix that quantitatively captures the subjective evaluations within the framework of fuzzy logic .

Table 2.
Linguistic variables [53].
Step 2-2: The expert evaluations contained within the SF-based criteria assessment matrix, constructed from individual expert judgments, are aggregated through the application of the SFYWA aggregation operator, which effectively synthesizes the diverse expert inputs while considering their associated weights. Subsequently, the aggregated SF-based criteria assessment matrix is computed by employing Equation (7), yielding a consolidated representation of the experts’ evaluations within the spherical fuzzy framework.
Herein, the expert weight matrix can be shown , wherein each and and .
Step 2-3: Defuzzification is conducted using the score function defined in Equation (8), which transforms the aggregated SF numbers into crisp values. As a result, the crisp-based aggregated criteria assessment matrix is obtained, providing a precise and interpretable format for further analysis. This matrix serves as the foundation for evaluating the criteria through the scoring procedure employed in the RANCOM method, while still retaining the advantages of the SF sets framework throughout the decision-making process.
Step 2-4: Once the criteria evaluation matrix is established in accordance with the RANCOM method, a comparative assessment among the criteria is conducted to determine their relative significance. This process involves the construction of the relative evaluation matrix , which is formulated by applying Equation (9), thereby enabling the systematic analysis of the interrelationships and relative importance of the criteria within the decision-making framework.
Step 2-5: The relative superiority values of the criteria are aggregated to capture their overall dominance within the evaluation context. Subsequently, the total relative evaluation matrix is derived by implementing Equation (10), providing a comprehensive representation of the cumulative relative importance of each criterion as part of the RANCOM-based analysis.
Step 2-6: The weights of the criteria are derived from the relative evaluation matrix, which encapsulates the aggregated relative superiority of each criterion. Accordingly, the criteria weight matrix , representing the perceived importance of each criterion from a qualitative standpoint, is calculated by applying Equation (11), thereby enabling a structured integration of expert judgment into the decision-making process.
Wherein, the criteria weight matrix is defined, where each , within the constraint as .
Stage 3: Constructing the alternative ranking matrix using the SF-ARLON method [7].
Step 3-1: Experts are engaged to evaluate the companies with respect to the defined criteria. Each expert assesses every alternative by referencing the criteria outlined in the decision model, employing the linguistic variables provided in Table 2. These linguistic evaluations are then translated into their corresponding SF Numbers, leading to the formation of the alternative evaluation matrix based on criteria
Step 3-2: The expert evaluations contained within the qualitative criteria-based alternative evaluation matrix—developed from individual expert assessments—are aggregated using the SFYWA aggregation operator, which accounts for the varying importance and reliability of expert opinions. As a result, the aggregated criteria-based alternative evaluation matrix is computed by applying Equation (12), providing a consolidated and balanced representation of expert judgments within the spherical fuzzy framework.
Herein, the expert weight matrix can be shown , wherein each and and .
Step 3-3: Defuzzification is carried out using the score function defined in Equation (13), which converts the aggregated spherical huzzy evaluations into crisp numerical values. Consequently, the crisp-based aggregated criteria-based alternative evaluation matrix is obtained, enabling a clear and quantifiable interpretation of the expert assessments for further analysis.
Step 3-4: The initial decision matrix generated in Step 3-3 is simultaneously designated as the foundational decision matrix for the alternative ranking process. Within the ARLON method framework, this initial decision matrix is computed by applying Equation (14). Moreover, the matrix serves to represent the performance values of the alternatives with respect to the established criteria, providing the basis for subsequent ranking analysis
Step 3-5: In this phase, two distinct logarithmic normalization procedures are applied to the initial decision matrix. The first normalized decision matrix is derived by implementing Equation (15), whereas the second normalized decision matrix is obtained through the application of Equation (16). These normalization steps are essential for standardizing the data prior to the computation of alternative rankings within the ARLON method framework.
Step 3-6: The aggregated normalized decision matrix is computed using the Heron Mean, as defined in Equation (17). This aggregation method enables the integration of the two previously normalized decision matrices, ensuring a balanced and representative synthesis of the normalized values for use in the subsequent ranking process.
Herein, indicates the tradeoff ratio for normalization process.
Step 3-7: The weighted aggregated normalized decision matrix is obtained by multiplying the aggregated normalized decision matrix by the criteria weights, as outlined in Equation (18). This step incorporates the relative importance of each criterion, adjusting the aggregated values to reflect their weighted significance in the decision-making process.
Herein, the criteria weight matrix is defined, where each , within the constraint as .
Step 3-8: The cost-based matrix is computed using Equation (19), while the benefit-based matrix is derived through the application of Equation (20). These matrices are calculated separately to distinguish between cost and benefit criteria, ensuring that each type of criterion is appropriately handled in the decision-making process.
Step 3-9: The ranking alternative matrix for the RPC pooling service providers selection problem is determined by applying Equation (21). This matrix provides the final ranking of the alternatives, based on the previously calculated weighted and normalized decision matrices, facilitating a structured comparison of the service providers.
Here, the variable represents the ratio of benefit-based matrix. It is calculated by determining the proportion of benefit criteria relative to the total number of criteria, offering a quantitative measure that reflects the share of criteria categorized as benefits within the entire set of criteria under consideration in the analysis.
Step 3-10: The final ranking alternative matrix for the RPC pooling service providers selection problem is derived by applying Equation (22). This matrix presents the conclusive ranking of the alternatives, integrating all previous evaluations and calculations to provide a comprehensive assessment of the service providers.
The algorithm for the SF-Yager-RANCOM-ARLON hybrid method is outlined in Algorithm 1. This algorithm provides a detailed step-by-step description of the methodology, offering a clear framework for implementing the hybrid approach in the context of decision-making and evaluation.
| Algorithm 1 The Objective of This Algorithm is to Present the SF-Yager-RANCOM-ARLON Hybrid Method for the Evaluation of the RPC Pooling Service Providers |
| Input: A set of alternatives , a set of criteria , a set of experts . Output: The expert weight matrix , the criteria weight matrix , the final ranking alternative matrix . Steps: Stage 1: Assessment of expert opinions utilizing SF sets;
|
4. Real-World Case Study
There are 13 criteria under 4 main headings that are determined to be effective in RPC pooling supplier selection and can be evaluated in terms of customer perspective and loyalty. An in-depth literature review was applied, and sectoral experiences were taken into consideration while determining the criteria.
4.1. Decision Model
4.1.1. Expert Group
Based on the scope and objectives of this study, a group of eight experts working in the retail industry was found to aid the assessment process. These experts were chosen due to their extensive experience and familiarity with logistics operations, supplier relationships, and sustainability practices within the sector. Their work assisted in identifying and prioritizing the key service provider choice criteria and alternative evaluation, particularly within the realms of ESG aspects of RPC systems.
4.1.2. Criteria
In this study the definition of the criteria for the ESG based RPC pooling service provider selection is based on several environmental, social, governance and operational factors. The criteria are individually explained as follows (Figure 2).

Figure 2.
The decision model.
Environmental Awareness : Environmental awareness has been a consistently increasing decisive factor of sustainable supplier selection, especially in complex MCDM frameworks. As [54] point out, the expansion of environmental awareness and demands for eco-friendly operations have led manufacturers to prioritize greener supply chains, with awareness being incorporated into supplier evaluation in the face of incomplete data settings. Furthermore, reference [55] writes that the incorporation of environmental concern in supplier selection is not simply a response to regulatory or social pressure but an integral part of the triple bottom line approach that improves long-term competitiveness. To this purpose, reference [56] demonstrate empirically that firms driven by relational and moral motives for sustainability—such as genuine environmental concern—outperform those driven solely by economic gain, concluding that awareness is not merely moral but strategically advantageous. Finally, reference [57] determines that environmental awareness, when expressed in tangible areas like supplier transparency and proactive behavior, significantly enhances resilience and environmental sustainability in supply chain networks.
Waste Management and Recycling : Effective waste management and recycling are increasingly being viewed as essential parameters in green supplier selection models. Reference [58] points out that sustainable supplier selection requires the integration of multiple environmental indicators between which waste recovery, eco-design, and recycling readiness are always ranked by experts as essential sub-criteria. Reference [59] further corroborates this perspective in a meta-review of 1098 studies, observing that waste and recycling-related measures are among the most operationalized elements in MCDM-based green supplier selection models. In agreement, reference [60] demonstrate how combined MCDM models such as BWM-TOPSIS can successfully represent qualitative and quantitative dimensions of recycling efficiency, especially for industries with high waste generation potential such as oil and gas. This concurrent evidence points towards the fact that the ability of the suppliers to minimize material wastage and attain closed-loop recycling processes is not just a sign of environmental awareness but also an applied necessity of green logistic models.
Occupational Health and Safety : Occupational health and safety is among the prominent features of the social pillar of sustainable supply chain management. Provision of healthy and safe work conditions is not only a legal requirement but also a sign of an organization’s ethical commitment and social sustainability. As argued by [61], safeguarding employees’ well-being is increasingly considered a critical factor in supplier selection as buyers seek to achieve procurement behaviors aligned with extended social responsibility ambitions. As highlighted by [62], implementing formal health and safety initiatives in suppliers’ operations plays a crucial role in enhancing workplace motivation, decreasing accidents, and thereby, supply chain resilience. Similarly, reference [63] identifies occupational health and safety as a social performance metric, emphasizing workers’ safety playing a role in the supplier’s reputation and ensuring long-term cooperation in sustainable sourcing practices. Together, these studies emphasize that occupational health and safety is more than a compliance issue but a strategic consideration in responsible supplier selection, especially in labor-intensive and risk-prone industries.
Employee Training and Development : This plays a great role in promoting social sustainability in supply chain systems, in general, by empowering them with capabilities to improve operational safety, workforce skills, and environmental practices. As argued by [64], strategic training provision to suppliers related to chains enhances an employee’s capabilities directly, while corresponding organizational advantages are enjoyed by promoting green supply chain best practices and improving common processes between different departments. Similarly, reference [65] also stresses that worker capacity building and knowledge sharing are crucial to achieve well-balanced sustainability performance in each of the three dimensions—economic, environmental, and social. In addition, reference [66] acknowledges “employment practices,” i.e., training and career development, as top-ranked social sustainability parameters in manufacturing supply chains, especially in the context of emerging economies where employment standards remain inconsistent. Second, reference [67] recognizes employee empowerment and lifelong learning as supply chain management strategic enablers important to boosting overall organizational performance and stakeholder satisfaction. Overall, these findings demonstrate that employee development is not merely an internal human resource process but a socially responsible investment ensuring supplier credibility, responsiveness, and alignment of sustainability goals.
The Interests and Rights of Employees : Protecting the interests and rights of employees is a cornerstone of social sustainability in supply chain management. This dimension consists of equitable compensation, non-discrimination, freedom of association for collective bargaining, and safeguard against exploitation or danger at work. Reference [68] observes that socially responsible supplier choice in circular supply chains not only suggests environmental responsibility but also labor practices being ethical and workers’ rights being maintained. Reference [69] also emphasizes that respect for employees’ interests, for instance, job security, dignity in the workplace, and representation, significantly affects a supplier’s overall performance in terms of sustainability via trust and cooperation in the long run with buyers. Further, reference [70] argues that criteria related to employees are typically underemphasized in traditional models but must take center stage in circular and resilient procurement models in view of the evolving global labor landscape post-COVID-19. To this end, giving regard to employee interests not only meets ethical procurement standards but also enhances organizational resilience and stakeholder trust along the supply chain.
Traceability and IT Systems : Traceability and integrated IT systems have become pillar components in achieving transparency, accountability, and responsiveness in sustainable supply chains. Development along Industry 4.0 and Industry 5.0 paradigms of digital technologies implies traceability mechanisms increasingly serve not only operational efficiency but also social responsibility functions. Reference [71] points out that the blockchain, IoT, and big data technologies significantly improve supply chain traceability and visibility, where stakeholders can track materials, verify ethical practices, and guarantee compliance across all tiers. Similarly, reference [72] sheds light on the fact that traceability systems designed with RFID, smart sensors, and real-time monitoring devices not only prevent product loss but also assist with better decision-making and less environmental impact by offering insightful information about product flows and quality parameters. These findings collectively indicate that traceability systems supported by IT infrastructure are no longer optional tools but business-critical facilitators of resilience, ethical sourcing, and sustainability for modern supply chains.
Information Disclosure : Disclosure of information is one of the most important pillars of accountability and transparency in sustainable supply chain management. It refers to the extent to which suppliers release pertinent ESG information on an obligatory or voluntary basis, e.g., labor practices, sourcing standards, and emissions data. Reference [63] points out that in circular supply chains, openness of data sharing and public reporting of sustainability data are the catalysts to generate stakeholder confidence and improve the decision-making processes. Reference [70] further argues that disclosure of information is a significant social requirement that is aligned with new digital instruments and supervisory pressures, enabling companies to assess not just the performance of suppliers but also their resilience and conformity with circular economic goals. In parallel, reference [68] highlights that in closed-loop systems, data openness directly facilitates traceability, risk management, and collaboration between supply chain stakeholders, thereby facilitating environmental and social impact optimization. As global supply chains become more complex and digitalized, strategic importance grows with information disclosure, promoting responsible sourcing and facilitating alignment with global sustainability frameworks.
Compliance and Regulatory Adherence : Compliance and regulatory adherence are pillars of sustainable supply chain management, which guarantee that the suppliers operate within the boundaries of legal and environmental standards. Companies are increasingly being called to adopt procurement practices that comply with international regulations as well as country-specific environmental regulations. Reference [73] points out that not only is regulatory adherence a legal safeguard, but it is also a strategic necessity, particularly in green supplier selection where compliance with evolving environmental standards is what earns long-term partnerships. Reference [74] also explains that firms must incorporate mechanisms of legal oversight within green supply chain systems to proactively address risks such as environmental violations, defects in data transparency, and loopholes of social responsibility. Reference [75] also argues that regulatory adherence, including compliance with labor rights, pollution control, and product safety standards, is a key sustainable supplier differentiator, reflecting the ethical dimension of supply chain business as well as economic and environmental factors. Overall, they highlight that complying with regulations goes beyond the issue of avoiding a fine and has a significant relationship with the mitigation of risk, brand credibility, and attainment of long-term goals of sustainability.
Cost of Service : In the context of sustainable supply chain practices, the notion of cost of service has evolved into a comprehensive evaluation criterion that extends beyond basic expense accounting. Rather than concentrating solely on reducing costs, modern approaches advocate for a balanced consideration of financial viability, environmental stewardship, and system resilience. According to [76], the process of selecting suppliers and assigning orders should account for the total cost of service, which includes not only initial pricing but also life-cycle expenditures and qualitative aspects aligned with green and social goals. Reference [77] further emphasizes that engaging with third-party logistics providers can result in more favorable service costs through enhanced coordination in transportation and inventory control, which in turn supports broader sustainability agendas. Additionally, research by [78] illustrates how combining environmental strategies with cost-optimization methods—particularly through MCDM tools—can improve service efficiency while aligning with ecological targets. Viewed from this lens, cost of service becomes more than a financial metric; it functions as a strategic instrument for responsible sourcing and long-term value creation within sustainable supply chains.
Service Flexibility : Service flexibility refers to the ability of a supplier to adapt to changing customer requirements, market situations, and supply chain disruptions by modifying its operations and products. Flexibility is particularly critical in sustainable and circular supply chains due to changing demand, reverse logistics, and product recovery operations. Reference [63] highlights that flexibility and effectiveness in services are the most significant economic considerations in supplier assessment, especially in circular supply chain models where response to product return, recycling strategies, and remanufacturing requirements is essential. Similarly, Reference [70] mentions the rising significance of flexibility as a driving force for resilience to allow suppliers to maintain service levels during shocks such as the COVID-19 pandemic or market fluctuations. Reference [74] further emphasizes that service flexibility enhances supplier viability through smoother adjustment with sustainability goals and shifting customer demand, especially in power battery industries where recycling and reuse logistics are an important consideration. Therefore, quantifying service flexibility is important to ensure continuity, efficiency, and sustainability in today’s procurement systems.
Delivery Reliability : Delivery reliability refers to the ability of a supplier to consistently deliver orders on time and in entirety, which is essential to provide continuity, minimize production disruptions, and keep customers satisfied. It is even more vital in sustainable and circular supply chains, where timing facilitates closed-loop logistics and return flows. Reference [79] points out that reliable and on-time delivery is one of the basics of supplier performance with a direct influence on production scheduling and supply chain effectiveness overall. Reference [68] also points out on-time delivery as one of the significant criteria for circular supplier selection, emphasizing that delays or inconsistency can have a crippling influence on achieving sustainability objectives. Reference [61] also highlights that delivery reliability, when combined with smart technologies in Industry 4.0, significantly enhances supply network visibility and responsiveness, resulting in eco-efficiency and resource optimization. Delivery reliability is therefore not only an operational imperative but also a strategic sustainability enabler.
Logistics Capability : Logistics competence is the competence of a service provider to manage effectively and efficiently the movement, storage, and flow of goods within and between supply chain networks. Logistics competence entails various forms of competencies, including transportation management, warehousing, distribution planning, and optimization. Reference [1] points out that logistics capability is one of the most important determinants in selecting pallet pooling service providers, especially for common and circular logistics models, since it has a direct correlation with the efficiency of operation and responsiveness of service. Reference [80] highlights that small e-retailers heavily depend on sound logistics functions to employ sustainable last-mile delivery strategies since the quality of logistics and the price are determinants of economic sustainability and customer satisfaction. Effective logistics infrastructure is not only determinative in providing customers’ demands efficiently but also in pursuing sustainability and competitiveness in dynamic supply chains.
Customer Relationship Management : Customer Relationship Management (CRM) is an important driver of sustainable supplier selection through building long-term relationships, enhancing the quality of service, and ensuring alignment between supply chain practices and customer expectations. CRM is being used more as a strategic driver for organizational performance in sustainable and resilient supply chain scenarios. Reference [81] asserts that CRM, when integrated with sustainable supply chain management (SSCM), increases organizational responsiveness, customer loyalty, and competitiveness, particularly in developing economies where customer engagement has traditionally been underemphasized. Likewise, reference [82] points out that in today’s uncertainty-prone business world, it is crucial to know dynamic customer preferences, and this is made possible by CRM using tools like Quality Function Deployment (QFD) and transition modeling so that supplier selection does not fall out of step with changing customer priorities. Moreover, reference [83] emphasizes that CRM, within ESG-driven supplier relationship management frameworks, contributes positively towards reputation building, winning customer confidence, and reducing risks in upstream supply chains. CRM is therefore not simply customer care—it is one aspect of sustainable procurement practice that supports environmental, social, and economic goals.
4.1.3. RPC Pooling Suppliers as Alternatives
In the specific case study addressing the issue of selecting RPC pooling suppliers, the potential provider options are explained below.
RPC pooling supplier-1 : This brand operates under a larger manufacturing group and specializes in collapsible logistics containers designed for sectors such as agriculture, food, automotive, and retail. Its modular transport solutions offer a combination of space efficiency, ease of handling, and durability. The products not only streamline material handling processes but also help reduce the environmental footprint of logistics operations. With the ability to provide customized production based on client needs, the company adds flexibility and adaptability to diverse supply chain systems.
RPC pooling supplier-2 : Offering innovative and eco-conscious solutions for the logistics industry, this provider specializes in foldable plastic crates and pallet systems. Its product range has been expanded to cater to a variety of sectors and is further enhanced by custom design services tailored to client needs. The transport systems developed help reduce logistics costs while promoting the use of sustainable packaging to minimize environmental impact. With durable and recyclable products, the company plays an active role in advancing reusable packaging systems within the industry.
RPC pooling supplier-3 : Specializing in plastic packaging and logistics solutions, this provider stands out with a range of eco-friendly and durable products. It offers reusable options such as collapsible crates, plastic pallets, and transport systems designed to enhance sustainability across supply chains. These systems are particularly beneficial in the food and retail sectors, where they support efficient handling and contribute to better use of warehouse space. With long-lasting designs made from recyclable materials, the company’s offerings are well-suited for environmentally conscious logistics operations.
RPC pooling supplier-4 : Recognized as one of the global leaders in reusable packaging solutions, the company stands out for its specialized RPC systems designed to handle and store fresh produce efficiently. Operating across international markets, it offers services such as crate rental, hygienic washing, and logistics optimization tailored to supply chain needs. Its solutions are widely adopted for their compliance with food safety standards, use of eco-friendly materials, and ability to reduce operational costs. Embracing a circular economy mindset, the company actively contributes to minimizing the carbon footprint across logistics operations.
RPC pooling supplier-5 : Operating on a global scale, this company is known for its forward-thinking RPC solutions, particularly in the areas of fresh food logistics, retail, and supply chain management. Its services across the EMEA region, including Turkey, focus on key priorities such as food safety, operational efficiency, and waste reduction. The product range includes foldable plastic crates, containers, and trackable logistics systems. With a rental-based service model that aligns with circular economy principles, the provider offers businesses both flexibility and a pathway toward more sustainable operations.
Finally, the criteria and alternatives for the research are presented in Figure 2.
4.2. Assessing RPC Pooling Suppliers Using the SF-Yager-RANCOM-ARLON Hybrid Model
At this stage, the steps outlined in the algorithm are sequentially implemented to identify the most suitable RPC pooling supplier, thereby demonstrating the applicability of the SF-Yager-RANCOM-ARLON Hybrid Model to the RPC pooling supplier selection problem. The implementation steps of the SF-Yager-RANCOM-ARLON Hybrid Model are as follows:
Application—Stage 1: Assessment of expert opinions utilizing SF sets.
Step 1-1: The expertise levels of the experts were determined using the linguistic variables presented in Table 1 and are summarized in Table 3. By converting the linguistic variables into SF numbers, the experts’ experience matrix was constructed and is also presented in Table 3.

Table 3.
The expert weight matrix.
Step 1-2: By applying the score function (Equation (5)), the SF numbers were defuzzified, resulting in the crisp-valued expert experience matrix , which is presented in Table 3.
Step 1-3: The expert weight matrix was obtained using Equation (6) and is presented in Table 3.
Application—Stage 2: Determining criteria weights through the SF-RANCOM method.
Step 2-1: To construct the criteria assessment matrix, each expert evaluated each criterion using the linguistic variables provided in Table 2, and the results are presented in Table S1 in Supplementary Document. Subsequently, the corresponding SF numbers were assigned to the linguistic variables, resulting in the formation of the SF-based criteria assessment matrix , which is shown in Table S2.
Step 2-2: The aggregated SF-based criteria assessment matrix was obtained using the SFYWA aggregation operator presented in Equation (7), and the resulting matrix is displayed in Table S3.
Step 2-3: By applying the score function (Equation (8)), the SF numbers were defuzzified, resulting in the crisp-based aggregated criteria assessment matrix , which is presented in Table S4.
Step 2-4: The relative evaluation matrix (scoring matrix) was constructed based on the conditions outlined in Equation (9), and the resulting matrix is presented in Table S5.
Step 2-5: The total relative evaluation matrix was calculated based on Equation (10).
Step 2-6: The criteria weight matrix was obtained using Equation (12) and is presented in Table 4.

Table 4.
The criteria weight matrix .
Application—Stage 3: Constructing the alternative ranking matrix using the SF-ARLON method.
Step 3-1: To construct the alternative assessment matrix, each expert evaluated each alternative by referencing the criteria using the linguistic variables provided in Table 2, and the results are presented in Table S6. Subsequently, the corresponding SF numbers were assigned to the linguistic variables, resulting in the formation of the SF-based alternative assessment matrix , which is shown in Table S7.
Step 3-2: The aggregated SF-based alternative evaluation matrix was obtained using the SFYWA aggregation operator presented in Equation (12), and the resulting matrix is displayed in Table S8.
Step 3-3: By applying the score function (Equation (13)), the SF numbers were defuzzified, resulting in the crisp-based aggregated alternative evaluation matrix , which is presented in Table S9.
Step 3-4: The initial decision matrix for the ARLON method was constructed using Equation (14), and it is presented in Table S10.
Step 3-5: By employing Equation (15) and Equation (16), the first normalized decision matrix and second normalized decision matrix were calculated and they are shown in Table S11 and Table S12, respectively.
Step 3-6: By employing Equation (17), the aggregated normalized decision matrix was calculated and shown in Table S13.
Step 3-7: By employing Equation (18), the weighted aggregated normalized decision matrix was calculated and shown in Table S14.
Step 3-8: By employing Equations (19) and (20), the cost-based matrix and benefit-based matrix were calculated and they are shown in Table S15.
Step 3-9: By employing Equation (21), the ranking alternative matrix for the RPC pooling service providers selection was calculated and shown in Table S15.
Step 3-10: The final ranking alternative matrix for the RPC pooling service providers selection problem is derived by applying Equation (22). This matrix presents the conclusive ranking of the alternatives, integrating all previous evaluations and calculations to provide a comprehensive assessment of the service providers.
By using Equation (22), the final ranking alternative matrix for the RPC pooling service providers selection was calculated and shown in Table 5.

Table 5.
The final ranking alternative matrix .
5. Results and Implications
The SF-Yager-RANCOM-ARLON hybrid method was proposed and implemented as a case study to address the RPC pooling service provider selection problem. Based on the outcomes derived from the algorithm, three core results were obtained through the application of this hybrid method. These outcomes include: (1) expert weights, (2) criteria weights, and (3) the ranking of RPC pooling service providers. The findings related to these three main outputs are summarized as follows:
Expert Weights Output: By utilizing SF sets and linguistic variables, expert weights were determined across three steps based on their experience levels. The ranking of expert influence is as follows: “Second expert = Fifth expert = Sixth expert = Eighth expert > First expert = Third expert = Fourth expert > Seventh expert ”. This approach prevents the assumption that all experts have equal influence, instead reflecting their differentiated impact on the decision-making process. In this application, the second, fifth, sixth, and eighth experts were identified as having the highest weights, indicating that their contributions are considered more influential than others.
Criteria Weights Output: The process of determining criteria weights begins with the experts’ evaluations using linguistic variables and is completed over six steps. A critical aspect of this process is the use of the SFYWA aggregation operator, which enables the generation of the scoring matrix required for the RANCOM-based calculation of criteria weights. The resulting criteria weight ranking is “Delivery Reliability > Service Flexibility > Customer Relationship Management > Compliance and Regulatory Adherence > Logistics Capability > Employee Training and Development > Traceability and IT Systems > Cost of Service > Waste Management and Recycling > The Interests and Rights of Employees > Environmental Awareness > Occupational Health and Safety > Information Disclosure ”. According to this ranking, the “Delivery Reliability” criterion is identified as the most important. This indicates that, in the selection process for RPC pooling service providers, operational performance is prioritized over environmental and social considerations.
RPC Pooling Service Provider Ranking Output: The ranking of RPC pooling service providers is performed using the SF-ARLON method, incorporating both SF sets and linguistic variables. Additionally, the SFYWA aggregation operator facilitates the integration of expert evaluations of alternatives. The ranking outcome is as follows: “RPC pooling supplier-4 > RPC pooling supplier-2 > RPC pooling supplier-5 > RPC pooling supplier-1 > RPC pooling supplier-3 ”, identifying the fourth RPC pooling service provider as the most suitable option. The inclusion of both expert and criteria in this determination enhances the accuracy and reliability of the decision-making process.
In conclusion, the successful implementation of the SF-Yager-RANCOM-ARLON hybrid method supports its suitability for RPC pooling service provider selection. However, to further verify the method’s robustness and consistency, sensitivity and comparative analyses are necessary. These analyses are presented in the following sections.
5.1. Sensitivity Analysis for the SF-Yager-RANCOM-ARLON Hybrid Method
To test the robustness of the SF-Yager-RANCOM-ARLON hybrid method in the context of RPC pooling service provider selection, three distinct sensitivity analysis scenarios were developed. Each scenario explores how changes in key parameters or model structure affect the final decision outcomes.
Scenario 1—Variation in the Parameter (ARLON Normalization Importance): In Scenario 1, different values ranging from 0 to 1 were assigned to the parameter used in the ARLON method. This parameter influences the relative importance of the normalization processes within the method. The purpose was to evaluate whether changes in normalization emphasis affect the final ranking of the alternatives. The results of Scenario 1 are illustrated in Figure 3, with the corresponding RPC pooling service provider rankings shown in Figure 4. Upon examination, no changes were observed in the overall ranking order of the alternatives. Although minor variations were noted in the ranking scores, these did not alter the final decision outcome. These findings indicate that the SF-Yager-RANCOM-ARLON hybrid method maintains its robustness under varying normalization weight conditions.
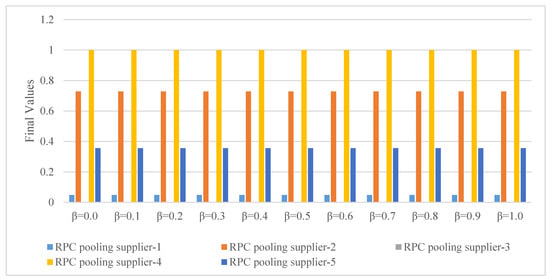
Figure 3.
Sensitivity Analysis-1 results.

Figure 4.
Sensitivity Analysis-1 ranks.
Scenario 2—Variation in the Parameter (SFYWA Aggregation Operator): In Scenario 2, the parameter , used in the SFYWA aggregation operator, was assigned values of 2, 3, 4, and 5. This parameter affects both the criteria weighting process and the aggregation of alternatives. By altering this value, the goal was to observe how changes in the aggregation behavior impact the final rankings. The aggregated final values for each sub-scenario are shown in Figure 5, and the corresponding rankings of RPC pooling service providers are presented in Figure 6. The results confirm that the order ranking remains stable across all variations in the parameter, further supporting the reliability and consistency of the hybrid method.
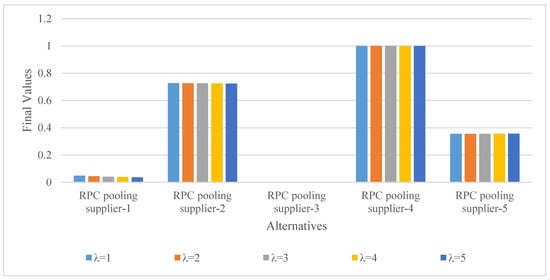
Figure 5.
Sensitivity Analysis-2 results.
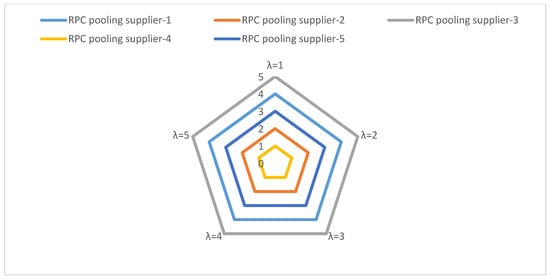
Figure 6.
Sensitivity Analysis-2 ranks.
Scenario 3—Removal of the Lowest-Ranked Alternatives from the Model: In Scenario 3, the alternative ranked lowest in the original model—RPC pooling supplier-3—was removed, and the decision-making process was repeated. Subsequently, supplier-1 and supplier-5 were also excluded one by one, with the method re-executed each time. Finally, the process was carried out with only RPC pooling suppliers 2 and 4 remaining in the model. The results of Scenario 3 are illustrated in Figure 7, with the corresponding RPC pooling service provider rankings shown in Figure 8. The results revealed that RPC pooling supplier-4 consistently emerged as the top-ranked provider, regardless of the removal of other alternatives. This indicates that the best-performing alternative remains unchanged under different model structures, providing additional evidence of the method’s robustness.
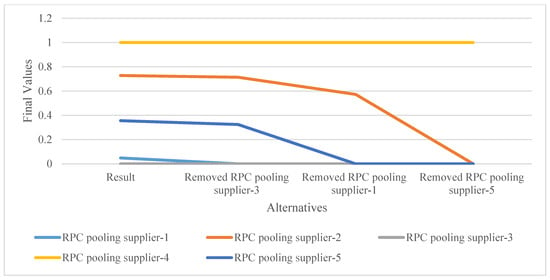
Figure 7.
Sensitivity Analysis-3 results.
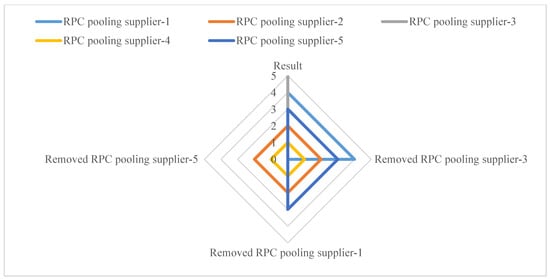
Figure 8.
Sensitivity Analysis-3 ranks.
Across all three sensitivity analysis scenarios, the SF-Yager-RANCOM-ARLON hybrid method demonstrated strong consistency and stability. The results remained reliable under variations in critical parameters and decision model structure, supporting the method’s suitability and robustness for RPC pooling service provider selection problems.
5.2. Comparative Analysis of the SF-Yager-RANCOM-ARLON Hybrid Method
To further validate the consistency and reliability of the SF-Yager-RANCOM-ARLON hybrid method for the RPC pooling service provider selection problem, a series of comparative analyses were conducted. These comparisons aimed to benchmark the proposed hybrid method against other well-established and widely recognized MCDM approaches that have demonstrated consistent performance in the literature.
For this purpose, the study of the same case was solved using the following alternative methods: ALWAS (Aczel-Alsina Weighted Assessment), AROMAN (An alternative ranking order method accounting for two-step normalization), ARTASI (Alternative ranking technique based on adaptive standardized intervals), MABAC (Multi-Attributive Border Approximation Area Comparison), RAM (Root Assessment Method), SAW (Simple Additive Weighting), TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), and WASPAS (Weighted Aggregated Sum Product Assessment). The final scores derived from each method’s application are presented in Figure 9.
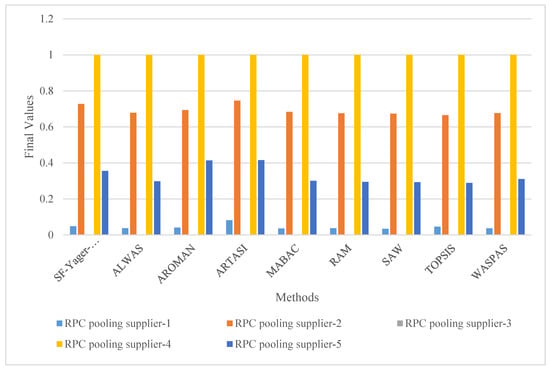
Figure 9.
Comparative analysis results.
Despite minor numerical differences in the final scores obtained from each method, the ranking of RPC pooling service providers remained identical across all approaches. According to the comparative analysis results, the correlations were determined as follows: ARLON–ALWAS correlation 0.9979, ARLON–AROMAN correlation 0.9970, ARLON–ARTASI correlation 0.9984, ARLON–MABAC correlation 0.9982, ARLON–MARCOS correlation 0.9975, ARLON–RAM correlation 0.9977, ARLON–SAW correlation 0.9976, ARLON–TOPSIS correlation 0.9968, and ARLON–WASPAS correlation 0.9984. The very high correlation values confirm that the results obtained are robust and consistent. This convergence in rankings across diverse methodological frameworks confirms that the SF-Yager-RANCOM-ARLON hybrid method yields consistent and dependable results. The analysis thus reinforces the method’s validity and suitability for solving complex decision-making problems in the context of RPC pooling service provider selection.
5.3. Research Implications
The findings and methodological contributions of this study offer several significant implications for both academic research and practical applications in the field of decision-making, particularly in the selection of RPC pooling service providers. The implications are presented below:
Academic Implications:
Advancement in Hybrid MCDM Approaches: The development of the SF-Yager-RANCOM-ARLON hybrid method introduces a novel decision-making framework that integrates SF sets with robust aggregation and ranking techniques, enhancing the flexibility and precision of MCDM applications.
Extension of Existing Methods with SF Theory: This study successfully extends the RANCOM and ARLON methods by incorporating SF numbers and Yager-based operations, enabling the use of more nuanced linguistic assessments and improving the representation of uncertainty in expert judgments.
Contribution to Aggregation Operators Literature: The effective implementation of the SFYWA aggregation operator, based on Yager t-norm and t-conorm, provides a valuable reference for researchers aiming to integrate advanced aggregation techniques into fuzzy decision models.
Case-Based Validation: The case study involving eight experts, thirteen criteria, and five alternatives serves as a benchmark for applying the hybrid model in complex real-world scenarios, offering a replicable framework for further academic studies.
Practical Implications:
Improved Decision Support for Logistics and Supply Chain Management: The hybrid method provides a structured and reliable tool for evaluating RPC pooling service providers, enabling decision-makers to incorporate expert opinion effectively and prioritize operational criteria like Delivery Reliability.
Enhanced Robustness and Consistency: The model’s reliability is demonstrated through comprehensive sensitivity analyses and comparative validation with established methods (e.g., TOPSIS, MABAC, WASPAS), which confirms its robustness and practical applicability across different evaluation settings.
Customization for Diverse Industrial Applications: Due to its modular structure and ability to accommodate linguistic variables, the proposed hybrid model can be adapted to various industries and decision problems involving subjective assessments and fuzzy environments.
Strategic Supplier Selection: The research supports more data-informed and systematic supplier selection processes, which can lead to improved efficiency, sustainability, and competitiveness in supply chain strategies.
6. Conclusions
In this study, a novel decision support system has been developed to address the RPC pooling service provider selection problem, utilizing the SF-Yager-RANCOM-ARLON hybrid method. This method integrates the spherical fuzzy logic framework with established multi-criteria decision-making techniques such as RANCOM and ARLON. By employing linguistic variables and transforming them into SF numbers, the proposed system effectively handles the inherent uncertainty in expert evaluations. The SFYWA aggregation operator, which is based on Yager’s t-norm and t-conorm, further enhances the robustness of the decision process. The application of this hybrid model in a case study demonstrates its practical value in making reliable and informed decisions in the selection of RPC pooling service providers.
The case study results revealed that Delivery Reliability was the most influential criterion in the selection process, and RPC pooling supplier-4 emerged as the optimal alternative based on the evaluation criteria. The sensitivity analysis conducted in three distinct scenarios confirmed the robustness of the SF-Yager-RANCOM-ARLON hybrid method. These scenarios tested variations in normalization processes, aggregation operator assignments, and decision model structures, yet the results remained consistent across all conditions. This stability underscores the method’s reliability and its ability to adapt to various decision-making contexts. Moreover, the comparative analysis with other well-established MCDM methods further affirmed the consistency and validity of the proposed approach.
This study contributes both theoretically and practically to the field of multi-criteria decision-making, particularly in the context of complex service provider selection problems. By extending the RANCOM and ARLON methods to incorporate spherical fuzzy numbers, this research provides a more accurate representation of expert judgments and decision criteria. The findings also offer valuable insights for practitioners in logistics and supply chain management, enabling more effective decision-making in selecting service providers. Future research could explore the application of this hybrid method in other decision-making domains and further refine the methodology by integrating additional factors such as risk assessment and cost analysis.
6.1. Limitations of the Study
Despite the methodological contributions and comprehensive findings, the present study has certain limitations that should be acknowledged to guide future research:
Dependency on Expert Judgments: The decision-making process relies heavily on expert evaluations, which may introduce subjectivity or bias, despite the use of SF sets to mitigate uncertainty.
Complexity of the Hybrid Framework: The integration of multiple methods (SF, Yager operators, RANCOM, ARLON) increases methodological complexity. This may limit the accessibility or practical adoption of the approach by practitioners unfamiliar with advanced fuzzy set theories.
Context-Specific Case Study: The proposed method is validated through a case study on RPC pooling service provider selection. While the results demonstrate reliability, the generalizability to other industries or decision problems requires further empirical testing.
Limited Number of Alternatives and Criteria: The case study involves a finite set of alternatives (five providers) and a specific set of criteria (thirteen), which may not capture the complexity of larger or more diverse decision environments.
Static Decision Environment: The study assumes a static evaluation context. Dynamic or real-time decision-making environments—common in logistics and supply chain domains—were not addressed in this research.
Scalability Issues: Due to the layered structure and repeated use of fuzzy computations, scalability to large-scale problems (e.g., with hundreds of criteria or alternatives) may pose computational challenges.
Software Implementation Limitations: The study does not provide open-source software or tool for the application of the proposed method, which might restrict its replication or real-world application by decision-makers without programming expertise.
6.2. Future Research Directions
Building on the findings and limitations of this study, several avenues for future research are proposed to enhance the development, applicability, and generalization of the SF-Yager-RANCOM-ARLON hybrid method in decision-making contexts:
Future studies can explore the applicability of the proposed hybrid method in different sectors such as healthcare service selection, sustainable supplier evaluation, smart city planning, or energy policy decisions.
Combining the hybrid method with Type-2 Fuzzy Sets, Spherical Fuzzy Sets, or Pythagorean Fuzzy Sets could be investigated to handle higher degrees of uncertainty and imprecision.
Future research could also examine the replacement of plastic with more environmentally friendly material alternatives in RPC systems, thereby aligning the method with the principles of the circular economy and contributing to greener and more sustainable logistics practices.
Future work may include the design and development of a user-friendly software platform or web-based decision support tool to facilitate the practical application of the hybrid methodology by industry practitioners. In addition, providing open-source implementations (e.g., in Python or Matlab) could further improve the transparency, replicability, and accessibility of the proposed method for both researchers and practitioners.
The current model assumes a homogeneous group of experts. Future studies could incorporate heterogeneous expert groups (e.g., different industries, departments, or regions) to examine inter-group consistency and consensus modeling using group decision-making strategies.
Developing real-time or automated sensitivity analysis tools can allow decision-makers to instantly observe the effect of input changes (e.g., expert weights or aggregation parameters) on final rankings.
Conducting longitudinal studies to evaluate how decisions made using the proposed method perform over time in terms of operational success or stakeholder satisfaction can provide empirical validation and improve methodological refinement.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/su17188356/s1, Table S1: The linguistic-based criteria assessment matrix , Table S2: The SF-based criteria assessment matrix , Table S3: The aggregated SF-based criteria assessment matrix , Table S4: The crisp-based aggregated criteria assessment matrix , Table S5: The crisp-based aggregated criteria assessment matrix , Table S6: The linguistic-based alternative assessment matrix , Table S7: The SF-based alternative assessment matrix , Table S8: The aggregated SF-based alternative evaluation matrix , Table S9: The crisp-based aggregated alternative evaluation matrix , Table S10: The initial decision matrix for the ARLON method, Table S11: The first normalized decision matrix , Table S12: The second normalized decision matrix , Table S13: The aggregated normalized decision matrix , Table S14: The weighted aggregated normalized decision matrix , Table S15: The cost-based matrix and benefit-based matrix and ranking alternative matrix
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article or Supplementary Material.
Conflicts of Interest
The author declares no conflicts of interest.
Notation
| Indices and Sets: | |
| index of RPC pooling service providers, | |
| index of criteria, | |
| index of experts, | |
| set of RPC pooling service providers, | |
| set of criteria, | |
| set of the cost-based criteria, | |
| set of the benefit-based criteria, | |
| set of experts. | |
| Parameters: | |
| number of PC pooling service providers, | |
| number of criteria, | |
| number of experts, | |
| parameter of aggregation operator, | |
| parameter of second normalization, | |
| parameter of ratio of benefit-based criteria, | |
| Variables: | |
| SF assessment of the expert , | |
| crisp value of the expert , | |
| weight of the expert , | |
| SF assessment of the criterion provided by the expert , | |
| aggregated value of the criterion , | |
| crisp value of the criterion , | |
| relative evaluation value of the criterion , depending on the criterion , | |
| total relative evaluation value of the criterion , | |
| weight of the criterion , | |
| SF assessment of the alternative depending on the criterion provided by the expert , | |
| aggregated value of the alternative depending on the criterion , | |
| crisp value of the alternative depending on the criterion , | |
| initial value of the alternative depending on the criterion , | |
| first normalized value of the alternative depending on the criterion , | |
| second normalized value of the alternative depending on the criterion , | |
| aggregated normalized value of the alternative depending on the criterion , | |
| cost-based value of the alternative | |
| benefit-based value of the alternative | |
| ranking value of the alternative | |
| final ranking value of the alternative | |
References
- Gürol, P.; Yurdabak, S.; Gül, A.Y.; Çakmak, E. Pallet pooling service provider selection with an intuitionistic fuzzy-based aroman model. J. Clean. Prod. 2025, 498, 145189. [Google Scholar] [CrossRef]
- Cristofaro, M.; Cucari, N.; Yamak, S.; Quiñones, P.G. Guest editorial: Environmental, social and governance (ESG) assets: A path of lights and shadows for management. Manag. Decis. 2025, 63, 389–400. [Google Scholar] [CrossRef]
- Behera, I.; Nanda, P. Green finance strategies: Driving sustainable business models through innovative financing solutions. In Sustainability, Crowdfunding and Digital Currencies; Springer: Berlin/Heidelberg, Germany, 2025. [Google Scholar] [CrossRef]
- Lou, S.; You, X.; Xu, T. Sustainable Supplier Evaluation: From Current Criteria to Reconstruction Based on ESG Requirements. Sustainability 2024, 16, 757. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Comput. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. RANCOM: A novel approach to identifying criteria relevance based on inaccuracy expert judgments. Eng. Appl. Artif. Intell. 2023, 122, 106114. [Google Scholar] [CrossRef]
- Kara, K.; Yalçın, G.C.; Simic, V.; Baysal, Z.; Pamucar, D. The alternative ranking using two-step logarithmic normalization method for benchmarking the supply chain performance of countries. Socio-Econ. Plan. Sci. 2024, 92, 101822. [Google Scholar] [CrossRef]
- Puschmann, T.; Alt, R. Sharing Economy. Bus. Inf. Syst. Eng. 2016, 58, 93–99. [Google Scholar] [CrossRef]
- Pouri, M.J.; Hilty, L.M. The digital sharing economy: A confluence of technical and social sharing. Environ. Innov. Soc. Transit. 2021, 38, 127–139. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, K. A systematic review and future directions of the sharing economy: Business models, operational insights and environment-based utilities. J. Clean. Prod. 2021, 290, 125209. [Google Scholar] [CrossRef]
- Reuschl, A.; Tiberius, V.; Filser, M.; Qiu, Y. Value configurations in sharing economy business models. Rev. Manag. Sci. 2022, 16, 89–112. [Google Scholar] [CrossRef]
- Benoit, S.; Merfeld, K.; Tunn, V.S.; Schaefers, T.; Andreassen, T.W. The B2B sharing economy: Framework, implications, and future research. J. Bus. Res. 2025, 191, 115244. [Google Scholar] [CrossRef]
- Peng, S. Sharing economy and sustainable supply chain perspective: The role of environmental, economic and social pillar of supply chain in customer intention and sustainable development. J. Innov. Knowl. 2023, 8, 100316. [Google Scholar] [CrossRef]
- Henry, M.; Schraven, D.; Bocken, N.; Frenken, K.; Hekkert, M.; Kirchherr, J. The battle of the buzzwords: A comparative review of the circular economy and the sharing economy concepts. Environ. Innov. Soc. Transit. 2021, 38, 1–21. [Google Scholar] [CrossRef]
- Thornton, H.C. Business model change and internationalization in the sharing economy. J. Bus. Res. 2024, 170, 114250. [Google Scholar] [CrossRef]
- Abdalla, S.; Amankwah-Amoah, J.; Hirekhan, M.; Temerak, M.S. Unlocking the potentials of hybrid business models in the sharing economy: An integrative review and new research agenda. Inf. Technol. Dev. 2024, 31, 8–32. [Google Scholar] [CrossRef]
- Köbis, N.C.; Soraperra, I.; Shalvi, S. The consequences of participating in the sharing economy: A transparency-based sharing framework. J. Manag. 2021, 47, 317–343. [Google Scholar] [CrossRef]
- Accorsi, R.; Cascini, A.; Cholette, S.; Manzini, R.; Mora, C. Economic and environmental assessment of reusable plastic containers: A food catering supply chain case study. Int. J. Prod. Econ. 2014, 152, 88–101. [Google Scholar] [CrossRef]
- Tua, C.; Biganzoli, L.; Grosso, M.; Rigamonti, L. Life Cycle Assessment of Reusable Plastic Crates (RPCs). Resources 2019, 8, 110. [Google Scholar] [CrossRef]
- Abejón, R.; Bala, A.; Vazquez-Rowe, I.; Aldaco, R.; Fullana-i-Palmer, P. When plastic packaging should be preferred: Life cycle analysis of packages for fruit and vegetable distribution in the Spanish peninsular market. Resour. Conserv. Recycl. 2020, 155, 104666. [Google Scholar] [CrossRef]
- Na, B.; Sim, M.K.; Lee, W.J. An optimal purchase decision of reusable packaging in the automotive industry. Sustainability 2019, 11, 6579. [Google Scholar] [CrossRef]
- Yadav, P.; Silvenius, F.; Katajajuuri, J.M.; Leinonen, I. Life cycle assessment of reusable plastic food packaging. J. Clean. Prod. 2024, 448, 141529. [Google Scholar] [CrossRef]
- Accorsi, R.; Battarra, I.; Guidani, B.; Manzini, R.; Ronzoni, M.; Volpe, L. Augmented spatial LCA for comparing reusable and recyclable food packaging containers networks. J. Clean. Prod. 2022, 375, 134027. [Google Scholar] [CrossRef]
- Huang, S.; Wang, R.; Yang, S.; Yao, J.; Gao, S. Review of life cycle cost analysis for reusable packaging for the retail industrial. In Proceedings of the 2024 7th International Conference on Humanities Education and Social Sciences (ICHESS 2024), Ningbo, China, 11–13 October 2024; Atlantis Press: Dordrecht, The Netherlands, 2024; pp. 780–792. [Google Scholar] [CrossRef]
- Glock, C.H. Decision support models for managing returnable transport items in supply chains: A systematic literature review. Int. J. Prod. Econ. 2017, 183, 561–569. [Google Scholar] [CrossRef]
- López-Gálvez, F.; Rasines, L.; Conesa, E.; Gómez, P.A.; Artés-Hernández, F.; Aguayo, E. Reusable plastic crates (RPCs) for fresh produce (case study on cauliflowers): Sustainable packaging but potential salmonella survival and risk of cross-contamination. Foods 2021, 10, 1254. [Google Scholar] [CrossRef] [PubMed]
- Suslow, T.V. Minimizing Risk in Multiple-Use Containers. Food Safety & Quality Magazine: Suslow UC Davis. 2015. Available online: https://ucfoodsafety.ucdavis.edu/sites/g/files/dgvnsk7366/files/inline-files/212397.pdf (accessed on 24 March 2025).
- Singh, J.; Shani, A.B.R.; Femal, H.; Deif, A. Packaging’s role in sustainability: Reusable plastic containers in the agricultural-food supply chains. In Organizing Supply Chain Processes for Sustainable Innovation in the Agri-Food Industry; Emerald Group Publishing Limited: Leeds, UK, 2016; pp. 175–204. [Google Scholar] [CrossRef]
- Sun, H.; Yang, Q.; Wu, Y. Evaluation and design of reusable takeaway containers based on the AHP–FCE model. Sustainability 2023, 15, 2191. [Google Scholar] [CrossRef]
- Li, T.-T.; Wang, K.; Sueyoshi, T.; Wang, D.D. ESG: Research progress and future prospects. Sustainability 2021, 13, 11663. [Google Scholar] [CrossRef]
- Todaro, D.L.; Torelli, R. From greenwashing to ESG-washing: A focus on the circular economy field. Corp. Soc. Responsib. Environ. Manag. 2024, 31, 4034–4046. [Google Scholar] [CrossRef]
- Qian, C.; Gao, Y.; Chen, L. Green supply chain circular economy evaluation system based on industrial internet of things and blockchain technology under ESG concept. Processes 2023, 11, 1999. [Google Scholar] [CrossRef]
- Banu, S.Z.; Vimala, V. Integration of ESG principles: An initiative for transformation from linear economy to circular economy. Theor. Appl. Econ. 2024, 31, 183–196. [Google Scholar] [CrossRef]
- Morri, G.; Colantoni, F.; De Paolis, A.M. ESG performance variability: Profitability and market implications for real estate entities in a worldwide context. J. Eur. Real Estate Res. 2024, 17, 373–394. [Google Scholar] [CrossRef]
- Chong, J.C. The Impact of Environmental, Social, and Governance (ESG) on the Performance of Sunway Reit Malaysia. Ph.D. Thesis, Tunku Abdul Rahman University of Management and Technology, Kuala Lumpur, Malaysia, 2025. [Google Scholar]
- Menicucci, E. ESG risks into the risk management framework. In Frameworks and Strategic Challenges for Financial Institutions; Springer: Cham, Switzerland, 2025. [Google Scholar] [CrossRef]
- Rezaee, Z.; Homayoun, S.; Poursoleyman, E.; Rezaee, N.J. Comparative analysis of environmental, social, and governance disclosures. Glob. Financ. J. 2023, 55, 100804. [Google Scholar] [CrossRef]
- Kim, J.; Kim, M.; Im, S.; Choi, D. Competitiveness of E-commerce firms through ESG logistics. Sustainability 2021, 13, 11548. [Google Scholar] [CrossRef]
- Tsang, A.; Frost, T.; Cao, H. Environmental, social, and governance (ESG) disclosure: A literature review. Br. Account. Rev. 2023, 55, 101149. [Google Scholar] [CrossRef]
- Farrokhizadeh, E.; Seyfi-Shishavan, S.A.; Gündoğdu, F.K.; Donyatalab, Y.; Kahraman, C.; Seifi, S.H. A spherical fuzzy methodology integrating maximizing deviation and TOPSIS methods. Eng. Appl. Artif. Intell. 2021, 101, 104212. [Google Scholar] [CrossRef]
- Mathew, M.; Chakrabortty, R.K.; Ryan, M.J. A novel approach integrating AHP and TOPSIS under spherical fuzzy sets for advanced manufacturing system selection. Eng. Appl. Artif. Intell. 2020, 96, 103988. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Alshamrani, A.M.; Alrasheedi, A.F.; Tirkolaee, E.B. Picture fuzzy compromise ranking of alternatives using distance-to-ideal-solution approach for selecting blockchain technology platforms in logistics firms. Eng. Appl. Artif. Intell. 2025, 142, 109896. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Dobryakova, L. Comparison of multi-criteria decision methods for customer-centered decision making: A practical study case. Procedia Comput. Sci. 2023, 225, 4824–4835. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pamucar, D.; Simic, V. Evaluation and prioritization of sustainable enterprise resource planning in SMEs using q-rung orthopair fuzzy rough set-based decision support model. IEEE Trans. Fuzzy Syst. 2024, 32, 3260–3273. [Google Scholar] [CrossRef]
- Kara, K.; Yalçın, G.C.; Ergin, E.A.; Simic, V.; Pamucar, D. A neutrosophic WENSLO-ARLON model for measuring sustainable brand equity performance. Socio-Econ. Plan. Sci. 2024, 94, 101918. [Google Scholar] [CrossRef]
- Kara, K.; Ergin, E.A.; Yalçın, G.C.; Çelik, T.; Deveci, M.; Kadry, S. Sustainable brand logo selection using an AI-supported PF-WENSLO-ARLON hybrid method. Expert Syst. Appl. 2025, 260, 125382. [Google Scholar] [CrossRef]
- Yalçın, G.C.; Kara, K.; Edinsel, S.; Kaygısız, E.; Simic, V.; Pamucar, D. Authentication system selection for performance appraisal in human resource management using an intuitionistic fuzzy CIMAS-ARLON model. Appl. Soft Comput. 2025, 171, 112786. [Google Scholar] [CrossRef]
- Yalçın, G.C.; Limon, E.G.; Kara, K.; Limon, O.; Gürol, P.; Devecş, M.; Demirayak, Ö.; Tomášková, H. A hybrid decision support system for transport policy selection: A case study on Russia’s Northern Sea Route in Arctic region. Socio-Econ. Plan. Sci. 2025, 98, 102171. [Google Scholar] [CrossRef]
- Ashraf, S.; Abdullah, S. Spherical aggregation operators and their application in multiattribute group decision-making. Int. J. Intell. Syst. 2019, 34, 493–523. [Google Scholar] [CrossRef]
- Yager, R.R. Aggregation operators and fuzzy systems modeling. Fuzzy Sets Syst. 1994, 67, 129–145. [Google Scholar] [CrossRef]
- Chinram, R.; Ashraf, S.; Abdullah, S.; Petchkaew, P. Decision support technique based on spherical fuzzy Yager aggregation operators and their application in wind power plant locations: A case study of Jhimpir, Pakistan. J. Math. 2020, 2020, 8824032. [Google Scholar] [CrossRef]
- Le, M.-T.; Nhieu, N.-L. A behavior-simulated spherical fuzzy extension of the integrated multi-criteria decision-making approach. Symmetry 2022, 14, 1136. [Google Scholar] [CrossRef]
- Sharaf, I.M. A new approach for spherical fuzzy TOPSIS and spherical fuzzy VIKOR applied to the evaluation of hydrogen storage systems. Soft Comput. 2023, 27, 4403–4423. [Google Scholar] [CrossRef]
- Chung, H.-Y.; Chang, K.-H.; Yao, J.-C. Addressing environmental protection supplier selection issues in a fuzzy information environment using a novel soft fuzzy AHP–TOPSIS method. Systems 2023, 11, 293. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, V.; Verma, P. Sustainable supplier selection in a construction company: A new MCDM method based on dominance-based rough set analysis. Constr. Innov. 2025, 25, 328–362. [Google Scholar] [CrossRef]
- Paulraj, A.; Chen, I.J.; Blome, C. Motives and performance outcomes of sustainable supply chain management practices: A multi-theoretical perspective. J. Bus. Ethics 2017, 145, 239–258. [Google Scholar] [CrossRef]
- Alimohammadlou, M.; Khoshsepehr, Z. Green-resilient supplier selection: A hesitant fuzzy multi-criteria decision-making model. Environ. Dev. Sustain. 2022. [Google Scholar] [CrossRef]
- Ulutaş, A.; Topal, A.; Pamučar, D.; Stević, Ž.; Karabašević, D.; Popović, G. A new integrated multi-criteria decision-making model for sustainable supplier selection based on a novel grey WISP and grey BWM methods. Sustainability 2022, 14, 16921. [Google Scholar] [CrossRef]
- Tronnebati, I.; El Yadari, M.; Jawab, F. A review of green supplier evaluation and selection issues using MCDM, MP and AI models. Sustainability 2022, 14, 16714. [Google Scholar] [CrossRef]
- Gidiagba, J.; Tartibu, L.; Okwu, M. Sustainable supplier selection in the oil and gas industry: An integrated multi-criteria decision making approach. Procedia Comput. Sci. 2023, 217, 1243–1255. [Google Scholar] [CrossRef]
- Ali, H.; Zhang, J.; Shoaib, M. A hybrid approach for sustainable-circular supplier selection based on industry 4.0 framework to make the supply chain smart and eco-friendly. Environ. Dev. Sustain. 2023, 26, 22587–22624. [Google Scholar] [CrossRef]
- Chai, N.; Zhou, W.; Jiang, Z. Sustainable supplier selection using an intuitionistic and interval-valued fuzzy MCDM approach based on cumulative prospect theory. Inf. Sci. 2023, 626, 710–737. [Google Scholar] [CrossRef]
- Alavi, B.; Tavana, M.; Mina, H. A dynamic decision support system for sustainable supplier selection in circular economy. Sustain. Prod. Consum. 2021, 27, 905–920. [Google Scholar] [CrossRef]
- Tramarico, C.L.; Salomon, V.A.P.; Marins, F.A.S. Multi-criteria assessment of the benefits of a supply chain management training considering green issues. J. Clean. Prod. 2017, 142, 249–256. [Google Scholar] [CrossRef]
- Matić, B.; Jovanović, S.; Das, D.K.; Zavadskas, E.K.; Stević, Ž.; Sremac, S.; Marinković, M. A new hybrid MCDM model: Sustainable supplier selection in a construction company. Symmetry 2019, 11, 353. [Google Scholar] [CrossRef]
- Khokhar, M.; Hou, Y.; Rafique, M.A.; Iqbal, W. Evaluating the social sustainability criteria of supply chain management in manufacturing industries: A role of BWM in MCDM. Probl. Ekorozwoju 2020, 15, 185–194. [Google Scholar] [CrossRef]
- Agrawal, V.; Mohanty, R.P.; Agrawal, A.M. Identification and analysis of enablers of SCM by using MCDM approach. Benchmarking Int. J. 2020, 27, 1681–1710. [Google Scholar] [CrossRef]
- Nasr, A.K.; Tavana, M.; Alavi, B.; Mina, H. A novel fuzzy multi-objective circular supplier selection and order allocation model for sustainable closed-loop supply chains. J. Clean. Prod. 2021, 287, 124994. [Google Scholar] [CrossRef]
- Liao, H.; Wen, Z. Capturing attitudinal characteristics of decision makers in multi-criterion sorting problems for performance evaluation of sustainable and circular suppliers. Ann. Oper. Res. 2023, 1–26. [Google Scholar] [CrossRef]
- Echefaj, K.; Charkaoui, A.; Cherrafi, A.; Garza-Reyes, J.A.; Khan, S.A.R.; Chaouni Benabdellah, A. Sustainable and resilient supplier selection in the context of circular economy: An ontology-based model. Manag. Environ. Qual. 2023, 34, 1461–1489. [Google Scholar] [CrossRef]
- Öztürk, C. Digitalization as a catalyst for social sustainability in supply chains: An ISM-fuzzy MICMAC and DEMATEL approach. Environ. Dev. Sustain. 2025, 1–61. [Google Scholar] [CrossRef]
- Islam, S.; Manning, L.; Cullen, J.M. A hybrid traceability technology selection approach for sustainable food supply chains. Sustainability 2021, 13, 9385. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. Green supplier selection using MCDM: A comprehensive review of recent studies. Spectr. Eng. Manag. Sci. 2024, 2, 1–16. [Google Scholar] [CrossRef]
- Wang, J. Intelligent management and legal regulation of enterprise green supply chain by fuzzy comprehensive evaluation. Heliyon 2024, 10, e39929. [Google Scholar] [CrossRef]
- Menon, R.R.; Ravi, V. Using AHP-TOPSIS methodologies in the selection of sustainable suppliers in an electronics supply chain. Clean. Mater. 2022, 5, 100130. [Google Scholar] [CrossRef]
- Mohammed, A.; Harris, I.; Govindan, K. A hybrid MCDM-FMOO approach for sustainable supplier selection and order allocation. Int. J. Prod. Econ. 2019, 217, 171–184. [Google Scholar] [CrossRef]
- Raut, R.; Kharat, M.; Kamble, S.; Kumar, C.S. Sustainable evaluation and selection of potential third-party logistics (3PL) providers: An integrated MCDM approach. Benchmarking Int. J. 2018, 25, 76–97. [Google Scholar] [CrossRef]
- Tsai, J.F.; Shen, S.P.; Lin, M.H. Applying a hybrid MCDM model to evaluate green supply chain management practices. Sustainability 2023, 15, 2148. [Google Scholar] [CrossRef]
- Mina, H.; Kannan, D.; Gholami-Zanjani, S.M.; Biuki, M. Transition towards circular supplier selection in petrochemical industry: A hybrid approach to achieve sustainable development goals. J. Clean. Prod. 2021, 286, 125273. [Google Scholar] [CrossRef]
- Bonilla, M.A.M.; Da Silva, B.S.; Schmitt, M.B.; Bouzon, M. Sustainable practices in last-mile logistics of small Brazilian e-retailers: An analysis using an MCDM approach. Acad. Rev. Latinoam. Adm. 2024, 37, 383–408. [Google Scholar] [CrossRef]
- Das, S.; Hassan, H.M.K. Impact of sustainable supply chain management and customer relationship management on organizational performance. Int. J. Product. Perform. Manag. 2022, 71, 2140–2160. [Google Scholar] [CrossRef]
- Tavakoli, M.; Tajally, A.; Ghanavati-Nejad, M.; Jolai, F. A Markovian-based fuzzy decision-making approach for the customer-based sustainable-resilient supplier selection problem. Soft Comput. 2023, 27, 15153–15184. [Google Scholar] [CrossRef]
- Li, Y.; Tsang, Y.P.; Lee, C.K.M.; Wu, C.H. Multi-criteria group decision analytics for sustainable supplier relationship management in a focal manufacturing company. J. Clean. Prod. 2024, 476, 143690. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).