Abstract
When power system equipment fails due to disasters, resulting in the isolation of parts of the network, the loads within the isolated system cannot be guaranteed a continuous power supply. However, for critical loads—such as hospitals or data centers—continuous power supply is of utmost importance. While distributed energy resources (DERs) within the network can supply power to some loads, outages may lead to compensation and fairness issues regarding the unsupplied loads. In response, this study proposes a methodology to determine the appropriate power contract price for key customers by estimating the unsupplied power demand for critical loads in isolated networks and incorporating both outage compensation costs and voltage stability penalties. The microgrid under consideration comprises DERs—including electric vehicles (EVs), fuel cell electric vehicles (FCEVs), photovoltaic (PV) plants, and wind turbine (WT) plants—as well as controllable resources such as battery energy storage systems (BESS) and hydrogen energy storage systems (HESS). It serves both residential load clusters and critical loads associated with social infrastructure. The proposed methodology is structured in two stages. In normal operating conditions, optimal scheduling is simulated using second-order conic programming (SOCP). In the event of a fault, mixed-integer SOCP (MISOCP) is employed to determine the optimal load shedding strategy. A case study is conducted using the IEEE 123 bus test node system to simulate the outage compensation cost calculation and voltage penalty assessment processes. Based on this analysis, a contract price for key customers that considers both disaster-induced outages and voltage impacts is presented.
1. Introduction
The modern electricity market is undergoing rapid transformation with the adoption of smart grids and distributed generation, highlighting the critical importance of managing key loads—such as data centers and hospitals—that require continuous and reliable power. Traditional power pricing models, which are designed around average consumption patterns and supply-demand balance, often fall short in guaranteeing uninterrupted power to these critical loads during disasters or outages. Consequently, there is an urgent need to develop optimization methodologies that ensure stable power delivery under normal conditions while also securing continuous supply during emergency situations.
Prior to the widespread integration of distributed generation into power systems in the 2000s, utilities had very few options to supply power when disasters or outages led to system separation. Although emergency or diesel generators could provide power to a limited number of loads, the isolated sections of the network typically remained without power until repairs were completed. However, with the substantial introduction of distributed energy resources (DERs) such as solar and wind, along with the integration of energy storage systems (ESSs) capable of storing excess energy, it has become possible to supply power even when the system is isolated due to a fault.
However, in an isolated distribution system, demand still outweighs supply, requiring decisions on which loads to serve and which to curtail. In most instances, the objective is to supply power to loads that are located near distributed generation or ESSs, taking power losses into account. However, when power is prioritized for key customers who require continuous supply, normal loads that would typically receive power may experience outages. In these cases, it becomes essential to determine appropriate compensation costs.
Moreover, key customers typically consume large amounts of power, which can adversely affect overall grid stability. The stability of the voltage is influenced by both the magnitude and the location of the connected capacity; when loads are overly concentrated in a particular area, the variability in the voltage increases, thereby compromising system stability. This instability forces the power company to incur additional costs related to network reinforcement, standby capacity operations, and ongoing maintenance. Consequently, it is anticipated that an appropriate penalty and investment cost-sharing mechanism will be required for large-scale loads to mitigate these impacts.
To address this issue, some companies have implemented customized contracts for large-scale industrial users or data centers, providing dedicated services such as continuous monitoring and emergency response systems, with power prices determined through separate agreements. However, clear evaluation criteria for cost sharing and quantifying the grid impact are generally lacking in these arrangements. Therefore, this paper aims to assess the grid impact of connecting key customers by using voltage drop as a metric, and to estimate the unsupplied power resulting from prioritized supply during disaster scenarios. This approach is intended to enable utilities to derive rational and fair cost allocations.
2. Related Work
A primary objective for utilities in grid operation is to ensure the reliability and safety of power supply. The power system can experience temporary outages due to various causes, which are often resolved by automatic reclosing devices activated by factors such as strong winds, lightning, or animal contact. However, high-impact, low-probability (HILP) events—such as typhoons, earthquakes, or wildfires—can inflict severe damage on the grid. Although these events rarely occur, the rising frequency of disasters due to climate change increases the need for ongoing monitoring and effective response strategies.
To quantify the grid damage caused by such disasters, the concept of resilience has been introduced, leading to extensive research and technological development aimed at enhancing grid resilience. Initially, resilience was understood primarily as the ability to quickly restore the affected areas and equipment after an outage. However, the Federal Energy Regulatory Commission (FERC) expanded the definition in January 2018 to include not only rapid recovery but also the ability to predict outages, respond effectively, and reduce damages [1].
In the post-disaster phase, when limited repair crews and resources are available to restore the affected areas and equipment, methodologies have been proposed to optimize the deployment of repair teams and resources for rapid restoration. For instance, efficient recovery strategies are proposed based on Mixed Integer Linear Programming (MILP) models that leverage the synergy between physical maintenance teams and load restoration systems [2,3]. An optimal recovery algorithm incorporates realistic recovery times by considering road conditions and repair team proficiency [4]. In [5], the optimal restoration plan is formulated using MILP, which accounts for environmental risks posed by disasters. However, these post-disaster response approaches have inherent limitations. As the duration of the disaster increases, so does the overall outage period. Since recovery efforts only commence after the disaster has ended, the outage persists throughout the restoration process, and recovery times can vary significantly between regions, leading to imbalanced power restoration across the affected network.
As the integration of renewable energy and ESSs within microgrids increases, strategies that leverage these DERs are being proposed. ESSs convert excess generated energy into chemical energy for storage, enabling their use when there is either an overproduction or a shortage in generation. By managing charging and discharging, ESSs can help balance supply and demand. This is particularly valuable for renewable energy sources, which cannot control their generation output. Thus, ESSs are frequently coupled with DERs. Numerous studies have introduced optimal scheduling techniques that focus on minimizing overall system operating costs by optimizing the use of energy storage. First, day-ahead and real-time co-optimization schemes have been proposed for industrial prosumers, improving profit while ensuring contract fulfilment. Secondly, distribution-level studies combine battery storage with demand response to reduce both total expenditure and renewable curtailment [6]. A separate line of work employs interval or affine-arithmetic formulations to capture uncertainty and battery degradation costs in microgrid scheduling [7,8]. Another contribution is a three-stage flexibility-provision framework that enables radial networks to meet TSO requests at minimal economic loss [9]. In [10,11], methodologies were proposed from a prosumer perspective that focus on maximizing energy management efficiency and profit. Furthermore, even if an incident leads to a portion of the network becoming isolated, the presence of distributed generation within that isolated system can maintain a continuous power supply, thereby reducing the duration of outages. However, despite the ability to supply power to the affected area using renewable energy and ESS, the intermittent nature and output limitations of renewable sources may still necessitate load shedding for certain loads. In such cases, determining which loads to disconnect becomes a critical consideration.
The most intuitive approach is to configure load shedding such that power losses are minimized. Typically, supplying power to loads that are located further away from generation sources results in increased losses. Another common strategy is to prioritize the supply for critical loads, such as hospitals, fire stations, and communication facilities. For example, loads are classified into critical and non-critical categories, and in one study, an optimized independent network operation strategy was proposed based on MILP for both battery energy storage systems (BESS) and renewable energy sources. In [12], a two-stage heuristic algorithm was developed to prioritize the recovery of critical loads following a disaster. Additionally, in [13], a methodology was introduced to enhance power supply reliability for critical loads in rural microgrids using hierarchical cooperative control. Furthermore, a hybrid hydrogen–battery storage system was proposed to improve system efficiency by targeting prioritized loads in [14]. In [15], a method was presented for improving resilience in microgrids integrated with hydrogen energy storage systems by leveraging mimetic wind turbines. Recently, approaches employing reinforcement learning have been proposed to optimize the control of distributed energy resources and energy storage [16,17] or to facilitate system reconfiguration [18].
Research has also been conducted to proactively control the system prior to a disaster, thereby enhancing resilience. In these cases, resources may be utilized even before an actual outage occurs, which can potentially lead to inefficiencies. For example, one method suggested enhancing grid resilience by integrating hydrogen systems into conventional demand response and distributed energy resource control frameworks, thereby enabling proactive cooperative control [19]. In [20], an optimal load sharing method was introduced for a hydrogen–battery hybrid storage system. Pre-setting a minimum SOC for ESS was suggested in [21] to secure the supply for critical loads in advance of anticipated disasters. Building on these preventive measures, ref. [22] introduced a resilience-focused microgrid control algorithm, supported by a novel resilience index, that enables prolonged autonomous operation of critical loads during extreme events. Additionally, ref. [23] evaluated how photovoltaic generation, stationary batteries, and vehicle-to-building integration enhance flexibility and economic performance in a building-scale microgrid.
However, most existing studies do not consider compensation for the loads that are shed, nor do they thoroughly address the grid impacts of prioritizing critical loads. Therefore, this paper proposes a pricing mechanism for power contracts between the utility and key customers that incorporates both compensation costs and investment expenses for grid reinforcement. This approach aims to ensure that the additional costs associated with compensating unsupplied loads and reinforcing the network are fairly allocated, thereby facilitating balanced and sustainable contract negotiations while maintaining grid stability and resilience.
The paper proposes a methodology for determining contract prices that account for compensation costs and voltage drop penalties, derived from optimal power supply and prioritized supply plans when a microgrid is partially separated and operates as an isolated network due to disasters. The contributions of this paper are as follows:
- It presents a two-stage optimization framework that utilizes second-order conic programming (SOCP) for normal operations and mixed-integer second-order conic programming (MISOCP) for rescheduling during outage scenarios, ensuring optimal dispatch of BESS and hydrogen energy storage systems (HESS) while considering load shedding.
- It quantifies the unsupplied power demand and voltage impacts when critical loads are prioritized in isolated networks, thereby reflecting both outage compensation and grid stability concerns.
- It proposes a novel pricing model for key customers that incorporates additional costs associated with disaster-induced outages and voltage degradation, promoting fair and balanced contractual negotiations.
- It demonstrates the practical application of the methodology through a case study using the IEEE 123 bus test node system, validating the proposed approach with realistic load and generation profiles.
Section 3 introduces the methodology for optimal scheduling and calculating power contract prices for key customers. In Section 4, a case study is presented that quantifies outage compensation costs by comparing conventional load shedding with prioritized load shedding, while also assessing the impact on the grid due to customer load connections. Finally, Section 5 provides the conclusion.
3. Methodology and Problem
3.1. Overall Process
Although the performance of meteorological observation equipment has continuously improved, predicting the timing, intensity, and location of disasters remains extremely challenging. Therefore, this study verifies the proposed methodology under various fault scenarios by dividing the process into two stages.
In the first stage, a day-ahead optimal scheduling for the subsequent 24 h is performed without prior information of an impending disaster. It is assumed that the profiles for DERs and load, which are essential for the optimization, are forecasted on an hourly basis for the entire day. Moreover, it is presumed that the microgrid’s BESS and HESS operate from 00:00 to 24:00 based on the optimal scheduling results obtained via SOCP. In the event of an unforeseen failure at any given time, the state-of-charge (SOC) of the ESSs at that moment serves as the initial condition for the subsequent disaster-specific optimization. This approach facilitates the estimation of initial values for the distributed generation units within the isolated section of the system caused by the failure, thereby ensuring a prompt and effective response.
In the second stage, it is assumed that a disaster-induced failure occurs at a minimum of one line or bus within the microgrid over 24 h. The associated protection devices isolate the affected branch, leaving the downstream section disconnected from both the upstream part of the radial feeder and the nearby lines. Consequently, this islanded segment must satisfy its own demand using only locally available assets—BESS, HESS, photovoltaic (PV), and wind turbine (WT) generators. If the external fault propagates to the point of common coupling, it can be assumed that the entire microgrid will be blacked out.
Furthermore, during the formulation of the power supply plan, data centers—which require a continuous power supply—are designated as critical loads to ensure that their power needs are prioritized. However, from the microgrid’s perspective, it is not feasible to supply power exclusively to the data center, especially considering associated economic losses. Therefore, a penalty mechanism is introduced based on voltage sensitivity and additional contractual costs, which may influence the prioritization of power supply depending on the break-even analysis. In scenarios where power generation is insufficient, supply priorities are established between general loads and critical loads based on the magnitude of the losses incurred. Conversely, in cases where there is surplus power generation, priority is given to charging the BESS and HESS. It is further assumed that if the power generation exceeds the maximum charging or discharging capacities of these ESSs, the PV and WT generation units may be temporarily curtailed.
The detailed definitions of all parameters used in the mathematical formulations and optimization processes are summarized in Appendix A for clarity regarding the variables used throughout the day-ahead scheduling and disaster response stages.
3.2. Microgrid Optimal Day-Ahead Scheduling
3.2.1. Objective Function
The objective function of this study is to minimize the total operational cost of the microgrid , with the BESS and HESS serving as control variables. The microgrid incorporates various DERs—including PV, WT, BESS, and HESS—and is equipped with both electric vehicle (EV) and fuel cell electric vehicle (FCEV) charging stations, enabling the provision of Vehicle-to-Grid (V2G) services.
The microgrid is inherently capable of exchanging power with the upstream grid, with the associated cost defined as the power trading cost , which is incorporated into the objective function. It is assumed that renewable energy is operated by the generation operators within the microgrid, and the costs are settled in accordance with the amount of renewable energy generated . Additionally, the ESSs incur maintenance costs during their charging and discharging cycles. The EV charging cost represents the revenue generated from supplying power to EVs. Finally, the revenue derived from buying and selling power to customers is defined as the customer power sales revenue . Each cost function is integrated into the objective function as follows:
The cost function for power transactions with the upstream grid is defined as the net difference between the cost of purchasing energy from the grid and the settlement revenue for exporting any surplus generation back to it as follows:
where τ denotes the time interval, which is set to 1 in this study. and represent the costs associated with purchasing and selling power at time , with the respective prices varying by time period. and denote the quantities of power purchased from or sold to the main grid at time .
The settlement cost for renewable energy generation is defined as the total amount paid to the renewable energy plant operators for the energy into the microgrid as follows:
where indicates the cost incurred by the power company when procuring power from RES within the system, while represents the power generated at time by the RES located on the bus. In order to maximize the economic efficiency of the system, the power generated from RES is given priority, and as a result, generation curtailment is not taken into account.
The maintenance-cost function for the BESS and HESS is given as follows:
where and denote the maintenance costs incurred by the power company when operating the BESS and the HESS, respectively. and represent the charging and discharging quantities of the BESS on the bus at time . Similarly, signifies the power generated at time by the HESS, which is operated in conjunction with fuel cells.
The revenue functions for selling electricity to EVs and customers are defined as follows:
where corresponds to the power supply price at time , and denotes the EV charging quantity. Finally, is defined as the price at which the power company sells power to customers, and represents the demand of the loads present within the system.
3.2.2. Power Flow and Power Balance Constraints
DERs and ESSs connected at different locations in the grid can affect power losses. For example, greater electrical distance between DERs and ESSs increases line losses during charging, reducing the net energy delivered to the storage device. Therefore, the power balance equations are incorporated as constraints in the scheduling to minimize such power losses. These power equations include voltage drops and current flows, reflecting the resistance and reactance of the lines; as a result, a voltage drop occurs corresponding to the amount of active and reactive power flowing through the line by the following equation.
where and represent the resistance and reactance of the line, respectively. and indicate the active and reactive power flowing through the line. represents the voltage of the bus , while represents the current flowing through the line connecting buses and , based on the definition of the power flow equation and Ohm’s law . Furthermore, the power loss in the line is modeled through the square of the line impedance.
Net power injection equals the difference between generation and consumption powers at each bus as follows:
where and denote the active and reactive power at bus . In essence, the voltage and current at each bus determine and for that bus, and these, in turn, determine the line losses and . Consequently, the constraints are designed to guide the optimization towards minimizing and .
Technically, the current flowing through the line should be equal to , , and . However, enforcing this equality directly can make the optimization problem non-convex. To improve the optimization convergence and convert the problem to SOCP, the condition has been relaxed with inequality as the following constraint. The detailed derivation of these SOCP conditions and relaxation formulations are contained in [24,25].
3.2.3. Bus Voltage and Line Current Constraints
Electric lines have a maximum thermal limit beyond which current cannot safely flow, while power generation facilities are constrained by factors such as each generator’s maximum and minimum output levels [26]. Consequently, the constraint formulations are designed to reflect these physical limitations and operational characteristics, ensuring that the optimization process adheres to realistic operating conditions. This approach not only safeguards the reliability and safety of the microgrid but also supports the overall economic viability of the system.
The voltage within the grid is expected to remain relatively stable, operating within an optimal range that avoids levels which are either excessively low or high. Consequently, a constraint is imposed to ensure that the voltage measured at each bus is maintained between the minimum and maximum limits as specified or agreed upon by the system as follows:
where and represent the minimum and maximum voltage ranges required for stable grid operation, respectively, while indicates the squared form of the voltage status at each bus .
A constraint is imposed to ensure that the current is maintained within a range from 0 (indicating no current flow) up to the maximum allowable current, which is defined by the thermal limit of the line as follows:
where represents the maximum allowable current, while denotes squared form of the current state in the distribution lines of the system. The squared-magnitude expressions of the voltage and current constraints are formulated so that they can be embedded directly into a SOCP framework.
3.2.4. Active/Reactive Power Ratio
The power flow within the microgrid is categorized into active and reactive power, with the ratio of these components varying according to the load type. Since this study focuses on the supply of active power, the reactive power demand of the microgrid is determined by referring to the power factor standards of conventional distribution systems as follows:
where and represent the active and reactive power within the grid, respectively. , , , and denote the total power generated by all generation units and the total load within the grid. refers to the ratio of reactive power to active power, while represents the reactive power supply capability of the renewable energy sources.
A target power factor is established as 0.95 to ensure both efficient operation and higher power quality within the microgrid. It is assumed that solar PV and wind power systems are capable of supplying reactive power when connected to the grid, operating at a power factor of 0.95 similar to that of the loads, which corresponds to a maximum reactive power supply capability of up to 31.2% relative to their active power output. Consequently, the reactive power flow within the microgrid is determined by the difference between the reactive power supplied by the renewable energy sources and the reactive power demanded by the loads.
The reactive power control functionalities of the ESSs and the potential reactive power generation from the EVs charging converters are excluded from the current scope. Future research will investigate the integration of ESS and EV charging converter reactive power control to develop comprehensive reactive power management strategies for the microgrid.
3.2.5. Electricity Trade with the Main Grid
When the resources within the microgrid are insufficient to achieve a power balance, power transactions with the main grid can be utilized. In scenarios where surplus power is available, the microgrid is permitted to sell electricity to the main grid at a predetermined price. Conversely, when there is a shortage, the microgrid can purchase power from the main grid to meet its demand. The power trade function can be calculated as follows:
where represent total power trade at time .
3.2.6. BESS Charging and Discharging Constraints
The BESS connected to the grid incorporates power control devices such as a Battery Management System (BMS) and Power Conversion System (PCS). Battery cells are assumed to be a typical lithium-ion battery. Lithium-ion batteries offer the advantage of rapidly charging or discharging power over short durations. The energy stored in the BESS must always remain within the bounds of zero and its maximum capacity, and its charge/discharge output cannot exceed the designated rated power. In practical applications, power conversion losses occur during the charging and discharging processes; hence, a conversion efficiency coefficient is applied to account for these losses. To ensure continuity in daily optimal scheduling, the initial and final SOC of the BESS are set to be identical.
where represents the summation of discharging and charging power of the BESS at bus at time . refers to the maximum output of the BESS, while indicates the rated energy capacity of the BESS. represents the state of charge of the BESS at time . Additionally, and denote the conversion efficiencies during charging and discharging, respectively. and correspond to the minimum and maximum allowable states of charge, and and represent the initial and final states of charge of the BESS.
Constraints (17)–(22) represent the operation constraints of the BESS. It includes a total summation of charging and discharging power (17), minimum and maximum power limits (18) and (19), the available amount of charging and discharging power considering efficiency (20), minimum and maximum SOC (21), and initial and final SOC (22).
3.2.7. HESS Charging and Discharging Constraints
It is assumed that the HESS comprises a hydrogen tank, a fuel cell for hydrogen-to-electricity conversion, and an electrolyzer for electricity-to-hydrogen conversion. The hydrogen tank utilizes high-pressure gas storage, and, similar to the BESS, it is equipped with a PCS and a Balance of Plant (BOP). Although the HESS can perform a function analogous to that of the BESS from a system perspective, it is constrained by its slower operational speed due to the need for preheating during charge and discharge processes. Consequently, the system is designed to preferentially utilize the BESS for rapid charge-discharge operations, while the HESS is reserved for longer-term charge-discharge activities. In the HESS, hydrogen is either released from or stored in the hydrogen tank via the fuel cell and electrolyzer, with the amount exchanged being proportional to the maximum output of each device.
where and represent the power generation from the fuel cell and the hydrogen production from the electrolyzer of the HESS at bus at time , respectively. and denote the conversion efficiencies between electricity and hydrogen. and indicate the maximum power output and the maximum hydrogen production at a given time, respectively. represents the proportion of hydrogen remaining in the hydrogen tank at bus at time . and refer to the amount of hydrogen produced by the electrolyzer and the amount of hydrogen consumed by the fuel cell, respectively. the capacity of the hydrogen tank, while and specify the minimum and maximum operating ranges for the tank’s state of charge. and represent the initial and final state of charge of the hydrogen tank. denotes the amount of hydrogen consumed by hydrogen fuel cell vehicles during charging. Unlike EVs, which can receive power at locations other than where the BESS is installed, hydrogen can only be supplied at the site where the HESS is located, thereby influencing the SOC constraints.
Constraints (23)–(30) represent the operation constraints of the HESS. It includes a total summation of fuel cell and electrolyzer (23), converting efficiency to electricity (24), converting efficiency to hydrogen (25), minimum and maximum power limits (26) and (27), the available amount of charging and discharging hydrogen considering efficiency (28), minimum and maximum SOC (29), and initial and final SOC (30).
3.3. Microgrid Optimal Rescheduling After Fault by Disaster
3.3.1. Fault Scenarios and Power Management
It is assumed that the microgrid operates the BESS and HESS in accordance with the day-ahead optimal scheduling results. In this study, the objective is to simulate an unforeseen sudden fault in the system triggered by a disaster. When a fault occurs within the microgrid, it is assumed that measurement devices can detect both the time of the fault and the affected bus or line. Subsequently, circuit breakers operate normally to isolate the fault, causing the remainder of the network connected to the affected bus or line to be separated from the main grid and lose its power supply. This isolated network must then rely on the renewable energy sources and energy storage devices available within the separated system to supply power to both critical and general loads. Consequently, it becomes necessary to develop a new optimal load shedding and power supply plan for the isolated network.
First, since the power generated by RESs is inherently uncontrollable and non-storable, it must be consumed on a priority basis. In instances where the generation from RES exceeds the load demand in the isolated network, any surplus energy can be stored in the ESSs for utilization during other periods. Conversely, if RES generation is insufficient to meet the load demand, the deficit must be compensated by discharging energy stored in the ESS. Moreover, if an anticipated outage period is expected to result in inadequate power supply for critical loads, it may be necessary to limit the use of ESS and, if required, implement load shedding for non-critical loads to conserve energy for essential services. Therefore, it becomes imperative to redefine the objective function and associated constraints to simultaneously minimize power losses and maximize power supply.
3.3.2. Reconstruction of the Objective Function and Constraints
In cases where continuous power supply to a critical load is prioritized, the resulting operational plan and power supply targets would differ from those obtained when only power losses are considered. Unlike the conventional approach where power is delivered to loads from the closest RESs and ESSs, prioritizing the critical load means that power is allocated to it even if it increases the line losses. This could lead to higher losses depending on the distance from the RES/ESS, ultimately reducing the overall power supply capability of the system and diminishing the number of loads that can be restored. While loads in a microgrid are generally close, feeder lengths can be several hundred meters to several kilometers long. Especially in distribution network environments, distance-induced voltage drops and energy loss can influence the prioritization and pricing of supply, particularly under constrained conditions. To simulate this scenario, objective function and constraints are formulated as follows:
where represents the total amount of power not supplied due to outages, summed over each time interval. The objective of the isolated network is to minimize the loads experiencing outages caused by power shortages. In this formulation, and are the disconnection switches for normal loads and critical loads, respectively; a value of 0 indicates that current flows, while 1 indicates that the circuit is interrupted. Here, refers to the bus number in the isolated network and denotes the time steps over the 24-h period following the outage. and are the weights assigned to normal loads and critical loads, respectively. The higher weighting for critical loads ensures that power supply to these loads is prioritized during the optimization process. and indicate the power demand required by the normal and critical loads at each time interval. represents the total renewable energy generation at each bus for each time period, with and denoting the power generated by PVs and WTs, respectively. Finally, represents the combined output from both the BESS and HESS.
Unlike the optimization process on the normal state, where the loads at each bus are aggregated to calculate the total load, fault scenarios require that the supply status of each load is evaluated individually. In such cases, loads must be defined and calculated on an individual basis. Critical loads are prioritized for power supply, meaning that, depending on the time-varying supply-demand balance, general household loads are disconnected first. If the available power is still insufficient to supply even the critical loads, power to these critical loads will also be disconnected. In contrast, the solar PV and wind generation in the isolated network are aggregated in the same manner as the original profile. However, if generation in certain time periods is excessive, some generation units may be temporarily disconnected through curtailment.
3.4. Electric Pricing for Key Customers
Key customers are generally those with high electricity consumption or those who significantly influence grid operation. Since these customers require a stable and continuous power supply, power companies must manage and respond to them separately. In this study, the prioritization of power supply to these customers during disaster scenarios is considered. Accordingly, a method is proposed for determining an appropriate power contract price that incorporates both the power compensation costs for general loads and a penalty reflecting the grid impact arising from large capacity connections.
3.4.1. Outage Compensation Cost
Rescheduling for the isolated network is conducted with the primary objective of minimizing line losses, except in cases where there is a specific rationale for deviation. This optimization is heavily influenced by the location and supply capabilities of the DERs within the isolated system. Consequently, loads that are not selected for supply will experience outages, potentially incurring outage compensation costs for the power company. However, if the prioritization of critical loads results in a reduction in power supply to normal loads compared to the original level, key customers are required to bear a certain proportion of the outage compensation cost corresponding to the decrease in supplied power. The outage cost functions for the general supply and prioritized supply cases are formulated as follows:
where represents the total outage compensation cost under the general supply scenario, while denotes the total outage compensation cost when power is prioritised for key customers. and indicate, respectively, the set of buses in the isolated network and the set of time intervals following the outage. represents the unsupplied load demand at bus i at time t, as determined by the optimization process. reflects the compensation limit corresponding to the duration of the outage.
3.4.2. Penalty Based on Voltage Sensitivity
Voltage sensitivity is a tool used to analyze how the system voltage changes in response to the magnitude of the loads connected to the grid. Moreover, even for identical loads, the impact on the system can vary depending on the connection location. Consequently, penalties can be established based on both the location and size of the load. These penalties are determined by comparing the system voltage before and after the connection of the contracted load, with the voltages calculated through power flow analysis. The overall voltage change across the system is then averaged, and the resulting voltage margin is computed. This margin is used to assess whether additional infrastructure enhancements are required, and the associated construction costs for transformers or lines are subsequently incorporated into the contract. The equipment-burden cost due to voltage drop is calculated by annualizing the additional line construction cost and multiplying by the average per-unit voltage drop across all buses as follows:
where represents the additional infrastructure expansion cost that may arise due to the capacity of the connected key customer. denotes the cost incurred for installing new power infrastructure required to enhance system stability in response to new network connections. is the system voltage at bus before the contracted load is connected, while represents the system voltage at bus when the contracted load is connected. denotes the total number of buses in the network.
3.4.3. Total Electricity Contract Price
The final contract price for key customers is determined by adding the system maintenance costs and the outage compensation costs to the existing time-dependent power selling prices for general loads. The final price can be calculated by following the equation:
where denotes the final contract price for key customers. To express this price on an hourly basis, the system maintenance costs, and outage compensation costs are calculated by dividing the total amounts by 365 days and 24 h.
4. Result Analysis
Based on the Modified IEEE 123 Node Feeder System as shown in Figure 1, the proposed process is implemented and validated by comparing the outcomes. To achieve this, profiles for each DER and load are defined, and equipment parameters are specified to closely resemble an actual system. Subsequently, a data preprocessing stage is conducted to synchronize the time intervals and eliminate errors. The refined data are then incorporated into the objective function and constraints for optimization.
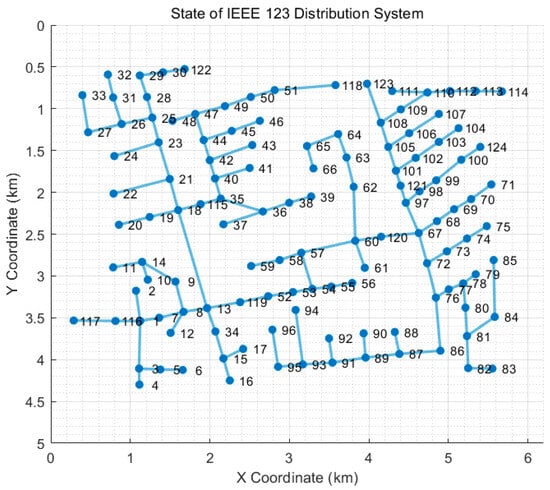
Figure 1.
Modified IEEE 123 Node Feeder system.
This approach allows for a comparison between the conventional pricing model—which considers only power losses—and the pricing model proposed in this study, which also accounts for voltage sensitivity and prioritized power supply. The mathematical formulation and optimization are performed using ‘Yalmip’ and ‘Gurobi’, with the simulation executed in MATLAB 2023b.
4.1. Load and RES Profiles
General loads are represented by arbitrary profile data that reflect the patterns observed in actual data and vary according to the types and numbers of loads present at each bus. The general load is composed of residential loads and commercial loads , each exhibiting different characteristics across time intervals. The final amount of general load consumed at a bus is determined by multiplying the number of loads allocated to that bus by the corresponding power consumption for each time interval. The total load at time interval is obtained by summing the individual demands of all loads as follows:
The key load consists of a data station , hospital , fire station , and communication station , with each component exhibiting distinct data patterns. In this study, it is assumed that the infrastructures for the hospital, fire station, and communication center are already connected, while the data center is being newly connected. Furthermore, the prioritized supply scenario is assumed to be exclusively applied to the data center. The load profile for key customers is structured as follows:
Total RES generation consists of PV and WT generation as the following equation. The PV component is modelled with a bell-shaped, consistent output profile, while the WT component incorporates the inherently variable nature of wind by adding random noise to its profile. Furthermore, the total power generated at each bus depends on the number of PV and WT units allocated to that bus.
It is assumed that the demand from EV is met via 100 kW-level DC fast chargers, and the charging profile reflects the typical daily pattern of EV charging. Generally, there is a high charging demand immediately after the start and end of the working day. A similar charging pattern is assumed for FCEVs .
4.2. Parameter Settings
To reflect the characteristics of the equipment, arbitrary values for the multi-energy sources and network facilities are assumed, as shown in Table 1. Most of these settings are based on a one-hour interval, and the scheduling time interval can be adjusted by multiplying with the time interval variable (). The capacities of the BESS and HESS are set to be identical, and their dynamic characteristics are not incorporated in the static state analysis. However, recognizing that the BESS has a fast response while the HESS is typically used for long-term, high-capacity storage, the parameters are configured such that the BESS operates within a robust, lower SOC range, whereas the HESS maintains a wider SOC range around a mid-level SOC.

Table 1.
Parameter settings of BESS, HESS and Microgrid.
4.3. Data Preprocessing
When utilizing actual load and generation data, the collected datasets often include measurement errors, outliers, and missing data. Consequently, it is essential to preprocess the data through filtering. This preprocessing involves normalization and interpolation, which helps to address and compensate for outliers and missing data.
Since the time intervals of each dataset are not aligned, it is essential to standardize these intervals across all data. Inconsistent time intervals can lead to variations in the results of correlation or pattern analyses between datasets. In this study, data are sorted based on the dataset with the largest time interval, which is one hour. Thereafter, linear interpolation is applied to adjust the data to the desired scheduling time interval. The distribution of load data across different time intervals is shown in Figure 2.
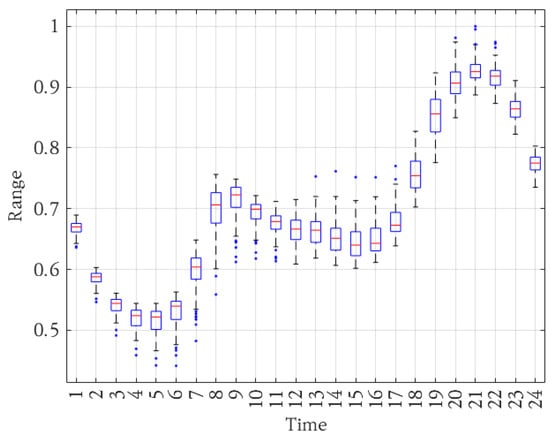
Figure 2.
The distribution of hourly load data. The red line represents the average value, and the blue box indicates the 25% to 75% confidence interval.
Outlier removal is performed on a per-time-interval basis, with data points falling outside the 95% confidence interval for each interval identified as outliers and subsequently removed. Furthermore, normalization is applied to preserve the inherent patterns of the actual data while enabling their use in generating diverse load capacity profiles. Based on the refined data, the distribution of values for each time interval is compiled. Sampling from these time interval distributions then allows for the creation of various scenarios, which can serve as test cases in the analysis.
4.4. Simulation Results and Analysis
4.4.1. Estimating Outage Compensation Cost Based on Optimal Scheduling
By aggregating the profiles, the total generation and load can be depicted as time-series graphs, as shown in Figure 3. This scenario assumes that, for most time intervals, the load exceeds the renewable generation; however, there are specific periods when the renewable generation surpasses the load.
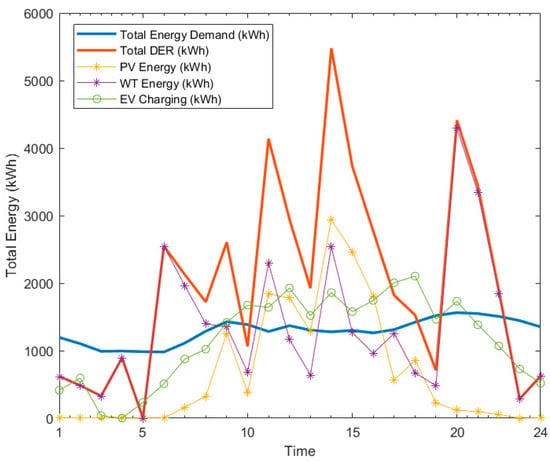
Figure 3.
Hourly total DER and load profile.
The microgrid is equipped with PV, WT, BESS, and HESS installations, and the system operator simulates the charge/discharge scheduling of the energy storage and electrolysis systems to minimize operational costs. In Figure 4, the optimal scheduling results for the BESS and HESS at each bus are illustrated, where the number following each device indicates its corresponding bus location. The sign of the BESS output indicates whether the system is charging or discharging. A positive value means that the BESS is discharging and supplying power to the grid, while a negative value indicates that the BESS is charging by receiving power from the grid. It is evident that the BESS does not exceed its maximum charge/discharge limit of 500 kW, and its SOC remains within the prescribed 20% to 80% range. Additionally, due to significant fluctuations in DER generation, the charge/discharge patterns of the BESS exhibit corresponding variability.
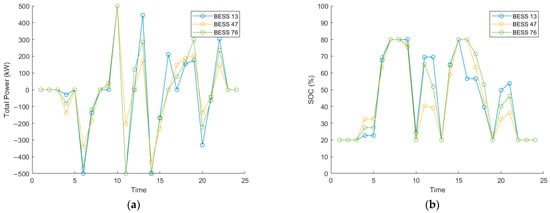
Figure 4.
Optimal scheduling of BESSs: (a) Hourly power of BESSs; (b) Hourly SOC of BESSs.
The proposed model defines the rated capacities, maximum/minimum state of charge (SOC) limits, charging/discharging rates, maintenance costs, and efficiencies of the BESS and HESS separately to reflect their distinct operational characteristics. The charging/discharging profiles and SOC results for the HESS are presented in Figure 5. It shows that HESS units on different buses exhibit varying charge/discharge amounts influenced by power flow and loss calculations. Compared to the BESS, which is characterized by rapid charge/discharge capabilities, the HESS—with its larger capacity and wider SOC operating range—shows a more stable charging/discharging profile and does not reach its maximum output. This outcome reflects the system constraints prioritizing the fast response of the BESS, while the HESS is intended for longer-term, less dynamic energy storage. Simultaneous charging of both BESS and HESS may occur under two main conditions: (1) when the surplus generation exceeds the maximum charging limit of the BESS or (2) when lower electricity prices are anticipated in the following period, prompting delayed charging to optimize cost-effectiveness.
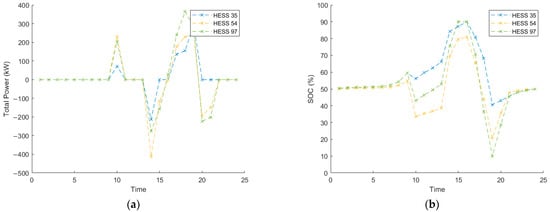
Figure 5.
Optimal scheduling of HESSs: (a) Hourly power of HESSs; (b) Hourly SOC of HESSs.
It is assumed that, prior to a disaster-induced line fault, the BESS and HESS operate according to the 24 h scheduling plan. The fault is assumed to occur randomly at a specific time and on a particular line. Upon the occurrence of the fault, it is assumed that the circuit breaker immediately isolates the affected line as intended, thereby creating an isolated network. To self-sustain power supply, the isolated network identifies the available resources within it and performs a new round of optimization based on those resources. The power generation profiles for solar PVs and WTs remain unchanged from those used in the day-ahead optimization. In this study, a fault on the line connecting bus 54 and bus 57 results in an isolated network that is separated from the main grid at 18:00. As illustrated in Figure 6, the isolated network retains a radial configuration, rendering it incapable of receiving external power. Figure 7 displays the time-series profiles of normal loads and critical loads for each bus within the isolated network.
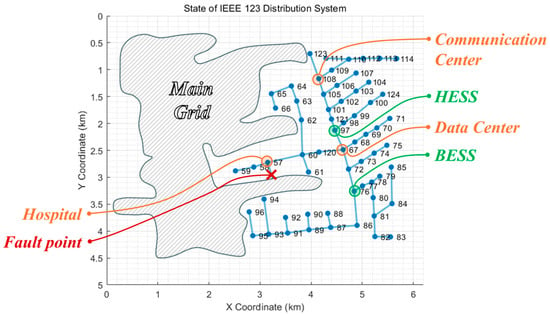
Figure 6.
Topology of isolated network.
Figure 7.
The time-series profiles of normal loads and critical loads for each bus: (a) Power demand of normal loads; (b) Power demand of critical loads.
In the isolated network, loads are connected at every bus, resulting in a total of sixty-two loads, with two of these classified as critical loads. There are also four wind generation plants and five solar PV plants connected. Figure 8 illustrates the total generation and load profiles over time. At the time of the outage, according to the optimal scheduling, the SOC of the BESS and HESS were 53.12% and 36.67%, respectively, which correspond to total stored energies of 265.6 kWh and 366.73 kWh. Considering safety requirements—with a minimum SOC of 20% for the BESS and 10% for the HESS—the available energy is reduced to 165.6 kWh for the BESS and 266.73 kWh for the HESS. Although the total renewable energy generation during the outage period is 5261.95 kWh, if renewable generation significantly exceeds load at certain times, the output limitations of the BESS and HESS may prevent the optimal utilization of all available energy. Accordingly, the available total energy and the required load are summarized in Table 2.
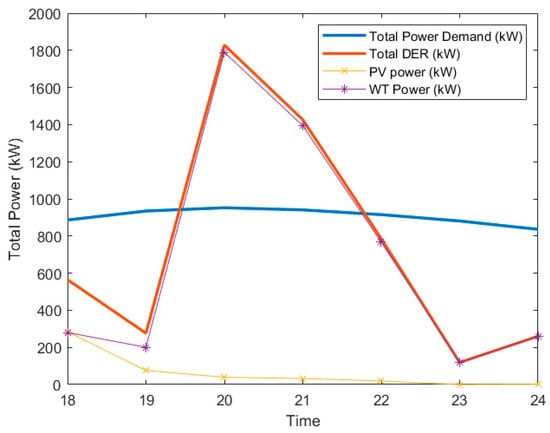
Figure 8.
Hourly total power of DER and load in isolated grid.

Table 2.
Post-fault total load and available energy in the islanded microgrid.
In the isolated network, one BESS and one HESS are connected. The optimal charging/discharging scheduling results are presented in Figure 9 and Figure 10. Between 20:00 and 22:00, the output from the DERs temporarily exceeds the network load, resulting in both the BESS and HESS operating in charging mode. However, due to the maximum charging capacity constraint of the BESS, its charging rate decreases more rapidly compared to that of the HESS.
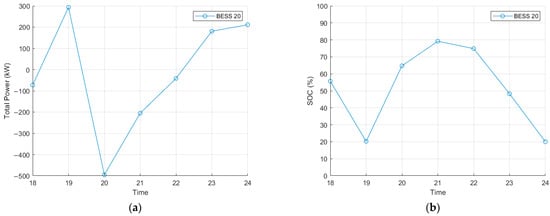
Figure 9.
Optimal rescheduling of BESSs: (a) Hourly power of BESSs; (b) Hourly SOC of BESSs.
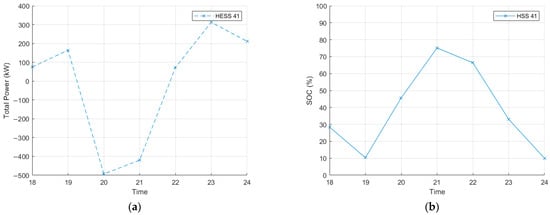
Figure 10.
Optimal rescheduling of BESSs: (a) Hourly power of HESSs; (b) Hourly SOC of HESSs.
Figure 11 shows the results of load shedding performed due to imbalances between supply and demand during the optimal scheduling process. Figure 11a presents the load shedding outcome when no distinction is made between critical and normal loads, focusing solely on minimizing power losses across the entire isolated network. In contrast, Figure 11b displays the results of optimization that exclusively considers continuous and prioritized power supply to key customers. Here, the x-axis represents the time from the occurrence of the disaster up to 24:00, while the y-axis denotes the buses in the isolated network. As shown in Figure 11b, when continuous and prioritized supply to key customers is implemented, the duration during which power is supplied to normal loads is reduced compared to the scenario without such prioritization. This outcome can be attributed to the significantly higher demand from key customers and the additional power losses incurred during the prioritization process, which together lead to a shorter supply period for normal loads.
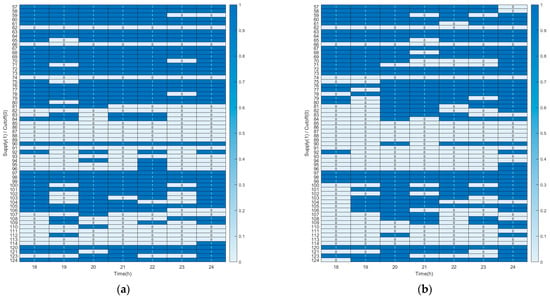
Figure 11.
The result of load shedding for normal load: (a) without considering key customers; (b) with considering continuous and prior supply for key customers.
Figure 12 and Figure 13 present the results before and after considering critical loads. When comparing the supply levels for normal loads versus critical loads, the scenario incorporating prioritized supply reveals that power is first allocated to critical loads before addressing normal loads. As a result, although the supply available to normal loads decreases, the power delivered to critical loads is maintained continuously for 7 h. In contrast, in scenarios where prioritized supply for critical loads is not implemented, the demand of critical loads is met only intermittently, rather than being sustained consistently over the period.
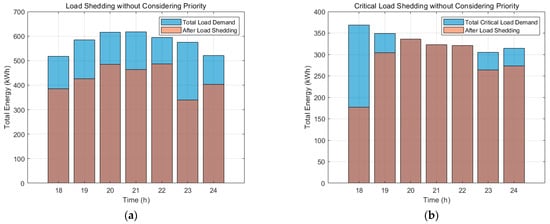
Figure 12.
Ratio of actual supplied power to total load demand without considering key customers: (a) supplied power to normal load; (b) supplied power to key customers.
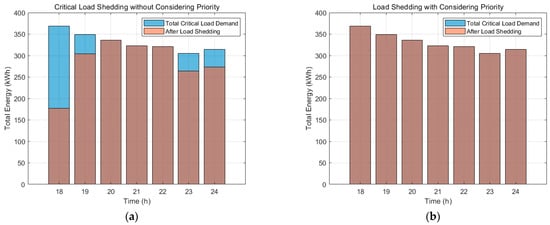
Figure 13.
Ratio of actual supplied power to total load demand with considering continuous and prior supply for key customers: (a) supplied power to normal load; (b) supplied power to key customers.
In Table 3, the results show the total supplied power for scenarios with and without prioritized supply. Without prioritization, the total power supply amounts to 4985.57 kWh. When prioritized supply is considered, the total supplied power increases to 5092.27 kWh. However, this prioritization results in an unsupplied power amount of 212.52 kWh for normal loads.

Table 3.
Power supply comparison between normal and critical loads with priority.
4.4.2. Estimating Voltage Stability Penalty Based on Voltage Variation
Figure 14 displays the average bus voltages obtained from power flow analysis over a 24-h profile of the IEEE 123 system. For example, Figure 14a shows the average voltage at each bus before the connection, whereas Figure 14b illustrates the average voltage when the data center is connected at bus 67. It is evident that, following the connection of the data center, the overall average voltage across the system decreases. In particular, it can be observed that the terminal buses located on the same feeder as the data center experience a slightly greater average voltage drop than other buses.
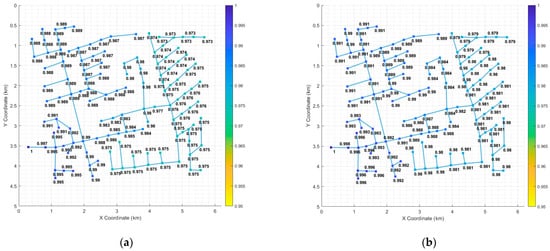
Figure 14.
Voltage analysis results for a 24-h profile: (a) base case; (b) case with a 200 kW data center connected.
As shown in Table 4, although the voltage drop does not fall below the minimum voltage threshold of 0.9 p.u., the overall reduction in system voltage can be interpreted as a decrease in grid stability. From the system operator’s perspective, this necessitates additional infrastructure installation or more frequent maintenance, which should be reflected in the power contract pricing. Specifically, the average voltage drop is 0.003 p.u., with the minimum voltage also decreasing by 0.003 p.u.

Table 4.
Average voltage drop of a 24 h profile when a 200 kW data center installed.
4.4.3. Estimating Electricity Price Based on Compensation Cost and Voltage Variation
Key customers, unlike other general loads, consume significantly more power and have a substantial impact on grid operations, thus necessitating additional management and response strategies by the utility. Accordingly, it is common practice to impose penalties that account for the impact on grid operations and to establish a customized contract price in the form of network contribution fees or burden charges. In particular, this study focuses on incorporating the cost of prioritized supply during disaster scenarios and the penalty cost associated with grid stability into the pricing framework.
In general, the weighting factor for outage compensation costs increases with longer outage durations. In this study, the 24 h period is divided into four segments, with compensation cost multipliers of 1, 3, 5, and 10 applied at every 6 h interval. In the fault scenario, an outage duration of 7 h falls into the second segment, corresponding to a multiplier of 3. Therefore, as shown in Table 5, the expected outage compensation cost is calculated by multiplying the maximum power price by the unsupplied load of normal loads resulting from prioritized supply, and then applying the weighting factor. Although this study assumes one outage per year, the compensation cost could be determined by reflecting the actual frequency of disaster events in the system.

Table 5.
Compensation cost estimation.
The grid stability penalty cost reflects the proportional voltage drop resulting from the connection of new contracted capacity. Typically, this involves estimating the additional line construction costs needed to alleviate congestion and the ongoing maintenance expenses. As shown in Table 6, if approximately 1 km of additional line construction is anticipated, a construction cost of $150,000 is assumed, with an annual operation and maintenance (O&M) cost of 2% of the installation expense.

Table 6.
Investment cost estimation.
Given that the power price typically varies on an hourly basis under a Time of Use (TOU) scheme, it is necessary to determine the hourly power price. Therefore, the total annual cost—which includes both compensation and investment costs—is divided by 365 days and 24 h to derive an hourly power contract price, as presented in Table 7. The hourly conversion of the compensation and investment costs amounts to $0.5407, and when this is factored in, the new TOU tariff is calculated to range between $0.6270 and $0.7715.

Table 7.
Final contract price estimation considering compensation and penalty.
4.5. Discussion
Both a single-profile scenario and an outage scenario are defined in this study, and SOCP and MISOCP methodologies are employed to estimate the unsupplied power for normal loads and to assess the impact on system voltage when critical loads are connected. Based on these analyses, the final contract price for key customers was calculated. The derived final contract price is approximately 3 to 6 times higher than the conventional rate. On this basis, additional conditions—such as demand response or power factor improvement measures—could be introduced to moderate the contract price. Moreover, the price for the first year reflects the cost-sharing of network reinforcement, while from the second year onward, only the maintenance cost is considered, potentially allowing for a lower-priced power supply.
This pricing strategy enables fair and balanced negotiations between critical loads and the grid operator, while contributing to the maintenance of grid stability and reliability. In addition, by explicitly reflecting outage compensation for normal loads in the event of prioritized supply during disasters, the proposed approach is expected to enhance social equity. For example, the grid operator could utilize the additional funds to invest in supplementary infrastructure to improve overall grid stability or to accumulate compensation funds for outages caused by prioritized supply, thereby mitigating financial risks associated with disasters.
While the current research assumes a single profile and scenario, future work can examine a broader range of scenarios to derive even more reasonable contract prices. Incorporating additional factors, such as mobile resources, may further improve the practicality and applicability of the proposed methodology.
5. Conclusions
In this study, the methodology is proposed for calculating the power contract price for key customers during outages by incorporating both outage compensation costs and voltage drop penalties. To simulate scenarios where parts of the microgrid become isolated due to faults, the proposed method includes SOCP-based optimization for the pre-outage scheduling of BESS and HESS, and MISOCP-based optimization to model both normal supply conditions and situations with prioritized supply to key customers.
Prior to an outage, the ESSs including BESS and HESS are optimized using SOCP. A fault scenario is then defined—for instance, a fault on the line connecting buses 54 and 57—which results in an isolated network. In this isolated network, the DERs must maintain supply–demand balance, and loads are categorized into critical loads and normal loads with set priorities. Rather than discharging energy solely based on the total load demand per time interval, the discharging strategy is designed to ensure continuous power supply to critical loads. To achieve this, the objective function assigns higher weights to critical loads, and the MISOCP optimization process determines the optimal timing and locations for load shedding.
This approach enables the system to maximize the supply available to normal loads while ensuring that the power supply to critical loads remains uninterrupted. Consequently, the unsupplied power for normal loads due to prioritization can be quantified, and the voltage drop caused by connecting critical loads is incorporated to propose a final power contract price. It is expected that the power company will be able to use the additional costs to expand network facilities and secure funding for outage compensation.
Author Contributions
Conceptualization, S.K. and S.C.; data curation, S.K. and Y.S.; formal analysis, Y.S., H.W. and X.Z.; funding acquisition, S.C.; investigation, S.C.; methodology, S.K., H.W., X.Z. and S.C.; project administration, S.C.; resources, S.K.; software, Y.S. and X.Z.; supervision, S.C.; validation, S.K., Y.S. and S.C.; visualization, S.K. and Y.S.; writing—original draft, S.K.; writing—review and editing, Y.S. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Korea Electric Power Corporation (No. R24XO02-2) and in part by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (No. RS-2023-00234707).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DER | Distributed energy resource |
| EV | Electric vehicle |
| FCEV | Fuel cell electric vehicle |
| PV | Photovoltaic |
| WT | Wind turbine |
| BESS | Battery energy storage system |
| HESS | Hydrogen energy storage system |
| SOCP | Second-order conic programming |
| MISOCP | Mixed-integer second-order conic programming |
| ESS | Energy storage system |
| HILP | High impact, low probability |
| FERC | Federal Energy Regulatory Commission |
| MILP | Mixed-integer linear programming |
| SOC | State-of-charge |
| V2G | Vehicle-to-Grid |
| BMS | Battery management system |
| PCS | Power conversion system |
| BOP | Balance of Plant |
| O&M | Operation and maintenance |
| TOU | Time of use |
Appendix A

Table A1.
The nomenclature for the defined parameters.
Table A1.
The nomenclature for the defined parameters.
| Parameter | Meaning |
|---|---|
| The total operation cost of the microgrid | |
| The total cost of power trade with outer grid | |
| The total cost of RES | |
| The total cost of ESS maintenance | |
| The total cost of EV charging | |
| The total revenue of customer sales | |
| The costs of purchasing power from the outer grid at time | |
| The costs of selling power to the outer grid at time | |
| The quantities of power purchased from the outer grid at time | |
| The quantities of power sold to the outer grid at time | |
| The purchasing cost of RES power at time | |
| The quantities of RES power generated at time located on bus | |
| The maintenance costs of the BESS | |
| The maintenance costs of the HESS | |
| The charging quantities of the BESS on the bus at time | |
| The discharging quantities of the BESS on the bus at time | |
| The quantities of the HESS output on the bus at time | |
| The EV charging price at time | |
| The quantities of EV charging on the bus at time | |
| The selling price of the power company to customers at time | |
| The demand of the loads on the bus at time | |
| The total demand of key customers | |
| The total demand of residential customers | |
| The total demand of key and residential customers | |
| The total demand of data station | |
| The total demand of hospital | |
| The total demand of communication station | |
| The total power generated by PV | |
| The total power generated by WT | |
| The total power generated by RES | |
| The total power generated by BESS | |
| The total power generated by HESS | |
| The total demand of customer | |
| The total demand of EV | |
| The total demand of FCEV | |
| The ratio of reactive power to active power | |
| The reactive power supplied by RES | |
| The sum of charging/discharging of the BESS on the bus at time | |
| The maximum output of the BESS | |
| The rated energy capacity of the BESS | |
| The SOC of the BESS on the bus at time | |
| The minimum SOC of the BESS | |
| The maximum SOC of the BESS | |
| The initial SOC of the BESS | |
| The final SOC of the BESS | |
| The conversion efficiency during charging of the BESS | |
| The conversion efficiency during discharging of the BESS | |
| The power from the fuel cell of the HESS on the bus at time | |
| The hydrogen from the electrolyzer of the HESS on the bus at time | |
| The maximum output of the fuel cell | |
| The maximum output of the electrolyzer | |
| The hydrogen produced by the electrolyzer | |
| The hydrogen consumed by the fuel cell | |
| The maximum capacity of hydrogen tank | |
| The hydrogen demand of FCEV | |
| The SOC of the HESS on the bus at time | |
| The minimum SOC of the HESS | |
| The maximum SOC of the HESS | |
| The initial SOC of the HESS | |
| The final SOC of the HESS | |
| The conversion efficiencies from hydrogen to electricity | |
| The conversion efficiencies from electricity to hydrogen | |
| The total amount of power not supplied due to outages | |
| The switches for normal loads on the bus at time | |
| The switches for critical loads on the bus at time | |
| The weights assigned to normal loads on the bus | |
| The weights assigned to critical loads on the bus | |
| The demand of normal loads on the bus at time | |
| The demand of critical loads on the bus at time | |
| The power generated by PVs on the bus at time | |
| The power generated by WTs on the bus at time | |
| The combined output from the BESS and HESS on the bus at time | |
| The total compensation cost under the general supply scenario | |
| The total compensation cost under the prioritized supply scenario | |
| The unsupplied load demand on the bus at time | |
| The compensation cost of the outage | |
| The additional infrastructure expansion cost | |
| The cost incurred for installing new power infrastructure | |
| The system voltage at bus before the contracted load is connected | |
| The system voltage at bus when the contracted load is connected | |
| The final contract price for key customers | |
| , | The voltage of the bus or |
| The current of the line between and | |
| The resistance of the line between and | |
| The reactance of the line between and | |
| The active power flowing through the line between and | |
| The reactive power flowing through the line between and | |
| The active power at bus | |
| The reactive power at bus | |
| The minimum voltage | |
| The maximum voltage | |
| The maximum current | |
| The total active power of the grid | |
| The total reactive power of the grid | |
| Time variable | |
| Time scale | |
| Bus number | |
| The total number of buses in the network | |
| The set of buses in the isolated network | |
| The set of time intervals following the outage |
References
- Stephanie, P. Federal Regulation for a “Resilient” Electricity Grid. Ecol. Law Q. 2019, 46, 417. [Google Scholar] [CrossRef]
- Sun, X.; Chen, J.; Zhao, H.; Zhang, W.; Zhang, Y. Sequential Disaster Recovery Strategy for Resilient Distribution Network Based on Cyber–Physical Collaborative Optimization. IEEE Trans. Smart Grid 2023, 14, 1173. [Google Scholar] [CrossRef]
- Qi, M.; Zhang, F.; Zhang, G. Sequential disaster recovery strategy for distribution network considering maintenance crew scheduling. J. Phys. 2024, 2823, 012062. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Q.; Qin, M.; Yang, Y. A Post-Disaster Fault Recovery Model for Distribution Networks Considering Road Damage and Dual Repair Teams. Energies 2024, 17, 5020. [Google Scholar] [CrossRef]
- Moglen, R.; Leibowicz, B.D.; Kwasinski, A.; Cruse, G. Optimal restoration of power infrastructure following a disaster with environmental hazards. Socio-Econ. Plan. Sci. 2024, 95, 101974. [Google Scholar] [CrossRef]
- Zhang, X.; Son, Y.; Choi, S. Optimal scheduling of battery energy storage systems and demand response for distribution systems with high penetration of renewable energy sources. Energies 2022, 15, 2212. [Google Scholar] [CrossRef]
- Zhang, X.; Son, Y.; Cheong, T.; Choi, S. Affine-arithmetic-based microgrid interval optimization considering uncertainty and battery energy storage system degradation. Energy 2022, 242, 123015. [Google Scholar] [CrossRef]
- Zhang, X.; Woo, H.; Choi, S. An interval power flow method for radial distribution systems based on hybrid second-order cone and linear programming. Sustain. Energy Grids Netw. 2023, 36, 101158. [Google Scholar] [CrossRef]
- Zhang, X.; Shin, D.; Son, Y.; Woo, H.; Kim, S.-Y.; Choi, S. Three-stage flexibility provision framework for radial distribution systems considering uncertainties. IEEE Trans. Sustain. Energy 2023, 14, 948. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Saraf, P.; Hadidi, R.; Makaram, E.B. Energy management system for enhanced resiliency of microgrids during islanded operation. Electr. Power Syst. Res 2016, 137, 133. [Google Scholar] [CrossRef]
- Zafar, R.; Mahmood, A.; Razzaq, S.; Ali, W.; Naeem, U.; Shehzad, K. Prosumer based energy management and sharing in smart grid. Renew. Sustain. Energy Rev. 2018, 82, 1675. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Y.; Xu, Y.; Liu, C.-C. Resilience-Oriented Critical Load Restoration Using Microgrids in Distribution Systems. IEEE Trans. Smart Grid 2016, 7, 2837. [Google Scholar] [CrossRef]
- Rajbhandari, Y.; Marahatta, A.; Shrestha, A.; Gachhadar, A.; Thapa, A.; Gonzalez-Longatt, F.; Guerrero, J.M.; Korba, P. Load prioritization technique to guarantee the continuous electric supply for essential loads in rural microgrids. Int. J. Elec. Power 2022, 134, 107398. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Jordehi, A.R.; Fernández-Lobato, L.; Jurado, F. Robust energy management in isolated microgrids with hydrogen storage and demand response. Appl. Energy 2023, 345, 121319. [Google Scholar] [CrossRef]
- Su, J.; Zhang, R.; Dehghanian, P.; Kapourchali, M.H.; Choi, S.; Ding, Z. Renewable-dominated mobility-as-a-service framework for resilience delivery in hydrogen-accommodated microgrids. Int. J. Electr. Power Energy Syst. 2024, 159, 110047. [Google Scholar] [CrossRef]
- Yoon, Y.; Son, Y.; Choi, S. Deep reinforcement learning-based operation strategy for high resilience distribution system. IET Conference Proceedings. IET Conf. Proc. 2025, 2024, 1132. [Google Scholar] [CrossRef]
- Hosseini, M.M.; Parvania, M. Resilient Operation of Distribution Grids Using Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2022, 18, 2100. [Google Scholar] [CrossRef]
- Gautam, M.; Abdelmalak, M.; MansourLakouraj, M.; Benidris, M.; Livani, H. Reconfiguration of Distribution Networks for Resilience Enhancement: A Deep Reinforcement Learning-based Approach. In Proceedings of the IEEE IAS, Detroit, MI, USA, 9–14 October 2022; p. 1. [Google Scholar] [CrossRef]
- Sharifpour, M.; Ameli, M.T.; Ameli, H.; Strbac, G. A Resilience-Oriented Approach for Microgrid Energy Management with Hydrogen Integration during Extreme Events. Energies 2023, 16, 8099. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Valverde, L.; Bordons, C. Optimal Load Sharing of Hydrogen-Based Microgrids With Hybrid Storage Using Model-Predictive Control. IEEE Trans. Ind. Electron. 2016, 63, 4919. [Google Scholar] [CrossRef]
- Son, Y.; Woo, H.; Noh, J.; Dehghanian, P.; Zhang, X.; Choi, S. Optimization of energy storage scheduling considering variable-type minimum SOC for enhanced disaster preparedness. J. Energy Storage 2024, 93, 112366. [Google Scholar] [CrossRef]
- Correia, A.F.M.; Antonio Goncalves Neves, M.; Isabel Casal Dos Reis, A.; Paulo Coimbra, A.; Richard de Oliveira de Almeida, T.; Moura, P.; de Almeida, A.T. Architecture and Operational Control for Resilient Microgrids—A University Case Study. IEEE Access 2025, 13, 51373. [Google Scholar] [CrossRef]
- Correia, A.F.M.; Moura, P.; de Almeida, A.T. Technical and Economic Assessment of Battery Storage and Vehicle-to-Grid Systems in Building Microgrids. Energies 2022, 15, 8905. [Google Scholar] [CrossRef]
- Masoud, F.; Steven, H.L. Branch Flow Model: Relaxations and Convexification-Part I. IEEE Trans. Power Syst. 2013, 28, 2554. [Google Scholar] [CrossRef]
- Woo, H.; Son, Y.; Cho, J.; Choi, S. Stochastic second-order conic programming for optimal sizing of distributed generator units and electric vehicle charging stations. Sustainability 2022, 14, 4964. [Google Scholar] [CrossRef]
- Qin, j.; Wan, Y.; Li, F.; Kang, Y.; Fu, W. Distributed Economic Operation in Smart Grid: Model-Based and Model-Free Perspectives, 1st ed.; Springer Nature: Singapore, 2023; p. 455. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).