Strength Iso-Responses of Shear-Deficient Ultra-High Performance Fiber Reinforced Concrete Beams

Abstract

The development of sustainable construction methods can be achieved by improving the performance of reinforced concrete elements, resulting in an increase in structural life expectancy. This paper presents a study of the structural performance of shear-deficient ultrahigh-performance concrete (UHPC) concrete beams to produce sustainable construction materials. In the first phase of the experimental campaign, performance-based optimizations were implemented for UHPC. The characteristic compressive strength of all mixes was kept at 130 ± 10 MPa. The elastic modulus of plain UHPC was obtained at 8 GPa, and for the fiber-reinforced one was 40 GPa. Additionally, 18 sets of reinforced UHPC beams were investigated for their structural behavior based on the overall depth, reinforcement ratio (ρ), and the shear-span-to-depth ratio (λ) as key variables. Here, λ was varied between 1 and 2 and ρ was varied between 0.56% and 3.15%. The experimental study determined the lowest shear strength as 4.56 MPa, and the highest shear strength was calculated as 11.34 MPa. The database of the current shear strength results and similar literature results were used to develop models for predicting shear capacity. This research focused on applying a statistical approach using neuro-fuzzy logic, the robust analytical model. The ratio of the experimentally calculated shear strength and the predicted shear strength for different values of λ and ρ was obtained between 0.75 and 1.25, which was in good agreement with the results of similar literature. The results of this study suggest that high-strength fiber may extend structural lifetimes in UHPC applications.

1. Introduction

Concrete is undoubtedly the most widely used manufactured material in the world for the construction of buildings and infrastructure, which can contribute to sustainable development [1,2,3]. Shear and bending are the two dominating responses to structural members, which are much investigated with the advances in concrete properties [4,5]. The failure pattern of reinforced concrete elements showed that the shear failure is more significant due to the weak performance of concrete [6,7]. Therefore, the literature review shows that an effort has been made to understand the shear behavior of RC structural members. Most of the research focused on investigating the influence of the controlling parameters, i.e., type of loading and support condition, the impact of effective depth to shear span ratio, application of transfer reinforcement, effects of strength, and performance of concrete [4,6,8,9,10].

The research findings revealed a significant enhancement in the properties of concrete, which contributed to a remarkable improvement in the shear behavior of structural members [11,12]. Therefore, ultra-high-performance concrete has become an exciting research subject for overcoming the challenges and issues faced in complex concrete structures [13,14]. It has been observed that normal concrete principally contributed to resisting compressive forces. Therefore, high or ultra-high-performance concrete (UHPC) enhanced mechanical properties, durability, pore structure, impact resistance, and, most importantly, post-cracking behavior [15,16].

UHPC has a wide range of applications, including building footbridges, using ABC systems to construct bridges more quickly, strengthening existing buildings, installing tunneling keystones using tunnel boring machines, constructing precast walls, marine platforms, overlaying damaged roads, urban furniture, and other architectural applications [17,18,19,20]. Sustainability in construction is of paramount importance to the scientific community [21], so it is imperative to keep in mind that special concretes must be produced in a way that not only ensures exceptional durability and mechanical properties but also is environmentally friendly and economically sustainable way.

In executing the concept of UHPC, the conventional concrete recipe was modified by adding ultra-fine reactive powder, and short discontinued fibers (steel and plastic composite) were mainly introduced. The American Concrete Institute, ACI committee 318 has presented fiber-reinforced concrete (FRC) mix design based on randomly oriented short steel fibers. ACI revision in 2008 showed that the randomly oriented short steel fibers could compensate for the requirements of minimum steel reinforcement in an RC beam. In further research, material models of steel-fiber-reinforced concrete were developed to widen the application of such composite [22,23].

With the encouraging results of fiber-reinforced concrete research and its recognition by various codes and standards for practical application, in the last 10 to 15 years, more synergetic research activities have been made in UHPC. The research outcome facilitated very high compressive strength, more than 100 MPa, ductility due to ultimate strain of up to 3%, refinement, and dispersion of cracks in the plastic zone. In such research, the main topics were investigating the effects of fiber characteristics (aspect ratio, shape, treatment, and texture) [24,25,26,27]. Table 1 compiled the findings of some research investigations dedicated to steel fiber; it can be viewed how the steel fiber behaved by different beam parameters.

Based on the objectives of the research, the UHPC mix design shows a considerable variation so the strength level, which made it not easy to develop a generalized mix design procedure. Furthermore, although the available research on UHPC is very diversified, there are very few guidelines available in various codes and standards for the structural design of UHPC members, especially members subjected to shear [28,29,30].

In the current studies, machine learning (ML) methods have been introduced in various structural engineering applications, for example, health monitoring, predictive material models, and seismic design of structures [30,31,32]. Various intelligent models were developed for predicting concrete mechanical and structural properties using ML algorithms [30,33]. For example, Vu and Hoang [34] used the least square support vector machine (LS-SVM) algorithm to predict the punching shear capacity of FRC slabs. Lee et al. [35] developed a computational model using the ANN technique to predict the shear capacity of slender FRC beams. Further, Lee et al. [35] reported that the ANN-based model yielded much better results than empirical relationships. Yan and Shi have also applied the SVM algorithm to predict Young’s modulus of concrete for normal and high-strength concrete [36].

For a possible application of UHPC in concrete structures, simplified design methodologies must be developed to optimize the properties of UHPC. Various recent articles have reported a computational framework for developing ML-based models to investigate the factors that influence the failure model and shear strength of UHPC beams [30,31,32,33,34,35,36,37]. For developing ML-based models, the experimental dataset from various studies has been compiled and used as input to the ML-based algorithms. Using pattern recognition techniques, the first step was determining which parameters affect the shear response of UHPC beams under load [30,38]. Then, most of the studies on UHPC concrete used support vector machines (SVMs), artificial neural networks (ANNs), and k-nearest neighbor analyses have been used to identify the majority of failure modes during experimentation with UHPC concrete, including shears, flexure-shears, and flexure-flexures. Based on the identified governing parameters for UHPC beams, genetic programming (GP) was used to develop correlations between the governing parameters in order to calculate the beams’ shear capacity. As reported in [30,31,32,33,34,35,36], shear capacity is affected by the geometric properties of beams, load configurations, and material properties, including fiber properties. To determine the shear capacity of UHPC beams, it is necessary to take into account geometric properties, loading configurations, and material properties. In the literature, three steps have been presented to predict UHPC performance using machine learning (ML): a priori data collection, failure mode classification, and prediction of shear capacity. The first step in the data collection was compiling UHPC beam data from numerous experimental programs. Next, features characteristic of UHPC beams were identified to identify critical parameters governing their shear response. Several patterns are modeled based on their key parameters, with particular emphasis on how they represent beams. In the next step, these patterns were input into the model to predict the failure mode. Finally, predictive equations were developed to estimate the shear capacity of UHPC beams GP [39,40,41,42,43].

As a result of their beneficial effects on strength and ductility, hybrid fiber system applications in UHPC are increasingly being pursued; however, their effects on the underlying materials and structures remain undetermined. Furthermore, the body of research lacks a comprehensive and reliable model for predicting the strength of UHPC beams that have been reinforced with bars for various applications.

The main objective of this paper was to investigate the structural performance of shear-deficient UHPC concrete beams and develop models for predicting shear capacity. This should improve the performance and lifespan of structures, thus contributing towards sustainable development. The literature mentioned that developing a structural design approach using UHPC is a complicated and complex issue. Some literature on the application of machine learning showed encouraging results. Therefore, this research focused on applying a statistical approach using a robust analytical model for predicting shear strength. A comprehensive experimental program was designed to determine the effects of controlling parameters. Eighteen sets of beams were cast with primary variables of the overall depth of the beam, reinforcement ratio, and the shear-span-to-depth ratio. A database of current results and related literature (66 beams in total) was developed to apply the neuro-fuzzy logic for shear strength prediction. Taking into account this relatively large number of analyzed data, the study will likely contribute to UHPC’s popularity by understanding the various factors influencing their behavior.

Table 1. An overview of studies on beam shear behavior in UHPC beams.

Ref.	Elements		Test		Dimensions (mm)				Material			Most Important Findings
	Type	No.	Type	Variables	$\mathit{h}$	$\mathit{L}$	$\mathit{a}$	${\mathit{b}}_{\mathit{w}}$	Type	Fibrous System	${\mathit{f}}_{\mathit{c}}^{\prime }$
[6]	Rectangular-beams	14	Four-point loading	$\lambda$, $\rho$, $\alpha$, $\zeta$, and longitudinal reinforcement strength	250	1800	Variable $\lambda$ = 1.51 to 3.02	150	UHPC	Micro steel fibers	80–116	The beam’s capacity was decreased due to an increase in $\lambda$ (in certain values); however, it marginally increased with increasing the tensile and transverse reinforcements. Additionally, the concrete plasticity model (CDM) was successfully employed to predict the behavior of beams with $\lambda$ of 1.75 to 3.0.
[40]	I-girders (Prestressed)	7	Three-point loading	$\zeta$	650	4000	2000	250	RPC	Micro steel fibers	150–170	The fibrous system significantly influences the cracking pattern and the ultimate load.
[41]		8		$\lambda$ and $\zeta$	650	4000, 8000	2000, 4000	500	UHPC	Micro steel fibers	122–140	The longitudinal shear failure could be a controlling design case for beams with a substantial moment gradient. Additionally, the CDM could be efficiently employed to design the UHPC beam under shear forces.
[42]	I-girders	11	Four-point loading	$\alpha$ (stirrups and/or fibers, or neither)	380	2000	760	230	UHPC	Micro steel fibers	151–194	The behavior of beams under shear was highly influenced by the fibrous content in the UHPC.
[37]	T-beams	12	Four-point loading	$\lambda$, $\rho$, and $\alpha$	500	2000–5000	Variable $\lambda$ = 1 to 4	140	RPC	Micro steel fibers	127–155	The response of girder to shear was notably influenced by $\lambda ,\rho$, and $\alpha$. For $\lambda =1-4$, the failure pattern was “shear compression” or “diagonal compression.”
[43]	T-beams reinforced with high-strength steel	11	Four-point loading	$\lambda$, $\zeta$, fiber type, $f_c^{\prime }$ and $\alpha$	140	1200	Variable $\lambda$ = 2.5 to 3.75	40	UHPC	Micro steel fibers	94–137 ($f_{cu}$)	Fibers are more practical in improving the shear behavior than the flexural behavior of beams. Additionally, both deformability and cracking strength have been enhanced by the use of fibers.

RPC: Reactive Powder Concrete; $\alpha =$ stirrup ratio; $\zeta =$ steel fiber dosage; $\lambda =$ Beam’s span-to-depth ratio ($a/d$), $d=$ effective depth of the beam.

Table 1. An overview of studies on beam shear behavior in UHPC beams.

Ref.	Elements		Test		Dimensions (mm)				Material			Most Important Findings
	Type	No.	Type	Variables	$\mathit{h}$	$\mathit{L}$	$\mathit{a}$	${\mathit{b}}_{\mathit{w}}$	Type	Fibrous System	${\mathit{f}}_{\mathit{c}}^{\prime }$
[6]	Rectangular-beams	14	Four-point loading	$\lambda$, $\rho$, $\alpha$, $\zeta$, and longitudinal reinforcement strength	250	1800	Variable $\lambda$ = 1.51 to 3.02	150	UHPC	Micro steel fibers	80–116	The beam’s capacity was decreased due to an increase in $\lambda$ (in certain values); however, it marginally increased with increasing the tensile and transverse reinforcements. Additionally, the concrete plasticity model (CDM) was successfully employed to predict the behavior of beams with $\lambda$ of 1.75 to 3.0.
[40]	I-girders (Prestressed)	7	Three-point loading	$\zeta$	650	4000	2000	250	RPC	Micro steel fibers	150–170	The fibrous system significantly influences the cracking pattern and the ultimate load.
[41]		8		$\lambda$ and $\zeta$	650	4000, 8000	2000, 4000	500	UHPC	Micro steel fibers	122–140	The longitudinal shear failure could be a controlling design case for beams with a substantial moment gradient. Additionally, the CDM could be efficiently employed to design the UHPC beam under shear forces.
[42]	I-girders	11	Four-point loading	$\alpha$ (stirrups and/or fibers, or neither)	380	2000	760	230	UHPC	Micro steel fibers	151–194	The behavior of beams under shear was highly influenced by the fibrous content in the UHPC.
[37]	T-beams	12	Four-point loading	$\lambda$, $\rho$, and $\alpha$	500	2000–5000	Variable $\lambda$ = 1 to 4	140	RPC	Micro steel fibers	127–155	The response of girder to shear was notably influenced by $\lambda ,\rho$, and $\alpha$. For $\lambda =1-4$, the failure pattern was “shear compression” or “diagonal compression.”
[43]	T-beams reinforced with high-strength steel	11	Four-point loading	$\lambda$, $\zeta$, fiber type, $f_c^{\prime }$ and $\alpha$	140	1200	Variable $\lambda$ = 2.5 to 3.75	40	UHPC	Micro steel fibers	94–137 ($f_{cu}$)	Fibers are more practical in improving the shear behavior than the flexural behavior of beams. Additionally, both deformability and cracking strength have been enhanced by the use of fibers.

RPC: Reactive Powder Concrete; $\alpha =$ stirrup ratio; $\zeta =$ steel fiber dosage; $\lambda =$ Beam’s span-to-depth ratio ($a/d$), $d=$ effective depth of the beam.

2. Materials and Methods

2.1. Materials

To develop the UHPC mix proportions, ordinary Portland cement (OPC, Type-I) complied with ASTM C150 specifications. In addition, two supplementary cementitious materials, silica fume (SF) and fly ash (FA)] were employed. Table 2 contains the physiochemical properties of these binders. Furthermore, a blend of locally available red and white sand was used for fine aggregate. The properties are given in Table 3. The grain size analysis of the binders mentioned above and sands is displayed in Figure 1. Moreover, a hybrid system of steel fibers (SF1, SF2, and SF3, as depicted in Figure 2) was incorporated into the UHPC. The properties of these fibers are given in Table 4, and their tensile strength was 2.6 GPa. Moreover, a polycarboxylate ether-based superplasticizer (Master Glenium 51, SP with 1080 kg/m³ unit weight and 65.2% moisture content) was used to develop self-compacted UHPC. Finally, the mixture design of the UHPC is presented in Table 5. A multi-objective design approach was used to develop the UHPC mixture to balance the materials’ performance with their cost while optimizing the efficiency of the process. An in-depth description of the design process can be found in [44], which provides an explanation of the process in detail.

Table 2. The properties of OPC, FA, and SF.

Oxides (%)	OPC	FA	SF
SiO2	20.41	55.23	86.20
Al2O3	5.32	25.95	0.49
Fe2O3	4.10	10.17	3.79
CaO	64.14	1.32	2.19
MgO	0.71	0.31	1.31
SO3	2.44	0.18	0.74
TiO2	0.30	-	-
Na2Oeq	0.10	0.86	2.80
L.O.I.	2.18	5.00	2.48
R.D.	3.15	2.70	2.20

Table 3. The properties of RS and WS.

Property	RS	WS
Bulk Specific Gravity (OD Basis)	2.64	2.73
Specific Gravity (SSD Basis)	2.65	2.74
Apparent Specific Gravity	2.67	2.76
Absorption, %	0.30	0.37
Fineness Modulus (range of 2.3–3.1)	1.11	1.46

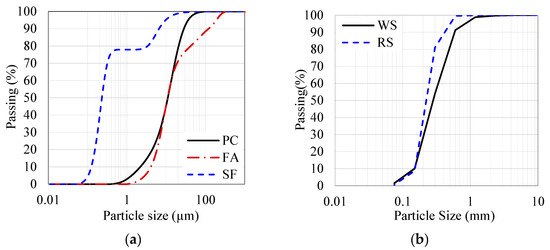
Figure 1. The particle size of (a) binders and (b) sands.

Figure 2. The steel fibers used in the study: (a) SF1, (b) SF2, and (c) SF3.

Table 4. The properties of steel fibers.

Type	Geometry	Length (mm)	Aspect Ratio
SF1		13	65
SF2		20	100
SF3		30	150

Table 5. Mixture design of the UHPC.

PC	SF	FA	WS	RS	Water	SP	Fiber
							A	B	C
1123.1	239.1	66.1	481.2	160.9	212.7	39.7	151.8	43.0	7.6

2.2. Mixing and Production of Concrete

As illustrated in Figure 3, the mixing process was conducted by utilizing a peculiar concrete mixture (MischTecnich, UEZ ZZ, 50-S, 95 L capacity). The UHPC was produced in about 18 min following the four stages depicted in Figure 3. At the end of the mixing procedure, the UHPC was cast in 50 mm layers in the beam’s forms, including the prepositioned steel rebars. Additionally, for the compressive strength test, 50 × 50 × 50 mm cubes and for flexural strength, 40 × 40 × 160 mm prisms were cast for all concrete mixes. Eventually, all test samples were stored in a water container under room conditions (19–23 °C and 100% RH) for curing for 28 days. Finally, the cube compressive strength of the UHPC was evaluated following ASTM C109 using a universal testing machine (3000 kN capacity) at a loading rate of 3.33 kPa/min. Although the concrete mixture was designed to achieve a characteristic strength of 130 ± 10 MPa, it was kept constant for the entire research program. At the same time, the flexural strength was conducted according to the ASTM C78 third-point loading test.

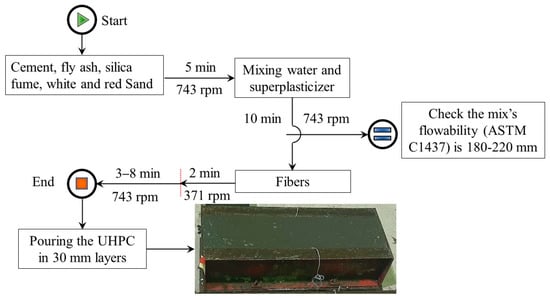
Figure 3. Mixing approach of the UHPC in Dissolver mixer.

2.3. Details of the UHPC Beams and Testing Arrangement

The experimental program for beam testing included the casting of 36 beams. The details are shown in Table 6, with 18 pairs of beams, each of which contained two beams. The primary variables for the beam testing program were the overall depth ($h$), reinforcement ratio ($\rho$), and shear span to depth ratio ($\lambda$). The entire experimental process is described in Figure 4; Figure 5 exhibits the typical geometry of the UHPC beam specimens (150 × 150 × 600 mm).

Table 6. Details of the UHPC beam specimens.

Beam	Batch	$\mathit{h}$	$\mathit{a}$	$\mathit{d}$	$\varnothing$	$\mathit{\rho }$	$\mathit{\lambda }$
B2	C1	150	225	125	8	0.536	1.80
B3		150	225	125	10	0.838	1.80
B4		150	225	125	12	1.206	1.80
B5	C2	150	225	125	16	2.145	1.80
B6		150	225	125	20	3.351	1.80
B7		150	207	115	12	1.311	1.80
B8	C3	150	171	95	12	1.587	1.80
B9		150	153	85	12	1.774	1.80
B10		150	135	75	12	2.011	1.80
B11	C4	150	250	125	12	1.206	2.00
B12		150	200	125	12	1.206	1.60
B13		150	175	125	12	1.206	1.40
B14	C5	150	150	125	12	1.206	1.20
B15		150	125	125	12	1.206	1.00
B16		140	250	120	12	1.257	2.08
B17	C6	130	220	110	12	1.371	2.00
B19		110	180	90	10	1.164	2.00
B20		100	160	80	10	1.309	2.00

Figure 4. An illustration of the experimental process.

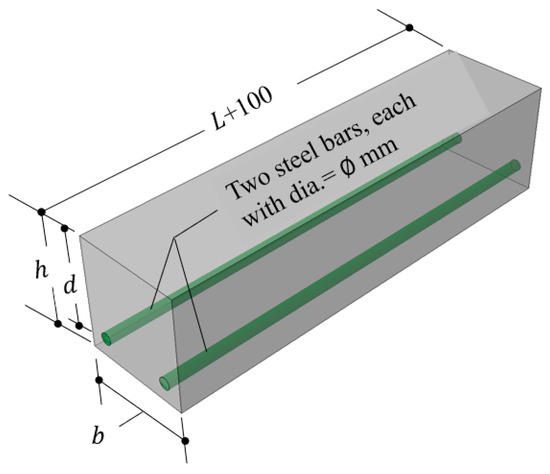
Figure 5. The geometry of the UHPC beams.

In this paper, we examined the structural behavior of UHPC beams (Table 6) under four-point loads. The beam testing setup is illustrated schematically in Figure 6. Test beams were run on an AMSLER hydraulic universal test machine with a capacity of 2000 kN and a loading rate of 0.4 mm/min. In total, five sets of equipment were used in the testing process. Three strain gauges measuring 60 mm were positioned at different locations on the concrete surface to assess strains. Prior to casting, two electrically sensitive strain gauges of 5 mm size were fastened to the steel rebars for strain measurements. Thirdly, two LVDTs were mounted vertically over the beam’s midspan to detect its vertical displacement. Attaching two horizontal LVDTs near the beam’s centerline allowed the beam’s crack width to be measured. Additionally, loads applied to actuators were measured directly through direct connections between actuators and load cells. The above-described instrumentation data was synchronized using Tokyo Sokki, model TDS-630, with a speed of 1000 channels in 0.1 s.

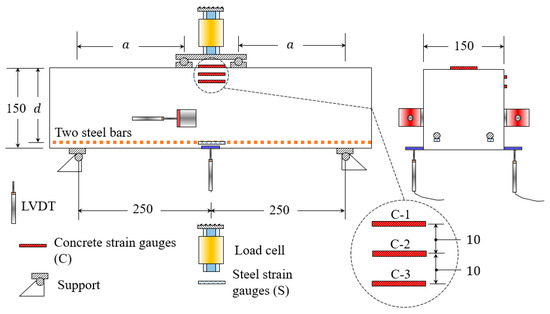
Figure 6. Schematic illustration of the beam testing setup (Dimensions are in mm).

2.4. Database of Parameters for Developing Neuro-Fuzzy Model

A database of the various parameters of beams was used for developing the Neuro-Fuzzy model. The parameters include the beams’ dimensions, fiber ratio, and estimated shear strength. In addition, the database contains data from the current study and similar studies reported in the literature, shown in Table 7.

Table 7. Database of the UHPC beams.

#	Beam	${\mathit{f}}_{\mathit{y}}$ (MPa)	$\mathit{b}$ (mm)	$\mathit{h}$ (mm)	Inputs					Output	Ref.
					${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	$\mathit{y}$
					$\mathit{\rho }$ (%)	$\mathit{\lambda }$	$\mathit{d}$ (mm)	${\mathit{f}}_{\mathit{c}}^{\prime }$ (MPa)	${\mathit{f}}_{\mathit{t}}^{\prime }$ (MPa)	${\mathit{V}}_{\mathit{u}}/\mathit{b}\mathit{h}$ (MPa)
1	B2	520	150	150	0.536	1.80	125	186.7	17.7	4.560	Current Study
2	B3	520	150	150	0.838	1.80	125	186.7	17.7	4.956
3	B4	520	150	150	1.206	1.80	125	186.7	17.7	5.991
4	B5	520	150	150	2.145	1.80	125	172.6	18.4	8.378
5	B6	520	150	150	3.351	1.80	125	172.6	18.4	9.693
6	B7	520	150	150	1.311	1.80	115	172.6	18.4	5.964
7	B8	520	150	150	1.587	1.80	95	185.8	24.9	6.662
8	B9	520	150	150	1.774	1.80	85	185.8	24.9	7.542
9	B10	520	150	150	2.011	1.80	75	185.8	24.9	7.449
10	B11	520	150	150	1.206	2.00	125	179.3	20.0	5.444
11	B12	520	150	150	1.206	1.60	125	179.3	20.0	7.382
12	B13	520	150	150	1.206	1.40	125	179.3	20.0	7.956
13	B14	520	150	150	1.206	1.20	125	186.7	27.6	9.267
14	B15	520	150	150	1.206	1.00	125	186.7	27.6	11.342
15	B16	520	150	140	1.257	2.08	120	186.7	27.6	5.052
16	B17	520	150	130	1.371	2.00	110	187.5	25.1	5.938
17	B19	520	150	110	1.164	2.00	90	187.5	25.1	4.885
18	B20	520	150	100	1.309	2.00	80	187.5	25.1	5.053
19	FHB2-2	442	125	250	1.517	2.00	212	63.8	5.88	5.090	[45]
20	FHB3-2	442	125	250	1.517	2.00	212	68.6	6.05	5.440
21	FHB2-3	442	125	250	1.517	3.00	212	63.8	5.88	3.090
22	FHB3-3	442	125	250	1.517	4.00	212	68.6	6.05	3.400
23	FHB2-4	442	125	250	1.517	4.00	212	63.8	5.88	2.410
24	FHB3-4	442	125	250	1.517	2.00	212	68.6	6.05	2.740
25	FNB2-2	442	125	250	1.517	2.00	212	30.8	3.83	4.040
26	FNB2-3	442	125	250	1.517	3.00	212	30.8	3.83	2.550
27	FNB2-4	442	125	250	1.517	4.00	212	30.8	3.83	2.000
28	BS-100-2.0	400	200	350	4.720	2.00	260	100.0	7.90 *	7.043	[46]
29	BS-200-2.0	400	200	350	4.720	2.00	260	200.0	11.17 *	8.114
30	SB1	600	150	290	8.002	3.00	220	166.9	11.5	3.954	[10]
31	L-0	522	150	250	8.177	2.26	160	117.2	6.9	9.493	[9]
32	LA-1	522	150	250	8.177	1.51	160	117.2	6.9	17.360
33	LA-2	522	150	250	8.177	1.75	160	117.2	6.9	10.267
34	LA-3	522	150	250	8.177	3.02	160	117.2	6.9	8.933
35	LC-3	522	150	250	8.177	2.26	160	101.2	6.9	11.093
36	LD-1	522	150	250	8.177	2.26	160	117.2	6.9	8.027
37	LD-2	522	150	250	8.177	2.26	160	117.2	6.9	11.333
38	LE-1	441	150	250	8.177	2.26	160	117.2	6.9	8.667
39	B4	400	152	152	5.905	1.20	127	137.0	37.165	16.339	[16]
40	B5	400	152	152	4.404	1.20	127	137.0	37.165	16.988
41	B21	400	152	152	4.880	1.20	127	125.0	22.495	15.106
42	B22	400	152	152	3.953	1.20	127	125.0	22.495	14.370
43	B23	400	152	152	4.880	1.20	127	125.0	22.495	14.500
44	B24	400	152	152	3.953	1.20	127	125.0	22.495	14.543
45	B29	400	102	203	3.459	0.90	77	125.0	22.597	19.753
46	B30	400	102	203	2.214	0.90	77	125.0	22.597	16.517
47	B35	400	152	76	5.954	2.80	127	125.0	22.134	9.176
48	B36	400	152	76	3.038	2.80	127	125.0	22.134	7.358
49	B37	400	152	76	3.038	2.80	127	125.0	22.134	6.146
50	B2	520	100	140	3.400	3.50	112	94.0	9.200	4.750	[47]
51	B3	520	100	140	3.400	3.50	112	98.0	11.000	5.000
52	B4	520	100	140	3.400	3.50	112	103.0	14.500	5.536
53	B5	520	100	140	3.400	3.50	112	110.0	15.400	5.893
54	B6	520	100	140	3.400	3.50	112	110.0	15.400	7.679
55	B7	520	100	140	4.900	3.50	112	110.0	15.400	8.036
56	B8	520	100	140	5.900	3.50	112	101.0	14.000	5.536
57	B9	520	100	140	3.400	3.50	112	93.0	14.000	5.357
58	B10	520	100	140	3.400	2.50	112	110.0	15.400	8.929
59	B11	520	100	140	3.400	3.00	112	110.0	15.400	6.964
60	B12	520	100	140	3.400	4.00	112	110.0	15.400	4.464
61	B13	520	100	140	3.400	4.50	112	110.0	15.400	4.250
62	B14	520	100	140	3.400	2.50	112	98.0	11.000	7.143
63	B15	520	100	140	3.400	4.50	112	98.0	11.000	3.929
64	B16	520	100	140	3.400	3.50	112	125.0	16.700	6.714
65	B17	520	100	140	3.400	3.50	112	142.0	17.900	7.214
66	B18	520	100	140	3.400	3.50	112	151.0	18.500	7.857

* Assumed $f_t^{\prime }=0.79\sqrt{f_c}$.

3. Results and Discussion

3.1. Flexural Strength of Concrete (with and without Fibers)

In general, fiber-reinforced UHPC has a tensile strength of 15–20 MPa. In comparison, UHPC without steel fibers exhibited almost half of this tensile strength [48]. According to several researchers, the compression strength should exceed 120 MPa [48,49,50]. As discussed above, all mixes were designed to achieve a characteristic compressive strength of 130 ± 10 MPa. The addition of fibers usually does not significantly affect the compressive strength. However, the principal benefit of adding fibers is improving the post-cracking performance of concrete. Therefore, a flexural strength test was conducted to assess the effects of fibers. Figure 7 shows the load-deflection curves of plain concrete prisms (40 × 40 × 160 mm) under the flexural strength test.

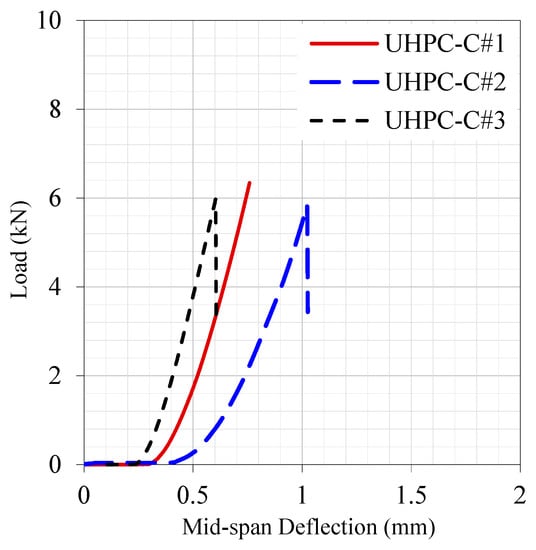
Figure 7. Load-deflection curve of plain concrete prisms.

Similarly, Figure 8 illustrates the load-deflection behavior of the fiber-reinforced concrete samples. It is observed that the plain concrete samples achieved an average peak load of 6 kN, whereas the FRC samples sustained an average peak load of 21 kN, which is almost 3.5 times the load carried by the plain concrete samples. Similarly, plain concrete samples failed soon after the first crack appeared. Hence, the deformation obtained at the first crack and failure was the same. Whereas the FRC samples attained an average of 0.8 mm deflection at the onset of the first crack, and the post-crack deflection reached 6 mm at the point of failure. It is a significant effect of the inclusion of fibers in concrete, so the concrete performance can be classified as ultra-high-performance concrete. The elastic modulus of plain and FRC reflects the load-deflection behavior. The elastic modulus of plain concrete was estimated as 8 GPa, and the elastic modulus of FRC was estimated as 40 GPa. As an important point to be noted, the elasticity modulus of the material was determined by calculating the flexural stress at the end of the elastic range.

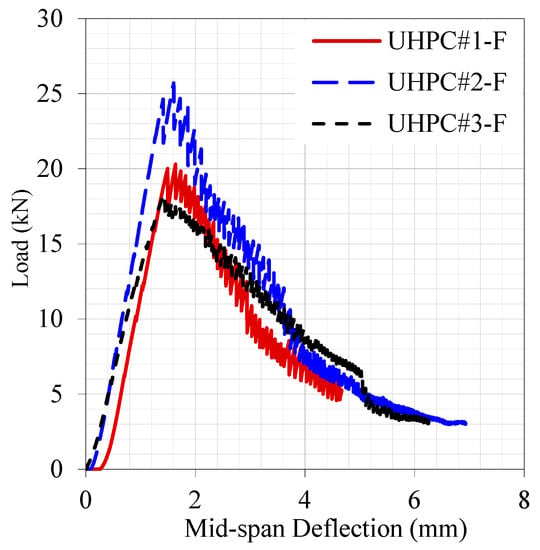
Figure 8. Load-deflection curve of fiber-reinforced concrete prisms.

3.2. Models for Predicting the $v_u$

In the literature, various researchers have proposed prediction equations for calculating the mean shear strength ($v_u$) of fiber-reinforced concrete (FRC) beams. Some of these equations are adopted by international design codes.

3.2.1. Sharma [51] Model

Sharma [51] has developed a simple model (Equation (1)) for evaluating the shear strength ($v_u$ in MPa) of FRC by conducting experimenatl investigations and used the results of Batson et al. [52].

$$v_u=\left(\frac{2}{3}\right)f_t^{\prime }{\left(\frac{1}{\lambda }\right)}^{0.25}$$

(1)

$$f_t^{\prime }=0.79\sqrt{f_c^{\prime }}$$

(2)

where,$f_t^{\prime }$ is the tensile strength of concrete (would be estimated by Equation (2), where $f_c^{\prime }$ is the cylindrical compressive strength of the FRC). Figure 9 shows that the mean of tested-to-predicted $v_u$ of Equation (1) and its coefficient of variance were 1.09 and 68.1%, respectively, and the error band was in the range of ±50%. The primary concern with regard to Equation (1) is that it does not account for the percentage of the longitudinal reinforcement ($\rho$). Figure 9a showed that Sharma’s model notably underestimated $v_u$ for beams with high $\rho$ (more than 6%). Additionally, Equation (1) generally undervalued the influence of $\lambda$. This formula is likely to provide an over-design of $\lambda$ less than two and would result in an unsafe design for slender beams ($\lambda >2$). It is worth noting that this finding is in accordance with that reported by Kwak et al. [45].

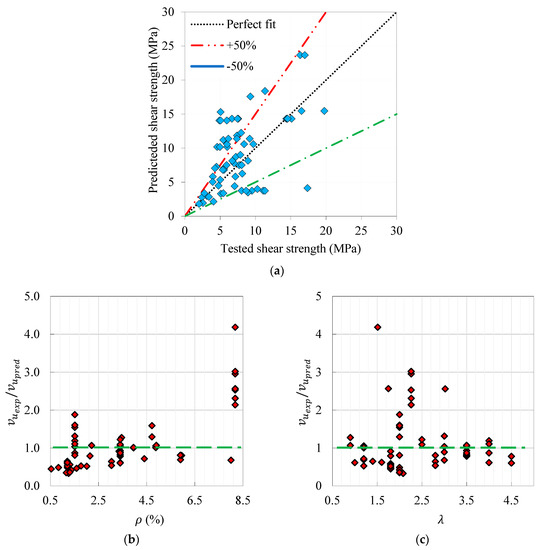
Figure 9. Prediction performance of Sharma model: (a) tested vs. predicted results and effect of (b) $\rho$, (c) $\lambda$.

3.2.2. Kwak et al. [45] Model

Kwak et al. [45] have proposed Equation (3) to calculate $v_u$ of FRC by using his own experiment results (12 beams) and others data (127 beams).

$$v_u=e{f}_t^{\prime }{}^{0.7}{\left(\frac{\rho }{\lambda }\right)}^{0.22}+1.36F$$

(3)

where e is 2.1 if $\lambda >3.5$ and is ($3.5/\lambda$) if $\lambda \le 3.5$ and $F$ are the fiber’s factors, which was considered 1 in this investigation. Future studies are needed on the effect of this factor ($F$) on the shear strength of UHPC beams. Figure 10 shows the prediction capability of Equation (3) in estimating $v_u$ of the current study database. This figure displays the average ratio of tested-to-predicted $v_u$ by utilizing Equation (3) and the associated variation coefficient were 1.22 and 41.9%, respectively, while the error band was in the range of ±30%.

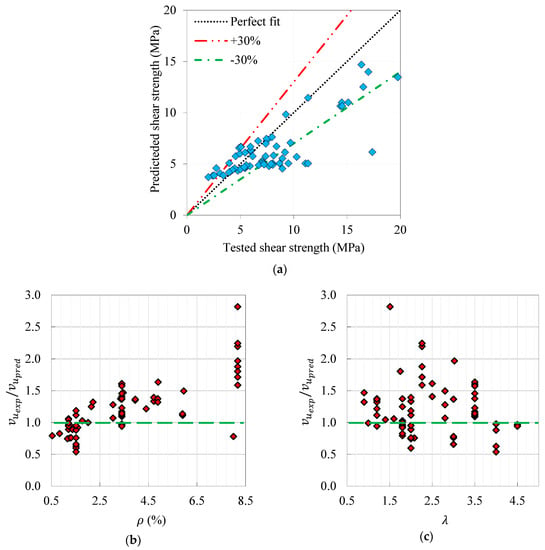
Figure 10. Prediction performance of Kwak et al. model: (a) tested vs. predicted results and effect of (b) $\rho$ and (c) $\lambda$.

3.2.3. Ahmad et al. [53] Model

Ahmad et al. [53] have proposed Equation (4) to compute $v_u$ of FRC. In their study, the prediction formula has been developed by the best curve fitting technique for the results of 10 tested beams and fairly well compared to 23 independent data.

$$v_u=0.35\sqrt{f_c^{\prime }}+\frac{1.32\rho }{\lambda }+\frac{14F}{{\lambda }^{1.1}}$$

(4)

Figure 11 depicts the prediction capacity of this model and the impact of $\rho$ and $\lambda$ on the tested-to-predicted $v_u$ of the current investigation database (Table 7). This figure demonstrated that Equation (4) had a prediction capability superior to the previous two moduli. Additionally, this formula underestimated $v_u$ for moderately reinforced beams (i.e., $\rho \approx$ 0.7–4.6%), and deeper ones (with $\rho$< 2.5). Figure 11 illustrates that the mean of tested-to-predicted $v_u$ of Equation (4) and its coefficient of variance were 1.23 and 33.9%, respectively, whereas the deviations of tested–predicted data from the perfect fit line were approx. in the range of ±30%.

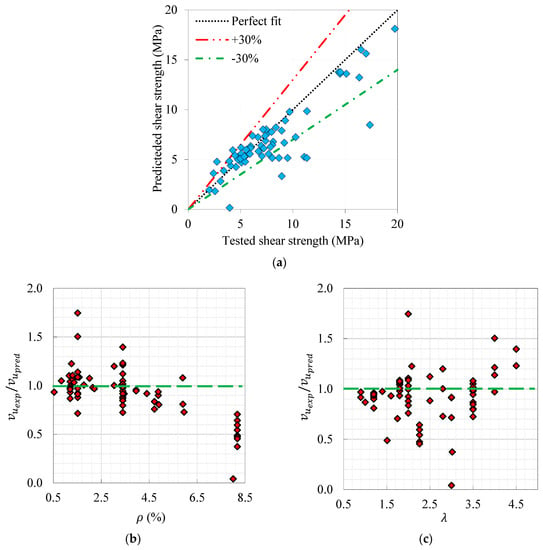
Figure 11. Prediction performance of Ahmad et al. model: (a) tested vs. predicted results and effect of (b) $\rho$ and (c) $\lambda$.

3.2.4. Wang et al. [9]

Wang et al. [9] have suggested the application of Equation (5) to predict $v_u$ of UHPC beams using their tested (14) rectangular beams and plasticity theory principles.

$$v_u=0.4f_c^{\prime }\left(\sqrt{1+{\lambda }^2}-\lambda \right)$$

(5)

Figure 12 displays the forecast ability of Equation (5) in estimating $v_u$ of the current study database. This figure displays the average ratio of tested-to-predicted $v_u$ by utilizing Equation (5) and the associated variation coefficient were 0.77 and 42.0%, respectively, whereas the deviations of tested–predicted data from the perfect fit line were approx. in the range of ±30%. The proposed model by Wang et al. [9] had the likelihood to overestimate the shear strength of UHPC beams.

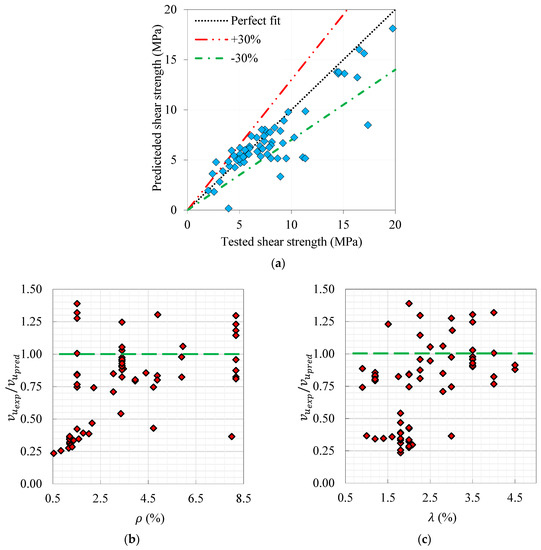
Figure 12. Prediction performance of Ahmad et al. model: (a) tested vs. predicted results, and effect of (b) $\rho$ and (c) $\lambda$.

3.3. Design of Experiments

3.3.1. Proposed Robust Model

In the current investigation, a robust analytical model for calculating $v_u$ was developed by utilizing the collected database (Table 7) and a general-purpose statistical program (Minitab [54]). The model’s independent variables ($x_1-x_5$) were $\rho (\%)$, $\lambda$, $d$, $f_c^{\prime }$, and $f_x^{\prime }$, respectively. The model was developed by employing the fully crossed design component that allows for investigation of the influence of the individual parameters on an independent variable, in addition to the impact of interactions among the dependent variable. Therefore, the response surface of $v_u$ could be predicted by Equation (6).

$$\begin{array}{c}{v}_u={\alpha }_1{x}_1+{\alpha }_2{x}_2+{\alpha }_3{x}_3+{\alpha }_4{x}_4+{\alpha }_5{x}_5+{\beta }_1{x}_1^2+{\beta }_2{x}_2^2+{\beta }_3{x}_3^2+{\beta }_4{x}_4^2+{\beta }_5{x}_5^2\hfill \\ +{\gamma }_{12}{x}_1{x}_2+{\gamma }_{13}{x}_1{x}_3+{\gamma }_{14}{x}_1{x}_4+{\gamma }_{15}{x}_1{x}_5+{\gamma }_{23}{x}_2{x}_3+{\gamma }_{24}{x}_2{x}_4\hfill \\ +{\gamma }_{25}{x}_2{x}_5+{\gamma }_{34}{x}_3{x}_4+{\gamma }_{35}{x}_3{x}_5+{\gamma }_{45}{x}_4{x}_5+\delta \hfill \end{array}{R}^2=94.2\%&$$

(6)

where, $\delta$ = 20.8, and the other mode’s parameters are given in Table 8 and Table 9.

Table 8. Linear and quadratic term constants of the robust proposed model (Equation (6)).

Terms	Coefficient
Linear	${\alpha }_1$	${\alpha }_2$	${\alpha }_3$	${\alpha }_4$	${\alpha }_5$
	5.06	(18.81)	0.119	(0.042)	(0.07)
Quadratic	${\beta }_1$	${\beta }_2$	${\beta }_3$	${\beta }_4$	${\beta }_5$
	(0.353)	1.412	(0.699 × 10−3)	(0.083 × 10−3)	12.67 × 10−3

Table 9. The cross-product constants of the robust proposed model (Equation (6)).

Terms	Coefficient
Cross-product	${\gamma }_{12}$	${\gamma }_{13}$	${\gamma }_{14}$	${\gamma }_{15}$
	(0.007)	(0.004)	(3.98 × 10−3)	(0.017)
		${\gamma }_{23}$	${\gamma }_{24}$	${\gamma }_{25}$
		0.035	0.0144	0.188
			${\gamma }_{34}$	${\gamma }_{35}$
			0.365 × 103	(4.42 × 103)
				${\gamma }_{45}$
				(0.46 × 103)

Figure 13 shows the prediction performance of the proposed robust model. With exception of two outliers, this figure established the rationality of the proposed model in the estimation of the shear strength of UHPC beams. The majority of the tested to predicted data points were in the range of 0.75 to 1.25, whereas the deviations of tested–predicted data from the perfect fit line were approx. in the range of ±20%.

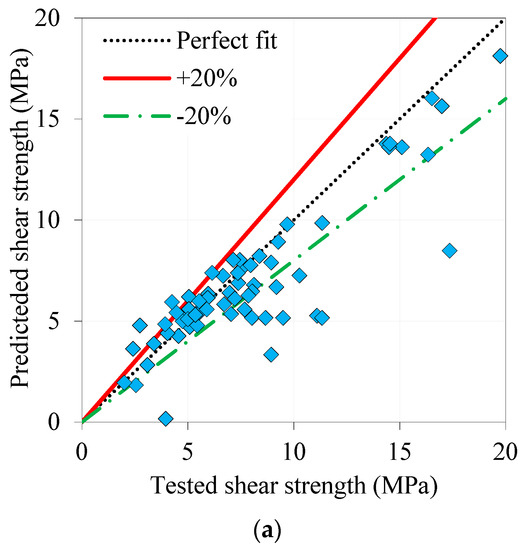
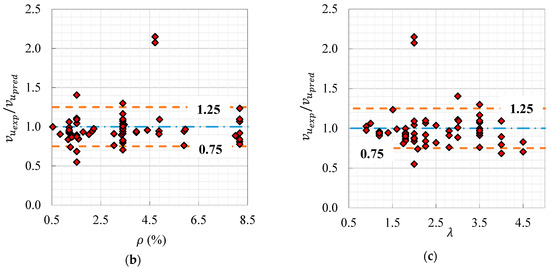
Figure 13. Prediction performance of the proposed robust model: (a) tested vs. predicted results, and effect of: (b) $\rho$ and (c) $\lambda$.

3.3.2. Isoresponses of the Shear Strength of UHPC Beams

The establishment of the previous factorial-based model (Equation (5)) aids the construction of the response contours that leads to an insight into the influence of various parameters on the response surface. Figure 14 shows the combined impact of different factors on the shear strength of UHPC beams. This figure may aid the design of such beams, as well as help in gaining and insightful understanding of the impact of these parameters on $v_u.$

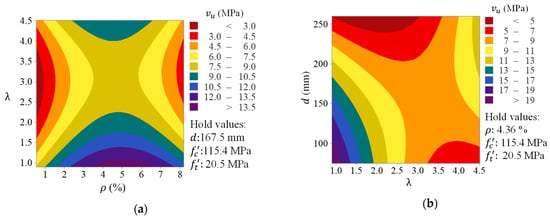
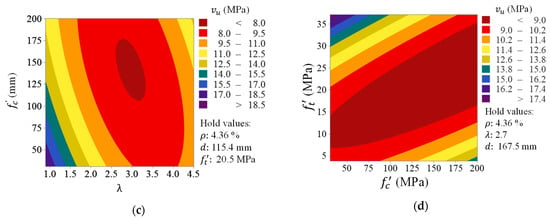
Figure 14. The combined influence shear strength isoresponses: (a) $\rho -\lambda$, (b) $\lambda -d$, (c) $\lambda -f_c^{\prime }$ and (d) $f_c^{\prime }-f_t^{\prime }$.

3.4. Simple Proposed Model for $v_u$

This investigation proposed a simplified design-oriented model for predicting the shear strength of UHPC beams, as given by Equation (7). This model was developed by employing nonlinear regression and taking into account the most influential parameters and the typical models forms available in the literature.

$$v_u=0.32\sqrt{f_c^{\prime }}+0.95\rho f_c^{\prime }{}^{0.36}\left(1/\lambda \right)$$

(7)

Figure 15 illustrates the ability of the proposed simplified model (Equation (7)) to predict the shear strength of UHPC beams of the current study. This figure shows that the proposed had reasonable reliability in calculating $v_u$, as most of the predicted strengths were close to the tested ones. The obtained tested-to-calculated results were in the 0.75–1.25 range. However, one beam was an exception (with a ratio of about 2.6), whereas most of tested–predicted data points were close ±85% accuracy range.

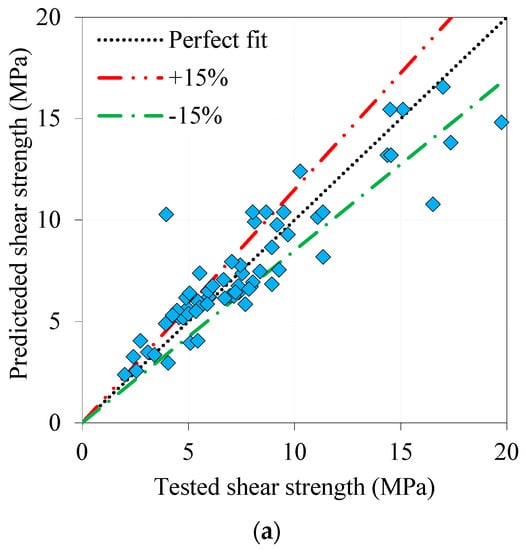
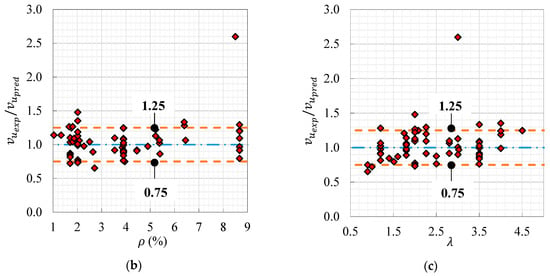
Figure 15. Prediction performance of the proposed simple model: (a) tested vs. predicted results and effect of (b) $\rho$ and (c) $\lambda$.

4. Conclusions and Prospective

The experimental program was based on the design of concrete mixes (with and without fibers) for characteristics compressive strength of 130 ± 10 MPa. The plain concrete mixes achieved an average elastic modulus of 8 GPa, and the FRC achieved a five-times-higher modulus of 40 GPa. Therefore, FRC showed a large post-cracking deformation, confirming the ultra-high performance. The prediction models developed for this study are in well agreement with the models presented in the literature. By studying the effects of ρ and λ, the ratio of shear strength of experimental and predicted results is between 0.75 to 1.25. The results of this study should lead to producing high strength concrete with a longer lifespan, thus improving the sustainability of concrete structures. Based on the findings of this study, we can draw the following conclusions:

• On the basis of the Sharma [51] model, it was found that the mean of the tested-to-predicted shear strength of the UHPC beams was 1.09 along with a coefficient of variation of 68.1%. A major concern with this model is that it does not account for the longitudinal reinforcement percentage and has underestimated the shear strength of beams with a high longitudinal reinforcement ratio (greater than 6%). This model seems inadequate for estimating the shear capacity of UHPC beams.
• In the Kwak et al. [45] model, the average ratio of measured-to-predicted shear strength and the variation coefficient associated with test-to-predicted shear strength was 1.22 and 41.9%, respectively, while the error band ranged between −30 and 30%. Thus, this model is likely to result in beams with shear capacities ranging from those of real values.
• The Ahmad et al. [53] model is likely to underestimate the performance of moderately reinforced beams and those with greater depths. According to this formula, the average ratio between the measured and predicted shear strengths was 1.23, with the variation coefficient for test-to-predicted shear strengths being 33.9%, and error bands ranging between −30 and 30%. As a result of the assumptions made in this model, beams will have shear capacities within a range of values that are widely separated from the real values of the beams.
• Based on Wang et al. [9], the test-to-predicted shear strength ratio was 0.77, with a variation coefficient of 42.1%, and error bands between −30 and 30%. The results of this model tended to overestimate the shear strength of UHPC beams in a large number of cases.
• A comparison of experimentally calculated shear strength with predicted shear strength using the proposed model for different beams was done in this study. Considering the experimentally calculated and predicted shear strength, it was found that the ratio was between 0.75 and 1.25 for the experimental and predicted shear strength, which corresponds to the results of similar literature.