Seismic Responses of Aqueducts Using a New Type of Self-Centering Seismic Isolation Bearing

Abstract

An aqueduct is a bridge-like structure that supports a canal passing over a river or low ground, and it is an important part of a water conveyance system. Aqueduct piers are extremely vulnerable to damage during strong earthquakes that can result in structural collapse. Further, excessive seismic displacement will also fracture an aqueduct’s rubber water-stop and interrupt the normal service of an aqueduct after an earthquake. Therefore, improving the seismic capacity and post-earthquake resilience of aqueducts is of great importance. In this paper, a new type of self-centering seismic isolation bearing, the inclined plane guide bearing (IPGB), is proposed for the seismic design of aqueducts, and it is studied both experimentally and numerically. Firstly, a typical aqueduct project and the setting of the IPGBs are introduced. Then, the test design, test cases, and test results of shaking table tests for two different pier-height aqueducts are presented. The seismic responses of the two models are studied, and the results show that the aqueduct that used IPGBs has a smaller bearing displacement and better post-earthquake resilience. Finally, a numerical simulation method applicable to aqueducts using IPGBs is proposed, and its accuracy is verified by comparing the results of the numerical simulation and the shaking table test.

1. Introduction

Water conveyance projects, such as the Valens Aqueduct in Turkey [1] and the South-to-North Water Diversion Project in China [2], can help alleviate water shortage problems in many large cities and promote sustainable economic development and ecological environmental protection. As an important part of a water conveyance system, an aqueduct is comprised of a superstructure with a large mass and piers with small lateral stiffnesses. The seismic safety of aqueducts in high seismic intensity areas has attracted researchers’ attention. Compared with bridges used for transportation, resuming normal service of aqueducts after strong earthquakes is more challenging. For a long-distance water conveyance system, if a certain part is damaged during an earthquake, and even if only a piece of the rubber water-stop is fractured, the normal service of the entire water conveyance system will be interrupted [3,4,5]. For example, several aqueducts were destroyed in the Lushan Earthquake and the Wenchuan Earthquake, and supplies of drinking water were interrupted. Therefore, the seismic design is very important for the seismic safety of aqueducts during strong earthquakes [6,7,8,9].

A series of studies have been carried out on aqueduct seismic issues, and they have primarily included the numerical modeling method for aqueducts during earthquakes [10,11,12,13,14,15], the interaction between the water and the aqueduct’s structure during earthquakes [16,17,18,19,20], the aqueduct’s seismic design method [20,21,22,23], etc. It has been shown that the seismic isolation method can significantly improve the seismic capacity of an aqueduct. Commonly used seismic isolation bearings, such as friction pendulum bearings (FPBs) and lead rubber bearings (LRBs) have satisfactory seismic isolation effects. However, the displacements and residual displacements of these bearings during strong earthquakes are much larger [24,25,26], resulting in damage to the rubber water-stop. Therefore, a newly developed self-centering seismic isolation bearing is applied to a typical aqueduct, and its seismic isolation effect is investigated in this paper.

It is well known that pier height significantly influences the seismic performance of a bridge. Therefore, the seismic performance of a taller pier aqueduct is different from that of a shorter pier aqueduct. Most past studies have focused on aqueducts with ordinary pier heights, such as the seismic performances and fragilities of shorter pier aqueducts [11,27,28,29,30,31,32,33,34]. However, the seismic performances of taller pier aqueducts are rarely investigated. In this paper, the seismic performances of aqueducts with two different pier heights are studied experimentally, and the test results are compared. The influence of pier height on the seismic performance of an aqueduct is investigated.

The seismic performances of aqueducts are investigated using the shaking table test method in this paper. In recent years, a series of shaking table tests were carried out to study the dynamic interaction between water and an aqueduct’s structure. Among them, Wang [35,36,37] studied the fluid structure coupling using shaking table tests, and the equivalent mass and load position of the water convection in U-shaped aqueducts were proposed quantitatively. Huang [38] and Duan [39] studied the tuned liquid damper (TLD) effect of an aqueduct during an earthquake using the shaking table test. It was shown that the shaking of the water and the breaking of the water waves had a TLD effect on the transverse dynamic response of the aqueducts. All of the shaking table tests noted above have focused on aqueducts with ordinary pier heights, and shaking table tests for tall-pier aqueducts have not been reported.

In this paper, an actual aqueduct project using a new type of self-centering seismic isolation bearing is taken as the research object, and a shaking table test is carried out to study the aqueduct’s seismic performance. The influence of pier height on the aqueduct’s seismic performance is also investigated.

2. An actual Aqueduct Project

2.1. Background Information

In this paper, an actual aqueduct project is taken as the research object, and the aqueduct’s seismic performance is studied using a new type of self-centering seismic isolation bearing. The aqueduct is located in a high seismic intensity area in southwest China, and the superstructure is a 30 m-span simply supported girder, as shown in Figure 1. The superstructure is a U-shaped reinforced concrete girder, and the substructure is a single-column hollow pier with a pile-group foundation. Typical cross-sections of the girder and the pier are shown in Figure 2.

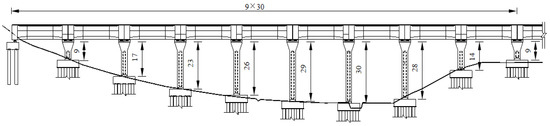
Figure 1. The elevation of a typical aqueduct structure (unit: meters).

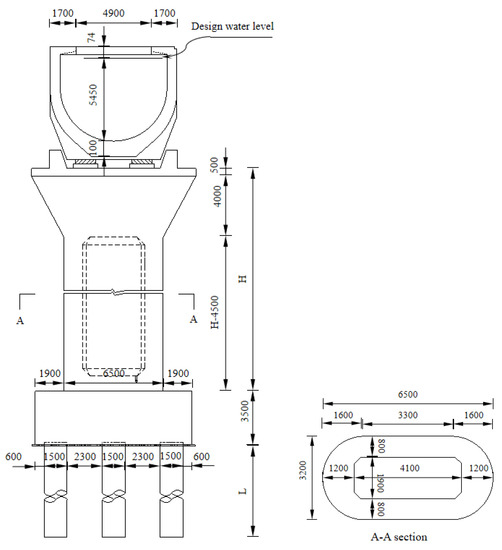
Figure 2. Cross-sections of the girder and the pier (unit: mm).

The horizontal peak ground acceleration for the design earthquakeis 0.30 g, which has an exceedance probability of 10% in 50 years.

2.2. Bearing Settings

This paper adopts a new type of self-centering seismic isolation bearing to improve the seismic performance of an aqueduct, i.e., an inclined plane guide bearing (IPGB). It can be classified into two categories to meet the requirements of normal service, i.e., fixed and expansion bearings. During an earthquake, the shear pins of the fixed bearings are cut off, and all bearings become expansion bearings for seismic resistance.

An expansion IPGB consists of five components, and they are, from top to bottom, an upper plate, a spherical cap, an upper slider, a lower slider, and a lower plate, respectively. Details of the bearing’s structure are shown in Figure 3. The upper plate, spherical cap, and upper slider form a spherical bearing to meet the rotation requirement of the bearing.

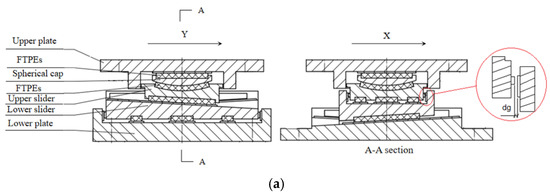
Figure 3. Components of the IPGB. (a) Details of the IPGB’s structure. (b) IPGB photos.

Three inclined planes with inclination angles of −3°, 3°, and −3° are arranged from left to right beneath the bottom surface of the upper slider, and a polytetrafluoroethylene (PTFE) plate is fixed on each inclined plane. Three inclined planes of the same inclination angles are arranged on the top surface of the lower slider, and a stainless-steel plate is fixed on each inclined plane. Two guide plates are set on both lateral sides of the lower slider to limit the upper slider to moving only in the Y-direction. When the horizontal displacement of the bearing along the Y-direction is zero, the three inclined planes beneath the bottom surface of the upper slider and the three inclined planes on the top surface of the lower slider will come into contact with each other. When the upper slider moves to the positive Y-direction, the left and right inclined planes beneath the bottom surface of the upper slider and those on the top surface of the lower slider will come into contact. Simultaneously, the two middle inclined planes will be out of contact. When the upper slider moves to the negative Y-direction, the left and right inclined planes beneath the bottom surface of the upper slider and those on the top surface of the lower slider will be out of contact. Simultaneously, the two middle inclined planes will come into contact.

Similarly, three inclined planes are arranged beneath the bottom of the lower slider, and a PTFE plate is fixed on each inclined plane. The inclination angles are −3°, 3°, and −3°, from left to right. Three inclined planes of the same inclination angles are also arranged on the top surface of the lower plate, and a stainless-steel plate is fixed on each inclined plane. Two guide plates are set on both lateral sides of the lower plate to limit the lower slider to moving only in the X-direction. When the horizontal displacement of the bearing along the X-direction is zero, the three inclined planes beneath the bottom surface of the lower slider and the three inclined planes on the top surface of the lower plate will come into contact with each other. When the lower slider moves to the positive X-direction, the left and right inclined planes beneath the bottom surface of the lower slider and those on the top surface of the lower plate will come into contact. Simultaneously, the two middle inclined planes will be out of contact. When the lower slider moves to the negative X-direction, the left and right inclined planes beneath the bottom surface of the lower slider and those on the top surface of the lower plate will be out of contact. Simultaneously, the two middle inclined planes will come into contact.

The hysteresis curve of an IPGB is shown in Figure 4. In the figure,

$$F_1=W\tan \theta +\mu W,$$

(1)

$$F_2=W\tan \theta -\mu W,$$

(2)

$$k=\frac{(F_1+F_2)}{2dg},$$

(3)

where W is the vertical load, θ is the inclination angle of inclined planes, μ is the sliding friction coefficient of the inclined planes, and $dg$ is the gap between the slider and the guide plate. To achieve the self-centering function, the following inequality should be satisfied:

$$\left|\sin \theta \right|>\mu \left|\cos \theta \right|.$$

(4)

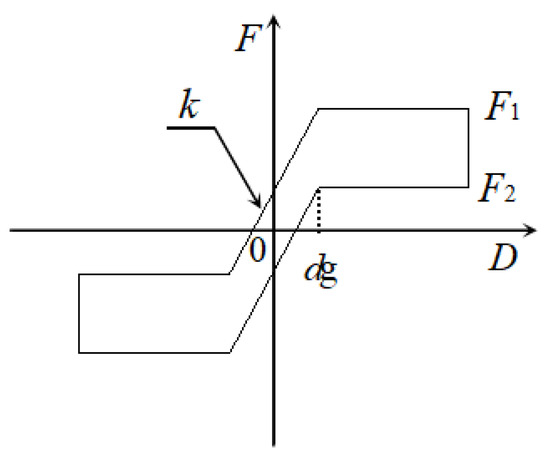
Figure 4. Hysteresis curve of an IPGB.

3. Design of the Shaking Table Test

3.1. Test Model Design

Two models are designed: Model I is an aqueduct with piers of 20 m in height and Model II is an aqueduct with piers of 40 m in height.

To study the seismic performance of an aqueduct using IPGBs, only four identical expansion bearings are set under the U-shaped girder. For the aqueduct using IPGBs, the horizontal stiffness of the substructure is composed of the IPGB stiffness and the pier stiffness in series. The bearing stiffness is much less than the pier stiffness, and so the horizontal stiffness of the substructure is primarily controlled by the bearing stiffness. Therefore, the longitudinal and lateral stiffnesses are nearly the same, and the longitudinal and lateral seismic responses are similar, as well. Because the longitudinal flexural capacity of the pier section is smaller than the transverse flexural capacity, the pier is more easily destroyed under longitudinal earthquakes, and so only the aqueduct seismic performance in the longitudinal direction is studied in this paper.

According to the test conditions, the length similarity ratio of the test model is determined to be 1:16. According to the length similarity ratio, an ideal model can be designed. However, if the similarity ratio is completely satisfied, there will be some problems that are difficult to cope with. For example, the diameters of the steel bars and the thicknesses of some concrete components will be too small to be fabricated. Therefore, the ideal model needs to be reformed to a test model according to equivalence principles. For instance, the superstructure of the test model is a Q235 I-shaped steel beam with some additional mass blocks according to the stiffness and mass equivalence principles [40]. The pier section of the test model is a filled rectangle, as shown in Figure 5.

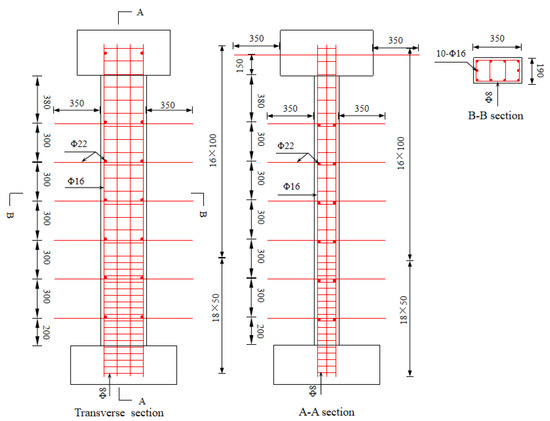
Figure 5. Design details of Model II (unit: mm).

The similarity ratios of the elastic modulus, the density, and the length are chosen to be fundamental physical quantities. The other similarity ratios are derived according to the similarity law [40].

The pier of the test model is made of C40 concrete and HRB400 reinforcement, which is consistent with the material of the prototype structure, and so the elastic modulus and density similarity ratios are equal to 1. In addition, with the acceleration similarity ratio being equal to 1, the remaining physical quantities of the test model can be derived according to the similarity law [41], as shown in Table 1.

Table 1. Scale factors of the test model.

Physical Quantity	Dimensional Calculation	Scale Factors
Length, l	$Sl$	0.625
Displacement, x	$Sx=Sl$	0.625
Elastic modulus, E	$SE$	1
Strain, $\epsilon$	$S\epsilon$	1
Stress, $\sigma$	$S\sigma =S\epsilon$	1
Density, $\rho$	$S\rho$	16
Acceleration, a	$Sa=Se/\left(S\rho Sl\right)$	1
Gravitational acceleration, g	$Sg=Se/\left(S\rho Sl\right)$	1
Concentrated load, P	$Sp=Se{S}_l^2$	0.390
Moment, M	$SM=S\sigma S_l^3$	0.244
Time, t	$St=1/S\omega$	0.25
Frequency, $\omega$	$S\omega =S_e^{0.5}{S}_{\rho }^{-0.5}/Sl$	4
Damping ratio, $\xi$	$S\xi$	1
Stiffness, k	$Sk=SeSl$	0.625
Mass, m	$Sm=S\rho S_l^3$	0.244

The density of the test model should be 16 times the actual density of the concrete, which is difficult to satisfy. The mass differences between the main components of the ideal and the actual test models are calculated, and additional mass blocks are designed to cover the shortage in density. The additional masses of the main components are listed in Table 2.

Table 2. The additional masses of the main components (unit: kg).

Components	Mass of the Ideal Model	Mass of the Test Model	Additional Mass
20 m-high pier	3920	1040	2880
40 m-high pier	6490	1180	5310
Girder	17,000	3000	14,000

3.2. Test Scheme

In the test, the displacement of the pier and the bearing, the horizontal force of the bearing, the structural acceleration, and the reinforcement strain in the plastic hinge area of the pier bottom were measured. The additional mass blocks and the transducers of the test model are shown in Figure 6, and the photo of the test model is shown in Figure 7.

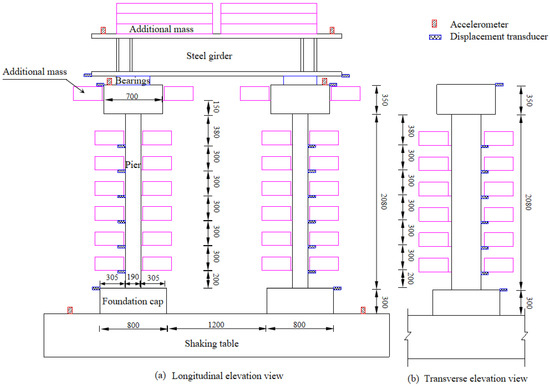
Figure 6. Additional mass blocks and transducers of Model II (unit: mm).

Figure 7. Photo of the test model.

3.3. Earthquake Excitations and Test Cases

The test is carried out in the State Key Laboratory of Disaster Reduction in Civil Engineering of Tongji University. The test equipment is an MTS two-direction and three-degree-of-freedom shaking table. The parameters of the shaking table are as follows: the table size is 6 m × 4 m, the maximum displacement is +/−0.5 m, the rated acceleration is 1.5 g, and the working frequency is 0.1–50 Hz.

Three earthquake excitations, named SJ1, SJ2, and SJ3, are artificially generated and input along the longitudinal direction. The compressed acceleration time histories are shown in Figure 8. In the shaking table test, the peak ground acceleration (PGA) of the earthquake excitations are scaled from 0.1 g to 0.75 g. These excitations correspond to seismic intensities of frequent earthquakes, design earthquakes, and rare earthquakes, respectively. Several white noise cases with a PGA of 0.05 g are also arranged to determine the state of the test model. All of the test cases are listed in Table 3.

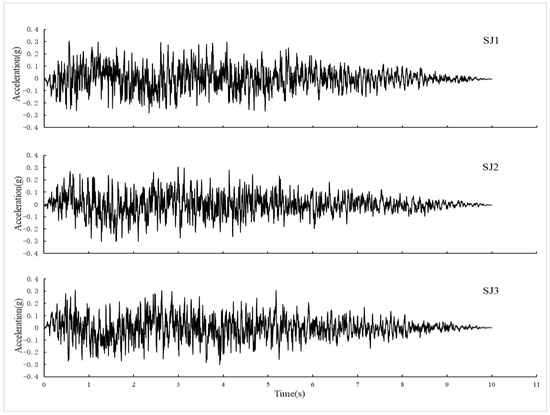
Figure 8. Artificial waves (unit: g).

Table 3. Test cases.

Case	Model	Earthquake Excitation	PGA (g)	Seismic Intensity Level
1	Model I and II	White noise	0.05
2		SJ1	0.1	Frequent earthquakes
3		SJ2	0.1
4		SJ3	0.1
5		SJ1	0.2
6		SJ2	0.2
7		SJ3	0.2
8		SJ1	0.3	Design earthquakes
9		SJ2	0.3
10		SJ3	0.3
11		SJ1	0.45	Rare earthquakes
12		SJ2	0.45
13		SJ3	0.45
14		White noise	0.05
15		SJ1	0.6	Rare earthquakes
16		SJ2	0.6
17		SJ3	0.6
18		SJ1	0.75
19		SJ2	0.75
20		SJ3	0.75
21		White noise	0.05

4. Analysis of Test Results

4.1. Test Phenomena

The material test results are: the average compressive strength of the concrete is 40 MPa, and the elastic modulus is 3.45 × 10⁴ MPa. The elastic modulus of the reinforcement is 2.08 × 10⁵ MPa, and the yield strength is 401 MPa.

In the test cases of frequent earthquakes, the bearing displacement of each test model is nearly zero, indicating that the IPGBs have not yet entered the seismic isolation state. In the test cases of PGA ≥ 0.3 g, the bearing displacement is visible and increases with the increase in PGA, which indicates that the IPGBs have entered the seismic isolation state for both design earthquakes and rare earthquakes.

After the test, there is no apparent residual crack in the aqueduct piers, indicating that the structure is basically in an elastic state.

4.2. Seismic Isolation Effect of IPGBs

The natural frequencies of each model in the white noise cases are shown in Table 4. It can be seen that structural natural frequencies of Model I and Model II decrease by 3.3% and 12.5%, respectively, by comparing the results of case 1 and case 14, respectively. The structural natural frequencies of Model I and Model II decrease by 6.7% and 18.8%, respectively, by comparing the results of case 1 and case 21, respectively. It is shown that the IPGB has an excellent seismic isolation effect and can protect the substructure of the aqueduct well during an earthquake.

Table 4. The natural frequency of each test model.

Model	Case 1	Case 14	Case 21
Model I	3.0 Hz	2.9 Hz	2.8 Hz
Model II	1.6 Hz	1.4 Hz	1.3 Hz

The maximum acceleration responses of the two models are shown in Figure 9. The acceleration responses of the pier tops increase with the PGAs, and the pier acceleration responses of Model II are less than those of Model I because of the minor horizontal stiffness of Model II. The girder acceleration responses of the two test models are relatively close and there is little change.

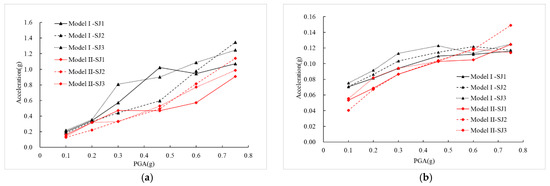
Figure 9. Maximum responses of the structural acceleration. (a) Pier acceleration. (b) Girder acceleration.

The seismic isolation rate R can be calculated to show the seismic isolation effect of the bearing as follows:

$$R=1-\frac{A_{max}^G}{A_{max}^P},$$

(5)

where $A_{max}^G$ is the maximum acceleration of the girder and $A_{max}^P$ is the maximum acceleration at the pier top.

The seismic isolation rates of all the test cases are listed in Table 5. All of the values are greater than 60% and increase with the PGAs, implying the IPGB has a satisfactory seismic isolation effect. Generally, the seismic isolation rates of Model I are higher than those of Model II, especially when the PGA is ≥0.3 g. Hence, the pier height has a certain influence on the bearing seismic isolation effect.

Table 5. Seismic isolation rate R.

Model	Earthquake Excitation	PGA (g)
		0.1	0.2	0.3	0.46	0.6	0.75
Model I	SJ1	64.9%	76.2%	83.5%	89.3%	88.1%	89.2%
	SJ2	61.1%	73.8%	76.6%	80.7%	87.5%	91.3%
	SJ3	65.4%	74.2%	86.0%	86.4%	89.6%	90.0%
Model II	SJ1	66.9%	78.4%	81.7%	78.1%	81.6%	86.2%
	SJ2	68.5%	69.6%	74.1%	78.9%	85.5%	86.9%
	SJ3	60.6%	74.3%	71.4%	80.5%	84.6%	88.4%

4.3. Displacement Responses of the IPGBs

The maximum displacements and residual displacements of the IPGBs in all the cases are shown in Figure 10. The time histories and hysteresis curves of the IPGBs in Model I for case 20 and Model II for case 16 are shown in Figure 11 and Figure 12, respectively.

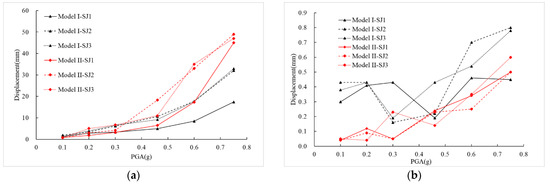
Figure 10. Seismic responses of the bearings. (a) Maximum displacement. (b) Residual displacement.

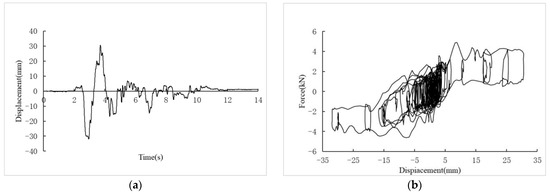
Figure 11. Time history and hysteresis curve of the IPGB of Model I for case 20. (a) Bearing displacement. (b) Hysteresis curve.

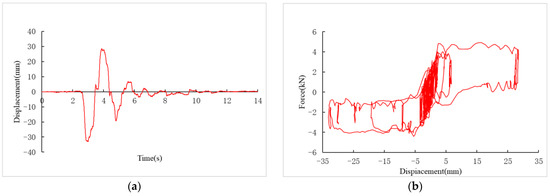
Figure 12. Time history and hysteresis curve of the IPGB of Model II for case 16. (a) Bearing displacement. (b) Hysteresis curve.

As shown in Figure 10, Figure 11 and Figure 12, the maximum bearing displacement increases with the PGAs, and the bearing displacement of Model II is larger than that of Model I. The bearing residual displacement of each model is less than 1 mm, which indicates the excellent post-earthquake resilience of the bearing.

4.4. Influence of Pier Height

As shown in Table 4, the natural frequencies of the two models are different, their reductions after rare earthquakes are also different, and the structural stiffness of Model II decreased significantly. Hence, it is demonstrated that the pier height has a significant influence on the aqueduct’s seismic performance.

Maximum reinforcement strains at the pier bottom for all the cases are shown in Figure 13. The reinforcement strain at the pier bottom of Model I remains nearly unchanged for cases of a PGA of ≥0.3 g. However, the reinforcement strain at the pier bottom for Model II increases with the PGA. The maximum reinforcement strains at the pier bottom for Model II are greater than 2000 με for the cases of a PGA of ≥0.6 g, and the pier has entered a slightly plastic state. It is demonstrated that the aqueduct’s seismic performances for Model I and Model II are quite different.

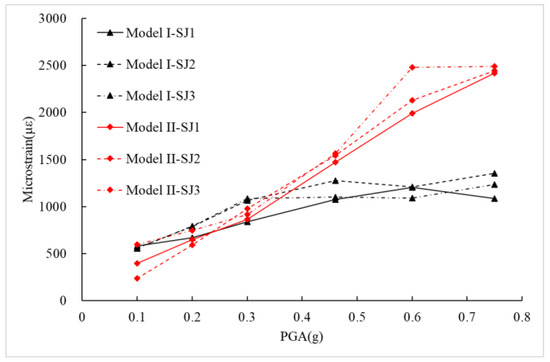
Figure 13. Maximum reinforcement strains at the pier bottom.

Displacement time histories at the top and half-height of the piers in Model I and Model II for cases 17 and 20 are shown in Figure 14 and Figure 15, respectively.

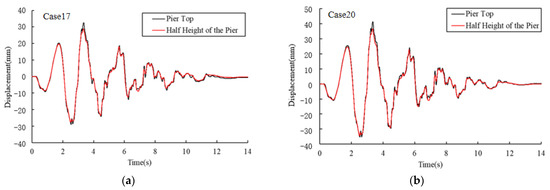
Figure 14. Displacement time histories in Model I. (a) For case 17. (b) For case 20.

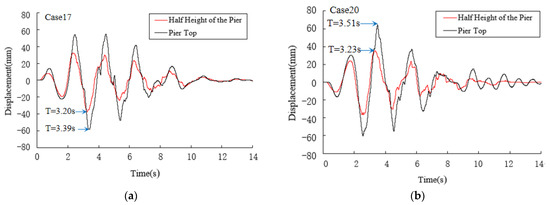
Figure 15. Displacement time histories in Model II. (a) For case 17. (b) For case 20.

It can be seen that in Model I, the displacement time histories at the top and half-height of the pier are very similar and the maximum values of the two curves appear at nearly the same time. However, in Model II, the two time history curves are totally different and the maximum values of the two curves do not appear at the same time. The maximum displacement at the half-height of the pier typically appears earlier than that at the pier’s top. It is indicated that the aqueduct’s seismic performance in Model II is affected by the high-order mode of the pier.

5. Numerical Simulation Method

According to the shaking table test results, the IPGB has an excellent seismic isolation effect and post-earthquake resilience. However, as a new type of bearing, the hysteresis curve of the IPGB is very unique. To further study the seismic performance of the aqueduct using IPGBs, a reasonable numerical simulation method is necessary. In this section, the numerical simulation method for the aqueduct using IPGBs is proposed, and its accuracy is verified by comparing it with the experimental results.

The girder of the aqueduct is simulated by elastic beam elements. The simulation methods of the reinforced concrete pier include a fiber beam element [42,43], an elastic beam element with reduced stiffness [44], and an elastic beam element with a plastic hinge. The aqueduct in this paper adopts the seismic isolation system, and the pier has no residual cracks after the test, which indicates that the pier is basically in an elastic state during earthquakes, and so the elastic beam element with a reduced stiffness is used to simulate the pier in this paper. The pier stiffness is reduced according to the AASHTO specification [45]. The reinforcement ratio and the axial compression ratio of the pier are 0.03 and 0.32, respectively, and so the reduction coefficient of the pier stiffness is 0.6.

The displacement–force relation of an IPGB cannot be simulated by a single element in existing finite element software. An ideal elastic–plastic element and a friction element are connected in parallel to simulate the IPGB connection element in this paper, as shown in Figure 16. The pre-yield stiffness of the ideal elastic–plastic element is provided by $k=\frac{F_1+F_2}{2}=W\tan \theta /dg,$ the yield force of the ideal elastic-plastic element is provided by $F_3=W\tan \theta$, and the yield force of the friction element is provided by $F_4=\mu W$.

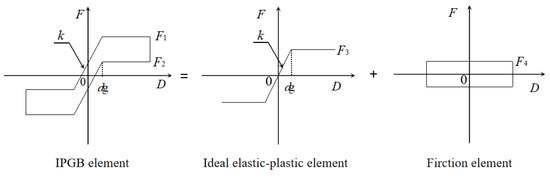
Figure 16. Simulation method for the IPGBs.

Relevant past research [46] has shown that using a constant friction coefficient to simulate sliding friction can well estimate the displacement of bearings and a structure, and a constant friction coefficient is also convenient for further parameter analysis of an aqueduct that uses IPGBs. Therefore, the friction coefficient used in the paper is constant and the value is 0.03.

With the above method, finite element models of aqueducts using IPGBs are established in SAP2000 finite element software, as shown in Figure 17. The results calculated with numerical models are compared with the test results, as shown in Figure 18 and Figure 19, and the maximum values of the numerical simulation and test results, as well as the errors between them, are listed in Table 6.

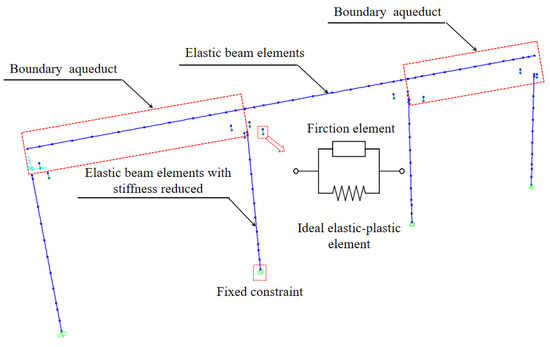
Figure 17. Numerical simulation model.

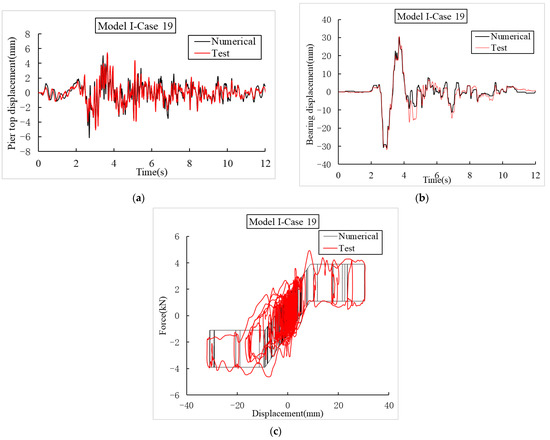
Figure 18. Comparison between the numerical and test results of Model I for case 19. (a) Time history of pier-top displacement. (b) Time history of bearing displacement. (c) Hysteresis curve of the bearings.

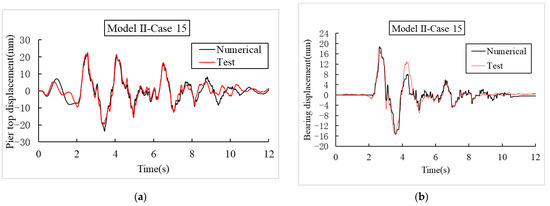
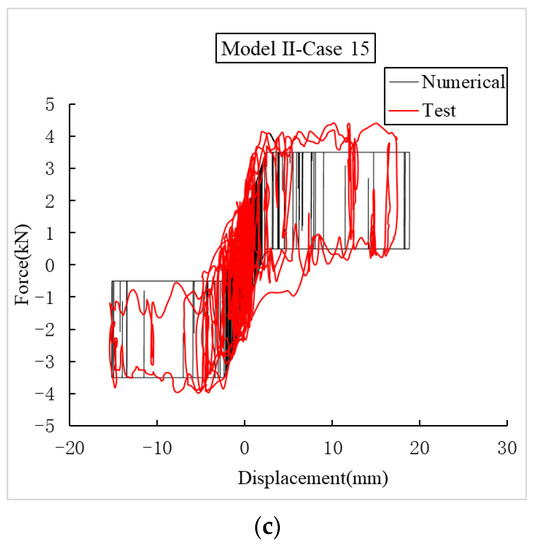
Figure 19. Comparison between the numerical and test results of Model II for case 15. (a) Time history of the pier-top displacement. (b) Time history of the bearing displacement. (c) Hysteresis curve of the bearings.

Table 6. Comparisons between the numerical and test results.

Model and Test Condition	Pier-Top Displacement (mm)			Bearing Displacement (mm)			Bearing Force (kN)
	Test	Numerical	Numerical/Test	Test	Numerical	Numerical/Test	Test	Numerical	Numerical/Test
Model I, case 19	5.47	5.32	0.97	30.62	30.35	0.99	4.58	3.90	0.85
Model II, case 15	22.63	22.26	0.98	17.46	18.45	1.06	4.21	3.50	0.83

As shown in Figure 18 and Figure 19, the simulation results of the time–history curve of the pier top displacement and the bearing displacement are highly coincident with the test results, and the simulation results of the bearing hysteresis curve are largely consistent with the test results. The maximum errors of pier-top displacement, bearing displacement, and bearing force are 3%, 6%, and 17%, respectively. The numerical simulation method proposed in this paper is applicable for aqueducts that use IPGBs with different pier heights in different test cases.

6. Conclusions

In this paper, a shaking table test is designed and carried out to study the seismic performance of an aqueduct that uses IPGBs, with the pier height and PGA as the parameters. Then, a numerical modeling method for aqueducts that use IPGBs is proposed, and its accuracy is verified by comparing the results of the numerical simulation method and the shaking table test. The main conclusions are as follows:

• The seismic isolation rate R is calculated to show the seismic isolation effect of the IPGB. The seismic isolation rate increases with the PGAs, and those of Model I are greater than those of Model II. The seismic isolation rates of both models are greater than 60%, indicating that the IPGBs have an excellent seismic isolation effect.
• The average bearing residual displacement of Model II is less than that of Model I, and the bearing residual displacements of both models are less than 1 mm. Therefore, the IPGBs have very good post-earthquake resilience, and the residual displacement of the bearing after the earthquake is minimal.
• The pier height has a distinct influence on the aqueduct’s seismic performance. When the PGA is ≥0.3 g, the reinforcement strain at the pier bottom in Model I does not increase with the PGAs. In contrast, the reinforcement strain at the pier bottom in Model II is positively correlated with the PGAs. The aqueduct’s seismic performance in Model II is affected by the high-order mode of the pier.
• The maximum errors of pier-top displacement, bearing displacement, and bearing force are 3%, 6%, and 17%, respectively, and the numerical simulation method proposed in this paper is applicable to aqueducts that use IPGBs.