A Hybrid Variable Weight Theory Approach of Hierarchical Analysis and Multi-Layer Perceptron for Landslide Susceptibility Evaluation: A Case Study in Luanchuan County, China

Abstract

Landslides, which can cause significant losses of lives or property damages, result from several different environmental factors whose influences are very complex. Thus, the statistical multi-layer perceptron (MLP) and heuristic analytical hierarchy process (AHP) are employed in the evaluation of landslide susceptibility. However, the landslide susceptibility maps drawn by these two methods are always affected by subjectivity and randomness. In the present study, we introduce variable weight theory (VW) to improve the MLP and AHP methods, and two novel hybrid models, AHP-VW and MLP-VW, are respectively proposed. VW theory is used to redistribute the weights of the factors in the two constant weight evaluations. This is so that the weights of the factors change with different evaluation units, thereby eliminating the subjectivity and randomness problems. The landslide susceptibility maps of the study area were categorized into very low, low, moderate, high, and very high susceptibility grades. The landslide susceptibility maps of the four models are validated by the receiver operating characteristic (ROC) curve. The area under the curve (AUC) is 0.825 for the AHP model, 0.879 for the MLP model, 0.873 for the AHP-VW model, and 0.915 for the MLP-VW model. The results show that the landslide susceptibility map drawn by statistical MLP is better than that drawn by heuristic AHP, which is consistent with many other current research results. Furthermore, VW can significantly improve the performance of constant-weight single models. Landslide susceptibility maps drawn by the statistical MLP model hybrid VW can be used for regional land use planning and landslide hazard mitigation purposes.

1. Introduction

Landslides are hazardous disasters that occur over the entire globe and significantly affect the development of an area, for example through loss of life and property damages [1]. The oldest landslide on record occurred in Hunan Province, China, in 1767 BC because of the triggering of an earthquake [2]. The World Health Organization (WHO) has reported that landslides at the global scale had caused approximately 18,000 deaths and affected 4.8 million people [3]. As a preliminary stage of future landslide management, landslide susceptibility mapping and zonation (LSMZ) not only provides an estimate of “where” landslides may be more likely to occur, but also divides the landslide susceptibility (LS) into different levels for further management in an area [4,5]. The factors that caused the landslides can be divided into conditioning and triggering groups [6]. The former mainly consists of the basis of the local terrain (e.g., slope, lithology, aspect, elevation, soil characteristics, etc.), while the latter normally refers to natural or anthropogenic slope failure caused in the short-term by factors such as precipitation, water level fluctuation, rapid snow melting, earthquake, and human activities [7,8].

Currently, a large number of methods for LSMZ have been shown in the literature and can be grouped into heuristic, deterministic, and statistical methods [9,10]. However, the three types of methods have different degrees of advantages and disadvantages in LSMZ [11,12,13]. Specifically, heuristic methods (e.g., analytic hierarchy process (AHP) model, multi-criteria evaluation, etc.) are mostly qualitative and based on prior knowledge and local experiences, as well as expert judgments [14]. Their reliability depends on how well the investigator understands the geomorphological processes acting upon the terrain. Therefore, heuristic methods are normally criticized for their subjectivity, uncertainty, and low model predictive performance. Deterministic methods (e.g., Newmark displacement, infinite slope stability model, etc.) rely on an understanding of the physical laws controlling slope instability to assess LS. These methods are only applicable in homogeneous geomorphic and geologic conditions, with simple landslide types, small-scale study areas, and previous data (e.g., soil characteristics, lithology, etc.) [15]. Lastly, statistical methods are based on the assumption that “the past and present are keys to the future” [11], and they mainly include the classic statistical models, such as the information value model [16], weight of evidence [17], and discriminant analysis [18], and machine learning methods, such as neural network analysis, support vector machine, and decision trees. Yong et al. reported that statistical methods are currently more popular than others, particularly machine learning methods [19]. However, criticisms of statistical methods have also been present in the vast literature, as they possess the following disadvantages:

(1) 

Statistical methods are also called “black box” models, with a lack of landslide-controlling processes [20,21].

(2) 

Statistical methods cannot be used when the landslide factors are dynamic (e.g., land use, climate, water table fluctuation) during the analytical period [22,23].

(3) 

Deep learning methods in LSMZ focus on finding out the global optimum, which takes significant time in the optimization process [24,25]. However, the machine learning methods of local optima solutions are concerned with model performance [26].

(4) 

Statistical methods are very dependent on data accuracy. On the one hand, the over-fitting issue may be prone to occur in statistical models [27]. On the other hand, the incompleteness of the landslide inventory may highly affect the model’s performance in these methods [28].

Considering the drawbacks of single heuristic, deterministic, and statistical methods, many scholars have commenced developing hybrid models for higher model performance, integrating different models and theories. For example, Shirzadi et al. presented a hybrid model with the integration of two machine learning methods, including naïve Bayes trees (NBT) and random subspace (RS), and obtained a higher AUC value (0.886) than with the single NBT model (0.811) [29]. Yan et al. introduced a cloud model (CM) to improve the performance of the existing analytical hierarchy process-normalized frequency ratio (AHP-NFR) model, which can effectively solve the issues of randomness and fuzziness [30]. Nguyen et al. demonstrated that a hybrid model combining particle swarm optimization (PSO) evolutionary algorithms and an artificial neural network (ANN) increased the model’s reliability and performance in LSMZ [31]. Aghdam et al. designed and compared two hybrid models (namely the frequency ratio-adaptive neuro-fuzzy inference system (FR-ANFIS) model and weights-of-evidence-adaptive neuro-fuzzy inference system (WOE-ANFIS) model) and demonstrated the great potential for hybrid model development [32]. The development of hybrid models effectively increased the predictive model’s performance more than a single heuristic, deterministic, and statistical model in LSMZ, and this has become the new tendency in this field.

Variable weight (VW) theory was first proposed by Wang [33] and well developed by Li in a comprehensive decision-making model [34,35]. This theory can eliminate the issue of one-sidedness for actual decision making by establishing a variable weight function [36]. It has been widely used in decision-making processes and weight determination in many fields [37,38,39]. In general, AHP obtains the weight of each factor by expert scoring, while MLP obtains the weight of each factor by statistical methods. Both evaluation models use static constant-weight evaluation, directly assigning weights to each evaluation factor or indirectly determining the weight of each evaluation factor by statistical methods, which can reflect the importance of each factor in the susceptibility evaluation. However, the weights of similar factors for different evaluation objects or the same evaluation object at different moments in the actual evaluation will keep changing. For LS, no matter how superior other factors are, as long as a certain factor is poor to a certain degree, the susceptibility of the evaluation unit will increase, so the weight of the factor should be increased. Otherwise, it may be “neutralized” by the superior factor, and the evaluation result will not match with the actual one. VW theory is used to redistribute the constant weights of each factor to each evaluation unit through the variable weight function, so that the weight of each factor changes with the change of the evaluation unit, to eliminate the problem of one-sidedness in actual decision making. However, there are limited studies applying VW theory in LSMZ. The only existing paper concerning VW theory and LSMZ comes from Zhang et al. [27]. They reported that the accuracy of the AHP-VW model has been greatly improved by introducing VW theory in LS evaluation. Currently, no studies show whether VW theory can improve the model performance of statistical MLP models. In this study, two hybrid models, namely the AHP-VW model and MLP-VW model, were designed to conduct LSMZ, taking Luanchuan County, Henan Province, China, as a case study. It is a hilly area that suffers from frequent recorded landslides. The two designed models represent the integration of VW theory and the heuristic model and statistical model, respectively. The performance of the single AHP model and multi-layer perceptron (MLP) model was compared with the two designed models. The receiver operating characteristic (ROC) curve was used to statistically compare the models’ performance. The objectives of this study include the following:

(1) 

Illustrate the significance of VW theory in LSMZ, including heuristic methods and statistical methods.

(2) 

Find out the optimal model for LSMZ in the study area.

(3) 

Provide suggestions for local landslide prevention and control (P&C) strategies based on LS maps.

2. Materials and Methods

The methodological framework adopted in this study is presented in Figure 1. Firstly, data from the study area were collected, including landslide inventory, climatic data, geological map, geomorphological map, digital elevation model (DEM), and land use data. Based on these data, landslide inventory maps and maps of eight causative factors (lithology, distance to fault, geomorphology, distance to river, elevation, aspect, slope, and land use) were produced, in which Pearson correlation analysis and multicollinearity analysis were also performed for the causative factors. It is worth noting that each landslide in the landslide inventory map can be represented by a point on a regional scale. In this paper, we use the geostatistical analysis tool in GIS to select 70% (148) of the landslides in the original database as the training dataset and the remaining 30% (64) as the validation dataset. Secondly, the values of each causative factor were calculated and rated by frequency ratios, constant weights for each causative factor were calculated using AHP and MLP, and variable weights were obtained using VW theory. The study area was also divided into 29,800 evaluation units. It should be noted that due to the small size of the study area and the large dispersion of factors, an irregular polygon grid method was used to divide the evaluation cells. Four different models, AHP, MLP, AHP-VW, and MLP-VW, were constructed for LS evaluation, and a series of LS maps were generated. Finally, the models are validated and discussed, and suggestions are made for local landslide P&C and future research.

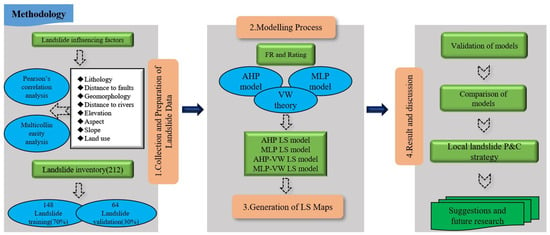
Figure 1. Methodological framework.

2.1. Study Area

Luanchuan, covering approximately 2463 km², is in the west of Henan province, China (111°11′ E–112°01′ E, 33°39′ N–34°11′ N), with a population of 0.33 million (Figure 2a,b). The climate is temperate continental monsoon with average annual precipitation of 738 mm. The terrain is generally high in the southwest and low in the northeast, with an average altitude of 750 m, forming different morphological classes including middle mountain areas, low mountain areas, and basins (Figure 2c). The peak of Baiyun mountain is the highest point, with an elevation of 2135 m (southeast of the region). The slopes of the whole study area are relatively gentle, normally less than 30°. The geology is characterized by ranging from Archean to Tertiary, with abundant carbonate rocks, metamorphic rocks, granites, sandstone, and argillaceous siltstone (Figure 2d). With significant tectonic activities and a large number of faults, geological disasters occur frequently in the study area, particularly landslides. Water resources, mineral resources, and forest resources are abundant in the study area. There are four major rivers and 604 tributaries in the study area, with a river network density of 0.59 km per square kilometer. More than 50 types of metal minerals, non-metal minerals, energy minerals, and water vapor minerals are distributed in the study area. Forest coverage exceeds 80% in the study area, ranking first in Henan province. The landslide inventory (Figure 2c) is collected from a field mapping report (2020) conducted by the Department of Natural Resources of Henan Province (DNRHP) in the study area, which identified a total of 212 landslide points.

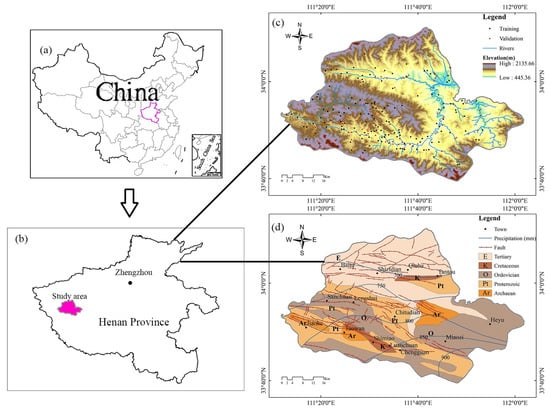
Figure 2. Study area information: (a) Henan province in China; (b) study area in Henan province; (c) study area with landslide inventory, elevation, and river systems; (d) study area with geology, fault, main counties, and precipitation.

2.2. Data Collection

Table 1 illustrates the data sources and corresponding causative factor layers used in this study, mainly including landslide inventory (training set and validation set), climate data (precipitation), geological (lithology and distance to faults) and geomorphologic maps (geomorphology and distance to river), DEM (elevation, aspect, and slope), and land use data (land use).

Table 1. The data layer, format, scale, source, and corresponding causative factors.

Data Layer		Data Format	Scale or Resolution	Data Source
Landslide inventory		Shape (point)	1:50,000	DNRHP
Geological map	Lithology	Tiff	1:50,000	DNRHP
	Distance to faults
Geomorphologic map	Geomorphology	Tiff	1:50,000	DNRHP
	Distance to river
DEM	Elevation	Grid	30 m	ASTER GDEM 30M
	Aspect
	Slope
Land use	Land use	Grid	30 m	Globeland30
Climate	Precipitation	Tiff	1:50,000	China Meteorological Data Network

2.3. Causative Factor Determination

2.3.1. Causative Factor

At present, there is no consensus on which landslide-influencing factors should be involved in the model design process [40]. In this study, based on site characteristics (from the field mapping report), data availability, previous research [41,42], and communication with local experts, the causative factors are determined from the geological aspect (lithology and distance to faults), morphological aspect (geomorphology, aspect, elevation, slope), hydrological aspect (distance to river), and land cover aspect (land use). According to the statistical analysis of causative factors, the factors selected above are all frequently used causative factors for modeling by LS researchers [10,43].

−

Lithology (LI)

Lithology provides the material support for the occurrence of landslides and forms the basis of landslide development. The materials in different lithologies vary in characteristics including strength, density, durability, permeability, and degree of weathering [44]. The weaker (e.g., from weathering or erosion) materials provide less resistance to driving force than the stronger materials and are thus more susceptible to landslides [45]. In this study, eight groups of lithology were manually classified by similar engineering geological characteristics: group 1: metamorphic rock with strong weathering (mainly quartzite); group 2: soft sandstone quartz sandstone; group 3: stratified clastic rock with fractures; group 4: hard massive intrusive rock group (mainly granite); group 5: hard thick intrusive rock group; group 6: sandstone and argillaceous siltstone with an argillaceous interlayer; group 7: hard limestone and dolomite; group 8: hard and thin carbonate rock (Figure 3a).

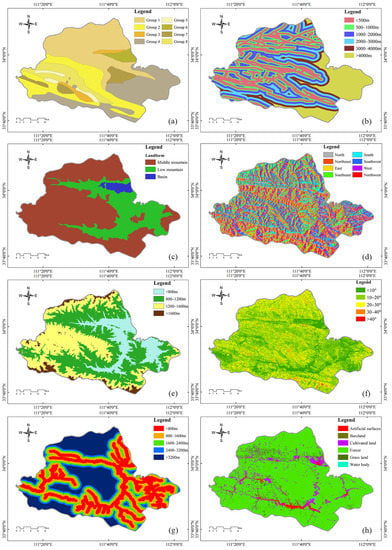
Figure 3. Causative factors: (a) lithology, (b) distance to faults, (c) geomorphology, (d) aspect, (e) elevation, (f) slope, (g) distance to rivers, (h) land use.

−

Distance to faults (F)

Active faults have essential roles in cracking stones and causing extensive weathering, which provide the materials for sliding [17,46]. In addition, rock and soil bodies more easily slide along the fracture zone, and the anti-sliding force is significantly reduced. The faults in the study areas are complex and widely distributed and were further divided into six classes by Euclidean distance: <500 m, 500–1000 m, 1000–2000 m, 2000–3000 m, 3000–4000 m, and >4000 m (Figure 3b).

−

Geomorphology (G)

Geomorphology is a composite result of morphology, soil characteristic, climate, vegetation, and aquatic ecosystem, thus further significantly affecting the regional distribution of landslides [47]. In LS research, geomorphology can also be presented by relative relief [48,49] and topographic position index (TPI) [50,51]. In this study, the geomorphology of the study area was divided into basin areas (0–500 m in relative relief), low mountain areas (500–1000 m in relative relief), and middle mountain areas (1000–3500 m in relative relief) (Figure 3c).

−

Aspect (A)

Aspect’s influence on landslide occurrence is a complicated effect of solar radiation intensity, precipitation, humidity, weathering, and wind direction [42,52]. Therefore, it is also a significant factor that influences landslide occurrence. In this study, aspects were created by DEM and divided into eight classes: north, northeast, east, southeast, south, southwest, west, and northwest. The plane aspect was ignored because the regions were too small (Figure 3d).

−

Elevation (E)

The elevation is usually considered a critical causative factor in regional LS prediction, especially for areas where elevations change dramatically [9]. It influences slope stability because the biophysical parameters and anthropogenic activities vary at different elevations [41]. The elevation produced by DEM in this study was divided into four classes: <800 m, 800–1200 m, 1200–1600 m, and >1600 m (Figure 3e).

−

Slope (S)

Slope controls the balance of the retaining and destabilizing forces acting on a slope [53]. It also indirectly affects the characteristics of both surface and subsurface flow and hence soil water content, soil formation, erosion potential, and many important geomorphic processes [41]. Therefore, the slope is also a significant causative factor that has been widely used in LS map modeling. In this study, the slope layer was created by DEM, and it was divided into five classes: 0–10°, 10–20°, 20–30°, 30–40°, and >40° (Figure 3f).

−

Distance to rivers (R)

The distance to rivers refers to the proximity of the rivers and drainages in the area [54]. Bank slopes are likely to be influenced by the erosion and downcutting of the river, which are prone to cause landslides over time [55]. Therefore, taking an equal interval of 800 m, the distance to river was identified as five buffer classes: <800 m, 800–1600 m, 1600–2400 m, 2400–3200 m, and >3200 m (Figure 3g).

−

Land use (LU)

The occurrence of landslides varies with land use pattern [56]. It is a characteristic of soil materials, vegetation cover, and human activities, which reflects the effects of people’s use intensity and natural contribution to landslide occurrence [57]. In this study, the land use was classified into artificial surfaces, bare land, cultivated land, forest, grassland, and water body (Figure 3h).

2.3.2. Pearson’s Correlation Analysis

Pearson’s correlation analysis measures the linear relationship of two variables with a value from −1 to 1, where 0 is no correlation, and 1 and −1 represent the total positive correlation and total negative correlation, respectively. The equation of Pearson’s correlation analysis is shown as follows:

$$r=\frac{{\displaystyle \sum }\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{\displaystyle \sum }{(x_i-\overline{x})}^2{\displaystyle \sum }{(y_i-\overline{y})}^2}}$$

(1)

where $r$ is the Pearson correlation coefficient, $x_i$ is the $x$ variable sample, $y_i$ is the $y$ variable sample, $\overline{x}$ is the mean of values in the $x$ variable, and $\overline{y}$ is the mean of values in the $y$ variable.

In this study, we consider an $r$ value higher than 0.7 to show a high linear relationship of two variables. Under this condition, one of the two variables should be removed.

2.3.3. Multicollinearity Analysis

In multiple regression models, the issue of multicollinearity may occur if two or more variables have linear relations, which may significantly influence the model’s accuracy. In this study, two indicators, namely variance inflation factor (VIF) (Equation (2)) and tolerances (TOL) (Equation (3)), are used to estimate the multicollinearity between the causative factors. In this study, we consider removing the causative factors with VIF < 10 and TOL > 0.1.

$$VIF=\frac{1}{1-R_i^2}$$

(2)

$$TOL=\frac{1}{VIF}$$

(3)

where $R_i^2$ is the coefficient of determination of the model

2.4. Modeling

2.4.1. Frequency Ratio (FR) Calculation and Ratings

FR is a widely used statistical approach in LS zonation. The FR is the ratio of the probability of an occurrence to the probability of a non-occurrence for given attributes. It is based on the observed relationships between the distribution of landslides and each conditional factor to reveal the correlation between future landslide locations and factors in the study area [58]. If this ratio is greater than 1, then the relationship between the landslide and the conditional factor’s range or classification is stronger. Otherwise, it is weaker [59]. For a total of $n$ conditional factors, the FR of conditional factor $x$ in the $i^{th}$ class is calculated by the following equation:

$$FR \left(x_i\right)=\frac{N_i/N}{S_i/S}$$

(4)

where $x_i$ represents the conditional factor $x$ in the $i^{th}$ class, $N_i$ is the number of landslides in the $i^{th}$ class of condition factor $x$, $N$ is the total number of landslides in the study area, $S_i$ is the area in the $i^{th}$ class of conditional factor $x$, and $S$ is the total area of the study area.

To conduct the subsequent calculations and evaluations, the FR results are normalized and empirically provided a score from 0.1 to 0.9.

2.4.2. AHP Model

AHP is a multi-criterion decision analysis (MCDA) technology introduced by Saaty, which allows subjective expert opinions as well as an objective comparative analysis to be considered in the decision-making process [60]. In AHP, the comparison factors are judged on a scale from 1 to 9 for relative importance. It is a common heuristic approach that empirically determines the weights of causative factors, taking expert knowledge into account [17]. The consistency ratio (CR) is used to ensure the consistency of weights determined by the AHP model, and the equation of CR calculation is shown in Equations (5) and (6). If the CR is less than 0.1, the weights determined by the AHP model can be considered reliable.

$$CR=\frac{CI}{RI}$$

(5)

$$CI=\frac{{\lambda }_{max}-m}{m-1}$$

(6)

where $CI$ is the consistency index, $RI$ is a random index (Table 2), ${\lambda }_{max}$ is the maximum eigenvalue, and $m$ is the total number of parameters.

Table 2. RI values for the pairwise comparisons in AHP analysis.

m	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49

The landslide susceptibility index $LSI$ for a unit in the AHP model is given by the following equation:

$$LSI={{\displaystyle \sum }}_{x=1}^n{W}_x{w}_{ix}$$

(7)

where $w_{ix}$ is the rating of the $i^{th}$ class in the causative factor $x$, $W_x$ is the weight of causative factor $x$, and $n$ is the number of causative factors.

2.4.3. MLP Model

As a commonly used artificial neural network (ANN) method, the MLP model can effectively solve the binary classification problem by learning algorithms [61]. The MLP model includes multiple inputs, represented by $x_1$, $x_2$,…, $x_n$, n ∈ N, respectively, and uses $f$($w_{1x}$ + $b_1$) for outputs (Figure 4). The influence of the input signal can be measured by the assigned weights, and then the function is used to determine whether to activate the neuron. The structures of the MLP have three parts: the input layer, hidden layer, and output layer. In this study, the input layer, hidden layer, and output layer are causative factors, model processing, and evaluation results, respectively.

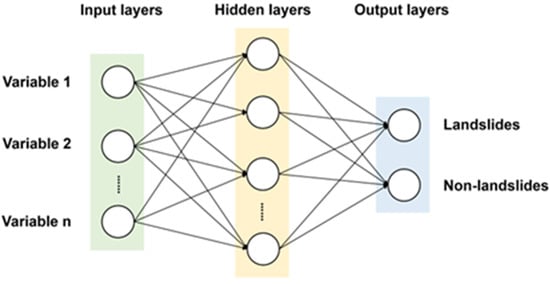
Figure 4. Schematic diagram of the MLP model.

2.4.4. VW Theory

VW theory was first proposed by Wang [33] and well-developed by Li in a comprehensive decision-making model [34,35]. In the weight determination process, one-sided deviations often occur in MCDA approaches, such as AHP, goal programming, and data envelopment analysis, while VW theory can eliminate the issue of one-sidedness for actual decision-making by establishing a variable weight function [36]. In the VW theory procedures used here, set $X=\left(x_1,\dots ,x_m\right)$ is the vector of factor $j$, and $S\left(X\right)=\left(S_1\left(X\right), \dots , S_m\left(X\right)\right)$ is the variable weight vector. VW theory shows that the variable weight vector is the Hadamard-normalized product of the constant weight vector and variable weight vector (See Equation (8)) [34].

$$W\left(X\right)=W\frac{S\left(X\right)}{{{\displaystyle \sum }}_{j=1}^m\left(W_j·S_j\left(X\right)\right)}$$

(8)

where $W\left(X\right)$ is the variable weight vector, $W$ is the constant weight vector, $S\left(X\right)$ is the state variable weight vector, $W_j$ is the constant weight vector of factor j, and $S_j\left(X\right)$ is the state variable weight vector of indicator j.

On this basis, Duan proposed the penalty-incentive segmented coordination theorem, which has been successfully applied to various decision-making problems (Equation (9)) (Figure 5) [62].

$$S_j\left(X\right)=\{\begin{array}{c}k\lambda ln\frac{\lambda }{x_j}+c x_j\in \left(0,\lambda \right]\\ c x_j\in \left(\lambda ,\alpha \right]\\ \frac{a-b}{2\left(\mu -\beta \right)\left(\beta -\alpha \right)}{\left(x_j-\alpha \right)}^2+c x_j\in \left(\alpha ,\beta \right]\\ \frac{a-b}{\mu -\beta }{x}_j+\frac{b\mu -a\beta }{\mu -\beta } x_j\in \left(\beta ,\mu \right]\\ \frac{a-b}{\mu -\beta }\left(1-\mu \right)ln\frac{\left(1-\mu \right)}{\left(1-x_j\right)}+a x_j\in \left(\mu ,1\right)\end{array}$$

(9)

where $x_j$ is the scoring; a, b, and c are the appraisal strategy; k is the adjustment coefficient; and λ, α, β, μ, c, b, and a are parameters with the following conditions (0 < λ < α < β < μ < 1, 0 < c < b < a < 1).

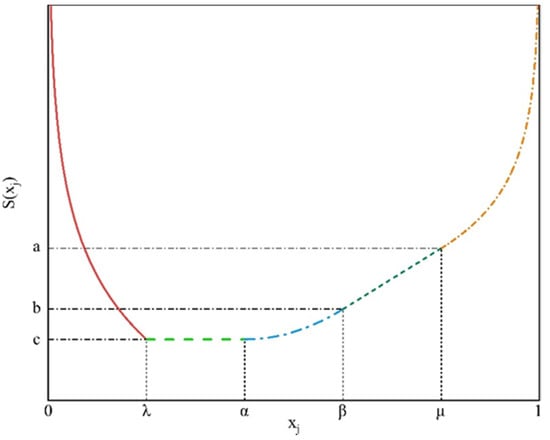
Figure 5. Penalty and incentive variable weight function.

2.4.5. ROC Curves

The ROC curve is a threshold-independent curve with some confusion matrices in which two statistics are calculated, namely TPR (true positive rate) and FPR (false positive rate) (Equations (10) and (11)) [63]. TP (true positive), FP (false positive), TN (true negative), and FN (false negative) represent the judgments of different confusion matrices, respectively. The ROC curve is constructed by plotting TPR and FPR (also called sensitivity and 1-specificity) on the y-axis and the x-axis. A higher AUC value indicates a better model, and a value of 1 indicates a perfect model [54].

$$TPR \left(sensitivity\right)=\frac{TP}{TP+FN}$$

(10)

$$FPR \left(1-specificity\right)=\frac{FP}{TN+FP}$$

(11)

In this study, we consider AUC values greater than 0.7 as “acceptable” models, greater than 0.8 as “good” models, and greater than 0.9 as “excellent” models.

3. Result and Discussion

3.1. Correlation and Multicollinearity Analysis

Table 3 shows the results of correlation analysis and multicollinearity analysis, respectively. It is found that all the $r$ values in Pearson’s correlation analysis are less than 0.7, and all the causative factors pass the multicollinearity diagnosis (VIF < 10 and TOL > 0.1). Therefore, all the causative factors can be used for the following LS map and analysis.

Table 3. Pearson’s correlation analysis and multicollinearity analysis.

Factors	LU	R	F	A	S	E	LI	G	VIEW	TOL
Land use (LU)	1.000	0.047	−0.014	−0.007	0.339	0.041	−0.002	0.192	1.167	0.857
Distance to river (R)	0.047	1.000	−0.183	0.038	0.015	0.362	0.033	0.355	1.313	0.761
Distance to fault (F)	−0.014	−0.183	1.000	0.089	−0.068	−0.180	0.271	−0.190	1.138	0.879
Aspect (A)	−0.007	0.038	0.089	1.000	0.098	−0.077	0.059	−0.062	1.037	0.964
Slope (S)	0.339	0.015	−0.068	0.098	1.000	0.114	−0.070	0.175	1.176	0.851
Elevation (E)	0.041	0.362	−0.180	−0.077	0.114	1.000	−0.331	0.502	1.538	0.650
Lithology (LI)	−0.002	0.033	0.271	0.059	−0.070	−0.331	1.000	−0.288	1.282	0.780
Geomorphology (G)	0.192	0.355	−0.190	−0.062	0.175	0.502	−0.288	1.000	1.533	0.652

3.2. Determination of Weight

3.2.1. Constant Weight Determination

Table 4 shows the results of AHP calculating the constant weights of factors. The specific calculations include constructing a judgment matrix, calculating the weight vector, and checking the consistency of the judgment matrix. The importance of the evaluation factors is compared between pairs by expert scoring, and then the corresponding judgment matrix is constructed, and the weight vector is calculated.

Table 4. The weights of causative factors determined by the AHP model.

Factors	LI	LU	G	A	E	F	R	S	Weight
Lithology (LI)	1	2	3	4	5	5	6	7	0.329
Land use (LU)		1	2	3	4	4	5	6	0.228
Geomorphology (G)			1	2	3	3	4	5	0.152
Aspect (A)				1	2	2	3	4	0.099
Elevation (E)					1	1	2	3	0.062
Distance to fault (F)						1	2	3	0.062
Distance to river (R)							1	2	0.040
Slope (S)								1	0.028
$n=8$;${\lambda }_{max}=8.2067$; $RI=1.41$;$CI=\frac{{\lambda }_{max}-n}{n-1}=0.0295$; $CR=\frac{CI}{RI}=0.0209<0.1$

In this paper, 70% of the landslide numbers were randomly selected as the training data set, and the remaining 30% were used as the validation data set. The MLP calculation weight is used to import the normalized FR value of the training set into SPSS26 for neural network training and testing. To make the prediction accuracy of the MLP model reach the optimal state, the cross-validation method is used to change the parameters in the model one by one to obtain the optimal model parameters. The model uses bagging to enhance the stability of the model and uses the gradient descent algorithm to adjust the parameters. Finally, the weight of each evaluation factor is obtained (Table 5).

Table 5. FR, normalized FR, ratings, and weights of MLP model.

Factors	Class	FR	Normalized FR	$\mathbf{Rating} \left({\mathit{x}}_{\mathit{j}}\right)$	Weight (MLP)
Geomorphology	Low mountain	1.2668	0.3418	0.5	0.053
	Basin	1.5701	0.4236	0.9
	Middle mountain	0.8696	0.2346	0.1
Lithology	Group 1	0.6353	0.0560	0.1	0.193
	Group 2	1.1584	0.1021	0.3
	Group 3	1.5295	0.1347	0.7
	Group 4	0.4802	0.0423	0.1
	Group 5	2.6449	0.2330	0.9
	Group 6	0.7483	0.0659	0.1
	Group 7	1.7640	0.1554	0.5
	Group 8	2.3900	0.2106	0.7
Aspect	North	0.6764	0.0839	0.1	0.094
	Northeast	1.0712	0.1328	0.7
	East	1.2785	0.1585	0.7
	Southeast	1.2385	0.1535	0.9
	South	0.7339	0.0910	0.1
	Southwest	1.1045	0.1369	0.3
	West	0.7681	0.0952	0.1
	Northwest	1.1958	0.1482	0.5
Elevation (m)	<800	1.3800	0.4236	0.9	0.228
	800–1200	1.2600	0.3868	0.7
	1200–1600	0.6178	0.1896	0.5
	>1600	0.0000	0.0000	0.3
Slope (°)	<10°	1.8183	0.5114	0.3	0.155
	10–20°	0.8654	0.2434	0.1
	20–30°	0.5646	0.1588	0.5
	30–40°	0.3071	0.0864	0.7
	>40°	0.0000	0.0000	0.9
Distance to fault (m)	<500	1.3237	0.2263	0.9	0.095
	500–1000	0.9308	0.1591	0.7
	1000–2000	1.0412	0.1780	0.5
	2000–3000	1.1888	0.2032	0.5
	3000–4000	0.8334	0.1425	0.3
	>4000	0.5321	0.0910	0.1
Land use	Grass land	2.0373	0.1672	0.5	0.137
	Cultivated land	3.7904	0.3110	0.9
	Artificial surfaces	1.6985	0.1394	0.5
	Bare land	0.0000	0.0000	0.3
	Forest	0.7094	0.0582	0.1
	Water body	3.9525	0.3243	0.7
Distance to river (m)	<800	1.5116	0.3064	0.9	0.045
	800–1600	1.0656	0.2160	0.5
	1600–2400	1.1587	0.2349	0.7
	2400–3200	0.7811	0.1583	0.5
	>3200	0.4163	0.0844	0.3

3.2.2. Variable Weight Determination

By spatially stacking all evaluation factors, 29,800 evaluation units can be obtained. The key to the calculation of the variable weight vector is the determination of the state variable weight vector, and the state variable weight vector can be constructed directly by using the mean value of the state vector, or it can be obtained by completing an equilibrium function. According to the classification of the evaluation factors and the final susceptibility classification requirements, each parameter in the state variable weight vector is determined by an equalization function. Considering λ = 0.2, α = 0.4, β = 0.6, μ = 0.7, adjustment coefficient k = 1.5, a = 0.5, b = 0.3, and c = 0.2, the state variable weight vector Equation (12) is obtained.

$$S_j\left(X\right)=\{\begin{array}{c}0.3ln\frac{0.2}{x_j}+0.2 x_j\in \left(0,0.2\right]\\ 0.2 x_j\in \left(0.2,0.4\right]\\ 5x_j^2-4x_j+1 x_j\in \left(0.4,0.6\right]\\ 2x_j-0.9 x_j\in \left(0.6,0.7\right]\\ 0.6ln\frac{0.3}{1-x_j}+0.5 x_j\in \left(0.7,1\right)\end{array}$$

(12)

Bring the rating ($x_j$) of each evaluation factor into Equation (12) to obtain S(X), and then use variable weight theory to calculate the variable weight of each factor in the evaluation unit. The output results are shown in Table 6 and Table 7.

Table 6. The variable weighting of AHP.

Unit	G	LI	A	E	S	F	LU	R
1	0.2327	0.1634	0.1229	0.1229	0.0143	0.1841	0.1389	0.0204
2	0.1869	0.3280	0.0987	0.0987	0.0115	0.1479	0.1115	0.0164
3	0.2256	0.1584	0.1191	0.1191	0.0444	0.1785	0.1346	0.0198
4	0.1823	0.3199	0.0962	0.0962	0.0359	0.1442	0.1088	0.0160
…	…	…	…	…	…	…	…	…
29,795	0.2133	0.1497	0.1442	0.1126	0.0420	0.0363	0.2546	0.0469
29,796	0.2189	0.1536	0.1480	0.1156	0.0168	0.0373	0.2613	0.0481
29,797	0.2446	0.1717	0.0516	0.1292	0.0150	0.0417	0.2920	0.0538
29,798	0.2367	0.1662	0.0500	0.1250	0.0466	0.0403	0.2826	0.0521
29,799	0.2196	0.1542	0.1485	0.1160	0.0135	0.0374	0.2622	0.0483
29,800	0.2415	0.1695	0.0637	0.1275	0.0148	0.0411	0.2883	0.0531

Table 7. The variable weighting of MLP.

Unit	G	LI	A	E	S	F	LU	R
1	0.0811	0.0923	0.1124	0.2727	0.0741	0.2636	0.0819	0.0215
2	0.0712	0.2027	0.0987	0.2395	0.0651	0.2315	0.0719	0.0189
3	0.0697	0.0793	0.0966	0.2344	0.2040	0.2266	0.0704	0.0185
4	0.0623	0.1773	0.0863	0.2095	0.1823	0.2025	0.0629	0.0165
…	…	…	…	…	…	…	…	…
29,795	0.0736	0.0837	0.1306	0.2474	0.2153	0.0515	0.1487	0.0488
29,796	0.0847	0.0964	0.1503	0.2848	0.0968	0.0593	0.1711	0.0562
29,797	0.0966	0.1099	0.0535	0.3247	0.0883	0.0676	0.1951	0.0640
29,798	0.0809	0.0920	0.0448	0.2719	0.2366	0.0566	0.1633	0.0536
29,799	0.0864	0.0983	0.1533	0.2904	0.0789	0.0605	0.1745	0.0573
29,800	0.0953	0.1084	0.0660	0.3204	0.0871	0.0667	0.1925	0.0632

3.3. Landslide Susceptibility Maps

The LSIs of the AHP model, the AHP-VW model, the MLP model, and the MLP-VW model were respectively calculated according to Equation (7). The LSI was divided into five grades: very-high-susceptibility area, high-susceptibility area, moderate-susceptibility area, low-susceptibility area, and very-low-susceptibility area by natural breakpoint method, and the LSMZ was compiled (Table 8). Although all mathematical classifications, such as equal interval, quantile, standard deviation, and geometrical interval, were tried in classifying the LSIs, the natural breaks method was selected as the logical method due to conformity with the actual conditions of the environment. Figure 6 shows that the LSMZ results compiled by the AHP model, AHP-VW model, MLP model, and MLP-VW model are generally consistent, but the MLP-VW model has the highest model performance, as almost all validated landslides are in very-high-LS areas. The distribution of LS in the study area is characterized by a striped spatial distribution along the river, while the density of landslide disasters is concentrated in the south and scattered in the north, showing the characteristics of being high in the south and low in the north.

Table 8. Grading of LSI in the study area.

Grading	Very-Low-Susceptibility Area	Low-Susceptibility Area	Moderate-Susceptibility Area	High-Susceptibility Area	Very-High-Susceptibility Area
AHP model	<0.2932	0.2932~0.4086	0.4086~0.5082	0.5082~0.6174	>0.6174
AHP-VW model	<0.2745	0.2745~0.4295	0.4295~0.5685	0.5685~0.6948	>0.6948
MLP model	<0.3368	0.3368~0.4336	0.4336~0.5152	0.5152~0.5992	>0.5992
MLP-VW model	<0.3267	0.3267~0.4656	0.4656~0.5817	0.5817~0.6887	>0.6887

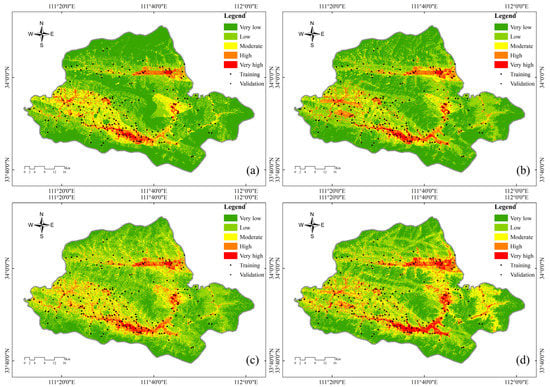
Figure 6. LS maps: (a) AHP model; (b) AHP-VW model; (c) MLP model; (d) MLP-VW model.

3.4. Validation of Models

To describe whether the compiled LSMZ is reasonable in an area, we use landslide density. The landslide density for each class in the study area was calculated by determining the number of landslides per square kilometer. This is used to determine the susceptibility class of an area, from very low to very high susceptibility class. Generally, a high value of landslide density indicates a high susceptibility class. According to Figure 7, firstly, the proportion of very-high-LS areas is very small, but the low-LS areas and very-low-LS areas are relatively large. Secondly, the landslide density in very-high-LS areas is significantly higher than in those areas’ sub-areas, which reflects the reasonability of the four models in LSMZ. In the MLP-VW model, there are 71 landslides in the very-high-susceptibility area, 43 landslides in the high-susceptibility area, 43 landslides in the moderate-susceptibility area, 46 landslides in the low-susceptibility area, and only 9 landslides in the very-low-susceptibility area, which has strong rationality.

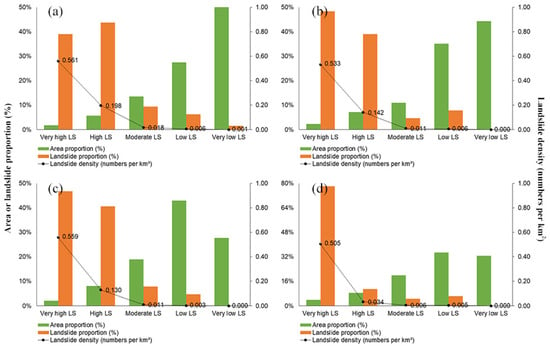
Figure 7. Landslide density: (a) AHP model; (b) AHP-VW model; (c) MLP model; (d) MLP-VW model.

ROC curve with the corresponding AUC value is a commonly used method to validate the accuracy of LSMZ [64]. Generally, when AUC > 0.5, the evaluation results are considered to have application value. For example, Zhao et al. used the logistic regression method to evaluate the susceptibility of landslides in Yueqing City, China, and they believed that results with an AUC value between 0.7 and 0.8 can be regarded as acceptable results [65]. Sun et al. and Zhang et al. also believe that a model with an AUC value > 0.7 can produce an acceptable LSMZ [27,66]. In addition, based on other related studies [67,68], it is reasonable to determine that the performance of the LS model is better with the AUC value > 0.7 as the threshold, and this has been widely recognized by many scholars. Figure 8 shows the ROC curves and corresponding AUCs of the four models. For the training data set (70% landslides), all the AUCs are higher than 0.8, which indicates the reasonability of the four models. For the verification data set (30% landslides), the MLP-VW model obtained the highest model performance (AUC = 0.915) among the four models, while the performance of the AHP model is the lowest (AUC = 0.825). The MLP-VW model can be considered an “excellent” model, and the other three models can be described as “good” models. In addition, VW theory effectively improves the model performance for both the AHP model and MLP model. From the AHP model to the AHP-VW model, the AUC increases from 0.825 to 0.873, while the performance of MLP-VW increases from 0.879 to 0.915 when VW theory is applied in the MLP model. From a long-term perspective, the AHP-VW and MLP-VW models break the traditional model’s inherent thinking that the “contribution” of each factor to the occurrence of geological disasters is not fully considered. Based on determining the constant weight of the indicator based on the AHP and MLP, using variable weights to assign different weights to evaluation units with different indicators can obtain an LSMZ that is more in line with actual geo-environmental conditions.

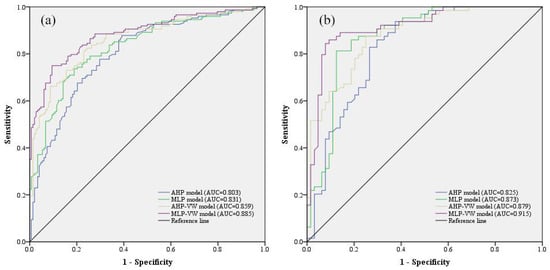
Figure 8. ROC curves: (a) training; (b) validation.

3.5. Comparison of Models

The number of causative factors considered in this study is comparatively lower, but the success rates obtained are fine. Increasing the number of causative factors considered does not necessarily increase the model success rate significantly [69,70]. Currently, this paper presents four different models, namely the AHP, MLP, AHP-VW, and MLP-VW models, in which the single model AHP and MLP represent heuristic and statistical models, respectively. In the AHP and AHP-VW models, land use, lithology, and geomorphology factors account for a large proportion of the LS evaluation (Table 4 and Figure 9). However, land use, elevation, slope, and lithology factors in the MLP and MLP-VW models account for a large proportion of LS evaluation (Table 5 and Figure 9). The difference in the proportions of these four models is because the initial constant weight of the AHP and AHP-VW models is determined by human subjective factors, while the initial constant weight of the MLP and MLP-VW models is determined based on previous landslide data. From this difference, we can see that land use and lithology should be paid attention to in LS evaluation in this area.

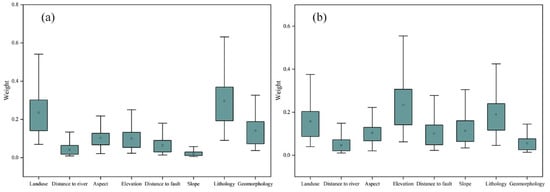
Figure 9. Boxplot of factors: (a) AHP-VW model; (b) MLP-VW model.

In addition, from the comparison of these two single models, it can be seen that the performance of the statistical MLP model is higher than that of the heuristic AHP, and a vast amount of literature has also demonstrated the higher performance of statistical methods in LSMZ compared to heuristic methods, particularly in machine learning models [71,72,73,74]. Pradhan reported that machine learning methods are known to be more efficient in solving many real-world problems compared to conventional methods, such as expert knowledge methods or analytic methods [75]. However, there is the fact that many governments and stakeholders still use a single method, such as the AHP model, information value model, or weight of evidence. In fact, in the pursuit of more accurate model performance and model optimization, deep learning algorithms are often used, with a lot of calculations and time consumption. Some decision-makers and landslide managers do not have sufficient time to optimize results in the preliminary stages of landslide management. After all, LSMZ is the preliminary stage of future landslide management and provides an estimate of “where” landslides may be more likely to occur. Too much time invested in this stage is a waste of human and computing resources. In this study, we consider combining VW theory with two typical heuristic and statistical models, respectively, and obtain two new hybrid models: AHP-VW and MLP-VW. According to the four model comparisons, when applying VW theory, it is evident that the model performance improves significantly, whether it is a heuristic model or a statistical model. This is because the heuristic AHP and statistical MLP evaluation models both use static constant weight evaluation. By directly or indirectly assigning fixed weights to each evaluation factor, it reflects the importance of each factor in susceptibility evaluation. However, in the actual evaluation, the weights of similar factors to different evaluation objects or to the same evaluation object at different times will constantly change. For LS, no matter how superior other factors are, as long as a factor is poor to a certain extent, the evaluation unit of the susceptibility of the factor will increase, so the weight of this factor should be increased; otherwise, it may be “neutralized” by a better factor, which makes the evaluation result inconsistent with the actual situation. VW theory is used to redistribute the weight of each factor in the constant weight evaluation, so that the factor weight changes with the different evaluation units, to solve the unreasonable problem of constant weight evaluation, thereby significantly improving the performance of the model. Zhang et al. and Huang et al. reported that the introduction of VW theory into heuristic AHP can significantly improve the accuracy and precision of the model [27,39]. As for the MLP-AHP model, there are no extensive related reports showing that it can significantly improve the model’s performance. The effect of the model presented in this paper is excellent. Therefore, it is an approach worthy of being promoted in practice.

3.6. Local Landslide P&C Strategy

Based on the LS map created by the MLP-VW model, an updated local landslide P&C strategy hierarchy is proposed, including basic P&C strategies, engineering activity management, and emergency P&C strategies. Firstly, the basic P&C strategies include landslide monitoring programs (LMP) and potential landslide stabilization. LMP should be conducted in the whole study area, and the landslide monitoring points should be increased accordingly in the high- and very-high-susceptibility areas. If necessary, stabilization measures such as anti-slip piles and anchor ropes should be used in the potential landslide sites. For engineering activity management in the high- and very-high-susceptibility areas, the stability of the slope should be a primary consideration for the selection of engineering project sites [76,77]. In addition, precautionary protection measures such as stone-blocking nets and retaining walls for slope management are required before engineering activities. For moderate- and low-susceptibility areas, attention should be paid to whether there are potential landslides in the surroundings of engineering activities. The loose soils beside these sites should be removed. Emergency P&C strategies are mainly to deal with high-intensity precipitation [78]. Different levels of susceptibility areas need to issue corresponding levels of warnings for rainstorms in advance. When the precipitation intensity is very high, evacuation of the masses should be efficiently conducted in the high- and very-high-susceptibility areas.

3.7. Suggestions and Future Research

In this study, we applied VW theory in two typical and single heuristic and statistical models and obtained a relatively higher model performance compared to initial models. Given that the discussion of VW theory has been limited, the following suggestions and future research are proposed:

• Although this study demonstrated higher performance in two models, it cannot be confidently said that VW theory can be generalizable to all the models in LSMZ. Designing more hybrid models with the integration of VW theory and comparing their model performance is suggested.
• Currently, many scholars strive to improve the performance of the models but ignore the difficulty of using the model in practice. Although deep-learning-based methods can significantly improve model performance, they consume a lot of time and human resources. We suggest that the following LSMZ framework is used to assess the applicability of the model in practice.
• The formulas of VW are diverse, and it is necessary to select the appropriate VW formula according to different issues. We only considered one common VW formula in the study, and it is necessary to discuss the performance and applicability of different VW formulas in the future.

4. Conclusions

As one of the most dangerous causes of fatalities, landslides have a wide range of effects around the globe. To control and prevent damages and losses brought about by landslides, it is essential to identify areas that are susceptible to landslides. An LSMZ that can solve this problem well not only provides an estimate of “where” landslides may occur more frequently, but also divides the LS into different levels for further management. In this study, a total of eight causative factors, including geomorphology, lithology, aspect, elevation, slope, distance to fracture, land use, and distance to river, were selected for LSMZ, and VW theory was introduced into the traditional heuristic AHP and statistical MLP models to obtain two novel hybrid models, AHP-VW and MLP-VW, respectively, for LSMZ. The LSMZ of the four models is roughly the same, showing a strip-like distribution along rivers, while the landslide hazard density is concentrated in the south and dispersed in the north, showing the characteristics of being high in the south and low in the north. However, as far as the performance of the single statistical MLP model is concerned, it is higher than that of the heuristic AHP model. The results of this study confirm that the statistical method is better than the heuristic method, and this is consistent with the results of previous studies. Furthermore, it was found that the MLP-VW model achieved the highest model performance (AUC = 0.915) among the four models, while the performance of the corresponding MLP model was lower (AUC = 0.873). Model performance is effectively improved when VW theory is applied. It can be reasonably concluded that the LSMZ constructed using the MLP-VW model in the study area can be used to improve LS evaluation and land use planning. However, the MLP-VW model was applied in the Luanchuan district only, just one of the landslide-affected areas in Henan province, and its applicability should also be tested in other parts of the world. Moreover, a fixed set of eight landslide-influencing factors was considered for modeling. However, it would be better to update the data set and explore more factors to further improve the model. Finally, we suggest designing more hybrid models, assessing the practical meanings of models, and discussing the performance and applicability of different VW formulas in the future.