Study on the Basic Mechanical Properties and Discrete Element Method Simulation of Permeable Concrete

Abstract

Permeable concrete pavement material has many voids and a good water permeability, which can reduce surface runoff and alleviate the problem of urban water logging. It also has the functions of acting as a supplementary source of groundwater, purifying water, bodies reducing the urban heat island effect, reducing road noise, and so on. It is an effective solution for urban infrastructures. However, at the same time, because it has a large number of pores, this also affects the strength of permeable concrete. The main factors affecting permeable concrete are particle size and the shape of the aggregate, the content of the cement paste and aggregate, the compaction degree of the mixture, and so on. In this study, the single-factor test method was used to study the effects of aggregate size, slurry-to-bone ratio and loose paving coefficient on the basic mechanical properties and permeability of permeable concrete. Here, the numerical model for permeable concrete is established by using the particle flow discrete element (Particle Flow Code (PFC)modeling method, and a numerical simulation test is carried out. It can be seen from the test results that the permeability coefficient of 50% 5–10 mm + 50% 10–15 mm mixed aggregate permeable concrete is slightly lower than that of 5–10 mm and 10–15 mm single-size aggregate, but has a higher compressive and splitting tensile strength. With the increase in paste-to-bone ratio, the permeability coefficient of permeable concrete decreases, and the compressive strength increases. The loose paving coefficient has a significant effect on the mechanics and permeability of permeable concrete with the increase in the loose paving coefficient, the water permeability decreases and the compressive strength increases. The numerical simulation results show that under the condition that the loose paving coefficient is 1.10 and the slurry-to-bone ratio is 0.5, compared with the experimental results, the error of the numerical simulation results of the compression test is less than 3%. The reliability of the simulation is verified. The discrete element modeling method in this study can be used to simulate the shape of the aggregate in permeable concrete, and the numerical model can effectively simulate the crack development and failure form of permeable concrete in compression tests.

1. Introduction

1.1. Research Background and Significance

In recent years, the concept of harmony between man and nature has been deeply rooted in the hearts of people. As a solution for the urban green infrastructure, permeable concrete has huge eco-environmental value and good economic value. In the 1970s, permeable concrete was first used in the United States to alleviate urban waterlogging and water pollution caused by impervious roads. Since then, to overcome the land subsidence caused by the excessive extraction of groundwater, the Japanese government formulated an underground restoration policy for rain water focusing on the pavement technology of permeable concrete., in which a large-scale study was carried out on the performance of permeable concrete. In recent years, the application of permeable concrete has gradually expanded from parks and square roads to parking lots, light-duty lanes, and so on, forming a positive development trend.

To strike a balance between the permeability and mechanical properties of permeable concrete, coarse aggregate with a small particle size is often selected for the preparation of permeable concrete, however. One of the important factors affecting the performance of permeable concrete is the slurry-to-bone ratio, but the influence of the slurry-to-bone ratio is not directly reflected in the current mix design methods. In addition, the forming process of permeable concrete also lacks of a unified standard, and the degree of compaction in the forming process is difficult to quantify.

At present, the research on permeable concrete still depends heavily on laboratory tests and field tests, and there are a lack of effective numerical simulation analysis methods. DEM is a numerical method to simulate discontinuous and discrete elements by establishing the relationship among force, acceleration, velocity, and displacement according to Newton’s second law. As a discrete element numerical simulation technology for the mechanics of granular materials, the discrete element method of particle flow has developed rapidly in recent years.

The meso-model of permeable concrete is established by using the discrete element numerical simulation method, and is compared with the macroscopic test results in the laboratory, therefore, the dependence on the actual test work can be minimized. In addition, the simulation test using the three-dimensional numerical model of permeable concrete particle flow can more truly reflect the structural characteristics, deformation characteristics, and failure mechanism of permeable concrete, as well as broaden the application range of permeable concrete.

1.2. Background and Significance

Permeable concrete (PC) is a type of environmentlly material with the characteristics of water permeability, sound absorption, and noise reduction as wel as being lightweight. Without fine aggregates, thin layers of grouting felt covered with coarse aggregate are bonded to each other to form a uniformly distributed honeycomb structure, with a certain strength and permeability, after which stagnant water on the road surface can quickly infiltrate into the ground. At present, PC is widely used in parks, squares, parking lots, light traffic roads, and so on.

The compressive strength is determined by the binding force between aggregate and cement paste, and it is greatly affected by the porosity of permeable concrete. The porosity of water concrete is affected by the size, shape, and compactness of coarse aggregate. Yu F et al. [1] tested eight kinds of permeable concrete specimens with 20% porosity, among them, the strength of permeable concrete with a coarse aggregate size of 2.36–4.76 mm was the lowest, while the strength of permeable concrete with a coarse aggregate strength of 4.76–9.5 mm was 52% higher. Another study [2,3] pointed out, under constant porosity, the strength of concrete containing 60% 8–16 mm and 30% 4–8 mm coarse aggregate was 21% higher than that of 60% 4–8 mm and 30% 8–16 mm aggregate. Some studies [4,5] have shown that in samples made of coarse aggregates with a single particle size (2.38 mm, 4.76 mm, and 9.51 mm), specimens made of smaller coarse aggregate sizes will lead to a decrease in strength due to an increase in the number of pores. However, some studies [6] have pointed out that in some cases, the use of smaller coarse aggregates can reduce the porosity and increase the compressive strength. Ignacio [7] found that the mechanical properties of permeable concrete could be improved by adding pumice instead of cement. Regarding the shape of coarse aggregate, some studies [8,9,10] have shown that the permeable concrete produced by angular aggregate had a higher porosity, and thus a higher permeability and lower strength. The porosity of permeable concrete determines the permeability of permeable concrete. Gao [11] studied the effect of polypropylene fiber on the properties of permeable concrete, when the content of the polypropylene fiber was 3 kg/m³, the permeability coefficient of permeable concrete decreased, and its mechanical properties and durability were the best. Lian [12] used three kinds of rock as a coarse aggregate to study the mechanical properties of permeable concrete. The results show that dolomite had the best wear resistance and bonding properties, and was found to be the best aggregate for making porous concrete. In addition, the study also found that the addition of silica fume had no great effect on the strength of permeable concrete. Qi [13] used waste rubber instead of coarse aggregate to prepare permeable concrete. It was found that the addition of an appropriate amount of waste rubber particles could improve the bearing capacity and permeability of permeable concrete. Liu [14] found that the early compressive strength and flexural strength of permeable concrete decreased with the addition of fly ash, and the higher the content of fly ash, the lower the compressive strength and flexural strength.

The porosity of permeable concrete determined the permeability of permeable concrete. The conventional method for testing the porosity of permeable concrete is the constant head method; this method does not need complex instruments and is fast and direct, so it has become popular. However, this method only provides the total porosity without considering the pore size distribution, and cannot quantify the zigzag voids that are difficult to enter or cannot be entered by water. Using an X-ray CT, the pore network can be visualized and further analyzed [15]. Zhang et al. [16] established the average pore size and its size distribution by using a 3D reconstruction model of permeable concrete specimens.

The research shows that the average pore sizes of permeable concrete samples with porosities of 13 %, 20 %, 25 %, and 28 % were 3.38, 4.74, 5.4, and 7.47 mm, respectively. There was also a study [17] that used X-ray CT to establish empirical relationships to calculate pore sizes based on mixture input parameters such as aggregate size. Another application of X-ray CT is to use scanned reconstructed 3D models of permeable concrete to model the mechanical or hydraulic behavior of permeable concrete and to determine clogging problems [18,19]. Marcaida [20] found that the permeability loss caused by particle plugging was affected by the size of the aggregates and plugged particles. When the pores of pervious concrete were fully covered by clogging particles, it appeared that, for some test cases, the permeability at the terminal stage may be limited by the infiltration capacity of the clogging materials. Amini [21] developed a regression model, which correlated the ultrasonic pulse velocity (UPV) with the permeability and compressive strength of permeable concrete; the average determination coefficient was 0.74–0.76. The constant head test method was more sensitive to the porosity level than the drop head test method, which made it more suitable for the permeability evaluation of permeable concrete [22,23]. Valerio [24] developed a new rainfall simulator that could control the simulated rainfall intensity in real time. The device could also collect infiltration water and surface runoff to evaluate the infiltration capacity of the specimen, as well as calculate the runoff coefficient of each porous surface. The study of Montes and Haselbach [25,26] pointed out that the water passing through permeable concrete holes was laminar, but other studies [27] showed that the flow state was transient; the Darcy−Forchheimer equation has been proposed to obtain the permeability more accurately. According to the test data of the physical and mechanical properties of permeable concrete, the researchers established a regression model to determine the relationship between the components and their proportions of porosity, permeability, and mix design [28]. Nassiri and AlShareedah [29] established a regression model to correlate compressive strength and flexural strength with porosity, cement content, and water−cement ratio. Chandrappa and Biligiri [30] tested 45 permeable concrete beams in 15 kinds of mixtures to study the effects of porosity and mixing ratio on the flexural strength and flexural stiffness of permeable concrete, and thus developed a regression model to predict the flexural strength. Ghafoori and Dutta [31] obtained the relationship between the compressive strength and the splitting tensile strength of permeable concrete based on the test results of four mixtures with a paste-to-bone ratio of 4:1 to 6:1.

The random particle model, which uses randomly distributed circular particles to represent the aggregate, fully considers the randomness of aggregate distribution, it was first proposed by Cundall and was later developed into the present DEM [32,33,34,35]. Permeable concrete can be conceptualized as a bonded granular material, which is suitable for modeling with a discrete element model [36,37]. S. Sinaie [38] studied the effectiveness of DEM in predicting the size effect of cylindrical concrete specimens under compression, the results showed that the DEM can effectively reproduce the effect of aspect ratio on compression performance. R. Pieralisi [39] presented a large-scale test scheme considering different aggregate shapes, gradation curves, and the ratio of aggregate to cement paste to evaluate the behavior of a permeable concrete mixture in a fresh state and to verify the numerical model. The fitting results between the numerical calculation results and the experimental results show that the model and constitutive relation reproduced the uniaxial under-compaction process of concrete. Azevedo [40] used DEM to simulate concrete and analyzed the two-dimensional tension−compression model. The results show that, by using the ductile tensile failure model and adding friction force to the simulation, the mechanical behavior of concrete could be simulated more accurately. TranVT [41] simulated the mechanical behavior of concrete under a triaxial load using DEM. Through the analysis of the calibrated uniaxial and triaxial experimental results, it was proven that the local interaction in the model could explain the macroscopic behavior of the samples under confining pressure well. R. Pieralisi et al. [42] proposed a comprehensive model that combined DEM with computational fluid dynamics (CFD). The permeability was evaluated using a numerical method, taking into account the influence of the mixture composition and compaction process. The compaction process of permeable concrete in a fresh state was simulated by DEM, and the meso-geometric structure was obtained. Based on the DEM-CFD model, extensive experimental studies on the permeability of permeable concrete were carried out, and the experimental results were used to verify the DEM-CFD model.

The purpose of this study was to optimize the mix design of permeable concrete and to improve its preparation technology, and to use the particle flow software PFC3D5.0 to establish the real aggregate model and randomly place it into the permeable concrete model. To study the uniaxial compression of permeable concrete using a simulation test, the numerical model was used to analyze the influence of the contact number of different proportions of mixed aggregate on the mechanical properties. The main research areas are as follows:

(1)

Optimize the mix proportion design method of permeable concrete and improve the preparation technology of permeable concrete. The effects of aggregate size, slurry-to-bone ratio, and loose paving coefficient on the basic mechanical properties and permeability of permeable concrete were studied seperately.

(2)

Based on the real aggregate shape, the discrete element numerical model of permeable concrete is established by using PFC3D5.0 software, and the numerical simulation test is carried out to verify the effectiveness of the model.

(3)

By using the numerical model, the failure mechanism of permeable concrete is analyzed, the influence of contact number on the mechanical properties of the numerical model is explored, and the aggregate size ratio of permeable concrete is optimized.

2. Materials and Methods

2.1. Experimental Materials

The main raw materials for preparing PC are cement, natural coarse aggregate, and tap water. The physical properties of PO42.5 ordinary Portland cement are shown in Table 1. To study the effect of aggregate size on the mechanical properties and permeability of permeable concrete, three kinds of aggregate were selected in this experiment, the aggregates were 5–10 mm single particle size, 10–15 mm single grain size, and 50% 5–10 mm + 50% 10–15 mm mixed particle size aggregate, respectively. The main physical properties of the natural coarse aggregate are shown in Table 2. The water used in this experiment was from the municipal water supply in Xinyang City.

Table 1. Physical and mechanical properties of cement.

Density (kg/m3)	Specific Surface Area (m2/kg)	Setting Time (min)		Flexural Strength (MPa)		Compressive Strength (MPa)
		Initial setting	Final coagulation	3d	28d	3d	28d
3100	3500	128	190	4.6	7.8	17.9	42.7

Table 2. Basic properties of natural coarse aggregate.

Kinds	Apparent Relative Density (kg/m3)	Crushing Value (%)	Compact Packing Density (kg/m3)	Stacked Porosity (%)	Apparent Density (kg/m3)	Water Absorption Rate
5–10 mm	2690	7.6	1456	45.67	2682	0.007

2.2. Test Method

The single factor test method was used in this experiment. In order to study the effect of mix design and the preparation technology on the compressive strength of permeable concrete, the aggregate size, paste-to-bone ratio, and loose paving coefficient were selected as factors, and three levels were set for each factor. The table of horizontal design of test factors is shown in Table 3.

Table 3. Horizontal design table of test factors.

Test Number	Aggregate Particle Size	Degree of Compaction	Plasma-Bone Ratio
A	50% 5–10 mm + 50% 10–15 mm	1.10	0.5
B1	50% 5–10 mm + 50% 10–15 mm	1.10	0.4
B2	50% 5–10 mm + 50% 10–15 mm	1.10	0.6
C1	100% 5–10 mm	1.10	0.5
C2	100% 10–15 mm	1.10	0.5
D1	50% 5–10 mm + 50% 10–15 mm	1.05	0.5
D2	50% 5–10 mm + 50% 10–15 mm	1.15	0.5

2.3. Mix Design

To study the effect of cement paste and aggregate content on the performance of permeable concrete, the volume method was improved in this experiment, the paste-to-bone ratio was introduced as a factor in the mix design of permeable concrete, and the effects of different contents of cement paste and aggregate on the compressive strength and permeability of permeable concrete were studied. The water−cement ratio of permeable concrete was 0.28 and the design porosity was 20%. The design method is shown in Formula (1).

In the formula:

$$(1+b)\times \frac{m_a}{{\rho }_a}+P=1$$

(1)

m_a—aggregate quality per cubic meter of mixture, kg,

b—Plasma-to-bone ratio,

${\rho }_{\mathrm{a}}$—Apparent density of coarse aggregate, kg/m³

$\rho$—Design porosity, %.

This design method quantifies the ratio of aggregate to cement slurry more directly and is not limited by the design porosity, it also studies the influence of cement paste and aggregate content on the performance of permeable concrete, in order to better guide the mix design of permeable concrete.

Three specimens were created in each group for compression tests. The actual consumption of materials used in each group is shown in Table 4.

Table 4. Actual consumption of materials in each group.

Serial Number	Cement (kg)	Water (kg)	Stone (kg)
			5–10 mm	10–15 mm
A	1.660	0.465	2.682	2.682
B1	1.138	0.319	2.299	2.299
B2	1.494	0.418	2.012	2.012
C1	1.660	0.465	5.364	0
C2	1.660	0.465	0	5.364
D1	1.660	0.465	2.682	2.682
D2	1.660	0.465	2.682	2.682

2.4. Experimental Process

The mixer usedin this study is a compulsory single horizontal shaft concrete mixer produced by model SYD-F02-20A (Shanghai Xinchangji Development, and the model is SYD-F02-20A. Co., Ltd., Shanghai, China). The mixing process refers to Technical Specifications for permeable cement pavement CJJ/T135-2009 [43]. To better wrap the cement paste around the aggregate, the cement paste method was used in this study. First, the cement was poured into the mixer and was addde half of the water, the mixture was stirred for 1 min. Then, the aggregate was poured in followed by stirring for 1 min. Finally the remaining half of the water was added and the mixture was stirred for 2 min to obtain the permeable concrete mixture. The stirring process is shown in Figure 1.

Figure 1. Mixing process of the cement-wrapped paste method: (a) weighing material, (b) cement wrapped paste; (c) mixed material mixing, and (d) discharge.

2.5. Specimen Forming and Maintenance

Before discharging the permeable concrete mixture, first, a thin layer of butter was plied on the inside of the mold to ensure the uniformity of the mixture in the compaction process. One third of the stirred mixture was discharged into the mold were repeated, the above steps twice more to make sure the mixture filled the whole mold uniformly, different according to the loose paving, a certain height, were used to determine an appropriate amount of the mixture is placed above the mold. Finally, the mixture was compressed into the mold. The forming process is shown in Figure 2. The maintenance process of the test block refers to Technical Specifications for permeable cement pavement CJJ/T135-2009 [43]. The dimensions of the dies used in this study are all 100 mm × 100 mm × 100 mm. After the specimen was molded, it was placed in water for maintenance, as shown in Figure 3. The curing water temperature was 25 ± 5 °C. After curing for 28 days, the mechanical properties and water permeability were tested.

Figure 2. Forming process of permeable concrete specimen: (a) brush grease, (b) assembly mold, (c) compaction, and (d) film mulching.

Figure 3. Maintenance of permeable concrete.

3. Performance Test and Analysis

3.1. Performance Test

3.1.1. Compressive Strength Test

The instrument used in this test was the microcomputer-controlled electro-hydraulic servo universal testing machine produced by using the model number WAW-3000 (Jinan Dongfang Test instrument, model number WAW-3000, Co. Ltd., Jinan, China) and the measuring range was 3000 kN and the accuracy is 0.5 grade. The compressive strength test referred to the Standard of Test methods for the physical and mechanical properties of concrete (GB/T50081-2019) [44]. Three samples were tested in each group, and the average value of the test results was taken. The compressive strength was calculated according to a Formula (2). In the formula:

$$f_{cc}=\frac{F}{A}$$

(2)

f_cc—Strength mixing, MPa

F—Test failure load, N

A—Test bearing area, mm².

3.1.2. Permeability Coefficient

The permeability coefficient is an important index to characterize the permeability of PC. In this experiment, the constant head method was used to determine the permeability coefficient. The measuring method of the permeability coefficient refers to the Technical Specification for permeable cement pavement CJJ/T135-2009 [43]. The calculation formula of the constant head method is Formula (3):

In the formula:

$$K_T=\frac{L}{H}\times \frac{Q}{A\times t}$$

(3)

K_t—When the water temperature is T °C, the permeability coefficient of the specimen, mm/s

L—thickness of the specimen, mm

Q—Water permeability of specimen, mL

H—Water level difference, mm

A—Cross-sectional area of specimen, mm²

t—Water permeation time of specimen, s.

3.2. Result Analysis

3.2.1. Influence and Analysis of Aggregate Size on Compressive Strength and Permeability Coefficient

Figure 4 shows the relationship between aggregate size and compressive strength and permeability coefficient. As can be seen, when the particle size of the aggregate was 5–10 mm, the compressive strength of the permeable concrete specimen was 8.3 MPa, and the permeability coefficient of the permeable concrete specimen was 3.65 mm/s. When the particle size of the aggregate was 10–15 mm, the compressive strength of the permeable concrete specimen was 10.6 MPa and the permeability coefficient of the permeable concrete specimen was 4.06 mm/s. When 50% 5–10 mm + 50% 10–15 mm aggregate was used, the compressive strength of the permeable concrete was the highest, reaching 11.9 MPa, while the permeability coefficient was the lowest.Which is 3.23 mm/s. It can be seen that compared with the 5–10 mm and 10–15 mm aggregate permeable concrete, the permeability coefficient of mixed aggregate permeable concrete decreased by 20.4% and 12%, respectively, but its compressive strength increased by 43.4% and 12.3%, respectively, compared with the 5–10 mm and 10–15 mm aggregates.

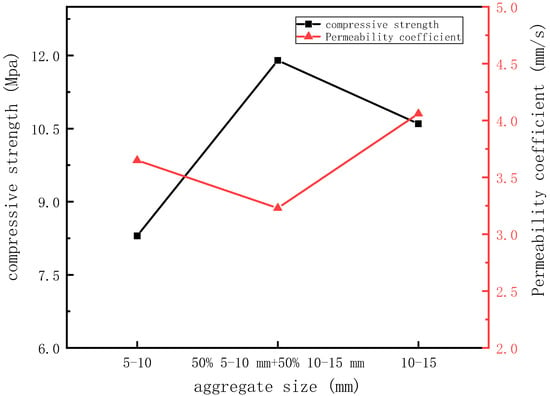
Figure 4. Relationship between aggregate size and compressive strength and permeability coefficient.

The bonding between different particle sizes is shown in Figure 5. As can be seen, there were more bonding sites between the mixed aggregates than the 10–15 mm size aggregates, and the staggered distribution of the 5–10 mm aggregate and 10–15 mm aggregate ensured the number of bonding sites between aggregates. Because of the increase in contact area between mixed aggregates, the interlocking effect between aggregates was enhanced. Therefore, compared with the single-size aggregate permeable concrete, the bond strength of the mixed-size aggregate permeable concrete specimen was enhanced, and the compressive performance was better, but the mixed water permeability was decreased. This was due to an increase in the number of bonds between the 50% 5–10 mm + 50% 10–15 mm mixed aggregates, with a high interpore and tortuosity, and the permeability was closely related to the zigzag degree of pores, the aggregate with a 10–15 mm particle size formed pores with less zigzag degrees, it makes easier, which made the spatial distribution and shape of the pores more reasonable.

Figure 5. Permeable concrete specimens with different aggregate sizes: (a) 5–10 mm aggregate specimen, (b) mixed aggregate specimen, and (c) 10–15 mm aggregate specimen.

3.2.2. Influence and Analysis of Loose Paving Coefficient on Compressive Strength and Permeability Coefficient

The relationship between the compressive strength, permeability rate, and loose paving coefficient of permeable concrete is shown in Figure 6. When the loose paving coefficient was 1.05, the compressive strength of permeable concrete was 9.7 MPa and the permeability coefficient was 3.45 mm/s. The compressive strength of the specimens with loose paving numbers of 1.10 and 1.15 was 11.9 MPa and 12.8 MPa, respectively, and the permeability coefficient was 3.23 mm/s and 3.04 mm/s, respectively. Compared with the permeable concrete with a loose paving coefficient of 1.05, the compressive strength increased by 22.7% and 31.9 %, respectively, and the permeability coefficient decreased by 6.4% and 11.9%, respectively. The compressive strength was positively correlated with the loose paving coefficient, and the permeability coefficient was negatively correlated with the loose paving coefficient, which close to the first-order function relationship.

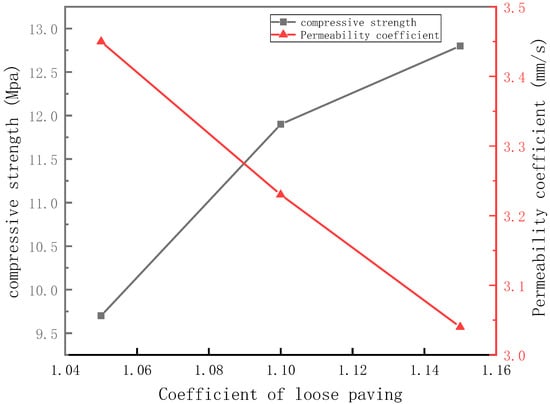
Figure 6. Relationship between the loose paving coefficient and compressive strength and permeability coefficient.

The state of permeable concrete specimens with different loose paving coefficients is shown in Figure 7. With the increase in loose paving coefficient, the compaction degree of the permeable concrete became closer, which increased the interlocking effect between aggregates, made the aggregates more compact, and squeezed each other. In addition, the relative lateral displacement of the aggregate in the compression process was limited and the compressive performance was improved. A denser extrusion between aggregates reduced the pore size and led to a decrease in the number of connected pores, increasing the tortuous degree of pores, and thus reducing the water permeability of the permeable concrete.

Figure 7. Morphology of permeable concrete specimens under different loose paving coefficients: (a) loose paving coefficient = 1.05, (b) loose paving coefficient = 1.10, and (c) loose paving coefficient = 1.15.

3.2.3. Influence and Analysis of Slurry-to-Bone Ratio on Compressive Strength and Permeability Coefficient

The relationship between compressive strength and the paste-to-bone ratio of permeable concrete is shown in Figure 8. When the paste-to-bone ratio was 0.4, the compressive strength of permeable concrete was 9.1 MPa and the permeability coefficient was 3.49 mm/s. The compressive strength of the specimens with a slurry-to-bone ratio of 0.5, 0.6 was 11.9 MPa and 14.8 MPa, respectively, and the permeability coefficient was 3.23 mm/s and 2.91 mm/s, respectively. Compared with the permeable concrete specimen with a slurry-to-bone ratio of 0.4, the compressive strength increased by 30.8% and 62.6 %, respectively, and the permeability coefficient decreased by 7.4% and 16.6 %, respectively. The permeable concrete specimens with different slurry-to-bone ratios are shown in Figure 9.

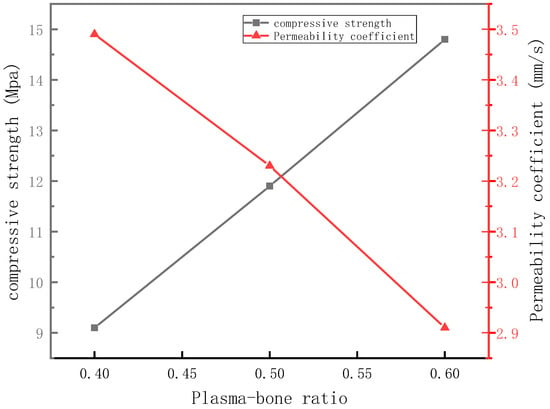
Figure 8. Relationship between slurry-to-bone ratio and compressive strength and permeability coefficient.

Figure 9. Morphology of permeable concrete specimens with different paste-to-bone ratios: (a) plasma-to-bone ratio = 0.4; (b) plasma-to-bone ratio = 0.5; (c) plasma-to-bone ratio = 0.6.

As can be seen from Figure 9, with the increase in paste-to-bone ratio, the content of cement paste in permeable concrete increased obviously, the content of cement paste wrapped in the aggregate also increased, and the content of aggregate in the mixture decreased; in the compression test, the improvement in the strength of the specimen was mainly due to the increase in bond area between aggregates. Because of its fluidity, cement occupies more and more pore space, the number of pores decreased, and the pore size decreased gradually, which reduced the permeability of the permeable concrete. Therefore, with the increase in the paste-to-bone ratio, the number of pores decreased, the pore size decreased, the compressive strength of the permeable concrete increased, and the permeability coefficient decreased.

4. Discrete Element Simulation

4.1. Aggregate Discrete Element Modeling

As the skeleton of permeable concrete, the size and shape of the aggregate have an important influence on the performance of permeable concrete. In the numerical simulation, the effective performance of the size and shape of the aggregate determines the outcome of the permeable concrete numerical simulation of.

4.1.1. Aggregate Classification

According to the size of aggregate used in the experiment, the aggregate was divided into two types: 5–10 mm particle size and 10–15 mm particle size. According to the shape of the aggregate, the aggregate was divided into three types: angular aggregate, flat aggregate, and slender aggregate. The shapes of the three aggregates are shown in Figure 10. According to the statistics of the number of aggregates of different shapes in the two kinds of aggregates, the proportion of the number of aggregates of each shape to the total number of aggregates was obtained. The shapes of 1000 aggregates of 5–10 mm and 10–15 mm size were calculated. The statistical results are shown in Table 5.

Figure 10. Aggregate shape classification: (a) 5–10 mm angular aggregate, (b) 5–10 mm flat aggregate, (c) 5–10 mm slender aggregate, (d) 5–10 mm angular aggregate, (e) 10–15 mm flat aggregate, and (f) 10–15 mm slender aggregate.

Table 5. The proportion of aggregate shapes.

Aggregate Particle Size	Angular Shape	Flat Form	Slender Shape
5–10 mm	53.1%	32.3%	14.6%
10–15 mm	64.5%	32.4%	3.1%

According to the statistical results and the proportion of aggregates of various shapes, the corresponding amount of aggregatewas selected and the aggregate was numbered. The numbering results are shown in Table 6. It should be pointed out that the content of slender aggregate in the 10–15 mm aggregate was less, only about 3%, so it was not included in the scope of modeling.

Table 6. Aggregate number.

Aggregate Particle Size	Angular Shape	Flat Form	Slender Shape
5–10 mm	A-1, A-2, A-3	A-4, A-5	A-6
10–15 mm	B-1, B-2, B-3, B-4	B-5, B-6	/

4.1.2. Aggregate Scanning

In this study, the particle flow modeling methodwas used to reconstruct the aggregate model by using PFC3D5.0 software to reconstruct the STL file of the outer contour information of the aggregate obtained by scanning. In this study, the aggregates were scanned one by one using the binocular Blu-ray 3D scanner produced by Fuzhou Minchuang 3D Electronic Technology, the scanning process is shown in Figure 11. The STL format file of the 3D scanned aggregate profile information was obtained and stored. The actual aggregate and the shape of the scanned aggregate are shown in Figure 12.

Figure 11. Using a Binocular Blu-ray 3D Scanner to scan the aggregate processes one by one.

Figure 12. (a) The true shape of the aggregate and (b) the shape of aggregate obtained from scanning.

4.1.3. Aggregate Discrete Element Modeling

PFC3D5.0 software is a discrete element simulation software of particle flow developed by Itasca Company. In this study, the STL file, which characterizes the outline information of the aggregate, was used to import it into PFC3D5.0 software to reconstruct the aggregate, which simulated the real shape. The specific steps are as follows:

• The STL file of each aggregate is named, and the STL file of aggregate Amurl is named shape_a1.
• Import the STL file of aggregate into the software by using the geometry import command of the PFC3D 5.0 built-in function to create geometry. Taking aggregate Amurl as an example, the command is written as follows: geometry import shape_a1.
• The imported geometry represents the surface of the aggregate, while the real aggregate is the solid. Therefore, it is necessary to fill the geometry with spherical particles, which can be achieved by the command of a clump template create in PFC3D 5.0. Import the geometry created in step (2) into PFC5.0 through the keyword geometry, and the particles are automatically filled into the geometry to create an aggregate cluster template.

The cluster template generated in step (3) was not the aggregate in the model, but the template used to generate the aggregate. According to the aggregate cluster template, the aggregate cluster was generated by the club generate command, which was used to simulate the shape and appearance of the aggregate.

When creating a cluster template using the clump template create command, the state of the created cluster template was mainly controlled by the following keywords: distance, ratio, and rad farad factor tor. Among them, the keyword distance corresponded to a smoothness angle measured from 0 to 180 degrees. The larger the distance, the smoother the particle distribution of discrete elements. Figure 13 shows the change in the cluster template as the distance increased gradually from 70 to 170. It can be seen that when the distance was 150, the cluster template was almost the same as the corresponding geometry. However, as the distance value increased, so did the number of discrete elements needed to form the cluster template. Figure 14 shows the number of discrete units required for the aggregate as the distance increased gradually from 50 to 170; it can be seen that when the distance value was greater than 150, the number of discrete elements increased sharply.

Figure 13. Aggregate template morphology under different distance values.

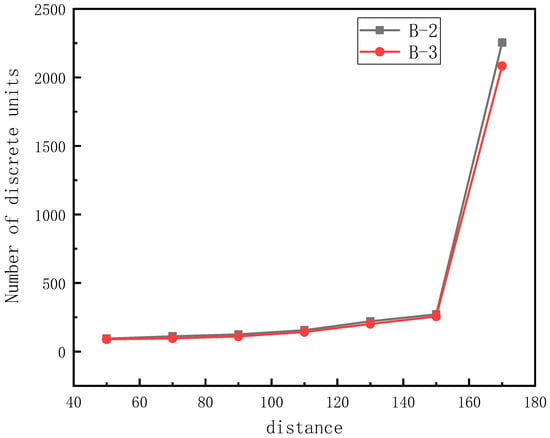
Figure 14. The number of discrete elements of aggregate under different distance values.

The keyword ratio referred to the ratio of the smallest to the largest particles retained in the cluster template when the value was between 0 and 1. The smaller the value of the ratio was, the more accurate the cluster template was in simulating the original aggregate shape, but it led to an increase in discrete elements needed to generate the cluster template. Figure 15 shows the shape of the cluster template generated under different ratio values. Figure 16 shows the number of discrete units required to generate the cluster template at different ratio values. It can be seen that when the ratio value was 0.3, the cluster template could accurately simulate the morphological characteristics of the original aggregate. When the ratio value was more than 0.3, the number of discrete elements needed to form the cluster template increased sharply.

Figure 15. Cluster template morphology under different ratio values.

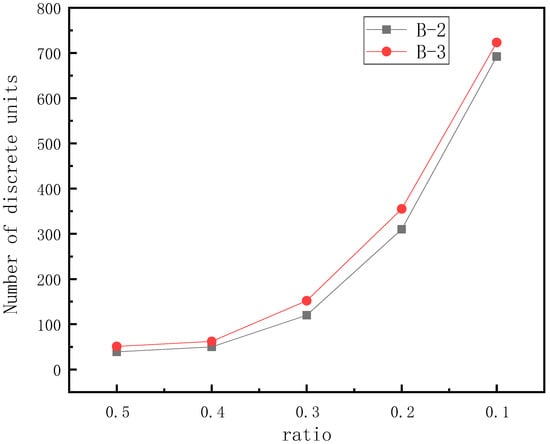
Figure 16. The number of discrete in the cluster template with ratio.

The computational efficiency of the model was closely related to the number of discrete elements. The more discrete elements, the lower the computational efficiency. In order to achieve a balance between calculation efficiency and simulation accuracy, in the aggregate discrete element model established in this paper, the distance value was 150 and the ratio value was 0.3.

4.2. Discrete Element Modeling of Permeable Concrete Specimen

4.2.1. Rigid Cluster Modeling of Permeable Concrete Specimen

After the STL file of the outer profile of the aggregate was introduced into PFC3D5.0 to establish the cluster template to characterize the aggregate, the cube test block was obtained by simulating the discharge process of the mixture and the preparation process of compaction molding according to the different particle size and loose paving coefficient of the test block. The specific steps were as follows:

1.

Specify the operation domain and use the wall generate command to generate a box of 50 mm × 50 mm × 300 mm, using the clump generate command, according to the aggregate size in the test block, different aggregate templates are selected to generate a certain number of aggregate models in the cuboid box. Figure 17 shows the aggregate model generated when simulating the 5–10 mm aggregate size permeable concrete test block. During the generation, the aggregate template with a 5–10 mm particle size was selected and each template generated 100 aggregates.

Figure 17. Aggregate clusters with a 5–10 mm diameter generated by using the clump generate command.

2.

The contact model between aggregates is set as a linear model and given a larger damping coefficient. The gravity acceleration of the aggregate model is set to make it fall naturally, to simulate the process of discharging the mixture into the mold. Figure 18 shows the process of aggregate falling, different colors represent different speeds of movement of aggregates. When the aggregate reaches a stable state, the specimen accumulates closely under the action of gravity, and the aggregate reaches the state of loose compaction without any external force.

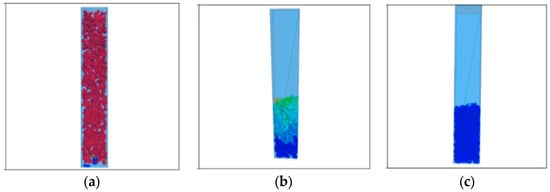Figure 18. Aggregate falling process: (a) the aggregate began to fall, (b) in the process of aggregate falling, and (c) the aggregate reaches a stable state.

3.

To realize the simulation of different loose paving coefficients of the specimen, the aggregate above a certain height is deleted by using the club deleted command. For example, delete the aggregate above 55 mm in the hexahedron under the loose paving factor of 1.10. Then, using the wall generate command, the wall is generated at a certain position above the aggregate, and the displacement direction, speed, and time of the wall are specified. The aggregate is compacted to a height of 50 mm by using the wall, and the cube model of 50 mm × 50 mm is obtained. The compaction process of the model is shown in Figure 19. The final cube test block is shown in Figure 20.

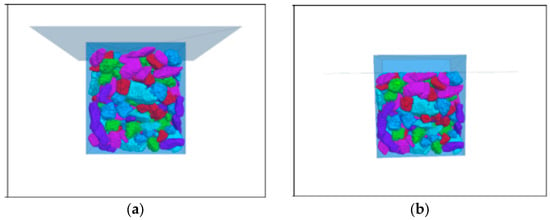Figure 19. Aggregate compaction process: (a) before compaction and (b) after compaction.

Figure 20. Compacted cube test block.

To improve the operation efficiency, the template generate command was used to generate the aggregate model. This command could only specify the amount of aggregate generated, not the volume fraction, because the test mix ratio was calculated according to the volume method; therefore, it was necessary to determine the quantity ratio between two kinds of aggregates under the same volume to ensure the volume ratio between aggregates with different particle sizes. We counted the number of two kinds of aggregates with the same quality, the statistical results are shown in Table 7. According to the statistical results, the ratio of the 5–10 mm aggregate to 10–15 mm aggregate was 7:1 at the same volume fraction.

Table 7. The number of two kinds of aggregates with the same quality.

Aggregate Quality/g	71	103	128	151
5–10 mm Aggregate quantity/unit	286	381	443	577
10–15 mm Aggregate quantity/unit	40	54	63	81

The aggregate size was controlled by the diameter size keyword in the template generate command; for example, when using a template with 5–10 mm particle size aggregate, the lower and upper limits of the size of the generated aggregate model were set to 5 mm and 10 mm, respectively. To distinguish the contact between clusters and the contacts within clusters in modeling, each aggregate was grouped separately (including the same aggregate generated by the same aggregate template). The number keyword was set to generate an aggregate, which was then grouped using the group keyword.

In the process of producing aggregates, on the one hand, the total amount of aggregates should not be too small, otherwise, the height of the tightly packed aggregates could not meet the requirements, which would affect the formation of cube specimens. On the other hand, too much aggregate and too much generating space will affect the operation efficiency of the following steps. Therefore, the size of the cuboid box generated in this study was 50 mm × 50 mm × 300 mm, which not only provided enough space to place the aggregate, but also ensured computational efficiency.

In this study, in the process of modeling, it was found that the reasonable setting of the aggregate generation order could effectively reduce the number of attempts and more aggregates could be generated in the same space. For example, the larger size aggregate was generated first, and then the smaller size aggregate was generated. To improve the computational efficiency, the cube size of 50 mm × 50 mm × 50 mm was used in this numerical simulation, and the maximum aggregate size was less than a third of the mold size.

In the above process, the aggregate model used rigid clusters, the spherical particles that made up the aggregate were whole, and there was no fracture and relative displacement between the particles.

4.2.2. Flexible Cluster Modeling of Permeable Concrete Specimens

The failure of permeable concrete was a result of the joint action of the bonding place of cement paste between aggregates and the failure of the aggregate itself. To simulate the real failure state of the specimen, it was necessary to transform the rigid cluster into a flexible cluster to simulate the fracture of the aggregate itself. The specific steps are as follows:

1.

Using the ball generate command, generate a regular arrangement of spherical particles in the space where the specimen model is located, to fill the space where the mold is located. At this point, as shown in Figure 21, the resulting particles overlap with the aggregate model. Using the ball generate command, generate regular arrangement of spherical particles in the space where the specimen model is located, so as to fill the space where the mold is located. At this point, as shown in Figure 21, the resulting particles overlap with the aggregate model.

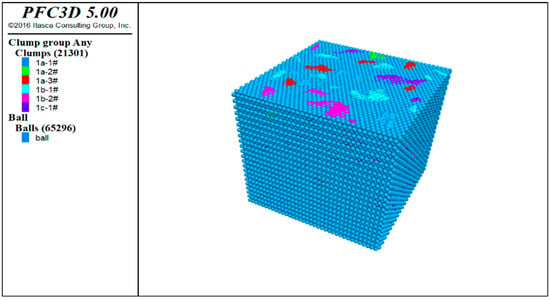Figure 21. Discrete element particles and aggregate clusters generated by the ball generate command.

2.

Using the FISH programming language that comes with the software, determine the position relationship between particles and the aggregate rigid cluster model, particles that do not overlap with the aggregate rigid cluster model are deleted, and the remaining particles are retained as flexible clusters representing aggregates. The resulting aggregate flexible cluster model is shown in Figure 22. The retained flexible cluster specimen model is used in the numerical simulation compression test and numerical simulation splitting tensile test.

Figure 22. Using FISH programming language to replace aggregate rigid clusters with flexible aggregate clusters.

For the ball generate command, the keyword radius was used to control the radius of the generated discrete element particles; the flexible clusters formed by smaller radius values could more truly simulate the shape characteristics of the aggregates. However, at the same time, the number of discrete element particles needed to form flexible aggregate clusters increased, and the computational efficiency decreased.

Figure 23 shows the morphology of aggregates B-2 and B-3 with different radius values; it can be seen that when the radius value is 0.5 mm, the aggregate flexible cluster can truly restore the morphological characteristics of the aggregate. Figure 24 shows the number of discrete unit particles required to replace aggregate 2a-2 and 2a-3 at different radius values. you can see, when the radius was greater than 0.5 mm, the number of discrete unit particles increased sharply. Therefore, to achieve a balance between computational efficiency and simulation accuracy, the aggregate DEM established in this study used discrete element particles with a radius value of 0.7 mm instead of aggregate rigid clusters.

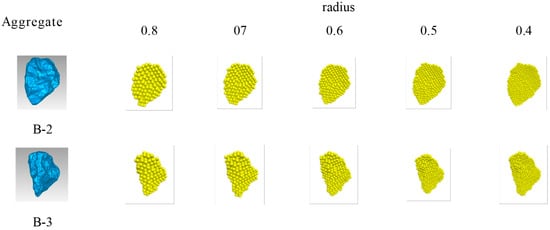
Figure 23. Morphology of flexible aggregate clusters under different radius values.

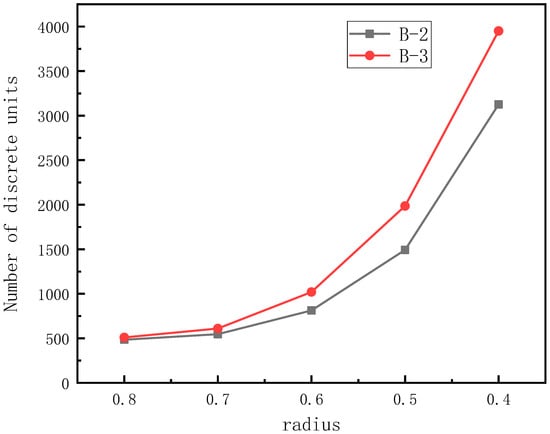
Figure 24. The number of discrete elements in the cluster template with different ratio values.

4.2.3. Contact Model Setting

After the aggregate was established with a flexible cluster aggregate, different contacts needed to be given to the corresponding contact model before a complete numerical model of permeable concrete could be formed. In this study, the linear parallel bonding model was used for the contact between flexible clusters, and the horizontal joint model was selected for the interior of flexible clusters. Figure 25 shows the set contact model, and Figure 26 shows the spatial distribution of the two contact models set by this method.

Figure 25. Linear parallel bond model set by cmat default command.

Figure 26. (a) Linear parallel bond model and (b) joint model after setting.

4.2.4. Parameter Calibration of Discrete Element Model of Permeable Concrete Specimen

Before the experiment, firstly, the parameters of the contact between the aggregate flexible clusters and the particles within the aggregate flexible clusters in the model were calibrated. The steps of parameter calibration are as follows:

• Permeable concrete specimens are prepared with a water−cement ratio of 0.28, aggregate particle size of 5–10 mm, slurry-to-bone ratio of 0.5, design porosity of 20%, and loose paving coefficient of 1.15. After curing in water for 28 days, the compression test is carried out, and the stress−strain curve and failure form of the specimen are recorded.
• The aggregate model with a 5–10 mm particle size is selected in PFC3D5.0 software, and the discrete element model of the permeable concrete specimen is established according to the loose paving coefficient of 1.15 and the ratio of paste to the bone.
• Select the corresponding contact model and default parameters, carry out the numerical simulation compression test, and adjust the contact model and parameters according to the test results, until the stress−strain curve of the numerical simulation specimen corresponds to the failure form.

In the numerical simulation in this study, the contact model between aggregate and aggregate were selected for the linear parallel bond model, and the contact model between the discrete element particles of the aggregate itself were chosen for the flat joint model.

In the process of parameter calibration, the stress−strain curve and failure form of the numerical model compression test measured by the results are shown in Figure 27. The stress−strain curve and failure form of the compression test of the specimen are shown in Figure 28.

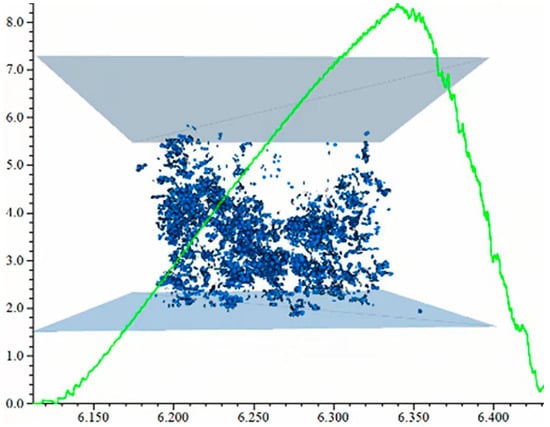
Figure 27. Stress-strain curve and failure form of the compression test of a numerical model.

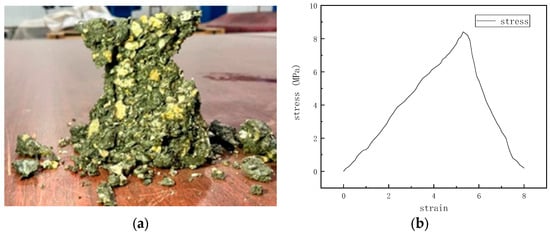
Figure 28. Stress−strain curve and failure form of specimen in a compression test: (a) failure form of compression test and (b) stress−strain curve test.

Figure shows the number and distribution of cracks after competing for the essive failure of the model; after the model was destroyed, cracks were mainly distributed at the edge of the model, and the distribution in the middle part was the densest, and the upper and lower fissures were less, the distribution of cracks were visible, the failure form of the specimen was the top cone failure and was consistent with the failure form of the specimen in Figure 28, and the peak values of the stress−strain curves were the same. This shows the effectiveness of parameter calibration; it was consistent with the failure form of the specimen after the compression test in Figure 28, and the stress−strain curves and peak values of the two were also the same, which shows the validity of parameter calibration and the reliability of the simulation.

5. Numerical Simulation of Particle Flow in Permeable Concrete by Discrete Element Method

5.1. Simulation Analysis and Verification of Compressive Strength of Permeable Concrete without Loose Paving Coefficient

After the contact model and parameters were determined, the compressive strength was tested using the numerical model of the corresponding specimen. The restore command to call was used to generate the specimen model and to generate corresponding walls above and below the model; after that, the speed and time of pressing under the wall were given, and the stress−strain curve during the testing process was recorded using the history command. The compression test process is shown in Figure 29.

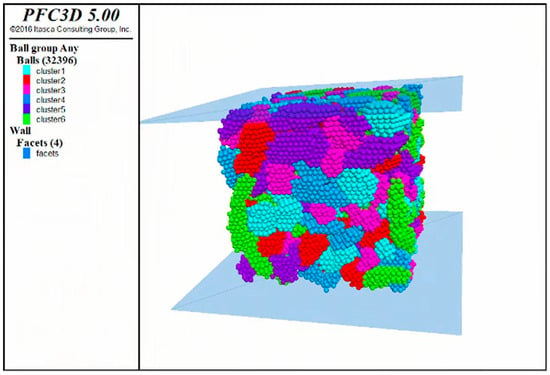
Figure 29. Compressive test of the specimen.

As can be seen from the test results, with the increase in the paste-to-bone ratio, the mechanical properties of permeable concrete increased and the permeability of permeable concrete decreased; therefore, considering the water permeability and mechanical properties of the specimen, 0.5 was selected as the slurry-to-bone ratio in the numerical simulation test. The aggregate model selected in this experiment was 50% 5–10 mm + 50 % 10–15 mm mixed aggregate. The compressive strength test results are shown in Figure 30. The results of numerical simulation compression test show that the compressive strength of the specimens with a loose paving factor of 1.05, 1.10, and 1.15 was 9.5 MPa, 12.1 MPa, and 13.1 MPa, respectively, and the errors between the results of the compression test and those of the compression test were 2.06 %, 2.52 %, and 2.34 % respectively. The accuracy of the simulation result was less than 3%, which proves the reliability of the simulation.

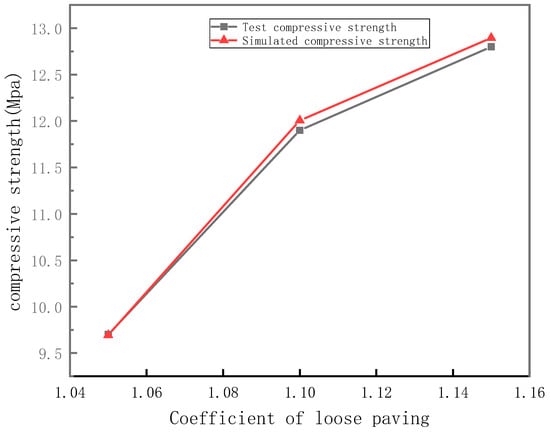
Figure 30. Compression simulation and test results of the numerical model.

In the numerical simulation test of compression, the failure forms of the specimen model under different loose paving coefficients were the same. Figure 31 and Figure 32 show the displacement of discrete elements and the distribution of cracks at different stages of the compression process, respectively. As can be seen from the figures, at the initial stage of the compression test, the particle displacement of the discrete element at the edge of the numerical model of the specimen was larger, and cracks started to appear in the corresponding part. It shows that the discrete elements at the edge of the permeable concrete numerical model peeled off at this time; this was consistent with the phenomenon that the first failure occurred at the edge of the specimen in the compression test of permeable concrete. With the increase in load, the number of cracks increased gradually, and the displacement at the edge of the test block model became larger and larger. As can be seen from Figure 31, when the specimen was destroyed, the displacement of the aggregate model in the cone-shaped area in the middle of the specimen was small, and, at this time, the distribution of cracks was less in the sub-region. This shows that the top cone damage occurred in the numerical simulation test of the specimen model.

Figure 31. Discrete element displacement and discrete element crack in the initial stage of compression: (a) displacement distribution of discrete elements and (b) numerical model fracture distribution.

Figure 32. Displacement and crack distribution of discrete element in compressive failure state: (a) displacement distribution of discrete elements and (b) numerical model fracture distribution.

Figure 33 shows the change in the number of cracks in the numerical model during compression simulation. As can be seen from the figure, at the initial stage of the specimen compression test, the number of cracks increased rapidly, and the discrete element particles at the edge of the model peeled off. With the increase in load, the number of cracks tended to be stable, which shows that stress redistribution occurred in the specimen model at this time, the specimen model entered a relatively stable state, and the compressive capacity was enhanced. As the load continued to increase, the stress and strain of the numerical model of the specimen continued to increase, the numerical model reached the limit of the compression test, fracture occurred between the aggregates inside the specimen and the aggregate, the number of cracks increased sharply, and then the specimen was destroyed.

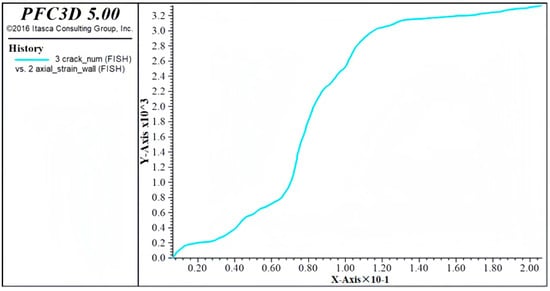
Figure 33. The change in the number of fractures in the process of compression simulation.

5.2. Relationship between the Number of Contacts and the Compressive Performance of the Numerical Model

In the numerical model, the number of discrete element particles and the number of contacts between the clusters representing aggregates had an important influence on the mechanical properties of the specimen. In this study, the number of discrete element particles under different compaction degrees and the contact number between rigid clusters before replacement were calculated. The statistical results of the compressive strength of the numerical model are shown in Table 8. Among them, the number of original particles refers to the number of discrete element particles filled with cube molds before replacing the rigid clusters, and the number of aggregate particles refers to the number of discrete element particles after replacement; the ratio between them could be used to measure the relative density of different numerical models of specimens. The number of linear parallel bond contacts represented the number and size of bonds between aggregates, and the contact number of horizontal joints represented the bonding number of discrete element particles between aggregates. The contact number of the aggregate model under the three loose paving coefficients is shown in Figure 34.

Table 8. The relationship between the number of particles, relative density, contact number, and loose spreading coefficient.

Loose Paving Coefficient	Number of Aggregate Particles (Unit)	Number of Original Particles (Unit)	Relative Density	Loose Paving Coefficient	Number of Aggregate Particles (Unit)
1.05	31,866	65,296	0.488	1.05	31,866
1.10	32,506	65,296	0.498	1.10	32,506
1.15	33,216	65,296	0.587	1.15	33,216

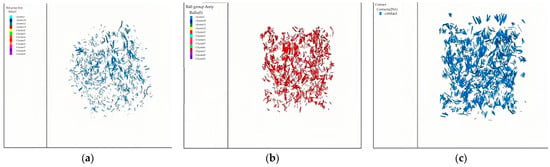
Figure 34. Numerical model of contact quantity and distribution between aggregates: (a) loose paving coefficient = 1.05, (b) loose paving coefficient = 1.10, and (c) loose paving coefficient = 1.15.

As can be seen from Figure 35, the compressive strength was positively correlated with the relative density and contact quantity; among them, the number of contacts between aggregates in the numerical model with loose paving coefficients of 1.10 and 1.15 increased by 37.04% and 60.77%, respectively, compared with the numerical model with a loose paving coefficient of 1.10, the relative density increased by 2.05% and 20.29%, respectively. This shows that the porosity of the specimen decreased with the increase in the compaction degree of the mixture. The increase in the content and contact of aggregates, led to an increase in compressive strength. The number of contacts was more suitable for measuring the mechanical properties of the numerical model.

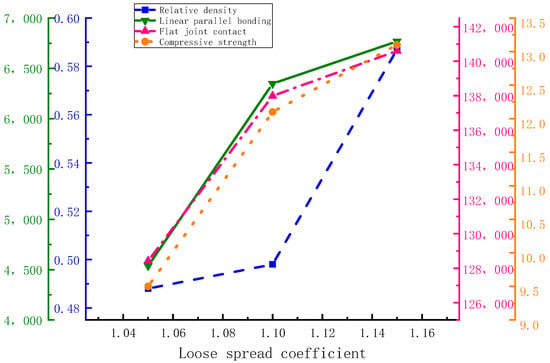
Figure 35. Relationship between the relative density, contact number, compressive strength, and loose paving coefficient.

The Influence of Different Proportion of Mixed Aggregate on the Contact Quantity of the Model and Its Analysis

In the numerical model, the number of contacts reflected the mechanical properties of the model to some extent. In the mixed particle size aggregate, the different proportions of aggregate with a single particle size affected the density of the permeable concrete mixture and the bond quantity between aggregates, thus affecting the mechanical properties. To study the effect of different proportions of mixed aggregate on the contact quantity of the model, a numerical simulation test was carried out by selecting a 0.5 slurry-to-bone ratio, 1.10 degrees of compaction, and setting different mixing ratios. The mixing ratio and the number of contacts are shown in Figure 36.

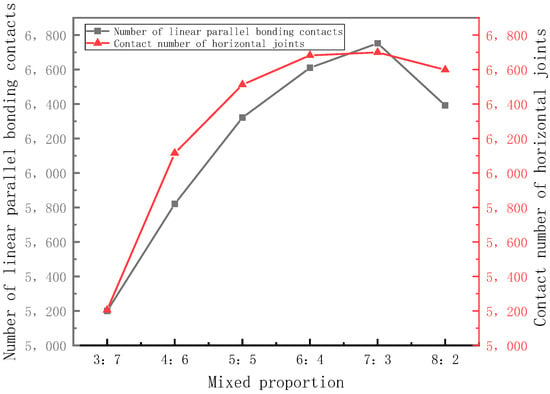
Figure 36. Relationship between contact quantity and aggregate mixing ratio.

As can be seen from Figure 36, when the proportion of aggregate particle size was 5–10 mm:10–15 mm = 7:3, the relative density of the mixture was the largest in the model, reaching 0.516, and the number of contacts between aggregates was the largest, reaching 2597. This shows that the mixed aggregate under this ratio had better mechanical properties.

Using the guidance of numerical simulation, we prepared a mixed aggregate with a particle size ratio of 5–10 mm:10–15 mm = 7:3 in the laboratory. For the preparation of permeable concrete, the slurry-to-bone ratio was 0.5 and the loose paving coefficient was 1.10. The 28-day compressive strength of the prepared permeable concrete specimen reached 13.4 MPa, compared with the specimen with a mixing ratio of 1:1, which increased by 12.6%. The results showed that the results of the numerical simulation could be effectively used to guide the experiment.

6. Discussion and Conclusions

In this paper, the effects of aggregate size, loose paving coefficient, and paste-to-bone ratio on the compressive strength and permeability of permeable concrete are studied. The test results show that the use of 50% 5–10 mm + 50% 10–15 mm mixed aggregate can effectively improve the compressive strength of permeable concrete, the loose paving coefficient has a positive correlation with the mechanical properties of concrete and a negative correlation with the permeability coefficient. Increasing the paste-to-bone ratio can effectively improve the mechanical properties of the permeable concrete, however, too high a slurry-to-bone ratio will lead to cohesion between aggregates and affect the permeability coefficient. The three factors of aggregate size, loose paving coefficient, and paste-to-bone ratio can be used as controlling factors to guide the mix design and preparation of permeable concrete. Table 9 shows the similarities and differences between the research content of this paper and that of predecessors.

Table 9. Comparison between this study and previous studies.

This Study	Previous Studies
The compressive performance of permeable concrete is simulated based on PFC3D, which is more clear and beautiful visually.	Liu Wei and others only use PFC2D to simulate ceramsite concrete, which has only planar a effect and no 3D clarity in vision.
Compared with the experimental results, the error of the numerical simulation results of the compressive strength is only 3%. Compared with the predecessors, the accuracy is higher and the simulation results are more accurate.	Liu Jinlong uses PFC for compressive strength numerical simulation results compared with the experimental results and the error is 10%; although it meets the accuracy requirements of the numerical simulation, the error is large.
A Binocular Blu-ray three-dimensional scanner is used to scan the aggregates one by one to obtain the true shape of the aggregate and establish a more realistic aggregate model.	Xu Hong, Zhao Long, and other scholars use ball particles instead of concrete aggregate, but the shape of concrete aggregate is irregular, so it is not accurate to use ball particles instead of aggregate.
Not only are the numerical simulations carried out using PFC3D software, but it is also proven that the mechanical properties are closely related to the number of contacts between the particles in the simulation model.	Most scholars such as he Shengdong only study the mechanical properties though numerical simulation but do not discuss why the mechanical properties of the specimens are different under different parameters.

The numerical model of permeable concrete specimens is established by using PFC3D5.0 software. The mechanism of the influence of the loose paving coefficient on the strength of permeable concrete is analyzed with a numerical simulation test, and the failure patterns are analyzed. The numerical model is used to analyze the influence of aggregate size on the relative density of the permeable concrete numerical model and the contact quantity between aggregates. The maximum error between the numerical simulation results and the experimental results of the permeable concrete discrete element model established by the modeling method in this paper is about 3 %; this proves that the numerical simulation method used in this study can effectively guide the mix design and preparation process of permeable concrete, and provides convenience for the follow-up research of permeable concrete.

However, there are still many deficiencies in this study on the factors affecting the mechanical properties and permeability of permeable concrete and the numerical simulation. The follow-up research can be improved from the following points:

• The flow performance of cement paste is not considered in the study of the paste-to-bone ratio. When the slurry-to-bone ratio is too large, too much cement paste can not be completely wrapped around the aggregate, resulting in cement paste blocking pores and reducing water permeability. In the follow-up study on the effect of the slurry-to-bone ratio on the performance of permeable concrete, the maximum thickness of aggregate can be taken as a reference factor, and the slurry-to-bone ratio can be controlled reasonably.
• Because of the limitation of computational efficiency, the cement paste is not represented by discrete element modeling in this study, and its function is realized by setting a reasonable contact model. The follow-up research can comprehensively consider the calculation efficiency and model accuracy, and bring the cement paste into the category of modeling.
• In the follow-up study, the discrete element method can be combined with the hydrodynamics method, and simulate the permeability of permeable concrete to realize the comprehensive consideration of the mechanical properties and permeability of permeable concrete by using numerical simulation method.