A Review of Load Frequency Control Schemes Deployed for Wind-Integrated Power Systems

Abstract

Load frequency control (LFC) has recently gained importance due to the increasing integration of wind energy in contemporary power systems. Hence, several power system models, control techniques, and controllers have been developed to improve the efficiency, resilience, flexibility, and economic feasibility of LFC. Critical factors, such as energy systems, resources, optimization approaches, resilience, and transient stability have been studied to demonstrate the uniqueness of the proposed design. This paper examines the most recent advances in LFC techniques for wind-based power systems. Moreover, the use of classical, artificial intelligence, model predictive control, sliding mode control, cascade controllers, and other newly designed and adopted controllers in the LFC area is thoroughly examined. Statistical analysis and a comparison table are used to evaluate the advantages, disadvantages, and applications of various controllers. Finally, this paper presents a comprehensive overview of contemporary and other widely used soft computing tools for the LFC issue. This detailed literature review will assist researchers in overcoming the gap between current progress, application, limitations, and future developments of wind energy in LFC.

1. Introduction

1.1. Background

Renewable energy generation has emerged as a global trend and a primary priority for governments globally in response to rising energy constraints and environmental degradation. Wind energy has fully recognized itself as humanity’s dominating alternative, more than any other green technology, owing to its minimal carbon footprint, low operating costs, and broad operational range [1,2]. The worldwide wind energy industry set a new milestone in 2020, reaching 743 GW, an increase of 14.3 percent over the previous year [3]. Additionally, wind energy is expected to provide 36% of the world’s electricity by 2050 [4]. Although wind energy is often abundant, it is extremely unpredictable owing to its reliance on adverse weather conditions. There may be instances where the wind energy generation does not meet the load requirement, resulting in power imbalance and high-frequency fluctuations [5,6]. These situations may degrade voltage stability and, in the worst scenario, trigger certain protective relays, resulting in a partial or total loss of power. As a result, integrating wind turbine generators (WTGs) into the load frequency control (LFC) of the power system may be a challenging task to address. LFC’s primary objective is to balance load-generation mismatches and to reduce frequency and tie-line power variations across various control regions [7,8,9]. To smooth the output power of WTGs, changes in the blade pitch angle have been proposed [10,11]. However, such strategies may compel the turbines to operate under substandard conditions, raising the WTG’s energy costs. It is also possible to adjust the output power by operating WTGs in a de-loaded state; but, this approach puts extra mechanical stress on the turbine rotor, potentially shortening the turbine’s life [12]. Additionally, storage devices (battery packs, supercapacitors) for smoothing the output power of WTGs have been a popular research topic over the last few decades [13,14,15]. While energy storage devices are effective for regulating wind power, they are expensive, mainly when used to manage large power systems [5]. The concept of vehicle-to-grid (V2G) has received considerable attention in recent years [16,17] and aggregating electric vehicles (EVs) as a storage reserve for a power system has shown to be an economical technique for minimizing wind power fluctuation. This approach enhances wind energy utilization in the power system while lowering the operating demands for separate energy storage devices [18]. When EV batteries are charged and discharged properly, they can feature bidirectional power regulation that supports LFC in the power system.

1.2. Literature Review

Numerous studies have been conducted on the LFC of WTG-integrated power systems, and innovative controllers and algorithms for effective coordination and damping in single-area [19], two-area [20], three-area [21], and multiple-area [22] configurations have been developed. For instance, traditional proportional–integral (PI) [23] and proportional–integral–derivative (PID) [24] controllers have been used to regulate system frequency using moth-flame optimization (MFO). However, due to the non-linear dynamics of the system, turbine strain, and load disturbance, such controllers cannot achieve the required efficiency. Fuzzy logic control (FLC) [25] based on differential evolution (DE) has shown excellent performance in the LFC problem of power systems. However, the authors did not consider renewable energy penetration, and membership functions (MFs) and criterion selection have certain limitations. These constraints may be overcome through the use of a multilayer recurring artificial neural network (ANN) coupled with a regressive and adjustable control mechanism [26]. The proposed recurrent ANN demonstrates the ability to restore LFC responses to their original values, even in the presence of parameter variations, peak load, and non-linearity. However, recurrent ANN is greatly reliant on training data, which requires a precise algorithm, adding significant computational complexity to the system. For enhanced dynamic performance in today’s power systems, the authors in [27] proposed FLC in conjunction with conventional PI/PID controllers using a novel teaching–learning-based optimization (TLBO) approach. However, an inappropriate selection of FLC features, including such MFs and baseline rules, might reduce the controller’s transient performance. Ref. [28] presents an approach for improving the resilience and transient stability of WTG’s integrated power systems by using sliding mode control (SMC). However, while developing the SMC controller, the authors assumed that all power system states were to be determined, which is challenging for actual power systems. In addition, SMCs continue to have limitations, such as the inability to achieve finite-time resolution, slow response to abrupt changes in disturbances, and the increased chattering of control signals [29]. Model predictive control (MPC) has been widely employed in recent years for several applications, including the integrated power system’s LFC issue. MPC has been deemed a suitable alternative to PI and PID controllers when it comes to achieving optimal performance in the LFC issue. It is also claimed that only MPCs are capable of dealing with constraints, in addition to their optimization capabilities [30]. Ref. [31] used a two-layer optimization technique to include the MPC into the LFC of a microgrid comprising wind turbines, base loads, and aggregated EVs. The results indicate that the proposed optimization can effectively manage uncertainty in microgrids and minimize forecasting errors. The LFC of a single-area power system has been optimized using an adaptive MPC based on a recursion algorithm [32]. These analyses made no attempt to account for the uncertainties and physical constraints inherent in the system operation. Ref. [33] addressed governor uncertainty, turbine parameter variations, and load changes; however, wind power fluctuations were not considered for the proposed controller. Ref. [34] proposed centralized MPC-based control techniques for managing dispersed power requirements and system constraints including the output power of WTGs. However, the optimization of MPC becomes increasingly complicated as the number of evaluative criteria, model parameters, and precise measurements increases.

1.3. Objectives and Contributions

Numerous surveys on LFC have been conducted, but they have predominantly focused on conventional power systems. In modern power systems, renewable energy, particularly wind energy, is increasingly integrated, which may have a detrimental effect on system inertia response and frequency stability. Consequently, a comprehensive review and study are required to address all recent trends of LFC within the wind-integrated power system. This paper presents a comprehensive review of the current state of knowledge and recent advancements in LFC for wind-interconnected power systems. Figure 1 depicts the survey segmentation conducted for this paper. As illustrated in the figure, three distinct aspects of LFC have been examined. First, the control area suitability of single-area, two-area, three-area, and four-area models for wind-integrated power system models have been discussed. Second, numerous control techniques for classifying LFC for wind-integrated power systems have been discussed. The use of soft computing for LFC classification has been examined further. Hence, the major contributions of this survey are briefly summarized below:

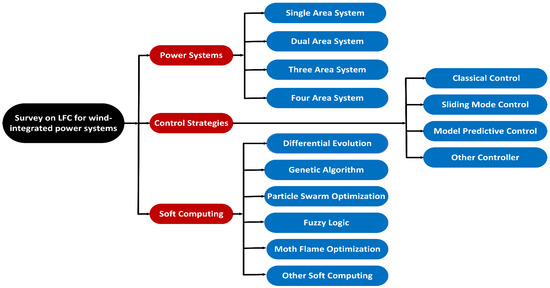
Figure 1. Flow chart on LFC survey.

• The impact of wind power on the frequency stability of interconnected power systems has been reviewed.
• The pros and cons of various wind-integrated power system models, as well as their influence on LFC, have been examined.
• The application and shortcomings of the most commonly employed control techniques for wind-integrated power systems have been investigated.
• The use of soft computing approaches to LFC models that can manage uncertainties and parameter variations in varied load disturbances has been outlined.
• Analysis of research gaps and future recommendations for LFC in wind-integrated power systems has been undertaken.

This manuscript is divided into six sections: Section 2 discusses the review of conventional and wind-integrated power systems. In Section 3, a description of the different types of wind-integrated power system models is discussed in relation to control area suitability for single-area, two-area, three-area, and four-area models. In the following Section 4, various control techniques are discussed to classify LFC for wind-integrated power systems. A further investigation of LFC classification is provided and investigated in Section 5 using soft computing and different control algorithms. The Section 6 of this literature review presents the conclusions.

2. Review of the Load Frequency Control Scheme

LFC is an ancillary service that plays an important role in the design and operation of modern power systems. It eliminates steady-state error in frequency and reduces unscheduled power flows between adjacent control areas [35]. During disturbances, it also maintains reasonable limits on overshoot and settling time. In the past, the frequency of the system was regulated by adjusting the governor positions of the generator; however, this mechanism was later found to be insufficient. Subsequently, the governor was equipped with supplementary analog control systems that relied on feedback signals from the generators, and load to regulate the frequency and output power of the power systems [36]. The introduction of power electronic converters, as well as renewable energy sources (RESs), such as wind and solar, poses new challenges for frequency regulation. This is because the RESs have very low inertia and limited reserves of power generation for frequency support. Therefore, modern LFC schemes use advanced control technologies to enable concurrent monitoring and control capabilities, even amidst the fluctuating nature of power systems.

2.1. LFC Scheme Considering Conventional Power Systems

Conventional power systems have been in use for many decades. These power systems heavily rely on the generation of electricity from multiple sources, including hydropower, thermal power, natural gas power, and nuclear power [37]. In such systems, it is standard practice to program the active power reserve on the generating side, allowing the generator to quickly ramp up or down the active power production. However, in recent years, researchers have been focusing on providing an active power reserve through demand response programs. Demand response is an effective technique for adjusting power system frequency. The switching-based control capability to load enables a quicker response to system disruptions than is possible with conventional synchronous generators. Together with recent technological advancements in processing, monitoring, and communication, this capability may empower load-side devices to improve frequency regulation in power systems. Considered an interconnected power system, tie-line power $\left(P_{tie}\right)$ may be expressed as [38,39]:

$$P_{tie,12}=\frac{\left|V_1\right|\left|V_2\right|}{X_{12}}\sin ({\delta }_1-{\delta }_2)$$

(1)

where $X_{12},\delta$ are the reactance and angles of end voltages $V_1,V_2$. For slight angle deviation, the tie-line power varies accordingly as:

$${\Delta P}_{tie,12}=\frac{\left|V_1\right|\left|V_2\right|}{X_{12}}\cos ({\delta }_1-{\delta }_2)(\Delta {\delta }_1-\Delta {\delta }_2)$$

(2)

$$K_{s12}=\frac{\left|V_1\right|\left|V_2\right|}{X_{12}}\cos \left({\delta }_1-{\delta }_2\right)$$

(3)

$${\Delta P}_{tie,12}=K_{s12}\left(\Delta {\delta }_1-\Delta {\delta }_2\right)$$

(4)

where $K_{s12}$ is the synchronizing coefficient of areas 1 and 2. Similarly, the incremental angle change caused by frequency deviation can be expressed as follows:

$$\mathsf{\Delta }\delta =2\pi {\int }_0^T\mathsf{\Delta }fdt$$

(5)

Putting the above value and taking Laplace transform:

$${\Delta P}_{tie,12}=\frac{2\pi K_{s12}}{s}({\Delta f}_1(s)-{\Delta f}_2(\mathrm{s}))$$

(6)

Consequently, the power deviation between the tie lines in regions 1–3 and 1–4 is determined as:

$${\Delta P}_{tie,13}=\frac{2\pi K_{s13}}{s}({\Delta f}_1(s)-{\Delta f}_3(\mathrm{s}))$$

(7)

$${\Delta P}_{tie,14}=\frac{2\pi K_{s14}}{s}({\Delta f}_1(s)-{\Delta f}_4(\mathrm{s}))$$

(8)

The generalized equation for tie-lines power deviation $({\Delta P}_{tie,i})$ can be expressed as:

$$\dot{{\Delta P}_{tie,i}}={\sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^n\Delta P_{tie}^{ij}={\sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^n{K}_{sij}({\Delta f}_i-{\Delta f}_j)$$

(9)

$${\Delta P}_{tie,ij}=-{\Delta P}_{tie,ji}$$

(10)

Auxiliary control in a multi-area power system should ensure that, as compared to regulating a region’s frequency, the tie-line power exchange with other areas maintains within set limits. Area control error (ACE) is often applied as an indicator to reduce these two variations [40,41]:

$${ACE}_i={\beta }_i{\Delta f}_i+{\Delta P}_{tie,i}$$

(11)

$${ACE}_i={\beta }_i{\Delta f}_i+{\sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^n{K}_{sij}({\Delta f}_i-{\Delta f}_j)$$

(12)

$${\beta }_i=D_i+\frac{1}{R_i}$$

(13)

where ${\beta }_i,D_i,$ and $R_i$ represent frequency bias, damping coefficient, and governor droop, respectively. The $D_i$ determines the LFC system’s ability to rapidly reduce frequency deviations in the power system. A higher $D_i$ indicates that the LFC system can respond quickly to frequency variations and stabilize the power system. The $D_i$ of conventional power systems can be calculated as follows:

$$D_i=4H_i{\omega }_n\mathsf{\xi }$$

(14)

where $H_i,{\omega }_n,$ and $\xi$ represent the inertia constant, natural frequency, and damping factor, respectively. Similarly, $H_i$ plays an essential role in determining the system’s capacity to respond to load demand variations and maintain frequency stability. The $H_i$ of a single generator can be determined as follows:

$$H_i=\frac{1}{2}\frac{j_i{{\omega }_m}^2}{S_{n,i}}$$

(15)

where $j_i$, ${\omega }_m$, and $S_{n,i}$ represent the moment of inertia, rotor speed, and rated power of the generator, respectively. Since conventional power systems consist of several interconnected generators, the total inertia constant ${(H}_{con})$ may be calculated using the following equation:

$$H_{con}=\frac{{\sum }_{i=1}^n{H}_i{S}_{n,i}}{S_n}$$

(16)

where $n$ and $S_n$ are the total number of connected generators and rated power of the power system. When addressing the optimization problem of LFC in interconnected power systems, various objective functions may be utilized to minimize the frequency and tie-lines power deviations. The frequency distortion and tie-lines power have been included in objective functions using a variety of techniques provided in the published research. Integral square error (ISE), integral absolute error (IAE), integral time square error (ITSE), and integral time absolute error (ITAE) are the four most significant objective functions for load frequency controller design [42]:

$$J_{\mathrm{I}\mathrm{S}\mathrm{E}}={\int }_0^T\{{(\Delta f_i)}^2+{({\Delta P}_{tie})}^2\}dt$$

(17)

$$J_{\mathrm{I}\mathrm{A}\mathrm{E}}={\int }_0^T\{|\Delta f_i|+|{\Delta P}_{tie}|\}dt$$

(18)

$$J_{\mathrm{I}\mathrm{T}\mathrm{S}\mathrm{E}}={\int }_0^T\left\{{(\Delta f_i)}^2+{({\Delta P}_{tie})}^2\right\}tdt$$

(19)

$$J_{\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{E}}={\int }_0^T\{|\Delta f_i|+|{\Delta P}_{tie}|\}tdt$$

(20)

2.2. LFC Scheme Considering Wind-Integrated Power Systems

The power system’s challenges have intensified as a consequence of the following factors: (a) increased integration of renewable sources [43]; (b) implementation of innovative technologies including microgrids [44]; and (c) reliance on insecure communications infrastructure. These factors have a direct impact on the performance, reliability, and stability of electric power systems. As wind power becomes increasingly integrated into power systems, the uncertainty associated with active power generation rises, leading to higher frequency deviations [45]. This requires that future LFC techniques for power systems must be more robust and efficient to overcome these challenges. Any variations in wind speed can impact the power output of WTs, which in turn can affect the equilibrium between power generation and consumption in the grid, resulting in deviations from the intended frequency. In the case of WTs, power output is directly proportional to the cube of the wind speed, as shown by the following equation:

$$P_w=1/2 \rho A{V}^3{C}_p(\mathsf{\lambda },\mathsf{\alpha })$$

(21)

where $P_w,\rho ,A,V$, $\mathsf{\lambda },\mathsf{\alpha },$ and $C_p$ represent power output, air density, turbine blade’s covered area, wind speed, tip speed, pitch angle, and power coefficient, respectively. A small change in wind speed can have a substantial effect on the output power of WTs, which alters the system’s inertia constant and increases the amplitude of oscillations. Hence, when WTGs are added to a system, the effectiveness of LFC decreases due to the relative loss of inertia and the system’s lower capacity to regulate the amount of generated power. The new system’s overall inertia ($H_{n,i})$ can be calculated as [46]:

$$H_{n,i}=H_{eq}+H_{wt}{L}_p$$

(22)

$$H_{eq}=H_{con}-H_{con}{L}_p$$

(23)

$$H_{eq}=H_{con}(1-L_p)=\frac{{\sum }_{i=1}^n{H}_i{S}_{n,i}}{S_n}(1-L_p)$$

(24)

where $L_p$, $H_{eq}$, and $H_{wt}$ are the wind penetration level, equivalent inertia of conventional generators, and inertia of WTGs, respectively. $L_p$ is the percentage of power produced by wind relative to the total power produced, which accounts for both conventional generators and WTGs. Similarly, $H_{wt}{L}_p$ represents the inertia contribution of the WTGs, while $H_{con}{L}_p$ represents the reduction in the inertia of conventional generation due to the presence of wind. WTG inertia $H_{wt}$ can be calculated using the following equation [46]:

$$H_{wt}=\frac{-\frac{T_{d}D}{lnx}-2H_{eq}(1-L_p)}{{2L}_p}$$

(25)

where $T_d$ and $D$ are the delay time and load damping constant. When WTGs are integrated into power systems, the regulatory constant, frequency bias, and damping coefficient also change, which can be calculated as follows:

$$R_{n,i}=\frac{R_i}{(1-L_p)}$$

(26)

$${\beta }_{n,i}=D_{n,i}+\frac{(1-L_p)}{R_i}$$

(27)

$$D_{n,i}=\frac{2\mathsf{\pi }{\Delta f}_i}{H_{n,i}}\ast S_{n,j}$$

(28)

where $S_{n,j}$ is the apparent power of the wind-integrated power system. Similarly, the system’s frequency deviation is described as follows:

$${\Delta f}_i(s)=\frac{{\sum }_{K=1}^N{TG}_{ki}\left(s\right)K\left(s\right){\Delta P}_{tie,i}(s)-{\Delta P}_{tie,i}(s)-{\Delta P}_{L,i}(s)}{{2H_{n,i}\left(s\right)+D}_{n,i}-{\sum }_{K=1}^N{TG}_{ki}\left(s\right)K\left(s\right){\beta }_{n,i}+\frac{{\sum }_{K=1}^N{TG}_{ki}(s)}{R_{n,i}}}$$

(29)

where ${TG}_{ki}$, ${\Delta P}_{L,i}$, and $K\left(s\right)$ represent turbine-governor transfer function, non-frequency-sensitive load change, and LFC controller, respectively. The above equation may be used to calculate the relation between frequency deviation and wind penetration levels. Several approaches are employed to alleviate the frequency impact of WTs integration, including the introduction of advanced control systems to modify the output of WTs in response to changes in wind speed and power grid conditions. These control systems have the capability to adjust the power output of the WTs in real time, thereby aiding in the stabilization of power grid frequency.

3. Taxonomy of LFC Based on the Types of Power Systems

The increasing use of renewable energy sources, notably wind power, has led to an increase in the operational complexity of the power system. Numerous control techniques and optimization algorithms have been proposed to enhance power quality and system response to irregularities.

3.1. Single-Area Wind-Integrated Power System

Planning and implementing a controller for a single-area system laid the foundation of the field’s research into regulating frequency deviations [47]. A single-area power system, which uses a WTG in addition to other traditional energy sources, is a basic system with uncomplicated power production and consumption. When operating a single-area system, the LFC’s primary responsibility is to adjust the frequency to match the system’s actual value since no tie-line power regulation is required. For wind-integrated power systems, a plethora of LFC control strategies have been proposed [7,19,48,49]. Ref. [32] developed an AMPC control scheme for resilient frequency regulation in a single-area power system, which was proven against a variety of unmatched variables and load disruptions. The linear representation of the turbine’s rotational speed implied by this technique does not guarantee continuous dependability. An intriguing technique based on non-linear MPC has been described with the goal of balancing power optimization and control, hence improving system dependability, and minimizing transient loads [50]. Similarly, as an alternative to the conventional LFC technique, the authors in [51] addressed the challenge of developing optimal linear time-invariant (LTI) designs at various operating points. In [19], a control strategy for wind-integrated single-area power systems was proposed that incorporates MPC and a linear quadratic gaussian (LQG) to account for physical constraints and load disturbances. The authors of [52] also used aggregated EVs in frequency control to limit wind-related system frequency changes by using a tube-based MPC (T-MPC). In this case, the influence of multiple disturbances was not considered concurrently. With these problems under consideration, a single-area microgrid system’s MPC controller has been designed to assess system performance while concurrently experiencing source and load disturbances [53]. The authors in [19,54] developed a mathematical model for wind-integrated power systems that considers the system’s frequency response during load disturbances. These models included traditional energy sources such as thermal and natural gas, as well as wind energy as a renewable energy source.

3.2. Dual-Area Wind-Integrated Power System

Dual-area power systems are connected by a tie line as shown in Figure 2, implying that both frequency and tie-line power regulation is required to ensure that the whole power system operates as designed and intended. Each area is equipped with many generators that are tightly connected to create a coherent group, guaranteeing that all generators in the power system respond in unison when the demand varies. During normal operation, the tie-line power for a dual-area system is calculated by the authors in [55,56]. Moreover, several studies have examined an overview of LFC systems in dual-area power systems and tie-line models, as well as their impacts on LFC systems that have been thoroughly investigated [16,20,26,54]. Multiple operating scenarios of the LFC of a dual-area power system comprised both thermal and wind turbine generators were explored using recurrent ANN and adaptive fuzzy control approaches [26]. Additionally, the authors in [16] introduced a modified fractional-order PID (FOPID) controller for wind energy and EVs based on two-area power systems. The cross-area power balance between demand and supply is more difficult to achieve, and it has an adverse effect on frequency stability and reduces auxiliary frequency control capabilities. To address the secondary frequency control issue in a deregulated dual-area power system, an enhanced SMC was developed that minimizes the optimum values of the objective functions while simultaneously requiring less computational effort [54]. Similarly, the authors in [20] compared the LFC capabilities of ANFIS, ANN, and fuzzy controllers, and their results indicate that the ANFIS controller improves dynamic response, including efficient execution, reduced fault magnitudes, and a lower transitory frequency. Additionally, several optimization strategies have been examined for the LFC problem in a dual-area power system in order to enhance the PID controller settings [57]. Reference [58] proposed using a tilt PID controller to regulate the frequency of traditional two-area deregulated power systems that also incorporate WTGs, EVs, and hybrid energy storage.

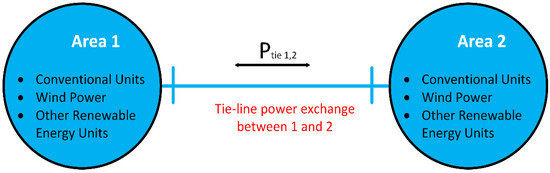
Figure 2. Schematic dual-area power system.

3.3. Three-Area Wind-Integrated Power System

These systems employ tie lines to interconnect the three control zones as depicted in Figure 3, each of which has a different combination of power generation resources and loads to control. As the control area associated with the fault level current expands, a more robust set of control mechanisms is needed to prevent disturbances from propagating. For a three-area wind-integrated power system, the ${\Delta f}_i,{\Delta P}_{tie,i},$ and area control error (ACE) were determined [55,56]. Moreover, several studies on LFC modelling for three-area connected power systems have been found in the literature. Ref. [59] presented an LFC technique based on RES integration and a novel algorithm for optimizing the parameters of a conventional PID controller. Assuming all of the system’s parameters have been adjusted to their nominal values, an LFC technique based on a full-order adaptive SMC has been developed [60]. The uncertainty associated with the parameters was not addressed in this system. Using a hybrid H₂/H_∞ controller, the parameter uncertainties and response latency of EVs to participate in multi-objective LFC with conventional sources were studied [22]. However, this technique does not provide an acceptable conclusion for voltage transients or any other constraint since the load is not scheduled during peak hours. Using the differential evolution (DE), the authors in [61] developed a resilient FOPID controller for a three-area power system that considers peak undershoots, convergence speed, and physical constraints. In a dynamic setting, the mathematical models of an unequal triple-area system with a diverse variety of energy resources, including wind energy, have been studied, and the results have been published [62,63]. The LFC of a composite power system that comprises thermal, solar, and EVs were studied, and an integral-double-derivative (IDD) controller was applied to assess the system performance [64].

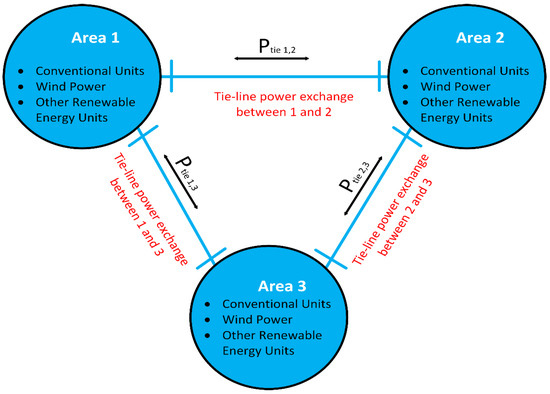
Figure 3. Schematic triple-area power system.

3.4. Four-Area Wind-Integrated Power System

In general, four-area power systems that are coupled by tie lines are separated into four regions, as illustrated in Figure 4, to maintain the frequency fluctuation within an acceptable range. The LFC model of four-area integrated power systems has been described by the authors in [51,65,66,67]. The initial design for a four-area LFC system using the generalized technique incorporated non-linear systems and dual controllers. On the other hand, as power systems become more complex and diverse, much research has been conducted on four-area integrated contemporary power systems with the goal of improving overall system performance [28]. The mathematical model for frequency regulation of wind-integrated power systems was investigated by the authors in [51]. The LFC model was investigated in a four-region design with identical reheated thermal units [68]. The formulation of the problem and the constraints associated with this model have been analyzed. Using a customized variant of the bat algorithm (BA) in conjunction with fuzzy logic, it is possible to obtain the optimum outputs of a traditional PI controller used for LFC in four-area systems [69]. However, unstable optimization outcomes and the tendency to slip into local optimums are some of BA’s shortcomings. While such algorithms provide the best coefficients, they are expensive and time intensive to apply, necessitating the use of cluster analysis and parallel computing to achieve the intended results.

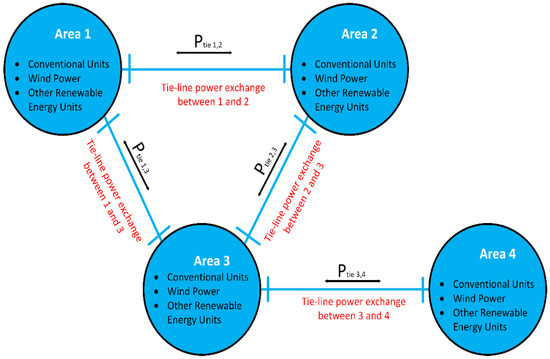
Figure 4. Schematic four-area power system.

4. Taxonomy of LFCs Based on Various Control Strategies

Since the inception of LFC, several controllers have been effectively devised and deployed. Some studies have upgraded existing control models, while others applied hybrid techniques to address power system LFC problems. This section examines the most common LFC control strategies in wind-integrated power systems. Table 1 details the advantages, disadvantages, and applications of these prevalent control strategies.

4.1. Classical Control Techniques

Most studies in the domain of LFC are devoted to the use of conventional controllers, the first in a succession of closed-loop systems designed to address the shortcomings of open-loop systems. To improve frequency regulation, the classic control paradigm uses integer order (IO) controllers that are usually coupled to the governor and are employed to reduce area control error [70]. Several conventional control approaches and optimization algorithms have been suggested in the past for LFC in power systems [63,64,69,71,72]. The innovative developed moth-flame optimization (MFO) technique has been used to obtain the required results while calibrating the PI parameters and the WTG’s speed regulator [23]. An MFO-optimized PID controller for wind-integrated power systems is being developed, which considers both local and large-scale uncertainty [24]. For a dual-area deregulated power network that incorporates EVs and WTGs along with conventional power sources, a tilt PID controller has been applied to investigate non-linear effects such as GRC, GDB, and boiler behavior [64]. An improved and optimized frequency response and tie-line power during a transient scenario have been achieved by using a PID controller and a PID acceleration controller [63]. The authors implemented three optimization strategies to obtain model parameters for an LFC in a multi-area wind interconnected system. Also, a 3DOF-PID controller has been offered to address the dynamic controller design issue of an integrated power system’s LFC [72]. For complex operations, a comparative study of three distinct PID controller design methods has been carried out [73]. Similarly, several studies [16,19,57,63,68] examined cascade controllers for LFC in an attempt to optimize the dynamic response of the power system. In a multi-area system, PID and PIDA controllers with three optimization algorithms have been presented to optimize frequency response and tie-line power under a transient condition [63]. For LFC of an integrated power system integrating EVs with various resources, including wind energy, a cascaded controller including TIDN and 1+PI has been proposed [68]. In addition, the authors developed an improved FO controller that integrates the features of two commonly used FOPID and TID controllers for LFC of two-area power networks [16]. Also, for concurrent variation in wind power and load fluctuation, a cascade PI-PD control strategy for LFC of an integrated power system with traditional and wind power sources was devised and tested [74]. Although, operational and physical constraints were not considered by the authors. Using a T-MPC and disturbance observer controllers, the authors of [57] applied aggregated EVs in frequency control to minimize wind-related system frequency variations. The following equations represent the transfer functions $G\left(s\right)$ of the controllers described previously:

$$G_{PI}\left(s\right)=K_p+\frac{K_i}{s}$$

(30)

$$G_{PID}\left(s\right)=K_p+\frac{K_i}{s}+K_{d}s$$

(31)

$$G_{PIDA}\left(s\right)=\frac{K_a{s}^3+K_d{s}^2+K_{p}s+K_i}{s^3+{as}^2+bs}$$

(32)

$$G_{tilt}\left(s\right)=\frac{K_p}{s^{1∕n}}+\frac{K_i}{s}+K_d\frac{N}{1+s}$$

(33)

$$G_{3DOF}\left(s\right)=\frac{S^2(K_{d}n{D}_{sw}+K_p{P}_{sw})+S(N{K}_e{P}_{sw}+K_i)+K_{i}N}{S(S+N)}$$

(34)

where $K_p,K_i,\mathrm{a}\mathrm{n}\mathrm{d} K_d$ denote the controllers’ proportional, integral, and derivative gain values. $P_{sw}$ and $D_{sw}$ are the proportional and derivative controller’s setpoint weights, respectively; $N$ and $n$ represent the filter coefficient and tilt-parameter. For cascade control, two controllers operate in such a manner that the output of the first controller serves as a setpoint for the succeeding controller. The transfer function of the system for a cascade controller is as follows:

$$Y\left(s\right)=\frac{\left(G_1\left(s\right)G_2\left(s\right)C_1\left(s\right)C_2\left(s\right)\right)·R\left(s\right)-G_1\left(s\right){·D}_1(s)}{1+G_2\left(s\right)C_2\left(s\right)+G_1(s)G_2(s)C_1(s)C_2(s)}$$

(35)

4.2. Sliding Mode Control Techniques

SMC is one of the various resilient controller techniques that may be used to modify a system’s behavior by applying pressure to allow it to slide over the system’s usual operating trajectory. It exhibits a resilient response to system disturbances and parameter variations, precluding the need for accurate modelling [75,76]. Consider a 2nd order system:

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\\ \dot{x_2}=b\sin (m{x}_1)+u\hspace{1em} \left|b\right|\le \beta \end{array}\right.$$

(36)

where $b \mathrm{a}\mathrm{n}\mathrm{d} m$ are possible unknown coefficients, and $\beta >0$ is a’s maximum limit of $b$. In state space, the sliding surface appears as,

$$s=x_2+c{x}_1$$

(37)

where $c$ is the positive constant. Now after using the controller:

$$u=-c{x}_2-\alpha sign(s)$$

(38)

The $sign(s)$ indicates the sign function, which is defined as:

$$sign\left(s\right)=\left\{\begin{array}{c}1\hspace{1em} for\hspace{1em} s>0\\ 0\hspace{1em} for\hspace{1em} s=0\\ -1\hspace{1em} for\hspace{1em} s<0\end{array}\right.$$

(39)

Multiple studies have shown that including SMC in a power system’s LFC may significantly assist in achieving the targeted control objectives due to its efficacy and simplicity of implementation [28,29,48,54,66,71]. SMC has been used to investigate the frequency fluctuations caused by power mismatch and transmission delays in wind-integrated power networks [28]. However, conventional SMCs continue to have limitations, including the increased chattering of control signals, a slow response to sudden changes in disturbances, and an inability to achieve finite-time resolution. To address these concerns, an adaptive fuzzy SMC with fast resolution and no singularity problem has been developed [29]. This approach, however, is still limited in its capacity to identify maximum boundary limits, the possibility of chattering, and high computation costs. An upgraded SMC has been developed to address the high computing costs and LFC problems in a deregulated dual-area power system by reducing the optimal values of the objective functions [54]. Reference [66] proposed an adaptive SMC-based LFC technique to recover the nominal values of all system parameters during external disturbances and parametric uncertainties. Also, a PSO-optimized SMC controller has been developed and evaluated for two and four areas with parameter uncertainties and load fluctuations using a third-order transfer function [71]. While such controls provide the best coefficients, they are expensive and time intensive to apply, necessitating the use of cluster analysis and parallel computing to obtain the intended results. Moreover, these control approaches are suitable for traditional generating units with a high system inertia and do not consider the probability of variable wind energy in the near future.

4.3. Model Predictive Control Techniques

MPC has been widely used in recent years for various applications, including solving the LFC problem of integrated power systems. For achieving optimal performance in the LFC issue, MPC has been considered an alternative to PI and PID controllers [41]. Consider MPC’s discrete linear state-space model, which is as follows [40]:

$$x_i(k+1)=A_i{x}_i(k)+B_i{u}_i(k)+E_i{w}_i(k)+{\sum }_{j\ne i}{A}_{ij}{x}_j\left(k\right)+B_{ij}{u}_j\left(k\right)$$

(40)

$$y_i(k)=C_i{x}_i(k)$$

(41)

The MPC predicts the states and outputs of all control regions n-steps ahead of time as follows:

$$\begin{array}{ll}{x}_i\left(k+n+1|k\right)=& A_n{L}_{i}x\left(k\right)+A^n\acute{L_i}x\left(k|k-1\right)+{\sum }_{s=1}^n{A}^{s-1}{B}_i{u}_i(k+n)|k\\ & +E_i{w}_i\left(k\right)+{\sum }_{\begin{array}{c}j\in \left\{1\dots .M\right)\\ j\ne i\end{array}}{\sum }_{s=1}^n{A^{s-1}B}_j{u}_j(k+n)|k-1)\end{array}$$

(42)

$$y_i(k+n+1|k)=C_i{x}_i(k+n+1|k)$$

(43)

where $x_i,u_i,w_i \mathrm{a}\mathrm{n}\mathrm{d} y_i$ indicate the state vector, input signal vector, disturbance vector, and output vector, respectively, and $A_i,B_i, \mathrm{a}\mathrm{n}\mathrm{d} E_i$ are the constants. It is also claimed that only MPCs, in addition to their optimization capabilities, can cope with constraints [30]. A two-layer optimization technique was used by the authors in [31] to include the MPC in the LFC of a microgrid that includes wind turbines, base loads, and aggregated EVs. An adaptive MPC based on a recursion algorithm was used to improve the LFC of a single-area power system [74]. Also, the authors in [53] examined a coordinated MPC-based design strategy for solving localized design problems and the effects of load disturbance changes on LFC on a four-area connected system with WTGs. The uncertainties and physical constraints that come with system operation were not considered in these analyses. The LFC’s MPC development process addressed the uncertainty in [33], but the fluctuation in wind power was ignored. Similarly, in [19], a control strategy for a wind-integrated single-area power system was proposed that incorporated MPC and an LQG to account for physical constraints and load disturbances. An intriguing technique based on non-linear MPC has been described with the goal of balancing power optimization and control, hence improving system dependability, and minimizing transient loads [60]. Ref. [34] proposed MPC-based control techniques for managing dispersed power requirements and system constraints including the output power of WTGs. However, optimization for MPC becomes increasingly complicated as the number of evaluative criteria, model parameters, and precise measurements increases. Reference [57] also employed aggregated EVs in frequency control to minimize wind-related system frequency fluctuations using a T-MPC; although, the impact of multiple disturbances was not examined concurrently in this situation. With these issues taken into account, the MPC controller of a single-area microgrid system has been designed to assess system performance while experiencing source and load disturbances [62].

4.4. Similar Designed and Deployed Controllers

During the early stages of LFC, basic conventional tuned controllers with mismatched parameter sets were extensively employed, resulting in poor performance under a broad variety of working circumstances and varied load perturbations. Therefore, a unique design is crucial to preserve the relationship between generation and load fluctuations to maintain the resilience of the LFC. Some newly designed controllers have been demonstrated to be reliable for LFC schemes in multi-area and microgrid systems [77,78]. As an alternative to the conventional LFC approach, the authors in [61] used a self-tuning regulator to address the challenge of developing optimal LTI designs at various operating points. The performance of LFC was improved by a resilient H∞ controller based on linear matrix inequality (LMI), which is suitable for conventional systems with HESS [79]. Using a hybrid H₂/H_∞ controller, the parameters uncertainties and response latency of EVs to participate in multi-objective LFC with conventional sources were studied [22]. A DRL-based LFC technique for controlling renewable power uncertainties and minimizing frequency deviation with a faster reaction time and better flexibility has been proposed [7]. However, these techniques do not provide an acceptable conclusion for voltage transients or any other constraints since the load is not scheduled during peak hours. The LFC of a composite power system composed of thermal, solar, and EVs under GRC and the time delay was investigated, and an IDD controller was used to evaluate system performance [80]. Recently, the authors in [68,81] proposed the preliminary implementation of the TI-TID controller for LFC of a conventional power system, taking physical constraints and load uncertainties into consideration. Similarly, a TIDN and 1+PI have been suggested for the LFC of an integrated power system integrating EVs with other resources, including wind energy [68]. Also, the author in [16] developed an enhanced FO controller that combines the capabilities of two commonly used FOPID and TID controllers for a two-area power network LFC. Nevertheless, due to the limitations of such control techniques, they cannot dampen out large fluctuations. Using linear matrix inequality, a mathematical model of a single-area system was developed to optimize the LFC’s resilience and reliability [79].

Table 1. Merits, demerits, and applications of various controllers.

Controllers	Advantages	Disadvantages	Applications	References
Model predictive control	Improved transient performance. Suitable for dealing with multivariable control systems. Simple and more efficient in terms of energy saving. Forecast for an upcoming disturbance. Employing time delays to regulate slow-moving operations	Time-consuming, sophisticated algorithm is required. Various models are restricted to merely steady, open-loop processes. Significant number of model parameters are required to characterize a response. Incorrect formulation of the prediction horizon will result in unsatisfactory control performance.	Chemical plants Steam pressure control Product processing Oil refineries Unmanned aerial vehicles Irrigation systems	[82,83,84,85]
Sliding mode control	Fast response time and simple practical implementation. Robust to unanticipated parameter changes and external disturbances. Effective against parameter uncertainty. Suitable for highly non-linear systems.	Only supports single-input systems. Difficult to handle complex plants. Change the existing system to a more specific and lower-order system. Sliding manifold is subjected to high-frequency oscillations.	Power Converters Electric drive Microcontroller Cooling Tower Unmanned aerial vehicles	[85,86,87,88]
Classical	Cost-effective and easy to design. The controller is not reliant on the processes. Well-researched and widely applied. Quick error correction leads to rapid process adjustments.	Relatively limited range of stability. Fine-tuning on a regular basis may affect longevity and robustness. Sensitive to variations in the gains of the controller. Not feasible to use with slow-changing variables. Lead to instability if not correctly tuned.	Industrial control Speed control Power converter Automobiles Power supply	[85,89,90]
Cascaded Control	Employ an additional controller to swiftly reduce disturbances that enhance the final output. Adapting more quickly to several disturbances. Minimizes the system’s dead time and phase lag time. Combines data from multiple sensors.	More tools and components are needed, which increases the cost of the systems. As additional parameters are needed, tuning becomes more challenging. Sensor failures can be highly sensitive. Might not offer the simplest solution for every circuit.	Boiler temperature control Heat exchanger’s flow rate Industrial heating processes Drum level control Material Dryer Process	[91,92,93]

Table 1. Merits, demerits, and applications of various controllers.

Controllers	Advantages	Disadvantages	Applications	References
Model predictive control	Improved transient performance. Suitable for dealing with multivariable control systems. Simple and more efficient in terms of energy saving. Forecast for an upcoming disturbance. Employing time delays to regulate slow-moving operations	Time-consuming, sophisticated algorithm is required. Various models are restricted to merely steady, open-loop processes. Significant number of model parameters are required to characterize a response. Incorrect formulation of the prediction horizon will result in unsatisfactory control performance.	Chemical plants Steam pressure control Product processing Oil refineries Unmanned aerial vehicles Irrigation systems	[82,83,84,85]
Sliding mode control	Fast response time and simple practical implementation. Robust to unanticipated parameter changes and external disturbances. Effective against parameter uncertainty. Suitable for highly non-linear systems.	Only supports single-input systems. Difficult to handle complex plants. Change the existing system to a more specific and lower-order system. Sliding manifold is subjected to high-frequency oscillations.	Power Converters Electric drive Microcontroller Cooling Tower Unmanned aerial vehicles	[85,86,87,88]
Classical	Cost-effective and easy to design. The controller is not reliant on the processes. Well-researched and widely applied. Quick error correction leads to rapid process adjustments.	Relatively limited range of stability. Fine-tuning on a regular basis may affect longevity and robustness. Sensitive to variations in the gains of the controller. Not feasible to use with slow-changing variables. Lead to instability if not correctly tuned.	Industrial control Speed control Power converter Automobiles Power supply	[85,89,90]
Cascaded Control	Employ an additional controller to swiftly reduce disturbances that enhance the final output. Adapting more quickly to several disturbances. Minimizes the system’s dead time and phase lag time. Combines data from multiple sensors.	More tools and components are needed, which increases the cost of the systems. As additional parameters are needed, tuning becomes more challenging. Sensor failures can be highly sensitive. Might not offer the simplest solution for every circuit.	Boiler temperature control Heat exchanger’s flow rate Industrial heating processes Drum level control Material Dryer Process	[91,92,93]

5. Using Soft Computing to Implement Control Techniques

The challenges of balancing customers’ demands with the availability of renewable and conventional power sources are becoming increasingly complicated. Thus, the growing recognition of the importance of frequency regulation in renewable and conventional power networks has resulted in a particular focus on soft computing techniques. The concept of soft computing, in contrast to hard computing, allows for implicit assumptions, imprecisions, ambiguities, and partial truths [94]. In recent years, soft computing, which is inspired by human brains, has become a popular research and study topic within the LFC scheme of power systems [95,96]. The reason for this predicament is the growing penetration of renewable energies into conventional power systems, which has resulted in an increase in scale and a change in system structure, making it impossible to implement classic LFC schemes. Hence, numerous control theories based on soft computing approaches have been proposed for resilient control and system reconfiguration. Some of these approaches for tuning and optimizing controller settings are as follows:

5.1. Differential Evolution Technique

DE is a heuristic technique for problem optimization that improves a candidate solution in accordance with a predefined competency measure. Such an algorithm requires no assumptions about the underlying optimization problem and may successfully investigate a wide design space while displaying robustness in multi-modal situations. DE differs from other algorithms in the evolution process [97,98]. Figure 5 depicts a flow chart of traditional differential evolution. Using a set of randomly generated initial populations, DE picks two distinct individual vectors from $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d} (\mathrm{0,1})$ according to a predetermined procedure and subtracts them together to produce a unique vector. In the first stage, preliminary parameter vectors are developed, and then the DE algorithm creates new individuals as shown below [98]:

$$x_o=x_{min}+\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}(\mathrm{0,1})(x_{max}-x_{min})$$

(44)

where $x_o{,x}_{min}$, and $x_{max}$ are the initial value, lower bound, and upper bound of search space, respectively. The next phase is the mutation, and the corresponding equation is given below:

$$v_{i,t+1}=x_{r1,t}+F(x_{r2,t}-x_{r3,t})$$

(45)

where $x_{r1,t},x_{r2,t},$ and $x_{r3,t}$ are all separate random individuals, $v_{i,t+1}$ represents the mutant vector, and $F$ is the scaling factor. Crossover is used to improve the diversity of the disturbed parameter vectors, and the following equation describes the trail vector $(u_{i,t+1}):$

$$u_{i,t+1}=u_{1i,t+1},u_{2i,t+1},u_{3i,t+1},\dots \dots ,u_{Di,t+1}$$

(46)

where

$$u_{k,i,t+1}=\left\{\begin{array}{r}{u}_{ki,t+1}| if {rand}_{k,i}\le CRork=I_{rand}\\ x_{ki,t}| if {rand}_{k,i}>CRork\ne I_{rand}\end{array}\right.$$

(47)

${rand}_{k,i},CR,I_{rand}$ represent the kth iteration of the regular random number, the crossover constant, and the arbitrarily chosen index 1, 2, ……,D. Several studies have examined DE for LFC to determine the optimal parameter settings for network stability. A PID controller with an optimum controller configuration was used in conjunction with a DE algorithm to ensure that LFC can be carried out efficiently in a regionally integrated power network that includes wind energy [99]. Similarly, a DE-based fuzzy-PID was presented for the LFC of conventional power networks with system fluctuations and modest load disturbances [25]. Using the DE, the authors in [67] developed a resilient FO-PIλD controller for a three-area power system that considers peak undershoots, convergence speed, and physical constraints. In reference [100], fuzzy and DE were combined to determine the optimum parameters of adaptive FOPID, which were evaluated for LFC problems during load disturbances.

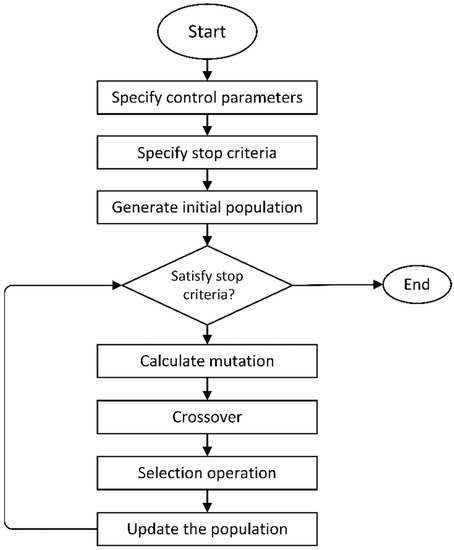
Figure 5. Flow chart of traditional DE [101].

5.2. Genetic Algorithm Technique

The GA is a stochastic selection-based approach for addressing non-linear, non-differentiable, irregular, and uncontrolled multi-objective optimization problems. The GA is continuously changing the population of candidate solutions, and at every phase, the GA picks out the best individuals in the existing population to be parents and employs them to produce offspring for the subsequent generation. Figure 6 depicts a flow diagram of a conventional GA. There have been several studies that investigated the effectiveness of GA for LFC to determine optimal parameter settings that help ensure network stability. A GA-based LFC for an EV microgrid was presented, and an assessment of a PID controller under uncertain conditions was performed to demonstrate system robustness [102]. Ref. [103] presented a GA-optimized FLC for frequency control in a dual-area thermal and solar power plant. In terms of dynamic performance, the suggested controller outperformed the PID, fuzzy logic, and GA-tuned PID controllers. For both conventional and unconventional microgrid systems with concurrent source and load fluctuations, a GA-optimized PI/PID controller was compared to the MPC design [62]. In [67], the DE and GA performances for three-area conventional power systems were examined, and a number of non-linear constraints such as GDB, GRC, and fuel dynamics were included. Similarly, the performance of a double-chain quantum GA on multi-area power systems was evaluated through application to real-world systems and its ability to handle non-linear constraints [104].

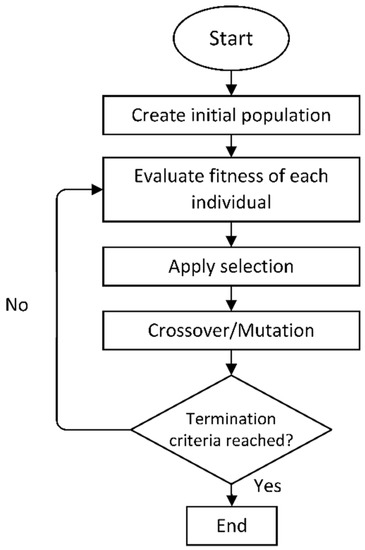
Figure 6. Flow chart of a traditional GA [105].

5.3. Particle Swarm Algorithmic Technique

PSO is one of the strategies inspired by the movements of flocks of birds and schooling fish, and it is used to determine the best candidate solution using bio-inspired techniques. The advantage of this optimization approach is that it just requires the objective function and is unaffected by the gradient, implying that the problems do not need to be differentiable. PSO is quite comparable to evolutionary computation approaches [106,107]. The system is seeded with a population of stochastic solutions, and the optimal response is discovered through iterative upgrades. To find the optimum response, the particles in the swarm move according to their previous optimal $(pbest)$ and global optimal $(gbest)$ positions. Figure 7 depicts the flowchart of a traditional PSO technique.

$$pbest\left(i,t\right)=\begin{array}{cc}\mathrm{a}\mathrm{r}\mathrm{g} \mathrm{m}\mathrm{i}\mathrm{n}\left[f\left(P_i\left(k\right)\right)\right],& iϵ\{\mathrm{1,2},\dots \dots {,N}_p\}\\ k=\mathrm{1,2},\dots \dots ,t& \end{array}$$

(48)

$$gbest\left(t\right)=\begin{array}{cc}\mathrm{a}\mathrm{r}\mathrm{g} \mathrm{m}\mathrm{i}\mathrm{n}\left[f\left(P_i\left(k\right)\right)\right],& iϵ\{\mathrm{1,2},\dots \dots {,N}_p\}\\ k=\mathrm{1,2},\dots \dots ,t& \end{array}$$

(49)

where $i,N,t,f, \mathrm{a}\mathrm{n}\mathrm{d} P$ denote the particle index, particle counts, current iteration’ number, fitness value, and position. Similarly, the below equation governs the velocity ($V)$ and position $(P)$ of each particle in the PSO:

$$V_i(t+1)=\omega V_i(t)+c_1{r}_1(pbest\left(i,t\right)-P_i(t))+c_2{r}_2(gbest\left(t\right)-P_i\left(t\right))$$

(50)

$$P_i\left(t+1\right)=P_i\left(t\right)+V_i(t+1)$$

(51)

where $c_1$ and $c_2$ represent two constants; $\omega$ is the inertia weight; $P_i$ is the best prior position of the ith individual, respectively. Similarly, $r_1$ and $r_2$ both represent a random number generated independently from the other. Several studies examined the performance of PSO for LFC to optimize controller settings for network stability. The authors in [5] provided a method for regulating the pitch angle of WTGs and EVs for LFC in a microgrid system while simultaneously tuning the parameters of MPC using PSO. A T-MPC was designed to regulate the frequency of renewable-penetrated power systems that contain a significant number of EVs [57]. During this process, the PSO algorithm was applied to tune the parameters to find the optimum solution. Similarly, [52] demonstrated the performance of a composite bacterial foraging-PSO tuned PI/PID controller in an LFC non-linear integrated power system with conventional and non-conventional energy sources. The authors compared a PSO-optimized PID controller with a layered recurrent ANN in a dual-area wind-integrated power system [26]. Also, an SMC design approach was proposed for frequency control in an integrated power system, and controller parameters were derived using GWO and PSO methods to achieve an optimal outcome [71].

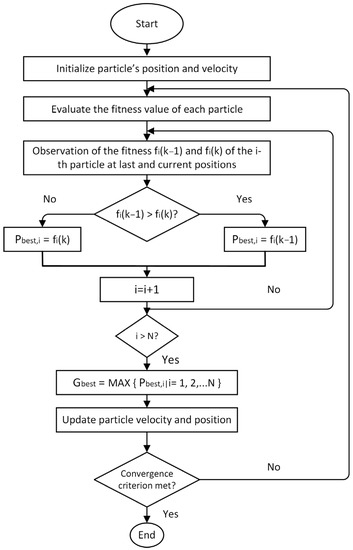
Figure 7. Flow chart of a traditional PSO [108].

5.4. Artificial Intelligence (AI) Control Techniques

As more renewable energy sources, such as wind and solar, are added to power networks, conventional control may not be able to provide the level of precision required. When it comes to addressing this challenge, AI control methods including ANN and fuzzy logic control have been shown to be particularly effective. An ANN is a learning mechanism that uses a network of connected nodes or neurons to replicate the structure of the human mind [109,110]. An ANN may be programmed to identify trends, categorize data, and anticipate future occurrences based on the data it has been provided. Figure 8 is a flowchart illustrating the ANN algorithm applied in the model’s development. The multilayer perceptron ANN systems were designed have a generic shape:

$$R_y=V_o+{\sum }_{j=1}^{N_h}{V}_{j}f\left(w_{oj}+{\sum }_{i=1}^{N_i}{w}_{ji}{u}_1\right)$$

(52)

where $R_y,u_1,N_i,w_{ji},f,N_h$, and $V_j$ indicate the system outputs, system inputs, multilayer perceptron inputs, weight of $i$ input to $j$ hidden layer neuron, activation function constant, and the number of hidden neurons, respectively. Numerous studies have employed fuzzy logic and ANN to develop autonomous controllers for the LFC in the power system [20,25,26,27,111]. In a triple-connected system, an ANN controller was utilized to adjust the PI controller’s gain, which enhances the LFC’s transient response [111]. Owing to the resilience and durability of fuzzy logic, it has been utilized to solve complex variable structure problems that conventional control systems cannot effectively resolve. An FLC [25] based on DE has shown excellent performance in the LFC problem of power systems; however, there are certain limitations in terms of MFs and criterion selection. These constraints may be overcome through the use of a multilayer recurring ANN coupled with a regressive and adjustable control mechanism [26], but this adds considerable computing complexity to the system. For enhanced dynamic performance in today’s power systems, the authors in [27] proposed FLC in conjunction with conventional PI/PID controllers using a novel TLBO approach. Also, the authors in [20] compared the LFC capabilities of ANFIS, ANN, and fuzzy controllers, and the results indicate that the ANFIS controller improves dynamic response, including efficient execution, reduced fault magnitudes, and lower transitory frequency.

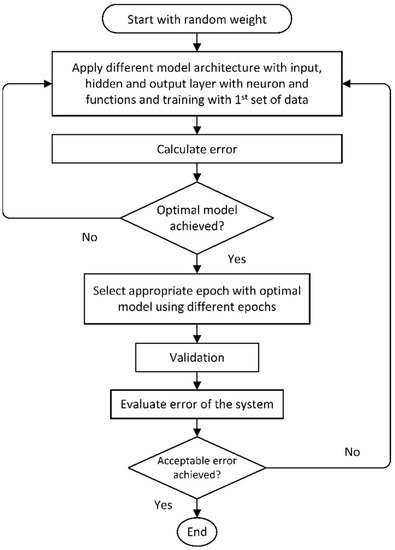
Figure 8. Flow chart of a traditional ANN [112].

5.5. Fuzzy Logic Approach

In recent years, an FL strategy for regulating system behavior has revived research interest due to its wide operating range and reasonable response times. More control scheme implementations are expected for complex power systems due to FL’s robustness, reliability, and capability to address difficulties without comprehending the mathematical functions of the system [12]. The FL control is made up of four major elements: the fuzzifier, the inference system, the rule base, and the de-fuzzifier, as shown in Figure 9. The fuzzifier converts numerical input into fuzzy sets, while the inference engine carries out all logic operations in FLC. The rule base is made up of MF and control rules, and the de-fuzzifier converts again the fuzzy set to numerical values. Various studies examined the dynamics of FL for LFC to optimize controller settings for network stability. A fuzzy-based SMC has been developed to deal with the maximum boundary limit of disturbances and instabilities in second-order systems [29]. The FL control system simulates the switching control law, which reduces disturbances and instabilities while eliminating input signal chattering. Reference [34] designed a fuzzy-based two-layer MPC to integrate ESSs in the LFC scheme of three-area power systems while considering a number of operational and physical constraints. Similarly, for the LFC of a hybrid system comprising conventional and non-conventional power sources, an IDD tuned by FL was used to examine the system’s performance and response to disturbances [80].

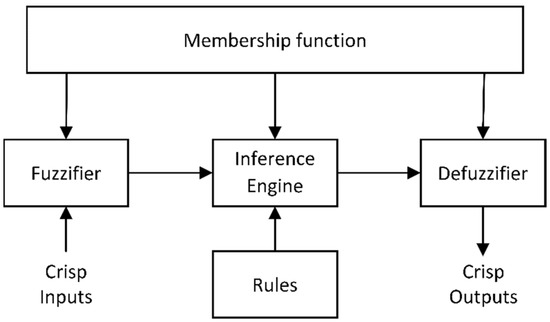
Figure 9. Flow chart of a traditional FL [113].

5.6. Moth-Flame Optimization Technique

The MFO technique was created in 2016 as one of the key attempts to simulate moth movement in computers and give an optimization strategy. Figure 10 depicts a traditional MFO algorithm’s flowchart. MFO determines the candidate solutions as moths, with their locations in space as the solution variable. Consequently, moths may fly in 1D, 2D, 3D, or multidimensional environments by altering their position vectors. Both moths and flames are viable solutions, but the difference lies in how we manage and adjust them during each cycle. The array of moths (M) and flames (F), as well as their fitness value vectors (OM, OF), may be expressed as follows [114]:

$$M=\left[\begin{array}{ccc}{m}_{\mathrm{1,1}}& \cdots & m_{1,d}\\ ⋮& \ddots & ⋮\\ m_{n,1}& \cdots & m_{n,d}\end{array}\right]$$

(53)

$$OM=\left[\begin{array}{c}{OM}_1\\ \begin{array}{c}{OM}_2\\ ⋮\end{array}\\ {OM}_n\end{array}\right]$$

(54)

$$F=\left[\begin{array}{ccc}{f}_{\mathrm{1,1}}& \cdots & f_{1,d}\\ ⋮& \ddots & ⋮\\ f_{n,1}& \cdots & f_{n,d}\end{array}\right]$$

(55)

$$OF=\left[\begin{array}{c}{OF}_1\\ \begin{array}{c}{OF}_2\\ ⋮\end{array}\\ {OF}_n\end{array}\right]$$

(56)

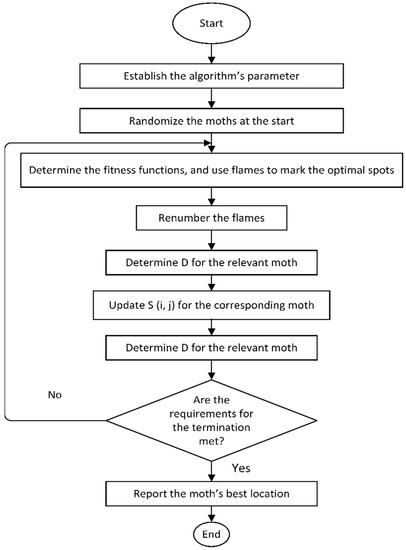
Figure 10. Flow chart of a traditional MFO [115].

In this case, $n \mathrm{a}\mathrm{n}\mathrm{d} d$ indicate the number of moths and control variables required, respectively. In the same way, the position of each moth relative to a flame can be determined by considering the following equation when studying a moth’s flying behavior:

$$M_j=S(M_j,F_k)$$

(57)

$M_j,F_k, \mathrm{a}\mathrm{n}\mathrm{d} S$ indicate the jth moth, kth flame, and helical function, respectively. The helical function is represented as:

$$S\left(M_j,F_k\right)=D_j·e^{bt}·cos(2\pi t)+F_k$$

(58)

$$t=(a-1)\ast rand+1$$

(59)

$$a=-1+Iteration\ast (-\frac{1}{T_{max}})$$

(60)

$$D_j=F_k-M_j$$

(61)

$D_j$, $b$, $t$, $T_{max}$, and $a$ are the linear distance, logarithmical helix shape constant, path coefficient, the maximum number of iterations, and constant, respectively. The performance of MFO for LFC has been analyzed in several studies to determine the appropriate settings for controllers. In [23], LFC was structured for multi-area power systems.

The MFO technique was employed to tune the PI controller and the WTG frequency regulator for optimum performance. Reference [24] employed MFO and PID techniques to design blade pitch controllers (BPC) to regulate voltage and power output oscillations, demonstrating the MFO technology’s efficacy. An algorithm that tunes the BPC’s settings was only applied to one wind turbine. An MFO-optimized 2-DOF PID controller was designed for frequency regulation of dual-areas interconnected power systems [116]. In addition, a comparison was performed between the MFO-optimized controller and the GA and cuckoo search algorithms (CSA). Similarly, an MFO was developed to optimize the controller parameters for the LFC of a two-area power system, and the algorithm’s performance was evaluated using sensitivity analysis in the presence of loaded scenarios and network instabilities [117].

5.7. Other Soft Computing Approaches

LFC solutions based on various recently developed soft computing approaches have been proposed for both conventional and unconventional power systems. For instance, a customized variant of the BA along with FL was used to obtain optimal results from a traditional PI controller for LFC in four-area systems [69]. For a concurrent variation in wind output and load fluctuation, a moth swarm algorithm (MSA)-tuned PI-PD controller for LFC of an integrated power system was designed and tested [74]. Using an MVO-optimized 3DOF-PID controller, the authors in [72] addressed the dynamic controller design challenge of a four-region integrated power system. The authors in [71] proposed an SMC controller for frequency regulation in an integrated power system, and the grey wolf optimization (GWO) technique was employed to build sliding surface parameters. The authors in [118] addressed the usage of an artificial bee colony (ABC) to give synchronized frequency management to a decentralized sustainable energy microgrid system. A novel LFC approach for interconnected power systems using biogeography-based optimization (BBO) was presented in [119] to improve controller settings. Three optimization techniques for adjusting controller settings in a dual-area power system were proposed, and the findings demonstrate that teaching-learning-based optimization (TLBO) had the highest performance during the dynamic test period [63]. To optimize the gains of an IDD controller, a sophisticated magnetotactic bacteria optimization (MBO) algorithm was being developed [80]. Various system changes, such as load disturbances, overloading, and solar irradiation, have been shown to demonstrate the robustness of the MBO-optimized IDD controller. Furthermore, a chimp optimization algorithm (COA) was used to fine-tune the constraints on the robust MPC controller design, and the controller design’s performance was demonstrated for a multi-area power system [19]. A newly developed water cycle algorithm (WCA) was also evaluated for its performance when used for configuring the TI-TID for LFC in a deregulated power system [81].

Table 2 provides an overview of recent controllers and soft computing tools developed for LFC conventional and renewable integrated power networks. Different controllers and soft computing techniques have been used for both conventional and renewable energy integrated power systems. Some authors have provided a detailed description of a wind-integrated power system, while others have focused on conventional power. The table also shows that further research on the LFC of wind-integrated power systems is required to develop more robust systems capable of supporting the anticipated growth in wind power production.

Table 2. A comparison of numerous studies on the LFC scheme.

References	Power System Types	Source of Generation	Controller Types	Soft Computing	Advantages	Disadvantages
[5]	Hybrid	Thermal, WTs, PHEV	MPC	-	Robust to parameter variations	Excludes short-term frequency stabilization
[7]	Hybrid	Steam, WTs, Generators	Deep reinforcement learning	-	Faster response speed, System dynamics adaptability	Incorporate offline training of agents, Heavy communication burdens
[11]	Hybrid	Thermal, WTs,	Pitch angle frequency control	-	Smooth WTG output power, Used less equipment	Force unsafe turbine operation, Increasing the WTG’s energy costs
[13]	Hybrid	Thermal, Gas units, Hydraulic, WTs, BSS	Centralized integral controller	-	Effective at all wind speeds, Robust to non-linearities	Costly for large power system operation
[14]	Hybrid	Thermal, Hydro, WTs, BSS	PI cascade	-	Reduce frequency fluctuations, Ensuring the reactive and active power adjustment	Non-linearities and WTG penetration levels are not considered
[16]	Hybrid	Thermal, Hydro, Solar, WTs, EV	FOPID, TID	Artificial ecosystem optimization	Increased robustness, Enhanced system stability for parameter uncertainty, Fast response during transients	Cross-area power balance is difficult to accomplish, Unable to dampen large fluctuations
[19]	Hybrid	Thermal, Wind	MPC, LQG	Chimp optimization algorithm	Robustness to system non-linearities and uncertainties, Support high wind power penetration	-
[20]	Hybrid	Hydro, Thermal	ANFIS	Fuzzy and Neural	Improves dynamic response, Reduces fault magnitudes, and lower transitory frequency	WTG penetration and its impact on LFC are ignored
[22]	Conventional	Thermal, EVs	H2/H∞	Linear matrix inequalities	Robustness to load fluctuation and parameter uncertainties	WTG penetration and its impact on LFC are ignored, Lacks peak-hour voltage transient or other constraints support
[24]	Hybrid	Thermal, WTs	PID	MFO	Adaptable to local and large-scale uncertainty	Load disturbances and system non-linearity reduce efficiency
[25]	Conventional	Thermal, Hydro, Gas	Fuzzy-PID	Tribe-DE	Excellent transient behavior, Resilience to disturbance, Robust to parameter variations	WTG penetration and its impact on LFC are ignored, MFs and criterion selection have certain limitations
[27]	Hybrid	Thermal, Hydro, PHEV	FO-fuzzy-PID	Teaching–learning based optimization	Good response to systems uncertainties and parameter variations	Not considered WTGs for LFC, MFs and baseline rules, might reduce the controller’s transient performance
[34]	Hybrid	Thermal, Solar, WTs, BSS	MPC	Fuzzy logic	Manage distributed power and system constraints, Good response to physical and operational constraints	Increasingly complex when more criteria for evaluation and model parameters are added
[52]	Hybrid	Steam, WTs	PI	Particle swarm optimization, Bacterial foraging algorithm	Reduces the settling time, Adaptable to parameter variations, Eliminate frequency area control error	Multiple disturbances are not evaluated simultaneously, Improperly configured PI/PID controllers may reduce dynamic performance
[54]	Hybrid	Thermal, WTs	SMC	Disrupted oppositional learned gravitational search algorithm	Good frequency response during load disturbances, Requiring less computational effort, Minimizes objective function optimal values	Variations in parameters and physical constraints are not examined, Reduce resilience in regard to time delays
[63]	Renewable	WTs	PID, PIDA	TLBO, Harmony search algorithm, Sine-cosine algorithm	Optimize transient frequency response and tie-line power, Excellent performance for load fluctuations	Increasing parametric uncertainty and plant non-linearities reduce efficiency
[64]	Hybrid	Thermal, Gas, Solar, WTs, EV, HES	Tilt-PID	Quasi Opposition Lion Optimization Algorithm	Reduced settling time. Suitable for varying wind power penetration, Good response to system non-linearity	-
[67]	Conventional	Reheat-Thermal	PIλD	Differential Evolution	Robustness to non-linear constraints and fuel dynamics, Resilience to increased load disturbance, and severe parametric fluctuation	WTG penetration and its impact on LFC are ignored
[68]	Hybrid	Wave, Geothermal, Hydro, Thermal, WTs	TIDN-(1+PI)	-	Lower peak overshoot/undershoot, Increased system-damping factor, Enhanced stability in the presence of numerous non-linearities and load disturbances	PI’s control theory remained unchanged, limiting the system’s adaptability to complex systems
[80]	Hybrid	Thermal, Solar, EV	IDD	Magnetotactic bacteria optimization	Robustness to load disturbances and overloading, Suitable for varying solar penetration	Not considered WTGs for LFC
[69]	Hybrid	Reheat-Thermal, Hydro	PI	Self-Adaptive Modified Bat Algorithm, Fuzzy Logic	Resilience against external disruptions and uncertainties, Optimizes system parameters and MFs concurrently	Unstable optimization outcomes, Tendency to slip into local optimums, WTGs are not considered for LFC
[72]	Conventional	Reheat-Thermal	3DOF-PID	Multi-verse optimization	Improve the design of dynamic controllers, Excellent performance for optimization constraints	WTG penetration and its impact on LFC are ignored
[74]	Renewable	Solar, Flywheel, EV, WTs	PI-PD	Moth Swarm Algorithm	Minimize the grid’s oscillation frequency, Simple design and tuning of the controller	Operational and physical constraints are not considered, Improperly configured PI-PD controller may reduce dynamic performance
[103]	Hybrid	Reheat-Thermal, Solar	FLC	Genetic algorithm	Reduce overshoot and settling time, Excellent dynamic response, Improved results for varied levels of solar energy penetration	WTGs are not considered for LFC, False data could cause unrealistic system efficiency
[104]	Hybrid	Thermal, Hydro, Gas	ADRC	Double chains quantum genetic algorithm	Ability to handle non-linear constraints, Reduce the stabilization time, Ability to handle non-linear constraints	Difficulty in adjusting parameters, Slow rate of convergence, WTGs are not evaluated
[120]	Conventional	Thermal	Fuzzy-PID	Differential evolution	Adaptable to parameter variations, Avoid re-tuning controller parameters under varied loading conditions	WTG penetration and its impact on LFC are ignored, Difficulty in attaining optimum controller gain, Needs considerable training data for implementation
[121]	Hybrid	Thermal, Hydro, Gas, Solar, WTs	PI	Multi-verse optimization	Robustness to loading disturbances, Adaptable to changes in input parameters	Not considering the impact of non-linearities, No detailed analysis of the proposed system, System is susceptible to large staring overshoot, and the controller gains

6. Conclusions

Over the last few decades, there has been an increase in the significance of renewable energy, particularly wind energy, which has placed an additional strain on the LFC capacity of the power system. As a consequence of the fluctuating wind speeds, WTGs are unable to offer continuous load monitoring and control, which may have a substantial effect on the system’s operating frequency. Thus, maintaining frequency stability is critical in minimizing power system failures and turbine blade damage caused by extreme vibrations. This survey examined the frequency stability issues in wind-integrated power systems. The pros and cons of various wind-integrated power system models, as well as the impact of these models on LFC, were examined. Critical factors, such as energy systems, resources, optimization approaches, resilience, and transient stability have been studied to demonstrate the uniqueness of the proposed design. In addition, this paper has outlined current research on LFC control strategies for wind-integrated power systems, including PI/PID/PIDF; SMC; MPC; cascade; and dual phase controllers. Finally, in terms of the LFC issue, many contemporary soft computing approaches including DE, GA, PSO, ANN, FL, MFO, and other widely used soft computing tools have been explored. The analysis concluded that although there have been significant advancements in control and optimization techniques, these techniques still have deficiencies that impact the operation of real power systems. Furthermore, these approaches did not account for the high level of wind energy integration in the future power system. Therefore, additional research on the LFC of wind-integrated power systems is necessary to develop more resilient systems capable of sustaining the anticipated increase in wind power production.

Future power systems may face frequent stability issues due to rising load demands and greater integration of renewable energy sources, notably wind and solar. Therefore, a modern control mechanism with appropriate optimization approaches that account for varying load demands and renewable energy penetrations are required to mitigate LFC concerns. Given the potential future of LFC research and the fact that wind and solar energies together account for more than 10% of global electricity production, it is imperative that a comparative study be conducted to analyze advanced controllers and optimization strategies for both wind- and solar-integrated power systems.