Study on Height Prediction of Water Flowing Fractured Zone in Deep Mines Based on Weka Platform

Abstract

Accurately predicting the height of water flowing fractured zone is of great significance to coal mine safety mining. In recent years, most mines in China have entered deep mining. Aiming at the problem that it is difficult to accurately predict the height of water flowing fractured zone under the condition of large mining depth, the mining depth, height mining, inclined length of working face and coefficient of hard rock lithology ratio are selected as the main influencing factors of the height of water flowing fractured zone. The relationship between various factors and the height of water flowing fractured zone is analyzed by SPSS software. Based on the data mining tool Weka platform, Bayesian classifier, artificial neural network and support vector machine model are used to mine and analyze the measured data of water flowing fractured zone, and the detailed accuracy, confusion matrix and node error rate are compared. The results show that, the accuracy rate of instance classification of the three models is greater than 60%. The accuracy of the artificial neural network model is the highest and the node error rate is the lowest. In general, the training effect of the artificial neural network model is the best. By predicting engineering examples, the prediction accuracy of the model reaches 80%, and a good prediction effect is obtained. The height prediction system of water flowing fractured zone is developed based on VB language, which can provide a reference for the prediction of the height failure grade of water flowing fractured zone.

1. Introduction

After the mining of the coal seam, under the action of the mine pressure, the overlying roof strata will move, which will lead to the fissure and fracture of the rock strata. According to the theory of “upper three zones” [1], the water flowing fractured zone refers to the sum of the caving zone and the fracture zone. The fracture channel is easily formed in the water flowing fractured zone. Once these fractures are penetrated, the water-conducting channel will be formed, which will lead to the increase of mine water inflow, which will lead to water inrush and other mine flood accidents, which will seriously threaten the safety of coal mining. Therefore, it is very important for coal mine safety production to accurately predict the development height of water flowing fractured zone.

Domestic and foreign research focus on the development height of water flowing fractured zone after coal mining. In order to ensure the safe mining under the aquifer, foreign countries have carried out long-term research on this. In the 1970s, Britain formulated regulations on coal mining under water bodies; in 1973, Russian researchers also proposed the calculation method of the height of the water flowing fractured zone and formulated the safety regulations for mining under water bodies; Japan has more than ten mines threatened by water damage, developed a special waterproof measure, for the composition and thickness of alluvium developed a safety procedure [2]. At present, the empirical formula given in ‘Regulations of Buildings, Water Bodies, Railways, Main Roadway Coal Pillar Setting and Coal Mining’ [3] is widely used in the calculation formula of water flowing fractured zone in China. These empirical formulas only consider the influence of mining thickness on the height of water flowing fractured zone, and are obtained by regression statistics. For example, the calculation formula of the height H_f of water flowing fractured zone in hard rock is as follows:

$$H_f=\frac{100{\displaystyle \sum M}}{1.2{\displaystyle \sum M+2.0}}\pm 8.9$$

(1)

or

$$H_f=30\sqrt{{\displaystyle \sum M}}+10$$

(2)

In the formula: $M$ is mining thickness.

With the continuous exploitation of coal resources, many mines in China have entered the deep mining stage of coal resources [4,5,6]. For example, the maximum mining depth of Suncun Coal Mine in Xinwen Coalfield has even reached 1350 m [7]. A large number of studies have shown [8,9,10,11,12] that the factors affecting the height of water flowing fractured zone are buried depth of coal seam, inclined length of working face, coefficient of hard rock lithology ratio and mining advance speed. Therefore, it is obviously unreasonable to use the empirical formula to calculate the height of the water flowing fractured zone.

V. Palchik [13,14,15,16] used the method of borehole detection to study the crack development law of overlying strata after coal mining in Donetsk coalfield, Ukraine, and divided the overlying strata into three zones, namely caving zone, fractured zone and continuous deformation zone. Domestic scholars mainly use theoretical analysis [17,18,19,20,21], numerical simulation [22,23,24] and similar material simulation [25,26,27,28], field measurement [29,30] and other methods to study the height of water flowing fractured zone. The calculation method in the ‘three under’ regulation is simple, but only one influencing factor of coal seam mining thickness is considered. Due to the large difference of mine occurrence conditions, it is only suitable for preliminary estimation. The theoretical calculation and numerical simulation method are better than the calculation method in the procedure, but there are shortcomings such as single calculation and simple model. The accuracy of similar material simulation test and field measurement is high, but the workload is heavy, the operation is complex and the cost is high. The prediction method proposed in this paper has comprehensive considerations, simple operation and high prediction accuracy. In this paper, on the basis of previous studies, collected 43 groups of coal seam mining depth greater than 400m of water flowing fractured zone development height of the measured data, using SPSS software to analyze the various factors and water flowing fractured zone relationship. Based on the data mining tool Weka platform, Bayesian classifier, artificial neural network and support vector machine model are used to mine and analyze the measured data of water flowing fractured zone. After comparing and analyzing the three models, the optimal model is obtained and the engineering example is predicted.

2. Modeling

In order to realize the accurate prediction of the height of the water flowing fractured zne [31,32,33], the prediction process is constructed, as shown in Figure 1.

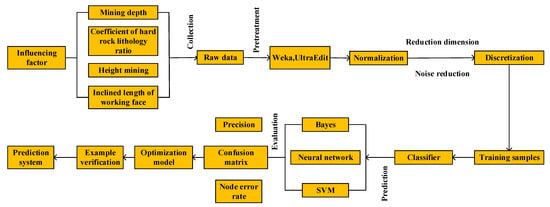
Figure 1. Prediction procedure.

2.1. Selection of Raw Data

By collecting and collating the actual data of the observation of the water flowing fractured zone in China, four influencing factors of mining depth, coefficient of hard rock lithology ratio, height mining and inclined length of working face are selected. Finally, 43 [34] sets of original data of water flowing fractured zone are selected. The first 33 sets of data are used as training samples. The specific data are shown in Table 1, and the last 10 sets of data are used as prediction samples. It can be seen from Table 1 that the mining depth of coal seam is mainly between 400~700 m, the thickness of coal seam is mainly medium thick coal seam and thick coal seam, and the inclined length of working face is between 110~230 m.

Table 1. Raw data.

Serial Number	Mining Depth s/m	Coefficient of Hard Rock Lithology Ratio b	Height Mining M/m	Inclined Length of Working Face l/m	Height of Water Flowing Fractured Zone H/m
1	412.4	0.09	2.2	157	35.4
2	489	0.47	4.5	160	54.79
3	472.5	0.53	4.5	132	57.45
4	424.42	0.26	3.4	120	45.1
5	590	0.51	9	220	76.37
6	420.5	0.52	3	209	52.01
7	649.1	0.23	3	186	42.99
8	475.2	0.28	3.9	209	49.05
9	568.6	0.65	3.65	132	60.14
10	557.25	0.45	5.8	186	65.25
11	412.55	0.08	2.2	157	35.2
12	679	0.46	2.1	180	44.54
13	403.2	0.1	1.8	120	22
14	665	0.19	7.5	222	70.3
15	433	0.52	7	168	47.55
16	434.1	0.35	3	145	38.41
17	485	0.36	4.8	175	43.43
18	441.97	0.36	3.4	120	28.63
19	437.17	0.05	3.4	120	86.4
20	463	0.62	7.6	116	22.61
21	403.1	0.08	2	136	57.49
22	476.4	0.63	3.65	132	55
23	515.7	0.35	4.5	147	86.8
24	450	0.72	8	170	51.4
25	499.9	0.47	4.8	150	45
26	490	0.52	4	135	45
27	420.06	0.14	3	145	30.29
28	516	0.74	2.95	206.1	54.5
29	434.4	0.46	3.4	136	45.1
30	445.4	0.07	4	195	38.81
31	499.92	0.47	4.8	150	54
32	419.03	0.16	3	145	32.83
33	550	0.81	2.4	180	55.32

2.2. Correlation Analysis

In order to study the development height of water flowing fractured zone under large buried depth (mining depth >400 m), mining depth (X₁), coefficient of hard rock lithology ratio (X₂), height mining (X₃) and inclined length of working face (X₄) are selected as the main influencing factors.

(1)

Mining depth

According to the theory of mine pressure control, in a certain range, the greater the mining depth, the greater the mine pressure, mine pressure is proportional to the size and depth of coal mining.

(2)

Coefficient of hard rock lithology ratio

The coefficient of hard rock lithology ratio refers to the ratio of hard rock to statistical height above the roof of coal seam. The hard rock participating in the statistics refers to sandstone, mixed rock and igneous rock. The specific calculation formula is as follows:

$$b=\frac{{\displaystyle \sum h}}{(15~20)M}$$

(3)

In the formula: $M$ is height mining; ${\displaystyle \sum h}$ is the cumulative thickness of hard rock strata within the height range of the estimated water flowing fractured zone.

(3)

Mining thickness

When the working face advances, periodic pressure will be generated, resulting in roof caving. With the increase of coal seam mining thickness, the plastic zone of overlying strata becomes larger, resulting in the height of caving zone is also larger.

(4)

Inclined length of working face

Before the coal seam is fully mined, the development height of the water flowing fractured zone gradually increases with the mining of the working face; when the coal seam is fully mined, the influence of the inclined length of the working face on the development of the high belt is not obvious.

In order to determine the relationship between the influencing factors and the height of the water flowing fractured zone, each scatter plot was established for research [35,36,37,38,39]. It can be seen from Figure 2 that there is a certain linear relationship between the mining depth (Figure 2a), the coefficient of hard rock lithology ratio (Figure 2b), the height mining (Figure 2c) and the inclined length of working face (Figure 2d) and the height of the water flowing fractured zone (y), as shown below:

y₁ = 0.083X₁ + 9.009

(4)

y₂ = 12.103X₂ + 44.711

(5)

y₃ = 2.667X₃ + 38.359

(6)

y₄ = 0.142X₄ + 26.698

(7)

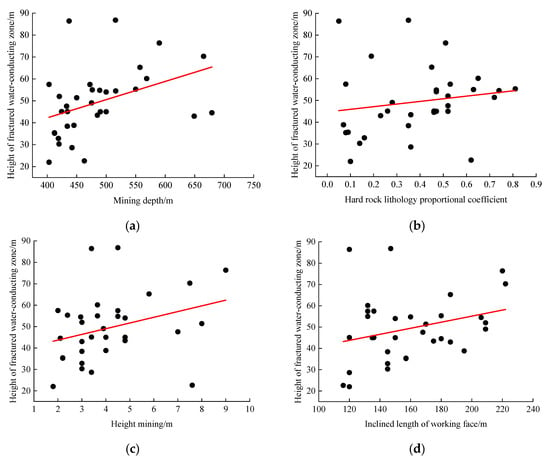
Figure 2. Relationship between influencing factors and height of water flowing fractured zone.

2.3. Normalization

In order to better retain valid data, it is necessary to reduce the dimension and noise of the raw data, that is, normalization and discretization. The purpose of normalization is to concentrate the values between 0 and 1, and the specific results are shown in Table 2. The normalized calculation formula is as follows:

$$Gij=\frac{Xij-\min (Xj)}{\max (Xj)-\min (Xj)}$$

(8)

In the formula: $Xij$ is the sample before normalization, $Gij$ is the normalized sample, $\min (Xj)$ is the minimum value in the original sample, $\max (Xj)$ is the maximum value in the original sample.

Table 2. Normalization results.

NO	X1	X2	X3	X4	Y
1	0.034	0.053	0.056	0.387	35.400
2	0.311	0.553	0.375	0.415	54.790
3	0.252	0.632	0.375	0.151	57.450
4	0.077	0.276	0.222	0.038	45.100
5	0.677	0.605	1.000	0.981	76.370
6	0.063	0.618	0.167	0.877	52.010
7	0.892	0.237	0.167	0.660	42.990
8	0.261	0.303	0.292	0.877	49.050
9	0.600	0.789	0.257	0.151	60.140
10	0.559	0.526	0.556	0.660	65.250
11	0.034	0.039	0.056	0.387	35.200
12	1.000	0.539	0.042	0.604	44.540
13	0.000	0.066	0.000	0.038	22.000
14	0.949	0.184	0.792	1.000	70.300
15	0.108	0.618	0.722	0.491	47.550
16	0.112	0.395	0.167	0.274	38.410
17	0.297	0.408	0.417	0.557	43.430
18	0.141	0.408	0.222	0.038	28.630
19	0.123	0.000	0.222	0.038	86.400
20	0.217	0.750	0.806	0.000	22.610
21	0.000	0.039	0.028	0.189	57.490
22	0.266	0.763	0.257	0.151	55.000
23	0.408	0.395	0.375	0.292	86.800
24	0.170	0.882	0.861	0.509	51.400
25	0.351	0.553	0.417	0.321	45.000
26	0.315	0.618	0.306	0.179	45.000
27	0.061	0.118	0.167	0.274	30.290
28	0.409	0.908	0.160	0.850	54.500
29	0.113	0.539	0.222	0.189	45.100
30	0.153	0.026	0.306	0.745	38.810
31	0.351	0.553	0.417	0.321	54.000
32	0.058	0.145	0.167	0.274	32.830
33	0.532	1.000	0.083	0.604	55.320

Table 2. Normalization results.

NO	X1	X2	X3	X4	Y
1	0.034	0.053	0.056	0.387	35.400
2	0.311	0.553	0.375	0.415	54.790
3	0.252	0.632	0.375	0.151	57.450
4	0.077	0.276	0.222	0.038	45.100
5	0.677	0.605	1.000	0.981	76.370
6	0.063	0.618	0.167	0.877	52.010
7	0.892	0.237	0.167	0.660	42.990
8	0.261	0.303	0.292	0.877	49.050
9	0.600	0.789	0.257	0.151	60.140
10	0.559	0.526	0.556	0.660	65.250
11	0.034	0.039	0.056	0.387	35.200
12	1.000	0.539	0.042	0.604	44.540
13	0.000	0.066	0.000	0.038	22.000
14	0.949	0.184	0.792	1.000	70.300
15	0.108	0.618	0.722	0.491	47.550
16	0.112	0.395	0.167	0.274	38.410
17	0.297	0.408	0.417	0.557	43.430
18	0.141	0.408	0.222	0.038	28.630
19	0.123	0.000	0.222	0.038	86.400
20	0.217	0.750	0.806	0.000	22.610
21	0.000	0.039	0.028	0.189	57.490
22	0.266	0.763	0.257	0.151	55.000
23	0.408	0.395	0.375	0.292	86.800
24	0.170	0.882	0.861	0.509	51.400
25	0.351	0.553	0.417	0.321	45.000
26	0.315	0.618	0.306	0.179	45.000
27	0.061	0.118	0.167	0.274	30.290
28	0.409	0.908	0.160	0.850	54.500
29	0.113	0.539	0.222	0.189	45.100
30	0.153	0.026	0.306	0.745	38.810
31	0.351	0.553	0.417	0.321	54.000
32	0.058	0.145	0.167	0.274	32.830
33	0.532	1.000	0.083	0.604	55.320

2.4. Discretization

The discretization is divided into supervised and unsupervised discretization of numerical attributes, which is used to discretize some numerical attributes in the data set to the classification attributes. The ‘mining depth’, ‘coefficient of hard rock lithology ratio’, ‘height mining’ and ‘inclined length of working face’ are equidistantly divided into 3 sections. Similarly, the height of water flowing fractured zone is also divided into 3 sections, 0~40 m is denoted by ‘1’ (water flowing fractured zone height grade ‘low’), 40~60 m is denoted by ‘2’ (water flowing fractured zone height grade ‘medium’), >60 m is denoted by ‘3’ (water flowing fractured zone height grade ‘high’). The calculation formula of discretization is as follows:

$$Lij=\{\begin{array}{cccc}& Q=\frac{\max (Gj)-\min (Gj)}{3}& & \\ 0,& \min (Gj)<Gij<\min (Gj)+Q& & \\ 1,& \min (Gj)+Q<Gij<\min (Gj)+2Q& & \\ 2,& \min (Gj)+2Q<Gij<\max (Gj)& & \end{array}$$

(9)

In the formula: $Lij$ is the discretized sample, $\max (Gj)$ is the maximum value of the normalized sample data, $\min (Gj)$ is the minimum value of the normalized sample data, $Q$ is the step size.

The repeated data from the discretization results are as follows: the first group and the 11th group of sample data are repeated, the second group and the 17th group of sample data are repeated, the fourth group and the 21st group of sample data are repeated, the 13th group, the 27th group and the 32nd group of sample data are repeated, the 16th group and the 18th group of sample data are repeated, the 25th group and the 31st group of sample data are repeated, and the 26th group and the 29th group of sample data are repeated. The first group, the second group, the fourth group, the thirteenth group, the sixteenth group, the twenty-fifth group, the twenty-sixth group and the twenty-seventh group were removed, and the remaining 25 groups of data were used as training samples, as shown in Table 3.

Table 3. Training samples.

NO	X1	X2	X3	X4	Y
1	1	2	2	1	2
2	3	2	3	3	3
3	1	2	1	3	2
4	3	1	1	2	2
5	1	1	1	3	2
6	2	3	1	1	3
7	2	2	2	2	3
8	1	1	1	2	1
9	3	2	1	2	2
10	3	1	3	3	3
11	1	2	3	2	2
12	1	2	2	2	2
13	1	2	1	1	1
14	1	1	1	1	3
15	1	3	3	1	1
16	1	1	1	1	2
17	1	3	1	1	2
18	2	2	2	1	3
19	1	3	3	2	2
20	2	3	1	3	2
21	1	2	1	1	2
22	1	1	1	3	1
23	2	2	2	1	2
24	1	1	1	1	1
25	2	3	1	2	2

3. Comparative Analysis of Model Prediction

This paper mainly from the confusion matrix, node error rate, detailed accuracy of the three aspects of comparative analysis.

3.1. Confusion Matrix

The confusion matrix is a special matrix used to show the performance of the algorithm. The larger the diagonal value of the confusion matrix, the more examples of classification. The confusion matrix results of the three models are shown in Table 4. Visualize Classifier errors, in which the instances of correct classification are represented by crosses, and the instances of wrong classification are represented by blocks. Blue indicates a low forecast grade, red indicates a medium forecast grade, green indicates a high forecast grade, The error scatter plots of the three models are shown in Figure 3.

Table 4. Confusion matrix.

Naive Bayes				Artificial Neural Network				Support Vector Machine
a	b	c	Classified As	a	b	c	Classified As	a	b	c	Classified As
2	3	0	a = 1	4	1	0	a = 1	0	5	0	a = 1
2	11	1	b = 2	2	12	0	b = 2	0	13	1	b = 2
1	2	3	c = 3	1	1	4	c = 3	0	2	4	c = 3

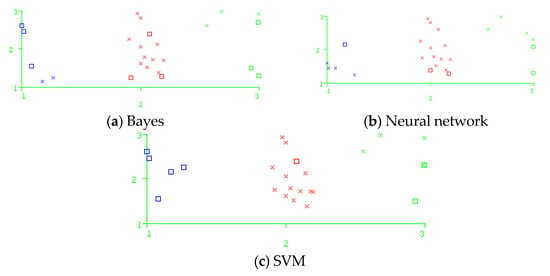
Figure 3. Error scatter plot.

The training samples are a total of 25 sets of data. It can be seen from Table 4 that there are 5 data with ‘low’ height grade of water flowing fractured zone in Naive Bayes model, 3 of which are predicted as ‘medium’; There are 14 data with a height grade of ‘medium’ in the water flowing fractured zone, of which 2 are predicted to be ‘low’ and 1 is predicted to be ‘high’; There are six data with a height grade of ‘high’ in the water flowing fractured zone, of which one is predicted to be ‘low’ and two are predicted to be ‘medium’. There are 16 correct classification examples and 9 wrong classification examples in Naive Bayes model. The correct rate is 64% and the error rate is 36%.

It can be seen from Table 4 that there are 5 data with ‘low’ height grade of water flowing fractured zone in artificial neural network model, of which 1 is predicted as ‘medium’; there are 14 data with a height grade of ‘medium’ in the water flowing fractured zone, of which 2 are predicted to be ‘low’. There are six data with a height grade of ‘high’ in the water flowing fractured zone, of which one is predicted to be ‘low’ and one is predicted to be ‘medium’. There are 20 correct classification examples and 5 wrong classification examples in the artificial neural network model. The correct rate is 80% and the error rate is 20%.

It can be seen from Table 4 that there are 5 data with ‘low’ height grade of water flowing fractured zone in support vector machine model, all of which are predicted as ‘medium’; there are 14 data with a height grade of ‘medium’ in the water flowing fractured zone, and one is predicted to be ‘high’. There are 6 data with a height grade of ‘high’ in the water flowing fractured zone, and 2 are predicted to be ‘medium’. There are 17 correct classification examples and 8 wrong classification examples in the support vector machine model. The correct rate is 68% and the error rate is 32%.

The accuracy of instance classification is: artificial neural network > support vector machine > Naive Bayes.

3.2. Node Error Rate

The node error rate is mainly reflected in the mean absolute error, root mean square error, absolute relative error and root relative square error. The node error rates of the three models are shown in Figure 4.

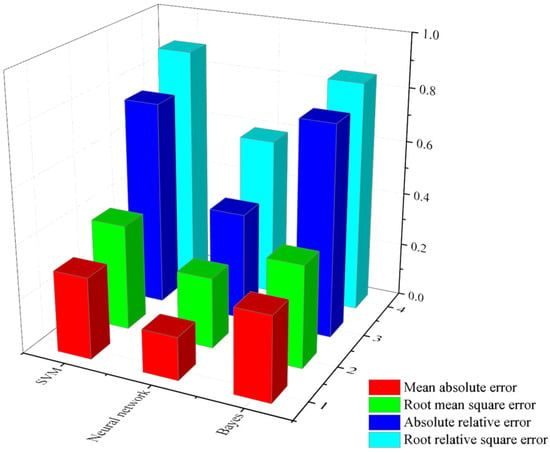
Figure 4. Node error rate.

It can be seen from Figure 4 that the Naive Bayesian model is slightly larger than the support vector machine in the mean absolute error and the absolute relative error. In terms of root mean square error and root relative square error, support vector machine is slightly larger than Naive Bayesian; the value of the node error rate of the two models is not much different. However, it is clear from the diagram that the value of the artificial neural network model is the lowest in the node error rate, and the training effect is the best.

3.3. Detailed Accuracy

The detailed accuracy is mainly reflected in TP Rate (true positive ratio), FP Rate (false positive ratio), Precision, Recall (recall ratio), F-Measure (harmonic average of precision and recall rates), MCC, Kappa statistics and characteristic curve area. The detailed accuracy of the three models is shown in Table 5.

Table 5. Detailed accuracy.

Model	TP Rate	FP Rate	Precision	Recall	F-Measure	MCC	Kappa
Naive Bayes	0.64	0.297	0.645	0.64	0.635	0.367	0.3608
Artificial neural network	0.8	0.132	0.834	0.8	0.805	0.68	0.6622
Support vector machine	0.68	0.369	0.556	0.68	0.603	0.36	0.3651

It can be seen from the detailed accuracy that in the TP Rate (TP Rate represents the proportion of the predicted positive class. The higher the value, the higher the accuracy of the positive class prediction.), artificial neural network > support vector machine > naive Bayes; the FP Rate represents the proportion of the negative class contained in the predicted positive class. The smaller the value of the FP Rate is, the better the effect is. The FP Rate of the artificial neural network model is the smallest, and the training effect is the best. The Precision, F-Measure, and MCC values are artificial neural network > naive Bayes > support vector machine. In terms of Recall and Kappa statistics, artificial neural network > support vector machine > naive bayes. In general, the artificial neural network model is optimal.

ROC Area (receiver operating characteristic curve area): Display the ROC area, the decimal range of [0, 1]. The ROC area is generally greater than 0.5, and the closer to 1, the better the classification effect of the model. When the value is between 0.5 and 0.7, the accuracy is low. When the value is between 0.7 and 0.9, it shows a certain accuracy. When the value is greater than 0.9, it shows a higher accuracy. The ROC values of the three models are shown in Table 6, and the ROC curves of the three models are shown in Figure 5.

Table 6. ROC value of the models.

	Naive Bayes	Artificial Neural Network	Support Vector Machine	Class
	0.86	0.95	0.75	1
	0.815	0.945	0.646	2
	0.829	0.978	0.851	3
Average weight	0.827	0.954	0.716

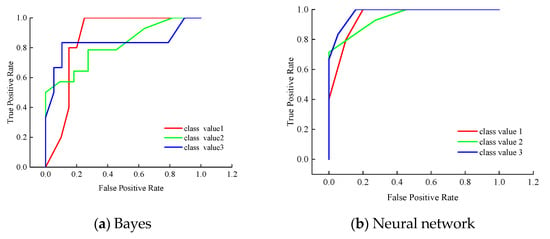
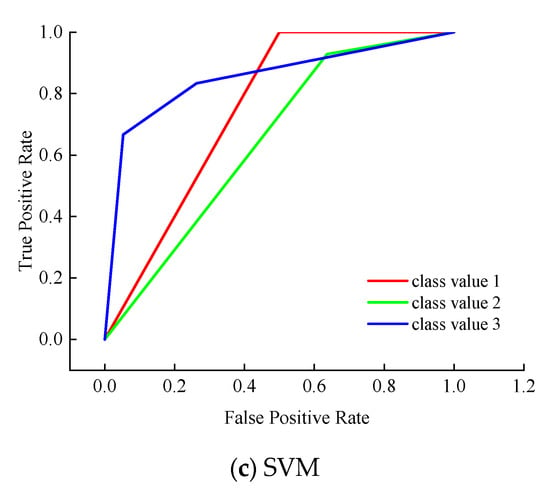
Figure 5. ROC.

It can be seen from Table 6 that the average ROC value of artificial neural network model is 0.954, with high accuracy. The ROC values of Naive Bayes model and support vector machine model are between 0.7 and 0.9, with certain accuracy. Overall, Artificial Neural Network > Naive Bayes > Support Vector Machine.

3.4. Prediction Using Artificial Neural Network Models

Through the above comparative analysis, it is concluded that the effect of the artificial neural network model is the best. The artificial neural network model is used to predict the measured data of 10 groups of water flowing fractured zone height. The prediction results are shown in Table 7.

Table 7. Comparison of prediction results.

Serial Number	Mining Depth/m	Coefficient of Hard Rock Lithology Ratio	Height Mining/m	Inclined Length of Working Face/m	Height of Water Flowing Fractured Zone/m	Height Grade of Water Flowing Fractured Zone		Comparison
						Actual	Prediction
1	420	0.71	3.7	70	56.8	medium	medium	correct
2	478.3	0.54	3.85	209	52.15	medium	medium	correct
3	568.4	0.85	2.94	180.4	57	medium	medium	correct
4	453.6	0.16	4	195	44.96	medium	medium	correct
5	412.5	0.24	2.2	136	35.2	low	low	correct
6	411.7	0.3	2.2	136	35.21	low	low	correct
7	475	0.37	6.1	170	64.6	high	low	error
8	453.5	0.42	1.6	180	30.3	low	medium	error
9	818.5	0.45	7.55	230	74.57	high	high	correct
10	427.3	0.43	4.6	120	56.6	medium	medium	correct

It can be seen from Table 7 that there are 10 groups of prediction data, only 2 groups of data prediction errors. The 7th group of samples to be tested is predicted to be ‘low’ (the actual damage level is ‘high’), and the 8th group of samples to be tested is predicted to be ‘medium’ (the actual damage level is ‘low’). The correct rate of prediction reaches 80%, and good prediction results are obtained.

4. Water Flowing Fractured Zone Height Prediction System Based on VB Language

Based on VB language, the height prediction system of water flowing fractured zone is developed. The software design flow chart is shown in Figure 6.

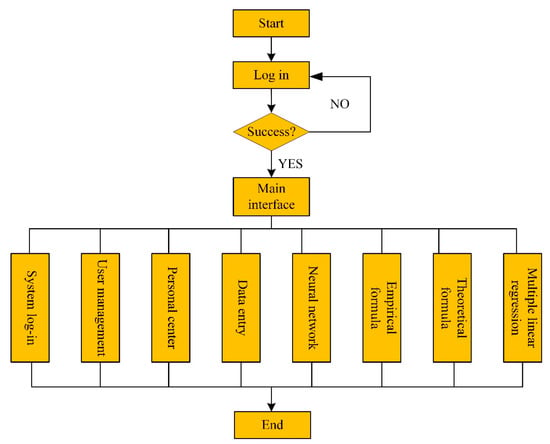
Figure 6. Process design of the software.

Some interfaces are shown in Figure 7. Mainly realized the following functions:

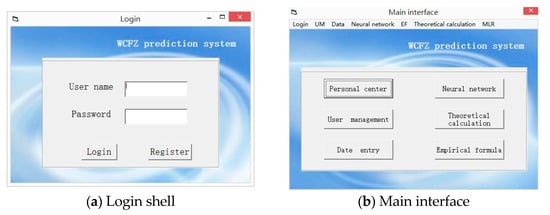
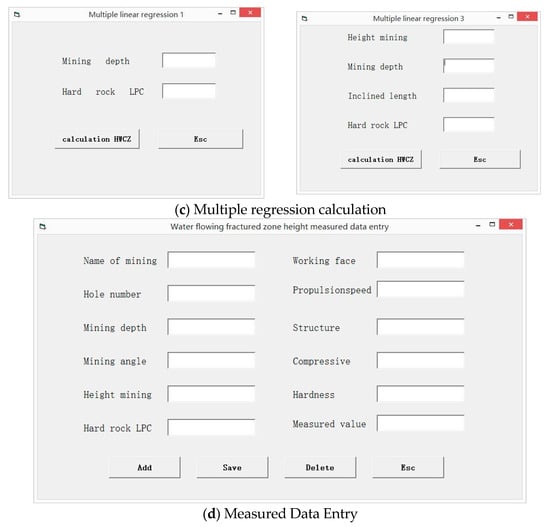
Figure 7. System interface.

(1)

User management module includes user’s department, login account, login password, user name, user role, mobile phone number and notes. User management interface is designed to give managers and ordinary users different permissions, user managers can also be real-time input measured data.

(2)

The factors affecting the height of water flowing fractured zone can be divided into three categories: geological factors, time factors and mining factors. In order to comprehensively collect the measured data of the height of water flowing fractured zone under various influencing factors, the measured data module of the height of water flowing fractured zone is designed, including the name of the mining area, the number of working face and the number of holes, the mining depth, the mining thickness, the dip angle of coal seam, the coefficient of hard rock lithology ratio, the inclined length of working face, the advance speed, the lithology combination structure of overburden rock, the compressive strength of roof, the hardness of coal seam and the measured value.

(3)

Prediction module mainly includes four methods, namely the neural network model, the empirical formula in the ‘three under’ procedure, theoretical calculation formula and multiple linear regression formula.

5. Conclusions

(1)

Based on the Weka platform, 33 groups of measured data of water flowing fractured zone height are used as training samples, and Naive Bayes, artificial neural network and support vector machine models are used for training respectively. The prediction results are compared and analyzed by confusion matrix, node error rate and detailed accuracy. It is concluded that the artificial neural network model is the best.

(2)

Based on artificial neural network, taking mining depth, coefficient of hard rock lithology ratio, height mining and inclined length of working face as the main factors, the accuracy of the height prediction model of water flowing fractured zone is 80%, which has achieved good prediction effect and can provide reference for the prediction of height failure grade of water flowing fractured zone.

(3)

Based on VB computer language, the height prediction system of water flowing fractured zone is developed. The system is simple to operate, practical and convenient, and realizes the height prediction of water flowing fractured zone under different methods.