Experimental and Numerical Analysis of Sustainable Use of Steel Slag for Geogrid-Encased Column Involving Its Clogging Effects

Abstract

This study investigates the sustainable use of steel slag for a geogrid-encased column involving its reinforcement and clogging effects on its consolidation performance in soft foundations through model tests and 3D hydromechanical-coupled finite element analyses. The 3D finite element model is first validated according to test results of an untreated and treated soft soil foundation. Then, a parametric study investigating the effect of clogging on the performance of the geogrid-encased steel slag column (GESSC) is carried out. Steel slags mixed with different percentages of fine (0%, 10%, 20%, and 40%) are used to simulate various clogging conditions. The numerical study shows that the percentage of fines in the GESSC has a notable effect on the dissipation of excess pore water pressure as well as foundation consolidation.

1. Introduction

A geogrid encased stone column (GESC) is considered an environmentally friendly foundation treatment technology due to its lower fuel consumption, low CO2 emission, and minor disposal of waste soil needed. With the wide application of GESCs, the contradiction between the demand for stones and restricted mining is increasingly prominent. Fortunately, a large amount of solid waste provides new material choices for GESCs.

Steel slag is a main byproduct of the steelmaking process; its cyclic utilization rate is only 29.5% in China. In the era of sustainable development, the management of steel slags brings opportunities and challenges. Although some researchers use steel slag powder to modify asphalt [1] or cement-based materials [2], the consumption of steel slag is still much less than its production. In addition, processing steel slags into powder also brings carbon emissions. Considering that steel slags have similar mechanical properties compared to traditional stone fillers, steel slags can be directly used as pavement fillers without processing [3]. It is also obvious that the geogrid-encased column is another potential application scenario for steel slag, but there is no relevant report yet.

The effectiveness of GESCs in foundation improvement is obvious. Experimental investigations on the performance of column-improved soil under static load have been conducted by researchers (e.g., [4,5,6,7,8,9,10]). GESC can also accelerate the consolidation process and reduce the foundation’s post-construction settlement. There are abundant numerical studies on the behavior of GESCs (e.g., [11,12,13]), which typically involve coupled seepage–stress finite element or finite difference analyses. However, one potential problem of GESC is that fine particles may migrate from the surrounding soft soil to the stone column, which results in clogging and undermines the drainage function of the GESC [14,15]. A clogged stone column typically has a much lower permeability compared to an unclogged one and the consolidation rate of a clogged system is also relatively lower [16]. The effect of clogging on the performance of stone columns has not received much attention. Only a few studies have addressed this issue. For example, Weber et al. [17] studied the formation of clogging during the installation of stone columns through centrifuge tests; Indraratna et al. [18] numerically demonstrated that the initial clogging of the stone column can reduce the degree of consolidation of surrounding soils; Deb et al. [19] suggested that time-dependent clogging should be included in design and analysis by considering reduced permeability over time; Tai et al. [20] provided a detailed model test where a stone column clogging can be assessed quantitatively.

The purpose of this study is to investigate the sustainable use of steel slag for a geogrid-encased column involving its reinforcement performance and clogging effects. Experiments are conducted to study the effectiveness of GESSC in soft foundation reinforcement. The coupled seepage–stress finite element model is first validated by small-scale experimental results that consist of two cases, i.e., (1) a drainage and consolidation test of a soft soil foundation without improvement; (2) a drainage and consolidation test of a soft soil foundation improved by one GESSC. Subsequently, the validated numerical model is used to conduct parametric studies to investigate the effect of clogging on the foundation consolidation. Four clogging conditions are considered, including no fines, 10%, 20%, and 40% of fines. The affected coefficient of permeability of GESSC is adjusted according to empirical equations obtained from experimental observations in the literature, which are related to the percentage of fines in the steel slag column. Finally, the influence of clogging on the excess pore water pressure, permeability, and foundation settlement due to consolidation are discussed.

2. Experimental Investigation

2.1. Column Fill Materials and Soft Clay

In recent years, engineers, governments, and environmentalists are searching for better ways to manage industrial wastes (e.g., fly ash, blast furnace slag, and steel slag). Many attempts have been made to use those wastes as alternative construction materials in civil engineering, such as ground improvement and road pavement subgrade. Steel slag is a byproduct of steel and iron producing processes and has been used in civil engineering for decades as an alternative for coarse aggregates [21]. In this study, steel slag from smelting in a basic oxygen furnace by a local steel mill with particle sizes ranging from 3 mm~20 mm was used as the fill material in the column. To assess the microstructural properties of the steel slag adopted in this experiment, scanning electron microscopy (SEM) and energy-dispersive spectroscopy (EDS) were performed for qualitative analysis of chemical elements. The SEM micrograph of steel slag is shown as an inset in Figure 1a, in which the typical mineral phases of dark gray fibrous type and grey-white irregular agglomeration can be seen. These two phases were analyzed by EDS. The dark gray fibrous type at spot A is mainly the calcium–iron phase, and it contains a small amount of P, Mn, Mg, V, and Ti; whilst the grayish white irregular agglomeration at point B mainly consists of calcium–silicon phase and a small amount of P, Mg, and Ti. In order to determine the mineral composition of steel slag, X-ray diffraction (XRD) analysis was carried out. The XRD results of steel slag are illustrated in Figure 1b. Different minerals were identified in the steel slag, such as magnetite (Fe₃O₄), srebrodolskite (Ca₂Fe₂O₅), and periclase (MgO). Due to the presence of heavy metal Mn in steel slag detected by EDS, it is imperative to conduct a quantitative analysis of the manganese element to evaluate its leaching toxicity. According to the method of “Solid Waste Leaching Toxicity with Sulfuric Acid and Nitric Acid” specified by HJ/T299-2007 (2007), a leaching test of steel slag was carried out. The detection results show that the determined concentration of Mn in steel slag is 0.66 mg/L, which is much lower than the toxicity limit of 2.0 mg/L from the Chinese code of “Hazardous Waste Identification Criteria-Leaching Toxicity Identification” specified by GB/T5085.3 (2007). Therefore, one can judge that the steel slag used in this test has no leaching toxicity and belongs to the category of environmental protection material.

Figure 1. Microstructural analysis of steel slag: (a) interface element analysis of steel slag through EDS with an inset of SEM image; (b) XRD patterns of steel slag.

The particle size distribution of the steel slag was determined by sieving test and the gradation curve was plotted as seen in Figure 2. The particle size of the steel slag at which 60%, 30%, 10% by mass was finer was 10.6, 7.4, and 4.8 mm, respectively. The coefficient of uniformity and curvature was 2.2 and 1.1, respectively. Based on the USCS classification system, the steel slag can be classified as poorly graded gravel (GP).

Figure 2. Gradation curve of steel slag.

The foundation soil examined was soft clay with a density of 1610 kg/m³, water content of 64%, hydraulic conductivity of 1.9 × 10^-8 m/s, and degree of saturation of 98%. Additional properties of the soft clay are presented in Table 1.

Table 1. Material properties of the soft clay.

Density $\mathit{\rho }$ (kg/m3)	Specific Gravity ${\mathit{G}}_{\mathit{s}}$	Initial Water Content $\mathit{\omega }$ (%)	Liquid Limit ${\mathit{L}}_{\mathit{L}}$	Plastic Limit ${\mathit{P}}_{\mathit{L}}$	Saturation ${\mathit{S}}_{\mathit{r}} (\%)$	Void Ratio $\mathit{e}$	Coefficient of Permeability $\mathit{k}$
1610	2.75	64%	40.0	25.4	98	1.80	1.9 × 10−8

2.2. Experimental Setup

The experiments were arranged in a large rigid model container with inside dimensions of 1.1 m × 1.1 m × 1.3 m (length × width × height), as shown in Figure 3. It is well known that boundary conditions significantly influence the results of drainage tests. According to the effective drainage range of 1.5D for a single-column composite foundation proposed by Meyerhof et al. [22], the boundary effect due to the dimension of the model container was negligible. Friction along the inside surface of the container was minimized by using a polyethylene sheet and a special lubricant, the special lubricant between the sheet and the sidewall of the container allowing the sheet to slip with very little resistance during the soft clay’s consolidation [23,24]. A drainage valve was connected to the bottom port of the model container to accelerate pore pressure dissipation within the soft clay. It should be noted that unlike the subsequent numerical analyses, the scenario of clogging was not experimentally simulated.

Figure 3. Schematic diagram of experiment setup and sensor layout: (a) horizontal view of various transducers’ positions and (b) vertical cross-sectional view of positions of various transducers. (Unit: cm).

Two small-scale model tests were conducted. The first one was a drainage and loading test of a soft clay foundation treated by the GESSC with a diameter D of 0.15 m and a length of 0.9 m. The second one was the same soft clay foundation but untreated. The preparation of the first model test includes the following steps:

(1)

A 0.25 m thick coarse sand layer was first placed at the bottom of the model container to facilitate the drainage of the pore water in the soft clay (see Figure 3b).

(2)

The GESSC was then placed on the coarse sand layer.

(3)

The soft clay was divided into several layers; care was taken to produce a flat surface for each layer during the placement.

(4)

At the top of the soft clay, a 0.1 m thick cushion layer, beneath the loading plate, consisting of gravel was constructed as the subgrade soil to increase the bearing capacity of the foundation and avoid the failure of foundation during loading.

(5)

A circular loading plate with a diameter of 0.4 m was used to apply the load at the surface of the gravel cushion later (see Figure 1).

(6)

During the experiment, the dissipation of excess pore water pressure within the soft clay at different depths was monitored. Three pore pressure gauges marked as P1, P2, and P3, respectively, were buried 0.15 m away from the perimeter of the column at different elevations, as shown in Figure 1.

The preparation of the second model test is the same as the first except the step (2).

The test consisted of two stages, i.e., the loading stage and the consolidation stage. During the loading stage, the drainage valve at the bottom of the container was closed. The load was applied via a computer-controlled hydraulic jack above the loading plate. For the test with the column-treated foundation, an incremental stress of 12 kPa was applied every 2 h, and there were eight increments in total. For the case of the untreated foundation, an incremental pressure of 2.5 kPa was applied every 4 h, and there were four increments in total. After reaching the final stress (i.e., finishing the loading stage), the drainage valve at the bottom of the box was opened in the consolidation stage. The pore water pressure was measured every 0.5 h for a total of 18 h to study the consolidation of the soft clay over time.

3. Three-Dimensional Coupled Seepage–Stress Finite Element Model

3.1. Finite Element Model

A 3D finite element analysis, using ABAQUS, was adopted in this paper to simulate the experimental results of the soft clay treated with a column. The same dimensions as the model test were adopted in the numerical analysis. The thickness of the upper gravel cushion layer, bottom sand drainage layer, and the soft clay layer was 0.10 m, 0.25 m, and 0.90 m, respectively. The steel slag column had a diameter of 0.15 m and a height of 0.9 m. The mesh of the finite element model is shown in Figure 4a. Historically, geogrid in the geosynthetic-encased steel slag column was simulated as a membrane [13,25], or a solid material [26,27,28], which did not consider the geometry of the geogrid’s aperture. Meanwhile, the aperture size has a great influence on material properties as well as drainage. The geogrid in the finite element model herein was simulated using the same geometry (i.e., aperture size) as the tested material, and the mesh of the geogrid is shown in Figure 4b. The size of the aperture was 0.01 m in this analysis. The vertical boundaries were restrained in the horizontal direction and only allowed for vertical settlement, whereas the bottom boundary was restrained in both horizontal and vertical directions.

Figure 4. Finite element mesh of (a) the whole model; (b) geogrid.

To reproduce the small-scale tests accurately, the in situ stress state of the model after the construction and the boundary conditions during loading and drainage stages need to be adjusted manually. Therefore, the finite element simulation was divided into three steps to facilitate the adjustments above. The gravity load and geostatic stress were applied in the first step, and the in situ stress state was achieved in this step; the gravel cushion layer and the sand drainage layer were considered as effective drainage boundaries. The second step was the loading stage; the sand layer was not considered as a drainage boundary since the bottom drainage port in the rigid container was closed during the loading; the external load was applied in the same manner as described in the experimental section. The last step was the consolidation step; the bottom sand drainage layer was considered as an effective drainage boundary and the external pressure from the last step was maintained in this step.

3.2. Constitutive Models

The modified cam–clay (MCC) model was used to simulate the behavior of soft clay. The properties of soft clay shown in Table 2 were obtained using one-dimensional consolidation tests, consolidated undrained triaxial compression tests, and permeability tests. The sand layer, steel slags, and gravels were all simulated as elastoplastic material governed using the Mohr–Coulomb (MC) failure criterion. The geogrid was considered as linear elastic (LE) with the elastic modulus measured by the tensile test.

Table 2. Material parameters in the finite element model.

Materials	Model	Cohesion c (kPa)	Internal Friction Angle φ (°)	Elastic Modulus E (MPa)	Poisson’s Ratio ν	λ	κ	M	e0	Coefficient of Permeability k (m/s)
Plate	LE			2 × 105	0.2
Geogrid	LE			100	0.3
Cushion	MC	8	30	35	0.3				0.8	1.6 × 10−3
Slag	MC	8	45	40	0.3				0.32	1.4 × 10−4
Sand	MC	5	40	30	0.3				0.6	1.2 × 10−5
Clay	MCC				0.35	0.41	0.102	0.42	1.8	1.9 × 10−8

Note: LE, MC, and MCC represent linear elasticity, Mohr–Coulomb, and modified cam–clay models, respectively.

3.3. Simulation of the Clogging Effect

The finite element model was first calibrated using the experimental results based on the tested column without clogging. Then, the model was modified to investigate the effect of column clogging on the dissipation of pore water within the soft clay. The most significant change for a clogged steel slag column is that the permeability of the column decreases due to the presence of fines. These fines are soft soil particles that migrate from the surrounding soft soil to slag column, which may block the drainage path within the column. In the finite element simulation, different coefficients of permeability were used to simulate the various extent of clogging. The coefficient of permeability for the column was calculated based on the empirical correlation proposed by Xu et al. [29] as follows:

$$k=\frac{n^3}{5{\left(1-n\right)}^2}{\left(\frac{D_{eff}}{6}\right)}^2$$

(1)

where $D_{eff}$ represents the average effective particle size of the porous material; n represents the porosity of the material. The porosity of the steel slag with a certain percentage of fines can be obtained by measuring the weight of the steel slag and fines mixture. In the finite element analyses, four different clogging conditions with no fines, 10% fines, 20% fines, and 40% fines were considered. The permeability calculated for each mixture according to Equation (1) is presented in Table 3. With the presence of fines increasing from 0 to 10%, 20%, and 40%, the void ratio of the steel slag column reduced by 25%, 47%, and 84%, respectively, and the coefficient of permeability reduced to 11.4%, 4.4%, and 0.15% of the original value of 1.4 × 10⁻⁴ m/s, respectively, showing the significant impact of clogging on the permeability of the column and protentional effect of clogging on the long-term drainage and consolidation of the soft clay foundation.

Table 3. Coefficient of permeability for various clogging conditions.

Cases	Steel Slag Weight m0 (kg)	Soil Particle Weight ms (kg)	Void Ratio	Coefficient of Permeability kv (m/s)
No fines	30	0	0.32	1.4 × 10−4
10% fines	30	3	0.24	1.6 × 10−5
20% fines	30	6	0.17	6.2 × 10−6
40% fines	30	12	0.05	2.1 × 10−7

4. Validation of the Finite Element Model

The relationship between the applied stress (denoted as P) and the settlement of the loading plate (denoted as s) is presented in Figure 5. S for the untreated foundation was notably larger than that for the treated foundation at the same applied stress, representing a notable improvement of the bearing capacity of the soft clay foundation treated with the column. The results between the numerical and experimental outcomes for the two cases tested provided a good correlation.

Figure 5. Load–settlement curves for the treated and untreated foundations.

Figure 6 shows the comparison between the model test and the finite element analysis results on the dissipation of excess pore water pressure over time in the consolidation stage at the monitored locations (P1, P2, and P3). It appears that the experimental and numerical results are in reasonable agreement. Because the treated foundation has a higher bearing capacity than the untreated one, the external load applied for the treated foundation was 98 kPa, significantly greater than that for the untreated foundation of 10 kPa, and hence there was much greater excess pore water pressure within the soil for the treated foundation. Nevertheless, it is clear that the excess pore water pressure for the foundation treated with GESSC dissipated faster than the untreated foundation at all locations due to the preferential flow path of the column.

Figure 6. Comparison of measured and estimated excess pore water pressure for treated and untreated foundations at: (a) P1; (b) P2; (c) P3 (note: the applied stress for the treated foundation was 98 kPa, and was 10 kPa for the untreated foundation).

5. Results and Discussions

Figure 7 shows the distribution of excess pore water pressure through depth after the loading stage at the center (Figure 7a) and the edge (Figure 7b) of the GESSC. Clogging affects the excess pore water pressure due to the decreasing permeability of the column. The accumulation of excess pore water pressure was affected by the water flow direction, which was directed horizontally towards the column and vertically downwards. Therefore, the maximum excess pore water pressure increased with the increasing fines content at each depth and the increasing vertical distance from the surface of the foundation. As Figure 7a shows, the excess pore water pressure increases with depth in all cases. In addition, for the cases of no fines, 10%, 20%, and 40% fines, the maximum excess pore water pressure at the bottom increases from 0.28 kPa to 1.88 kPa, 3.20 kPa, and 5.12 kPa, respectively. Figure 7b shows that clogging has no effect on excess pore water pressure at the edge of the column within the depth of 0.50 m below the soil surface. For the depth deeper than 0.60 m, the larger percentage of fines leads to higher excess pore water pressure at the edge of the column. The higher the fines content, the deeper the location of the maximum pore water pressure.

Figure 7. Distribution of excess pore water pressure through depth after loading stage at (a) the center of GESSC; (b) the edge of the GESSC.

Figure 8 shows the dissipation of excess pore water pressure at P1, P2, and P3 with different percentages of fines for the GESSC. The excess pore water pressure decreases over time for all the cases examined. The speed of excess pore water pressure dissipation increased with the decreasing fines content within the column, and the column without fines (i.e., no clogging) had the greatest dissipation speed. The effect of clogging on the dissipation of excess pore water pressure was more prominent at deeper depths (P1 and P2) than at shallow depths (P3). Since P1’s position had the maximum accumulation of excess pore water pressure (Figure 6), the value of the hydraulic gradient in that position was consequently maximum among those three pore pressure gauge positions; therefore, the dissipation rate in P1 was highest. For the experiments conducted, all excess pore water pressure decreased to practically zero at day 10 due to the boundary of the experiments. In a field condition with no lateral boundary and commonly no bottom drainage sand beneath the soft clay, the excess pore water pressure could take a much longer time to dissipate, especially when the soft soil has a greater thickness. Three functions were generated to quantify the relationship between time x, excess pore water pressure y, and fines z at the positions of P1, P2, and P3. The functions are generated by high-degree polynomials:

$${\mathrm{z}=\mathrm{p}}_{\mathrm{ij}}{\displaystyle \sum }_1^{\mathrm{i}\ast \mathrm{j}}{\mathrm{x}}^{\mathrm{i}}{\mathrm{y}}^{\mathrm{j}}$$

(2)

where i and j are the orders of the time and the excess pore water pressure. The coefficients ${ p}_{ij}$ for each depth are listed in the Table 4, Table 5 and Table 6. The predictions of the equations are shown in Figure 9. The prediction results are highly consistent with the numerical results; the R² (R: Coefficient of determination) of the three functions are 0.95, 0.97, and 0.97 for P3, P2, and P1, respectively. All functions show that there is a linear relationship between excess pore water pressure and fines content at the same time. Therefore, Equation (2) can be rewritten as:

$$\mathrm{z}=\mathrm{Ay}+\mathrm{B}$$

(3)

$$A={{\displaystyle \sum }}_0^i{p}_{1i}{x}^i$$

(4)

$$B={{\displaystyle \sum }}_0^i{p}_{0i}{x}^i$$

(5)

where A is the time factor and B is the time constant. p_0i and p_1i are related to the geometry of the GESSC, materials, positions, and so on.

Figure 8. Dissipation of excess pore water pressure with different percentages of fines at (a) P3; (b) P2; (c) P1.

Table 4. Coefficients p_ij of P3.

	i	0	1	2
j
0		−1.531	0.2966	−0.0141
1		0.4804	0.1861	0

Table 5. Coefficients p_ij of P2.

	i	0	1	2	3	4
j
0		−0.9963	0.4464	−0.08832	0.007918	−0.0002592
1		0.284	0.01542	−0.008269	0.003191	0

Table 6. Coefficients p_ij of P1.

	i	0	1	2	3	4
j
0		−0.4725	0.2414	−0.05727	0.006017	−0.000227
1		0.1369	0.04979	−0.01344	0.003763	0

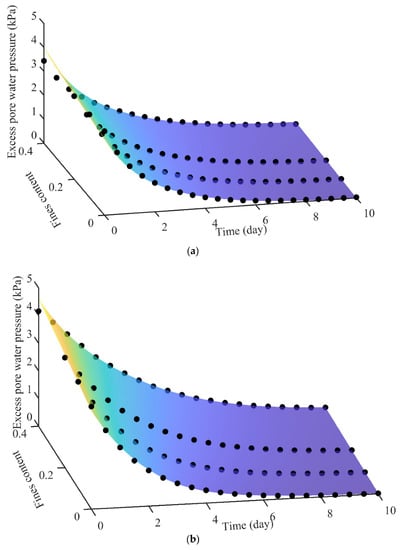
Figure 9. Predictions of the equations at (a) P3; (b) P2; (c) P1.

Figure 10 shows the time history curve of radial seepage velocity under different degrees of clogging. The radial seepage velocity at all locations decreased as the soft soil consolidated. The fine particles have a negligible effect on the radial seepage velocity at P3, where the excess pore water pressure was small. At the middle and bottom depths of the foundation, due to the higher excess pore water pressure, the radial seepage velocity within the first two days was notably decreased by the percentage of fines due to the clogging effect.

Figure 10. Time history curves of radial seepage velocity with different percentage of fines at (a) P3; (b) P2; (c) P1.

As the clogging reduced the dissipation of excess pore water pressure (Figure 8), it is expected that the consolidation rate was reduced as well. Figure 11 shows the effect of fines content within the column and the resultant clogging on the degree of consolidation over time. A larger percentage of fines leads to slower consolidation, especially when the time factor T_v falls within the range between 0.001 and 0.1.

Figure 11. Effect of clogging on the consolidation of the soft soil foundation.

6. Conclusions

In this study, experiments were carried out to study the performance of a geogrid-encased column filled with sustainable steel slag and then numerical models focusing on the influence of clogging on the consolidation of a soft foundation improved by the geogrid-encased steel slag column (GESSC) were developed. The numerical model was first validated by a small-scale laboratory test without considering clogging effect foundations. Subsequently, the validated 3D hydromechanical-coupled finite element model was used to conduct parametric studies considering different clogging conditions represented by the percentage of fines in the GESSC. It was found that clogging can lead to an increase of excess pore water pressure inside the GESSC as well as the soils around the column, especially at the bottom. In addition, clogging can significantly reduce the dissipation rate of excess pore water pressure, radial seepage velocity of surrounding soils, and the consolidation rate of the loaded foundation. The equations between time, excess pore water pressure, and fines content show that there is a linear relationship between excess pore water pressure and fines content at the same time. Lastly, it should be noted that the conclusions drawn from the finite element models are based on small-scale tests. Therefore, more accurate and representative results and conclusions applicable to full-scale GESSC structures need further investigation.