A Hybrid Algorithm for Parameter Identification of Synchronous Reluctance Machines

Abstract

In rail transit traction, synchronous reluctance machines (SynRMs) are potential alternatives to traditional AC motors due to their energy-saving and low-cost characteristics. However, the nonlinearities of SynRMs are more severe than permanent magnet synchronous motors (PMSM) and induction motors (IM), which means the characteristics of SynRMs are challenging to model accurately. The parameter identification directly influences the modeling of nonlinearity, while the existing algorithms tend to converge prematurely. To overcome this problem, in this paper, a hybrid optimizer combining the SCA with the SSO algorithm is proposed to obtain the parameters of SynRMs, and the proposed Sine-Cosine self-adaptive synergistic optimization (SCSSO) algorithm preserves the self-adaptive characteristic of SSO and the exploration ability of SCA. Comprehensive numerical simulation and experimental tests have fully demonstrated that the proposed method has obviously improved parameter identification accuracy and robustness. In the dq-axis flux linkage, the mismatch between reference and estimated data of proposed algorithm is below 1% and 6%, respectively. Moreover, the best d-axis RMSE of SCSSO is 50% of the well-known algorithm CLPSO and 25% of BLPSO and its performance has improved by two orders of magnitude compared to traditional simple algorithms. In the q-axis, the best RMSE is 10% of CLPSO and 50% of Rao-3 and Jaya. Moreover, the performance of the proposed algorithm has improved nearly 90 times compared to traditional simple algorithms.

1. Introduction

Due to their high efficiency, simple structure, low cost, wide speed range, and high environmental adaptability, Synchronous Reluctance Machines (SynRMs) are good alternatives to induction motors (IM) in fans, pumps, and compressors [1] and powerful competitors of permanent magnet synchronous machines (PMSM) in traction applications [2]. SynRMs are a highly nonlinear and strongly coupled system due to their self- and cross-saturation effects, which directly affect the torque output, power factor, excitation level, and stable operation area. To control SynRMs effectively, it is critical to evaluate the actual nonlinear behaviors of magnetic circuits based on accurate models [3,4,5]. Therefore, a nonlinear magnetic model [6] that satisfies the reciprocity conditions and inherent properties is introduced. However, the accuracy of the model is still limited by the rationality of the parameter identification algorithm because of the multimodal problems.

Many researchers have contributed to the parameter identification algorithms to obtain optimal solutions in recent decades [7], such as genetic algorithm (GA) [8], ant colony optimizer (ACO) [9], particle swarm optimization (PSO) [10], monarch butterfly optimization (MBO) [11], and grey wolf optimization (GWO) [12]. These metaheuristic algorithms have achieved satisfactory results in single objective optimization. However, the multimodality of parameter identification places more stringent requirements on traditional metaheuristic algorithms. To cope with the problems mentioned above of traditional metaheuristic algorithms in multimodality, various algorithms have been developed. In [13], multistage ant colony optimization (MSACO) was raised for direct instantaneous torque control of switched reluctance motor drives. This algorithm considered the multi-dimension condition. However, it overemphasized the exploitation ability, similar to the original ant colony optimization, which induced the solution trapped into pause best solution. Paper [14] combined Harris Hawks optimization with a Sine-Cosine algorithm and applied it to a hybrid renewable energy system. Paper [15] mixed biogeography-based optimization with a Sine-Cosine algorithm to satisfy high-dimensional global optimization problems [16]. Mohamed I. Abdelwanis mixed Particle Swarm Optimization (PSO) with Jaya optimization to fit the rapid response demand of induction motors [17]. Rahimi, A. promoted a Bat-inspired algorithms by considering chaotic behavior of PMSM [18]. Dalia Yousri promoted Grey Wolf Optimization (GWO) by introducing a chao map for applications to PMSM [19].Moreover, researchers made many efforts to promote the stochastic optimization algorithms applied in the parameter identification for induction motors [20,21]. However, their mutation directions are uncertain, and their mutation strategies are based on gradient. Thus, their calculation speed is relatively slow, and they tend to converge prematurely when dealing with multimodal problems. Additionally, an uncomplicated but valid algorithm named the Rao algorithm is proposed [22]. The distinguishing feature of Rao algorithms from other metaheuristic algorithms is the novel update mechanism of the optimal solution search path. The interaction of the algorithm among individuals was guided by fitness evaluation, which enhanced the exploitability. However, the interaction process ignored diversity’s value, which also induced premature convergence.

To solve the problem of early convergence, a self-adaptive synergistic optimization (SSO) was proposed to identify the parameters of the SynRM magnetic model [23]. The mutation strategy of the algorithm is guided by introduced parameters based on probability, which could offer updated directions in the global scope and avoid falling into local optimums. However, when the current solutions are certainly not at the global optimum, the searchability is provided by algorithm Rao-3 [24]. The searchability of Rao-3 is relatively weak, so it is hard to get rid of the current worst solutions. Recently, a simple yet effective metaheuristics method named the Sine-Cosine algorithm (SCA) has attracted much attention [14] due to its strong exploration ability, simple structure and self-adaptive balance capability.

However, SCA tends to get stuck in adjacent optima and uneven exploitation [25], resulting from its weak exploitability. In [26], SCA was used in urban traffic light scheduling. In [27], SCA was applied to constrained engineering optimization problems. However, when the complexity of the problem increased, SCA will over-consume calculation resources in exploration, also inducing premature convergence.

Based on the above factors, a hybrid optimizer for the parameter identification of SynRM is proposed in this paper, with superior exploration and exploitation. The main contributions of this paper can be summarized as follows:

1)

An improved position updating mechanism with hybridized SCA, weighted fitness values, and personal historical best is designed in SSO search;

2)

A collaboration-based hybrid SSO-SCA optimizer (SCSSO) is developed.

The rest of the paper is organized as follows. Section 2 presents the magnetic model of SynRMs. Section 3 and Section 4 briefly introduced the SSO algorithm and SCA, respectively. The working principle of the proposed SCSSO algorithm has been illustrated in Section 5. Section 6 revealed the statistical results of SCSSO and other compared algorithms. Finally, the conclusions are drawn in Section 7.

2. Problem Formulation

This section introduces a magnetic model of SynRMs expressed only by currents to simplify the equation. Objective functions considering self-saturation and cross-saturation are introduced. We focus on the model in the d-q reference frame (the d-axis aligns to the direction of maximum permeance) synchronous to the rotor. Additionally, the magnetic energy change caused by the iron loss change is minimal compared to that caused by the current change. Thus, the magnetic model is established under three hypotheses: (1) The iron loss has been omitted. (2) The stator flux linkages only relate to the stator current. (3) The effect of temperature on stator resistance is neglected.

2.1. Nonlinear Model of SynRMs Magnetic Behaviors

The electromagnetic torque of SynRMs is generated by an anisotropic rotor with a magnetic barrier in the coupled magnetic field [28]. The main rotor topologies are axial lamination (ALA) and transverse lamination (TLA). In general, the two rotor structures’ internal mechanism of the torque generated is the same. As shown in Figure 1, due to the material properties of the rotor, there is inevitably a self-saturation effect in the d-axis and q-axis magnetic circuits. In addition, due to the sharing of magnetic circuits, there is a cross-coupling effect between the d- and q-axis magnetic linkages. The nonlinear behavior mechanism of the two rotors is the same, and the following general modeling method can be used.

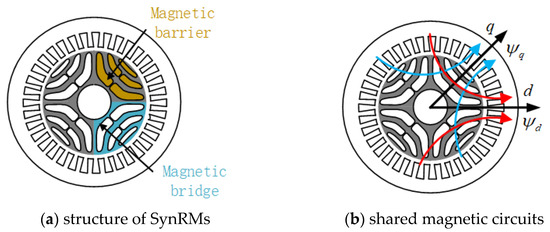
Figure 1. The magnetic circuit of the SynRMs rotor.

As Hypothesis (2), the stator flux linkages can be expressed by stator currents, which means the mapping can characterize magnetic circuit nonlinearity among magnetic linkages (${\psi }_s$) and stator currents ($i_s$) as follows [29]:

$$\{\begin{array}{c}{\psi }_d={\psi }_d\left(i_d,i_q\right)\\ {\psi }_q={\psi }_q\left(i_d,i_q\right)\end{array}$$

(1)

where $i_s={\left(i_d,i_q\right)}^T$, ${\psi }_s={\left({\psi }_d,{\psi }_q\right)}^T$ are stator currents and flux linkages, respectively. The subscripts d and q represent the d- and q-axis.

The energy conversion mechanism determines the nonlinearity for modeling the magnetic model. As illustrated in Figure 2, SynRMs is a typical singly excited electromechanical energy conversion device. It can be observed that the electrical and mechanical systems are coupled by the magnetic energy (W_m) transformation.

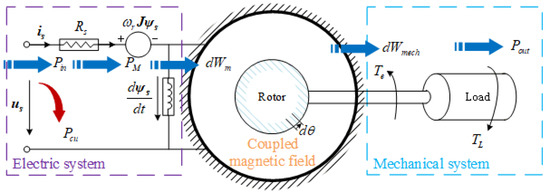
Figure 2. The electromechanical energy conversion process of SynRMs.

The mechanical work of SynRMs merely originates from electric energy, while electric energy transfers to three main parts: stator resistance loss, electronic-magnetic resistance, and mechanical. Thus, energy conserved in SynRMs can be expressed as follows:

$$i_s^T{u}_s=R_s{\Vert i_s\Vert }^2+\frac{d{W}_m}{dt}+T_e\left(i_s\right){\omega }_m$$

(2)

where $u_s={\left(u_d,u_q\right)}^T$, $R_s$, $T_e\left(i_s\right)$, $W_m$, ${\omega }_m$ are stator voltage, stator winding resistance, electromagnetic torque, magnetic energy and mechanical velocity of the motor, respectively.

In the coupling field, the change of magnetic energy mediates energy conversion. For simplifying the calculation, the variation of magnetic energy can be expressed equivalently by the co-magnetic energy (W_c) [30].

$$\frac{d{W}_c}{dt}={\psi }_d\left(i_d,i_q\right)\frac{d{i}_q}{dt}+{\psi }_q\left(i_d,i_q\right)\frac{d{i}_d}{dt}$$

(3)

Resulting from a shared magnetic circuit, the flux linkage on the d- and q-axis has a redistribution in the working process, which is the main reason for self-saturation and cross-saturation [23]. In other words, the saturation phenomenon is from the magnetic field, a typical conservative field. Under the concept of the traditional field, the relationship between ${\psi }_s$ and $i_s$ can be formulated as

$$\frac{\partial {\psi }_d\left(i_d,i_q\right)}{\partial i_q}=\frac{\partial {\psi }_q\left(i_d,i_q\right)}{\partial i_d}$$

(4)

Combining (2) and (3), the cross saturation-flux linkage is as follows:

$$\{\begin{array}{c}{\psi }_d\left(i_d,i_q\right)={\psi }_d\left(i_d\right)-\frac{\partial \Delta W_c}{\partial i_d}\\ {\psi }_q\left(i_d,i_q\right)={\psi }_q\left(i_q\right)-\frac{\partial \Delta W_c}{\partial i_q}\end{array}$$

(5)

where ${\psi }_d\left(i_d\right)$, ${\psi }_q\left(i_q\right)$ are merely the flux linkage under self-saturation, and $\Delta W$ represents co-magnetic energy converted between the d- and q-axis [31]. Under restrictions (4) and (3), the flux linkage model based on the Gaussian’s function is established as

$$\{\begin{array}{c}{\psi }_d(i_d,i_q)={\alpha }_d(2-e^{-{\gamma }_d{i}_d}-e^{-{\gamma }_{d1}{i}_d^2})+{\beta }_d{i}_d-k\left(2W{i}_d{e}^{-W{i}_d{}^2}\right)\left(V_1{i}_q^2-i_q{e}^{-V{i}_q}+{\kappa }_q{i}_q-e^{-V{i}_q}\right)\\ {\psi }_q(i_d,i_q)={\alpha }_q(2-e^{-{\gamma }_q{i}_q}-e^{-{\gamma }_{q1}{i}_q^2})+{\beta }_q{i}_q-k\left(1-e^{-W{i}_d{}^2}\right)\left(2V_1{i}_q+V{i}_q{e}^{-V{i}_q}+{\kappa }_q\right)\end{array}$$

(6)

where {α, γ, β} are non-negative self-saturation coefficients for the d-, and q-axis, and {k, W, V, V₁, κ_q} are cross-saturation coefficients. The subscripts d and q represent the d-axis and the q-axis. Based on (3), (4), and (5), the reciprocity condition and ΔW_c are expressed as

$$\frac{\partial {\psi }_d(i_d,i_q)}{\partial i_q}=\frac{\partial {\psi }_q(i_d,i_q)}{\partial i_d}=-k\left(2W{i}_d{e}^{-W{i}_d{}^2}\right)\left(2V_1{i}_q+V{i}_q{e}^{-V{i}_q}+{\kappa }_q\right)$$

(7)

$$\Delta W_c=k\left(e^{-W{i}_d^2}-1\right)\left(V_1{i}_q^2-i_q{e}^{-V{i}_q}+{\kappa }_q{i}_q-e^{-V{i}_q}\right)$$

(8)

Therefore, the analytical expressions of apparent inductances and incremental inductances can be obtained as

$$\{\begin{array}{l}{L}_d^{ai}(i_d,i_q)=\frac{{\alpha }_d(2-e^{-{\gamma }_d{i}_d}-e^{-{\gamma }_{d1}{i}_d^2})}{i_d}+{\beta }_d-k\left(2W{e}^{-W{i}_d{}^2}\right)\left(V_1{i}_q^2-i_q{e}^{-V{i}_q}+{\kappa }_q{i}_q-e^{-V{i}_q}\right)\\ L_q^{ai}(i_d,i_q)=\frac{{\alpha }_q(2-e^{-{\gamma }_q{i}_q}-e^{-{\gamma }_{q1}{i}_q^2})}{i_q}+{\beta }_q-k\left(1-e^{-W{i}_d{}^2}\right)\left(2V_1+V{e}^{-V{i}_q}+\frac{{\kappa }_q}{i_q}\right)\end{array}$$

(9)

$$\{\begin{array}{cc}{L}_d^{ii}(i_d,i_q)\hfill & ={\alpha }_d\left({\gamma }_d{e}^{-{\gamma }_d{i}_d}+2{\gamma }_{d1}{i}_d{e}^{-{\gamma }_{d1}{i}_d^2}\right)+{\beta }_d\hfill \\ & -2kW\left(e^{-W{i}_d{}^2}-2W{i}_d^2{e}^{-W{i}_d{}^2}\right)\left(V_1{i}_q^2-i_q{e}^{-V{i}_q}+{\kappa }_q{i}_q-e^{-V{i}_q}\right)\hfill \\ L_q^{ii}(i_d,i_q)\hfill & ={\alpha }_q\left({\gamma }_q{e}^{-{\gamma }_q{i}_q}+2{\gamma }_{q1}{i}_q{e}^{-{\gamma }_{q1}{i}_q^2}\right)+{\beta }_q\hfill \\ & -k\left(1-e^{-W{i}_d{}^2}\right)\left(2V_1+V{e}^{-V{i}_q}-V^2{i}_q{e}^{-V{i}_q}\right)\hfill \\ L_{dq}^{ii}(i_d,i_q)\hfill & =L_{qd}^{ii}(i_d,i_q)=-k\left(2W{i}_d{e}^{-W{i}_d{}^2}\right)\left(2V_1{i}_q+V{i}_q{e}^{-V{i}_q}+{\kappa }_q\right)\hfill \end{array}$$

(10)

where $L_{}^{ai}$ and $L_{}^{ii}$ are apparent inductance and incremental inductances, respectively.

2.2. Objective Function

To extract model parameters effectively, parameter extraction needs to be transformed into an optimization problem by solving the objective function between the proposed model and the flux linkage-current dataset. The cross-saturation parameters shared by the d- and the q-axis model are the premise of the optimization problem. The algorithm should be able to identify the no-load characteristics, self-saturation and cross-saturation characteristics cooperatively. Some researchers applied the least square (LS) method in the extraction of magnetic model parameters [29], but it is sensitive to initial solution and dataset noise. Alternatively, Root Mean Square Error (RMSE) is introduced for this objective function.

In this paper, the reference dataset was d- and q-axis flux linkage. As deduced above, ${\psi }_d\left(i_d\right)$, ${\psi }_q\left(i_q\right)$ are set as an intermediate function, as in following:

$$\{\begin{array}{l}{f}_k^d({\psi }_{FE}^d,i_{FE}^d,i_{FE}^q,{\mathbf{x}}_d)={\alpha }_d\left(2-e^{-{\gamma }_d{i}_{FE}^d}-e^{-{\gamma }_{d1}{\left(i_{FE}^d\right)}^2}\right)+{\beta }_d{i}_{FE}^d\\ -k\left(2W{i}_{FE}^d{e}^{-W{\left(i_{FE}^d\right)}^2}\right)\left(V_1{\left(i_{FE}^q\right)}^2-i_{FE}^q{e}^{-V{\left(i_{FE}^q\right)}^2}+{\kappa }_q{i}_{FE}^q-e^{-V{i}_{FE}^q}\right)-{\psi }_{FE}^d\\ {\mathbf{x}}_d=\left\{{\alpha }_d,{\gamma }_d,{\beta }_d,k,W,V,V_1,{\kappa }_d\right\}\end{array}$$

(11)

$$\{\begin{array}{l}{f}_k^q({\psi }_{FE}^q,i_{FE}^d,i_{FE}^q,{\mathbf{x}}_q)={\alpha }_q\left(2-e^{-{\gamma }_q{i}_{FE}^q}-e^{-{\gamma }_{q1}{\left(i_{FE}^q\right)}^2}\right)+{\beta }_q{i}_{FE}^q\\ -k\left(1-e^{-W{\left(i_{FE}^d\right)}^2}\right)\left(2V{i}_{FE}^q+V{i}_{FE}^q{e}^{-V{i}_{FE}^q}+{\kappa }_q\right)-{\psi }_{FE}^q\\ {\mathbf{x}}_q=\left\{{\alpha }_q,{\gamma }_q,{\beta }_q,k,W,V,V_1,{\kappa }_q\right\}\end{array}$$

(12)

The objective function was transferred to RMSE

$${\mathrm{RMSE}}_d\left({\mathbf{x}}_d\right)=\sqrt{\frac{1}{N}{\displaystyle \sum _{k=1}^N{f}_d^k{({\psi }_d^{FE},i_d^{FE},i_d^{FE}{,\mathbf{x}}_d)}^2}}$$

(13)

$${\mathrm{RMSE}}_q\left({\mathbf{x}}_q\right)=\sqrt{\frac{1}{N}{\displaystyle \sum _{k=1}^N{f}_q^k{({\psi }_q^{FE},i_q^{FE},i_q^{FE}{,\mathbf{x}}_q)}^2}}$$

(14)

where x is the decision variable, N is the sample number, ψ_FE, i_FE are stator flux linkages and currents in the collected FEA dataset. x_d, x_q are the obtained parameter vectors, where x_d = [x_d1, x_c], and x_q = [x_q1, x_c]. x_d1 and x_q1 are the unique parameters involved in x_d and x_q, respectively, and x_c = [k, W, V, κ_d, κ_q] is the common parameter sub-vector. Here, the subscripts “d” and “q” represent d- and q-axis respectively. N is the number of FEA data.

3. SSO Algorithm

Yuanzhe Zhao and Linjie Ren proposed SSO in 2021.The basic idea is to introduce a self-adaptive mechanism to balance the exploration and exploitation [23]. In this section, the framework of SSO algorithm is briefly provided. P. Guglielmi concludes that in the evolution of a population, exploitation and exploration are often in a trade-off relationship [32]. For evaluating the probability of exploration and exploitation, a probability-based synergistic performance (SP) for the kth candidate solution x_k is defined as

$$P_s\left(x_k,NP\right)=P_d\left(x_k,NP\right)\cdot c_{k,s}+P_f\left(x_k,NP\right)\cdot (1-c_{k,s})$$

(15)

where, $P_s\left(x_k,NP\right)$, $P_f\left(x_k,NP\right)$, $P_d\left(x_k,NP\right)$, represent the SP, fitness performance (FP) and diversity performance (DP) for the candidate, respectively. c_k,s is a random number in the range [0, 1].

3.1. Core Parameters Calculation

The objective function ($f\left(x_k\right)$) is selected as the fitness function ($f_{fitness}\left({\mathit{x}}_k\right)$) for each candidate solution.

$$f_{\mathrm{fitness}}\left({\mathit{x}}_k\right)=f\left({\mathit{x}}_k\right)$$

(16)

Then the candidates are sorted in ascending order according to the value of $f_{\mathrm{fitness}}\left({\mathit{x}}_k\right)$, and finally we calculate probability by the sorting results.

$$R_{\mathrm{fitness} }\left({\mathit{x}}_k,N\right)=NP+1-i_k,i_k=1,2,\dots ,NP$$

(17)

$$P_{k,f }\left({\mathit{x}}_k,NP\right)={\left(\frac{R_{\mathrm{fitness} }\left({\mathit{x}}_k,NP\right)}{NP}\right)}^2$$

(18)

where i_k represents the fitness ranking of x_k in the population.

On the other hand, owing to avoiding local optima, diversity should guarantee the ability to search a wider range. Therefore, the diversity function based on Euclidean distance between candidates [27] is defined as

$$f_{\mathrm{diversity}}\left({\mathit{x}}_k\right)=-{\displaystyle \sum _{w=1}^{NP}\Vert {\mathit{x}}_k-{\mathit{x}}_w\Vert },w=1,2,\dots ,NP$$

(19)

where $\Vert {\mathit{x}}_k-{\mathit{x}}_w\Vert$ represents the Euclidean distance between x_k and x_w. The diversity ranking and DP are presented as follows.

$$R_{\mathrm{diversity} }\left({\mathit{x}}_k,NP\right)=NP+1-j_k,j_k=1,2,\dots ,NP$$

(20)

$$P_{k,d }\left({\mathit{x}}_k,NP\right)={\left(\frac{R_{\mathrm{diversity} }\left({\mathit{x}}_k,NP\right)}{NP}\right)}^2$$

(21)

where j_k represents the fitness ranking of x_k in the population.

The way to select best candidate needs to be redesigned, as Algorithm 1 shows.

Algorithm 1 The Synergistic performance comparison method

1: if $P_s\left(x_k,NP\right)\ne P_s\left(x_l,NP\right)$ then

2:    if $P_s\left(x_k,NP\right)>P_s\left(x_l,NP\right)$ then

3:     return xk

4:   else

5:     return xl

6:   end if

7: else

8:    if $P_d\left(x_k,NP\right)\ne P_d\left(x_l,NP\right)$ then

9:     if $P_d\left(x_k,NP\right)>P_d\left(x_l,NP\right)$ then

10:      return xk

11:     else

12:      return xl

13:    end if

14:   else

15:     if $P_f\left(x_k,NP\right)\ne P_f\left(x_l,NP\right)$ then

16:      if $P_f\left(x_k,NP\right)>P_f\left(x_l,NP\right)$ then

17:       return xk

18:     else

19:       return xl

20:     end if

21:    else

22:      return xk

23:     end if

24:   end if

25: end if

3.2. Framework of SSO

SSO’s evolutionary strategy comes from three Rao Algorithms [22]. The mutation processes are

$${x^{\prime }}_{fbest,v}=x_{fbest,v}+r_{1,fbest,v}\left(x_{fb,v}^R-x_{fw,v}^R\right)$$

(22)

where the superscript “R” represents the randomly selected candidate. x_fb,v, x_fw,v represent the vth variable for the better and worse candidate, respectively. x′_fbest,v is the updated value of x′_k,v. r_1,fbest,v is random numbers for the vth variable in the range [0, 1].

$${x^{\prime }}_{k,v}=x_{k,v}+r_{1,k,v}\left(x_{best,v}^s-x_{worst,v}^s\right)$$

(23)

$${x^{\prime }}_{k,v}=x_{k,v}+r_{1,k,v}\left(\left|x_{best,v}\right|-\left|x_{worst,v}\right|\right)+r_{2,k,v}\left(\left|x_{k,v}\mathrm{or} x_{l,v}\right|-\left|x_{l,v}\mathrm{or} x_{k,v}\right|\right)$$

(24)

where the superscript “s” represents the candidate for quantitative selection based on SP. x_best,v, x_worst,v represent the vth variable for the best and worst candidate, respectively. x′_k,v is the updated value of x_k,v. r_1,k,v and r_2,k,v are the two random numbers for the vth variable in the range [0, 1].

The pseudo code of SSO algorithm is shown in Algorithm 2.

The SSO algorithm has a simple structure and removes algorithm-specific parameters. In the searching process, exploration and exploitation are dynamically balanced.

Algorithm 2 Pseudo code of SSO algorithm

1: Initialize population size (NP) and maximum number of   function evaluations (Max_FES);

2: Generate the initial population randomly,   evaluate the objective function value of each individual;

3: FES = NP;

4: While FES < Max_FES do

5:  Compute fitness performance Pf of each individual xk;

6:  Compute diversity performance Pd of each individual xk;

7:  Get fitness best individual xfbestand fitness worst individual xfworst;

8:  For k = 1 to NP do

9:    if k = fbest  then

10:      Modify the best solution by using (21);

11:   else

12:     Randomly select ck,s∈{0, 1};

13:     Compute Ps each individual according to (14);

14:     Get Ps bestindividual $x_{best}^s$ and Ps wrost individual $x_{worst}^s$;

15:     Select xl1, xl2 from population randomly (l1 ≠ l2);

16:     Ps comparison of xl1and xl2by using Algorithm 1;

17:     if rand > Ps(k)

18:      Modify candidate solution by using (23);

19:     else

20:      Modify candidate solution by using (22);

21:     end if

22:   end if

23:   Compute Pf of the updated individual;

24:   FES = FES + 1;

25:   Accept the new solution if it is better than the old one;

26:  end for

27: End while

4. Sine-Cosine Algorithm

Seyedali Mirjalili proposed the Sine-Cosine algorithm in 2016. The algorithm introduced a trigonometric function to stochastic population-based optimization [14] and realized a wide range search and gradually approaching solutions in the exploitation process. The working principle of SCA is introduced.

Its mutation strategy is as follow:

$$\begin{array}{l}{x}_{k,v}^{\prime }=\{\begin{array}{c}{x}_{k,v}+r_{1,k,v}\sin \left(r_2\right)\times \left|r_3{x}_{best,v}^{}-x_{k,v}\right|,if\hspace{1em}{r}_4<0.5\\ x_{k,v}+r_{1,k,v}\cos \left(r_2\right)\times \left|r_3{x}_{best,v}^{}-x_{k,v}\right|,if\hspace{1em}{r}_4\ge 0.5\end{array}\\ \end{array}$$

(25)

$$r_{1,k,v}=a-\frac{at}{T}$$

(26)

where $x_{k,v}^{\prime }$, $x_{k,v}$, $x_{best,v}^{}$ are the same as ones in (21) to (23), a, t, T represents constant, the current number of iteration and the maximum number of iteration, respectively. The range of $r_{1,k,v}$ and search detail of SCA are as Figure 3 shows.

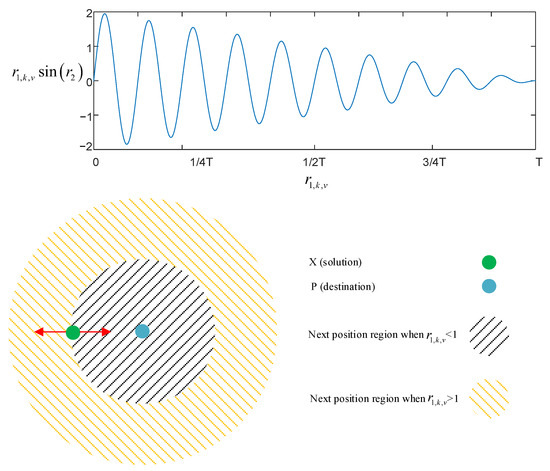
Figure 3. The range of $r_{1,k,v}\cdot \sin \left(r_2\right)$ and search detail of SCA.

As Figure 3 shows, the value of $r_{1,k,v}$ decided the search direction of the SCA algorithm. Additionally, four parameters decide the search path of SCA. $r_{1,k,v}$ defines the direction. $r_2$ dictates how far the movement should be towards or outwards the destination. $r_3$ provides a random weight for the destination in order to stochastically emphasize ($r_3>1$) or deemphasize ($r_3<1$) the effect of destination in defining the distance. Finally, the parameter $r_4$ equally switches between the sine and cosine components. As mentioned above, SCA holds much randomness. Algorithm 3 shows the pseudo code of SCA.

Algorithm 3 Pseudo code of Sine-Cosine algorithm

1: Initialize a set of serach agents (solutions)(X);

2: Do

3: Evaluate each of the search agents by the objective function;

4: Update the best solution obtained so far (P = X*);

5: Update r1, r2, r3, and r4;

6: Update the position of search agents using (24);

7: While (t < maximum number of iterations)

8: Return the best solution obtained so far as the global optimum.

In Algorithm 3, X* represents the best individual in current searching process. The Sine-Cosine algorithm’s search process is adaptive. There is not another parameter that needs to be trained. Moreover, it has a wider search range.

5. Sine-Cosine Self-Adaptive Synergistic Optimization

As stated above, when the current candidate is absolutely not the best solution, and the value of $P_f\left(x_k,NP\right)$ is small, SSO uses Equation (24) to update the direction of exploration. The searching process is shown as Figure 4.

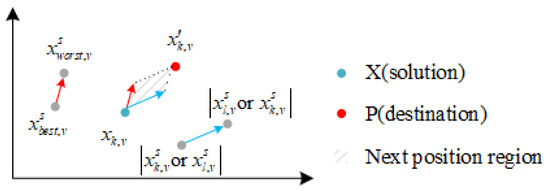
Figure 4. The search detail of SSO.

The next position region is restricted by two reasons. One is the worst solutions. Another is the last candidates. Resulting from the two factors, the next position region is the Rhombic region.

As stated above, the search region of SCA is relatively narrow. However, the search range of SCA is a circle around current candidate, as shown in Figure 3. Moreover, SCA and SSO both automatically balance exploration and exploitation, and SCA has a much wider search range. Thus, if we combine SSO with SCA, the new SC-SSO remains self-adaptive. In addition, SCA replaced Rao-3, offering stronger searching ability. Figure 5 shows the framework of SC-SSO.

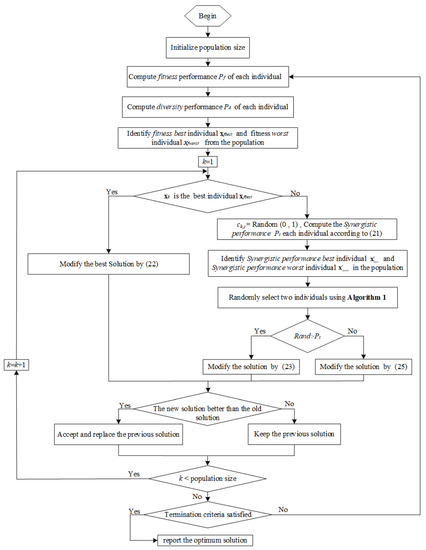
Figure 5. Framework of SCSSO.

As shown in Figure 5, Rao-3 was replaced after the random selection process. When two individuals are randomly selected, a random number decides the equal to modify the solution. If Ps > rand, it proves that current solutions are still valuable and thus continue to exploit around the solution. However, Ps < rand proves that current solutions are worse than surrounding candidates. Then, we use a method to explore.

The standard SSO uses the Rao-3 algorithm to explore, while Rao-3’s search ability is relatively weak. Therefore, SCA is a better alternative.

As shown in Figure 5, the structure of the self-organization mechanism is simple and clear and has no extra parameters. During the operation of the algorithm, the direction of evolution is automatically balanced, which means the convergence strength is self-adaptively managed.

In SCSSO, P_s remains the index of evaluating the capability of current candidates. When the x_k is the best individual, the next searching direction is decided by Equation (21), as Figure 6 shows.

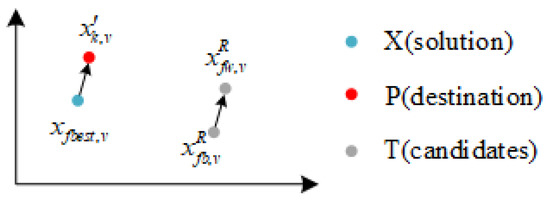
Figure 6. Searching direction when the the x_k is the best individual.

When the x_k is not the best solution, a method of comparing P_s with random numbers has been carried out. If P_s is greater than a random number, we could use Equation (23) to search the best solution around current solutions, but if P_s is smaller than a random number, a much larger search region should be carried out. The search region of SCA is a circle around the destination, as shown in Figure 3, so it could help to get rid of the current worst solution.

6. Experimental Results

In the field of optimization using meta-heuristics and evolutionary algorithms, several tests and experiments should be carried out in order to test the efficiency, accuracy, and robustness of proposed algorithms. In these experiments, FEA data are selected as a benchmark, while the error between the calculation results of object functions and reference data are inferred to RMSE, so that the accuracy and robustness could be evaluated. The analysis software used in this paper is MATLAB. Algorithms are compared by the best RMSE values in 30 populations. Through the best (B), and worst (W) values, we can evaluate the accuracy of them, and the standard deviation (SD) and mean (M) represent the stability of them.

6.1. Reference Data

The reference data come from the finite element analysis of the designed 2 kW prototype SynRMs. The design parameters of the prototype are summarized in Table 1.

Table 1. Parameters of prototype.

Parameters	Values	Parameters	Values
Rated Power (kw)	2	Rated Voltage (V)	60
Rated Speed (r·min−1)	1500	Rated Current (A)	30
Rated Torque (N·m)	12.7	Number of pole pairs	2
Stator resistance (Ω)	0.3	Moment of inertia (kg·m−2)	0.025

The result of FEA illustrated the nonlinearity of SynRMs flux linkage. As i_s increases, the nonlinearity of ψ_s becomes increasingly obvious. As shown in Figure 7a, when i_d reaches 10A, the curve of ψ_d rising becomes slower. The same phenomena appeared in ψ_q. This is so-called self-saturation. Additionally, when i_d is fixed, the value of ψ_d decreases as i_q increases. In Figure 7b, the ψ_q decreases more rapidly than ψ_d in (a). This i_d, i_q influencing mutual flux linkage phenomena is called cross-saturation.

Figure 7. Flux linkage results of FEA. (a) Nonlinear flux linkage of d-axis. (b) Nonlinear flux linkage of q-axis.

To prove the performance metrics of the enhanced SC-SSO, comparative experiments are carried out with other well-performed algorithms, including original Rao algorithms, Ant Lion Optimization (ALO) algorithm [33], differential evolution with biogeography-based optimization (DE/BBO) [34] and JAYA algorithm [35]. For the sake of fairness, different algorithms retain the same parameter configurations, as Table 2 shows.

Table 2. Parameter configurations.

Model	Population Size	Run Times	Max_FES	Parameters Range
				Lower	Upper
q-axis flux linkage model	NP = 30	30	30,000	0	2
d-axis flux linkage model	NP = 30	30	30,000	0	2

6.2. Results on q-Axis Flux Linkage Model

For the q-axis flux linkage model, 11 algorithms are independently implemented 30 times to obtain their self-saturation and cross-saturation parameters. RMSEq is taken as the index of accuracy evaluation. The best parameters and best RMSE are shown to compare in Table 3.

Table 3. Comparison Among Different Algorithms on q-axis Flux Linkage Model.

Algorithm	Self-Saturation Coefficients				Cross-Saturation Coefficients					RMSEq
	αq	βq	γq	γq1	k	W	V	V1	κq
SCSSO	0.0071	0.8712	0.1336	7.8411 × 10−4	0.0255	0.0019	0.012184	0.2528	6.1885	2.2339 × 10−4
SSO	0.0071	0.7738	0.1345	7.8854 × 10−4	0.0060	0.0021	0.0106	0.3756	1.0311	3.5053 × 10−4
SCA	0.0071	0.8712	0.1336	7.8411 × 10−4	0.0255	0.1804	0.079904	0.0012	0	0.0021
GWO	0.0071	1.0610	0.1251	7.8437 × 10−4	0.0198	0.0021	0.0112	0.2685	0.1083	2.3034 × 10−4
ALO	0.0140	0.0014	0.3133	7.7888 × 10−4	0.0197	0.0033	0.0109	0.2151	0.0041	6.9356 × 10−4
BLPSO	0.0070	0.4307	0.4166	7.9459 × 10−4	0.0180	0.0021	0.0121	0.2915	0.1393	2.9613 × 10−4
CLPSO	0.0127	0.0218	0.6777	6.2413 × 10−4	0.0105	1.1194	0.0049	0.4572	0.1498	0.0022
DE/BBO	0.0072	0.4329	0.3368	7.7735 × 10−4	0.0212	0.0023	0.0450	0.2157	2.0000	2.6629 × 10−4
CMM-DE/BBO	0.0070	0.8631	0.2983	7.9557 × 10−4	0.0226	0.0020	0.01150	0.2808	0.0640	2.4377 × 10−4
Rao-1	0.0071	1.0297	0.1238	7.8393 × 10−4	0.0215	0.0020	0.0115	0.2633	0.0751	2.2443 × 10−4
Rao-2	0.0079	0.2632	0.6453	7.0144 × 10−4	0.0215	0.0020	0.0115	0.2633	0.0751	5.8524 × 10−4
Rao-3	0.0072	1.6691	0.0597	7.6864 × 10−4	0.0042	0.0016	0	2.0000	2.0000	7.0207 × 10−4
JAYA	0.0141	0.4671	0	7.6524 × 10−4	0.0050	0.0012	0.0072	0.9533	1.7820	6.9965 × 10−4
PSO	0.0214	0.5025	0.4511	0.0108	0.1847	0.4574	0.0431	0.0306	0.0750	0.1971
GA	0.0029	0.0026	0.0022	0.0013	0.0043	1.11 × 10−5	2.39 × 10−5	5.20 × 10−11	2.99 × 10−6	0.0052

In Table 4, B M and W mean the best mean and worst RMSE values in 30 populations. SD represents standard deviation of 30 RMSE values for each algorithm. As Table 4 shows, the SCSSO offered the best RMSEq value (2.2339 × 10⁻⁴); the second-best value (2.2443 × 10⁻⁴) was offered by RAO-1; and the worst value (0.0022) was offered by CLPSO, which was ten times that of SCSSO. The best RMSEq of SSO and SCA was 1.56 times and 10 times that. of SCSSO. Compared with other well-known algorithms, SCSSO is highly performed. To further illustrate the excellent results of the parameter identification, the q-axis flux linkage map is reconstructed using the best results of the SCSSO algorithm. Table 4 explains the statistical results, and SCSSO ranks first in the comparison. Moreover, the RAO-1 was the second best RMSE, but its mean value was 0.0017, nearly 20 times that of SCSSO. The second-best mean value (4.8678 × 10⁻⁴) was provided by BLPSO, 1.76 times that of the proposed algorithms. Additionally, SCSSO is superior to SCA in statistical results. Although the standard deviation of SCSSO is inferior to SSO, the best RMSEq, worst RMSEq and mean value are superior.

Table 4. Statistical Results of RMSE of Different Algorithms for q-axis Model.

Model	Population Size	Algorithm	RMSE
			B	M	W	SD
q-axis flux linkage model	NP = 30	SCSSO	2.2339 × 10−4	2.7572 × 10−4	6.5841 × 10−4	5.7682 × 10−4
		SSO	3.5053 × 10−4	4.7825 × 10−4	9.1071 × 10−4	1.2444 × 10−4
		SCA	0.0021	0.0036	0.0086	0.0015
		GWO	2.3034 × 10−4	0.0018	0.0050	0.0012
		ALO	6.9356 × 10−4	0.0022	0.0049	0.0010
		BLPSO	2.9613 × 10−4	4.8678 × 10−4	8.5550 × 10−4	6.3891 × 10−4
		CLPSO	0.0022	0.0059	0.0420	0.0077
		DE/BBO	2.6629 × 10−4	0.0012	0.0121	0.0024
		CMM-DE/BBO	2.4377 × 10−4	7.4912 × 10−4	0.0024	6.7630 × 10−4
		Rao-1	2.2443 × 10−4	0.0017	0.0238	0.0043
		Rao-2	5.8524 × 10−4	0.0053	0.0238	0.0074
		Rao-3	7.0207 × 10−4	0.0073	0.0238	0.0093
		JAYA	6.9965 × 10−4	0.0031	0.0074	0.0016
		PSO	0.1935	0.2346	0.9040	0.1270
		GA	0.0052	0.1937	0.3833	0.1106

Figure 8 is the plots of the best RMSEq of the proposed algorithm and other compared ones. As indicated above, the standard deviation of the new algorithm was the smallest in the 11 algorithms, and the best value was the smallest in this comparison.

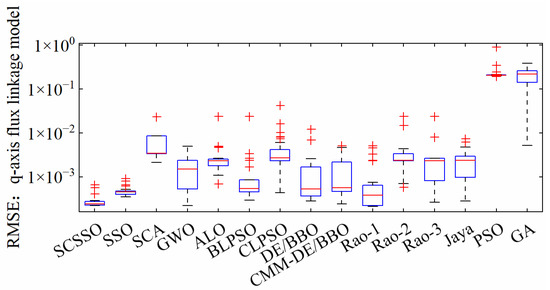
Figure 8. Best boxplot over 30 runs of different algorithms for q-axis flux linkage model.

It can be seen in Table 3 and Table 4 that the best value, mean value and worst value of traditional simple algorithms are one hundred times larger than other improved algorithms. The standard deviation is at least ten times larger than the other 13 algorithms. This proved that the traditional algorithms are not suitable for multidimensional problems.

Figure 9a takes FEA data as a surface and uses the SCSSO algorithm data as the fitting ball to illustrate the accuracy of the SCSSO algorithm. Figure 9b illustrates the mismatch between estimated data and FEA data.

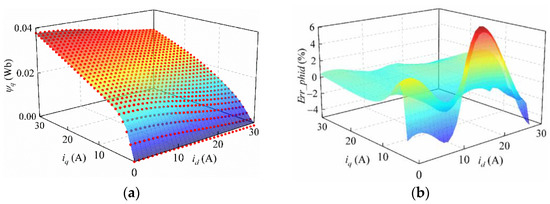
Figure 9. FEA data vs estimated data of q-axis. (a) Comparation between FEA and estimated data. (b) Mismatch of q-axis flux linkage, estimated vs. FEA.

As shown in Figure 9b, the calculation results of the proposed algorithm have only a 6% mismatch with the reference data in the edge of the model, which is attributed to the modeling method and the calculation error of FEA at the model boundary. Under many circumstances, the error of mismatch does not exceed 1%, which means the model with the identified parameters can be applied in actual engineering.

6.3. Results on d-Axis Flux Linkage Model

As the second stage of SynRMs magnetic model parameter identification, the extraction of the d-axis model parameters is similar to the process mentioned in the previous subsection. The best cross-saturation coefficients are obtained in the previous process. Therefore, only four self-saturation parameters need to be identified.

It can be seen from Figure 10 that the estimated data suit the reference perfectly. Moreover, the errors of d-axis flux linkage are below 1%. Table 5 lists the best estimated parameters and the best RMSEd (4.0816 × 10⁻⁴) of different algorithms. The SCSSO keeps the best RMSEd value (4.0816 × 10⁻⁴). Table 6 illustrates that the best RMSE values of the 11 algorithms are resultant, but the mean value, the worst RMSE and standard deviation of the 11 compared algorithms are orders of magnitude larger than the proposed algorithm. Especially with DE\BBO, its mean value was almost 10 times that of SCSSO. The worst RMSE value of GWO was nearly 20 times that of the proposed algorithms. Additionally, the standard deviation of GWO was nearly 60 times that of SCSSO. The SCSSO has superior performance to SCA and SSO in any aspect.

Figure 10. FEA data vs estimated data of d-axis. (a) Comparation between FEA and estimated data. (b) Mismatch of d-axis flux linkage, estimated vs. FEA.

Table 5. Comparison among different algorithms for d-axis flux linkage model.

Algorithm	Self-Saturation Coefficients				RMSEd
	αd	βd	γd	γd1
SCSSO	0.0616	0.1495	0.0100	0.0013	4.0816 × 10−4
SSO	0.0615	0.1498	0.0100	0.0013	4.0854 × 10−4
SCA	0.0602	0.1587	0.0112	0.0015	4.8188 × 10−4
GWO	0.0615	0.1498	0.0100	0.0013	4.0818 × 10−4
ALO	0.0623	0.1484	0.0098	0.0013	4.2398 × 10−4
BLPSO	0.0595	0.1491	0.0108	0.0015	5.2488 × 10−4
CLPSO	0.0613	0.1665	0.0086	0.0014	9.0099 × 10−4
DE/BBO	0.0602	0.1509	0.0104	0.0014	4.5824 × 10−4
CMM-DE/BBO	0.0615	0.1498	0.0100	0.0013	4.0818 × 10−4
Rao-1	0.0615	0.1500	0.00995	0.0013	4.0866 × 10−4
Rao-2	0.0616	0.1497	0.0100	0.0013	4.0821 × 10−4
Rao-3	0.0615	0.1498	0.0100	0.0013	4.0817 × 10−4
JAYA	0.0619	0.1499	0.0099	0.0013	4.0828 × 10−4
PSO	0.0378	0.0745	0.3731	0.0033	0.0384
GA	0.0131	0.0675	1.9945	0.0704	0.0140

Table 6. Statistical results of RMSE of different algorithms for d-axis model.

Model	Population Size	Algorithm	RMSE
			B	M	W	SD
d-axis flux linkage model	NP = 30	SCSSO	4.0816 × 10−4	4.6754 × 10−4	7.5682 × 10−4	9.1699 × 10−5
		SSO	4.0854 × 10−4	7.0770 × 10−4	0.0022	4.2779 × 10−4
		SCA	4.8188 × 10−4	0.0012	0.0020	4.2928 × 10−4
		GWO	4.0818 × 10−4	0.0029	0.0232	0.0056
		ALO	4.2398 × 10−4	0.0032	0.0180	0.0017
		BLPSO	5.2488 × 10−4	0.0012	0.0020	4.2742 × 10−4
		CLPSO	9.0099 × 10−4	0.0036	0.0100	0.0018
		DE/BBO	4.5824 × 10−4	0.0036	0.0079	0.0022
		CMM-DE/BBO	4.0818 × 10−4	0.0021	0.0058	0.0016
		Rao-1	4.0866 × 10−4	0.0010	0.0034	0.0014
		Rao-2	4.0821 × 10−4	0.0028	0.0232	0.0041
		Rao-3	4.0817 × 10−4	0.0023	0.0034	0.0012
		JAYA	4.0828 × 10−4	0.0018	0.0036	0.0013
		PSO	0.0384	0.0787	0.3728	0.0781
		GA	0.0140	0.0784	0.6984	0.1395

Figure 11 shows the plots of the best RMSEd of the proposed algorithm and other compared algorithms. As shown above, the best and worst RMSE, mean value and standard deviation were the smallest of all.

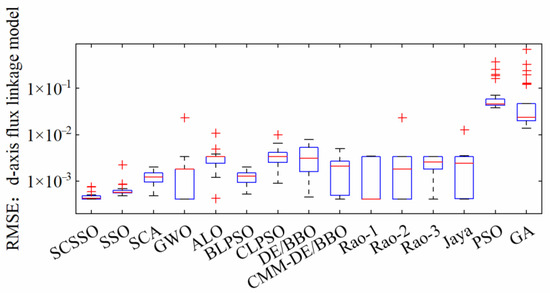
Figure 11. Best boxplot over 30 runs of different algorithms for d-axis flux linkage model.

An experiment in an SynRM prototype was carried out based on the 2 kW SynRM prototype and MicroLabBox dSPACE experimental platform, as shown in Figure 12. Its parameters are shown in Table 1. The hysteresis brake is used as the brake load. The torque sensor is installed on the shaft between the SynRM prototype and the hysteresis brake to measure the torque generated by the SynRM; the customized 55 kW three-phase inverter is powered by the 9 kW DC power supply to drive the motor; a MicroLabBox dSPACE ds1202 with a 2 GHz dual-core real-time processor and programmable FPGA is used as the system controller for implementing the control algorithm, sending pulses to the inverter, and sampling and analyzing information of the measured currents, position and torque of the motor. In the experiment tests, the sampling time is chosen as 100 μs.

Figure 12. Experimental platform of SynRM prototype: (a) PC with software of dSPACE ControlDesk; (b) Torquemeter; (c) 9 kW DC power supply; (d) MicroLabBox dSPACE ds1202; (e) Customized three-phase inverter; (f) Oscilloscope; (g) 2 kW SynRM prototype with resolver; (h) Torque sensor; (I) Hysteresis brake.

To verify the applicability of the proposed algorithm, the results of the proposed algorithm obtained were compared with the traditional look-up table method.

The experimental results are shown in Figure 13.

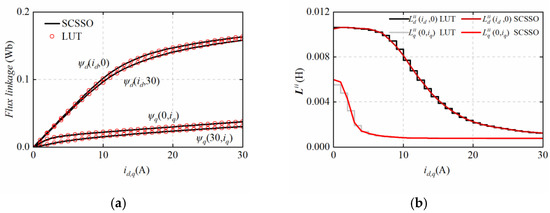
Figure 13. Comparison between LUT and SCSSO. (a) Flux linkages between LUT VS SCSSO. (b) Incremental inductances LUT VS SCSSO.

It can be seen from Figure 13 that the flux linkages and incremental inductances can highly fit the traditional method. Additionally, because of the differentiability of objective function, the incremental inductances are continuous.

6.4. Results Discussion

The comparison results demonstrate that the proposed SCSSO algorithm has much better accuracy and effectiveness for solving the parameters identification problem of the SynRMs magnetic model, and its performance is competitive in contrast with all compared algorithms. The difference between the best RMSEd and the best RMSEq provided by the proposed SCSSO algorithm can be clearly observed. On one hand, the accuracy of the experimental results in the q-axis model is considerable, and the algorithm error is inevitably introduced into the d-axis model with the application of cross-saturation parameters. On the other hand, the energy loss of the rotor region corresponding to the d- and q-axis is different. Those losses are not reflected in the cross-saturation parameters under conservative field assumptions. This makes the influence of the loss contained in the standard datasets equivalent to a kind of noise, which is accumulated and introduced into the identification result of the d-axis self-saturation parameters. Fortunately, the values of best RMSEd and RMSEq are in the same order of magnitude. Thus, the superior accuracy and robustness of the proposed SCSSO algorithm can be explained in one aspect, while its stability was contrasted by itself under a different NP. Thus, an experiment was carried out to test the robustness and stability of SCSSO. In this experiment, the SCSSO algorithm with NP = 10, 20, 30, 40 and 50 was tested and compared, maintaining the Max_FES at 30,000. The statistical results are presented in Table 7.

Table 7. Statistical results of SCSSO algorithm with varying NP for SynRMs magnetic model (30,000 function evaluations).

Model	RMSE	Population Size
		NP = 10	NP = 20	NP = 30	NP = 40	NP = 50
q-axis flux linkage model	B	3.15164 × 10−4	3.4644 × 10−4	2.2339 × 10−4	6.4685 × 10−4	8.7220 × 10−4
	M	5.1534 × 10−4	4.5315 × 10−4	2.7572 × 10−4	0.0031	0.0045
	W	0.0045	0.0053	6. 5841 × 10−4	0.0034	0.0045
	SD	1.4531 × 10−3	1.4153 × 10−4	5.7682 × 10−4	6.4845 × 10−4	6.6546 × 10−4
d-axis flux linkage model	B	4.0828 × 10−4	4.0925 × 10−4	4.0816 × 10−4	4.1557 × 10−4	5.4685 × 10−4
	M	9.3769 × 10−4	4.9046 × 10−4	4.6754 × 10−4	6.4842 × 10−4	9.4531 × 10−4
	W	0.0076	6.9249 × 10−4	7.5682 × 10−4	0.0048	0.0081
	SD	1.5883 × 10−3	7.3260 × 10−4	9.1698 × 10−5	4.5151 × 10−4	0.0048

It can be clearly seen that due to the different dimensions of the problem, the optimal population size for different problems is also different. Hence, the most appropriate population size for the parameter identification of d- and q-axis flux models is set to 30.

7. Conclusions

In this paper, an SCSSO algorithm based on SSO and SCA is proposed to extract the parameters of the SynRMs nonlinear magnetic model. Compared with traditional and simple algorithms, the proposed algorithm has improved more than 80 times. Additionally, the proposed algorithm has improved by 10% (even by 50% compared to some outstanding algorithms). Experiment results elaborated that the SCSSO algorithm is effective enough to solve the parameter identification problems of the SynRMs nonlinear magnetic model. Moreover, through the verification of the proposed SynRMs model parameter identification, it can be inferred that the proposed algorithm can be extended to the solution of the multi-parameter and multi-peak problem. Furthermore, through the verification of SynRM prototype, the practicability of the proposed method could better describe the nonlinearity of the magnetic circle than the traditional method. In our future work, the iron loss and the variation of resistance could be taken into consideration. On the basis of the research in this study, in view of the noise characteristics of the measured reference data, it is necessary to further study the evolution strategy of metaheuristic algorithms with higher robustness to further improve the accuracy of SynRMs magnetic model parameter identification.