Over-Current Relays Coordination Including Practical Constraints and DGs: Damage Curves, Inrush, and Starting Currents

Abstract

In this paper, an integrated optimization model based on Gradient-Based Optimizer (GBO) for overcurrent relays coordination along with the challenging practical constraints is proposed. The current proposed effort aims to facilitate the coordination strategy and minimize the technical problems facing the protection/site engineers. The objective function is adapted to minimize the total operating time of the primary relays (TOT) concurrently with satisfying a set of constraints. The algorithm endeavors to fine-tune the relay tripping curve to avoid the false tripping in the case of motor starting and/or transformer inrush conditions. Bear in mind that the selected optimized settings should guarantee that the relay would operate in less time than the thermal withstand capability time of the protected equipment. The proposed model is examined over the distribution portion of the Qarun petroleum isolated network (located in West desert/Egypt), which presents a practical test case including some scenarios after validating its performance with the IEEE 15-bus network. The proposed complicated optimization problem comprises 128 discrepant inequality constraints for overcurrent relays coordination only having 16 relays with 14 relay pairs. Eventually, GBO demonstrates that it is an efficient algorithm for solving this highly constrained optimization problem by comparing its performance to other robust and well-known algorithms such as particle swarm optimizer (PSO) and water cycle optimizer (WCA). The performance metrics confirm the GBO’s viability over the others. For sake of quantification, (i) for scenario1 of the Qarun test case, the GBO achieves a TOT of 0.7381 s, which indicates 63% and 57% reductions for those obtained by the PSO and WCA, respectively, and (ii) for the 15-bus test case, reductions in the TOT of 14.3% and 16.5% for scenarios 1 and 2, respectively. The proposed tool based on GBO can enhance the protection co-ordination including some practical constraints.

1. Introduction

Directional Over-Current Relays (DOCRs) can be considered as the primary protection in distribution and sub-transmission systems [1]. The primary relay is responsible for clearing the fault first, and if it fails, the backup one should act after a particular value called the Coordination Time Interval (CTI) [2]. The settings of digital OCRs are mainly the pickup current ($I_p$), time dial ($T_D$), and the Time Current Characteristic (TCC) type, which determines the inverse degree of the tripping curve [3]. International Electrotechnical Commission (IEC 60255-3) [4] and IEEE C37.112 [5] define the most commonly used standardized tripping Characteristics (CCs). However, the utilization of nonstandard tripping CCs was proposed in [6] by also optimizing the tripping equation coefficients.

The main objective of the DOCR coordination problem is to minimize the total operating time of the relays in addition to achieving the problem constraints [7]. Previously, it has been solved using conventional techniques such as Linear Programming (LP), Non-Linear Programming (NLP), and Mixed-Integer LP (MILP), as presented in [8]. Moreover, metaheuristic-based algorithms either nature-inspired, swarm-based, or evolutionary-based have been tackled to upgrade the results and the convergence rate [9]. Afterward, hybrid techniques have been implemented such as Cuckoo Search Algorithm and LP in [10] for solving the optimal coordination of DOCRs in microgrids with grid-connected and islanded modes [11]. In this sense, the optimal coordination proposed in [12] complicated the problem by including energy storage systems and inverter-based Distributed Generators (DGs) in the tested networks. The dual-setting DOCR approach was utilized in [13,14,15] for automated distribution networks. The optimal sizing of fault current limiters was investigated to preserve the coordination in the case of DG penetration, as illustrated in [16,17,18].

Various methodologies and formulas of Objective Functions (OFs) have been tackled in the literature, which can be found summarized in [19]. A new approach was discussed in [20] taking into account the topology transient changes using a complete model of all network elements. Various topologies were also discussed in [21] by optimizing the relay-type CCs as in [22] for the microgrid’s optimal protection coordination considering N-1 contingency. However, DOCR coordination was solved using the critical fault point instead of the near-end fault point, as found in [23], which improved the results accuracy. Afterward, active settings of digital OCRs by using the setting group concept were utilized in [24] to be adapted with the current topology of the network. New time–current–voltage CCs in [25] and double-inverse CCs in [26] were proposed to enhance the DOCR coordination in the presence of DGs. Moreover, a modified depth-first search algorithm was proposed in [27], while it was hybridized with MILP in [28] for determining the minimum breakpoint set along with the coordination of OCRs. In this regard, a hybrid variable neighborhood search and LP algorithm was formulated in [29] to cope with diverse DOCRs for online optimal coordination. Furthermore, a stochastic fractal search algorithm was exploited in [30], while the arc flash hazards were assessed along with the optimal OCRs coordination in [31].

This research aims to develop a comprehensive optimization model for OCR coordination integrated with various types of constraints [32,33,34,35,36,37]. These constraints are discrepant in nature, which simulates the real network operating conditions. The objective of this methodology is to minimize the operating time of the primary relays along with satisfying as many of these constraints as possible. Minimum operating time, transient condition, and equipment damage curve constraints represent the main contributions inserted into the optimization model. This highly constrained optimization model is solved through a new optimization approach called Gradient-Based Optimizer (GBO) [32]. It is selected based on the NFL theorem that states that no particular algorithm can solve all optimization problems efficiently. GBO combines the principles of gradient and heuristic-based techniques by enhancing both exploration and exploitation phases [32]. It is worth mentioning that the GBO performance is validated against one of the powerful algorithms for solving power system optimization problems: Slime Mold Algorithm (SMA). Moreover, the GBO results are validated by a fair comparison with other robust algorithms such as Particle Swarm Optimizer (PSO) and Water Cycle Algorithm (WCA).

The main contributions of this work may be summarized as follows: (i) a novel optimization model including practical constrains such as transformer inrush, and motor starting and damage curves are considered, (ii) a novel attempt is made to test the performance of the GBO in solving the OCR problem, and (iii) demonstrations are made on a typical isolated distribution network.

The body of this article is organized into five sections. The formulation of the proposed model is announced in Section 2. Section 3 gives the procedures of the GBO, and the numerical simulations are demonstrated in Section 4 along with various validations. Finally, the findings and concluding remarks are summarized in Section 5.

2. Optimization Model Formulation

The relay operating time $\left(t_{ri}\right)$ can be calculated through (1) by optimizing the relay settings, i.e., ($I_p$, $T_D,$ and $TCC$ type). Table 1 gives the constant values of $a,b,\mathrm{and}c$ for various IEC and IEEE CCs. The objective of the OCR coordination problem is to minimize the Total Operating Time (TOT) of the primary relays ($t_{pri})$ in addition to preserving the problem constraints, as declared in (2). Boundary, selectivity, and operating constraints should be met for achieving feasible results.

$$t_{ri}=\left(\frac{a}{{\left(\frac{I_f}{I_p}\right)}^b-1}+c\right)T_D$$

(1)

$$OF={\displaystyle \sum }_{i=1}^M{t}_{pri}+W{F}_m{\displaystyle \sum }_{i=1}^M\Delta t_{mi}+W{F}_c{\displaystyle \sum }_{j=1}^K\Delta t_j+W{F}_t{\displaystyle \sum }_{i=1}^{M1}\Delta t_{ti}+W{F}_d{\displaystyle \sum }_{i=1}^{M2}\Delta t_{di}$$

(2)

Table 1. Constants for common standardized tripping curves.

CCs Type	Std		$a$	$b$	$c$
	IEC	IEEE
SI	✓	✕	0.1400	0.0200	0.0000
VI	✓	✕	13.5000	1.0000	0.0000
EI	✓	✕	80.0000	2.0000	0.0000
LI	✓	✕	120.0000	1.0000	0.0000
MI	✕	✓	0.0515	0.0200	0.1140
VI	✕	✓	19.6100	2.0000	0.4910
EI	✕	✓	28.2000	2.0000	0.1217

SI: standard inverse, VI: very inverse, EI: extremely inverse, LI: long inverse, MI: moderately inverse.

2.1. Boundary Constraints

The optimized decision variables should be bounded between lower and upper limits for feasible solution, as shown in (3) and (4).

$$T_{Dmin,i}\le T_{D,i}\le T_{Dmax,i}$$

(3)

$$I_{pmin,i}\le I_{p,i}\le I_{pmax,i}$$

(4)

2.2. Selectivity Constraints

The backup relay should act after a specified period called $CTI$ if the primary relay fails to trip, as shown in (5). The value of $CTI$ is also bounded between the minimum value ($CT{I}_{min})$ and maximum value ($CT{I}_{max})$ to restrict the coordination criteria inside a practical time range.

$$CT{I}_{min,j}\le \Delta t_j\le CTI{}_{max,j},\Delta t_j=t_{bri}-t_{pri}$$

(5)

2.3. Operating Constraints

These constraints can be divided into three sets to simulate the real network operating conditions as follows.

2.3.1. Minimum Operating Time Constraint

As the coordination optimization problem tends to minimize the relay operating time, the results may contain an infeasible tripping time not included in any commercial relay. A penalty term $(\Delta t_{mi})$ is inserted in the OF to guarantee that the relay tripping time $(t_{ri})$ is greater than or equal to a specific value $\left(t_{min,i}\right)$, as demonstrated in (6).

$$t_{ri}-t_{min,i}\ge \Delta t_{mi}\ge 0$$

(6)

2.3.2. Transient Conditions Constraints

It is worth mentioning that induction motors have a starting current range of (3–8) of the motor full load current depending on the starting method and conditions. In this regard, a high inrush current drawn from the supply during transformer energizing has a range of (8–12) for transformer full load current. These transient high currents may lead to a false tripping of the relay during these transient conditions. Figure 1 depicts a typical motor starting curve and a standardized relay tripping CC with the methodology of the practical coordination rules illustrated on it. To avoid the intersection between the two curves, a current margin of (75%$.I_{starting}$) and a time margin ($t_{rt,i}-t_{t,i}$) of (2–10) s shall be considered and may be extended to 1 s, as shown. The same practical coordination rules mentioned earlier should also be considered in the case of a transformer overcurrent relay protection feeder, as shown in Figure 2.

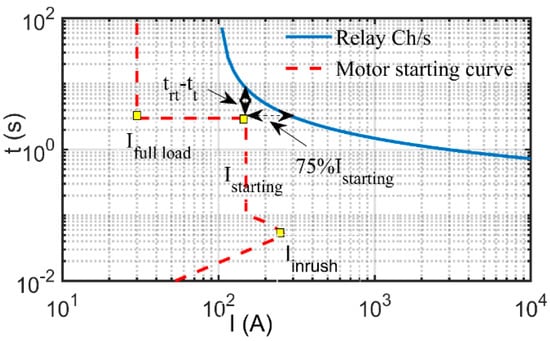
Figure 1. Motor starting curve with the practical coordination rules.

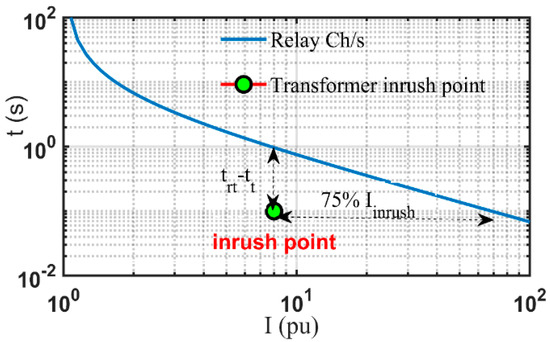
Figure 2. Transformer inrush point with the practical coordination rules.

Consequently, a penalty term is added to the OF $\left(\Delta t_{ti}\right)$ to ensure that the relay tripping curve is higher than the motor starting curve or the transformer inrush point, as expressed in (7). $t_{rt,i}$ is the relay operating time at the transient current and $t_{t,i}$ is the motor starting time or the transformer inrush current period.

$$t_{rt,i}-t_{t,i}\ge \Delta t_{ti}$$

(7)

2.3.3. Equipment Damage Curves Constraints

All electrical equipment in power systems has a thermal withstand capability curve called a “damage curve”. The damage curve is an inverse relation between the current passing through the equipment and the withstand time. The larger the current that flows $\left(I\right)$, the lower the equipment withstand time $\left(t_{d,i}\right)$. The equipment damage curve can be expressed in (8) where $LTE$ is the Let Through Energy that represents the withstand electrical capability that, in turn, is a constant value. The relation between the fault current passing through a feeder $(I_f)$ in amperes and $t_{d,i}$ for a given Cross-Sectional Area ($A$) is shown in (9) [38]. $k_c\mathrm{and}\mathrm{ß}$ depend on the conductor type, while the initial temperature $\left(T_o\right)$ and the final temperature $\left(T_d\right)$ depend on the insulation type, as declared in Table 2. The constants presented in (9) are lumped together for a single constant $\left(k\right)$, as shown in (10) and depicted in Figure 3, while $A$ is in $m{m}^2.$ The value of $k$ depends on the feeder construction, as declared in Table 2, whose value can be found in [38,39] with a slight difference. The distribution transformers used in this research are classified as category 2, as mentioned in [40], whose $k$ constant value equals 1250 per unit.

$$I^2\times t_{d,i}=LTE\left(k{A}^2·s\right)$$

(8)

$${\left(\frac{I_f}{1973.525\times A}\right)}^2\times t_{d,i}=k_c{\log }_{10}\left(\frac{T_d+\mathrm{ß}}{T_o+\mathrm{ß}}\right)$$

(9)

$$t_{d,i}={\left(\frac{k\times A}{I_f}\right)}^2$$

(10)

$$t_{d,i}-t_{pri}\ge \Delta t_{di}$$

(11)

Table 2. Feeder constants under various conductor and insulation materials.

Power Cables
Conductor	Type	${\mathit{k}}_{\mathit{c}}$	$\mathrm{ß}$	Insulation	Type	${\mathit{T}}_{\mathit{o}}$(°C)	${\mathit{T}}_{\mathit{d}}$(°C)	Transmission Lines
	Copper (CU)	0.0297	234		PVC	70	160
					XLPE/EPR	90	250	Type	$k$
	Aluminum (AL)	0.0125	228		Rubber	75	200	AAC/ACAR	132.4235
					Paper	85	200	ACSR	170.1179

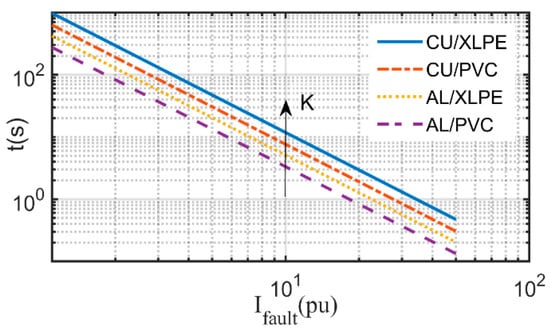
Figure 3. Cable damage curves with various constructions.

To ensure a safe operation, the relay should trip in less time than the equipment withstand time $\left(t_{d,i}\right)$ at the maximum fault point, as shown in (11) and Figure 4. Therefore, a penalty term $\left(\Delta t_{di}\right)$ is added to the OF to satisfy this constraint. It is worth mentioning that there is a conflict of constraints in the optimization model of OCR coordination. This represents a challenging task to the algorithm to pick the optimal settings preserving all these types of constraints. The conflict appears in the algorithm’s attempt to minimize the relay operating time besides positioning the tripping curve above the starting or the inrush curves. Furthermore, the algorithm aims at tripping in less time than the equipment withstand time along with preserving the minimum operating time constraint. Hereinafter, GBO and its behavior concept are discussed in brief in the next section.

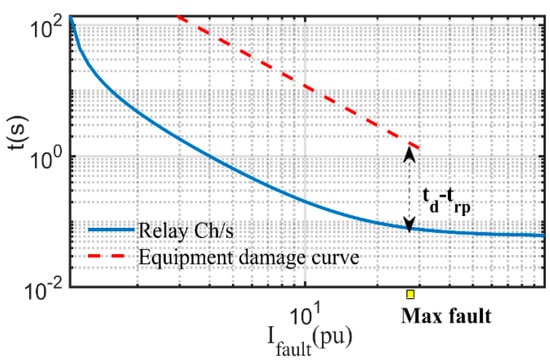
Figure 4. Equipment damage curve with a standard relay CC.

3. Gradient-Based Optimizer

The optimization techniques can be classified into two main categories based on the optimization behavior process [33,34]. Gradient-based techniques such as Newton’s method estimate the derivatives of the OF along with the constraints by identifying an extreme point whose gradient equals zero. The second category is the non-gradient-based approaches such as all metaheuristic algorithms that randomly generate initial populations, and the optimal solution is attained by updating these search vectors. The GBO combines the principles of the two techniques by enhancing both exploration and exploitation phases. GBO has two main operators: Gradient Search Rule (GSR) that is responsible for enhancing the exploration phase for better convergence in the search agents. The other operator is the Local Escaping Operator (LEO) that prevents GBO from becoming trapped in local minima; more details of the mathematical model of GBO can be found in [32,35,36].

$$X_n=X_{lower}+rand\left(0,1\right)\times \left(X_{upper}-X_{lower}\right),n\in N$$

(12)

GBO starts with the population initialization by randomly generating the initial vectors according to (12), where $rand\left(0,1\right)$ is a random number between 0 and 1. $X_n$ represents the solution at iteration n, while $X_{lower}$ and $X_{upper}$ are the boundaries of the decision variable $X$.

$$MOD=rand\left(0,1\right)\times {\rho }_b\times \left(X_{best}-X_n\right)$$

(13)

$${\rho }_b=2\times rand\left(0,1\right)\times \alpha -\alpha$$

(14)

GSR is deemed as the main brain of GBO as it controls the vector’s movement and enhances the exploration phase. The Movement of Direction ($MoD$) of the decision variables can be estimated from (13), where ${\rho }_b$ is a random parameter assessed from (14). The term $X_{best}-X_n$ expresses the convergence process by moving the current vector $X_n$ into the best vector obtained $X_{best}$. The parameter $\alpha$ varies with the number of iterations and its value is changed at each iteration, as shown in a figure depicted in [32,36].

$$X_{n+1}=X_n-\frac{2\Delta X\times \mathrm{ƒ}\left(X_n\right)}{\mathrm{ƒ}\left(Y_n+\Delta X\right)-\mathrm{ƒ}\left(Y_n-\Delta X\right)}$$

(15)

$$GSR=rand\left(0,1\right)\times {\rho }_a\times \frac{2\Delta X\times X_n}{\left(Y{p}_n-Y{q}_n+ϵ\right)}$$

(16)

As GBO inspires its procedures from Newton’s method, as expressed in (15), the GSR performance is improved by calculating it from (16). ${\rho }_a$ is the parameter that balances the exploration and exploitation phases and varies with the parameter $\alpha$.

$$X_{rand}=X_{lower}+rand\left(0,1\right)\times \left(X_{upper}-X_{lower}\right)$$

(17)

$$X_k^m=L_2\times X_p^m+\left(1-L_2\right)\times X_{rand}$$

(18)

To promote the efficacy of the proposed algorithm, the LEO is implemented in the subroutine represented briefly in (17) and (18). $X_{rand}$ is a new solution, while $X_p^m$ is selected randomly over the population and $X_k^m$ is the newest randomly generated vector. $L_2$ is a binary number that takes a value of 0 or 1 based on the random assessing of other parameters for obtaining the global optimal solution. The relations of the other variables presented in (15)–(18) can be found in detail in [32,36] to avoid making the paper too long. The general procedures of the GBO are depicted in Figure 5 [35,36].

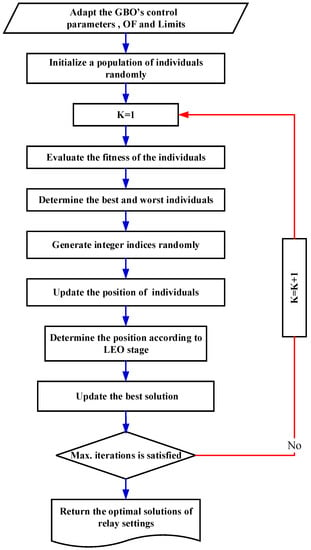
Figure 5. General procedures of the GBO.

4. Simulation Results and Discussions

The GBO performance is evaluated on two different test cases with various optimization models. The first one is the IEEE 15-bus network that is considered as a test bench tackled by several optimization techniques in the literature. The second one is the medium-voltage distribution portion of the Qarun petroleum company, which is considered an isolated network. New microprocessor-based relays are implemented in both networks coping with continuous decision variables. The limits of $I_p$ are 100% and 150% of the full load current, while the boundaries of $T_D$ are 0.05 s and 1 s, and $CTI$ ranges from 0.2 s to 0.4 s. A $t_{min}$ of 50 ms is selected as the minimum relay operating time in this research to emulate most of the recent digital relays. The simulation results are executed in the MATLAB environment and implemented using a PC with an AMD A8 processor, 6 GB RAM, and a Windows 10 operating system.

4.1. Test Case 1: IEEE 15-Bus Test Network

To validate the efficacy of the proposed optimization model, GBO performance is examined on the IEEE 15-bus network, which is depicted in Figure 6. This highly penetrated DG network consists of 6 DGs, 21 lines, 42 relays, and 82 Primary/Backup (P/B) relay pairs that are given along with the fault currents in [41]. The optimized settings of DOCRs using the three scenarios are tabulated in Table 3. Scenario 1 achieves a fitness function of 10.2601 s by optimizing 84 decision variables considering the fixed SI tripping curve. In addition, 2.0474 s is the best fitness function obtained by extending the problem to optimize 126 decision variables by selecting the best curve between IEC standardized tripping curves. A fair comparison between GBO and SMA [42] is studied and clarifies that GBO is an efficient optimizer for solving the DOCR coordination. GBO achieves a notable reduction in the total operating time compared to SMA of about 14.3% and 16.5% for scenarios 1 and 2, respectively. In scenario 2, some relays trip in a very small time, which violates the real network conditions. Therefore, the minimum operating time constraints are added to the optimization model in scenario 3, attaining a total time of 2.8198 s. In this context, Table 4 illustrates the operating times of P/B relay pairs and their associated CTI values using the three scenarios. Moreover, GBO attempts all the selectivity constraints in all scenarios with diverse convergence characteristics, as depicted in Figure 7.

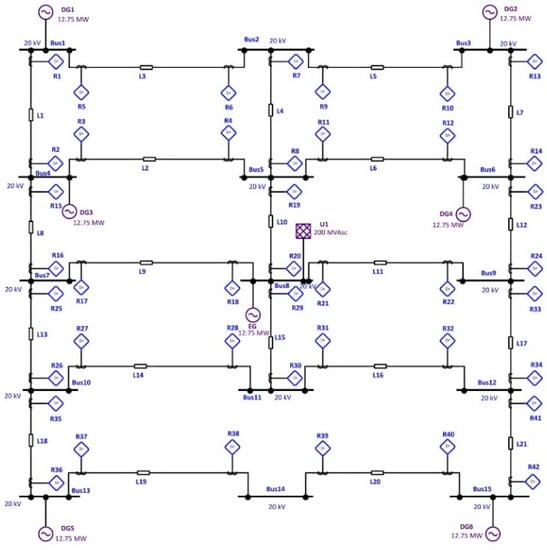
Figure 6. IEEE 15-bus test network single-line diagram.

Table 3. DOCRs optimal settings of IEEE 15-bus test network.

Relay ID	Scenario 1		Scenario 2			Scenario 3
	${\mathit{I}}_{\mathit{p}}\left(\mathit{A}\right)$	${\mathit{T}}_{\mathit{D}}\left(\mathit{s}\right)$	${\mathit{I}}_{\mathit{p}}\left(\mathit{A}\right)$	${\mathit{T}}_{\mathit{D}}\left(\mathit{s}\right)$	$\mathit{T}\mathit{C}\mathit{C}$	${\mathit{I}}_{\mathit{p}}\left(\mathit{A}\right)$	${\mathit{T}}_{\mathit{D}}\left(\mathit{s}\right)$	$\mathit{T}\mathit{C}\mathit{C}$
1	245.2154	0.0769	198.8608	0.0558	EI	200.6693	0.0674	VI
2	242.1648	0.0959	230.0005	0.0512	EI	230.0000	0.0734	VI
3	446.2669	0.0722	326.1272	0.0521	EI	387.1645	0.0548	VI
4	295.0000	0.0986	318.7285	0.0542	EI	407.6785	0.0490	VI
5	345.0000	0.0976	345.1292	0.0467	EI	349.3123	0.0558	EI
6	271.5379	0.0866	263.3328	0.0645	EI	250.0000	0.0739	EI
7	291.3159	0.0881	303.9544	0.0356	EI	271.9109	0.0539	EI
8	501.6190	0.0755	402.4457	0.0434	EI	396.0000	0.0574	VI
9	340.0234	0.0647	297.1377	0.0337	EI	340.4649	0.0374	VI
10	320.6639	0.0857	278.4108	0.0460	EI	293.2507	0.0516	VI
11	402.3677	0.0793	300.0018	0.0782	EI	303.3797	0.0730	VI
12	429.9626	0.0806	336.1315	0.0643	EI	447.4937	0.0542	EI
13	349.1431	0.0704	347.6792	0.0363	VI	357.7547	0.0360	VI
14	288.0940	0.0903	298.0157	0.0405	EI	271.1177	0.0648	VI
15	328.8095	0.0731	247.5089	0.0499	EI	303.5143	0.0538	VI
16	204.1901	0.0797	170.3275	0.0538	EI	209.0682	0.0529	VI
17	134.3431	0.0893	127.1071	0.0720	EI	135.0273	0.0645	VI
18	364.5879	0.0872	330.0068	0.0603	VI	393.5179	0.0755	VI
19	393.5610	0.0720	304.8611	0.0648	EI	333.1832	0.0609	VI
20	495.9189	0.0852	415.0082	0.0614	EI	441.5143	0.0647	VI
21	426.8790	0.0795	380.7279	0.0374	EI	460.0089	0.0638	VI
22	138.4039	0.0916	166.7603	0.0571	VI	137.5225	0.0689	VI
23	300.8530	0.0829	276.7387	0.0512	VI	322.4169	0.0527	VI
24	195.8838	0.0862	174.9163	0.0571	VI	170.0000	0.0648	VI
25	299.2712	0.0796	242.0540	0.0515	EI	266.1785	0.0456	EI
26	303.5105	0.0679	205.0000	0.0664	EI	223.3536	0.0620	VI
27	306.8094	0.0806	239.6638	0.0651	VI	236.8383	0.0602	EI
28	381.8977	0.0783	303.2900	0.0582	EI	300.0001	0.0577	EI
29	620.8050	0.0755	450.4305	0.0525	EI	493.8575	0.0588	VI
30	138.8182	0.0951	137.0251	0.0691	EI	181.7429	0.0564	EI
31	263.4773	0.0816	221.5581	0.0559	VI	220.0000	0.0570	VI
32	255.4869	0.0702	190.0056	0.0426	EI	203.5645	0.0615	VI
33	354.8464	0.0779	299.0247	0.0437	EI	332.4263	0.0538	VI
34	263.2423	0.0829	200.0010	0.0767	EI	217.5601	0.0643	EI
35	323.5058	0.0748	255.6778	0.0602	VI	271.2643	0.0367	EI
36	353.9631	0.0816	355.4702	0.0550	VI	290.0001	0.0607	VI
37	438.0994	0.0886	400.0012	0.0630	VI	407.2676	0.0421	EI
38	290.5859	0.0724	229.4515	0.0500	EI	246.0091	0.0414	EI
39	264.6272	0.0778	201.6115	0.0613	EI	249.5618	0.0385	EI
40	485.1641	0.0792	489.8822	0.0428	VI	522.3651	0.0382	VI
41	261.9881	0.0748	200.0461	0.0574	EI	252.4027	0.0438	VI
42	269.6373	0.0884	252.0226	0.0548	VI	303.9431	0.0428	VI
OF (s)	10.2601		2.0474			2.8198

Table 4. Operating times of P/B relay pairs and their associated CTI values of IEEE 15-bus test network.

P/B Relay Pair		Scenario 1			Scenario 2			Scenario 3
P	B	${\mathit{t}}_{\mathit{p}\mathit{r}}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{b}\mathit{r}}\left(\mathit{s}\right)$	$\mathit{C}\mathit{T}\mathit{I}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{p}\mathit{r}}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{b}\mathit{r}}\left(\mathit{s}\right)$	$\mathit{C}\mathit{T}\mathit{I}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{p}\mathit{r}}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{b}\mathit{r}}\left(\mathit{s}\right)$	$\mathit{C}\mathit{T}\mathit{I}\left(\mathit{s}\right)$
1	6	0.1946	0.3948	0.2002	0.0135	0.2465	0.2329	0.0534	0.2536	0.2002
2	4	0.2213	0.4217	0.2004	0.0103	0.2117	0.2014	0.0522	0.2521	0.1999
2	16	0.2213	0.4264	0.2050	0.0103	0.2386	0.2284	0.0522	0.2796	0.2275
3	1	0.2260	0.4264	0.2004	0.0281	0.2567	0.2286	0.0797	0.2799	0.2003
3	16	0.2260	0.4264	0.2004	0.0281	0.2386	0.2105	0.0797	0.2796	0.1999
4	7	0.2490	0.4548	0.2058	0.0230	0.2302	0.2072	0.0678	0.2749	0.2071
4	12	0.2490	0.4552	0.2062	0.0230	0.2867	0.2636	0.0678	0.4480	0.3801
4	20	0.2490	0.4549	0.2059	0.0230	0.2734	0.2504	0.0678	0.2823	0.2144
5	2	0.2949	0.4953	0.2004	0.0409	0.2718	0.2309	0.0500	0.3293	0.2793
6	8	0.2603	0.4634	0.2031	0.0515	0.2514	0.1999	0.0532	0.2661	0.2129
6	10	0.2603	0.4810	0.2207	0.0515	0.2517	0.2001	0.0532	0.2533	0.2000
7	10	0.2811	0.4810	0.1999	0.0428	0.2517	0.2089	0.0518	0.2533	0.2015
8	3	0.2309	0.4308	0.1999	0.0257	0.2308	0.2051	0.0713	0.2765	0.2051
8	12	0.2309	0.4552	0.2243	0.0257	0.2867	0.2610	0.0713	0.4480	0.3766
8	20	0.2309	0.4549	0.2240	0.0257	0.2734	0.2477	0.0713	0.2823	0.2109
9	5	0.2054	0.4815	0.2761	0.0278	0.2429	0.2152	0.0660	0.2974	0.2314
9	8	0.2054	0.4634	0.2580	0.0278	0.2514	0.2237	0.0660	0.2661	0.2001
10	14	0.2432	0.4431	0.1999	0.0225	0.2225	0.2000	0.0624	0.2625	0.2001
11	3	0.2277	0.4308	0.2031	0.0300	0.2308	0.2008	0.0740	0.2765	0.2024
11	7	0.2277	0.4548	0.2271	0.0300	0.2302	0.2002	0.0740	0.2749	0.2009
11	20	0.2277	0.4549	0.2272	0.0300	0.2734	0.2434	0.0740	0.2823	0.2082
12	13	0.2421	0.4418	0.1997	0.0332	0.2414	0.2082	0.0500	0.2499	0.1999
12	24	0.2421	0.4419	0.1998	0.0332	0.2331	0.1999	0.0500	0.2552	0.2053
13	9	0.2117	0.4119	0.2002	0.0558	0.2561	0.2003	0.0571	0.2569	0.1999
14	11	0.2217	0.4216	0.1999	0.0136	0.2698	0.2562	0.0547	0.2552	0.2004
14	24	0.2217	0.4419	0.2203	0.0136	0.2331	0.2195	0.0547	0.2552	0.2005
15	1	0.1871	0.4264	0.2392	0.0111	0.2567	0.2457	0.0500	0.2799	0.2300
15	4	0.1871	0.4217	0.2346	0.0111	0.2117	0.2006	0.0500	0.2521	0.2021
16	18	0.2280	0.4685	0.2405	0.0254	0.2713	0.2460	0.0741	0.4332	0.3591
16	26	0.2280	0.4306	0.2026	0.0254	0.2874	0.2620	0.0741	0.2742	0.2001
17	15	0.2308	0.4684	0.2376	0.0266	0.2788	0.2522	0.0676	0.3310	0.2634
17	26	0.2308	0.4306	0.1998	0.0266	0.2874	0.2608	0.0676	0.2742	0.2066
18	19	0.1884	0.3983	0.2099	0.0332	0.2692	0.2361	0.0500	0.2639	0.2139
18	22	0.1884	0.4117	0.2233	0.0332	0.2704	0.2372	0.0500	0.2537	0.2037
18	30	0.1884	0.4117	0.2233	0.0332	0.2331	0.1999	0.0500	0.3458	0.2958
19	3	0.2123	0.4308	0.2186	0.0303	0.2308	0.2004	0.0748	0.2765	0.2017
19	7	0.2123	0.4548	0.2426	0.0303	0.2302	0.1999	0.0748	0.2749	0.2001
19	12	0.2123	0.4552	0.2430	0.0303	0.2867	0.2564	0.0748	0.4480	0.3732
20	17	0.2118	0.4118	0.1999	0.0145	0.2715	0.2570	0.0534	0.2534	0.2000
20	22	0.2118	0.4117	0.1999	0.0145	0.2704	0.2559	0.0534	0.2537	0.2003
20	30	0.2118	0.4117	0.1999	0.0145	0.2331	0.2187	0.0534	0.3458	0.2923
21	17	0.1815	0.4118	0.2303	0.0062	0.2715	0.2653	0.0500	0.2534	0.2034
21	19	0.1815	0.3983	0.2168	0.0062	0.2692	0.2631	0.0500	0.2639	0.2139
21	30	0.1815	0.4117	0.2302	0.0062	0.2331	0.2269	0.0500	0.3458	0.2958
22	23	0.2362	0.4860	0.2498	0.0721	0.2722	0.2001	0.0706	0.3492	0.2785
22	34	0.2362	0.4389	0.2027	0.0721	0.2723	0.2003	0.0706	0.2723	0.2016
23	11	0.2020	0.4216	0.2195	0.0413	0.2698	0.2286	0.0500	0.2552	0.2052
23	13	0.2020	0.4418	0.2398	0.0413	0.2414	0.2002	0.0500	0.2499	0.1999
24	21	0.2391	0.4858	0.2467	0.0635	0.2690	0.2054	0.0700	0.4572	0.3872
24	34	0.2391	0.4389	0.1998	0.0635	0.2723	0.2088	0.0700	0.2723	0.2023
25	15	0.2682	0.4684	0.2002	0.0466	0.2788	0.2322	0.0500	0.3310	0.2810
25	18	0.2682	0.4685	0.2003	0.0466	0.2713	0.2247	0.0500	0.4332	0.3832
26	28	0.2301	0.4758	0.2457	0.0426	0.3223	0.2797	0.0900	0.3121	0.2221
26	36	0.2301	0.4944	0.2643	0.0426	0.3501	0.3075	0.0900	0.2902	0.2002
27	25	0.2945	0.4987	0.2043	0.1189	0.3191	0.2002	0.0677	0.3468	0.2791
27	36	0.2945	0.4944	0.1999	0.1189	0.3501	0.2312	0.0677	0.2902	0.2225
28	29	0.2846	0.4844	0.1998	0.0682	0.2713	0.2032	0.0661	0.2941	0.2280
28	32	0.2846	0.4844	0.1998	0.0682	0.2737	0.2055	0.0661	0.3426	0.2765
29	17	0.1983	0.4118	0.2135	0.0123	0.2715	0.2592	0.0500	0.2534	0.2034
29	19	0.1983	0.3983	0.2000	0.0123	0.2692	0.2570	0.0500	0.2639	0.2139
29	22	0.1983	0.4117	0.2134	0.0123	0.2704	0.2581	0.0500	0.2537	0.2037
30	27	0.2568	0.4569	0.2001	0.0346	0.2634	0.2288	0.0500	0.2638	0.2138
30	32	0.2568	0.4844	0.2276	0.0346	0.2737	0.2390	0.0500	0.3426	0.2926
31	27	0.2338	0.4569	0.2232	0.0632	0.2634	0.2002	0.0639	0.2638	0.1999
31	29	0.2338	0.4844	0.2507	0.0632	0.2713	0.2081	0.0639	0.2941	0.2302
32	33	0.2299	0.4542	0.2243	0.0290	0.2479	0.2189	0.0906	0.2910	0.2004
32	42	0.2299	0.5037	0.2738	0.0290	0.2846	0.2556	0.0906	0.2910	0.2004
33	21	0.2860	0.4858	0.1998	0.0598	0.2690	0.2091	0.1224	0.4572	0.3348
33	23	0.2860	0.4860	0.2000	0.0598	0.2722	0.2123	0.1224	0.3492	0.2268
34	31	0.3037	0.5038	0.2001	0.0846	0.2847	0.2002	0.0841	0.2872	0.2031
34	42	0.3037	0.5037	0.2000	0.0846	0.2846	0.2000	0.0841	0.2910	0.2069
35	25	0.2752	0.4987	0.2235	0.1130	0.3191	0.2061	0.0500	0.3468	0.2968
35	28	0.2752	0.4758	0.2006	0.1130	0.3223	0.2093	0.0500	0.3121	0.2621
36	38	0.2508	0.4511	0.2003	0.0901	0.2904	0.2003	0.0794	0.2795	0.2001
37	35	0.3008	0.5013	0.2005	0.1173	0.3175	0.2002	0.0521	0.2859	0.2338
38	40	0.3166	0.5168	0.2002	0.1099	0.3097	0.1997	0.1051	0.3061	0.2011
39	37	0.3168	0.5166	0.1998	0.0989	0.3291	0.2302	0.0962	0.2959	0.1997
40	41	0.2915	0.4961	0.2046	0.1067	0.3570	0.2503	0.1030	0.3030	0.2000
41	31	0.2544	0.5038	0.2494	0.0478	0.2847	0.2369	0.0868	0.2872	0.2003
41	33	0.2544	0.4542	0.1998	0.0478	0.2479	0.2001	0.0868	0.2910	0.2042
42	39	0.2410	0.4411	0.2001	0.0612	0.2615	0.2002	0.0587	0.2590	0.2003
∑		19.5582	37.2361	17.6782	3.5536	21.9888	18.4356	5.4143	24.4764	19.0615

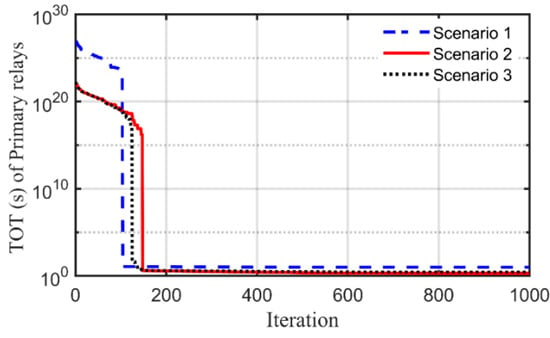
Figure 7. OF convergence of IEEE 15-bus test network.

4.2. Test Case 2: Qarun Test Network

The single-line diagram of this network is implemented using Electrical Transient Analyzer Program (ETAP) software [43], as shown in Figure 8. This network consists of two 4 MW, 0.8 PF generators connected to a main 3.3 kV sectionalized busbar with a normally open bus coupler. In addition, it consists of eight Dyn11 distribution transformers with an inrush current magnitude of 8 per unit continuing for 100 ms. The starting current of oil-well medium-voltage motors is 5 per unit, continuing for 3 s, and they have a stalling time of 33 s. All cables in this network are CU conductors with XLPE insulation. The system data regarding all elements including generators, transformers, feeders, motors, and MCCs (Motor Control Centers) are given in Appendix A (see Table A1, Table A2, Table A3, Table A4 and Table A5).

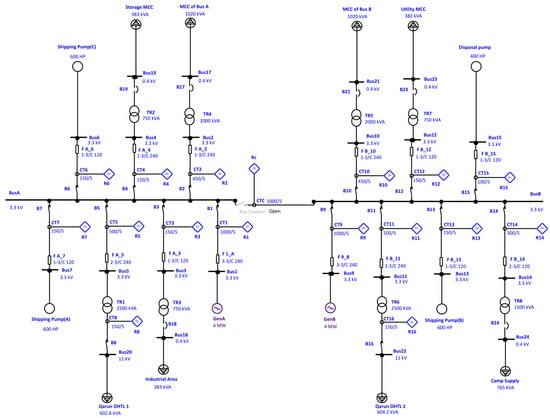
Figure 8. Qarun test network single-line diagram.

This network consists of 16 OCRS with 14 P/B relay pairs. The symmetrical three-phase and two-phase fault currents are given in Table 5, while the initial load flow currents are given in Table 6. These power system studies are performed using ETAP software considering only the worst-case faults as inputs to the optimization model, i.e., three-phase fault currents. Motors’ starting and stall times are obtained through the manufacturer’s recommendation, while the transformers’ LTE is assumed to be 1250 per unit, according to [35]. The formulation comprises 128 discrepant inequality constraints including 48 constraints related to OCR settings. Furthermore, there are 14 selectivity constraints, 16 minimum operating time constraints, and 24 transient condition constraints. This optimization problem also contains 26 equipment damage curve constraints; 14 of them concern the power cables that are fulfilled by default.

Table 5. Fault currents passing through P/B relay pairs of Qarun test network.

P/B Relay Pair		3-Phase Fault		2-Phase Fault
P	B	${\mathit{I}}_{\mathit{f}\mathit{p}}\left(\mathit{k}\mathit{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{b}}\left(\mathit{k}\mathit{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{p}}\left(\mathit{k}\mathit{A}\right)$	${\mathit{I}}_{\mathit{f}\mathit{b}}\left(\mathit{k}\mathit{A}\right)$
2	1	6.174	4.537	5.567	4.045
3	1	6.211	4.317	5.565	3.836
4	1	5.712	3.97	5.101	3.516
5	1	6.349	4.535	5.716	4.043
6	1	4.865	3.493	4.293	3.086
7	1	4.865	3.493	4.298	3.083
8	5	0.945	3.15	0.834	3.209
10	9	6.185	4.531	5.548	4.041
11	9	6.367	4.535	5.705	4.044
12	9	6.442	4.464	5.759	3.977
13	9	4.869	3.484	4.287	3.081
14	9	5.656	4.008	5.03	3.549
15	9	5.812	4.078	5.147	3.62
16	11	0.946	3.154	0.833	3.206

Table 6. OCRs optimal settings of Qarun test network.

Relay ID	${\mathbf{I}}_{\mathbf{fl}}\left(\mathbf{A}\right)$	Scenario 1					Scenario 2
		${\mathit{I}}_{\mathit{p}}\left(\mathit{A}\right)$	${\mathit{T}}_{\mathit{D}}\left(\mathit{s}\right)$	$\mathit{T}\mathit{C}\mathit{C}$			${\mathit{I}}_{\mathit{p}}\left(\mathit{A}\right)$	${\mathit{T}}_{\mathit{D}}\left(\mathit{s}\right)$	$\mathit{T}\mathit{C}\mathit{C}$
				Curve	IEC	IEEE			Curve	IEC	IEEE
1	628.3	707.0480	0.3356	VI	✕	✓	779.6370	0.3040	VI	✕	✓
2	180.8	180.8000	0.2147	VI	✓	✕	269.4136	0.5192	EI	✕	✓
3	68	91.8804	0.3239	EI	✓	✕	91.5472	0.7414	EI	✕	✓
4	68	88.8047	0.3466	EI	✓	✕	91.9678	0.5890	EI	✕	✓
5	106	122.5999	0.4077	VI	✓	✕	137.8547	0.4262	VI	✓	✕
6	103.9	142.2529	0.9076	EI	✓	✕	144.7595	0.9375	EI	✓	✕
7	103.9	143.2030	0.8946	EI	✓	✕	147.0365	0.8538	EI	✓	✕
8	31.8	31.8000	0.1000	EI	✓	✕	41.4839	0.1000	VI	✓	✕
9	663.9	881.5404	0.2451	VI	✕	✓	866.5552	0.2168	MI	✕	✓
10	180.9	267.8911	0.5228	EI	✕	✓	269.8280	0.3294	EI	✓	✕
11	106.3	120.0446	0.4168	VI	✓	✕	146.3529	0.3806	VI	✓	✕
12	67.8	88.9917	0.6138	EI	✕	✓	73.8600	0.7654	EI	✕	✓
13	103.9	141.1091	0.9240	EI	✓	✕	151.3325	0.8243	EI	✓	✕
14	135.9	165.2193	0.4009	EI	✓	✕	166.0149	0.7253	EI	✓	✕
15	71.5	105.8773	0.7745	EI	✓	✕	107.2474	0.9999	EI	✓	✕
16	31.9	31.9000	0.1000	EI	✓	✕	46.1682	0.2648	EI	✕	✓
TOT (s)		0.7381					1.0387

The proposed optimization model mentioned in Section 2 is run and solved using GBO for this test case with two scenarios. The settings of recent digital relays are optimized with extracting the optimal tripping curve among IEC and IEEE standardized curves, as illustrated in Table 6. Scenario 1 achieves a TOT of 0.7381 s while Scenario 2 achieves a TOT of 1.0387 s with zero boundary and selectivity constraints violations in both scenarios. Table 7 clarifies the operating times of P/B relay pairs, CTI values, and their associated operating constraints for scenario 1. It can be noted that there are six violations in the minimum operating time constraint found in relay pairs 2, 3, 7, 12, 13, and 14. Therefore, the optimization problem becomes more complicated by adding an extra 14 minimum operating time constraints in Scenario 2.

Table 7. P/B relay pairs operating times and their associated constraint values of Qarun test network for scenario 1.

Relay Pair ID	P/B Relay Pair		${\mathit{t}}_{\mathit{p}\mathit{r}}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{b}\mathit{r}}\left(\mathit{s}\right)$	$\mathit{CTI}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{r}\mathit{t}}\left(\mathit{s}\right)$	$\begin{array}{c}\Delta {\mathit{t}}_{\mathit{t}}\left(\mathit{s}\right)=\\ {\mathit{t}}_{\mathit{r}\mathit{t}}-{\mathit{t}}_{\mathit{t}}\end{array}$	${\mathit{t}}_{\mathit{d}}\left(\mathit{s}\right)$	$\begin{array}{c}\Delta {\mathit{t}}_{\mathit{d}}\left(\mathit{s}\right)=\\ {\mathit{t}}_{\mathit{d}}-{\mathit{t}}_{\mathit{p}\mathit{r}}\end{array}$
	P	B
1	2	1	0.0874	0.3286	0.2411	0.2002	0.1002	4.0142	3.9268
2	3	1	0.0057	0.3462	0.3405	0.1999	0.0999	0.5581	0.5525
3	4	1	0.0067	0.3804	0.3737	0.1998	0.0998	0.6600	0.6533
4	5	1	0.1084	0.3287	0.2204	0.1999	0.0999	5.9320	5.8237
5	6	1	0.0621	0.4459	0.3838	5.9974	2.9974	0.3698	0.3077
6	7	1	0.0621	0.4459	0.3839	5.9973	2.9973	0.3698	0.3077
7	8	5	0.0091	0.2229	0.2138	-	-	-	-
8	10	9	0.0913	0.3094	0.2181	0.1999	0.0999	4.0000	3.9086
9	11	9	0.1081	0.3091	0.2010	0.1999	0.0999	5.8986	5.7905
10	12	9	0.0780	0.3154	0.2374	0.1999	0.0999	0.5188	0.4409
11	13	9	0.0621	0.4491	0.3870	6.0000	3.0000	0.3691	0.3070
12	14	9	0.0274	0.3647	0.3373	0.2000	0.1000	2.6899	2.6625
13	15	9	0.0206	0.3560	0.3354	5.9975	2.9975	0.1240	0.1035
14	16	11	0.0091	0.2226	0.2135	-	-	-	-
∑			0.7381	4.8249	4.0869

Scenario 2 achieves better results than Scenario 1 by canceling the violations in the minimum operating time constraint in all pairs except for pair 13. Moreover, the transient condition constraints are improved by expanding the time difference gap, as declared in pairs 2, 4, 5, and 13 and clarified in Table 8. It can be observed that there are no equipment damage curve violations in both scenarios, as declared in Table 7 and Table 8. Pair 13 represents a challenge to the algorithm in bounding the tripping time between $t_{min}$ of 50 ms and $t_d$ of 124 ms. It is violated in both scenarios by obtaining a very small primary relay tripping time of 20.6 ms in scenario 1 and 27.2 ms in scenario 2. In this context, Figure 9 depicts a TCC sample of a motor feeder with some current time indications, as shown using scenario 2 settings.

Table 8. P/B relay pairs operating times and their associated constraint values of Qarun test network for scenario 2.

Relay Pair ID	P/B Relay Pair		${\mathit{t}}_{\mathit{p}\mathit{r}}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{b}\mathit{r}}\left(\mathit{s}\right)$	$\mathit{CTI}\left(\mathit{s}\right)$	${\mathit{t}}_{\mathit{r}\mathit{t}}\left(\mathit{s}\right)$	$\begin{array}{c}\Delta {\mathit{t}}_{\mathit{t}}\left(\mathit{s}\right)=\\ {\mathit{t}}_{\mathit{r}\mathit{t}}-{\mathit{t}}_{\mathit{t}}\end{array}$	${\mathit{t}}_{\mathit{d}}\left(\mathit{s}\right)$	$\begin{array}{c}\Delta {\mathit{t}}_{\mathit{d}}\left(\mathit{s}\right)=\\ {\mathit{t}}_{\mathit{d}}-{\mathit{t}}_{\mathit{p}\mathit{r}}\end{array}$
	P	B
1	2	1	0.0911	0.3307	0.2395	0.2001	0.1001	4.0142	3.9231
2	3	1	0.0948	0.3503	0.2555	0.2504	0.1504	0.5581	0.4634
3	4	1	0.0760	0.3884	0.3124	0.2001	0.1001	0.6600	0.5840
4	5	1	0.1277	0.3308	0.2031	0.2360	0.1360	5.9320	5.8044
5	6	1	0.0665	0.4618	0.3954	6.4341	3.4341	0.3698	0.3033
6	7	1	0.0624	0.4618	0.3994	6.0619	3.0619	0.3698	0.3073
7	8	5	0.0620	0.2633	0.2013	-	-	-	-
8	10	9	0.0502	0.3566	0.3064	0.2472	0.1472	4.0000	3.9497
9	11	9	0.1209	0.3565	0.2356	0.2243	0.1243	5.8986	5.7777
10	12	9	0.0960	0.3597	0.2637	0.2005	0.1005	0.5188	0.4229
11	13	9	0.0638	0.4204	0.3566	6.2322	3.2322	0.3691	0.3054
12	14	9	0.0500	0.3837	0.3336	0.3653	0.2653	2.6899	2.6399
13	15	9	0.0272	0.3796	0.3524	7.9646	4.9646	0.1240	0.0968
14	16	11	0.0501	0.2500	0.2000	-	-	-	-
	∑		1.0387	5.0936	4.0549

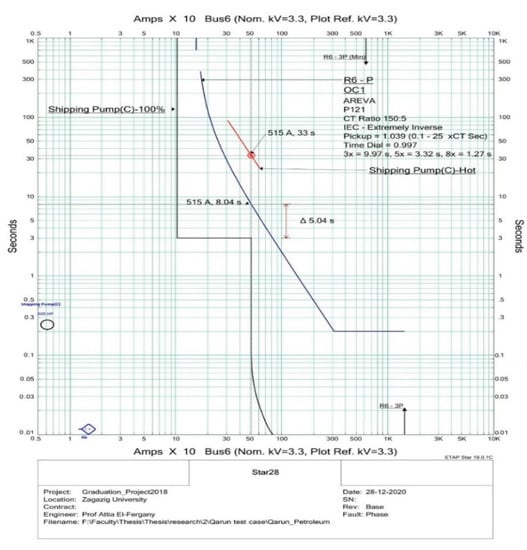
Figure 9. TCC sample of a motor feeder using scenario 2 settings.

The OF values and statistical measures obtained using GBO, PSO, and WCA are reported in Table 9, while the settings using PSO and WCA are not reported, to avoid making the paper too long. It is clear that GBO achieves a notable reduction in the OF value and better convergence compared to PSO and WCA, as declared in Figure 10 and Figure 11. The data tips shown in these figures are related to the minimum obtained OF value through whole iterations using GBO. There is a slight difference between OF and TOT values due to some violations in the operating constraints, which are multiplied by large factors, as declared in Table 9.

Table 9. Performance measures of GBO compared to PSO and WCA in Qarun test network.

Scenario 1
	TOT	Min	Max	Mean	Median	SD	$\mathit{W}{\mathit{F}}_{\mathit{m}}$	$\mathit{W}{\mathit{F}}_{\mathit{c}}$	$\mathit{W}{\mathit{F}}_{\mathit{t}}$	$\mathit{W}{\mathit{F}}_{\mathit{d}}$	Elapsed Time (s)
GBO	0.7381	0.7385	1.2336	1.0116	1.0396	0.1774	0	1000	1000	10000	185.9983
PSO	1.1614	1.1610	3036.6235	1126.6009	40.2700	1532.762	0	1000	1000	10000	227.2286
WCA	1.0614	1.0619	42.7392	12.9535	1.2226	18.3029	0	1000	1000	10000	400.4712
Scenario 2
GBO	1.0387	3.3137	4.3728	3.6892	3.4044	0.4815	100	10	10	100	175.8350
PSO	1.3181	3.9370	35.1902	10.3495	4.2033	13.8870	100	10	10	100	176.1993
WCA	1.1281	3.4031	4.7424	4.1908	4.2593	0.4858	100	10	10	100	420.3673

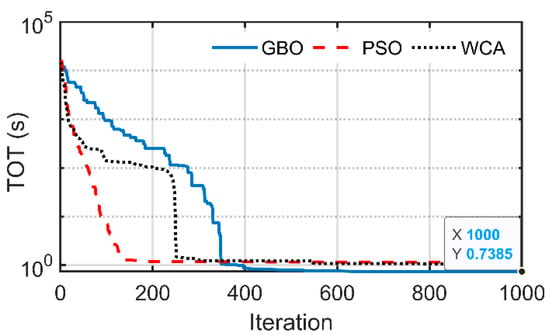
Figure 10. Scenario 1 OF convergence of Qarun test network.

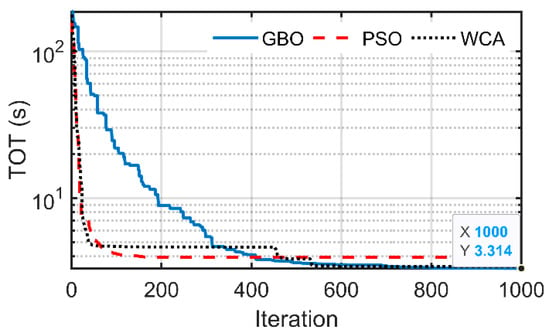
Figure 11. Scenario 2 OF convergence of Qarun test network.

5. Conclusions

This work represents a forward step in the optimization model of overcurrent relay coordination by solving the practical technical problems facing the protection engineers. This model aims to eliminate the false tripping actions due to energizing inductive equipment such as transformers and motors. Moreover, it is ensured that the OCR will trip before the breakdown of the protected equipment with preserving the minimum operating time condition for each commercial relay. First, the effectiveness of the proposed GBO is interrogated by a fair comparison with SMA for solving the IEEE 15-bus network using various scenarios. In this regard, GBO manifests its superiority by attaining a reduction in the total operating time of 14.3% and 16.5% for scenarios 1 and 2, respectively. Afterward, the proposed optimization model is applied on the medium voltage distribution network of the Qarun petroleum company, which is deemed as an isolated network. GBO achieves a notable reduction in the TOT compared to PSO and WCA with better OF convergence. Moreover, GBO employs the tradeoff technique between the problem constraints with a very low number of violations. Consequently, GBO exhibits only one minimum time constraint violation and zero equipment damage curve constraint violations for Scenario 2. Although scenario 2 complicates the optimization problem, it attains better and feasible results than Scenario 1. Eventually, this model paves the way for researchers to develop and augment the overcurrent relay coordination problem.