A Model Proposal for Occupational Health and Safety Performance Measurement in Geothermal Drilling Areas

Abstract

The energy sources required for general development and maintenance cause environmental pollution due to the carbon emissions released into the atmosphere. For these reasons, countries have turned to renewable energy sources. Energy production methods also cause serious problems in terms of the health and safety of employees. This study aimed to create an occupational health and safety performance model in geothermal energy fields, which generate renewable energy sources, using multi-criteria decision-making methods. A two-stage model was created for OHS performance index measurement. In the first stage, a literature screening was performed, risk analysis criteria were examined, and performance measurement criteria were determined with geophysical engineers and OHS experts. Seven main criteria and forty-seven subcriteria were set. An analytical hierarchy process method (AHP) and a fuzzy analytical hierarchy process (F-AHP) using the main criteria and subcriteria were determined. In the second stage, exposure rates were obtained using the Promethee method in three geothermal wells. The risks in these three wells are listed according to their importance. A performance model was created. The Results section includes conclusions and suggestions. This study, by creating an OHS performance model, can be used by managers and OHS professionals working in geothermal energy production fields to solve problems.

1. Introduction

Global energy requirements have dramatically escalated due to increasing urbanization and population. This energy has great potential in terms of supporting economic growth, particularly in developing countries [1]. In recent centuries, fossil fuel waste has increased greenhouse gas emissions, which is the cause of concerns regarding global warming, climate change, and a loss of biodiversity. As a result, sustainable energy has been the center of attention owing to its positive contribution to climate change and economic growth. Establishing more environmentalist, sustainable, and renewable energy systems is needed to diminish global environmental threats [2].

Today, the renewable energy share is below 15%. Renewable energy continued to grow annually by about 0.9% between 2009 and 2019. Renewable power generation is expected to increase from 21% in 2021 up to 44% in 2050. The contribution of hydropower is expected to remain largely unchanged until 2050, and other renewable sources of power generation, such as geothermal and biomass, are expected to collectively constitute less than 3% of total generated energy. In addition, new studies are continuously carried out with the aim of developing more efficient and green energy sources. For example, the development of solar panels that work at night is studied in the fields of infrared technology, biomass energy, hydrogen energy, and wave/ocean energy. The direct usage of geothermal energy for thermal implementations has been quite intensified geographically, and it constitutes three-fourths of the energy consumed in countries such as China, Turkey, Iceland, and Japan. The direct use of geothermal energy resources has recently grown by approximately 8%, and it is the primary driving force of heating. The amount of geothermal energy power generated globally, based on data from late 2018, is 14.9 GWe. The top five countries generating electricity from geothermal energy are the USA, the Philippines, Indonesia, Turkey, and New Zealand. Non-electrical use has surpassed 70,000 MWt, with the United States, China, Sweden, Belarus, and Norway leading the globe in direct use applications [3].

As indicated in Figure 1, the generation of renewable energy, which was 8.7% in 2009, reached 11.7% in 2019. Despite the negative impact of the COVID-19 pandemic, the generation of renewable energy has risen to 12.6%. Due to this rate of increase, a “zero emission” objective for 2050 has been imposed by the Paris Treaty, signed by 135 countries.

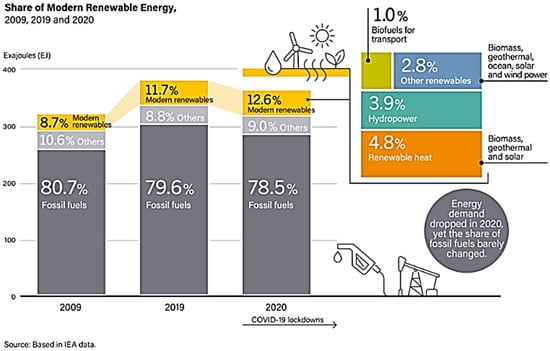
Figure 1. Distribution of renewable energy usage between 2009 and 2020 [3].

Even though renewable and clean energy is considered positive, geothermal energy may cause environmental and socio-economic problems that can impact the ecological balance. Its greatest disadvantage is that it involves the use of hazardous chemicals. Although it does not emit greenhouse gases like fossil fuels do, hydrogen sulfur stored under the earth’s crust as well as carbon dioxide, ammoniac, methane, and boron may emerge at low rates. Naturally, these rates are higher in places near geothermal drilling. To provide sustainable geothermal energy, water needs to be pumped. Heat is measured in underground reservoirs. Since water is circulated in power plants and sent back again, a decrease in water quality may occur. Furthermore, it is also likely that geothermal drilling is associated with earthquake risks due to the creation of wells that are drilled in search of springs or produce water. Drilling into the crust while pumping hot water out of the ground may harm tectonic structures and cause earthquake risks [4].

Geothermal energy is generated by hot water and steam in underground reservoirs, being pumped out of the ground through drilled wells, using moving turbines that work via electric generators [1]. For this process, a vast area is needed for the establishment of drilling machines. When designing wells to be drilled by a drilling machine, reservoir depth, production pipe diameter, reservoir fluid type and features, and geologic and tectonic structures are of great importance. In geothermal drilling, the depth of the geothermal reservoir and the well diameter need to be chosen based on the capacity of the machine and pump. Wells that do not exceed 2000 m are considered shallow, and those above that depth are considered deep [5].

Drilling is a complex and expensive operation. To drill a geothermal well in an area, first, geological studies, geochemical analyses, and research via more than one geophysical method must be conducted. The drilling area must be designated as the most appropriate spot based on geological sections acquired from geological studies in the area. By laying a concrete foundation where the drilling machine will be placed, the stability of the drilling machine is ensured. As the depth of the well increases, risks increase too, in terms of drilling equipment and well security. Well diameter is important for that reason. When the diameter of the well is large, the success rate of well tests increases. Mud ponds need to be prepared, and mud quality must be determined; the well is observed through constant measurements of viscosity and temperature. In the wells at the production phase, pressure tests (decrease and increase), fluid production tests, water/steam ratio measurements and static and dynamic temperature tests are conducted [6].

Because of the constant shifting pattern from the time of construction to deconstruction, it is also known that the number and variety of occupational hazards that employees face are too high, and many involve various tasks and duties. Employees are exposed to various hazards that can cause many different accidents, such as cuts, falls, sprains, strains, and contact with hazardous chemicals. It is known these accidents may cause death and injuries, which would decrease the productivity of drilling operations.

Proactively predetermining all risks that might be posed in drilling operations is necessary for the sake of employees and for the continuity of drilling. Planning geothermal activities properly, using appropriate techniques, and taking necessary precautions not only reduce costs but also reduce environmental harm and unexpected accidents. Therefore, to determine criteria involved in this complex structure, and to measure and increase performance, fuzzy multi-criteria decision making is used, as the most appropriate method.

When the phases of pumping geothermal energy out of the ground are examined, occupational health and safety elements are seen to be involved in every step of the project, including worksite construction, artesian well production, and gas extraction and usage. Hence, 242 studies have been examined. Some of the studies carried out in Table 1 via multi-criteria decision-making (MCDM) methods in the field of OHS, particularly on risk analysis, are as follows:

Table 1. Summary chart of literature review.

Summary Chart of Literature Review
Year	Author	Name of Article	Implementation Area	Objective of Study	MCDM Method Used
2006	Law and Chan [7]	Prioritizing the safety management elements	Press, electronic, textile	Weighting OHS performance indicators	AHP
2009	Chang and Liang [8]	Performance evaluation of process safety management systems of paint manufacturing facilities	Pigment production	OHS performance measurement	AHP
2009	Grassi et al. [9]	A fuzzy multi-attribute model for risk evaluation in workplaces	Nutrition	A new risk assessment method	Fuzzy TOPSIS
2009	Hu et al. [10]	Risk evaluation of green components to hazardous substance using FMEA and FAHP	Electronic	A new risk assessment method	Fuzzy AHP
2011	Beriha et al. [11]	Occupational health and safety management using gray relational analysis: An Indian perspective	Construction, steel, ceramics	Comparison of security culture	GRA
2013	Janackovic [12] et al.	Selection and Ranking Of Occupational Safety Indicators Based On Fuzzy AHP: A Case Study In Road Construction Companies	Construction	Weighting OHS performance indicators	Fuzzy AHP
2014	Mahdevari et al. [13]	Human health and safety risks management in underground coal mines using fuzzy TOPSIS	Mining	A new risk assessment method	Fuzzy TOPSIS
2014	Kısa [14]	Assessment of OHS conditions in Molding Workshops via Multi-Criteria Decision-Making Methods	Molding workshop	Prioritizing OHS risks	AHP
2014	Özdemir [15]	Assessment of OSH conditions in Textile Workshops via Multi-Criteria Decision-Making Methods	Textile workshop	OHS performance measurement	ANP, DEMATEL
2015	Podgorski [16]	Measuring operational performance of an OHS management system: A demonstration of AHP-based selection of leading key performance indicators	None	Weighting OHS performance indicators	AHP
2015	Güneri et al. [17]	A fuzzy AHP methodology for selection of risk assessment methods in occupational safety	Press	Comparison between risk assessment methods	Fuzzy AHP
2015	Djapan et al. [18]	A new fuzzy model for determining risk level on the workplaces in manufacturing small and medium enterprises	Manufacturing	Prioritizing OHS risks	Fuzzy AHP
2015	Vahdani et al. [19]	A new FMEA method by integrating fuzzy belief structure and TOPSIS to improve risk evaluation process	Steel	Prioritizing OHS risks	Fuzzy TOPSIS
2015	Liu et al. [20]	A novel approach for failure mode and effects analysis using combination weighting and fuzzy VIKOR method	Health	Prioritizing OHS risks	Fuzzy AHP, fuzzy VIKOR
2016	Khalil et al. [21]	Ranking the indicators of building performance and the users’ risk via Analytical Hierarchy Process (AHP): Case of Malaysia	Educational buildings	Weighting OHS performance indicators	AHP
2016	Delice and Zegerek [22]	Ranking Occupational Risk Levels of Emergency Departments Using a New Fuzzy MCDM Model: A Case Study In Turkey	Health	Prioritizing OHS risks	Fuzzy GRA, Fuzzy DEMATEL
2016	Efe et al. [23]	Analysis of Error Types and Impacts via Fuzzy Promethee Method in Occupational Safety: An Implementation in a construction firm	Construction	A new risk assessment method	Fuzzy PROMETHEE
2016	Yılmaz and Şenol [24]	A fuzzy multi-criteria model and its implementation for risk assessment in occupational health and safety	Metal	A new risk assessment method	Fuzzy AHP, Fuzzy TOPSIS
2017	Raviv et al. [25]	AHP-based analysis of the risk potential of safety incidents: Case study of cranes in the construction industry	Crane sector	Prioritizing OHS risks	AHP
2017	Gül et al. [26]	Occupational health and safety risk assessment in hospitals: A case study using two-stage fuzzy multi-criteria approach	Health	A new risk assessment method	Fuzzy AHP, Fuzzy VIKOR
2017	İnan et al. [27]	A multiple attribute decision model to compare the firms’ occupational health and safety management perspectives	None	Weighting OHS performance indicators	VIKOR
2017	Kokangül et al. [28]	A new approximation for risk assessment using the AHP and Fine Kinney methodologies	Production	A new risk assessment method	AHP
2017	Öztürk and Toptancı [29]	An Integrated MCDM Model for Occupational Safety Specialist Selection	None	Choosing OHS experts	AHP
2017	Efe et al. [30]	An integrated intuitionistic fuzzy set and mathematical programming approach for an occupational health and safety policy	Construction, textile, metal	A new risk assessment method	AHP, VIKOR
2017	Liu et al. [31]	Failure mode and effect analysis with extended gray relational analysis method in cloud setting	Paper production	A new risk assessment method	GRA
2017	Ediz et al. [32]	Assessment of Occupational Health and Safety Administration System Performance Indicators via AHP	None	Weighting OHS performance indicators	AHP
2017	Janackovic et al. [33]	Selection of key indicators for the improvement of occupational safety system in electricity distribution companies	Electricity	Weighting OHS performance indicators	Fuzzy AHP
2018	Ilbahar et al. [34]	A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system	Construction	A new risk assessment method	Fuzzy AHP

Even though there are a high number of studies in the field of risk assessment and performance measurement by multi-criteria decision-making methods in the literature, there are scarcely any studies in the field of occupational health and safety, especially on geothermal drilling areas. Moreover, there is no study on weighting occupational health and safety or risk assessment performances or making performance comparisons in geothermal drilling areas via multi-criteria decision-making methods. In this study, occupational health and safety performance factors in geothermal wells examined in the literature were studied by means of multi-criteria decision-making methods for the first time. This study integrated a model with results involving studies in the literature that measure OHS performance in drilling areas. Occupational health and safety vulnerability in drilling areas were determined, and a method providing performance development is provided.

2. Materials and Methods

The data received from the geothermal drilling area contain numerous criteria, so it was decided that multi-criteria decision-making methodologies would be used. Seven main criteria and forty-seven subcriteria obtained from the statistical study were weighted by the AHP method, one of the multi-criteria decision-making methodologies. The same process was performed using the F-AHP method. Criteria are listed in a table according to the order of importance.

Finally, the calculated weighting was evaluated by the Promethee method, and the OHS model was created and interpreted for geothermal wells.

2.1. Analytical Hierarchy Process

The analytical hierarchy process (AHP), suggested by Myers and Alpert in 1968 and developed as a model by Professor Thomas Lorie Saaty in 1977, is used to reach solutions to decision-making problems [35]. The AHP is a method that does not compel one to use a method for decision making; rather, it provides an opportunity to learn one’s own decision-making mechanisms and thus ensures that better decisions are made [36]. The AHP is an approach wherein the knowledge, experience, thoughts, and intuitions of individuals are combined in a logical framework [37]. Hence, the AHP is a mathematical method that takes the priorities of groups and individuals into consideration in decision making and evaluates qualitative and quantitative variables. This makes the AHP more substantial than other decision-making methods [38].

In the implementation phase of the AHP, first, the problem must be defined clearly and the objective in the problem must be determined. Starting with the objective, the main criteria, the subcriteria, and the lowest-level alternatives are established in a certain hierarchical structure. A hierarchical structure related to criteria and alternatives is constituted in accordance with the research topic, similar to the structure shown in Figure 2. The numbers of subfactors under each factor at the same level must be close to each other [39].

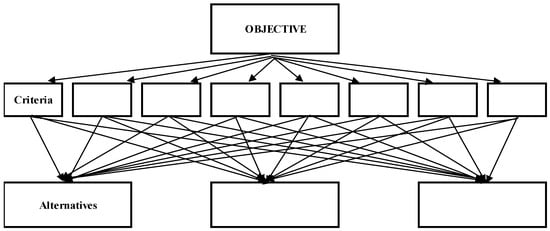
Figure 2. General structure of the AHP hierarchy.

To determine the significance level in the relations between criteria and alternatives, pairwise comparisons between alternatives and criteria are made by decision makers. A square matrix in the dimension of a comparison matrix (n × n) is shown in Equation (1) below.

$$A=\left. [\begin{array}{c}\begin{array}{cccc}a11& a12& \dots & a1n\\ a21& a22& \dots & a2n\\ .& .& .& .\\ .& .& .& .\\ .& .& .& .\\ .& .& .& .\\ a1n& a2n& \dots & ann\end{array}\end{array}\right]$$

(1)

A: alternatives, a: binary comparison result, n: number of factors.

While making comparisons and forming matrices, the pairwise comparison scale shown in Table 2 is used.

To normalize each column in the pairwise comparison matrix, columns are added, and by dividing the matrix elements by the related column sum, a normalized matrix is formed. In the next step, by calculating the line sum of the normalized matrix formed for each alternative or criterion, a priority vector matrix is formed. Priority values determined for each criterion or alternative in the priority matrix formed via the priority vector are multiplied by column elements of the pairwise comparison matrix belonging to that particular criterion or alternative, and a weighted total matrix is obtained. The line value sum of the weighted total matrix is divided by the line values of the priority vector matrix, and the arithmetic mean of matrix elements formed in the (nx1) dimension is calculated, so the priority values of the criteria or alternatives are acquired. Priority values are calculated via the formula in Equation (2) [40].

$$Wi=\frac{{\sum }_{j=1}^n cij}{n}$$

(2)

W: relative level importance of i alternative to j criteria, n: number of factors, $cij$ comparative importance of i alternative and j criterion.

In the final step, to determine whether pairwise comparisons of decision criteria and decision options of the decider are consistent, a consistency ratio is calculated. A low consistency ratio indicates that the decisions of the decider in the pairwise comparisons are consistent; a high ratio means that they are inconsistent. In the AHP method, a consistency value of up to 0.1 can be accepted. If this ratio is higher than 0.1, it is necessary for the decider to review his/her decisions in the pairwise comparisons again and repeat the steps [41]. While calculating the consistency index, the first CI value is determined [42].

2.2. Fuzzy Analytical Hierarchy Process

Even though the AHP method considers the information of experts, it cannot completely reflect uncertainties or fuzziness. Therefore, by combining fuzzy logic with the AHP, Fuzzy AHP (F-AHP) is formed. Unlike the AHP, where net values are used, comparison ratios in F-AHP are given in the range of a certain value [43]. The first study on Fuzzy AHP was conducted in 1983 by van Laarhoven and Pedrycz, who compared fuzzy ratios using triangle fuzzy numbers [44]. Buckley (1985) created a model using trapezoid fuzzy numbers [45]. In Buckley’s approach, the weightiness of measures is acquired, the performance of alternatives is designated, and the geometrical mean method in the fuzzy area is used. Considering this method, while the comparison matrix is being formed, as in the traditional AHP method, a part of the diagonal matrix is filled in, and the reverse of the assessment for the other part of the diagonal is conducted [46].

Fuzzy Logic: Mathematical interpretations of the real world are now more complex and therefore can be more widely applied. Rather than precise (crip) values of binary logic, looser, non-strict evaluations can take place. Fuzzy set theory is suggested to improve overly simplified models and thus analyze the complex systems of the real world [47]. The term “fuzzy” is used for situations where movement or observation sets do not have well-defined boundaries.

Hierarchical structures regarding criteria and alternatives are constituted in accordance with the research topic. Subfactor numbers under each factor at the same level must be close to each other [39].

After the step of constituting a hierarchy, criteria, subcriteria, and alternatives are evaluated via pairwise comparisons using linguistic terms. In Equation (3), a pairwise comparison matrix belonging to the expert is given [48].

$${\tilde{A}}^k=\left. [\begin{array}{cccc}{\tilde{a}}_{11}^k& {\tilde{a}}_{12}^k& \cdots & {\tilde{a}}_{1n}^k\\ {\tilde{a}}_{21}^k& {\tilde{a}}_{22}^k& \dots & {\tilde{a}}_{2n}^k\\ \dots & \dots & \dots & \dots \\ {\tilde{a}}_{m1}^k& {\tilde{a}}_{m2}^k& \dots & {\tilde{a}}_{mn}^k\end{array}\right]$$

(3)

A: result of matrix, a: fuzzy numbers

An indication of this equation via fuzzy numbers is given in Equation (4) [49].

$$\begin{array}{cc}\check{A}=& \left({\tilde{a}}_{ij}\right){.}_{n\times n}\end{array}=\left. [\begin{array}{cccc}\left(1,1,1\right)& \left(l_{12},m_{12},u_{12}\right)& \cdots & \left(l_{1n},m_{1n},u_{1n}\right)\\ \left(l_{21},m_{21},u_{21}\right)& \left(1,1,1\right)& \dots & \left(l_{2n},m_{2n},u_{2n}\right)\\ \dots & \dots & \dots & \dots \\ \left(l_{n1},m_{n1},u_{n1}\right)& \left(l_{n2},m_{n2},u_{n2}\right)& \dots & \left(1,1,1\right)\end{array}\right]$$

(4)

A: result of matrix, (l, m, u): fuzzy numbers, n: number of factors.

Examples of linguistic scales used for qualitative evaluation in the literature are shown in Table 3.

After obtaining value judgments, a consensus matrix is acquired by taking expert weights into consideration. When there is more than one decider in an evaluation, a consensus matrix is obtained using Equation (5).

$${\tilde{a}}_{ij}=\frac{{\sum }_{k=1}^K{a}_{ij}^k}{K},$$

(5)

K: indicates the number of deciders, $a$: fuzzy numbers.

To calculate the consistency of expert opinions, the consistency of comparison matrices needs to be calculated. Through the defuzzification of matrix elements in a fuzzy decision matrix, a pairwise comparison matrix is obtained. After sustaining the consistency of the pairwise comparison matrix, the step of weight calculation can follow. Fuzzy geometrical mean values for each line of each decision matrix are calculated [50].

2.3. The Promethee Method

The PROMETHEE method is a method of listing alternatives, which can be perceived and used easily by a decider. Six different functions can be used to evaluate criteria. Based on the nature of criteria, which one will be used is determined by the decider. Function types vary depending on the problem [51].

This method was developed by J. P. Brans in 1982, and first implementations were conducted in the same year. After two years, B. Mareschal and J. P. Brans improved the method, and, in their article published in 1985, put the program into its final form. In 1988, these authors proposed GAIA, a visual interaction module. Thanks to GAIA, it was possible to create detailed images regarding the results of problems solved via the PROMETHEE method [52]. The PROMETHEE method is widely and successfully used mostly because of its mathematical characteristics and practical usage [53].

Table 2. Pairwise comparison scale [54].

Intensity of Importance	Definitions	Explanation
1	Equally importance	Two activities contribute equally to the abjective
3	Modarate importance	Experience and judgement slightly favour one activity over another
5	Strong importance	Experience and judgement strongly favour one activity over another
7	Very strong or demonstrated importance	An activity is favour very strongly over another; its dominance demostrated in practice
9	Expreme importance	The evidance favouring one activity over another is of the highest possible order of affirmation
2, 4, 6, 8	For compromise between the above values	Sometimes one needsto interpolate a compromise justment numerically because there is no good word to

Table 2. Pairwise comparison scale [54].

Intensity of Importance	Definitions	Explanation
1	Equally importance	Two activities contribute equally to the abjective
3	Modarate importance	Experience and judgement slightly favour one activity over another
5	Strong importance	Experience and judgement strongly favour one activity over another
7	Very strong or demonstrated importance	An activity is favour very strongly over another; its dominance demostrated in practice
9	Expreme importance	The evidance favouring one activity over another is of the highest possible order of affirmation
2, 4, 6, 8	For compromise between the above values	Sometimes one needsto interpolate a compromise justment numerically because there is no good word to

Table 3. The linguistic scale used for pairwise comparison [49].

Saaty’s Relative Importance	Linguistic terms	Fuzzy Score
Cij = 1	Equally important	(1,1,1)
Cij = 2	Intermittent value between two adjesent scale	(1,2,3)
Cij = 3	Weekly important	(2,3,4)
Cij = 4	Intermittent value between two adjesent scale	(3,4,5)
Cij = 5	Fairly important	(4,5,6)
Cij = 6	Intermittent value between two adjesent scale	(5,6,7)
Cij = 7	Strongly important	(6,7,8)
Cij = 8	Intermittent value between two adjesent scale	(7,8,9)
Cij = 9	Absolutaly important	(8,9,9)

Table 3. The linguistic scale used for pairwise comparison [49].

Saaty’s Relative Importance	Linguistic terms	Fuzzy Score
Cij = 1	Equally important	(1,1,1)
Cij = 2	Intermittent value between two adjesent scale	(1,2,3)
Cij = 3	Weekly important	(2,3,4)
Cij = 4	Intermittent value between two adjesent scale	(3,4,5)
Cij = 5	Fairly important	(4,5,6)
Cij = 6	Intermittent value between two adjesent scale	(5,6,7)
Cij = 7	Strongly important	(6,7,8)
Cij = 8	Intermittent value between two adjesent scale	(7,8,9)
Cij = 9	Absolutaly important	(8,9,9)

A data matrix is formed based on designated alternatives, criteria, criteria weights, and values acquired by alternatives regarding the related criteria. The data matrix on alternatives A = (a, b, c,…), evaluated by w = (w1, w2,…,wk) weights and criteria c = (f1, f2,…,fk), is formed, as shown in Table 4 [54].

Table 4. Data matrix [53].

Criteria	a	b	c	……	w
f1	f1(a)	f1(b)	f1(c)	……	w1
f2	f2(a)	f2(b)	f2(c)	……	w2
……	……	……	……	……	……
fk	fk (a)	fk (b)	fk (c)	……	wk

f: criteria, k: number of criteria, (a, b, c…): alternatives, w: weight.

A choice function for the criteria is defined. Choice functions are determined in accordance with the nature of the criteria and the fundamental features of the alternatives. Six different choice functions used in the method are shown in Table 5 [55].

Table 5. PROMETHEE choice functions [52].

Usual-criterion $P_{ij}^k=\left\{\begin{array}{c}0, If d_{ij}^k\le 0 \left(\mathrm{in\; difference}\right)\\ 1, If d_{ij}^k>0 \left(\mathrm{Strict\; preference}\right)\end{array}\right.$
Quasi-criterion $P_{ij}^k=\left\{\begin{array}{c}0, If d_{ij}^k\le q_k \left(\mathrm{in\; difference}\right)\\ 1, If d_{ij}^k>q_k \left(\mathrm{Strict\; preference}\right)\end{array}\right.$
Criterion with linear preference $P_{ij}^k=\left\{\begin{array}{c}\frac{d_{ij}^k}{P_k}, If d_{ij}^k\le P_k \left(\mathrm{Weak\; Preferance}\right)\\ 1, If d_{ij}^k>P_k \left(\mathrm{Strict\; preference}\right)\end{array}\right.$
Level-criterion $P_{ij}^k=\left\{\begin{array}{c}0, If d_{ij}^k\le q_k \left(\mathrm{in\; difference}\right)\\ \frac{1}{2}, If q_k<d_y^k\le P_k \left(\mathrm{Weak\; preference}\right) \\ 1, If d_{ij}^k>P_k \left(\mathrm{Strict\; preference}\right)\end{array}\right.$
Criterion with linear preference and indifference area $P_{ij}^k=\left\{\begin{array}{c} 0, If d_{ij}^k\le q_k \left(\mathrm{in\; difference}\right)\hfill \\ \frac{d_{ij}^k-q_k}{P_k-q_k}, If q_k<d_y^k\le P_k \left(\mathrm{Weak\; preference}\right) \\ 1, If d_{ij}^k>P_k \left(\mathrm{Strict\; preference}\right)\end{array}\right.$
Gaussian criterion $P_{ij}^k=\left\{1-exp \left\{\frac{-{\left(d_{ij}^k\right)}^2}{2{\sigma }_k^2}\right\}\begin{array}{c}0, If d_{ij}^k\le 0\\ If d_{ij}^k>0\end{array}\right.$

Based on these choice functions, common choice functions are determined for alternative pairs [52].

$$P\left(a,b\right)=\left\{\begin{array}{c}0 f\left(a\right)\le f\left(b\right)\\ p\left. [f\left(a\right)-f\left(b\right)\right] f\left(a\right)>f\left(b\right)\end{array}\right.,$$

(6)

P (a, b): preference function, f: alternatives.

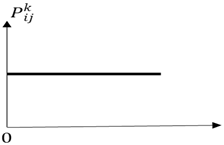
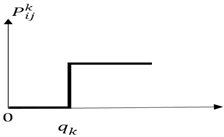
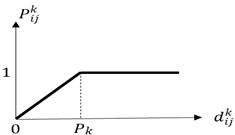
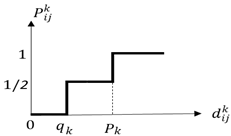
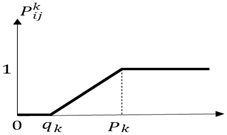
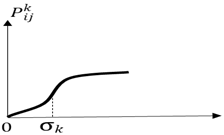
A schematic indication of common choice functions determined for alternatives is given in Figure 3. In the pairwise comparison of decision points, whether an evaluation factor has a maximization or minimization aspect is considered [52].

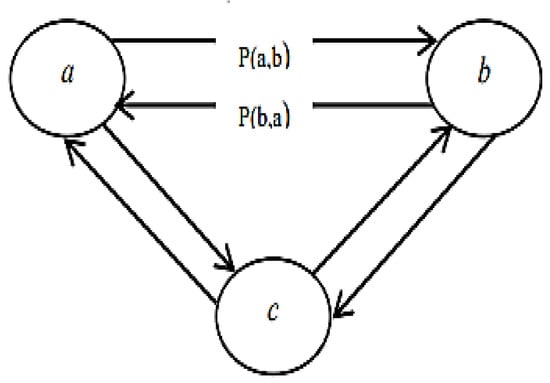
Figure 3. Schematic indication of common choice functions [56].

Based on the common choice functions, choice indices are determined for each alternative pair. The choice index of alternatives a and b evaluated by criterion c with a weight of $w_i$ (i = 1, 2, …, k) is calculated by Equation (7) [54].

$$\pi \left(a,b\right)={{\displaystyle \sum }}_i^k{w}_i{P}_i\left(a,b\right),$$

(7)

π: preference index, w: weight, i: criteria, P (a, b): preference function, and k: number of criteria.

Positive ($\phi$⁺) and negative ($\phi$⁻) superiority values are calculated by Equations (8) and (9) [54].

$${\phi }^{+}=\frac{1}{m-1} \sum \pi \left(a, x\right),$$

(8)

$${\phi }^{-}=\frac{1}{m-1} \sum \pi \left(x,a\right),$$

(9)

$\phi$: superiority π: preference index, m: number of alternatives.

Partial priorities for alternatives are determined via Promethee 1. Partial priorities ensure the determination of the preference status of alternatives, the determination of alternatives that are no different from each other, and the determination of alternatives that are incomparable with each other.

There are three conditions in defining partial priorities for alternatives a and b [54].

If any of the conditions below are met, alternative a is preferred to alternative b and calculated by Equations (10)–(12) [54].

$${\phi }^{+}\left(a\right)>{\phi }^{+}\left(b\right) ve {\phi }^{-}\left(a\right)<{\phi }^{-}\left(b\right),$$

(10)

$${\phi }^{+}\left(a\right)>{\phi }^{+}\left(b\right) ve {\phi }^{-}\left(a\right)={\phi }^{-}\left(b\right),$$

(11)

$${\phi }^{+}\left(a\right)={\phi }^{+}\left(b\right) ve {\phi }^{-}\left(a\right)<{\phi }^{-}\left(b\right),$$

(12)

$\phi$: superiority, $a$ or $b$ alternatives

If the condition given below is met, alternative a and b are no different and are calculated by Equation (13) [54].

$${\phi }^{+}\left(a\right)={\phi }^{+}\left(b\right) ve {\phi }^{-}\left(a\right)={\phi }^{-}\left(b\right),$$

(13)

$\phi$: superiority, $a$ or $b$ alternatives

If any of the conditions below are met, alternative a cannot be compared with alternative b, and they are, respectively, calculated by Equations (14) and (15) [54].

$${\phi }^{+}\left(a\right)>{\phi }^{+}\left(b\right) ve {\phi }^{-}\left(a\right)>{\phi }^{-}\left(b\right),$$

(14)

$${\phi }^{+}\left(a\right)>{\phi }^{+}\left(b\right) ve {\phi }^{-}\left(a\right)>{\phi }^{-}\left(b\right),$$

(15)

$\phi$: superiority, $a$ or $b$ alternatives

Whole priorities are calculated for each alternative. The total order is designated and calculated by Equation (16) [54].

$$\phi \left(a\right)={\phi }^{+}\left(a\right)-{\phi }^{\mp }\left(b\right),$$

(16)

$\phi$: superiority, $a$ or $b$ alternatives

Based on the whole priority value calculated for alternatives a and b, the following decisions are made [54].

If $\phi \left(a\right)>\phi \left(b\right)$, alternative a is superior, If $\phi \left(a\right)=\phi \left(b\right)$, alternative a and b are no different.

$\phi$: superiority,$a$or$b$alternatives

While sorting, a sequence starting from the alternative with a high index value to the alternative with a low index value is carried out. When index values are equal, there is no difference between/among alternatives [53].

3. Results

Proposal of Drilling Area Performance Measurement OHS Model

Taking the increase in renewable energy into consideration, an annotated chart and a hierarchic structure of criteria formed for drilling areas in the model proposed are given below. The main objective of the proposed index model is to find each determined criterion’s importance weight in the OHS performance. The process of defining the weight importance of criteria and subcriteria in the model proposed is as follows:

Step 1: To establish a decision-making team, criteria and subcriteria were determined by considering insufficiencies and basic concepts through a detailed literature review regarding the sector. The criteria determined and their definitions are shown in Table 6.

Table 6. The criteria and descriptions of the performance index.

	Main Criterion	Criterion Description
Level 1 Criterion 1	Errors Caused by Employees	The criterion designating the importance of errors in geothermal drilling performance, including the physical, spiritual, and mental negativity of employees.
Level 1 Criterion 2	Errors Caused by Insufficient Registry	The criterion indicating errors caused by unfortunate incidents in education, health, occupational accidents, and investigations in the past and errors arisen by insufficient legal forms stating the current situation.
Level 1 Criterion 3	Past Occupational Accidents	The criterion indicating the repetition of errors caused by insufficient statistical data defining past occupational accident registry and precautions taken.
Level 1 Criterion 4	Errors Caused by Insufficient Administration	The criterion indicating errors caused because the employer or the employer’s representative and the responsible authority do not make decisions required by OHS or do not structure the budget properly for that reason.
Level 1 Criterion 5	Risks Posed by Equipment	The criterion indicating errors caused because proper equipment is not purchased, either intentionally or unintentionally, or because proper equipment is not used for the proper work or necessary maintenance is not carried out.
Level 1 Criterion 6	Mass Protection Precautions	The criterion indicating errors caused because decisions to be made for mass protection precautions are not made and processes are not monitored.
Level 1 Criterion 7	Environmental Conditions	The criterion indicating errors caused by natural difficulties because the drilling area is founded under harsh physical conditions.
Employee-Caused Error Subcriteria		Criterion Description
Level 2 Criterion 1	Depression-Driven Errors	The criterion indicating depression and accompanying psychological problems and medication taken for errors caused by human beings.
Level 2 Criterion 2	Insufficient Stress Management	Conclusions arising because of sudden and quick psychological stress and no ability to manage that stress.
Level 2 Criterion 3	Insufficient Body Strength	The criterion indicating cases caused because one is not physically healthy due to various health problems.
Level 2 Criterion 4	Errors Caused by Incomplete Information	Risks posed because orientation trainings for work are not carried out properly, and the employee cannot perceive what should be done.
Level 2 Criterion 5	Errors Caused by Physical Disability and Ailment	Risk posed because an employee cannot carry out work safely due to a lack of the physical strength that the work requires.
Level 2 Criterion 6	Errors Caused by Excessive Self-Confidence	Taking too many risks as a result of excessive self-confidence arising from repetitive work routine and expertise.
Level 2 Criterion 7	Errors Caused by Fatigue	Feeling fatigue and attention deficits due to irregular eating habits and sleep caused by shift changes or excessive working.
Insufficient Registry Subcriteria		Criterion Description
Level 2 Criterion 1	Incomplete Personnel File	Incomplete personnel files including SSI (Social Security Institution) entries of working personnel
Level 2 Criterion 2	Insufficient Past Accidents Registry	Legal gaps caused by not informing the SSI of occupational accident registries and statistical gaps caused by a lack of log keeping.
Level 2 Criterion 3	Insufficient Occupational Diseases Registry	Legal gaps caused by not informing the SSI of occupational disease registries or statistical gaps caused by a lack of log-keeping.
Level 2 Criterion 4	Insufficient Inspection Report	Not filing registries stemming from inspections and not conducting necessary improvements in that respect.
Level 2 Criterion 5	Educational Insufficiency and Not Recording	Involves risks posed by not carrying out trainings required by law and the employee’s failure to understand the occupational security conditions of the work.
Level 2 Criterion 6	Insufficient Medical Reports	Risks posed by not conducting necessary tests at the beginning of a work period and periodically and by the uncertainty of an employee’s health condition.
Level 2 Criterion 7	Insufficient Organizational Chart	A complex structure caused by insufficient organizational charts and job definitions at an institute.
Past Occupational Accident Subcriteria		Criterion Description
Level 2 Criterion 1	Electricity-Caused Reasons	Accidents caused by the generator and electrical components are not sufficient measures and the electrician did not do their job.
Level 2 Criterion 2	Caused by Working in Heat	Burns caused by erupting hot water and gas extraction in geothermal work.
Level 2 Criterion 3	Intoxication	Intoxication caused by food or chemicals used.
Level 2 Criterion 4	Caused by Working at High Altitude	Falling or hanging in the air because of a failure to attach safety belts to ridge ropes while working in towers.
Level 2 Criterion 5	Caused by Falling Equipment and Material	Being injured as a result of leaving equipment and tools at slab edges, which then fall off due to tower resonance.
Level 2 Criterion 6	Caused by Vehicle Accidents	Vehicle accidents due to parking outside marked areas in the field.
Level 2 Criterion 7	Biological Risks	Being threatened by large and small organisms as a result of constantly working in open air and all negative situations caused by the COVID-19 pandemic
Level 2 Criterion 8	Chemical Risks	Being exposed to acids and chemicals used to drill various rocks during drilling operations.
Level 2 Criterion 9	Being Jammed or Crushed	Crushes and sprains that occur as a result of either materials getting stuck or displaced materials in the field falling on the employee.
Administration Insufficiency Subcriteria		Criterion Description
Level 2 Criterion 1	Insufficient Number of Staff	Insufficient labor power due to having too few employees for the task at hand.
Level 2 Criterion 2	Wage Policy	Not paying the same wage to employees of different genders doing the same job/work.
Level 2 Criterion 3	Lack of Motivation and Mobbing	Not appreciating or awarding employees with bonuses or praise for their work and tasks carried out or various pressures put on employees by administrations.
Level 2 Criterion 4	Lack of Corporate Identity	Not having a corporate culture/identity, not being serious about occupational safety, and ignoring the occupational safety of employees.
Level 2 Criterion 5	Lack of Procedures	Not defining directions, procedures, and standards to be used by a corporation.
Level 2 Criterion 6	Long Work Hours	Employees working three shifts due to nonstop drilling operations and not having occupational handover procedures during shift changes.
Level 2 Criterion 7	Lack of Job Definition	Employees’ failure to work in accordance with their job descriptions on organizational charts.
Errors Caused by Insufficient Equipment Subcriteria		Criterion Description
Level 2 Criterion 1	Usage of Wrong Equipment	Not having required equipment in the area or not purchasing it.
Level 2 Criterion 2	Inappropriate Usage for Work	Using equipment out of the usage area and in areas that are not of use.
Level 2 Criterion 3	Insufficient Maintenance	Not having periodical or regular maintenance of equipment or hindering maintenance.
Level 2 Criterion 4	Unlicensed Usage	Breaking, opening, or removing the seals/disregarding safety procedures for materials and the equipment used.
Level 2 Criterion 5	PPE Errors	Risks posed by errors caused by a lack of standard personal protective equipment, CE certificates, or manufacturing defects.
Level 2 Criterion 6	Design Problem	Not designing tools and equipment in accordance with occupational safety during the design process.
Level 2 Criterion 7	Storing	Not having appropriate storing according to the proper procedures of the machine and equipment used; not shelving materials or shelving at the wrong height.
Level 2 Criterion 8	Calibration	Not calibrating machines used in certain periods and making measuring errors as a result.
Insufficient Mass Protection Precaution Subcriteria		Criterion Description
Level 2 Criterion 1	Technical Equipment Precautions	Technical equipment not being present for mass protection.
Level 2 Criterion 2	Shift Change Procedure	Risks posed by malfunctions that might occur during shift changes between staff working at different hours.
Level 2 Criterion 3	Health and Safety Signs	Not having the health and safety signs needed in a working environment or having inaccurate signs.
Level 2 Criterion 4	Lack of Emergency Procedure	Not prepared for emergencies or not knowing how to handle them.
Level 2 Criterion 5	Following Directions	Not following definitions/directions for precautions regarding machines, tools, equipment, and occupational safety; now knowing how to conduct construction work and use materials.
Level 2 Criterion 6	Lack of Emergency Staff	Not having adequate first-aid teams for emergencies.
Environmental Factor Subcriteria		Criterion Description
Level 2 Criterion 1	Physical Conditions	Conditions regarding the heading resonance, noise, radiation, thermal comfort, and dust in the surroundings.
Level 2 Criterion 2	Climate	Climate conditions of countries or regions where work is carried out, whose impacts are important to consider for employees working in open fields.
Level 2 Criterion 3	Location Choice	Conditions regarding the fields where drilling areas will be established and the conditions related to the relevant situation and position worksite; conditions minimizing the influence of climate conditions.

Step 2: A hierarchic building model is formed in Figure 4. In the hierarchical building model, the main criteria are shown at the highest level, and the subcriteria are shown at lower levels. Alternatives are not defined in the model because importance weights of drilling area alternatives for which criteria are determined will be designated by the Promethee method.

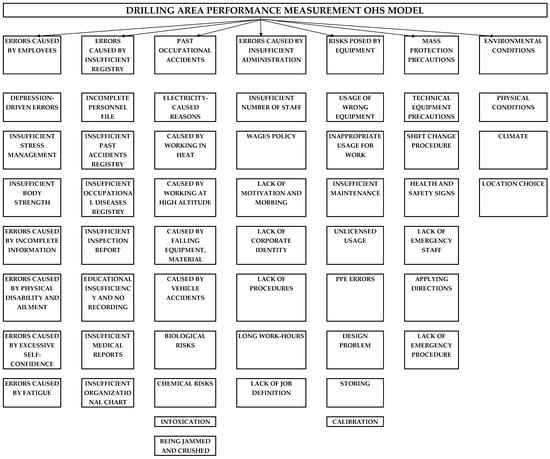
Figure 4. The geothermal drilling hierarchical building model.

Step 3: The model formed was transformed into super-decision package software used for the AHP method. After providing relationship establishment among criteria in the program, pairwise comparison questionnaires on the designated criteria using a 1–9 Saaty scale were completed by eight engineers, three of whom were also occupational safety experts; they were asked to evaluate criteria related to drilling areas. While data were being input into the program, the geometrical mean of points obtained from experts was calculated.

Program screenshots for the drilling area performance index are shown in Figure 5 and Figure 6.

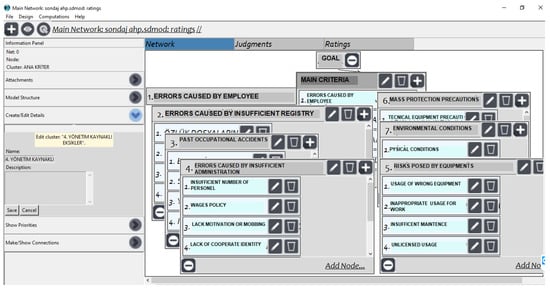
Figure 5. Model screenshot for hierarchical structure.

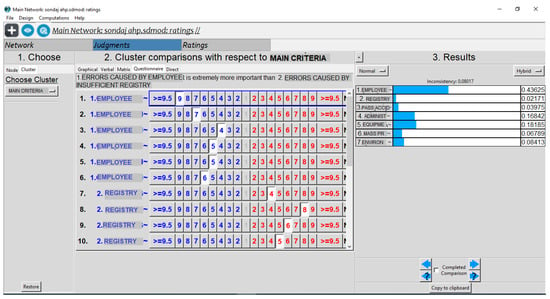
Figure 6. Model screenshot for criteria weighting.

Step 4: After completing pairwise comparison questionnaires, the importance weight for each criterion was obtained. The consistency ratio was checked at each step. If it was higher than 0.10, the pairwise comparison conducted was revised and revaluated. Program screenshots for the consistency ratio is shown in Figure 7.

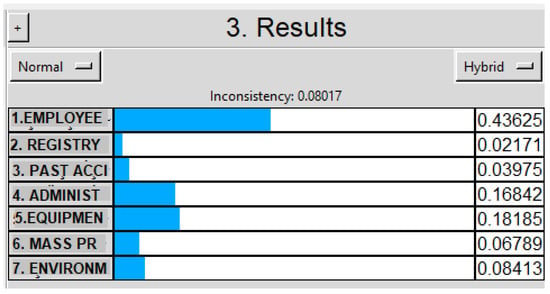
Figure 7. Screenshot of the pairwise comparison survey.

Step 5: The results of the evaluations yielded the importance weight of each designated criterion according to their OHS performance. Data belonging to the results are interpreted in Section 4.

Step 6: In the final step, the Visual Promethee program was used. Alternatives were requested from drilling supervisors of three geothermal drilling areas for which performance measurements were conducted. Taking criteria at the lowest level of each branch hierarchically into consideration, 47 subcriteria were input into the program, and the V-type was considered suitable as a choice function. Together with program outcomes, drilling area alternatives of those criteria were evaluated. Information regarding the results is explained in Section 4.

4. Discussion

Studies on multi-criteria decision-making methodologies and occupational health and safety in different sectors were examined. These studies have been examined and a framework for OHS performance modeling in geothermal energy fields has been established. The methodology and process of the four studies presented below were used.

Multi-criteria decision-making methods are the closest implementations to the ideal truth in answering multivariate questions. Through examining mostly studies conducted in the mining sector while designating multi-criteria decision-making methodologies, determining the required criteria for the designation of the most appropriate location in the mining fields and the mining method and also weighting the determined criteria have guided this article. In this way, the problems experienced in our country and other countries regarding occupational health and safety, especially in geothermal drilling fields, were compared and the criteria used in the study were reviewed [56]. Regarding the methods used, the AHP, F-AHP and PROMETHEE far outnumber the rest. Furthermore, through examining economic, environmental, and social dimensions of renewable energy in some OECD countries, the future significance of the sector was studied. In determining the locations of potential geothermal sources correctly, we also discussed which of the multi-criteria decision-making methodologies were used and why, and this contributed to our study [1,40]. Moreover, multi-criteria decision-making methods were used in order to study spatial distribution and spatial relationship among open geoscience data sets on a regional scale. It was observed that the AHP has been used for a long while as an essential method and is preferred since accurate results can be easily acquired thanks to programs such as Super Decision. Other methodologies used were F-AHP, PROMETHEE, Electre, TOPSIS, Fry Analysis, Data Envelopment and Weights of Evidence [39].

In the first step, the geometrical mean values of points obtained from all experts for each criterion were calculated via the AHP and F-AHP, and entry to the Super Decision program was carried out for the AHP. Fuzzy AHP calculations were conducted on Excel via Buckley F-AHP. Inconsistency ratios were checked. In the next step, the importance weight of each sub-criteria for OHS performance was acquired (Table 7).

Table 7. According to the AHP method weights of the lower criteria of the geothermal drilling OHS performance index.

Fuzzy Ahp		Ahp
Importance Weights		Importance Weights
Physical Conditions	0.086	Errors Caused By Fatigue	0.170
Errors Caused By Fatigue	0.075	Errors Caused By Incomplete Information	0.088
Lack Of Procedures	0.067	Wage Policy	0.066
Shift Change Procedure	0.065	Errors Caused By Excessive Self-Confidence	0.061
Errors Caused By Physical Disability And Ailment	0.060	Lack Of Emergency Procedure	0.046
Errors Caused By Excessive Self-Confidence	0.045	Physical Conditions	0.045
Depression-Driven Errors	0.036	Insufficient Body Strength	0.045
Insufficient Stress Management	0.035	Lack Of Emergency Staff	0.040
Wage Policy	0.035	Depression-Driven Errors	0.039
Usage Of Wrong Equipment	0.033	Lack Of Corporate Identity	0.034
Lack Of Emergency Procedure	0.033	Shift Change Procedure	0.032
Technical Equipment Precautions	0.029	Insufficient Number Of Staff	0.026
Lack Of Motivation And Mobbing	0.029	Applying Directions	0.025
Applying Directions	0.023	Climate	0.025
Lack Of Job Definition	0.023	Insufficient Stress Management	0.021
Caused By Working In Heat	0.021	Health And Safety Signs	0.020
Lack Of Corporate Identity	0.020	Technical Equipment Precautions	0.019
Insufficient Body Strength	0.020	Design Problem	0.018
Intoxication	0.019	Lack Of Motivation And Mobbing	0.016
Location Choice	0.018	Lack Of Job Definition	0.015
Inappropriate Usage For Work	0.017	Location Choice	0.014
Unlicensed Usage	0.015	Errors Caused By Physical Disability And Ailment	0.012
Ppe Errors	0.015	Electricity-Caused Reasons	0.011
Insufficient Past Accidents Registry	0.012	Caused By Working In Heat	0.009
Errors Caused By Incomplete Information	0.012	Usage Of Wrong Equipment	0.009
Design Problem	0.012	Incomplete Personnel File	0.008
Insufficient Maintenance	0.012	Ppe Errors	0.008
Being Jammed Or Crushed	0.011	Unlicensed Usage	0.008
Lack Of Emergency Staff	0.011	Inappropriate Usage For Work	0.008
Climate	0.011	Long Work-Hours	0.006
Electricity-Caused Reasons	0.010	Storing	0.006
Health And Safety Signs	0.010	Lack Of Procedures	0.006
Long Work-Hours	0.010	Insufficient Maintenance	0.006
Insufficient Occupational Diseases Registry	0.009	Calibration	0.005
Insufficient Number Of Staff	0.008	Caused By Vehicle Accidents	0.005
Insufficient Inspection Report	0.008	Caused By Working At High Altitude	0.005
Calibration	0.008	Educational Insufficiency And No Recording	0.004
Storing	0.007	Insufficient Medical Reports	0.004
Incomplete Personnel File	0.004	Being Jammed Or Crushed	0.002
Educational Insufficiency And No Recording	0.004	Chemical Risks	0.002
Biological Risks	0.004	Biological Risks	0.002
Caused By Vehicle Accidents	0.004	Insufficient Organizational Chart	0.002
Caused By Working At High Altitude	0.004	Caused By Falling Equipment And Material	0.002
Chemical Risks	0.003	Intoxication	0.002
Caused By Falling Equipment And Material	0.003	Insufficient Past Accidents Registry	0.001
Insufficient Medical Reports	0.002	Insufficient Occupational Diseases Registry	0.001
Insufficient Organizational Chart	0.002	Insufficient Inspection Report	0.001
Total	1.000		1.000

When Table 7 is examined, if the sequence is examined based on the weighting made by the AHP method, “Errors Caused By Fatigue” (0.170) is the first problem, while the F-AHP is in second place, “Errors Caused By Fatigue” (0.075). “Errors Caused By Incomplete Information” (0.088) and “Wage Policy” (0.066) rank second and third, while the F-AHP study does not appear in the first six weighting categories. “Errors Caused By Excessive Self-Confidence” (0.061) is in sixth place in the study with F-AHP. The “Lack Of Emergency Procedure” (0.046) ranks fifth and is not included in the F-AHP ranking. “Physical Conditions” (0.045) is in sixth place, and the F-AHP ranking (0.086) takes first place.

In the F-AHP methodology weighting study, “Lack Of Procedures” (0.067) takes third place, “Shift Change Procedure” (0.065) takes fourth place, and “Errors Caused By Physical Disability Additionally, Ailment” (0.060) takes fifth place. These three categories do not rank in the first six items in the AHP study.

At the second step, for all criteria designated, geometrical mean values of scores obtained from all experts are calculated and put into the Visual Promethee program, and performance index results are obtained. Based on these results, partial sorting/sequencing is determined via PROMETHEE I. In the step with pairwise comparisons of positive and negative superiority values regarding decision points, three situations are likely to occur: the superiority of one decision point over another, a lack of difference between decision points, and incomparable decision points. In accordance with the criteria weights shown in Figure 8, there is a sequence from best to worst. According to PROMETHEE I, out of the three drilling areas, AREA 2 ranks first in terms of OHS criteria performance, followed by AREA 3 and AREA 1 in second and third, respectively.

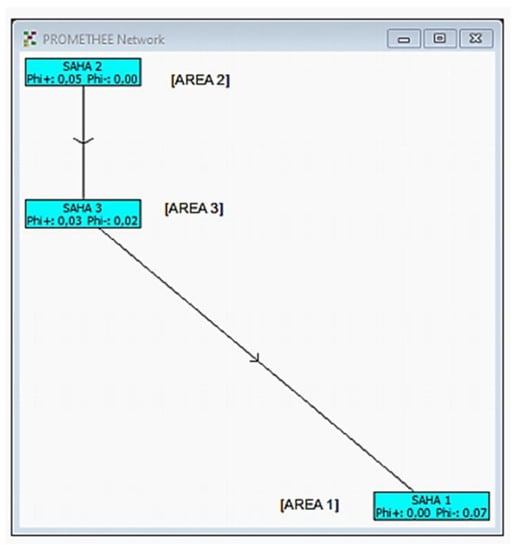
Figure 8. Sorted results calculated with PROMETHEE I.

5. Conclusions

Occupational accidents not only cause death and injuries. Invisible expenses are involved, including: labor loss, expertise loss together with experienced employees, compensations, various penalties, and insurance payouts. Hence, preventing accidents in every line of work requires research. It is economically and socially important to prevent accidents that might occur in the geothermal drilling of wells, which is one of the clean energy branches in the energy sector and is gradually gaining importance. Thus, it is necessary to conduct accurate analyses, use management systems, become knowledgeable about legislation, estimate risks beforehand, and understand how to work with equipment properly. It is important to apply occupational safety procedures according to standards such as OSHA and ISO45001. This paper covers and evaluates criteria and performance index proposals designated as a result of different studies on occupational health and safety in geothermal drilling areas. Table 7 shows that the weighting results of the AHP and fuzzy AHP subcriteria are similar. Errors caused by employees are frequent and include: fatigue, stress, a lack of physical strength, a lack of information, excessive self-confidence, wage policies, and an insufficient number of staff. The last two indirectly depend on the human factor. Following those, it is striking that errors caused by administration and insufficient mass protection precautions are also frequent. This emphasizes the importance of the spiritual, mental, and physical well-being of employees. It is clear that, along with being physically suitable for the work, the spiritual health of an employee is critical. In addition, occupational accidents in the past, the misuse of equipment and work machines, incorrect definitions of general protection measures, environmental conditions, location selection, PPE errors, vehicle accidents, chemical risk factors, and physical risk factors should also be considered in terms of occupational health and safety. In fact, there are human-induced risk factors influencing these factors. Mass protection precautions to be taken by administration and procedures to be implemented need to be studied further. Drilling works are continuous from beginning to end. It is important to financially satisfy working staff who are far from their homes and engaging in physically demanding work for long periods of time, to encourage them to pay attention to working hours, and to satisfy them spiritually by taking stress, depression, and fatigue criteria into consideration. In this regard, supportive actions from the Ministry of Energy and the Ministry of Labor and Social Security can be increased.

While we only expected this work to serve as a basis for the preparation of a risk assessment suitable for the sector, this study is considered to be significant not only for drilling areas through its OHS performance index model proposal, which provides an evaluation of performance measurement, but also in other sectors as well in terms of solving and clarifying obscurities and answering questions.

To conclude, drilling operations involve many complex elements, and elements originating from the work of human beings are also complex and important for drilling areas. Through a consideration of employee-based occupational health and security systems in economic, social, and ecologic dimensions, problems regarding health and sustainability can be overcome.