Abstract
As an important part of intelligent transportation systems, traffic state classification plays a vital role for traffic managers when formulating measures to alleviate traffic congestion. The proliferation of traffic data brings new opportunities for traffic state classification. In this paper, we propose a hybrid new traffic state classification method based on unsupervised clustering. Firstly, the k-medoids clustering algorithm is used to cluster the daily traffic speed data from multiple detection points in the selected area, and then the cluster-center detection points of the cluster with congestion are selected for further analysis. Then, the self-tuning spectral clustering algorithm is used to cluster the speed, flow, and occupancy data of the target detection point to obtain the traffic state classification results. Finally, several state-of-the-art methods are introduced for comparison, and the results show that performance of the proposed method are superior to comparable methods.
1. Introduction
With the development of social economy and the expansion of urban population, the traffic flow on urban roads continues to increase, and traffic congestion intensifies, which seriously affects the traffic efficiency of urban roads and the normal operation of transportation systems [1]. Intelligent transportation systems (ITS) can effectively solve the traffic congestion problem of urban roads through traffic management and traffic flow guidance, and traffic state classification can reflect the traffic’s overall operation state. Traffic managers can formulate corresponding measures to alleviate traffic congestion through traffic state information provided [2,3,4]. Therefore, traffic state classification has for a long time been a significant research topic in the field of transportation. Researchers have developed a variety of different types of traffic state classification methods.
At present, the traffic state classification methods are mainly divided into direct and indirect classification methods. Direct classification methods can visually classify the traffic state through information such as video images. Although this method has high classification accuracy, it is difficult to obtain clear video image information, and different visibility also affects classification accuracy. In addition, this method is inefficient in dealing with large amounts of traffic information. Indirect classification methods can classify the traffic state by analyzing the traffic data obtained by traffic detectors distributed in different sections. These methods have the advantages of high classification efficiency and easy data acquisition. The method adopted in this study involved indirect classification [5]. We classified and evaluated the traffic state through the existing traffic data, and the classification results had a positive effect on improving traffic congestion. In addition, many scholars have proved that the use of historical traffic parameters can accurately predict future traffic parameters. For example, Ma et al. [6] used a self-adaptive two-dimensional forecasting method to predict short-term traffic flow, and obtained excellent prediction results. Therefore, through clustering analysis of future traffic parameters, prediction of future traffic conditions can be achieved.
As an unsupervised learning method, clustering analysis can classify traffic flow data without any prior conditions. So far, many clustering algorithms have been selected to analyze different traffic states. In recent years, clustering algorithms have achieved good results in the field of traffic state classification. For example, in 2019, Nguyen et al. [7] proposed using a clustering analysis algorithm to extract highway congestion characteristics. In 2020, Tišljarić et al. [8] extracted the Speed Transition Matrix by analyzing traffic data, and estimated traffic state according to the centroid of the Speed Transition Matrix. In 2021, Pei et al. [9] realized traffic congestion identification of main roads in cities in cold climates by clustering analysis algorithm. Clustering analysis divides the dataset into multiple classes and allocates data with high similarity into the same class. For traffic flow data, clustering results are usually divided into normal and congestion. In 1979, Herman and Prigogine [10] divided traffic state into smooth flow and congestion, and most of the subsequent traffic state classifications have been based on this. In 2004, Kerner [11] proposed a three-phase traffic flow theory, which divides traffic flow into free flow, synchronized flow, and wide moving jam. This classification method has been widely used; in 2018, Esfahani et al. [12] used the three-phase traffic flow theory as the classification standard when conducting cluster analysis on traffic flow data. In 2020, Wang et al. [13] divided traffic flow data into three traffic flow states using FCM clustering algorithm, and traffic flow state recognition based on ensemble learning, to determine the traffic flow parameters corresponding to each traffic state. Cheng et al. [14] proposed an improved FCM clustering algorithm to classify urban traffic states, and traffic state was divided into five levels: smooth, basic flow, slight congestion, basic congestion, and severe blockage.
The current clustering methods used for traffic flow data are mainly the FCM clustering algorithm, the k-means method, and its improved method. The k-means algorithm was published by Lloyd [15], and this clustering method was later applied to different fields. So far, scholars continue to use the k-means algorithm to classify different types of data. For example, Montazeri-Gh et al. [16] used the k-means algorithm to identify traffic conditions based on driving characteristics. In 2019, Rao et al. [17] used the k-means method to cluster traffic flow variables (volume to capacity ratio, queue length, and delay) collected from intersections. In 2021, Zhao et al. [18] proposed a self-organizing map (SOM) and k-means fusion algorithm to classify network traffic. The FCM algorithm is also a popular clustering analysis technique in the field of transportation, and an improved FCM algorithm has been used for urban traffic state classification [14]. In 2021, Liu et al. [19] used the FCM algorithm to evaluate the traffic state of an expressway network. Furthermore, the improved algorithm and other methods based on the k-means algorithm have been widely used in the study of traffic state. For example, Yang et al. [20] used the spectral clustering algorithm to cluster urban traffic flow data from the perspective of the road network, and Zhang et al. [21] used the k-medoids clustering method to analyze relevant traffic flow information from the spatial dimension.
Many researchers have chosen speed, flow and occupancy for clustering analysis, Zhang et al. [22] chose speed, flow, and occupancy as the main parameters in the study of traffic state classification using a weighted FCM method. According to the addition of other traffic data on the basis of basic traffic parameters, good classification results have been achieved. For example, Cheng et al. [14] proposed a new classification index, namely road network adequacy, and established an evaluation system for the traffic state index by combining road network adequacy with speed, flow, and occupancy. In addition, the change trends of traffic parameters such as traffic flow differ daily at different detection points. Clustering based on the change trends of traffic parameters in different locations over a period of time has also been used for studying traffic state classification. Su et al. [23] took as samples the time variation trends of traffic flow within a day at multiple intersections in a city, converted the traffic flow sequence data of different detection points into a gray image, and then clustered the image.
Clustering is the process of grouping similar objects into different groups. Clustering analysis of different datasets can obtain different classification results. So, the selection of datasets is particularly important. Some researchers obtained useful traffic state classification criteria by directly studying single detection-point data (for example, Wang et al. [13] identified clustering centers of different traffic states by analyzing the traffic parameters of the detection point). When traffic congestion occurs in a region, the traffic conditions of different sections in that region are different. Some researchers have classified sections with different traffic conditions through cluster analysis of traffic parameters for different sections. For example, Yang et al. [20] used spectral clustering technology to analyze the daily traffic state changes of a regional road network, so as to detect traffic congestion sections and traffic state during holidays. In 2019, Mondal et al. [24] used the k-means algorithm to classify different sections based on traffic density and average vehicle speed, and identified sections of cities where there were serious traffic congestion problems. In Section 3.3, this paper compares the traffic state partition results of single detection-point data and detection-point data filtered by clustering algorithm. It can be seen from the comparison results that the traffic data used in this paper can improve the accuracy of traffic state classification, by selecting the appropriate detection point data through clustering algorithm. Therefore, the analysis provided in this study suggests that traffic parameters directly selected by a single detection point cannot accurately represent the overall traffic situation in a region. The traffic pressure at the selected detection point may be significantly higher or lower than that of the surrounding road section, affecting to a certain extent the accuracy of the traffic state classification results. The above situation can be avoided or minimized by analyzing different road sections. Therefore, state classification of traffic parameters using the clustering method needs to solve two main problems; the need to select sections containing different traffic states for clustering; and selection of the appropriate clustering algorithm to obtain accurate classification results.
Firstly, we collected speed data from multiple detectors in a certain area of the city on a single day, and divided different detection points into multiple categories by using the k-medoids clustering method according to changes of speed during the day. Then, the central cluster detection point in a category was selected as representative of this kind of detection point, and the traffic parameters of the selected detection point for two consecutive months were clustered. When analyzing the traffic flow parameters of a single detection point, we use the self-tuning spectral clustering method to cluster the parameters of speed, flow, and occupancy. The self-tuning spectral clustering algorithm [25] does not require manual selection of scale parameters, which improves its clustering performance compared with the traditional spectral clustering algorithm. Finally, two evaluation criteria, i.e., the classification accuracy and normalized mutual information (NMI) were applied to evaluate the proposed method and other comparison methods (FCM algorithm by Liu et al., 2021 [19]; k-means algorithm by Esfahani et al., 2019 [12]; and spectral clustering algorithm by Shang et al., 2017 [26]). The main contributions of this paper can be summarized as follows:
- The k-medoids algorithm and self-tuning spectral clustering algorithm were combined for traffic state classification in the target area. The k-medoids algorithm was used to divide different sections into multiple clusters based on daily traffic speed data, and then the cluster-center detection points were selected to classify the traffic state using the self-tuning spectral clustering algorithm based on traffic parameters. This process included for the first time the application of the k-medoids algorithm for classification of different sections.
- The first use of the self-adjusting spectral clustering algorithm for traffic state discrimination based on traffic parameters.
Using the silhouette coefficient, Davies–Bouldin (DB) index, and Krzanowski–Lai (KL) index to determine the number of clusters k in the k-medoids algorithm. The rest of this paper is arranged as follows. In Section 2, we propose the definition of traffic state classification level, determine the traffic indicators needed for clustering analysis, and introduce the principles of the k-medoids clustering algorithm and self-tuning spectral clustering algorithm. Section 3 illustrates the data source and empirical results. In Section 4, we discuss the comparison results and summarize the differences between the results obtained by different methods, indicating the superiority of the method proposed in this study. Section 5 draws conclusions and discusses recommendations for future work.
2. Materials and Methods
2.1. Definition of Traffic State Classification Levels
Due to the unique characteristics of traffic flow parameters in different traffic states, it is not accurate to distinguish traffic states only by numerical characteristics. To correctly distinguish different traffic conditions, it is necessary to identify the accuracy of clustering results. This paper refers to the American Highway Capacity Manual (HCM) [27]. The Highway Capacity Manual divides the service level of urban expressways into six categories: A, B, C, D, E and F. Service level A indicates that vehicles can travel at free flow speed, and vehicles in the traffic flow can implement maneuver operations without interference. In this study, times when the service level was in category A are defined as a “smooth” state. Level B, level C, and level D service respectively indicate that vehicles are limited in varying degrees during driving, and that small accidents are likely to cause queuing phenomena. Road traffic is under pressure to enter the congestion state. In this study, B, C, and D service levels are categorized as “slow” states. When the highway is at service level E, the traffic density is close to its maximum, and the vehicle speed is significantly affected, so driving freedom in the traffic flow is greatly limited. F-level service indicates blocked traffic. Therefore, this study defines the traffic state of E and F highway service levels into “congestion”. In this study, occupancy is defined as a standard when determining the classification level of traffic state. Because traffic flow is significantly reduced when road congestion occurs, the size of traffic flow cannot fully explain the traffic state. Similarly, when traffic flow is low, traffic speed is easily affected by many factors. Increase in occupancy rate obviously indicates an increase in traffic pressure, and the change in the number of occupants in the traffic flow does not decrease significantly when the road is jammed; thus, it is reasonable to define traffic state by occupancy. In addition, the detectors selected in this study were located on a four-lane urban highway, and the traffic state classification level was calculated according to the standards of the Highway Capacity Manual. In summary, we divided different service levels into different traffic states by occupancy rate, and traffic states were divided into smooth, slow, and congestion (shown in Table 1).

Table 1.
Traffic state classification levels.
2.2. Traffic State Classification Index
Many previous studies have shown that speed, flow, and occupancy are the most commonly used indicators of traffic state. These three traffic data are relatively easy to obtain, and many research results have shown that ideal results can be obtained by analyzing these three indicators. The purpose of this study was to classify traffic state, so the speed, flow, and occupancy data were selected for analysis. In terms of traffic flow data, to avoid variations in traffic flow caused by different road types and numbers of lanes affecting the clustering results, the data collection object of this paper was the traffic flow of a four-lane urban highway.
2.3. K-Medoids Method
The k-means algorithm takes as the center point the average value of all data points in the current cluster, and the k-medoids algorithm is a variant of the k-means algorithm. The center point in the current cluster satisfies the minimum sum of the distance between each point and the other points in the current cluster. Therefore, compared with the k-means algorithm, the center point of k-medoids is selected from the existing data. We chose the data characteristics of the center points obtained by the k-medoids algorithm as representative of all the detection points of a category, and obtained the characteristics of various types of data through analysis of the selected data for multiple centers.
The k-medoids algorithm selects the centroid from existing data points, so it has better robustness to noise. In addition, although the running time of the k-medoids algorithm is longer than that of the k-means algorithm, due to the computational complexity, there is no obvious difference between the running time of the model and that of the k-means algorithm when calculating datasets with small amounts of data. In summary, the k-medoids algorithm is suitable for clustering all-day velocity data of multiple detection points. The main steps of the k-medoids algorithm are as follows.
- (1)
- Randomly select k data points from the dataset as the center points.
- (2)
- Calculate the distance between each data point and the center point, divide the data point and the nearest center point into one class, and finally divide all data points into k clusters.
- (3)
- Calculate the distance between all data points in each cluster, and select the point with the smallest sum of distances as a new medoid to calculate the cost function generated by the new medoids. If it is negative, replace it, or if not then replace and restore the center point.
- (4)
- Repeat steps (2) and (3) until medoids no longer change, or reach the set number of iterations.
2.4. Self-Tuning Spectral Clustering Method
Spectral clustering evolved from graph theory and was later widely used in clustering techhniques. Spectral clustering does not require a specific data structure; in contrast, the k-means method requires that the data must be convex. In addition, the essence of spectral clustering is graph cutting, so it avoids the amalgamation of discrete clusters. The spectral clustering method involves clustering the eigenvectors of the Laplacian matrix of the sample data. This transforms the data from high-dimensional to low-dimensional space, so as to reduce the computational complexity and improve the clustering effect, then clustering in low-dimensional space through other methods (k-means was selected in this study).
The first step of spectral clustering is to construct the similarity matrix, which is the distance measurement of any two points in the sample data. The higher the similarity of distance leap between two points, the lower the distance similarity. The traditional spectral clustering algorithm constructs a similarity matrix using the full connection method, which represents the distance between two sample points through Gaussian distance; the formula is shown in Equation (1). In the formula, the neighborhood width of the sample data is controlled by the scale parameter , which indicates that the larger the value of , the greater the similarity between the sample point and other sample points with a long distance is:
The similarity matrix is obtained by the full connection method. Because the scale parameters have a great influence on the clustering results, the traditional spectral clustering algorithm requires manual selection of the parameters . In previous studies, researchers have used their clustering algorithms to determine repeatedly the scale parameters. This method not only requires manually setting the range of values to be tested, but also greatly increases the computational time. In addition, the research of Zelnik-Manor et al. [15] showed that when data contained different scales, the fixed scale parameters could not obtain good clustering results.
To avoid the negative impact of parameter selection difficulties on clustering results, we chose to calculate a local scale parameter for each data point. This method can solve the problem of unsuitability of clustering results obtained by the traditional spectral clustering algorithm in the face of multi-scale data, and reduces the calculation time of the model. The calculation method for local scale parameters is shown in Equation (2). is the Kth nearest neighbor data of , and represents the distance between each data point and the kth nearest neighbor data:
After calculating the scale parameters corresponding to each data point, we can improve Equations (1)–(3):
After obtaining the similarity matrix , we further calculated the degree matrix , as shown in Equation (4):
By reconstructing the adjacency matrix and calculating the diagonal matrix , the Laplacian matrix can be calculated according to Equation (5):
Then the normalized Laplacian matrix can be constructed, see Equation (6):
After obtaining the Laplacian matrix, the eigenvalues of were calculated. Then sorting the eigenvalues from small to large, we calculated the eigenvectors corresponding to the first k eigenvalues . Feature vectors were standardized to form feature matrix , see Equation (7):
Let be the vector of the ith row of , where , forming a new sample .
Finally, we used the k-means algorithm to cluster the new sample point and obtain the final clustering result.
2.5. The Proposed Method
Figure 1 shows the steps of the method used in this study.
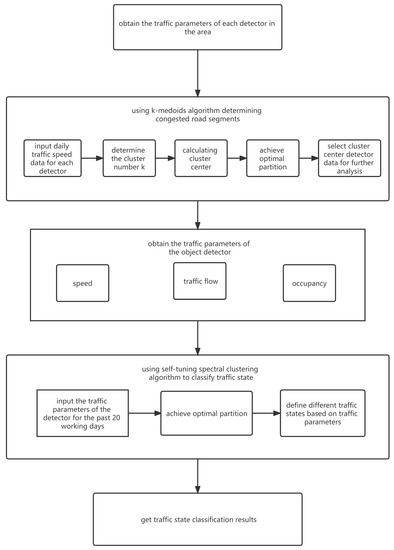
Figure 1.
Flowchart of the method.
The specific steps of the proposed method are as follows:
- (1)
- In this study, a total of 27 loop detectors in a region of California were selected from the Performance Measurement System (PeMS) public database, and the speed data with 1 h interval were extracted for the working day.
- (2)
- The k-medoids clustering algorithm was used to cluster the velocity data for different detection points, and the detection points were divided into different partitions according to the clustering results.
- (3)
- We identified the congestion categories in the evening peak period, and then prepared to further analyze the speed, flow, and occupancy data for 20 working days from the cluster-center detection point.
- (4)
- According to the road transport manual standards, the traffic state was divided into three categories according to the level of road service. The standards of different traffic states were formulated based on the occupancy data, as a reference for determining the accuracy of the clustering results.
- (5)
- The extracted traffic data were clustered by spectral adaptive clustering algorithm, and the classification accuracy, confusion matrix, and NMI values were obtained by combining the definitions of traffic state classification levels.
3. Results
3.1. Data Description
In this study, we first clustered the traffic speed dataset obtained by the detector, and selected the traffic speed data for the whole day of 23 September 2021. The time intervals were 1 h. The traffic speed data was taken from from the PeMS database, which collects traffic data from more than 39,000 individual detectors; the arrangement of sensors covers the expressway system in all metropolitan areas of California. The study area selected in this study contained 27 detection points, and the positions of the detection points each covered four lanes. The study area is shown in Figure 2, where the blue points are the positions of the detection points. After clustering the traffic speed dataset, we further clustered the speed, flow, and occupancy parameters obtained by the detection points of each cluster center. In terms of the data selection of this cluster analysis research, we selected for analysis the traffic parameters of all working days from 23 September to 20 October 2021.
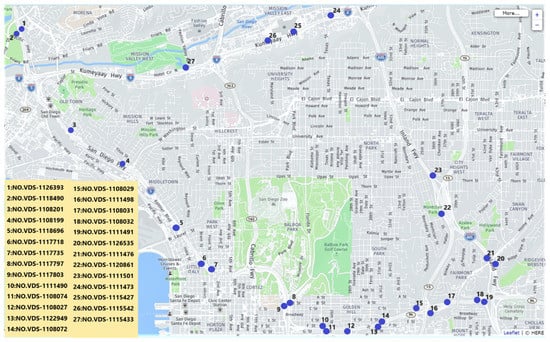
Figure 2.
Detector Locations in Regional Road Networks.
According to the traffic speed data from all detection points in the study area (Figure 3), it can be seen that the traffic speed remained in a stable interval for most of the day. When the traffic speed decreased significantly during a certain period of time, it indicated that the normal operation of traffic flow on the road was hindered for this period, and the most common reason for the decrease of traffic speed was traffic congestion. Figure 3 shows that the traffic speed data from different detectors decreased at different time periods. We used the clustering algorithm to classify these results.
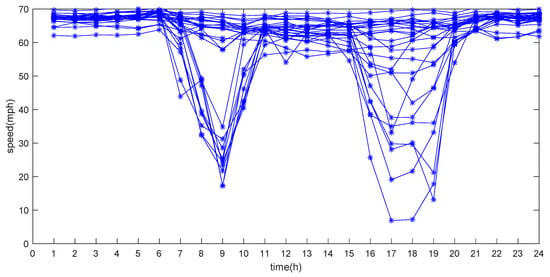
Figure 3.
Daily traffic speed variation for all detectors.
3.2. Analysis for Clusters
3.2.1. Analysis of Congested Road Sections Based on Daily Traffic Speed Data at Detection Points
The samples were collected from 27 detectors in an area of California, USA. The data were monitored for all-day traffic speeds on 23 September 2021, with intervals of 1 h. We used the k-medoids algorithm to cluster different detection points. This method divides detection points with similar characteristics into one category, by analyzing the characteristics of traffic speed at different detection points. At the same time, k detection points are selected by the k-medoids algorithm as the clustering centers of the clustering results, and each clustering center represents the characteristics of its corresponding category. After obtaining the initial clustering results, this study selected other traffic parameters of the cluster-center detection point for further analysis, in order to identify the traffic state.
In this study, the k-medoids clustering algorithm was used to cluster all-day traffic flow velocity data from different road detectors, to divide different types of road traffic flow characteristics. To select the appropriate number of clusters to ensure the accuracy and effectiveness of clustering results, it is necessary to compare through internal indicators the clustering results obtained from different cluster numbers. If the number of clusters is too small, the difference between detectors in the same cluster is large, and if the number of clusters is too large, the difference between different clusters in the clustering results will not be obvious. Determining the appropriate number of clusters is the key to ensuring the accuracy of clustering results. In order to ensure the accuracy of clustering results, this study used silhouette coefficient, Davies–Bouldin (DB) index, and Krzanowski–Lai (KL) index to determine the number of clusters. The smaller the Davies–Bouldin value, the higher the similarity between samples in the same cluster, and the smaller the similarity between samples in different clusters. Silhouette coefficient is another indicator to evaluate the clustering effect; the closer the contour coefficient is to one, the more reasonable the clustering result. Similarly, a higher Krzanowski–Lai (KL) value indicates better clustering results. In order to reduce the complexity of the clustering process and ensure the practicability of the clustering results, we initially determined the number of clusters as 2–6.
Silhouette coefficient is an index to evaluate clustering effect. This method combines the factors of cohesion and separation, to evaluate the clustering effect according to different numbers of clusters and different clustering methods.
In above formula, is the average distance between sample point and other sample points in the same cluster, is the average distance between sample point and all sample points in the other cluster. The better the clustering effect, the smaller the average distance from the sample point to the sample point in the same cluster, and the larger the average distance from the sample point in other clusters. So, the bigger the contour coefficient, the better the clustering performance.
The Davies–Bouldin index first requires calculation of the variable , which is the average distance from the intra-cluster data to the cluster center, and represents the dispersion of the intra-cluster data. The calculation formula of is as follows:
where represents the jth data point in class ; represents the center of category ; represents the number of data points in Category ; is the distance from each point to the center, indicates standard deviation of distance from each point to the center, which together can be used to measure dispersion.
Then, the distance between variables can be calculated according to Equation (10):
where represents the value of the attribute of the center point of the class , and is the distance between the center of the class and the center of the class .
On the basis of the above variables, we calculated the similarity variable, representing the similarity of categories and . The calculation formula is as follows:
Finally, we determined the maximum value of , which represents the maximum similarity between category and other categories. The Davies–Bouldin index is defined as the mean value of the maximum similarity of all classes, which can be calculated as:
The Krzanowski–Lai (KL) index can be used to determine the number of clusters :
where is the sum of squares from all sample points to the cluster center in the class , and is the dimension of the sample.
As shown in Equation (14), taking the appropriate value to maximize the KL index indicated that the clustering performance was optimal.
Figure 4 shows the corresponding silhouette coefficient, Davies–Bouldin (DB) index and Krzanowski–Lai (KL) index, when the number of clusters was 2, 3, 4, 5 and 6.
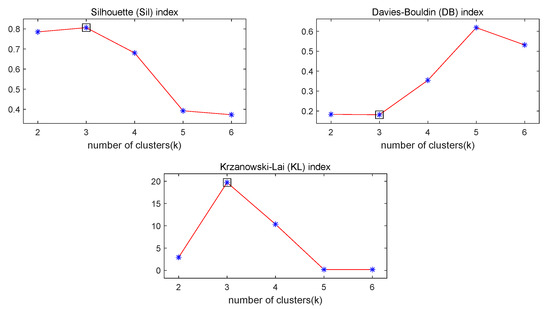
Figure 4.
Evaluation indicators for different numbers of clusters.
It can be seen from Figure 4 that when the number of clusters was three, the DB index was the lowest and the Sil index and KL index were the highest, which indicated the best clustering performance. After determining the number of clusters, we applied further clustering by use of the k-medoids algorithm. The traffic speed data from 27 detection points within a day were divided into three categories, and the images for each cluster are shown in Figure 5. The red curve in the figure is the clustering center.
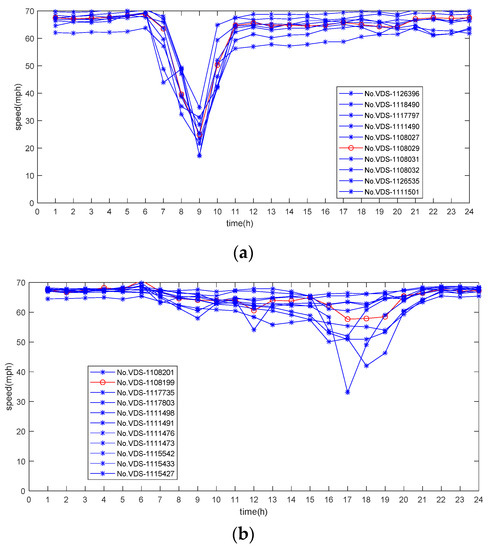
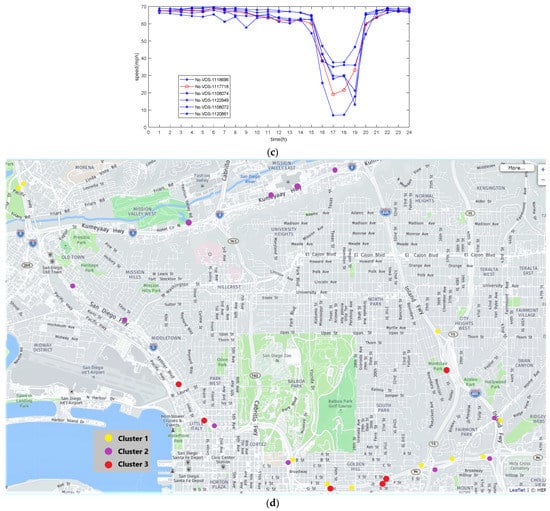
Figure 5.
Clustering results for the k-medoids algorithm and clustering centers of each cluster: (a) Cluster 1; (b) Cluster 2; (c) Cluster 3; (d) location of detectors belonging to different clusters in regional road networks.
It can be seen from the image that in the first cluster, between 8.00 a.m. and 9.00 a.m., the traffic speed on the road was significantly reduced. Combined with the flow and occupancy data at this time, according to the traffic flow operation law, it can be concluded that this was in the early peak period, and the number of vehicles on the road was significantly increased, which affected the traffic capacity of vehicles on the road, thus affecting the traffic speed. In the second cluster the variation range of all-day traffic speed was less than for the other two types. In the results for this cluster, it can be seen that the traffic capacity of the section where the sample detection point was located was able to meet the traffic flow most of the time; even if the increase of traffic volume affected the traffic speed of the vehicles, it recovered in a short time. In the third cluster, the road traffic speed decreased significantly between 5.00 p.m.–7.00 p.m. This period belongs to the late peak period, and the sharp increase in the number of vehicles on the road led to the decline of traffic capacity, and the traffic speed of vehicles was affected. In general, the traffic speeds were basically stable late at night, and some sections of the road demonstrated reduced traffic speed to a certain extent in the daytime. Overall, the changes of traffic speed conformed to the traffic operation law.
Through analysis of the changes of traffic speed at multiple detection points, we distinguished sections with and without traffic congestion at different periods. The early peak duration of the first cluster was shorter, the speed of congestion period was unstable; the late peak duration of the third cluster was longer and the traffic flow parameters were more stable in the congestion period, so we chose Cluster 3 as the further research object. The sample points of the clustering center obtained by the k-medoids algorithm were those with the highest similarity with the data of other sample points in the same cluster. Therefore, we represented all the detection points in Cluster 3 through the sample points of the clustering center (No. VDS-1117718), and further analyzed the speed, flow, and occupancy data of this detection point to obtain different traffic state results.
3.2.2. Traffic State Classification Based on Traffic Flow Parameters
Figure 6 is the result of the adaptive spectral clustering method for detection point 1,117,718 for all working days in the 20 days of speed, flow, and occupancy data using the self-tuning spectral clustering algorithm; the total number of sample points was 5760. We divided the sample points into three different traffic states, i.e., smooth, slow, and crowded. The clustering results clearly showed different traffic states. The boundaries between different traffic states were clear, with almost no noise, indicating the effectiveness of the clustering model. Clustering centers under different traffic conditions are shown in Table 2. In addition, the confusion matrix (Figure 7) and accuracy (Table 3) illustrate the effectiveness of the clustering results according to the occupancy standard of the highway transportation manual. More than 95% accuracy shows that the clustering results are in line with the actual situation of various traffic conditions, and the confusion matrix also shows the accuracy of the clustering results.
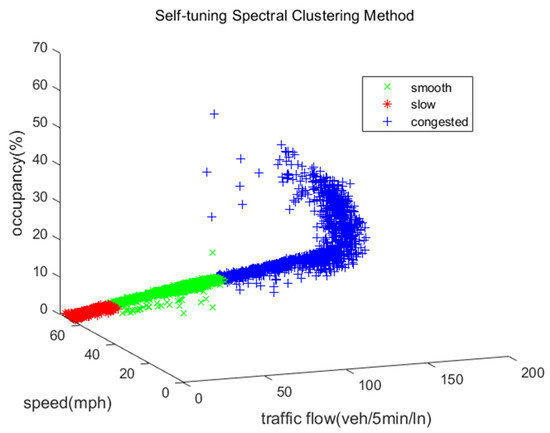
Figure 6.
Traffic state identification results based on the self-tuning spectral clustering model.

Table 2.
Cluster centers determined by self-tuning spectral clustering.
Figure 7.
Confusion matrix for accuracy comparison of each method: (a) Self-tuning spectral clustering method (NO.VDS-1117718); (b) self-tuning spectral clustering method (NO. VDS-1115542); (c) K-means method (NO. VDS-1117718); (d) spectral clustering method (NO. VDS-1117718); (e) traditional FCM method (NO. VDS-1117718).

Table 3.
User accuracy and producer accuracy in different traffic states.
3.3. Method Comparison
In order to prove the superiority of the proposed method, we evaluated the classification accuracy of different methods by two comparison schemes, and the results are shown here. First, we compared the clustering results of random detector data and detector data filtered by k-medoids clustering, to illustrate the effectiveness of k-medoids clustering in improving the clustering accuracy. Then in the second comparison scheme, we compared the clustering accuracy of the self-tuning spectral clustering algorithm and other clustering algorithms, including the k-means algorithm, FCM algorithm, and traditional spectral clustering algorithm. The purpose of the comparison is to prove the superiority of self-tuning spectral clustering algorithm for traffic flow parameter clustering. Two different comparison schemes reflect the performance of the combination method proposed in this study.
3.3.1. Comparison of the Classification Accuracy
According to the occupancy standard determined above, we calculated the classification accuracy of the clustering results through the labels obtained by clustering. Classification accuracy included three indexes: overall classification accuracy, user accuracy, and production accuracy. According to these indicators, this part of the study first compared the self-tuning spectral clustering results from random detectors, against the results of detector data obtained by k-medoids clustering. Then, the clustering results of the selected detector data after k-medoids clustering were compared by different clustering algorithms, including k-means algorithm, FCM algorithm, and traditional spectral clustering algorithm. To better show the classification accuracy, we show the confusion matrix. In the confusion matrix, x coordinates represent the real category, and y coordinates represent the predicted category. The samples with correct clustering results are distributed along the diagonal. Figure 7 shows the confusion matrix generated from different detector data and different methods. The confusion matrix contains the overall classification accuracy, user accuracy, and production accuracy values of the three different traffic states. In the confusion matrix, congestion, slowness, and unimpededness are represented by digits 1, 2, and 3, respectively.
Production accuracy refers to the proportion of samples correctly classified as category i in all measured samples (a column of the confusion matrix), calculated as the proportion of diagonal elements represented as a class in the confusion matrix to the number of all elements in this column.
User accuracy refers to the proportion of samples classified as type i in all samples (a row of the confusion matrix). In fact, the measurement type is also the proportion of samples classified as type i, calculated by the proportion of diagonal elements represented as a class in the confusion matrix to all elements in this row.
Overall classification accuracy is the ratio of the correct classification sample to the total number of samples, which is expressed as the ratio of the sum of diagonal elements to all elements in the confusion matrix.
3.3.2. Normalized Mutual Information (NMI)
Standardized mutual information (NMI) as an evaluation index of clustering results can objectively evaluate the accuracy between clustering results and classification criteria. The range of NMI is zero to one, and the closer the value is to one, the higher the accuracy. This study selected this index as a basis for judging the clustering effect. The NMI results are shown in Figure 8; it can be seen from the image that the NMI of the spectral clustering algorithm was closer to one, indicating that compared with the traditional spectral clustering algorithm, k-means algorithm, and FCM algorithm, the clustering results of the self-tuning spectral clustering algorithm were closer to the reference standard.
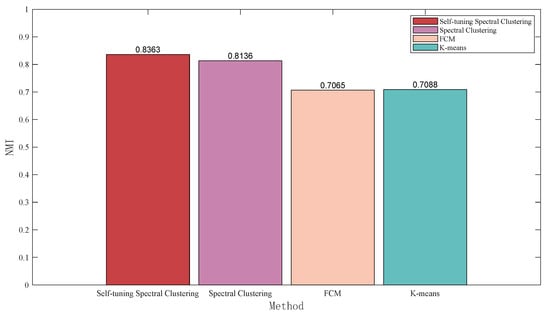
Figure 8.
NMI comparison between reference standards and different methods.
4. Discussion
In this section, the results of the proposed method and the results of the comparative methods are discussed, to prove the effectiveness of the proposed method.
First, in order to verify the effectiveness of the k-medoids clustering algorithm for traffic state identification, we selected for comparison the data of a detector (No. VDS-1115542) from the second cluster that had shown no obvious congestion. From the classification accuracy of the clustering results for the detectors screened by k-medoids clustering and those for the random detectors in the confusion matrix (Figure 7), it can be seen that the accuracy of the clustering results of the detector data selected by k-medoids clustering was significantly better than that of the random detector data. The reason for this result is that the k-medoids clustering method divided the night-time sections for the detector into one category, and this category of cluster-center sections included the traffic conditions when the traffic pressure increased at night, and also the conditions when the road traffic was normal during the daytime. However, the whole-day traffic conditions of different sections in each region were different, and the method of random selection of section detector data was not rigorous enough. For example, during some sections of the whole day road vehicles ran smoothly, and there was no significant difference between different traffic conditions obtained by clustering. The influence of traffic pressure on traffic flow parameters of some sections during peak hours was not obvious, and was not representative of the traffic capacity of most sections in the region. Table 4 shows the comparison of the data clustering centers divided into congestion categories in the clustering results of detectors VDS-1117718 and VDS-1115542. It can be seen that the traffic data for the road where detector VDS-1115542 was located were divided into congestion categories, and the speed showed no obvious change compared with other states. The speed at detector VDS-1117718 was significantly reduced, and the occupancy rate was also significantly higher than that of the other detector. This showed that the congestion of the road section where the detector VDS-1115542 was located was not obvious, which affected the effect of the clustering algorithm. To sum up, it was effective to select the appropriate detector data by k-medoids algorithm.

Table 4.
Congestion state cluster-center data for different detectors (self-tuning spectral clustering method).
On the basis of selecting the appropriate road detector data through the k-medoids clustering algorithm, we can see that the self-tuning spectral clustering algorithm, FCM algorithm, k-means algorithm, and traditional spectral clustering algorithm obtained excellent results in analyzing traffic flow parameters for traffic state clustering. It can be seen from the histogram (Figure 9) that the overall classification accuracy of the self-tuning spectral clustering algorithm was the highest, reaching 95.7%. Compared with the traditional spectral clustering algorithm (91.7%), k-means algorithm (89.1%), and FCM algorithm (89.1%), they increased by 3.7%, 6.3% and 6.3%, respectively. On the other hand, the user accuracy and production accuracy of the adaptive spectral clustering algorithm were higher than those of other methods. The average user accuracy of self-tuning spectral clustering algorithm from class one to class three was 95.83%, which was 3.6%, 5.82%, and 6% higher than the traditional spectral clustering algorithm, k-means algorithm, and FCM algorithm, respectively. Compared with the traditional spectral clustering algorithm (92.37%), k-means algorithm (90.16%), and FCM algorithm (90.23%), the average production accuracy of the adaptive spectral clustering algorithm from class one to class three (95.37%) increased by 3%, 5.21%, and 5.14%, respectively. Therefore, the self-tuning spectral clustering method was more suitable for analyzing traffic flow data than the traditional general clustering algorithm, k-means method, or FCM method. In addition, it can be seen from the confusion matrix and classification accuracy that the producer accuracies of the third category for the FCM method and k-means method were 16.1% and 14.4% lower, respectively, than that of self-tuning spectral clustering. Combined with the clustering results of the FCM and k-means methods, Figure 7 of the confusion matrix image shows that in the case of high occupancy rate, where the speed was significantly lower than the free flow speed and the traffic flow was within a certain scale part of the data were divided into “smooth” and “slow” states. Combined with the actual situation, analysis indicates that this part of the data meets the standard of congestion. Therefore, we can conclude that the FCM method and k-means method produced obvious errors in distinguishing congestion states. In summary, the hybrid algorithm of k-medoids clustering and self-tuning spectral clustering proposed in this study was superior to other comparison methods, from its overall classification accuracy to its accuracy in various categories.
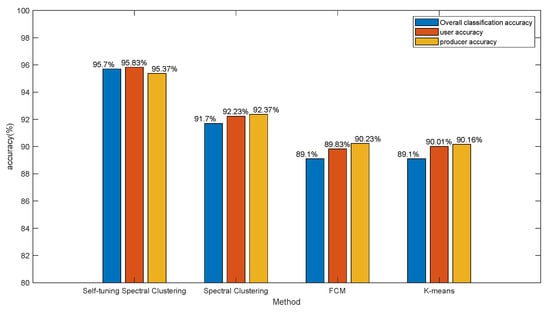
Figure 9.
Comparison of the overall classification accuracy, average user accuracy, and average producer accuracy of different methods.
To further prove the effectiveness of the proposed method in traffic state clustering, we introduced NMI as a performance comparison index. It can be seen from Figure 9 that the NMI (0.8363) between the self-tuning spectral clustering algorithm and the reference standard was greater than that of other comparison methods (k-means, FCM, and traditional spectral clustering methods’ NMI wer 0.7088, 0.7065 and 0.8136, respectively). The NMI index results also show that the proposed method can obtain better results than other comparison methods.
5. Conclusions
In urban transportation systems, congestion often occurs in the evening peak period, which seriously reduces the travel efficiency of urban residents and also causes economic losses. Accurate and rapid traffic state discrimination can release traffic information in more accurate detail and implement corresponding measures to prevent traffic congestion, which has a positive impact on the smooth operation of the transportation system. However, the traffic-carrying capacity of roads differs between regions, and the unified standard that has been formulated is often not applicable to all roads. In this study, a combination method including two unsupervised clustering learning algorithms was proposed to cluster traffic flow data, and a comprehensive classification index system for traffic state has been established based on speed, occupancy, and traffic flow. We used the k-medoids clustering algorithm to classify different roads in the region by analyzing the all-day speed data of the road detectors. The clustering algorithm separated into one category the sections with high traffic pressure in the evening rush hour, and then the speed, flow, and occupancy data of this category of cluster-center section for the previous 20 working days were extracted for further analysis. In the analysis of traffic flow data for classification of traffic state, we used the adaptive spectral clustering algorithm. Compared with the traditional spectral clustering algorithm, the self-tuning spectral clustering algorithm does not require manual selection of sigma parameters. In order to prove the clustering performance of the proposed method, this study referred to the standard of traffic flow parameters in the highway capacity manual (HCM) at different service levels, and divided different traffic states according to occupancy data as a reference for the accuracy of clustering results. We compared the results of traffic state classification from randomly selected detection points with results from the detection points selected by the k-medoids clustering algorithm through adaptive spectral clustering. Through comparison of NMI and classification accuracy, we proved the effectiveness of the k-medoids algorithm for selecting detection points. Next, we compared the gap between NMI and classification accuracy for the self-tuning spectral clustering algorithm, traditional spectral clustering algorithm, k-means algorithm, and FCM algorithm, and further proved the superiority of the proposed method in this study. Finally, this method was verified by taking highways data from a certain area in the PeMS database as an example. The results show that the proposed method can accurately classify the data into different traffic states after clustering analysis of the flow data. Therefore, the method proposed in this study is effective in highway traffic state classification.
The research results of this paper demonstrate that the method can effectively screen out sections with high traffic pressure in the evening rush hour, so that traffic managers can understand the road traffic situation more clearly and intuitively, as allowing them to quickly publish traffic information and implement corresponding traffic measures to alleviate traffic pressure. At the same time, different roads in different regions have different traffic-carrying capacities due to varying environmental and human factors. Through analysis of local real traffic flow data, this method can determine more accurate traffic state identification criteria according to the actual situation of roads in different regions. However, this study still has room for improvement in some aspects. For example, traffic accidents can also lead to changes in traffic flow parameters that affect traffic conditions, and at certain times lower traffic speeds and higher occupancy on roads are caused by traffic accidents rather than traffic congestion. In future research, the authors should combine traffic flow data and traffic accident data for a more comprehensive study. In addition, the traffic state classification level set in this study only included occupancy data. In future research, we will combine more data including traffic flow and speed, to develop more detailed traffic state classification standards. Similarly, this study divided traffic state into three categories, but the proposed method can also achieve more detailed classification based on more comprehensive traffic data. In summary, we will solve these problems in future research.
Author Contributions
Methodology, Q.S. and Y.Y.; software, Q.S. and Y.Y.; validation, Y.Y. and T.X.; writing—original draft preparation, Q.S. and Y.Y.; writing—review and editing, Q.S.; project administration, Q.S.; funding acquisition, Q.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MOE (Ministry of Education in China) Project of Humanities and Social Sciences (Grant No. 21YJC630110), and the Shandong Provincial Natural Science Foundation project (Grant No. ZR2021MF109).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, M.; Debbage, N. Urban morphology and traffic congestion: Longitudinal evidence from US cities. J. Comput. Environ. Urban Syst. 2021, 89, 101676. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Y.; Wang, W. ITS-frame: A framework for multi-aspect analysis in the field of intelligent transportation systems. J. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2893–2902. [Google Scholar] [CrossRef]
- Kaffash, S.; Nguyen, A.T.; Zhu, J. Big data algorithms and applications in intelligent transportation system: A review and bibliometric analysis. J. Int. J. Prod. Econ. 2021, 231, 107868. [Google Scholar] [CrossRef]
- Nama, M.; Nath, A.; Bechra, N. Machine learning-based traffic scheduling techniques for intelligent transportation system: Opportunities and challenges. J. Int. J. Commun. Syst. 2021, 34, e4814. [Google Scholar] [CrossRef]
- Wang, W.X.; Guo, R.J.; Yu, J. Research on road traffic congestion index based on comprehensive parameters: Taking Dalian city as an example. J. Adv. Mech. Eng. 2018, 10, 1687814018781482. [Google Scholar] [CrossRef]
- Ma, M.; Liang, S.; Guo, H. Short-term traffic flow prediction using a self-adaptive two-dimensional forecasting method. J. Adv. Mech. Eng. 2017, 9, 1687814017719002. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Krishnakumari, P.; Calvert, S.C. Feature extraction and clustering analysis of highway congestion. J. Transp. Res. Part C Emerg. Technol. 2019, 100, 238–258. [Google Scholar] [CrossRef]
- Tišljarić, L.; Carić, T.; Abramović, B. Traffic state estimation and classification on citywide scale using speed transition matrices. J. Sustain. 2020, 12, 7278. [Google Scholar] [CrossRef]
- Pei, Y.; Cai, X.; Li, J. Method for Identifying the Traffic Congestion Situation of the Main Road in Cold-Climate Cities Based on the Clustering Analysis Algorithm. J. Sustain. 2021, 13, 9741. [Google Scholar] [CrossRef]
- Herman, R.; Prigogine, I. A two-fluid approach to town traffic. Science 1979, 204, 148–151. [Google Scholar] [CrossRef]
- Kerner, B.S. Three-phase traffic theory and highway capacity. J. Phys. A Stat. Mech. Its Appl. 2004, 333, 379–440. [Google Scholar] [CrossRef]
- Esfahani, R.K.; Shahbazi, F.; Akbarzadeh, M. Three-phase classification of an uninterrupted traffic flow: A k-means clustering study. J. Transp. B Transp. Dyn. 2019, 7, 546–558. [Google Scholar] [CrossRef]
- Wang, Z.; Chu, R.; Zhang, M. An Improved Selective Ensemble Learning Method for Highway Traffic Flow State Identification. J. IEEE Access 2020, 8, 212623–212634. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, W.; Lu, J. Classifying the traffic state of urban expressways: A machine-learning approach. J. Transp. Res. Part A Policy Pract. 2020, 137, 411–428. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. J. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Fotouhi, A. Traffic condition recognition using the k-means clustering method. J. Sci. Iran. 2011, 18, 930–937. [Google Scholar] [CrossRef]
- Rao, W.; Xia, J.; Lyu, W. Interval data-based k-means clustering method for traffic state identification at urban intersections. J. IET Intell. Transp. Syst. 2019, 13, 1106–1115. [Google Scholar] [CrossRef]
- Zhao, S.; Xiao, Y.; Ning, Y.; Zhou, Y.; Zhang, D. An optimized K-means clustering for improving accuracy in traffic classification. Wirel. Pers. Commun. 2021, 120, 81–93. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Li, Y.; Kang, X.; Gao, L. Method of Evaluating and Predicting Traffic State of Highway Network Based on Deep Learning. J. Adv. Transp. 2021, 2021, 8878494. [Google Scholar] [CrossRef]
- Yang, S.; Wu, J.; Qi, G.; Tian, K. Analysis of traffic state variation patterns for urban road network based on spectral clustering. Adv. Mech. Eng. 2017, 9, 1687814017723790. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, Y.; Zhu, Q. Mining related information of traffic flows on lanes by k-medoids. In Proceedings of the 2014 11th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Xiamen, China, 19–21 August 2014; pp. 390–396. [Google Scholar]
- Zhang, L.; Jia, Y.; Sun, D.; Yang, Y. A fuzzy weighted c-means classification method for traffic flow state division. Mod. Phys. Lett. B 2021, 35, 2150341. [Google Scholar] [CrossRef]
- Su, M.T.; Zheng, J.; Zhang, Z.P. Clustering Mining of Urban Traffic Flow Based on CVAE. J. Traffic Logist. Eng. 2020, 8, 34–44. [Google Scholar] [CrossRef]
- Mondal, M.A.; Rehena, Z. Identifying traffic congestion pattern using k-means clustering technique. In Proceedings of the 2019 4th International Conference on Internet of Things: Smart Innovation and Usages (IoT-SIU), Ghaziabad, India, 18–19 April 2019; pp. 1–5. [Google Scholar]
- Zelnik-Manor, L.; Perona, P. Self-tuning spectral clustering. Adv. Neural Inf. Process. Syst. 2004, 17. Available online: https://proceedings.neurips.cc/paper/2004/file/40173ea48d9567f1f393b20c855bb40b-Paper.pdf (accessed on 30 July 2022).
- Shang, Q.; Lin, C.Y.; Yang, Z.S.; Bing, Q.C.; Tian, X.J.; Wang, S.X. Traffic state identification for urban expressway based on spectral clustering and RS-KNN. J. South China Univ. Technol. 2017, 45, 52–58. [Google Scholar]
- Manual, H.C. HCM2010; Transportation Research Board; National Research Council: Washington, DC, USA, 2010; p. 1207.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).