Rock Mass Classification Method Based on Entropy Weight–TOPSIS–Grey Correlation Analysis

Abstract

The accurate and reliable classification of rock mass is the basis of a reasonable engineering design. In the Xishan mining region of Sanshandao Gold Mine, three conventional rock mass classification methods of Tunneling Quality Index (Q), Rock Mass Rating (RMR) and China National Standard-basic quality (BQ), were compared in the burial depth area above 780 m, and it was discovered that the classification results of different rock mass classification methods had a low coincidence rate in the deep area; Therefore, this paper adopted entropy weight method, TOPSIS method and grey correlation analysis method to calculate the entropy weight and relative closeness of different methods in different middle sections. The study’s findings revealed that in the deep area, the relative closeness between each classification mass was: RMR > Q > BQ; Based on the above results, the IRMR method with modified RMR was selected for comprehensive analysis, and the concept of importance degree of evaluation index was defined; it was found that the importance degree of evaluation index of in-situ stress loss was the highest, while the importance degree of joint direction was the lowest; The “ETG” rock mass classification method based on “site-specific” is established, which provides a reference for the establishment of deep rock mass classification method.

1. Introduction

The engineering rock mass grade is a comprehensive reflection of the multi-faceted characteristics of complex rock masses, which can assist engineers in grasping engineering characteristics of rock masses, providing a reliable basis for engineering stability analysis, reasonable use of rock masses, and reasonable engineering support, as well as providing effective guidance for engineering design and construction [1,2]. Yet, in the practical application process, there is no unified standard for rock mass classification. When different methods are used to classify the same area, normally different rock mass grades will be obtained, at the same time, the importance of different indicators may differ under different geological conditions, which sometimes makes it difficult for engineers and technicians to choose a reasonable rock mass grade. Therefore, at least the employment of at least two rock classification methods is recommended in engineering practice.

Rock mass classifications have been developed in the literature. Since the first attempt to classify rocks by Russian Vernier at the end of the 18th century [2], Scholars from all over the world continue to improve and expand the rock classification methods [3]. According to the modified type of rock mass classification, it can be roughly divided into the traditional classification method (later called “traditional method”), the modified method of the traditional classification method (later called “modified method”) and the new classification method using the modern science and technology (later called “new method”). Traditional methods include Rock Mass Rating (RMR) by South African Bieniawski [4,5], Q index (Q) by Norwegian Barton [6], Geological Strength Index classification (GSI) by Zimbabwean Hoke [7] and BQ classification in Chinese engineering rock classification standards [8]. Modification methods include the Romana SMR method for slope after modification based on RMR method [9,10]. Based on the RMR-SMR evaluation system, the rock mass classification system CSMR was established by the China Water Resources and Hydropower Slope Engineering Special Panel in 1997 [11]. Chen et al. [12] established the rock mass engineering quality evaluation method QHLW for high-level radioactive waste disposal engineering based on Q system. Guo et al. [13] proposed the anisotropic rock mass classification system A-BQ, based on the Chinese rock mass classification standard BQ; With the development of computer science, increasing amounts of cutting-edge science and technology are applied to rock mass classification, so some new methods are proposed: Zhou et al. [14] proposed a fuzzy RES-multidimensional cloud rock mass classification model based on the one-dimensional cloud from the system perspective. Santos et al. [15] had presented a new methodology for achieving rock mass classifications based on mathematical and statistical fundamentals, aiming at optimizing the selection of variables and consequent reduction of subjectivity in the parameters and classification methods. Salimi et al. [16] had presented the better represented influence of rock mass properties on TBM performance using multivariate regression analysis and artificial intelligence algorithms, including regression tree and genetic programming. Dai et al. [17] applied the unconfirmed mean method to the rock detonation classification and found that the predicted results matched the measured results with an accuracy of up to 100%.

This paper compares the results of three rock mass classification methods, the anastomosis rate in the deep buried area, and finds out the most suitable rock mass classification method (RMR) in this area by means of entropy weight method, TOPSIS method and grey correlation analysis method. At the same time, the importance of each evaluation index is obtained through analysis. The entropy weight-TOPSIS-grey correlation analysis rock mass classification model is established, which provides a reference for deep rock mass classification.

2. Materials and Methods

2.1. Rock Mass Classification Evaluation Index System

2.1.1. Selection of Evaluation Indicators

Rock mass classification is influenced by various factors such as structural surface characteristics, rock integrity, geological factors, rock strength index and engineering factors. Among the many classification methods of rock mass, Q (1974 version) [6], RMR (1989 version, the versions not specifically marked below are those of this version) [5] and BQ (2015 version) [8] are widely used because of their comprehensive consideration, wide range of application and strong representability. The factors considered by each method are shown in Table 1.

Table 1. Influence factors of three rock mass classification methods.

Classification Method	Influencing Factors
Q	Rock quality designation (RQD)	Joint set number (Jn)	Joint roughness number (Jr)	Joint alteration number (Ja)	Joint water reduction factor (Jw)	Stress Reduction factor (SRF)
RMR	Rock compressive strength (R1)	Rock quality designation (R2)	Spacing of discontinuities (R3)	Condition of discontinuities (R4)	Ground water conditions (R5)	Orientation of discontinuities (R6)
[BQ] *	Rock compressive strength ($\mathsf{\sigma }$cw)	Rock mass integrity (KV)	Correction coefficient of the groundwater (K1)	Correction coefficient of the main structural plane (K2)	Correction coefficient of the initial stress state (K3)

* [BQ] is the result after the modification of BQ classification method, K₁ K₂ K₃ are the correction coefficient, both of which come with BQ method.

2.1.2. Evaluation System Construction

This paper takes Sanshandao Gold Mine as an example, according to the literature [18], the main rocks of the mine are porphyritic biotite granite, ferric sericite granite and ferric sericite. The surrounding rock of the upper and lower wall of the ore body is sericite, and the indirect surrounding rock is black cloud amphibolite or black cloud plagiotic gneiss, black cloud metamorphic rock, etc. The research employs a total of 7 middle sections from $-$780 to $-$915 of Xishan Mining area, Sanshandao Gold Mine, according to the data provided by the mine authorities, the evaluation index scores of the three rock mass classification methods are shown in Table 2, Table 3 and Table 4.

Table 2. Q classification evaluation index scores.

Middle Section	Evaluation Indicators
	RQD	Jn	Jr	Ja	Jw	SRF
$-$780-1 *	87.4	7	2	4	0.65	1
$-$795-1	91.7	7	1.5	4	0.6	1.5
$-$825-1	75.9	9	2	4	0.6	2
$-$870-1	22.5	7	2	4	0.65	2
$-$885-1	82.1	8	2	4	0.58	2
$-$900-1	82.6	10	2	4	0.55	2
$-$915-1	64.6	9	2	4	0.58	2

* $-$ 780-1 means the number of the first measurement point in the middle section of $-$ 780, the same method was used to number the regions later.

Table 3. RMR classification evaluation index scores.

Middle Section	Evaluation Indicators
	R1 *	R2 *	R3 *	R4	R5	R6
$-$780-1	9.8	16.4	11.9	17	0	−5
$-$795-1	9.7	17.6	12.2	20	7	−5
$-$825-1	10.0	13.4	12.8	22	7	−5
$-$870-1	9.4	3.4	12.2	18	12	−5
$-$885-1	10.1	15.0	12.5	20	4	0
$-$900-1	10.4	15.1	12.7	19	7	−10
$-$915-1	9.3	10.7	11.5	16	0	−5

* R₁, R₂ and R₃ are obtained according to the equation provided by the paper [18], which about Sanshandao mine, thereinto, $R_1=-0.0003{\mathsf{\sigma }}_{cw}^2+0.135{\sigma }_{cw}+0.9023$, $R_2=0.0012RQ{D}^2+0.0692\mathrm{RQD}+1.23$, $R_3=3.5411\ln D_V+0.9023$, $D_V$ is the distance between joints, and its unit is m.

Table 4. BQ * classification evaluation index scores.

Middle Section	Evaluation Indicators
	$\mathit{\sigma }$cw	KV	K1	K2	K3
$-$780-1	80.23	0.461	0.3	0.3	1.0
$-$795-1	79.38	0.555	0.3	0.2	1.0
$-$825-1	82.74	0.741	0.3	0.2	1.0
$-$870-1	76.04	0.693	0.3	0.05	1.0
$-$885-1	88.90	0.401	0.1	0.25	1.0
$-$900-1	87.30	0.412	0.5	0.2	1.0
$-$915-1	75.76	0.453	0.3	0.3	1.0

* A brief description of the BQ classification is provided in Appendix A.

2.1.3. Comparison of Classification Results

Different classification methods are inconsistent in the selection of indicators, the emphasis degree of each indicator and the value method of indicators, which leads to certain differences in the classification results of rock mass in the same area by different classification methods. Therefore, it is very important to study the relationship between different methods. The first correlation was proposed by Bieniawski [19], between the RMR index and the Q index, with the equation: RMR = 9lnQ + 44, using values from tunnels from all over the world and with a determination coefficient of R2 = 0.59. Rutledge and Preston [20] conducted a similar study and obtained an R2 of 0.66. Sunwoo et al. [21] used the linear regression analyses were undertaken in order to assess a possible correlation between Q classification and RMR classification system with rock types, with an R2 of 0.79. R., K. [22] proposed a new method to express the relationship between Q and RMR, which is proved to be highly reliable. Palmstrm et al. [23] by used the common input tables, and significantly more reliable correlations between the RMR, Q and RMi can be found than the existing transition equations in use. With the aim of improving the quality between the correlations, some authors developed correlations in the same lithology. Castro-Fresno et al. [24] analyzed of the correlation between RMR and Q Index in Low-Quality Soils, with an R2 of 0.49. Fernández-Gutiérrez et al. [25] studied the correlation between Bieniawski’s RMR index and Barton’s Q index in fine-grained sedimentary rock formations, an R2 value of 0.915, which obtained a high correlation. Campos et al. [26] found new correlations between GSI and RMR, resulting in satisfactory results and showed the potential of aiding in the decision-making process in projects involving soft (poor) rock masses, composed by low-strength lithotypes and similar weathering grades.

The correlation equation between RMR classification and Q classification was established by summarizing the references [27] in Table 5. According to Table 5, the relationship between RMR value and Q value can be calculated, and the results are divided into 5 grades. The calculation results are shown in Table 6.

Table 5. The correlation equation of RMR classification and Q classification [27].

Number *	Author(s) and Time	Equation
1	Bieniawski (1976)	RMR = 9lnQ + 44	(1)
2	Rutledge and Preston (1978)	RMR = 5.9lnQ + 43	(2)
3	Moreno (1980)	RMR = 5.4lnQ + 55.2	(3)
4	Cameron-Clarke and Budavari (1981)	RMR = 5lnQ + 60.8	(4)
5	Abad et al. (1983)	RMR = 10.5lnQ + 41.8	(5)
6	Kaiser and Gale (1985)	RMR = 8.7lnQ + 38	(6)
7	Al-Harthi (1993)	RMR = 9lnQ + 49	(7)
8	Choquet and Hadjigogiu (1993,2016)	RMR = 10lnQ + 39	(8)
9	El-Naqa (1994)	RMR = 7lnQ + 44	(9)
10	Barton (1995)	RMR = 15lnQ + 50	(10)
11	Tugrul (1998)	RMR = 7lnQ + 36	(11)
12	Sari and Pasamehmetoglu (2004)	RMR = 3.7lnQ + 53.1	(12)
13	Kumar et al. (2004)	RMR = 6.4lnQ + 49.6	(13)
14	Cosar (2004)	RMR = 2.8lnQ + 45.19	(14)
15	Hashemi et al. (2010)	RMR = 5.37lnQ + 40.48	(15)
16-1	Laderian and Abaspoor (2012)	RMR = 8.15lnQ + 44.88	(16)
16-2	Laderian and Abaspoor (2012)	RMR = 42.87Q0.162	(17)
17	Ranasooriya and Nikraz (2012)	RMR = 6.3lnQ + 43	(18)
18	Rafiee (2013)	RMR = 8.09lnQ + 43.08	(19)
19	Castro Caicedo and Pérez Pérez (2013)	RMR = 5.7lnQ + 43.65	(20)
20	Ali et al. (2014)	RMR = 2.87lnQ + 48.71	(21)
21	Senra (2016)	RMR = 6.55lnQ + 59.53	(22)
22	Sayeed and Khanna (2015)	RMR = 4.52lnQ + 43.635	(23)

* Numbers 1–6 are RMR classification for 1976 edition.

Table 6. The corresponding results of RMR classification and Q classification.

Number	I	II	III	IV	V
RMR	81~100	60~81	41~60	20~41	<20
Q1	>61.01	5.92~61.01	1.40~5.92	0.07~1.40	<0.07
Q2	>626.83	17.84~626.83	0.71~17.84	0.02~0.71	<0.02
Q3	>118.84	2.43~118.84	0.07~2.43	0.0001~0.07	<0.0001
Q4	>56.83	0.85~56.83	0.02~0.85	0.0003~0.02	<0.0003
Q5	>41.82	5.66~41.82	0.93~5.66	0.13~0.93	<0.13
Q6	>140.12	12.54~140.12	1.41~12.54	0.13~1.41	<0.13
Q7	>35.01	3.39~35.01	0.41~3.39	0.04~0.41	<0.04
Q8	>66.69	8.17~66.69	1.22~8.17	0.15~1.22	<0.15
Q9	>197.50	9.83~197.50	0.65~9.83	0.03~0.65	<0.03
Q10	>7.90	1.95~7.90	0.55~1.95	0.14~0.55	<0.14
Q11	>619.29	30.83~619.29	2.04~30.83	0.10~2.04	<0.10
Q12	>1882.85	6.46~1882.85	0.04~6.46	0.0001~0.04	<0.0001
Q13	>135.13	5.08~135.13	0.26~5.08	0.01~0.26	<0.01
Q14	>358,357.26	198.20~358,357.26	0.22~198.20	0.0001~0.22	<0.0001
Q15	>1892.44	37.90~1892.44	1.10~37.90	0.02~1.10	<0.02
Q16-1	>84.09	6.39~84.09	0.62~6.39	0.05~0.62	<0.05
Q16-2	>50.79	7.97~50.79	0.76~7.97	0.01~0.76	<0.01
Q17	>416.44	14.86~416.44	0.73~14.86	0.03~0.73	<0.03
Q18	>108.56	8.10~108.56	0.77~8.10	0.06~0.77	<0.06
Q19	>701.09	17.61~701.09	0.63~17.61	0.02~0.63	<0.02
Q20	>76,946.92	51.10~76,946.92	0.07~51.10	0.00005~0.07	<0.00005
Q21	>26.52	1.07~26.52	0.06~1.07	0.002~0.06	<0.002
Q22	>3891.67	37.36~3891.67	0.56~37.36	0.01~0.56	<0.01

Results Two decimal places are reserved. If two decimal places cannot display a valid result, one significant digit is reserved.

The data in Table 6 are analyzed and the boxplot [28] is drawn, and the results are shown in Figure 1; it can be seen from the figure that the corresponding median Q value is 135.13 when RMR = 81, 8.1 when RMR = 60, and 0.63 when RMR = 41. When RMR = 20, the median value of Q was 0.02. Except for RMR = 81, the median is close to the average in other data, and the gap between them is slightly larger when RMR = 60; however, when RMR = 81, the Q value obtained by some methods is more than 350,000, and there are many abnormal points in the data, due to some correlations can provide anomalous values because they are intended for specific lithotypes, and therefore, outside from their range of application they are useless. Therefore, the median was selected for analysis of this content.

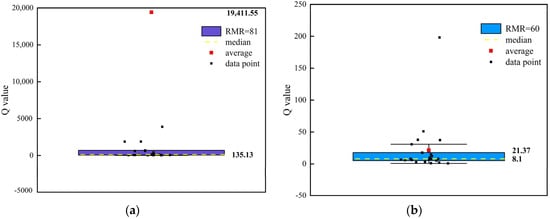
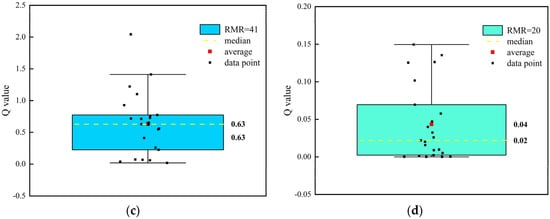
Figure 1. RMR classification and Q classification corresponding to the results of the boxplot. Where: (a) is the boxplot when RMR = 81, at the same time, a partial magnification of the Y-axis is performed for ease of observation; (b) is the boxplot when RMR = 60; (c) is the boxplot when RMR = 41; (d) is the boxplot when RMR = 20.

The median value of Q in Figure 1 is taken as the correlation value between Q classification and RMR classification, and the rock mass is divided into 5 grades to make the three classification methods correspond to each other. The results are shown in Table 7. The classification results of rock mass in each section obtained by this method are shown in Table 8.

Table 7. The correspondence between the rock types of the three methods.

	I	II	III	IV	V
Q	>135.13	8.1~135.13	0.63~8.1	0.02~0.63	<0.02
RMR	81~100	60~81	41~60	20~41	<20
[BQ]	>550	451~550	351~450	251~350	<250

Table 8. Results of the three methods of rock mass classification.

Middle Section	Classification Results
	Q Value	Grade	RMR Value	Grade	[BQ] Value	Grade
$-$780-1	2.86	III	50.1	III	419.72	III
$-$795-1	28.21	II	61.5	II	466.89	II
$-$825-1	5.55	III	60.2	II	523.47	II
$-$870-1	0.41	IV	50.0	III	491.37	II
$-$885-1	7.94	III	61.6	II	388.52	III
$-$900-1	10.00	II	54.2	III	394.24	III
$-$915-1	0.02	V	42.5	III	415.56	III

The sum of the areas where the classification results of different methods are the same and the ratio of all the tested areas is the coincidence rate, expressed as a percentage, and the mutual anastomosis rate between the three methods were analyzed, and the results are shown in Figure 2 in the deeper areas, the traditional rock mass classification methods are difficult to produce consistent results due to different factors considered by each method.

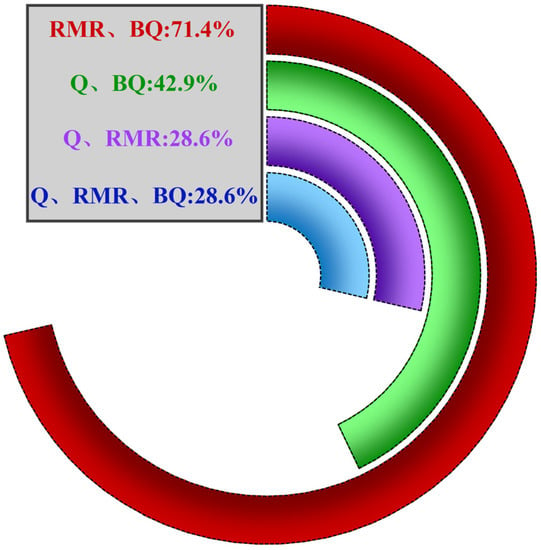
Figure 2. Coincidence rate of the results of the three classification methods.

The classification results of each method are shown in Figure 3, in which the proportion of Grade III surrounding rocks exceeds 40% in all types of methods, classification IV and V surrounding rocks only appear in Q classification, and Grade II surrounding rocks account for more than 40% in RMR and BQ classification. From the overall classification results, RMR and BQ classification results are generally more adventurous, while the influence of RQD values in Q classification is too great, leading to large variability in classification results.

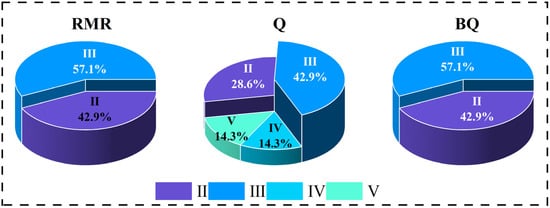
Figure 3. Classification results of the three classification methods.

2.2. Comprehensive Assessment of Rock Mass Classification

More and more scholars apply scientific theories and methods to various aspects of mine [29,30,31], which plays an important role in promoting the development of mining engineering field. Choosing appropriate scientific theories and methods to be applied to rock mass classification can help people better describe the rock mass grade. The entropy weight [32] is an objective assignment method that calculates the degree of variation in indicator data and uses the quantity of information offered by each indicator’s entropy value to establish indicator weights. Gray correlation method is derived from gray system theory in system science theory [33], which can avoid the situation where the quantitative results do not match the qualitative analysis. TOPSIS method [34] is a common decision technique for multi-objective decision analysis of limited solutions in systems engineering, and is now also often used in the comprehensive evaluation of multiple indicators. In this paper, the three approaches are combined to provide a full evaluation of rock mass classification, and a new method of rock mass classification is attempted to be built on this premise. Figure 4 depicts the exact procedure.

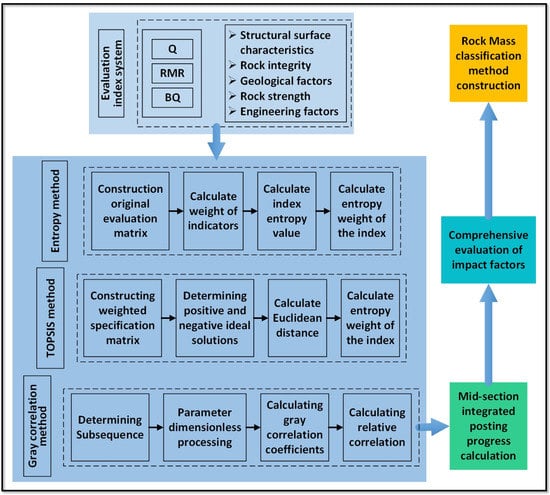
Figure 4. Rock mass assessment process based on entropy weight-TOPSIS-grey correlation analysis.

2.2.1. Entropy Weight Method

Firstly, entropy weight method is used to determine the weight of the rock mass classification evaluation index. Entropy is used to measure uncertainty in information theory. The smaller the entropy value of something is, the smaller the uncertainty is, and the more information it contains. On the contrary, the larger the entropy value, the less information it contains, and thus the entropy value can be used to determine the size of the influence of the indicator on the evaluation system, i.e., the corresponding weight of the indicator [35]. With n evaluation objects $X=\left\{X_1,X_2,\cdots ,X_{\mathrm{n}}\right\}$ and m evaluation indicators $Y=\left\{Y_1,Y_2,\cdots ,Y_{\mathrm{m}}\right\}$, the original evaluation matrix $Z={\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{\mathrm{n}\times \mathrm{m}}=\left(\mathrm{i}=1,2,\cdots ,\mathrm{n};\mathrm{j}=1,2,\cdots ,\mathrm{m}\right)$, and ${\mathrm{z}}_{\mathrm{ij}}^{‘}$ is the j-th original evaluation indicator of the i-th evaluation object. The specific steps of the entropy weight method are shown below.

1.

Dimensionless processing

Because the dimensions of the values in the matrix are not consistent, the original data need to be dimensionless processing. At the same time, the values in the matrix can be divided into positive type and negative type. The larger the positive type is, the more favorable the negative type is, the smaller the positive type is, the more favorable the negative type is. Therefore, the following two dimensionless processing equations are used for disposing.

$$z_{ij}^{+}=\frac{{\mathrm{z}}_{\mathrm{ij}}^{‘}-{\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{min}}{{\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{max}-{\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{min}}$$

(24)

$$z_{ij}^{-}=1-\frac{{\mathrm{z}}_{\mathrm{ij}}^{‘}-{\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{min}}{{\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{max}-{\left({\mathrm{z}}_{\mathrm{ij}}^{‘}\right)}_{min}}$$

(25)

where, $\mathrm{i}=1,2,\cdots ,\mathrm{n}$.$\mathrm{j}=1,2,\cdots ,\mathrm{m}.z_{ij}^{+}$ is the treatments for positive indicators and $z_{ij}^{-}$ is the treatment of negative indicators (Use the same method to distinguish positive indicators and negative indicators below).

The results of the dimensionless normalization of the positive and negative type indicators are normalized by the following equation.

$$z_{ij}=\frac{z_{ij}^{*}}{\sqrt{{\sum }_{i=1}^n{\left(z_{ij}^{*}\right)}^2}}$$

(26)

where, $z_{ij}^{*}$ is the evaluation indicators after the positive or negative dimensionless treatment, and $z_{ij}$ is the evaluation indicator after normalization.

2.

Specific gravity calculation

Calculate the weight of the i-th evaluation object under the j-th indicator $A_{ij}$.

$$A_{ij}=\frac{z_{ij}}{{\sum }_{i=1}^n{z}_{ij}}$$

(27)

3.

Entropy calculation

Calculate the entropy value $B_j$ accounted for by the i-th evaluation unit under the j-th indicator.

$$B_j=-\frac{1}{\ln n}{{\displaystyle \sum }}_{i=1}^n{A}_{ij}\ln A_{ij}$$

(28)

4.

Entropy weighting calculation

Calculate the entropy weight $C_j$ accounted for by the i-th evaluation unit under the j-th indicator.

$$C_j=\frac{1-B_j}{{\sum }_{i=1}^n{B}_j}$$

(29)

2.2.2. TOPSIS Method

1.

Construction of a weighted normalization matrix

The weighted normalization matrix D is obtained by multiplying the normalization matrix with the weight.

$$\mathrm{D}={\left({\mathrm{C}}_{\mathrm{j}}{\mathrm{z}}_{\mathrm{ij}}\right)}_{\mathrm{n}\times \mathrm{m}}=\left[\begin{array}{ccc}{\mathrm{C}}_1{\mathrm{z}}_{11}& \cdots & {\mathrm{C}}_{\mathrm{m}}{\mathrm{z}}_{11}\\ ⋮& \ddots & ⋮\\ {\mathrm{C}}_1{\mathrm{z}}_{\mathrm{n}1}& \cdots & {\mathrm{C}}_{\mathrm{m}}{\mathrm{z}}_{\mathrm{nm}}\end{array}\right]=\left[\begin{array}{ccc}{\mathrm{d}}_{11}& \cdots & {\mathrm{d}}_{1\mathrm{m}}\\ ⋮& \ddots & ⋮\\ {\mathrm{d}}_{\mathrm{n}1}& \cdots & {\mathrm{d}}_{\mathrm{nm}}\end{array}\right]$$

2.

Determine the positive and negative ideal solution of D

Calculate the positive ideal solution of the weighted decision matrix $d^{+}$ and negative ideal solutions $d^{-}$.

The equation are, respectively, as follows.

$$D^{+}=\left(d_1^{+},d_2^{+},\cdots ,d_n^{+}\right)$$

(30)

$$D^{-}=\left(d_1^{-},d_2^{-},\cdots ,d_n^{-}\right)$$

(31)

of which $d_j^{+}=ma{x}_i{d}_{ij}$, $d_j^{-}=mi{n}_i{d}_{ij}$.

3.

Calculate the Euclidean distance

Calculate each solution to a positive ideal solution $d_j^{+}$ and the negative ideal solution $d_j^{-}$ the Euclidean distance ${\mathrm{E}}_{\mathrm{i}}^{+}$ and ${\mathrm{E}}_{\mathrm{i}}^{-}$.

The equation are, respectively, as follows.

$${\mathrm{E}}_{\mathrm{i}}^{+}=\sqrt{\left\{{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{d}}_{\mathrm{ij}}-d_j^{+}\right)}^2\right\}}$$

(32)

$${\mathrm{E}}_{\mathrm{i}}^{-}=\sqrt{\left\{{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{d}}_{\mathrm{ij}}-d_j^{-}\right)}^2\right\}}$$

(33)

2.2.3. Grey Correlation Analysis

1.

Calculation of grey correlation coefficient

Based on the weighted normalization matrix D, calculate the i-th evaluation solution $d_j^{+}$ with the positive ideal solution $d_j^{-}$ and the negative ideal solution with respect to the j-th indicator with the grey correlation coefficient F.

The equation are, respectively, as follows.

$$F_{ij}^{+}=\frac{mi{n}_{i}mi{n}_j\left|d_j^{+}-d_{ij}\right|+\gamma ma{x}_{i}ma{x}_j\left|d_j^{+}-d_{ij}\right|}{\left|d_j^{+}-d_{ij}\right|+\gamma ma{x}_{i}ma{x}_j\left|d_j^{+}-d_{ij}\right|}$$

(34)

$$F_{ij}^{-}=\frac{mi{n}_{i}mi{n}_j\left|d_j^{-}-d_{ij}\right|+\gamma ma{x}_{i}ma{x}_j\left|d_j^{-}-d_{ij}\right|}{\left|d_j^{-}-d_{ij}\right|+\gamma ma{x}_{i}ma{x}_j\left|d_j^{-}-d_{ij}\right|}$$

(35)

where $\mathsf{\gamma }\in \left(0,1\right)$ is the resolution factor, generally taken as 0.5.

2.

Calculation of grey correlation degree

Calculate the grey correlation degree G of the positive and negative ideal solutions.

The equation are, respectively, as follows.

$$G_i^{+}=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{f}_{ij}^{+}$$

(36)

$$G_i^{-}=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{f}_{ij}^{-}$$

(37)

3.

Calculation of relative closeness

① Dimensionless processing

For the derived${ \mathrm{E}}_{\mathrm{i}}^{+}$, ${\mathrm{E}}_{\mathrm{i}}^{-}$, ${\mathrm{G}}_{\mathrm{i}}^{+}$ and ${\mathrm{G}}_{\mathrm{i}}^{-}$ and dimensionless processing is performed to obtain, in turn${ \mathrm{e}}_{\mathrm{i}}^{+}$ and ${\mathrm{e}}_{\mathrm{i}}^{-}$, ${\mathrm{g}}_{\mathrm{i}}^{+}$ and ${\mathrm{g}}_{\mathrm{i}}^{-}$.

The calculation equation is as follows.

$${\mathrm{e}}_{\mathrm{i}}^{+}=\frac{{\mathrm{E}}_{\mathrm{i}}^{+}}{{\mathrm{maxE}}_{\mathrm{i}}^{+}}$$

(38)

$${\mathrm{e}}_{\mathrm{i}}^{-}=\frac{{\mathrm{E}}_{\mathrm{i}}^{-}}{{\mathrm{maxE}}_{\mathrm{i}}^{-}}$$

(39)

$${\mathrm{g}}_{\mathrm{i}}^{+}=\frac{{\mathrm{G}}_{\mathrm{i}}^{+}}{{\mathrm{maxG}}_{\mathrm{i}}^{+}}$$

(40)

$${\mathrm{g}}_{\mathrm{i}}^{-}=\frac{{\mathrm{G}}_{\mathrm{i}}^{-}}{{\mathrm{maxG}}_{\mathrm{i}}^{-}}$$

(41)

② Combined dimensionless weighted Euclidean distance and grey correlation

The closer the index to be evaluated is to the positive ideal solution and the farther it is to the negative ideal solution, the better it is. The higher the correlation with the positive ideal solution and the lower the correlation with the negative ideal solution, the better. That is, the greater the values of ${ \mathrm{e}}_{\mathrm{i}}^{-}$ and ${\mathrm{g}}_{\mathrm{i}}^{+}$, the closer the evaluation object is to the positive ideal solution. The greater the values of ${\mathrm{e}}_{\mathrm{i}}^{+}$ and ${\mathrm{g}}_{\mathrm{i}}^{-}$, the further away the evaluation object is from the positive ideal solution.

The specific form of expression is as follows.

$$H_i^{+}=\alpha {\mathrm{e}}_{\mathrm{i}}^{-}+\beta {\mathrm{g}}_{\mathrm{i}}^{+}$$

(42)

$$H_i^{-}=\alpha {\mathrm{e}}_{\mathrm{i}}^{+}+\beta {\mathrm{g}}_{\mathrm{i}}^{-}$$

(43)

Of these, the $\alpha$ and $\beta$ are the degrees of preference, the $\mathsf{\alpha }+\mathsf{\beta }=1, \mathsf{\alpha },\beta \in \left(0,1\right)$, whose values are determined by the decision maker according to his or her preferences, and both are taken as 0.5 in this paper. $H_i^{+}$ and $H_i^{-}$ and reflect the degree of proximity and distance from the ideal solution, respectively.

4.

Calculating the relative closeness of the scheme I.

$$I_i=\frac{H_i^{+}}{H_i^{+}+H_i^{-}}$$

(44)

3. Results and Discussion

3.1. Entropy Weight Analysis of Evaluation Indicators

Analysis of the evaluation indicators in the three rock mass classification methods to determine the positive and negative types of each factor is shown in Table 9.

Table 9. Types of indicators for the three classification methods.

Q		RMR		BQ
Indicators	Type	Indicators	Type	Indicators	Type
RQD	Positive	R1	Positive	$\mathsf{\sigma }$cw	Positive
Jn	Negative	R2	Positive	KV	Positive
Jr	Positive	R3	Positive	K1	Negative
Ja	Negative	R4	Positive	K2	Negative
Jw	Positive	R5	Positive	K3	Negative
SRF	Negative	R6	Positive

Using Equations (24)–(26) for dimensionless normalization, the following matrix is obtained.

$$\mathrm{ZQ} =\left[\begin{array}{cccccc}0.9379& 1.0000& 1.0000& 0.0000& 1.0000& 1.0000\\ 1.0000& 1.0000& 0.0000& 0.0000& 0.5000& 0.0000\\ 0.7717& 0.3333& 1.0000& 0.0000& 0.5000& 0.0000\\ 0.0000& 1.0000& 1.0000& 0.0000& 1.0000& 0.0000\\ 0.8613& 0.6667& 1.0000& 0.0000& 0.3000& 0.0000\\ 0.8685& 0.0000& 1.0000& 0.0000& 0.0000& 0.0000\\ 0.6084& 0.3333& 1.0000& 0.0000& 0.3000& 0.0000\end{array}\right]$$

$$\mathrm{ZRMR} =\left[\begin{array}{cccccc}0.4545& 0.9155& 0.3077& 0.1667& 0.0000& 0.5000\\ 0.3636& 1.0000& 0.5385& 0.6667& 0.5833& 0.5000\\ 0.6364& 0.7042& 1.0000& 1.0000& 0.5833& 0.5000\\ 0.0909& 0.0000& 0.5385& 0.3333& 1.0000& 0.5000\\ 0.7273& 0.8169& 0.7692& 0.6667& 0.3333& 1.0000\\ 1.0000& 0.8239& 0.9231& 0.5000& 0.5833& 0.0000\\ 0.0000& 0.5141& 0.0000& 0.0000& 0.0000& 0.0000\end{array}\right]$$

$$\mathrm{ZBQ} =\left[\begin{array}{ccccc}0.3402& 0.1765& 0.5000& 0.0000& 0.0000\\ 0.2755& 0.4529& 0.5000& 0.4000& 0.0000\\ 0.5312& 1.0000& 0.5000& 0.4000& 0.0000\\ 0.0213& 0.8588& 0.5000& 1.0000& 0.0000\\ 1.0000& 0.0000& 1.0000& 0.2000& 0.0000\\ 0.8782& 0.0324& 0.0000& 0.4000& 0.0000\\ 0.0000& 0.1529& 0.5000& 0.0000& 0.0000\end{array}\right]$$

The above matrix was substituted into the entropy weight method calculation equation, and all values of the normalized matrix were shifted to all values +0.0001 to avoid errors caused by the denominator being equal to 0 in the calculation process, to obtain the entropy value B and entropy weight C for the three classification methods, and the results are shown in Table 10.

Table 10. Entropy weight method results.

Q			RMR			BQ
Indicators	B	C	Indicators	B	C	Indicators	B	C
RQD	0.9148	0.0771	R1	0.8391	0.1985	$\mathsf{\sigma }$cw	0.7840	0.2607
Jn	0.8725	0.1155	R2	0.9105	0.1105	Kv	0.7349	0.3200
Jr	0.9208	0.0717	R3	0.8867	0.1398	K1	0.8982	0.1228
Ja	1.0000	0.0000	R4	0.8580	0.1752	K2	0.7543	0.2965
Jw	0.8604	0.1265	R5	0.7969	0.2505	K3	1.0000	0.0000
SRF	0.3273	0.6092	R6	0.8982	0.1255

3.2. Relative Closeness Analysis of Each Section

TOPSIS method and grey correlation analysis were used to analyze the relative closeness of the grading results of each section. The results were shown in Table 11, and the relative proximity degree was shown in Figure 5; it can be seen from the table that the relative proximity degree of each method is between 0.35 and 0.70. In Q classification, the middle segment of $-$795 has the best effect, while the middle segment of $-$915 has the worst. In the RMR classification, the middle segment of $-$825 had the best effect, and the middle segment of $-$780 had the worst effect. In BQ classification, $-$870 middle segment had the best effect, and $-$780 middle segment had the worst effect. In general, the average value of RMR was the highest and the overall grading effect was the best. Due to different considerations and the interference of subjective factors, different classification methods show great differences in the relative closeness between different sections. When different methods are used to classify the same area, normally different rock mass grades will be obtained, therefore, at least the employment of at least two rock classification methods is recommended.

Table 11. Results of the relative closeness analysis.

Classification Method	Parameters	Middle Section
		$-$780-1	$-$795-1	$-$825-1	$-$870-1	$-$885-1	$-$900-1	$-$915-1
Q	E+	0.0048	0.3192	0.6175	0.6140	0.6169	0.6329	0.6211
	E−	0.6409	0.3407	0.1190	0.1857	0.1301	0.0982	0.1013
	G+	0.6985	0.4762	0.4212	0.5238	0.4475	0.3988	0.3913
	G−	0.7143	0.2402	0.3810	0.4038	0.4286	0.3935	0.5284
	I	0.5551	0.6379	0.4552	0.5044	0.4504	0.4321	0.3784
RMR	E+	0.3304	0.1959	0.1453	0.2579	0.1889	0.1866	0.3990
	E−	0.1582	0.2490	0.3123	0.2759	0.2773	0.3056	0.0847
	G+	0.4231	0.5151	0.6075	0.4481	0.5845	0.5693	0.3344
	G−	0.8571	0.5352	0.3977	0.3548	0.5373	0.3633	0.4320
	I	0.4054	0.5836	0.6925	0.6248	0.6138	0.6861	0.4505
BQ	E+	0.4367	0.3190	0.2244	0.2662	0.3983	0.3790	0.4828
	E−	0.1217	0.2098	0.3734	0.4090	0.2942	0.2580	0.0785
	G+	0.2346	0.2629	0.3529	0.3740	0.3883	0.2761	0.2197
	G−	0.5714	0.4049	0.3179	0.2677	0.3086	0.3401	0.4082
	I	0.3563	0.4796	0.6284	0.6668	0.6125	0.5233	0.3889

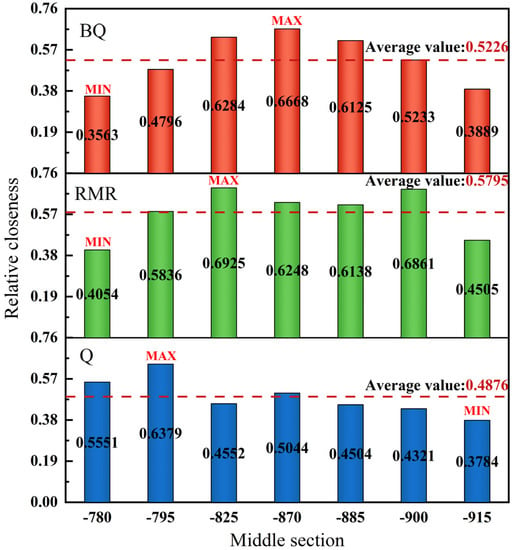
Figure 5. The statistics and comparison of the relative closeness of the three methods.

Combined with Table 6, the five middle sections with different grading results ($-$825, $-$870, $-$885, $-$900 and $-$915) were graded according to the relative closeness. The data with a relatively large degree of closeness were taken as the results, and the final grading results were obtained as shown in Table 12. The results show that the rock classification results obtained by this method are not conservative.

Table 12. Final classification results.

Middle Section	$-$780-1	$-$795-1	$-$825-1	$-$870-1	$-$885-1	$-$900-1	$-$915-1
Mass grade	III	II	II	II	II	III	III
Classification method	Q	Q	RMR	BQ	RMR	RMR	RMR
Relative closeness	0.5551	0.6379	0.6925	0.6668	0.6138	0.6861	0.4505

3.3. Entropy-Weighted-TOPSIS-Grey Correlation Rock Mass Classification Method

From the above study, RMR classification has a high overall approximation in the Xishan mining region of Sanshandao Gold Mine. Therefore, the IRMR classification method [36], which is based on the RMR method considering ground stress damage, was selected to obtain the entropy weight and relative closeness of each factor in a more section area.

3.3.1. Entropy-TOPSIS Analysis

Using the raw data available on Sanshandao Gold Mine as an example, the raw matrix was created as shown in Table 13.

Table 13. Raw data matrix.

Serial Number	Location of Measurement Points	Evaluation Indicators
		R1	R2	R3	R4	R5	R6	R7
1	$-$780-1	9.8	16.4	11.9	17	0	−5	−4.3
2	$-$780-2	9.8	16.4	12	17	0	−5	−4.3
3	$-$795-1	9.7	17.6	12.2	20	7	−5	−4.3
4	$-$795-2	9.7	17.6	12.2	19	7	−5	−4.2
5	$-$825-1	10	13.4	12.8	22	7	−5	−9.5
6	$-$825-2	10	13.4	12.4	21	7	−5	−9.5
7	$-$825-3	10	13.4	12.8	20	7	−5	−8.2
8	$-$825-4	10	13.4	12.4	20	7	−5	−9
9	$-$870-1	9.4	3.4	12.2	18	12	−5	−9.5
10	$-$885-1	10.1	15	12.5	20	4	0	−9.5
11	$-$900-1	10.4	15.1	12.7	19	7	−10	−9.2
12	$-$915-1	9.3	10.7	11.5	16	0	−5	−9.2
13	$-$915-2	9.3	10.7	11.5	17	1	−6	−9.2

The processing steps are the same as above, and the results of the entropy weighting method analysis of each influencing factor are obtained, as shown in Table 14, where R₇ has the largest entropy weight and R₆ the smallest. The information carried by the geo stress damage index is the most effective.

Table 14. Results of entropy weight method analysis.

Evaluation Indicators	R1	R2	R3	R4	R5	R6	R7
B	0.8971	0.9605	0.9124	0.9160	0.8615	0.9572	0.6800
C	0.1263	0.0485	0.1074	0.1030	0.1699	0.0525	0.3925

3.3.2. Grey Correlation Analysis

The core of grey correlation analysis is to establish the parent series of variation with the scheme according to certain rules, and to find the correlation degree between each sub-series and the parent series, so that the degree of influence of each evaluation indicator on the scheme can be obtained [37]. In this paper, the positive Euclidean distance and IRMR values determined by entropy weight-TOPSIS analysis were used as the parent series, and seven evaluation indicators, such as R₁-R₇, were used as the sub-series, and the series were dimensionless, and the grey correlation degree of each evaluation indicator was calculated using Equations (10)–(13), and the results are shown in Table 15.

Table 15. Grey correlation for each evaluation indicator.

Evaluation Indicators	R1	R2	R3	R4	R5	R6	R7
RMR correlation	0.1774	0.1763	0.1036	0.1071	0.1402	0.1503	0.1451
E+ relevance	0.1457	0.1467	0.1881	0.1834	0.1048	0.1031	0.1284

3.3.3. Rock Mass Classification Method Construction

On the basis of the above study, the entropy weight, RMR value and E⁺ correlation are integrated, 3 groups of parameters of the same indicator are added, R₁-R₅ indicators are normalized, R₆ and R₇ are changed in equal proportion, and the final parameter obtained is defined as the evaluation indicator importance J, as shown in Table 16, where R₁-R₅ are moderately important and close, R6 is the least important, and in the deep region, high ground stress is one of the main causes of channel destabilization damage, so R₇ is the largest, at 0.3284, which is in line with the actual situation. Based on the above study, the entropy weight-TOPSIS-grey correlation rock mass grading method (referred to as “ETG” rock mass grading method) was established, with R₁-R₅ as a positive number and a full score of 100, and R₆ and R₇ as negative numbers, which are correction indicators. To avoid “jumps” in the grading process, a linear grading method is adopted, i.e., the upper limit of the evaluation index is used as the upper limit of the score, and the detailed grading criteria are shown in Figure 6.

Table 16. “ETG” rock mass classification method.

Evaluation Indicators	R1	R2	R3	R4	R5	R6	R7
J	0.2216	0.1831	0.1967	0.1941	0.2046	0.1507	0.3284
Rating value	22.16	18.31	19.67	19.41	20.46	15.07	32.84

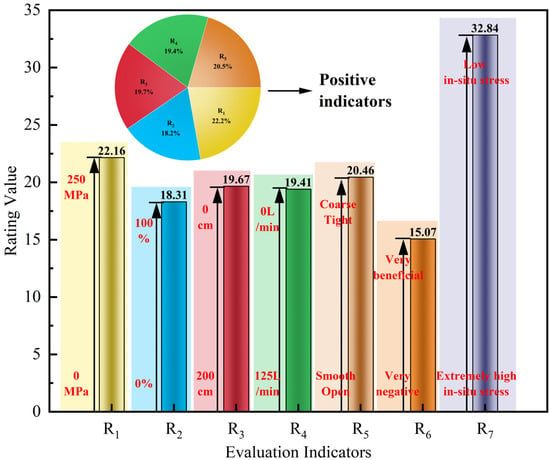
Figure 6. Detailed classification criteria.

The method is based on actual data in the field and uses Entropy weight, TOPSIS and Grey Correlation analysis to try to establish a “site-specific” rock mass classification method, it may be more suitable for specific areas than other common methods.

3.3.4. Project Examples

The above “ETG” rock mass classification method was applied to the middle section of the Sanshandao mine, and the “ETG” grading results were compared with the IRMR method grading results, and the results are shown in Table 17. As can be seen from the table, in section $-$870, the grading results of the two grading methods differed, with IRMR being grade III and ETG being grade IV. The rest of the results were the same, but the ETG values were all lower than the IRMR values, and the grading results were more conservative, reducing the risk of damage to the roadway due to errors in grading the rock mass classification.

Table 17. ETG and IRMR Grade Results.

Serial Number	1	2	3	4	5	6	7	8	9	10	11	12	13
IRMR value	45.8	45.9	57.2	56.3	50.7	49.3	50	48.8	40.5	52.1	45	33.3	34.3
Grade	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅳ	Ⅳ
ETG value	43.2	43.3	54.6	53.8	45.1	43.7	45.3	43.6	35.9	45.1	40.8	28.1	29.3
Grade	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅲ	Ⅳ	Ⅲ	Ⅲ	Ⅳ	Ⅳ