Refined Network Topology for Improved Reliability and Enhanced Dijkstra Algorithm for Optimal Path Selection during Link Failures in Cluster Microgrids

Abstract

Cluster microgrids are a group of interoperable smart microgrids, connected in a local network to exchange their energy resources and collectively meet their load. A microgrid can import/export energy to the neighboring microgrid in the network based on energy deficit/availability. However, in executing such an operation, a well-established communication network is essential. This network must provide a reliable communication path between microgrids. In addition, the network must provide an optimal path between any two microgrids in the network to optimize immediate energy generation, import requirements, and export possibilities. To meet these requirements, different conventional research approaches have been used to provide reliable communication, such as backup/alternative/Hot Standby Router Protocol (HSRP)-based redundant path concepts, in addition to traditional/renowned Dijkstra algorithms, in order to find the shortest path between microgrids. The HSRP-based mechanism provides an additional path between microgrids, but may not completely solve the reliability issue, especially during multiple link failures and simultaneous failures of the actual path and redundant path. Similarly, Dijkstra algorithms discussed in the literature do not work for finding the shortest path during link failures. Thus, to enhance reliability, this paper proposes a refined network topology that provides more communication paths between microgrids, while retaining the same number of total links needed, as in conventional HSRP-based networks. In addition, this paper proposes an enhanced Dijkstra algorithm to find the optimum path during link failures. Simulations are executed using NetSim^TM by implementing test cases such as single-link and multiple-link failures. The results prove that the proposed topology and method are superior to conventional approaches.

1. Introduction

The microgrid is a small entity that generates power using renewable sources, such as solar, wind, etc., to meet its load demand. If any excess power is generated at the microgrid level, then it will be sent to the main grid; if there is a deficiency, it will utilize main grid power. Currently, there is an increase in community culture, where microgrids of different load profiles are situated in the same locality [1,2]. However, instead of operating the microgrids independently, if they are operated together, any excess energy can be shared among the microgrids, depending on their requirement. These interoperable microgrids are called cluster microgrids [3]. This cluster microgrid network creates a new opportunity for the energy market, and these energy operations are executed at the central monitoring and control unit (CMCU).

To explain the scenario of a cluster microgrid network, a cluster of four interconnected microgrids is defined and shown in Figure 1. Here, all the microgrids are connected to a common electrical bus for energy transactions (import or export) among them. Similarly, all the microgrids are connected to the CMCU for communication exchange (data and control transmission). Various sources and loads associated with each of these microgrids are given in Table 1 as an example. The effectiveness of energy transactions among microgrids depends on effective decisions within the network. This further depends on effective information tracing from the microgrids, passing this information to the CMCU, then passing these control decisions from CMCU to the microgrids; overall, the communication network plays a crucial role in these operations.

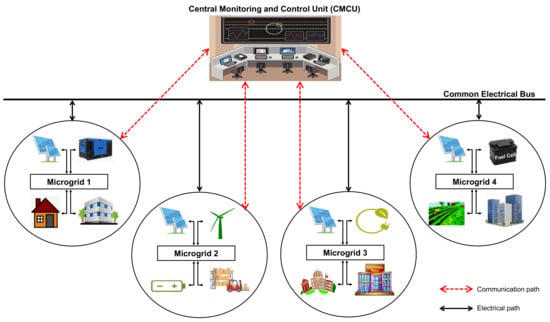
Figure 1. Traditional interoperable microgrid architecture.

Table 1. Sources and loads associated with each microgrid.

Microgrid	Sources	Loads
Microgrid1 (MG1)	Solar, Diesel Generator	Individual house, Apartment
Microgrid2 (MG2)	Solar, Wind, Battery	Warehouse
Microgrid3 (MG3)	Solar, Biomass	University building, Shopping mall
Microgrid4 (MG4)	Solar, Fuel Cell	Farm, Large community

The CMCU executes energy operations based on availability, demand, and supply of each microgrid in the network; therefore, a continuous data supply to the CMCU is required. However, these networks are often affected by link failures, which in turn affect communication reliability [4]. If the communication link between a microgrid and the CMCU fails, then that particular microgrid cannot participate in the energy transactions that are taking place in the cluster microgrid network.

From the above discussion, it can be seen that the communication network must be highly reliable in order to enhance the operation of cluster microgrids. To address the link failure issue in the network, a backup link/alternate path/HSRP (hot standby router protocol)-based approach is used, which recommends using a redundant path for every actual path between the microgrid and the CMCU [5]. However, this approach is not very efficient in achieving reliability at higher levels as the requirement of having a redundant path for each actual path increases deployment and network infrastructure costs, as well as making the whole network more complex. Hence, instead of using a backup path for every actual path, we must identify an optimal configuration that can enhance communication reliability. Furthermore, selecting the shortest path between any microgrid and the CMCU is also highly recommended, in order to reduce (or avoid) latency issues.

Recently, various graph theory-based approaches/algorithms have been introduced by researchers working on communication networking, with varying objectives. Some of these key works for the applications of power systems, microgrids, power electronics, medical, and other general industrial scenarios, are listed in Table 2. These works have proved how important the graph theory-based solution is for communication network applications, in order to achieve different goals such as fault isolation, power management, autonomous tasking, data center establishment, control of power electronics converter, and multi-AGV routing, etc. Using a graph theory-based approach is a key motivation for this paper as it helps to establish a robust communication network in the proposed cluster microgrid scenario.

Table 2. Summary of graph theory-based key works executed in diverse applications.

Objective	Key Points	Year
Fault isolation scheme in power system [6]	The tripping path of the circuit breaker linking each protected electrical component to establish fault isolation can be identified using the Floyd-Warshall algorithm.	2022
Power management in interconnected multi-microgrid systems [7]	In both deterministic and probabilistic scenarios, the multi-objective JAYA algorithm is used to solve the power management of a multi-microgrid system. This is validated by simulation results and advised as an efficient approach to achieve the cost and environmental goal functions.	2022
Autonomous tasking in industrial usages [8]	A new algorithm called Dijkstra optimal tasking (DOT), which is inspired by Dijkstra is designed for optimal task scheduling in industrial applications.	2021
Proof of Floyd-Warshall algorithm [9]	Alpha to C++ generation system helps in verifying the correctness and validating the Floyd-Warshall algorithm.	2021
Refined Floyd-Warshall algorithm [10]	Floyd-Warshall algorithm is inefficient, especially for large complicated/dense graphs, various improved version of this algorithm is discussed.	2021
Topology for building the network for the data center [11]	In building the network for the data center, there are various types of network topologies, one of which is the Jellyfish Topology. The issues faced during the link failures in the network are addressed by the Floyd-Warshall algorithm.	2021
Modeling and control methodology of lattice converters [12]	Lattice converters combine the merits of both cascaded-bridge converters and multi-paralleled converters. With modularity and scalability, they can handle huge currents and voltages. This study provides a unified modeling and control methodology for diverse lattice converter topologies based on graph theory, resulting in the achievement of their key control objectives.	2021
Evaluation of transmission properties of networks [13]	The use of unevenness coefficients to evaluate transmission qualities of networks with regular graphs is discussed. The analysis shows that usage of graph edges depends on two factors, namely, the total number of minimum length paths and a number of parallel paths connecting the graph nodes.	2021
Multi-AGV routing problem [14]	The efficiency of the automated guided vehicle (AGV) system depends on avoiding multi-automated guided vehicle path conflicts. To optimize the routing of multi-AGVs, a bi-level path planning algorithm is proposed. The suggested bi-level path planning algorithm outperformed the Dijkstra algorithm and the standard A* algorithm in terms of search efficiency.	2020
Application of graph theory in health care [15]	During emergency cases in health care scenarios, a regular traffic system will create trouble for the concerned person (patient/doctor/etc.) to reach the hospital in time. The graph theory-based approaches help to address this issue by traffic splitting (stratification).	2020
End-to-end quality of wireless community networks [16]	Individuals create community networks to provide free Internet access. End-to-end quality (EtEQ) tracking is used by link-state routing systems to pick pathways that maximize delivery rate while minimizing traffic congestion. According to the results of the trial, the EtEQ prediction approach outperforms ETX + Dijkstra in terms of Packet Delivery Ratio and Link ETX.	2019

Further, algorithms such as Breadth-first search, Dijkstra, Bellman-Ford, Floyd-Warshall, and A* were developed for finding the optimal (shortest) path between any two nodes in a communication network of various applications [17,18,19]. A summary of all such key algorithms is given in Table 3. Among these algorithms, Dijkstra is the most popular and widely used algorithm in real-time applications (e.g., geographical mapping), due to its less time complexity, when compared to the other algorithms. In addition, the Dijkstra algorithm is used for surface optimal path planning, and for identifying collision-free optimized paths [20,21]. Further, modified Dijkstra algorithms were proposed to calculate the shortest path in networks with deterministically time-varying links, and for vehicle path planning [22,23]. With the massive deployment of sensor nodes, quality of measurements should be guaranteed, which is effectively tackled by the calibration technique. For effective search solutions in these environments, the Prim-Dijkstra algorithm was proposed [24]. However, these state-of-the-art algorithms cannot be used during link failures in the network.

Table 3. Comparison of various conventional algorithms used for optimal path selection.

Parameter	Dijkstra’s Algorithm [8]	Floyd-Warshall Algorithm [9]	A* Algorithm [17]	Bellman-Ford Algorithm [25]
Shortest path	Single source	All pairs	Single source	Single source
Edges/Links	Positive	Positive or negative	Positive	Positive or negative
Type	Undirected or directed	Undirected or directed	Undirected or directed	Directed
Time complexity	θ ((V × logV) + E)	θ (V3)	Heuristic dependent	θ (E × V)
Space complexity	θ (V)	θ (V2)	Heuristic dependent	θ (V)

where ‘Ɵ’ is the complexity function, ‘E’ is the number of links, and ‘V’ is the number of nodes.

Hence, by considering all of the above-mentioned issues in state-of-the-art approaches, this paper proposes a refined network topology that provides more communication paths between microgrids, while retaining the same number of total links needed as in conventional HSRP-based networks. This enhances the reliability of the network. In addition, this paper proposes a graph theory-based enhanced Dijkstra algorithm to find the optimum path between nodes during link failures.

The rest of the paper is structured as follows. Reliability enhancement through the proposed topology is described in Section 2. Section 3 provides a discussion on finding the shortest path during link failures, using the enhanced Dijkstra algorithm. Section 4 presents the results and discussion, and finally, Section 5 concludes this paper.

2. Refined Network Topology for Improved Reliability

To make graph representation clear, all the microgrids are considered as nodes, and are connected with the help of links. Here, communication between nodes and the CMCU is bidirectional, so the network is represented using an undirected graph. Single-path topology, double-path topology, and the proposed multipath topology to represent the cluster microgrids (Figure 1) network is shown in Figure 2. Here, node representation of microgrid 1 is considered as A, node representation of microgrid 2 is considered as B, node representation of microgrid 3 is considered as C, node representation of microgrid 4 is considered as D, and the representation of the CMCU node is considered as E. Here, the graph is undirected, so the representation of A → E, B → E, C → E, D → E, A → B, A → C, B → D, and C → D is same as the representation of E→ A, E → B, E → C, E → D, B → A, C → A, D → B, and D → C, respectively.

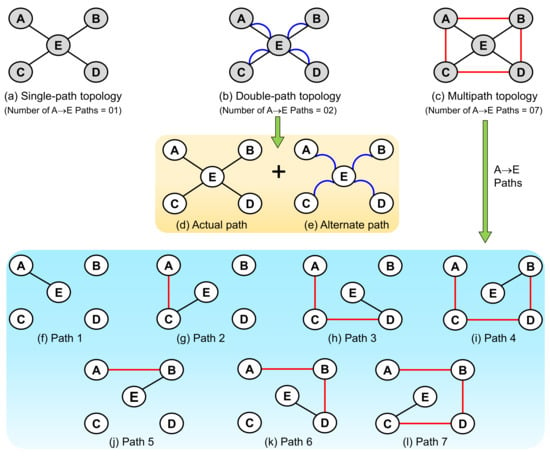
Figure 2. Graph representation of the cluster microgrids network using conventional single-path topology, conventional double-path topology, and the proposed multipath topology.

The total number of links and paths that are formed in single-path topology, double-path topology, and multipath topology, is shown in Figure 3. From this, it is observed that the total links available in single-path topology are four, double-path topology are eight, and the multipath topology are eight. Similarly, between any two nodes, for example, A→ E, there is only one path in single-path topology, two paths in double-path topology, and seven paths in the multipath topology. Hence, the multipath topology is a restructured representation of the double-path topology, without increasing the number of links, but providing more paths for connecting source and destination nodes. This shows the indication of a more robust structure that can establish an effective cluster microgrids network with improved reliability.

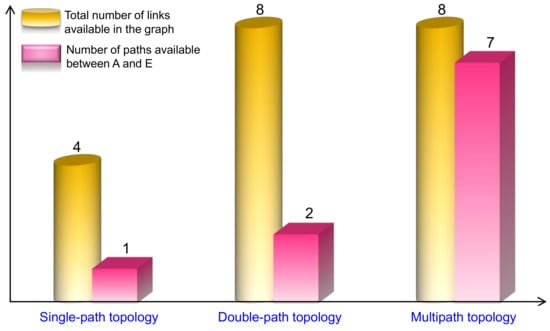
Figure 3. Number of links versus paths in single-path, double-path, and multipath topologies.

In the single-path topology, there exists only one link between each of nodes A, B, C, and D to E. i.e., A → E, B → E, C → E, D → E as shown in Figure 2a. If link failure happens between nodes (e.g., A → E: node A and node E), communication cannot be established between them. Additionally, the same scenario can be observed for other links i.e., B → E, C → E, D → E. This is the major drawback of single-path topology. The drawback of the single-path topology can be eliminated, however, by using an alternate path/HSRP-based approach, as shown in Figure 2b, where an alternate path is provided in addition to the actual path [5]. Therefore, in this case, two links exist between each of the nodes, A, B, C, D to E, which forms an actual path and an alternate path. The links present here are: A → E, B → E, C → E, D → E corresponding to the actual path, as shown in Figure 2d, and A → E, B → E, C → E, D → E corresponding to the alternate path, as shown in Figure 2e. Therefore, if an actual path fails, communication happens through the alternate path.

To further enhance reliability, this paper proposes a new topology as shown in Figure 2c. This requires the same number of links that the double-path topology (Figure 2b) requires, but enhances reliability, compared to the double-path topology, by providing more paths between nodes. For example, Figure 2f–l shows all the possible paths between nodes A and E. From this, it is observed that there are seven possible paths between A and E for communication in the proposed case; whereas, it was only one in single-path topology, and only two in double-path topology. This is the major benefit of the proposed multipath topology. In the multipath topology, to reach node E from node A (for example), the seven available paths are: A → E, A → C → E, A → C → D → E, A → C → D → B → E, A → B → E, A → B → D → E, A → B → D → C → E.

Therefore, in the case of multipath topology, to reach from a source node to a destination node, even if one path fails (due to link failures), there are six more paths available; whereas, in double-path topology, only one more path was available. Further, if two paths fail between any two nodes in the double-path topology, communication is completely lost between them; whereas, in the proposed approach, if two paths fail, five more paths will be available.

Thus, the proposed multipath topology can work even in the case of multi-path or multi-link failures. Hence, multipath topology increases reliability without increasing the number of links, when compared with double-path topology.

3. Enhanced Dijkstra Algorithm for Optimal Path Selection during Link Failures

In a real-time scenario, all the microgrids may not be placed at equidistance to the CMCU. Thus, a conceptual graph of the multipath topology, shown in Figure 2c, can be redrawn as Figure 4 by considering the practical nature of the cluster microgrids. The graph shown in Figure 4 is therefore considered, to analyze the shortest path between microgrid nodes (A, B, C, D) and CMCU (E). Here, each link is represented with the cost, which refers to the distance between nodes. The cost of the links is assumed as: A → C:2 (i.e., the cost of the link A to C is 2); A → B:13; A → E:12; C → E:8; C → D:3; D → E:1; D → B:5; and B → E:1, based on the distance between the two nodes, where the link is formed. To understand the problem statement, initially, two key state-of-the-art algorithms (namely, the Dijkstra algorithm [8] and the Floyd-Warshall algorithm [9]) that were discussed in Section 1 for finding the shortest path, are implemented in Section 3.1. Further, Section 3.2 describes the proposed enhanced Dijkstra algorithm, and its implementation.

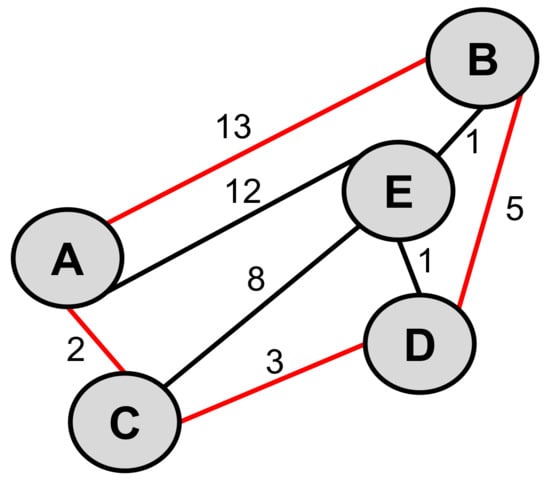
Figure 4. Graph representation of cluster microgrids with costs.

3.1. Implementation of Key State-of-the-Art Algorithms

Achieving reliability through an effective topology, along with optimum path communication, is vital for successful cluster microgrids’ deployment. Therefore, with this motivation, the topology shown in Figure 4 is investigated for optimal path search. For example, travel from node A (source node) to node E (destination node) is considered for implementing the algorithms to find the shortest path for A to E communication, based on the cost (distance) calculation. To calculate the cost of this travel, there exist many possible paths. For the direct path between node A and node E, the cost is 12; however, other possible paths exist which costs less than 12. It is necessary, therefore, to execute all such possibilities between the source node and destination node, in order to finally identify the shortest path for communication. To achieve this objective, the Dijkstra algorithm and the Floyd-Warshall algorithm are implemented.

3.1.1. Implementation of the Conventional Dijkstra Algorithm

The Dijkstra algorithm (Algorithm 1) gives the shortest distance from the source node to all other nodes, finally outputting the shortest path between source node and destination node as per user set values. It is a greedy algorithm, which means it uses a local optimum approach. The implementation of the Dijkstra algorithm for the considered case study (Figure 4) is shown in Figure 5 and is described as follows:

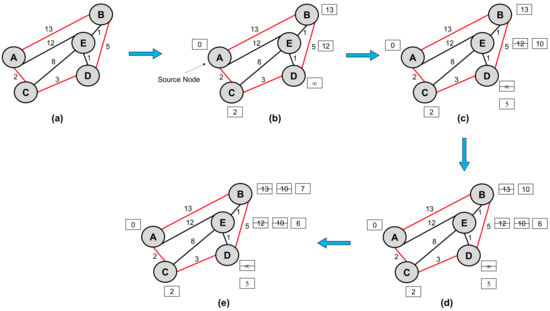
Figure 5. Implementation of conventional Dijkstra algorithm.

• Assume node ‘A’ as the source node (initial node of observation) and assign the costs, for the source node as 0, directly connected nodes (B, E, and C with the cost of 13, 12, and 2 respectively), and indirectly connected nodes (‘D’) as ‘∞’, as shown in Figure 5b. From this, node ‘C’ is identified as the shortest node from the node of observation.
• From ‘C’, the directly connected nodes observed are D (with cost 3) and E (with cost 8). So, their costs are updated as 5 and 10, respectively, as shown in Figure 5c, and are computed as follows.

  -

  If cost (D) > cost (C) + cost (C → D) (i.e., ∞ > 2 + 3, which is true), therefore, the cost of ‘D’ is updated as 5.

  -

  If cost (E) > cost (C) + cost (C → E) (i.e., 12 > 2 + 8, which is true), therefore, the cost of ‘E’ is updated as 10.

• From this computation, as the cost of ‘D’ is lesser than other nodes, the node ‘D’ is selected as the node of observation (or shortest node) for further analysis. From ‘D’, the directly connected nodes observed are E (with cost 10) and B (with cost 13). So, their costs are updated as 6 and 10 respectively as shown in Figure 5d, and are computed as follows.

  -

  If cost (E) > cost (D) + cost (D → E) (i.e., 10 > 5 + 1, which is true), therefore, the cost of ‘E’ is updated as 6.

  -

  If cost (B) > cost (D) + cost (D → B) (i.e., 13 > 5 + 5, which is true), therefore, the cost of ‘B’ is updated as 10.

• From this computation, as the cost of ‘E’ is lesser than other nodes, the node ‘E’ is selected as the node of observation (or shortest node) for further analysis. From ‘E’, only one directly connected node ‘B’ is observed with a cost of 10. So, its cost is further updated as 7 as shown in Figure 5e and is computed as follows.

  -

  If cost (B) > cost (E) + cost (E → B) (i.e., 10 > 6 + 1, which is true), therefore, the cost of ‘B’ is updated as 7.

• Thus, all the nodes in the graph are relaxed. Finally, joining all the above identified directly connected shortest nodes produce the least cost path between the source node ‘A’ and destination node ‘E’, which is found as A → C → D → E path with a cost of 6.

Algorithm 1 Conventional Dijkstra Algorithm.

Input: Graphical representation of the network with indications of source and destination nodes. Step 1. Assign the cost of source-node as ‘0’, directly connected nodes with their cost, and all other nodes (indirectly connected nodes) as ‘∞’. Further, assign the source node as the node of observation. Step 2. Select the shortest node out of all the directly connected nodes from the node of observation. Step 3. Identify all directly connected nodes to the shortest node identified in Step 2 (say, node ‘b’) and update their costs. Further, pick up the shortest node among them (say, node ‘c’), whose cost can be updated as mentioned in Step 4. Step 4. Update the cost of ‘c’ as per the following formulae If cost (c) > cost (b) + cost (b → c) then update cost (c) = cost (b) + cost (b → c) else retain the same cost Step 5. Now consider node ‘c’ as the node of observation and repeat Step 2 to Step 4 for node ‘c’. Step 6. In this way, continue the process for the entire graph until all other nodes are relaxed, which finally indicates the least cost possible path (shortest path) from the source node. Here, the visited node should not be rechecked. Output: Optimal path recommendation.

3.1.2. Implementation of the Conventional Floyd-Warshall Algorithm

The Floyd-Warshall algorithm (Algorithm 2) is an “all-pair” shortest path algorithm, which calculates the shortest path from each node of the network graph to all other nodes, finally outputting the shortest path between source and destination nodes as per user set values. The execution of the Floyd-Warshall algorithm is given in Figure 6 and is described as follows:

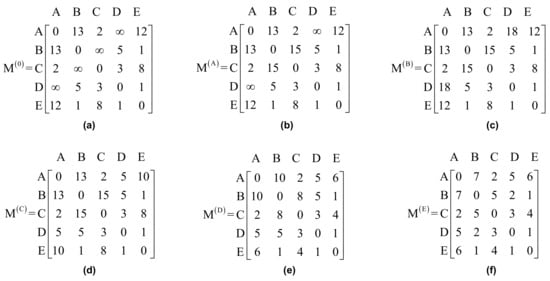
Figure 6. Implementation of conventional Floyd-Warshall algorithm.

• Assign the costs as follows.

  -

  All self-nodes (A to A, B to B, C to C, D to D, and E to E) are assigned with cost ‘0′.

  -

  From each one of the nodes to all other directly connected nodes, the costs are assigned as A → B:13, A → C:2, A → E:12, B → A:13, B → D:5, B → E:1, C → A:2, C → D:3, C → E:8, D → B:5, D → C:3, D → E:1, E → A:12, E → B:1, E → C:8, E → D:1.

  -

  Indirectly connected nodes (A to D, B to C, C to B, D to A) are given with cost ‘∞’.

• Represent Step 1 in the form of a matrix (M⁰), as shown in Figure 6a. In this matrix,

  -

  the first row is assigned with costs 0, 13, 2, ∞, 12; which represents the cost of the paths of nodes A to A, B, C, D, and E.

  -

  the second row is assigned with costs 13, 0, ∞, 5, 1; which represents the cost of the paths of node B to A, B, C, D, and E.

  -

  the third row is assigned with 2, ∞, 0, 3, 8; which represents the cost of the paths of node C to A, B, C, D, and E.

  -

  the fourth row is assigned with costs ∞, 5, 3, 0, 1; which represents the cost of the paths of node D to A, B, C, D, and E.

  -

  the fifth row is assigned with 12, 1, 8, 1, 0; which represents the cost of the paths of node E to A, B, C, D, and E.

• Now consider the first intermediate node ‘A’ and update the elements in the matrix by using Equation (1) and representing it as M^(A), as shown in Figure 6b.

  -

  here, the cost of the matrix elements is updated by considering the path via the intermediate node. If the cost is less than the actual, then it should be updated.

• Repeat the above step for each of the other nodes as an intermediate node and calculate the matrices as shown in Figure 6c–f.
• Hence, for A → E travel in the considered case study, finally, the shortest path and cost calculated through this conventional Floyd-Warshall algorithm are obtained as A → C → D → E and 6, respectively.

Algorithm 2 Conventional Floyd-Warshall Algorithm.

Input: Graphical depiction of the network with indications of source and destination nodes. Step 1. Assign the cost of source-node as ‘0’, directly connected nodes with their cost, and all other nodes (indirectly connected nodes) as ‘∞’. Step 2. Create a matrix (M0) with nodes vs. nodes (as rows vs. columns), which are mapped with the costs assigned in Step 1. Step 3. Consider the first intermediate node(a) and check for the shortest paths for all other nodes via node(a). The first intermediate node refers to the first node in the graph. Using this analysis, form a new matrix (Ma), whose values (Ma [i, j]) are calculated by using Equation (1). Here, all the costs in the ath row and ath column remain unchanged. Step 4. Repeat Step 3 for all the other nodes by selecting each of the nodes as the intermediate node, one at a time, sequentially. Step 5. The sequentially improved final matrix (M∞) obtained in Step 4 represents the least cost possible path (shortest path) between any two nodes. Output: Optimal path recommendation.

$${\mathrm{M}}^{\mathrm{a}}[\mathrm{i}, \mathrm{j}]=\mathrm{Minimum}\left\{\left({\mathrm{M}}^{\mathrm{a}-1}[\mathrm{i}, \mathrm{j}]\right), \left({\mathrm{M}}^{\mathrm{a}-1}{[\mathrm{i},\mathrm{a}]+\mathrm{M}}^{\mathrm{a}-1}[\mathrm{a}, \mathrm{j}]\right)\right\}$$

(1)

3.2. Proposed Enhanced Dijkstra Algorithm

From Figure 5 and Figure 6, it is observed that both the key state-of-the-art algorithms lead to the same solution for finding the optimal path (A → C → D → E) between the considered two nodes (A and E). However, if there is any link failure in this shortest path (for example, assume D → E link failure), then the conventional Dijkstra algorithm stops working and finds no communication establishment between node A and node E, as shown in Figure 7a. Therefore, these algorithms work only when there is continuous communication between nodes (i.e., no link failure exists in the path connected between the two nodes in the network). This is a typical scenario of exhibiting link failures in communication networks, where the conventional path finding algorithms fail, and requires the invention of new algorithms to achieve this objective.

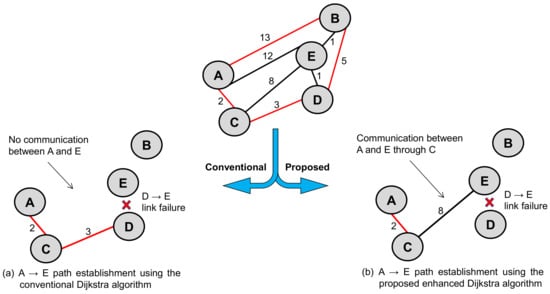
Figure 7. Resultant paths during link failures in both conventional and proposed algorithms.

To address the abovementioned problem with conventional algorithms, this section proposes a new algorithm, which is inspired by the conventional Dijkstra algorithm, namely, the “enhanced Dijkstra algorithm”.

In the case of the proposed enhanced Dijkstra algorithm (Algorithm 3), when any link failures are found in the communication path, the algorithm searches for a new shortest path and establishes communication between desired nodes. This is the unique feature of the proposed algorithm. Therefore, as shown in Figure 7b, when there is D → E link failure, the algorithm continues the search and finds the next best shortest path (i.e., next least cost possible path), i.e., path A → C → E with a cost of 10. This is how the proposed enhanced Dijkstra algorithm addresses the link failure issues, which shows superior performance over conventional algorithms.

Algorithm 3 Proposed enhanced Dijkstra algorithm

Input: Graphical depiction of the network with indications of source and destination nodes. Step 1. Define the number of nodes (N) in the graph. for i = 1 to N, connect the links by assigning the cost from each node to all other directly connected nodes. Step 2. Assign the cost of source-node as ‘0’, directly connected nodes with their cost, and all other nodes (indirectly connected nodes) as ‘∞’. Further, assign the source node as the node of observation. Step 3. Identify the link failures and update the graph with only available links. Step 4. Now using this new graph, identify the directly connected nodes (v) from the source node (u) and perform the following on the graph.  If cost (v) > cost (u) + cost (u → v)  then update cost (v) = cost (u) + cost (u → v)  else    retain the same cost. Step 5. Mark ‘u’ as visited and the visited node should not be rechecked while performing Step 4. Step 6. Select the minimum cost neighbor while performing Step 4 and repeat this step until all the nodes are marked as visited. This finally indicates the least cost possible path (shortest path) from the source node. Output: Optimal path recommendation.

The implementation of the proposed enhanced Dijkstra algorithm for the considered case study is given as follows:

• Defining the graph ‘G’ as given in Equation (2). For A → E travel in the case study shown in Figure 4,

  -

  assign the value of the number of nodes (‘N’) as 5.

  -

  cost assignment as A → B:13, A → C:2, A → E:12, B → A:13, B → E:1, B → D:5, C → A:2, C → E:8, C → D:3, D → C:3, D → B:5, D → E:1, E → A:12, E → C:8, E → B:1, E → D:1.

$$\left.\begin{array}{l}\mathrm{G}=\{\\ ‘\mathrm{A}’:\text{{}‘\mathrm{B}’:13,‘\mathrm{C}’:2,‘\mathrm{E}’:12\}, ‘\mathrm{B}’:\left\{‘\mathrm{A}’:13,‘\mathrm{E}’:1,‘\mathrm{D}’:5\right\}, \\ ‘\mathrm{C}’:\left\{‘\mathrm{A}’:2,‘\mathrm{E}’:8,‘\mathrm{D}’:3\right\}, ‘\mathrm{D}’:\left\{‘\mathrm{C}’:3,‘\mathrm{B}’:5,‘\mathrm{E}’:1\right\}, \\ ‘\mathrm{E}’:\left\{‘\mathrm{A}’:12,‘\mathrm{C}’:8,‘\mathrm{B}’:1,‘\mathrm{D}’:1\right\}\\ \} \end{array}\right\}$$

(2)

• Identify the link failures and update the graph G1 as given in Equation (3).

  -

  define the graph with costs A → B:13, A → C:2, A → E:12, B → A:13, B → E:1, B → D:5, C → A:2, C → E:8, C → D:3, D → C:3, D → B:5, E → A:12, E → C:8, E → B:1.

$$\left.\begin{array}{l}\mathrm{G}1=\{\\ ‘\mathrm{A}’:\text{{}‘\mathrm{B}’:13,‘\mathrm{C}’:2,‘\mathrm{E}’:12\}, ‘\mathrm{B}’:\left\{‘\mathrm{A}’:13,‘\mathrm{E}’:1,‘\mathrm{D}’:5\right\},\\ ‘\mathrm{C}’:\left\{‘\mathrm{A}’:2,‘\mathrm{E}’:8,‘\mathrm{D}’:3\right\}, ‘\mathrm{D}’:\left\{‘\mathrm{C}’:3,‘\mathrm{B}’:5\right\},\\ ‘\mathrm{E}’:\left\{‘\mathrm{A}’:12,‘\mathrm{C}’:8,‘\mathrm{B}’:1\right\}\\ \} \end{array}\right\}$$

(3)

• Define the source node ‘A’. Here, node ‘C’ (with costs of 2) is identified as the directly connected shortest node from the source node ‘A’.

If cost (C) > cost (A) + cost (A → C)
⇒ If 2 > 0 + 2, which is false.
So, retain the same cost.

• This process continues by shifting the source node to the next shortest direct node, until all nodes are traced, or, until reaching the destination node.
• Finally, joining all these direct shortest paths will produce the shortest path between the source node ‘A’ and the destination node ‘E’.
• From Figure 7b, the shortest path and cost calculated through this enhanced Dijkstra algorithm are A → C → E and 10 respectively.

Hence, for A → E travel in the case study shown in Figure 4, when a link D → E failure is considered, the shortest path and cost calculated through this proposed enhanced Dijkstra algorithm are obtained as A → C → E and 10, respectively.

In each of the steps, the shortest path is calculated as shown in Table 4, and the visited node is marked. This continues until all the nodes are marked. Various possible paths that are found are traced, as shown in Figure 8, from which it can be noted that for the considered case, path A → C → E, with a cost of 10, is the shortest among all other possible paths.

Table 4. Computations of the proposed enhanced Dijkstra algorithm.

Nodes	A	B	C	D	E
A	0	13(A)	2(A)	∞	12(A)
C		13(A)	2(A)	5(C)	10(C)
D		10(D)		5(C)	10(C)
B		10(D)			10(C)
E					10(C)

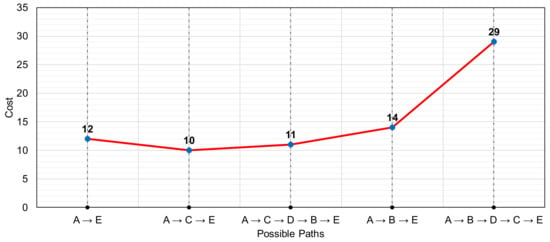
Figure 8. The cost involved in all possible paths between node A and node E during D → E failure.

4. Results and Discussion

To prove the importance of the proposed enhanced Dijkstra algorithm over the conventional Dijkstra algorithm, graphs of single-path topology, double-path topology, and the proposed multipath topology, are considered, as shown in Figure 9, with their link costs indicated. Three test scenarios were implemented on these graphs, namely, the no-link failure scenario, single-link failure scenario, and multiple-link failure scenario. All of these are explained, with results as given in Section 4.1, Section 4.2 and Section 4.3, respectively. The system configuration used for the simulation is given in Appendix A.

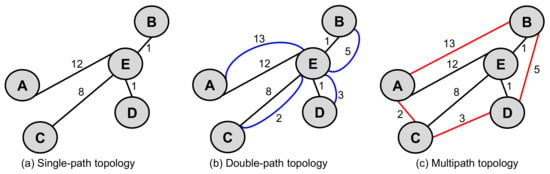
Figure 9. Various topologies for representing the cluster microgrids.

4.1. Results of No-Link Failure Scenario

In this case study, various paths available in the network to reach from A to E in single-path topology, double-path topology, and multipath topology, are shown in Figure 10. There is only one possible path in the single-path topology, with a cost of 12, as shown in Figure 10a.

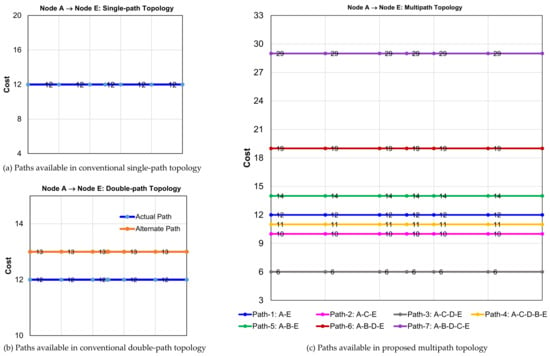
Figure 10. Node A to node E paths available in single-path, double-path, and multipath topologies, when there is no link failure in the network.

In the double-path topology, two possible paths exist, one with cost 12 (actual path) and the other with cost 13 (alternate path), as shown in Figure 10b. Out of these two paths, the path with a cost of 12 is selected for communication establishment, as it is the least cost path. On the other hand, in the case of multipath topology, seven possible paths exist to reach from node A to node E, which are: A → E:12; A → C → E:10; A → C → D → E:6; A → C → D → B → E:11; A → B → E:14; A → B → D → E:19; and A → B → D → C → E:29, as shown in Figure 10c. Out of these seven possible paths, the path with a cost of 6 (A → C → D → E) is selected for communication between A and E, as it is the least cost path.

From the above discussion, the proposed topology enhances the reliability of the network by providing the highest number of possible paths (=7), compared to single-path topology (=1), and double-path topology (=2). In addition, the proposed topology with an enhanced Dijkstra algorithm ensures the least cost path (with a cost of 6), when compared to the single-path/double-path topologies (both with a cost of 12).

4.2. Results of Single-Link Failure Scenario

To understand link failure in the network, a single-link (link A → E) failure is simulated. During a normal scenario, as there is only one possible path in the single-path topology to reach from A to E, with the cost of 12, this path collapses for the link failure, as shown in Figure 11a. There will not be any further communication between node A and node E once the link failure is observed. In double-path topology, as two possible paths exist, up to the instant of a link failure the communication between node A and node E takes place through the actual shortest path (i.e., the path with cost 12). Once this link fails, then communication is carried through the alternate path that is available in the network (whose cost is 13), as shown in Figure 11b. On the other hand, in the case of multipath topology, even though the direct link A → E failed, communication between node A and node E is continued through the path A → C → D → E (with a cost of 6), which is the same as when there is no link failure. As shown in Figure 11c, A → C → D → E is the lowest cost path retained by the network, with or without single-link failure execution. This clearly shows that there is no effect from a single-link failure on the multipath topology.

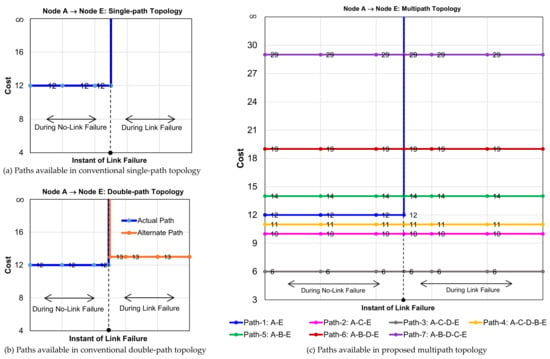
Figure 11. Node A to node E paths available in single-path, double-path, and multipath topologies, when there is a single-link failure in the network.

Thus, it is concluded that multipath topology can tolerate single-link failure cases, thereby providing robust communication in the network.

4.3. Results of Multiple-Link Failure Scenario

Multiple links (two or more) failures cannot be established in single-path topology as there is only one path available from A to E. Similarly, in the case of double-path topology, as the maximum links available between A and E are only two, the failure of these two links completely collapses communication between those two nodes. Hence, single-path and double-path topologies cannot handle multi-link failure cases. However, in multipath topology, as seven paths are possible between source node (A) and destination node (E), it can tolerate two-link failure cases effectively. The proposed enhanced Dijkstra algorithm continuously iterates the search process during link failures and finds the optimum communication path. For the simulation, all such possible pairs of link failures are executed and, in each case, the possible paths for A → E communication are identified. Out of all of these possible combinations, the optimum cost path is finalized for communication between A and E nodes, as shown in Table 5.

Table 5. Possible paths and optimum paths available between A → E during two-link failures.

S. No	Links Failed	A → E Paths Available (Cost)	A → E Optimum Path (Cost)
1	(A → B), (A → C)	A → E (12)	A → E (12)
2	(A → B), (A → E)	A → C → E (10), A → C → D → E (6), A → C → D → B → E (11)	A → C → D → E (6)
3	(A → B), (B → D)	A → E (12), A → C → E (10), A → C → D → E (6)	A → C → D → E (6)
4	(A → B), (B → E)	A → E (12), A → C → E (10), A → C → D → E (6)	A →C→D→E (6)
5	(A → B), (C → D)	A → E (12), A → C → E (10)	A → C → E (10)
6	(A → B), (C → E)	A → E (12), A → C → D → E (6), A → C → D → B → E (11)	A → C → D → E (6)
7	(A → B), (D → E)	A → E (12), A → C → E (10), A → C → D → B → E (11)	A → C → E (10)
8	(A → C), (A → E)	A → B → E (14), A → B → D → E (19), A → B → D → C → E (29)	A → B → E (14)
9	(A → C), (B → D)	A → E (12), A → B → E (14)	A → E (12)
10	(A → C), (B → E)	A → E (12), A → B→ D → E (19), A → B → D → C → E (29)	A → E (12)
11	(A → C), (C → D)	A → E (12), A → B → E (14), A → B → D → E (19)	A → E (12)
12	(A → C), (C → E)	A → E (12), A → B → E (14), A → B → D → E (19)	A → E (12)
13	(A → C), (D → E)	A → E (12), A → B → E (14), A → B → D → C → E (29)	A → E (12)
14	(A → E), (B → D)	A → C → E (10), A → C → D → E (6), A → B → E (14)	A → C → D → E (6)
15	(A → E), (B → E)	A → C → E (10), A → C → D → E (6), A → B → D → E (19), A → B → D → C → E (29)	A → C → D → E (6)
16	(A → E), (C → D)	A → C → E (10), A → B → E (14), A → B → D → E (19)	A → C → E (10)
17	(A → E), (C → E)	A → C → D → E (6), A → C → D → B → E (11), A → B → E (14), A → B → D → E (19)	A → C → D → E (6)
18	(A → E), (D → E)	A → C → E (10), A → C → D → B → E (11), A → B → E (14), A → B → D → C → E (29)	A → C → E (10)
19	(B → D), (B → E)	A → E (12), A → C → E (10), A → C → D → E (6)	A → C → D → E (6)
20	(B → D), (C → D)	A → E (12), A → C → E (10), A → B → E (14)	A → C → E (10)
21	(B → D), (C → E)	A → E (12), A → C → D → E (6), A → B → E (14)	A → C → D → E (6)
22	(B → D), (D → E)	A → E (12), A → C → E (10), A → B → E (14)	A → C → E (10)
23	(B → E), (C → D)	A → E (12), A → C → E (10), A → B → D → E (19)	A → C → E (10)
24	(B → E), (C → E)	A → E (12), A → C → D → E (6), A → B → D → E (19)	A → C → D → E (6)
25	(B → E), (D → E)	A → E (12), A → C → E (10), A → B → D → C → E (29)	A → C → E (10)
26	(C → D), (C → E)	A → E (12), A → B → E (14), A → B → D → E (19)	A → E (12)
27	(C → D), (D → E)	A → E (12), A → C → E (10), A → B → E (14)	A → C → E (10)
28	(C → E), (D → E)	A → E (12), A → C → D → B → E (11), A → B → E (14)	A → C → D → B → E (11)

In total, out of the eight links available in multipath topology (refer to Figure 3), 28 combinations of pairs of links can be generated using Equation (4). The resultant network graphs for A to E communication in the proposed topology, subjected to different two-link failures, are shown in Figure 12.

$$\mathrm{Number} \mathrm{of} \mathrm{Link} \mathrm{Pairs}={}^{\mathrm{n}}\mathrm{C}_{\mathrm{r}}=\frac{\mathrm{n}!}{\mathrm{r}!(\mathrm{n}-\mathrm{r})!}$$

(4)

where n is the number of available links and r is the number of failed links in the graph.

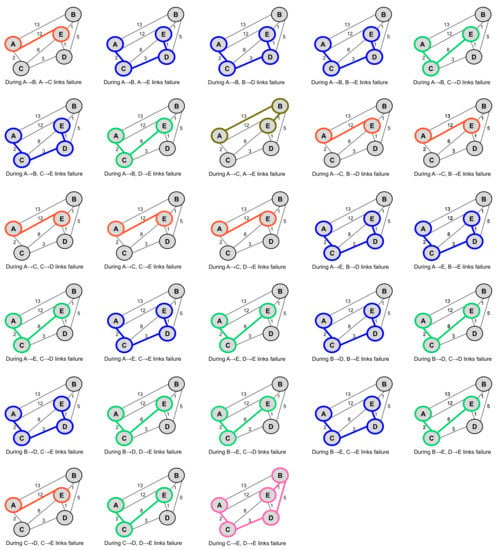
Figure 12. Resultant network graphs with respect to A to E communication in multipath topology, subjected to different two-link failures.

Similarly, the resultant optimum paths available between A and E in multipath topology, before and after the execution of different two-link failures in the network, are shown in Figure 13. From this, it is observed that the proposed enhanced Dijkstra algorithm always ensured the optimum path from the available paths, to reach node E from node A. Once there is a two-link failure initiated, then out of all available paths, the least cost path is identified, through which further communication is carried.

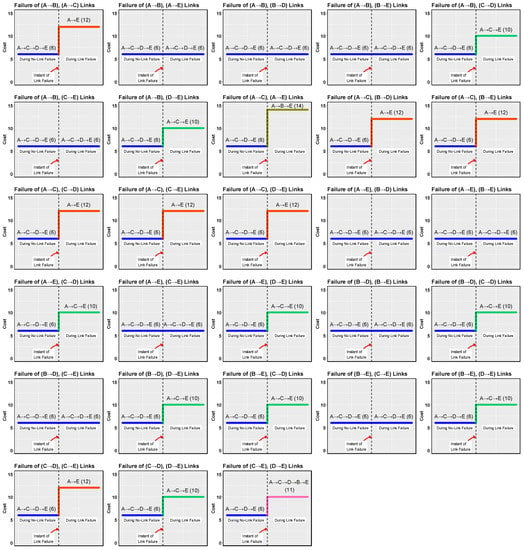
Figure 13. Resultant optimum paths available between A and E in multipath topology, before and after the execution of different two-link failures in the network.

For example, when the links (A → B) and (A → C) failed, the algorithm identifies the one possible path i.e., A → E (with a cost of 12). When the links (A → B) and (A → E) failed, the algorithm identifies the possible paths as A → C → E (with a cost of 10), A → C → D → E (with a cost of 6), and A → C → D → B → E (with the cost of 11). Out of these possible paths, path A → C → D → E is selected as its cost is less than all other possible paths. The same process continues for all other combinations of link failures. At any given point of time, in a two link failure scenario, a minimum of one path and a maximum of four paths are possible.

In Figure 12, all the highlighted paths indicate the shortest distance (optimum path) that is derived by the proposed enhanced Dijkstra algorithm, corresponding to different combinations of two-link failures. In Figure 13, when there is no link failure, the path A → C → D → E (with a cost of 6) is always used for communication between node A and node E. Further, when the two-link failures are injected, corresponding to each such combination, the optimum paths are derived differently. So, the path (A → C → D → E) gets transferred to this newly derived path.

Similarly, the simulation was carried out for 56 combinations of three-link failures (⁸C₃), 70 combinations of four-link failures (⁸C₄), 56 combinations of five-link failures (⁸C₅), 28 combinations of six-link failures, and eight combinations of seven-link failures. From all these simulations, it is found that the proposed multipath topology, with an enhanced Dijkstra algorithm, can tolerate all the link failures (except in only one combination, i.e., failure of A → B, A → C, and A → E all at once, for establishing travel between node A and node E), thereby ensuring reliability and optimum communication in the network.

5. Conclusions

Two important issues faced in the interoperable microgrid communication network, namely reliability and optimum path communication during link failures, are addressed in this paper by proposing a new topology with an enhanced Dijkstra algorithm. The achievements of this paper are summarized as follows.

• From Figure 10, it is observed that the number of paths available in single-path topology is one and double-path topology is two, whereas in the proposed multipath topology, it is seven. From this, it is clear that the proposed topology enhances reliability by providing more communication paths in the network.
• From Figure 11, it is observed that multipath topology resulted in shortest path identification with an optimum cost for communication between the considered source and destination nodes, even when the scenario changed from no-link failure to single-link failure. Whereas, double-path topology failed in retaining the shortest path during this single-link failure scenario.
• From Figure 13, it is observed that multipath topology has effectively provided an optimum communication path even during multiple-link failure cases, whereas double-path topology has completely failed during a two-link failure scenario.

Thus, the combination of the proposed refined network topology and enhanced Dijkstra algorithm, provide an effective solution for the establishment of successful interoperable smart microgrids. The proposed topology and algorithm can be extended to any number of microgrids that enter into the interoperable network.