Indirect Analysis of Concrete Slump Using Different Metaheuristic-Empowered Neural Processors
Abstract
:1. Introduction
2. Data and Modeling Methodology
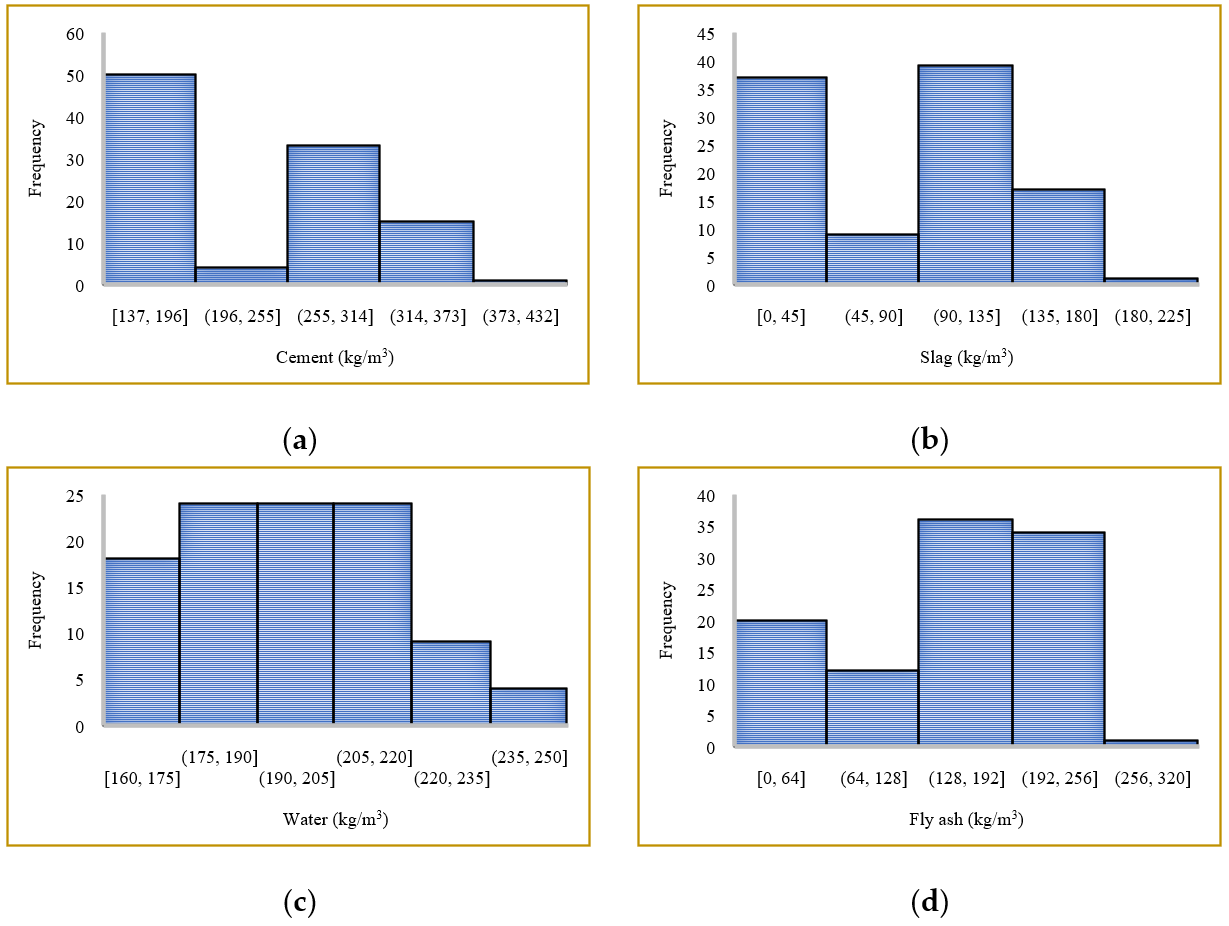
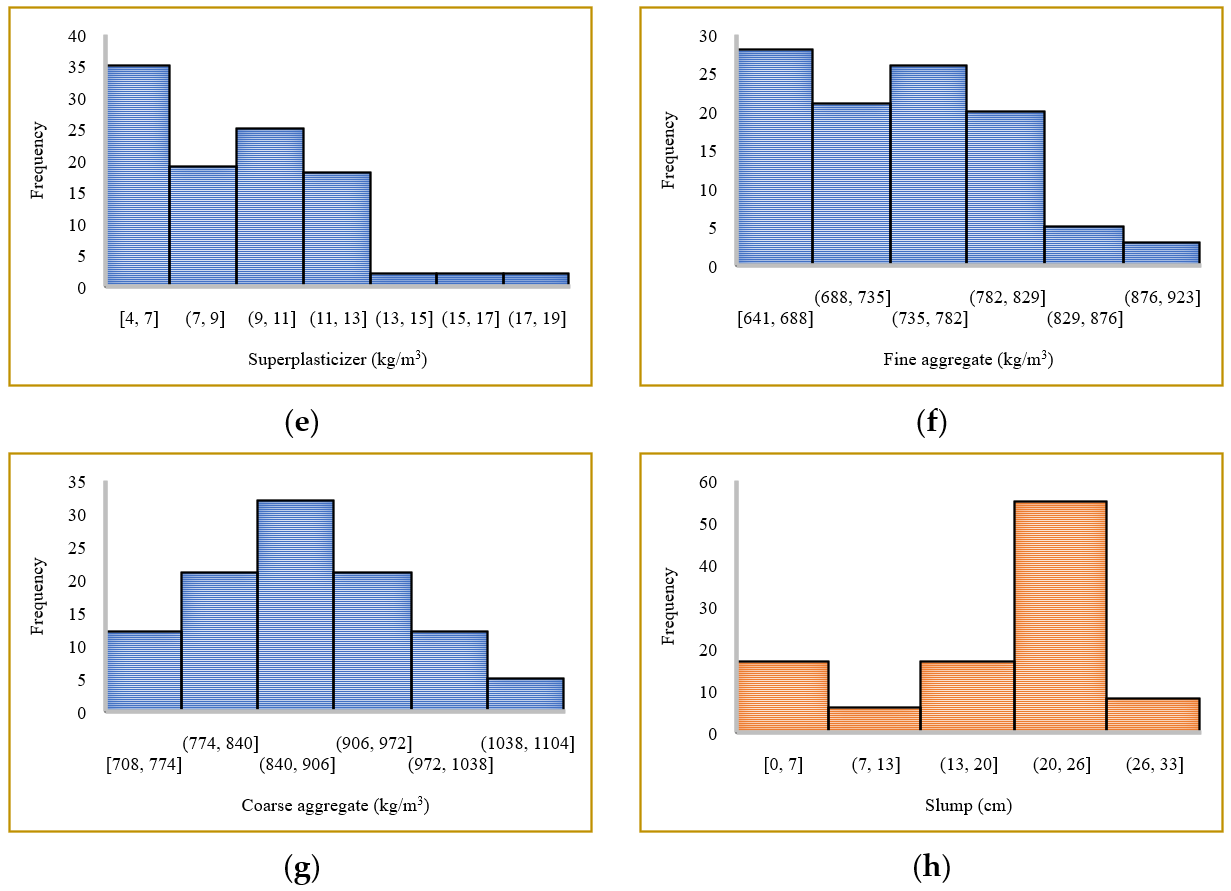
2.1. Data
2.2. Methodology
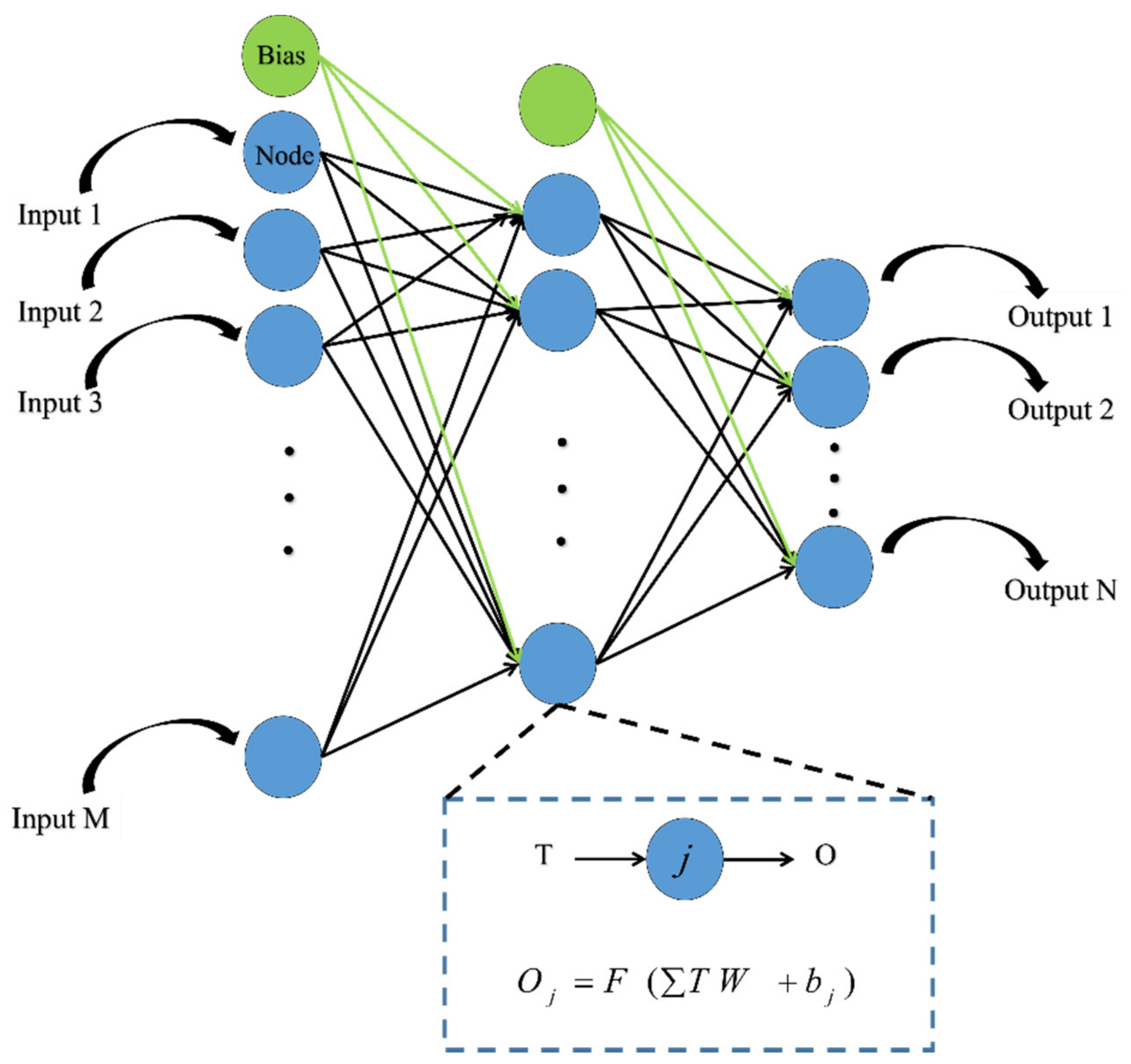
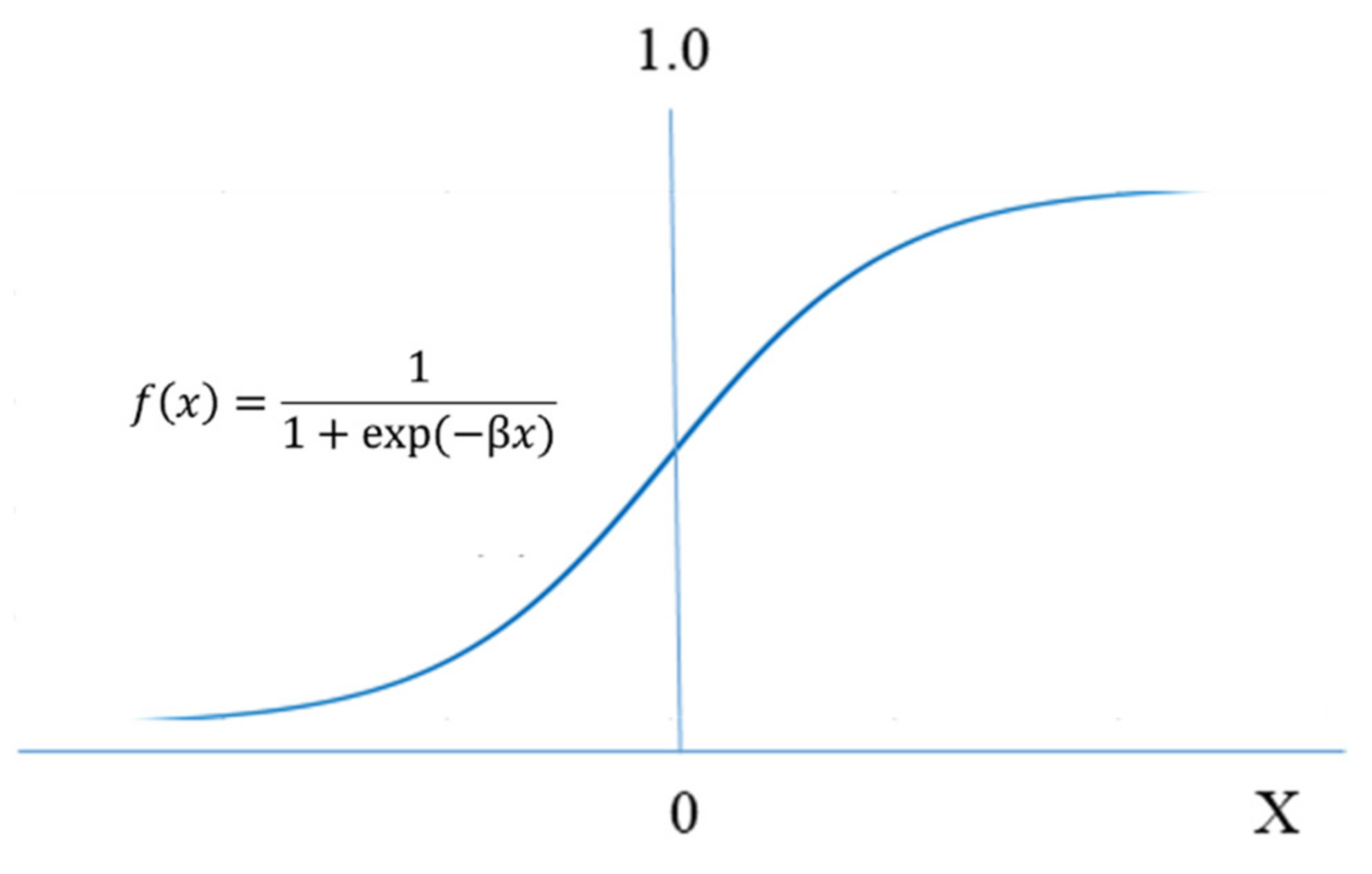
2.2.1. Artificial Neural Network
2.2.2. Metaheuristic Optimizers
2.2.3. Hybridization Process
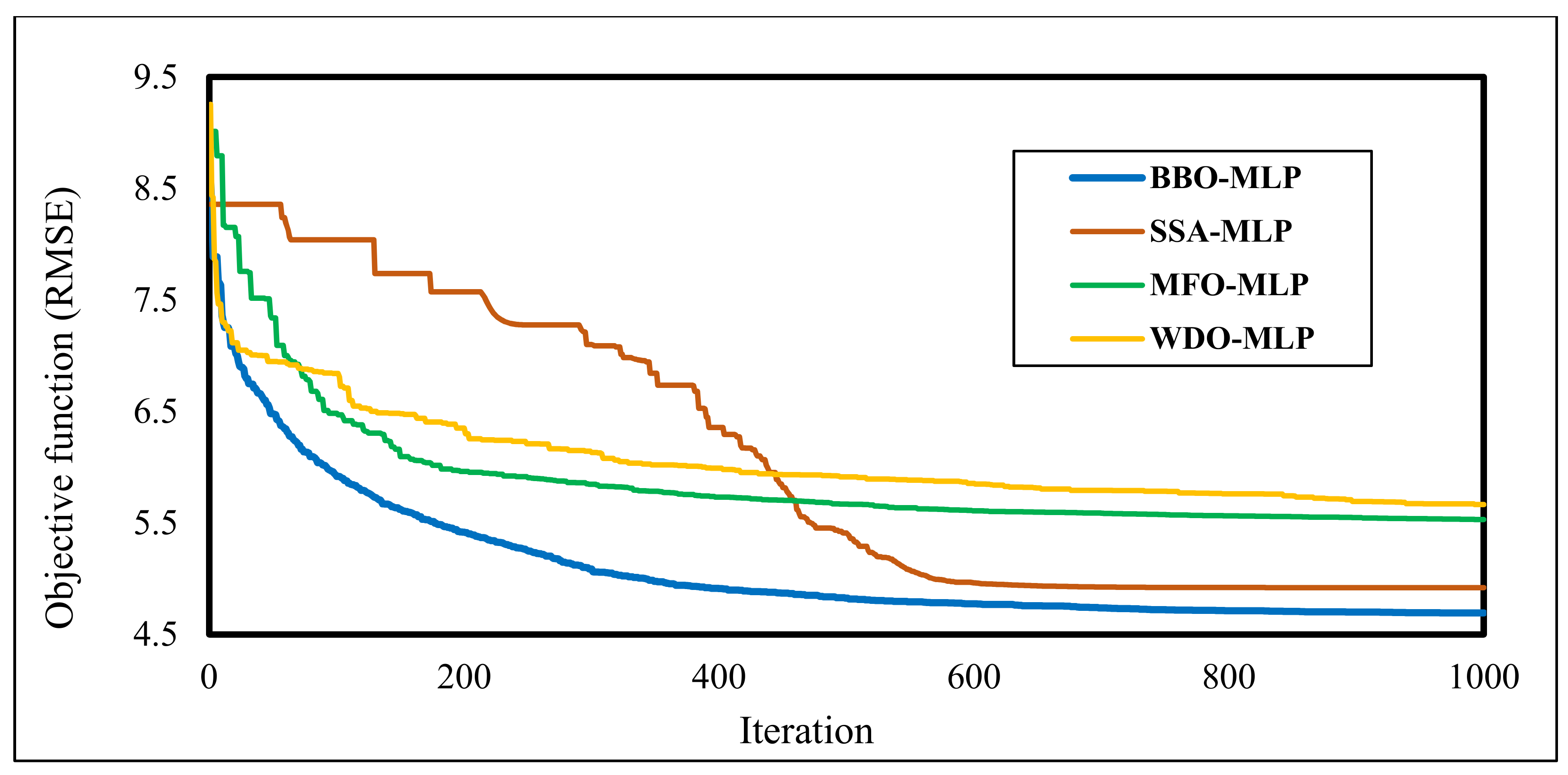
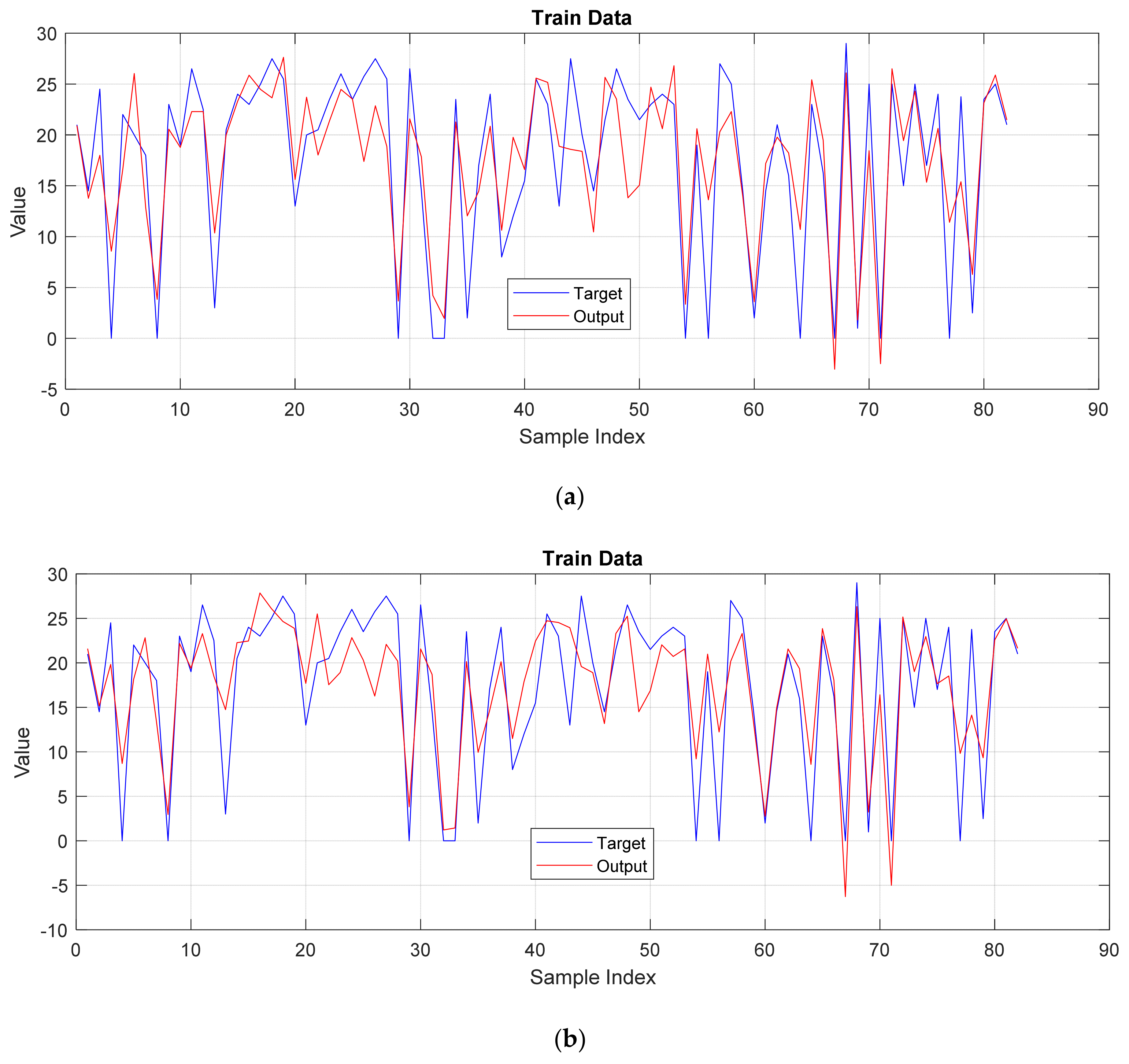
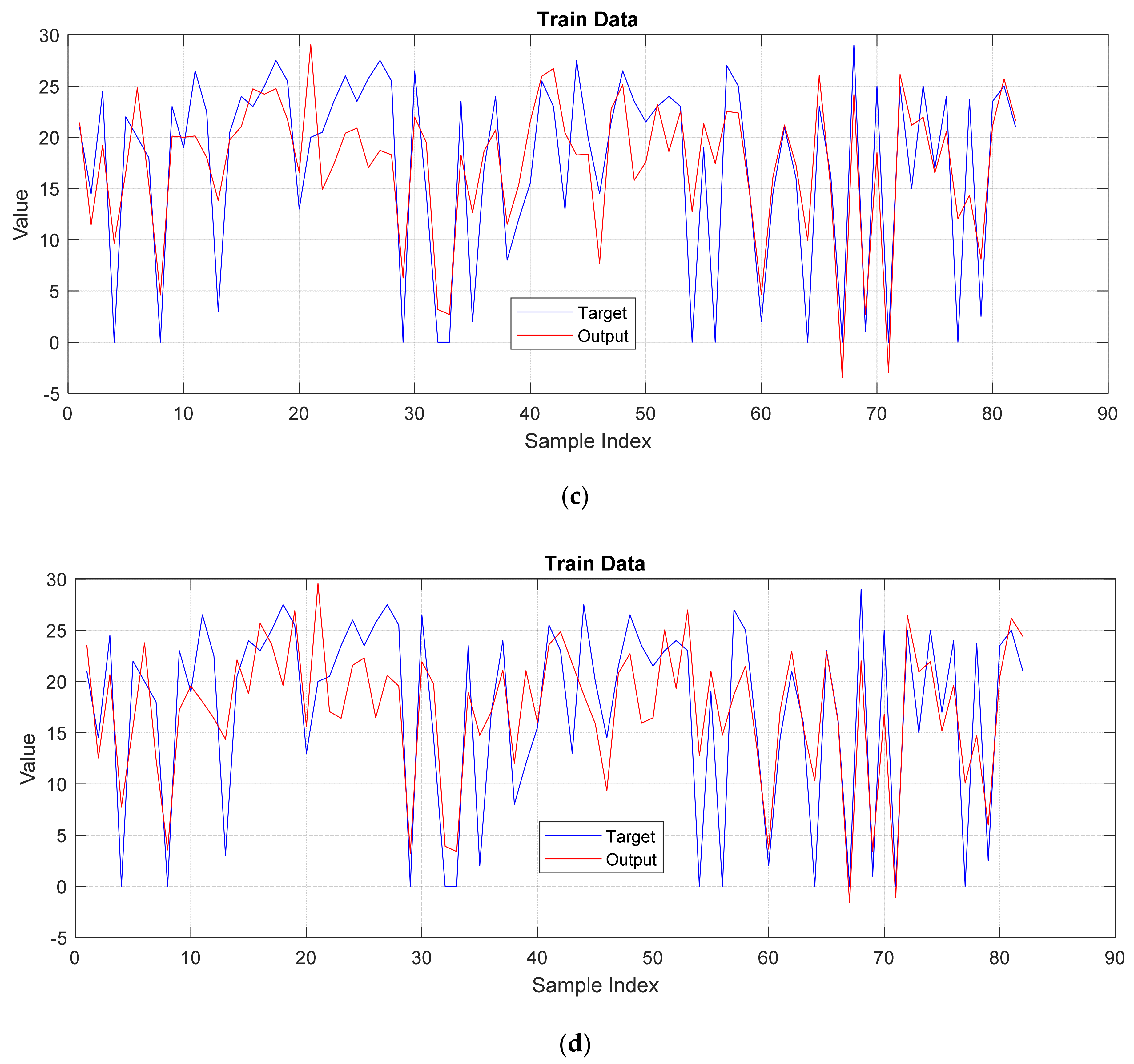
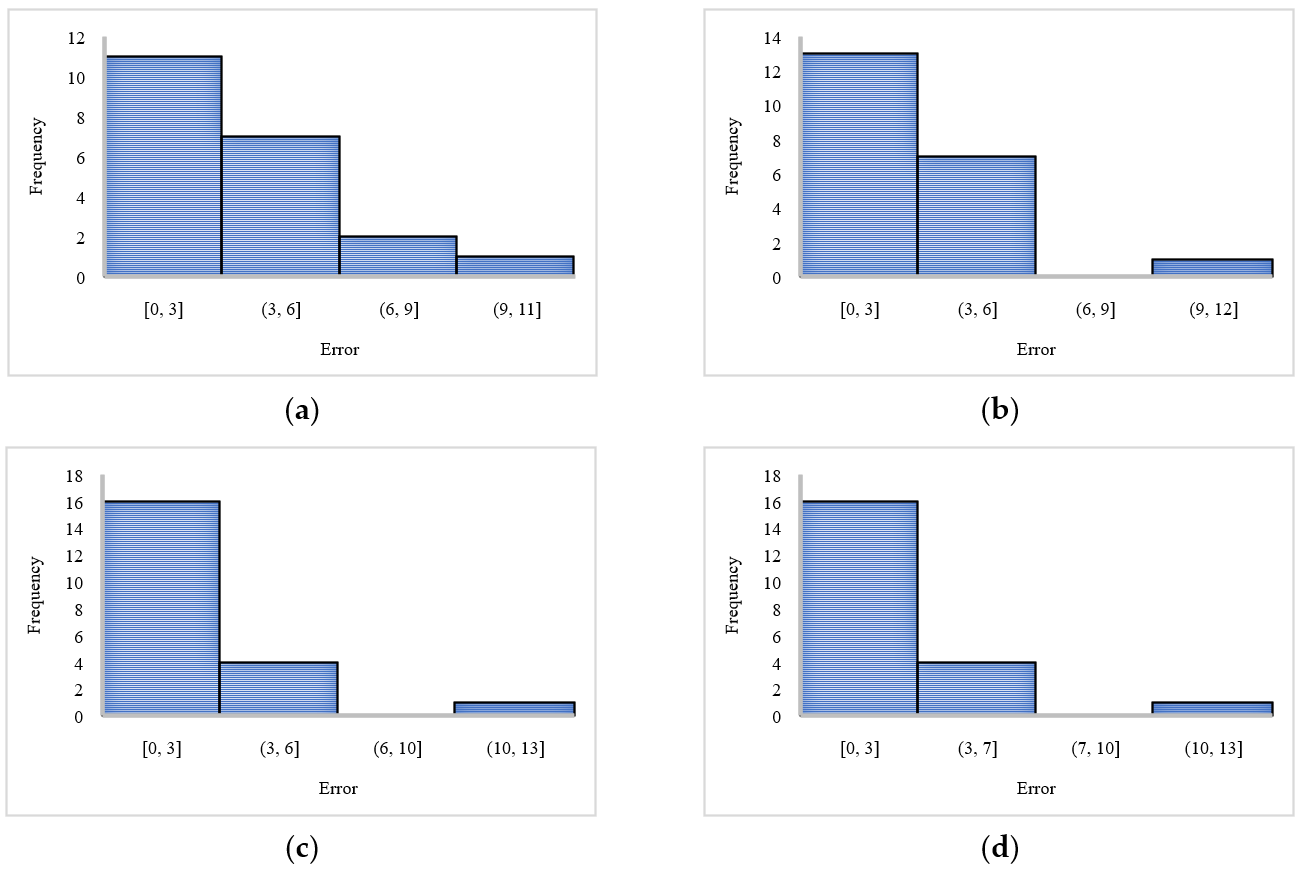
3. Results and Discussion
3.1. Accuracy Criteria
3.2. Performance Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Antiohos, S.; Papadakis, V.; Tsimas, S. Rice husk ash (RHA) effectiveness in cement and concrete as a function of reactive silica and fineness. Cem. Concr. Res. 2014, 61, 20–27. [Google Scholar] [CrossRef]
- Chandwani, V.; Agrawal, V.; Nagar, R. Modeling slump of ready mix concrete using genetic algorithms assisted training of Artificial Neural Networks. Expert Syst. Appl. 2015, 42, 885–893. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel approach for dam break flow modeling using computational intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Zhao, C.; Liao, F.; Li, X.; Du, Y. Macroscopic modeling and dynamic control of on-street cruising-for-parking of autonomous vehicles in a multi-region urban road network. Transp. Res. Part C Emerg. Technol. 2021, 128, 103176. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Cao, R.; Zhang, C. Slope stability analysis considering different contributions of shear strength parameters. Int. J. Geomech. 2021, 21, 04020265. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Y.; Kong, Z.; He, J. Development of Similar Materials for Liquid-Solid Coupling and Its Application in Water Outburst and Mud Outburst Model Test of Deep Tunnel. Geofluids 2022, 2022, 8784398. [Google Scholar] [CrossRef]
- Shan, Y.; Zhao, J.; Tong, H.; Yuan, J.; Lei, D.; Li, Y. Effects of activated carbon on liquefaction resistance of calcareous sand treated with microbially induced calcium carbonate precipitation. Soil Dyn. Earthq. Eng. 2022, 161, 107419. [Google Scholar] [CrossRef]
- Zhou, X.; Bai, Y.; Nardi, D.C.; Wang, Y.; Wang, Y.; Liu, Z.; Picón, R.A.; Flórez-López, J. Damage Evolution Modeling for Steel Structures Subjected to Combined High Cycle Fatigue and High-Intensity Dynamic Loadings. Int. J. Struct. Stab. Dyn. 2022, 22, 2240012. [Google Scholar] [CrossRef]
- Hao, R.-B.; Lu, Z.-Q.; Ding, H.; Chen, L.-Q. A nonlinear vibration isolator supported on a flexible plate: Analysis and experiment. Nonlinear Dyn. 2022, 108, 941–958. [Google Scholar] [CrossRef]
- Shi, L.; Xiao, X.; Wang, X.; Liang, H.; Wang, D. Mesostructural characteristics and evaluation of asphalt mixture contact chain complex networks. Constr. Build. Mater. 2022, 340, 127753. [Google Scholar] [CrossRef]
- Cheng, H.; Sun, L.; Wang, Y.; Chen, X. Effects of actual loading waveforms on the fatigue behaviours of asphalt mixtures. Int. J. Fatigue 2021, 151, 106386. [Google Scholar] [CrossRef]
- Yan, B.; Ma, C.; Zhao, Y.; Hu, N.; Guo, L. Geometrically Enabled Soft Electroactuators via Laser Cutting. Adv. Eng. Mater. 2019, 21, 1900664. [Google Scholar] [CrossRef]
- Yuan, J.; Lei, D.; Shan, Y.; Tong, H.; Fang, X.; Zhao, J. Direct Shear Creep Characteristics of Sand Treated with Microbial-Induced Calcite Precipitation. Int. J. Civ. Eng. 2022, 20, 763–777. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, J.; Chen, H.; Shao, L.; Zhou, X.; Wang, S. Shear strength and mesoscopic characteristics of basalt fiber–reinforced loess after dry–wet cycles. J. Mater. Civ. Eng. 2022, 34, 04022083. [Google Scholar] [CrossRef]
- Xie, S.-J.; Lin, H.; Chen, Y.-F.; Wang, Y.-X. A new nonlinear empirical strength criterion for rocks under conventional triaxial compression. J. Cent. South Univ. 2021, 28, 1448–1458. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Bai, L.; Tang, M.; Chen, H.; Su, D. Fragility analyses of bridge structures using the logarithmic piecewise function-based probabilistic seismic demand model. Sustainability 2021, 13, 7814. [Google Scholar] [CrossRef]
- Zhao, Y.; Joseph, A.J.J.M.; Zhang, Z.; Ma, C.; Gul, D.; Schellenberg, A.; Hu, N. Deterministic snap-through buckling and energy trapping in axially-loaded notched strips for compliant building blocks. Smart Mater. Struct. 2020, 29, 02LT03. [Google Scholar] [CrossRef]
- Huang, S.; Liu, C. A computational framework for fluid–structure interaction with applications on stability evaluation of breakwater under combined tsunami–earthquake activity. Comput.-Aided Civ. Infrastruct. Eng. 2022, 1–28. [Google Scholar] [CrossRef]
- Huang, S.; Huang, M.; Lyu, Y. Seismic performance analysis of a wind turbine with a monopile foundation affected by sea ice based on a simple numerical method. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1113–1133. [Google Scholar] [CrossRef]
- Alam, Z.; Sun, L.; Zhang, C.; Samali, B. Influence of Seismic Orientation on the Statistical Distribution of Nonlinear Seismic Response of the Stiffness-Eccentric Structure. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 387–404. [Google Scholar]
- Bai, Y.; Nardi, D.C.; Zhou, X.; Picon, R.A.; Florez-Lopez, J. A new comprehensive model of damage for flexural subassemblies prone to fatigue. Comput. Struct. 2021, 256, 106639. [Google Scholar] [CrossRef]
- Chen, H.; Liu, M.; Chen, Y.; Li, S.; Miao, Y. Nonlinear Lamb Wave for Structural Incipient Defect Detection with Sequential Probabilistic Ratio Test. Secur. Commun. Netw. 2022, 2022, 9851533. [Google Scholar] [CrossRef]
- Sun, D.; Huo, J.; Chen, H.; Dong, Z.; Ren, R. Experimental study of fretting fatigue in dovetail assembly considering temperature effect based on damage mechanics method. Eng. Fail. Anal. 2022, 131, 105812. [Google Scholar] [CrossRef]
- Lan, Y.; Zheng, B.; Shi, T.; Ma, C.; Liu, Y.; Zhao, Z. Crack resistance properties of carbon nanotube-modified concrete. Mag. Concr. Res. 2022, 1–11. [Google Scholar] [CrossRef]
- Shi, T.; Liu, Y.; Zhang, Y.; Lan, Y.; Zhao, Q.; Zhao, Y.; Wang, H. Calcined attapulgite clay as supplementary cementing material: Thermal treatment, hydration activity and mechanical properties. Int. J. Concr. Struct. Mater. 2022, 16, 10. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, L.; Hu, K.; Li, Y.; Zhou, X.; Wang, S. Influence of wet-dry cycles on uniaxial compression behavior of fissured loess disturbed by vibratory loads. KSCE J. Civ. Eng. 2022, 26, 2139–2152. [Google Scholar] [CrossRef]
- Hu, Z.; Shi, T.; Cen, M.; Wang, J.; Zhao, X.; Zeng, C.; Zhou, Y.; Fan, Y.; Liu, Y.; Zhao, Z. Research progress on lunar and Martian concrete. Constr. Build. Mater. 2022, 343, 128117. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Huang, Y.; Tong, M.-N. Reliability-based analysis of the flexural strength of concrete beams reinforced with hybrid BFRP and steel rebars. Arch. Civ. Mech. Eng. 2022, 22, 171. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Yang, R.; Liu, P. Experimental Analysis of Bearing Capacity of Basalt Fiber Reinforced Concrete Short Columns under Axial Compression. Coatings 2022, 12, 654. [Google Scholar] [CrossRef]
- Wei, J.; Xie, Z.; Zhang, W.; Luo, X.; Yang, Y.; Chen, B. Experimental study on circular steel tube-confined reinforced UHPC columns under axial loading. Eng. Struct. 2021, 230, 111599. [Google Scholar] [CrossRef]
- Huang, H.; Guo, M.; Zhang, W.; Huang, M. Seismic Behavior of Strengthened RC Columns under Combined Loadings. J. Bridge Eng. 2022, 27, 05022005. [Google Scholar] [CrossRef]
- Huang, H.; Huang, M.; Zhang, W.; Pospisil, S.; Wu, T. Experimental investigation on rehabilitation of corroded RC columns with BSP and HPFL under combined loadings. J. Struct. Eng. 2020, 146, 04020157. [Google Scholar] [CrossRef]
- Chen, H.; Li, S. Collinear Nonlinear Mixed-Frequency Ultrasound with FEM and Experimental Method for Structural Health Prognosis. Processes 2022, 10, 656. [Google Scholar] [CrossRef]
- Du, Y.; Qin, B.; Zhao, C.; Zhu, Y.; Cao, J.; Ji, Y. A novel spatio-temporal synchronization method of roadside asynchronous MMW radar-camera for sensor fusion. IEEE Trans. Intell. Transp. Syst. 2021, 1–12. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yang, M.; Geng, G. Toward concurrent video multicast orchestration for caching-assisted mobile networks. IEEE Trans. Veh. Technol. 2021, 70, 13205–13220. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Z.; Chen, H.; Shao, L.; Zhou, X.; Wang, S. Study on strength behavior of basalt fiber-reinforced loess by digital image technology (DIT) and scanning electron microscope (SEM). Arab. J. Sci. Eng. 2021, 46, 11319–11338. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z. Subset simulation with adaptable intermediate failure probability for robust reliability analysis: An unsupervised learning-based approach. Struct. Multidiscip. Optim. 2022, 65, 172. [Google Scholar] [CrossRef]
- Li, Y.; Che, P.; Liu, C.; Wu, D.; Du, Y. Cross-scene pavement distress detection by a novel transfer learning framework. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 1398–1415. [Google Scholar] [CrossRef]
- Liu, C.; Wu, D.; Li, Y.; Du, Y. Large-scale pavement roughness measurements with vehicle crowdsourced data using semi-supervised learning. Transp. Res. Part C Emerg. Technol. 2021, 125, 103048. [Google Scholar] [CrossRef]
- Liu, K.; Ke, F.; Huang, X.; Yu, R.; Lin, F.; Wu, Y.; Ng, D.W.K. DeepBAN: A temporal convolution-based communication framework for dynamic WBANs. IEEE Trans. Commun. 2021, 69, 6675–6690. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Z.; Liu, X.; Wang, L.; Xia, X. Efficient image segmentation based on deep learning for mineral image classification. Adv. Powder Technol. 2021, 32, 3885–3903. [Google Scholar] [CrossRef]
- Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of mechanical properties of silica fume-based green concrete using machine learning techniques. Polymers 2021, 14, 30. [Google Scholar] [CrossRef] [PubMed]
- Shah, M.I.; Memon, S.A.; Khan Niazi, M.S.; Amin, M.N.; Aslam, F.; Javed, M.F. Machine learning-based modeling with optimization algorithm for predicting mechanical properties of sustainable concrete. Adv. Civ. Eng. 2021, 2021, 6682283. [Google Scholar] [CrossRef]
- Kumar, A.; Arora, H.C.; Kapoor, N.R.; Mohammed, M.A.; Kumar, K.; Majumdar, A.; Thinnukool, O. Compressive strength prediction of lightweight concrete: Machine learning models. Sustainability 2022, 14, 2404. [Google Scholar] [CrossRef]
- Salami, B.A.; Olayiwola, T.; Oyehan, T.A.; Raji, I.A. Data-driven model for ternary-blend concrete compressive strength prediction using machine learning approach. Constr. Build. Mater. 2021, 301, 124152. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Song, C.; Wang, Z. Predicting compressive strength of manufactured-sand concrete using conventional and metaheuristic-tuned artificial neural network. Measurement 2022, 194, 110993. [Google Scholar] [CrossRef]
- Jiang, G.; Keller, J.; Bond, P.L.; Yuan, Z. Predicting concrete corrosion of sewers using artificial neural network. Water Res. 2016, 92, 52–60. [Google Scholar] [CrossRef] [Green Version]
- Parichatprecha, R.; Nimityongskul, P. Analysis of durability of high performance concrete using artificial neural networks. Constr. Build. Mater. 2009, 23, 910–917. [Google Scholar] [CrossRef]
- Demir, F. Prediction of elastic modulus of normal and high strength concrete by artificial neural networks. Constr. Build. Mater. 2008, 22, 1428–1435. [Google Scholar] [CrossRef]
- Bilgil, A. Estimation of slump value and Bingham parameters of fresh concrete mixture composition with artificial neural network modelling. Sci. Res. Essays 2011, 6, 1753–1765. [Google Scholar]
- Zhang, X.; Akber, M.Z.; Zheng, W. Predicting the slump of industrially produced concrete using machine learning: A multiclass classification approach. J. Build. Eng. 2022, 58, 104997. [Google Scholar] [CrossRef]
- Gomaa, E.; Han, T.; ElGawady, M.; Huang, J.; Kumar, A. Machine learning to predict properties of fresh and hardened alkali-activated concrete. Cem. Concr. Compos. 2021, 115, 103863. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.A.; Kanca, E.; Caglar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Jain, A.; Jha, S.K.; Misra, S. Modeling and analysis of concrete slump using artificial neural networks. J. Mater. Civ. Eng. 2008, 20, 628–633. [Google Scholar] [CrossRef]
- Nehdi, M.; Djebbar, Y.; Khan, A. Neural network model for preformed-foam cellular concrete. Mater. J. 2001, 98, 402–409. [Google Scholar]
- Dias, W.; Pooliyadda, S. Neural networks for predicting properties of concretes with admixtures. Constr. Build. Mater. 2001, 15, 371–379. [Google Scholar] [CrossRef]
- Moayedi, H.; Osouli, A.; Tien Bui, D.; Foong, L.K. Spatial Landslide Susceptibility Assessment Based on Novel Neural-Metaheuristic Geographic Information System Based Ensembles. Sensors 2019, 19, 4698. [Google Scholar] [CrossRef] [Green Version]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimisation of retaining walls using hybrid adaptive gravitational search algorithm. Civ. Eng. Environ. Syst. 2014, 31, 229–242. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimization of foundation using global-local gravitational search algorithm. Struct. Eng. Mech. Int. J. 2014, 50, 257–273. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A. Optimization and coordination of damping controls for optimal oscillations damping in multi-machine power system. Int. Rev. Electr. Eng. (IREE) 2011, 6, 1984–1993. [Google Scholar]
- Khajehzadeh, M.; Keawsawasvong, S.; Sarir, P.; Khailany, D.K. Seismic Analysis of Earth Slope Using a Novel Sequential Hybrid Optimization Algorithm. Period. Polytech. Civ. Eng. 2022, 66, 355–366. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, Q.; Yang, Z.; Yu, X.; Jia, B. A novel artificial bee colony algorithm for structural damage detection. Adv. Civ. Eng. 2020, 2020, 3743089. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Moayedi, H.; Bahiraei, M.; Foong, L.K. Employing TLBO and SCE for optimal prediction of the compressive strength of concrete. Smart Struct. Syst. 2020, 26, 753–763. [Google Scholar]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Kalantar, B.; Abdullahi Mu’azu, M.; Rashid, A.S.; Foong, L.K.; Nguyen, H. Novel hybrids of adaptive neuro-fuzzy inference system (ANFIS) with several metaheuristic algorithms for spatial susceptibility assessment of seismic-induced landslide. Geomat. Nat. Hazards Risk 2019, 10, 1879–1911. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Foong, L.K. Predicting Electrical Power Output of Combined Cycle Power Plants Using a Novel Artificial Neural Network Optimized by Electrostatic Discharge Algorithm. Measurement 2022, 198, 111405. [Google Scholar] [CrossRef]
- Bui, D.T.; Ghareh, S.; Moayedi, H.; Nguyen, H. Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete. Eng. Comput. 2019, 37, 701–712. [Google Scholar]
- Bui, D.-K.; Nguyen, T.; Chou, J.-S.; Nguyen-Xuan, H.; Ngo, T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018, 180, 320–333. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhong, X.; Foong, L.K. Predicting the splitting tensile strength of concrete using an equilibrium optimization model. Steel Compos. Struct. Int. J. 2021, 39, 81–93. [Google Scholar]
- Moayedi, H.; Kalantar, B.; Foong, L.K.; Tien Bui, D.; Motevalli, A. Application of three metaheuristic techniques in simulation of concrete slump. Appl. Sci. 2019, 9, 4340. [Google Scholar] [CrossRef] [Green Version]
- Foong, L.K.; Zhao, Y.; Bai, C.; Xu, C. Efficient metaheuristic-retrofitted techniques for concrete slump simulation. Smart Struct. Syst. Int. J. 2021, 27, 745–759. [Google Scholar]
- Xu, J.; Shen, Z.; Ren, Q.; Xie, X.; Yang, Z. Geometric Semantic Genetic Programming Algorithm and Slump Prediction. arXiv 2017, arXiv:1709.06114. [Google Scholar]
- Chen, L.; Kou, C.-H.; Ma, S.-W. Prediction of slump flow of high-performance concrete via parallel hyper-cubic gene-expression programming. Eng. Appl. Artif. Intell. 2014, 34, 66–74. [Google Scholar] [CrossRef]
- Yeh, I.-C. Modeling slump flow of concrete using second-order regressions and artificial neural networks. Cem. Concr. Compos. 2007, 29, 474–480. [Google Scholar] [CrossRef]
- ASTMC 143; American Society for Testing and Materials. Standard Test Method for Slump of Hydraulic Cement Concrete. ASTM International: West Conshohocken, PA, USA, 2005.
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Orr, M.J. Introduction to Radial Basis Function Networks; Technical Report; Center for Cognitive Science; University of Edinburgh: Edinburgh, UK, 1996. [Google Scholar]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Kişi, Ö.; Adamowski, J.; Ramezani-Charmahineh, A. Evaluation of data driven models for river suspended sediment concentration modeling. J. Hydrol. 2016, 535, 457–472. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Keawsawasvong, S.; Mirzaei, H.; Jebeli, M. An Effective Artificial Intelligence Approach for Slope Stability Evaluation. IEEE Access 2022, 10, 5660–5671. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. Effective hybrid soft computing approach for optimum design of shallow foundations. Sustainability 2022, 14, 1847. [Google Scholar] [CrossRef]
- Mehrabi, M.; Moayedi, H. Landslide susceptibility mapping using artificial neural network tuned by metaheuristic algorithms. Environ. Earth Sci. 2021, 80, 804. [Google Scholar] [CrossRef]
- Mehrabi, M. Landslide susceptibility zonation using statistical and machine learning approaches in Northern Lecco, Italy. Nat. Hazards 2021, 111, 901–937. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Al-Shammari, E.T.; Keivani, A.; Shamshirband, S.; Mostafaeipour, A.; Yee, L.; Petković, D.; Ch, S. Prediction of heat load in district heating systems by Support Vector Machine with Firefly searching algorithm. Energy 2016, 95, 266–273. [Google Scholar] [CrossRef]
- Nguyen, H.; Mehrabi, M.; Kalantar, B.; Moayedi, H.; Abdullahi, M.A.M. Potential of hybrid evolutionary approaches for assessment of geo-hazard landslide susceptibility mapping. Geomat. Nat. Hazards Risk 2019, 10, 1667–1693. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an adaptive neuro-fuzzy inference system for spatial prediction of landslide susceptibility using four state-of-the-art metaheuristic techniques. Sensors 2020, 20, 1723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Ala’M, A.-Z.; Mirjalili, S.; Fujita, H. An efficient binary salp swarm algorithm with crossover scheme for feature selection problems. Knowl.-Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A Novel Nature-Inspired Optimization Algorithm and Its Application to Electromagnetics. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar]
- Bhattacharya, A.; Chattopadhyay, P.K. Solving complex economic load dispatch problems using biogeography-based optimization. Expert Syst. Appl. 2010, 37, 3605–3615. [Google Scholar] [CrossRef]
- Roy, P.; Ghoshal, S.; Thakur, S. Biogeography based optimization for multi-constraint optimal power flow with emission and non-smooth cost function. Expert Syst. Appl. 2010, 37, 8221–8228. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Sayed, G.I.; Khoriba, G.; Haggag, M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl. Intell. 2018, 48, 3462–3481. [Google Scholar] [CrossRef]
- Ahmed, S.; Mafarja, M.; Faris, H.; Aljarah, I. Feature Selection Using Salp Swarm Algorithm with Chaos. In Proceedings of the 2nd International Conference on Intelligent Systems, Metaheuristics & Swarm Intelligence, Phuket, Thailand, 24–25 March 2018; ACM: New York, USA, 2018; pp. 65–69. [Google Scholar]
- Abbassi, R.; Abbassi, A.; Heidari, A.A.; Mirjalili, S. An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers. Manag. 2019, 179, 362–372. [Google Scholar] [CrossRef]
- Savsani, V.; Tawhid, M.A. Non-dominated sorting moth flame optimization (NS-MFO) for multi-objective problems. Eng. Appl. Artif. Intell. 2017, 63, 20–32. [Google Scholar] [CrossRef]
- Yamany, W.; Fawzy, M.; Tharwat, A.; Hassanien, A.E. Moth-flame optimization for training multi-layer perceptrons. In Proceedings of the 2015 11th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 29–30 December 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 267–272. [Google Scholar]
- Yıldız, B.S.; Yıldız, A.R. Moth-flame optimization algorithm to determine optimal machining parameters in manufacturing processes. Mater. Test. 2017, 59, 425–429. [Google Scholar] [CrossRef]
- Ranjan, P.; Choubey, A.; Mahto, S.K. A novel approach for optimal design of multilayer wideband microwave absorber using wind driven optimization technique. AEU-Int. J. Electron. Commun. 2018, 83, 81–87. [Google Scholar] [CrossRef]
- Qureshi, T.N.; Javaid, N.; Naz, A.; Ahmad, W.; Imran, M.; Khan, Z.A. A novel meta-heuristic hybrid enhanced differential harmony wind driven (EDHWDO) optimization technique for demand side management in smart grid. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 454–461. [Google Scholar]
- Bao, Z.; Zhou, Y.; Li, L.; Ma, M. A hybrid global optimization algorithm based on wind driven optimization and differential evolution. Math. Probl. Eng. 2015, 2015, 389630. [Google Scholar] [CrossRef] [Green Version]

| Np | BBO-MLP | SSA-MLP | MFO-MLP | WDO-MLP | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | Time (s) | RMSE | Time (s) | RMSE | Time (s) | RMSE | Time (s) | |
| 10 | 5.505577 | 139.4756 | 6.355048 | 144.6717 | 5.8897 | 127.0382 | 6.215144 | 127.2421 |
| 25 | 4.730596 | 347.3891 | 5.748444 | 344.6891 | 5.540889 | 334.6007 | 5.942362 | 324.4255 |
| 50 | 4.974088 | 690.5993 | 5.569974 | 666.6998 | 5.610954 | 673.13 | 6.144947 | 632.0315 |
| 75 | 4.858011 | 1031.498 | 5.522838 | 953.5088 | 5.817214 | 1000.989 | 6.133931 | 986.733 |
| 100 | 4.816898 | 1310.805 | 4.920222 | 1263.715 | 5.530195 | 1255.081 | 5.664862 | 1398.88 |
| 200 | 4.74319 | 3025.854 | 5.10271 | 2532.209 | 5.815933 | 2505.335 | 6.285705 | 3270.84 |
| 300 | 4.692921 | 3870.514 | 5.104293 | 3770.992 | 5.728259 | 4225.847 | 6.166536 | 30,623.5 |
| 400 | 5.043938 | 5170.186 | 5.553021 | 5051.865 | 5.658828 | 5861.167 | 6.11727 | 5550.942 |
| 500 | 5.061255 | 6856.051 | 4.950267 | 7814.967 | 5.676524 | 6622.55 | 6.178576 | 6720.605 |
| Ensemble Models | Network Results | |||||
|---|---|---|---|---|---|---|
| Training Phase | Testing Phase | |||||
| RMSE | MAE | R2 | RMSE | MAE | R2 | |
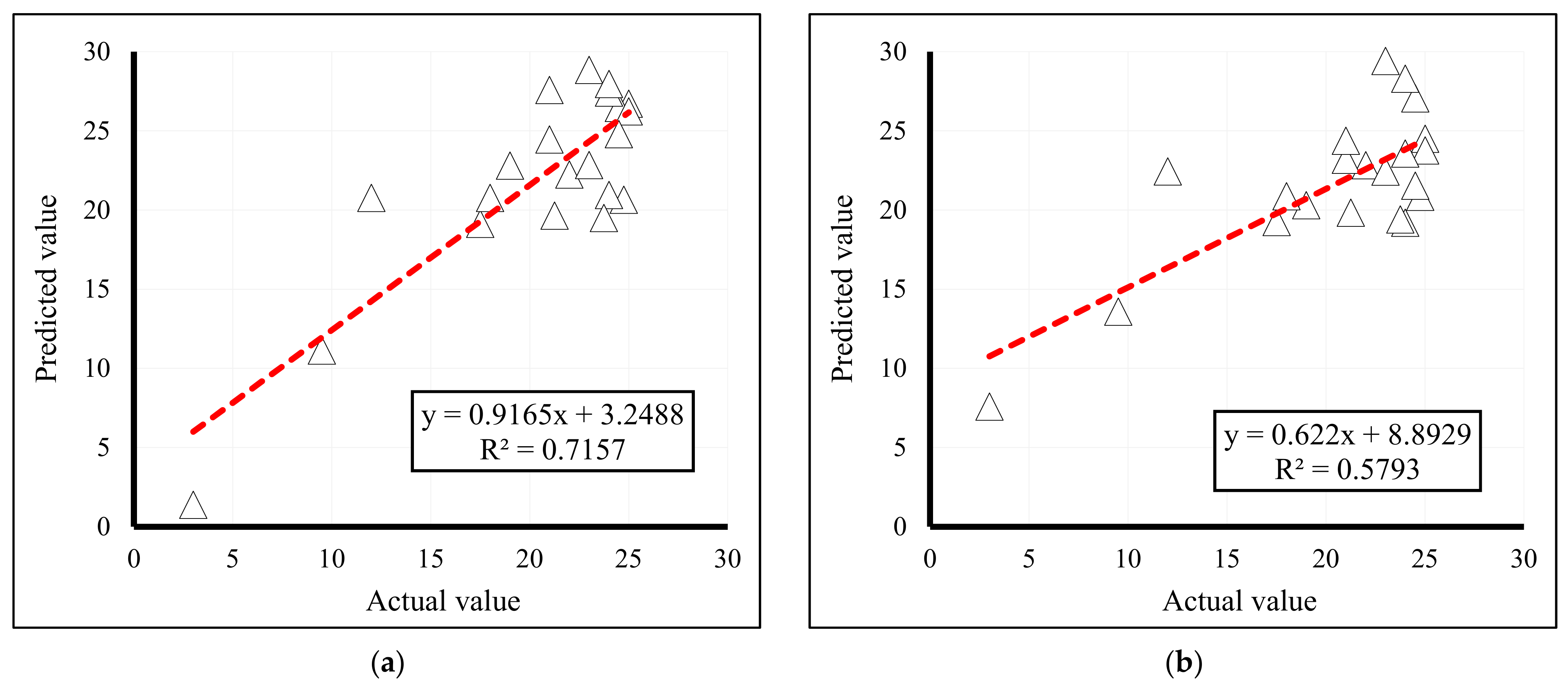
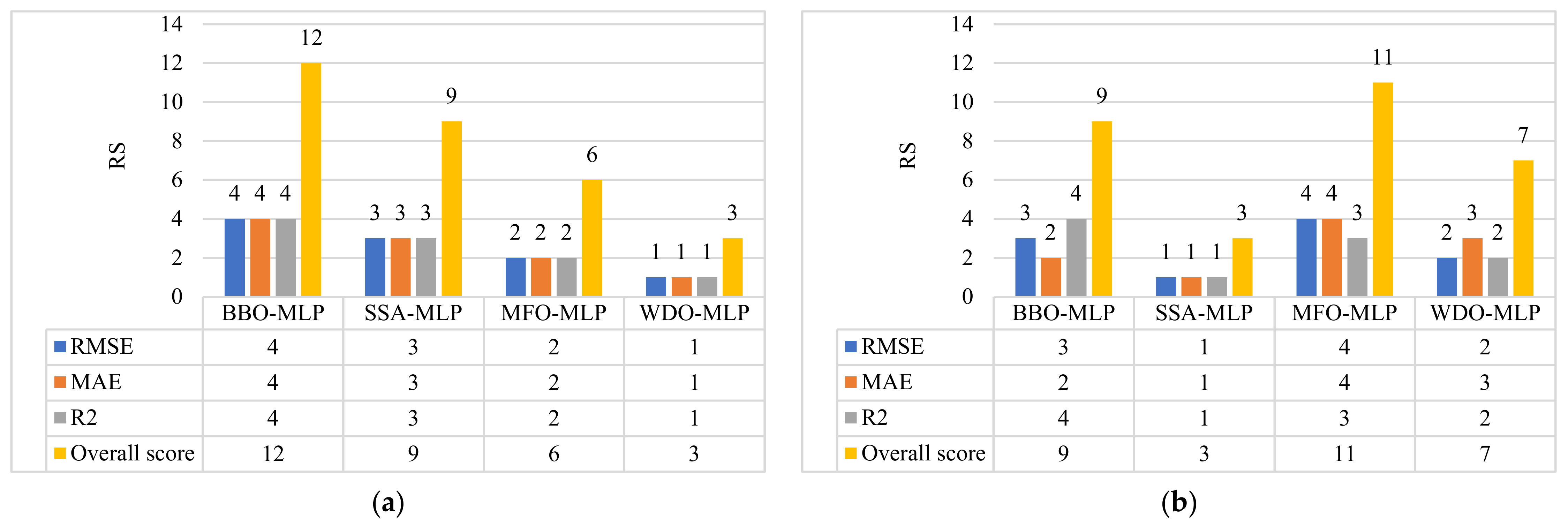
| BBO-MLP | 4.6929 | 3.6729 | 0.7479 | 3.6399 | 2.9521 | 0.7157 |
| SSA-MLP | 4.9202 | 3.8692 | 0.7202 | 3.8572 | 3.0871 | 0.5793 |
| MFO-MLP | 5.5302 | 4.3970 | 0.6472 | 3.3309 | 2.3156 | 0.6748 |
| WDO-MLP | 5.6649 | 4.6087 | 0.6283 | 3.7540 | 2.8368 | 0.6438 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safayenikoo, H.; Nejati, F.; Nehdi, M.L. Indirect Analysis of Concrete Slump Using Different Metaheuristic-Empowered Neural Processors. Sustainability 2022, 14, 10373. https://doi.org/10.3390/su141610373
Safayenikoo H, Nejati F, Nehdi ML. Indirect Analysis of Concrete Slump Using Different Metaheuristic-Empowered Neural Processors. Sustainability. 2022; 14(16):10373. https://doi.org/10.3390/su141610373
Chicago/Turabian StyleSafayenikoo, Hamed, Fatemeh Nejati, and Moncef L. Nehdi. 2022. "Indirect Analysis of Concrete Slump Using Different Metaheuristic-Empowered Neural Processors" Sustainability 14, no. 16: 10373. https://doi.org/10.3390/su141610373
APA StyleSafayenikoo, H., Nejati, F., & Nehdi, M. L. (2022). Indirect Analysis of Concrete Slump Using Different Metaheuristic-Empowered Neural Processors. Sustainability, 14(16), 10373. https://doi.org/10.3390/su141610373







