Abstract
There is an increasing awareness on the major benefits of using soil-geosynthetic composite (SGC) to achieve and maintain the stability of earth-filled embankment. Unlike the mechanically stabilized earth wall, the mechanism of the composite mass is still not fully understood. For examples, current analyses have been limited to an SGC mass with a reinforcement spacing of 0.2 m only; the combined effect of reinforcement and backfill properties is rarely studied; the equation for the estimation of the load-carrying capacity of the SGC mass has only been validated for backfill with maximum particle size between 10 mm and 33 mm and an ratio between 6 and 20. The consequences of backfill compaction on an SGC mass with different reinforcement spacings are yet to be validated and whether the load-carrying capacity equation would still be applicable for materials with properties falling outside the above ranges. Through the simulation and validation of a field scale SGC mass, this study aims to assess the influence of various reinforcement and backfill parameters on the mechanical responses of a large-scale experimental SGC mass under its working load and failure conditions; the results are presented in terms of the wrapped face lateral displacement, reinforcement axial strain, and load-carrying capacity.
1. Introduction
A soil mass with closely spaced (reinforcement spacing ≤ 0.3 m) geosynthetic reinforcement is referred to as GRS, which differs from the conventional mechanically stabilized earth (MSE) walls where the reinforcement is a tensile tieback member in the soil mass; whereas in GRS, the reinforcement is an inclusion to improve the stiffness and strength of soil-geosynthetic composite (SGC). There has been an increasing awareness of the major benefits of using GRS to achieve and maintain stability of earth-filled embankment.
Laboratory large-scale model tests have been carried out and loaded to failure to examine the load-carrying capacity of GRS. Early GRS research has mainly focused on the effect of reinforcement spacing by means of field-scale experiments [1,2,3]. Elton and Parawaran [1] conducted a series of large cylindrical GRS compression tests with nonwoven geotextiles in unconfined condition using different reinforcement spacings and reinforcement strengths to evaluate the load-carrying capacity of reinforced soil. Adam et al. [2] and Pham [3] evaluated the influence of reinforcement spacing and reinforcement strength on the performance of five GRS mini piers and five large-scale soil-geosynthetic composites (SGC) specimens, respectively. Note that field-scale GRS experiment is referred to as the SGC test by Pham [3] and Wu and Pham [4]. These experiments not only showed that the reinforcement spacing plays a more prominent role than the reinforcement strength but also revealed that the behavior of closely spaced reinforced soil can be designated as a nonhomogeneous GRS.
Two-dimensional (2D) finite element (FE) analyses have also been performed by References [3,4,5,6,7,8,9] with the aim to appraise the composite behavior of the GRS mass experimented by Pham [3]. In particular, Pham [3] performed a number of finite element analyses and examined the effect of specimen sizes on the overall stress–strain and volumetric change distributions of the SGC mass with the aim to determine a generic dimension for the SGC mass that would produce a sufficiently close load-deformation behavior of a large GRS mass. Wu et al. [5,6] conducted a number of parametric studies to investigate the effect of reinforcement spacing, reinforcement stiffness, and soil stiffness on the volumetric change behavior and the stresses and deformations of SGC mass. In addition, FE studies have also been carried out to evaluate the composite behavior of the geosynthetic-reinforced soil–integrated bridge system (GRS–IBS) by References [10,11,12,13,14,15]. In particular, Ardah et al. [11] conducted a 2D FE analysis to mimic the performance of the GRS–IBS under different loading conditions, while Abu-Farsakh et al. [10] conducted a series of parametric study and investigated the effect of abutment height, span length, reinforcement spacing, and reinforcement stiffness on the behavior of the GRS–IBS.
On-site construction of a GRS mass generally involves a compaction process that leads to an increase in both the vertical and horizontal stresses in the soil mass. After compaction, the increase in the vertical load is reduced to a very small value or totally removed, but the increase in horizontal stress might only be slightly reduced. Such a net increase in the horizontal stress or the lock-in stress could affect the performance of the reinforcement. References [16,17,18,19,20,21,22,23,24] assessed the compaction effect by modeling the compaction load as a uniformly distributed load applied to the top surface of every newly placed fill as the wall was built from the base to the top, while Mirmoradi and Ehrlich [25,26,27] simulated the effect by applying the uniformly distributed load to the top and bottom surfaces of the fill layer. Gui et al. [8] and Phan et al. [9] conducted a series of numerical analyses on an SGC mass to evaluate the influence of compaction loads, compaction procedures, and surcharge loads on the response of the SGC mass. Gui et al. [8] found that the compaction procedures and the compaction loads of 44 kPa and 70 kPa used throughout the construction of the SGC mass had negligible effect on the reinforcement strain and the lateral displacement of the wrapped-faces of the SGC mass. However, their analyses were limited to the SGC mass with a reinforcement spacing of 0.2 m only; the compaction effect on SGC masses with different reinforcement spacings has yet to be validated. Esen et al. [28] investigated the performance of a GRS retaining wall (GRS-RW) via a comprehensive full-scale laboratory experiment and found that the wall reached its active state during the compaction process, and that the GRS was self-supporting under its own weight and train load, and thus resulted only in an insignificant pressure increment on the wall.
The lateral displacement of the facing and vertical compression of the soil mass are two vital considerations in the serviceability design of GRS bridge abutments while the load-carrying capacity is a crucial consideration for the strength limit condition [14]. For example, Raja and Shukla [29] developed an analytical expression to estimate the ultimate bearing capacity of a strip footing resting on GRS with reinforcement ends being wraparound to provide an additional shearing resistance and passive resistance to the GRS mass. Wu and Pham [30] proposed a semiempirical equation to evaluate the ultimate load-carrying capacity of the GRS mass:
where is the external confining pressure exerted on the SGC mass; c the apparent cohesion of soil; the coefficient of Rankine passive earth pressure; the tensile strength of reinforcement; the vertical spacing of reinforcement; and is the reference reinforcement spacing, which can be approximated empirically as , where is the maximum particle size of the soil. The equation was derived based on an inferred assumption that there was significant interaction between the soil and geosynthetic reinforcement in the soil mass [31]. Equation (1) was validated by at least 15 available field-scale experiments, if which some of them were conducted by the Federal Highway Administration [32], for materials with properties falling in the range of and . It is unclear whether the accuracy of the equation would still be consistent in materials with properties falling outside the above ranges, for example, for the case with the maximum aggregate size of 33 mm and .
Failure modes are also important in determining the load-carrying capacity of GRS mass. The failure or rupture surface of the GRS mass in the field can be difficult to observe but it can be easily observed through the laboratory experiment. For example, Pham [3] dismantled their SGC specimens and removed all the geotextile sheets at the end of their stage loading and discovered that the rupture surface of their SGC mass corresponded to the location of the tensile rupture of the geotextile sheets. The failure mode of geosynthetic-reinforced soil–integrated bridge system (GRS–IBS) has also been examined by, for examples, References [10,11,14,15]. Abu–Farsakh et al. [10] conducted a finite element analysis to investigate the location of the maximum strains in the reinforcement of a GRS–IBS under service loading. Ardah et al. [11] simulated the performance of a fully instrumented GRS–IBS bridge abutment of the Maree Michel Bridge in Louisiana under various loading conditions and found that the active wedge failure analysis, which involved a rupture plane inclined at , was not valid in the case of GRS–IBS abutments for which the failure envelope was found to extend beyond the theoretical active wedge by 40%. Zheng et al. [14] conducted a parametric study to investigate the effect of various parameters on abutment deformation and failure behavior of GRS bridge abutments using the finite-difference program FLAC2D and concluded that the failure surface followed a bilinear path, which initiated from the heel of the bridge seating. Zheng et al. [15] performed a numerical study on the maximum reinforcement tensile forces for GRS bridge abutments and found that the locus of the maximum reinforcement tensile forces at failure followed a Y-shaped pattern, initiated from the toe and heel of the bridge seating, and converges at a certain depth before extending downward to the toe of the GRS wall.
The primary goal of this study is to assess the influence of various reinforcement and backfill parameters on the mechanical responses of a large-scale experimental SGC mass in terms of wrapped-face lateral displacement, reinforcement axial strain, load-carrying capacity, and an understanding in the failure mode of the SGC mass. The influence of compaction effort on the SGC mass for closely spaced reinforcement is also studied.
2. Materials and Methods
Three large-scale SGC specimens, simulating the behavior of an on-site GRS mass, strengthened by (i) nine layers of single-sheet Geotex 4 × 4 at a vertical spacing of 0.2 m (test no. 1), (ii) four layers of single-sheet Geotex 4 × 4 at a vertical spacing of 0.4 m (test no. 2) and (iii) four layers of double-sheet Geotex 4 × 4 at a vertical spacing of 0.4 m (test no. 3) were experimentally studied by Pham [3]. The SGC specimens were 2 m high and 1.4 m wide, with an ratio of 0.7. Rowe and Ho [33,34] and Ho and Rowe [35] concluded that there was little variation in the reinforcement forces and lateral wall deformation when the ratio was greater than or equal to 0.7; in addition, the ratio of has also been recommended by AASHTO [36] for practical use.
The backfill material used in the tests consisted of crushed diabase from a source near Washington D.C. and well-graded gravelly soil with the largest particle size of 33 mm and compacted to 98% maximum dry density. The basic physical properties of the backfill were: specific gravity of soil solids = 3.0, percentage of fines = 14.6%, maximum dry unit weight = 24 kN/m, and optimum water content = 5.2%. The triaxial test were conducted for specimens with a diameter of 150 mm and a height of 300 mm. Figure 1a shows that for the confining pressures of 5, 15, and 30 psi, the shear strength parameters, i.e., the peak internal friction angle and the apparent cohesion obtained were 70 kPa (10.3 psi) and 50, respectively, while for the confining pressures of 30, 70, and 110 psi, the shear strength parameters were 240 kPa (35.1 psi) and 38, respectively. However, for most reinforced walls, the maximum confining pressure is always less than 30 psi [3]; therefore, the chosen shear strength parameters for the analysis were kPa and .
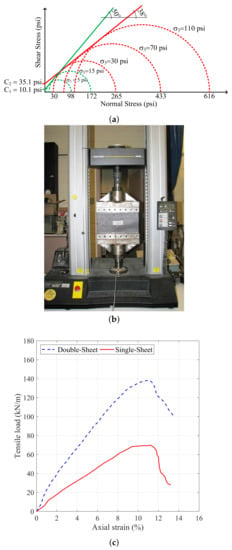
Figure 1.
Materials properties: (a) shear strength parameters of the study backfill; (b) uniaxial tensile test of a 300 mm wide by 150 mm long Geotex 4 × 4 PP-woven geotextile; (c) obtained tensile strength of the single- and double-sheet geotextiles (Pham [3]).
The single- and double-sheet reinforcement used in this study was the Geotex 4 × 4 polypropylene (PP)-woven geotextile, which has an ultimate tensile strength—obtained using the “wide width tensile test (Figure 1b)”, in accordance with ASTM 4595 [37]—of 70 kN/m and 140 kN/m, respectively, (Figure 1c); the breakage strain of both reinforcements was at about 11.5%, and the average tensile stiffness at about 1% strain was 1000 kN/m and 2000 kN/m, respectively, for the single- and double-sheet reinforcements. During the preparation of the specimen, hollow modular concrete blocks with a dimension of 397 mm × 194 mm × 194 mm were used as a temporary facing at the wrapped-faces of the SGC mass, but they were removed prior to the application of the surcharge. The entire surfaces of the SGC specimen were vacuum-sealed with a 0.5 mm thick latex membrane; a prescribed confining pressure of 34 kPa was applied for tests 1 to 3 by connecting the latex membrane to a suction device through two 6 mm diameter flexible plastic tubes. The other two sides (front and rear) of the specimen were supported by the rigid steel framed plexiglass, for which the rupture surface could be directly observed. In addition, the principal strain normal to the direction of the plexiglass was constrained and could therefore be assumed to be constant; consequently, there was effectively zero incremental strain along the plexiglass and, hence, yielding a plane strain condition [38].
A 500-metric-tonne hydraulic jack was used to apply the vertical load via a 30 cm thick concrete pad placed on the top surface of the specimen. Linear variable displacement transducers (LVDTs) and digital dial indicators were installed on top of the concrete pad and at the discrete height of the specimens for monitoring the vertical and lateral displacements of the SGC mass. A vertical load was gradually applied until failure. The vertical failure stress and strain for test specimens no. 1, 2 and 3 were found to be approximately 2700 kPa and 6.75%, 1750 kPa and 6.1%, and 1300 kPa and 4.0%, respectively.
Figure 2 depicts the typical geometry, loading condition, interface elements, and finite element mesh configured in the simulated SGC mass. The sensitivity of mesh sizes was examined, for examples, by Wu and Pham [4] and Gui et al. [8]; the numerical results suggested that, to produce sufficiently accurate results, fine mesh without refinement should be chosen when performing simulation on the GRS problem. Thus, a fine mesh without refinement was used to discretize the model. The simulation was conducted using the two-dimensional FE program Plaxis–2D [39]. The soil and facing block were represented by the fourth-order, 15-noded triangular elements. To describe the axial forces, the geotextile was represented by a special tension 5-noded elements, while the stress–strain behavior of the granular backfill material was represented using the advanced second-order hyperbolic elastoplastic hardening soil model. This model not only separated hardening into deviatoric and volumetric hardening, by utilizing a shear and a cap yield surface, but also employed the nonlinear elastic behavior that related the elastic modulus to the stress level [40]. In this model, the limiting states of stress were described by means of the angle of friction, the apparent cohesion, and the dilatancy angle. Soil stiffness was described in the program by using three different input stiffness: the triaxial secant modulus , the triaxial unloading modulus , and the oedometer loading modulus . Note that the secant modulus is defined as the slope of a line between the origin and a specific point, i.e., the ultimate strength, in a stress–strain curve; thus, it is often called the secant modulus at 50% strength.
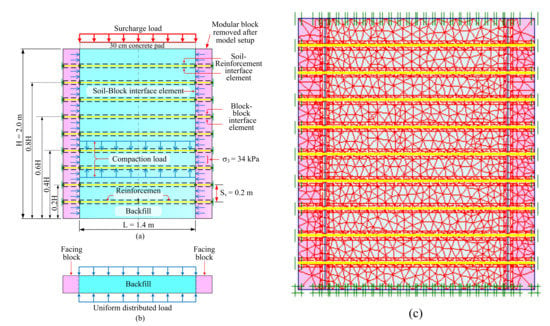
Figure 2.
(a) Schematic diagram and configuration of a typical SGC mass; (b) uniformly distributed load adopted in the simulation of the compaction effect of the SGC specimen; (c) a typical finite element mesh used in the numerical simulation.
The input parameters for the following numerical analyses are tabulated in Table 1. The interface between the block–block, soil–block, and soil–reinforcement were simulated using the ”zero-thickness” interface elements, as characterized by the Mohr–Coulomb failure criterion, and they were defined via an interface friction angle , an interface apparent cohesion , an interface dilation angle , and a given Poisson’s ratio of 0.45 [39]. For simplicity, Reference [39] suggested that the values of the interface properties might also be defined via a strength/stiffness reduction factor , where represents a fully bonded interface, to the properties of the adjacent soil via the following equations:

Table 1.
Parameters involved in the experimental and finite element analyses.
The numerical analysis was carried out in two stages: (i) backfilling and compaction and (ii) surcharge application to the top surface of the SGC mass. The SGC mass was constructed in stages with various thicknesses of soil lift (depending on the reinforcement vertical spacing) placed and compacted until its full height of 2 m was reached. The compaction of each soil lift was modeled by assigning an equivalent uniformly distributed load to the top and bottom surfaces of each soil lift, defined as a Type-II compaction procedure in [27], during the staged construction process (Figure 2b). Two compaction pressures: 44 and 70 kPa were considered in the FE simulation. The compaction pressure of 70 kPa represented the upper limit of the compaction-induced stress of 28.3 kPa or an equivalent total force per unit width of 53.2 kN/m produced by a light compaction equipment, whereas the compaction pressure of 44 kPa represented the compaction pressure induced by the plate compactor MBW–GP1200, as used in the SGC tests by Pham [3]. This compactor and hence the compaction pressure were different from the ones that were used by Mirmoradi and Ehrlich [27]. A confining pressure of 34 kPa, representing the vacuum pressure applied to the SGC mass, was applied to the sides and top boundaries of the following simulated SGC masses. Both the lateral and vertical displacements of the bottom boundary were restrained in the numerical model.
The vertical pressure–axial strain relationship and the lateral displacement along one of the wrapped-faces of the specimens are presented in Figure 3. Both the simulated and measured stress–strain curve, Figure 3a, were in good agreement for a vertical pressure of up to 1200 kPa for tests 2 and 3. As for that in test no. 1, the result revealed that the experimental specimen was stiffer than that adopted in the numerical simulation and hence causing a deviation in the stress–strain profile. In accordance with the requirement of References [41,42], the allowable bearing pressure of a bridge sill over reinforced-soil retaining walls is limited to 200 kPa, thus these load-carrying capacities of SGC masses are at least 6 times larger than the typical bridge abutment design load. The simulation taking into consideration the compaction effort gave a better simulation result, in particular, for test no. 1. However, the variation between the results produced using compaction pressures of 44 kPa and 70 kPa was found to be insignificant; therefore, the compaction pressure of 44 kPa was adopted in the subsequent study.
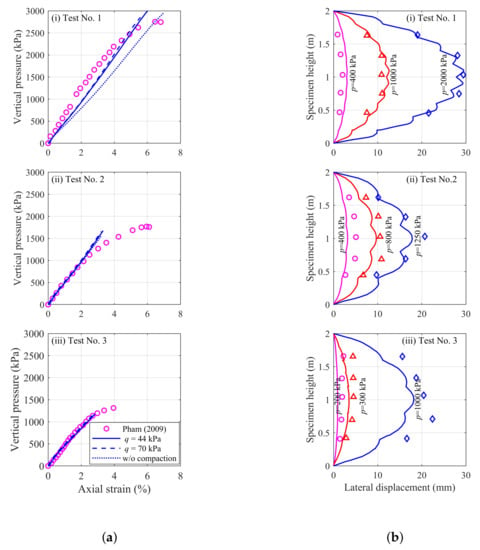
Figure 3.
(a) Simulated and measured applied vertical pressure vs. axial strain and (b) simulated (with a compaction pressure of 44 kPa) and measured lateral displacement along the specimen height of the three SGC tests performed by Pham [3].
Figure 3b compares the simulated and measured lateral displacement profiles of the three SGC tests. Surcharges of 400 kPa, 1000 kPa, and 2000 kPa; 400 kPa, 800 kPa, and 1250 kPa; and 200 kPa, 300 kPa, and 1000 kPa were separately considered for tests 1, 2, and 3, respectively; for each of these surcharges a compaction pressure of 44 kPa was applied in the simulation. The compaction pressure value of 44 kPa was calculated from the actual compactor used for the experimental tests. It can be seen that there is a good agreement between the simulated and the measured lateral displacement profiles for the three SGC tests. In all the simulations, the location of the maximum lateral displacement was found to be located at the middle height of the specimens and coincided with that observed in the experiments except that in test no. 3. Based on these comparisons, we concluded that the numerical procedures and the input parameters adopted in this study were reliable and accurate.
Figure 4 shows the failure surfaces observed from the three large-scale loading tests on the SGC masses, which were conducted by Pham [3]. Tests 1 and 3 utilized a single-sheet reinforcement but in test no. 1, the reinforcement’s vertical spacing was 0.2 m while that in test no. 3, the vertical spacing was 0.4 m. Test no. 2 utilized a double-sheet reinforcement spaced at a vertical spacing of 0.4 m (Table 1). On the one hand, as seen from Figure 4, the specimen of test 1 and 3 generated a failure active wedge, which was similar to that in a bearing capacity problem, beneath the 30 cm thick concrete pad mounted on top of the specimen surface for which the surcharge load was applied. On the other hand, the specimen of test no. 2, which adopted the double-layer reinforcement, revealed a failure mode of localized-ductile failure with only one failure plane as commonly observed in a triaxial test.

Figure 4.
Failure patterns observed from the experimental SGC masses performed by Pham [3]. (a) Test no. 1; (b) test no. 2; and (c) test no. 3.
3. Results
A series of parametric studies was carried out to investigate the influence of reinforcement spacing , reinforcement strength , reinforcement axial stiffness , backfill material’s average secant modulus , and angle of internal friction on the response of the study SGC mass. Unless otherwise stated, a surcharge of 200 kPa, representing both the limiting design load and the serviceability stage of a bridge abutment, was applied to all the simulations; the angle of internal friction and the apparent cohesion of the backfill was 50 and 70 kPa, respectively; and the tensile strength and the axial stiffness of the reinforcement was 70 kN/m and 1000 kN/m, respectively. The responses of the reinforcement and the backfill material were expressed in terms of the load-carrying capacity and wrapped-face lateral displacement of the specimen, and the axial strain and the location of the maximum axial strain of the reinforcement at which the failure plane was most likely initiated.
3.1. Influence of Reinforcement Vertical Spacing
In this study, three different vertical spacings of 0.1 m, 0.2 m, and 0.4 m were considered and evaluated. The tensile strength of the reinforcement was 70 kN/m. Figure 5 shows the influence of the reinforcement vertical spacing, located across the specimen heights of 0.2 H, 0.4 H, 0.6 H, and 0.8 H from the base (Figure 2a), on the distribution of its axial strain. In general, the magnitude of the reinforcement axial strain increases with the increase of the reinforcement spacing, which is reasonable since a specimen with a closely spaced reinforcement would be stronger than that with a widely spaced reinforcement and hence mobilized at a relatively small strain level. For example, the maximum axial strain for the reinforcement placed across the height of 0.2 H increased from 0.10% to 0.12% when the vertical spacing was increased from 0.1 m to 0.4 m. It can also be seen that the reinforcement across the lowest (0.2 H) and highest (0.8 H) heights, in particular the one placed across the height of 0.2 H, generated their maximum axial strain near both ends of its reinforcement, i.e., at a distance of about 10% to 15% of its length from both ends, while the reinforcement at the middle two layers (0.4 H, 0.6 H) generated their maximum axial strain at the midlength of the reinforcement. In addition, it is also obvious that the variation in the axial strain profiles generated with and without the compaction effort was no more than 5%; thus, the numerical result implies that the influence of the compaction effort during the construction stage of the GRS mass had an insignificant effect on the elongation of the reinforcement axial strain.
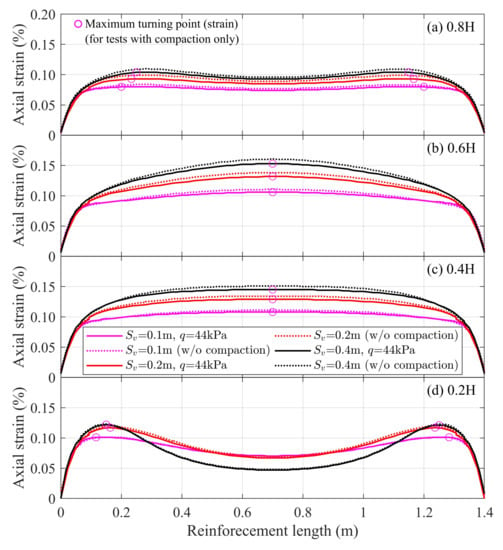
Figure 5.
Influence of reinforcement vertical spacing, under a surcharge (service load) of 200 kPa, on the distribution of reinforcement’s axial strain at (a) 0.8 H, (b) 0.6 H, (c) 0.4 H, and (d) 0.2 H of the specimen.
Figure 6 shows the relation between the load-carrying capacity, the reinforcement spacing, and the reinforcement tensile strength of the studied SGC specimen. The simulation procedure for the load-carrying capacity of the SGC specimen was essentially the procedure used in the simulation of the bearing capacity of a footing as outlined in Reference [39], which is via the application of a small incremental load using the multipliers option in the program until failure. In general, the numerical result shows that the load-carrying capacity increases with the increase of the reinforcement strength but decreases with the increase of the reinforcement spacing; hence, using a closer reinforcement spacing allows the use of a reduced reinforcement strength. This finding is in agreement with the result obtained, for examples, by Leshchinsky [43], who found that the spacing between the reinforcement layers could have a major impact on the bearing capacity of an MSE wall-supported footing, and by Xu et al. [44] who found that the load-carrying capacity of a GRS mass was affected by the reinforcement spacing and the reinforcement strength.
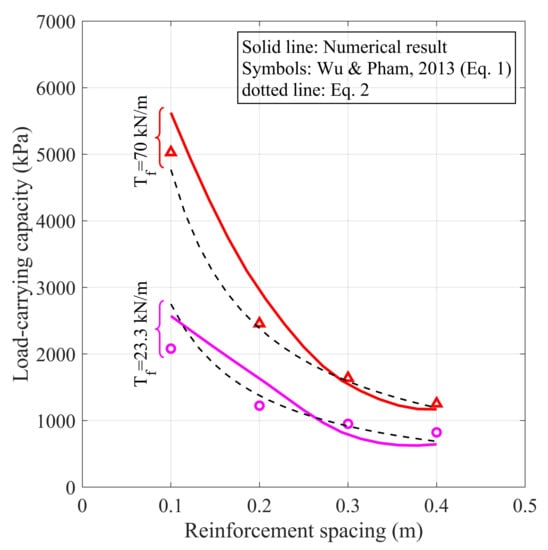
Figure 6.
Relation between load-carrying capacity and reinforcement spacing of the study SGC mass.
In Figure 6, the analytical load-carrying capacity was obtained using Equation (1), which was proposed by Wu and Pham [30]; in this equation, the confining pressure used was 34 kPa, the largest particle size was 33 mm, the angle of internal friction of the backfill—required for calculating the coefficient of Rankine passive earth pressure —was 50, and the apparent cohesion was 70 kPa. The numerical result for 23.3 kN/m and 70 kN/m are in good agreement with the analytical result.
One of the major findings in this paper is proposing a semiempirical equation, which is simple and conservative, for quickly estimating the load-carrying capacity of the studied SGC mass with only two reinforcement parameters:
Since it is a semiempirical equation, the unit for , , and must be in kN/m, m, and kPa, respectively. The equation implicitly considers the shear strength of the backfill ( kPa) adopted in the numerical analysis and, therefore, may be unsuitable for estimating the load-carrying capacity of a backfill with different shear strength values. However, it shows that the ultimate load-carrying capacity of the SGC mass is proportional to the square root of the tensile strength and inversely proportional to the vertical spacing of the geotextile. A comparison of the load-carrying capacity result obtained using Equation (5) and the numerical analysis is shown in Figure 6, where the black dotted lines denote the load-carrying capacity profiles estimated using Equation (5) for reinforcement strengths of 23.3 kN/m and 70 kN/m. A numeric comparison between the result of the FE simulation and Equation (5) was also made and is discussed later in Table 2. The load-carrying capacity estimated using Equation (5) is in good agreement with that of Equation (1) for a reinforcement with tensile strengths of 23.3 and 70 kN/m; the result of the black dotted line seems to be much more closer to that derived from the numerical analysis.

Table 2.
Load-carrying capacity of SGC mass under various combinations of reinforcement spacing and strength.
3.2. Influence of Reinforcement Axial Stiffness
The axial stiffness of a geotextile can be defined as the ratio of the tensile strength and the average width elongation. Aging may promote the degradation of the reinforcement and hence its axial stiffness during the serviceability stage of the SGC mass. Therefore, it is necessary to examine the influence of the axial stiffness on the axial strain and the load-carrying capacity of the reinforcement. A common value for the axial stiffness is about 1000 kN/m; adopting a factor of three, three different reinforcement axial stiffness were considered: 333 kN/m, 1000 kN/m, and 3000 kN/m. The vertical spacing of the reinforcement was fixed at 0.2 m. Figure 7 presents the distribution of the axial strain of the reinforcement placed across the specimen heights of 0.2 H, 0.4 H, 0.6 H, and 0.8 H, as measured from the base of the specimen. As in the study on the influence of reinforcement vertical spacing, it can be seen that the reinforcement placed at the lowest (0.2 H) and the highest (0.8 H) heights generated their largest axial strain near both ends of the reinforcement, and at a distant of about 10% to 20% of its length, whereas the reinforcements of the middle two layers (0.4 H, 0.6 H) generated their largest axial strain at the midlength of the reinforcement. In addition, it was found that the magnitude of the maximum axial strain decreased with the increase of the reinforcement stiffness. For example, the maximum axial strain for the reinforcement placed across the specimen height of 0.2 H decreased from 0.14% to 0.08% when the reinforcement stiffness increased from 333 kN/m to 3000 kN/m.
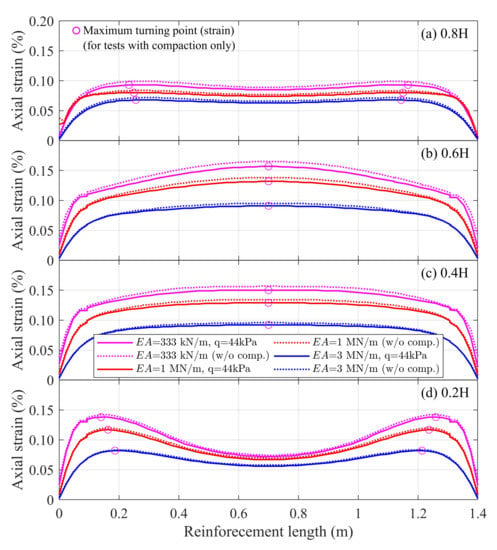
Figure 7.
Influence of reinforcement axial stiffness , under a surcharge (service load) of 200 kPa, on the distribution of reinforcement axial strain at (a) 0.8 H, (b) 0.6 H, (c) 0.4 H, and (d) 0.2 H of the specimen.
Figure 8 shows the effect of the reinforcement stiffness on the load-carrying capacity of the studied SGC specimen. The tensile strength of the reinforcement was 70 kN/m. The reinforcement stiffness had different effects on the load-carrying capacity of the SGC specimen; for a particular spacing, the effect of the reinforcement stiffness on the load-carrying capacity was greater between the values of 333 kN/m and 1000 kN/m. In other words, the numerical result showed that the effect of was more apparent between 333 kN/m and 1000 kN/m than that between 1000 kN/m and 3000 kN/m. This effect was magnified when the vertical spacing of the reinforcement was reduced from 0.4 m to 0.1 m. The result suggested that for a consistent performance of the reinforcement, the reinforcement to be adopted should have a stiffness of at least 1000 kN/m.
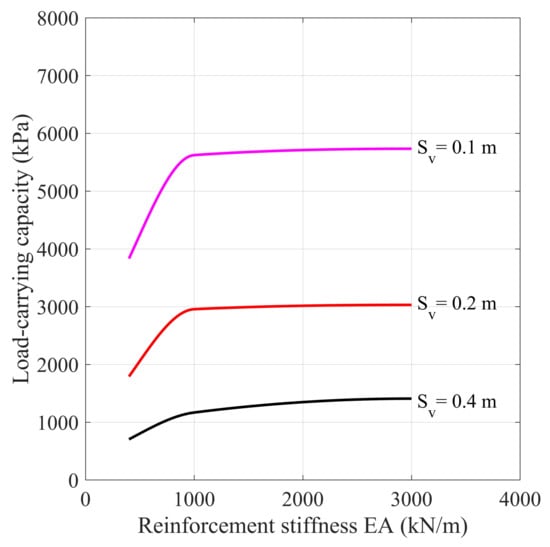
Figure 8.
Relation between load-carrying capacity and reinforcement stiffness of the study SGC mass.
3.3. Influence of Secant Modulus
In Plaxis [39], the shear behavior of the soil was represented by the secant modulus and the unloading–reloading modulus , while the volumetric behavior was represented by the tangent modulus for a primary oedometer loading . Schanz and Vermeer [45] reported that the secant modulus of sandy soils was closely related to the one-dimensional oedometer modulus , i.e., , and that the unloading–reloading modulus was about three times the secant modulus , i.e., . Three different values of were considered and evaluated in this study: , , and , where was taken as 62.4 MPa—the value obtained and adopted by Pham [3] in their simulation of the behavior of a series of large-size generic soil-geosynthetic composite (GSGC); as before, the tensile strength of the reinforcement was 70 kN/m.
Figure 9 presents the distribution of the reinforcement axial strain placed across the specimen heights of 0.2 H, 0.4 H, 0.6 H, and 0.8 H. Again, it can be seen that the reinforcements located at the lowest (0.2 H) and the highest (0.8 H) heights generated their largest axial strain near both ends of the reinforcement, about 0.2∼0.3 m from its ends, while the reinforcement placed at the middle height of the specimen (0.4 H, 0.6 H) generated their largest axial strain at the midlength of the reinforcement. In general, the axial strain profile increases with a decrease in the secant modulus . For example, for the reinforcement across the height of 0.2 H from the base of the specimen and with a vertical spacing of 0.2 m, the maximum axial strain increased from about 0.12% to about 0.24% when the secant modulus was decreased from 187.1 MPa to 20.8 MPa. Obviously, the secant modulus had a significant influence on the axial strain of the reinforcement. Under the same applied load, as the soil became stiffer, the internal force mobilized in the reinforcement was smaller. This finding is in agreement with the results obtained by Wu et al. [6] and Hoffman and Pham [46]; both reported that the secant modulus was the most important factor influencing the stress–deformation behavior of the GRS mass. However, the variation in the axial strain due to the various compaction effort was, again, found to be insignificant.
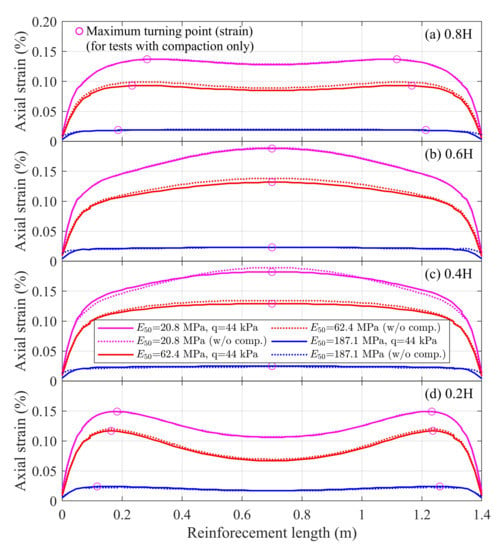
Figure 9.
Influence of secant modulus of soil, under a surcharge (service load) of 200 kPa, on the distribution of reinforcement axial strain at (a) 0.8 H, (b) 0.6 H, (c) 0.4 H, and (d) 0.2 H of the specimen.
3.4. Influence of Angle of Internal Friction
Three different angles of internal friction, 40, 45, and 50, of the backfill were considered and evaluated in this study. Figure 10 shows the axial strain distribution of the reinforcement placed at various heights of the specimen. As in the previous cases, it can be seen that the reinforcement across the lowest (0.2 H) and highest (0.8 H) heights generated their maximum axial strain near both ends of its reinforcement, while the reinforcement at the middle two layers (0.4 H, 0.6 H) generated their maximum axial strain at the midlength of the reinforcement. The magnitude of the reinforcement’s maximum axial strain decreased with an increase in the angle of internal friction. For example, for the reinforcement placed at 0.2 H from the base of the specimen, the maximum axial strain increased from 0.11% for an angle of internal friction of 50 to about 0.19% for an angle of internal friction of 40.
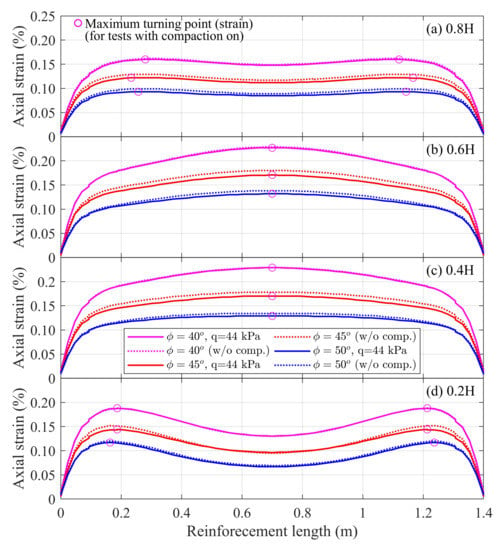
Figure 10.
Influence of angle of internal friction, under a surcharge (service load) of 200 kPa, on the distribution of reinforcement axial strain at (a) 0.8 H, (b) 0.6 H, (c) 0.4 H, and (d) 0.2 H of the specimen.
Figure 11 shows the effect of the angle of internal friction of the backfill on the load-carrying capacity of the studied SGC specimen. The load-carrying capacity was found to be proportional to the angle of internal friction, but inversely proportional to the vertical spacing. This numerical finding agrees with the results of Xu et al. [44], in which they concluded that the angle of internal friction of the backfill had a significant effect on the load-carrying capacity of the GRS mass. The numerical result was also compared to the analytical result calculated using Equation (1); both the numerical and analytical results showed the same trend of a nonlinear relation on the load-carrying capacity for the values of the angle of internal friction considered here. In general, the numerical result underestimated the load-carrying capacity calculated by the analytical Equation (Equation (1)).
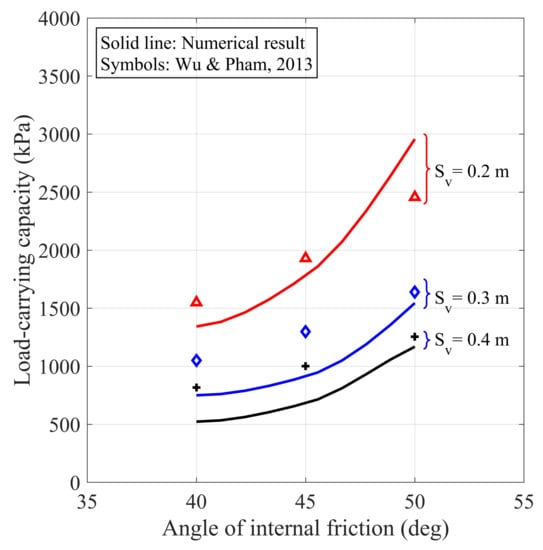
Figure 11.
Relations between load-carrying capacity and angle of internal friction of the study SGC specimen with various vertical spacing.
4. Discussion
4.1. Influence of Reinforcement Stiffness and Spacing on Lateral Displacement
Figure 12 reveals the effect of varying the ratio of the reinforcement stiffness and reinforcement spacing on the lateral displacement of the SGC specimen’s wrapped face. For an of 0.2 m, the corresponding range of the reinforcement stiffness was kN/m, while for an of 0.4 m, the corresponding range was kN/m. The simulated result showed that the lateral displacement reduced significantly with the increase of the ratio of ; specifically, for a particular vertical spacing, the lateral displacement reduced with the increase of the reinforcement stiffness. For the range of values considered here, for 0.4 m, the reduction was 48.9% while for 0.2 m the reduction was 54.8%, leading to an average reduction of about 50% in the magnitude of the lateral displacement. For a constant ratio of 10,000 kN/m/m, the variation between the simulated lateral displacements for an of 0.2 m ( = 2000 kN) and 0.4 m ( = 4000 kN) was only 1.25 mm. The result implies that the reinforcement stiffness plays a slightly greater role than the reinforcement spacing in the lateral displacement of the SGC specimen.
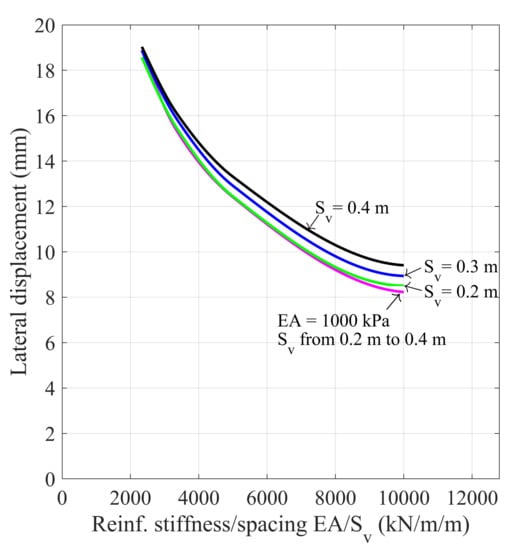
Figure 12.
Relation between the open face lateral displacement and the ratio of reinforcement stiffness and reinforcement spacing of the study GRS mass.
4.2. Influence of Reinforcement Strength and Spacing on Load-Carrying Capacity
Figure 13 reveals the effects of reinforcement spacing and reinforcement strength on the load-carrying capacity of the study SGC specimen obtained from the FE analysis. To achieve the ratio of 175, 233, 350, and 700, a variety of reinforcement strengths between 17.5 kN/m and 280 kN/m and reinforcement spacings between 0.1 m and 0.4 m were considered. The figure shows that the load-carrying capacity of SGC specimen increases with the increase of the reinforcement strength but decreases with the increase of the reinforcement spacing. On one hand, it can be seen that at the reinforcement strength of 17.5 kN/m, the load-carrying capacity is decreasing linearly with the increase of the reinforcement spacing, while at the reinforcement strength of 280 kN/m, the load-carrying capacity is decaying exponentially with the increase of the reinforcement spacing. On the other hand, the load-carrying capacity is exponentially correlated to the reinforcement strength at the reinforcement spacing of 0.1 m but is logarithmically correlated at the reinforcement spacing of 0.4 m. The logarithmic relation indicates that the reinforcement strength in the SGC specimen could not be efficiently mobilized for enhancing the shear strength of the composite mass and hence its load-carrying capacity.
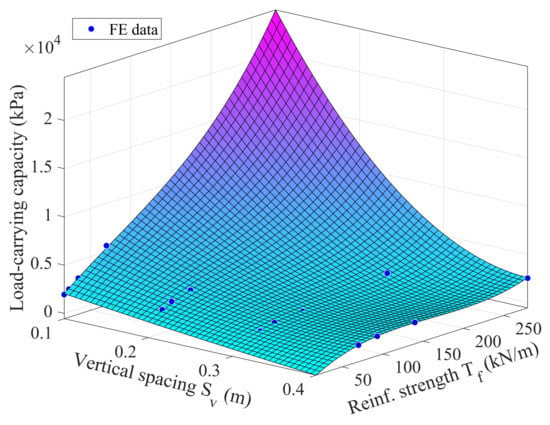
Figure 13.
Relation between load-carrying capacity, reinforcement strength, and reinforcement spacing of the study GRS mass.
Table 2 shows that by reducing both the reinforcement strength and reinforcement spacing simultaneously to produce a fixed ratio of reinforcement strength/reinforcement spacing, i.e., = 350, the load-carrying capacity of the SGC specimen doubled from 1656 kPa ( = 140 kN/m and = 0.4 m) to 3181 kPa ( = 35 kN/m and = 0.1 m). The load-carrying capacity of the composite mass in the case of = 140 kN/m and = 0.4 m was only 56% of the load-carrying capacity in the case = 70 kN/m and = 0.2 m, while in the case of = 70 kN/m and = 0.2 m, the load-carrying capacity was about 93% of that in the case of = 35 kN/m and = 0.1 m. Perhaps the reinforcement spacing played a much more important role than the strength of the reinforcement in the load-carrying capacity of the studied SGC specimen. The numerical result is in good agreement with the data observed by Pham [3], where the load-carrying capacity of their experimented composite mass in test no. 2 (2 = 140 kN/m and = 0.4 m) was 65% of the load-carrying capacity of their test specimen no. 1 ( = 70 kN/m and = 0.2 m). Pham [3] attributed this disproportionate decrease to the composite behavior created by the interface friction between the geosynthetic reinforcement layers and the backfill materials, in which a closer spacing resulted in increasing the lateral confinement and, hence, increasing the stiffness and load-carrying capacity of the SGC mass. Using the combination of a very close reinforcement spacing such as 0.1 m and a high reinforcement strength such as 280 kN/m resulted in an unnecessary high load-carrying capacity of the SGC mass. Figure 13 implies that a reasonable combination of would be between (0.1 m, 70 kN/m) and (0.4 m, 280 kN/m), for which the load-carrying capacity reduces linearly between 5600 kPa and 2500 kPa, respectively.
4.3. Failure Surface of SGC Mass
Pham [3] observed that the failure surface of their SGC mass corresponded to the location of the tensile rupture or maximum strain of their geogrid layers. Figure 14 denotes the location of the reinforcement’s maximum axial strain with normalized depth observed from all the analyses. It can be seen that the location of the maximum axial strain developed in the reinforcement as a result of altering the reinforcement vertical spacing, reinforcement stiffness, soil secant modulus, and angle of internal friction did not vary a lot.
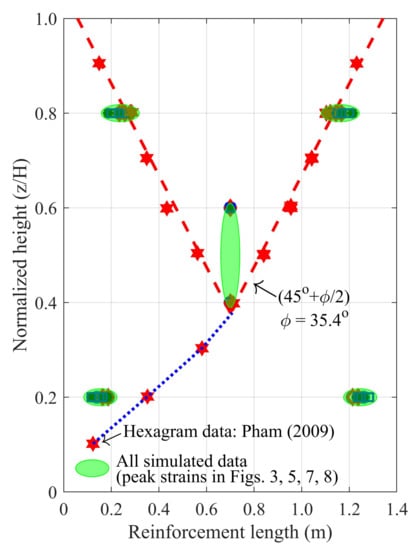
The failure surface observed in the SGC test specimen no. 1 of Pham [3], Figure 14, was also added to this figure using the hexagram; clearly the failure surface is incompletely developed. The failure surface on the right-hand-side of the active wedge continued to develop diagonally downwards following the path of the blue dotted line, which could well be the failure surface or the –slip line of the radial shear (fan) zone. Obviously, one should not expect a complete development of the failure surface beneath the concrete pad (footing) as the composite specimen did not have sufficiently far side boundaries. A rigid boundary, if not a sufficiently far boundary, is required for the generation of a complete failure surface that eventually extends to the top surface [47]. In addition, the soil mass supporting the concrete pad might have insufficient restraint at the side boundaries, which were both wrapped-faces and supported by a confining pressure of only 34 kPa, which was constantly maintained during testing by a vacuum pressure of 34 kPa.
The experimental failure surface (red dotted line) has an inclination angle of about 62.7. According to the Mohr–Coulomb failure criterion, failure occurs on the plane with the maximum ratio of shear stress and normal stress; thus, the theoretical inclination angle of the Rankine active wedge is , leading to a backcalculated internal friction angle of 35.4, which is smaller than the peak internal friction angle of 50 obtained from a series of 150 mm diameter by 300 mm high triaxial tests performed on unreinforced soil. A similar result was also observed in [32]. Based on the rupture pattern of the geotextiles in their test specimen no. TF–6 and an inclination angle of 62.9, Nicks et al. [32] obtained a backcalculated internal friction angle of 35.8, which was 25% smaller than the peak internal fiction angle obtained from the triaxial test of unreinforced soil. At first, one may argue that the shear strength of soil decreased with an increase in the specimen size [48] and hence the 2 m high by 1.4 m wide SGC mass should possess a smaller angle of friction than that measured from the medium size (150 mm diameter by 300 mm high) triaxial apparatus. However, such a direct comparison might be impractical because the SGC mass was a reinforced mass while that used in the triaxial test was unreinforced specimen.
The failure surface generated in the study SGC mass cannot be compared to that observed in the geosynthetic-reinforced soil–integrated bridge system (GRS–IBS). For examples, Zheng et al. [14], who investigated the pattern of the failure surface of GRS–IBS, found that the failure surface developed from the heel of the bridge seat to the toe of the abutment but their failure surface first migrated downward from the heel of the bridge seat and then diagonally to a point beneath the toe of the GRS wall; while Ardah et al. [11] found out that the failure envelope of GRS–IBS abutments extends beyond the theoretical value () by as much as 40%. Although both the GRS–IBS and SGC mass have the same design philosophy, i.e., the reinforcements mechanism is considered to be part of a composite material due to the interaction between closely spaced reinforcements and backfill material, their surcharge loading is different. In the SGC mass, the surcharge was uniformly applied to the entire surface of the soil mass, while in the GRS–IBS, the surcharge was applied to the bridge seating located only on one side of the soil mass [11]. This may be the reason for the variation in the pattern of failure surface observed in the SGC mass and GRS–IBS. A series of performance tests for GRS revealed that the failure surfaces of reinforced soil composite were not the same as those in Rankine’s theory and the backcalculated angle of friction for the composite mass was about 15% to 25% smaller than that of the unreinforced soil [49]; therefore, the method of determining friction angles from failure surfaces for unreinforced soil was not suitable for reinforced soil mass.
5. Conclusions
A series of numerical analyses were performed to simulate the responses of an experimental soil-geosynthetic composite (SGC) mass under various parameters such as the reinforcement spacing, reinforcement stiffness, soil modulus, and angle of internal friction of the backfill. The responses of the studied SGC mass were evaluated in terms of the reinforcement axial strain, lateral deformation of wrapped faces, and load-carrying capacity of the specimen. The failure surface of the SGC mass was also compared to that in the GRS–IBS system. Based on the results from this parametric study, the following conclusions can be made:
- In general, the variation of the reinforcement spacing, reinforcement stiffness, soil modulus, and angle of friction of the backfill had negligible effect on the level of the reinforcement’s maximum axial strain, which corresponded to the possible rupture or failure surface of the composite mass.
- The study showed that the influence of the reinforcement stiffness on the load-carrying capacity of the composite mass was more apparent when was between 333 kN/m and 1000 kN/m than between 1000 kN/m and 3000 kN/m. The result suggested that for a consistent performance, the geotextile reinforcement to be adopted should have an axial stiffness of at least 1000 kN/m.
- Wu–Pham’s equation performed well in estimating the load-carrying capacity of the composite mass with reinforcement strengths of 23.3 kN/m and 70 kN/m, a range of internal friction angles of 40, and a range of reinforcement spacings of .
- Based on the result of the same reinforcement strength and reinforcement spacing ratio (Table 2), the reinforcement spacing was found to have a more profound effect than the reinforcement strength on the load-carrying capacity of the composite mass. This behavior was mainly attributed to the composite behavior created by the interface friction between the closely spaced geosynthetic-reinforcement layers and the backfill, in which a closer spacing resulted in an increased lateral confinement and hence, increasing the stiffness and load-carrying capacity of the SGC mass. A reasonable combination of was recommended, which is between (0.1 m, 70 kN/m) and (0.4 m, 280 kN/m), for which the load-carrying capacity reduced linearly between 5600 kPa and 2500 kPa, respectively.
- The failure surface of the composite soil mass beneath the concrete pad was found to be different from that observed in the GRS–IBS system, and that of the unreinforced soil; using the Rankine active wedge theory and the Mohr–Coulomb failure criterion, the backcalculated angle of friction of the SGC mass was found to be about 15% to 25% less than that of unreinforced soil. Thus, the failure mode of the GRS composite was different from that of the unreinforced soil and did not follow the Rankine—Mohr–Coulomb failure mode.
More work on the mechanical properties of the GRS composite, the combined effect of reinforcement and soil properties, and Wu–Pham’s load-carrying capacity equation would be necessary before such advantage could be realized in practice. Furthermore, it is recommended that artificial intelligence (AI) or machine learning (ML) be considered in future studies to extract useful relationships from the results of this parametric study, which was validated via experimental data.
Author Contributions
Conceptualization, T.T.T.P., T.P. and M.-W.G.; numerical analysis, T.T.T.P.; experimental data curation, T.P.; numerical data curation, T.T.T.P.; writing—original draft preparation, T.T.T.P.; writing—review and editing, T.P. and M.-W.G.; supervision, M.-W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GRS | Geosynthetic-reinforced soil |
| IBS | Integrated bridge system |
| PP | Polypropylene |
| SGC | Soil-geosynthetic composite |
| GRS–IBS | Geosynthetic-reinforced soil–integrated bridge system |
References
- Elton, D.J.; Patawaran, M.A.B. Mechanically Stabilized earth reinforcement tensile strength from tests of geotextile-teinforced soil. Transp. Res. Rec. 2004, 1868, 81–88. [Google Scholar] [CrossRef] [Green Version]
- Adams, M.T.; Ketchart, K.; Wu, J.T.H. Mini pier experiments: Geosynthetic reinforcement spacing and strength as related to performance. In Proceedings of the Geo-Denver 2007: Geosynthetics in Reinforcement and Hydraulic Applications (Geotechnical Special Publication 165); Gabr, M.A., Bowders, J.J., Eds.; ASCE Geo-Institute: Reston, VA, USA, 2007. [Google Scholar] [CrossRef]
- Pham, T.Q. Investigating Composite Behavior of Geosynthetic-reinforced soil (GRS) mass. Ph.D. Thesis, University of Colorado, Denver, CO, USA, 2009; p. 378.
- Wu, J.T.H.; Pham, T.Q. An Analytical model for evaluation of compaction-induced stresses in a reinforced soil mass. Int. J. Geotech. Eng. 2010, 4, 549–556. [Google Scholar] [CrossRef]
- Wu, J.T.H.; Yang, K.H.; Mohamed, S.; Pham, T.Q.; Chen, R.H. Suppression of soil dilation—A reinforcing mechanism of soil-geosynthetic composites. Transp. Infrastruct. Geotechnol. 2014, 1, 68–82. [Google Scholar] [CrossRef]
- Wu, J.T.H.; Tung, C.; Adams, M.T.; Nicks, J.E. Analysis of stress-deformation behavior of soil-geosynthetic composites in plane strain condition. Transp. Infrastruct. Geotechnol. 2018, 5, 210–230. [Google Scholar] [CrossRef]
- Yang, K.H.; Wu, J.T.H.; Chen, R.H.; Chen, Y.S. Lateral bearing capacity and failure mode of geosynthetic-reinforced soil barriers subject to lateral loadings. Geotext. Geomembr. 2016, 44, 799–812. [Google Scholar] [CrossRef]
- Gui, M.W.; Phan, T.T.; Pham, Q.T. Impacts of compaction load and pocedure on stress-deformation behaviors of a soil-geosynthetic composite (SGC) mass—A case study. Appl. Sci. 2020, 10, 6339. [Google Scholar] [CrossRef]
- Phan, T.T.T.; Gui, M.W.; Pham, Q.T. Numerical Simulation of Compaction Load on Stress Deformation Behavior of Soil-Geosynthetic Composite Mass Advances in Transportation Geotechnics IV (LNCE 165). In Advances in Transportation Geotechnics IV: Proceedings of the 4th International Conference on Transportation Geotechnics; Tutumluer, E., Nazarian, S., Al-Qadi, I., Qamhia, I.I.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 2, pp. 945–956. [Google Scholar] [CrossRef]
- Abu-Farsakha, M.; Ardah, A.I.S.; Voyiadjis, G.Z. Numerical parametric study to evaluate the performance of a geosynthetic-reinforced soil–integrated bridge system (GRS-IBS) under service loading. Transp. Geotech. 2019, 20, 100238. [Google Scholar] [CrossRef]
- Ardah, A.; Abu-Farsakh, M.; Voyiadjis, G. Numerical evaluation of the performance of a geosynthetic-reinforced soil-integrated bridge system (GRS-IBS) under different loading conditions. Geotext. Geomembr. 2017, 45, 558–569. [Google Scholar] [CrossRef]
- Zheng, Y.W.; Fox, P.J. Numerical investigation of geosynthetic-reinforced soil bridge abutments under static loading. J. Geotech. Geoenviron. Eng. 2016, 142, 04016004. [Google Scholar] [CrossRef]
- Zheng, Y.W.; Fox, P.J. Numerical investigation of the geosynthetic-reinforced soil–integrated bridge system under static loading. J. Geotech. Geoenviron. Eng. 2017, 143, 04017008. [Google Scholar] [CrossRef]
- Zheng, Y.W.; Fox, P.J.; McCartney, J.S. Numerical simulation of deformation and failure behavior of geosynthetic-reinforced soil bridge abutments. J. Geotech. Geoenviron. Eng. 2018, 144, 04018037. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.W.; Fox, P.J.; McCartney, J.S. Numerical study on maximum reinforcement tensile forces in geosynthetic-reinforced soil bridge abutments. Geotext. Geomembr. 2018, 46, 634–645. [Google Scholar] [CrossRef] [Green Version]
- Broms, B. Lateral Pressure Due to Compaction of Cohesionless Soils. In Proceedings of the 4th Budapest Conference on Soil Mechanics and Foundation Engineering: 3rd Danube-European Conference, Budapest, Hungary, 12–15 October 1971; pp. 373–384. [Google Scholar]
- Aggour, M.S.; Brown, C.B. The Prediction of earth pressure on retaining walls due to compaction. Géotechnique 1974, 24, 489–502. [Google Scholar] [CrossRef]
- Seed, R. Compaction-Induced Stresses and Deflections on Earth Structure. Ph.D. Dissertation, Department of Civil Engineering, University of California, Berkeley, CA, USA, 1983; 447p. [Google Scholar]
- Duncan, J.M.; Seed, R.B. Compaction-induced earth pressures under K0-conditions. J. Geotech. Eng. ASCE 1986, 112, 1–22. [Google Scholar] [CrossRef]
- Seed, R.; Duncan, J. FE Analyses: Compaction-induced stresses and deformations. J. Geotech. Eng. ASCE 1986, 112, 23–43. [Google Scholar] [CrossRef]
- Hatami, K.; Bathurst, R.J. Development and verification of a numerical model for the analysis of geosynthetic-reinforced soil segmental walls under working stress conditions. Can. Geotech. J. 2005, 42, 1066–1085. [Google Scholar] [CrossRef]
- Hatami, K.; Bathurst, R.J. Numerical model for reinforced soil segmental walls under surcharge loading. J. Geotech. Geoenviron. Eng. 2006, 132, 673–684. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Nernheim, A.; Walters, D.L.; Allen, T.M.; Burgess, P.; Saunders, D.D. Influence of reinforcement stiffness and compaction on the performance of four geosynthetic-reinforced soil walls. Geosynth. Int. 2009, 16, 43–59. [Google Scholar] [CrossRef]
- Yu, Y.; Bathurst, R.J.; Allen, T.M. Numerical modelling of two full-scale reinforced soil wrapped-face walls. Geotext. Geomembr. 2017, 45, 237–249. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M. Modeling of the Compaction-induced stresses in numerical analyses of GRS walls. Int. J. Comput. Methods Spec. Issue Comput. Geomech. 2014, 11, 1342002. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M. Modeling of the compaction-induced stress on reinforced soil walls. Geotext. Geomembr. 2015, 43, 82–88. [Google Scholar] [CrossRef]
- Mirmoradi, S.H.; Ehrlich, M. Numerical simulation of compaction-induced stress for the analysis of RS walls under working conditions. Geotext. Geomembr. 2018, 46, 354–365. [Google Scholar] [CrossRef]
- Esen, A.F.; Woodward, P.K.; Laghrouche, O.; Connolly, D.P. Stress distribution in reinforced railway structures. Transp. Geotech. 2022, 32, 100699. [Google Scholar] [CrossRef]
- Raja, M.N.A. and Shukla, S.K. Ultimate bearing capacity of strip footing resting on soil bed strengthened by wraparound geosynthetic reinforcement technique. Geotext. Geomembr. 2020, 48, 864–874. [Google Scholar] [CrossRef]
- Wu, J.T.H.; Pham, T.Q. Load-carrying capacity and required reinforcement strength of closely spaced soil-geosynthetic composites. J. Geotech. Geoenviron. Eng. 2013, 139, 1468–1476. [Google Scholar] [CrossRef]
- Hoffman, P.F.; Pham, T.Q.; Wu, J.T.H. Discussion: Xu, C., Liang, C., and Chen, P. “Experimental and theoretical studies on the ultimate bearing capacity of geogrid-reinforced sand. Geotextiles and Geomembranes. 2019, 47(3), 417–428”. Geotext. Geomembr. 2019, 47, 692–694. [Google Scholar] [CrossRef]
- Nicks, J.E.; Adams, M.T.; Ooi, P.S.K. Geosynthetic-Reinforced Soil Performance Testing: Axial Load Deformation Relationships; Report No. FHWA-HRT-13-066; Federal Highway Administration: McLean, VA, USA, 2013; p. 169. Available online: https://www.fhwa.dot.gov/publications/research/infrastructure/structures/13066/index.cfm (accessed on 2 February 2022).
- Rowe, R.K.; Ho, S.K. Some insights into reinforced wall behavior on finite element analysis. In Earth Reinforcement Practice; Ochiai, H., Ed.; A.A. Balkema: Rotterdam, The Netherlands, 1993; pp. 485–490. [Google Scholar]
- Rowe, R.K.; Ho, S.K. Horizontal deformation in reinforced soil walls. Can. Geotech. J. 1998, 35, 312–327. [Google Scholar] [CrossRef]
- Ho, S.K.; Rowe, R.K. Effect of wall geometry on the behavior of reinforced soil walls. Geotext. Geomembr. 1997, 14, 521–541. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). Standard Specifications for Highway Bridges, 17th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2002; p. 1051. [Google Scholar]
- ASTM D4595-17; Standard Test Method for Tensile Properties of Geotextiles by the Wide-Width Strip Method. ASTM International: West Conshohocken, PA, USA, 2017. [CrossRef]
- Wikipedia Contributors. Plane Stress; Wikipedia, The Free Encyclopedia. Available online: https://en.wikipedia.org/w/index.php?title=Plane_stress&oldid=1046695456 (accessed on 4 January 2022).
- Plaxis 2D—Version 8: Reference Manual; Delft University of Technology: Delft, The Netherlands, 2002; Available online: https://www.plaxis.com/support/manuals/plaxis-2d-manuals/ (accessed on 30 June 2021).
- Schanz, T.; Vermeer, P.A.; Bonnier, P.G. The hardening soil model: Formulation and verification. In Beyond 2000 in Computational Geotechnics; Ronald, B., Brinkgreve, J., Eds.; Taylor & Francis Group: London, UK, 1999; pp. 281–296. [Google Scholar]
- Elias, V.; Christopher, B.R.; Berg, R.R. Mechanically Stabilized Earth Walls and Reinforced Soil Slopes Design and Construction Guidelines; National Highway Institute Course No. 132042, FHWA NHI-00-043, Federal Highway Administration: Washington, DC, USA, 2001; Available online: http://www.coripa.com.ar/view/uploads/articles/article_file-332.PDF (accessed on 2 February 2022).
- Wu, J.T.H.; Lee, K.Z.Z.; Pham, T. Allowable bearing pressures of bridge sills on GRS abutments with flexible facing. Geotech. Geoenviron. Eng. 2006, 132, 830–841. [Google Scholar] [CrossRef]
- Leshchinsky, B. Limit analysis optimization of design factors for mechanically stabilized earth wall-supported footings. Transp. Infrastruct. Geotechnol. 2014, 1, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Liang, C.; Shen, P.P. Experimental and theoretical studies on the load-carrying capacity of geogrid-reinforced sand. Geotext. Geomembr. 2019, 47, 417–428. [Google Scholar] [CrossRef]
- Schanz, T.; Vermeer, P.A. On the Stiffness of Sands. In Géotechnique Symposium in Print: Pre-Failure Deformation Behaiour of Geometricals; Jardine, R.J., Davies, M.C.R., Hight, D.W., Smith, A.K.C., Stallebrass, S.E., Eds.; Thomas Telford Publishing: London, UK, 1998; pp. 383–387. Available online: https://www.icevirtuallibrary.com/doi/abs/10.1680/pdbog.26421.0027 (accessed on 20 February 2022).
- Hoffman, P.; Pham, T. The search for internal stability in reinforced soil. Transp. Infrastruct. Geotechnol. 2020, 7, 378–389. [Google Scholar] [CrossRef]
- Gui, M.W. Centrifuge and Numerical Modelling of Pile and Penetrometer in Sand. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1995. [Google Scholar]
- Wu, P.K.; Matsushima, K.; Tatsuoka, F. Effects of specimen size and some other factors on the strength and deformation of granular soil in direct shear tests. Geotechnical. Test. J. 2008, 31, GTJ100773. [Google Scholar] [CrossRef]
- Wu, J.T.H.; Pham, T.Q.; Adams, M.T. Composite Behavior of Geosynthetic-Reinforced Soil (GRS) Mass; Report No. FHWA-HRT-10-077; Federal Highway Administration: McLean, VA, USA, 2013; p. 211. Available online: https://www.fhwa.dot.gov/publications/research/infrastructure/10077/index.cfm (accessed on 2 February 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).