Abstract
Traditional landslide hazard assessment methods generally use the same evaluation model to carry out assessments under different working conditions. Due to the differences in landslide influence factors and model calculation methods considered under different working conditions, the evaluation results obtained using traditional methods are different from those of real-world scenarios. Therefore, research on optimal landslide hazard assessment methods for different working conditions is important for disaster prevention and mitigation in areas along fault zones. Taking the section along the Lixian–Luojiabu fault zone in Gansu province in China as the research area, a landslide hazard assessment was carried out under rainfall and earthquake conditions. A method based on the fractal theory–information coupling model is proposed for the rainfall condition, and a method based on an improved Newmark model considering matric suction is proposed for the earthquake condition. Under the rainfall condition, a landslide hazard assessment was carried out using the information model, the logistic regression model, the fractal theory model, the logistic regression–information coupling model and the fractal theory–information coupling model. Meanwhile, under the earthquake condition, an assessment was carried out using the traditional Newmark model and the improved Newmark model considering matric suction. Finally, the ROC curve and Kappa coefficient were used to test the accuracy of these evaluation models and to determine the optimal model under different working conditions. The results showed that the fractal theory–information coupling model had the largest AUC value and Kappa coefficient value under the rainfall condition (0.856 and 0.807, respectively). The test value of the logistic regression–information coupling model was second, and the values of the other three models were all lower than 0.8. This shows that the evaluation of the fractal theory–information coupling model is better than those of the other models under the rainfall condition. The AUC value and Kappa coefficient of the improved Newmark model under the earthquake condition were 0.805 and 0.794, respectively, which were larger than the test values of the traditional Newmark model. This shows that the evaluation of the proposed model is better than that of the traditional Newmark model under the earthquake condition. These research results provide a reference for landslide hazard assessments in areas with similar characteristics.
1. Introduction
The occurrence of geological disasters such as landslides has become a restricting factor in terms of the development of society. In recent decades, many countries have been paying more and more attention to landslide research, and a number of scholars have carried out studies on landslide susceptibility, hazard and risk assessments [1,2,3,4,5,6].
Landslide hazard assessment models can be divided into two types: deterministic and nondeterministic. Deterministic models are able to determine slope stability in a certain range based on mechanical or hydrological models and relevant basic geospatial information. Among them, the most widely used is based on the analysis of slope deformation by cumulative displacement, as proposed by Newmark [7]. When combined with the Newmark sliding body displacement analysis model, this procedure is able to calculate the permanent displacement of a slope body under earthquake conditions and serves as the seismic basis for landslide hazard zoning [8]. Based on the Newmark cumulative displacement method, Jibson et al. [9] conducted an inverse analysis of the seismic landslide risk induced by the 1994 Northridge earthquake in California, USA. Rathje et al. [10] improved the Newmark model using the peak acceleration of ground motion under different exceedance probability conditions and compiled earthquake landslide hazard distribution maps under different exceedance probability conditions in Southern California. Wang et al. [11,12] proposed a rapid emergency assessment method of earthquake landslide risk based on a simplified Newmark displacement model, taking 11 counties and cities in areas that were severely affected by the Wenchuan (Ms8.0) earthquake as examples. Those authors presented an in-depth discussion on the concept and mechanical assessment method of earthquake landslide hazards. Based on the Newmark model, Chen et al. [13,14,15] analyzed potential earthquake landslide hazard areas in earthquake disaster areas in Lushan, Sichuan, Ludian, Yunnan and Jiuzhaigou (China). Yang et al. [16] used the Newmark model to rapidly evaluate the spatial distribution of landslide hazard induced by the Ms8.1 earthquake that occurred in Nepal on April 25, 2015; the evaluation results reflected the basic characteristics of earthquake-induced landslide hazard distribution in the region. Nondeterministic models include the information quantity model, analytic hierarchy process model, logistic regression model, fuzzy comprehensive evaluation model and so on. Ayalew et al., Lee et al. and Gregory et al. [17,18,19] used the logistic regression model to create landslide susceptibility zoning maps or analyze and predict landslide susceptibility. Akbar and Ha [20] obtained landslide-related data in the Kaghan region of Pakistan using 3S technology and realized a landslide hazard analysis using the information quantity model. Pourghasemi et al. [21] used a combination of the fuzzy comprehensive evaluation, logistic regression and analytic hierarchy process models to conduct landslide hazard susceptibility zoning in the Haraz Basin, Iran. Gao et al. [22] carried out a landslide hazard assessment study in the Wanzhou District of Chongqing, China, based on the information quantity model. Tang et al. [23] carried out landslide hazard assessment studies in the Shanxi–Shaanxi Loess Plateau region, China, using the information, logistic regression and evidence weight models.
Through research and comparisons, it was found that for the deterministic model, Jibson et al., Rathje et al., Wang et al., Chen et al. and Yang et al. ignored the influence of the suction effect of the matrix in the soil, which led to overly conservative evaluation results. For the non-deterministic model, Ayalew et al., Lee et al., Ohlmacher et al. and Pourghasemi et al. did not consider the impact of the sub-interval hazard effect of each influencing factor of landslides. Additionally, Akbar et al., Gao et al. and Tang et al. did not consider the contribution weights of different factors on the occurrence of landslides. As a result, the calculated results were inconsistent with those of real-life situations. In addition, these scholars did not use different evaluation models to carry out research under different working conditions. Since geological disasters along fault zones have the characteristics of multiple points and wide areas, the question of how to scientifically and reasonably carry out hazard assessments under different working conditions has become a major problem in disaster prevention and mitigation.
This paper took the area along the Lixian–Luojiabu fault zone in Gansu province in China as the research area. On the basis of the 1:50,000 geological disaster survey, combined with the characteristics of the fault zone itself, landslide hazard assessment research was carried out. Under the rainfall condition, the traditional fractal theory model was applied to the field of landslide hazard assessment, and a landslide hazard assessment method based on a fractal theory–information coupling model was proposed. Under the earthquake condition, combined with the shear strength formula of unsaturated soil, taking the effect of matrix suction into account, an improved Newmark model evaluation method considering the effect of matrix suction was proposed. Through comparisons with traditional evaluation methods, the authors actively explored the optimal evaluation model under different working conditions, which has exploration significance for landslide hazard assessments along fault zones.
2. Evaluation Model
2.1. Evaluation Model under the Rainfall Condition
(1) Information model
The theoretical basis of the information volume model is information theory, which was proposed by the American mathematician C.E. Shannon and has been continuously enriched and improved upon by scholars at home and abroad [24]. The information content analysis model can be used as a quantitative index of zoning by calculating the information content Ii value of a landslide provided by a certain unit under the combination of P kinds of influencing factors. The specific calculation formula is as follows:
where Ii is the total information quantity of landslide occurrence that objectively reflects the possibility of landslide occurrence, Ni is the number of landslide points or landslide area under the existing index, N is the total number of landslide points or the total landslide area in the study area, Si is the distribution area under the existing index and S is the total area of the research area.
According to the size of Ii, the corresponding grade is determined for the unit. Ii < 0 means that the possibility of a landslide in this unit is less than the possibility of a landslide in the research area; Ii = 0 means that the possibility of a landslide in this unit is equal to the possibility of a landslide in the research area; Ii > 0 means that the possibility of a landslide in this unit is more than the possibility of a landslide in the research area. In short, the larger the unit information value is, the more likely a landslide is to occur [25,26].
(2) Logistic regression model
The logistic regression model is a widely used probabilistic, nonlinear multivariate statistical model [27]. The landslide hazard assessment method based on the logistic regression model takes single factor data as independent variables and the occurrence of landslides as a classified dependent variable (0 represents the non-occurrence of landslide, and 1 represents the occurrence of landslides) [28]. P is set as the probability of landslide occurrence, Q = 1 − p is the probability of a landslide not happening and the natural logarithm of P/Q is taken as ln(P/Q); that is, the logit transformation of P is performed, which is denoted as LogitP. Taking the probability of landslide occurrence P as the dependent variable, the influencing factor set x1, x2, …, xn is the independent variable, and the regression equation is established:
where LogitP is the objective function of landslide occurrence probability, the linear combination of xn, b0, b1, b2, …, bn is the logistic regression coefficient and P represents the probability of landslide occurrence, which has a range of [0, 1].
(3) Fractal theory model
To date, few scholars at home or abroad have carried out landslide hazard assessment based on the fractal theory model. Based on accumulative and transform fractal theory [29,30,31], the authors propose a landslide risk assessment method based on the fractal theory model. The method is based on the landslide distribution density and fractal dimension calculated by accumulative and transform fractal theory, and the percentage conversion of landslide distribution density and fractal dimension is carried out. The fractal dimension value after conversion is taken as the weight calculation value, and the landslide distribution density value after conversion under each influence factor is weighted. The fractal dimension value after conversion is used as the weight calculation value, the landslide distribution density value after conversion under each influence factor is weighted and the final calculation result is used as the quantitative index of risk assessment.
where xn is the landslide distribution density factor value after percentage conversion under the nth influence factor and an is the component weight value corresponding to the nth impact factor after percentage conversion.
The fractal theory model objectively reveals the complex relationship between landslides and their influencing factors, and fractal dimension values after percentage conversion can quantitatively express the degree of contribution of different landslide impact factors, making it a relatively objective evaluation method.
(4) Logistic regression–information coupling model
Although the logistic regression model can determine the weight of influencing factors, it cannot solve the problem of landslide sensitivity at different levels within each evaluation factor well. In the information model, the information value can extract the influence of the internal grade of the factors that influence the occurrence of landslides, but the information value of each influencing factor has an equal weight superposition, so it cannot reflect the contribution weight of different factors to the occurrence of landslides or the differences in the degrees of influence. In order to give full play to the advantages of the logistic regression model and information model, the authors calculated the information model of each evaluation factor as the index of a logistic regression analysis and then used the binomial logistic regression analysis to plot the regression coefficients of each impact factor on the basis of constructing a logistic regression–information coupling model. The specific calculation formula is as follows:
where Ii is the total information quantity of landslide occurrence and objectively reflects the possibility of landslide occurrence, Ni is the number of landslide points or landslide areas under the existing index, N is the total number of landslide points or the total area of landslides in the study area, Si is the distribution area under the existing index, S is the total area of the research area, b0, b1, b2, …, bn is the logistic regression coefficient and PLI represents the probability of landslide occurrence, which has a range of [0,1].
(5) Fractal theory–information coupling model
The authors combine the fractal theory model and the information model and propose a landslide hazard assessment method based on the fractal theory–information coupling model. In this method, the fractal weight value after percentage conversion in the above fractal theoretical model is used as the weighted value for calculation, the information value calculated under each influencing factor is weighted and calculated and the final calculation result is used as the quantitative index of hazard assessment. The specific calculation formula is as follows:
where Ii is the total information quantity of landslide occurrence and it objectively reflects the possibility of landslide occurrence, Ni is the number of landslide points or landslide area under the existing index, N is the total number of landslide points or the total area of landslide in the study area, Si is the distribution area under the existing index, S is the total area of the research area, Iik is the information value of the j factor under the ith influence factor and an is the component weight value corresponding to the nth impact factor after percentage conversion.
The model not only takes into account the size of the disaster-causing effect of each influencing factor sub-interval but also takes into account the contribution weights of different factors to the occurrence of landslides, which theoretically improves the accuracy of landslide hazard assessment.
2.2. Evaluation Model under the Earthquake Condition
(1) Traditional Newmark model
Based on the limit equilibrium theory, the Newmark model considers the sliding body as a rigid body and assumes that there is no internal deformation of the sliding body. When the external force acts on the sliding body with less than the critical acceleration, the slope body does not produce permanent displacement. Finite displacement occurs when the external force is greater than the critical acceleration [7]. The model evaluates slope stability by calculating the accumulated permanent displacement of the sliding body during the process of ground motion acceleration.
At present, when calculating slope stability, the formula of safety factors considering the influence of rainfall infiltration is generally adopted [9], and its stress state is shown in Figure 1.
where is the effective internal friction Angle, is the effective cohesion, is slope Angle, is the weight of slope material, is the weight of water, is the thickness of the slope body and is the ratio of the buried depth of groundwater above the damaged surface to the depth of the damaged surface.
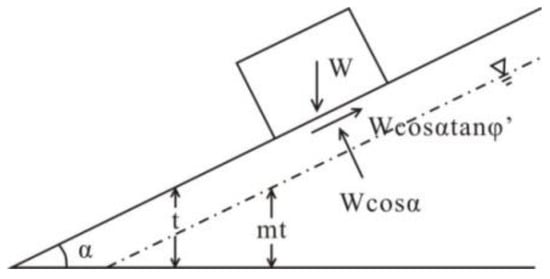
Figure 1.
Static force analysis diagram of Newmark model.
The critical acceleration [32] is expressed as:
where g is the acceleration of gravity.
The Newmark displacement calculation adopts the empirical formula obtained by Jibson and Harp et al.:
where is the Newmark cumulative displacement and is the earthquake intensity.
The general formula of is:
where is the time program column of single component ground motion acceleration in a strong earthquake, is the total duration recorded for ground motion acceleration and is time.
The cumulative displacement calculated by the Newmark model is not directly related to slope instability and thus does not indicate that a landslide disaster will definitely occur in this area. Only when the slope displacement reaches a certain level will the slope become unstable and slide along the sliding surface, resulting in a landslide disaster. Therefore, the statistical relationship between slope displacement and landslide occurrence is used to calculate the probability of an earthquake landslide [9], and hazard zoning is carried out.
where is the probability of the occurrence of an earthquake landslide and k, a and b are constant parameters in the fitting function. In this paper, k is 0.335, a is 0.048 and b is 1.565.
(2) Improved Newmark model
On the basis of summarizing the traditional model, the authors think that there are some limitations in the calculation of the safety factor in the traditional Newmark evaluation model. This formula does not take into account the shear strength provided by the negative pore water pressure above the groundwater level, which is reasonable when the main part of the sliding surface is below the groundwater level, but the matric suction cannot be ignored for slope sliding at a deep or shallow groundwater level. However, there are a large number of shallow surface landslides in earthquake-induced landslides, and most of the landslides are located above the groundwater level, so it is necessary to improve the safety factor formula.
According to the shear strength formula of unsaturated soil proposed by Fredlund [33]:
where is the net normal stress on the failure surface, is the matric suction and is the rate at which the shear strength increases with matric suction.
Based on the shear strength formula of unsaturated soil and taking matric suction into account, this paper improves the static safety factor formula of the Newmark model and expresses it as:
The parameters in the formula have the same meanings as before.
3. Findings
3.1. Overview of the Research Area
The Lixian–Luojiabu fault zone in Gansu province is mainly composed of three oblique secondary fault segments on the plane, with a total length of about 150 km and a strike of 60°. The western section is about 90 km long from Dangchang East to Lixian East. The middle section is about 40 km long from the south of Lixian County to the northeast of Luojiabu. The eastern section is about 20 km long from the west of Tianshui Town to the east of Pingnan Town [34]. This paper takes the core area (middle section) of the fault zone as the research area. The lithology of the strata exposed in the area includes Yanshanian biotite porphyritic granite, Devonian sandstone and slate, Carboniferous siltstone and limestone, Paleogene conglomerate and sandstone, Neogene red clay, Middle–late Pleistocene loess and Holocene alluvial gravel. The rock and soil structure along the Lixian–Luojiabu fault zone is broken. Under the action of rainfall, earthquakes and other factors, geological disasters such as landslides and collapses are relatively common in the area. Through data collection, remote sensing interpretation and field investigation, it was found that 588 landslides have occurred on both sides of the Lixian–Luojiabu fault zone with a high density of landslides (Figure 2).
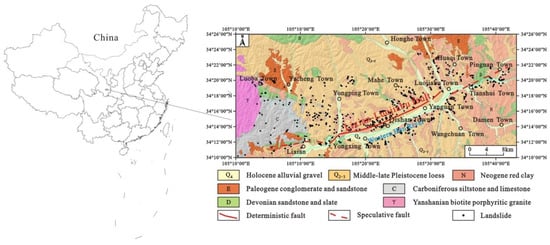
Figure 2.
Geographical location map of the study area.
3.2. Hazard Assessment
3.2.1. The Rain Condition
The eight main factors of slope gradient, slope height, slope type, slope aspect, engineering geological rock group, fault distance, river distance and precipitation in the study area were selected as the risk evaluation indicators under rainfall conditions. The following five models were used to carry out landslide risk assessments.
(1) Information model
Through statistical analysis, the information scale provided by each evaluation factor to the induced landslide is obtained (Table 1). After the information value of each influencing factor layer was calculated, all the factor layers were superimposed and the total information values ranged from −5.653300285 to 3.809999943. The larger the value, the greater the contribution to the occurrence of landslides, and the more likely it is landslides will occur. Finally, a landslide risk assessment map based on the information model was established (Figure 3).

Table 1.
Information provided by each evaluation factor for induced landslides.
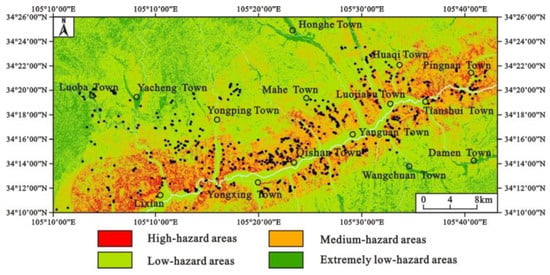
Figure 3.
Landslide hazard assessment map under the rainfall condition in the research area (information model).
(2) Logistic regression model
Firstly, the normalized value of landslide incidence was taken as the independent variable and the occurrence of landslides was taken as the dependent variable. Secondly, the statistical data of 588 landslide points were taken as one part of the training sample, the data of 588 non-landslide points randomly generated by ArcGIS software (selected outside the distribution area of landslide surface) were taken as the other part of the training sample and a total of 1176 training sample sets were obtained for calculation and analysis. Thirdly, modeling was carried out in combination with the evaluation index factors of the study area. Data on 1176 sample sets were imported into the SPSS software for calculation and logistic regression analysis (Table 2). Finally, the landslide hazard assessment diagram based on the logistic regression model was obtained (Figure 4).

Table 2.
Table of calculation results based on the logistic regression model.
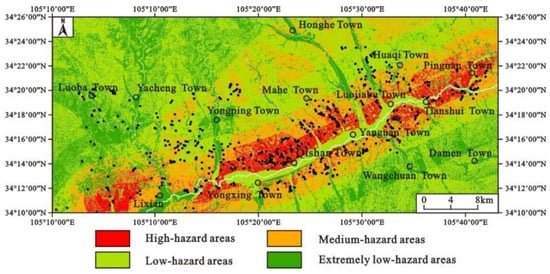
Figure 4.
Landslide hazard assessment map under the rainfall condition in the research area (logistic regression model).
(3) Fractal theory model
Firstly, based on the accumulation and transformation fractal theory, using the Origin software, the classification and variable dimension statistical analysis of landslide distribution density and various evaluation factors was carried out. The cumulative sum fractal sequence diagram of landslide distribution density and various first-order S1(r), second-order S2(r) and third-order S3(r) evaluation factors were obtained (Figure 5), and the fractal dimension values of various evaluation factors were determined according to the fitting relationship. Secondly, parameter assignment and weight calculation were carried out for various evaluation factors to form a quantitative statistical table of landslide risk based on the fractal theoretical model (Table 3). Finally, all factor layers were superimposed and calculated according to the above converted fractal weight values, and the calculation results were normalized to obtain the landslide hazard assessment map based on the fractal theoretical model (Figure 6).
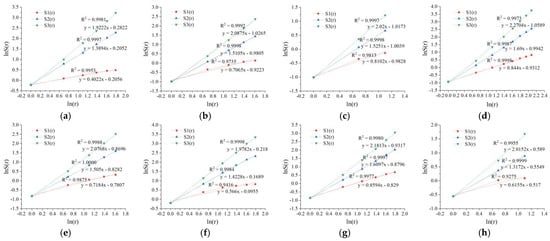
Figure 5.
The cumulative sum fractal sequence diagram of landslide distribution density and various evaluation factors. (a) Slope; (b) Slope height; (c) Slope type; (d) Aspect; (e) Engineering geological rock group; (f) Fracture distance; (g) River distance; (h) Precipitation.

Table 3.
Quantitative statistical table of landslide risk based on the fractal theory model.
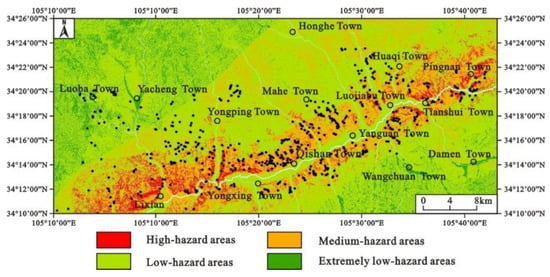
Figure 6.
Landslide hazard assessment map under the rainfall condition in the research area (fractal theory model).
(4) Logistic regression–information coupling model
Based on the basic principle of the logistic regression–information coupling model, after constructing the logistic regression–information model in the study area using regression coefficients (Table 4), the corresponding calculations were further completed with reference to the logistic regression calculation method. Finally, the AHP-Information-based model was formed. The landslide risk assessment map of the coupled model is presented in (Figure 7).

Table 4.
Landslide hazard calculation based on the logistic regression–information coupling model.
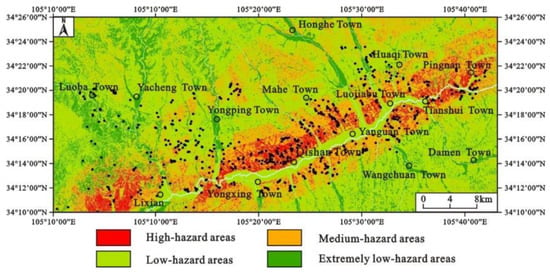
Figure 7.
Landslide hazard assessment map under the rainfall condition in the research area (logistic regression–information coupling model).
(5) Fractal theory–information coupling model
Based on the basic principle of the fractal theory–information coupling model, a summary of the analysis and the calculation of various evaluation factors is shown in Table 5. The landslide risk assessment map of the coupled model is shown in Figure 8.

Table 5.
Statistical table of landslide risk calculation based on the fractal theory–information coupling model.
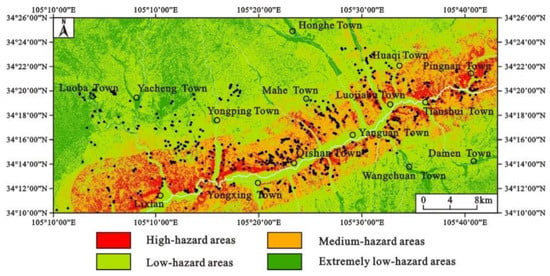
Figure 8.
Landslide hazard assessment map under the rainfall condition in the research area (fractal theory–information coupling model).
3.2.2. The Earthquake Condition
(1) Traditional Newmark model
When selecting engineering geological rock groups according to the classification results of rainfall conditions, the rock and soil mass in the research area is divided into the hardest rock group (I), the harder rock group (II), the softer rock group (III), the weak rock group (IV) and the loose rock group (V). Combined with the test results of the regional drilling sampling and trench sampling and synthesizing the existing achievements and data in the area, the mechanical parameters of various engineering geological rock groups used in the research area were obtained (Table 6). When selecting the terrain slope, the existing 1:50,000 DEM data are used to calculate the ratio between the height difference and the horizontal distance between adjacent grid cells.

Table 6.
Mechanical parameters of engineering geology rock group (traditional Newmark model).
When analyzing the stability of the landslide, the state of the sliding body is considered the dry state and the ratio m of the buried depth of the groundwater above the failure surface to the depth of the failure surface is taken as 0. Due to the shallow depth of most of the landslide failure surfaces in the study area, the thickness t of the sliding mass here is approximately 5 m. Using Equation (7), the distribution of the static safety factor Fs of the regional slope body was calculated, and then, the corresponding regional critical acceleration distribution was obtained.
The cumulative displacement value of the landslide is based on the calculation of the regional static safety factor and the regional critical acceleration, and the Arias strength calculation was carried out. Since the sequence of the ground motion acceleration and other related parameters were not collected in this area, the empirical formula for fitting the Arias intensity was derived from Roberto, who analyzed 190 acceleration time history records of 17 strong earthquakes in Italy [35]:
where PGA is the peak acceleration of the seismic vibration.
According to the zoning of seismic parameters corresponding to a 10% probability of exceedance in 50 years, prepared by the Lanzhou Seismological Institute of the China Earthquake Administration, the corresponding Ia distribution is obtained. Then, Equation (9) is used to obtain the cumulative displacement value of Newmark under the condition of 10% probability of exceedance in 50 years in the research area
The probability of landslide occurrence is obtained by Equation (11) on the basis of the calculation result of the cumulative displacement of the landslide. According to the international research results on earthquake landslide hazard zoning [9,36], the earthquake landslide hazard level is divided into high-hazard areas (earthquake landslide occurrence probability is greater than 25%), medium-hazard areas (earthquake landslide occurrence probability is 15–25%), low-hazard areas (earthquake landslide occurrence probability is 5–15%) and extremely low-hazard areas (earthquake landslide occurrence probability less than 5%) (Figure 9).
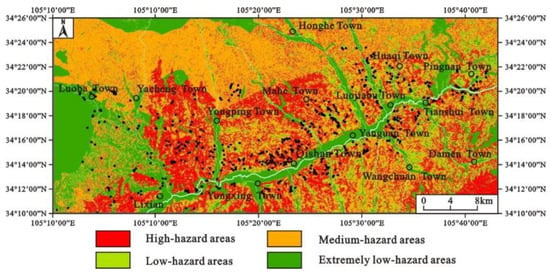
Figure 9.
Landslide hazard assessment map under the earthquake conditions in the research area (traditional Newmark model).
(2) Improved Newmark model
When selecting engineering geological rock group parameters, due to the existence of an unsaturated zone in loose rock groups and weak rock groups, it is necessary to consider the effect of matrix suction. Based on the test results of regional drilling sampling and trench sampling, and synthesizing the existing results in this area, the mechanical parameters of the engineering geology rock group, matrix suction (Table 7) and soil–water characteristic curves of loose rock groups and weak rock groups were finally obtained (Figure 10). The terrain slope parameters are the same as in the previous section.

Table 7.
Value table of mechanical parameters of engineering geology rock group (improved Newmark model).
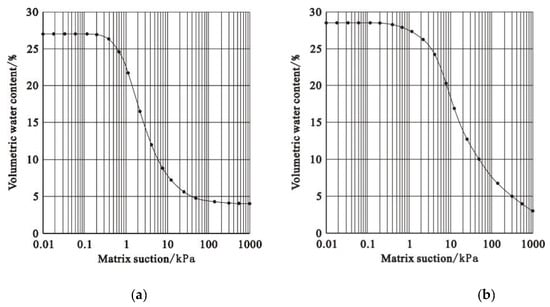
Figure 10.
Soil–water characteristic curve of the research area. (a) Loose rock group; (b) Weak rock group.
When carrying out the landslide hazard assessment, referring to the traditional Newmark model method, the landslide hazard assessment map under the condition of 10% probability of exceedance in 50 years in the research area was finally obtained (Figure 11).
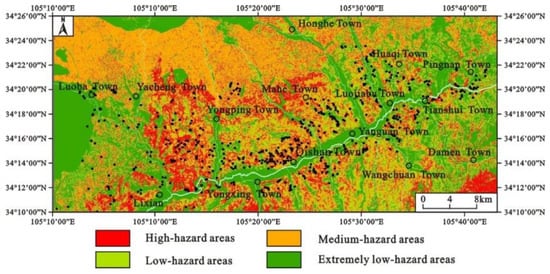
Figure 11.
Landslide hazard assessment map under the earthquake condition in the research area (improved Newmark model).
3.3. Data Validation and Comparative Analysis
In order to analyze and compare the landslide hazard assessment results calculated by various models, the receiver operating characteristic curve method (referred to as ROC curve, Receiver Operating Characteristic) and the Kappa coefficient method were used to verify the calculation results. The ROC curve method is based on the area under the ROC curve (referred to as AUC value; area under the curve) as an indicator to measure the accuracy. It is generally believed that AUC values between 0.7 and 0.9 indicate that the results have certain reliability, and the closer the value is to 1, the higher the reliability [37]. The Kappa coefficient method is a classification accuracy evaluation index based on the confusion matrix algorithm, which reflects the consistency between the observed value and the simulation result and is also called the consistency test [38]. It is generally believed that when the Kappa coefficient is greater than 0.75, the accuracy of the model prediction is better.
3.3.1. The Rain Condition
The comparison shows that the evaluation results of the five models under the rainfall condition mainly shows low-hazard areas and extremely low-hazard areas, and the high-hazard areas account for a small area. The existing landslides are concentrated in high-hazard areas and medium-hazard areas, and the density of landslide points shows a gradual increasing trend from extremely low-hazard areas to high-hazard areas. The test results of the ROC curve method and the Kappa coefficient method show that the evaluation results of the fractal theory–information coupling model are more advantageous (Table 8 and Figure 12). This method not only considers the magnitude of the hazard-causing effect in the sub-intervals of each influencing factor but also takes into account the contribution weights of different factors to the occurrence of landslides, which improves the accuracy of landslide hazard assessment. The model can be used as the optimal model for the evaluation of landslide hazards along the Lixian–Luojiabu fault zone in Gansu province under the rainfall condition.

Table 8.
Summary table of accuracy of test results of different model evaluation methods under the rainfall condition.
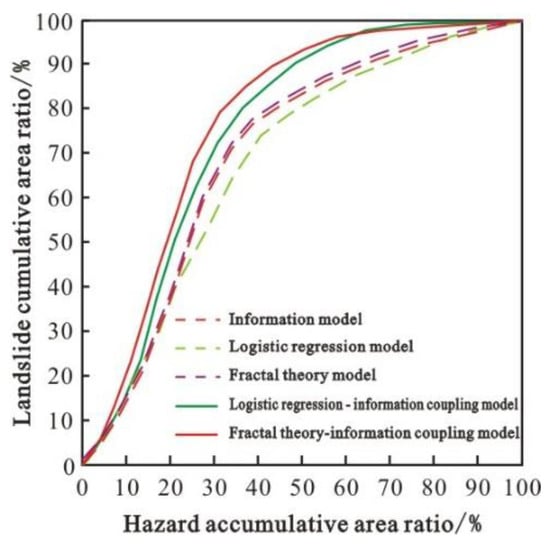
Figure 12.
ROC curves of different model evaluation methods under the rainfall condition.
3.3.2. The Earthquake Condition
The comparison shows that the evaluation results of the two models under the earthquake condition are mainly medium-hazard areas and extremely low-hazard areas, followed by high-hazard areas and finally low-hazard areas. Existing landslides are concentrated in high-hazard areas and medium-hazard areas, and the density of landslide points shows a gradual increasing trend from extremely low-hazard areas to high-hazard areas. The test results of the ROC curve method and the Kappa coefficient method show that evaluation results calculated by the improved Newmark model considering the effect of matrix suction are more reasonable (Table 9 and Figure 13). The model can be used as the optimal model for the evaluation of landslide hazards along the Lixian–Luojiabu fault zone in Gansu province under the earthquake condition.

Table 9.
Summary table of accuracy test results of different model evaluation methods under the earthquake condition.
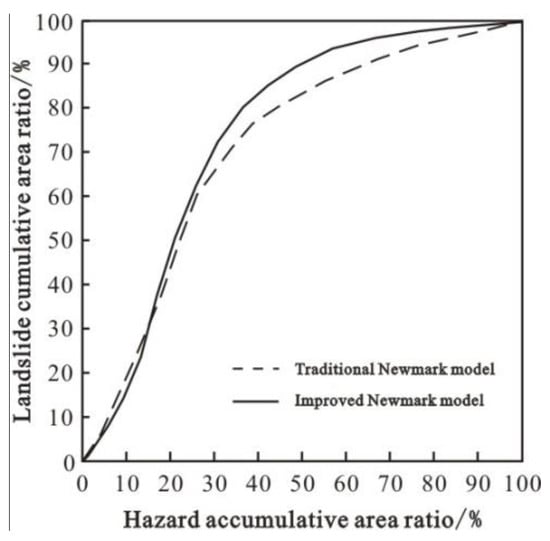
Figure 13.
ROC curves of different model evaluation methods under the earthquake condition.
4. Conclusions
Taking the area along the Lixian–Luojiabu fault zone in Gansu province in China as the research area, the landslide hazard assessment method based on the fractal theory–information coupling model was proposed for the rainfall condition, and a landslide hazard assessment method based on the improved Newmark model considering the matrix suction effect was proposed for the earthquake condition. The evaluation results of these two models were compared with those of traditional models, and the accuracy test was carried out by using the ROC curve and Kappa coefficient to explore the optimal evaluation model under different working conditions.
The results showed that the fractal theory–information coupling model had the largest AUC value and Kappa coefficient value under the rainfall condition, which were 0.856 and 0.807, respectively. The test value of the logistic regression–information coupling model was second, and the test values of the other three models were all lower than 0.8. This showed that the evaluation of the fractal theory–information coupling model was better than those of other models under the rainfall condition. This is mainly because the method not only takes into account the size of the disaster-causing effect of each influencing factor sub-interval but also takes into account the contribution weights of different factors to the occurrence of landslides, which improves the accuracy of landslide hazard assessment. The AUC value and Kappa coefficient value of the improved Newmark model considering the effect of matrix suction under the earthquake condition were 0.805 and 0.794, respectively, which were larger than the test values of traditional the Newmark model. This shows that the evaluation of the improved Newmark model considering matric suction was better than that of traditional the Newmark model under the earthquake condition. This is mainly because this method makes up for the defect of ignoring the effect of matrix suction in the traditional model, making the evaluation results more reliable and reasonable.
It is worth noting that the fractal theory–information coupling model for landslide hazard assessment needs to be more accurate when the number of landslide samples is large enough and the fractal calculation process is cumbersome. Simpler calculation methods need to be further explored in the future. When the improved Newmark model considering matric suction is used to evaluate landslide hazard assessment, the matric suction values are mainly based on empirical parameters, and the accuracy of the parameters affects the calculation accuracy.
Author Contributions
Writing—original draft, conceptualization, methodology, resources, data analysis, W.F.; investigation, methodology, writing—review, B.H.; project administration, Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Geological Survey Project of China Geological Survey (No. 12120114035701, DD20160276, DD20190642 and DD20221739).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, S.; Ryu, J.-H.; Kim, I.-S. Landslide susceptibility analysis and its verification using likelihood ratio, logistic regression, and artificial neural network models: Case study of Youngin, Korea. Landslides 2007, 4, 327–338. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Yin, K.L. Landslide Disaster Risk Analysis; Science Press: Beijing, China, 2010. [Google Scholar]
- Tang, Y.M.; Zhang, M.S.; Li, L.; Xue, Q. Discrimination to the landslide susceptibility, hazard and risk assessment. Hydrogeol. Eng. Geol. 2011, 38, 125–129. [Google Scholar]
- Wu, S.R. Landslide Risk Assessment Theory and Technology; Science Press: Beijing, China, 2012. [Google Scholar]
- Tang, Y.M.; Zhang, M.S.; Li, Z.G.; Feng, W. Review and comparison oninland and overseas Geo-hazards risk management. Northwestern Geol. 2015, 48, 238–246. [Google Scholar]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.B.; Wu, S.R. Key theory and method of landslide hazard risk assessments. Geol. Bull. China 2008, 27, 1764–1770. [Google Scholar]
- Jibson, R.W.; Harp, E.L.; Michael, J.A. A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef]
- Rathje, E.M.; Saygili, G. Probabilistic Seismic Hazard Analysis for the Sliding Displacement of Slopes: Scalar and Vector Approaches. J. Geotech. Geoenviron. Eng. 2008, 134, 804–814. [Google Scholar] [CrossRef]
- Wang, T.; Wu, S.R.; Shi, J.S.; Xin, P. Case study on rapid assessment of regional seismic landslide hazard based on simplified Newmark displacement model: Wenchuan Ms 8.0 earthquake. J. Eng. Geol. 2013, 21, 16–24. [Google Scholar] [CrossRef]
- Wang, T.; Wu, S.R.; Shi, J.S.; Xin, P. Concepts and mechanical assessment method for seismic landslide hazard: A review. J. Eng. Geol. 2015, 23, 93–104. [Google Scholar]
- Chen, X.L.; Yuan, R.M.; Yu, L. Applying the Newmark’s model to the assessment of earthquake-triggered landslides during the Lushan earthquake. Seismol. Geol. 2013, 35, 661–670. [Google Scholar]
- Chen, X.L.; Zhang, L.; Wang, M.M. Study on the distribution pattern of earthquake-triggered landslides based on seismic landslide susceptibility analysis: A case study of landslides triggered by the Ms6.5 Ludian earthquake in 2014. Seismol. Geol. 2018, 40, 1129–1139. [Google Scholar]
- Chen, X.L.; Shan, X.J.; Zhang, L.; Liu, C.G.; Han, N.N.; Lan, J. Quick assessment of earthquake-triggered landslide hazards: A case study of the 2017 Ms 7.0 Jiuzhaigou earthquake. Earth Sci. Front. 2018, 25, 312. [Google Scholar]
- Yang, Z.H.; Zhang, Y.S.; Guo, C.B.; Du, G.L. Landslide hazard rapid assessment in the Ms 8.1 nepal earthquake-impacted area, based on Newmark model. J. Geomech. 2017, 23, 115–124. [Google Scholar]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Lee, S. Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Gregory, C.; Ohlmacher; Davis, J.C. Using multiple logistic regression and GIS technology to predict landslide hazard in northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar]
- Akbar, T.; Ha, S. Landslide hazard zoning along Himalayan Kaghan Valley of Pakistan-by integration of GPS, GIS, and remote sensing technology. Landslides 2011, 8, 527–540. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Gao, K.C.; Cui, P.; Zhao, C.Y.; Wei, F.Q. Landslide hazard evaluation of Wanzhou based on GIS information value method in the three gorges reservoir. Chin. J. Rock Mech. Eng. 2006, 25, 991–996. [Google Scholar]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 2020, 277, 124159. [Google Scholar] [CrossRef]
- Zhao, P.D.; Hu, W.L.; Li, Z.J. Statistical Prediction of Mineral Deposits; Geological Press: Beijing, China, 1983. [Google Scholar]
- Falsaperla, S.; Graziani, S.; Nunnari, G.; Spampinato, S. Automatic classification of volcanic earthquakes by using Multi-Layered neural networks. Nat. Hazards 1996, 13, 205–228. [Google Scholar] [CrossRef]
- Ruan, S.Y.; Huang, R.Q. Application of GIS-based information model on assessment of geological hazards risk. J. Chengdu Univ. Technol. 2001, 28, 89–92. [Google Scholar]
- Peterson, H.B.; Kleinbaum, D.G. Interpreting the literature in obstetrics and gynecology: II. Logistic regression and related issues. Obstet. Gynecol. 1991, 78, 717–720. [Google Scholar]
- Cong, W.Q.; Pan, M.; Li, T.F.; Wu, Z.X.; Lv, G.X. Key research on landslide and debris flow hazard zonation based on GIS. Earth Sci. Front. 2006, 13, 185–190. [Google Scholar]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.H. Fractal analyses for parameters of wind, wave and current. Port Eng. Technol. 1996, 3, 6–9. [Google Scholar]
- Xue, T.F.; Yang, Q.; Luan, M.T. Research on fractal characters of spatial distribution of landslide based on GIS. Rock Soil Mech. 2007, 28, 347–350. [Google Scholar]
- Wilson, R.C.; Keefer, D.K. Dynamic analysis of a slope failure from the 6 August 1979 Coyote Lake, California, earthquake. Bull. Seism. Soc. Am. 1983, 73, 863–877. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Yang, X.P.; Feng, X.J.; Huang, X.N.; Song, F.M.; Li, G.Y.; Chen, X.C.; Zhang, L.; Huang, W.L. The late quaternary activity characteristics of the lixian-luojiabu fault: A discussion on the seismogenic mechanism of the lixian M8 earthquake in 1654. Chin. J. Geophys. 2015, 58, 504–519. [Google Scholar]
- Roberto, R. Seismically induced landslide displacements: A predictive model. Eng. Geol. 2000, 58, 337–351. [Google Scholar]
- Yang, Z.H.; Guo, C.B.; Wu, R.A.; Zhong, N.; Ren, S.S. Predicting seismic landslide hazard in the Batang fault zone of the Qinghai-Tibet Plateau. Hydrogeol. Eng. Geol. 2021, 48, 91–101. [Google Scholar]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, W.; Hu, J.; Zhang, H.; Wu, P.; He, H. Kappa coefficient: A popular measure of rater agreement. Shanghai Arch Psychiatry 2015, 27, 62–67. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).