Minimum Safety Factor Evaluation of Slopes Using Hybrid Chaotic Sand Cat and Pattern Search Approach
Abstract
:1. Introduction
- An efficient hybrid metaheuristic approach based on chaotic sand cat and pattern search techniques, known as CSCPS, was developed.
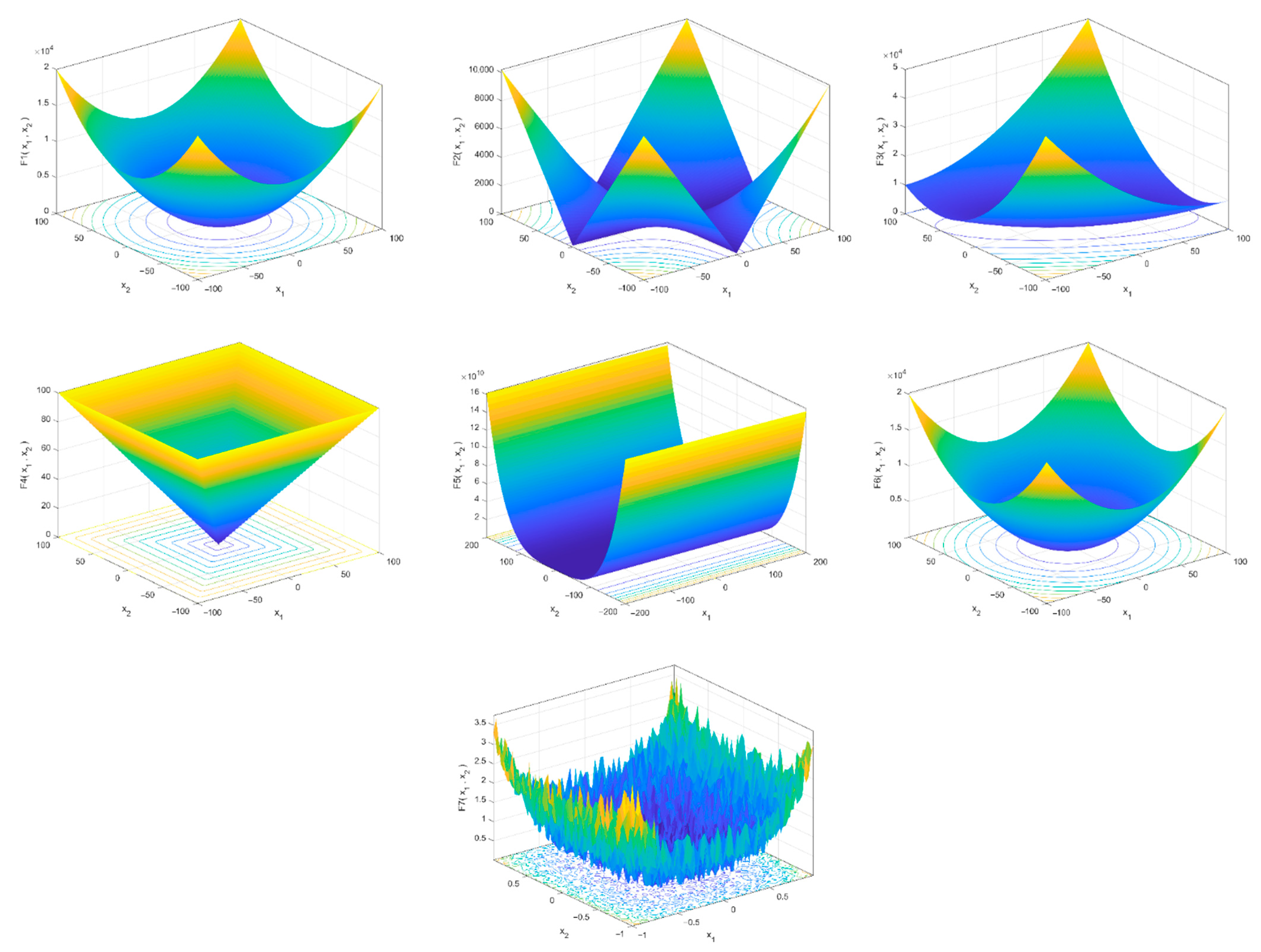
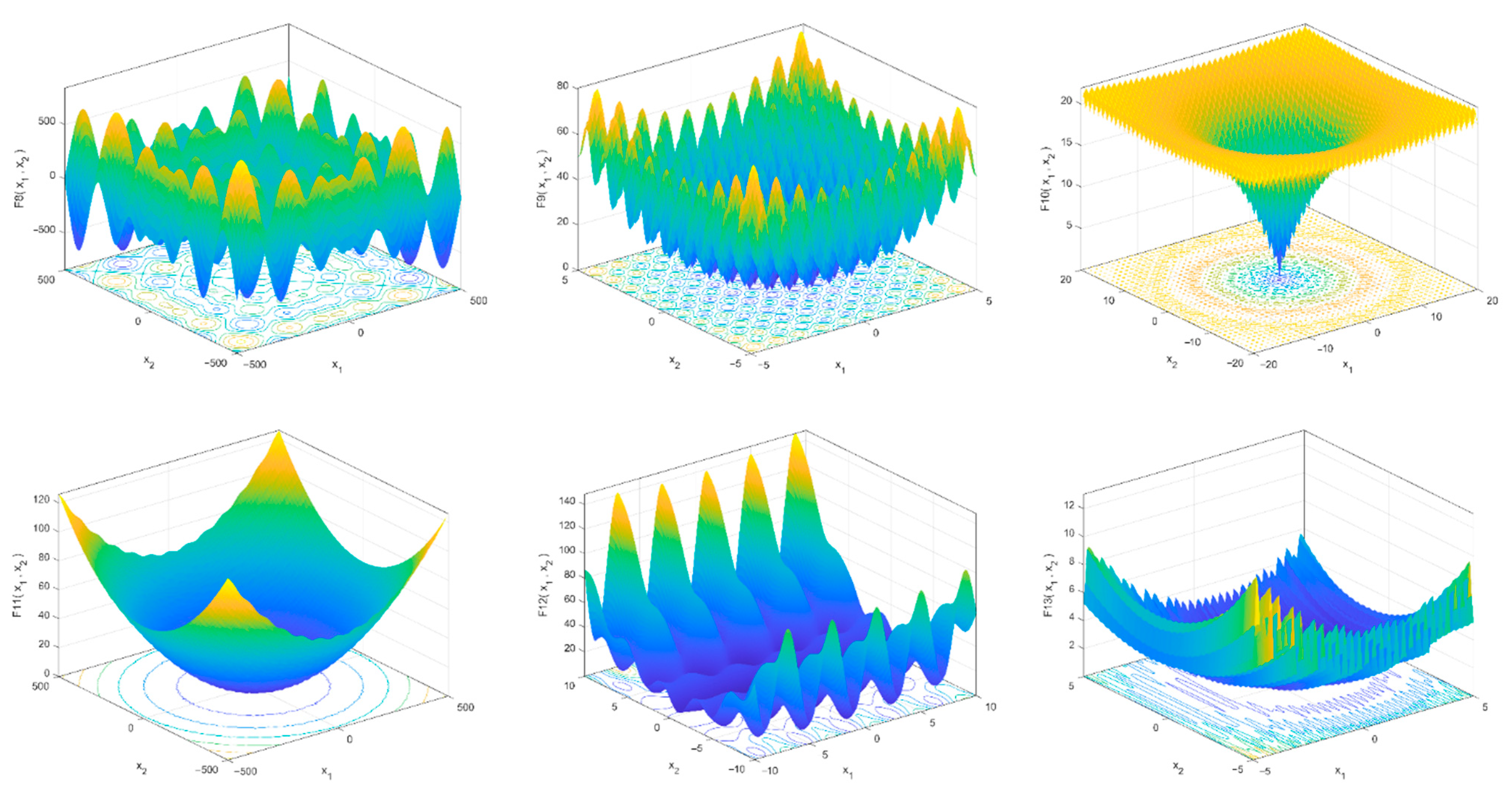
- The performance of CSCPS for numerical function optimization was assessed on thirteen common benchmarking functions, and the results were compared with existing commonly used optimization algorithms.
- To demonstrate the efficiency of the proposed technique in solving real-world problems, the new method was used to determine the minimum factor of safety of earth slopes.
- The objective function of a slope stability problem was modeled by using the Morgenstern–Price limit equilibrium approach for the slip surface’s overall shape.
- The efficiency of the proposed CSCPS for slope stability assessment was investigated by using two benchmark problems based on the literature, and the obtained results were compared with those evaluated previously by the other techniques.
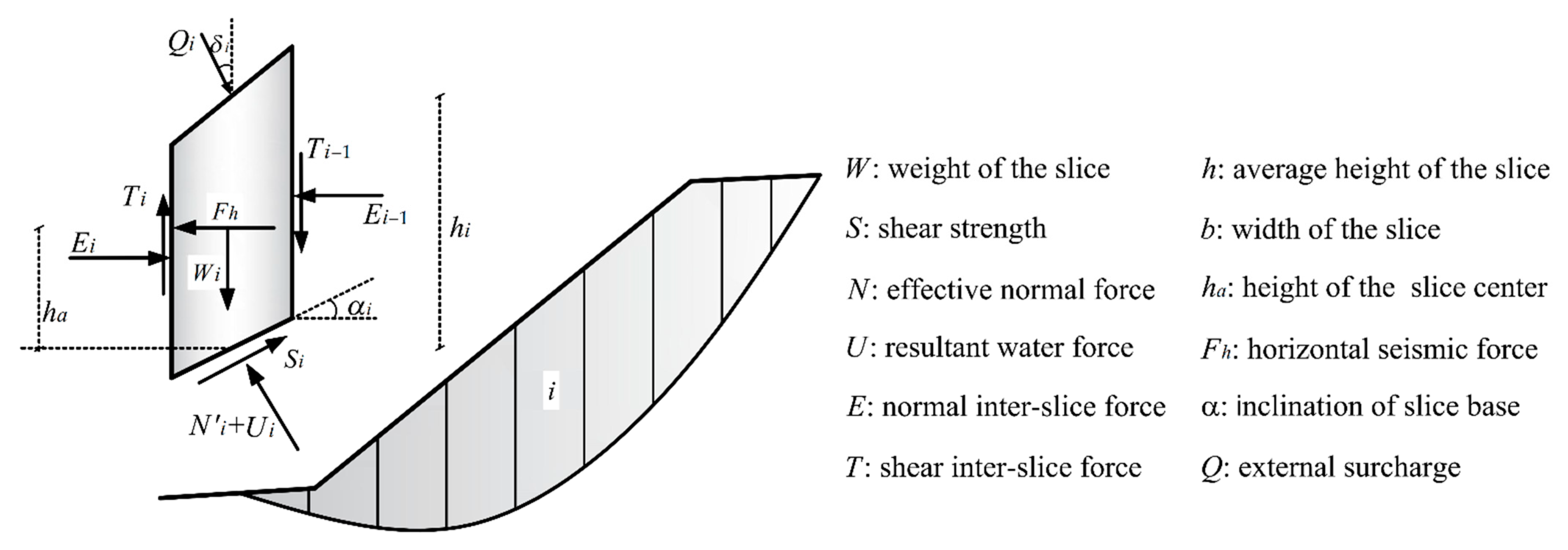
2. Safety Factor Formulation
- Step 1.
- Create a trial slip surface and divide it into n vertical segments.
- Step 2.
- Determine Ri and Ti by using the equations below:
- Step 3.
- Pick the function for inter-slice forces; f(x) = 1 is assumed in this study.
- Step 4.
- Consider FOS and λ initial amounts according to the following criteria:The λ and FOS might be set to 0 and 1, respectively, as their initial values [64].
- Step 5.
- Evaluate Φi and i−1 based on Equations (6) and (7).
- Step 6.
- Calculate FOS based on Equation (8):
- Step 7.
- Compute Φi and i−1 and calculate FOS once more by performing Steps 5 and 6 again.
- Step 8.
- Define Ei and λ based on the Equations (9) and (10).
- Step 9.
- Reevaluate FOS by using the obtained λ, and this process ends when the distinction between the found FOS and λ falls below 0.005 and 0.01, respectively. For the analysis in this paper, the generation failure surface approach developed by Cheng et al. [65] was implemented for the general form of the failure surface, which divides the assumed failure soil mass into some vertical sections of equal width.
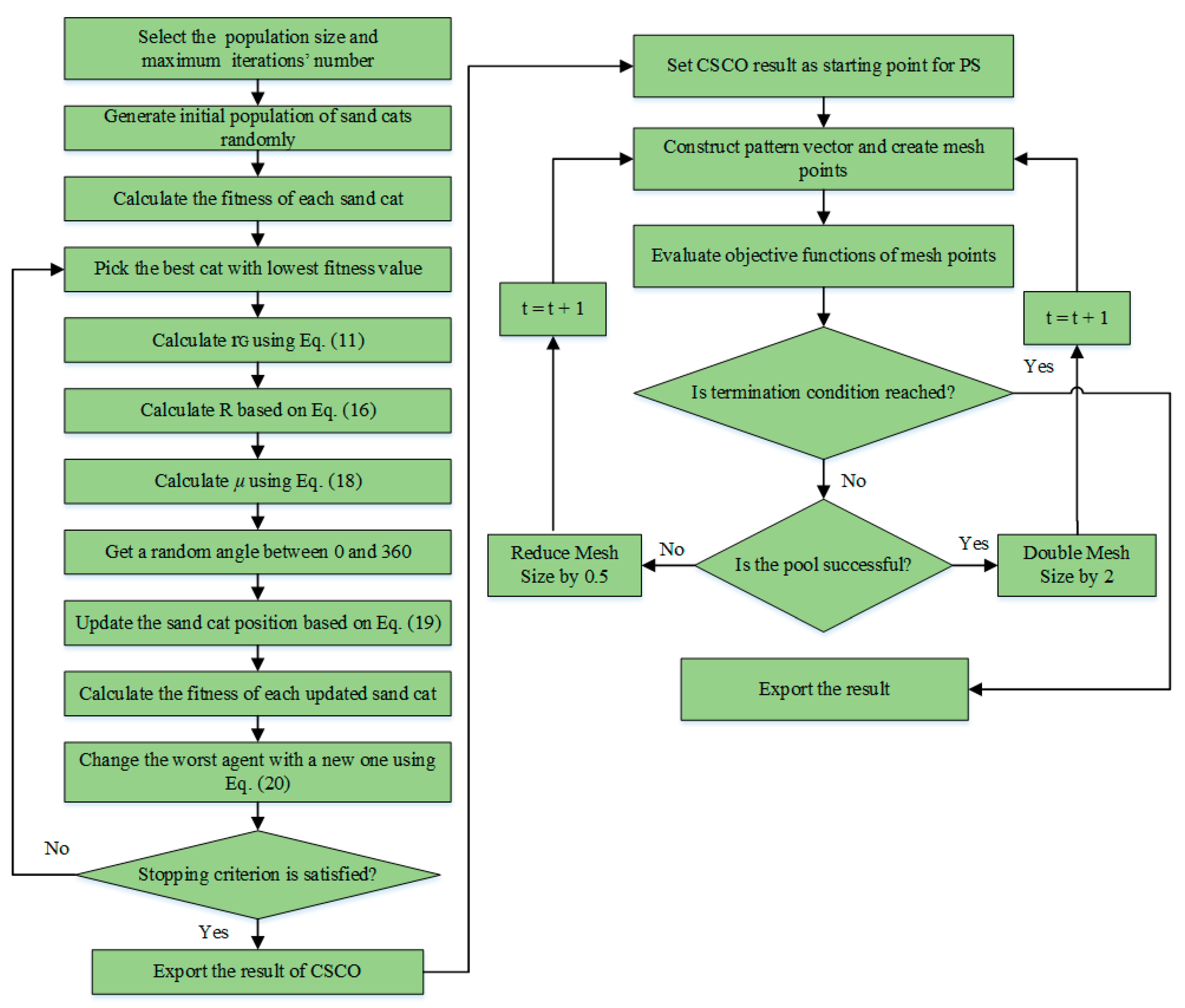
3. Proposed Chaotic Sand Cat and Pattern Search
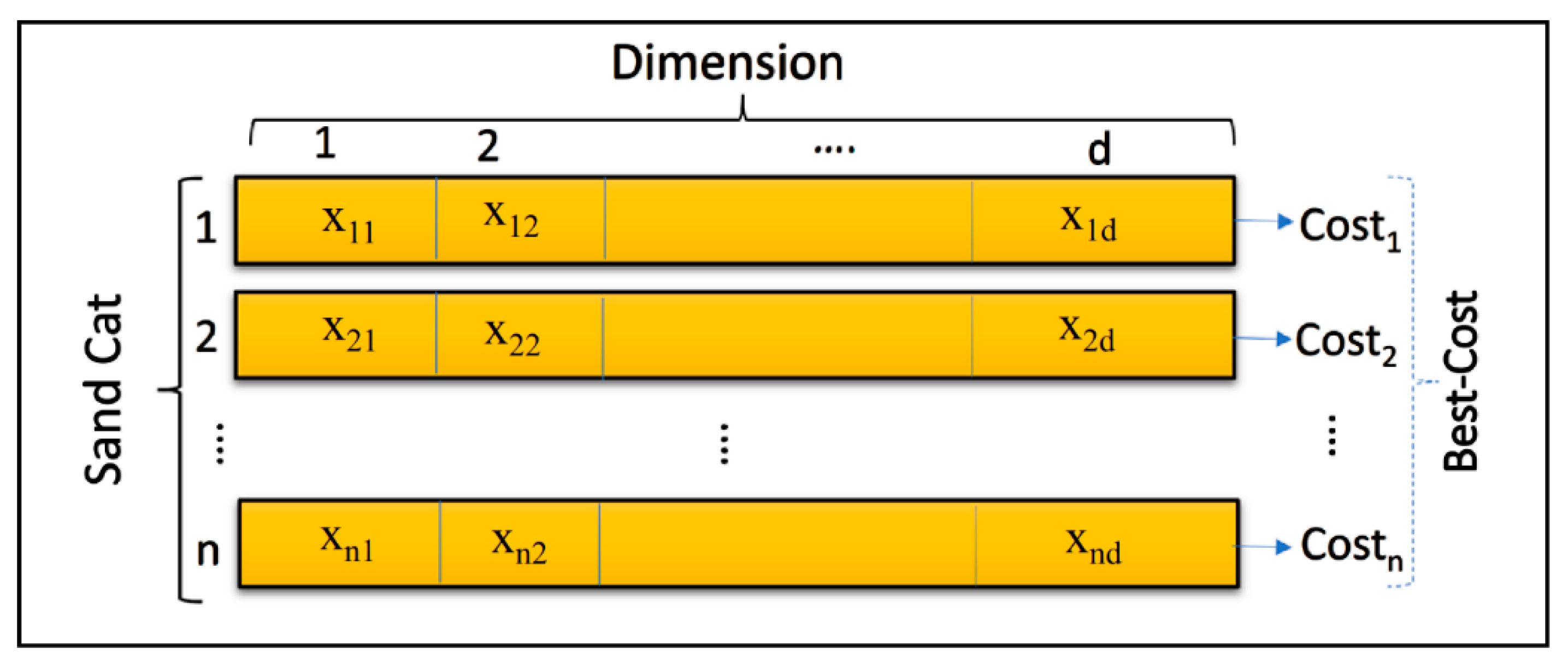
3.1. Sand Cat Optimization
| Algorithm 1. Sand cat optimization algorithm. |
| Initialize the population Calculate the fitness function based on the objective function Initialize the r, rG, R While (t ≤ tMax) For each sand cat Get a random angle θ ( If (|R| ≤ 1) Update the search agent based on exploitation part of Equation (17); Else Update the search agent based on the exploration part of Equation (17); End End t = t+1 End |
3.2. Chaotic Sand Cat Optimization
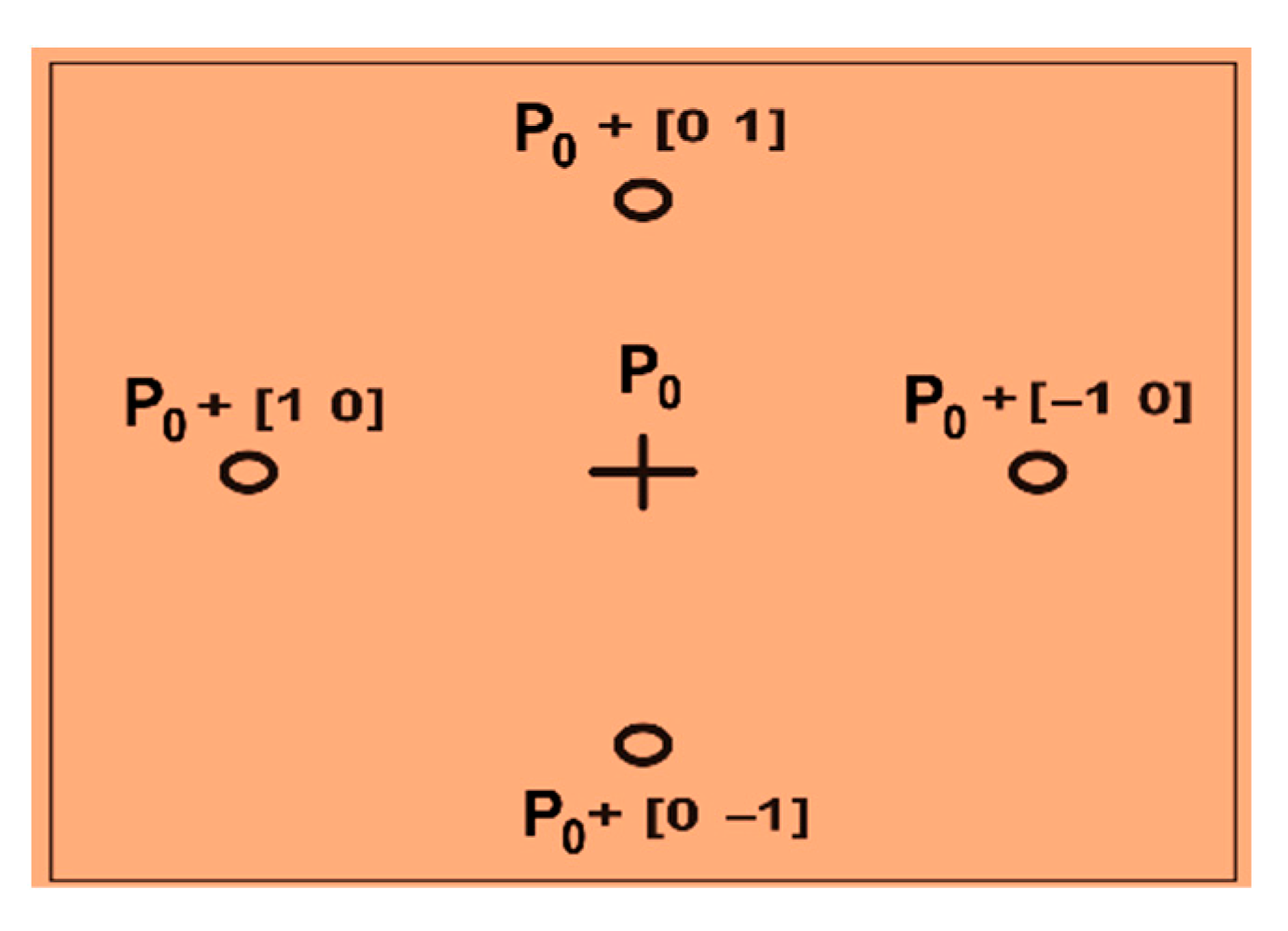
3.3. Pattern Search (PS)
3.4. Chaotic Sand Cat–Pattern Search
4. Model Verification
5. Model Application
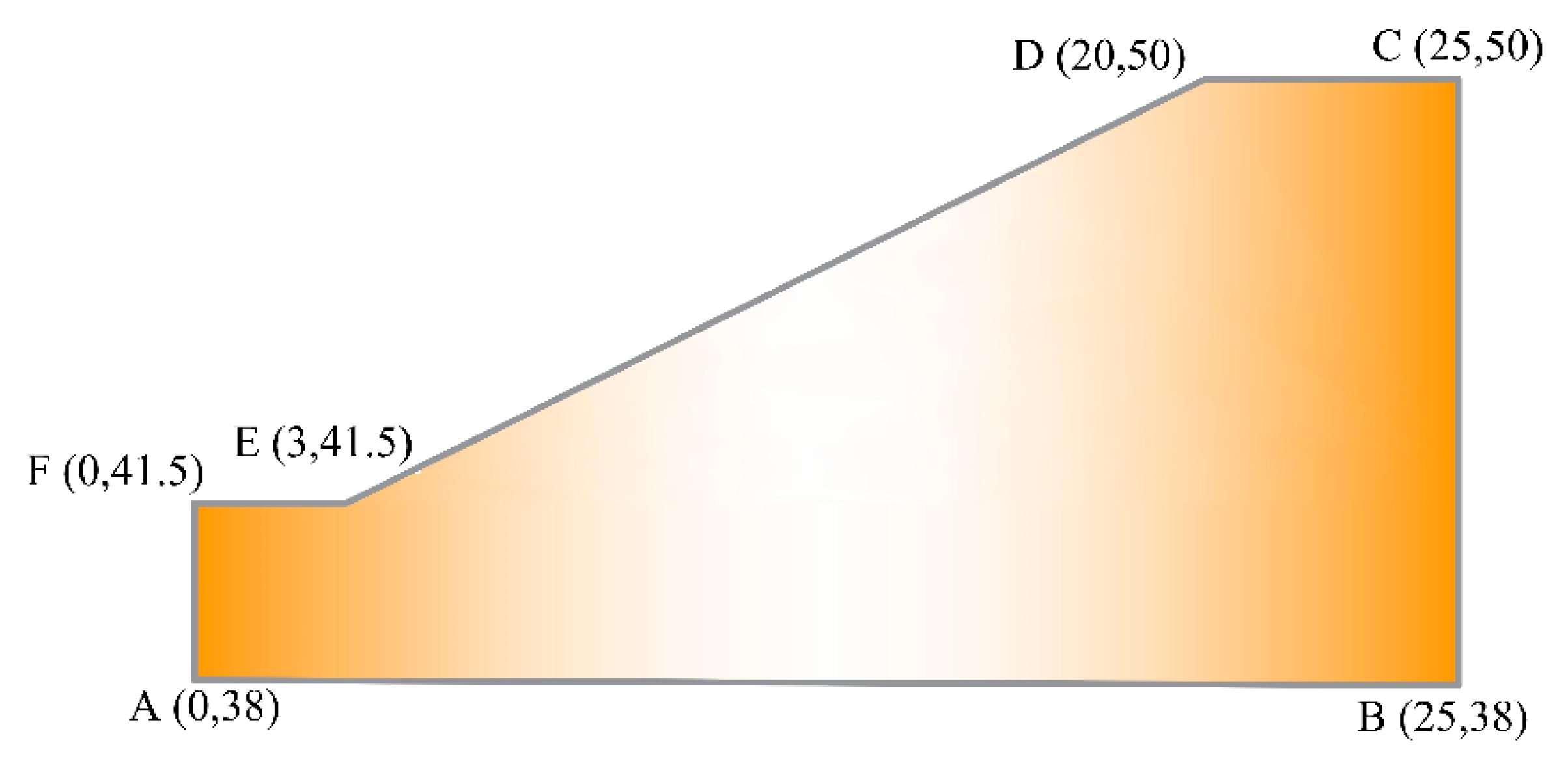
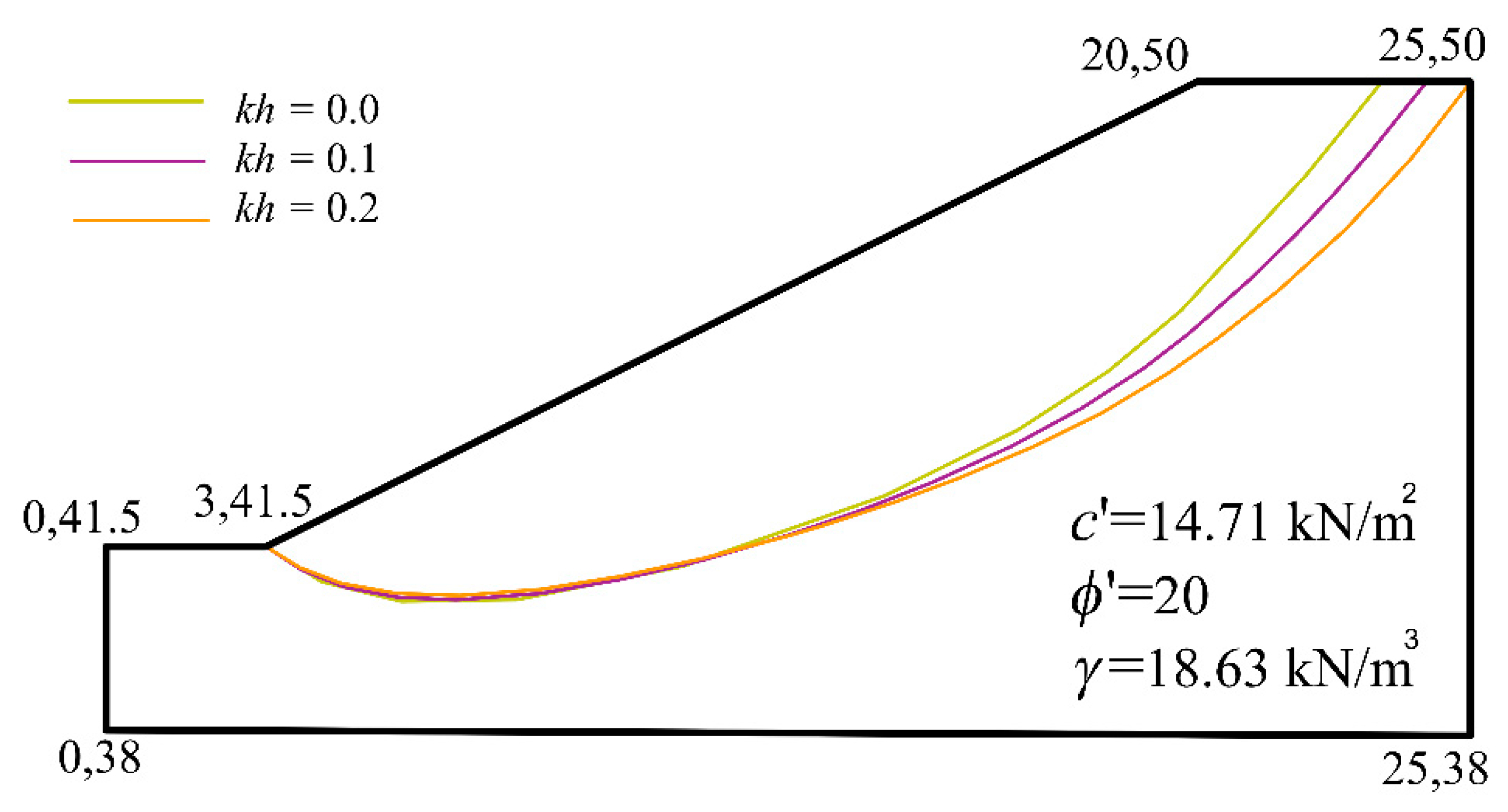
5.1. A Uniform Soil Slope
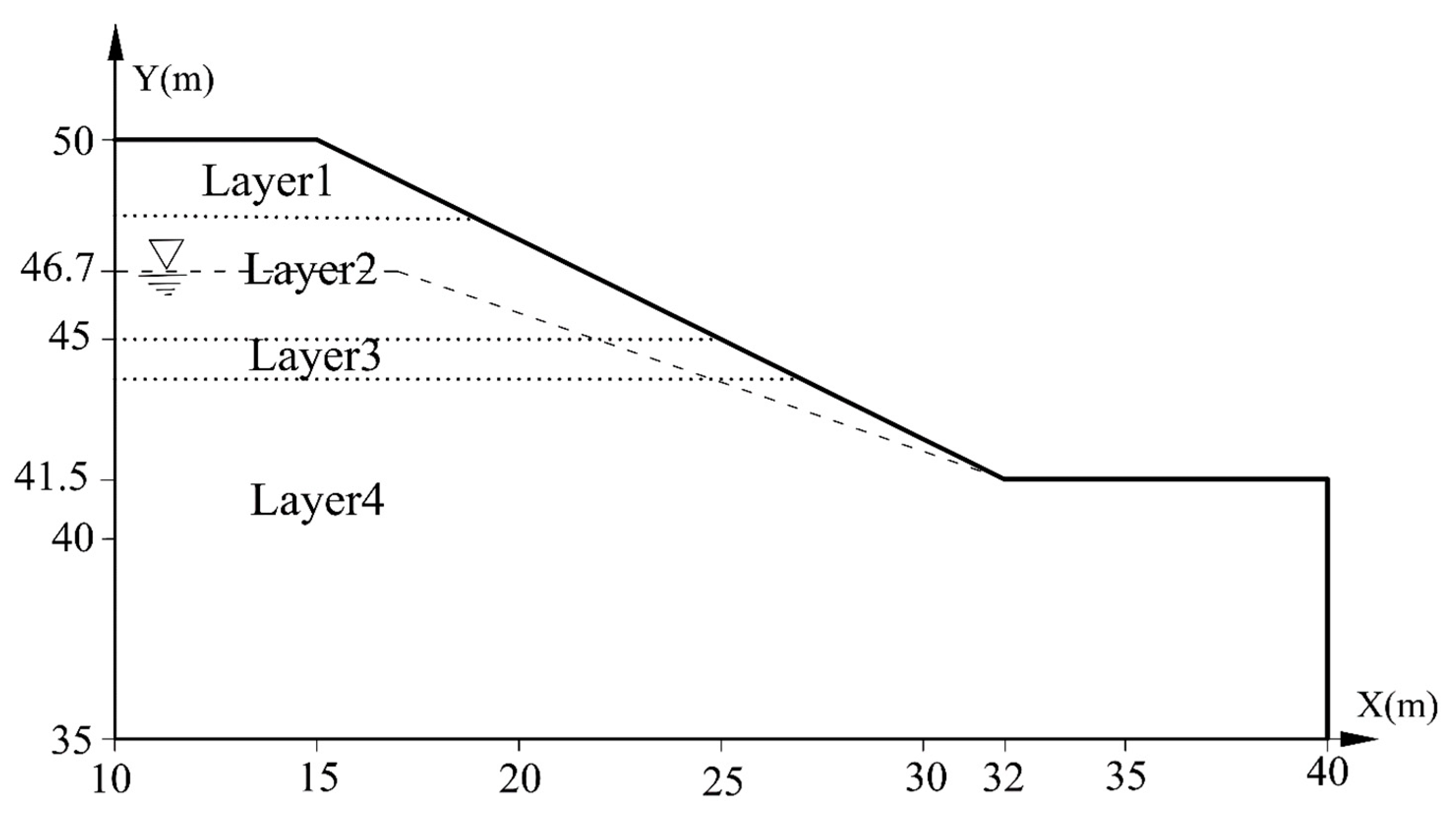
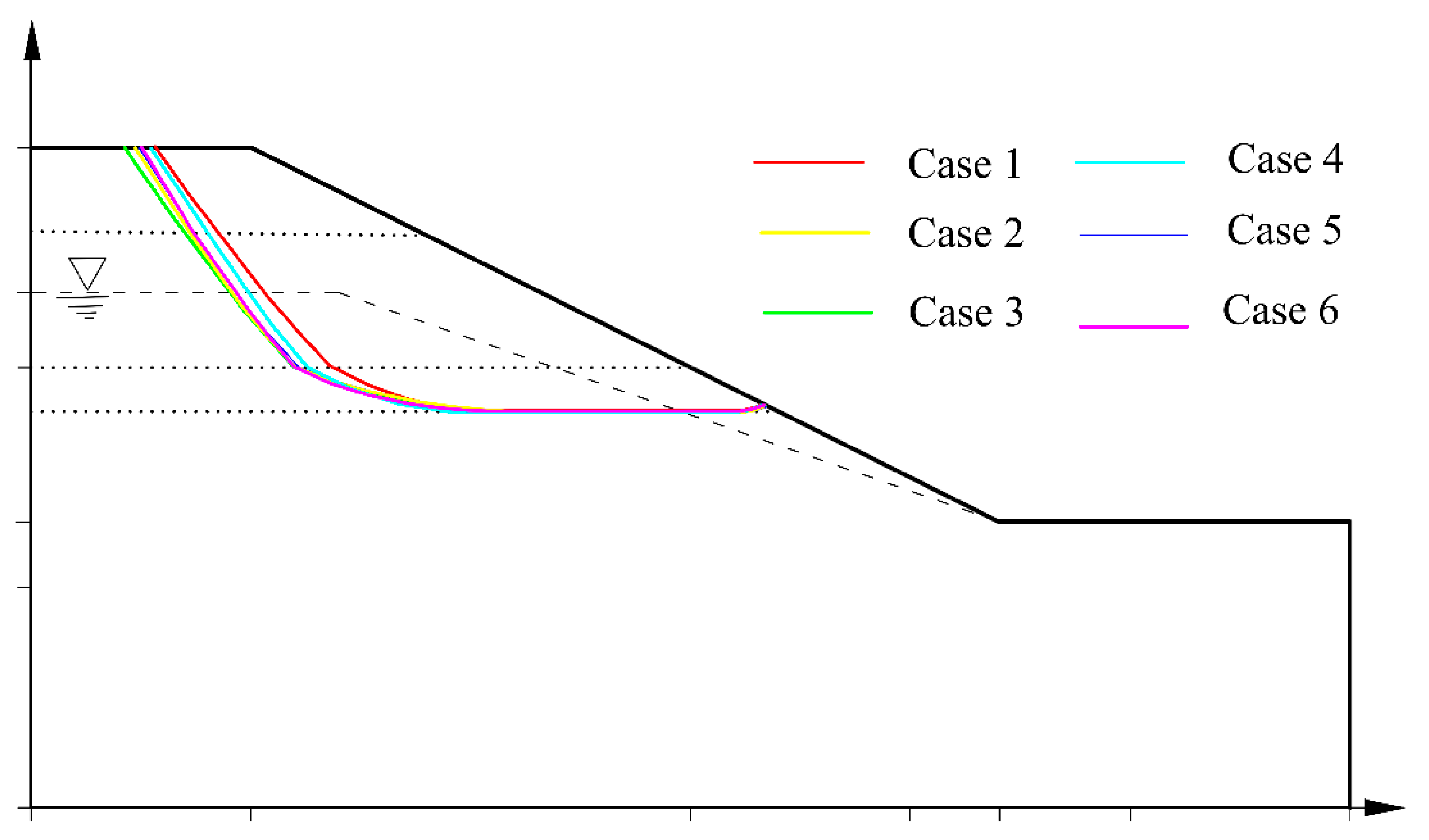
5.2. Slope in a Multi-Layered Soil
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. Locating the general failure surface of earth slope using particle swarm optimization. Civ. Eng. Environ. Syst. 2012, 29, 41–57. [Google Scholar] [CrossRef]
- Chen, Z.; Shao, C. Evaluation of minimum factor of safety in slope stability analysis. Can. Geotech. J. 1988, 25, 735–748. [Google Scholar] [CrossRef]
- Aryal, K.; Sandven, R.; Nordal, S. Slope stability evaluation by limit equilibrium and finite element methods. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; pp. 2471–2476. [Google Scholar]
- Baker, R.; Shukha, R.; Operstein, V.; Frydman, S. Stability charts for pseudo-static slope stability analysis. Soil Dyn. Earthq. Eng. 2006, 26, 813–823. [Google Scholar] [CrossRef]
- Tang, H.; Liu, X.; Xiong, C.; Wang, Z.; Ez Eldin, M. Proof of nondeterministic polynomial-time complete problem for soil slope-stability evaluation. Int. J. Geomech. 2016, 16, C4015004. [Google Scholar] [CrossRef]
- Zolfaghari, A.R.; Heath, A.C.; McCombie, P.F. Simple genetic algorithm search for critical non-circular failure surface in slope stability analysis. Comput. Geotech. 2005, 32, 139–152. [Google Scholar] [CrossRef]
- Wang, H.; Moayedi, H.; Kok Foong, L. Genetic algorithm hybridized with multilayer perceptron to have an economical slope stability design. Eng. Comput. 2021, 37, 3067–3078. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, L.; Chi, S. Performance studies on six heuristic global optimization methods in the location of critical slip surface. Comput. Geotech. 2007, 34, 462–484. [Google Scholar] [CrossRef]
- Kashani, A.R.; Gandomi, A.H.; Mousavi, M. Imperialistic competitive algorithm: A metaheuristic algorithm for locating the critical slip surface in 2-dimensional soil slopes. Geosci. Front. 2016, 7, 83–89. [Google Scholar] [CrossRef] [Green Version]
- Gandomi, A.; Kashani, A.; Mousavi, M.; Jalalvandi, M. Slope stability analysis using evolutionary optimization techniques. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 251–264. [Google Scholar] [CrossRef]
- Himanshu, N.; Burman, A. Determination of critical failure surface of slopes using particle swarm optimization technique considering seepage and seismic loading. Geotech. Geol. Eng. 2019, 37, 1261–1281. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.; El-Shafie, A. Reliability analysis of earth slopes using hybrid chaotic particle swarm optimization. J. Cent. South Univ. Technol. 2011, 18, 1626–1637. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Optimal location of PSS using improved PSO with chaotic sequence. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; pp. 253–258. [Google Scholar]
- Delice, Y.; Aydoğan, E.K.; Özcan, U.; İlkay, M.S. A modified particle swarm optimization algorithm to mixed-model two-sided assembly line balancing. J. Intell. Manuf. 2017, 28, 23–36. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A. Optimization and coordination of damping controls for optimal oscillations damping in multi-machine power system. Int. Rev. Electr. Eng. 2011, 6, 1984–1993. [Google Scholar]
- Cheng, Y.; Li, L.; Lansivaara, T.; Chi, S.; Sun, Y. An improved harmony search minimization algorithm using different slip surface generation methods for slope stability analysis. Eng. Optim. 2008, 40, 95–115. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimisation of retaining walls using hybrid adaptive gravitational search algorithm. Civ. Eng. Environ. Syst. 2014, 31, 229–242. [Google Scholar] [CrossRef]
- Ji, Y.; Tu, J.; Zhou, H.; Gui, W.; Liang, G.; Chen, H.; Wang, M. An adaptive chaotic sine cosine algorithm for constrained and unconstrained optimization. Complexity 2020, 2020, 6084917. [Google Scholar] [CrossRef]
- Hegazy, A.E.; Makhlouf, M.; El-Tawel, G.S. Improved salp swarm algorithm for feature selection. J. King Saud Univ.-Comput. Inf. Sci. 2020, 32, 335–344. [Google Scholar] [CrossRef]
- Gao, W. Modified ant colony optimization with improved tour construction and pheromone updating strategies for traveling salesman problem. Soft Comput. 2021, 25, 3263–3289. [Google Scholar] [CrossRef]
- Duan, D.; Poursoleiman, R. Modified teaching-learning-based optimization by orthogonal learning for optimal design of an electric vehicle charging station. Util. Policy 2021, 72, 101253. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, Z.-F.; Tseng, M.-L.; Zheng, S.-J.; Lim, M.K. Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 2021, 108, 107504. [Google Scholar] [CrossRef]
- Ali, M.H.; Kamel, S.; Hassan, M.H.; Tostado-Véliz, M.; Zawbaa, H.M. An improved wild horse optimization algorithm for reliability based optimal DG planning of radial distribution networks. Energy Rep. 2022, 8, 582–604. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- Azarafza, M.; Akgün, H.; Ghazifard, A.; Asghari-Kaljahi, E.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis by limit equilibrium approaches—A review. Int. J. Digit. Earth 2021, 14, 1918–1941. [Google Scholar] [CrossRef]
- Azarafza, M.; Akgün, H.; Feizi-Derakhshi, M.-R.; Azarafza, M.; Rahnamarad, J.; Derakhshani, R. Discontinuous rock slope stability analysis under blocky structural sliding by fuzzy key-block analysis method. Heliyon 2020, 6, e03907. [Google Scholar] [CrossRef] [PubMed]
- Azarafza, M.; Akgün, H.; Ghazifard, A.; Asghari-Kaljahi, E. Key-block based analytical stability method for discontinuous rock slope subjected to toppling failure. Comput. Geotech. 2020, 124, 103620. [Google Scholar] [CrossRef]
- Goh, A. Search for critical slip circle using genetic algorithms. Civ. Eng. Environ. Syst. 2000, 17, 181–211. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Li, L.; Chi, S.-C.; Wei, W. Particle swarm optimization algorithm for the location of the critical non-circular failure surface in two-dimensional slope stability analysis. Comput. Geotech. 2007, 34, 92–103. [Google Scholar] [CrossRef]
- Chan, C.M.; Zhang, L.; Ng, J.T. Optimization of pile groups using hybrid genetic algorithms. J. Geotech. Geoenviron. Eng. 2009, 135, 497–505. [Google Scholar] [CrossRef]
- Kahatadeniya, K.S.; Nanakorn, P.; Neaupane, K.M. Determination of the critical failure surface for slope stability analysis using ant colony optimization. Eng. Geol. 2009, 108, 133–141. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; El-Shafie, A.; Eslami, M. Modified particle swarm optimization for optimum design of spread footing and retaining wall. J. Zhejiang Univ.-Sci. A 2011, 12, 415–427. [Google Scholar] [CrossRef]
- Camp, C.V.; Akin, A. Design of retaining walls using big bang–big crunch optimization. J. Struct. Eng. 2012, 138, 438–448. [Google Scholar] [CrossRef]
- Camp, C.V.; Assadollahi, A. CO2 and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. A new hybrid firefly algorithm for foundation optimization. Natl. Acad. Sci. Lett. 2013, 36, 279–288. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Ma, Z. An artificial bee colony algorithm for locating the critical slip surface in slope stability analysis. Eng. Optim. 2013, 45, 207–223. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-objective optimization of foundation using global-local gravitational search algorithm. Struct. Eng. Mech. Int. J. 2014, 50, 257–273. [Google Scholar] [CrossRef]
- Gordan, B.; Jahed Armaghani, D.; Hajihassani, M.; Monjezi, M. Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 2016, 32, 85–97. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Kashani, A.R. Construction cost minimization of shallow foundation using recent swarm intelligence techniques. IEEE Trans. Ind. Inform. 2017, 14, 1099–1106. [Google Scholar] [CrossRef]
- Aydogdu, I. Cost optimization of reinforced concrete cantilever retaining walls under seismic loading using a biogeography-based optimization algorithm with Levy flights. Eng. Optim. 2017, 49, 381–400. [Google Scholar] [CrossRef]
- Mahdiyar, A.; Hasanipanah, M.; Armaghani, D.J.; Gordan, B.; Abdullah, A.; Arab, H.; Majid, M.Z.A. A Monte Carlo technique in safety assessment of slope under seismic condition. Eng. Comput. 2017, 33, 807–817. [Google Scholar] [CrossRef]
- Gandomi, A.; Kashani, A.; Zeighami, F. Retaining wall optimization using interior search algorithm with different bound constraint handling. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1304–1331. [Google Scholar] [CrossRef]
- Chen, H.; Asteris, P.G.; Jahed Armaghani, D.; Gordan, B.; Pham, B.T. Assessing dynamic conditions of the retaining wall: Developing two hybrid intelligent models. Appl. Sci. 2019, 9, 1042. [Google Scholar] [CrossRef] [Green Version]
- Koopialipoor, M.; Jahed Armaghani, D.; Hedayat, A.; Marto, A.; Gordan, B. Applying various hybrid intelligent systems to evaluate and predict slope stability under static and dynamic conditions. Soft Comput. 2019, 23, 5913–5929. [Google Scholar] [CrossRef]
- Yang, H.; Koopialipoor, M.; Armaghani, D.J.; Gordan, B.; Khorami, M.; Tahir, M. Intelligent design of retaining wall structures under dynamic conditions. Steel Compos. Struct. Int. J. 2019, 31, 629–640. [Google Scholar]
- Xu, C.; Gordan, B.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M.; Zhang, X. Improving performance of retaining walls under dynamic conditions developing an optimized ANN based on ant colony optimization technique. IEEE Access 2019, 7, 94692–94700. [Google Scholar] [CrossRef]
- Kalemci, E.N.; İkizler, S.B.; Dede, T.; Angın, Z. Design of reinforced concrete cantilever retaining wall using Grey wolf optimization algorithm. Structures 2020, 23, 245–253. [Google Scholar] [CrossRef]
- Kaveh, A.; Hamedani, K.B.; Bakhshpoori, T. Optimal design of reinforced concrete cantilever retaining walls utilizing eleven meta-heuristic algorithms: A comparative study. Period Polytech. Civ. Eng. 2020, 64, 156–168. [Google Scholar] [CrossRef]
- Kashani, A.R.; Gandomi, M.; Camp, C.V.; Gandomi, A.H. Optimum design of shallow foundation using evolutionary algorithms. Soft Comput. 2020, 24, 6809–6833. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Tang, L.; Zhang, W.; Lacasse, S.; Liu, H.; Gao, L. Efficient reliability analysis of earth dam slope stability using extreme gradient boosting method. Acta Geotech. 2020, 15, 3135–3150. [Google Scholar] [CrossRef]
- Moayedi, H.; Osouli, A.; Nguyen, H.; Rashid, A.S.A. A novel Harris hawks’ optimization and k-fold cross-validation predicting slope stability. Eng. Comput. 2021, 37, 369–379. [Google Scholar] [CrossRef]
- Sharma, S.; Saha, A.K.; Lohar, G. Optimization of weight and cost of cantilever retaining wall by a hybrid metaheuristic algorithm. Eng. Comput. 2021, 1–27. [Google Scholar] [CrossRef]
- Kaveh, A.; Seddighian, M.R. Optimization of Slope Critical Surfaces Considering Seepage and Seismic Effects Using Finite Element Method and Five Meta-Heuristic Algorithms. Period. Polytech. Civ. Eng. 2021, 65, 425–436. [Google Scholar] [CrossRef]
- Temur, R. Optimum design of cantilever retaining walls under seismic loads using a hybrid TLBO algorithm. Geomech. Eng. 2021, 24, 237–251. [Google Scholar]
- Li, S.; Wu, L. An improved salp swarm algorithm for locating critical slip surface of slopes. Arab. J. Geosci. 2021, 14, 1–11. [Google Scholar] [CrossRef]
- Arabali, A.; Khajehzadeh, M.; Keawsawasvong, S.; Mohammed, A.H.; Khan, B. An Adaptive Tunicate Swarm Algorithm for Optimization of Shallow Foundation. IEEE Access 2022, 10, 39204–39219. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. Effective hybrid soft computing approach for optimum design of shallow foundations. Sustainability 2022, 14, 1847. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Kalhor, A.; Tehrani, M.S.; Jebeli, M. Optimum design of retaining structures under seismic loading using adaptive sperm swarm optimization. Struct. Eng. Mech. 2022, 81, 93–102. [Google Scholar]
- Kashani, A.R.; Camp, C.V.; Azizi, K.; Rostamian, M. Multi-objective optimization of mechanically stabilized earth retaining wall using evolutionary algorithms. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 3352. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 1–25. [Google Scholar] [CrossRef]
- Dolan, E.D.; Lewis, R.M.; Torczon, V. On the local convergence of pattern search. SIAM J. Optim. 2003, 14, 567–583. [Google Scholar] [CrossRef]
- Duncan, J.M. State of the art: Limit equilibrium and finite-element analysis of slopes. J. Geotech. Eng. 1996, 122, 577–596. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Geotechinque 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Zhu, D.; Lee, C.; Qian, Q.; Chen, G. A concise algorithm for computing the factor of safety using the Morgenstern–Price method. Can. Geotech. J. 2005, 42, 272–278. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y. Location of critical failure surface and some further studies on slope stability analysis. Comput. Geotech. 2003, 30, 255–267. [Google Scholar] [CrossRef]
- Huang, G.; Rosowski, J.; Ravicz, M.; Peake, W. Mammalian ear specializations in arid habitats: Structural and functional evidence from sand cat (Felis margarita). J. Comp. Physiol. A 2002, 188, 663–681. [Google Scholar]
- Torczon, V. On the convergence of pattern search algorithms. SIAM J. Optim. 1997, 7, 1–25. [Google Scholar] [CrossRef]
- Cherki, I.; Chaker, A.; Djidar, Z.; Khalfallah, N.; Benzergua, F. A Sequential Hybridization of Genetic Algorithm and Particle Swarm Optimization for the Optimal Reactive Power Flow. Sustainability 2019, 11, 3862. [Google Scholar] [CrossRef] [Green Version]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995; pp. 1942–1948. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. Lect. Notes Comput. Sci. 2009, 5792, 169–178. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]



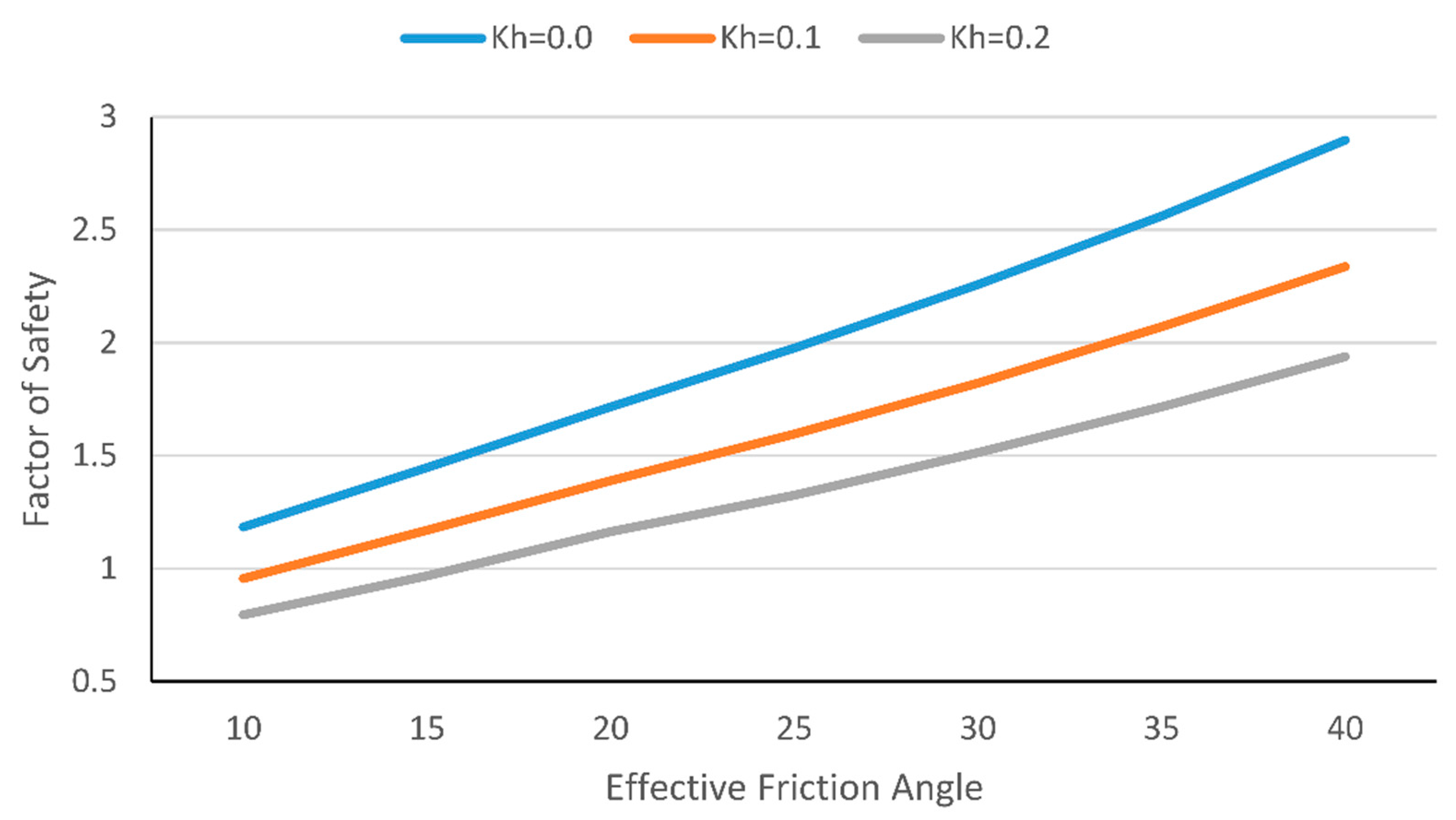
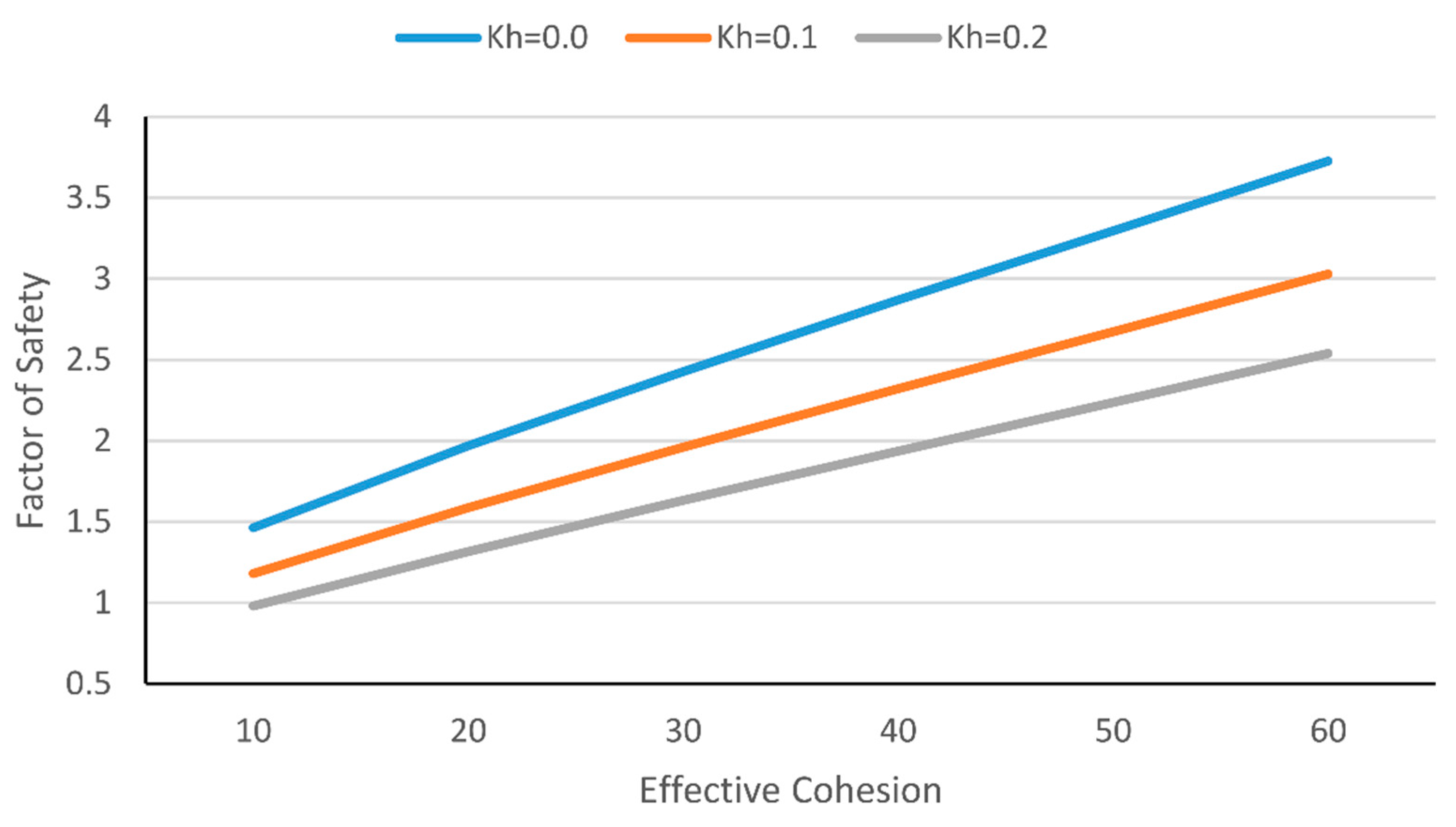
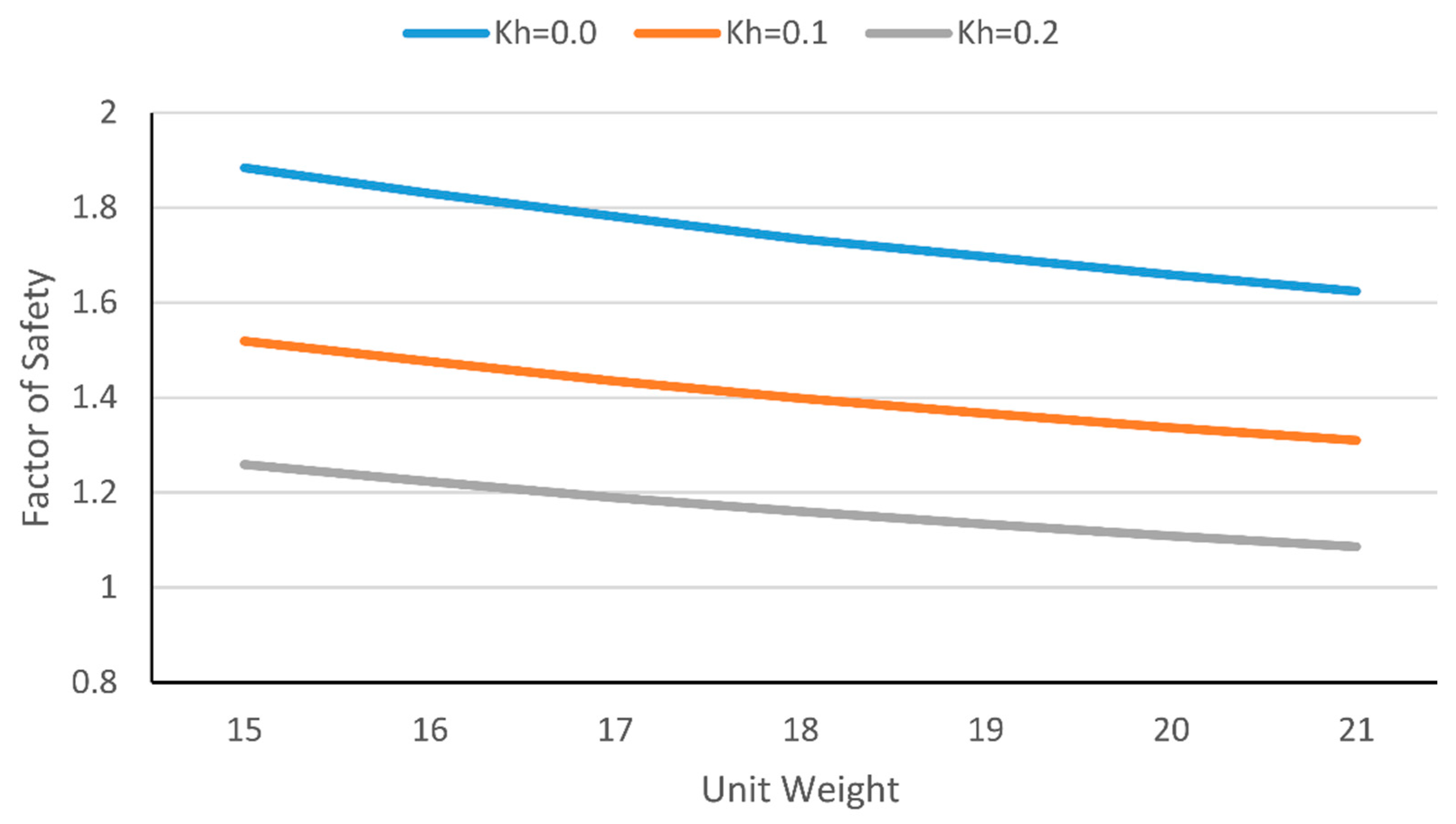
| Author, Year | Reference | Optimization Method | Application |
|---|---|---|---|
| Goh, 2000 | [28] | Genetic algorithm | Locate the critical circular slip surface in slope stability analysis |
| Zolfaghari, Heath, and McCombie, 2005 | [6] | Genetic algorithm | In slope stability, look for critical non-circular failure surfaces. |
| Cheng et al., 2007 | [29] | Particle swarm optimization | Two-dimensional slope stability analysis |
| Cheng et al., 2008 | [16] | Improved harmony search algorithm | Slope stability analysis |
| Chan, Zhang, and Ng, 2009 | [30] | Hybrid genetic algorithms | Optimization of pile groups |
| Kahatadeniya, Nanakorn, and Neaupane, 2009 | [31] | Ant colony optimization | Determination of the critical failure surface of earth slope |
| Khajehzadeh et al., 2011 | [32] | Modified particle swarm optimization | Optimum design of spread footing and retaining wall |
| Camp and Akin, 2012 | [33] | Big bang–big crunch optimization | Optimum design of retaining wall |
| Camp and Assadollahi, 2013 | [34] | Hybrid big bang–big crunch algorithm | Optimizing the cost and CO2 of concrete footings |
| Khajehzadeh, Taha, and Eslami, 2013 | [35] | hybrid firefly algorithm | Minimize of total cost and CO2 emissions of the foundation subjected to geotechnical and structural requirements. |
| Kang, Li, and Ma, 2013 | [36] | Artificial bee colony algorithm | In slope stability, finding the critical slip surface |
| Khajehzadeh, Taha, and Eslami, 2014 | [37] | Adaptive gravitational search algorithm | Multi-objective optimization of foundation |
| Kashani, Gandomi, and Mousavi, 2016 | [9] | Imperialistic competitive algorithm | Locating the critical slip surface of earth slope |
| Gordan et al., 2016 | [38] | Particle swarm optimization and neural network | Prediction of seismic slope stability |
| Gandomi and Kashani, 2017 | [39] | Accelerated particle swarm optimization, firefly algorithm, levy-flight krill herd, whale optimization algorithm, ant lion optimizer, grey wolf optimizer, moth–flame optimization algorithm, and teaching-learning-based optimization algorithm | Construction cost minimization of shallow foundation |
| Aydogdu, 2017 | [40] | Biogeography-based optimization algorithm | Cost optimization of retaining wall |
| Gandomi et al., 2017 | [10] | Genetic algorithm, differential evolution, evolutionary strategy, and biogeography-based optimization | Slope stability analysis |
| Mahdiyar et al., 2017 | [41] | Monte Carlo simulation technique | Safety assessment of slope |
| Gandomi, Kashani, and Zeighami, 2017 | [42] | Interior search algorithm | Retaining wall optimization |
| Chen et al., 2019 | [43] | Hybrid imperialist competitive algorithm and artificial neural network | Prediction of safety factor values of retaining walls |
| Koopialipoor et al., 2019 | [44] | Imperialist competitive algorithm, genetic algorithm, particle swarm optimization, and artificial bee colony combined with artificial neural network | Predict the slope safety exposed to static and dynamic conditions |
| Yang et al., 2019 | [45] | Neural network system | Design retaining wall structures based on smart and optimal systems |
| Xu et al., 2019 | [46] | Hybrid artificial neural network and ant colony optimization | Dynamic conditions of retaining wall structures |
| Himanshu and Burman, 2019 | [11] | Particle swarm optimization | Determination of critical failure surface considering seepage and seismic loading |
| Kalemci et al., 2020 | [47] | Grey wolf optimization algorithm | Optimization of retaining walls |
| Kaveh, Hamedani, and Bakhshpoori, 2020 | [48] | Eleven meta-heuristic algorithms | Optimal design of cantilever retaining walls |
| Kashani et al., 2020 | [49] | Differential algorithm, evolution strategy, and biogeography-based optimization algorithm | Optimum design of shallow foundation |
| Wang et al., 2020 | [50] | Extreme gradient boosting method | Evaluating the earth dam slopefailure probability. |
| Moayedi et al., 2021 | [51] | Harris hawks’ optimization | Predicting the factor of safety in the presence of rigid foundations |
| Sharma, Saha, and Lohar, 2021 | [52] | Hybrid butterfly and symbiosis organism search algorithm | Optimization of retaining wall |
| Kaveh and Seddighian, 2021 | [53] | Black hole mechanics optimization, firefly algorithm, evolution strategy, sine cosine algorithm | Slope critical surfaces optimization with seepage and seismic effects |
| Temur, 2021 | [54] | Teaching-learning based optimization | Optimization of retaining wall |
| Li and Wu, 2021 | [55] | Improved salp swarm algorithm | Locating critical slip surface of slopes |
| Arabali et al., 2022 | [56] | Adaptive tunicate swarm algorithm | Optimization of construction cost and CO2 emissions of shallow foundation |
| Khajehzadeh, Keawsawasvong, and Nehdi, 2022 | [57] | Artificial neural networks combined with rat swarm optimization | Prediction of the ultimate bearing capacity of shallow foundations and their optimum design |
| Khajehzadeh, Kalhor, et al., 2022 | [58] | Adaptive sperm swarm optimization | Optimum design of retaining structures under seismic load |
| Kashani et al., 2022 | [59] | Multi-objective particle swarm optimization, multi-objective multi-verse optimization, and Pareto envelope-based selection algorithm | Multi-objective optimization of mechanically stabilized earth retaining wall |
| Function | Range | n (Dim) | |
|---|---|---|---|
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 |
| Function | Range | n (Dim) | |
|---|---|---|---|
| 428.9829 × n | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 |
| F | Index | CSCPS | SCO | PSO | FA | MVO | SSA | TSA |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 0.00 | 2.42 × 10−97 | 4.98 × 10−9 | 7.11 × 10−3 | 2.81 × 10−1 | 3.29 × 10−7 | 8.31 × 10−56 |
| SD | 0.00 | 7.22 × 10−97 | 1.40 × 10−8 | 3.21 × 10−3 | 1.11 × 10−1 | 5.92 × 10−7 | 1.02 × 10−58 | |
| F2 | Mean | 0.00 | 1.16 × 10−52 | 7.29 × 10−4 | 4.34 × 10−1 | 3.96 × 10−1 | 1.9111 | 8.36 × 10−35 |
| SD | 0.00 | 2.55 × 10−52 | 1.84 × 10−3 | 1.84 × 10−1 | 1.41 × 10−1 | 1.6142 | 9.86 × 10−35 | |
| F3 | Mean | 0.00 | 7.84 × 10−81 | 1.40 × 10 | 1.66 × 103 | 4.31 × 10 | 1.50 × 103 | 1.51 × 10−14 |
| SD | 0.00 | 3.49 × 10−80 | 7.13 | 6.72 × 102 | 8.97 | 707.05 | 6.55 × 10−14 | |
| F4 | Mean | 0.00 | 4.57 × 10−46 | 6.00 × 10−1 | 1.11 × 10−1 | 8.80 × 10−1 | 2.44 × 10−5 | 1.95 × 10−5 |
| SD | 0.00 | 9.98 × 10−46 | 1.72 × 10−1 | 4.75 × 10−2 | 2.50 × 10−1 | 1.89 × 10−5 | 4.49 × 10−4 | |
| F5 | Mean | 7.22 × 10−8 | 2.80 × 10 | 4.93 × 10 | 7.97 × 10 | 1.18 × 102 | 136.56 | 28.4 |
| SD | 4.78 × 10−9 | 8.73 × 10−1 | 3.89 × 10 | 7.39 × 10 | 1.43 × 102 | 154.00 | 0.842 | |
| F6 | Mean | 0.00 | 2.15 | 6.92 × 10−2 | 6.94 × 10−3 | 2.02 × 10−2 | 5.72 × 10−7 | 3.67 |
| SD | 0.00 | 4.47 × 10−1 | 2.87 × 10−2 | 3.61 × 10−3 | 7.43 × 10−3 | 2.44 × 10−7 | 0.3353 | |
| F7 | Mean | 1.39 × 10−5 | 1.51 × 10−4 | 8.94 × 10−2 | 6.62 × 10−2 | 5.24 × 10−2 | 8.82 × 10−5 | 0.0018 |
| SD | 2.65 × 10−5 | 1.33 × 10−4 | 0.0206 | 4.23 × 10−2 | 1.37 × 10−2 | 6.94 × 10−5 | 4.62 × 10−4 |
| F | Index | CSCPS | SCO | PSO | FA | MVO | SSA | TSA |
|---|---|---|---|---|---|---|---|---|
| F8 | Mean | −1.25 × 104 | −1.01 × 104 | −6.01 × 103 | −5.85 × 103 | −6.92 × 103 | −7.46 × 103 | −7.89 × 103 |
| SD | 0.00 | 1.70 × 103 | 1.30 × 103 | 1.61 × 103 | 9.19 × 102 | 634.67 | 599.26 | |
| F9 | Mean | 0.00 | 0.00 | 4.72 × 10 | 1.51 × 10 | 1.01 × 102 | 55.45 | 151.45 |
| SD | 0.00 | 0.00 | 1.03 × 10 | 1.25 × 10 | 1.89 × 10 | 18.27 | 35.87 | |
| F10 | Mean | 8.88 × 10−16 | 8.77 × 10−16 | 3.86 × 10−2 | 4.58 × 10−2 | 1.15 | 2.84 | 2.409 |
| SD | 0.00 | 0.00 | 2.11 × 10−1 | 1.20 × 10−2 | 7.87 × 10−1 | 6.58 × 10−1 | 1.392 | |
| F11 | Mean | 0.00 | 0.00 | 5.50 × 10−3 | 4.23 × 10−3 | 5.74 × 10−1 | 2.29 × 10−1 | 0.0077 |
| SD | 0.00 | 0.00 | 7.39 × 10−3 | 1.29 × 10−3 | 1.12 × 10−1 | 1.29 × 10−1 | 0.0057 | |
| F12 | Mean | 1.57 × 10−32 | 1.25 × 10−1 | 1.05 × 10−2 | 3.13 × 10−4 | 1.27 | 6.82 | 6.373 |
| SD | 2.88 × 10−48 | 5.41 × 10−2 | 2.06 × 10−2 | 1.76 × 10−4 | 1.02 | 2.72 | 3.458 | |
| F13 | Mean | 1.35 × 10−32 | 1.99 | 4.03 × 10−1 | 2.08 × 10−3 | 6.60 × 10−2 | 21.31 | 2.897 |
| SD | 2.95 × 10−48 | 2.51 × 10−1 | 5.39 × 10−1 | 9.62 × 10−4 | 4.33 × 10−2 | 16.99 | 0.643 |
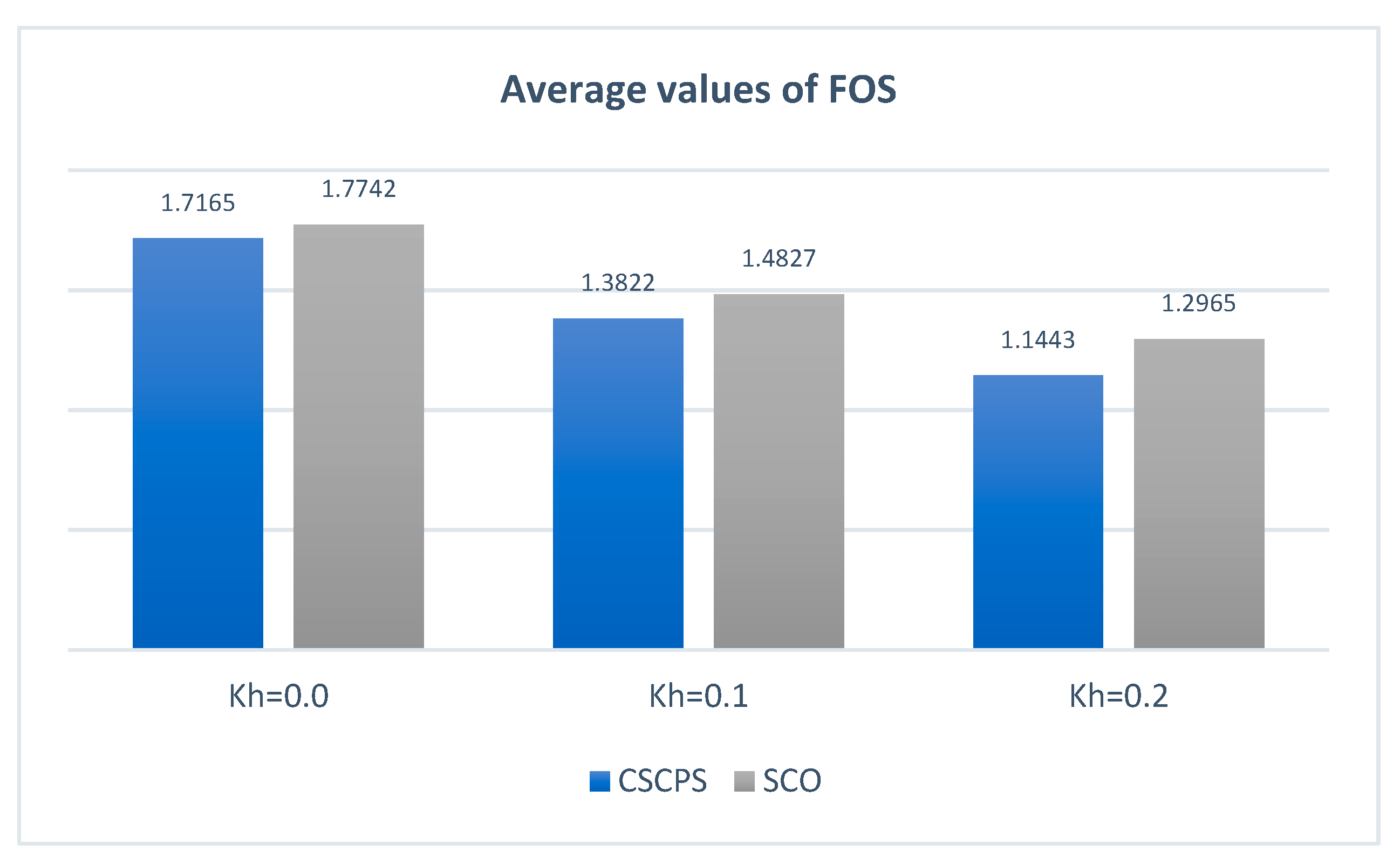
| Optimization Method | Analysis Method | Number of Slices | Minimum FOS | ||
|---|---|---|---|---|---|
| Kh = 0.0 | Kh = 0.1 | Kh = 0.2 | |||
| GA [6] | Morgenstern–Price | - | 1.75 | _ | _ |
| SA [8] | Spencer’s method | 40 | 1.7267 | _ | _ |
| HS [8] | Spencer’s method | 40 | 1.7264 | _ | _ |
| PSO [11] | Bishop’s method | 40 | 1.7195 | _ | _ |
| SCO (current study) | Morgenstern–Price | 40 | 1.7275 | 1.4012 | 1.1897 |
| CSCPS (current study) | Morgenstern–Price | 40 | 1.7132 | 1.3803 | 1.1424 |
| Soil Properties | Unit | Layer Number | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Unit weight, γ | kN/m3 | 18.63 | 18.63 | 18.63 | 18.63 |
| Cohesion, c′ | kPa | 14.7 | 16.7 | 4.9 | 34.3 |
| Friction angle, ϕ′ | Degree | 20 | 21 | 10 | 28 |
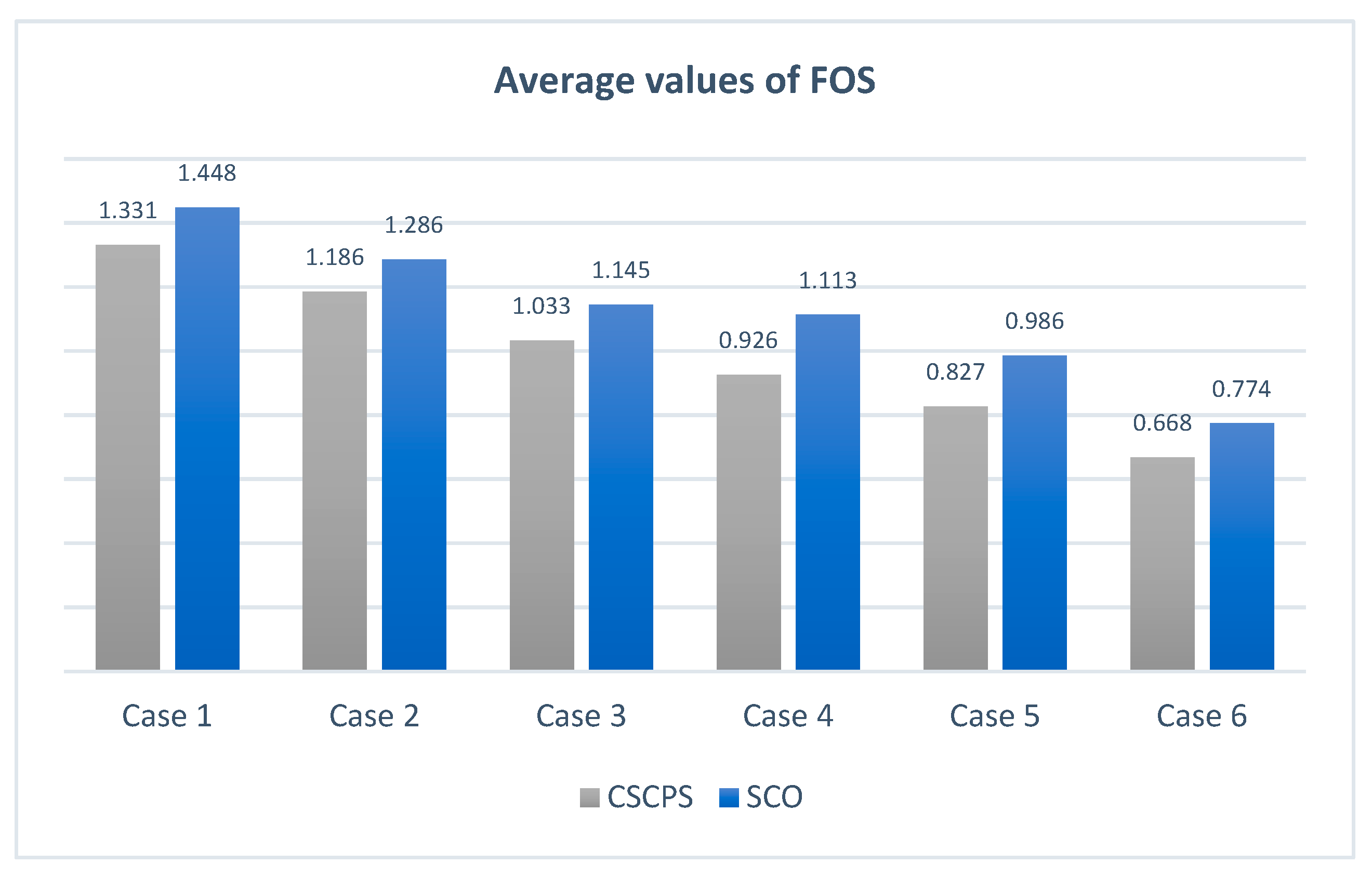
| Optimization Method | Analysis Method | Loading Case | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| GA [6] | Morgenstern–Price | 1.48 | 1.36 | 1.37 | 0.98 | _ | _ |
| PSO [8] | Spencer method | 1.3372 | 1.21 | 1.0474 | 0.9451 | _ | _ |
| SCO (current study) | Morgenstern–Price | 1.342 | 1.206 | 1.0546 | 0.985 | 0.849 | 0.69 |
| CSCPS (current study) | Morgenstern–Price | 1.322 | 1.178 | 1.019 | 0.916 | 0.814 | 0.657 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iraji, A.; Karimi, J.; Keawsawasvong, S.; Nehdi, M.L. Minimum Safety Factor Evaluation of Slopes Using Hybrid Chaotic Sand Cat and Pattern Search Approach. Sustainability 2022, 14, 8097. https://doi.org/10.3390/su14138097
Iraji A, Karimi J, Keawsawasvong S, Nehdi ML. Minimum Safety Factor Evaluation of Slopes Using Hybrid Chaotic Sand Cat and Pattern Search Approach. Sustainability. 2022; 14(13):8097. https://doi.org/10.3390/su14138097
Chicago/Turabian StyleIraji, Amin, Javad Karimi, Suraparb Keawsawasvong, and Moncef L. Nehdi. 2022. "Minimum Safety Factor Evaluation of Slopes Using Hybrid Chaotic Sand Cat and Pattern Search Approach" Sustainability 14, no. 13: 8097. https://doi.org/10.3390/su14138097
APA StyleIraji, A., Karimi, J., Keawsawasvong, S., & Nehdi, M. L. (2022). Minimum Safety Factor Evaluation of Slopes Using Hybrid Chaotic Sand Cat and Pattern Search Approach. Sustainability, 14(13), 8097. https://doi.org/10.3390/su14138097








