Abstract
The analytic solution for surrounding rock of roadway is of significance for stability analysis and roadway support. However, analytical solution for surrounding rock of roadway which took influences of water seepage, strain softening, dilatancy and intermediate principal stress all into account did not receive much reporting. To promote research in this aspect, a mechanical model simultaneously considering water seepage, strain softening, rock dilatancy, and intermediate principal stress was established based on porous elastoplastic mechanics, and then unified analytical solution for surrounding rock of roadway was obtained. Based on an example, influences of water seepage, strain softening, rock dilatancy, residual cohesion and intermediate principal stress on surrounding rock of roadway were thoroughly investigated using single factor analysis. The obtained results are as follows: radii of plastic zones and surface displacement of roadway would increase exponentially with water pressure increasing and their magnitudes are greater than corresponding values without water seepage considered; with softening modulus increasing, peak circumferential stress location would slightly shift to deeper surrounding rock, while broken zone radius and surface displacement of roadway would increase in a decay velocity; rock dilatancy has little effect on peak circumferential stress and plastic softening zone radius, while broken zone radius and surface displacement of roadway increase linearly with dilatancy coefficient α1 increasing indicating their magnitudes are overestimated if associated flow rule is adopted; with weighted coefficient increasing, stress components in plastic zones at the same distance from roadway center would increase, while radii of two plastic zones and surface displacement of roadway are reduced, i.e., self-bearing capacity of rock is enhanced considering intermediate principal stress effect compared to Mohr–Coulomb criterion; with residual cohesion increasing, peak circumferential stress remains unchanged, while stress components in plastic zones at the same distance from roadway center would increase and radii of two plastic zones decrease significantly. The above results implicated that water seepage effect should be carefully considered for roadway stability under groundwater environment; strain-softening and flow rule of rock should be reasonably analyzed and chosen to accurately predict surface displacement and broken zone radius of roadway; rock bolt length should be increased with softening modulus increasing, while it can be decreased with intermediate principal stress effect considered; grouting measure is an effective measure to improve roadway stability. In short, the research provides a theoretical basis and some practical engineering implication for roadway support.
1. Introduction
Coal is of significance for the development of China’ s society and economy. With exhaustion of shallow coal resources, the coal exploitation has gradually entered deeper rock mass with mechanical characteristics of “three highs and one disturbance” [1], which affects the stability of underground roadway. Determination of deformation and plastic zone of roadway is of significance for stability analysis and roadway support. Analytic solution for surrounding rock of roadway, which provides direct understanding of plastic zones and deformation, is a hot issue studied by scholars [2,3,4,5,6]. There are many factors to be considered in deriving analytic expressions for surrounding rock of roadway. Firstly, groundwater always exists in underground rock mass of mining engineering. When the roadway is excavated, the original stress state would be destroyed, thus simultaneously generating a seepage field because of groundwater flow. The water seepage would then influence stress distribution of surrounding rock [7,8,9]. Hence, an accurate theoretical solution for surrounding rock should take the influence of groundwater into account. Besides, when circumferential stress of surrounding rock reaches its compressive strength during stress redistribution process, its stress would be reduced to its residual strength gradually; namely, surrounding rock of roadway would present post-peak strain-softening behavior [3,4,5,6]. Thus, elastoplastic analysis of surrounding rock should consider strain-softening characteristics. Furthermore, related studies have demonstrated that there is little volume change of rock in the pre-peak process, while rock dilatancy exists at the post-peak process, which would affect the deformation characteristics of surrounding rock [3,5,10,11]. Therefore, rock dilatancy should be also considered. Last but not least, surrounding rock of roadway is generally in three-dimensional stress state, while related studies showed that intermediate principal stress would affect surrounding rock strength to an extent [10,11,12]. Hence, to accurately describe failure or deformation characteristics for surrounding rock, influences of water seepage, strain softening, dilatancy and intermediate principal stress should be all considered [11,12,13,14,15,16].
Recently, regarding solutions for surrounding rock of roadway, numerous achievements have been obtained. Zhang [9] and Gao [15] obtained elastoplastic solution which considered effects of dilatancy, strain softening and seepage, while influence of second principal stress is ignored. Based on unified strength theory, Liu [17] obtained analytical expressions considering dilation characteristics and intermediate principal stress, but effect of strain softening and seepage were not considered. Considering effects of strain softening, dilatancy and intermediate principal stress, scholars [11,18,19,20,21] obtained analytic solutions based on different strength criteria, such as generalized spatially mobilized plane criterion, generalized three-dimensional Hoek–Brown criterion, modified Lade criterion and Drucker–Prager criterion, which indicated that intermediate principal stress had influenced on stress distributions, but the seepage effect was not considered. In comparison of four different strength criteria, Pan [12] and Fan [16] analyzed influences of seepage, rock dilatancy and intermediate principal stress, which indicated that the rock dilatancy was related to plastic potential function, but they did not distinguish the strain-softening zone and broken zone. For bolted roadway, Gu [10] had analyzed roadway stability in consideration of intermediate principal stress and dilatancy, but seepage effect was not considered; Zhou [22] proposed a new analytical solution with seepage, dilatancy, intermediate principal stress considered, but an elastic–brittle model is used, which is not suitable for describing strain-softening characteristics of surrounding rock without rock bolt or other support measures. Furthermore, scholars [23,24,25,26] obtained numerical solutions for surrounding rock of roadway considering influences of confining pressure and seepage on rock parameters, in which extra relatively complex calculation procedures were needed and not all factors were considered. In conclusion, both analytic and numerical solutions for circular roadway have been extensive studied recently, and the previous literature has analyzed influences of factors including water seepage, strain softening, dilatancy and intermediate principal stress on roadway stability, respectively. However, to our best knowledge, there is little reporting regarding analytical solution for surrounding rock of roadway, which takes influences of seepage, strain softening, dilatancy and intermediate principal stress all into account, and how these factors influence stress, plastic zone radius or displacement was not fully understood. The goal of the present study is to promote and improve research in this aspect. Therefore, based on existing studies, a mechanical model considering water seepage, strain softening, rock dilatancy, and intermediate principal stress was established according to porous elastoplastic mechanics in Section 3, and then unified analytical solutions for surrounding rock of roadway were obtained, which can represent analytical solutions for an ordered series of solutions. Based on an example, influences of each factor on stress distribution, radii of plastic zones and displacement were further studied using single factor analysis. The results provide a theoretical basis and some practical engineering implication for roadway support.
2. Unified Strength Theory
As mentioned above, the Mohr–Coulomb and Hoek–Brown criteria had widely been applied in rock mechanics. However, both two criteria have only considered the influence of minimum and maximum principal stresses, whereas intermediate principal stress has not been considered. Existing studies [10,11,12] revealed that intermediate principal stress would influence rock failure and deformation in a certain extent, which demonstrated intermediate principal stress should not be ignored. Hence, to obtain a reasonable analytical solution for surrounding rock of roadway, the unified strength theory proposed by Yu et al. [27] is adopted:
where φ and c represent internal friction angle and cohesion; σ3, σ2 and σ1 represent minor, intermediate and major principal stresses, respectively; b represents weighted coefficient accounting for influencing of σ2 which ranges from zero to one. In the present paper, positive value is for compressive stress.
3. Mechanical Model for Surrounding Rock of Roadway
3.1. Distribution of Pore Water Pressure
A mechanical model, which is used to calculate deformation and stress calculation for surrounding rock of roadway, is established based on following assumptions: (1) the roadway is approximately considered as an equivalent circular cavern with infinite length, so the surrounding rock is in a plane strain state; (2) surrounding rock is assumed as elastoplastic porous media with homogeneous, isotropic characteristics; (3) the weight of surrounding rock, which is subjected to hydrostatic stress and pore water pressure, is ignored; (4) the permeability of surrounding rock is a constant in all directions. As illustrated in Figure 1, the roadway radius is r0, and it is imposed by a hydrostatic stress of σ0 before excavation. If the support pressure pi is not great enough, two plastic zones, namely broken zone with radius being Rb and plastic softening zone with radius being Rp, would be commonly formed around the roadway, while the surrounding rock with radius greater than Rp is still under elastic state.
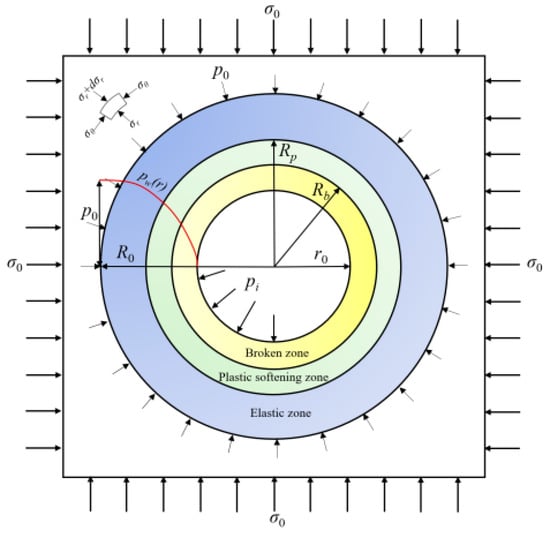
Figure 1.
Mechanical model for circular roadway under seepage influence.
Before excavation of roadway, an initial pore water pressure p0 is existed throughout surrounding rock (Figure 1). After roadway excavation, internal water pressure is decreased to zero. As is well known, the subsurface water will flow due to pore water pressure difference between inner and outer domain. According to above assumptions, the water seepage would only occur in radial direction, which results in the axisymmetric redistribution of pore water pressure. To obtain analytical solution of water pressure distribution, a boundary on which water pressure is unaltered should be determined. Related studies [2] showed that when a point is located on boundary with radius of R0 ≥ 30 r0, the alternation of pore water pressure pw and stress can be negligible compared to infinite condition. Thus, the mechanical model is established with a maximum radial dimension of R0 = 30r0 (shown in Figure 1). In this study, neglecting the buoyancy part of seepage body force and compressibility of water, the governing equation for steady water seepage can be obtained [11]:
where r denotes radial distance from roadway center.
Based on seepage boundary conditions of pw(r)|r=r0 = 0 and pw(r)|r=R0 = p0, the distribution of water pressure around roadway surrounding rock is given:
where s = p0/ln(r0/R0).
3.2. Elastoplastic Solution of Mechanical Model
3.2.1. Basic Equations under Polar Coordinate System
The stresses in circumferential and radial directions under polar coordinate system are denoted by σθ and σr, respectively. Under the assumption of (1), the strain in axial direction of roadway is zero, and then stress σz in axial direction can be expressed by σz = a(σr + σθ)/2, in which a is a constant. If the surrounding rock is in elastic zone, then a = 2v in which v represents Poisson’s ratio with value interval of [−1, 0.5]; while if the surrounding rock is in the two plastic zones, then a = 1 [13]. Hence, the relations among minor, intermediate and major principal stresses under polar coordinate system are σ3 = σr ≤ σ2 = σz ≤ σ1 = σθ, and then intermediate principal stresses in surrounding rock satisfy the relation of σ2 ≥ (σ1 + σ3)/2 − (σ1 − σ3)sin φ/2. Then unified strength theory of Equation (1) can be rewritten as an alternative form:
where , and . When weighted coefficient b is zero, unified strength theory will be simplified as Mohr–Coulomb criterion.
According to elastoplastic mechanics and principle of effective stress [15,28], the equilibrium equation for surrounding rock of roadway under seepage effect is
and the displacement-strain equations of surrounding rock is
where η represents effective pore pressure coefficient; εθ and εr denote circumferential strain and radial strain, respectively; and u denotes displacement in radial direction.
3.2.2. Analytical Solutions of Displacement and Stress in Elastic Zone
The constitutive relationship of surrounding rock in elastic zone under plane strain condition is given by:
where and denote circumferential and radial stresses of elastic zone; E is elastic modulus; and and are circumferential strain and radial strain in elastic zone, respectively.
Substituting Equations (6) and (7) into (5), the displacement and stress components in elastic zone are obtained:
where , and , are constants given below in Equation (11).
At the plastic–elastic interface, r = Rp, the surrounding rock is on the verge of yielding, which satisfies yield condition of Equation (4); and the boundary condition of radial stress at r = R0 is σ0 + p0, namely
Substituting Equation (9) into Equation (10), the constants of and are given by
As the strains induced by initial stress σ0 have been accomplished before excavation of roadway, so the actual strain components are given by [29,30]:
For elastic zone, the actual radial displacement ue* is solved by substituting Equation (12) into left-hand side equation of Equation (6):
3.2.3. Analytical Solutions of Displacement and Stress in Plastic Softening Zone
Related studies [18] demonstrated that surrounding rock has characteristics of strain softening after the peak stress is reached. Figure 2 shows that compressive strength of rock would gradually decrease to the residual strength after peak stress reaches. The residual strength represents the constant stress when the strain softening of rock would no longer occur after failure. The experimental strain–stress curve of rock [25,29] could be simplified and subdivided into a three-line segment as illustrated in Figure 2.
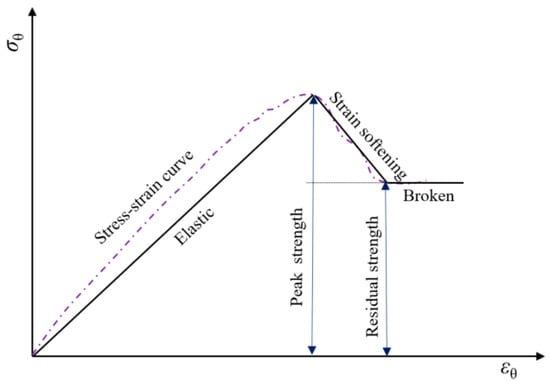
Figure 2.
Strain–stress curve for rock.
Generally, elastic strains occurring in plastic softening zone would be much smaller in contrast to plastic strains.
Hence, elastic strains in softening zone are assumed to the same as corresponding strains at the plastic–elastic interface [6]. For plastic softening zone, the radial and circumferential strains are expressed by the following [12,18]:
where and represent radial and circumferential strains; and represent increments of circumferential and radial plastic strains, respectively.
According to plastic potential theory [18], the increment of plastic strain is given by
where is increment of plastic strain; is the plastic factor increment; g is the plastic potential function; and is the stress tensor. Assuming the plastic potential function g has the same form of unified strength theory of Equation (4):
where is , is , and is dilatancy angle.
Substituting (16) into (15), the plastic strain increment could be expressed by
Existing studies [3,5] have demonstrated that there is little volume change of rock in the pre-peak process, while there is a volumetric dilatancy of rock at the post-peak process. Therefore, rock dilatancy occurs both at broken zone and plastic softening zone. Relationships between strains and dilatancy coefficients are illustrated in Figure 3.
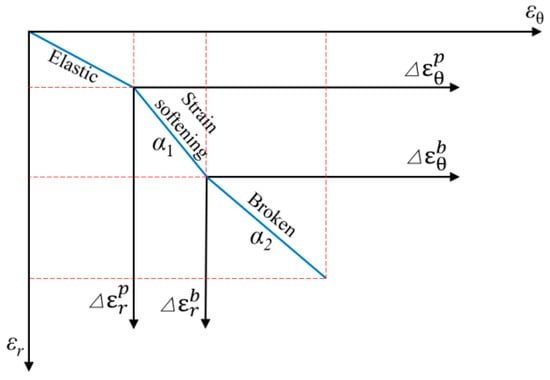
Figure 3.
Relationships between strains and dilatancy coefficients.
Based on flow rule of volumetric dilatancy in plastic softening zone [12,18]:
where α1 (α1 ≥ 1) denotes dilatancy coefficient, which is slope between increments of radial and circumferential plastic strains shown in Figure 3. When α1 = 1, it represents a condition of surrounding rock without volumetric dilatancy.
Combined with Equations (17) and (18), the dilatancy coefficient is obtained by plastic potential function:
Similarly, for broken zone, the circumferential and radial strains are expressed as [12,18]:
where and represent the total circumferential and radial strains; and represent increments of radial and circumferential plastic strains, respectively.
Based on flow rule of volumetric dilatancy in the broken zone [12,18],
where α2 (α2 ≥ 1) denotes dilatancy coefficient, which is slope between increments of radial and circumferential plastic strains in broken zone as illustrated in Figure 3, and it can be calculated similarly to Equation (19). When α2 = 1, it means that no volumetric dilatancy occurs in the broken zone.
For the plastic softening zone, substituting Equation (14) into Equation (6), we obtain
Multiplying the first equation in Equation (22) by , which is then added to the second Equation in Equation (22), the following expression are obtained:
According to Equation (18), Equation (23) can be simplified as
where and are circumferential and radial strains at the interface of plastic softening zone and elastic zone, which can be obtained by solving Equation (12) with r being Rp.
Combining with the continuity condition for displacement up* = ue* at r = Rp (see Equation (13)), we obtain the displacement up* and circumferential strain through solving ordinary differential Equations (24) and (6):
The rock within plastic softening zone is yielding, which satisfies the following relation:
where and denote circumferential stress and radial stress, respectively; np denotes compressive strength of surrounding rock as illustrated in Figure 4.
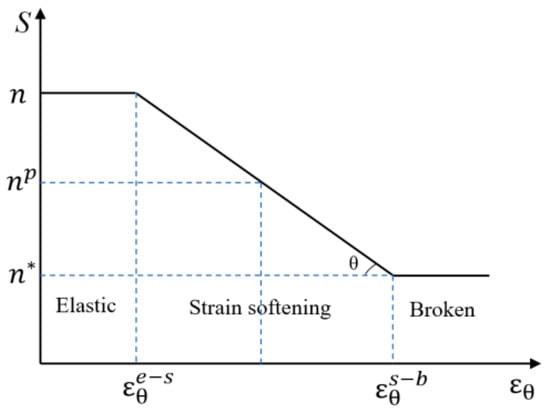
Figure 4.
Evolution model for compressive strength parameter.
In Figure 4, S denotes the compressive strength parameter of the last term on the left side in Equation (4), M = tan θ represents the softening modulus of rock. For rock in strain softening region, its compressive strength parameter of cohesion would be significantly influenced, while internal friction angle is minimally affected [25], which means that the internal friction angle can be assumed as a constant. Therefore, the evolution model for compressive strength parameter S, i.e., the evolution of cohesion, is subdivided into three-line segment (Figure 4). The greater of plastic strain increment, the smaller is np. The compressive strength of surrounding rock, np, is given by
Substituting Equations (12) and (26) into (28) gives
Furthermore, substituting Equation (22) into (20) leads to
In combination with continuity condition of stress = at r = Rp, and substituting Equation (30) into Equation (5), the stress components in plastic softening zone are expressed as
3.2.4. Analytical Solutions for Displacement and Stress in Broken Zone
For surrounding rock of broken zone, it satisfies unified strength theory:
where and denote circumferential and radial stresses, respectively; n* denotes the residual strength.
Combining with the stress condition |r=r0 = pi, and substituting Equation (30) into Equation (5), stress components in broken zone are then given as:
Similarly, combining with Equations (6), (20) and (21) and the displacement continuity condition of at , then is obtained:
where A and B are constants given by
3.2.5. Radii of Plastic Zones
According to the interface condition np = n* at r = Rb and Equation (29), we obtain
Then relationship between softening zone radius and broken zone radius can be given by
Utilizing the stress continuity condition = at r = Rb, the radius of softening zone is be given by
3.3. Validation of Unified Analytical Solution
The proposed analytical solution for surrounding rock of roadway has taken influences of water seepage, strain softening, dilatancy and intermediate principal stress all into account. Therefore, it can be deemed as a unified solution for an ordered series of solutions. Obviously, the series of solutions obtained should involve analytic solution for elastic and perfectly plastic surrounding rock. The simplification process of unified solution is as follows: = 0 and p0 = 0, the water seepage influence is not regarded; , the strain softening of surrounding rock is ignored; , the rock dilatancy is not considered; b = 0, the unified strength theory is simplified as Mohr–Coulomb criterion. For the analytic solution of plastic zone radius (i.e., strain-softening zone radius or broken zone radius in present study, as the two radii are the same under such condition), substituting the above parameters into Equation (42), and with combination of Equations (33), (11), and (4), the plastic zone radius is given:
Let , substituting the above parameters into Equation (37), and with combination of Equations (38) and (39), then surface displacement of roadway can be obtained:
As can be seen, both Equations (43) and (44) are consistent with the classical Kastner’s solution in literature [30], which validates the correctness of the unified solution for surrounding rock of roadway. Thus, the unified solution obtained can indeed represent an ordered series of solutions.
4. Example Analysis
To further investigate influences of water seepage, strain softening, rock dilatancy and intermediate principal stress on radii of plastic zone, displacement and stress in surrounding rock of roadway, an engineering example is thoroughly studied using the single factor analysis. Namely, one of the influencing factors, such as pore water pressure, softening modulus, dilatancy coefficient and weighted coefficient are changed each time. The radius of the circular roadway r0 is 2 m with uniform original stress σ0 being 15 MPa. Table 1 lists the calculation parameters for mechanical model of surrounding rock of roadway.

Table 1.
Calculation parameters for mechanical model.
4.1. Influence of Water Seepage
Figure 5a illustrates the distributions of stresses with water seepage considered (η = 1) and without water seepage considered (η = 0). As can be seen, variation laws of stresses under both conditions are coincident with each other; namely, the circumferential stresses present tendency of increasing firstly and decreasing next, radial stresses present a gradually increasing trend, and peak circumferential stresses occur at plastic–elastic interface; however, water seepage plays a significant role in distributions of two stress components; the peak circumferential stress with water seepage considered is greater than that of without water seepage considered, and location of peak stress would shift to the righthand side; with initial pore water pressure increasing, the peak circumferential stresses and its corresponding distances from roadway center would both increase. The results obtained agree well with existing study in literatures [22,25]. When p0 is increased from 1 MPa to 3 MPa, peak circumferential stress increases by 18% from 28.7 MPa to 33.8 MPa. Figure 5b,c shows variations of radii of plastic zones and of roadway surface displacements under different water pressure. As can be seen, radii of broken and plastic softening zones and surface displacement with water seepage considered are greater than that of without water seepage considered. The reason is that effective stress in surrounding rock would increase with seepage effect considered [2,6]; moreover, radii of two plastic zones and surface displacement of roadway all present an increase trend as water pressure increases with water seepage considered and without water seepage considered although their tendencies are different. The former increases exponentially with water pressure, while the latter increases linearly with water pressure. For instance, with p0 increasing from 1 MPa to 3 MPa, plastic softening zone radius increases by 22% from 3.2 m to 3.9 m, surface displacement of roadway increases by 80% from 0.05 m to 0.09 m. In short, the obtained results indicate that water seepage plays a significant role in radii of plastic zones and surface displacement of roadway, and its influence should be carefully considered for the stability of roadway under groundwater occurrence environment.
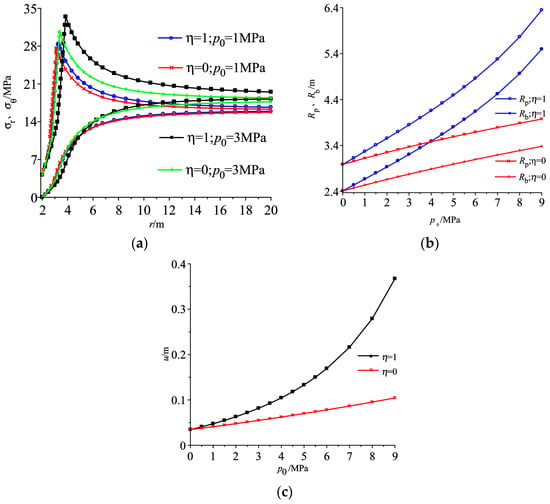
Figure 5.
Influence of water seepage on (a) stress distributions, (b) radii of plastic zones, (c) surface displacements of roadway.
4.2. Influence of Strain Softening
Three softening modulus M, i.e., 1000 MPa, 2000 MPa and 3000 MPa, are chosen to investigate effect of strain softening on stress distribution. As illustrated in Figure 6a, with increase of softening modulus, the magnitude of peak circumferential stress is kept unchanged, which is consistent with analysis in literature [30] indicating that stresses at interface of elastic zone and plastic softening zone would not be influenced by strain softening in plastic zones. Besides, location of peak circumferential stress would slightly shift to the righthand side when softening modulus increases from 1000 MPa to 3000 MPa; and the greater of softening modulus, the smaller of two stress components in plastic zones at the same distance from roadway center. The reason is that the softening modulus denotes the compressive strength reduction per unit of plastic strain increment, the greater of softening modulus, the greater of strength reduction per unit of plastic strain increment.
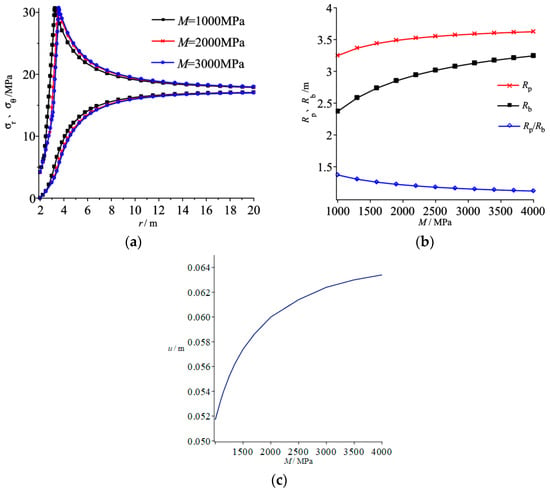
Figure 6.
Influence of strain softening on (a) stress distributions, (b) radii of plastic zones, (c) surface displacements of roadway.
Furthermore, softening modulus M has a greater influence on Rb but less influence on radius of strain-softening zone as illustrated in Figure 6b. With the increase in M, Rb would gradually expand with expansion velocity decreasing. For instance, when softening modulus M is increased from 1000 MPa to 2000 MPa, radius of broken zone increases by 21% from 2.4 m to 2.9 m; while softening modulus M is increased from 2000 MPa to 3000 MPa, radius of broken zone increases by 7% from 2.9 m to 3.1 m. Ratio of Rp and Rb decreases in a decay form with softening modulus increasing, which further indicates that softening modulus has a greater influence on Rb than Rp. The variation curve between softening modulus and surface displacement of roadway. As seen from Figure 6c, when softening modulus M is increased from 1000 MPa to 3000 MPa, surface displacement of roadway only increases from 51.8 mm to 62.3 mm with its slope between softening modulus, and surface displacement of roadway is decreasing gradually, which showed that softening modulus M would affect surface displacement of roadway to an extent. In short, the obtained results indicate that strain-softening characteristics of surrounding rock should be analyzed to accurately predict broken zone radius and surface displacement of roadway; for bolting support roadway, the length of rock bolt is usually determined by the radius of plastic zones [1], so the length of rock bolt should be increased with softening modulus increasing.
4.3. Influence of Dilatancy
The dilatancy characteristics of rock are described by dilatancy coefficient α1 and α2 in this paper (see Figure 3). As described in theoretical analysis of Section 3, dilatancy coefficient α2 has no influence on radii of broken and softening zones. Noting that when rock dilatancy coefficient is 3.4, it is corresponding to associated flow rule (i.e., internal friction angle is equal to dilatancy angle); while rock dilatancy coefficient is set to 1, it is corresponding to the condition without dilatancy considered (i.e., dilatancy angle is set to zero).
Figure 7a illustrates the distributions of stresses around roadway. As can be seen, the rock dilatancy has no effect on magnitude of peak circumferential stress, which is consistent with the results in the literature [22,30]. Figure 7b shows that the dilatancy coefficient has little influence on strain-softening zone radius, but the greater of dilatancy coefficient α1, the greater of radius of broken zone, which agrees well with the related literature [18]. The broken zone radius increases linearly with dilatancy coefficient α1 increasing. Dilatancy coefficients play an important role in surface displacements of roadway (Figure 7c). As can be seen, surface displacements of roadway increase linearly with dilatancy coefficient α1. When dilatancy coefficient α1 is increased from 1 to 3.4, surface displacement of roadway increases by 32.4% from 50.0 mm to 66.2 mm under condition of α2 = 1; while surface displacement of roadway increases by 37.8% from 52.6 mm to 72.5 mm under condition of α2 = 1.6, the increment of surface displacement of roadway is about 7.52 mm with dilatancy coefficient increasing by one. Relevant studies showed that the general value of dilatancy coefficient is 1.5 [22]. Hence, the radius of broken zone and surface displacement of roadway is underestimated with dilatancy not considered, while it is overestimated using the associated flow rule of rock.
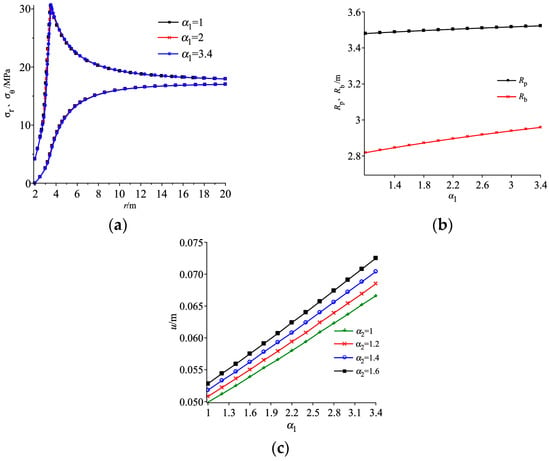
Figure 7.
Influence of dilatancy on (a) stress distributions, (b) radii of plastic zones, (c) surface displacements of roadway.
4.4. Influence of Intermediate Principal Stress
As mentioned in Section 2, intermediate principal stress effect is manifested by weighted coefficient b. Figure 8a illustrates the distribution of stresses under different weighted coefficient.
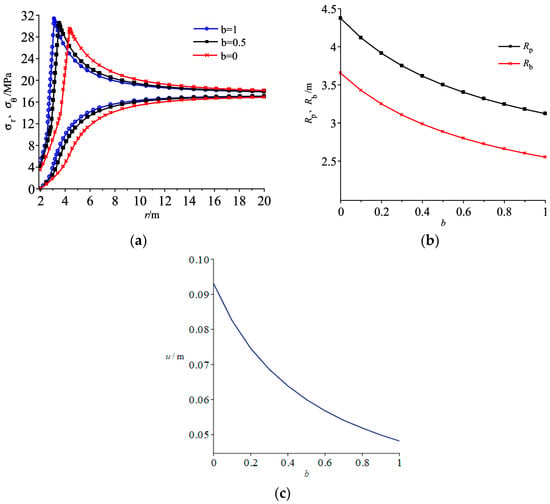
Figure 8.
Influence of intermediate principal stress on (a) stress distributions, (b) radii of plastic zones, (c) surface displacements of roadway.
As can be seen, the greater the weighted coefficient, the larger the two stress components in plastic zones at the same distance from roadway center and corresponding peak circumferential stress; however, with a smaller weighted coefficient, the circumferential stress is increased while radial stress is decreased, which is consistent with results in the literature [17]. Moreover, the location of peak circumferential stress would move to the lefthand side with weighted coefficient increasing. The farther away from roadway center, the less influence of weighted coefficient on stresses. It can be explained that the compressive strength of rock would be increased with effect of intermediate principal stress considered as shown in unified strength theory of Equation (4). Figure 8b shows the relation between weighted coefficient and radii of plastic zones. Both radii of broken and plastic softening zones are reduced exponentially with weighted coefficient increasing. When weighted coefficient is increased from 0 to 1, peak circumferential stress increases by 6% from 29.5 MPa to 31.2 MPa, radius of plastic softening zone decreased by 28% from 4.4 m to 3.15 m, surface displacement of roadway decreased by 48% from 92 mm to 48 mm. Results demonstrate that limit strength of surrounding rock has been enhanced with influence of intermediate principal stress considered. Noting when b is set to zero, unified strength criterion is equivalent to Mohr–Coulomb criterion, which is more conservative in predicting radii of plastic zones and surface displacement of roadway. Therefore, in engineering practice, self-bearing capacity enhancement of surrounding resulting from intermediate principal stress must be considered. Due to length of rock bolt is mainly determined by plastic zone radius, so rock bolt length can be decreased with effect of intermediate principal stress considered. If grouting measure is adopted, the grouting range can also be decreased. The results obtained are helpful for reasonable measure selection of surrounding rock, which can save support cost.
4.5. Influence of Residual Cohesion
Figure 9a presents the distribution of stresses under different residual cohesion c*. As can be seen, the greater the residual cohesion, the larger the two stress components in plastic zones at the same distance from roadway center, and the smaller the distance of plastic–elastic interface from roadway center. However, the peak circumferential stress remains unchanged, which is in good agreement with the literature [30].
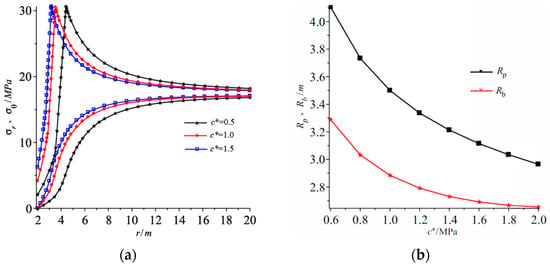
Figure 9.
Influence of residual cohesion on (a) stress distributions, (b) radii of plastic zones.
Variations of radii of plastic zones under different residual cohesions are illustrated in Figure 9b. The broken zone and softening zone decreased exponentially with the increase of residual cohesion. For instance, the radius of broken zone decreases by 20% from 3.3 m to 2.65 m with residual cohesion changes from 0.6 MPa to 2.0 MPa. Hence, the grouting measure, which will improve residual cohesion, can be adopted in roadway to ensure its stability.
5. Conclusions
In this paper, a mechanical model which can simultaneously consider water seepage, strain softening, rock dilatancy, and intermediate principal stress was established, and then unified analytical solutions for pore water pressure, stress, displacement, radii of plastic zones were obtained for surrounding rock of roadway. Based on an example, influences of water seepage, strain softening, rock dilatancy, residual cohesion and intermediate principal stress on surrounding rock of roadway were thoroughly investigated using single factor analysis. The main conclusions are as follows:
- (1)
- With water pressure increasing, peak circumferential stress, radii of two plastic zones and surface displacement of roadway with water seepage considered would increase, and their magnitudes are all greater than their corresponding conditions with water seepage not considered. Particularly, radii of plastic zones and surface displacement of roadway increases exponentially with water pressure increasing, water seepage influence should be carefully considered to ensure roadway stability under groundwater environment.
- (2)
- With softening modulus increasing, the magnitude of peak circumferential stress is kept unchanged, and location of peak circumferential stress would slightly shift to the deeper surrounding rock. Softening modulus has a greater influence on broken zone radius than that of strain-softening zone radius, and it also affects surface displacement of roadway to an extent. To accurately predict broken zone radius and surface displacement of roadway, strain-softening characteristics of surrounding rock should be analyzed; and length of rock bolt should be increased with softening modulus increasing for bolting support roadway.
- (3)
- Rock dilatancy coefficient has little effect on magnitude of peak circumferential stress and plastic softening zone radius, while radius of broken zone and surface displacement of roadway increase linearly with dilatancy coefficient α1 increasing. For actual engineering, surface displacement of roadway would be underestimated with rock dilatancy not considered, while they are overestimated if associated flow rule is adopted, indicating that flow rule of rock should be reasonably chosen for calculating roadway surface displacement and broken zone radius of roadway.
- (4)
- With weighted coefficient increasing, stress components in plastic zones at the same distance from roadway center would increase; while the distance of peak circumferential stress location from roadway center, radii of broken and plastic softening zones, and surface displacement of roadway are reduced. Self-bearing capacity enhancement of surrounding rock resulting from effect of intermediate principal stress should be considered. The traditional Mohr–Coulomb criterion is more conservative. Rock bolt length and grouting range can be decreased after considering effect of inter-mediate principal stress, which is helpful for reasonable measure selection of surrounding rock.
- (5)
- With residual cohesion increasing, peak circumferential stress remains unchanged, stress components in plastic zones at the same distance from roadway center would increase, and the distance of plastic–elastic interface from roadway center decreases, which implicates that grouting measure can be adopted to improve roadway stability effectively.
Author Contributions
Conceptualization, Z.Y. and J.Z.; methodology, S.L.; validation, Z.Y., Z.J. and F.H.; formal analysis, Z.Y.; investigation, J.Z.; resources, Z.Y.; data curation, J.Z.; writing—original draft preparation, Z.Y.; writing—review and editing, Z.J.; visualization, S.L.; supervision, S.L.; project administration, F.H.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Natural Science Foundation of China] grant number [51974121 and 51604111], [Scientific Research Fund of Hunan Provincial Education Department] grant number [16C0654].
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used to support findings of this study are included within this paper.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Kang, H.P. Seventy years development and prospects of strata control technologies for coal mine roadways in China. Chinese J. Rock Mech. Eng. 2021, 40, 1–30. [Google Scholar]
- Li, Z.L.; Ren, Q.W.; Wang, Y.H. Elasto -plastic analytical solution of deep-buried circle tunnel considering fluid flow field. Chin. J. Rock Mech. Eng. 2004, 23, 1291–1295. [Google Scholar]
- Yao, G.S.; Li, J.P.; Gu, S.C. Analytic solution to deformation of soft rock tunnel considering dilatancy and plastic softening of rock Mass. Rock Soil Mech. 2009, 30, 463–467. [Google Scholar]
- Zhang, Q.; Wang, S.L.; Ge, X. Elastoplastic analysis of circular openings in strain-softening rock masses. Chin. J. Rock Mech. Eng. 2010, 29, 1031–1035. [Google Scholar]
- Zhang, X.B.; Zhao, G.M.; Meng, X.R. Elastoplastic solution for surrounding rock of circular roadway based on D-P criterion by considering post-peak strain softening and dilatancy. J. Min. Saf. Eng. 2013, 30, 903–910. [Google Scholar]
- Lv, A.; Ramandi, H.L.; Masoumi, H.; Saadatfar, M.; Regenauer-Lieb, K.; Roshan, H. Analytical and experimental investigation of pore pressure induced strain softening around boreholes. Int. J. Rock Mech. Min. Sci. 2019, 113, 1–10. [Google Scholar] [CrossRef]
- Xie, S.Y.; Shao, J.F. Elastoplastic deformation of a porous rock and water interaction. Int. J. Plast. 2006, 22, 2195–2225. [Google Scholar] [CrossRef]
- Zhang, K.X.; Huang, Z.H.; Zhang, J.H.; Wang, X.; Ma, Z.; Yang, Y. Failure features and instability mechanism of mine mudstone roadway under role of high-pressure seepage water. Coal Sci. Technol. 2015, 43, 1–5. [Google Scholar]
- Zhang, B.Q.; Chen, F.Q.; Wang, Q.Y. Elastoplastic solutions for surrounding rock masses of deep-buried circular tunnels with non-darcian flow. Int. J. Geomech. 2019, 19, 301–317. [Google Scholar] [CrossRef]
- Gu, S.C.; Zhou, P.; Sun, W.; Hu, C.; Li, Z.; Wang, C. Analysis of surrounding rock stability of bolted roadway considering dilatancy and intermediate principal stress. J. Min. Saf. Eng. 2019, 36, 429–436. [Google Scholar]
- Pan, J.L.; Ren, F.H. Analytical solution for surrounding rock of circular roadway based on generalized SMP criterion considering seepage and dilatancy. Coal Geol. Explor. 2019, 47, 32–39. [Google Scholar]
- Pan, J.L.; Guo, Q.F.; Ren, F.H.; Cai, M. Comparative analysis of different strength criteria for deep-buried rock roadway under seepage. J. China Coal Soc. 2019, 44, 3369–3378. [Google Scholar]
- Liu, Z.Q.; Yu, D.M. Elastoplastic stress and displacement analytical solutions to deep-buried circular tunnels considering intermediate principal stress and dilatancy. Eng. Mech. 2012, 29, 289–296. [Google Scholar]
- Zhang, Q.; Jiang, B.S.; Wang, S.L.; Ge, X.R.; Zhang, H.Q. Elasto-plastic analysis of a circular opening in strain-softening rock mass. Int. J. Rock Mech. Min. Sci. 2012, 50, 38–46. [Google Scholar] [CrossRef]
- Gao, Z.N.; Meng, X.R.; Fu, Z.L. Elasto-plastic analysis on surrounding rock of roadways based on seepage, strain softening and dilatancy. J. Chongqing Univ. 2014, 37, 96–101. [Google Scholar]
- Fan, H.; Liu, W.R.; Fu, T.F.; Li, S. Stability analysis of surrounding rock of tunnel considering seepage, shear dilation and intermediate principal stress. China Saf. Sci. J. 2016, 26, 139–145. [Google Scholar]
- Liu, W.R. Analysis of deformation of circular roadway considering effects of intermediate principal stress and dilatancy. Geotech. Geol. Eng. 2019, 2020, 529–536. [Google Scholar] [CrossRef]
- Guo, Q.F.; Pan, J.L.; Wu, X.H.; Xi, X.; Cai, M. A new unified solution for circular tunnels based on generalized smp criterion considering the strain softening and dilatancy. Adv. Civ. Eng. 2019, 2019, 1684707. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Bai, J.B.; Yan, S.; Chang, Z.G.; Song, Y.B.; Zhang, W.G.; Xu, J. The elastoplastic solutions of deep buried roadway based on the generalized 3D hoek-brown strength Criterion considering strain-softening properties. Geofluids 2021, 2021, 5575376. [Google Scholar] [CrossRef]
- Deng, Y.S.; Wang, J.X.; Zou, B.P. Elastoplastic analysis for circular tunnel based on modified lade criterion considering strain softening and dilatancy. Adv. Civ. Eng. 2021, 2021, 4872558. [Google Scholar] [CrossRef]
- Wang, R.; Liu, X.D.; Bai, J.B.; Yan, S.; Xu, J. An innovative elastoplastic analysis for soft surrounding rock considering supporting opportunity based on drucker-prager strength criterion. Adv. Civ. Eng. 2021, 2021, 5555839. [Google Scholar] [CrossRef]
- Zhou, P.; Li, J.P.; Gu, S.C. A new analytical solution for deep-buried circular cavern with anchor reinforcement under seepage field. Arab. J. Geosci. 2021, 2021, 968–985. [Google Scholar] [CrossRef]
- Zhang, Q.; Shao, C.; Wang, H.Y.; Jiang, B.S.; Liu, R.C. A fully coupled hydraulic-mechanical solution of a circular tunnel in strain-softening rock masses. Tunn. Undergr. Space Technol. 2020, 99, 103375. [Google Scholar] [CrossRef]
- Deng, Y.S.; Wang, J.X.; Jiang, M.J.; Zou, B. Elasto-plastic analysis of circular tunnel in rock mass with confining stress-dependent strain-softening behavior considering intermediate principal stress. Arab. J. Geosci. 2021, 14, 2191. [Google Scholar] [CrossRef]
- Fan, H.; Wang, L.G.; Wang, S.; Jiang, C. A New Unified Solution for Deep Tunnels in Water-Rich Areas considering Pore Water Pressure. Geofluids 2021, 2021, 6696757. [Google Scholar] [CrossRef]
- Wang, L.; Zou, J.F.; Sheng, Y.M. An improved stress and strain increment approaches for circular tunnel in strain-softening surrounding rock considering seepage force. Adv. Mater. Sci. Eng. 2019, 2019, 2075240. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.H.; Zan, Y.W.; Zhao, J.; Yoshimine, M. A unified strength criterion for rock material. Int. J. Rock Mech. Min. Sci. 2002, 39, 975–989. [Google Scholar] [CrossRef]
- Yuan, Z.G.; Shao, Y.H. Numerical modeling on hydraulic fracturing in coal-rock mass for enhancing gas drainage. Adv. Civ. Eng. 2018, 2018, 1485672. [Google Scholar] [CrossRef]
- Fang, Z.; Harrison, J.P. A mechanical degradation index for rock. Int. J. Rock Mech. Min. Sci. 2001, 38, 1193–1199. [Google Scholar] [CrossRef]
- Wu, S.C. Rock Mechanics; Higher Education Press: Beijing, China, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).