Three-Dimensional Modeling and Performance Study of High Temperature Solid Oxide Electrolysis Cell with Metal Foam

Abstract

Optimizing the flow field of solid oxide electrolysis cells (SOECs) has a significant effect on improving performance. In this study, the effect of metal foam in high temperature SOEC electrolysis steam is investigated by a three-dimensional model. The simulation results show that the SOEC performance is improved by using metal foam as a gas flow field. The steam conversion rate of the SOEC increases from 72.21% to 76.18% and the diffusion flux of steam increases from 2.3 × 10⁻⁴ kg/(m²∙s) to 2.5 × 10⁻⁴ kg/(m²∙s) at 10,000 A/m². In addition, the permeability, temperature, steam mole fraction, and gas utilization are investigated to understand the effect of the improved performance of the SOEC with metal foam. The results of this study provide a baseline for the optimal design of SOECs with metal foam.

1. Introduction

The concerns regarding dramatic climate change, population growth, industrial pollution, and energy independence have stimulated the development of renewable energy resources [1,2,3]. However, renewable energy has the characteristics of intermittency and volatility [4]. Converting renewable energy electricity into hydrogen has the advantages of a large storage capacity, a high power density, a long duration, and a good development prospect [5,6,7]. Using renewable energy for electrolyzing water to produce hydrogen can achieve zero carbon dioxide emissions, which is ideal hydrogen production technology [5,8]. Ekhtiari et al. [9] and Hafsi et al. [10] utilized natural gas network pipelines for hydrogen storage and transportation solutions. Recently, there are four main technologies: alkaline electrolysis cell (AEC), proton exchange membrane electrolysis cell (PEMEC), alkaline anion exchange membranes electrolysis cell (AEMEC) and solid oxide electrolysis cell (SOEC), for hydrogen production by electrolysis of steam [11]. Although AEC technology is the most mature, it can have low efficiency, strong corrosiveness and potential safety hazards [12]. PEMEC can adapt to a fluctuating power supply while the overall hydrogen production efficiency is still low. Moreover, precious metal catalysts are required and the equipment cost is high [13,14]. In contrast, SOECs can produce hydrogen at a high temperature of 600–1000 °C with a lower power demand and higher chemical reaction rate, which can effectively reduce power consumption and improve conversion efficiency [15,16].

Due to the structural characteristics and material of SOECs, their performance SOEC is limited by gas diffusion [17,18,19]. A large number of studies have shown that metal foam materials can be used as alternative materials for flow field, because metal foam materials have the advantages of high electrical conductivity, high thermal conductivity, high porosity, low cost and low permeability [20]. Meanwhile, many experiments and simulations have verified the obvious effects of metal foam, i.e., its reducing of diffusion resistance and enhancing of gas transport [21,22,23,24,25,26,27,28]. However, there are few numerical simulation studies on SOEC with metal foam which show that they have great potential in term of improving gas diffusion and the electrochemical reaction rate.

The energy of an SOEC can be derived from renewable energy sources. For example, Chen et al. [29] proposed a novel solar hydrogen production system. The sCO₂ Brayton cycle provided electrical energy for an SOEC, and the ammonia-based thermochemical energy storage system provided thermal energy (high temperature steam) for SOEC. Sigurvinsson et al. [30] established a technical and economic optimization model. This included an SOEC electrolytic cell and high temperature heat exchanger network, which helped with investigateions into the feasibility of coupling geothermal energy with SOEC electrolysis. The study found that even with geothermal temperatures as low as 230 °C, it is still economically competitive compared to alkaline electrolysis. Harvego et al. [31] proposed a reference design scheme for a commercial-scale high temperature electrolysis hydrogen production plant, in which the electrolytic cell is driven by the high-temperature helium-cooled reactor coupled with the Brayton cycle. Through economic analysis, it is found that the high temperature electrolysis hydrogen production driven by the high-temperature helium-cooled gas-cooled reactor, would be competitive in term of cost. Zhang et al. [32] investigated the cost of high temperature steam electrolysis (HTSE) from greenhouse gas emissions to hydrogen production using a life cycle assessment approach. The results showed HTSE greenhouse gas emissions from 3 to 20 kg CO_2e/kg H₂ and costs from $2.5 to 5/kg H₂ over the life cycle. It is estimated that this figure could drop to $50/tonne CO_2e with future technological advancements.

The schematic diagram of a three-dimensional SOEC model established in this study is shown in Figure 1. As shown in Figure 1a, the gas flow field is the SOEC without metal foam. Moreover, the gas flow field (the SOEC with metal foam) is shown in Figure 1b. The purpose of this study was to fully understand SOECs with metal foam in terms of the performance of electrolysis steam. The effects of permeability, temperature, steam mole fraction, and gas utilization on the performance of an SOEC were studied.

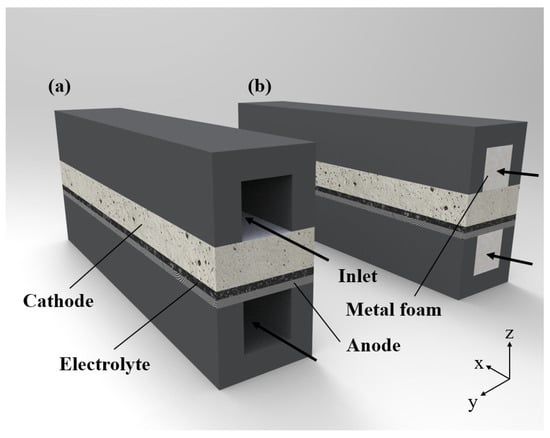
Figure 1. Schematic of the SOEC: (a) without metal foam, (b) with metal foam.

2. Modeling Description

2.1. Physical Model and Assumptions

The schematic of an SOEC is shown in Figure 2. In the middle of the SOEC is a dense electrolyte layer that separates the gases on both sides and transports oxygen ions. There are porous cathodes and anodes on both sides of the electrolytic cell and the porous structure is conducive to the diffusion and transmission of gases. On the cathode side, steam molecules are transported from the flow channel to the cathode-electrolyte interface (the three-phase boundary (TPB) [33,34,35]). Water molecules split into hydrogen ions and oxygen ions at the cathode-electrolyte interface. Two hydrogen ions gain electrons to form a hydrogen molecule. Hydrogen molecules are transported from the porous cathode to the cathode flow channel. The oxygen ions are transported to the anode side through the electrolyte. On the anode side, oxygen ions lose electrons and become oxygen molecules. The generated oxygen molecules are transported from the anode-electrolyte interface to the anode flow channel. The generated electrons are transported from the anode side to the cathode side through the external circuit.

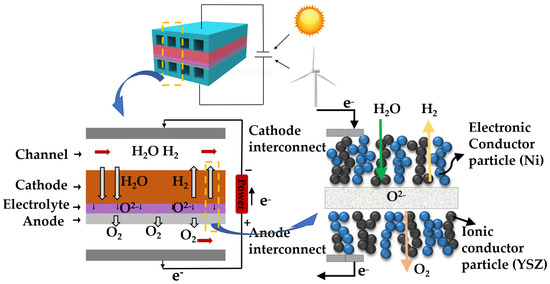
Figure 2. Schematic diagram of hydrogen production from steam electrolysis by the SOEC.

At the cathode-electrolyte interface:

$${\mathrm{H}}_2{\mathrm{O}+2\mathrm{e}}^{-}\to {\mathrm{H}}_2{+\mathrm{O}}^{2-}$$

(1)

At the anode-electrolyte interface:

$${\mathrm{O}}^{2-}\to \frac{1}{2}{\mathrm{O}}_2{+2\mathrm{e}}^{-}$$

(2)

The overall reaction of SOEC electrolysis steam can be expressed as:

$${\mathrm{H}}_2\mathrm{O}\to {\mathrm{H}}_2+\frac{1}{2}{\mathrm{O}}_2$$

(3)

In the study, there are a few main assumptions, listed as follows:

• All the gases involved in the reaction are ideal gases.
• The SOEC is operating in a steady state.
• The SOEC is operating under isothermal condition.
• The permeability of the gas species and electrons in the electrolyte are neglected.

2.2. Governing Equations

2.2.1. Mass Conservation Equation

The equation of mass conservation is as follows:

$$\nabla (\epsilon \rho \overrightarrow{u})=S_m{}_{,i}$$

(4)

where $\rho$ is the density of the gas mixture, u (m/s) is the velocity, S_m,i (kg/(m³∙s)) is the mass source term and ε is the porosity of the porous electrode.

$$S_m{}_{,i}=\{\begin{array}{l}{S}_{m,a}=\frac{j_a}{4F}{M}_{O_2}\hspace{1em}Anode\\ S_{m,c}=S_{H_{2}O}+S_{H_2}=-\frac{j_c}{2F}{M}_{H_{2}O}+\frac{j_c}{2F}{M}_{H_2}\hspace{1em}Cathode\\ 0\hspace{1em}Other\end{array}$$

(5)

where F (C/mol) is Faraday’s constant, M (kg/mol) is the mole mass of the components, and j (A/m²) is the current density.

2.2.2. Momentum Conservation Equation

The equation of momentum conservation is as follows:

$$\epsilon \nabla \cdot (\rho \overrightarrow{u}\overrightarrow{u})=-\epsilon \nabla p+\nabla \cdot (\epsilon \mu \nabla \overrightarrow{u})+S_u$$

(6)

where μ (kg/(m∙s)) is the dynamic viscosity of the mixed gas, P (Pa) is the pressure and S_u (kg/(m²∙s²)) is the momentum source term.

$$S_u=\{\begin{array}{l}-\frac{\mu \overrightarrow{u}{\epsilon }^2}{K}\hspace{1em}Porous electrode, metal foam channel\\ 0\hspace{1em}Other\end{array}$$

(7)

where K (m²) is the porous electrode permeability. The Carman-Kozeny correlation determines the flow permeability as [36]:

$$K=\frac{d_p^2{\epsilon }^3}{180{(1-\epsilon )}^2}$$

(8)

where d_p is the diameter of the electronic particles.

2.2.3. Species Conservation Equation

The equation of species conservation is as follows:

$$\nabla \cdot (\epsilon \rho Y_i\overrightarrow{u})=\nabla \cdot (\rho D_i^{eff}\nabla Y_i)+S_i$$

(9)

$$\begin{array}{l}{S}_{H_2}=\frac{j_c}{2F}{M}_{H_2}\\ S_{H_{2}O}=-\frac{j_c}{2F}{M}_{H_{2}O}\\ S_{O_2}=\frac{j_a}{4F}{M}_{O_2}\end{array}$$

(10)

where Y_i is the mass fraction of component i, D_i (m²/s) is the effective diffusion coefficient and S_i is the component i mass source term.

In the channel, the binary molecular diffusion coefficient is used to simulate gas diffusion [37].

$$D_{ij}=\frac{3.198\times T^{1.75}}{P(v_i^{\mathrm{1/3}}+v_j^{\mathrm{1/3}})}{\left(\frac{1}{M_i}+\frac{1}{M_j}\right)}^{0.5}$$

(11)

where M_i (g/mol) is the relative molecular mass of component i and v_i (cm⁻³ mol⁻¹) is the diffusion volume of the component. The effective diffusion coefficient in the channel is expressed as:

$$D_i^{eff}=\frac{1-x_i}{{\displaystyle \sum _{j\ne i}{x}_j/D_{ij}}}$$

(12)

In the porous electrode, Knudsen diffusion and binary molecular diffusion should be considered, because of the effects of porosity and tortuosity on gas diffusion. The Knudsen diffusion coefficient is expressed as [36]:

$$D_{ik}^{}=\frac{d_p\epsilon }{3\tau }\sqrt{\frac{8RT}{\pi M_i}}$$

(13)

where T (K) is the temperature and τ is the tortuosity. Considering both Knudsen diffusion and binary molecular diffusion, the effective diffusion coefficient in the porous electrode is formally expressed as [37]:

$$D_i^{eff}=\frac{D_{ij}^{}{D}_{ik}^{}}{D_{ij}^{}+x_i{D}_{ik}^{}+x_j{D}_{ik}^{}}$$

(14)

2.2.4. Charge Conservation Equation

The equation of charge conservation is as follows:

$$\nabla \cdot (-{\sigma }_{el}^{eff}\nabla {\varphi }_{el})=S_{el}=j_i\cdot S_V$$

(15)

$$\nabla \cdot (-{\sigma }_{io}^{eff}\nabla {\varphi }_{io})=S_{io}=j_i\cdot S_V$$

(16)

where ${\sigma }_{io}^{eff}$ and ${\sigma }_{el}^{eff}$ (J/mol) are the effective ionic and electronic conductivities, respectively. S_el and S_io (A/m³) are the source terms of electronic and ionic potentials, respectively.

$$S_{el}=\{\begin{array}{l}{j}_c\cdot S_{TPB}\hspace{1em}Cathode\\ -j_a\cdot S_{TPB}\hspace{1em}Anode\end{array}$$

(17)

$$S_{io}=\{\begin{array}{l}-j_c\cdot S_{TPB}\hspace{1em}Cathode\\ j_a\cdot S_{TPB}\hspace{1em}Anode\end{array}$$

(18)

where j_a and j_c (A/m²) are the current density, respectively. S_TPB (m²/m³) is TPB’s active area per unit volume. The parameter S_TPB can be expressed as a particle coordination number and percolation theory in the binary random packing of spheres [38]:

$$S_{TPB}=\pi {\sin }^2\theta r_e^2{n}_t{n}_i\frac{Z_e{Z}_i}{6}{P}_e{P}_i$$

(19)

where θ is the contact angle between the electronic and ionic conductors; r_e (mm) is the radius of the electronic conductors; n_t is the total number of particles per unit volume; n_e and n_i (n_i = 1 − n_e) are the number fractions of electronic and ionic conductors, respectively; Z_e and Z_i are average coordination numbers of electronic/ionic conductors and finally P_e and P_i are the probability of the electronic/ionic particles connecting to the porous media.

The parameters of n_t and n_e are computed as [39]:

$$n_t=\frac{1-\epsilon }{(4/3)\pi r_e^3\left[n_e+(1-n_e){(r_i/r_e)}^3\right]}$$

(20)

and

$$n_e=\frac{\Phi }{\Phi +(1-\Phi )/{(r_i/r_e)}^3}$$

(21)

where ε is the porosity of the electrode, r_i (mm) is the radius of the ionic conductors and Φ is the volumetric fraction of electronic conductors in the porous electrode.

The parameters Z_e and Z_i can be determined as:

$$Z_e=3+\frac{3}{n_e+(1-n_e){(r_i/r_e)}^2}$$

(22)

and

$$Z_i=3+\frac{3{(r_i/r_e)}^2}{n_i+(1-n_i)(r_i/r_e{)}^2}$$

(23)

The parameters P_e and P_i are calculated as:

$$P_e={\left[1-{(\frac{4.236-Z_{e-e}}{2.472})}^{2.5}\right]}^{0.4}$$

(24)

and

$$P_i={\left[1-{(\frac{4.236-Z_{i-i}}{2.472})}^{2.5}\right]}^{0.4}$$

(25)

where Z_e−e and Z_i−i are the average coordination numbers of electronic/ionic particles to electronic/ionic particles. The parameters Z_e−e and Z_i−i are defined as:

$$Z_{e-e}=\frac{6n_e}{n_e+(1-n_e){(r_i/r_e)}^2}$$

(26)

and

$$Z_{i-i}=\frac{6n_i}{n_i+\left(1-n_i\right){\left(r_i/r_e\right)}^{-2}}$$

(27)

2.3. Electrochemical Reaction Model

During the operation, SOEC voltage can be expressed by the following expression:

$$V=E+{\eta }_{conc,c}+{\eta }_{conc,a}+{\eta }_{act,c}+{\eta }_{act,a}+{\eta }_{ohm}$$

(28)

where E (V) is the equilibrium voltage; η_conc,c and η_conc,a are the concentration overpotentials at the cathode and anode, respectively; η_act,,a and η_act,c are the activation overpotentials at the anode and cathode, respectively and finally η_ohm is the ohmic overpotential.

The equilibrium voltage E is determined by the Nernst equation:

$$E=E_0+\frac{RT}{2F}ln[\frac{P_{H_2}^0{(P_{O_2}^0)}^{1/2}}{P_{H_{2}O}^0}]$$

(29)

where R (J/(mol∙K)) is the universal gas constant, F (C/mol) is the Faraday constant, $P_{H_{2}O}^0$, $P_{H_2}^0$ and $P_{O_2}^0$ are the partial pressures of steam, hydrogen, and oxygen on the electrode—electrolyte surfaces, respectively, and finally E₀ is the standard Nernst potential.

$$E_0=\frac{-\Delta G_0}{nF}$$

(30)

The concentration overpotential is expressed as:

$$\begin{array}{l}{\eta }_{conc,c}=\frac{RT}{2F}ln(\frac{P_{H_2}^I\cdot P_{H_{2}O}^0}{P_{H_2}^0\cdot P_{H_{2}O}^I})\\ {\eta }_{conc,a}=\frac{RT}{2F}ln\left[{(\frac{P_{O_2}^I}{P_{O_2}^0})}^{1/2}\right]\end{array}$$

(31)

where P₀ and P_I are the partial pressures at the electrode surface and electrode—electrolyte interface, respectively, and subscripts H₂O, H₂, and O₂ represent the steam reactant, hydrogen, and oxygen products, respectively.

The relationship between the activation overpotential and the current density is expressed by the Butler—Volmer equation [40]:

$$j_i{}_{=a,c}=J_{0,i}[\exp (\frac{{\alpha }_{a}nF{\eta }_{act,i}}{RT})-(\frac{(1-{\alpha }_c)nF{\eta }_{act,i}}{RT})]$$

(32)

where J_0,a (A/m³) and J_0,c are the exchange current densities at the anode and cathode, respectively, η_act is the activation overpotential and α is the charge transfer coefficient. The activation overpotential is calculated as:

$${\eta }_{act,i}=\frac{RT}{nF}{\sin \mathrm{h}}^{-1}\left(\frac{J_i}{2J_{0,i}}\right)$$

(33)

The parameter J_0,i is calculated as:

$$J_{0,i}={\gamma }_i\exp (-\frac{E_{act,i}}{RT})$$

(34)

where γ_i (A/m²) is the pre-exponential factors and E_act,i (J/mol) is the activation energy.

The ohmic overpotential is calculated as [41]:

$${\eta }_{ohm}=2.99\times {10}^{-5}jL\exp (\frac{10300}{T})$$

(35)

where L (mm) is the thickness of the electrolyte.

2.4. Boundary Conditions

The boundary settings of the conservation equation are shown in Table 1.

Table 1. Boundary conditions or settings for the SOEC model.

Equation	Channel	Electrode/Channel Interfaces	Electrode/Electrolyte Interfaces	Other
Mass Conservation	Mole Fraction	Continuous	Insulation	Insulation
Momentum Conservation	Mass Flow Rate (Equation (36))	Continuous	No Slip	No Slip
Ionic charge Conservation	Insulation	Insulation	Continuous	Insulation
Electronic charge Conservation	Insulation	Electric Potential	Electric Potential	Insulation

The cathode inlet mass flow is given as [42]:

$$m={\displaystyle \sum _1^i(x_i{M}_i)\times \frac{\left|j_{ca}\right|A_{act}{\delta }_{ca}}{2F{u}_f}}$$

(36)

where x_{i(i = H20, H2)} is the mole fraction, A_act (m²) is the effective reaction area of the cathode layer, δ_c (mm) is the thickness of the cathode layer, and u_f is the gas utilization.

3. Model Validation

In this section, the governing equations of the SOEC given in the previous section were used to simulate the experimental results of Momma et al. [43]. The model was verified by the commercial software COMSOL Multiphysics. In their experiments, the accuracy of the modeling results was closely related to the characteristic parameters of the microstructure. The specific parameters of the model in this study are shown in Table 2, Table 3 and Table 4. As shown in Figure 3, the simulated results of the model were basically consistent with the reference data at different temperatures.

Table 2. Parameters used in the SOSE electrochemistry modeling analysis.

Parameter	Value
Operating pressure, P (atm)	1
Pre-exponential factor for anode exchange current density, γa (A/m2)	2.051 × 109 [44]
Pre-exponential factor for cathode exchange current density, γc(A/m2)	1.344 × 1010 [44]
Activation energy for anode, Eact,a (J/mol)	1.2 × 105
Activation energy for cathode, Eact,c (J/mol)	1.0 × 105
Electrode porosity, ε	0.48 [44]
Electrode tortuosity, τ	5.4 [44]
Faraday’s constant, F (C/mol)	96,485
Gas constant, R (J/(mol∙K))	8.3145
Average pore radius, re (μm)	1.07 [44]
Volumetric fraction of electronic particles in the porous electrode, Φ	0.5 [45]
Contact angle between the electronic and ionic particles, θ	15° [46]
Transfer coefficient in anode/cathode, αa/αc	0.5/0.5 [47]

Table 3. Microstructural and geometrical parameters.

Electrolyte-Supported Electrolyzer: For Model Validation
Electrolyte thickness, L (mm)	1
Cathode thickness, dc (mm)	0.1
Anode thickness, da (mm)	0.1
Cathode-supported electrolyzer: For Parametric Analyses
Electrolyte thickness, L (mm)	0.05
Cathode thickness, dc (mm)	0.5
Anode thickness, da (mm)	0.05

Table 4. Material parameters of the SOEC [42,48].

Parameter	Cathode	Electrolyte	Anode
Material	Ni-YSZ	YSZ	LSM-YSZ
Ionic conductivities (S/m)	3.34 × 104 ∙exp(−10300/T)	3.34 × 104 × exp(−10300/T)	3.34 × 104 × exp(−10300/T)
Electronic conductivities (S/m)	3.27 × 106 − 1065.3 T	-	4.2 × 107 × exp(−1150/T)/T

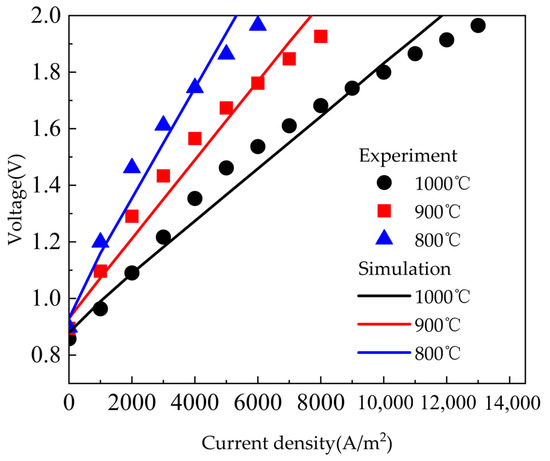
Figure 3. Comparison between simulation results and reference data [44] at different temperatures.

4. Results and Discussion

4.1. Effect of Permeability

The permeability of metal foam can affect the performance of the SOEC. Permeability is related to the porosity, tortuosity, and pore size of metal foam. In this section, four kinds of metal foams with the a permeability of 1 × 10⁻⁷ m², 1 × 10⁻⁸ m², 1 × 10⁻⁹ m², and 1 × 10⁻¹⁰ m² were selected for analysis. The steam conversion rate, voltage, the steam diffusion flux, and pressure drop curve at different permeabilities are shown in Figure 4a–d. We can see that the metal foam improved the performance of the SOEC without metal foam. The steam conversion rate of the SOEC increased from 72.21% to 76.18%, while the diffusion flux of the steam increased from 2.3 × 10⁻⁴ kg/(m²∙s) to 2.5 × 10⁻⁴ kg/(m²∙s) at 10,000 A/m². It can be said that with the decrease of permeability, the steam conversion rate increases, and the voltage required by the electrolytic cell increased gradually. Zhan et al. [49] also obtained similar results using metal foam as a cathode flow distributor in an SOFC. It can be said that a higher output voltage was always accompanied with a larger pressure drop. The voltage drop generated in the channel also increased with the decrease of permeability. The steam diffusion flux increased and then decreased with the decrease of permeability decreasing. At 15,000 A/m², the voltage increased from 2.4358 V to 2.4401 V and the steam conversion rate increased from 76.95% to 79.26% as the permeability decreased from 1 × 10⁻⁷ m² to 1 × 10⁻⁹ m². However, the voltage drop increased significantly from 8.28 Pa to 1772.49 Pa and the diffusion flux of steam decreased from 7.96 × 10⁻⁴ kg/(m²∙s) to 7.57 × 10⁻⁴ kg/(m²∙s). Due to the decrease in permeability, the tortuosity inside the foam became larger, which increases the gas flow resistance. As a result, the pressure drop becomes larger, which led to a decrease in the steam diffusion flux. Therefore, selecting the appropriate metal foam permeability could effectively improve SOEC performance. Tseng et al. [50] studied the effects of different metal foams on PEM fuel cells. Their results indicated that the conductivity of metal foam was an important factor in fuel cell performance. As shown in Figure 4b, with the metal foam introduced into the flow channel in this paper, the voltage of the SOEC with metal foam was larger than the SOEC without metal foam. Since the metal foam could transmit gas and is also a conductive medium, the transmission area of conductive electrons was increased. Electrons can be transported vertically to the porous electrode through the shortest path, which not only shortens the electron transport path, but also makes the electron distribution more uniform, thus reducing the cell activation overpotential, increasing the conductivity, and increasing the voltage.

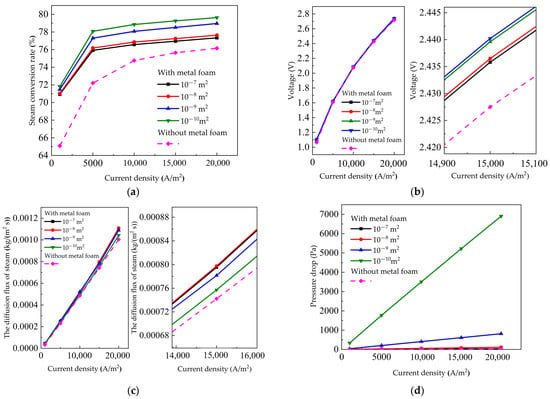
Figure 4. Influence of metal foam permeability: (a) steam conversion rate curve; (b) voltage curve; (c) the diffusion flux of steam curve; (d) pressure drop curve.

4.2. Effect of Temperature

In this section, the operating temperature of 800/900/1000 °C was selected for analysis. Figure 5a–c show the variation trend of the steam conversion rate, cathode activation overpotential, and the diffusion flux of steam in the different gas flow channels. The steam conversion rate, the cathode activation overpotential voltage and the diffusion flux of steam decreased as the temperature increased. These three figures reveal that the performance of the SOEC with metal foam was better than without metal foam. When the temperature reached 1000 °C and the current density reached 10,000 A/m², the steam conversion rate increased from 74.76 to 76.86%. The diffusion flux of H₂O increased from 4.86 × 10⁻⁴ kg/(m²∙s) to 5.13 × 10⁻⁴ kg/(m²∙s), and the cathode activation overpotential voltage decreased from 0.088764 V to 0.088758 V. Because metal foam occupied the SOEC without metal foam flow channel, the longitudinal mass transfer performance of the SOEC was increased. Kumar and Reddy [51] found that the tortuous pathway in the metal foam porous structure significantly improved the gas flow uniformity and convection normal to the electrode surface. According to Meng et al. [46], the effects of operating temperatures on SOEC overpotential was similar to the trend shown in this paper. As the temperature increased, the overpotential, shown in Figure 5b, decreased. The decrease of temperature caused both the exchange current density and the ionic conductivity to decrease, which resulted in the activation overpotential increasing.

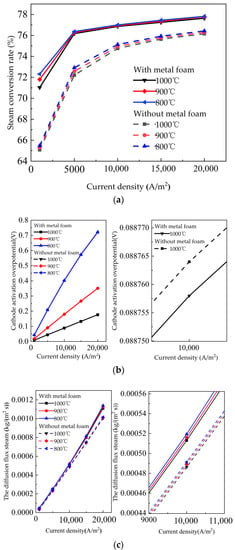
Figure 5. Influence of temperature on the SOEC with metal foam and the SOEC without metal foam (a) steam conversion rate curve; (b) the cathode activation overpotential voltage; (c) the diffusion flux of steam.

4.3. Effect of Steam Mole Fraction

When the temperature and permeability were constant, the gas composition had an effect on the performance of the SOEC. In this section, the operating temperature was kept at 1000 °C and permeability at 10⁻⁸ m². The steam to hydrogen molar ratios of 50%/50%, 60%/40% and 70%/30% were selected for analysis. The influence curves of SOEC with metal foam and SOEC without metal foam on steam conversion rate under different inlet steam mole fractions are shown in Figure 6a, the voltage curve is shown in Figure 6b, the cathode activation overpotential is shown in Figure 6c, and the steam diffusion flux curve is shown in Figure 6d. As shown in the four figures, the steam conversion rate of the SOEC with metal foam is significantly higher than that of the SOEC without metal foam. When the mole fraction of steam to hydrogen mole ratio is 50%/50% and the current density is 10,000 A/m², the steam conversion rate increases from 77.52% to 79.77%. Additionally, the diffusion flux of H₂O increases from 5.68 × 10⁻⁴ kg/(m²∙s) to 6.01 × 10⁻⁴ kg/(m²∙s). The cathode activation overpotential decreased from 0.088744 V to 0.088729 V, indicating that the metal foam contributed to gas diffusion. As shown in Figure 6b, the cell voltage decreases with the vapor mole fraction increasing, which can be explained by the Nernst equation (Equation (29)). Figure 6c,d show metal foam increase the diffusion rate and decrease the overpotential. Metal foam reduces the gas transport resistance and increases steam conversion. Meng et al. [44] studied the effect of steam mole fraction on SOEC J-V characteristics. The voltage also decreases with steam mole fraction increasing.

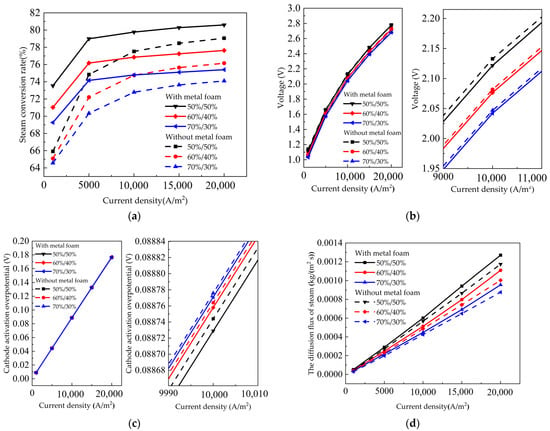
Figure 6. Influence of steam mole fraction on the SOEC with metal foam and without metal foam (a) steam conversion rate curve; (b)voltage curve; (c) cathode activation overpotential; (d) the diffusion flux of steam.

4.4. Effect of Gas Utilization

Besides permeability, temperature, and steam mole fraction, gas utilization had a significant effect on the SOEC’s dynamic behavior. To prevent a shortage of reaction gas for the SOEC, the reaction gas provided was more than the gas needed for the SOEC. In this section, the operating temperature as kept at 1000 °C, the permeability was kept at 10⁻⁸ m² and the steam molar fraction was kept at 0.6. The gas utilization of 0.5/0.6/0.7/0.8 was selected for analysis.

Figure 7a shows the influence of the SOEC with metal foam and without metal foam on the steam conversion rate under different gas utilization. The gas utilization had a great effect on the water conversion rate. The conversion rate of steam varied greatly with different gas utilization. Du et al. [42] studied the co-electrolysis of water and carbon dioxide in solid oxide electrolysis cells. As the gas utilization rate decreased, the voltage decreasesd and the electrolysis efficiency increased. As shown in Figure 7a, the gas utilization is increased from 0.5 to 0.8, and the steam conversion rate increased by more than 30%. This sharp change was expected because the steam conversion rate was strongly dependent on the inlet fuel flow. Nevertheless, the figure indicated that the SOEC with metal foam steam conversion rate was better than SOEC without metal foam. Figure 7b,c show the cathode activation overpotential and steam diffusion flux curve, respectively. The steam conversion rate increased from 86.39% to 88.6% when the gas utilization was 0.8 and the current density was 15,000 A/m². The steam diffusion flux increases from 8.58 × 10⁻⁴ kg/(m²∙s) to 9.26 × 10⁻⁴ kg/(m²∙s). The cathode activation overpotential decreases from 0.13276 V to 0.13038 V. This was mainly due to the increase in the concentration of reactants at the TPB reaction interface as the gas utilization rate decreased, thus reducing the activation overpotential voltage.

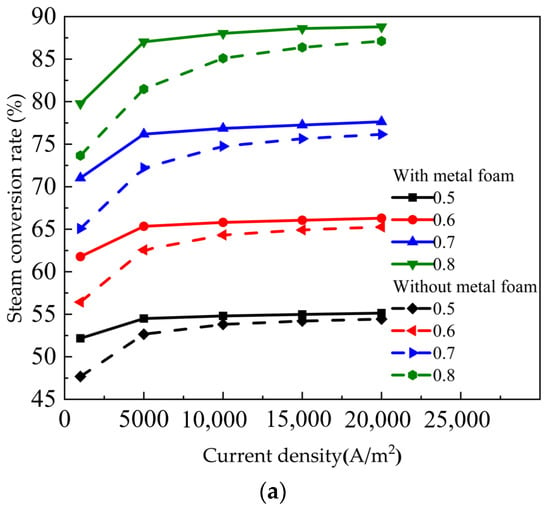
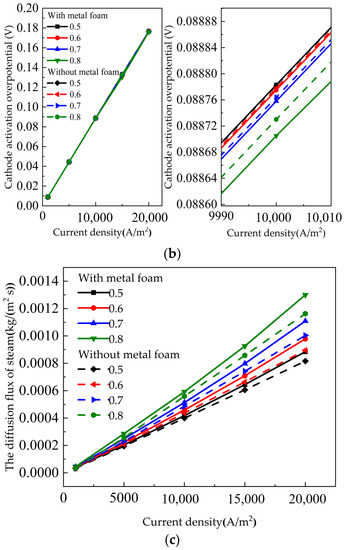
Figure 7. Influence of gas utilization on the SOEC with metal foam and without metal foam: (a) steam conversion rate curve; (b) cathode activation overpotential; (c) the diffusion flux of steam.

5. Conclusions

In this study, the effect of metal foam used in high temperature SOECs, have been investigated in a three-dimensional model. Conservation equations for mass, momentum, matter and charge were used in this model. Through the analysis and discussion of the simulation results, it was found that metal foam could effectively improve SOEC performance. The steam conversion rate of the SOEC increased from 72.21% to 76.18% and the diffusion flux of steam increased from 2.3 × 10⁻⁴ kg/(m²∙s) to 2.5 × 10⁻⁴ kg/(m²∙s) at 10,000 A/m². The SOEC with metal foam could have improved conductivity and promoted the gas diffusion from the channel to the porous electrode layer, which would have helped to reduce diffusion resistance and to enhance gas transport.

Furthermore, the effects of permeability, temperature, steam mole fraction and gas utilization on the SOEC performance were studied. The results show that the performance of the SOEC with metal foam was better than the SOEC without metal foam in terms of the steam conversion rate, cathode activation overpotential and diffusion flux of steam. For example, higher permeability metal foam performed better, but with a greater pressure drop. Therefore, selecting the appropriate metal foam permeability was beneficial to the improvement of SOEC performance. The results of this paper provide a baseline for the optimal design of SOECs with metal foam.