Abstract
The induction faucet has been widely used in public due to its advantages of convenience, sanitation, water, and electricity saving. To solve the problem of environmental pollution caused by dry batteries used in induction faucets, a suitable micro pipe mixed-flow turbine installed in a tap-water system with only 15 mm in diameter, that uses the pipeline water pressure to generate electricity for the induction faucet was designed and developed, based on computational fluid dynamics (CFD) and model tests. According to the specific speed, a preliminary design of each flow component of the turbine was first produced. Then, using the multi-objective orthogonal optimization method, the optimum test schemes were determined, and the influence of various test factors on the turbine’s hydraulic performance was revealed. Under the design flow rate, the turbine’s power output and efficiency were 6.40 W and 87.13%, respectively, which were 34.45% and 4.99% higher than those of the preliminary scheme. Both the power output and efficiency of the optimized turbine met the design requirements. Numerical and model test results showed good agreement, where the deviation in turbine power output predictions was below 5% under large flow condition. Model test results also showed that the turbine can be started as long as the inlet flow is greater than 0.14 kg/s. Overall, the micro-pipe turbine designed in this paper exploits the (mostly wasted) water kinetic energy in induction faucets for power production, contributing to environmental pollution reduction and realizing energy conservation.
1. Introduction
Water is essential for life and plays an irreplaceable role in the human production and proper functioning of the Earth’s ecosystems [1]. Water quality and quantity are major environmental problems, and important factors affecting human health and safety [2]. With the current global progress in science and technology there has been an improvement in people’s awareness of energy conservation and environmental protection and the induction faucet has been become widely used in various public places. This has come as a result of several advantages being linked to its use, such as convenience, sanitation, and water and electricity saving. However, many sensors in the induction faucet have relied on battery power supply due to the fact that their locations make it hard to connect to local utility grid power [3]. Generally speaking, the batteries in an induction faucet need to be replaced every two to three months. Extensive use of an induction faucet will require a large number of batteries, which will cause pollution to the environment and soil if the batteries are not properly handled [2,4]. However, the environmental pollution from batteries usage can be solved by changing the power supply mode of sensors in the induction faucet, which would make the induction faucet more energy-saving and environmentally friendly.
Therefore, this has become the main challenge for many researchers. McNabola et al. [5] indicated that water supply is a core service on which civilized society depends, and which involves considerable energy consumption and economic cost. They showed that a break pressure tank installed in water supply networks to resolve the high flow pressure provides the opportunity to recover energy from networks through a hydropower turbine system. Moreover, they proved that the above approach showed preliminary technical and economic feasibility, so as to minimize energy consumption. Eventually, more and more investigators turned their attention to the utilization of micro-hydropower in water systems to take advantage of the excess energy in the pipelines. In a recently conducted study [6], a micro-pipe turbine (MPT) installed in a tap-water pipeline was gradually developed and utilized. Its working principle is as follows: this micro-pipe turbine is designed to be driven by water kinetic energy, where, through the connecting shaft, the MPT drives the generator to produce usable electrical power. Then the generator charges the battery of the sensor after sending out an AC electric signal, thus providing power for the detection equipment of the water supply pipeline (WSP). Finally, the conversion of fluid kinetic energy, mechanical energy, and electric energy is realized. The entire MPT system is closed in a rectangular box, only leaving out the inlet and outlet pipes. The box is fully installed in the tap-water pipeline connected to the induction tap, and the bottom of the box is fixed to the wall or floor. The water flows through the MPT to drive the generator, and the electrical energy is stored in the rechargeable battery to realize the constant power supply for the induction faucet. In the production process of the MPT, the engineering plastic polyamide material would be selected for its advantages such as the low cost, long service life, small volume, and light weight. 3D printing technology has been used to manufacture MPT, which is convenient and cost-effective. The excellent features of this MPT system are, among others, the associated convenient installation, small size, simple production process, stable power supply, long service life and replacement cycles, environment-friendliness, and energy conservation ability.
Some investigations have been done to study the hydro energy harvest in the water pipelines, and several attempts have been made to select or design proper turbines [7,8]. For example, Du et al. [9] investigated the impact of the runner inlet arc angle on the performance of an inline cross-flow turbine in urban water mains. Sinagra et al. [10] suggested a cross-flow with positive outlet pressure (a power recovery system), which could provide potential energy consumption service with additional significant hydropower production. Generally, in line with the placement mode of the main shaft, micro hydro turbines can be divided into horizontal axis and vertical axis types, which are derived from the wind turbines [11]. Sakti et al. [12] studied a horizontal-axis type in-pipe hydro-turbine by using the SolidWorks simulation method, where the best combination of deflector design and blade curvature angle was realized. Li et al. [13] designed an ultra-low head turbine, which was similar to a marine and hydrokinetics turbine, but their research focus was on the performance of composite runner blades. Several mini bulb propeller turbines which also can be installed inside water pipelines have been developed [14]. Ferro et al. [15] designed the rotor blades of a mini hydraulic turbine using a quasi-three-dimensional method and the results validated the design hypothesis of small flow velocity through the rotor. Samora et al. [16] optimized and tested a new five-blade tubular propeller turbine with an 85 mm diameter for pipe inline installation. Study results showed that this turbine has potential for further development since the efficiencies were around 60%. Compared to the horizontal axis type, vertical axis type of pipeline turbines have attracted more attention due to linked advantages of flow direction holding, simple structure, small space, and easy installation. Chen et al. [3] developed a novel vertical-axis water turbine for hydropower harness inside water pipelines and found that the rotor with a hollow structure combined with an eye-shaped slanted block in a pipeline could achieve the maximum power as compared with other types of vertical-axis rotors. The vertical-axis-type micro-turbines mainly consist of two sub-types. One is the lift-type and the other is the drag-type. The lift type hydro turbine, also known as the Darrieus type, was developed for big water pipelines (pipe diameters larger than 25 inch) by Lucid Energy [17]. Langroudi et al. [18] conducted new spherical lift-based in-pipe turbine modelling and parameterization research, and the power coefficient, the probability of cavitation, and the pressure coefficient obtained by using a reasonable numerical methods were validated with some experiments. Oladosu et al. [19] generated a pipeline lift-based spherical turbine with NACA 0020 airfoil cross-section, which showed appropriate energy extraction in water distribution pipelines with diameters of 250 mm. Though this lift-type MPT exhibits good energy performance after reasonable design, the start-up performance is still a big problem due to the dynamically stalled blade characteristics [20,21]. The drag-type turbine, sometimes named the Savonius turbine, has also been successfully developed and utilized on different occasions. Payambarpour et al. [22,23] performed a parametric study on a 3D modified Savonius turbine with a deflector in a 100 mm water pipe by using both experimental and numerical methods, where they found that the relationship between the flow rate and aspect ratio depended on the blockage coefficient. Chen et al. [24] designed a drag-type vertical-axis hydro-turbine for pico-hydropower in water pipelines and conducted an optimization study based on previous design scheme. The proposed turbine showed good performance at the velocity rage from 1.5 m/s to 3.5 m/s and the rotating speed range from 100 rpm to 1000 rpm. Yang et al. [25] compared the start-up hydraulic performances of a lift-type and a drag-type hydro-turbine. The results showed that the lift-type turbine gives better hydraulic characteristics in terms of tip speed ratio and power coefficient than those of the drag-type turbine, while the drag-type turbine displays better start-up performance than the lift-type.
Compared to other turbines, energy recovery from water supply systems using pumps as turbines (PATs) presents many advantages such as the marketable availability, low investment cost, and easy installation and maintenance. This has increasingly attracted the attention from many field players and researchers, where PATs have been considered to be an effective way to generate power in water pipelines. Different studies have been carried out to verify the feasibility of PAT technology in water pipelines, using computational fluid dynamics (CFD) techniques [26,27,28]. Fontana et al. [29] investigated the water distribution system in one district of Naples (Italy) to assess the hydropower generation potential using the PATs, where it was found that the PATs could achieve a good balance between hydropower recovery and head reduction. Du et al. [30] numerically and experimentally studied the performance of a PAT, which was selected through the application of empirical equations, based on the given working conditions in one typical high-rise building. The results verified that the PATs are a good way for avoiding excessive water-head reduction at higher flow rates. Kramer et al. [31] investigated a PAT device both in the laboratory and in the field to improve the economic profitability of energy recovery plants at low installed capacities (around 15 kW). Buono et al. [32] used 3D CFD modeling methodology to study a PAT installed in a hydraulic urban network. The maximum efficiency was found to be 66.3%. De Marchis et al. [33] developed a hydrodynamic model of a PAT, which was applied in the Palermo district network (Italy). Their analysis indicated that a really attractive capital payback period could be achieved if PATs are installed in the pipes located close the water supply node. Pérez-Sánchez et al. [34] defined a new approach to estimating the PAT best efficiency point and predicting its energy performance curve, the accuracy of which was verified using an experimental database. However, due to the fixed geometrical characteristics and inner flow space, the PAT performance in terms of head reduction was easily affected by the variation of flow discharge. To solve this problem, Carravetta et al. [35] designed a PAT installation scheme, which ensured that PAT operating conditions stayed around their best efficiency point, where at the same time, PAT’s water pressure reduction task was effectively performed. For PATs, the fundamental blade design only considers its pump mode of operation (normal hydraulic pump operation). Therefore, PAT flow dynamics under reverse operating mode do not conform to the conventional turbine design concept. Meanwhile, due to PAT’s lack of guide vanes (GV), it is difficult to form an appropriate in-flow velocity at the runner inlet, resulting in a relatively low efficiency.
Due to their comparatively big sizes, existing MPT designs don’t fit the power generation task within micro-pipes (pipe diameter less than 15 mm) with very small flows. Moreover, their operational efficiency has been less than 65% for most of the so-far-tested pipe turbines, which indicates the associated low extraction rate of water-contained energy within water pipelines. In this paper, a high-efficiency and stable mixed-flow turbine was applied to a micro tap-water-pipe power generation system that was only 15 mm in diameter. This turbine uses the water pressure in the WSP to kick off its rotational motion, and generates the electrical power to feed the induction faucet batteries. The main goal of this study was to design and develop an efficient micro turbine that specifically met two performance requirements, namely low-flow-rates start-up and having enough output power. To this end, the design process is shown in Figure 1 and the structure of the paper is as follows: In Section 1, which is the introductory section, the research background to the present study is discussed. In Section 2, the preliminary design of the MPT is explained. Then the hydraulic design and optimization of the concerned turbine, based on orthogonal optimization method and numerical simulation, are discussed in Section 3. In the same section, these methods are verified through experimental testing. Finally, Section 4 contains the study’s main concluding remarks.
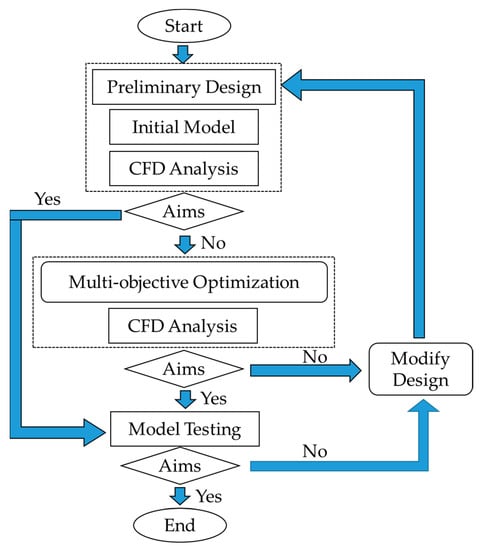
Figure 1.
Design process of the MPT.
2. Preliminary Design of the MPT
2.1. Determination of Basic Parameters
2.1.1. Design Head
The pressure at the end of the urban water supply network is 0.14 Mpa, that is, the water head is 14 m according to the requirements of the national water supply pressure service code of China. However, the kinetic hydraulic power inside WSP is mainly used to drive the water flow, and only superfluous head or small part of water energy can be used by turbines to generate electricity. Considering the pressure loss of water flow in the pipeline, the head is taken as 3 m.
2.1.2. Design Discharge
On the basis of the actual specification and size of the WSP, the diameter of the four-branch pipe is 15 mm, and the flow rate is set at 1.5 m/s [36], so the discharge Q can be calculated by the following equation:
where d is the pipe diameter, ρ is the water flow density (1000 kg/m3), and u is the water flow velocity. Based on the known conditions, the design flow rate can be calculated as 0.265 kg/s.
2.1.3. Design Power Output
In order to offer continuous and stable power for the monitoring system in induction faucet, a rechargeable storage battery is installed between the control circuit and the induction faucet. The electric energy emitted by the generator first charges the battery, and then the battery supplies power to the induction faucet, since the power consumption of the induction faucet is less than 6 W.
2.1.4. Design Rotational Speed
The operating voltage of the rechargeable battery is 4 V, and the output current of the generator needs to reach 1.5 A in order to meet the power supply requirements. Due to the small size of the MPT and the high speed rotation driven by the water flow, a micro-sized high-speed generator independently developed by a company in Zhejiang Province, China was adopted. When the speed of the generator is 3500 r/min, the output current is 1.5 A. Thus, the design speed of the MPT is 3500 r/min.
2.2. Determination of Turbine Type
The specific speed ns is an important characteristic parameter of water turbine classification, and its definition can be expressed as follows [37]:
where n, P, and H are the rotational speed, power output, and water head of the MPT, respectively.
According to the above basic design parameters of MPT, the calculated specific speed is about 50 m·kW, which is a low specific speed. Generally, micro hydro turbines can be classified into two general types based on their working principle: (1) impulse turbines used for high heads of water and low flow rates and (2) reaction turbines normally employed for heads below about 450 m and moderate or high flow rates. Meanwhile, according to the different types of reaction turbine applicable speed range, the Francis turbine was selected. Finite element studies have been widely used in structural analysis [38,39,40]. Many studies show that Francis turbines not only perform well, but also have a stable and reliable structure [41,42]. Moreover, the flow in WSPs is usually unstable, so the energy performance of axial flow hydraulic machinery is obviously affected by the tip leakage flow [43], and the mixed flow structure has better stability. A Francis turbine consists of spiral casing, water guiding mechanism, runner, and draft tube.
2.3. Initial Modelling
For initial models (Figure 2), the diameter of runner was 30 mm, a curved-shape upper crown and lower ring were adopted, the number of runner blades was preliminarily selected as 13, and the blade thickness was 1mm. The distribution circular diameter of GV was 33 mm, the number of GV was temporarily 12, and negative curvature blade profile was initially chosen. The volute form employed a combination of circular and elliptical sections with an wrap angle of 345°. The draft tube adopted a straight, tapered shape with a cone angle of 12° and the length and outlet diameter of draft tube outlet were both 15 mm, which was limited by the diameter of the tap-water pipeline.
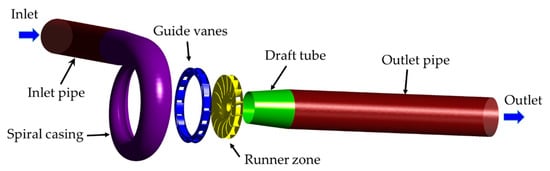
Figure 2.
MPT computational domain and components.
2.4. Numerical Simulation of the Initial MPT
2.4.1. Governing Equations
The water flow in the WTP is an incompressible viscous and turbulent fluid, so the continuity and the quasi-steady-state Reynolds-Averaged Navier–Stokes equations can be expressed as follows [44]:
where ui and uj are the velocity components in different direction, i, j = 1,2,3, and to simplify the equation form, Einstein summation convention were used for the subscript i and j; xi and xj are the Cartesian coordinate components, i, j = 1,2,3; ρ is the density of fluid, Fi is the mass force, p is the pressure, and µ is kinematic viscosity.
The finite volume method was adopted to discretize the controlling system of equations [45]. The Menter’s shear stress transport k − ω turbulence model was chosen to close the governing equations due to its effective prediction for cases involving flow separation under adverse pressure gradient conditions [46,47]. To obtain an accurate calculation, the second-order center-difference scheme for the pressure term was employed and the second-order upwind scheme and implicit solution were applied for momentum item, turbulent dissipation rate, and turbulent kinetic energy. The semi-implicit method for pressure-linked equations-consistent method was adopted for the coupling of velocity and pressure of turbulent flow.
2.4.2. Grid Partition and Boundary Condition
The CFD calculation domain consists of six parts: the inlet passage, the guide vanes, the spiral casing, the runner, the draft tube, and the outlet passage. The grid partition method was applied for grid generation, and the interfaces were defined to connect different parts. Generally, the quality and quantity of the grid have a major impact on the accuracy of numerical simulation results [48]. The ANSYS-ICEM meshing software is used to generate the grid. Considering the complexity of turbine’s geometry, the unstructured mesh was generated throughout the whole MPT model due to its superiority in terms of fast-generation speed and good adaptability for most complex structures [49]. The local mesh-refinement method was adopted for runner and the guide vanes, and the fluid regions were directly divided in volume grids.
In this paper, 10 layers of grids were defined in the boundary layer around the guide vanes and runner blades wall to reduce the y+ value near the wall region, and finally the y+ region was 8~60, since the main concern of this research was the turbine’s power output. In order to reduce the influence of grid number on the simulation results, five grid schemes were tested (Table 1). From the table, when the grid number of the whole model came to 4.0 × 106 (S3), the relative variation ratio of turbine’s efficiency was no more than 0.1%. After weighing computing resources and grid computing accuracy, the grid-division S4 was chosen, where the total grid number of flow components was 4.7 × 106, and the minimum quality was no less than 0.3.

Table 1.
Mesh independency verification.
In addition, the mass flow inlet with a value of Q = 0.265 kg/s was chosen as the inlet and the pressure outlet was applied to outlet for MPT. The interfaces were used for information transmission between the calculation areas. The runner zone was simulated by the moving reference frames method with the rotational speed of 3500 r/min. A no-slip boundary condition was imposed to the solid walls, and standard wall functions used for the near-wall region [42]. The convergence criteria of the residuals at each iteration were below a typical criterion of 10−5.
2.4.3. CFD Results of the Initial MPT
Table 2 shows the calculation results of the initial MPT model. The power output and efficiency of the initial MPT model were 4.76 W and 82.99%, respectively, which were close to the design requirements but did not yet meet them. So optimization should be carried out to reach the design goal, where the power output of 6 W and an 85% efficiency are the target.

Table 2.
CFD results of the initial MPT model.
3. Hydraulic Performance Improvement of the MPT
3.1. Orthogonal Experiment Design
The orthogonal experiment is also known as a multi-factor preferred design. When there are multiple investigated factors and multiple values for each parameter, the orthogonal experiment method is very suitable for exploring the influence among the factors. Through comprehensive design, integrated comparison, and statistical analysis, this method can give out better results. Due to the characteristics of balance and dispersion by balanced sampling in the range of factors for the orthogonal table, each test scheme has strong representative, so the tests can achieve the purpose of the experiment. Based on the structural parameters discussed above, the orthogonal experiment method was adopted to analyze the influence of the parameters on the WPT’s hydraulic performance and to explore the best combination of them by extremum difference analysis.
The purpose of the orthogonal experiment was to improve the power output P and efficiency η of the MPT, so the power output and efficiency were selected as the test evaluation index. Blade number zb (factor A), guide vane profile G (factor B), guide vane number zg (factor C), and guide vane opening (GVO) α (factor D) were selected for the orthogonal experimental study, and three levels were taken for each factor. The three levels of the blade numbers were 11, 13, and 15, respectively. The three levels of the guide vane type were negative curvature profile (B1), symmetric curvature profile (B2), and positive curvature profile (B3). The three levels of guide vane number were 12, 14, and 16, respectively. And the three levels of guide vane opening were 23°, 25°, and 27°, respectively. The factors and levels are shown in Table 3.

Table 3.
Factors and levels of orthogonal experiment design.
The orthogonal layout is represented by Ll(tc). In this layout, L stands for orthogonal layout, l is the number of experiments, t is the level of factor, and c is the number of columns (the maximum factors). So the orthogonal experiment design adopted a L9(34) layout (Table 4) in this study. The L9(34) design was carried out pursuant to the orthogonal principal in order to examine the influences of the four factors on the power output and efficiency at the design condition of the MPT.

Table 4.
L9(34) orthogonal experiment schemes.
According to the table, only trail No. 5 and 7 achieved the required power output at the design discharge point. Therefore, the superior scheme was as follows: the optimal scheme in terms of power output was trail No. 5 (A2B2C3D1, named Scheme (a)) and the optimal scheme in terms of efficiency was trail No. 7 (A3B1C3D2, named Scheme (b)).
3.2. Extremum Difference Analysis
The extremum difference value (R) can represent the level of a factor’s influence on the indicators. The larger the R value, the greater the influence a certain factor imposes on the indicator. The analysis of extremum difference requires the Kr and Kravg values. These can be defined as follows:
where r is the number of levels, m is total test times for each level, Kr is the sum of test results when number of the level is r, Yk is the kth index value, and Kravg is the arithmetic mean value of Kr.
The analysis of different R values is displayed in Table 5 and Table 6. According to the table, the impact of each factor level on the two test indicators can be obtained.

Table 5.
Extremum difference analysis of test results for MPT’s power output P (W).

Table 6.
Extremum difference analysis of test results for MPT’s efficiency η (%).
Based on the extremum difference analysis, the influence degree of each factor on the two evaluation indicators was different. To intuitively demonstrate the influence of each factor on the evaluation index, we took the factors as the horizontal coordinate and each evaluation index as the vertical coordinate, and the horizontal index relationship is shown in Figure 3.
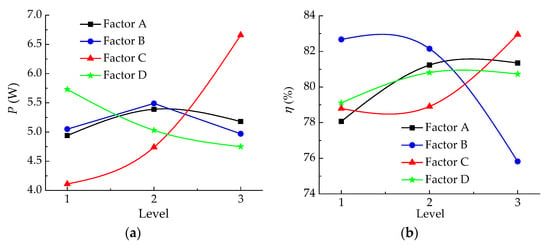
Figure 3.
Relationship between levels of each factor and evaluation indicators, (a) output index and (b) efficiency index.
With the increase of zb, the power output first increased and then decreased, the efficiency continuously rose to a certain value then slowed down. On one hand, as the zb increased, the extrusion effect of the blades on the water flow increased, causing the climb of the head and the turbine’s power output. On the other hand, after zb increased, the total area of the blade increased, and the pressure difference between the front and back of the blade decreased, resulting in the drop of turbine’s power output. The common action between the blades’ extrusion effect on the water flow and the blades’ surface pressure difference affected the power output and efficiency of the turbine.
In terms of the guide vane profile (factor B), the positive curvature guide vane had the minimum power output and efficiency, so this type is not suitable for this MPT. The symmetrical guide vane had the largest power output because of large volume, which enhanced the extrusion effect on the water flow, leading to large head and power output. The negative curve guide vane had the highest efficiency and a higher utilization rate of water flow energy.
As zg increased, both the MPT’s efficiency and the power output increased. The increase of zg within a certain range was conducive to guiding the water flow into the rotating runner and forming a certain circulation amount, which then improved the MPT’s power output and efficiency.
With the increase of α, the power output continuously decreased, and the efficiency increased first and then decreased. At the same flow rate condition, the water head rose and the power output dropped after the α rose. The excessively small or large GVO led to a large angle of attack at the inlet of the guide vane, resulting in flow separation and greater hydraulic loss. The large GVO did not allow the water flowing through the guide mechanism to form circulation before the runner, reducing the power output and efficiency of the MPT. Therefore, the proper GVO should be determined in the design of the turbine to improve the power output and efficiency.
From the extremum difference analysis, the superior test scheme of power output and efficiency index were A2B2C3D1 (named Scheme (c)) and A3B1C3D2 (named Scheme (d)), respectively. According to the calculation of extremum difference value R, the significant order of four test factors on the test index was: C > D > B > A for power output and B > C > A > D for efficiency.
3.3. Optimized Scheme Determination
The two evaluation indicators of this orthogonal test are of the equal importance. According to the test schemes (a) and (b) obtained from the intuitive analysis above and the test schemes (c) and (d) obtained from the extremum difference analysis of each index, the comprehensive frequency analysis of the corresponding levels of the four factors A, B, C and D was carried out, as shown in Table 7.

Table 7.
Factors A, B, C, and D correspond to different horizontal frequency tables.
From Table 6, both schemes A2B2C3D1 and A3B1C3D2 were superior according to the integrated frequency analysis method. However, the calculated water head of scheme A2B2C3D1 was 3.52 m, while the calculated head of scheme A3B1C3D2 was 2.85 m, which was closer to the design water head of 3m. Furthermore, the efficiency of scheme A3B1C3D2 was the highest when the power output reached 6 W, so the optimal test scheme was initially determined to be A3B1C3D2. The results of the orthogonal experiment showed that the ideal design model was as follows: the number of runner blades zb = 15, the guide vane type is negative curvature profile, the number of guide vanes zg = 16, and the GVO α = 25°. After CFD verification, the MPT’s power output and efficiency at design condition were 6.4 W and 87.13%, respectively.
3.4. Analysis of the Optimized Scheme
To verify the optimization results, the average internal flow streamlines in the guide vane and runner zone were extracted at the design discharge, as shown in Figure 4. The streamlines in the blade channel at the three spans all presented some obvious vortices on the front and back of the blades, resulting in disorderly flow pattern and large hydraulic loss before optimization. The vortex in blade channel of the optimized model is significantly reduced, and only small vortices appear on the back of the individual blades. The velocity distribution is relatively uniform, and the streamlines are overall smooth and the flow pattern is good. After optimization, the flow velocity on blades increased.
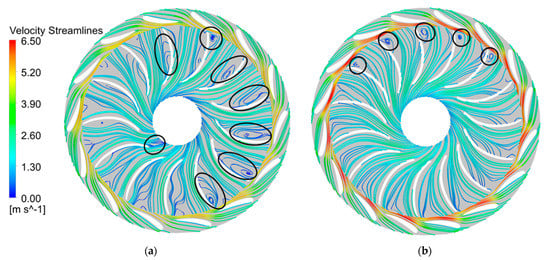
Figure 4.
Streamline distribution in guide vane and runner zone at design flow rate, (a) before optimization and (b) after optimization.
Figure 5 presents the pressure contour of the blade surface under design flow rate. The blade surface pressure decreases uniformly along the inlet edge to the outlet edge of the blade, and there are obvious negative pressure areas near the lower ring of the blade. Obviously, the negative pressure zone on the optimized blade surface is significantly reduced (Figure 5b). Local high pressure appears at the back surface of the blade before the optimization, while the high pressure area basically disappeared after optimization. Moreover, the pressure difference on the two sides of the blade increases significantly after optimization, which improves the working capacity of the blade and the power output of the MPT, so the optimization effect is better.
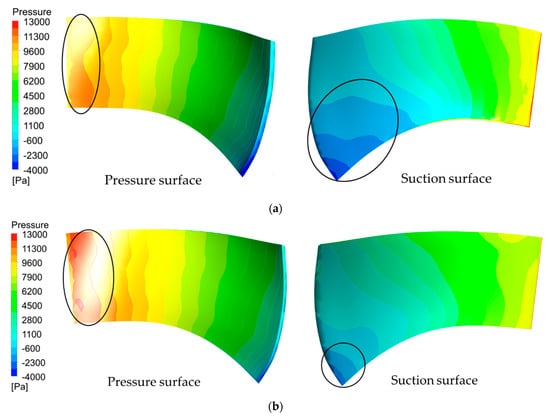
Figure 5.
Blade contour on blade surface at design flow rate, (a) before optimization and (b) after optimization.
4. Experimental Validation and Analysis
4.1. Test Bench Set-Up
The model MPT was made according to the 1:1 model scale (Figure 6), in order to reduce the difficulty of production and financial cost. The spiral casing and draft tube were made of engineering plastic polyamide material and produced by 3D printing technology.

Figure 6.
Photo of the physical WPT model.
The MPT experimental test was carried out on a flow test machine, which was independently developed by a company in Zhejiang province, China (Figure 7). The spiral casing inlet was installed at the water pipe outlet on the test bench, and the inlet flow value was input through the flow test machine. After the test instrument was started, the multimeter was used to measure the current and calculate the power. The measuring current range of the multimeter was 2 mA–20 mA–200 mA–20 A, and the measurement accuracy was ±1.8%.

Figure 7.
Model test bench of MPT, (a) photo of the test bench, (b) flow test machine, and (c) multimeter.
4.2. Analysis of the Experimental Results
Table 8 shows the results of comparison between numerical simulation results and experimental test results. During the test, the power output of the turbine under different flow conditions was measured by changing the input flow value of the flow tester. Since the flow velocity in the tap-water pipeline is generally 1~3 m/s, the measured flow velocities in the experiment were 1 m/s, 1.5 m/s, 2 m/s, 2.5 m/s, and 3 m/s, and the corresponding inlet mass flow rates were 0.177 kg/s, 0.265 kg/s, 0.353 kg/s, 0.442 kg/s, and 0.53 kg/s, respectively. With the experimental results of the flow rate of 0.8 m/s (0.14 kg/s), the MPT could still start, but the power output was only 0.44 W. Multiple experimental results showed that the turbine could start when the inlet flow was greater than 0.14 kg/s.

Table 8.
Comparison of numerical simulation results and experimental results under different working conditions.
According to Table 8, the power output measured by the model test was lower than the obtained value through numerical simulation. The main reason for this is that the index measured in the experiments was the actual power of the MPT after the generator conversion, while the one obtained through numerical simulation was the power output of the MPT without considering the generator conversion. Also, the MPT model made during the experiment used a plastic material inducing friction between the runner and the runner chamber, and this was not considered in numerical simulation. Moreover, the size of MPT was very small, and the blade and guide vane actually made for model testing deviated from the numerical simulation. There were also some measurement errors, especially when measuring the current with an electric meter. In addition, under the small flow rate condition, the flow pattern was poor, which led to large fluctuations of measured values. This also considerably contributed to the appearance of large errors between the test and numerical predictions. Overall, the error value was within 10% under low flow conditions, while it reduced to within 5% under large flow conditions. The generated power met the design target under design flow conditions.
5. Conclusions
In this study, an MPT used to generate electric power for induction faucet sensors within a 15 mm pipeline was developed. The fundamentally expected MPT performance characteristics were the power output larger than 6 W when the pipe water velocity is 1.5 m/s and the turbine efficiency of no less than 85%. The initial design was done by using the 3D CFD method, where multi-objective optimization through orthogonal experiments was later applied to improve its hydraulic performance. Finally, the optimized version of the MPT model was experimentally tested.
After simulating and comparing a variety of schemes, the optimal MPT was achieved with the output power of 6.40 W at the design flow rate, representing an increase of 34.45% as compared to the preliminary design scheme. In the same respect, the optimal efficiency was 87.13%, representing an increase of 4.99% as compared to the preliminary design scheme. The feasibility of combining the numerical simulation technology and comprehensive frequency analysis method through the multi-objective orthogonal optimization test for MPT studies, has been verified. For the optimized turbine model, the inter-blade vortex and negative pressure area on the blade surface were significantly reduced, and the high-pressure area on the back of the blade basically disappeared, which improved the power capacity of the blades, collectively leading to the improved MPT power output and efficiency. A good and effective optimization was therefore achieved.
According to the model test results, the MPT-generated energy reached 6 W at the design flow rate, which meets the design requirements. The numerical simulation error as compared to test data was within 10%. Under large flow conditions, the error was around 5%, indicating that numerical simulation outcomes can offer a good guidance for micro turbine design even though the difference between the simulation and experimental results is fairly large. The experimental measurement showed that the MPT can start when the inlet flow rate is greater than 0.14 kg/s.
So far, the literature on the application of mixed-flow turbines for energy generation task within water supply pipelines with extra-small diameters (less than 15 mm) is still limited. This study creatively applies the mixed flow water turbine to the micro tap-water pipeline, changing the induction faucet power supply system from the battery-dependent one to a hydropower-fed one. This technology not only gives a long-term solution to energy saving issues within these systems, but also contributes to the environmental pollution control by eliminating the usage of batteries. The kind of MPT design presented in this article pays more attention to the turbine’s efficiency and ensures that the output power meets the power requirements of induction faucet sensors.
Future studies could also consider runner blade profile and the frame line of flow components, which may also have a large impact on the machine performance. In the future, more factors can be selected to explore a more complete and faster optimization method, so as to more comprehensively reflect the impact of various design parameters on the turbine performance. Furthermore, a WPT for smaller discharge can be designed to achieve the power demand when the flow velocity in the pipeline is less than 1.5 m/s.
Author Contributions
Conceptualization, K.K. and H.C.; methodology, H.C. and H.W.; software, H.C. and H.W.; validation, Y.Z., K.K. and M.B.; formal analysis, H.C. and H.W.; investigation, K.K.; resources, Y.Z. and H.X.; data curation, H.W., Y.Z. and H.X.; writing—original draft preparation, H.C. and K.K.; writing—review and editing, Y.Z., M.B. and H.X.; visualization, K.K.; supervision, Y.Z. and H.X.; funding acquisition, H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52006053), the Natural Science Foundation of Jiangsu Province (BK20200508), the China Postdoctoral Science Foundation (2021M690876), and the Open Research Subject of Key Laboratory of Fluid Machinery and Engineering (Xihua University), Sichuan Province (grant number LTJX2021-001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The computational work was supported by High Performance Computing Platform, Hohai University. The support of Hohai University, China is also gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| CFD | Computational fluid dynamics |
| GV | Guide vane |
| GVO | Guide vane opening |
| MPT | Micro-pipe turbine |
| WSP | Water supply pipeline |
| c | Number of columns |
| d | Pipe diameter |
| Fi | Mass force |
| H | Water head |
| Kr | Sum of test results when number of the level is R |
| Kravg | Arithmetic mean value of Kr |
| l | Number of experiments |
| m | The total test times of each level |
| n | Rotational speed |
| ns | Specific speed |
| P | Power output |
| p | Pressure |
| Q | Discharge |
| R | Extremum difference value |
| r | Number of levels |
| t | The level of factor |
| Yk | The kth index value |
| u | Water flow velocity |
| ui | Velocity component in i direction |
| uj | Velocity component in j direction |
| zb | Blade number |
| zg | Guide vane number |
| ρ | Water flow density |
| μ | Kinematic viscosity |
| η | Efficiency |
| α | Guide vane opening |
References
- Water and Sustainable Development. Available online: https://www.un.org/waterforlifedecade/water_and_sustainable_development.shtml (accessed on 27 September 2021).
- Schwarzenbach, R.P.; Egli, T.; Hofstetter, T.B.; von Gunten, U.; Wehrli, B. Global Water Pollution and Human Health. Annu. Rev. Environ. Resour. 2010, 35, 109–136. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.X.; Liu, C.P.; Lau, C.H.; Lo, M. A novel vertical axis water turbine for power generation from water pipelines. Energy 2013, 54, 184–193. [Google Scholar] [CrossRef]
- Semu, E.; Singh, B.R.; Selmer-Olsen, A.R. Mercury pollution of effluent, air, and soil near a battery factory in Tanzania. Water Air Soil Pollut. 1986, 27, 141–146. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A.P. The technical and economic feasibility of energy recovery in water supply networks. Renew. Energy Power Qual. J. 2011, 1, 1123–1127. [Google Scholar] [CrossRef]
- Aqel, M.O.A.; Issa, A.; Qasem, E.; El-Khatib, W. Hydroelectric Generation from Water Pipelines of Buildings. In Proceedings of the 2018 International Conference on Promising Electronic Technologies (ICPET), Deir El-Balah, Palestine, 3–4 October 2018; IEEE: New York, NY, USA, 2018; pp. 63–68. [Google Scholar] [CrossRef]
- Zhou, D.; Deng, Z. Ultra-low-head hydroelectric technology: A review. Renew. Sustain. Energy Rev. 2017, 78, 23–30. [Google Scholar] [CrossRef]
- Campbell, R.J. Small Hydro and Low-Head Hydro Power Technologies and Prospects. 2010. Available online: https://www.researchgate.net/profile/Ammar-Kamel/project/Small-dams-for-electric-power-production/attachment/57bd6c6908ae98f5947f2f9a/AS:398544616869890@1472031849894/download/Small_hydro_and_Low-head_hydro_power.pdf?context=ProjectUpdatesLog (accessed on 27 September 2021).
- Du, J.; Shen, Z.; Yang, H. Numerical study on the impact of runner inlet arc angle on the performance of inline cross-flow turbine used in urban water mains. Energy 2018, 158, 228–237. [Google Scholar] [CrossRef]
- Sinagra, M.; Sammartano, V.; Morreale, G.; Tucciarelli, T. A New Device for Pressure Control and Energy Recovery in Water Distribution Networks. Water 2017, 9, 309. [Google Scholar] [CrossRef] [Green Version]
- Dhadwad, A.; Balekar, A.; Nagrale, P. Literature review on blade design of hydro-microturbines. Int. J. Sci. Eng. Res. 2014, 5, 72–75. [Google Scholar]
- Sakti, A.; Prasetyo, A.; Tjahjana, D.; Hadi, S. The horizontal axis type of savonius water turbine in pipe using SolidWork simulation. In Proceedings of the 4th International Conference on Industrial, Mechanical, Electrical, and Chemical Engineering, Solo, Indonesia, 9–11 October 2018. [Google Scholar]
- Li, H.D.; Zhou, D.Q.; Martinez, J.J.; Deng, Z.D.; Johnson, K.I.; Westman, M.P. Design and performance of composite runner blades for ultra low head turbines. Renew. Energy 2019, 132, 1280–1289. [Google Scholar] [CrossRef]
- Saftner, D.A.; Hryciw, R.D.; Green, R.A.; Lynch, J.P.; Michalowski, R.L. The use of wireless sensors in geotechnical field applications. In Proceedings of the 15th annual Great Lakes Geotechnical/Geoenvironmental Conference, Indianapolis, IN, USA, 9 May 2008. [Google Scholar]
- Ferro, L.M.C.; Gato, L.M.C.; Falcao, A.F.O. Design of the rotor blades of a mi Water and sustainable development ni hydraulic bulb-turbine. Renew. Energy 2011, 36, 2395–2403. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Munch-Alligne, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blade tubular propeller turbine for pipe inline installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]
- Lucid Energy Inc. How Drinking Water Pipes Can Also Deliver Electric Power. Available online: http://www.pbs.org/newshour/bb/drinking-water-pipes-can-also-deliver-electric-power (accessed on 27 September 2021).
- Langroudi, A.T.; Afifi, F.Z.; Nobari, A.H.; Najafi, A.F. Modeling and numerical investigation on multi-objective design improvement of a novel cross-flow lift-based turbine for in-pipe hydro energy harvesting applications. Energy Convers. Manag. 2020, 203, 15. [Google Scholar] [CrossRef]
- Oladosu, T.L.; Koya, O.A. Numerical analysis of lift-based in-pipe turbine for predicting hydropower harnessing potential in selected water distribution networks for waterlines optimization. Eng. Sci. Technol.-Int. J.-Jestech 2018, 21, 672–678. [Google Scholar] [CrossRef]
- Mcalister, K.W.; Carr, L.W.; Mccroskey, W.J. Dynamic Stall Experiments on the NACA 0012 Airfoil; NASA Technical Paper 1100; NASA Ames Research Center: Moffett Field, CA, USA, 1978.
- Carr, L.W.; Mcalister, K.W.; Mccroskey, W.J. Analysis of the Development of Dynamic Stall Based on Oscillating Airfoil Experiments; NACA Technical Paper D-8382; NASA Ames Research Center: Moffett Field, CA, USA, 1977.
- Payambarpour, S.A.; Najafi, A.F.; Magagnato, F. Investigation of deflector geometry and turbine aspect ratio effect on 3D modified in-pipe hydro Savonius turbine: Parametric study. Renew. Energy 2020, 148, 44–59. [Google Scholar] [CrossRef]
- Payambarpour, S.A.; Najafi, A.F. Experimental and numerical investigations on a new developed Savonius turbine for in-pipe hydro application. Proc. Inst. Mech. Eng. Part A-J. Power Energy 2020, 234, 195–210. [Google Scholar] [CrossRef]
- Chen, J.; Lu, W.; Hu, Z.; Lei, Y.; Yang, M. Numerical studies on the performance of a drag-type vertical axis water turbine for water pipeline. J. Renew. Sustain. Energy 2018, 10, 44503. [Google Scholar] [CrossRef]
- Yang, W.; Hou, Y.; Jia, H.; Liu, B.; Xiao, R. Lift-type and drag-type hydro turbine with vertical axis for power generation from water pipelines. Energy 2019, 188, 116070. [Google Scholar] [CrossRef]
- Rossi, M.; Comodi, G.; Piacente, N.; Renzi, M. Effects of viscosity on the performance of Hydraulic Power Recovery Turbines (HPRTs) by the means of Computational Fluid Dynamics (CFD) simulations. Energy Procedia 2018, 148, 170–177. [Google Scholar] [CrossRef]
- Sekar, K.; Kumar, N.; Vasanthakumar, P. Centrifugal pump as turbine for micro-hydro power scheme in rural areas of India: A review. Int. J. Chem. Tech. Res. 2017, 10, 106–109. [Google Scholar]
- Capurso, T.; Bergamini, L.; Camporeale, S.; Fortunato, B.; Torresi, M. CFD analysis of the performance of a novel impeller for a double suction centrifugal pump working as a turbine. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics ETC13, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Portolano, D. Losses Reduction and Energy Production in Water-Distribution Networks. J. Water Resour. Plan. Manag. 2012, 138, 237–244. [Google Scholar] [CrossRef]
- Du, J.Y.; Yang, H.X.; Shen, Z.C.; Chen, J. Micro hydro power generation from water supply system in high rise buildings using pump as turbines. Energy 2017, 137, 431–440. [Google Scholar] [CrossRef]
- Kramer, M.; Terheiden, K.; Wieprecht, S. Pumps as turbines for efficient energy recovery in water supply networks. Renewable Energy 2018, 122, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Buono, D.; Frosina, E.; Mazzone, A.; Cesaro, U.; Senatore, A. Study of a Pump as Turbine for a Hydraulic Urban Network Using a Tridimensional CFD Modeling Methodology. Energy Procedia 2015, 82, 201–208. [Google Scholar] [CrossRef] [Green Version]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Messineo, A.; Milici, B.; Napoli, E.; Notaro, V.; Puleo, V.; Scopa, A. Energy Recovery in Water Distribution Networks. Implementation of Pumps as Turbine in a Dynamic Numerical Model. Procedia Eng. 2014, 70, 439–448. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water 2020, 12, 468. [Google Scholar] [CrossRef] [Green Version]
- Carravetta, A.; del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef] [Green Version]
- Yeung, A.T.C. Asset management of drainage facilities using advanced technologies. In Proceedings of the 2014 Drainage Services Department International Conference (DSDIC 2014), Hong Kong, China, 12–14 November 2014. [Google Scholar]
- Turbine Selection on the Basis of Specific Speed. Available online: https://www.britannica.com/technology/turbine/Turbine-selection-on-the-basis-of-specific-speed (accessed on 27 September 2021).
- Chu, W.; Jiang, T.; Ho, P.S. Effect of Wiring Density and Pillar Structure on Chip Packaging Interaction for Mixed-Signal Cu Low k Chips. IEEE Trans. Device Mater. Reliab. 2021, 21, 290–296. [Google Scholar] [CrossRef]
- Chu, W.; Spinella, L.; Shirley, D.R.; Ho, P.S. Effects of Wiring Density and Pillar Structure on Chip Package Interaction for Advanced Cu Low-k Chips. In Proceedings of the 2020 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 28 April–30 May 2020; pp. 1–4. [Google Scholar]
- Kawase, Y.; Yamaguchi, T.; Masuda, T. Magnetic field analysis of micro turbine generator using finite element method. In Proceedings of the 10th International Symposium on Electromagnetic Field, ISEF 2001, Krakow, Poland, 20–22 September 2001; pp. 237–241. [Google Scholar]
- Zhu, D.; Tao, R.; Xiao, R.F.; Pan, L.T. Solving the runner blade crack problem for a Francis hydro-turbine operating under condition-complexity. Renew. Energy 2020, 149, 298–320. [Google Scholar] [CrossRef]
- Chen, Z.; Singh, P.M.; Choi, Y.D. Structural Safety Evaluation of a Francis Hydro Turbine Model at Normal Operation Condition. KSFM J. Fluid Mach. 2017, 20, 12–18. [Google Scholar] [CrossRef]
- Kan, K.; Yang, Z.; Lyu, P.; Zheng, Y.; Shen, L. Numerical study of turbulent flow past a rotating axial-flow pump based on a level-set immersed boundary method. Renew. Energy 2021, 168, 960–971. [Google Scholar] [CrossRef]
- Zhou, D.; Chen, H.; Zheng, Y.; Kan, K.; Yu, A.; Binama, M. Development and Numerical Performance Analysis of a Pump Directly Driven by a Hydrokinetic Turbine. Energies 2019, 12, 4264. [Google Scholar] [CrossRef] [Green Version]
- Kversteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Wiley: New York, NY, USA, 1995; pp. 4–30. [Google Scholar]
- Menter, F.; Rumsey, C. Assessment of two-equation models for transonic flows. In Proceedings of the Fluid Dynamics Conference, Colorado Spring, CO, USA, 20–23 June 1994; pp. 1994–2343. [Google Scholar]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Devals, C.; Vu, T.C.; Zhang, Y.; Dompierre, J.; Guibault, F. Mesh convergence study for hydraulic turbine draft-tube. In Proceedings of the 28thIAHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016; Volume 49. [Google Scholar]
- Chen, H.; Zhou, D.; Kan, K.; Guo, J.; Zheng, Y.; Binama, M.; Xu, Z.; Feng, J. Transient characteristics during the co-closing guide vanes and runner blades of a bulb turbine in load rejection process. Renew. Energy 2021, 165, 28–41. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).