Abstract
Due to growing concerns for environmental problems and food quality, consumers pay more attention to the carbon emission and freshness of fresh food. The booming e-commerce also accelerates the development of the dual-channel supply chain. In the dual-channel supply chain of fresh food, the carbon emission and freshness of fresh food are becoming important factors affecting consumers’ purchase demand. This paper focuses on the optimal decision of carbon emission reduction and pricing, which is investigated by a Stackelberg game-theoretic approach in three dual-channel supply chain sales models (retailer dual channel, producer dual channel, and mixed dual channel). A two-stage fresh food supply chain system composed of a producer and a retailer is explored. The sensitivity analysis and the comparison of three dual-channel models are carried out. The results show the following: (1) the sales price, carbon emission reduction, market demand, producer’s profit, retailer’s profit, and supply chain’s profit of fresh food under the three dual-channel supply chains show the same change on different levels of consumers’ low-carbon preference coefficient and freshness level, respectively; (2) the optimal decision of carbon emission reduction and pricing, demand, and profit of the three dual-channel models need to be determined according to the value of consumers’ purchasing preferences for the retailer’s offline channel. The paper gives some enlightenment to the decision-making members in the fresh dual-channel supply chain.
1. Introduction
In recent years, with the rapid development of e-commerce and the rise of online shopping [1], fresh food enterprises add online sales channels to expand sales and enhance their competitiveness. Therefore, they gradually form the dual-channel sales model, which includes offline and online sales channels [2,3]. Especially in 2020, affected by the “COVID-19” epidemic, fresh food e-commerce has become the main way for residents to buy fresh food. The epidemic has led to the popularization of fresh food e-commerce and introduced rare development opportunities for many companies [4]. The dual-channel sales model including both online and offline channels is very likely to dominate the market of fresh food for some time to come.
The fresh dual-channel supply chain can be divided into a retailer dual-channel model, producer dual-channel model, and mixed dual-channel model [5,6,7,8]. In the retailer dual-channel model, the producer sells products wholesale to the retailers. In addition to the traditional offline sales channels, retailers plan to open new online sales channels. For example, Hema Fresh, 7 Fresh, and Super Species adopt the retailer dual-channel supply chain model. In the producer dual-channel model, producers also intend to establish an extra online channel for sales alongside the original retailer’s offline sales channels. The mode of direct supply from the production base or community group belongs to the producer dual-channel model, which is adopted by enterprises such as Dolly Farm and Pagoda. A mixed dual-channel model means that the producer sells fresh food wholesale to the retailer at first. Then, the retailer sells it through online and offline channels, and the producer also plans to sell it online. For example, RT-Mart carries out both offline and online channels, while COFCO, one of its suppliers, has built its online sales channel named Womai.com.
Fresh food is perishable, and a lot will be lost in the operation of the food supply chain [9]. Statistical analysis shows that the loss rate of fresh food in China has reached 25–35% [10]. Therefore, companies must pay more efforts to prevent fresh food from spoiling. The improvement of freshness level may increase the sales price. However, consumers will pay more attention to the freshness of products than the price with the improvement of people’s living standards [8]. Thus, the consumers’ freshness preference plays an important role in the supply chain operation.
Greenhouse gas emissions have attracted the attention of countries around the world and become the focus of the international community [11]. The European Union aims to reduce its carbon emissions by 40% from 1990 levels by 2030. Some environmental labels (such as carbon labels) have been introduced internationally to guide consumers’ green purchase [12,13,14]. Carbon labels specify the amount of carbon emission emitted or reduced during the product’s life cycle. China is using internationally accepted certification methods to establish its carbon labeling system to guide Chinese consumers to achieve low-carbon consumption. The implementation of carbon labels will have a major impact on the retail sector, putting huge pressure on product manufacturing and supply chains. At the same time, the public is paying more and more attention to environmental issues. With the gradual popularity of the concept of low-carbon consumption, many environmentally conscious consumers choose to buy products according to carbon emissions or even buy environment-friendly products with higher prices [15]. As a result, the carbon emissions of commodities will affect market demand.
The perishability of fresh food and consumers’ preference for low carbon emission and freshness make it harder to make decisions for enterprises in the fresh food supply chain when making decisions. Furthermore, poor decision-making will make the supply chain expensive. Meanwhile, a convenient online shopping experience brings about the transfer of consumers’ purchasing channels, and it also impacts the offline channels and affects each company’s economic interest. Therefore, it is particularly important for supply chain members to study the decision-making problem of the dual-channel supply chain of fresh food. Based on the above analysis, this paper mainly studies the following questions.
- (1)
- What are the optimal sales price and carbon emission reduction decisions in a fresh food dual-channel supply chain?
- (2)
- What are the effects of the low carbon preference coefficient of consumers, freshness level, and channel preference coefficient on the optimal decision and profit of supply chain members?
- (3)
- From the perspective of the producer and retailer, what is the difference between the best decision and profit for different dual-channel sales models?
The purpose of this study is to provide a theoretical basis and decision support for the fresh food dual-channel supply chain pricing processes considering the consumers’ preference for low-carbon emission and freshness.
To solve the above problems, this paper studies a producer–retailer fresh food supply chain considering consumers’ low-carbon and freshness preference under three dual-channel sales models: retailer dual channel, producer dual channel, and mixed dual channel. The demand for fresh food is affected by sales price, carbon emission reduction, and freshness level. The Stackelberg game is used for solving the problem. The producer, as the leader in the Stackelberg game, decides the carbon emission reduction, while the retailer, as the follower, decides the sales price. Firstly, we study the optimal carbon emission reduction and pricing decisions under three dual-channel supply chain models. Secondly, we explore the impact of important parameters on supply chain decisions and profits. Finally, we compare the optimal decisions and profits under three dual-channel models.
This paper has the following innovations. First, we consider that market demand for fresh food is affected by sales price, carbon emission reduction, and freshness level simultaneously. Most of the fresh food decision-making studies focus on considering that the market demand is only influenced by sales price and freshness. However, as public awareness of the environment increases, the demand for fresh food will be affected by its carbon emissions. Second, this paper studies a mixed dual-channel supply chain and makes a comparative analysis with two single dual-channel supply chain models. Previous studies for the dual-channel supply chain are mainly aimed at the single dual-channel supply chain (retailer dual channel, producer dual channel). With the development of e-commerce, more and more producers and retailers open online sales channels, and the mixed dual-channel supply chain model is becoming common.
The reminder of the paper is organized as follows. Section 2 provides a review of the relevant literature. Section 3 describes the problem and introduces the notations and assumptions used throughout this paper. Section 4 illustrates three dual-channel models of fresh food and carries out sensitivity analysis. Section 5 provides a comparative analysis. Section 6 describes the numerical experiments. Section 7 shows the managerial implications for business and government. Section 8 summarizes our main findings and gives some directions for future research. All proofs are relegated to Appendix A.
2. Literature Review
2.1. Consumer Preference
With the development of a low-carbon economy, consumers’ preference for low-carbon products has become an important factor affecting supply chain operation. The impact of consumers’ environmental awareness on market demand is called carbon emission sensitive demand [16]. Consumers’ awareness of environmental protection is increasing, and more and more consumers are paying attention to the carbon emission of products when making purchase decisions.
Consumers’ low-carbon preference behavior has attracted extensive attention from many scholars. Seyfangs analyzed the impact of consumers’ low-carbon preference behavior on market demand and price and constructed a scientific demand function that is influenced by low-carbon emission [17]. Du et al. constructed a carbon emissions-dependent demand function and analyzed the impact of consumers’ low-carbon preference on carbon emissions and supply chain performance. They found that the profit of the supply chain and consumers’ preference for low-carbon consumption increase with the greater reduction of carbon emission in the supply chain [14]. Zhou et al. discussed the coordination of the low-carbon supply chain under an advertising and emission reduction cost-sharing contract under the condition that retailers have concerns for fairness and consumers have low-carbon preference [18]. Liu et al. evaluated the impact of carbon emission reduction’s cost sharing on supply chain profits using a theoretical model incorporating changes in consumer preferences. The results showed that consumers’ preference for low-carbon products makes the members of the supply chain share the cost of carbon emission reduction, which increases the order quantity and supply chain’s profit, and encourages the supply chain enterprises to cooperate [19]. Wang et al. studied the impact of cap-and-trade regulation and consumers’ low-carbon preference on the supply chain in a dual-channel supply chain [20]. Zhang and Yu explored the impact of consumers’ reference low-carbon effect and the goodwill of a low-carbon product on the balanced emission reduction decisions and profit of dual-channel supply chain members, and they realized supply chain coordination by using cost-sharing contracts in a dual-channel supply chain [21].
In the fresh food industry, consumers’ preference for freshness is an important factor affecting the operation of the supply chain. Scholars have also done some studies on consumers’ preference for freshness. Cai et al. considered a fresh product supply chain whose market demand is sensitive to freshness [22]. Herbon explored the impact of the heterogeneity of consumers’ preference for freshness on supply chain profits and consumer welfare [23]. Yang et al., based on considering consumers’ preference for freshness, made a comparative study on the optimal decision and profit under the traditional retail model, O2O model, and dual-channel model [8]. Considering that consumers have a preference for freshness, Zhang and Ma studied the optimal equilibrium strategy of a fresh dual-channel supply chain under different return modes [24].
2.2. Fresh Food Supply Chain Decision Making
Fresh food is easy to rot and spoil. Many scholars have studied the influence of fresh products’ freshness on supply chain decision making and supply chain coordination. For example, Cai et al. [22] and Ma et al. [25] studied the decision-making and coordination strategy of a three-level supply chain, which consists of a producer, third party logistics (3PL), and distributor, given that price and freshness affect the market demand of fresh food. Zhu et al. took into account the impact of food freshness and sales efforts on consumer demand and realized supply chain coordination through cost-sharing contracts [26]. Feng et al. regarded the demand of perishable products as a multivariate function of their unit price, freshness, and inventory level, and they studied the optimal unit price, cycle time, and ending inventory level to maximize the total profit [27].
Many scholars have also studied pricing, ordering, and preservation strategies in the case of carrying out fresh-keeping efforts. Hsu et al. introduced the retailer’s fresh-keeping efforts into the supply chain decision model and studied the retailer’s optimal order strategy and fresh-keeping effort level [28]. Dye and Hsieh, based on Hsu’s research, constructed a fresh agricultural product inventory model with the change of deterioration rate over time, and they studied the optimal replenishment strategy and fresh-keeping effort level of retailers [29]. Zhang et al. studied pricing and investment in fresh-keeping technology in the case of centralization and decentralization, and they realized supply chain coordination by revenue sharing and cooperative investment contract [30]. Yang et al. studied the optimal pricing and fresh-keeping effort decisions in a fresh food supply chain under three sales models (retail model, dual-channel model, and O2O model) and made a comparative analysis [8].
2.3. Multi-Channel Supply Chain
The research on the multi-channel supply chain mainly focuses on channel pricing, channel coordination, and profit decision [31]. Chen et al. studied the pricing strategy, supply chain cooperation strategy, and profit strategy in a dual-channel supply chain with two alternative manufacturers [32]. In the case that manufacturers use the same and different wholesale prices for traditional retailers and online retailers, Erjiang et al. discussed the channel coordination strategies adopted by manufacturers to alleviate channel conflicts [33]. Opening online sales channels in addition to traditional sales channels may not bring greater profits to the whole supply chain. Therefore, many scholars have conducted comparative studies on different channels, which provide references for enterprises in channel selection. By comparison, Keen et al. comprehensively analyzed the impact of three sales modes on the profits of the overall supply chain, including a traditional retail mode, online direct sales mode, and dual-channel sales mode, and they found that only the dual-channel sales mode could maximize the profits of the supply chain [34]. Moutaz et al. studied the channel selection and pricing decision of manufacturers. The analysis showed that unit variable costs is the most critical factor for channel selection in a vertically integrated supply chain. In the case of the existence of independent retailers, the scale of consumer groups dominated by retail will become the main factor in channel selection [35].
In recent years, different dual-channel supply chain models extended by the development of e-commerce have become the focus of academic research. Introducing online sales channels and implementing a dual-channel supply chain strategy are effective to expand sales channels and market space for most enterprises, especially manufacturers and retailers of consumable products. According to the relevant models of dual-channel supply chain research, the dual-channel supply chain is divided according to the channel structure and the channel control subject. The details are shown in Table 1.

Table 1.
Classification of dual-channel supply chain model.
2.4. Research Gap
In order to further emphasize the difference between this paper and the published relevant literature, the relevant literature is reviewed in Table 2.

Table 2.
Some literature most relevant to this paper.
Through the literature review, the following research gaps can be concluded. First, studies on decision making considering consumers’ low-carbon preference are mainly concentrated in the supply chain of manufacturing enterprises, and there are a few studies focusing on other industries. With the improvement of public environmental awareness and the gradual popularization of the carbon labeling system, the public will increase low-carbon preference in every aspect of life and will be more willing to carry out environment-friendly activities.
Second, the research on fresh food supply chain decision making mainly focuses on the issues considering the impact of sales price and freshness on market demand. However, the increase in public environmental awareness will make the market demand for fresh food be affected by carbon emissions. Therefore, considering the impact of freshness and carbon emission reductions on the fresh food market demand, studying the decision-making problems of the fresh food supply chain will be of great research value.
Third, the study of the mixed dual-channel model in which both manufacturers and retailers open online sales channels are few. In the study of dual-channel supply chain decision making, there are studies of the manufacturer’s dual channel and the retailer’s dual channel. However, the development of the Internet and e-commerce has led to the emergence of more and more mixed dual-channel supply chains. Therefore, incorporating the mixed dual channel into the dual-channel supply chain decision-making research can make it more comprehensive.
3. Problem Description, Notations, and Assumptions
Considering a two-echelon fresh food supply chain consisting of one producer and one retailer, we assume that the supply chain operates in a Stackelberg game framework where the producer is a leader and the retailer is a follower. The market demand for fresh food is affected by sales prices, carbon emission reduction, and freshness level. The retailer decides the sales price, and the producer decides the wholesale price and carbon emission reduction. There are three sales models: retailer dual-channel model, producer dual-channel model, and mixed dual-channel model, as shown in Figure 1. For each model, we will find the optimal decision.
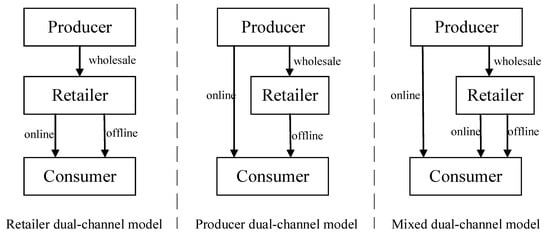
Figure 1.
Three dual-channel models.
To be specific, we summarize notations in Table 3. In the notations, superscripts “1”, “2”, and “3” respectively represent the retailer dual-channel model, producer dual-channel model, and mixed dual-channel model. In addition, the superscript “*” represents the optimal decision variable, demand, and profit. The subscript “r-off”, “r-on”, and “p-on” represent the offline sales of the retailer, online sales of the retailer, and online sales of the producer respectively.

Table 3.
Notations.
In order to establish the model, the following basic assumptions are provided.
Assumption 1.
In economics, it is often assumed that market demand is a linear function. A linear demand hypothesis on price and non-price variables has also been made in many studies in the literature about operation management and marketing (Ghosh et al. [16], Basiri et al. [40]). Similarly, this paper assumes that fresh food market demand has a linear relationship with sales price, carbon emission reduction, and freshness level [41].
Assumption 2.
The investment in carbon emission reduction is one-off, which does not affect the production cost of fresh food. Meanwhile, the paper let the unit production cost [42] to simplify the analysis. The cost function of carbon emission reduction is [43]. This formula shows that the higher the carbon emission reduction of the product, the higher the cost of emission reduction that will be paid. The added value of emission reduction cost shows an increasing trend, which means the producer cannot cut carbon emissions indefinitely [44].
Assumption 3.
To reduce channel conflicts, this paper applies the same pricing strategy for fresh food sold online and offline [45], and the sales price is decided by the retailer. The sensitivity coefficient of consumer demand to the price is 1 [46], and to avoid trivial trouble, let [45,47].
Assumption 4.
For simplicity, we assume that the supply chain only provides customers with a single fresh food [15]. The carbon emission of fresh food is mainly generated in the operation link of the producer [48], and consumers can know the carbon emission reduction of fresh food through the carbon label. The development of carbon labels makes it possible for consumers to understand carbon emissions reduction of fresh food through carbon labels.
Assumption 5.
is the freshness level of fresh food, assuming that the freshness levels of fresh food sold online and offline are the same.
4. The Models
4.1. Retailer Dual-Channel Model
Combined with the literature [16,49,50], the demand function of the online direct channel and offline channel of fresh food are given by
In the retailer dual-channel supply chain, the producer obtains profits mainly by selling wholesale products to the retailer, and the retailer obtains profits mainly by selling products through offline and online channels.
The profits of the producer, retailer, and supply chain are as follows.
We use the Stackelberg game led by the producer to process this model. The producer determines the wholesale price and carbon emissions reduction. Then, the retailer, as the follower, decides the sales price. To obtain the optimal solution, we first obtain . ; we know that is a concave function of . Let , we get
Substituting Equation (6) into Equation (3), we can derive an expression for in terms of and : ., . , , , , we get, and When , the Hessian matrix is negative definite, and is jointly concave on and . Let and , and we have the optimal solution as follows:
Furthermore, substituting and for Equation (6), we can obtain the optimal sales price:
Substituting into , , we obtain the total market demand and the producer’s profit, the retailer’s profit, and the total supply chain’s profit:
Proposition 1.
There is a retailer’s online dual-channel sales model when the consumers’ purchasing preference for the retailer’s offline channel is in a certain range: . Here, .
The proof is shown in Appendix A.
The right hand of the inequality indicates that when consumers’ purchasing preference for the retailer’s offline channel () is less than a certain threshold, the retailer is willing to open the direct channel. If is too large, then the demand in the direct channel is negative. In this case, the retailer does not open the direct channel.
From the optimal solution, we can directly obtain the following results.
Corollary 1.
(1),,; (2); (3),,.
Corollary 1 shows that the sales price, wholesale price, producer’s carbon emission reduction, total market demand, retailer’s profit, producer’s profit, and the whole supply chain’s profit show the same change with consumers’ low-carbon preference coefficient () in the retailer dual-channel model. The greater the value is, the more likely it is to promote the producer to conduct carbon emission reduction. The investment of carbon emission reduction will increase the costs of the producer, and the producer will increase the wholesale prices to obtain profits. Higher wholesale prices add to retailers’ costs, and retailers raise their sales price. Under the combined effect of carbon emission reduction and higher price, market demand increases. The increase in market demand, sales price, and wholesale price brings greater profits for producers, retailers, and the whole supply chain.
Corollary 2.
(1),,; (2); (3),,.
Corollary 2 shows that the sales price, wholesale price, producer’s carbon emission reduction, market demand, retailer’s profit, producer’s profit, and whole supply chain’s profit show the same change with freshness level () in the retailer dual-channel model. This is because retailers will raise the sales price to get more profits with fresher product. After the increase in sales price, the producer will also increase the wholesale price to gain more profits. At the same time, it will carry out carbon emission reduction to make up for the loss of consumer demand caused by the increase in sales price. Finally, the combined effect of carbon emissions reduction and higher sales price will increase the market demand. Profits will also increase.
4.2. Producer Dual-Channel Model
Similar to the retailer dual-channel model, it is assumed that fresh food demand is linearly related to carbon emission reduction and freshness level [41], and the market demand functions of the producer dual-channel mode are as follows:
In the producer dual-channel supply chain, the producer obtains profits mainly by selling wholesale products to retailers and selling fresh food with the online channel, while the retailer obtains profits mainly through selling fresh food with the offline channel.
The profits of the producer, retailer, and supply chain are as follows.
To obtain the optimal solution, we first obtain . , the is a concave function of . Let , we get
Substituting Equation (12) into Equation (9), we can derive an expression for in terms of and : . ; . , , , , we get, and When , the Hessian matrix is negative definite, and is jointly concave on and . Let and ; then, we have the optimal solution as follows:
Furthermore, substituting and for Equation (12), we can obtain the optimal sales price:
Substituting , , and into , , , , and , we obtain the total market demand, the producer’s profit, the retailer’s profit, and the total supply chain’s profit:
Proposition 2.
There exist a producer dual-channel sales model when the consumers’ purchasing preference for the retailer’s offline channel is in a certain range: . Here,, .
The left hand of the inequality indicates that when the consumers’ purchase preference for the retailer’s offline channel () is higher than a certain threshold, the retailer is willing to cooperate with the producer, who has his own offline channel. If is too small, the retailer is faced with negative demand, or the sales price is less than the wholesale price, which means the retailer is unwilling to participate in the game. The right hand of the inequality indicates that when is less than a certain threshold, the producer is willing to open the direct channel. If is too large, the demand faced by the producer in the direct channel is zero or negative. In this case, the producer does not open the direct channel or accept the consistent pricing strategy.
Corollary 3.
(1),,; (2); (3),,.
Corollary 3 shows the impacts of the consumers’ low-carbon preference coefficient (γ) on the sales price, wholesale price, producer’s carbon emission reduction, total market demand, retailer’s profit, producer’s profit, and the whole supply chain’s profit in the producer dual-channel model. Similar to the retailer dual channel, all of them are increasing with . The reason is the same as Corollary 1.
Corollary 4.
(1),,; (2); (3),,.
Corollary 4 indicates that the sales price, wholesale price, producer’s carbon emission reduction, total market demand, retailer’s profit, producer’s profit, and the whole supply chain’s profit increase with respect to freshness level () in the producer dual-channel model. A high freshness level motivates the retailer to raise the sales price. Since the online pricing of the producer is consistent with the offline pricing of the retailer, the online pricing of the producer will also rise, which may lead to the reduction of demand. To suppress the reduction of market demand, the producer will carry out carbon emissions reduction to obtain more market demand. At the same time, the producer’s carbon emission reduction increases their costs, so the producer will raise their wholesale prices. Finally, there is more demand for fresh food, and greater demand leads to greater profits.
Corollary 5.
- (1)
- ,;
- (2)
- When,,; when,;
- (3)
- ,,;
- (4)
- When,; when,,
Corollary 5 indicates in the producer dual-channel model:
- (1)
- The producer’s carbon emission reduction and wholesale price decrease with the increase of the consumers’ purchase preference for the retailer’s offline channel (). When is small, the online demand of the producer is larger, and the producer can obtain larger profits. The increasing profits will also stimulate the producer to carry out carbon emissions reduction to further increase market demand and profit. With the relatively high cost of carbon emission reduction, the wholesale price is also high. With the increase of , the online demand of the producer decreases, and the motivation for carbon emission reduction is lacking. Therefore, the wholesale price also decreases.
- (2)
- When the carbon emissions reduction investment cost coefficient () is less than a threshold value, the sales price decreases with the increase of , because the wholesale price is decreasing. In addition, the rate of change of the wholesale price is greater than that of the sales price. As a result, when is greater than a threshold, the sales price increases as increases.
- (3)
- The market demand decreases with the increase of , because the carbon emissions reduction decreases with the increase of . The producer’s profit decreases with the increase of . This is because with the increase of , the offline sales channel of the retailer occupies a larger market demand, leading to the decrease of the producer’s profit.
- (4)
- When is small, the retailer’s profit decreases with the increase of . Under these circumstances, the producer’s profit also decreases, so the profit of the whole supply chain decreases. When is large, the retailer’s profit increases with the increase of . The sales price and market demand jointly affect the retailer’s profit and eventually lead to the increase of the profit. In this case, the reduction rate of the producer’s profit is greater than the increase rate of the retailer’s profit, and the profit of the whole supply chain decreases.
4.3. Mixed Dual-Channel Model
Similar to the retailer dual-channel model, it is assumed that fresh food demand is linearly related to carbon emissions reduction and freshness level [41], and the market demand function of the mixed dual-channel model is as follows:
The profits of the producer, retailer, and supply chain are as follows.
Substitute expressions (13), (14), (15), and into the above formula, and we obtain:
Let ; substituting it into (16), (17), the profit functions of the producer, retailer, and the whole supply chain can be obtained as follows:
To obtain the optimal solution, we first obtain . , the is a concave function of . Let , we get:
Substituting Equation (21) into Equation (19), we can derive an expression for in terms of and : . ; . , , , , and we get, and When , the Hessian matrix is negative definite, and is jointly concave on and. Let and , and we have the optimal solution as follows:
Furthermore, substituting and for Equation (21), we can obtain the optimal sale price:
Substituting , , and into , , , , , and , we obtain the total market demand and the producer’s profit, the retailer’s profit, and the total supply chain’s profit:
Proposition 3.
There is a mixed dual-channel sales model when the consumers’ purchasing preference for the retailer’s offline channel is in a certain range:. Here,,, and.
This proposition shows that the mixed dual-channel sales model only exists when the consumers’ purchasing preference for the retailer’s offline channel () is within a certain range. If is too small, the sales price may be lower than the wholesale price. It means that the retailer is unwilling to participate in the game, or the producer’s online sales demand is zero or negative. In this case, the producer will not open an online sales channel. If is too large, the retailer’s online demand is zero or negative. In this case, the retailer will not open an online sales channel.
Corollary 6.
(1),,; (2); (3),,.
Corollary 6 indicates that in the mixed dual-channel model, sales price, carbon emission reduction, market demand, retailer’s profit, producer’s profit, and the whole supply chain’s profit show the same change with consumers’ low-carbon preference coefficient (). The higher the is, the more it can promote the carbon emission reduction of the producer, and the more it is conducive to the increase of the retailer’s profit, producer’s profit, and the whole supply chain’s profit.
Corollary 7.
(1),,; (2); (3),,.
Corollary 7 explores the impacts of freshness level () on the sales price, wholesale price, carbon emission reduction, market demand, retailer’s profit, producer’s profit, and the whole supply chain’s profit, and it indicates that all of them are positively related to in the mixed dual-channel model. The reason is the same as Corollary 4.
Corollary 8.
- (1)
- ,;,;
- (2)
- When,,and,; When,,;
- (3)
- ,,;,,;
- (4)
- When,,; when,,, and,
Corollary 8 indicates the following for the mixed dual-channel model: (1) The producer’s carbon emission reduction and wholesale price decrease with the increase of the consumers’ purchasing preferences for the retailer’s offline channel () or the consumers’ purchasing preferences for the retailer’s online channel (). (2) When the carbon emission reduction investment cost coefficient () is less than a threshold value, the sales price decreases with the increase of or . When is greater than a threshold, the sales price increases as or increases. (3) The market demand increases with the increase of or . The producer’s profit decreases with the increase of or . (4) When is less than a threshold, the retailer’s profit decreases with the increase of or . The producer’s profit also decreases with the increase of or , so the profit of the whole supply chain also decreases. When is greater than a threshold, the retailer’s profit shows the same change with or . The reason is the same as Corollary 5.
5. Comparison
The supply chain participants behave differently in various sales models. We compare the single dual-channel and mixed dual-channel supply chains to judge the change of optimal decision and market demand and determine whether it is beneficial to supply chain members when supply chain members open another online sales channel based on the two kinds of the single dual-channel supply chain (retailer dual channel and producer dual channel). According to the results, the optimal decision, market demand, and profit under the three dual-channel supply chains are sorted out as shown in Table 4.

Table 4.
The optimal decision, market demand, and profit under the three dual-channel supply chains.
According to the above results, Proposition 4 to Proposition 8 can be obtained as follows.
Proposition 4.
(1) When,; when,; (2) When,; when,.
Here ,
.
Proposition 4 shows that when the consumers’ purchasing preference for the retailer’s offline channel () is small, the sales price of the mixed dual-channel model is higher than that of two single dual-channel supply chains. Meanwhile, when is large, the sales price of the mixed dual-channel model is lower than that of two single dual-channel supply chains.
Proposition 5.
(1) When,; when,; (2) When,; when,. Here,,.
Proposition 5 indicates that when is small, the carbon emission reduction of the producer dual-channel model is higher than that of the mixed dual-channel model, while the carbon emission reduction of the mixed dual-channel model is higher than that of the retailer dual-channel model. As increases, the carbon emission reduction of the mixed dual-channel model is higher than that of the producer dual-channel model, while the carbon emission reduction of the retailer dual-channel model is higher than that of the mixed dual-channel model.
Proposition 6.
(1) When,; when,; (2) when,; when,.
Proposition 6 shows that when is small, the market demand of the producer dual-channel model is higher than that of the mixed dual-channel model, while the market demand of the mixed dual-channel model is higher than that of the retailer dual-channel model. As increases, the market demand of the mixed dual-channel model is higher than that of the producer dual-channel model, while the market demand of the retailer dual-channel model is higher than that of the mixed dual-channel model.
Proposition 7.
For the retailer:
- (1)
- a: When,exist. If, then; if,;b: When,does not exist, in this case,.Here, when,.
- (2)
- a: When,exists. If,; if,;b: When,does not exist, in this case,.Here, when,.
Proposition 7 shows that when is small, the profit gained by retailers in the retailer dual-channel model is greater than that of the mixed dual-channel model. This is because when is small, the offline demand of retailers is smaller. In the mixed dual-channel model, the producer opens online channels to share part of the demand of retailers, and the retailer’s profit decreases. As increases, the retailer’s profit in the retailer dual-channel model will be less than that in the mixed dual-channel model. When is small, the retailer gains more profits in the mixed dual-channel model than in the producer dual-channel model. When is small, retailers’ offline demand is small, but retailers open their online sales channel to obtain more demand, which brings more profits. With the increase of , the profit gained by retailers in the producer dual-channel model will be greater than that of the mixed dual-channel model. This is because the increase of offline market demand brought by the increase of is greater than that brought by the opening of online sales channels.
Proposition 8.
For the producer:
- (1)
- a: When],exists. If,; if,;b: When,does not exist, in this case,.Here, when,.
- (2)
- a: When,exists. If,; if,;b: When,does not exist, in this case,.Here, when,.
Proposition 8 shows that when is small, the producer’s profit in the mixed dual-channel model is greater than that of the retailer dual-channel model. This is because the producer opens online channels to share part of the demand of the retailer, so the producer’s profit increases. With the increase of , the producer’s profit in the mixed dual-channel model will be less than that of the retailer dual-channel model, because the producer loses more profits in the mixed dual-channel model than in the producer dual-channel model. When is small, the producer gains more profits in the producer dual-channel model than in the mixed dual-channel model, because the retailer opens the online sales channel to share part of the producer’s demand in the mixed dual-channel model. With the increase of , the profit gained by the producer in the producer dual-channel model will be less than that of the mixed dual-channel model. It is probably because the online market demand for the producer is more affected by .
6. Numerical Analysis
In order to verify corollaries in Section 4 and propositions in Section 5, numerical experiments are conducted in this section. Based on previous literature on fresh supply chain decisions [40] and low-carbon supply chain decisions [40,47], some relevant parameters are set as follows:; ; ;;;.
6.1. Impact of
This subsection illustrates how consumers’ purchasing preference for retailers’ offline channels () influences the three dual-channel supply chains. Here, we let vary between 0 and 1. Figure 2 shows that when is small, the sales price of the mixed dual-channel supply chain is higher than that of two single dual-channel supply chains, while when is large, the sales price of the mixed dual-channel supply chain is lower than that of two single dual-channel supply chains. This is consistent with Proposition 4. Figure 3 shows that when is small, the carbon emission reduction of the producer dual-channel supply chain is higher than that of the mixed dual-channel supply chain, while the carbon emission reduction of the mixed dual-channel supply chain is higher than that of the retailer dual-channel supply chain. As increases, the carbon emission reduction of the mixed dual-channel supply chain is higher than that of the producer dual-channel supply chain, while the carbon emission reduction of the retail dual-channel supply chain is higher than that of the mixed dual-channel supply chain. This is consistent with Proposition 5. Figure 4 shows that when is small, the market demand of the producer dual-channel supply chain is higher than that of the mixed dual-channel supply chain, while the market demand of the mixed dual-channel supply chain is higher than that of the retailer dual-channel supply chain. As increases, the market demand of the mixed dual-channel supply chain will be higher than that of the producer dual-channel supply chain, while the market demand of the retailer dual-channel supply chain will be higher than that of the mixed dual-channel supply chain. This is consistent with Proposition 6.
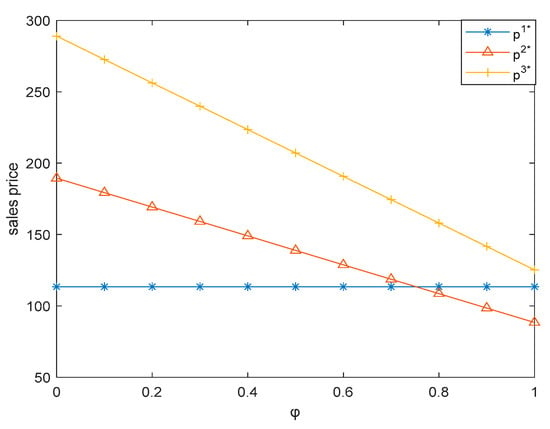
Figure 2.
Effect of on sales price.
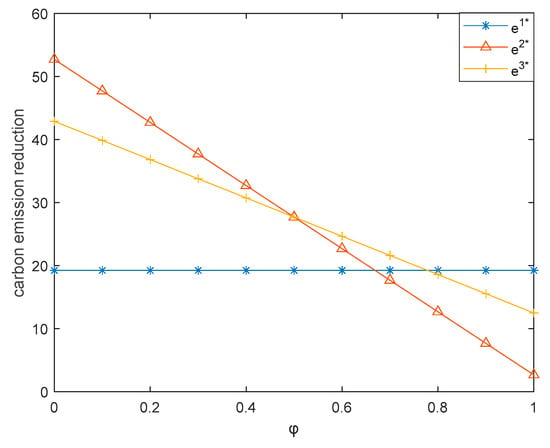
Figure 3.
Effect of on carbon emission reduction.
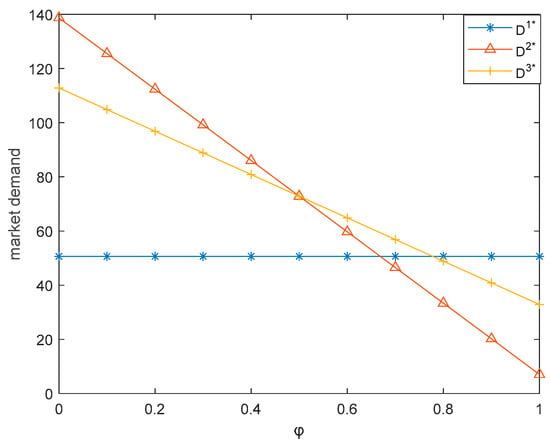
Figure 4.
Effect of on market demand.
Figure 5 shows that when is small, the producer’s profit in the producer dual-channel supply chain is larger than that in the mixed dual-channel supply chain. As increases, the producer’s profit in the producer dual-channel supply chain is smaller than that in the mixed dual-channel supply chain. When is small, the producer’s profit in the mixed dual-channel model is greater than that of the retailer dual-channel model. With the increase of , the producer’s profit in the mixed dual-channel model is smaller than that of the retailer dual-channel model. This is consistent with Proposition 7.
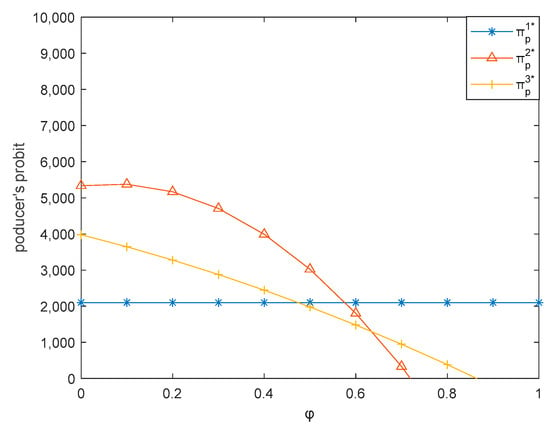
Figure 5.
Effect of on producer’s profit.
Figure 2, Figure 3, Figure 4 and Figure 5 also respectively demonstrate that the sales price, carbon emission reduction, market demand, and producer’s profit decrease with the increase of in the producer dual-channel model and mixed dual-channel model.
Figure 6 depicts that when is small, retailers gain more profits in the mixed dual-channel model than the producer dual-channel model. As increases, the retailer’s profit in the producer dual-channel model will be greater than that in the mixed dual-channel model. When is small, the retailer’s profit in the retailer dual-channel model is greater than that in the mixed dual-channel model. As increases, the retailer’s profit in the retailer dual-channel model will be less than that in the mixed dual-channel model. This is consistent with Proposition 8. Figure 6 also demonstrates that the producer’s profit increases with the increase of in the producer dual-channel model and mixed dual-channel model.
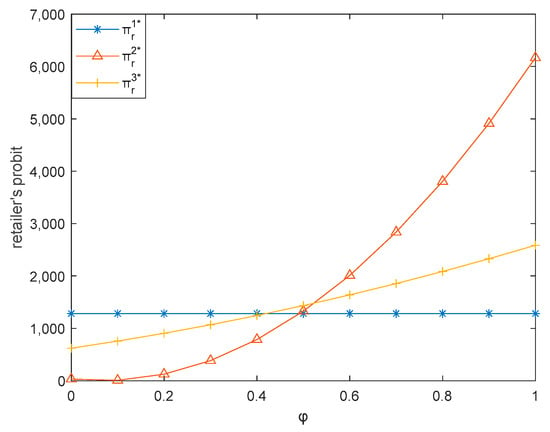
Figure 6.
Effect of on retailer’s profit.
6.2. Impact of
This subsection illustrates how the low-carbon preference coefficient of consumers () influences the three dual-channel supply chains. Here, we let vary between 0 and 1. Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 respectively demonstrates that sales price, carbon emission reduction, market demand, retailer’s profit, and producer’s profit increase with the increase of in three dual-channel supply chains, which is consistent with Corollaries 1, 3, and 6.
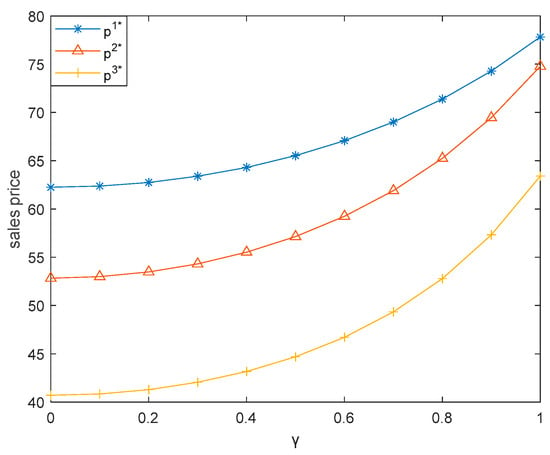
Figure 7.
Effect of on sales price.
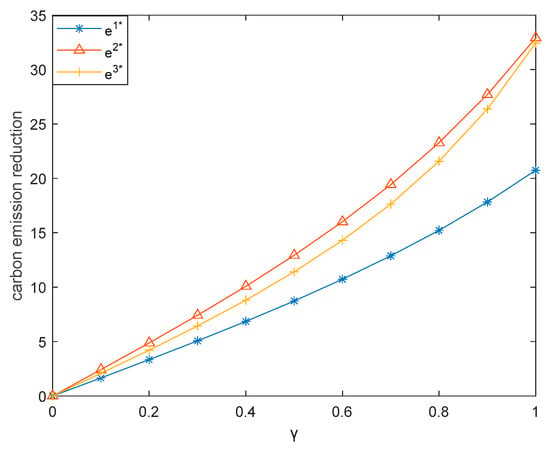
Figure 8.
Effect of on carbon emission reduction.
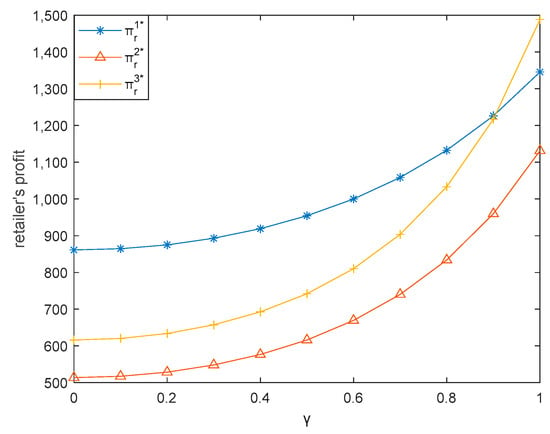
Figure 9.
Effect of on market demand.
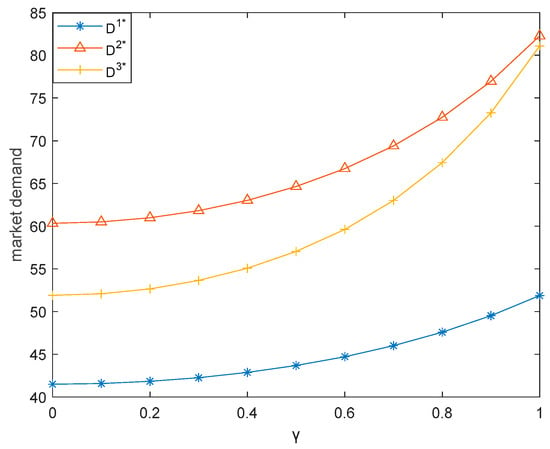
Figure 10.
Effect of on retailer’s profit.
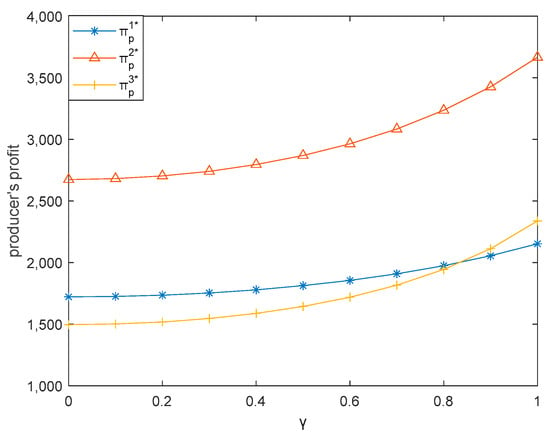
Figure 11.
Effect of on producer’s profit.
6.3. Impact of
This subsection illustrates how the freshness level of fresh food () influences the three dual-channel supply chains. Here, we let vary between 1 and 10. Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 respectively demonstrate that sales price, carbon emission reduction, market demand, retailer’s profit, and producer’s profit increase with the increase of in the three dual-channel supply chains, which is consistent with Corollaries 2, 4, and 7.
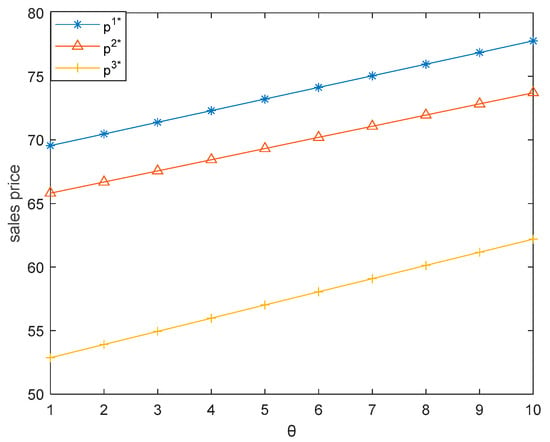
Figure 12.
Effect of on sales price.
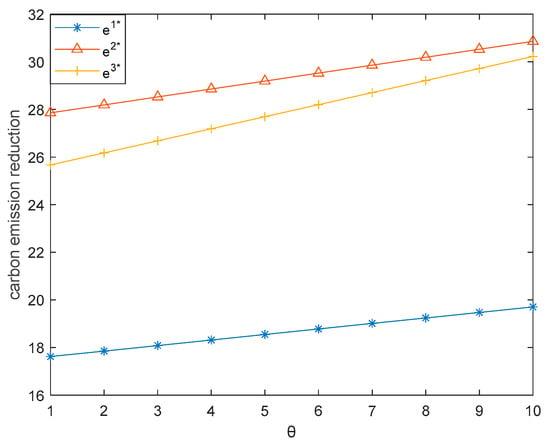
Figure 13.
Effect of on carbon emission reduction.
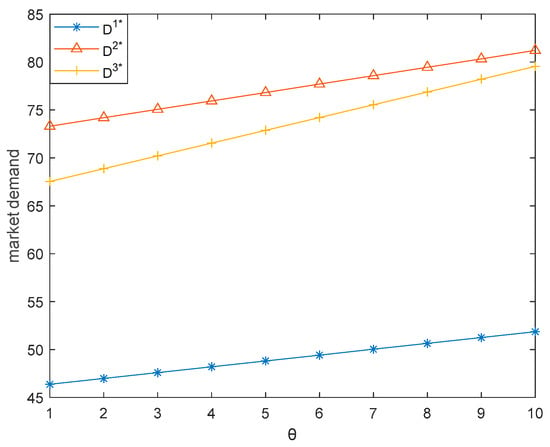
Figure 14.
Effect of on market demand.
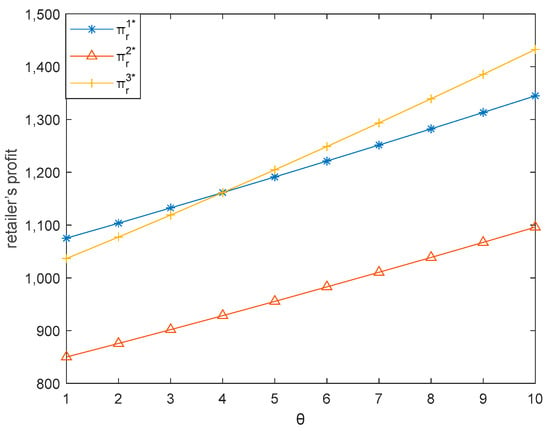
Figure 15.
Effect of on retailer’s profit.
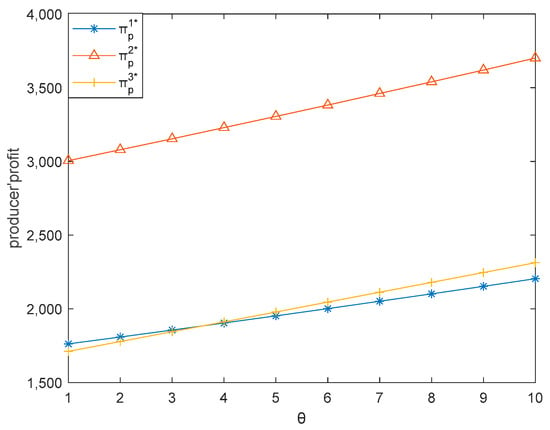
Figure 16.
Effect of on producer’s profit.
7. Managerial Implication
- (1)
- Since the freshness of fresh food has an important impact on the profit of members of the supply chain, and the loss of fresh food in the circulation process is the most important factor affecting its freshness, enterprises in the supply chain should try to control the circulation loss of fresh food and improve the freshness of food. On the one hand, enterprises can improve technical equipment by putting in special refrigerated transport vehicles and cold storage facilities to improve the level of specialization and standardization. Then, enterprises could ensure that the temperature control of the fresh food supply chain is under control and keep products efficient and high quality on their way into the sales market. On the other hand, enterprises can strengthen staff training, teach them to operate in accordance with the cold chain standard, and reduce the loss in the circulation process of fresh food by human reason.
- (2)
- Consumers’ low-carbon preference for fresh food makes both manufacturers and retailers more profitable. Therefore, enterprises in the supply chain should understand the preferences of consumers and make corresponding measures to reduce emissions in a timely manner. Enterprises can take measures such as increasing the use of clean energy, reducing the use or recycling of packaged products to meet consumers’ low-carbon preferences, and improve the profits of the supply chain. In addition, in order to further enhance consumers’ preference for low carbon and achieve the goal of low-carbon emission reduction, the government can advocate and promote the whole society’s low-carbon consumption by popularizing environmental protection knowledge and providing subsidies for low-carbon consumption.
- (3)
- In production dual-channel and mixed dual-channel models, the change of consumers’ channel preference will also have an impact on supply chain members. This requires supply chain enterprises to timely understand consumers’ channel preferences by means of market research or big data analysis, so as to adjust market supply and channel selection strategies in a timely manner and enhance their competitiveness.
- (4)
- Supply chain members can consider transforming single dual-channel supply chain model to mixed dual-channel supply chain model to increase the profit of the whole supply chain. Enterprises can judge whether to open mixed dual channels according to the carbon emission reduction investment cost coefficient and consumers’ purchasing preference for offline sales channels of retailers and then make profit maximization decisions.
8. Conclusions
This research studies a decision-making problem in a dual-channel supply chain of fresh food considering consumers’ low-carbon and freshness preferences. Three dual-channel sales models, including a retailer dual-channel model, producer dual-channel model, and mixed dual-channel model, are constructed. First, the optimal pricing and carbon emission reduction decisions of the three dual-channel models are solved respectively. Then, we compare the single dual-channel supply chain with the mixed dual-channel supply chain. The study presents three main results.
- (1)
- We explore the impacts of the low-carbon preference coefficient of consumers and freshness level on the three dual-channel supply chains. We find that a higher low-carbon preference coefficient of consumers and freshness level can increase the sales price, producer’s carbon emission reduction, market demand, retailer’s profit, producer’s profit, and supply chain’s profit. Therefore, enterprises in the supply chain should understand the preferences of consumers and take corresponding measures in a timely manner to reduce carbon emissions and keep the freshness of fresh food, which will improve the profits of the supply chain.
- (2)
- The impact of the consumers’ purchasing preferences on the three dual-channel supply chains is investigated. In the producer dual-channel model and the mixed dual-channel model, the increase of the consumers’ purchasing preferences for the retailer’s offline channel or the consumers’ purchasing preferences for the retailer’s online channel will reduce the wholesale price, carbon emission reduction, market demand, producer’s profit, and supply chain’s profit. The value of the carbon emission reduction investment cost coefficient decides the relationship between the sales price and the consumers’ purchasing preference for the retailer’s offline channel or the consumers’ purchasing preference for the retailer’s online channel. It also decides how the retailer’s profit changes with the consumers’ purchasing preference for the retailer’s offline channel or the consumers’ purchasing preference for the retailer’s online channel.
- (3)
- The comparison of the optimal decision, market demand, and profit in the three dual-channel models need to be determined according to the value of the consumers’ purchasing preference for the retailer’s offline channel. Therefore, if the supply chain members want to add an online channel on a single dual-channel supply chain to improve the profit, it can be specifically judged according to the value of consumers’ purchasing preference for the retailer’s offline channel.
The study can be extended in several directions in future research. On the one hand, we assume that the supply chain members adopt unified pricing determined by retailers while the sale price is not uniform online and offline in most cases. Therefore, the decision-making research of the three kinds of fresh food dual-channel supply chain models can be carried out under the condition that online and offline pricing are not unified. On the other hand, we assume that the supply chain members have symmetrical information. The rationality of this assumption is based on the long-term cooperative relationship between the producer and the retailer. However, some enterprises in the supply chain will conceal their information. Therefore, under the condition of asymmetric information, the comparative study of the three kinds of fresh food dual-channel supply chains is also worth studying.
Author Contributions
Conceptualization, J.X., Q.M. and J.L.; Formal analysis, J.X., Q.M. and J.L.; Writing—original draft, J.X. and J.L.; Writing—review and editing, J.X., Q.M., X.H. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 71772106), Humanities and Social Sciences Foundation of the Ministry of Education of China (No. 17YJCZH198), and Shandong Provincial Natural Science Foundation, China (No. ZR2017MG012).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the editors and referees for their valuable comments and suggestions to help improve this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
For the retailer, is required; therefore, substituting their expressions into the inequality, we obtain . At the same time, the market demand for online sales of retailers shall meet the following requirements:. □
Proof of Corollary 1.
- (1)
- , , ;
- (2)
- ;
- (3)
- , , . □
Proof of Corollary 2.
- (1)
- , ,;
- (2)
- ;
- (3)
- , , . □
Proof of Proposition 2.
For the retailer, is required; therefore, substituting their expressions into the inequality, we obtain , ; then, we get .
For the producer, is required; therefore, substituting their expressions into the inequality, we obtain ,, and we obtain. □
Proof of Corollary 3.
- (1)
- , , ;
- (2)
- ;
- (3)
- .
According to Proposition 2, we know , then we have .
, . □
Proof of Corollary 4.
- (1)
- , , ;
- (2)
- ;
- (3)
- , , . □
Proof of Corollary 5.
- (1)
- , ;
- (2)
- , when ,; We know, so when , ;
- (3)
- ; , ; Similarly, ;
- (4)
- , , ; when , . □
Proof of Proposition 3.
For the retailer, , is required; therefore, substituting their expressions into the inequality, we obtain Meanwhile, the market demand of online sales should meet the following requirements:
For the producer, is required; therefore, substituting their expressions into the inequality, we obtain. □
Proof of Corollary 6.
- (1)
- , , . We know ; thus (), and we can deduce , ,;
- (2)
- ;
- (3)
- , From Proposition 3, we have , then ; ;. □
Proof of Corollary 7.
- (1)
- , ,;
- (2)
- ;
- (3)
- , From Proposition 3, we have , then ; ; . □
Proof of Corollary 8.
- (1)
- , ; , ;
- (2)
- , . When , we have , ; Because , thus when , we have , ;
- (3)
- ; .,.
From Proposition 3, we have , thus, ; Similarly we have, ;
- (4)
- , . From Proposition 3, we have , so when , then , ; when , then , . □
Proof of Proposition 4.
, and . When , we have ; when , we have .
, and B = , when , we have ; when , we have . □
Proof of Proposition 5.
, . When , we have ; when , we have .
, . When , we have ; when , we have . □
Proof of Proposition 6.
,. When , we have ; when , we have .
, . When , ; when , we have . □
Proof of Proposition 7.
- (1)
- Let , we get that, we have .
According to Propositions 1 and 3, we know that when , the retailer dual-channel and mixed dual-channel models exist simultaneously. Here, , , , . If , we get , so does not exist. Therefore, when , it is only possible that .
- (2)
- Same as above. □
Proof of Proposition 8.
The proof is similar to that of Proposition 7 (1), so we omit it. □
References
- Dominici, A.; Boncinelli, F.; Gerini, F.; Marone, E. Determinants of online food purchasing: The impact of socio-demographic and situational factors. J. Retail. Consum. Serv. 2021, 60, 102473. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, D.Q.; Yue, X. E-business system investment for fresh agricultural food industry in China. Ann. Oper. Res. 2017, 257, 379–394. [Google Scholar] [CrossRef]
- He, B.; Gan, X.; Yuan, K. Entry of online presale of fresh produce: A competitive analysis. Eur. J. Oper. Res. 2019, 272, 339–351. [Google Scholar] [CrossRef]
- Cang, Y.M.; Wang, D.C. A comparative study on the online shopping willingness of fresh agricultural products between experienced consumers and potential consumers. Sustain. Comput. Inform. Syst. 2020, 30, 100493. [Google Scholar]
- Cai, G. Channel Selection and Coordination in Dual-Channel Supply Chains. J. Retail. 2010, 86, 22–36. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Yang, L. Comparisons of initial carbon allowance allocation rules in an O2O retail supply chain with the cap-and-trade regulation. Int. J. Prod. Econ. 2017, 187, 68–84. [Google Scholar] [CrossRef]
- Chen, J.; Liang, L.; Yao, D.-Q.; Sun, S. Price and quality decisions in dual-channel supply chains. Eur. J. Oper. Res. 2017, 259, 935–948. [Google Scholar] [CrossRef]
- Yang, L.; Tang, R. Comparisons of sales modes for a fresh product supply chain with freshness-keeping effort. Transp. Res. Part E Logist. Transp. Rev. 2019, 125, 425–448. [Google Scholar] [CrossRef]
- Liu, C.; Chen, W.; Zhou, Q.; Mu, J. Modelling dynamic freshness-keeping effort over a finite time horizon in a two-echelon online fresh product supply chain. Eur. J. Oper. Res. 2020, in press. [Google Scholar]
- Yang, L.; Tang, R.; Chen, K. Call, put and bidirectional option contracts in agricultural supply chains with sales effort. Appl. Math. Model. 2017, 47, 1–16. [Google Scholar] [CrossRef]
- Liao, Z.; Zhu, X.; Shi, J. Case study on initial allocation of Shanghai carbon emission trading based on Shapley value. J. Clean. Prod. 2015, 103, 338–344. [Google Scholar] [CrossRef]
- Hicks, R.L. Can Eco-Labels Tune a Market? Evidence from Dolphin-Safe Labeling. J. Environ. Econ. Manag. 2002, 43, 339–359. [Google Scholar]
- Song, M. Low-carbon production with low-carbon premium in cap-and-trade regulation. J. Clean. Prod. 2016, 134, 652–662. [Google Scholar]
- Du, S.; Zhu, J.; Jiao, H.; Ye, W. Game-theoretical analysis for supply chain with consumer preference to low carbon. Int. J. Prod. Res. 2014, 53, 3753–3768. [Google Scholar] [CrossRef]
- Liu, B.; Li, T.; Tsai, S.-B. Low Carbon Strategy Analysis of Competing Supply Chains with Different Power Structures. Sustainability 2017, 9, 835. [Google Scholar]
- Ghosh, D.; Shah, J. Supply chain analysis under green sensitive consumer demand and cost sharing contract. Int. J. Prod. Econ. 2015, 164, 319–329. [Google Scholar] [CrossRef]
- Seyfang, G. Community action for sustainable housing: Building a low-carbon future. Energy Policy 2010, 38, 7624–7633. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, M.; Chen, X.; Xu, X. Co-op advertising and emission reduction cost sharing contracts and coordination in low-carbon supply chain based on fairness concerns. J. Clean. Prod. 2016, 133, 402–413. [Google Scholar] [CrossRef]
- Liu, M.L.; Li, Z.H.; Anwar, S.; Zhang, Y. Supply chain carbon emission reductions and coordination when consumers have a strong preference for low-carbon products. Environ. Sci. Pollut. Res. 2021, 28, 19969–19983. [Google Scholar] [CrossRef]
- Xiaoyan, W.; Minggao, X.; Lu, X. Analysis of Carbon Emission Reduction in a Dual-Channel Supply Chain with Cap-And-Trade Regulation and Low-Carbon Preference. Sustainability 2018, 10, 580. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, L. Dynamic Optimization and Coordination of Cooperative Emission Reduction in a Dual-Channel Supply Chain Considering Reference Low-Carbon Effect and Low-Carbon Goodwill. Int. J. Environ. Res. Public Health 2021, 18, 539. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Chen, J.; Xiao, Y.; Xu, X.; Yu, G. Fresh-product supply chain management with logistics outsourcing. Omega 2013, 41, 752–765. [Google Scholar] [CrossRef]
- Herbon, A. Dynamic pricing vs. acquiring information on consumers’ heterogeneous sensitivity to product freshness. Int. J. Prod. Res. 2013, 52, 918–933. [Google Scholar] [CrossRef]
- Zhang, K.; Ma, M. Differential Game Model of a Fresh Dual-Channel Supply Chain under Different Return Modes. IEEE Access 2021, 9, 8888–8901. [Google Scholar] [CrossRef]
- Ma, X.; Wang, S.; Islam, S.M.N.; Liu, X. Coordinating a three-echelon fresh agricultural products supply chain considering freshness-keeping effort with asymmetric information. Appl. Math. Model. 2019, 67, 337–356. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, X.; Zhao, S. Cost-sharing models for green product production and marketing in a food supply chain. Ind. Manag. Data Syst. 2018, 118, 654–682. [Google Scholar] [CrossRef]
- Feng, L.; Chan, Y.L.; Cárdenas-Barrón, L.E. Pricing and lot-sizing polices for perishable goods when the demand depends on selling price, displayed stocks, and expiration date. Int. J. Prod. Econ. 2017, 185, 11–20. [Google Scholar] [CrossRef]
- Hsu, P.H.; Wee, H.M.; Teng, H.M. Preservation technology investment for deteriorating inventory. Int. J. Prod. Econ. 2010, 124, 387–393. [Google Scholar] [CrossRef]
- Dye, C.Y.; Hsieh, T.P. An optimal replenishment policy for deteriorating items with effective investment in preservation technology. Eur. J. Oper. Res. 2012, 218, 106–112. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, G.; Zhang, Q.; Bai, Z. Coordinating a supply chain for deteriorating items with a revenue sharing and cooperative investment contract. Omega 2015, 56, 37–49. [Google Scholar] [CrossRef]
- Liang, X.; Jiang, Q. Pricing strategy of manufacturer in dual-channel considering competition between online retailers and offline retailers. Control.Decision 2019, 34, 1501–1513. [Google Scholar]
- Chen, Y.C.; Fang, S.-C.; Wen, U.-P. Pricing policies for substitutable products in a supply chain with Internet and traditional channels. Eur. J. Oper. Res. 2013, 224, 542–551. [Google Scholar] [CrossRef]
- Peng, G.; Tian, X.; Chen, Q. Online Cooperative Promotion and Cost Sharing Policy under Supply Chain Competition. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar]
- Keen, C.; Wetzels, M.; De Ruyter, K.; Feinberg, R. E-tailers versus retailers. J. Bus. Res. 2004, 57, 685–695. [Google Scholar] [CrossRef]
- Khouja, M.; Park, S.; Cai, G. Channel selection and pricing in the presence of retail-captive consumers. Int. J. Prod. Econ. 2010, 125, 84–95. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, D.; He, L. Contracting emission reduction for supply chains considering market low-carbon preference. J. Clean. Prod. 2016, 120, 72–84. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Alizadeh-Basban, N.; Sarker, B.R. Coordinated contracts in a two-echelon green supply chain considering pricing strategy. Comput. Ind. Eng. 2018, 124, 249–275. [Google Scholar] [CrossRef]
- Yu, B.; Wang, J.; Lu, X.; Yang, H. Collaboration in a low-carbon supply chain with reference emission and cost learning effects: Cost sharing versus revenue sharing strategies. J. Clean. Prod. 2020, 250, 119460. [Google Scholar] [CrossRef]
- Guo, C.R.; Chen, G.Y. Price Competition and Equilibrium Analysis in Supply Chain with Double Hybrid Distribution Channels. Chin. J. Manag. Sci. 2009, 17, 65–71. [Google Scholar]
- Basiri, Z.; Heydari, J. A mathematical model for green supply chain coordination with substitutable products. J. Clean. Prod. 2017, 145, 232–249. [Google Scholar] [CrossRef]
- Fujiwara, O.; Perera, U.L.J.S.R. EOQ models for continuously deteriorating products using linear and exponential penalty costs. Eur. J. Oper. Res. 1993, 70, 104–114. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; You, J. Consumer environmental awareness and channel coordination with two substitutable products. Eur. J. Oper. Res. 2015, 241, 63–73. [Google Scholar] [CrossRef]
- Wang, S.Y.; Choi, S.H. Pareto-efficient coordination of the contract-based MTO supply chain under flexible cap-and-trade emission constraint. J. Clean. Prod. 2020, 250, 119571. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Q.; Zhang, Z.Y. Channel selection and carbon emissions reduction policies in supply chains with the cap-and-trade scheme. J. Manag. Sci. China 2017, 20, 75–87. [Google Scholar]
- Li, B.; Zhu, M.; Jiang, Y.; Li, Z. Pricing policies of a competitive dual-channel green supply chain. J. Clean. Prod. 2016, 112, 2029–2042. [Google Scholar] [CrossRef]
- Xie, Q.H.; Huang, P.Q. A Quantity Discount Model for Coordination of Internet-based Hybrid Channels. Syst. Eng. Theory Pract. 2007, 8, 1–11. [Google Scholar]
- Ranjan, A.; Jha, J.K. Pricing and coordination strategies of a dual-channel supply chain considering green quality and sales effort. J. Clean. Prod. 2019, 218, 409–424. [Google Scholar] [CrossRef]
- Svanes, E.; Aronsson, A.K.S. Carbon footprint of a Cavendish banana supply chain. Int. J. Life Cycle Assess. 2013, 18, 1450–1464. [Google Scholar] [CrossRef]
- Li, T.; Zhang, R.; Zhao, S.; Liu, B. Low carbon strategy analysis under revenue-sharing and cost-sharing contracts. J. Clean. Prod. 2019, 212, 1462–1477. [Google Scholar] [CrossRef]
- Yang, H.; Chen, W. Retailer-driven carbon emission abatement with consumer environmental awareness and carbon tax: Revenue-sharing versus Cost-sharing. Omega 2018, 78, 179–191. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).