Abstract
Computational fluid dynamics (CFD) provides a flexible tool for investigation of separation processes within membrane hollow fiber modules. By enabling a three-dimensional and time dependent description of the corresponding transport phenomena, very detailed information about mass transfer or geometrical influences can be provided. The high level of detail comes with high computational costs, especially since species transport simulations must discretize and resolve steep gradients in the concentration polarization layer at the membrane. In contrast, flow simulations are not required to resolve these gradients. Hence, there is a large gap in the scale and complexity of computationally feasible geometries when comparing flow and species transport simulations. A method, which tries to cover the mentioned gap, is presented in the present article. It allows upscaling of the findings of species transport simulations, conducted for reduced geometries, on the geometrical scales of flow simulations. Consequently, total transmembrane transport of complete modules can be numerically predicted. The upscaling method does not require any empirical correlation to incorporate geometrical characteristics but solely depends on results acquired by CFD flow simulations. In the scope of this research, the proposed method is explained, conducted, and validated. This is done by the example of CO2 removal in a prototype hollow fiber membrane oxygenator.
1. Introduction
Design optimization of hollow fiber membrane modules is crucial to improve separation performance as well as energy and resource efficiency of membrane processes. To be able to effectively do so, a detailed understanding of the underlying phenomena is needed [1]. Computational fluid dynamics (CFD) allows us to deepen our understanding and can be considered as a suitable platform for the investigation of a wide spectrum of membrane separation processes [2].
In CFD, the geometry is decomposed into finite volumes. The relevant transport equations, which describe the membrane separation process—mainly mass, momentum, species, and energy balance—are then discretized for the entirety of the finite volumes (computational mesh) and subsequently solved numerically. Since the module geometry is introduced into the CFD model via the computational mesh, empirical correlations that incorporate the geometry (e.g., Sherwood correlations) can be avoided. This is of high relevance during an optimization process, as these correlations are not fully applicable to all design iterations [3]. In contrast, the discretization of a geometry into finite volumes provides CFD with the necessary grade of flexibility that is a prerequisite for the performance evaluation of new prototype designs.
Due to the high number of computational cells that are necessary to resolve the narrow spacings of a fiber packing, the geometric flexibility gained by CFD comes with high computational costs. Owing to high Schmidt numbers in mass transfer problems, the numerical effort is further increased by steep concentration gradients at the membrane surface. These gradients built up due to the diffusion limited transport of the permeating species in the laminar boundary layer [4]. They represent a substantial contribution to the transport resistance and therefore must be resolved adequately. This requires an additional high level of cell refinement perpendicular to the membrane surface [5]. To conclude, it is computationally feasible to perform flow simulations on macroscopic scales such as membrane modules and larger parts of fiber packings. However, the required high cell refinement at the membrane wall and the associated higher numerical effort limits the simulation of species transport to microscopic scales such as two-dimensional flat membranes, single fibers, or small fiber arrangements. This gap in the geometrical scale and complexity of flow and species transport simulations can be observed when studying previous publications in related research fields.
In process and environmental science, hollow fiber packings are often simplified by modelling a two-dimensional flat sheet membrane for fundamental CFD investigations of transmembrane transport or studies on the concentration polarization layer [6,7,8,9]. If larger parts of the membrane module design are included into the CFD geometry, the fiber packing is often modeled as a porous structure [10,11]. Here, the momentum equation is modified with a porous media approach (e.g., Darcy’s law). Transmembrane flux is then estimated using Sherwood models, therefore again including geometry dependent correlations. Compared to the porous media approach, CFD simulations of resolved hollow fiber packings are often limited to small packings when including transmembrane transport [12] or are only investigating hydrodynamic phenomena if larger packings are examined [13,14,15].
In medicine, hollow fiber membranes are utilized in numerous applications as hemodialysis, hemofiltration, and plasmapheresis [16]. However, a particular important role in the development of CFD membrane modelling can be attributed to blood oxygenation. In this framework, highly efficient membrane modules are necessary to reduce the extrinsic membrane surface, to limit the blood priming volume [17], and to develop compact para- and intracorporeal devices [18]. As the transmembrane transport of CO2 and O2 in an oxygenator has no significant impact on hydrodynamics, numerical complexity is, to some extent, reduced. Hence, substantial progress has been achieved in this field. For instance, simulations of transmembrane CO2 transport are not limited to two-dimensional flat sheet models, but are extended towards periodic fiber arrangements [3] or parts of packings [19]. Kaesler et al. [20] used an Eulerian-Eulerian approach to model the O2 transfer in an prototype oxygenator and treated blood as two phases, red blood cells and blood plasma, to account for the heterogenous distribution of hemoglobin. As the concentration polarization layer in blood is the main transport resistance [21], most simulations include only the blood side of the oxygenator. Taskin et al. [22] additionally resolved the membrane wall and simulated the oxygen transport in a small packing of an experimental oxygenator. Harasek et al. [23] extended this approach and included the hollow fiber lumen to the simulation domain. Deviation of the real packing from an ideal packing states a challenge when generating computational meshes. D’Onofrio et al. [24] proposed a workflow to convert microcomputer tomography data of an oxygenator into a computational grid. To conclude, CFD simulations of oxygenator membrane modules are relatively advanced. Nevertheless, a significant gap in geometric scale and complexity can be observed in the literature when comparing flow and species transport simulations of oxygenator membrane modules.
In this study, a method is proposed, which tries to cover this gap and allows to give accurate predictions of hydrodynamic phenomena and transmembrane transport on the same macroscopic scale.
The proposed method, illustrated in Figure 1, includes the following steps:
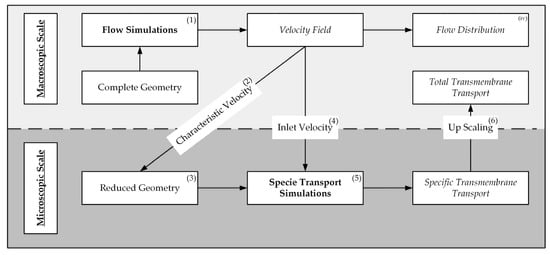
Figure 1.
Workflow of the presented upscaling method for prediction of hydraulic and transmembrane transport on a macroscopic scale.
- Flow simulations for computation of the velocity field in the complete geometry,
- Identification of characteristic velocity components with significant influence on the transmembrane species transport,
- Development of a reduced packing geometry based on the velocity distribution,
- Numerical conversion of the characteristic velocity to an inlet velocity for the reduced geometry,
- Species transport simulations of the reduced geometry to predict transmembrane flux,
- Upscaling of the transmembrane flux to predict the total transmembrane transport of the whole module.
For the last step, no empirical correlations that incorporate geometric parameters have to be utilized. While this upscaling method is, in general, suitable for membrane processes where hydrodynamic transport is not influenced by transmembrane transport, it has been specifically developed, conducted, and validated for the CO2 removal process of an oxygenator prototype.
2. Experimental and Numerical Methods
2.1. Ex Vivo Tests
To validate the prediction capabilities of the proposed upscaling method, data sets of ex vivo tests (tests outside the living test animal) were exploited. In these tests, the CO2 removal performance of a prototype oxygenator (see Figure 2) was determined. As test animals, two pigs were chosen, which were provided by the teaching and research farm of the University of Veterinary Medicine, Vienna. All tests were performed under the ethics proposal ZI. 8/115-97/98. For stable experimental conditions, the animals were sedated and mechanically ventilated via an endotracheal tube. Oxygen saturation and CO2 partial pressure were controlled via the ventilator (Servo 900C, Siemens). To maintain physiological blood pressure, Ringer’s solution (mixture of sodium chloride, sodium lactate, potassium chloride, and calcium chloride in water) was administered. To prevent blood coagulation, which could cause clotting of the hollow fiber bundles, heparin was injected intravenously. Blood pressure, cardiac output (blood flow rate provided by the heart), body temperature (approximately 37 °C), and heart rate were monitored (PiCCO plus, Pulsion Medical System). Blood was pumped (BPX-80, Medtronic) from the vena femoralis (largest vein of the leg) out of the pig to the prototype oxygenator and back in, via the vena jugularis (largest vein in the neck, Figure 2a). These veins were chosen because they are capable of providing and taking over the necessary blood flow rates. Blood flow rate was measured with a clamp-on ultrasonic flow probe (SONOFLOW CO.55/080). CO2 was removed from blood flowing at the shell side of the prototype oxygenator. For each measuring point, three blood samples (BG, Figure 2a) were taken before and after the prototype module and analyzed with a blood gas analyzer (ABL500 FLEX, Radiometer Medical A/S). The device allows the measurement of CO2 partial pressure as well as Hematocrit (volume percentage of red blood cells in blood) and other blood parameters relevant for clinical monitoring. The prototype module fiber lumen were swept with pure O2 (1 L STP/min) to remove the CO2 from the circuit. Sweep gas flow of the prototype oxygenator was regulated by a mass flow controller (GF40, Brooks). Flow rate of the outgoing sweep gas flow was recorded using a piston stroke volumetric measurement device (Defender 510, Bios DryCal). Furthermore, CO2 concentration of the sweep gas flow exiting the prototype module was measured (BINOS 100 M, Emerson). By combining volumetric and concentration measurement, the CO2 removal was determined. A parameter study was conducted to examine the influence of CO2 partial pressure and blood flow on the CO2 removal. CO2 partial pressure of blood entering the prototype oxygenator was set to three different levels (50, 70, 100 mmHg). For each partial pressure, three blood flows (1000, 1300, 1600 mL/min) were tested. Pressure was measured before and after the modules on blood and gas side (PR, Figure 2a), using miniaturized pressure transmitters (AMS 4711, Analog Microelectronics).
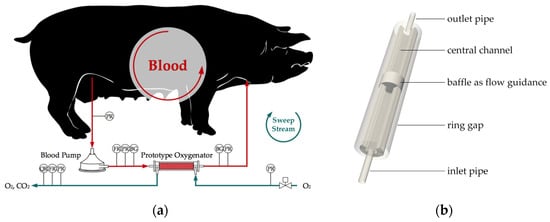
Figure 2.
Ex vivo test set up: (a) Scheme of ex vivo loop with pig, prototype oxygenator, blood pump, pressure sensors (PR), flow rate sensors (FR), and CO2 concentration sensor (QR); (b) Blood guiding parts of the prototype oxygenator with cut through the membrane packing.
A Physica MCR302 rheometer (Anton Paar, Austria), equipped with a double gap cylinder system (internal gap: 0.417 mm; external gap: 0.462 mm; cup length: 42 mm), was used to determine the blood viscosity of the test animals. Due to agglomeration of blood components on the shell side and condensation of pervaporated blood plasma on the fiber lumen side, permeances of unused and dry fibers are considered unrepresentative. Hence, membrane pure gas permeances were measured after the experiments to evaluate the impact of ex vivo tests on the membrane resistance.
The prototype module can be seen in Figure 2b. A hollow fiber mat was coiled up around the coaxially positioned inlet and outlet pipe (outer diameter, 6 mm). Hence, a hollow fiber packing in the form of a hollow cylinder was shaped. The packing has a central cylindrical channel with 6 mm diameter as well as an outer diameter of 16 mm and is inserted into a pipe with 20 mm inner diameter as the module shell. This leaves a 2 mm ring gap between packing and shell. In the middle of the module, a baffle blocks the blood flow in the central channel and forces a transverse flow through the packing. The hydraulic diameter of the central channel and the ring gap are comparable, to promote homogenous blood distribution. The packing with an active fiber length of 100 mm is potted on both ends of the shell pipe. Sweep gas is distributed or collected at the end of the lumen via end caps (not shown in Figure 2b). Approximately 500 fibers (Membrana Oxyplus® 90/200 PMP, 3M) were incorporated into the module. Tangential and radial spacing between the fibers measures 200 µm.
2.2. Computational Fluid Dynamics
To predict the transmembrane transport with the proposed upscaling method, two types of CFD simulations are necessary. First, flow simulations of the complete module or module parts, large enough to show the actual flow distribution in the module. Second, species transport simulations on a simplified (reduced) geometry, derived from the flow simulation results. In order to be able to upscale the species transport simulation results to the complete geometry, the inlet velocities of the reduced geometry are computed based on the velocity distribution of the flow simulations. In this work, the proposed upscaling method was applied specifically to predict the CO2 removal of the prototype oxygenator described in Section 2.1. However, the method can be used generically for membrane processes where there is no significant influence of transmembrane transport on hydrodynamic transport. All CFD simulations were carried out using the opensource toolbox OpenFOAM® 4.1 (ESI Group). The simulations were run on server nodes equipped with 32 core CPUs (16 cores in two physical modules, EPYC 7351, AMD).
2.2.1. Flow Simulation of the Complete Membrane Module
Blood flow of the complete prototype oxygenator was simulated. Therefore, the finite volume formulation of the steady incompressible Navier–Stokes equation was solved by applying the Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm [25] (simpleFoam). The computational grid, consisting of hexahedron cells, was generated using commercial meshing software (Gambit 2.4.6, ANSYS) and was additionally longitudinally refined with OpenFOAM®. The final computational mesh used for flow simulations contained 32 Mio. cells. Mesh resolution within the packing was matched to the cell refinement of the reduced geometry (Section 2.2.3). Average cell size outside the packing was significantly larger to reduce computational costs. The cell length in the longitudinal direction was set uniformly to 0.35 mm. Cell size in the radial and tangential direction variated from 0.087 (cells close to walls or the packing) to 0.175 mm (cells within the main flow), depending on the position in the module. Flow within the packing can be assumed laminar based on the Reynolds number (Repacking = u·L/ν ≈ 0.1 m/s · 200 µm / 2.3E-6 m2/s ≈ 8.7). In contrast, the Reynolds number of the inlet pipe is slightly elevated at maximum blood flow rates (1600 mL/min, Reinlet = u·L/ν ≈ 2.1 m/s · 4 mm / 2.3E-6 m2/s ≈ 3650). Hence, additional flow simulations were conducted utilizing the k-ω turbulence model. These turbulent flow simulations showed similar flow distribution and pressure loss when compared to laminar flow simulations. Consequently, the numerically less expensive method (laminar flow simulation) was chosen. The governing equations were discretized utilizing second order schemes (Van Leer). A uniform inlet velocity at the beginning of the inlet pipe was matched to inlet flow rates ranging from 1000 to 1600 mL/min. At all walls, including membrane surfaces, a no-slip velocity boundary condition was applied. At the end of the outlet pipe, a fixed uniform value of 0 Pa was set for relative pressure. The remaining boundary conditions for velocity and pressure were set to zero gradient (Neumann conditions). Blood was modelled as a single phase fluid. To account for the shear thinning rheological behavior of porcine blood, a power law viscosity model (Equation(1)) was utilized [26] and fitted to experimental data (Section 3.1). The power law was extended by an upper and lower limiter. At high shear rates, the viscosity converges towards its minimum, the Newtonian viscosity (µmin = µNewtonian). To improve numerical stability during the first solver iterations, viscosity is limited to max 100 Pa s at low shear rates.
µ = max(µmin, min(µmax, µ0 × ɣ̇η-1))
2.2.2. Derivation of the Reduced Geometry, Computation of Inlet Velocities
In order to accomplish a high prediction performance of the upscaling method proposed in this work, the reduced geometry and the corresponding inlet velocities have to be representative for the whole module (complete geometry). Therefore, the development of the reduced geometry is strongly dependent on the results of the flow simulations of the complete geometry (Section 3.1). In the examined module, the hollow fiber packing is, in general, positioned in a crossflow mode within the blood flow. Only the first fiber layer of the packing is hit frontally by the crossflow. Most of the remaining fibers are positioned in the slipstream of the neighbor fibers upstream. Hence, the blood flow hits the fibers located in the inner part of the packing tangentially, at their sides (Section 3.1). Thus, the packing was simplified to a non-staggered arrangement, which generates similar flow behavior. Additionally, no significant flow perpendicular to the main cross flow was observed in the packing. Consequently, the influence of neighboring fibers positioned perpendicular to the flow direction are considered relatively insignificant. Therefore, the packing was reduced to a single line of eight parallelly aligned fibers, representing the eight fiber mat windings. The crossflow is modeled by the inlet velocity boundary condition of the reduced geometry. The reduced geometry is illustrated in Figure 3c, where it is also compared to the real geometry (Figure 3b). Spacing between fibers is matched to the spacing of used fiber mats (200 µm) and the distance between two fiber mat layers (200 µm), defined by the in-house module building process. As the flow in longitudinal direction was negligibly small within the packing, flow in the species transport simulations was reduced to an idealized cross flow (quasi two-dimensional). Hence, the length of the fibers in the reduced geometry (10 mm) has no physical representation in the complete module.
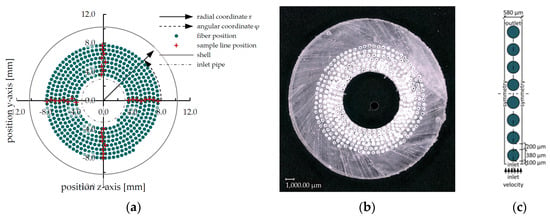
Figure 3.
Packing geometry: (a) Scheme of the prototype oxygenator fiber arrangement, including sampling line positions and polar coordinate system; (b) Slice of fiber potting to illustrate real geometry; (c) Scheme of reduced geometry for CO2 transport simulations.
By setting appropriate inlet velocities, a representative cross flow can be modelled. To calculate the inlet velocities, the characteristic velocity components that define the cross flow character have to be identified. This is done by calculating the ratio between a velocity component in an arbitrary direction (xj) and the velocity magnitude |U|:
ψ = xj · U ÷ |U|
Computing the velocity fraction of the radial velocity component (ψradial, xj = xradial) returns values close to one within the packing (Section 3.1). In this study, the radial velocity component was therefore considered as the characteristic velocity for calculation of the cross flow in the reduced geometry. It can be calculated by projecting the velocity field on a polar coordinate system with the coordinate plane perpendicular to the module length axis (Figure 3a).
The radial velocities were sampled on lines parallel to the longitudinal axis, which were positioned exactly between two fibers. Sample lines were positioned at four different angles (0°, 90°, 180°, 270°—Figure 3a) to eliminate dependencies from the angular position. Due to the higher flow cross-sections at outer fiber mat windings, the radial velocity magnitude decreases in a radial direction. As the rectangular reduced geometry cannot account for this velocity decrease, sample lines were defined for all eight windings (layers). This allows the computation of an inlet velocity, which can represent the average radial velocity of blood flowing through a packing segment similar to the reduced geometry. Effects of this simplification on the prediction performance of the proposed method are discussed in Section 3.4. Two hundred samples, distributed homogeneously on the longitudinal axis, were taken per line (Figure 4). The arithmetic average of all samples on all lines (6400 points) was calculated to gain a representative mean radial velocity (uradial).

Figure 4.
Blood guiding parts of the prototype oxygenator (complete geometry) with a cut through the membrane packing. Red dotted lines: line sources at the angular position ϕ = 0° used for sampling of radial velocity profiles, shown in Section 3.1. Turquoise dot-and-dashed line: cross-sections at five different longitudinal positions (20, 40, 50, 60, and 80 mm) used for velocity magnitude and radial velocity fraction contour plots, shown in Section 3.1.
The sampled velocities, acquired by flow simulations of the complete geometry, represent the maximum velocity (umax = uradial) between two fibers. The uniform inlet velocity of the reduced geometry can be adapted iteratively to produce velocity profiles within the reduced geometry, which fit to the maximum velocities of the complete geometry. In Figure 5a, the velocity distribution between fibers is illustrated. The presented profiles were gained by the quasi two-dimensional CFD simulations of the reduced geometry (full lines, Figure 5a). They represent the distribution of radial velocities in the packing of the complete geometry. In addition to the profiles, their average is inserted into the graph (ū, dashed lines, Figure 5a). The average is calculated based on the arithmetic mean of the velocity profiles between the fibers. As can be seen in Figure 5a, following correlation between maximum (umax) and mean (ū) velocity was found to be in good agreement with the CFD simulations of the reduced geometry:
ū = umax ÷ (2)0.5 = uradial ÷ (2)0.5
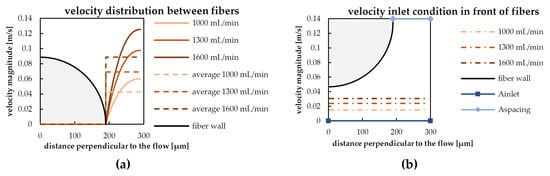
Figure 5.
(a) Velocity distribution and velocity average between fibers gained by computational fluid dynamics (CFD) simulations of reduced geometry; (b) Uniform inlet velocity condition (reduced geometry) in front of the fibers. Fibers are inserted schematically into the graph.
Applying the continuity equation, a uniform inlet velocity (uinlet, dotted and dashed line, see Figure 5b) for the reduced packing segment can be calculated using the mean velocity, the inlet boundary area (Ainlet), and the cross-section between two fibers (Aspacing). Utilizing Equation (3) and Equation (4) allowed the avoidance of the iterative determination of the uniform inlet velocity.
uinlet = ū × Aspacing ÷ Ainlet
2.2.3. Species Transport Simulations of the Reduced Geometry
Species transport simulations including transmembrane transport were conducted for the reduced geometry. The computational grid of the simplified packing was generated with the blockMesh utility of OpenFOAM®. It comprises 8000 hexahedron cells in the cross-section. At the membrane surface, the mesh was refined to adequately resolve the concentration polarization. Therefore, ten cell layers were applied. The cell layer thickness was decreased successively towards the membrane with an expansion ratio of 5 (ratio of most outer layer thickness to most inner layer thickness). The thickness of the most inner layer measured 1.4 µm. Grid convergence index (GCI) [27], determined for the used mesh, predicts an error due to the discretization of about 3%.
For the species transport simulations, an in-house solver membraneFoam [28] was applied. The multi-region solver was developed based on OpenFOAM®. The transport equations of the single regions, which are divided by the membrane surface, are computed separately but are coupled by transmembrane transport (Ji). The later is implemented as a volumetric source term for cells attached to the membrane surface in all solved transport equations. It is calculated based on membrane permeance (P) and membrane surface area (A) of the computational cell. Since membrane resistance was found to be increased as a result of the ex vivo trials, pure gas permeances of used fibers were applied for the CO2 transport simulation. As a driving force, the partial pressure difference (Δpi) between the computational cell and its neighbor cell, on the other side of the membrane, is utilized. If there is no direct neighbor cell, the partial pressure can be interpolated based on nearby values using various schemes.
JCO2 = P × A × ΔpCO2
Due to the generic implementation of membraneFoam, every region (blood-, membrane-, and lumen-side) of the prototype module could be resolved, but preceding studies [23] showed that the main drop of CO2 partial pressure (the driving force of transmembrane transport) is located at the blood side and the outer selective membrane layer. Hence, the porous sub-structure and the lumen of the hollow fiber membrane were neglected and not added as an additional region to the computational domain. The multi-region solver membraneFoam was therefore utilized in a single region mode. Based on previous findings [23], the partial pressure on the gas side of the selective layer was assumed to be uniformly 0 mmHg. This reduces Eq(5) for CO2 to:
JCO2 = P × A × (pCO2,Blood − 0)
To model the CO2 transport, the different CO2-related species, dissolved CO2 and bicarbonate (HCO3−), were summarized to one total CO2 species. The CO2 partial pressure (pCO2) was then calculated based on the concentration of this single species (cCO2,total) [29].
cCO2,total = q × pCO2t with q = 0.128 and t = 0.369
A diffusion coefficient for total CO2 (DCO2,total) was derived by enforcing the diffusion of total CO2 to be equal to the combined diffusion of dissolved CO2 and bicarbonate. DCO2,total can then be expressed as a function of the dissociation slope (λ = (δ cCO2,total / δ pCO2,Blood)), the solubility of dissolved CO2 (αCO2), and the diffusion coefficients of dissolved CO2 (DCO2) and bicarbonate (DHCO3-). Thereby, λ can be assumed constant at clinically relevant CO2 partial pressures above 50 mmHg. All parameter values, necessary for the calculation of DCO2,total, are summarized in Table 1.
DCO2,total = DHCO3- + (DCO2 − DHCO3-) × αCO2 ÷ λ

Table 1.
Summary of diffusion model parameters. Values were taken from [29].
For CO2 transport simulations, the finite volume formulation of the transient, laminar, and incompressible Navier–Stokes equation was solved by applying the Pressure Implicit Method for Pressure-Linked Equations (PIMPLE) algorithm. Discretization schemes and the viscosity model were set equally to the flow simulations described above (Section 2.2.1). The inlet velocity was calculated based on Equation (3–4) and was applied uniformly on the inlet patch. Mass fractions of blood and CO2 were set to match the CO2 partial pressure at the blood inlet of the prototype oxygenator during the ex vivo trials. To model the influence of neighboring fibers, symmetry conditions were applied at the sides of the geometry. The remaining boundary conditions were set analogous to the flow simulation.
By adequately defining the reduced geometry and the corresponding inlet velocities, the predicted CO2 removal (JCO2,reduced geometry) can be up-scaled relatively simply to the complete geometry (JCO2,complete geometry) by the use of the membrane area of complete and reduced geometry (Amembrane,i):
JCO2,complete geometry = JCO2,reduced geometry × Amembrane,complete geometry ÷ Amembrane,reduced geometry
While in the prototype oxygenator, O2 is transported from the sweep gas into the blood via the membrane; this study solely focuses on the CO2 transport. The dependency of the CO2 solubility from the O2 saturation (Haldane effect), or any other coupling between transmembrane CO2 and O2 transport, was neglected.
3. Results and Discussion
To validate the proposed method, the transmembrane CO2 removal performance of a prototype oxygenator was determined in ex vivo trials and predicted by our upscaling method. The experimentally and numerically determined results are compared in the following section. While the presented results are specific, the proposed method itself is generic and can be applied to a wide range of hollow fiber membrane separation processes where hydrodynamic transport is not influenced by transmembrane transport.
3.1. Hydrodynamic Results
In total, the ex vivo trials were conducted with two pigs. The blood viscosity measurements showed low variation between the two test animals (Figure 6). The power law model coefficients were determined as µ0 = 8.81 mPa s and n = 0.792, with an acceptable coefficient of determination (R2 = 0.96). The whole blood viscosity, which converges towards Newtonian viscosity at high shear rates, amounts to 2.38 mPa s (µmin). A maximal viscosity of 19.4 mPa s was measured at shear rates of 1.0 s−1. In Figure 6, the correlation between shear rate and dynamic viscosity given by the power law model is compared to the experimental data.
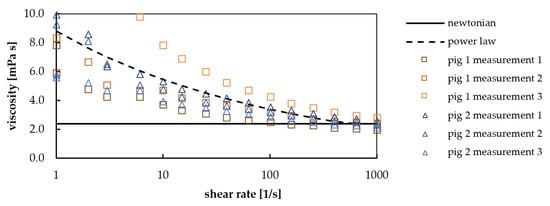
Figure 6.
Shear rate dependency of dynamic viscosity given by the power law model fitted to porcine blood. The Newtonian viscosity (2.38 mPa s) is entered in the graph for comparison.
The relation between blood side pressure loss in the prototype oxygenator and blood flow rate is shown in Figure 7a. Blood side pressure loss in the prototype module ranges from 29 mmHg at 1055 mL/min to approximately 72 mmHg at 1559 mL/min. Pressure drop is predicted accurately by CFD flow simulations at flow rates ranging from 1300 to 1600 mL/min, but is slightly overpredicted by approximately 10 mmHg at 1055 mL/min. The average deviation between numerically and experimentally determined blood side pressure drop amounts to 15%. This indicates that the description of blood as a single phase, shear thinning fluid is an appropriate modelling approach.
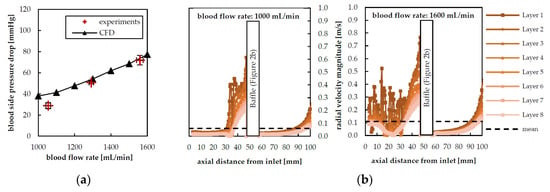
Figure 7.
(a) Pressure drop in the prototype module in dependency of blood flow rate, determined by experiments (+) and CFD (▲, flow simulations complete geometry); (b) Radial velocity profiles determined by CFD flow simulations of the complete geometry.
Flow simulations give a detailed insight into the macroscopic blood distribution of the prototype membrane oxygenator. Figure 7b shows the distribution of the radial velocity magnitude over the longitudinal axis of the complete module, based on CFD flow simulations. No significant dependence of the radial velocity from the angular position was detected. Therefore, only the profiles for ϕ = 0 (see Figure 4) are presented and considered representative for all other angles. The flow cross-section increases with the number of fiber mat windings (layers). It is lowest in the inner layer (Layer 1, Figure 7b) and highest in the outer layer (Layer 8, Figure 7b). As can be seen in Figure 7b, this leads to a drop of radial velocity magnitude with increasing layer number. The average radial velocity in Layer 1 is 2.7 times higher than in Layer 8. The variation of radial velocity is in general stronger in front of the baffle (axial distance < 50 mm, standard deviation 0.12 m/s) than behind the baffle (axial distance > 50 mm, standard deviation 0.05 m/s). This suggests that the blood distribution can be considered significantly more homogenous in the second half of the membrane module. The similarly sized hydraulic diameter of the ring gap (4 mm) and central channel (6 mm) were not able to promote a homogenous transverse flow over the whole module length. Furthermore, radial velocity variations are more distinct in inner layers (e.g., Layer 1) than outer layers (e.g., Layer 8). With increasing blood flow rate, the radial velocity (mean) and the radial velocity variation increases in general. The strong increase of radial velocity shortly before the baffle (on average +86% in the last 10 mm) raises momentum in radial directions. As the membrane shell deflects this momentum in both, negative and positive axial direction, backflow is generated at higher blood flow rates. This leads to a rise of radial velocity magnitude in proximity to the blood inlet (axial distance, 0–20 mm).
In Figure 8a, the blood side velocity magnitude distribution of the prototype oxygenator at a flow rate of 1300 mL/min can be seen. Five cross-sections perpendicular to the longitudinal axis of the module are presented at five different longitudinal positions (20, 40, 50, 60, and 80 mm distance from the beginning of the fiber packing, Figure 4). The flow profiles show that, in coiled up fiber mats with parallel aligned fibers and a tangential and radial spacing of 200 µm, the fibers tend to stay in the slipstream of each other. Therefore, the packing can be approximated by a non-staggered fiber arrangement in the reduced geometry. High velocities and main flows can be assigned to pathways running in between the fibers in a radial direction (Figure 3a, radial coordinate). Pathways that are aligned with the tangential direction (Figure 3a, angular coordinate) show low velocities and flows. Another indication for cross flow mostly occurring in a radial direction can be given by the fraction of the radial velocity component with the velocity magnitude (radial velocity fraction). This fraction is a simple measure to evaluate the influence of the radial velocity component on the flow and in consequence on the transmembrane transport. Of course, this method can be applied to every other velocity component when evaluating different module designs. The distribution of the radial velocity fraction is shown in Figure 8b. In areas with higher flows/velocities (pathways aligned radially), the fraction is close to one (main flow direction is in a radial direction). In areas with lower flows/velocities (pathways aligned tangentially) the radial velocity component accounts for half of the total velocity (radial velocity fraction of approximately 0.5). The radial velocity was therefore considered as representative to determine the inlet velocity for the reduced geometry (CO2 transport simulations).
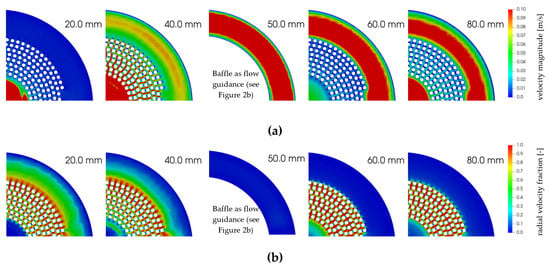
Figure 8.
Contour plots at five different longitudinal positions of the complete geometry (Figure 4): (a) Velocity magnitude; (b) Fraction of radial velocity component and velocity magnitude.
Table 2 summarizes the maximum radial velocities between two fibers (umax), averaged for multiple positions (Figure 3a). The maximum radial velocities were computed based on the flow simulation results of the complete geometry. The inlet velocity for the reduced geometry was calculated by using Eq(3) and Eq(4). It increases approximately linear (R2 = 0.98) with the blood flow rate (Figure 9).

Table 2.
Maximum radial velocity between two fibers averaged for multiple positions in the complete module and inlet velocity for the reduced geometry at different blood flow rates.
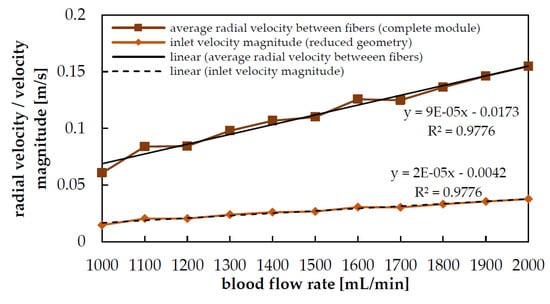
Figure 9.
Uniform inlet velocity for reduced geometry and maximum radial velocity between two fibers averaged for multiple positions in the complete geometry.
3.2. Species Transport Results
In Figure 10, the specific CO2 removal determined in the ex vivo tests is illustrated. Transmembrane CO2 flux rises slightly with higher blood flow rates. With higher CO2 partial pressures at the blood inlet, this dependency gets stronger. This can be seen by comparing the slopes of the linear regressions shown in Figure 10. They approximate the dependency of the specific CO2 removal from the blood flow rate. The slope for an inlet pCO2 of 100 mmHg is 15 times higher compared to the slope at 50 mmHg. In general, the specific CO2 removal is more sensitive to the inlet pCO2 than to the blood flow rate. The CO2 removal performance predicted by CFD species transport simulations were compared to experimental data (Figure 10). Transmembrane flux is predicted most accurately (within the error margins) at flow rates of 1300 mL/min or at an inlet pCO2 of 70 mmHg. In general, the accuracy of the numerical model is satisfactory. The highest deviation (approximately 7%) occurs at a pCO2 of 100 mmHg and a blood flow rate of 1600 mL/min. On average, the error is low, at 3.2%. The largest errors, and therefore a systemic deviation, can be observed at high pCO2 (100 mmHg). At this stage of research, it cannot be differentiated if these deviations are caused by the CO2 solubility model or by the proposed upscaling method. The upscaling is done relatively simply by multiplying the specific transmembrane CO2 removal of the reduced geometry with the outer membrane area of the complete module.
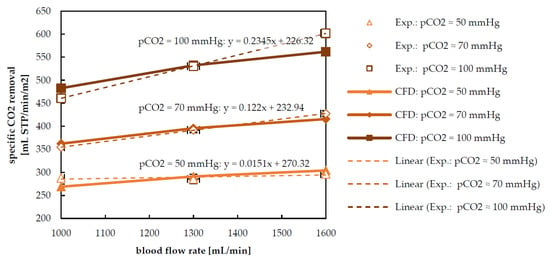
Figure 10.
Experimentally and numerically determined specific CO2 removal at different flow rates and pCO2 at the blood inlet of the prototype oxygenator.
The satisfying match between numerically and experimentally predicted CO2 removal suggests that the computed inlet velocities for the reduced geometry are representative for the different blood flow rates. Hence, the presented method is able to account for complex flow phenomena. This includes fluctuations of radial velocities along a sample line, with deviations of up to ±84% from the average. Furthermore, the dependency from the radial position in the packing can be considered reasonably. This is important because the radial velocities at the first fiber mat winding are 2.7 times higher compared to the radial velocities in the last winding. While in the reduced geometry blood flow is modelled only as a single pass, the method remains stable at higher blood flow rates, where back flow can be detected in parts of the complete geometry.
CO2 pure gas permeance determined experimentally after the ex vivo tests amounts to 0.7 mL STP/min/bar/m2.
3.3. Computational Costs
The stationary flow simulations of the complete prototype oxygenator converged, on average, after 206 CPU hours of calculation. The computational effort was reduced by using the simulation solution of a lower flow rate as a starting condition for a higher flow rate. Transient species transport simulations of the reduced packing took approximately 272 CPU hours per 4 s of simulated time. Solution convergence was monitored by checking the species balance. As a strict criterion, the error in the CO2 species balance was normalized with the transmembrane CO2 transport. This relative error (ε) amounted to 2.46% and 0.28% at 2 and 4 s of simulated time, respectively (Figure 11, ε—porcine). As a test case, a species transport simulation was conducted for bovine blood on the mesh of the flow simulation. Due to the less pronounced shear thinning behavior of bovine blood (see Table 3) and shear rates significantly higher than 1.0 s-1, a Newtonian viscosity model (µ = 5.8 mPa s) was chosen [30]. Membrane permeances were set to pure gas permeances measured for unused membranes (4.23 mL/min/bar/m2). The remaining settings were defined equally to the species transport simulations for porcine blood.
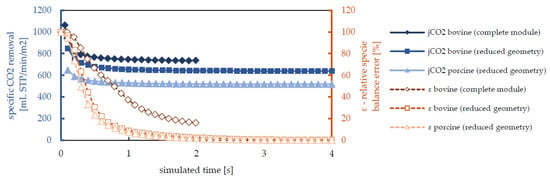
Figure 11.
Convergence of specific CO2 removal (jCO2) and decline of relative CO2 species balance error (ε) with increasing simulated time.

Table 3.
Comparison of bovine and porcine blood viscosity.
The predicted blood side pressure drop and the specific CO2 removal (jCO2) of bovine and porcine blood cannot be compared directly. This is due to the different viscosities and the chosen permeances. Nevertheless, the analogous decline of the relative species balance error (Figure 11) indicates that the numerical effort can be considered similar. To compute 2 s of simulated time for the complete geometry, it took 62,244 CPU hours. At this point, the relative species balance error amounted to 16.1%. To reach this level of convergence, the species transport simulation on the reduced geometry takes significantly less computation time. Approximately 200 CPU hours were needed for 0.7 s of simulated time (ε = 16.6%). This equals a reduction of computation time by 99.3% when considering the time effort of both, the species simulation, and the corresponding flow simulation necessary for the prediction of the inlet velocity. The number of cells in the numerical grid was reduced from 32 Mio. cells for the whole module (complete geometry) to 202,000 cells for the reduced packing (cell number decrease of 99.4%).
The given data suggests that, for relative species balance errors lower than 30%, the predicted CO2 removal differs from the converged solution by maximally 10%. The CO2 removal for bovine blood, determined by the simulations of the complete and reduced geometry, deviates by approximately 10% (Figure 11). The error introduced by the reduction of the geometry can therefore be regarded as acceptable. The difference in transmembrane CO2 flux for bovine and porcine blood (jCO2, Figure 11) can be explained by the chosen permeances (new fibers—bovine simulation versus used fibers—porcine simulations).
The maximum residence time of the reduced geometry was determined as 0.57 s (Figure 12a). In comparison, the maximum residence time of the complete geometry is approximately 16 s (Figure 12a). To reach a relative CO2 species balance error below 1%, 2.7 s of simulated time (4.7 times the maximum residence time) have to be calculated on the reduced geometry. As multiples of the maximum residence time have to be simulated to gain simulation results with a high level of convergence (ε < 1%), even more tremendous numerical effort for the complete geometry would arise.
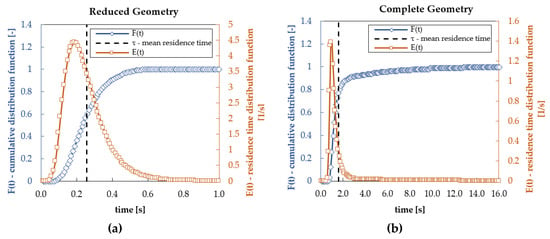
Figure 12.
Residence time distribution, E(t), and cumulative distribution function, F(t), for (a) reduced geometry; (b) complete geometry.
3.4. Radial Dependency of Transmembrane Transport
The uniform inlet velocity of the reduced geometry is calculated based on samples taken from the velocity field of the complete geometry. To gain representative inlet velocities, the sample points should be distributed homogenously within the packing. The radial distribution of sample lines (Figure 3a) gives the average velocity of blood flowing through a packing segment similar to the reduced geometry. This allows the species transport simulations to account for the mean reduction of transmembrane flux due to a decline in driving force in flow direction. Furthermore, the influence of upstream fibers on the flow distribution downstream can be considered. The velocity decrease in radial direction, and its influence on transmembrane flux cannot be modelled with the reduced geometry. To evaluate the effect of this simplification, the dependency of transmembrane flux from the radial position (fiber mat layer) is illustrated in Figure 13 for the reduced and complete geometry. It shows the area weighted average of transmembrane flux for the eight different fiber mat layers (1—most inner, 8—most outer). The presented results were generated by the species transport simulations for bovine blood and gas permeances of unused fibers (Section 3.3).
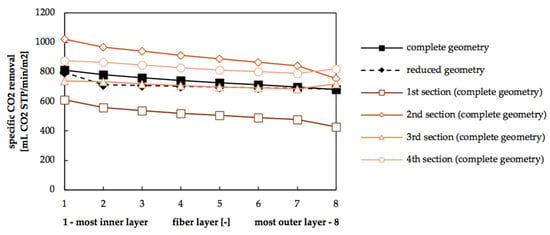
Figure 13.
Average specific CO2 removal of the eight different fiber mat layers (complete geometry) or fiber positions (reduced geometry). Average specific CO2 removal (complete geometry) is additionally given for four different longitudinal sections (1st: 0.0–22.5 mm, 2nd: 22.5–45.0 mm, 3rd: 55.0–77.5 mm, 4th: 77.5–100.0 mm, see Figure 4).
In the reduced geometry, each fiber represents one fiber layer. As can be seen in Figure 13, species simulation results of the reduced geometry predict only a small influence of the fiber position on the transmembrane flux. While the first fiber (Layer 1) shows the highest transmembrane flux (796 mL STP CO2/min/m2), transmembrane transport reduces only slightly (14%) with increasing layer number. As more fibers are accommodated in the outer than in the inner fiber mat layers, multiple averaging methods for transmembrane flux could be considered. In this study, two averaging methods, given in Eq(10), were compared. The arithmetic average (jCO2,arithmetic average = 710 mL STP CO2/min/m2) weights the transmembrane flux (jCO2,i) of each fiber layer (i) equally. The weighted average (jCO2,weighted average = 704 mL STP CO2/min/m2) accounts for the fact that the total number of fibers (n) is unequally distributed among the fiber mat layers, which accommodate varying numbers of fibers (ni). Due to small variations of transmembrane flux between the fiber layers, the two averaging methods give similar results.
jCO2,arithmetic average = (∑ jCO2,i) / (∑ i), jCO2,weighted average = (∑ (jCO2,i · ni)) / (∑ ni), i … layer number
Species transport simulation results of the complete geometry also show a low dependency of transmembrane flux from the radial position. The standard deviation between the different layers accounts for 6% of the mean transmembrane flux. Additionally, Figure 13 shows the radial dependency of transmembrane flux for four different longitudinal sections of the complete geometry. The longitudinal ranges of the sections (1st section: 0.0–22.5 mm, 2nd section: 22.5–45.0 mm, 3rd section: 55.0–77.5 mm, 4th section: 77.5–100.0 mm) can be tracked in Figure 4. Similar to the complete geometry, the different longitudinal sections show only a small dependency of transmembrane flux from the radial position. The highest standard deviation between fiber layers (10% of average) occurs in the first section, closest to the blood inlet. Nevertheless, weighted averaging, which considers the unequal distribution of fibers among the different fiber layers, could play a crucial role if a high radial dependency of the transmembrane flux is observed.
Compared to the radial dependency, the longitudinal dependency of transmembrane flux is significantly stronger. The standard deviation of transmembrane transport between the four longitudinal sections of a specific fiber layer equals, on average, 20% of the mean value. The presented sample ensemble provides a homogenous longitudinal distribution of sample points within the packing (Figure 4). Calculation of the inlet velocity (Section 2.2.2) therefore adequately considers the longitudinal variation of the cross flow within the packing. To summarize, the average transmembrane flux of the different fiber layers matches reasonably when comparing the simulations of complete and reduced geometry (Figure 13). This is due to the higher sensitivity of transmembrane flux on the longitudinal position and lower dependency on the radial position.
4. Conclusions
A simple CFD method was developed, which allows a numerically efficient prediction of the transmembrane transport of larger hollow fiber membrane modules. The method bridges the gap between the geometric complexity of flow and species transport simulations that can be observed when examining previously published CFD studies of hollow fiber membrane modules. The method comprises the following steps:
- Flow simulations of a complete module to gain the velocity distribution,
- Identification of velocity components characteristic for transmembrane species transport,
- Development of a simplified hollow fiber packing geometry based on flow simulation results,
- Calculation of matching inlet velocities for the reduced geometry, to account for different flow rates in the complete geometry,
- Species transport simulations of the simplified (reduced) geometry for different flow rates and species compositions,
- Upscaling of the transmembrane transport to the complete geometry.
For the last step, no empirical correlations that incorporate geometric parameters have to be utilized.
The method was validated based on the CO2 removal performance of a prototype oxygenator in ex vivo trials. The prediction performance of the proposed method is satisfactory. A mean deviation of 3% between experimental and numerically determined CO2 removal was recorded. The saving of computational costs is significant. For the same level of convergence, the upscaling method reduces the necessary CPU hours to conduct the CFD simulations by 99.3% (factor of 150). The proposed method can therefore be considered as a significant reduction in computational effort for CFD species transport simulations of hollow fiber membrane modules and similar units.
Author Contributions
Conceptualization, B.L. and M.H.; methodology, B.L.; software, B.L., M.E., and B.H.; validation, B.L., P.E., and M.E.; formal analysis, B.L., P.E., and M.E.; investigation, B.L., P.E., M.E., and Christoph Janeczek; resources, C.K., R.U., M.G., and M.H; data curation, B.L., P.E., and M.E; writing—original draft preparation, B.L.; writing—review and editing, B.H. and Christian Jordan; visualization, B.L.; supervision, Christoph Janeczek and Christian Jordan; project administration, M.G. and M.H.; funding acquisition, C.K., R.U., M.G., and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Austrian Research Promotion Agency (FFG). Project: Minimal Invasive Liquid Lung (MILL). FFG project number: 857859.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Acronyms | |
| CFD | Computational Fluid Dynamics |
| CO2 | Carbon dioxide |
| HCO3− | Bicarbonate |
| Latin Symbols | |
| A | Membrane area of a computational cell attached to the membrane surface |
| Amembrane,i | Membrane area of reduced (i = reduced) or complete geometry (i = complete) |
| Ainlet | Flow cross-section at inlet |
| Aspacing | Area between two fibers |
| cCO2,total | Total CO2 concentration (dissolved CO2 and bicarbonate) |
| DCO2 | Diffusivity of CO2 in blood |
| DCO2,total | Diffusivity of total CO2 in blood |
| DHCO3- | Diffusivity of HCO3− in blood |
| E(t) | Residence time distribution |
| F(t) | Cumulative distribution function |
| JCO2 | Transmembrane CO2 transport |
| jCO2 | Transmembrane CO2 flux (Transmembrane CO2 Transport per membrane area) |
| L | Characteristic length of Reynolds number |
| n | Total number of fibers |
| ni | Number of fibers in fiber layer (fiber mat winding) i |
| P | Permeance |
| pCO2 | CO2 partial pressure |
| pi | Partial pressure of component i |
| q | Empirical coefficient of CO2 solubility model |
| Re | Reynolds number |
| t | Empirical exponent of CO2 solubility model |
| u | Characteristic velocity of Reynolds number |
| U | Velocity vector field |
| ū | Mean velocity between two fibers |
| uinlet | Uniform inlet velocity |
| umax | Maximum velocity between two fibers |
| uradial | Velocity component in radial direction |
| xj | Unit vector in direction j |
| Greek Symbols | |
| αCO2 | Solubility of CO2 in blood |
| ɣ̇ | Shear rate |
| ΔpCO2 | CO2 partial pressure difference |
| Δpi | Partial pressure difference of component i |
| ε | CO2 species balance error normalized with transmembrane CO2 transport |
| η | Empirical exponent of power law model |
| λ | Slope of CO2 dissociation curve |
| µ | Dynamic viscosity |
| µ0 | Empirical coefficient of power law model |
| µmax | Maximum viscosity of whole blood at low shear rates |
| µmin | Minimum viscosity of whole blood at high shear rates |
| µNewtonian | Newtonian viscosity of whole blood (at high shear rates) |
| ν | Kinematic viscosity |
| τ | Mean residence time |
| ψj | Fraction of velocity component in direction j and velocity magnitude |
References
- Qi, R.; Henson, M.A. Membrane system design for multicomponent gas mixtures via mixed-integer nonlinear programming. Comput. Chem. Eng. 2000, 24, 2719–2737. [Google Scholar] [CrossRef]
- Ghidossi, R.; Veyret, D.; Moulin, P. Computational fluid dynamics applied to membranes: State of the art and opportunities. Chem. Eng. Process. Process. Intensif. 2006, 45, 437–454. [Google Scholar] [CrossRef]
- Low, K.W.Q.; Loon, R.V.; Rolland, S.A.; Sienz, J. Formulation of Generalized Mass Transfer Correlations for Blood Oxygenator Design. J. Biomech. Eng. 2017, 139, 031007. [Google Scholar] [CrossRef] [PubMed]
- Fimbres-Weihs, G.A.; Wiley, D.E. Review of 3D CFD modeling of flow and mass transfer in narrow spacer-filled channels in membrane modules. Chem. Eng. Process. Process. Intensif. 2010, 49, 759–781. [Google Scholar] [CrossRef]
- Dzhonova-Atanasova, D.B.; Tsibranska, I.H.; Paniovska, S.P. CFD Simulation of Cross-Flow Filtration. Ital. Assoc. Chem. Eng. 2018, 70, 2041–2046. [Google Scholar]
- Ghidossi, R.; Daurelle, J.V.; Veyret, D.; Moulin, P. Simplified CFD approach of a hollow fiber ultrafiltration system. Chem. Eng. J. 2006, 123, 117–125. [Google Scholar] [CrossRef]
- Hajilary, N.; Rezakazemi, M. CFD modeling of CO2 capture by water-based nanofluids using hollow fiber membrane contactor. Int. J. Greenh. Gas. Control. 2018, 77, 88–95. [Google Scholar] [CrossRef]
- Miramini, S.A.; Razavi, S.M.R.; Ghadiri, M.; Mahdavi, S.Z.; Moradi, S. CFD simulation of acetone separation from an aqueous solution using supercritical fluid in a hollow-fiber membrane contactor. Chem. Eng. Process. Process. Intensif. 2013, 72, 130–136. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, Y.; Zhang, L.; Chen, Y.; Ju, S. CFD investigation of CO2 capture by methyldiethanolamine and 2-(1-piperazinyl)-ethylamine in membranes: Part B. Effect of membrane properties. J. Nat. Gas. Sci. Eng. 2014, 19, 311–316. [Google Scholar] [CrossRef]
- Cai, J.J.; Hawboldt, K.; Abdi, M.A. Analysis of the effect of module design on gas absorption in cross flow hollow membrane contactors via computational fluid dynamics (CFD) analysis. J. Membr. Sci. 2016, 520, 415–424. [Google Scholar] [CrossRef]
- Wang, Y.; Brannock, M.; Cox, S.; Leslie, G. CFD simulations of membrane filtration zone in a submerged hollow fibre membrane bioreactor using a porous media approach. J. Membr. Sci. 2010, 363, 57–66. [Google Scholar] [CrossRef]
- Kavousi, F.; Syron, E.; Semmens, M.; Casey, E. Hydrodynamics and gas transfer performance of confined hollow fibre membrane modules with the aid of computational fluid dynamics. J. Membr. Sci. 2016, 513, 117–128. [Google Scholar] [CrossRef]
- He, K.; Zhang, L.-Z. Cross flow and heat transfer of hollow-fiber tube banks with complex distribution patterns and various baffle designs. Int. J. Heat Mass Transf. 2020, 147, 118937. [Google Scholar] [CrossRef]
- Wu, S.-E.; Lin, Y.-C.; Hwang, K.-J.; Cheng, T.-W.; Tung, K.-L. High-efficiency hollow fiber arrangement design to enhance filtration performance by CFD simulation. Chem. Eng. Process.—Process. Intensif. 2018, 125, 87–96. [Google Scholar] [CrossRef]
- Zhuang, L.; Guo, H.; Dai, G.; Xu, Z. Effect of the inlet manifold on the performance of a hollow fiber membrane module-A CFD study. J. Membr. Sci. 2017, 526, 73–93. [Google Scholar] [CrossRef]
- Perepechkin, L.P.; Perepechkina, N.P. Hollow fibres for medical applications. A review. Fibre Chem 1999, 31, 411–420. [Google Scholar] [CrossRef]
- Jaffer, I.H.; Reding, M.T.; Key, N.S.; Weitz, J.I. Hematologic Problems in the Surgical Patient. In Hematology; Elsevier: Amsterdam, The Netherlands, 2018; pp. 2304–2312.e4. ISBN 978-0-323-35762-3. [Google Scholar]
- Federspiel, J.W.; Svitek, G.R. Lung, Artificial: Current Research and Future Directions. Encycl. Biomater. Biomed. Eng. 2008. [Google Scholar]
- Hormes, M.; Borchardt, R.; Mager, I.; Rode, T.S.; Behr, M.; Steinseifer, U. A validated CFD model to predict O₂ and CO₂ transfer within hollow fiber membrane oxygenators. Int. J. Artif. Organs 2011, 34, 317–325. [Google Scholar] [CrossRef]
- Kaesler, A.; Rosen, M.; Schmitz-Rode, T.; Steinseifer, U.; Arens, J. Computational Modeling of Oxygen Transfer in Artificial Lungs. Artif. Organs 2018, 42, 786–799. [Google Scholar] [CrossRef]
- Federspiel, W.J.; Henchir, K.A. Lung, Artificial: Basic Principles and Current Applications. In Encyclopedia of Biomaterials and Biomedical Engineering, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; pp. 1661–1672. [Google Scholar]
- Taskin, M.E.; Fraser, K.H.; Zhang, T.; Griffith, B.P.; Wu, Z.J. Micro-scale Modeling of Flow and Oxygen Transfer in Hollow Fiber Membrane Bundle. J. Memb. Sci. 2010, 362, 172–183. [Google Scholar] [CrossRef]
- Harasek, M.; Lukitsch, B.; Ecker, P.; Janeczek, C.; Elenkov, M.; Keck, T.; Haddadi, B.; Jordan, C.; Neudl, S.; Krenn, C.; et al. Fully Resolved Computational (CFD) and Experimental Analysis of Pressure Drop and Blood Gas Transport in a Hollow Fibre Membrane Oxygenator Module. Ital. Assoc. Chem. Eng. 2019, 76, 193–198. [Google Scholar]
- D’Onofrio, C.; van Loon, R.; Rolland, S.; Johnston, R.; North, L.; Brown, S.; Phillips, R.; Sienz, J. Three-dimensional computational model of a blood oxygenator reconstructed from micro-CT scans. Med. Eng. Phys. 2017, 47, 190–197. [Google Scholar] [CrossRef] [PubMed]
- Caretto, L.; Gosman, A.; Patankar, S.; Spalding, D. Two Calculation Procedures for Steady, Three-Dimensional Flows with Recirculation. In Proceedings of the 3rd Conference on Numerical Methods in Fluid Mechanics, Lecture Notes in Physics, 19th ed.; Springer-Verlag: Berlin Heidelberg, Germany, 1973; pp. 60–68. [Google Scholar]
- Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non-Newtonian blood flow in human right coronary arteries: Steady state simulations. J. Biomech. 2004, 37, 709–720. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Haddadi, B.; Jordan, C.; Miltner, M.; Harasek, M. Membrane modeling using CFD: Combined evaluation of mass transfer and geometrical influences in 1D and 3D. J. Membr. Sci. 2018, 563, 199–209. [Google Scholar] [CrossRef]
- Svitek, R.G.; Federspiel, W.J. A Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators. Ann. Biomed. Eng. 2008, 36, 992–1003. [Google Scholar] [CrossRef] [PubMed]
- Windberger, U.; Baskurt, O.K. Comparative hemorheology. In Handbook of Hemorheology and Hemodynamics; IOS Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Rauen, H.M. (Ed.) Biochemisches Taschenbuch, 2nd ed.; Springer-Verlag: Berlin Heidelberg, Germany, 1964; ISBN 978-3-642-85768-3. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).